Towards a Clinically Applicable Computational Larynx Model
Abstract
Featured Application
Abstract
1. Introduction
2. Materials and Methods
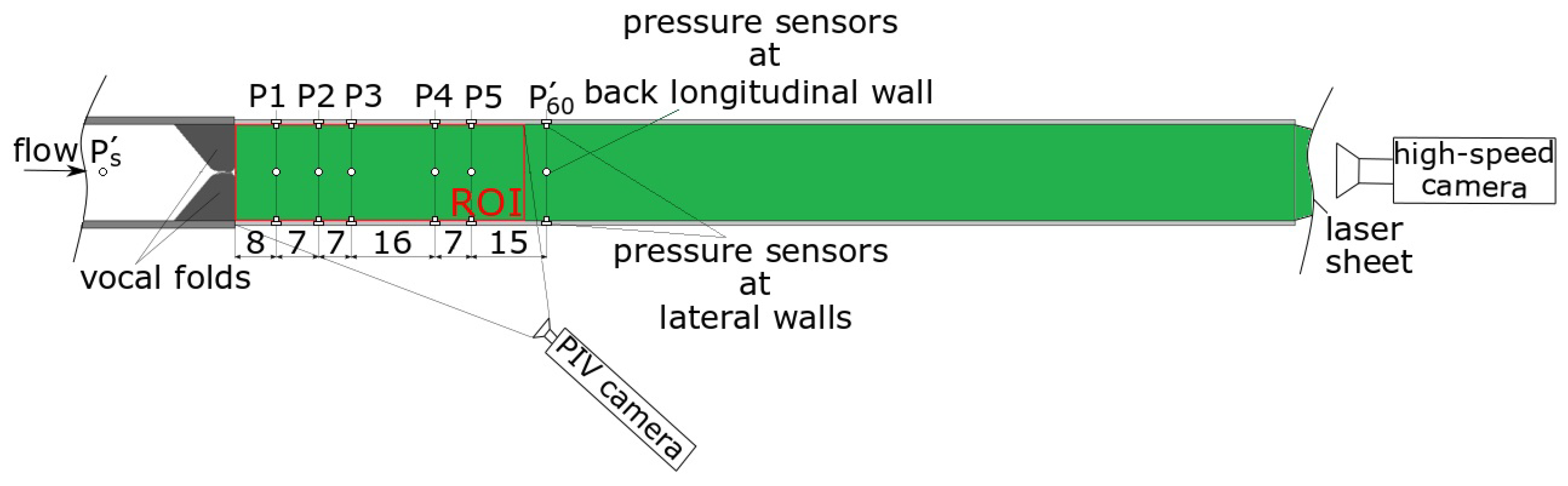
2.1. Experimental Model and Measuring Techniques
2.2. Numerical Model and Methods
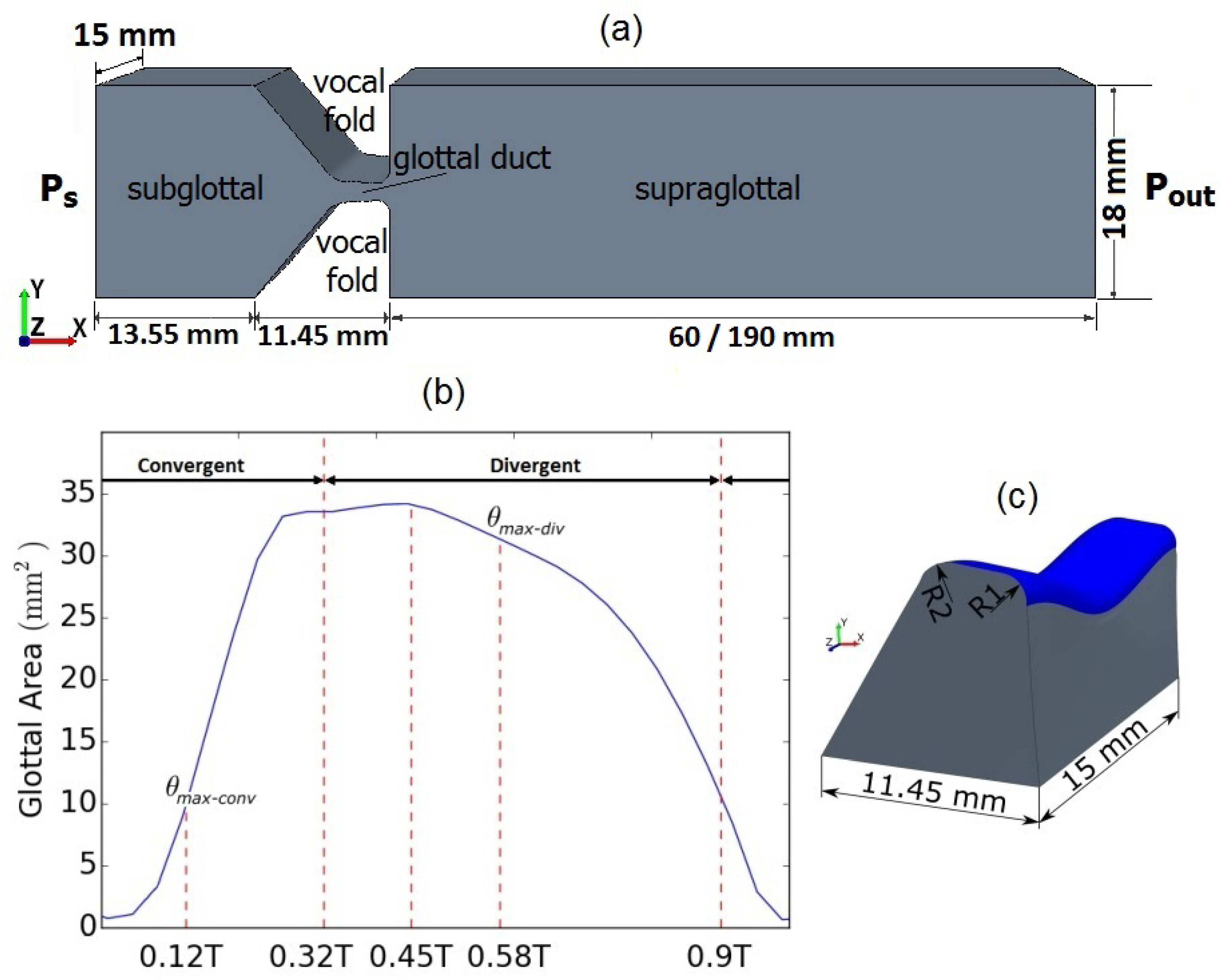
2.2.1. Geometry of Computational Model and Vocal Fold Motion
2.2.2. Numerical Methods
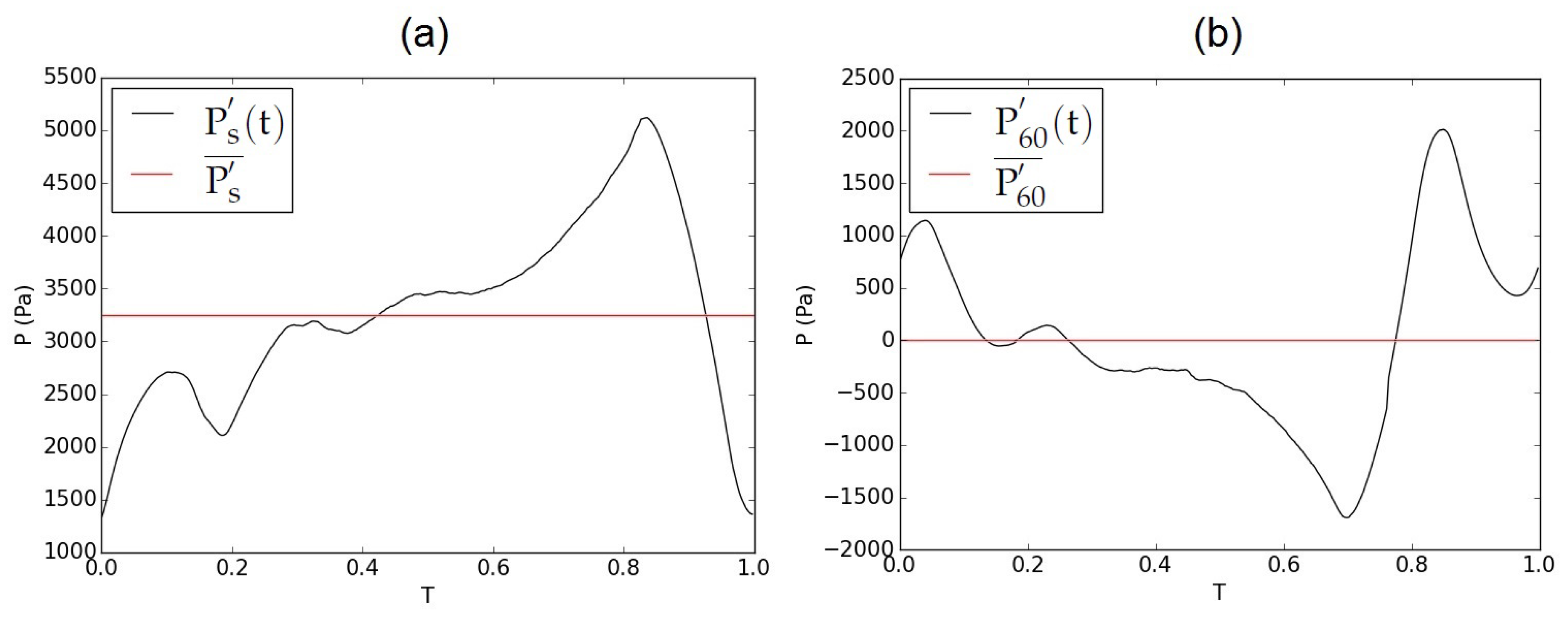
2.2.3. Boundary Conditions
2.2.4. Mesh Generation and Mesh Motion
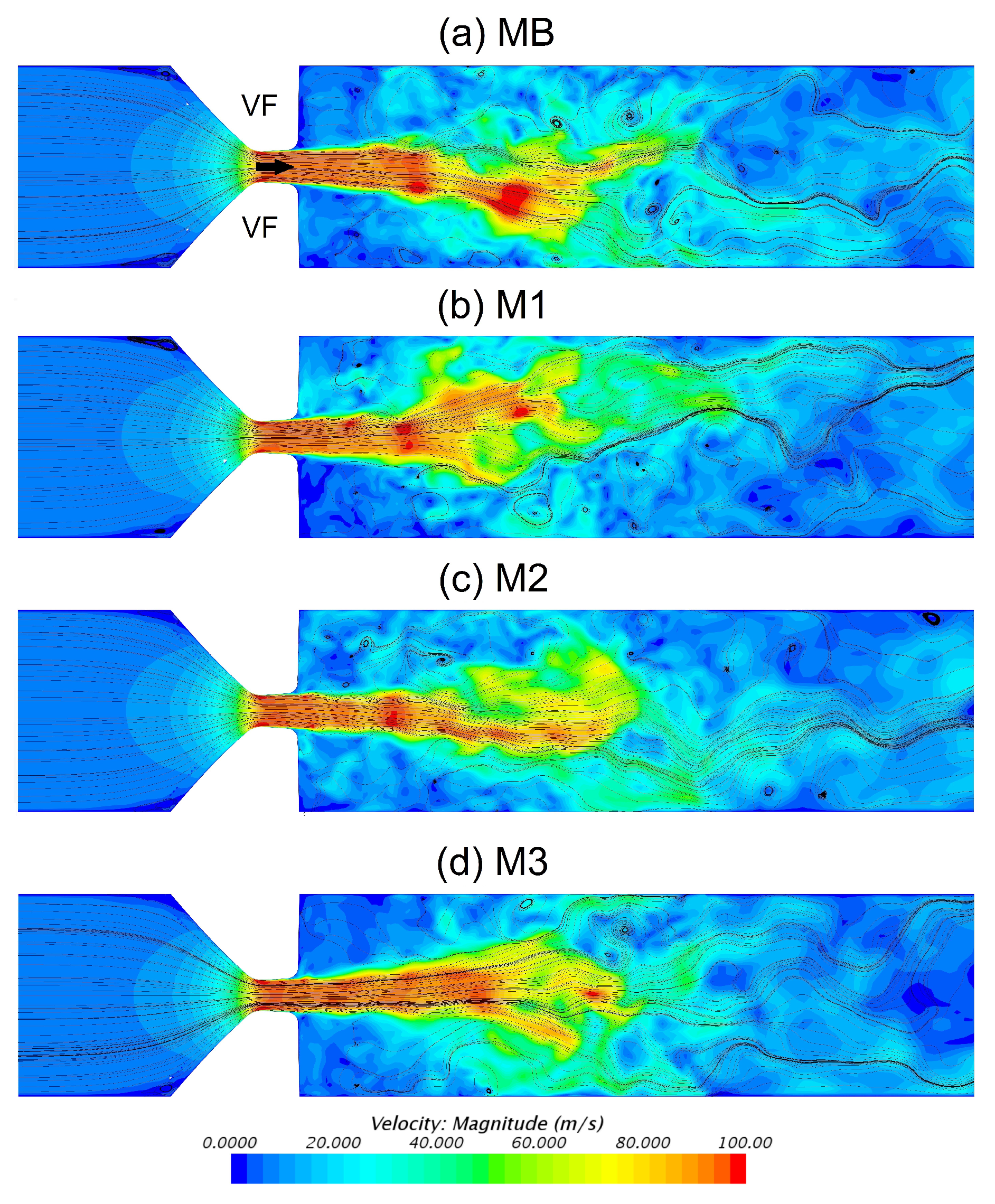
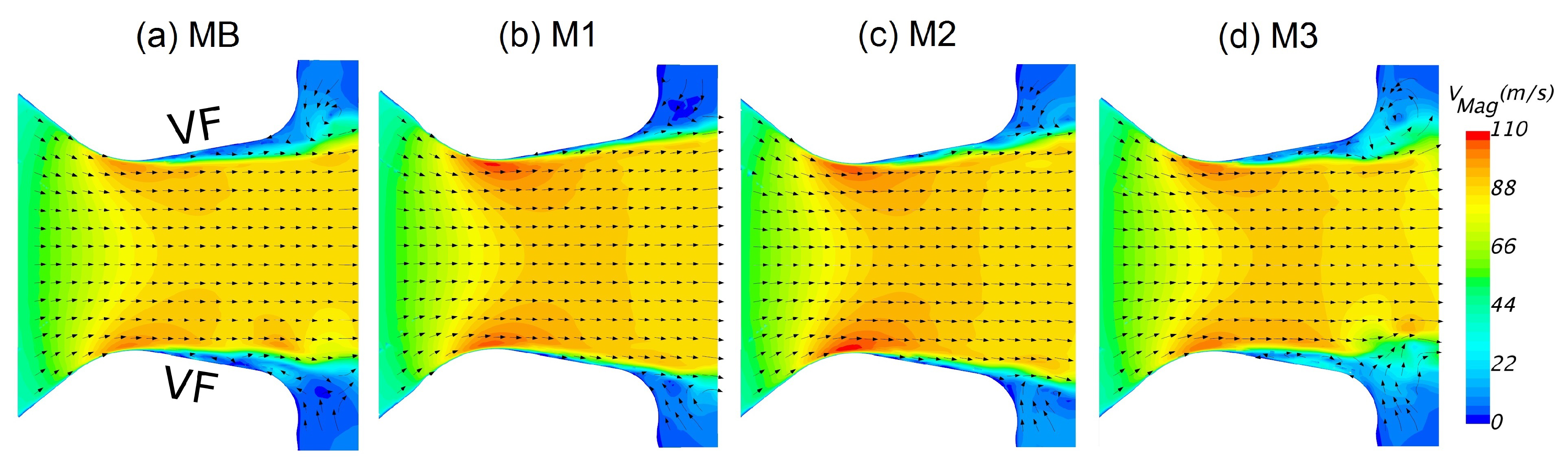
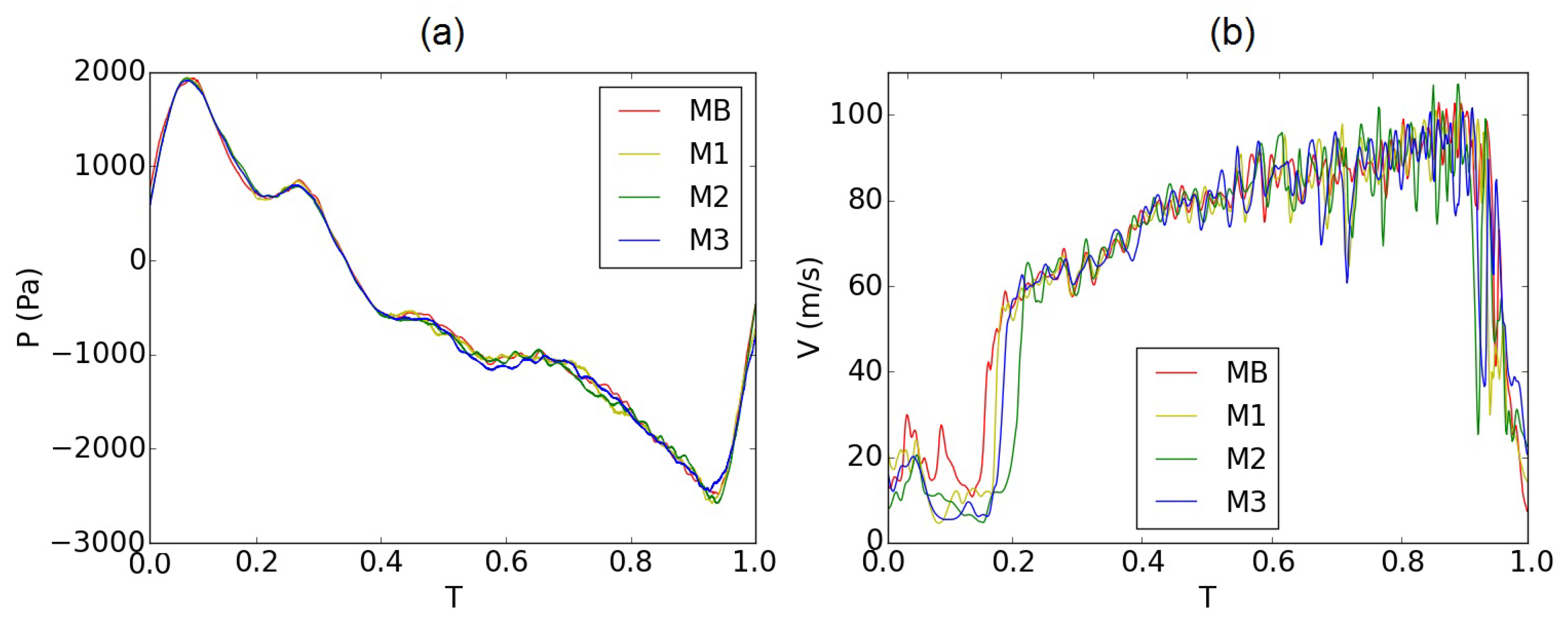
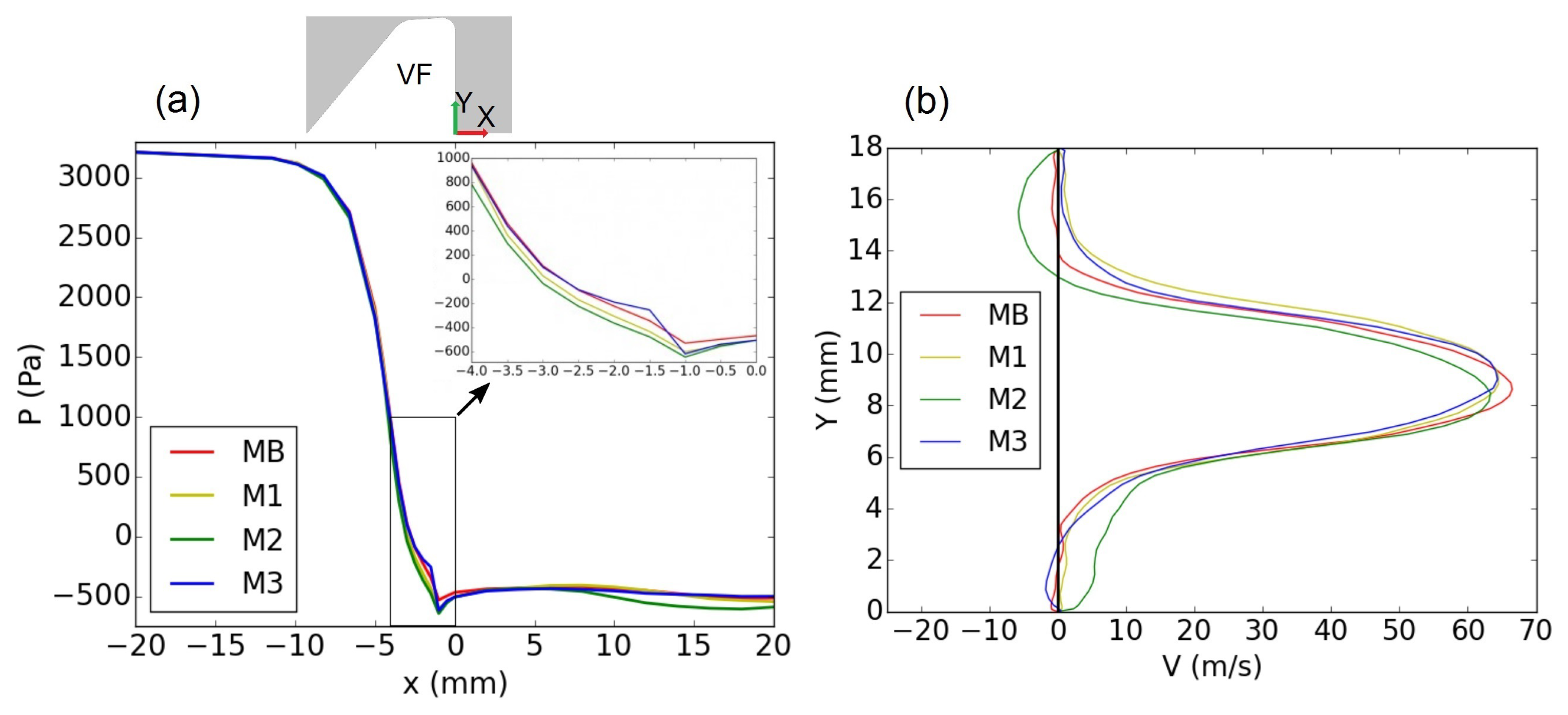
2.2.5. Reduction of Mesh Resolution
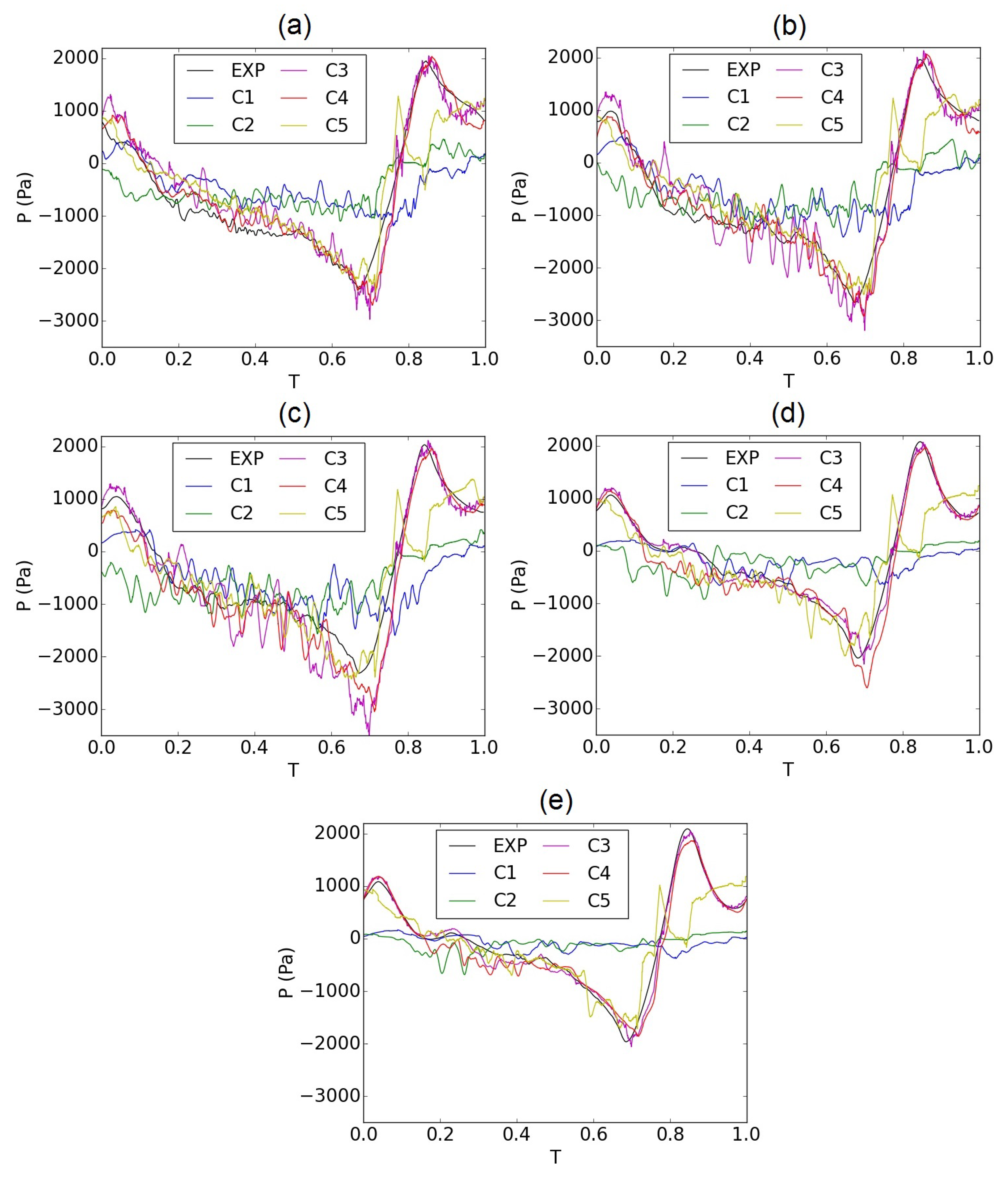
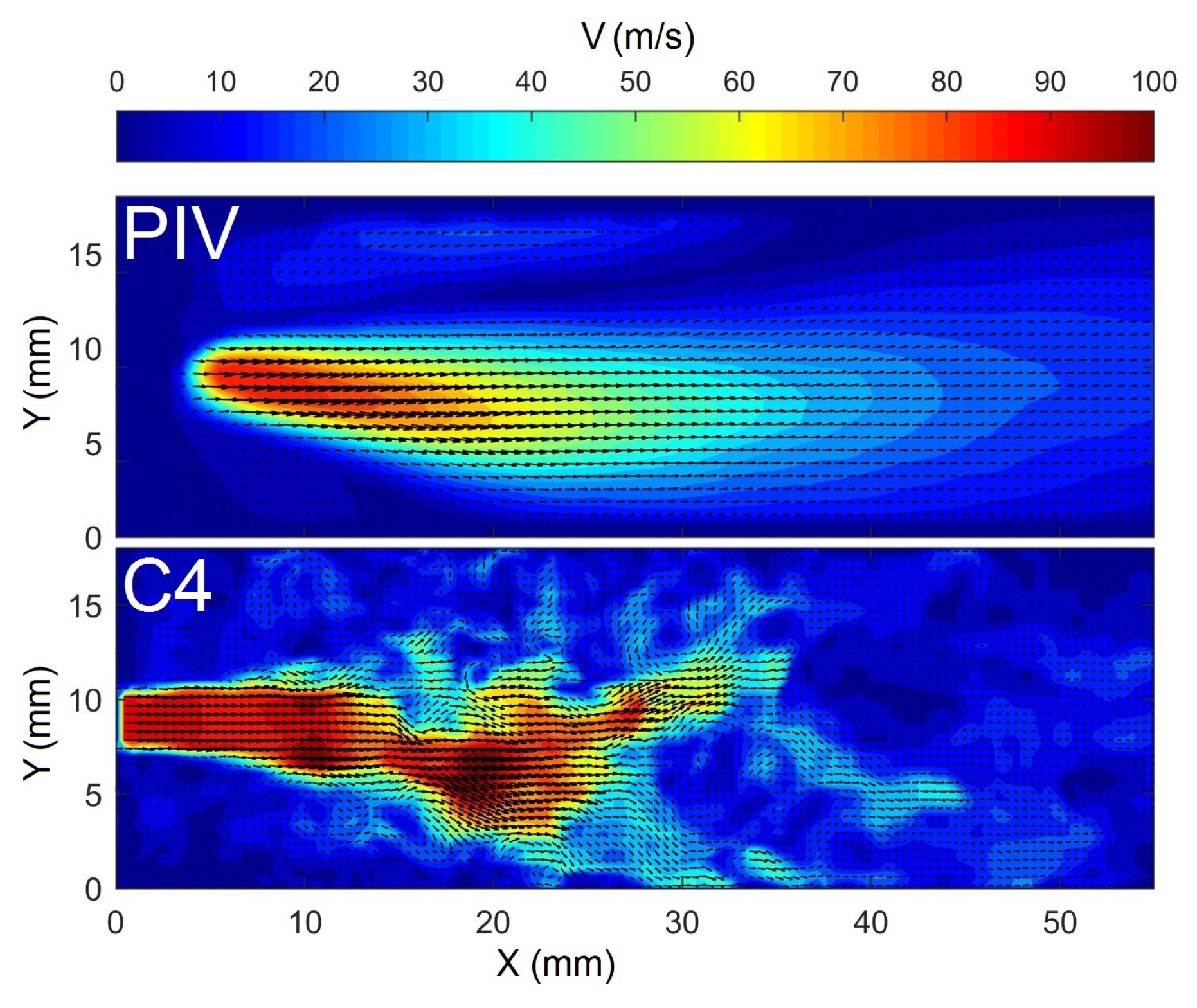
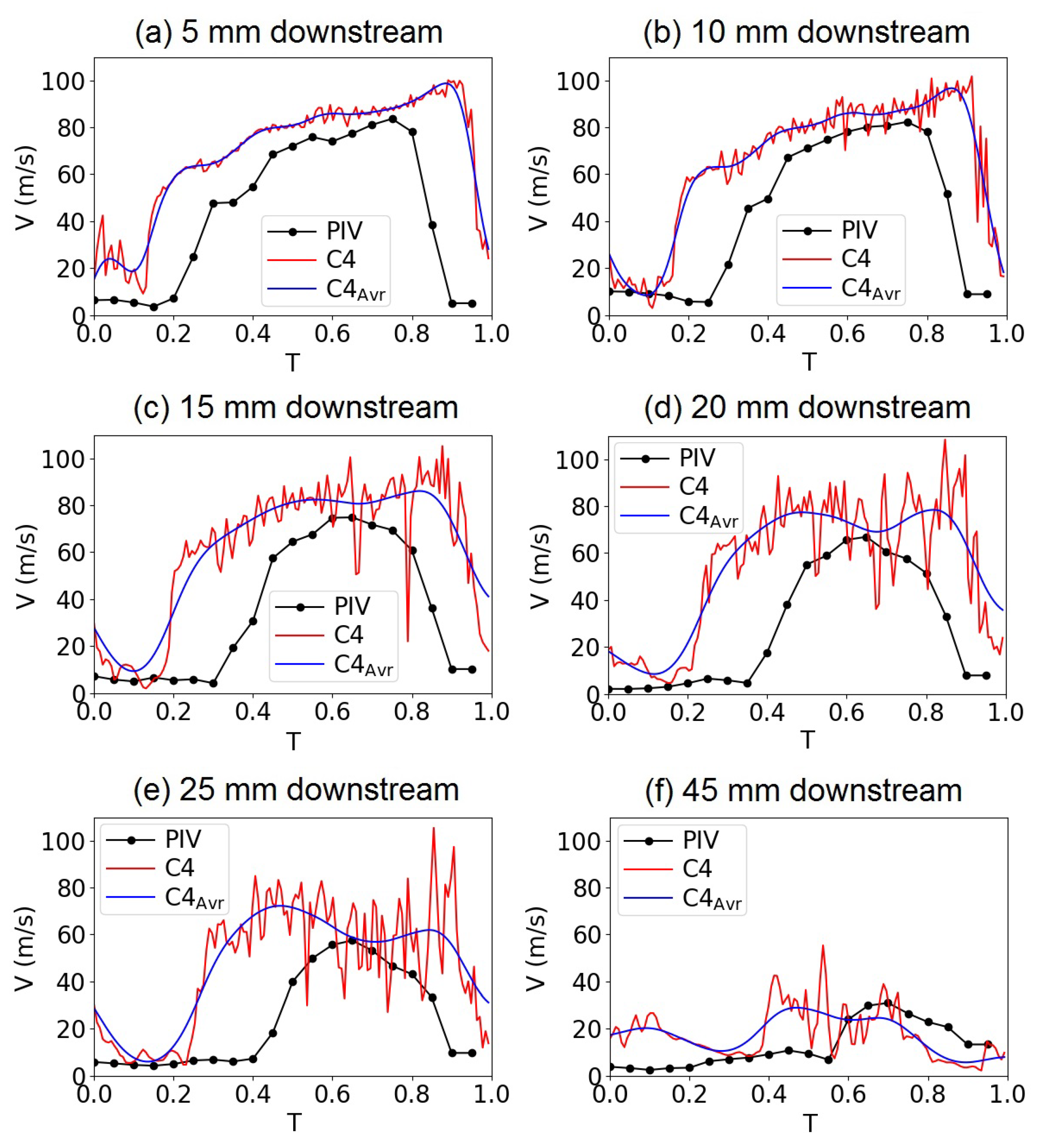
3. Validation of the Computational Model
4. Results and Discussion
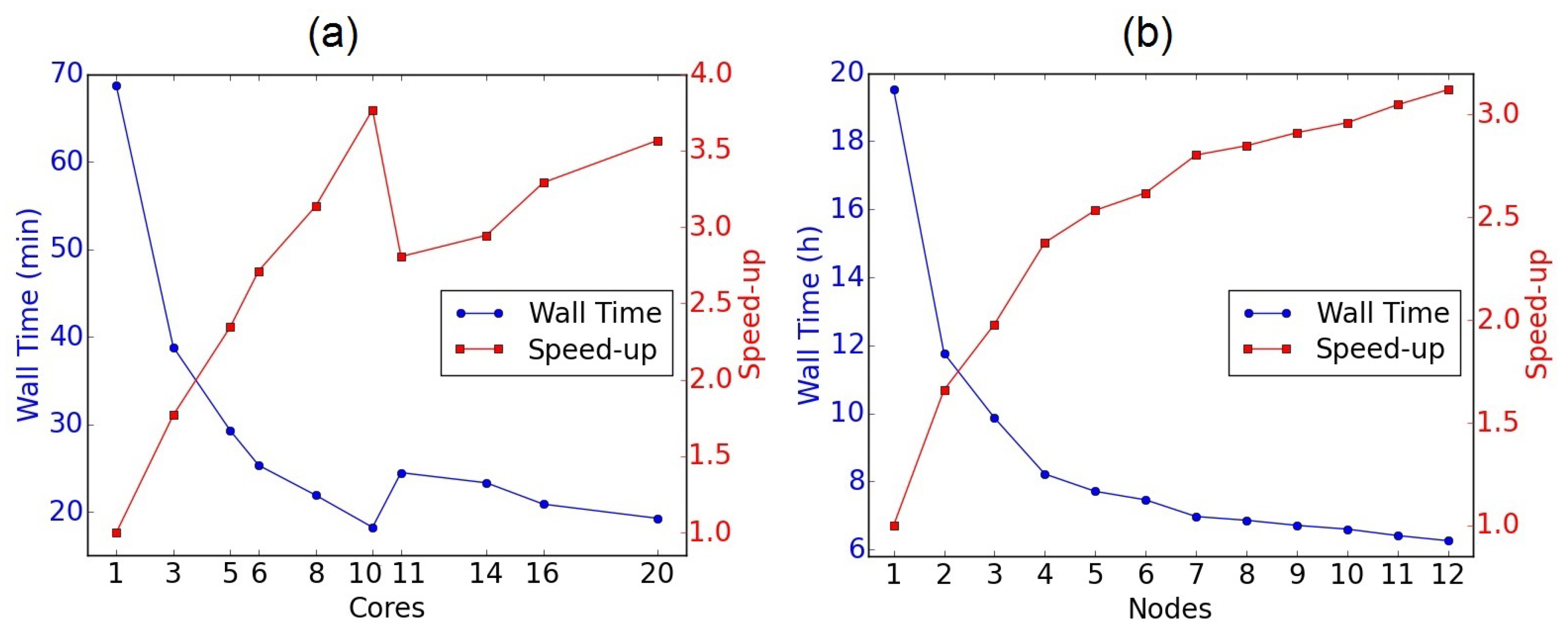
4.1. Reduction of Computational Costs
4.2. Using HPC Resources to Reduce the Time-to-Solution
5. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Titze, I.R. Principles of Voice Production; National Center for Voice and Speech: Iowa City, IA, USA, 2000. [Google Scholar]
- Aronson, A.; Bless, D. Clinical Voice Disorders, 4th ed.; Thieme: New York, NY, USA, 2009. [Google Scholar]
- Smith, E.; Verdolini, K.; Gray, S.; Nichols, S.; Lemke, J.; Barkmeier, J.; Dove, H.; Hoffman, H. Effect of voice disorders on quality of life. J. Med. Speech-Lang. Pathol. 1996, 4, 223–244. [Google Scholar] [CrossRef]
- Cohen, S. Self-reported impact of dysphonia in a primary care population: An epidemiological study. Laryngoscope 2010, 120, 2022–2032. [Google Scholar] [CrossRef] [PubMed]
- Merrill, R.; Anderson, A.; Sloan, A. Quality of life indicators according to voice disorders and voice-related conditions. Laryngoscope 2011, 121, 2004–2010. [Google Scholar] [CrossRef] [PubMed]
- Roy, N.; Merrill, R.; Gray, S.; Smith, E. Voice disorders in the general population: Prevalence, risk factors, and occupational impact. Laryngoscope 2005, 115, 1988–1995. [Google Scholar] [CrossRef]
- Cohen, S.; Kim, J.; Roy, N.; Asche, C.; Courey, M. The impact of laryngeal disorders on work-related dysfunction. Laryngoscope 2012, 122, 1589–1594. [Google Scholar] [CrossRef] [PubMed]
- Ruben, R. Redefining the survival of the fittest: communication disorders in the 21st century. Laryngoscope 2000, 110, 241. [Google Scholar] [CrossRef] [PubMed]
- Cohen, S.; Kim, J.; Roy, N.; Asche, C.; Courey, M. Direct health care costs of laryngeal diseases and disorders. Laryngoscope 2012, 122, 1582–1588. [Google Scholar] [CrossRef]
- Wilson, J.; Deary, I.; Millar, A.; Mackenzie, K. The quality of life impact of dysphonia. Clin. Otolaryngol. Allied Sci. 2002, 27, 179–182. [Google Scholar] [CrossRef]
- Cohen, S.; Dupont, W.; Courey, M. Quality-of-life impact of non-neoplastic voice disorders: A meta-analysis. Ann. Otol. Rhinol. Laryngol. 2006, 115, 128–134. [Google Scholar] [CrossRef]
- Zraick, R.; Risner, B. Assessment of quality of life in persons with voice disorders. Curr. Opin. Otolaryngol. Head Neck Surg. 2008, 16, 188–193. [Google Scholar] [CrossRef]
- Slavych, B.; Engelhoven, A.; Zraick, R. Quality of life in persons with voice disorders: A review of patient-reported outcome measures. Int. J. Ther. Rehabil. 2013, 20, 308–315. [Google Scholar] [CrossRef]
- Merrill, R.; Tanner, K.; Merrill, J.; McCord, M.; Beardsley, M.; Steele, B. Voice symptoms and voice-related quality of life in college students. Ann. Otol. Rhinol. Laryngol. 2013, 122, 511–519. [Google Scholar] [CrossRef] [PubMed]
- Wendler, J. Stroboscopy. J. Voice 1992, 6, 149–154. [Google Scholar] [CrossRef]
- Döllinger, M. The next step in voice assessment: High-speed digital endoscopy and objective evaluation. Curr. Bioinf. 2009, 4, 101–111. [Google Scholar] [CrossRef]
- Döllinger, M.; Lohscheller, J.; McWhorter, A.; Kunduk, M. Variability of normal vocal fold dynamics for different vocal loading in one healthy subject investigated by phonovibrograms. J. Voice 2009, 23, 175–181. [Google Scholar] [CrossRef] [PubMed]
- Kitzing, P. Clinical applications of electroglottography. J. Voice 1990, 4, 238–249. [Google Scholar] [CrossRef]
- Murray, P.; Thomson, S. Synthetic, multi-Layer, self-Oscillating vocal fold model fabrication. J. Vis. Exp. JoVE 2011, e3498. [Google Scholar] [CrossRef]
- Luo, R.; Kong, W.; Wei, X.; Lamb, J.; Jiang, J. Development of excised larynx. J. Voice 2018. [Google Scholar] [CrossRef]
- Scherer, R.; Torkaman, S.; Afjeh, A. Intraglottal pressures in a three-dimensional model with a non-rectangular glottal shape. J. Acoust. Soc. Am. 2010, 128, 828–838. [Google Scholar] [CrossRef]
- Mihaescu, M.; Khosla, S.M.; Murugappan, S.; Gutmark, E. Unsteady laryngeal airflow simulations of the intra-glottal vortical structures. J. Acoust. Soc. Am. 2010, 127, 435–444. [Google Scholar] [CrossRef]
- Šidlof, P.; Horáček, J.; Řidký, V. Parallel CFD simulation of flow in a 3D model of vibrating human vocal folds. Comput. Fluids 2013, 80, 290–300. [Google Scholar] [CrossRef]
- Zörner, S.; Kaltenbacher, M.; Döllinger, M. Investigation of prescribed movement in fluid-structure interaction simulation for the human phonation process. Comput. Fluids 2013, 86, 133–140. [Google Scholar] [CrossRef] [PubMed]
- Alipour, F.; Scherer, R.C. Time-dependent pressure and flow behavior of a self-oscillating laryngeal model with ventricular folds. J. Voice 2015, 29, 649–659. [Google Scholar] [CrossRef] [PubMed]
- Duncan, C.; Zhai, G.; Scherer, R.C. Modeling coupled aerodynamics and vocal fold dynamics using immersed boundary methods. J. Acoust. Soc. Am. 2006, 120, 2859–2871. [Google Scholar] [CrossRef] [PubMed]
- Smith, S.L.; Thomson, S.L. Effect of inferior surface angle on the self-oscillation of a computational vocal fold model. J. Acoust. Soc. Am. 2012, 131, 4062–4075. [Google Scholar] [CrossRef] [PubMed]
- Xue, Q.; Mittal, R.; Zheng, X.; Bielamowicz, S.A. Computational modeling of phonatory dynamics in a tubular three-dimensional model of the human larynx. J. Acoust. Soc. Am. 2012, 132, 1602–1613. [Google Scholar] [CrossRef]
- Zhang, C.; Zhao, W.; Frankel, S.; Mongeau, L. Computational aeroacoustics of phonation, Part II: Effects of flow parameters and ventricular folds. J. Acoust. Soc. Am. 2002, 112, 2147–2154. [Google Scholar] [CrossRef]
- Bae, Y.; Moon, Y.J. Computation of phonation aeroacoustics by an INS/PCE splitting method. Comput. Fluids 2008, 37, 1332–1343. [Google Scholar] [CrossRef]
- Šidlof, P.; Zörner, S.; Hüppe, A. A hybrid approach to the computational aeroacoustics of human voice production. Biomech. Model. Mechanobiol. 2015, 14, 473–488. [Google Scholar] [CrossRef]
- Lodermeyer, A.; Tautz, M.; Becker, S.; Döllinger, M.; Birk, V.; Kniesburges, S. Aeroacoustic analysis of the human phonation process based on a hybrid acoustic PIV approach. Exp. Fluids 2018, 59, 13. [Google Scholar] [CrossRef]
- Jeong, W.; Rhee, K. Hemodynamics of cerebral aneurysms: Computational analyses of aneurysm progress and treatment. Comput. Math. Methods Med. 2012, 2012. [Google Scholar] [CrossRef] [PubMed]
- Radaelli, A.; Augsburger, L.; Cebral, J.; Ohta, M.; Rüfenacht, D.; Balossino, R.; Benndorf, G.; Hose, D.; Marzo, A.; Metcalfe, R.; et al. Reproducibility of haemodynamical simulations in a subject-specific stented aneurysm model—A report on the Virtual Intracranial Stenting Challenge 2007. J. Biomech. 2008, 41, 2069–2081. [Google Scholar] [CrossRef] [PubMed]
- Pereira, V.; Brina, O.; Gonzalez, A.; Narata, A.; Ouared, R.; Karl-Olof, L. Biology and hemodynamics of aneurismal vasculopathies. Eur. J. Radiol. 2013, 82, 1606–1617. [Google Scholar] [CrossRef] [PubMed]
- Brown, A.; Shi, Y.; Marzo, A.; Staicu, C.; Valverde, I.; Beerbaum, P.; Lawford, P.; Hose, D. Accuracy vs. computational time: Translating aortic simulations to the clinic. J. Biomech. 2012, 45, 516–523. [Google Scholar] [CrossRef] [PubMed]
- Morris, P.; Narracott, A.; Kobligk, H.; Soto, D.; Hsiao, S.; Lungu, A.; Evans, P.; Bressloff, N.; Lawford, P.; Hose, D.; et al. Computational fluid dynamics modelling in cardiovascular medicine. Heart 2016, 102, 18–28. [Google Scholar] [CrossRef]
- Ueda, T.; Suito, H.; Ota, H.; Takase, K. Computational fluid dynamics modeling in aortic diseases. Cardiovasc. Imaging Asia 2018, 2, 58–64. [Google Scholar] [CrossRef][Green Version]
- Zachow, S.; Steinmann, A.; Hildebrandt, T.; Weber, R.; Heppt, W. CFD simulation of nasal airflow: Towards treatment planning for functional rhinosurgery. Int. J. Comput. Assist. Radiol. Surg. 2006, 165–167. [Google Scholar] [CrossRef]
- Xiong, G.; Zhan, J.; Zuo, K.; Li, J.; Rong, L.; Xu, G. Numerical flow simulation in the post-endoscopic sinus surgery nasal cavity. Med. Biol. Eng. Comput. 2008, 46, 1161–1167. [Google Scholar] [CrossRef]
- Chen, X.; Leong, S.; Lee, H.; Chong, V.; Wang, D. Aerodynamic effects of inferior turbinate surgery on nasal airflow: a computational fluid dynamics model. Rhinology 2010, 48, 394–400. [Google Scholar]
- Mylavarapu, G.; Mihaescu, M.; Fuchs, L.; Papatziamos, G.; Gutmark, E. Planning human upper airway surgery using computational fluid dynamics. J. Biomech. 2013, 46, 1979–1986. [Google Scholar] [CrossRef]
- Markow, M.; Janecki, D.; Orecka, B.; Misiołek, M.; Warmuziński, K. Computational fluid dynamics in the assessment of patients’ postoperative status after glottis-widening surgery. Adv. Clin. Exp. Med. 2017, 26, 947–952. [Google Scholar] [CrossRef]
- Mittal, R.; Zheng, X.; Bhardwaj, R.; Seo, J.H.; Xue, Q.; Bielamowicz, S.A. Toward a simulation-based tool for the treatment of vocal fold paralysis. Front. Physiol. 2011, 2. [Google Scholar] [CrossRef] [PubMed]
- Xue, Q.; Zheng, X.; Mittal, R.; Bielamowicz, S.A. Computational study of effects of tension imbalance on phonation in a three-dimensional tubular larynx model. J. Voice 2014, 28, 411–419. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z. Toward real-time physically-based voice simulation: An eigenmode-based approach. Proc. Mtgs. Acoust. 2017, 30, 060002. [Google Scholar] [CrossRef]
- Triep, M.; Brücker, C. Three-dimensional nature of the glottal jet. J. Acoust. Soc. Am. 2010, 127, 1537–1547. [Google Scholar] [CrossRef]
- Mattheus, W.; Brücker, C. Asymmetric glottal jet deflection: Differences of two- and three-dimensional models. J. Acoust. Soc. Am. 2011, 130, EL373–EL379. [Google Scholar] [CrossRef]
- Chisari, N.E.; Artana, G.; Sciamarella, D. Vortex dipolar structures in a rigid model of the larynx at flow onset. Exp. Fluids 2011, 50, 397–406. [Google Scholar] [CrossRef]
- Sadeghi, H.; Kniesburges, S.; Kaltenbacher, M.; Schützenberger, A.; Döllinger, M. Computational models of laryngeal aerodynamics: potentials and numerical costs. J. Voice 2018. [Google Scholar] [CrossRef]
- Zörner, S.; Šidlof, P.; Hüppe, A.; Kaltenbacher, M. Flow and acoustic effects in the larynx for varying geometries. Acta Acust. United Acust. 2016, 102, 257–267. [Google Scholar] [CrossRef]
- Kniesburges, S. Fluid-Structure-Acoustic Interaction during Phonation in a Synthetic Larynx Model. Ph.D. Thesis, Friedrich-Alexander University Erlangen-Nürnberg, Shaker, Aachen, Germany, 2014. [Google Scholar]
- Kniesburges, S.; Hesselmann, C.; Becker, S.; Schlücker, E.; Döllinger, M. Influence of vortical flow structures on the glottal jet location in the supraglottal region. J. Voice 2013, 27, 531–544. [Google Scholar] [CrossRef]
- Kniesburges, S.; Birk, V.; Lodermeyer, A.; Schützenberger, A.; Bohr, C.; Becker, S. Effect of the ventricular folds in a synthetic larynx model. J. Biomech. 2017, 55, 128–133. [Google Scholar] [CrossRef] [PubMed]
- Lodermeyer, A.; Becker, S.; Döllinger, M.; Kniesburges, S. Phase-locked flow field analysis in a synthetic human larynx model. Exp. Fluids 2015, 56, 77. [Google Scholar] [CrossRef]
- Scherer, R.C.; Shinwari, D.; Witt, K.J.D.; Zhang, C.; Kucinschi, B.R.; Afjeh, A.A. Intraglottal pressure profiles for a symmetric and oblique glottis with a divergence angle of 10 degrees. J. Acoust. Soc. Am. 2001, 109, 1616–1630. [Google Scholar] [CrossRef]
- Thomson, S.; Mongeau, L.; Frankel, S. Physical and numerical flow-excited vocal fold models. In Proceedings of the Third International Workshop on Models and Analysis of Vocal Emissions for Biomedical Applications, Florence, Italy, 10–12 December 2003. [Google Scholar]
- Rasp, O.; Lohscheller, J.; Döllinger, M.; Eysholdt, U.; Hoppe, U. The pitch rise paradigm: A new task for real-time endoscopy of non-stationary phonation. Folia Phoniatr. Logop. 2006, 58, 175–185. [Google Scholar] [CrossRef] [PubMed]
- Zheng, X.; Mittal, R.; Bielamowicz, S. A computational study of asymmetric glottal jet deflection during phonation. J. Acoust. Soc. Am. 2011, 129, 2133–2143. [Google Scholar] [CrossRef] [PubMed]
- Kucinschi, B.; Scherer, R.; DeWitt, K.; Ng, T. Flow Visualization and Acoustic Consequences of the Air Moving Through a Static Model of the Human Larynx. J. Biomech. Eng. 2005, 128, 380–390. [Google Scholar] [CrossRef] [PubMed]
- Nicoud, F.; Ducros, F. Subgrid-scale stress modelling based on the square of the velocity gradient tensor. Flow Turbul. Combust. 1999, 62, 183–200. [Google Scholar] [CrossRef]
- Issa, R.I. Solution of the implicitly discretised fluid flow equations by operator-splitting. J. Comput. Phys. 1986, 62, 40–65. [Google Scholar] [CrossRef]
- Anderson, J. Computational Fluid Dynamics: The Basics with Applications; McGraw-HILL, Inc.: New York, NY, USA, 1995. [Google Scholar]
- Hirsch, C. Numerical Computation of Internal and External Flows: The Fundamentals of Computational Fluid Dynamics, 2nd ed.; Elsevier Science: Amsterdam, The Netherlands, 2007. [Google Scholar] [CrossRef]
- Pope, S. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar] [CrossRef]
- Ipsen, I. Numerical Matrix Analysis: Linear Systems and Least Squares; Society for Industrial and Applied Mathematics: Pliladelphia, PA, USA, 2009. [Google Scholar] [CrossRef]
- Mittal, R.; Erath, B.; Plesniak, M. Fluid dynamics of human phonation and speech. Annu. Rev. Fluid Mech. 2013, 45, 437–467. [Google Scholar] [CrossRef]
- Khosla, S.; Oren, L.; Ying, J.; Gutmark, E. Direct simultaneous measurement of intraglottal geometry and velocity fields in excised larynges. Laryngoscope 2014, 124, S1–S13. [Google Scholar] [CrossRef]
- Oren, L.; Khosla, S.; Gutmark, E. Intraglottal pressure distribution computed from empirical velocity data in canine larynx. J. Biomech. 2014, 47, 1287–1293. [Google Scholar] [CrossRef] [PubMed]
- Hussain, F.; Husain, H.S. Elliptic jets. Part 1. Characteristics of unexcited and excited jets. J. Fluid Mech. 1989, 208, 257–320. [Google Scholar] [CrossRef]
- Mattheus, W.; Brücker, C. Characteristics of the pulsating jet flow through a dynamic glottal model with a lens-like constriction. Biomed. Eng. Lett. 2018, 8, 309–320. [Google Scholar] [CrossRef]
- Zhao, W.; Frankel, S.H.; Mongeau, L. Numerical simulations of sound from confined pulsating axisymmetric jets. AIAA J. 2001, 39, 1868–1874. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Hager, G.; Wellein, G. Introduction to High Performance Computing for Scientists and Engineers, 1st ed.; CRC Press, Taylor & Francis Inc.: Boca Raton, FL, USA, 2010. [Google Scholar]
- Amdahl, G.M. Validity of the single processor approach to achieving large scale computing capabilities. In AFIPS ’67 (Spring), Proceedings of the Spring Joint Computer Conference; ACM: New York, NY, USA, 1967; pp. 483–485. [Google Scholar] [CrossRef]



| Supraglottal Channel Length | |||
|---|---|---|---|
| C1 | 60 mm | ||
| C2 | 60 mm | ||
| C3 | 60 mm | ||
| C4 | 60 mm | ||
| C5 | 190 mm |
| Mesh | Base Size (mm) | Basic Refinement (mm) | Glottis Refinement (mm) | Average No. of Cells | (s) |
|---|---|---|---|---|---|
| MB | 0.5 | 0.25 | 0.0625 | 2.4 M | 1.00 |
| M1 | 0.56 | 0.28 | 0.070 | 1.8 M | 1.12 |
| M2 | 0.64 | 0.32 | 0.080 | 1.3 M | 1.28 |
| M3 | 0.68 | 0.34 | 0.085 | 1.1 M | 1.36 |
| P1 | P2 | P3 | P4 | P5 | |
|---|---|---|---|---|---|
| C1 | 0.76 | 0.71 | 0.78 | 0.93 | 0.99 |
| C2 | 0.69 | 0.72 | 0.77 | 0.91 | 0.95 |
| C3 | 0.50 | 0.46 | 0.53 | 0.28 | 0.22 |
| C4 | 0.22 | 0.20 | 0.33 | 0.28 | 0.22 |
| C5 | 0.47 | 0.44 | 0.49 | 0.60 | 0.60 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sadeghi, H.; Kniesburges, S.; Falk, S.; Kaltenbacher, M.; Schützenberger, A.; Döllinger, M. Towards a Clinically Applicable Computational Larynx Model. Appl. Sci. 2019, 9, 2288. https://doi.org/10.3390/app9112288
Sadeghi H, Kniesburges S, Falk S, Kaltenbacher M, Schützenberger A, Döllinger M. Towards a Clinically Applicable Computational Larynx Model. Applied Sciences. 2019; 9(11):2288. https://doi.org/10.3390/app9112288
Chicago/Turabian StyleSadeghi, Hossein, Stefan Kniesburges, Sebastian Falk, Manfred Kaltenbacher, Anne Schützenberger, and Michael Döllinger. 2019. "Towards a Clinically Applicable Computational Larynx Model" Applied Sciences 9, no. 11: 2288. https://doi.org/10.3390/app9112288
APA StyleSadeghi, H., Kniesburges, S., Falk, S., Kaltenbacher, M., Schützenberger, A., & Döllinger, M. (2019). Towards a Clinically Applicable Computational Larynx Model. Applied Sciences, 9(11), 2288. https://doi.org/10.3390/app9112288






