Analytical Electromechanical Modeling of Nanoscale Flexoelectric Energy Harvesting
Abstract
1. Introduction
2. Electromechanical System and Mathematical Formation
3. Closed-Form Expressions of Electromechanical Frequency Response Functions
3.1. Electromechanical Governing Equations in Modal Coordinates
3.2. Closed-Form Frequency Response Functions
4. Numerical Results and Discussion
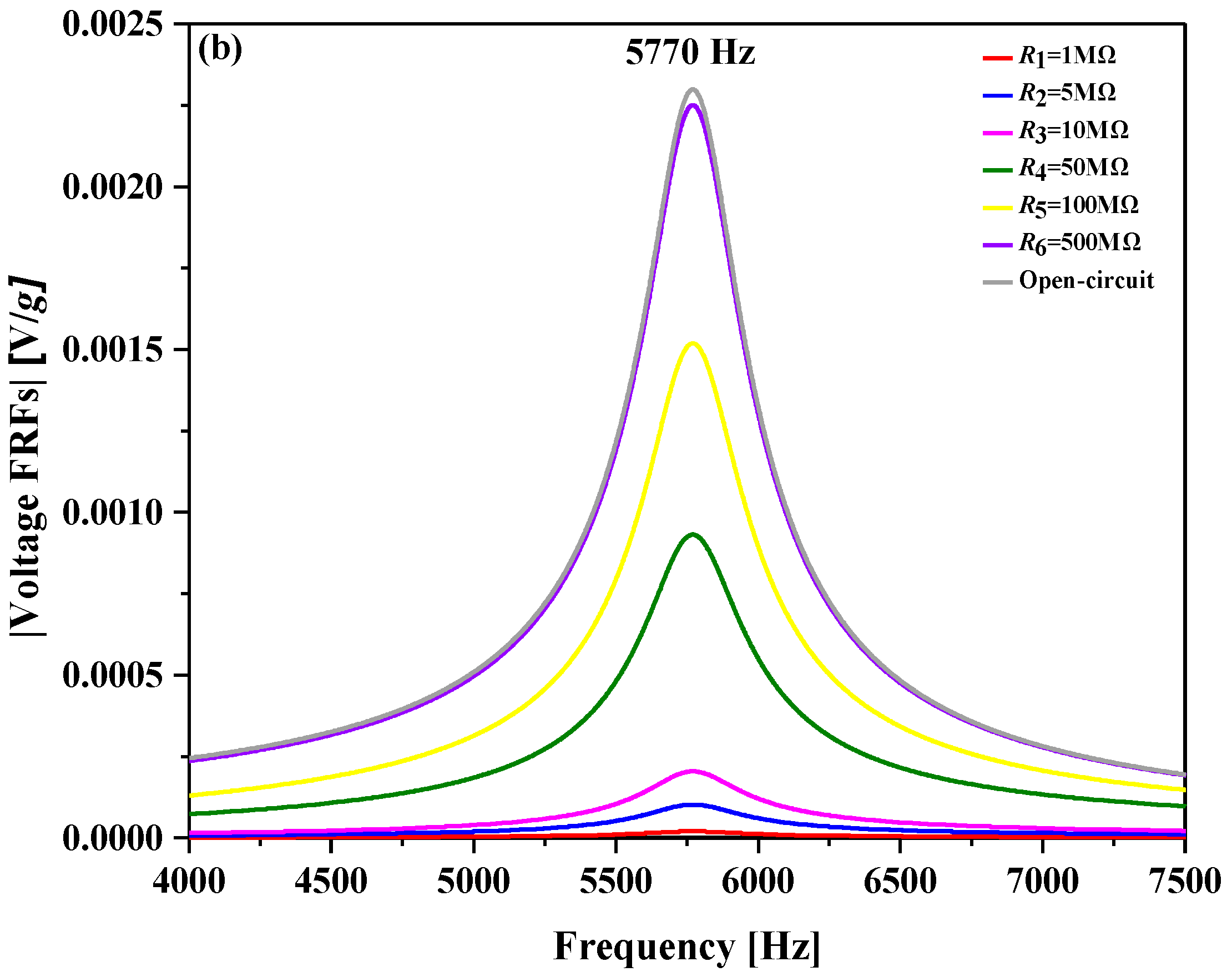
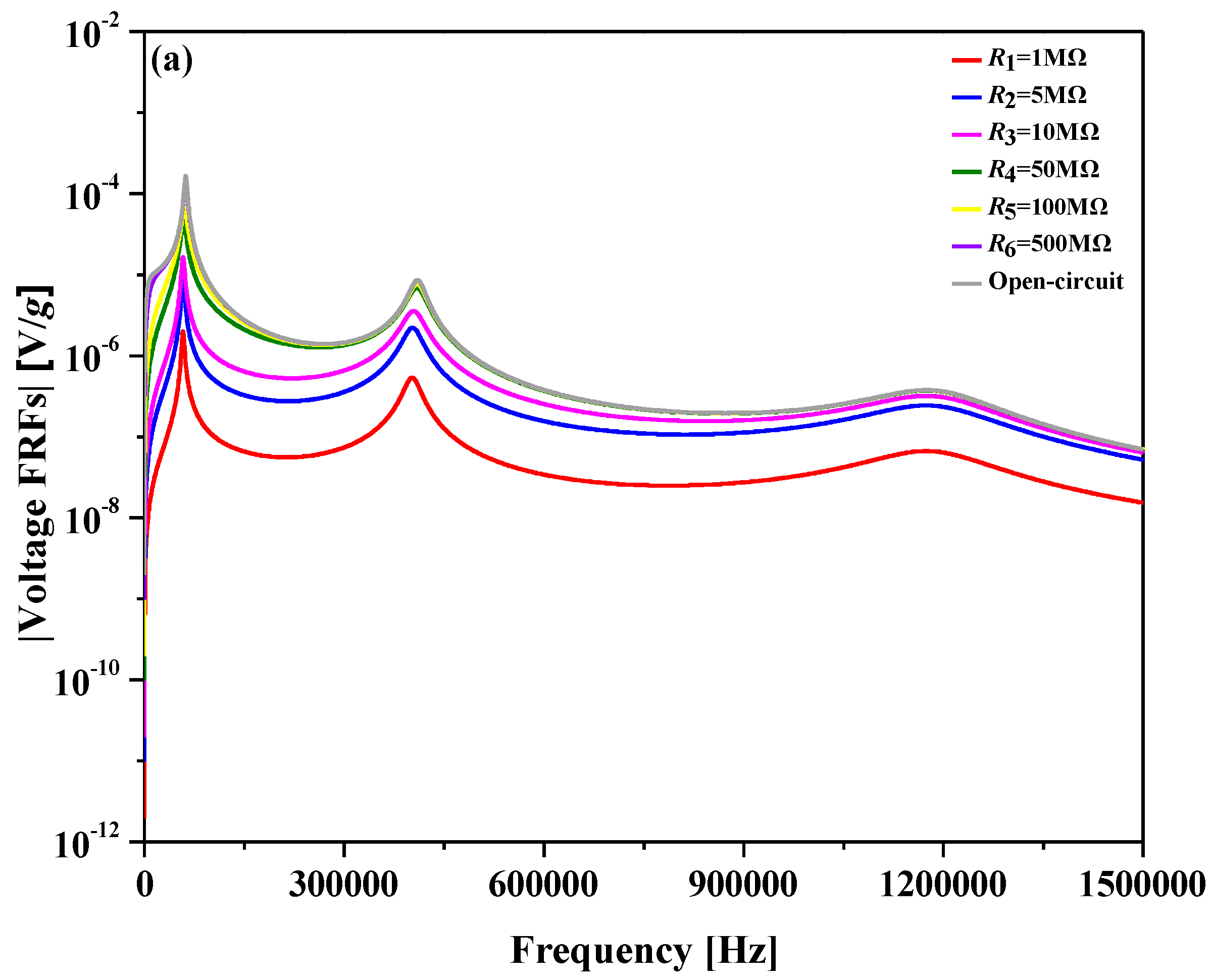
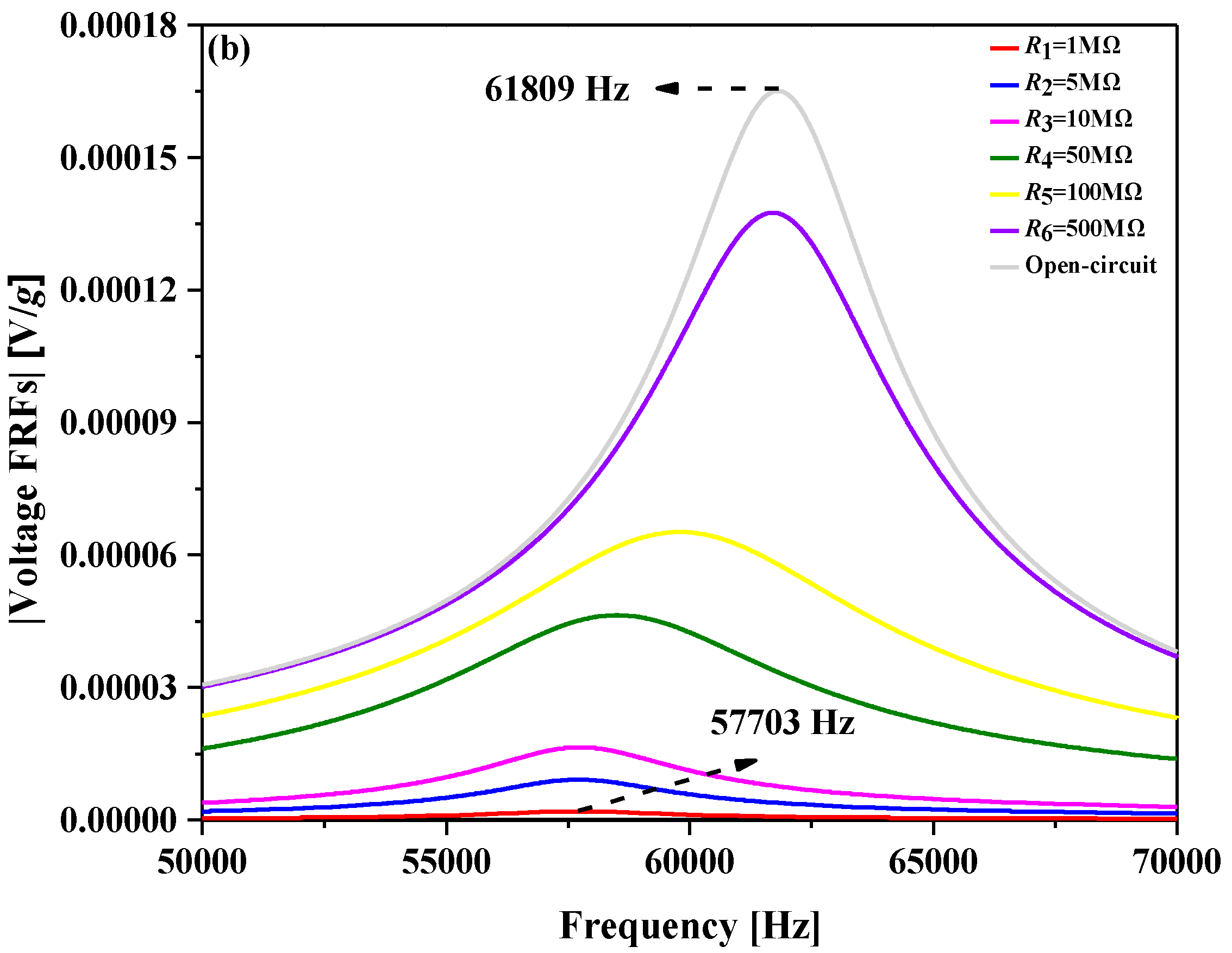
4.1. Voltage FRFs
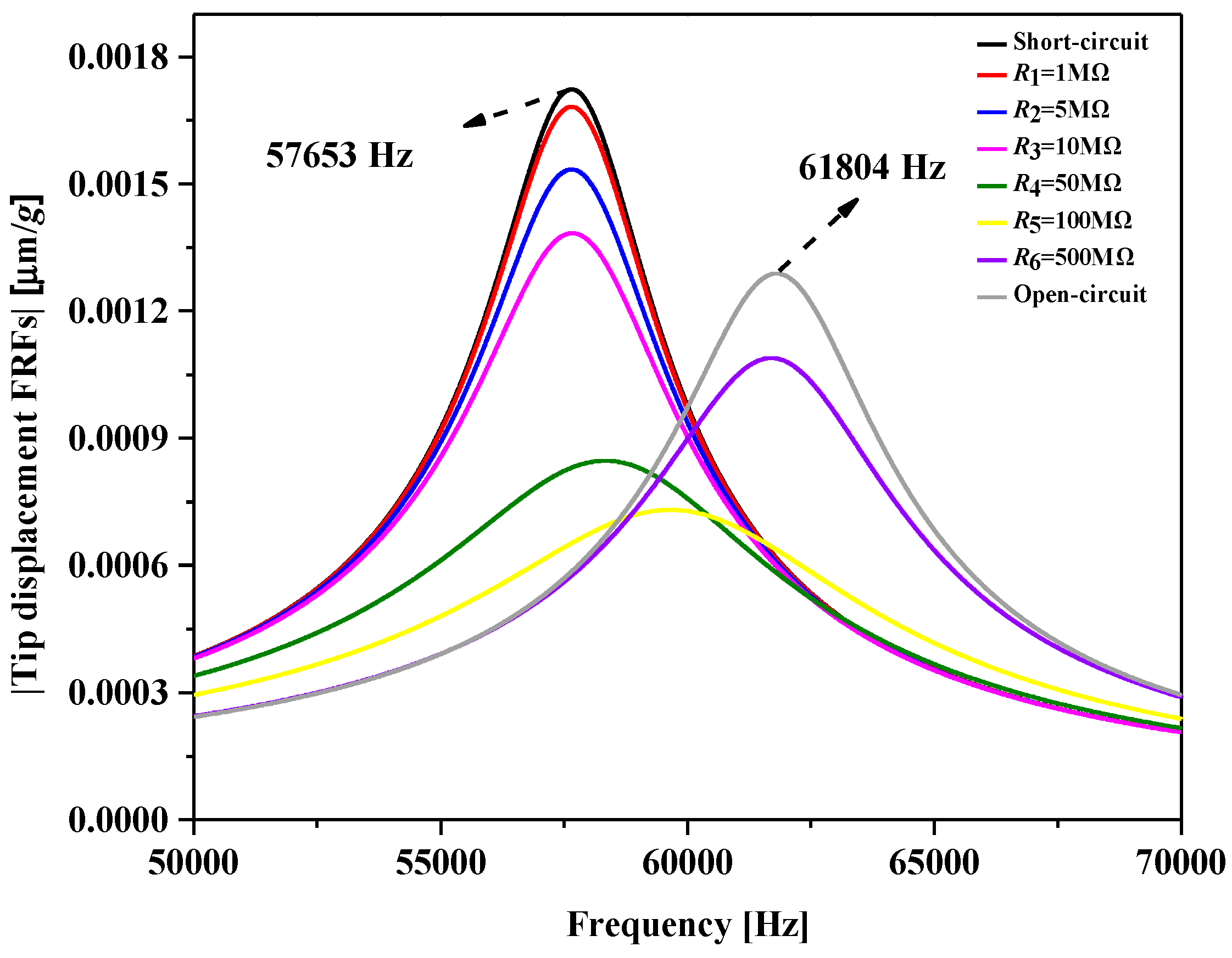
4.2. Tip Displacement FRFs
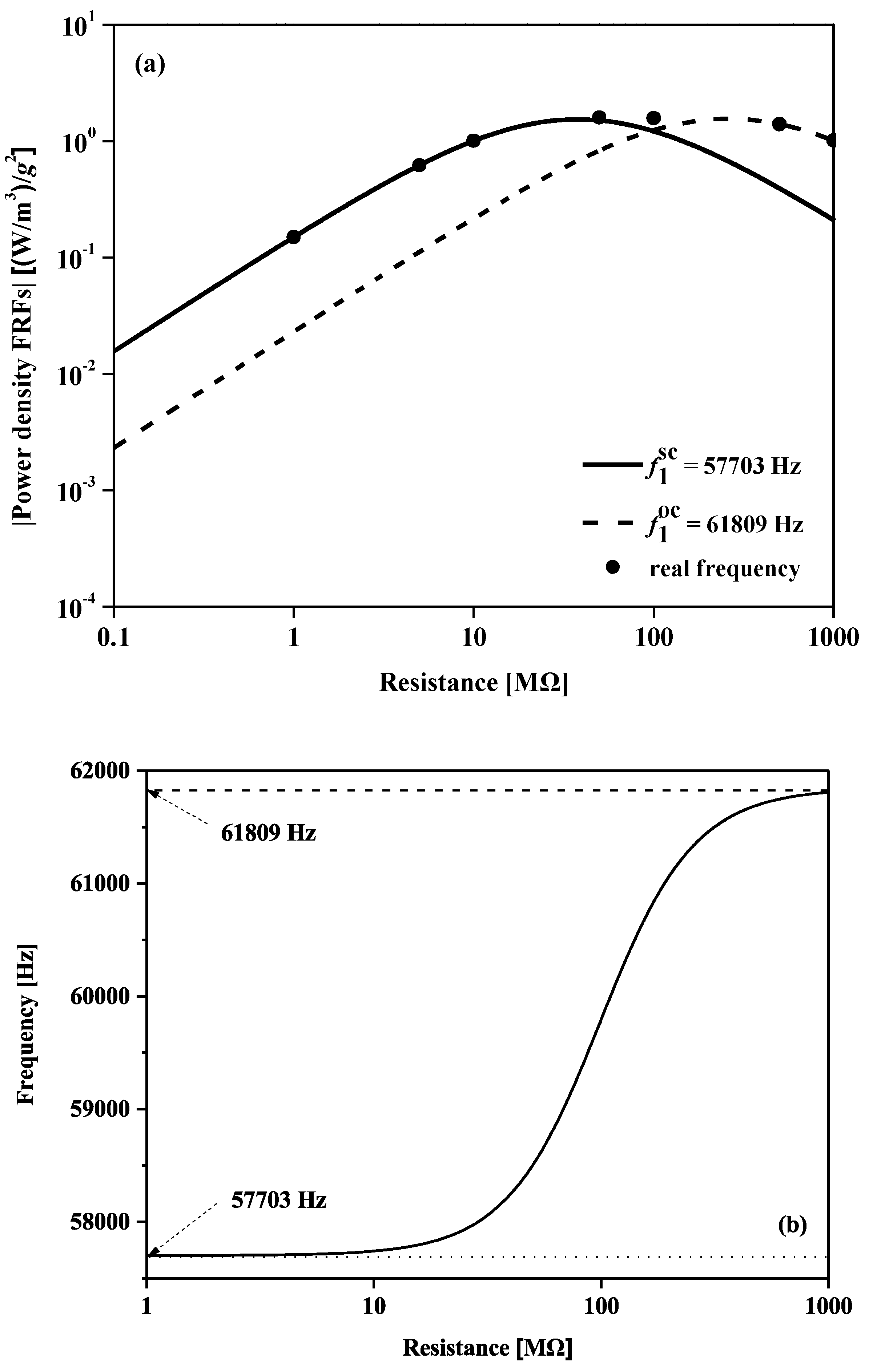
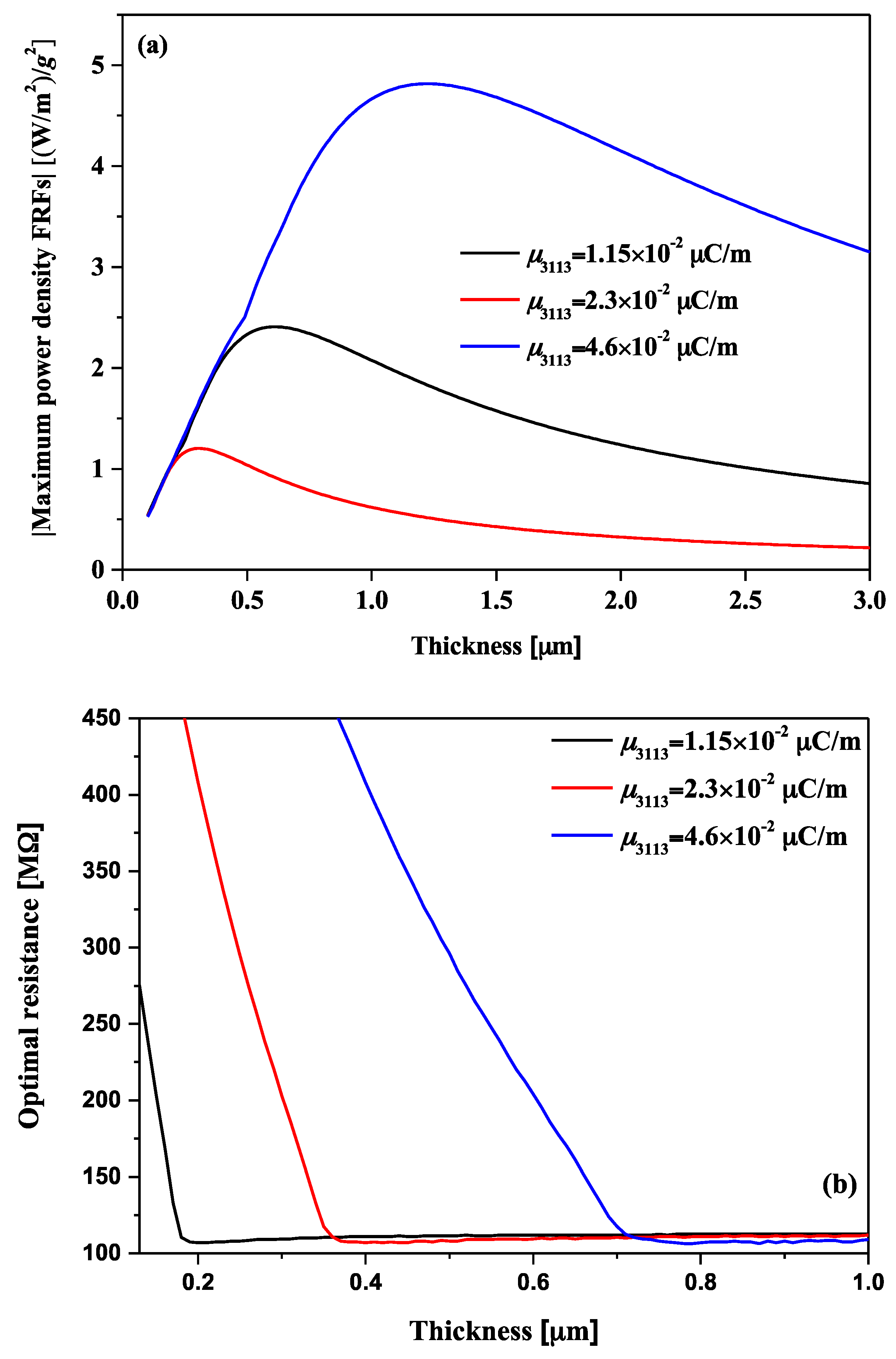
4.3. Power Density FRFs
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hudak, N.S.; Amatucci, G.G. Small-scale energy harvesting through thermoelectric, vibration, and radiofrequency power conversion. J. Appl. Phys. 2008, 103, 101301. [Google Scholar] [CrossRef]
- Williams, C.B.; Yates, R.B. Analysis of a micro-electric generator for microsystems. Sens. Actuat. A Phys. 1996, 52, 8–11. [Google Scholar] [CrossRef]
- Glynne-Jones, P.; Tudor, M.J.; Beeby, S.P.; White, N.M. An electromagnetic, vibration-powered generator for intelligent sensor systems. Sens. Actuat. A Phys. 2004, 110, 344–349. [Google Scholar] [CrossRef]
- Mathúna, C.O.; O’Donnell, T.; Martinez-Catala, R.V.; Rohan, J.; O’Flynn, B. Energy scavenging for long-term deployable wireless sensor networks. Talanta 2008, 75, 613–623. [Google Scholar] [CrossRef] [PubMed]
- Mitcheson, P.D.; Miao, P.; Stark, B.H.; Yeatman, E.M.; Holmes, A.S.; Green, T.C. MEMS electrostatic micropower generator for low frequency operation. Sens. Actuat. A Phys. 2004, 115, 523–529. [Google Scholar] [CrossRef]
- Roundy, S.; Wright, P.K.; Rabaey, J. A study of low level vibrations as a power source for wireless sensor nodes. Comput. Commun. 2003, 26, 1131–1144. [Google Scholar] [CrossRef]
- Jeon, Y.B.; Sood, R.; Jeong, J.H.; Kim, S.G. MEMS power generator with transverse mode thin film PZT. Sens. Actuat. A Phys. 2005, 122, 16–22. [Google Scholar] [CrossRef]
- Anton, S.R.; Sodano, H.A. A review of power harvesting using piezoelectric materials (2003–2006). Smart Mater. Struct. 2007, 16, R1–R21. [Google Scholar] [CrossRef]
- Lu, C.; Tsui, C.Y.; Ki, W.H. A batteryless vibration-based energy harvesting system for ultra low power ubiquitous applications. IEEE Int. Sym. Circuit Syst. 2007, 1349–1352. [Google Scholar]
- Lu, C.; Tsui, C.Y.; Ki, W.H. Vibration energy scavenging system with maximum power tracking for micropower applications. IEEE Trans. VLSI Syst. 2011, 19, 2109–2119. [Google Scholar] [CrossRef]
- Lu, C.; Raghunathan, V.; Roy, K. Efficient design of micro-scale energy harvesting systems. IEEE J. Emerg. Sel. Top. Circuit Syst. 2011, 1, 254–266. [Google Scholar] [CrossRef]
- Ma, W.; Cross, L.E. Large flexoelectric polarization in ceramic lead magnesium niobate. Appl. Phys. Lett. 2001, 79, 4420–4422. [Google Scholar] [CrossRef]
- Ma, W.; Cross, L.E. Strain-gradient-induced electric polarization in lead zirconate titanate ceramics. Appl. Phys. Lett. 2003, 82, 3293–3295. [Google Scholar] [CrossRef]
- Zubko, P.; Catalan, G.; Buckley, A.; Welche, P.R.L.; Scott, J.F. Strain-gradient-induced polarization in SrTiO3 single crystals. Phys. Rev. Lett. 2007, 99, 167601. [Google Scholar] [CrossRef]
- Sharma, N.D.; Maranganti, R.; Sharma, P. On the possibility of piezoelectric nanocomposites without using piezoelectric materials. J. Mech. Phys. Solids 2007, 55, 2328–2350. [Google Scholar] [CrossRef]
- Sharma, N.D.; Landis, C.M.; Sharma, P. Piezoelectric thin-film superlattices without using piezoelectric materials. J. Appl. Phys. 2010, 108, 024304. [Google Scholar] [CrossRef]
- Majdoub, M.S.; Sharma, P.; Cagin, T. Enhanced size-dependent piezoelectricity and elasticity in nanostructures due to the flexoelectric effect. Phys. Rev. B 2008, 77, 125424. [Google Scholar] [CrossRef]
- Qi, Y.; Kim, J.; Nguyen, T.D.; Lisko, B.; Purohit, P.K.; McAlpine, M.C. Enhanced piezoelectricity and stretchability in energy harvesting devices fabricated from buckled PZT ribbons. Nano Lett. 2011, 11, 1331. [Google Scholar] [CrossRef]
- Zhu, W.; Fu, J.Y.; Li, N.; Cross, L. Piezoelectric composite based on the enhanced flexoelectric effects. Appl. Phys. Lett. 2006, 89, 192904. [Google Scholar] [CrossRef]
- Chu, B.; Zhu, W.; Li, N.; Cross, L.E. Flexure mode flexoelectric piezoelectric composites. J. Appl. Phys. 2009, 106, 104109. [Google Scholar] [CrossRef]
- Zubko, P.; Catalan, G.; Tagantsev, A.K. Flexoelectric effect in solids. Ann. Rev. Mater. Res. 2013, 43, 387–421. [Google Scholar] [CrossRef]
- Lee, D.; Noh, T.W. Giant flexoelectric effect through interfacial strain relaxation. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2012, 370, 4944–4957. [Google Scholar] [CrossRef]
- Petrov, A.G. Electricity and mechanics of biomembrane systems: Flexoelectricity in living membranes. Anal. Chim. Acta 2006, 568, 70–83. [Google Scholar] [CrossRef]
- Abdollahi, A.; Peco, C.; Millan, D.; Arroyo, M.; Arias, I. Computational evaluation of the flexoelectric effect in dielectric solids. J. Appl. Phys. 2014, 116, 093502. [Google Scholar] [CrossRef]
- Hu, S.L.; Sheng, S.P. Electric field gradient theory with surface effect for nano-dielectrics. Comput. Mater. Conit. 2009, 13, 63–87. [Google Scholar]
- Zhang, Z.; Yan, Z.; Jiang, L. Flexoelectric effect on the electroelastic responses and vibrational behaviors of a piezoelectric nanoplate. J. Appl. Phys. 2014, 116, 014307. [Google Scholar] [CrossRef]
- He, L.; Lou, J.; Zhang, A.; Wu, H.; Du, J.; Wang, J. On the coupling effects of piezoelectricity and flexoelectricity in piezoelectric nanostructures. AIP Adv. 2017, 7, 105106. [Google Scholar] [CrossRef]
- Xiang, S.; Li, X.F. Elasticity solution of the bending of beams with the flexoelectric and piezoelectric effect. Smart Mater. Struct. 2018, 27, 105023. [Google Scholar] [CrossRef]
- Su, Y.X.; Zhou, Z.D.; Yang, F.P. Electromechanical analysis of bilayer piezoelectric sensors due to flexoelectricity and strain gradient elasticity. AIP Adv. 2019, 9, 015207. [Google Scholar] [CrossRef]
- Toupin, R.A. The elastic dielectric. Arch. Ration. Mech. Anal. 1956, 5, 849–915. [Google Scholar] [CrossRef]
- Shen, S.P.; Hu, S.L. A theory of flexoelectricity with surface effect for elastic dielectrics. J. Mech. Phys. Solids 2010, 58, 655–677. [Google Scholar] [CrossRef]
- Liang, X.; Hu, S.; Shen, S. Effects of surface and flexoelectricity on a piezoelectric nanobeam. Smart Mater. Struct. 2014, 23, 035020. [Google Scholar] [CrossRef]
- Yan, Z.; Jiang, L.Y. Flexoelectric effect on the electroelastic responses of bending piezoelectric nanobeams. J. Appl. Phys. 2013, 113, 194102. [Google Scholar] [CrossRef]
- Liang, X.; Hu, S.; Shen, S. Size-dependent buckling and vibration behaviors of piezoelectric nanostructures due to flexoelectricity. Smart Mater. Struct. 2015, 24, 105012. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, R.; Jiang, L. A study of the flexoelectric effect on the electroelastic fields of a cantilevered piezoelectric nanoplate. Int. J. Appl. Mech. 2017, 9, 1750056. [Google Scholar] [CrossRef]
- Zhou, Z.D.; Yang, C.P.; Su, Y.X.; Huang, R.; Lin, X.H. Electromechanical coupling in piezoelectric nanobeams due to flexoelectric effect. Smart Mater. Struct. 2017, 26, 095025. [Google Scholar] [CrossRef]
- Deng, Q.; Kammoun, M.; Erturk, A.; Sharma, P. Nanoscale flexoelectric energy harvesting. Int. J. Solids Struct. 2014, 51, 3218–3225. [Google Scholar] [CrossRef]
- Moura, A.G.; Erturk, A. Electroelastodynamics of flexoelectric energy conversion and harvesting in elastic dielectrics. J. Appl. Phys. 2017, 121, 064110. [Google Scholar] [CrossRef]
- Yan, Z. Modeling of a nanoscale flexoelectric energy harvester with surface effects. Physical E 2017, 88, 125–132. [Google Scholar] [CrossRef]
- Liang, X.; Zhang, R.; Hu, S.; Shen, S. Flexoelectric energy harvesters based on Timoshenko laminated beam theory. J. Intell. Mater. Syst. Strust. 2017, 28, 2064–2073. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. An experimentally validated bimorph cantilever model for piezoelectric energy harvesting from base excitations. Smart Mater. Struct. 2009, 18, 025009. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. Piezoelectric Energy Harvesting; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Tang, L.; Wang, J. Size effect of tip mass on performance of cantilevered piezoelectric energy harvester with a dynamic magnifier. Acta Mech. 2017, 228, 3997–4015. [Google Scholar] [CrossRef]
- Chu, B.; Salem, D.R. Flexoelectricity in several thermoplastic and thermosetting polymers. Appl. Phys. Lett. 2012, 101, 103905. [Google Scholar] [CrossRef]
- Daqaq, M.F.; Stabler, C.; Qaroush, Y.; Seuaciuc-Osorio, T. Investigation of power harvesting via parametric excitations. J. Intell. Mater. Syst. Struct. 2009, 20, 545–557. [Google Scholar] [CrossRef]
- Ferrari, M.; Ferrari, V.; Guizzetti, M.; Ando, B.; Baglio, S.; Trigona, C. Improved energy harvesting from wideband vibrations by nonlinear piezoelectric converters. Sens. Actuat. A Phys. 2010, 162, 425–431. [Google Scholar] [CrossRef]
- Mahmoudi, S.; Kacem, N.; Bouhaddi, N. Enhancement of the performance of a hybrid nonlinear vibration energy harvester based on piezoelectric and electromagnetic transductions. Smart Mater. Struct. 2014, 23, 075024. [Google Scholar] [CrossRef]
- Drezet, C.; Kacem, N.; Bouhaddi, N. Design of a nonlinear energy harvester based on high static low dynamic stiffness for low frequency random vibrations. Sens. Actuat. A Phys. 2018, 283, 54–64. [Google Scholar] [CrossRef]
- Yang, B.; Lee, C.; Xiang, W.; Xie, J.; He, J.H.; Kotlanka, R.K.; Low, S.P.; Feng, H. Electromagnetic energy harvesting from vibrations of multiple frequencies. J. Micromech. Microeng. 2009, 19, 035001. [Google Scholar] [CrossRef]
- Sari, I.; Balkan, T.; Kulah, H. An electromagnetic micro power generator for wideband environmental vibrations. Sens. Actuat. A Phys. 2008, 145–146, 405–413. [Google Scholar] [CrossRef]
- Abed, I.; Kacem, N.; Bouhaddi, N.; Bouazizi, M.L. Multi-modal vibration energy harvesting approach based on nonlinear oscillator arrays under magnetic levitation. Smart Mater. Struct. 2016, 25, 025018. [Google Scholar] [CrossRef]
- Abed, I.; Kacem, N.; Bouhaddi, N.; Bouazizi, M.L. Nonlinear dynamics of magnetically coupled beams for multi-modal vibration energy harvesting. In Proceedings of the 2016 SPIE Smart Structures and Materials + Nondestructive Evaluation and Health Monitoring, Las Vegas, NV, USA, 15 April 2016; p. 97992C. [Google Scholar]
- Lin, X.H.; Su, Y.X.; Zhou, Z.D.; Yang, J.P. Analysis of the natural frequency for flexoelectric cantilever beams under the open-circuit condition. Chin. Q. Mech. 2018, 39, 383–394. (In Chinese) [Google Scholar]
- Dutoit, N.E.; Wardle, B.L. Experimental verification of models for microfabricated piezoelectric vibration energy harvesters. AIAA J. 2007, 45, 1126–1137. [Google Scholar] [CrossRef]
- Baskaran, S.; Ramachandran, N.; He, X.; Thiruvannamalai, S.; Lee, H.J.; Heo, H.; Chen, Q.; Fu, J.Y. Giant flexoelectricity in polyvinylidene fluoride films. Phys. Lett. A 2011, 375, 2082–2084. [Google Scholar] [CrossRef]





© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, Y.; Lin, X.; Huang, R.; Zhou, Z. Analytical Electromechanical Modeling of Nanoscale Flexoelectric Energy Harvesting. Appl. Sci. 2019, 9, 2273. https://doi.org/10.3390/app9112273
Su Y, Lin X, Huang R, Zhou Z. Analytical Electromechanical Modeling of Nanoscale Flexoelectric Energy Harvesting. Applied Sciences. 2019; 9(11):2273. https://doi.org/10.3390/app9112273
Chicago/Turabian StyleSu, Yaxuan, Xiaohui Lin, Rui Huang, and Zhidong Zhou. 2019. "Analytical Electromechanical Modeling of Nanoscale Flexoelectric Energy Harvesting" Applied Sciences 9, no. 11: 2273. https://doi.org/10.3390/app9112273
APA StyleSu, Y., Lin, X., Huang, R., & Zhou, Z. (2019). Analytical Electromechanical Modeling of Nanoscale Flexoelectric Energy Harvesting. Applied Sciences, 9(11), 2273. https://doi.org/10.3390/app9112273




