A Full Coupled Thermal–Hydraulic–Chemical Model for Heterogeneity Rock Damage and Its Application in Predicting Water Inrush
Abstract
1. Introduction
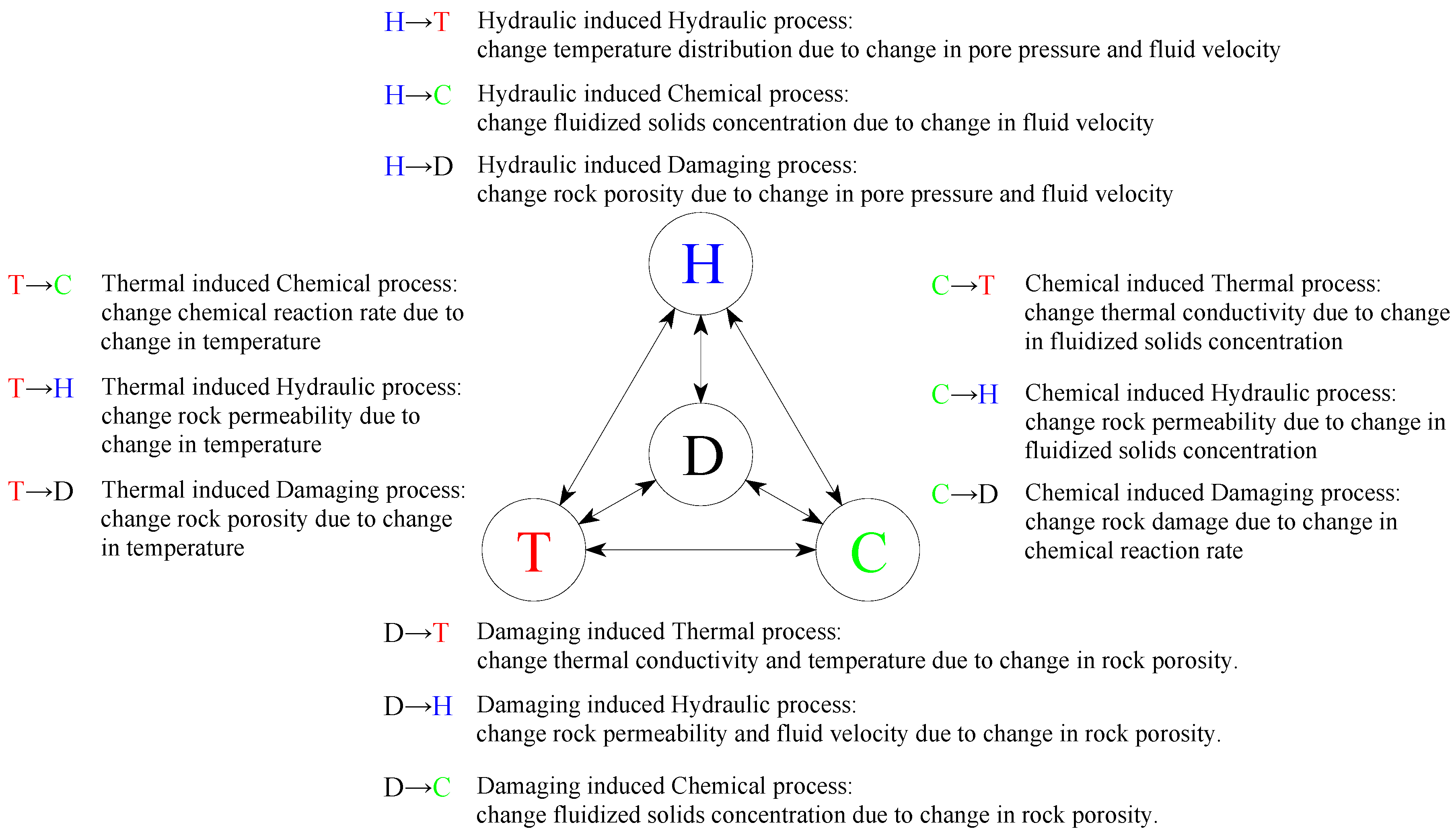
2. The Equations of Coupled THC Model
2.1. The Hydrochemical and Hydraulic Erosion Equation
2.1.1. Basic Equations
2.1.2. Governing Equations
2.2. The Flow Equation
2.3. The Heat Transfer Equation
3. Numerical Model Setup
4. Results
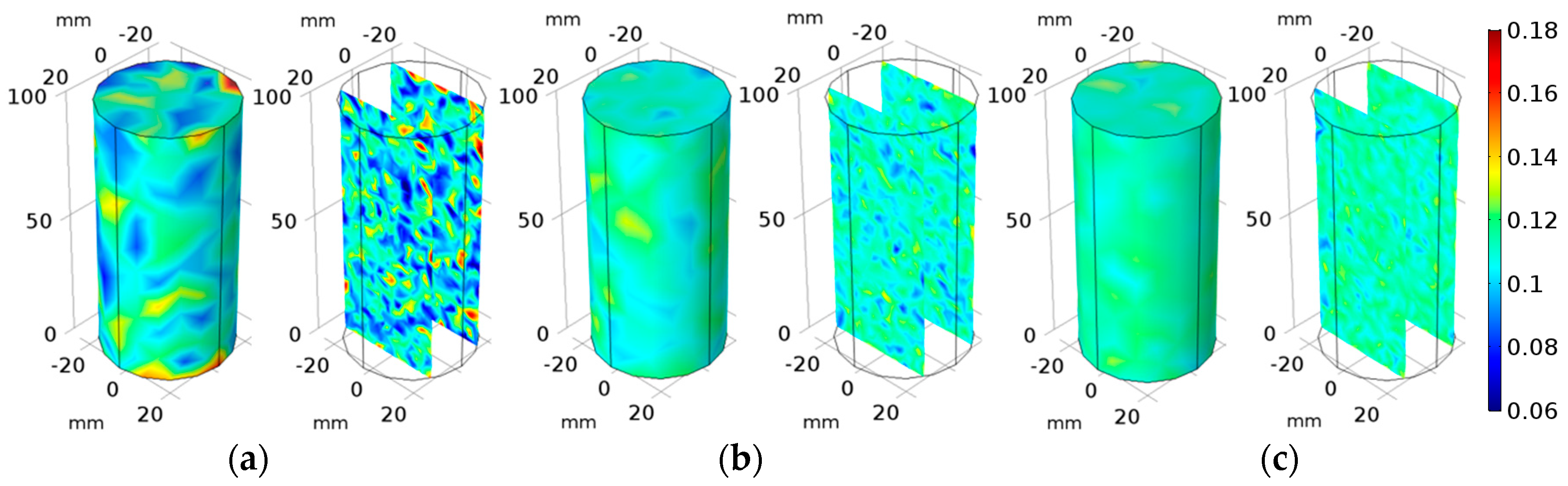
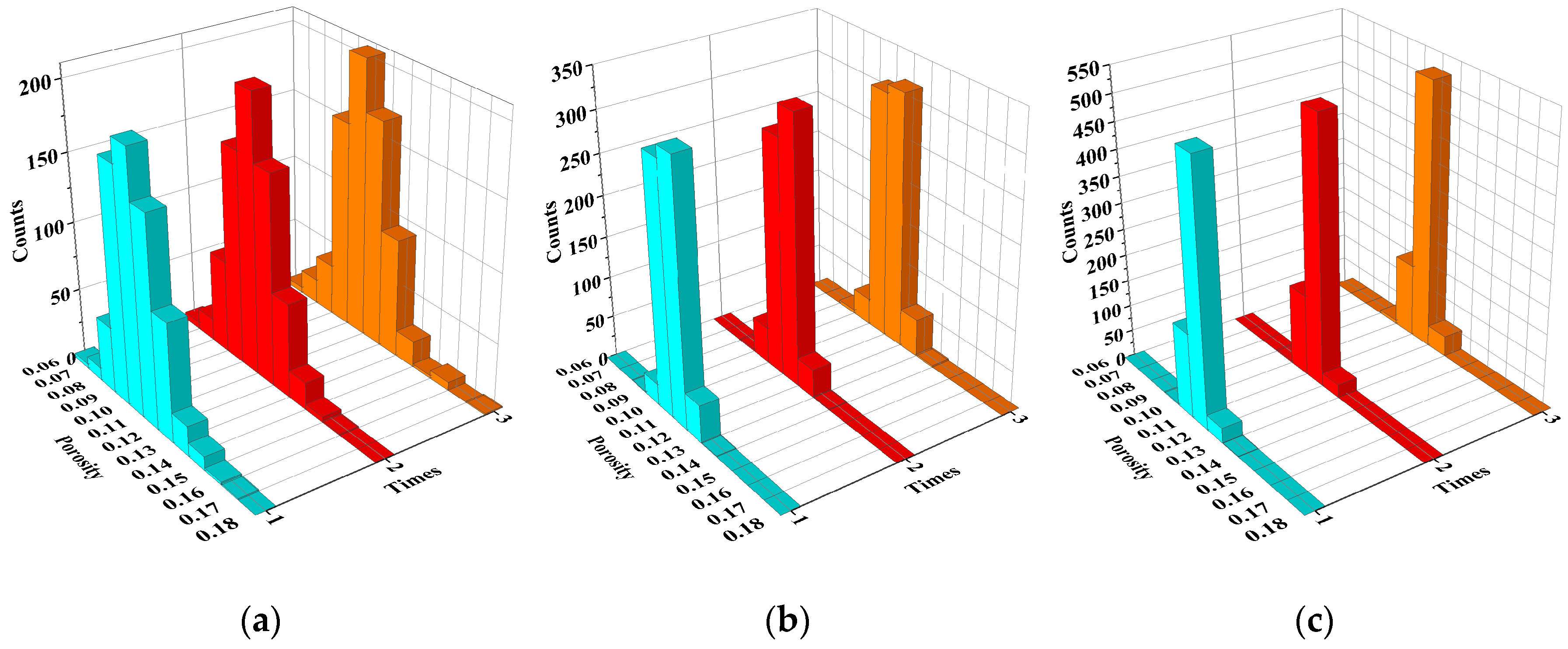
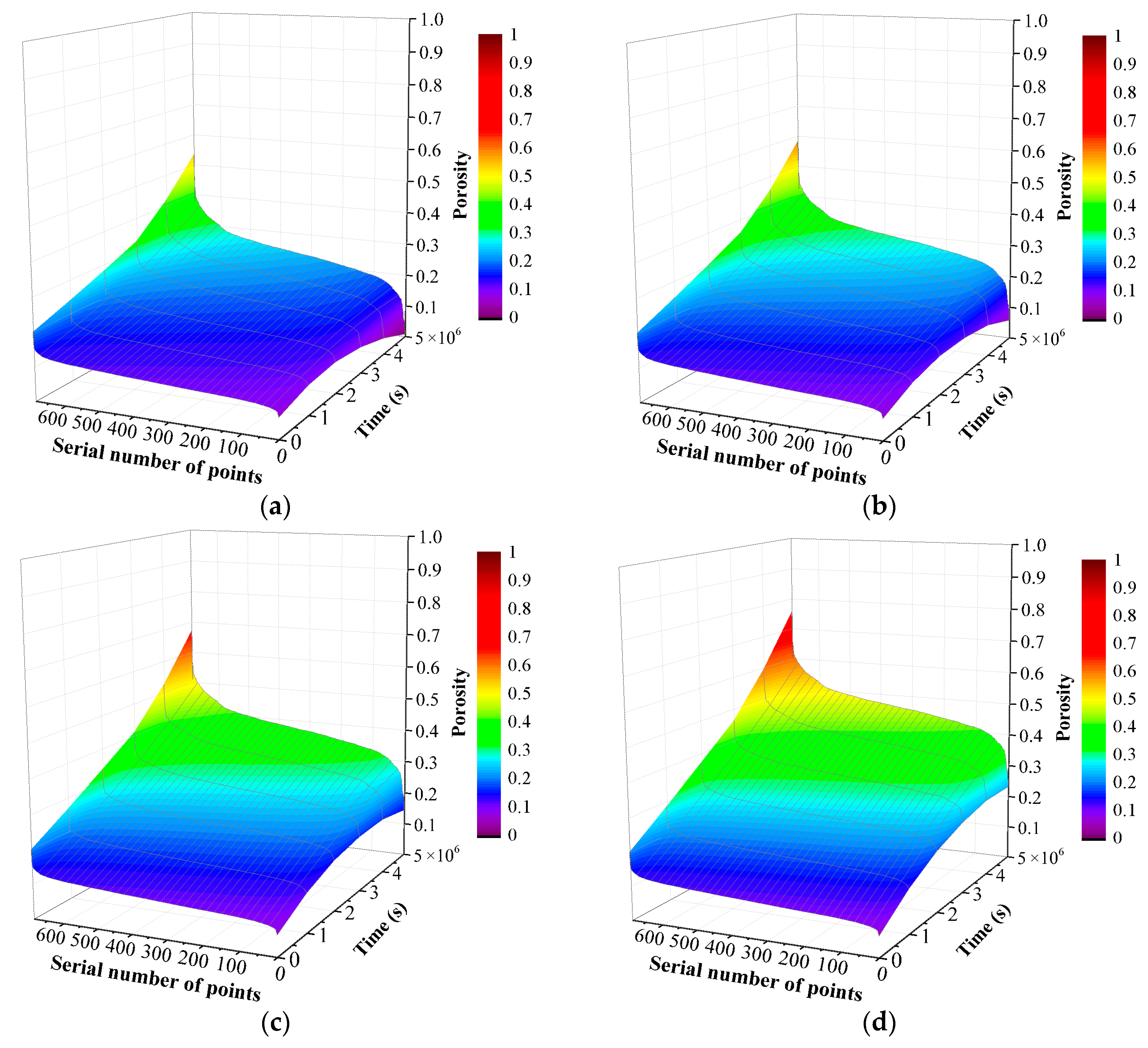
4.1. The Porosity
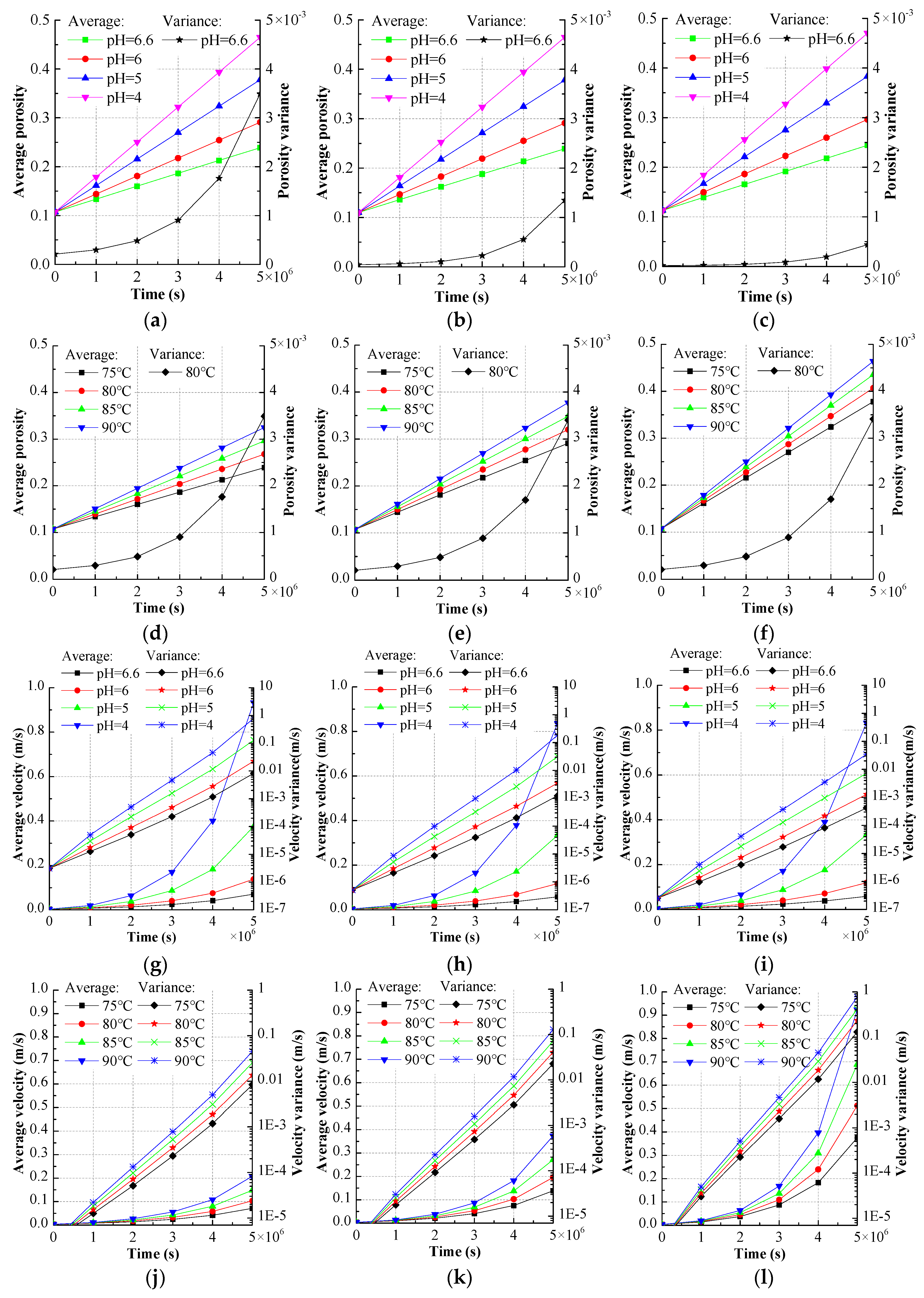
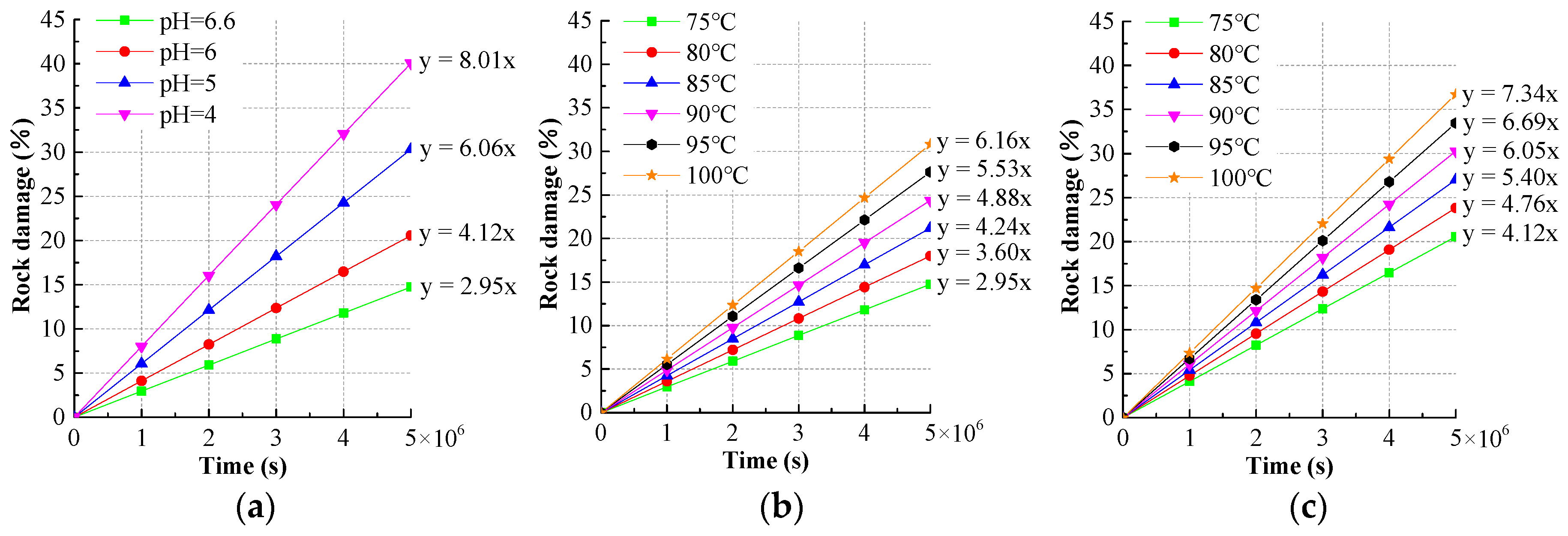
4.1.1. The Influence of Hydrochemistry
4.1.2. The Influence of Temperature
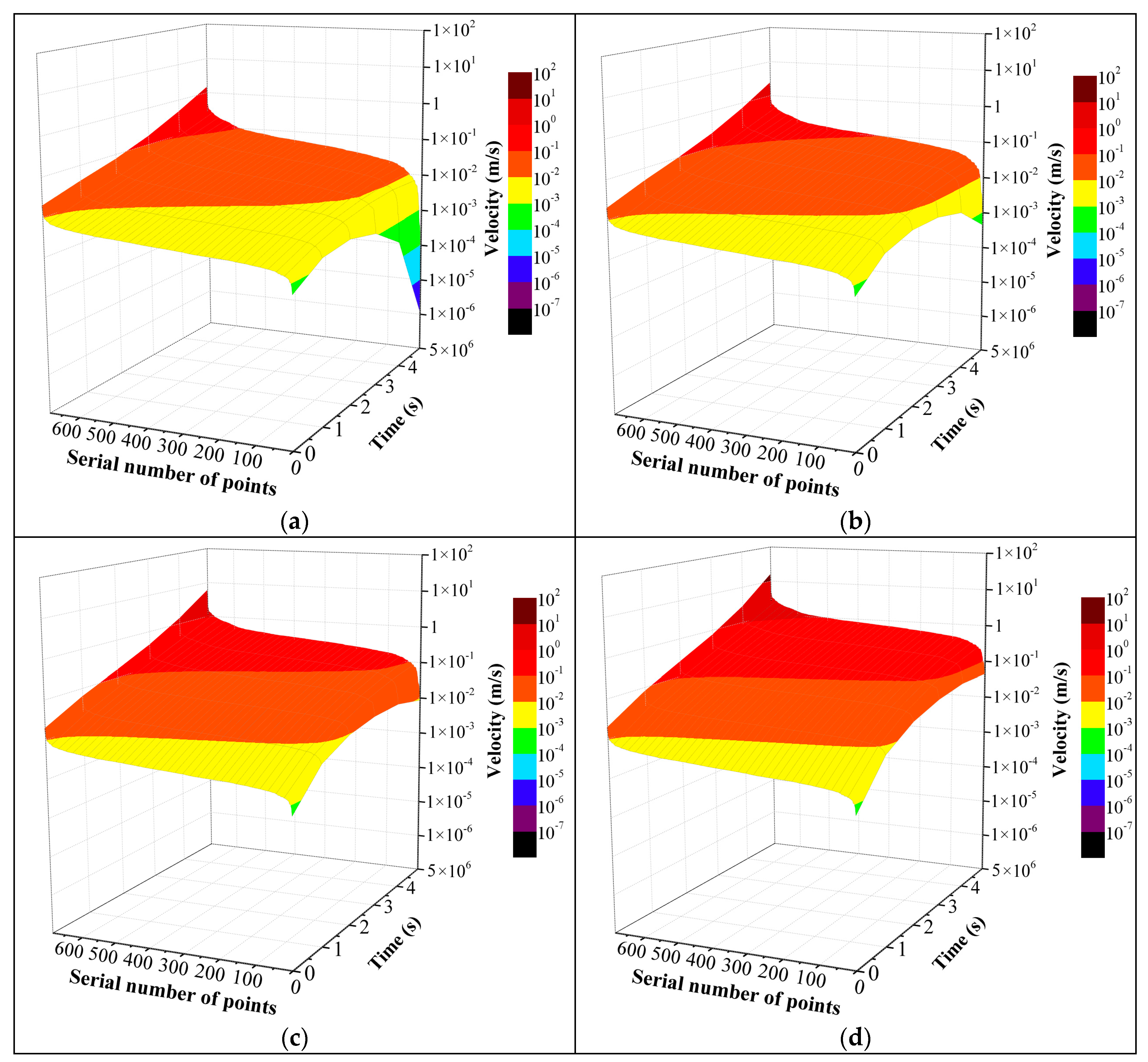
4.2. The Fluid
4.2.1. The Influence of Hydrochemistry
4.2.2. The Influence of Temperature
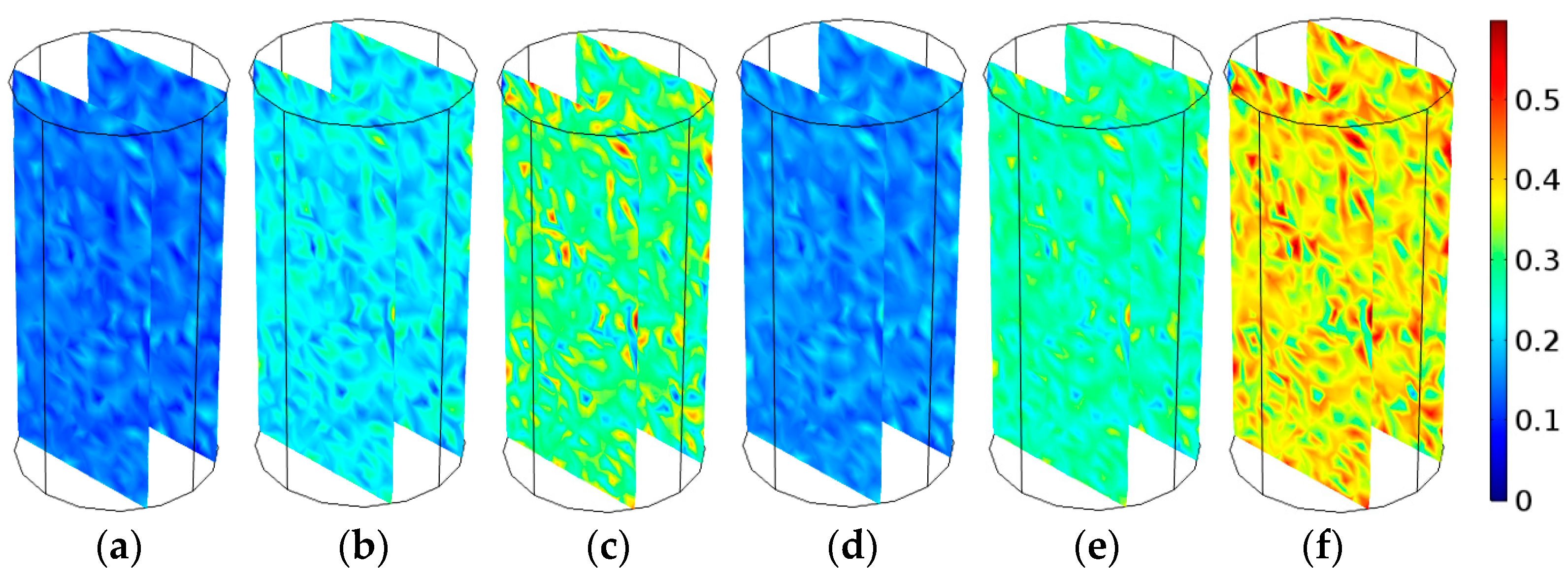
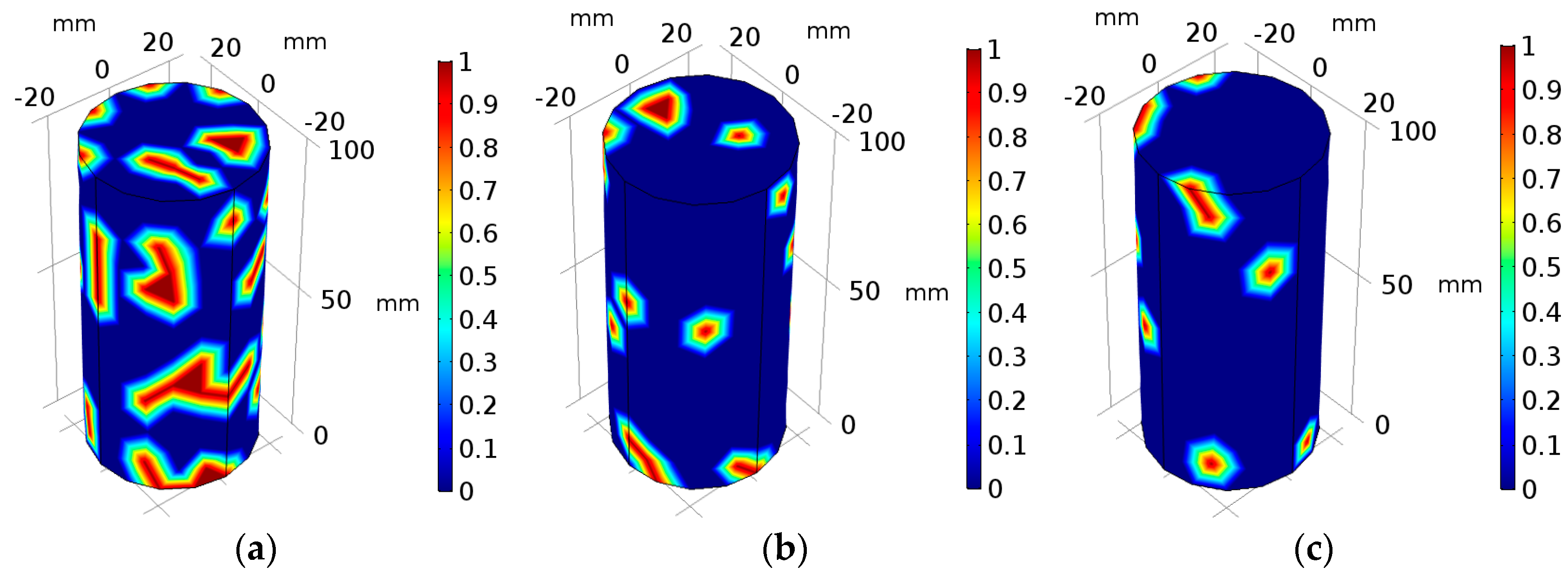
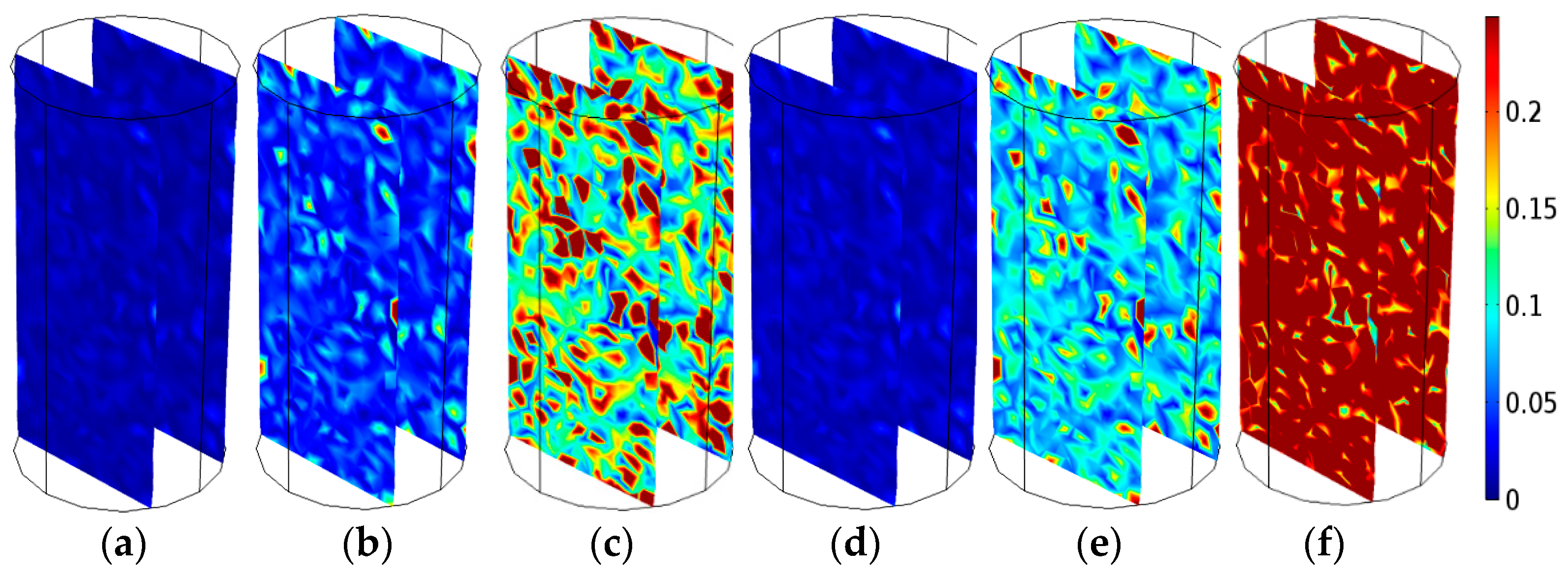
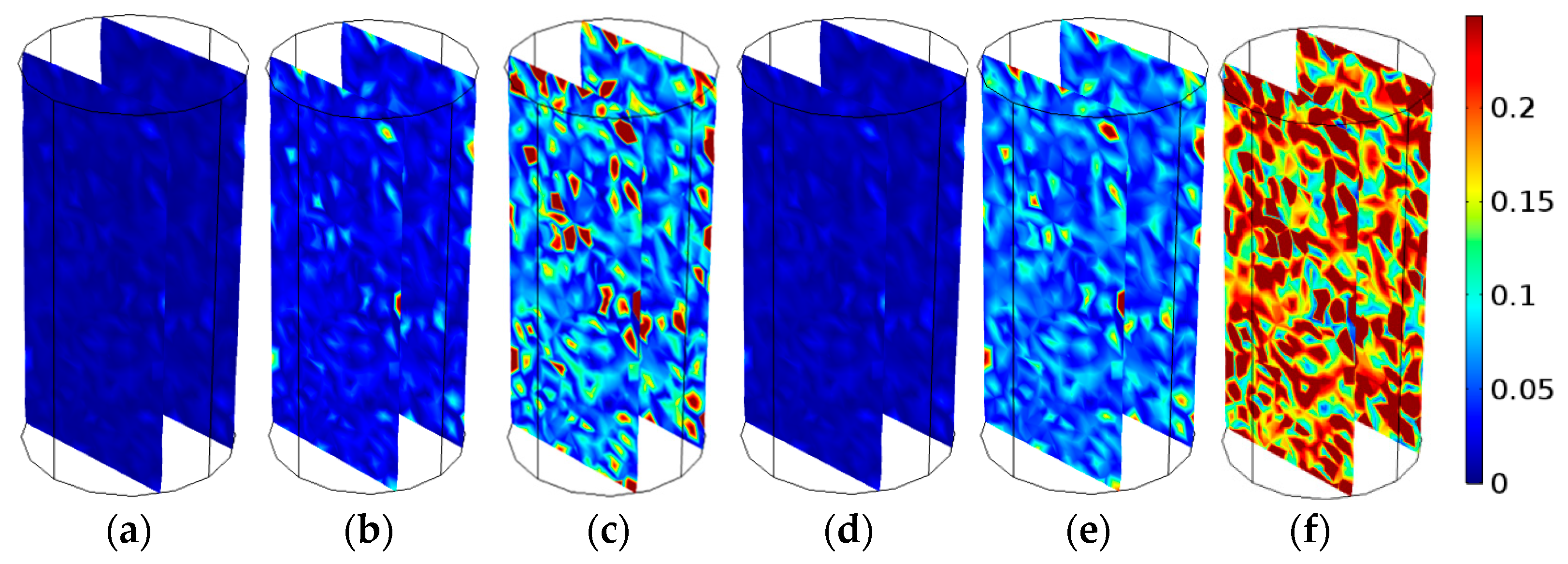
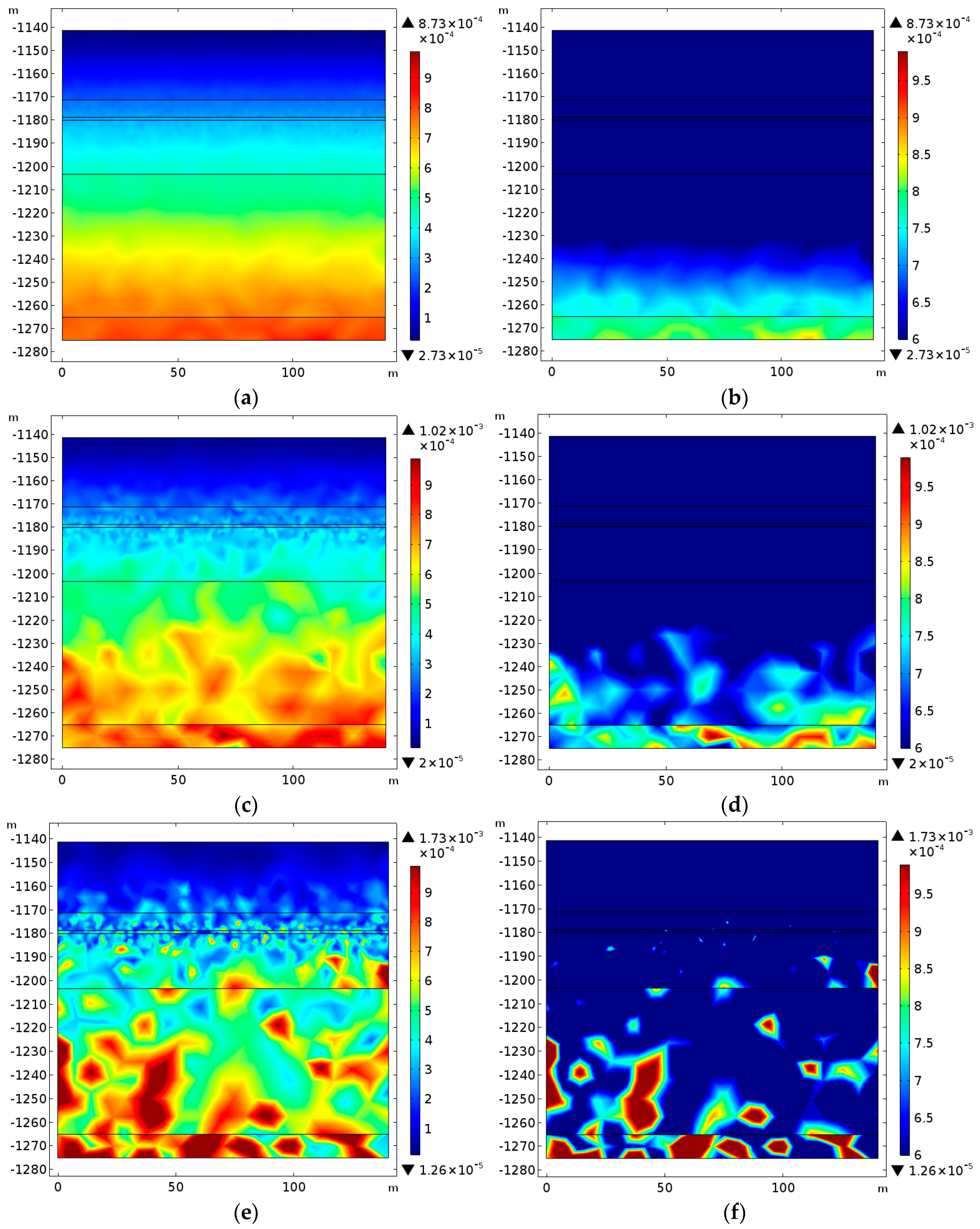
4.3. The Rock Damage
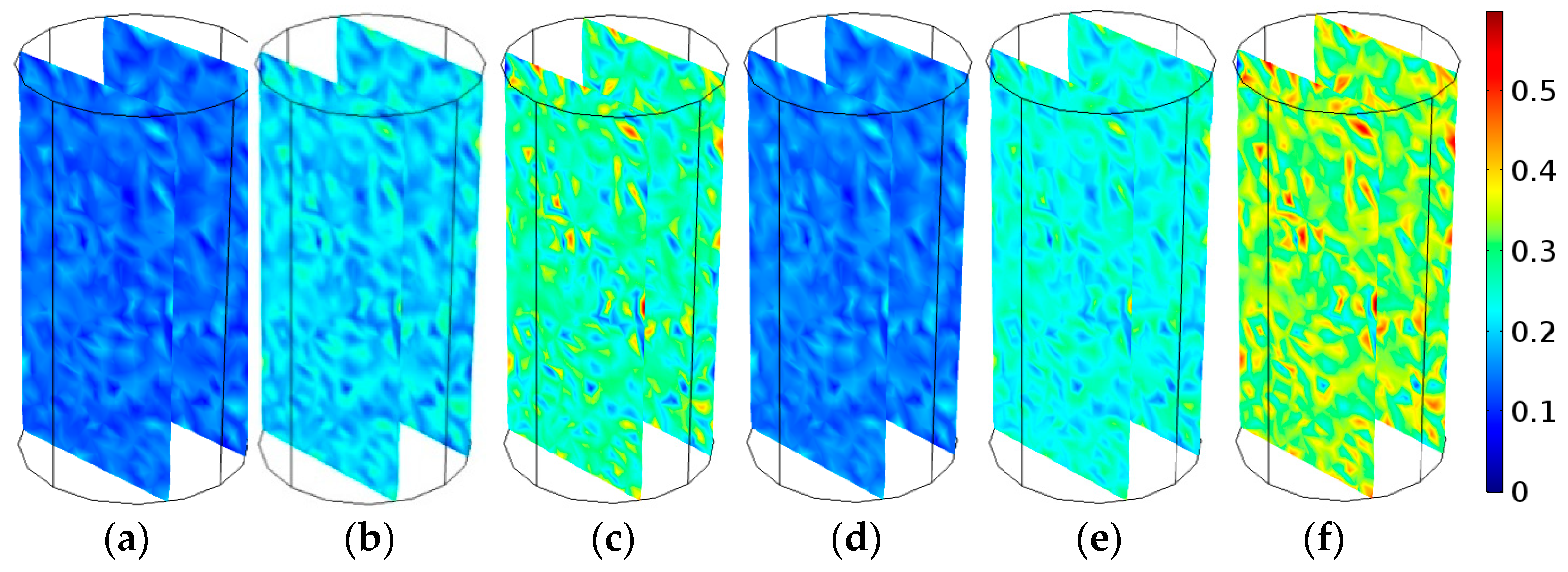
5. Application in Predicting Water Inrush
6. Discussions
- In alkaline conditions and high temperature that make the chemical reaction rate decrease, the rock damage change rule is not studied. In addition, the impact of thermal expansion on rock damage is not considered.
- The relationship between the external stress and porosity change is not established. Therefore, the change in porosity due to mechanical compression or expansion is not studied. The rock damage is only defined by the porosity change. The strength parameters (e.g., the elastic modulus), are not considered to define the damage.
7. Conclusions
- With increasing time, the average porosity approximately shows linear growth, and the average fluid velocity approximately shows exponential growth, and their growth rates increase with decreasing pH value and increasing temperature in a certain acidity and temperature range.
- The Weibull distribution is adopted to govern the heterogeneity of the initial rock porosity distribution, and the variance is used to express the heterogeneity. The increase of initial porosity heterogeneity has little influence on porosity change, but it can increase the fluid velocity growth rate. The porosity heterogeneity and fluid velocity heterogeneity approximately show exponential growth with increasing time. The increase of temperature and decrease of pH value have little influence on the porosity heterogeneity, but they can increase the growth rate of the fluid velocity heterogeneity. The rock heterogeneity growth contributes to rock fracture, which is corresponding to the results reported by the previous research.
- The porosity change is used to define the rock damage. The rock damage growth rate increases with a decreasing pH value and increasing temperature in a certain acidity range and temperature range.
- The water inrush is more likely to occur through the rock with greater heterogeneity.
Supplementary Files
Supplementary File 1Author Contributions
Funding
Conflicts of Interest
References
- Kong, B.; Wang, E.; Li, Z. The effect of high temperature environment on rock properties—An example of electromagnetic radiation characterization. Environ. Sci. Pollut. Res. 2018, 25, 29104–29114. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Tang, C.A.; Li, L.C.; Liang, Z.Z. Numerical simulation of 3d hydraulic fracturing process. Chin. J. Geotech. Eng. 2010, 32, 1875–1881. [Google Scholar]
- Zheng, Y.J.; Chen, M. Lab investigation of dissolution velocity of carbonate rock boreholes. Petrol. Drill. Tech. 2003, 31, 1–3. (In Chinese) [Google Scholar]
- Jing, L.; Tsang, C.F.; Stephansson, O. DECOVALEX—An international co-operative research project on mathematical models of coupled THM processes for safety analysis of radioactive waste repositories. Int. J. Rock Mech. Min. Sci. 1995, 32, 389–398. [Google Scholar] [CrossRef]
- Tsang, C.F.; Jing, L.; Stephansson, O.; Kautsky, F. The DECOVALEX III project: A summary of activities and lessons learned. Int. J. Rock Mech. Min. Sci. 2005, 42, 593–610. [Google Scholar] [CrossRef]
- Rutqvist, J.; Wu, Y.S.; Tsang, C.F.; Bodvarsson, G. A modeling approach for analysis of coupled multiphase fluid flow, heat transfer, and deformation in fractured porous rock. Int. J. Rock Mech. Min. Sci. 2002, 39, 429–442. [Google Scholar] [CrossRef]
- Graupner, B.J.; Shao, H.; Wang, X.R.; Nguyen, T.S.; Li, Z.; Rutqvist, J.; Chen, F.; Birkholzer, J.; Wang, W.; Kolditz, O.; et al. Comparative modelling of the coupled thermal–hydraulic-mechanical (THM) processes in a heated bentonite pellet column with hydration. Environ. Earth Sci. 2018, 77, 84. [Google Scholar] [CrossRef]
- Xiao, Y.; Guo, J.; Wang, H.; Lu, L.; Mclennan, J.; Chen, M. Coupled THM and matrix stability modeling of hydroshearing stimulation in a coupled fracture-matrix hot volcanic system. Math. Probl. Eng. 2018. [Google Scholar] [CrossRef]
- Sun, Z.; Pin, Y.; Yao, J.; Zhang, K.; Zhuang, L.; Zhu, X.; Wang, T.; Jiang, C. Numerical Investigation on the Heat Extraction Capacity of Dual Horizontal Wells in Enhanced Geothermal Systems Based on the 3-D THM Model. Energies 2018, 11, 280. [Google Scholar] [CrossRef]
- Zhu, W.; Wei, C.; Tian, J.; Yang, T.; Tang, C. Coupled thermal-hydraulic-mechanical model during rock damage and its preliminary application. Rock Soil Mech. 2009, 30, 3851–3857. (In Chinese) [Google Scholar]
- Guo, W.; Zhao, J.; Yin, L.; Jiang, N. Study on Fault Water Inrush Mechanism and Nonlinear Seepage-stress Coupling. J. Shandong Univ. Sci. Technol. 2017, 6, 1–7. (In Chinese) [Google Scholar]
- Yeh, G.T.; Tripathi, V.S. A Model for Simulating Transport of Reactive Multispecies Components: Model Development and Demonstration. Water Resour. Res. 1991, 27, 3075–3094. [Google Scholar] [CrossRef]
- Xu, T.; Sonnenthal, E.; Spycher, N.; Pruess, K. TOUGHREACT—A simulation program for non-isothermal multiphase reactive geochemical transport in variably saturated geologic media: Applications to geothermal injectivity and CO geological sequestration. Comp. Geosci. 2006, 32, 145–165. [Google Scholar] [CrossRef]
- Cui, Q.; Feng, X.; Xue, Q.; Zhou, H.; Zhang, Z. Mechanism study of porosity structure change of sandstone under chemical corrosion. Chin. J. Rock Mech. Eng. 2008, 27, 1209–1216. (In Chinese) [Google Scholar]
- Liu, J.; Sheng, J.; Polak, A.; Elsworth, D.; Yasuhara, H.; Grader, A. A fully-coupled hydrological–mechanical–chemical model for fracture sealing and preferential opening. Int. J. Rock Mech. Min. Sci. 2006, 43, 23–36. [Google Scholar] [CrossRef]
- Karrech, A. Non-equilibrium thermodynamics for fully coupled thermal hydraulic mechanical chemical processes. J. Mech. Phys. Solids 2013, 61, 819–837. [Google Scholar] [CrossRef]
- Yasuhara, H.; Elsworth, D. A numerical model simulating reactive transport and evolution of fracture permeability. Int. J. Numer. Anal. Methods Geomech. 2006, 30, 1039–1062. [Google Scholar] [CrossRef]
- Poulet, T.; Karrech, A.; Regenauer-Lieb, K.; Fisher, L.; Schaubs, P. Thermal–hydraulic–mechanical–chemical coupling with damage mechanics using ESCRIPT RT and ABAQUS. Tectonophysics 2012, 526–529, 124–132. [Google Scholar] [CrossRef]
- Bond, A.E.; Bruský, I.; Cao, T.; Chittenden, N.; Fedors, R.; Feng, X.T.; Gwo, J.P.; Kolditz, O.; Lang, P.; McDermott, C.; et al. A synthesis of approaches for modelling coupled thermal–hydraulic–mechanical–chemical processes in a single novaculite fracture experiment. Environ. Earth. Sci. 2017, 76, 12. [Google Scholar] [CrossRef]
- Heap, M.J.; Xu, T.; Chen, C.F. The influence of porosity and vesicle size on the brittle strength of volcanic rocks and magma. Bull. Volcanol. 2014, 76, 856. [Google Scholar] [CrossRef]
- Tang, C.A.; Liu, H.Y. Influence of heterogeneity on crack propagation modes in brittle rock. Chin. J. Geophys. 2000, 43, 117–125. [Google Scholar] [CrossRef]
- Zhang, K.; Yao, B.H.; Wu, S.G.; Zhang, H.T. Study on the characteristics of variable mass seepage and water inrush mechanism of collapse column. J. Min. Saf. Eng. 2013, 30, 892–896. (In Chinese) [Google Scholar]
- Zhu, W.C.; Tang, C.A. Micromechanical model for simulating the fracture process of rock. Rock Mech. Rock Eng. 2004, 37, 25–56. [Google Scholar] [CrossRef]
- Wang, Q.Y.; Zhu, W.C.; Xu, T.; Niu, L.L.; Wei, J. Numerical simulation of rock creep behavior with a damage-based constitutive law. Int. J. Geomech. 2016, 17, 04016044. [Google Scholar] [CrossRef]
- Zheng, C.; Kizil, M.S.; Aminossadati, S.M.; Chen, Z. Effects of geomechanical properties of interburden on the damage-based permeability variation in the underlying coal seam. J. Nat. Gas Sci. Eng. 2018, 55, 42–51. [Google Scholar] [CrossRef]
- Papamichos, E.; Vardoulakis, I. Sand erosion with a porosity diffusion law. Comput. Geotech. 2005, 32, 47–58. [Google Scholar] [CrossRef]
- Bear, J.; Bachmat, Y. Introduction to modeling of transport phenomena in porous media. Theory Appl. Transp. Porous Med. 1990, 4, 481–516. [Google Scholar]
- Nasir, O. Coupled Thermo-Hydro-Mechanical-Chemical (THMC) Responses of Ontario’s Host Sedimentary Rocks for Nuclear Waste Repositories to Past and Future Glaciations and Deglaciations. Ph.D. Thesis, University of Ottawa, Ottawa, ON, USA, 2013. [Google Scholar]
- Ding, W.X.; Chen, J.P.; Xu, T.; Chen, H.J.; Wang, H.Y. Mechanical and chemical characteristics of limestone during chemical erosion. Rock Soil Mech. 2015, 36, 1825–1830. (In Chinese) [Google Scholar]
- Tan, F.; Zhang, Y.F.; Wang, Z.Y.; Dong, Z.X.; Huang, Z.L.; Wang, Q.P.; Gao, J.W. Simulation Experiment for the Burial Dissolution of Different Petrofabric Carbonate Rocks of Ordovician in the Ordos Basin. Acta Sedimentol. Sin. 2017, 35, 413–424. (In Chinese) [Google Scholar]
- Yang, J.; Huang, S.; Zhang, W.; Huang, Y.; Liu, G.; Xiao, L. Experimental simulation of dissolution for carbonate with different composition under the conditions from epigenesis to burial diagenesis environment. Acta Sedimentol. Sin. 1995, 13, 49–54. (In Chinese) [Google Scholar]
- Wang, J.X. Study on Elastoplastic Damage and MHC Coupling Model of Rock and Numerical Algorithm. Ph.D. Thesis, Dalian Maritime University, Dalian, Liaoning, China, 2014. (In Chinese). [Google Scholar]
- Guo, W.J.; Liu, W.T.; Zhang, W.Q. Special Mining Method of Coal Mine, 1st ed.; China Coal Industry Publishing House: Beijing, China, 2008; pp. 150–151. (In Chinese) [Google Scholar]
- Li, W.; Liu, Y.; Qiao, W.; Zhao, C.; Yang, D.; Guo, Q. An improved vulnerability assessment model for floor water bursting from a Confined Aquifer Based on the Water Inrush Coefficient Method. Mine Water Environ. 2017, 37, 11–19. [Google Scholar] [CrossRef]
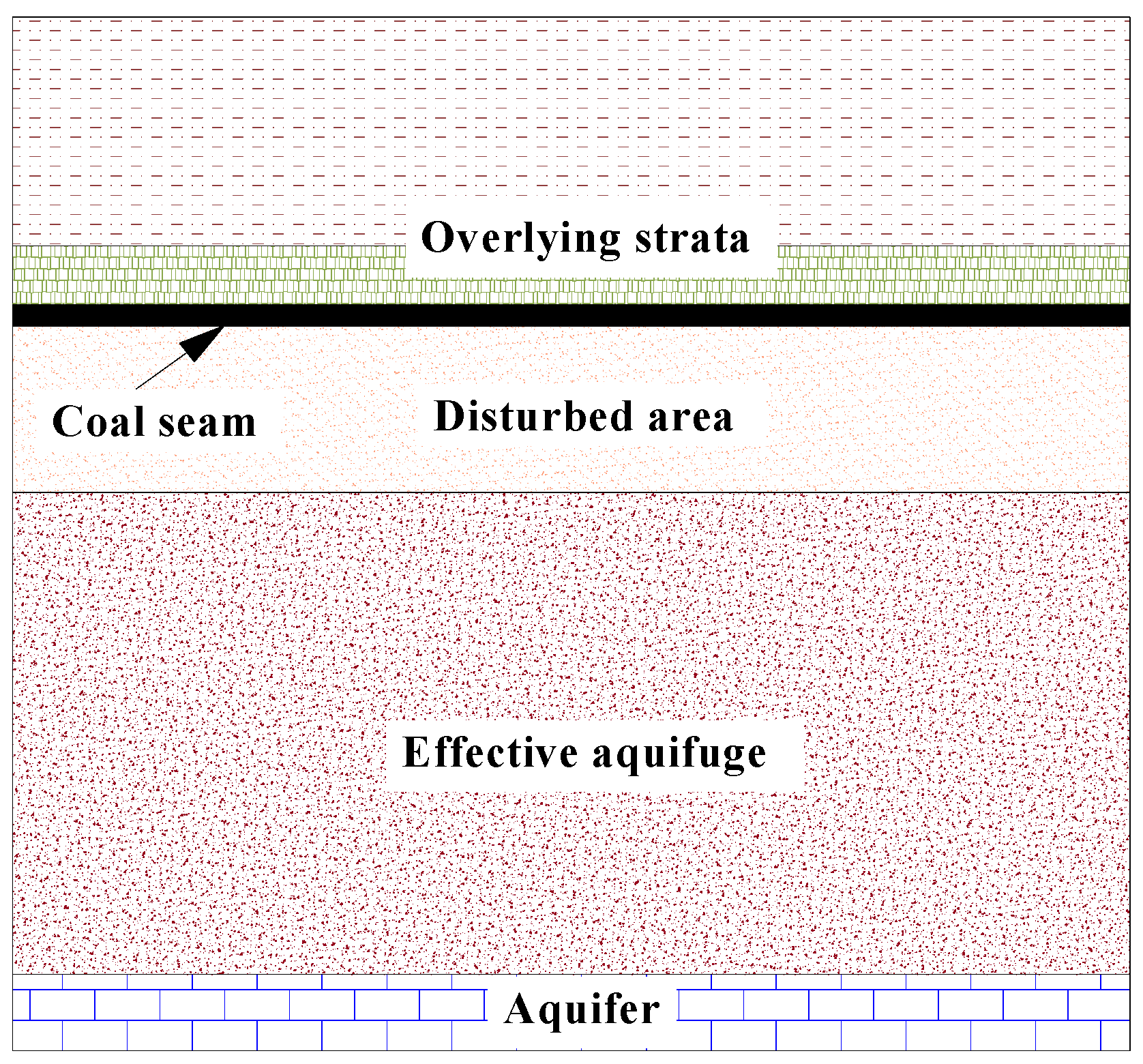
| Parameter Name | Value |
|---|---|
| Confining pressure | 5 MPa |
| Axial pressure | 20 MPa |
| Initial average porosity | 0.11 |
| Solid density | 2660 m3/kg |
| Bulk modulus | 9.896 × 109 N/m2 |
| Shear modulus | 8.051 × 109 N/m2 |
| Fluid density | 1000 m3/kg |
| Dynamic viscosity | 1 × 10−3 Pa·s |
| Thermal conductivity of fluid | 0.6 W/(m·K) |
| Heat capacity of fluid | 4.2 × 103 J/(kg·K) |
| Thermal conductivity of solid matrix | 2.8 W/(m·K) |
| Heat capacity of solid matrix | 9.21 × 102 J/(kg·K) |
| Permeability parameter | 1.1 × 10−10 m2 |
| Porosity diffusivity coefficient | 1 × 10−11 m2/s |
| Scale parameter | 0.12 |
| The Shape Parameter | The pH Value | 0 s | 1 × 106 s | 2 × 106 s | 3 × 106 s | 4 × 106 s | 5 × 106 s |
|---|---|---|---|---|---|---|---|
| 2 | 6.6 | 0.000209 | 0.000297 | 0.000483 | 0.000903 | 0.001762 | 0.003491 |
| 6 | 0.000209 | 0.000297 | 0.000483 | 0.000886 | 0.0017 | 0.0034 | |
| 5 | 0.000209 | 0.000297 | 0.000483 | 0.000886 | 0.0017 | 0.003409 | |
| 4 | 0.000209 | 0.000297 | 0.000483 | 0.000886 | 0.0017 | 0.003395 | |
| 5 | 6.6 | 4.12 × 10−5 | 6.14 × 10−5 | 0.000107 | 0.000226 | 0.000555 | 0.001347 |
| 6 | 4.12 × 10−5 | 6.14 × 10−5 | 0.000112 | 0.000241 | 0.000538 | 0.001326 | |
| 5 | 4.12 × 10−5 | 6.14 × 10−5 | 0.000112 | 0.000241 | 0.000613 | 0.001689 | |
| 4 | 4.12 × 10−5 | 6.14 × 10−5 | 0.000112 | 0.000241 | 0.000613 | 0.001788 | |
| 8 | 6.6 | 1.77 × 10−5 | 2.51 × 10−5 | 4.31 × 10−5 | 8.6e × 10−5 | 0.000194 | 0.000437 |
| 6 | 1.77 × 10−5 | 2.51 × 10−5 | 4.31 × 10−5 | 8.6e × 10−5 | 0.000194 | 0.000438 | |
| 5 | 1.77 × 10−5 | 2.51 × 10−5 | 4.31 × 10−5 | 8.61 × 10−5 | 0.000195 | 0.000439 | |
| 4 | 1.77 × 10−5 | 2.51 × 10−5 | 4.22 × 10−5 | 8.19 × 10−5 | 0.000182 | 0.000405 |
| Rock and Coal | Elastic Modulus (MPa) | Poisson Ratio | Density (m3/kg) |
|---|---|---|---|
| Overlying strata | 9.988 | 0.27 | 2657 |
| Coal seam | 3.609 | 0.39 | 1490 |
| Disturbed area | 8.055 | 0.28 | 2635 |
| Aquifuge | 13.434 | 0.20 | 2687 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.; Zhao, J.; Nie, R.; Zeng, Y.; Xu, B.; Sun, X. A Full Coupled Thermal–Hydraulic–Chemical Model for Heterogeneity Rock Damage and Its Application in Predicting Water Inrush. Appl. Sci. 2019, 9, 2195. https://doi.org/10.3390/app9112195
Liu W, Zhao J, Nie R, Zeng Y, Xu B, Sun X. A Full Coupled Thermal–Hydraulic–Chemical Model for Heterogeneity Rock Damage and Its Application in Predicting Water Inrush. Applied Sciences. 2019; 9(11):2195. https://doi.org/10.3390/app9112195
Chicago/Turabian StyleLiu, Weitao, Jiyuan Zhao, Ruiai Nie, Yifan Zeng, Baichao Xu, and Xi Sun. 2019. "A Full Coupled Thermal–Hydraulic–Chemical Model for Heterogeneity Rock Damage and Its Application in Predicting Water Inrush" Applied Sciences 9, no. 11: 2195. https://doi.org/10.3390/app9112195
APA StyleLiu, W., Zhao, J., Nie, R., Zeng, Y., Xu, B., & Sun, X. (2019). A Full Coupled Thermal–Hydraulic–Chemical Model for Heterogeneity Rock Damage and Its Application in Predicting Water Inrush. Applied Sciences, 9(11), 2195. https://doi.org/10.3390/app9112195





