Abstract
Strong designated verifier signature can provide an efficient way to protect the identity privacy of the signer and the integrity of the data transmitted over the public channel. These characteristics make it very useful in outsourcing computing, electronic voting, electronic bidding, electronic auction and other fields. However, most strong designated verifier signature schemes are unable to identify the real signature generator when the signer and the designated verifier dispute a signature. In addition, the existing strong designated verifier signature schemes in the standard model rarely satisfy strong unforgeability, and thus cannot prevent the attacker from forging a valid signature on any previously signed message. Therefore, designing a strong designated verifier signature scheme without random oracles that satisfies strong unforgeability and undeniability is very attractive in both practice and theory. Motivated by these concerns, we design the first undeniable strong designated verifier signature scheme without random oracles, in which the arbiter can independently perform the judgment procedure to prove whether a controversial signature is generated by the signer or the designated verifier. Under standard assumptions, the scheme is proved to be strongly unforgeable in standard model. Furthermore, it not only achieves non-transferability and privacy of the signer’s identity but also satisfies the undeniable property of traditional digital signature schemes. Performance analysis results show that the length of the signer’s private key, the designated verifier’s private key and signature length are 40 bits, 40 bits and 384 bits, respectively. Compared with he related schemes, the proposed scheme has higher performance in signature length, private key size and computational overhead. Finally, we show how to apply it to implement outsourcing computation in cloud computing.
1. Introduction
Digital signature is a very important information security technology, which can realize data integrity, non-repudiation, identity authentication and other functions. It plays an important role in network security communication [1], e-commerce [2], e-government [3] and other systems [4,5,6]. To deal with specific application scenarios, some digital signature schemes with special properties have been proposed. Among them, designated verifier signature (DVS) [7] is a significant variant of digital signature. In DVS, the signer is allowed to designate a verifier to confirm the authenticity of a signature, but the designated verifier is unable to convince anyone that the signature was generated by the real signer. The reason is that the simulated signature produced by the designated verifier is computationally indistinguishable from the original signature created by the signer for the same message. This feature of DVS is called non-transferability, which is very useful in the fields of electronic voting, electronic tendering and software copyright [8,9]. To avoid the signer’s identity information being leaked, Jakobsson et al. [7] introduced the concept of strong designated verifier signature (SDVS). In SDVS, the validation of a signature must require the designated verifier’s private key, and any third party cannot determine the real creator of the signature. That is to say, only the designated verifier knows the real identity of the signer. Thus, SDVS enhances the privacy of the signer’s identity (PSI) and can be applied to some new fields [10]. For example, in cognitive computation [11], an intelligent robot authenticates the identity of its owner, but it must protect the owner’s identity information.
However, in a SDVS scheme, any third party does not know who generated the signature when the signer and the designated verifier dispute a signature. In this scenario, the undeniability property is very essential for SDVS. There are a few SDVS schemes with undeniability, and they were proved to be secure in the random oracle model [12,13,14]. Unfortunately, Canetti et al. [15] showed that the cryptographic scheme in the random oracle model may be insecure when the random oracle is instantiated by a concrete hash function. Therefore, it is of practical significance to study the SDVS scheme without random oracles.
Most existing SDVS schemes in the standard model only possess existential unforgeability [16,17,18]. Namely, an adversary can easily obtain a new legal signature of the same message by modifying an existing message-signature pair. Strong unforgeability can prevent the above-mentioned modification and protect the integrity of a signature [19]. A SDVS scheme is said to be strongly unforgeable if it satisfies existential unforgeability and the adversary cannot produce a legal signature of a message that has previously been signed. Although strong unforgeability has already been considered in several SDVS schemes [20], none of them has the undeniable property in the standard model.
1.1. Our Contribution
Motivated by the above concerns, we construct a new SDVS scheme with undeniability and strong unforgeability, which is named the SDVS-USU scheme in this paper. The main contributions of this paper are as follows.
- The proposed scheme is the first strongly unforgeable SDVS scheme with the undeniability property in the standard model, while the existing SDVS schemes are secure in the random oracle model.
- In the SDVS-USU scheme, the signer assigns a verifier to validate the signature, and designates an arbiter to determine the actual generator of the signature. For a controversial signature, the arbiter can independently identify the real signature generator without the help of the signer or the designated verifier.
- The SDVS-USU scheme is proved to be strongly unforgeable against adaptive chosen message attacks under the bilinear Diffie–Hellman (BDH) assumption, while the privacy of the signer’s identity relies on the decisional bilinear Diffie–Hellman (DBDH) assumption. At the same time, it has the property of non-transferability.
- Compared with the existing SDVS schemes without random oracles, the SDVS-USU scheme has better performance in terms of signature length, private key size and computational cost.
1.2. Paper Organization
The rest of this paper is organized as follows. Section 2 describes the work related to SDVS. Section 3 introduces some preliminaries, such as bilinear parings, complexity assumptions and the security definition of SDVS. Section 4 presents the SDVS-USU scheme. Section 5 demonstrates the security of the SDVS scheme. Section 6 analyzes the performance of the SDVS-USU scheme. Section 7 illustrates the application of the SDVS-USU scheme in outsourcing computation. Section 8 is the conclusions.
2. Related Work
The concept of SDVS was first introduced by Jakobsson et al. [7], and formalized by Saeednia et al. [21]. Since then, some efficient SDVS schemes were proposed [22,23,24,25,26,27], but the security of those schemes is based on the ideal random oracle. To deal with this problem, Hung et al. [17] designed a SDVS scheme in the standard model. However, its security is highly dependent on the security of the pseudo-random function. If the pseudo-random function leaks the associated index, the attacker can easily generate legitimate signatures for arbitrary messages on behalf of the signer or the designated verifier. Based on the q-Strong Diffie–Hellman assumption, Zhang et al. [16] constructed another SDVS scheme without random oracles. However, their SDVS scheme could not protect the privacy of the signer’s identity and did not give formal security proof. Besides, Asaar et al. [18] presented a secure SDVS scheme based on Waters’ scheme [28], but their scheme is malleable. Tian et al. [20] showed that the above three SDVS schemes [16,17,18]. do not satisfy strong unforgeability. Later, Tian et al. [20] used the OR proof [29] and Kang et al.’s scheme [30] to design a basic signature scheme with existential unforgeability. Then, Tian et al. [20] constructed a SDVS scheme using their basic scheme and the Cramer–Shoup scheme [31]. To shorten the signature length, Tian et al. [20] proposed another SDVS scheme based on their basic signature scheme and Tian et al.’s encryption scheme [32]. Although Tian et al.’s two SDVS schemes [20] satisfy strong unforgeability, neither provides undeniability. To overcome this shortcoming, Yang et al. [12] designed an undeniable SDVS scheme using chameleon hash function [33]. However, the signer needs to store all previous signature data to identify the real generator in a signature, and the judgment process needs the help of the signer. To improve the fairness of the judgment, Hu et al. [14] designed two undeniable SDVS schemes in which the arbiter can independently identify the real signer in a disputed signature. However, Yang et al.’s scheme [12] and Hu et al.’s schemes [14] were provably secure in the random oracle model. Unfortunately, there is no strongly unforgeable SDVS scheme with the undeniable property in the standard model. Thus, in this paper, we put forward such construction for SDVS.
3. Preliminaries
3.1. Bilinear Paring
Suppose p is a prime, and are two cyclic groups of order p, and g is any generator of . A map is called a bilinear pair if it satisfies the following conditions [18]:
- Bilinearity: For any , .
- Non-degeneracy:.
- Computability: For any , can be calculated efficiently.
3.2. Complexity Assumptions
Given , where are unknown, the BDH problem is to calculate .
Definition 1.
The BDH assumption is that the probability of any probabilistic polynomial-time (PPT) algorithm solving the BDH problem is negligible.
Given and , where unknown , the DBDH problem is to determine whether holds.
Definition 2.
The DBDH assumption is that there is no PPT algorithm to solve the DBDH problem with a probability of more than [18].
3.3. Strong Designated Verifier Signature
An SDVS scheme with undeniable property is defined as follows:
- : On the input of a security parameter , this algorithm produces the public parameters .
- : On the input of , this algorithm produces a public/private key pair for a signer S, for a designated verifier V and for an arbiter A.
- : On the input of public keys of S, V and A, the signer S’s private key and a message m, this algorithm produces a signature on m.
- : Given public keys of S, V and A, this algorithm returns 1 if the designated verifier V’s private key can be used to verify that is a legal signature for a message m; otherwise, it returns 0.
- : On the input of public keys of S, V and A, the designated verifier V’s private key and a message m, this algorithm produces a simulated signature that is indistinguishable from .
The correctness of SDVS requires that both the original signature and the simulated signature are valid. That is, for any key pairs , and , any message m, any signature =, and any simulated signature =, , the following two equations must hold:
A secure SDVS scheme with undeniable property should achieve the security requirements of strong unforgeability, non-transferability, privacy of the signer’s identity (PSI) and undeniability.
The unforgeability requires that only the signer and the designated verifier can produce a valid signature. Formally, the strong unforgeability of an SDVS scheme is defined by the following game between a challenger and an adversary .
- Setup: executes the algorithm to output the public parameters , and runs the algorithm to generate the signer’s key pair , the designated verifier’s key pair and the arbiter’s key pair . Then, sends to .
- Signing queries: When initiates a signature query for message , runs the , algorithm to obtain a signature on and returns to .
- Simulating queries: When asks for a simulated signature on a message , runs the , , algorithm to obtain a signature on and returns to .
- Verifying queries: When submits a signature on a message , sends the signature verification result output by the algorithm , to .
- Output: Finally, outputs a message/signature pair . wins the game if
- 1.
- =1.
- 2.
- has not been produced by the Simulating query.
- 3.
- is not one of all tuples during the Signing queries.
Definition 3.
If the probability of any PPT attacker winning in the above game is negligible, then an SDVS scheme is said to be strongly unforgeable against adaptive chosen message attacks.
The non-transferability requires that no third party can tell the signature on a message was created by the signer or was simulated by the designated verifier.
Definition 4.
An SDVS scheme is said to be non-transferable if it is not feasible for any PPT algorithm to differentiate that a given signature is produced by the signer or the designated verifier without knowing the signer’s private key , the designated verifier’s private key or the arbiter’s private key . That is, the probability ε of distinguishing between simulated signatures and real signatures is negligible.
In other words, the signature generated by the signer is computationally indistinguishable from the signature simulated by the designated verifier, i.e.,
PSI requires that no one other than the designated verifier knows the identity of the signer, but any third party is unable to identify the designated verifier and the signer. That is, if there are two signers and , it is infeasible for any PPT adversary to differentiate whether the signature of a message is signed by or without knowing the designated verifier’s private key. PSI is formally defined by the following security game between a distinguisher and a challenger .
- Setup: runs the algorithm to produce the public parameters , and runs the algorithm to generate the signer ’s key pair , , the signer ’s key pair , the designated verifier V’s key pair and the arbiter A’s key pair . Then, sends , to .
- Query phase 1: adaptively initiates a series of inquiries to as follows.
- -
- Signing queries: When issues a signature query on a message and an index , executes the , algorithm to obtain a signature on and returns to .
- -
- Simulating queries: When issues a simulated signature query on a message and an index , runs the , , algorithm to obtain a signature on and returns to .
- -
- Verifying queries: After receiving a message , a signature and an index , responds to with the output of the algorithm , .
- Challenge: After receiving the challenge message submitted by , obtains a random value by flipping a coin. Then, returns the signature generated by the algorithm , to .
- Query phase 2: continues to make queries as in Query phase 1 except that is unable to submit a signature verification query on for any .
- Output: returns a value . If , wins the game.
Definition 5.
An SDVS scheme is secure about PSI if there is no PPT distinguisher wins the game with a probability of more than .
For a controversial signature, the undeniability requires that the arbiter can correctly identify the real identity of the generator in the signature.
Definition 6.
An SDVS scheme is said to be undeniable if there exists a PPT arbiter, with inputting the signer’s public key , the designated verifier’s public key , the arbiter’s private key and a disputed signature on a message , can prove whether the signer S or the designated verifier V generated with an overwhelming probability, namely,
Here, the output S indicates is created by the signer, while the output V indicates is generated by the designated verifier.
4. The SDVS-USU Scheme
In this section, we design a strongly unforgeable SDVS scheme with undeniable property on the basis of a variant of Waters’ scheme [28]. Although a few SDVS schemes [12,13,14] satisfy undeniability, their security depends on ideal random oracles, which might be insecure in reality. Most of the SDVS schemes [17,18] without random oracles are malleable, so they cannot achieve strong unforgeability. To overcome these problems, the SDVS-USU scheme uses two collision-resistant hash functions to protect the integrity of the signature. This method can not only generate non-malleable signatures, but also achieve strong unforgeability and undeniability. Since we design the SDVS-USU scheme using a direct construction rather than a general conversion method, it basically maintains the performance of the Waters’ scheme [28] in terms of signature size and computational overhead. Additionally, it should be emphasized that the employed collision-resistant hash functions are not considered as random oracles in our security proof.
There are three participants in the SDVS-USU scheme: the signer S, the designated verifier V and the arbiter A. In the following, we assume that all signed messages are bit strings of length n. To achieve this assumption, messages of arbitrary length can be converted into messages of fixed length n by using a secure hash function . The SDVS-USU scheme is described as follows.
- : Let and be two multiplicative cyclic groups of prime order p. g is any generator of , is a bilinear pair, and is a vector of length n, where . Let and be two collision-resistant hash functions. The public parameters are .
- : The signer S picks two random elements as the private key , , and computes the corresponding public key . Similarly, and are the designated verifier V’s private key and public key respectively. The arbiter A’s public/private key pair is , where .
- : To generate the signature of a n-bit message , the signer proceeds as follows.
- 1.
- Select randomly and calculate .
- 2.
- Compute , and .
- 3.
- Compute .
- 4.
- Output a signature on m.
- : After receiving a signature on a n-bit message from the signer, the designated verifier calculates and uses its private key to verify whetherIf it holds, the designated verifier believes that is legal and outputs 1; else, the designated verifier considers to be illegal and outputs 0.
- : To produce a simulated signature on a message , the designated verifier performs the following:
- 1.
- Select randomly and compute .
- 2.
- Compute , and .
- 3.
- Compute .
- 4.
- Output a simulated signature on m.
Correctness: If is correctly produced by the algorithm, then we have
The above equation indicates that the signature of message m generated by the signer using the private key can be verified by the signature verification algorithm . That is, is a legal signature.
If is correctly produced by the algorithm, then we have
It shows that the simulated signature produced by the designated verifier using its private key can also be verified by the signature verification algorithm . Therefore, the SDVS-USU scheme satisfies correctness.
Compared with the previous similar schemes, the novelty of the SDVS-USU scheme is as follows:
- In the algorithm, is embedded in a part of a signature . Since the hash function is collision-resistant, any modification of m, and T will make fail the signature verification equation. In other words, an attacker cannot generate a legitimate signature for a previously signed message if the attacker does not know the private key of the signer or the designated verifier. Hence, the SDVS-USU scheme possesses strong unforgeability.
- The value contains the arbiter’s public key , the signer’s private key and the hash value , which shows that only the arbiter can use its own private key and T to identify the real generator in a signature. In addition, and are two collision-resistant hash functions, and T is a part of and the signature . Therefore, any modification of the value T will result in the failure of the validation of the signature . That is, the SDVS-USU scheme provides undeniability.
- The Waters’ scheme [28] is malleable and satisfies existential unforgeability in the standard model. The proposed SDVS scheme is based on Waters’ scheme [28], but the SDVS-USU scheme is no-malleable and strongly unforgeable in the standard model. Therefore, the SDVS-USU scheme is different from Waters’ scheme [28] in terms of design and security proof.
5. Security Analysis
In this section, we demonstrate that the SDVS-USU scheme holds strong unforgeability, non-transferability, PSI and undeniability.
Theorem 1.
If the BDH assumption holds, then the SDVS-USU scheme is strongly unforgeable against adaptive chosen message attacks in the standard model.
Proof of Theorem 1.
Suppose there exists a polynomial-time adversary who breaks the strong unforgeability of the SDVS-USU scheme with non-negligible probability, where can make at most signing queries, simulating queries and verifying queries. Then, we construct another algorithm who can solve the BDH problem by using the ’s forgery. Given a random BDH problem instance , the goal of is to calculate . will act as ’s challenger and respond to ’s queries as follows.
- Setup: simulates the algorithm in the following way.
- 1.
- Select randomly, and set to satisfy .
- 2.
- Select two random values , and set the signer’s public key , the designated verifier’s public key and the arbiter’s public key . Note that a, b and c are unknown to .
- 3.
- Select and , randomly.
- 4.
- Select a random integer , assign , and for , and set a vector .
- 5.
- Pick two collision-resistant hash functions and .
- 6.
- Send the public parameters , and to .
For a n-bit message , we define two functionsHence, we obtain the following equation - Signing queries: When issues a signature query on a message , computes the value of . Note that if , there exists an unique value such that . On the other hand, implies . If , aborts. If , first searches in Table which is initially empty. If there is a tuple in , extracts from ; otherwise, randomly selects and adds in . Then, picks a random element , and computes , , andFinally, returns a signature on to . Correctness: We show that is a valid signature on as follows:
- Simulating queries: responds to this kind of query in the same way as in Signing queries.
- Verifying queries: requests a verification query on a signature on a message . If , aborts. Otherwise, finds in Table and extracts from . Then, computes , and , and checks whetherIf this equation holds, returns 1 to ; otherwise, returns 0 to .
- Output: outputs a forged signature on a message . If , aborts. Otherwise, calculates and , and outputs as follows:
Here, we discuss the probability of successfully solving the BDH problem instance. If does not abort in the above simulation, then the following conditions must hold:
- : during the Signing, Simulating and Verifying queries.
- : in the forgery phase.Hence, the probability that completes the whole simulation is . According to Waters’ proof [21], we have
Therefore, if breaks the strong unforgeability of the SDVS-USU scheme with probability , then can solve the BDH problem with probability at least . □
Theorem 2.
The SDVS-USU scheme is non-transferable.
Proof of Theorem 2.
The form of the original signature for a message m is
and the form of the simulated signature on m is
The randomness of is determined by the random value , and the randomness of depends on the random value . Since r and s are randomly selected from , the distribution of the real signature and the simulated signature is computationally indistinguishable. Namely, it is infeasible to distinguish and without knowing the private key of the signer, the designated verifier or the arbiter. Hence, the SDVS-USU scheme satisfies the non-transferable property. □
Theorem 3.
Our SDVS scheme is secure against the privacy of the signer’s identity under the DBDH assumption.
Proof of Theorem 3.
Suppose there exists a PPT distinguisher who breaks the privacy of the signer’s identity of the SDVS-USU scheme. Then, we can construct an algorithm to solve the DBDH problem. Given a random instance of the DBDH problem, where unknown and , the ’s goal is to determine if Z is equal to .
- Setup: simulates the algorithm by performing the following steps:
- 1.
- Choose random integers , , and set , and a vector , where for .
- 2.
- Select four random values , and set the signer ’s public key , the signer ’s public key , the designated verifier’s public key and the arbiter’s public key . Note that a, b and c are unknown to .
- 3.
- Set as the common secret key between and V, and as the common secret key between and V.
- 4.
- Pick two collision-resistant hash functions and .
- 5.
- Send the public parameters , and to .For a message , we also define a function , and thus we have .
- Query phase 1: answers ’s queries as follows.
- -
- Signing queries: When issues a signature query on a message and an index , does the following.
- 1.
- Select a random integer , and compute .
- 2.
- Pick a random element , and compute and , .
- 3.
- Compute .
- 4.
- Return a signature on to .
- -
- Simulating queries: responds to this query in the same way as in Signing queries.
- -
- Verifying queries: On receiving a signature of a message and a value , first calculates , and . Then, uses to verify whetherIf this equation holds, indicating is valid, sends 1 to ; otherwise, returns 0 to .Correctness: We show that the above signature produced by the Signing query is correct since
- Challenge: When submits a challenge message , proceeds as follows:
- 1.
- Pick randomly, and compute .
- 2.
- Pick a random element , and compute and .
- 3.
- Flip a fair coin to obtain a random bit .
- 4.
- Compute .
- 5.
- Return a signature on to .
- Query phase 2: continues to issue various queries as in Query phase 1 except that cannot make a signature verification query on for any .
- Output: outputs a value . If , indicating , outputs 1; else, indicating Z is a random element in , outputs 0.
From the above simulation, we can see that does not exit in the whole simulation. Therefore, if breaks the PSI property of the SDVS-USU scheme with probability , then can solve the DBDH problem instance with probability of . □
Theorem 4.
The SDVS-USU scheme is undeniable.
Proof of Theorem 4.
On receiving a disputed signature on a message , the arbiter performs the following:
- 1.
- Obtain the signer’s public key and the designated verifier’s public key .
- 2.
- Compute and , where is the arbiter’s private key.
- 3.
- Check or . If , the arbiter confirms is created by the signer. If , the arbiter confirms is produced by the designated verifier.
In the proposed scheme, a signature from the signer has the form , while a signature from the designated verifier has the form . The arbiter can independently prove the real signer of any valid signature by verifying or with probability 1. Therefore, the SDVS-USU scheme holds the undeniability property. □
6. Comparison
The SDVS-USU scheme is compared with other SDVS schemes [14,18,20] in terms of performance and security properties. In Table 1 and Table 2, the Size, Sign and Verify columns represent the size of a signature, and the computational cost of signature generation and signature verification, respectively. The SU column shows whether the scheme is strongly unforgeable. The PSI column indicates whether the scheme has the PSI property. The Undeniability column shows whether the scheme is undeniable. The SM column indicates whether the scheme is secure in the standard model. Let p and q be two primes such that . Since the computational cost of some cryptographic operations such as modular multiplication, hash function or inverse is relatively small after being optimized by various technologies [34], we consider only the computationally expensive bilinear pairing and exponentiation operations in Table 1. We use the symbol P to denote one paring operation. , and denote one exponentiation operation in , and , respectively. , , and represent the length of an element in , , and , respectively.

Table 1.
Comparison of performance.

Table 2.
Comparison of security properties.
As can be seen in Table 1 and Table 2, two SDVS schemes of Hu et al. [14] outperform other schemes in both signature length and computational overhead, but their two schemes are not proven to be secure in the standard model. For the length of signature, the SDVS-USU scheme has one more element in than Asaar et al.’s scheme [18] but is superior to Tian et al.’s two schemes [20]. The SDVS-USU scheme is able to perform some pre-computation, such as in the signature generation phase and in the verification phase. Thus, the SDVS-USU scheme has comparable computation complexity with other schemes [18,20]. However, Asaar et al.’s scheme [18] does not have strong unforgeability and the PSI property. Moreover, none of Asaar et al.’s scheme [18] and Tian et al.’s [20] schemes holds the undeniable property. The SDVS-USU scheme has strong unforgeability and the PSI property in the standard model. Moreover, it achieves undeniability. Therefore, the SDVS-USU scheme has stronger security.
We carried out simulation experiments to evaluate the performance of the SDVS-USU scheme. The experimental environment was a laptop with Intel Core i7-6500 CPU@2.5 GHz and 8 GB memory. All simulation programs running on Microsoft Windows 10 operating system were based on PBC-0.47-VC library.
Figure 1 illustrates that the signature size of the SDVS-USU scheme, Asaar et al.’s scheme [18] and Tian et al.’s two schemes [20] is 384 bits, 256 bits, 532 bits and 404 bits, respectively. Hence, the SDVS-USU scheme has shorter signature length.
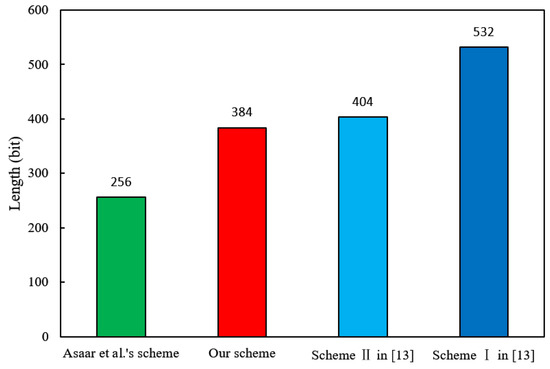
Figure 1.
Comparison of signature size.
As shown in Figure 2, the length of the signer’s private key in the SDVS-USU scheme is 40 bits, which is the same as that of Asaar et al.’s scheme [18] but larger than that of Tian et al.’s two schemes [20]. Moreover, the length of the designated verifier’s private key in the SDVS-USU scheme is 40 bits, which is larger than that of Asaar et al.’s scheme [18] but smaller than that of Tian et al.’s two schemes [20].

Figure 2.
Comparison of private key size.
In the signing phase, Asaar et al.’s scheme [18] requires two exponentiations and one pairing operation. The first SDVS scheme and the second SDVS scheme of Tian et al. [20] need six and five exponentiations, respectively. The SDVS-USU scheme requires four exponentiations and one pairing operation. Figure 3 shows that the computational performance of signature generation in the SDVS-USU scheme is comparable with other schemes [18,20].
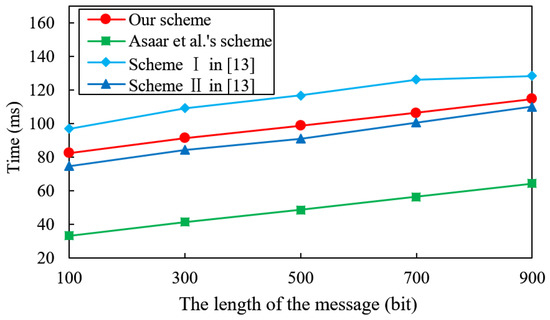
Figure 3.
Comparison of time cost of signing.
We consider the optimization of the verifying process by pre-computing so that the signature verification algorithm of each scheme achieves the highest performance. In the verification phase, Asaar et al.’s scheme [18] actually requires one exponentiation and one pairing operation. The first SDVS scheme of Tian et al. [20] needs three hash functions, three exponentiations, one inverse and two pairing operations. The second SDVS scheme of Tian et al. [20] requires three hash functions, two exponentiations, one inverse and two pairing operations. The SDVS-USU scheme requires two exponentiations and one pairing operation. Figure 4 demonstrates that the computational cost of signature verification of the SDVS-USU scheme is more than that of Asaar et al.’s scheme [18] but less than Tian et al.’s two schemes [20].
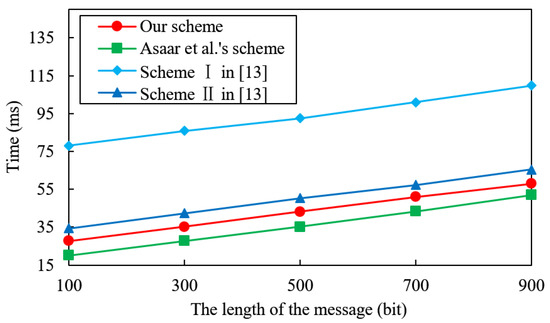
Figure 4.
Comparison of time cost of verifying.
7. Application in Outsourcing Computing in Cloud Computing
Cloud computing has strong computing power and storage capacity of big data. However, the cloud service provider (CSP) is not trusted by the user, and may steal the user’s private information or deceive the user. Cloud computing allows resource-constrained users to outsource expensive computations to the CSP. Hence, it is very important to ensure the integrity of the computing task and the authenticity of the remote user’s identity. Due to the limited computing ability of the user, the heavy computing task is outsourced to the CSP to complete. The CSP is able to authenticate a computing task outsourced by the user through a signature-based protocol. For the protection of private information, the user wants the designated CSP to be the only entity that can verify the legality of the signature on a computing task, and the CSP cannot reveal the signature to any third party at will. Since the ordinary digital signature has public verifiability and transferability, anyone can verify the validity of signatures by using the public key of the signer and obtain the real identity of the signer. Obviously, the ordinary digital signature scheme is not suitable for this scenario. The SDVS scheme is considered as one of the solutions to these problems, which can provide secret authentication service to the user in an outsourcing computation task. SDVS guarantees that a designated CSP can validate the user’s signature on a computing task. At the same time, it ensures that the designated CSP does not convince others that the user is involved in a computing task.
However, most of the SDVS schemes cannot identify the real signature generator when the user and the cloud service provider dispute a signature, which may cause huge economic losses to the user or the CSP. Hence, the SDVS scheme without undeniability cannot handle a controversial computing task. For example, if the user denies the submission of a computing task for some reasons, then the CSP is forced to stop it. At the same time, if the CSP forges a user’s signature on the computing task, then the user will take on the responsibility to pay for expensive computing cost. These economic losses are undesirable to the user or the CSP. The SDVS-USU scheme given in Section 3.2 is undeniable and strongly unforgeable, so it is more suitable for outsourcing computation in a cloud computing environment. The system model of outsourcing computation in cloud computing based on the SDVS-USU scheme is shown in Figure 5.
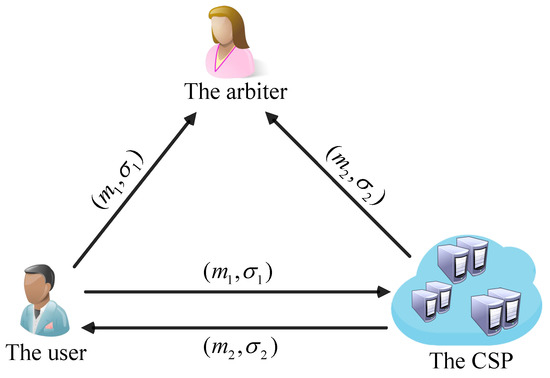
Figure 5.
The system model of outsourcing computation in cloud computing based on the SDVS-USU scheme.
There are three entities in the system: the user, the CSP and the arbiter. The process of outsourcing calculation is as follows.
- 1.
- A user with limited computing resources uses his private key and the SDVS-USU scheme to generate a signature for a computing task and sends to the CSP.
- 2.
- The CSP has powerful computing power. After verifying the validity of the signature on to confirm this submission, the CSP performs the computational task of . Then, the CSP uses its private key and the SDVS-USU scheme to generate the signature of the corresponding calculation result , and returns to the user.
- 3.
- If is the valid signature of , the user accepts the calculation result returned by the CSP; otherwise, the user refuses to accept and accuses the CSP of malicious behavior.
- 4.
- For a controversial computing task, the arbiter determines whether the user or the CSP is responsible for the economic loss of the computing task based on and .
The SDVS-USU scheme is easily implemented as a software in cloud computing environments. For example, the signature algorithm is installed on the user side, and the verification algorithm is installed on the CSP side. On the one hand, the user sends the computing task and the corresponding signature to the designated CSP. On the other hand, only the designated CSP can check the integrity of the computing task and the authenticity of the user’s identity by verifying the validity of the signature, and vice versa. From the performance analysis results in Section 5, the SDVS-USU scheme has better computational performance while achieving the undeniable property. The length of the signer’s private key, the designated verifier private key and signature are 40 bits, 40 bits and 384 bits, respectively. If the message length is 900 bits, the time cost for signing and verifying is approximately 0.12 s and 0.06 s, respectively. At present, an ordinary laptop configuration is at least Intel Core i3 CPU@2.1 GHz, 4 G memory and 256 GB hard disk storage space. The CSP has more computing power, thus the SDVS-USU scheme can be practically applied to cloud computing environments.
8. Conclusions
In this paper, we construct an undeniable SDVS scheme that satisfies strong unforgeability in the standard model. The performance analysis results show that the SDVS-USU scheme has better performance in terms of private key size, signature length and computational overhead. In the SDVS-USU scheme, strong unforgeability prevents hackers from using the existing message/signature pair to create a legal signature of the same message. Non-transferability ensures that hackers cannot know the identity of the real signer in a signature. PSI further protects the privacy of the signer’s identity. Undeniability ensures that the signer and the designated verifier cannot deny messages that they have previously sent. Therefore, our SDVS scheme can guarantee the integrity of outsourced computing tasks and authenticate the identity of users in cloud computing. In the future, we will design an instance scenario to illustrate the feasibility of implementing the SDVS-USU scheme in the real world.
Author Contributions
X.Y., and G.C. wrote the paper; T.L., and R.L. proved the security; and M.W. and C.W. designed the experiments.
Funding
This research was funded by the National Natural Science Foundation of China (No. 61662069), China Postdoctoral Science Foundation (No. 2017M610817), Science and Technology Project of Lanzhou City of China (No. 2013-4-22), and Foundation for Excellent Young Teachers by Northwest Normal University (No.NWNU-LKQN-14-7).
Acknowledgments
The authors would like to thank the anonymous reviewers.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jenefa, J.; Anita, E.M. Secure vehicular communication using ID based signature scheme. Wirel. Pers. Commun. 2018, 98, 1383–1411. [Google Scholar] [CrossRef]
- Mason, S. World electronic signature legislation. Digit. Evid. Electron. Signat. Law Rev. 2018, 15, 146–163. [Google Scholar] [CrossRef]
- Yang, X.; Gao, G.; Zhou, Q.; Li, Y.; Wang, C. E-government data security exchange scheme based on proxy re-signature. Comput. Eng. 2017, 43, 183–188. [Google Scholar]
- Baker, T.; Asim, M.; MacDermott, Á.; Iqbal, F.; Kamoun, F.; Shah, B.; Alfandi, O.; Hammoudeh, M. A secure fog-based platform for SCADA-based IoT critical infrastructure. Softw. Pract. Exp. 2019, 2688, 1–16. [Google Scholar]
- Tariq, N.; Asim, M.; Al-Obeidat, F.; Zubair Farooqi, M.; Baker, T.; Hammoudeh, M.; Ghafir, I. The security of big data in fog-enabled IoT applications including blockchain: A survey. Sensors 2019, 19, 1788. [Google Scholar] [CrossRef] [PubMed]
- Abbas, N.; Asim, M.; Tariq, N.; Baker, T.; Abbas, S. A mechanism for securing IoT-enabled applications at the fog layer. J. Sens. Actuator Netw. 2019, 8, 16. [Google Scholar] [CrossRef]
- Jakobsson, M.; Sako, K.; Impagliazzo, R. Designated verifier proofs and their applications. In Proceedings of the Eurocrypt’96, Saragossa, Spain, 12–16 May 1996; pp. 143–154. [Google Scholar]
- Shim, K.A. On delegatability of designated verifier signature schemes. Inf. Sci. 2014, 281, 365–372. [Google Scholar] [CrossRef]
- Noh, G.; Jeong, I.R. Strong designated verifier signature scheme from lattices in the standard model. Secur. Commun. Netw. 2016, 18, 6202–6214. [Google Scholar] [CrossRef]
- Ghafir, I.; Saleem, J.; Hammoudeh, M.; Faour, H.; Prenosil, V.; Jaf, S.; Jabbar, S.; Baker, T. Security threats to critical infrastructure: The human factor. J. Supercomput. 2018, 74, 4986–5002. [Google Scholar] [CrossRef]
- Tian, H.; Chen, X.; Zhang, F.; Wei, B.; Jiang, Z.; Liu, Y. A non-delegatable strong designated verifier signature in id-based setting for mobile environment. Math. Comput. Model. 2013, 58, 1289–1300. [Google Scholar] [CrossRef]
- Yang, B.; Yu, Y.; Sun, Y. A novel construction of SDVS with secure disavowability. Clust. Comput. 2013, 16, 807–815. [Google Scholar] [CrossRef]
- Hu, X.; Zhang, X.; Ma, C.; Xu, H.; Wang, J.; Tan, W. A designated verifier signature scheme with undeniable property in the random oracle. In Proceedings of the IEEE International Conference on Software Engineering and Service Science, Beijing, China, 26–28 August 2016; pp. 960–963. [Google Scholar]
- Hu, X.; Tan, W.; Xu, H.; Wang, J.; Ma, C. Strong designated verifier signature schemes with undeniable property and their applications. Secur. Commun. Netw. 2017, 2017, 7921782. [Google Scholar] [CrossRef]
- Canetti, R.; Goldreich, O.; Halevi, S. The random oracle methodology, revisited. J. ACM 2004, 51, 557–594. [Google Scholar] [CrossRef]
- Zhang, H.; Ji, C. An efficient designated verifier signature scheme without random oracles. In Proceedings of the IEEE The First International Symposium on Data, Privacy, and E-Commerce, Beijing, China, 26–28 August 2016; pp. 338–340. [Google Scholar]
- Huang, Q.; Yang, G.; Wong, D.; Susilo, W. Efficient strong designated verifier signature schemes without random oracles or delegatability. Int. J. Inf. Secur. 2011, 10, 373–385. [Google Scholar] [CrossRef]
- Asaar, M.; Salmasizadeh, M. A Pairing Based Strong Designated Verifier Signature Scheme without Random Oracles. Available online: https://eprint.iacr.org/2012/061.pdf (accessed on 5 May 2019).
- Pang, L.; Zhao, H.; Zhou, X.; Li, H. Strongly unforgeable and efficient proxy signature scheme with fast revocation secure in the standard model. Int. J. Distrib. Sens. Netw. 2016, 12, 1–12. [Google Scholar] [CrossRef]
- Tian, H.; Jiang, Z.; Liu, Y.; Wei, B. A systematic method to design strong designated verifier signature without random oracles. Clust. Comput. 2013, 16, 817–827. [Google Scholar] [CrossRef]
- Saeednia, S.; Kremer, S.; Markowitch, O. An efficient strong designated verifier signature scheme. In Proceedings of the 6th International Conference Information Security and Cryptology, Seoul, Korea, 27–28 November 2003; pp. 40–54. [Google Scholar]
- Kang, B.; Boyd, C.; Dawson, E. A novel identity-based strong designated verifier signature scheme. J. Syst. Softw. 2009, 82, 270–273. [Google Scholar] [CrossRef]
- Tian, H.; Chen, X.; Li, J. A short non-delegatable strong designated verifier signature. In Proceedings of the ACISP, Wollongong, NSW, Australia, 9–11 July 2012; pp. 261–279. [Google Scholar]
- Sharma, N.; Sahu, R.A.; Saraswat, V.; Sharma, B.K. Adaptively secure strong designated signature. In Proceedings of the Progress in Cryptology-IndoCrypt, India, Kolkata, India, 11–14 December 2016; pp. 43–60. [Google Scholar]
- Hu, X.; Xu, H.; Liu, Y.; Wang, J.; Tan, W.; Zhang, X. An efficient designated verifier signature scheme with pairing-free and low cost. Secur. Commun. Netw. 2016, 18, 5724–5732. [Google Scholar] [CrossRef]
- Khan, A.U.; Ratha, B.K. A secure strong designated verifier signature scheme. Int. J. Netw. Secur. 2017, 19, 599–604. [Google Scholar]
- Wei, J.; Yang, G.; Mu, Y. Designated verifier proxy re-signature for deniable and anonymous wireless communications. Wirel. Pers. Commun. 2017, 97, 3017–3030. [Google Scholar] [CrossRef]
- Waters, B. Efficient identity-based encryption without random oracles. In Proceedings of the Eurocrypt’05, Aarhus, Denmark, 22–26 May 2005; pp. 114–127. [Google Scholar]
- Cramer, R.; Damgård, I.; Schoenmakers, B. Proofs of partial knowledge and simplified design of witness hiding protocols. In Proceedings of the Annual International Cryptology Conference, Santa Barbara, CA, USA, 21–25 August 1994; pp. 174–187. [Google Scholar]
- Kang, L.; Tang, X.; Lu, X.; Fan, J. A Short Signature Scheme in the Standard Model. Available online: https://pdfs.semanticscholar.org/dd25/6b488873276c7ddd7986a8ef306b045cb8d1.pdf (accessed on 5 May 2019).
- Cramer, R.; Shoup, V. A practical public-key encryptosystem provable secure against adaptive chosen ciphertext attack. In Proceedings of the CRYPTO’98, Santa Barbara, CA, USA, 23–27 August 1998; pp. 13–25. [Google Scholar]
- Tian, H.; Sun, X.; Wang, M. A new public key encryption scheme. J. Comput. Sci. Technol. 2007, 22, 95–102. [Google Scholar] [CrossRef]
- Krawczyk, H.; Rabin, T. Chameleon hashing and signatures. In Proceedings of the Network and Distributed System Security Symposium, San Diego, CA, USA, 27–29 March 2000; pp. 143–154. [Google Scholar]
- Chang, C.; Yao, S.; Yu, D. Vectorized big integer operations for cryptosystems on the intel mic architecture. In Proceedings of the 2015 IEEE 22nd International Conference on High Performance Computing, Bengaluru, India, 16–19 December 2015; pp. 194–203. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).