Width Dependent Two-Photon Absorption in Monolayer Black Phosphorus Nanoribbons
Abstract
1. Introduction
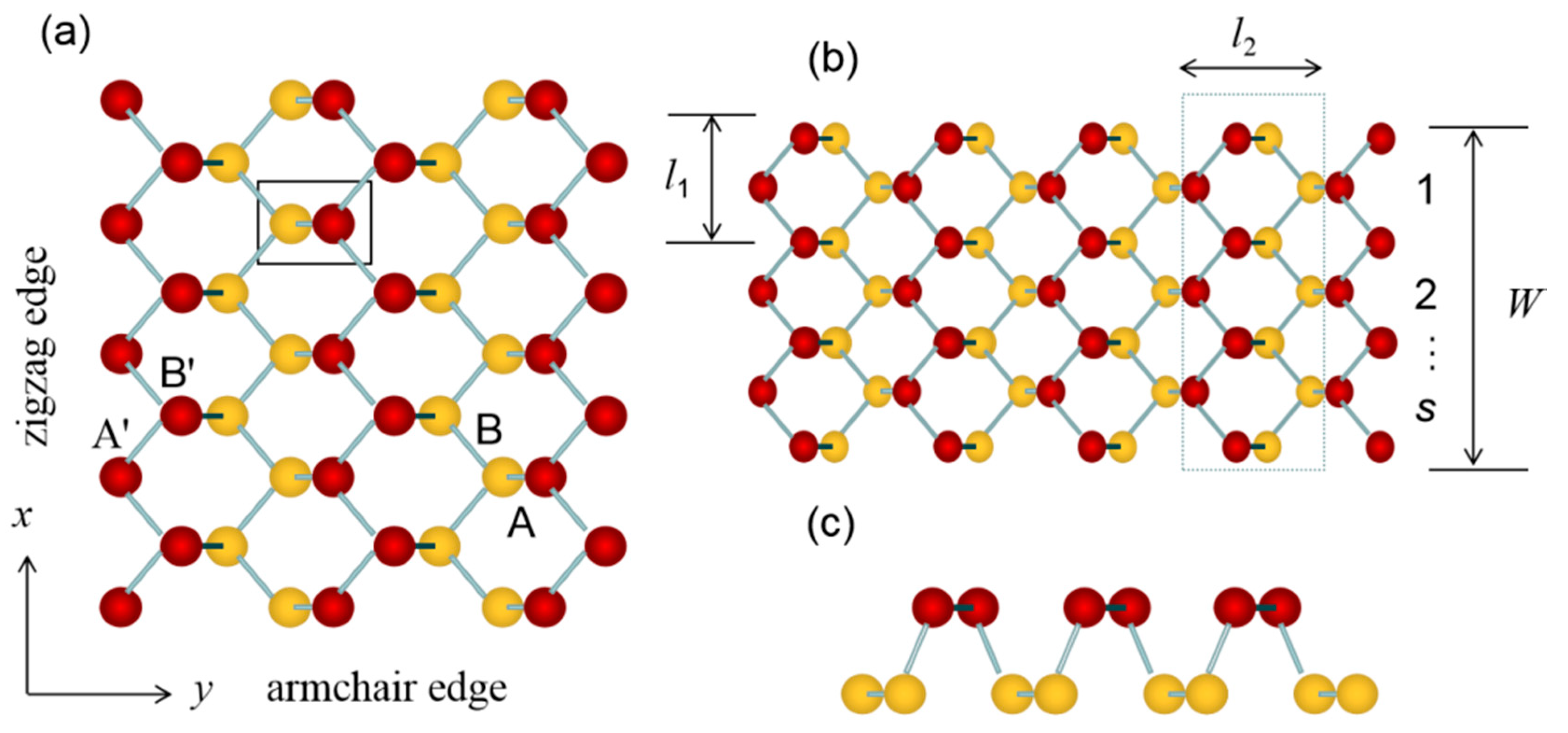
2. Theory and Calculations
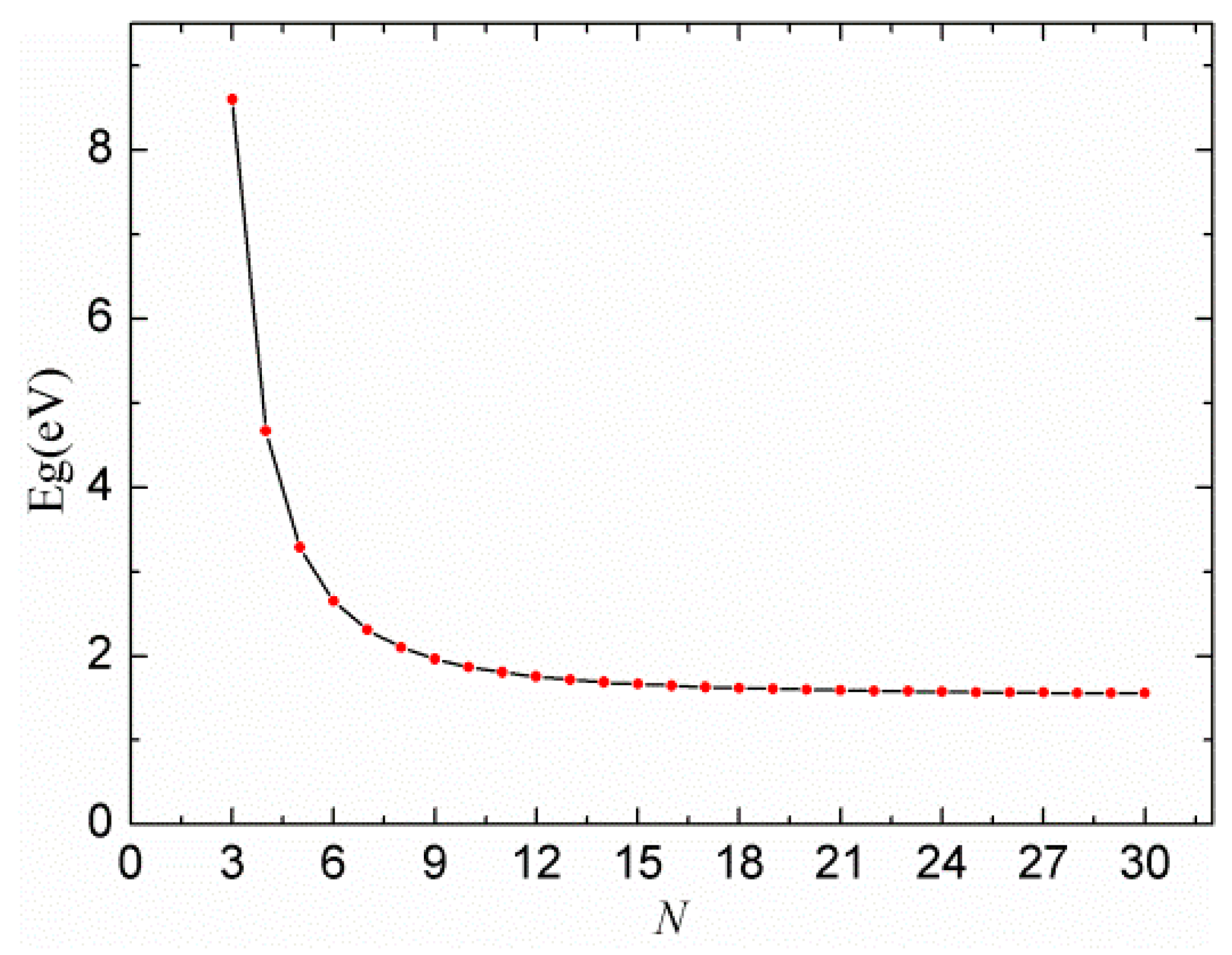
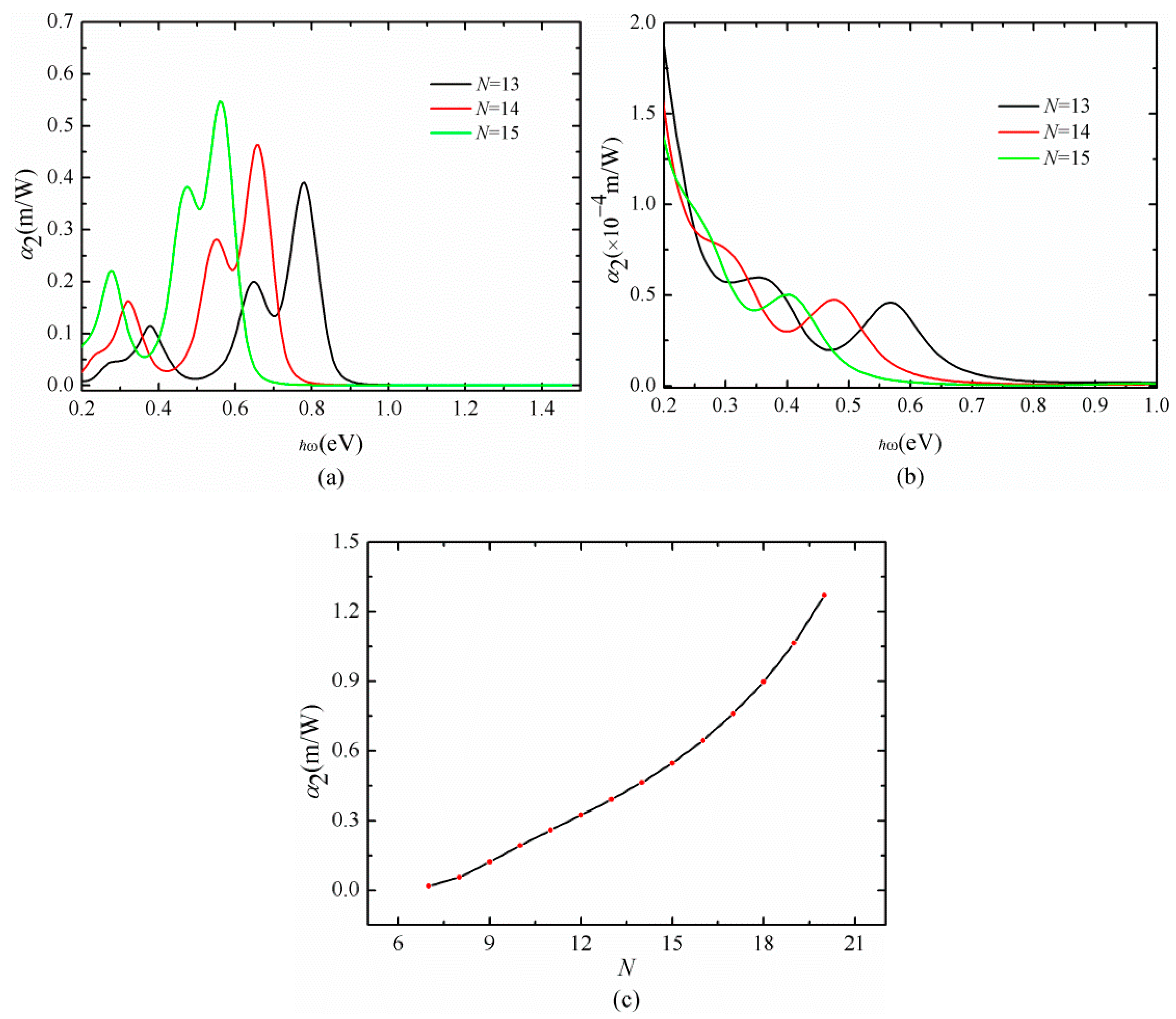
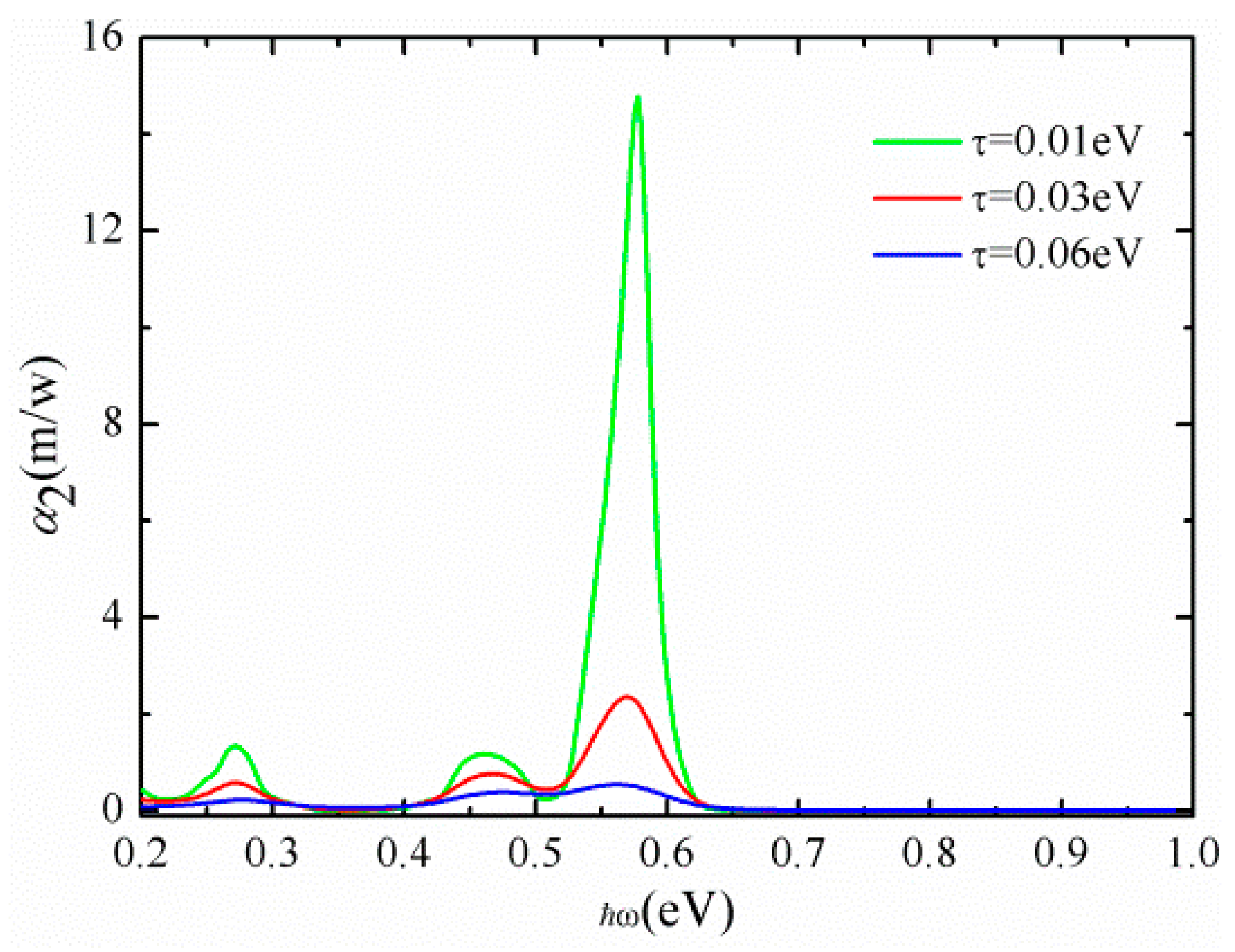
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Reich, S.E. Phosphorene excites materials scientists. Nature 2014, 506, 19. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Neal, A.T.; Zhu, Z.; Luo, Z.; Xu, X.; Tománek, D.; Ye, P.D. Phosphorene: An Unexplored 2D Semiconductor with a High Hole Mobility. ACS Nano 2014, 8, 4033–4041. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Chen, Y.; Zhang, Y.H.; Liu, S.F. Recent advance in black phosphorus: Properties and applications. Mater. Chem. Phys. 2017, 189, 215–229. [Google Scholar] [CrossRef]
- Xia, F.N.; Wang, H.; Jia, Y.C. Rediscovering black phosphorus as an anisotropic layered material for optoelectronics and electronics. Nat. Commun. 2014, 5, 5458-1–5458-6. [Google Scholar] [CrossRef]
- Ling, X.; Wang, H.; Huang, S.; Xia, F.; Dresselhaus, M.S. The renaissance of black phosphorus. PNAS 2015, 112, 4523–4530. [Google Scholar] [CrossRef]
- Li, D.; Jussila, H.; Karvonen, L.; Ye, G.; Lipsanen, H.; Chen, X.; Sun, Z. Polarization and thickness dependent absorption properties of black phosphorus: New saturable absorber for ultrafast pulse generation. Sci. Rep. 2015, 5, 15899-1–15899-9. [Google Scholar] [CrossRef]
- Li, L.; Yu, Y.; Ye, G.J.; Ge, Q.; Ou, X.; Wu, H.; Feng, D.; Chen, X.; Zhang, Y. Black phosphorus field-effect transistors. Nat. Nanotechnol. 2014, 9, 372–377. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.L.; Han, C.; Hu, Z.H.; Wang, L.; Liu, L.; Wee, A.T.S.; Chen, W. 2D phosphorene: Epitaxial growth and interface engineering for electronic devices. Adv. Mater. 2018, 30, 1802207-1–1802207-11. [Google Scholar] [CrossRef] [PubMed]
- Lu, S.B.; Miao, L.L.; Guo, Z.N.; Qi, X.; Zhao, C.J.; Zhang, H.; Wen, S.C.; Tang, D.Y.; Fan, D.Y. Broadband nonlinear optical response in multi-layer black phosphorus: An emerging infrared and mid-infrared optical material. Opt. Express 2015, 23, 11183–11194. [Google Scholar] [CrossRef]
- Peng, X.; Copple, A.; Wei, Q. Edge effects on the electronic properties of phosphorene nanoribbons. J. Appl. Phys. 2014, 116, 144301-1–144301-6. [Google Scholar] [CrossRef]
- Rodin, A.S.; Carvalho, A.; Castro Neto, A.H. Strain-Induced Gap Modification in Black Phosphorus. Phys. Rev. Lett. 2014, 112, 176801-1–176801-5. [Google Scholar] [CrossRef] [PubMed]
- Abate, Y.; Akinwande, D.; Gamage, S.; Wang, H.; Snure, M.; Poudel, N.; Cronin, S.B. Recent progress on stability and passivation of black phosphorus. Adv. Mater. 2018, 30, 1704749-1–1704749-13. [Google Scholar] [CrossRef]
- Brey, L.; Fertig, H.A. Electronic states of graphene nanoribbons studied with the Dirac equation. Phys. Rev. B 2006, 73, 235411-1–235411-5. [Google Scholar] [CrossRef]
- Barone, V.; Hod, O.; Scuseria, G.E. Electronic structure and stability of semiconducting graphene nanoribbons. Nano Lett. 2006, 6, 2748–2754. [Google Scholar] [CrossRef] [PubMed]
- Sisakht, E.T.; Zare, M.H.; Fazileh, F. Scaling laws of band gaps of phosphorene nanoribbons: A tight-binding calculation. Phys. Rev. B 2015, 91, 085409-1–085409-8. [Google Scholar] [CrossRef]
- de Sousa, D.J.P.; de Castro, L.V.; da Costa, D.R.; Pereira, J.M. Boundary conditions for phosphorene nanoribbons in the continuum approach. Phys. Rev. B 2016, 94, 235415-1–235415-10. [Google Scholar] [CrossRef]
- Zeng, B.W.; Li, M.J.; Zhang, X.J.; Yi, Y.G.; Fu, L.P.; Long, M.Q. First-Principles Prediction of the Electronic Structure and Carrier Mobility in Hexagonal Boron Phosphide Sheet and Nanoribbons. J. Phys. Chem. C 2016, 120, 25037–25042. [Google Scholar] [CrossRef]
- Carvalho, A.; Rodin, A.S.; Neto, A.H.C. Phosphorene nanoribbons. EPL 2014, 108, 47005-1–47005-6. [Google Scholar] [CrossRef]
- Margulis, V.A.; Muryumin, E.E.; Gaiduk, E.A. Optical Kerr effect and two-photon absorption in monolayer black phosphorus. J. Opt. 2018, 20, 055503-1–055503-10. [Google Scholar] [CrossRef]
- Chen, R.; Tang, Y.; Zheng, X.; Jiang, T. Giant nonlinear absorption and excited carrier dynamics of black phosphorus few-layer nanosheet in broadband spectra. Appl. Opt. 2016, 55, 10307–10312. [Google Scholar] [CrossRef]
- Wang, K.; Szydlowska, B.M.; Wang, G.; Zhang, X.; Wang, J.J.; Magan, J.J.; Zhang, L.; Coleman, J.N.; Wang, J.; Blau, W.J. Ultrafast nonlinear excitation dynamics of black phosphorus nanosheets from visible to mid-infrared. ACS Nano 2016, 10, 6923–6932. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Jiang, X.; Ge, Y.; Guo, Z.; Zeng, Z.; Xu, Q.; Zhang, H.; Yu, X.F.; Fan, D.Y. Size-dependent nonlinear optical properties of black phosphorus nanosheets and its applications in ultrafast photonics. J. Mater. Chem. C 2017, 5, 3007–3013. [Google Scholar] [CrossRef]
- Jiang, X.F.; Zeng, Z.K.; Li, S.; Guo, Z.N.; Zhang, H.; Huang, F.; Xu, Q.H. Tunable broadband nonlinear optical properties of black phosphorus quantum dots for femtosecond laser pulses. Materials 2017, 10, 210. [Google Scholar] [CrossRef]
- Shao, J.; Xie, H.; Huang, H.; Li, Z.; Sun, Z.; Xu, Y.; Xiao, Q.; Yu, X.; Zhao, Y.; Zhang, H.; Wang, H.; Chu, P.K. Biodegradable black phosphorus-based nanospheres for in vivo photothermal cancer therapy. Nat. Commun. 2016, 7, 12967-1–12967-14. [Google Scholar] [CrossRef]
- Pereira, J.M.; Katsnelson, M.I. Landau levels of single-layer and bilayer phosphorene. Phys. Rev. B 2015, 92, 075437-1–075437-9. [Google Scholar] [CrossRef]
- Nathan, V.; Guenther, A.H.; Mitra, S.S. Review of multiphoton absorption in crystalline solids. J. Opt. Soc. Am. B 1985, 2, 294–316. [Google Scholar] [CrossRef]
- Rudenko, A.N.; Katsnelson, M.I. Quasiparticle band structure and tight-binding model for single- and bilayer black phosphorus. Phys. Rev. B 2014, 89. [Google Scholar] [CrossRef]
- Gong, H.M.; Wang, X.H.; Du, Y.M.; Wang, Q.Q. Optical nonlinear absorption and refraction of CdS and CdS-Ag core-shell quantum dots. J. Chem. Phys. 2006, 125, 024707-1–024707-4. [Google Scholar] [CrossRef]
- Yu, B.L.; Zhu, C.S.; Gan, F.X. Nonlinear optical absorption and refraction by CdTe microcrystals doped in glass. J. Appl. Phys. 2000, 87, 1759–1761. [Google Scholar] [CrossRef]
- Yang, H.; Feng, X.; Wang, Q.; Huang, H.; Chen, W.; Wee, A.T.S.; Ji, W. Giant Two-Photon Absorption in Bilayer Graphene. Nano Lett. 2011, 11, 2622–2627. [Google Scholar] [CrossRef]
- Zheng, X.; Zhang, Y.; Chen, R.; Cheng, X.; Xu, Z.; Jiang, T. Z-scan measurement of the nonlinear refractive index of monolayer WS2. Opt. Express 2015, 23, 15616–15623. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Dong, N.; Zhang, S.; Zhang, X.; Feng, Y.; Wang, K.; Zhang, L.; Wang, J. Giant two-photon absorption in monolayer MoS2. Laser Photon. Rev. 2015, 9, 427–434. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, G.; Mu, H.; Lin, S.; Chen, J.; Xiao, S.; Bao, Q.; He, J. Ultrafast recovery time and broadband saturable absorption properties of black phosphorus suspension. Appl. Phys. Lett. 2015, 107, 091905-1–091905-5. [Google Scholar] [CrossRef]
| Materials | Size | Wavelength | α2 (m/W) | |
|---|---|---|---|---|
| (nm) | Experiment | Theory | ||
| CdS QDs [28] | 6.4 nm | 790 | 3.9 × 10−13 | |
| CdS-Ag QDs [28] | 10.1 nm | 790 | 1.68 × 10−10 | |
| CdTe QDs [29] | 20 nm | 1060 | 10−10 | |
| Graphene [30] | bilayer | 780 | (1 ± 0.2) × 10−7 | |
| 1100 | (2 ± 0.4) × 10−7 | |||
| 3000 | 2 × 10−3 | |||
| WS2 [31] | monolayer | 800 | (3.7 ± 0.28) × 10−6 | |
| MoS2 [32] | monolayer | 1030 | (7.62 ± 0.15) × 10−8 | |
| BP nanosheets [20] | 2000 | (4.16 ± 0.4) × 10−8 | ||
| BP QDs [23] | 2–3 nm | 500 | (7.49 ± 0.23) × 10−14 | |
| 700 | (1.68 ± 0.078) × 10−14 | |||
| 900 | (0.81 ± 0.03) × 10−14 | |||
| acBPNs | 2 nm | 700 | 5 × 10−6 | |
| 800 | 2.3 × 10−6 | |||
| 900 | 5.7 × 10−6 | |||
| 1100 | 9.7 × 10−5 | |||
| 1300 | 1.8 × 10−3 | |||
| 2000 | 0.16 | |||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Feng, X.; Qin, Y.; Wang, Q. Width Dependent Two-Photon Absorption in Monolayer Black Phosphorus Nanoribbons. Appl. Sci. 2019, 9, 2014. https://doi.org/10.3390/app9102014
Liu Y, Feng X, Qin Y, Wang Q. Width Dependent Two-Photon Absorption in Monolayer Black Phosphorus Nanoribbons. Applied Sciences. 2019; 9(10):2014. https://doi.org/10.3390/app9102014
Chicago/Turabian StyleLiu, Yu, Xiaobo Feng, Yonggang Qin, and Qianjin Wang. 2019. "Width Dependent Two-Photon Absorption in Monolayer Black Phosphorus Nanoribbons" Applied Sciences 9, no. 10: 2014. https://doi.org/10.3390/app9102014
APA StyleLiu, Y., Feng, X., Qin, Y., & Wang, Q. (2019). Width Dependent Two-Photon Absorption in Monolayer Black Phosphorus Nanoribbons. Applied Sciences, 9(10), 2014. https://doi.org/10.3390/app9102014




