Short Transient Parameter-Varying IIR Filter Based on Analog Oscillatory System

Featured Application

Presented filtering structure can be used to improve the dynamics of sensors.

Abstract

This paper presents a concept for digital infinite impulse response (IIR) lowpass filter with reduced transient response. The proposed digital filtering structure is based on an analog oscillatory system. In order to design the considered digital filter, the analog prototype is subjected to a discretization process and, then, the parameters describing the dynamical properties of the oscillatory system are temporarily varied in time, so as to suppress the transient response of the designed filter. An optimization method, aimed at reducing the settling time by proper parameter manipulation, is presented. Simulation results, along with a real-life application proving the usefulness of the proposed concept, are also shown and discussed.

1. Introduction

Measuring devices usually operate in noised environments. The source of the noise can vary, depending on the measured physical quantity [1,2]. In the electrical engineering area, one of the most-often measured quantities is the voltage value, derived from sensors (e.g., the weight transformed to the voltage output of tensometers). Unfortunately, voltage measurements can be easily noised by other electrical equipment around the sensors. The noise source is often an integral part of the measured object itself [3]. For example, the measurement of DC motor speed is conducted by magnetic encoders which are usually placed at the end of the motor shaft. Significant noise can be also generated by equipment placed within a close vicinity of the sensor [4]. For example, power lines can affect the measurements of biomedical signals [5].

One of the most important problems in filtering measurement signals is the transient response of the filters used. The duration of the transient depends mainly on the order and the selectivity of the filter. Long transients may cause very significant problems, particularly when short time-signals are processed, or when the initial stage of a filtered signal is of great importance. In such situations, a useful signal can be considerably distorted due to the presence of the transient of the filter, or the signal can be entirely lost in the transient state.

In this paper, a concept for a digital parameter-varying infinite impulse response (IIR) lowpass filter with a transient response of short duration is presented. The proposed digital filter is based on an analog oscillatory system, which is subjected to the discretization process. The improvement of the dynamic behavior attained by the proposed filter structure is based on temporary changes in the value of dynamical parameters of the analog filter prototype [6,7].

The methodology proposed for the variation of filter parameters has been used, with some modifications, in a few applications. For example, in [8], a time-varying analog filter was used to eliminate the oscillatory response exhibited by the load cells used in weighing applications. Another time-varying filter was used, in [9], to reduce the time employed in the acquisition of evoked potentials generated through auditory stimuli. Moreover, in [10], the parameter-varying strategy was used to reduce the transient response of filters with a compensated group delay response. As the concept was proved to be very useful, the methodology was only tested with exponential decay functions as the time-varying base, dictated by the implementation reliability and repeatability demands with analog passive elements. This paper is a further extension of our research into the time-varying coefficients concept in the digital signal processing area, where more complex time-varying base functions are easily achieved. We propose to use a known analog oscillatory system as the basis for the digital time-varying filtering structure. We also present a new method for obtaining the sets of coefficients that improve the transient response of the considered system.

The paper is organized as follows: In Section 2, the considered oscillatory system and its discrete counterpart are presented. The idea of the IIR filter with time-varying parameters is presented in Section 3. In Section 4, the strategy used to optimize the variability of filter parameters, in order to reduce the transient response, is presented. Section 5 presents and discusses the real-life implementation and measurement of the rotary speed of a motor with the proposed parameter-varying filtering structure. Finally, some concluding remarks are given in Section 6.

2. Time-Invariant Analog and Digital Filter Prototype

In this paper, we use the well-known analog model of the oscillatory system. The considered system can be regarded as a second-order lowpass filter section. The transfer function describing the second order filter in the frequency domain is given, as follows:

$$H\left(s\right)=\frac{k}{{\omega }_0^{-2}{s}^2+2\zeta {\omega }_0^{-1}s+1},$$

(1)

where k stands for the gain coefficient, $\zeta$ for the damping ratio, and ${\omega }_0$ for the natural frequency of the filter. By using the well-known bilinear transform, in the form of:

$$s\to \frac{2}{t_s}\frac{z-1}{z+1},$$

(2)

where $t_s$ stands for the sampling time, one can obtain a digital oscillatory model with the entangled gain, damping ratio, and natural frequency parameters. The obtained transfer function of the discretized filter is as follows:

$$H\left(z\right)=\frac{k{t}_s^2(z^2+2z+1)}{[4{\omega }_0^{-2}+4\zeta {\omega }_0^{-1}{t}_s+t_s^2]z^2+[-8{\omega }_0^{-2}+2t_s^2]z+4{\omega }_0^{-2}-4\zeta {\omega }_0^{-1}{t}_s+t_s^2}.$$

(3)

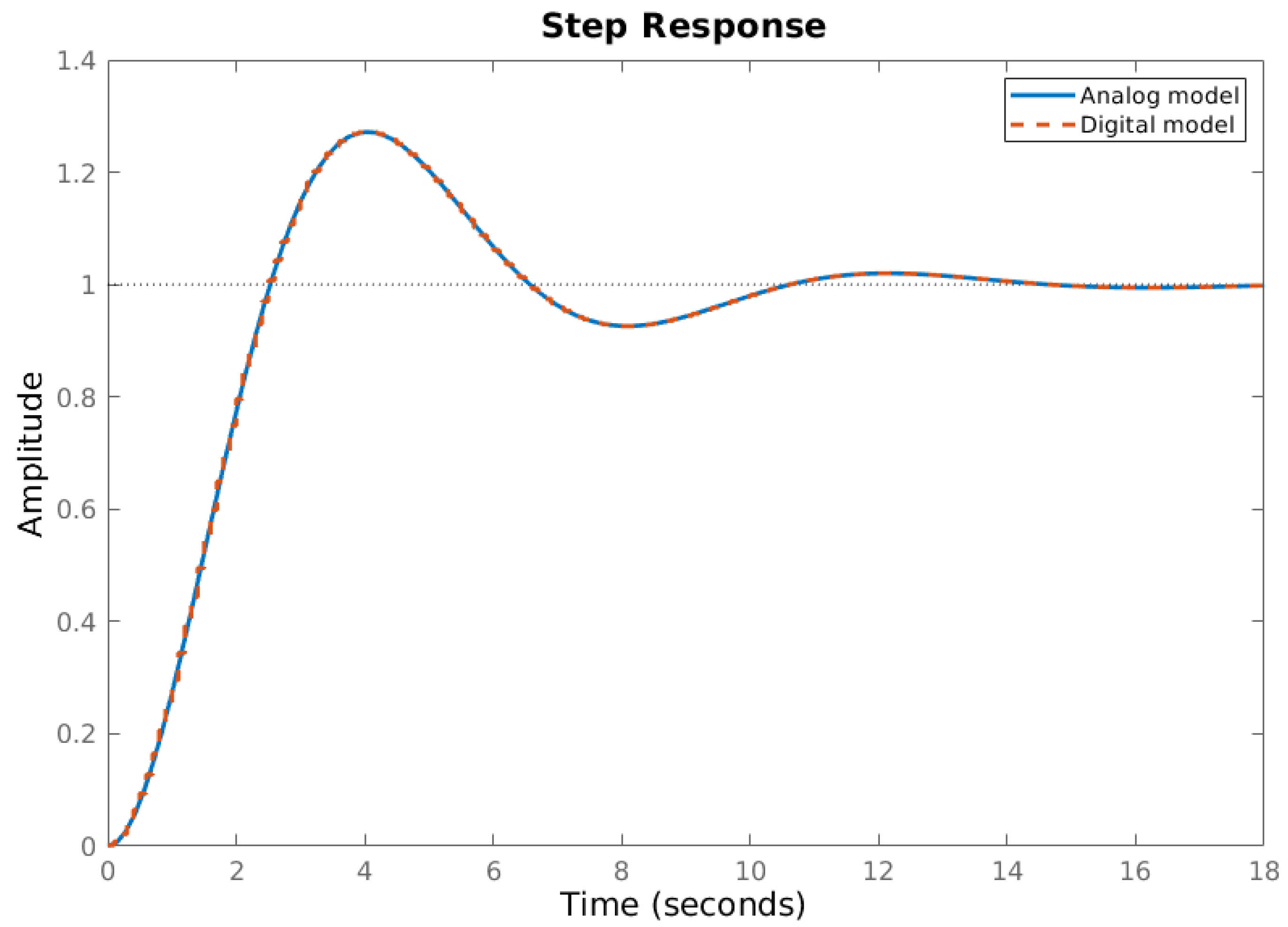
Figure 1 presents the step responses of exemplary digital and analog second-order oscillatory systems, proving the correctness of the proposed discretization process. In this paper, the second-order Chebyshev type-I filter, with passband peak-to-peak ripple $R_p$ = 3 dB and normalized cutoff frequency ${\omega }_c$ = 1 rad/s, is considered as a study case.

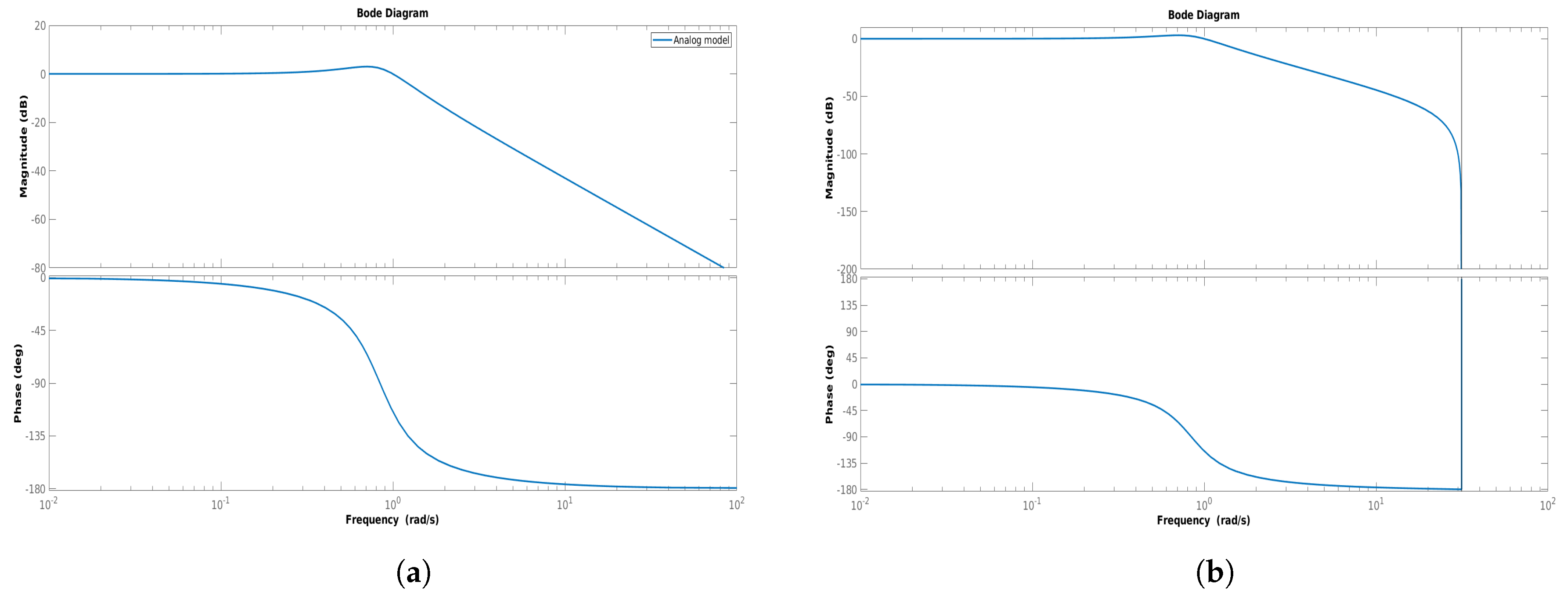
Figure 2a,b present the Bode diagrams of both the analog and digital filters.

3. Filter Dynamics

The dynamic properties of the second-order lowpass analog and discretized filters are described by the natural frequency ${\omega }_0$, the damping ratio $\zeta$, and the gain coefficient k. All these parameters affect the duration of the transient response of the considered filter.

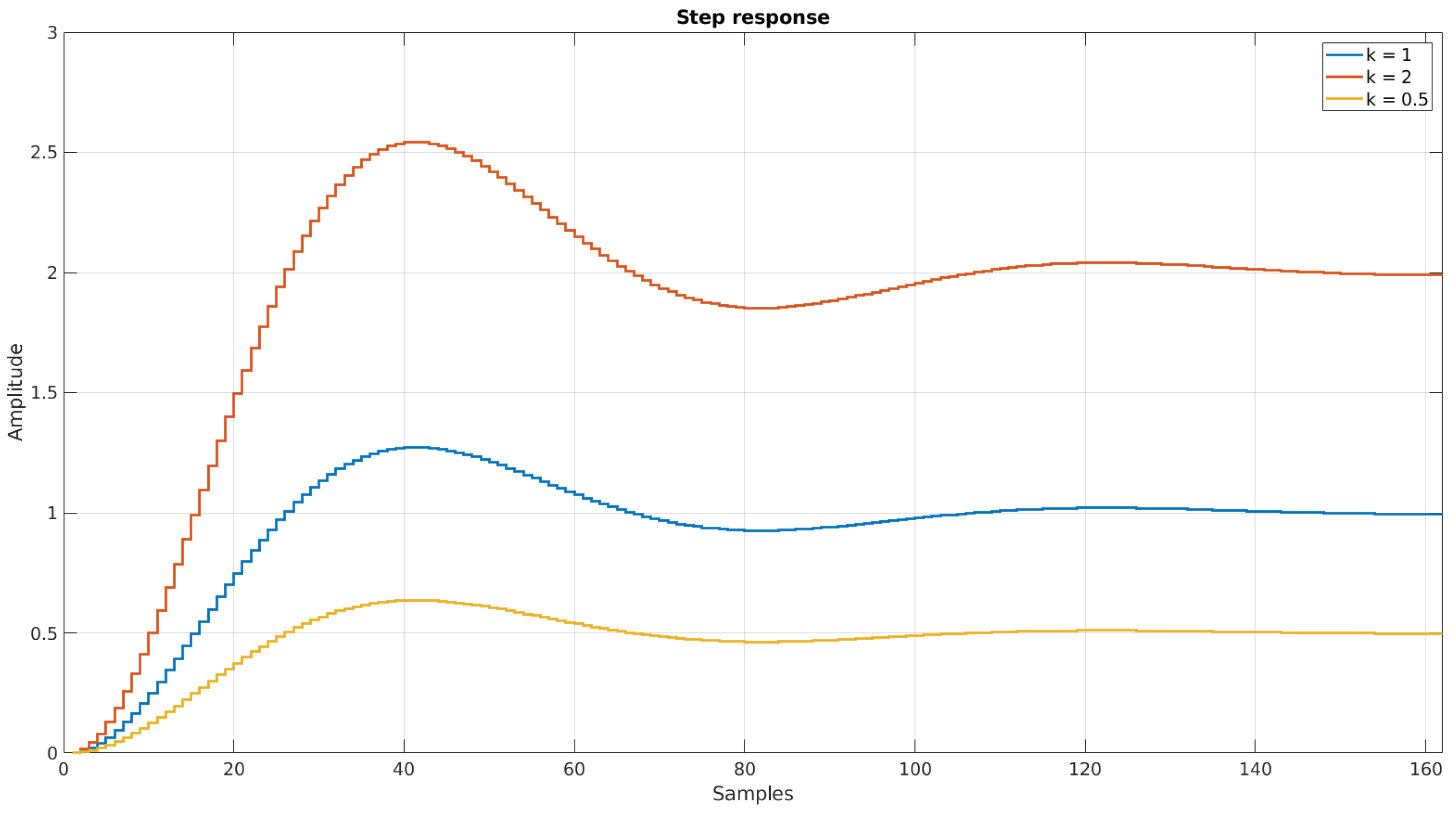
Figure 3 presents the step response of the digital filter with three different values of the gain k, ${\omega }_0$ = 8.41$·{10}^{-1}$, $\zeta$ = 3.83$·{10}^{-1}$, and $t_s$ = 1/10 s.

Table 1. Step response characteristics for k = 0.5, 1, and 2. RiseTime—time it takes for the response to rise from 10% to 90% of the steady-state response; SettlingTime—time it takes for the error to fall to within 2% of steady-state response; SettlingMin—minimum value once the response has risen; SettlingMax—maximum value once the response has risen; Overshoot—percentage overshoot; and PeakTime—time at which the peak value occurs.

	k = 0.5	k = 1	k = 2
RiseTime	16.9859	16.9859	16.9859
SettlingTime	132.1759	132.1759	132.1759
SettlingMin	0.4630	0.9260	1.8520
SettlingMax	0.6360	1.2720	2.5440
Overshoot	27.9031	27.9031	27.9031
PeakTime	41	41	41

presents the detailed characteristics of the presented step responses.

As one can notice, the k parameter does not have a direct influence on the settling time values. On the other hand, let us assume that the k parameter is initially larger than the base value but, further on (with the right timing), is set back to the aforementioned pre-determined number. One could expect the final value of the response as expected with this design, but with a reduced settling time characteristic. As the change of the parameter k would happen only for a brief moment and only at the beginning of the processing, one can expect the frequency characteristic to be as designed.

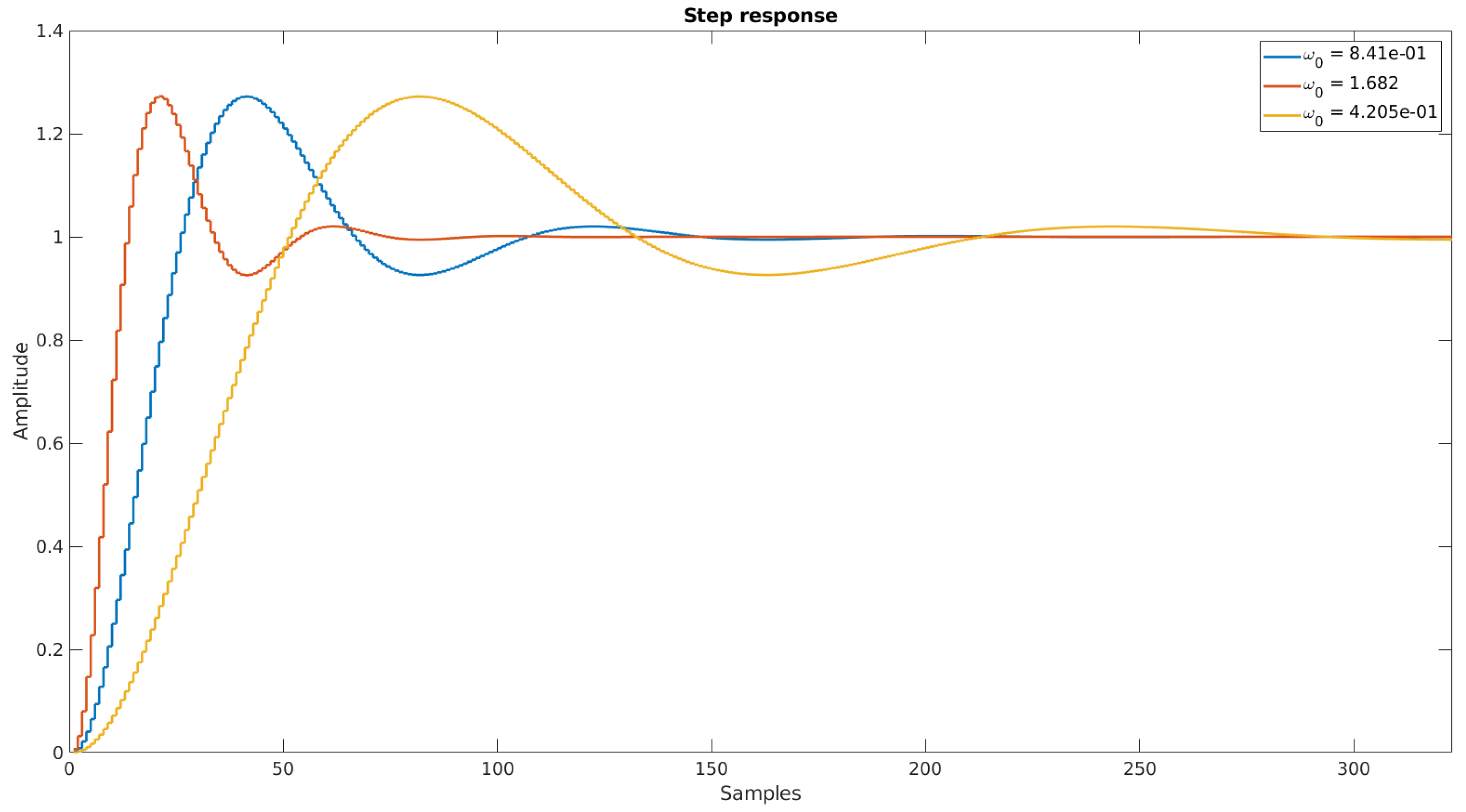
Figure 4 presents the step response of the filter with three different values of $w_0$, k = 1, $\zeta$ = 3.83$·{10}^{-1}$, $t_s$ = 1/10 s.

Table 2. Step response characteristics for ${\omega }_0$ = 4.205$·{10}^{-1}$, 8.41$·{10}^{-1}$, and 1.682.

	${\mathit{\omega }}_0$ = 4.205$·{10}^{-1}$	${\mathit{\omega }}_0$ = 8.41$·{10}^{-1}$	${\mathit{\omega }}_0$ = 1.682
RiseTime	33.9803	16.9859	8.5523
SettlingTime	263.5927	132.1759	50.7959
SettlingMin	0.8983	0.9260	0.9068
SettlingMax	1.2718	1.2720	1.2723
Overshoot	27.8830	27.9031	27.0523
PeakTime	81	41	21

presents the detailed characteristic of the step responses, similar to Table 1.

This example shows that, by increasing ${\omega }_0$, the settling time reduced. Similar to the gain coefficient, one can deduce that it is desirable for the filter to behave as a model with large ${\omega }_0$ at the beginning of the response and, once reaching a close proximity to the steady state, ${\omega }_0$ should be set back to the predefined value to preserve the frequency characteristic demands.

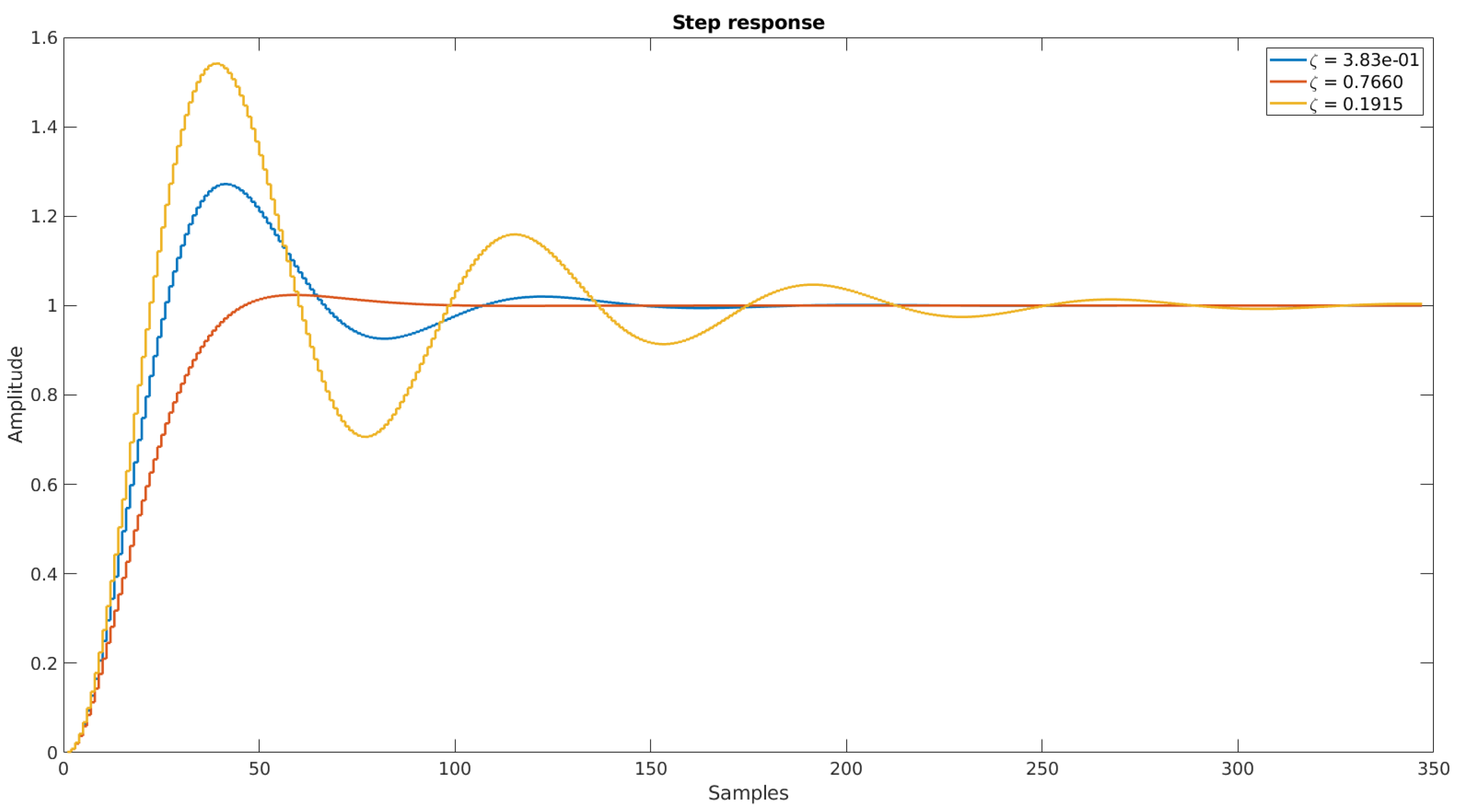
Figure 5 presents the step response of the filter with three different values of the $\zeta$ parameter, k = 1, ${\omega }_0$ = 8.41$·{10}^{-1}$, and $t_s$ = 1/10 s.

Table 3. Step response characteristics for $\zeta$ = 1.915$·{10}^{-1}$, 3.83$·{10}^{-1}$, and 7.66$·{10}^{-1}$.

	$\mathit{\zeta }$ = 1.915$·{10}^{-1}$	$\mathit{\zeta }$ = 3.83$·{10}^{-1}$	$\mathit{\zeta }$ = 7.66$·{10}^{-1}$
RiseTime	14.2378	16.9859	27.9770
SettlingTime	240.1456	132.1759	63.3110
SettlingMin	0.7065	0.9260	0.9079
SettlingMax	1.5413	1.2720	1.0237
Overshoot	53.5289	27.9031	2.1483
PeakTime	39	41	59

presents the detailed characteristic of the step responses, similar to Table 1 and Table 2.

Similar to the ${\omega }_0$ parameter, one can draw the conclusion that increasing the value of $\zeta$ improves the settling time of the system response.

4. Time-Varying Filter

In the previous section, we showed the way in which the coefficients of the oscillatory system affect the settling time. Our research aims to use this knowledge to reduce the transient state of the given system. We propose to vary the parameters of the system, in a pre-defined way and at a specified horizon. After reaching the horizon, the values of the system are set to be constant, to preserve the initial frequency characteristic demands.

As the well-known transfer function is only defined for time-invariant systems, one can describe the time-varying system with a difference equation, which is defined as follows:

$${\displaystyle \sum _{i=0}^q}{a}_i\left(n\right)y[n-i]={\displaystyle \sum _{i=0}^m}{b}_i\left(n\right)x[n-i],$$

(4)

where $a_i\left(n\right)$ and $b_i\left(n\right)$ are the time-varying coefficients, $y\left(n\right)$ is the output, $x\left(n\right)$ is the input, q and m are the numbers of coefficients, i is the auxiliary index, and n is the discrete time-index. As this is a system which is recursive in nature, one must also remember to check the stability of the designed filter. In previous research, we proposed a method, based on [11,12], to calculate the time-varying poles of the filtering structure and proposed a methodology for assessing the stability of the design.

4.1. Coefficient Sets

In order to choose the right sets of coefficients, one must first determine the horizon, before which the parameters should vary. Our experimental research proved that the most efficient horizon lies between the settling time, calculated as a 2% border around the steady state and 1.5 times that value.

As for the rest of the parameters, we designed an optimization routine to propose the sets of coefficients that reduce the settling time of the given system. The fitness of each candidate in the mentioned routine is evaluated as the time value needed to achieve the 2% border around the steady state of the response of the time-varying filter prototype to the step signal. In this paper, we assume that all parameters (k, ${\omega }_0$, and $\zeta$) can vary in time. Of course, as stated earlier, the parameters settle down to the pre-determined values, according to the time-invariant design, after reaching the defined horizon.

The first stage of the optimization process assumes that the parameters can change linearly through a given horizon. The starting value of the linear change is picked randomly and the objective is the reduction of the settling time value. One can choose the number of random steps in this stage. Figure 6 presents the first stage of the optimization routine.

Once the starting point for each linear set of coefficients is determined, the second stage of optimization starts. During our research, we noticed that, often, the linear change of parameters can be further improved, in terms of reducing the settling time of the whole time-varying design. The next step of our optimization routine introduces Bézier-like curves as a basis for the parameter sets. The freedom they offer in shaping the dynamics of those sets is very useful. The mentioned curves are calculated according to the following equation:

$$B\left(t\right)={\displaystyle \sum _{i=0}^n}\left(\genfrac{}{}{0pt}{}{n}{i}\right){(1-t)}^{n-i}{t}^i{P}_i,$$

(5)

where n is the degree of the polynomial, $P\left(i\right)$ is the control point, i is the auxiliary index, and $t\in [0,1]$. The first control point is the one calculated in the first optimization stage. The last point is given by the final, pre-determined by the time-invariant design value at the time equal to the chosen horizon. The time basis of the curve is also re-calculated, according to the mentioned horizon. In this paper, we use a random placement of one middle control point. In this stage, one can also choose the number of steps. The aim is the same as before, which is the reduction of the settling time of the system. Figure 7 presents the second stage of the optimization routine.

As one can notice, introducing the Bézier curves results in a non-linear change of the coefficients in the chosen horizon. In most test cases, it allowed for an additional 10% improvement of the settling time, in comparison to first stage optimization alone.

4.2. Simulation Results

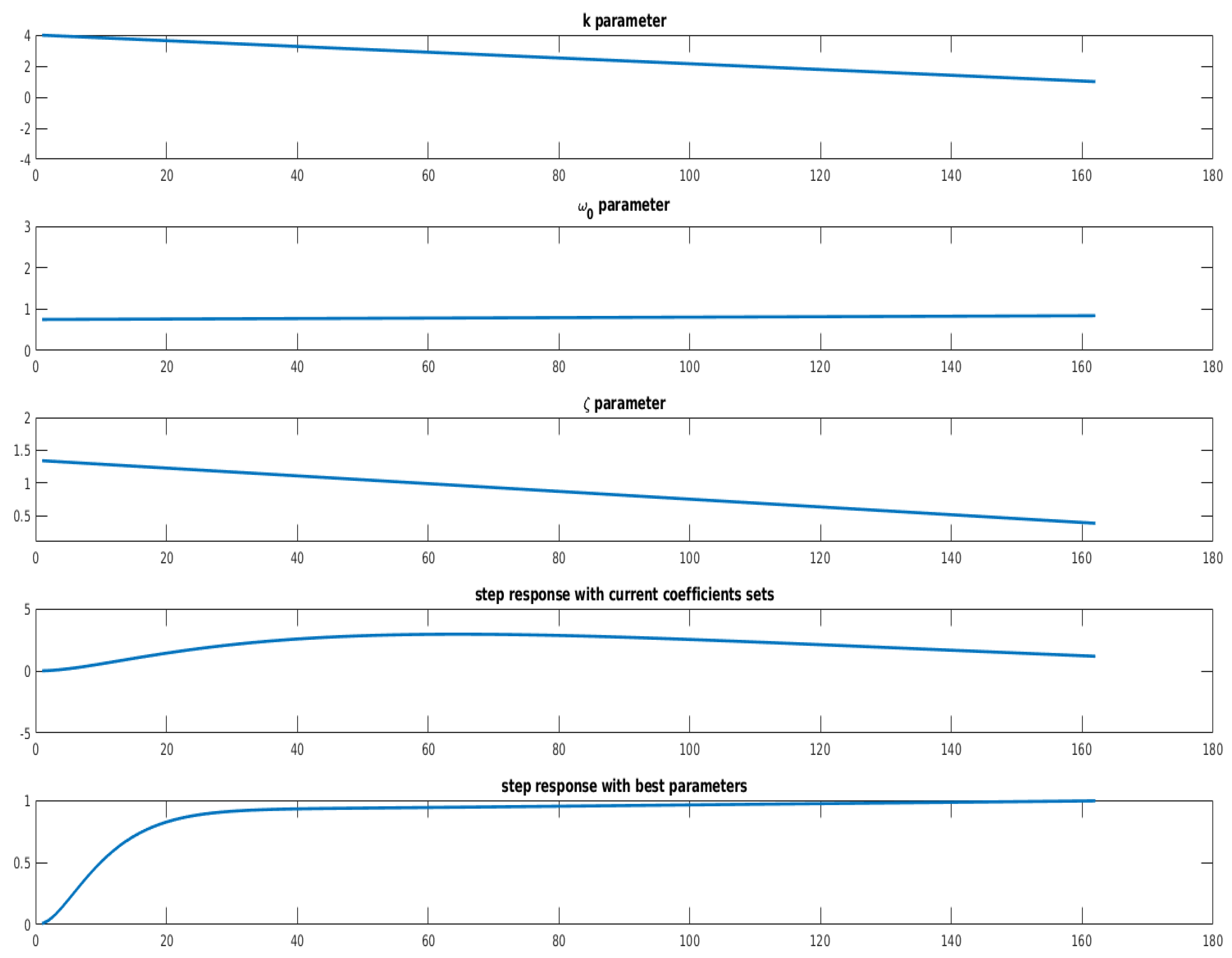
Figure 8 presents the sets of coefficients calculated with the optimization routine, using 3000 steps for each stage.

As one can notice, the sets correspond to the conclusions made in Section 3. The k parameter was proved not to affect the settling time when changed and one can notice, in Figure 8, that the optimization routine also hardly varied this parameter. In Section 3, it was concluded that higher values of the ${\omega }_0$ parameter reduces the settling time. The optimization routine has also designed the system that initially acts as a filter with a high value of ${\omega }_0$ and later moves to the pre-defined final value at the end of the horizon, to preserve the frequency demands of the filtering structure. One can observe the same phenomenon, in terms of the $\zeta$ parameter. Figure 9 presents the comparison of the step responses of the time-invariant and time-varying systems.

As one can notice in

Table 4. Comparison of the linear time-invariant (LTI) and time-varying (LTV) systems.

	LTI System	LTV System
RiseTime	16.9859	10.7465
SettlingTime	132.1759	17.0687
SettlingMin	0.9260	0.9193
SettlingMax	1.2720	1.0107
Overshoot	27.9031	1.0311
PeakTime	41	23

, the improvement of the settling time reached 87%. Along with reducing the transient time, the overall overshoot was also significantly lowered.

5. Experimental Results

To test our time-varying filtering structure with a real-life signal, we measured the output of a magnetic encoder mounted on a geared DC motor. Figure 10 presents the measurement setup to acquire the test signal.

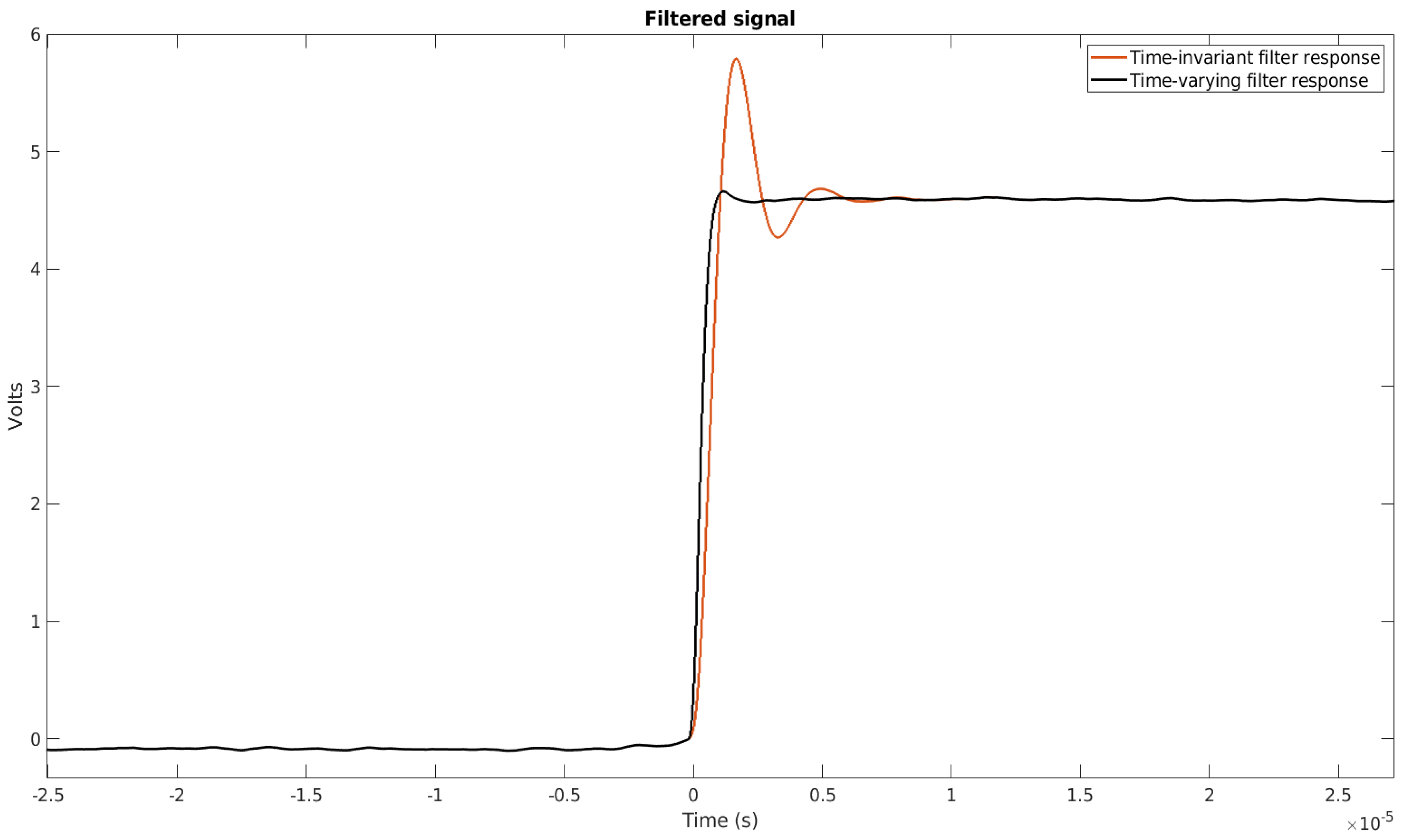
The obtained measurement is presented in Figure 11, along with the responses of the time-invariant and time-varying filters.

Figure 12 presents the closeup of the most interesting part of the responses.

As one can notice, the time-varying filter had a much better performance, in terms of settling time, than the time-invariant counterpart. Furthermore, the time-varying filter was characterised by a considerably reduced overshoot.

6. Conclusions

This paper presents an approach for a digital IIR filtering structure, by using an analog oscillatory system (along with its parameters) as a basis. We aimed to reduce the settling time of the digital design. To achieve this goal, the time-varying coefficient concept was proposed in Section 4. As the concept requires calculating the right sets of coefficients, we introduced an optimization routine in Section 4.1, and proved that its outcome is consistent with the time-invariant observations made in Section 3. The time-varying structure, obtained by the proposed optimization routine, decreased the settling time by 87% for the given example. To further test the time-varying structure, we used a magnetic encoder of a DC motor to gather a noised signal. This real-life example also proved that the time-varying filter allows for a reduction of the settling time, while still maintaining the ability to de-noise a useful signal.