The Impact of Intermittent Androgen Suppression Therapy in Prostate Cancer Modeling

Abstract

Previous studies on prostate cancer modeling under hormonal therapy successfully fit clinical serum androgen data, under the assumption that the levels of intracellular and serum androgen are similar. However, such an assumption may not hold throughout the course of treatment. In this paper, we propose a model that directly accounts for serum androgen and its interaction with intracellular androgen. We establish biological links between the model and clinical data, and discuss in detail parameter ranges and the initialization of model variables. We further investigate parameter sensitivity over time, which gauges the maximum effect of varying each parameter and allows us to fix some parameters, to increase the robustness of the parameter fitting process. By relying on the characteristics of intermittent androgen suppression therapy (IAS), we employ a two-part weighted error function for fitting. We also carry out mathematical analyses to study the dynamic aspects of the system with different androgen thresholds. We find that the proposed model shows superior forecasting ability, compared to its predecessor. Furthermore, we demonstrate the impact of androgen on the dynamics of the androgen-dependent and -independent cancer cells, which suggests the discrete description of androgen dependency may not give a realistic characterization of the cancer population. We show that IAS has certain characteristics that need to be considered for parameter estimation. Our results demonstrate that the model and the fitting scheme are viable for similar applications of prostate cancer modeling under hormonal therapy.

1. Introduction

Prostate cancer (PCa) is the second most common cancer found in American men. The estimated lifetime chance of being diagnosed with prostate cancer is 1 in 7. While prostate cancer is commonly found in men over 50 years old, it can start to develop in men in their twenties and takes decades to progress. Survival rates for localized prostate cancer have been improved significantly, due to advances in treatment; however, once cancer metastasizes beyond the prostate, the survival rate drops to about 28% [1,2]. It has been noted that the growth of prostate cancer is highly dependent on androgen, a male characteristic hormone like testosterone. Thus, for metastasized cancer, the standard hormonal treatment is androgen deprivation therapy (ADT), which dates back to Huggins’ Nobel Prize-winning discovery that castration causes rapid regression of PCa. While the treatment is successful in making the tumor regress initially, the cancer cells eventually mutate and adapt to be able to grow in an environment with low-androgen level, leading to the ineffectiveness of hormonal therapy or hormonal resistance [3]. Additionally, ADT comes with many side effects, for instance, impotence, depression, bone demineralization, and an increased risk of dementia. Thus, intermittent androgen suppression therapy (IAS) was introduced. During IAS, the patients are put on treatment until their prostate-specific antigen (PSA—a prostate cancer biomarker) level reaches a desired low threshold, then they are taken off the treatment until the PSA level rises above a predetermined threshold. The process is then repeated until the patients reach hormonal resistance [1].

Various mathematical models have been developed, in the past two decades, to study many aspects of prostate cancer, especially under androgen suppression therapy. The first experimentally- driven model of PCa under continuous androgen suppression therapy (CAS) is credited to Jackson in 2004 [4]. This inspired a series of works that study PCa under IAS and compare the effect of CAS versus IAS [5,6,7,8]. Furthermore, theoretical perspectives on population dynamics and spatial structure have also been explored in subsequent works [9,10,11]. In addition, a biologically detailed model with a complex biochemical network has also been developed and verified with experimental data [12]. On a more applicable note, optimal scheduling, complex algorithms to predict hormonal resistance, and stochastic models have been used to provide insights into clinical aspects of prostate cancer treatment [13,14,15,16]. For a detailed review of recent work, the authors refer to [17].

In this paper, we focus on a previous approach by Baez and Kuang, which was the first successful attempt at using both PSA and androgen data for fitting and forecasting [8]. A recent work by Phan et al. [18] shows that, with the available types of data (e.g., PSA and androgen data), the model in Baez and Kuang (BK model) has the optimal population structure to describe and to forecast the dynamics of prostate cancer under IAS. On the other hand, the model fails to completely capture the growth phase of the PSA level when the patient is taken off treatment. Additionally, fitting of the androgen data is done by assuming similar levels of body androgen and intracellular androgen, which may not hold throughout the course of treatment. Thus, we extend the BK model to directly take into account serum androgen separately from intracellular androgen. We carry out numerical comparisons between the two models, in terms of fitting and forecasting. Finally, we study the mathematical properties of the new model, to show the effect that androgen has on the survival of cancer cells.

The data is taken from a clinical study from the Vancouver Prostate Center [19]. Similar to [18], we select 26 patients with sufficient data for fitting and forecasting comparisons, over 2.5 cycles of treatment.

2. Model and Method

2.1. The BK Model

Baez and Kuang [8] introduced a two-subpopulation model for prostate cancer undergoing androgen suppression therapy. This model is a simplification from the model in Portz et al. [7]. The model takes the form:

$$\frac{d{x}_1}{dt}=\underset{\mathrm{growth}}{\underbrace{{\mu }_m\left(1-\frac{q_1}{Q}\right)x_1}}-\underset{\mathrm{death}}{\underbrace{\left(D_1\left(Q\right)+{\delta }_1{x}_1\right)x_1}}-\underset{\mathrm{cell}\mathrm{transformation}}{\underbrace{\lambda \left(Q\right)x_1}}$$

(1)

$$\frac{d{x}_2}{dt}=\underset{\mathrm{growth}}{\underbrace{{\mu }_m\left(1-\frac{q_2}{Q}\right)x_2}}-\underset{\mathrm{death}}{\underbrace{\left(D_2\left(Q\right)+{\delta }_2{x}_2\right)x_2}}+\underset{\mathrm{cell}\mathrm{transformation}}{\underbrace{\lambda \left(Q\right)x_1}}$$

(2)

$$\frac{dQ}{dt}=\underset{\mathrm{diffusion}:\mathrm{serum}\to \mathrm{intracellular\; androgen}}{\underbrace{\gamma (Q_m-Q)}}-\underset{\mathrm{cell}\mathrm{uptake}\mathrm{of}\mathrm{androgen}}{\underbrace{\frac{\mu (Q-q_1)x_1+\mu (Q-q_2)x_2}{x_1+x_2}}}$$

(3)

$$\frac{dP}{dt}=\underset{\mathrm{baseline}\mathrm{PSA}\mathrm{production}}{\underbrace{bQ}}+\underset{\mathrm{tumor}{}^{\prime }\mathrm{s}\mathrm{PSA}\mathrm{production}}{\underbrace{\sigma (Q{x}_1+Q{x}_2)}}-\underset{\mathrm{degradation}}{\underbrace{ϵP}}$$

(4)

$$D_i\left(Q\right)=d_i\frac{R_i}{Q+R_i},\lambda \left(Q\right)=c\frac{K}{Q+K}$$

(5)

$$\gamma ={\gamma }_{1}u\left(t\right)+{\gamma }_2,u\left(t\right)=\left\{\begin{array}{c}0,\mathrm{on}\mathrm{treatment}\hfill \\ 1,\mathrm{off}\mathrm{treatment}\hfill \end{array}\right..$$

(6)

In this model, $x_1$ and $x_2$ represent the androgen-dependent (AD) and androgen-independent (AI) cells, respectively. P is the PSA level, and Q is the intracellular androgen level. In [8], the authors assumed that the level of intracellular androgen is the same as that of the serum androgen. Since only serum androgen data is available (and not intracellular androgen data), this assumption allows data fitting using clinical androgen data with the variable Q, along with the data fitting of tumor biomarker PSA. The model assumes $q_1>q_2$, which biologically means that the AI cell subpopulation can grow in an environment with lower androgen levels than AD cells can. A more thorough derivation of this model can be found in [8,18]. As pointed out in [18], the mutation from AD to AI cells is sufficient to describe the transformation between these two cells, due to the lack of clinical data types.

As mentioned in [18], the equation governing the dynamics of Q has a significant biological flaw. Since the diffusion is scaled with the difference between $Q_m$ and the current value of Q, it means that immediately after the patient is taken off treatment, the serum androgen level reaches its max (e.g., $Q_m$). Scaling the growth of intracellular androgen in this way is perhaps one of the causes for the sudden jump in PSA level between the on- and off-treatment intervals.

2.2. The New Model

In the BK model, the assumption of similarity in the levels of serum androgen and intracellular androgen may not hold consistently throughout the treatment. This motivates the following model, which directly takes into account body androgen production and its diffusion to intracellular androgen. Additionally, previous work by Portz et al. [7] extrapolated serum androgen data with an exponential growth/decay function. The serum androgen values are then fed into a five-compartmental model, known as the PKN model. Extending upon this idea, we explicitly include a compartment that governs the dynamics of serum androgen. The following model is presented as an extension of the BK model:

$$\frac{d{x}_1}{dt}=\underset{\mathrm{growth}}{\underbrace{{\mu }_1\left(1-\frac{q_1}{Q}\right)x_1}}-\underset{\mathrm{death}}{\underbrace{\left(D_1\left(Q\right)+{\delta }_1{x}_1\right)x_1}}-\underset{\mathrm{cell}\mathrm{transformation}}{\underbrace{\lambda \left(Q\right)x_1}}$$

(7)

$$\frac{d{x}_2}{dt}=\underset{\mathrm{growth}}{\underbrace{{\mu }_2\left(1-\frac{q_2}{Q}\right)x_2}}-\underset{\mathrm{death}}{\underbrace{\left(D_2\left(Q\right)+{\delta }_2{x}_2\right)x_2}}+\underset{\mathrm{cell}\mathrm{transformation}}{\underbrace{\lambda \left(Q\right)x_1}}$$

(8)

$$\frac{dQ}{dt}=\underset{\mathrm{androgen}\mathrm{diffusion}:A\to Q}{\underbrace{m(A-Q)}}-\underset{\mathrm{cells}\mathrm{uptake}\mathrm{of}\mathrm{androgen}}{\underbrace{\frac{{\mu }_1(Q-q_1)x_1+{\mu }_2(Q-q_2)x_2}{x_1+x_2}}}$$

(9)

$$\frac{dA}{dt}=\underset{\mathrm{androgen}\mathrm{production}}{\underbrace{{\gamma }_2+{\gamma }_1(A_0-A)}}\underset{\mathrm{suppression}\mathrm{of}\mathrm{production}}{\underbrace{-A_0{\gamma }_1(1-u)}}$$

(10)

$$\frac{dP}{dt}=\underset{\mathrm{baseline}\mathrm{PSA}\mathrm{production}}{\underbrace{bQ}}\underset{\mathrm{tumor}{}^{\prime }\mathrm{s}\mathrm{PSA}\mathrm{production}}{\underbrace{+\sigma (Q{x}_1+Q{x}_2)}}\underset{\mathrm{degradation}}{\underbrace{-ϵP}}$$

(11)

$$D_i\left(Q\right)=d_i\frac{R_i}{Q+R_i},\lambda \left(Q\right)=c\frac{K}{Q+K}$$

(12)

In contrast to the BK model, the variable A in this model represents serum androgen. While the treatment is on, the rate of change of A is strongly influenced by a negative exponential term, indicating the effect of the total androgen blockage drug. While the treatment is off, the production of A takes the form of a logistic-type growth, where $A_0$ is the maximum serum androgen, which is akin to the carrying capacity in the logistic equation. The uptake rate of intracellular androgen, Q, depends on the current level of serum androgen. This is a biological improvement over the BK model as, after the patient is taken off treatment, it takes time for the serum androgen to recover to its maximum. As a consequence, the intracellular androgen level will take more time to recover its normal level.

2.3. Sensitivity Analysis for the New Model

Sensitivity analysis of the parameters plays an important part in evaluating and improving the robustness of a model. Previous studies focus on the local sensitivity at a fixed time point [8,18]. While this can provide valuable information, the dynamics of IAS therapy are broken down into on- and off-treatment intervals, with distinct characteristics in both parts. Additionally, understanding the effect each parameter has on the dynamics of the model can lead to the fixing of certain parameters, during the parameter estimation process. If some of the less sensitive parameters can be fixed, then we essentially reduce the uncertainty in the remaining parameters, which increases their identifiability. Here, we employ the normalized sensitivity equation from section 5.5 in [20], to carry out the sensitivity analysis of the new model:

$$S_p=\frac{\partial x}{\partial p}\frac{p}{x},$$

where p is the parameter, and x is the variable of interest; for example, $\mu$ and PSA level, respectively. Note that, since we will be varying each parameter by 1% with respect to their value, we can use the following approximation of the sensitivity equation:

$$S_p=\frac{\partial x}{\partial p}\frac{p}{x}\approx \frac{x_{varied}-x}{0.01p}\frac{p}{x}=\frac{x_{varied}-x}{0.01x},$$

(13)

where $x_{varied}$ is the value of x after increasing a parameter by 1%. The result of the sensitivity analysis is summarized in

Table 1. Order of sensitivity. The number represents the maximum order of sensitivity of a variable with respect to a parameter. For instance, at the intersection of ${\mu }_1$ and $x_1$, 0 means changing ${\mu }_1$ by $1\%$ will affect at most a change of order 0 in $x_1$. In this table, 0 corresponds to most sensitive and $-8$ means least sensitive. The most insensitive parameters with combined order less than $-10$ are c, K, ${\delta }_1$, and ${\delta }_2$. Thus, we fix them in the new model. Note that $d_2$ also has a combined order of sensitivity less than −10; however, since $d_1$ is sensitive, we do not fix $d_2$. Also, we do not carry out the sensitivity for ${\gamma }_2$, since we fix it as 0 for the new model, due to its small range.

Param	${\mathit{\mu }}_1$	${\mathit{\mu }}_2$	${\mathit{q}}_1$	${\mathit{q}}_2$	b	$\mathit{\sigma }$	$\mathit{ϵ}$	${\mathit{d}}_1$	${\mathit{d}}_2$	${\mathit{\delta }}_1$	${\mathit{\delta }}_2$	${\mathit{R}}_1$	${\mathit{R}}_2$	c	K	${\mathit{\gamma }}_1$	m	${\mathit{A}}_0$
$x_1$	0	0	0	−1	0	−1	−1	0	−2	−1	−2	0	−3	−5	−6	0	−1	0
$x_2$	0	0	−2	0	−3	−3	−2	−2	−1	−3	−1	−2	−1	−5	−5	0	−2	−1
A	−3	−3	−3	−4	−4	−3	−3	−3	−4	−4	−4	−4	−4	−8	−8	0	−3	0
Q	−1	−1	−2	−1	−3	−3	−2	−2	−3	−3	−3	−2	0	−7	−7	0	−1	−1
P	0	0	−1	−1	0	−1	0	0	−1	−1	−1	0	−2	−6	−6	0	−1	0

.

While the sensitivity process is perhaps more relevant when carried out on patient data, there is a large variation in the data between patients, and so finding a consensus among all patients can be difficult. Instead, we: (1) Synthesize a set of parameters within the range in

Table 2. Parameter definition and range, established via clinical data and previous computational work. Note that the parameters with an asterisk next to their fitting range are fixed in the new model, e.g., c, K, ${\delta }_1$, ${\delta }_2$, and ${\gamma }_2$ are fixed at $0.00015$, 1, 5, 5, and 0, respectively. The ranges of parameters with a double asterisk are dependent on the data from the first $1.5$ cycles for each patient.

Param	Description	Range	Unit
$\mu$	max proliferation rate	0.001–0.09	[day]${}^{-1}$
${\mu }_1$	max proliferation rate (AD cells)	0.001–0.09	[day]${}^{-1}$
${\mu }_2$	max proliferation rate (AI cells)	0.001–0.09	[day]${}^{-1}$
$q_1$	min AD cell quota	0.41–1.73 **	[nmol][day]${}^{-1}$
$q_2$	min AI cell quota	0.01–0.41 **	[nmol][day]${}^{-1}$
b	baseline PSA production rate	0.0001–0.1	[$\mathsf{\mu }$g][nmol]${}^{-1}$[day]${}^{-1}$
$\sigma$	tumor PSA production rate	0.001–1	[$\mathsf{\mu }$g][nmol]${}^{-1}$[L]${}^{-1}$[day]${}^{-1}$
$ϵ$	PSA clearance rate	0.0001–0.1	[day]${}^{-1}$
$d_1$	max AD cell death rate	0.001–0.09	[day]${}^{-1}$
$d_2$	max AI cell death rate	0.01–0.001	[day]${}^{-1}$
${\delta }_1$	density death rate	1–90 *	[L]${}^{-1}$[day]${}^{-1}$
${\delta }_2$	density death rate	1–90 *	[L]${}^{-1}$[day]${}^{-1}$
$R_1$	AD death rate half-saturation	0–3	[nmol][L]${}^{-1}$
$R_2$	AI death rate half-saturation	1–6	[nmol][L]${}^{-1}$
c	maximum mutation rate	0.00001–0.0001 *	[day]${}^{-1}$
K	mutation rate half-saturation level	0.8–1.7 *	[nmol][day]${}^{-1}$
${\gamma }_1$	primary androgen production rate	0.008–0.8	[day]${}^{-1}$
${\gamma }_2$	secondary androgen production rate	0.001–0.1 *	[day]${}^{-1}$
m	diffusion rate from A to Q	0.01–0.9	[day]${}^{-1}$
$A_0$	maximum serum androgen level	27–35 **	[nmol][day]${}^{-1}$
$x_1\left(0\right)$	Initial subpopulation of AD cells	0.009–0.02	[L]
$x_2\left(0\right)$	Initial subpopulation of AI cells	0.0001–0.001	[L]

, and a treatment schedule that produces the expected dynamics observed in clinical data. (2) Using these parameters, we carry out the sensitivity process by increasing one parameter at a time by $1\%$ of its value. (3) We approximate $S_p$ at each time point for 1 treatment cycle using Equation (13). The process is repeated for all parameters. Finally, we record the maximum order of sensitivity in Table 1.

Table 1 shows the maximum effect that changing a parameter by $1\%$ has on the variables. For instance, by looking at the intersection between c and A, we see that changing c by $1\%$ can cause A to change by a maximum order of $-8$. To compare the sensitivity of these parameters, we add up their sensitivity coefficients. Doing so, we find that the parameters with combined order less than $-10$ (least sensitive) are c, K, ${\delta }_1$, ${\delta }_2$, and $d_2$. Since $d_1$ and $d_2$ serve similar purposes and $d_1$ is a sensitive parameter, we choose to not to fix $d_2$. In summary, for the fitting process of the new model, we fix c, K, ${\delta }_1$, ${\delta }_2$, and ${\gamma }_2$. Note that we do not carry out the sensitivity analysis for ${\gamma }_2$, due to its small value; in fact, we fix ${\gamma }_2$ to 0 for the new model (although a small value would suffice). The values that we fix for c, K, ${\delta }_1$, and ${\delta }_2$ are $0.00015$, 1, 5, and 5, respectively.

2.4. Parameter Range

Previous work employed various parameter ranges without a detailed discussion of how the parameter range is obtained. This caused an unnecessary inconsistency across the literature. Here, we present our method of approximation of the parameter range used for fitting in Table 2. This is possible, partially because our model has clear biological links to clinical data and previous work. In doing so, we hope to build upon this, in future work, for coherency across models. First, we note that the units of $x_i$, Q, A, and P are respectively L, nmol/L, nmol/L, and $\mathsf{\mu }$g/L. From this, the following ranges and unit of parameters are established:

• ${\mu }_1$ is the maximum proliferation rate for the AD cancer subpopulation. Its unit is [day]${}^{-1}$. Berges et al. [21] studied the proliferation and death rates of prostate cancer cells. We interpret their result for metastatic prostate cancer cells from hormonally untreated patients to be suitable for AD cells because, before hormonal treatment, most cancer cells should be androgen-dependent. This gives us a range of (0.004–0.081) for ${\mu }_1$. Similarly, for ${\mu }_2$ (the maximum proliferation rates for AI cancer subpopulation), its range (0.001–0.046) is derived from the result for hormonally failing patients. This is because we expect AI cells to take over, once the patients become hormonal refractory. Taking into account experimental and survey errors (especially in this case, where the cancer population size is small), we use (0.001–0.09) as the range for both ${\mu }_1$ and ${\mu }_2$ in the parameter fitting process.
• $d_1$ is the maximum death rate for AD cells. Its unit is [day]${}^{-1}$. Its range is also derived from Berges et al. [21], under similar assumptions in the case of the proliferation rates. The ranges for $d_1$ and $d_2$ are (0.001, 0.0525) and (0.015, 0.0775), respectively. For parameter fitting, we use the ranges (0.001, 0.09) and (0.01, 0.09) for $d_1$ and $d_2$, respectively.
• $q_1$ is the minimum androgen cell quota for AD cells. It has the same unit as Q, [nmol/L]. Tsutomu Nishiyama [22] showed in his review paper that hormonal suppression therapy aims to reduce serum androgen to below 0.69 nmol/L, which is considered the castration level (this threshold varies in practice, but no more than 1.73 nmol/L). The lowest threshold recorded in Nishiyama [22] is 0.41 nmol/L. This gives us an approximate bound for $q_1$, (0.41–1.73) because, once serum androgen drops below this range, the growth of AD cells is repressed. $q_2$, the minimum androgen cell quota for AI cells, should be smaller than 0.41 nmol/L, to allow AI cells some growth during castration. Since no information is available on the lower bound of $q_2$, we approximate the range to be (0.01–0.41). Since the value of $q_i$ is patient-specific, a fixed range will not suffice for every patient. Thus, we find the minimum serum androgen ($mi{n}_A$) in the first 1.5 cycles (from the data) and use the ranges ($mi{n}_A+0.2,mi{n}_A+0.5$) and ($0.01,mi{n}_A+0.2$), respectively, for $q_1$ and $q_2$ to reflect the condition $q_1>q_2$ and to represent the effect of cell quota on growth.
• The ${\delta }_i$’s are the density death rates. Their unit is [L]${}^{-1}$[day]${}^{-1}$. No experimental information is available for the density death rate of cancer cells. Additionally, our sensitivity results in Table 1 indicate that their importance is negligible, thus we fix them at 10${}^{-5}$ [mm${}^3$]${}^{-1}$[day] ${}^{-1}$, or 10 [L]${}^{-1}$[day]${}^{-1}$ using the value taken from Baez and Kuang [8]. We keep ${\delta }_i$ in our model to avoid unrealistic overgrowth of the cancer cell population.
• K is the half-saturation level of the androgen-dependent mutation rate from AD cells to AI cells. Its unit is [nmol][L]${}^{-1}$. Baez and Kuang used the range (0–1), while Portz et al. [7] used (0.08–1.7). Since no experimental validation is available, and as K is one of the least sensitive parameters, we fix K to be 1 [nmol][L]${}^{-1}$.
• $R_i$ are the half-saturation level of androgen-dependent death rates for AD and AI cells. Its unit is nmol/L. While no experimental information is available, computation results in [8,23] show that (0–3) and (1–6) are reasonable ranges for $R_1$ and $R_2$, respectively. Thus, we employ these ranges.
• c is the maximum mutation rate from AD cells to AI cells. Its unit is [day]${}^{-1}$. While there is no experimental ranges for c, numerical experimentation using a mathematical prostate model from Ideta et al. [5] established a reasonable range for c to be (${10}^{-5}$–${10}^{-4}$). This is often fixed at about 0.00015 in the literature [7,23]. Since c is one of the most insensitive parameters, we choose to fix it at 0.00015 [day]${}^{-1}$.
• b is the baseline PSA production rate. Its unit is [$\mathsf{\mu }$g][nmol]${}^{-1}$[day]${}^{-1}$. Baez and Portz [7,8] used two different ranges for b. Taking the lower and upper limits of both, we will use (0.0001–0.1) as the range for b. We note that, intuitively, the baseline production of PSA is produced by normal prostate cells; however, to simplify the model, we assume that this production is proportional to the intracellular androgen level, because the lack or abundance of androgen directly affects the product from prostate cells.
• $\sigma$ is the androgen-dependent PSA production rate of the cancer cells. Its unit is [$\mathsf{\mu }$g][nmol]${}^{-1}$[L]${}^{-1}$[day]${}^{-1}$. Everett et al. [23] used several ranges within (0.001–1), so we employ (0.001–1) as the range for $\sigma$.
• $ϵ$ is the PSA clearance rate. Its unit is [day]${}^{-1}$. While no clinical experiment supports a range for $ϵ$, Portz et al. [7] used 0.08, and Baez and Kuang [8] extended this to (0.001–0.01). We further extend the range to (0.0001–0.1) for our parameter estimation.
• ${\gamma }_1$ is the androgen production rate associated with the testes, the primary source of androgen production. Its unit is [day]${}^{-1}$. Previously, the value used in Baez et al. [8] seemed large, which resulted in an instantaneous increase in androgen level after the on-treatment interval stopped [18]. On the contrary, Ideta et al. [5] set ${\gamma }_1$ to be 0.08. Thus, for our purpose, we use (0.008–0.8) as a possible range for ${\gamma }_1$.
• ${\gamma }_2$ is the secondary androgen production rate, produced from sources other than the testes, such as the adrenal gland. The range established from [8] is (0.001–0.1) for ${\gamma }_2$, where their ${\gamma }_1=20$. However, the value of ${\gamma }_2$ should only be a small fraction of ${\gamma }_1$. Thus, in our case, the value of ${\gamma }_2$ is negligible. Hence, we fix it at 0 for the fitting process.
• m is the diffusion rate that links serum androgen level with intracellular androgen level. It is unitless. This rate is taken at 1 implicitly in [7,8]. Here, We allow m to vary from 0.01 to 0.9, to incorporate the level of synergy between A and Q.
• $A_0$ is the maximum serum androgen level. Clinical data shows that typical serum androgen range is below 27 [nmol][L]${}^{-1}$ [19]. Furthermore, computational work often assumed $A_0<35$ [nmol][L]${}^{-1}$ [5,8]. Since this range is patient-specific, for parameter fitting
  we find the maximum serum androgen ($ma{x}_A$) in the first 1.5 cycles (from data) and use the range ($ma{x}_A-5,ma{x}_A+5)$ for $A_0$.

Aside from the ranges for parameters, we also discuss the initial conditions for the model. $A\left(0\right)$ and $P\left(0\right)$ are taken as the first recorded serum androgen and PSA level (pre-treatment), respectively, from patient data. We assume $Q\left(0\right)$ to be $90\%$ of $A\left(0\right)$. This assumption means, prior to treatment, the level of serum androgen and intracellular androgen are approximately the same. For $x_1\left(0\right)$ and $x_2\left(0\right)$, we use experimental data on the effect of androgen suppression therapy on prostate volume (not tumor) from Bruchovsky et al. [19]. To derive this value, we compare the prostate volume pre-treatment (mean 24.7 cm${}^3$) and after the first treatment (mean 14.7 cm${}^3$). We assume that the AD cells are mostly responsible for this initial reduction, or an approximate initial size (for metastasized tumor) of 10 cm${}^3$, or 0.01 L. This indicates a biologically reasonable range for the initial volume of $x_1$. Since other factors can affect this value, we use a range of (0.009–0.02) as our possible range for $x_1\left(0\right)$. Additionally, if we assume that the initial subpopulation of $x_2\left(0\right)$ is about $1\%$ of $x_1\left(0\right)$, then we obtain the range (0.00001–0.001) for $x_2\left(0\right)$. The parameter ranges and initialization are summarized in Table 2.

2.5. Parameter Estimations

For parameter fitting, we use function fmincon from MATLAB (version 2018b), which utilizes an interior point algorithm to minimize an objective error function within the range provided in Table 2. Previously, the objective error function was calculated as the sum of the mean squared error (MSE) fitting error for PSA and androgen, because MSE punishes particularly large errors (which is undesirable in clinical applications). This emphasis on good fit can be problematic for forecasting, as the peak PSA level (during the off-treatment interval) is much larger than the PSA level during the on-treatment interval. Specifically, MSE will prioritize large errors, thus fmincon will estimate parameter values to achieve high PSA level to match the data at peak level, which leads to overestimated forecasts. This problem is escalated, as the time for on- and off-treatment intervals are taken from data. Furthermore, the problem is not resolved using other error measures. For instance, using the relative error metric causes the fitting to skew toward smaller data points due to their number, and so forecasting is often significantly underestimated [18]. Instead, taking into account the characteristic of the treatment schedule and its effect on PSA level, we employ a weighted least square error that will allow emphasis on the recent data, and a controlled weight on the error contribution from the peak level. First, we introduce the weighted error function:

$$Erro{r}_{MSE}=\frac{1}{N}\sum _{i=1}^N{(y_i-{\widehat{y}}_i)}^2{e}^{-\alpha (t_f-t_i)},$$

where N is the total number of data points, y is either the PSA or androgen data generated from the model, and $\widehat{y}$ is the respective observed data. $t_f$ is the final time of the second treatment period, and $t_i$ is the time of data point ${\widehat{y}}_i$. Here $\alpha$ is the exponential weight, which is usually taken to be between 0 and 1. The larger $\alpha$ is, the more memory-less the process becomes, e.g., earlier data points become weightless. Since we want to control the error contribution from before and after the peak PSA level, and as the data are collected somewhat irregularly, we employ the following scheme to give sufficient weights to the data before and after the peak:

$$Erro{r}_{MSE}=W_1\frac{1}{N_1}\sum _{i=1}^{peak}{(y_i-{\widehat{y}}_i)}^2{e}^{-{\alpha }_1(t_f-t_i)}+W_2\frac{1}{N_2}\sum _{i=peak+1}^{end}{(y_i-{\widehat{y}}_i)}^2{e}^{-{\alpha }_2(t_f-t_i)}$$

Here, $W_1$ and $W_2$ are the desired contributions of error from prior and after the peak PSA level, respectively. Similarly, $N_1$ and $N_2$ are the total number of data points, for the respective part. We find that setting ${\alpha }_1=0.01={\alpha }_2$ and $W_1=W_2=0.5$, meaning equal contribution of error from both parts, provides consistent results. Note that, in practice, the values of ${\alpha }_i$ and $W_i$ should be specialized to each patient. Here, we only wish to show their effectiveness in fitting and forecasting. The objective error function that is minimized by fmincon is the sum of PSA and androgen residuals, which takes the form:

$$Objectiv{e}_{MSE}=Erro{r}_{MSE,PSA}+Erro{r}_{MSE,androgen}.$$

3. Numerical Results

For comparison purposes, we calculate the errors from the fitting and forecasting of BK and the new model.

Table 3. Fitting mean squared error (MSE) comparison (median, 1st quartile, 3rd quartile). Two models are compared, using 26 patient’s data. Both models show comparable good fitting results. Note that the fitting ability of model 2 has been shown to be superior, among existing work [8,18]. Additionally, the incorporation of serum androgen in the new model does not significantly improve the fitting of androgen.

Model	PSA			Androgen
	Median	${\mathit{Q}}_1$	${\mathit{Q}}_3$	Median	${\mathit{Q}}_1$	${\mathit{Q}}_3$
BK model	1.43	0.85	3.72	4.15	2.42	7.65
New model	2.03	0.88	4.52	3.68	2.12	12.69

shows a comparable good fit in the first one and a half cycles, for both models. On the other hand,

Table 4. Forecasting mean squared error (MSE) comparison (median, 1st quartile, 3rd quartile). Two models are compared, using 26 patient’s data. The new model demonstrates a slightly better forecasting ability, compared to the BK model. Furthermore, the forecasting ability of model 2 has been shown to be superior, among existing work under different metrics [8,18]. Additionally, the forecasting of androgen is comparable between the two models.

Model	PSA			Androgen
	Median	${\mathit{Q}}_1$	${\mathit{Q}}_3$	Median	${\mathit{Q}}_1$	${\mathit{Q}}_3$
BK model	9.02	4.34	17.32	11.99	4.70	27.81
New model	6.78	4.20	14.60	12.56	5.22	28.32

shows that, while both models produce good forecasting, the new model outperforms the BK model in term of forecasting. Note that, for the BK model, we fit 17 parameters and 2 initial conditions, while the new model fitting accounts for 14 parameters and 2 initial conditions. Thus, information criteria (like the AIC) can be used to further the comparison between the two models, as done in [24]. However, such comparison does not evaluate the biological mechanism of the model, thus we omit it here. We select representatives of fitting and forecasting results, and present it in Figure 1 and Figure 2.

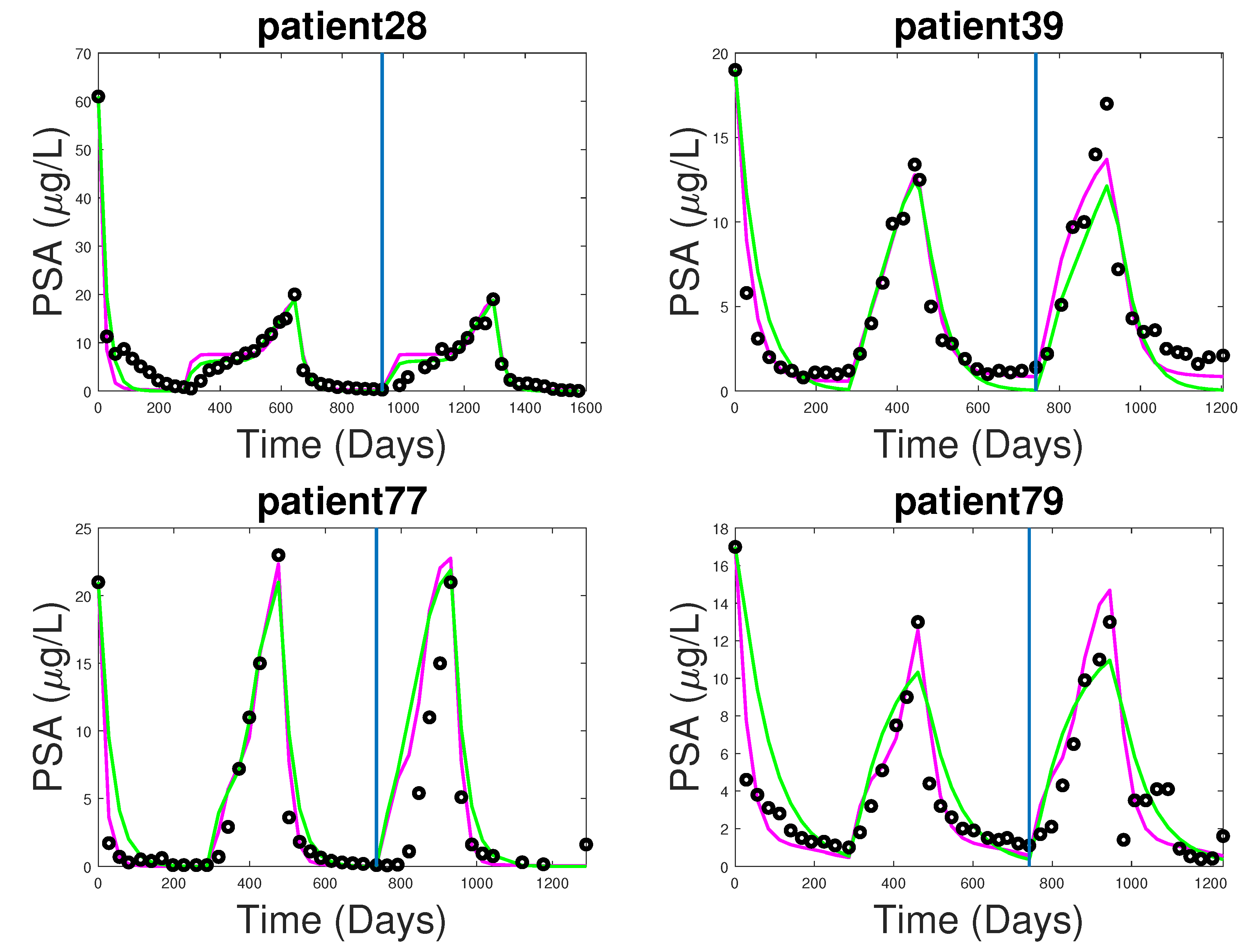
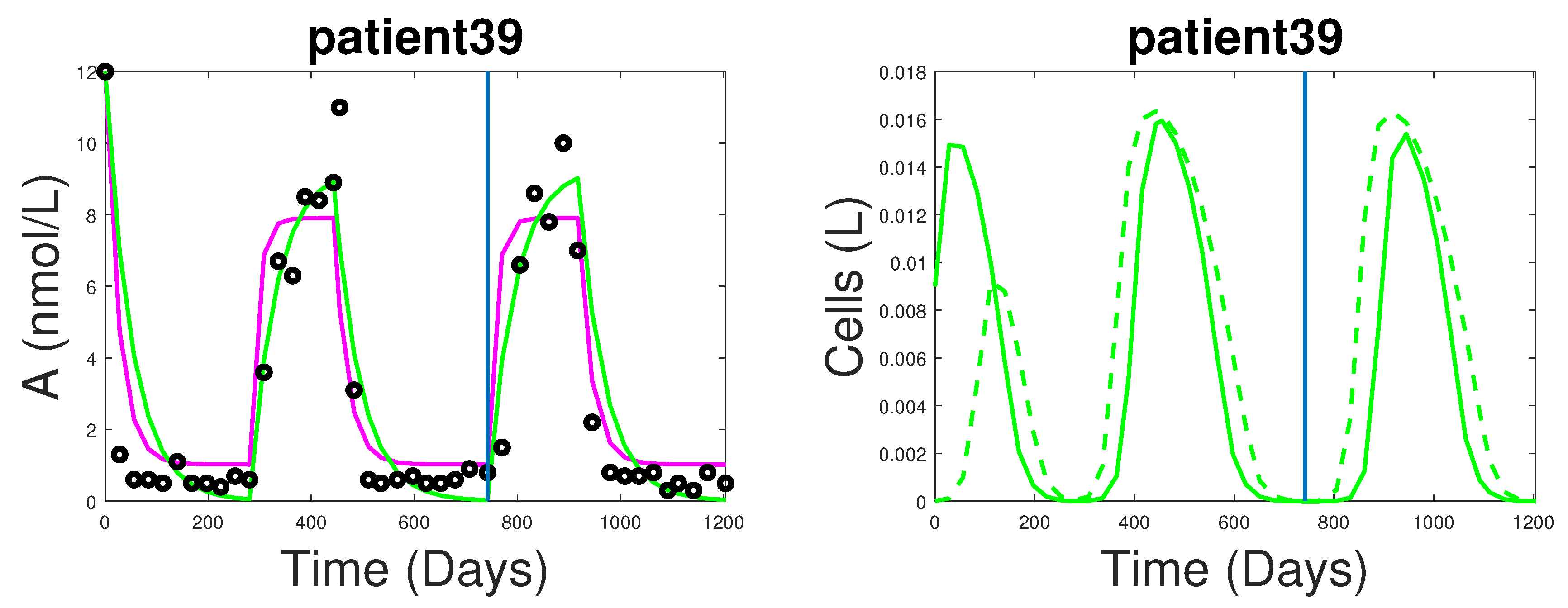
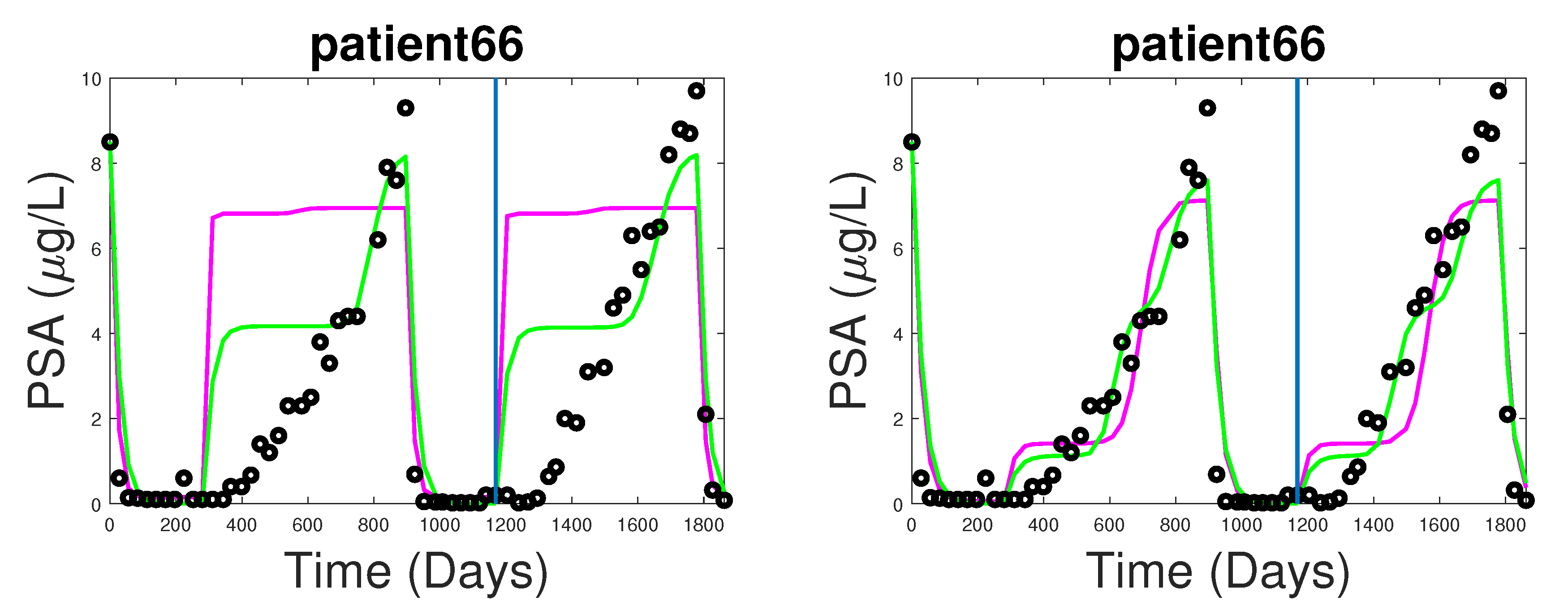
3.1. Fitting and Forecasting of Androgen and Cancer Cell Dynamics

We provide an example of fitting and forecasting comparisons for androgen on the left figure in Figure 2. Note that while both models fit and forecast the dynamics of androgen comparatively well, the new model exhibits a higher flexibility, in contrast to the square-like shape of androgen in the BK model. dWe also provide an example of cancer cell dynamics, in the right figure in Figure 2. The result from cancer dynamics suggests that the onset of hormonal resistance can develop early into the treatment. Additionally, since cancer subpopulations can go into near extinction (during the on-treatment interval) before bouncing back, this suggests that the mechanism used to incorporate androgen into growth and death rates needs improvement, or perhaps the problem asks for an optimization of parameter values using analytical means. Finally, since the cancer population can stay under control after AI cells overtake AD cells in number, it suggests against the intuitive definition that hormonal resistance occurs when AI cells overtake AD cells.

3.2. Note on Numerical Fitting Using Two-Part Weighted Error

Different patients react differently to the treatment, especially during the first cycle of treatment—the time for PSA to fully relapse varies between patients. Figure 3 shows an example where PSA level takes over two years to reach the upper PSA threshold. Recall that our fitting scheme utilizes a fixed exponential weight that works well for most patients, but fails in this case due to the abnormally long time it takes PSA to relapse (left figure). This indicates that our choices of ${\alpha }_i=0.01$ and $W_i=0.5$ are not suitable for this particular case. As a counter-example, by reducing the exponential weight and readjusting the contribution of errors from each section of data (e.g., adjusting ${\alpha }_1$ to $0.001$, $W_1=0.7$, and $W_2=0.3$), the fitting and forecasting results significantly improve (right figure).

4. Dynamics of the New Model

In this section, we carry out mathematical analyses for the newly proposed model, which help to justify its coherence with biological expectations. Previous studies [8,18] have already examined some standard properties of the BK model and its variations, so we only focus on the new model here. We remark that, while PSA serves as an important indicator of how good the model is against clinical data, the dynamics of the system are independent of the dynamics of PSA. In addition, if the dynamics of $x_i$, Q, and A are known, one can immediately infer the dynamics of P. Thus we will only carry out our analysis with $x_i$, Q, and A. The first proposition establishes a positively invariant region, which is also bounded. This supports the biological validity of the model since we expect $x_i$, Q, and A to stay non-negative and never become infinite.

Proposition 1.

Let $\overline{A}=\frac{{\gamma }_2+{\gamma }_1{A}_0}{{\gamma }_1}$ and assume $q_2\le q_1<\overline{A}$ and ${\gamma }_2>{\gamma }_1{q}_2$. Furthermore, we assume that when androgen is abundant, the growth rate is larger than the death rate, meaning ${\mu }_i(1-q_i/\overline{A})>D_i\left(\overline{A}\right)$ for $i=1,2$. Then, the solutions that start in the region $\{(x_1,x_2,Q,A):0<x_1\le M_x,0<x_2\le M_y,Q,A\in [q_2,\overline{A}]\}$, stay in that region. Here, $M_x=\frac{1}{{\delta }_1}\left({\mu }_1(1-q_1/\overline{A})-D_1\left(\overline{A}\right)\right)$ and

$$M_y=\frac{1}{2{\delta }_2}\left(\left({\mu }_2(1-q_2/\overline{A})-D_2\left(\overline{A}\right)\right)+\sqrt{4\lambda \left(q_2\right)M_x{\delta }_2+{\left({\mu }_2(1-q_2/\overline{A})-D_2\left(\overline{A}\right)\right)}^2}\right).$$

Proof. 

Since $A^{\prime }\left(t\right)={\gamma }_2+{\gamma }_1{A}_0(1-\frac{A}{A_0})-{\gamma }_1{A}_0(1-u)$, we see that $A^{\prime }\left(q_2\right)\ge 0$ and $A^{\prime }\left(\overline{A}\right)\le 0$. It follows that $q_2\le A\left(t\right)\le \overline{A}$ for all $t>0$ with initial condition in the same region. Similarly, since $Q^{\prime }\left(t\right)=m(A-Q)-\frac{{\mu }_1(Q-q_1)x_1+{\mu }_2(Q-q_2)x_2}{x_1+x_2}$, we find that $Q^{\prime }\left(q_2\right)\ge 0$ and $Q^{\prime }\left(\overline{A}\right)\le 0$. Thus, a similar conclusion follows. Consider the rate of change of $x_1$,

$$\begin{array}{cc}\hfill x_1^{\prime }& ={\mu }_1\left(1-\frac{q_1}{Q}\right)x_1-(D_1\left(Q\right)+{\delta }_1{x}_1)x_1-\lambda \left(Q\right)x_1\hfill \\ & \le \left({\mu }_1\left(1-\frac{q_1}{\overline{A}}\right)-D_1\left(\overline{A}\right)\right)x_1-{\delta }_1{x}_1^2.\hfill \end{array}$$

This implies that the limit supremum of $x_1\left(t\right)$ is bounded by $\frac{1}{{\delta }_1}\left({\mu }_1(1-q_1/\overline{A})-D_1\left(\overline{A}\right)\right)=:M_x$. Now consider the rate of change of $x_2$,

$$\begin{array}{cc}\hfill x_2^{\prime }& ={\mu }_2\left(1-\frac{q_2}{Q}\right)x_2-(D_2\left(Q\right)+{\delta }_2{x}_2)x_2+\lambda \left(Q\right)x_1.\hfill \end{array}$$

In the limit $t\to \infty$, $x_2^{\prime }$ is bounded above by

$$\begin{array}{cc}\hfill x_2^{\prime }& \le {\mu }_2\left(1-\frac{q_2}{\overline{A}}\right)x_2-(D_2\left(\overline{A}\right)+{\delta }_2{x}_2)x_2+\lambda \left(q_2\right)M_x\hfill \\ & =\lambda \left(q_2\right)M_x+\left({\mu }_2\left(1-\frac{q_2}{\overline{A}}\right)-D_2\left(\overline{A}\right)\right)x_2-{\delta }_2{x}^2=:h\left(x_2\right).\hfill \end{array}$$

The function $h\left(x_2\right)$ is a concave-down parabola. Thus ${lim\; sup}_{t\to \infty }{x}_2\left(t\right)$ is bounded above by the larger solution of $h\left(x_2\right)=0$. Solving for $h\left(x\right)=0$, we obtain the upper bound of the limit supremum of $x_2$,

$$M_y=\frac{1}{2{\delta }_2}\left(\left({\mu }_2(1-q_2/\overline{A})-D_2\left(\overline{A}\right)\right)+\sqrt{4\lambda \left(q_2\right)M_x{\delta }_2+{\left({\mu }_2(1-q_2/\overline{A})-D_2\left(\overline{A}\right)\right)}^2}\right).$$

Since $x_1\left(0\right)<M_x$ and $x_2\left(0\right)<M_y$, $x_1$ and $x_2$ are bounded above by $M_x$ and $M_y$, respectively. Additionally, if $x_i\left(0\right)>0$, then the positivity of $x_i\left(t\right)$ follows immediately.  ☐

The second proposition shows that the system has a boundary equilibrium where AD cells become extinct, during the off-treatment interval. Additionally, it establishes sufficient conditions for the existence of a unique positive steady-state.

Proposition 2.

In the case of $u=1$, assume $q_1>q_2$, then $E_1=(0,\frac{{\mu }_2(1-q_2/Q_{*})-D_2\left(Q_{*}\right)}{{\delta }_{22}},Q_{*},A_{*})$, where $Q_{*}=\frac{m{A}_{*}+{\mu }_1{q}_1}{m+{\mu }_1}$ and $A_{*}=({\gamma }_2+{\gamma }_1{A}_0)/{\gamma }_1$, is the only equilibrium state where the AD subpopulation becomes extinct. Furthermore, suppose conditions (1) and (2) hold:

• $\frac{m{A}_0}{m+max\{{\mu }_1,{\mu }_2\}}>q_1$
• $\frac{m{A}_0+min\{{\mu }_1{q}_1,{\mu }_2{q}_2\}}{m+max\{{\mu }_1,{\mu }_2\}}>\frac{1}{2}\left(\Delta +\sqrt{{\left(\Delta \right)}^2-4max\{R_1,K\}}\right)>0$,

where $\Delta =q_1+\left(1+\frac{d_{1}c}{{\mu }_1}\right)max\{R_1,K\}$. Then the system has a unique positive steady-state $(x_1^{*},x_2^{*},Q^{*},A^{*})$.

Proof. 

For $u=1$ (off-treatment interval), we first consider the boundary equilibria of the system. Since $(x_1,x_2)=(0,0)$ is undefined for the system and $x_{2*}=0$ implies $x_{1*}=0$, the only equilibrium involving an extinction of a cancer subpopulation takes place when $x_{1*}=0$. In this case, solving $x_2^{\prime }=0$ yields $x_{2*}=\frac{{\mu }_2(1-q_2/Q_{*})-D_2\left(Q_{*}\right)}{{\delta }_{22}}$. Additionally, solving $Q^{\prime }=0$ and $A^{\prime }=0$ yields $Q_{*}=\frac{m{A}_{*}+{\mu }_1{q}_1}{m+{\mu }_1}$ and $A_{*}=({\gamma }_2+{\gamma }_1{A}_0)\setminus {\gamma }_1$.

For the positive steady state, suppose that $x_1^{*},x_2^{*},Q^{*},A^{*}>0$. Then solving for $x_1^{\prime }=0$ and $x_2^{\prime }=0$ gives:

$$\left\{\begin{array}{cc}0\hfill & =A_1{x}_1^{*}-{\delta }_{11}{\left(x_1^{*}\right)}^2\hfill \\ 0\hfill & =A_2{x}_2^{*}-{\delta }_{22}{\left(x_2^{*}\right)}^2+\lambda \left(Q^{*}\right)x_1^{*}\hfill \end{array}\right.\Rightarrow \left\{\begin{array}{cc}{\delta }_{11}{\left(x_1^{*}\right)}^2\hfill & =A_1{x}_1^{*}\hfill \\ {\delta }_{22}{\left(x_2^{*}\right)}^2\hfill & =A_2{x}_2^{*}+\lambda \left(Q^{*}\right)x_1^{*}\hfill \end{array}\right.$$

(14)

where $A_i$ are the coefficients of $x_i^{*}$, e.g., $A_1={\mu }_1(1-\frac{q_1}{Q^{*}})-D_1\left(Q^{*}\right)-\lambda \left(Q^{*}\right)$. Dividing the previous two equations to obtain

$$\frac{{\delta }_{11}}{{\delta }_{22}}{\left(\frac{x_1^{*}}{x_2^{*}}\right)}^2=\frac{A_1\left(\frac{x_1^{*}}{x_2^{*}}\right)}{A_2+\lambda \left(Q^{*}\right)\left(\frac{x_1^{*}}{x_2^{*}}\right)}$$

(15)

Set $y=\left(\frac{x_1^{*}}{x_2^{*}}\right)$, then

$$f\left(y\right)=\left(\lambda \left(Q^{*}\right)\frac{{\delta }_{11}}{{\delta }_{22}}\right)y^2+\left(A_2\left(Q^{*}\right)\frac{{\delta }_{11}}{{\delta }_{22}}\right)y-A_1\left(Q^{*}\right)=0.$$

(16)

Note that $\lambda \left(Q^{*}\right)=c\frac{K}{Q^{*}+K}>0$, so if $A_1>0$, then by Descartes’s rule of sign, the system has a unique solution y, regardless of the sign for $A_2$. The uniqueness of y implies that the ratio $\frac{x_1^{*}}{x_2^{*}}$ is constant. We proceed to establish the positivity of $A_1$. Explicitly, $A_1$ takes the form

$$\begin{array}{cc}\hfill A_1\left(Q^{*}\right)& ={\mu }_1\left(1-\frac{q_1}{Q^{*}}\right)-D_1\left(Q^{*}\right)-\lambda \left(Q^{*}\right)\hfill \\ & ={\mu }_1\left(1-\frac{q_1}{Q^{*}}\right)-d_1\frac{R_1}{Q^{*}+R_1}-c\frac{K}{Q^{*}+K}\hfill \end{array}$$

Note that, since the treatment is off, biologically $Q\left(t\right)>>q_1$, which allows strong growth of the AD cell subpopulation. We will establish later that there is indeed a lower bound of $Q\left(t\right)$ satisfying $lim\; infQ\left(t\right)>q_1$, under reasonable biological constraints. For the moment, we assume such lower bound exists. Then

$$\begin{array}{cc}\hfill lim\; inf{A}_1& \ge {\mu }_1\left(1-\frac{q_1}{Q_m}\right)-d_1\frac{R_1}{Q_m+R_1}-c\frac{K}{Q_m+K}\hfill \\ & \ge {\mu }_1\left(1-\frac{q_1}{Q_m}\right)-(d_1+c)\frac{max\{R_1,K\}}{Q_m+max\{R_1,K\}}\hfill \end{array}$$

where $Q_m>>q_1$ is a lower bound of $Q\left(t\right)$ for the off-treatment interval. We would like for $A_1>0$, thus rearranging terms give the condition:

$$Q_m^2-\left(q_1+\left(1+\frac{d_{1}c}{{\mu }_1}max\{R_1,K\}\right)\right)Q_m-max\{R_1,K\}>0.$$

(17)

Next we examine the expression for $Q^{\prime }\left(t\right)$ to find an appropriate lower bound. Note that, since as $t\to \infty ,A\left(t\right)\to \frac{{\gamma }_2}{{\gamma }_1}+A_0=:A^{*}$, we have the following:

$$\begin{array}{cc}\hfill \underset{t\to \infty }{lim}{Q}^{\prime }\left(t\right)& =m(A^{*}-Q)-\frac{{\mu }_1(Q-q_1)x_1+{\mu }_2(Q-q_2)x_2}{x_1+x_2}\hfill \\ & =\left(m{A}^{*}+\frac{{\mu }_1{q}_1+x_1+{\mu }_2{q}_2{x}_2}{x_1+x_2}\right)-\left(m+\frac{{\mu }_1{x}_1+{\mu }_2{x}_2}{x_1+x_2}\right)Q\hfill \\ & \ge \left(m{A}_0+\frac{{\mu }_1{q}_1+x_1+{\mu }_2{q}_2{x}_2}{x_1+x_2}\right)-\left(m+\frac{{\mu }_1{x}_1+{\mu }_2{x}_2}{x_1+x_2}\right)Q.\hfill \end{array}$$

This implies

$$\underset{t\to \infty }{lim\; inf}Q\left(t\right)\ge \underset{t\to \infty }{lim}\frac{m{A}_0+\frac{{\mu }_1{q}_1{x}_1+{\mu }_2{q}_2{x}_2}{x_1+x_2}}{m+\frac{{\mu }_1{x}_1+{\mu }_2{x}_2}{x_1+x_2}}+\left(Q\left(0\right)-\frac{m{A}_0+\frac{{\mu }_1{q}_1{x}_1+{\mu }_2{q}_2{x}_2}{x_1+x_2}}{m+\frac{{\mu }_1{x}_1+{\mu }_2{x}_2}{x_1+x_2}}\right)e^{-\left(m+\frac{{\mu }_1{x}_1+{\mu }_2{x}_2}{x_1+x_2}\right)t}.$$

Then as $t\to \infty$, the exponential term approaches 0, so

$$\begin{array}{cc}\hfill \underset{t\to \infty }{lim\; inf}Q\left(t\right)& \ge \frac{m{A}_0(x_1+x_2)+{\mu }_1{q}_1{x}_1+{\mu }_2{q}_2{x}_2}{m(x_1+x_2)+({\mu }_1{x}_1+{\mu }_2{x}_2)}\hfill \\ & \ge \frac{m{A}_0(x_1+x_2)+min\{{\mu }_1{q}_1,{\mu }_2{q}_2\}(x_1+x_2)}{m(x_1+x_2)+max\{{\mu }_1,{\mu }_2\}(x_1+x_2)}\hfill \\ & =\frac{m{A}_0+min\{{\mu }_1{q}_1,{\mu }_2{q}_2\}}{m+max\{{\mu }_1,{\mu }_2\}}.\hfill \end{array}$$

This means that, eventually, $Q\left(t\right)$ will be bounded below by $\frac{m{A}_0+min\{{\mu }_1{q}_1,{\mu }_2{q}_2\}}{m+max\{{\mu }_1,{\mu }_2\}}>q_1$, which is true because of our biologically reasonable condition $\frac{m{A}_0}{m+max\{{\mu }_1,{\mu }_2\}}>q_1$ (e.g., $A_0>>q_1$). Thus, we establish that indeed there is a lower bound of $Q\left(t\right)$ that satisfies $lim\; infQ\left(t\right)>q_1$. Now, the condition in Equation (17) is satisfied in the limit of $t\to \infty$, if $\frac{m{A}_0+min\{{\mu }_1{q}_1,{\mu }_2{q}_2\}}{m+max\{{\mu }_1,{\mu }_2\}}$ is greater than the larger solution for $Q_m$ (or smaller than the smaller solution) in Equation 17. Therefore, $A_1>0$ requires either

$$\frac{m{A}_0+min\{{\mu }_1{q}_1,{\mu }_2{q}_2\}}{m+max\{{\mu }_1,{\mu }_2\}}>\frac{1}{2}\left(\Delta +\sqrt{{\left(\Delta \right)}^2-4max\{R_1,K\}}\right),$$

(18)

or,

$$\frac{m{A}_0+min\{{\mu }_1{q}_1,{\mu }_2{q}_2\}}{m+max\{{\mu }_1,{\mu }_2\}}<\frac{1}{2}\left(\Delta -\sqrt{{\left(\Delta \right)}^2-4max\{R_1,K\}}\right)$$

(19)

where $\Delta =q_1+\left(1+\frac{d_{1}c}{{\mu }_1}\right)max\{R_1,K\}$. Since the condition in Equation (19) is not possible (e.g., the right hand side is negative, but the left hand side is positive), the only possible condition is Equation (18), which is the condition in the proposition. This establishes the existence of positive $x_1^{*}$ and $x_2^{*}$, which have a fixed ratio $y^{*}$. Solving $Q^{\prime }=0$ for $Q^{*}$ gives the positive steady state

$$Q^{*}=\frac{m{A}^{*}+\frac{{\mu }_1{q}_1{x}_1^{*}+{\mu }_2{q}_2{x}_2^{*}}{x_1^{*}+x_2^{*}}}{m+\frac{{\mu }_1{x}_1^{*}+{\mu }_2{x}_2^{*}}{x_1^{*}+x_2^{*}}}=\frac{m{A}^{*}(x_1^{*}+x_2^{*})+{\mu }_1{q}_1{x}_1^{*}+{\mu }_2{q}_2{x}_2^{*}}{m(x_1^{*}+x_2^{*})+{\mu }_1{x}_1^{*}+{\mu }_2{x}_2^{*}}>0.$$

(20)

Finally, to show uniqueness, recall that the ratio of $x_1^{*}$ and $x_2^{*}$ is a fixed constant, $y^{*}$. Thus, substitute $x_2^{*}=x_1^{*}/y^{*}$ in Equation (20) to obtain

$$\begin{array}{cc}\hfill Q^{*}& =\frac{m{A}^{*}{x}_1^{*}(1+\frac{1}{y^{*}})+({\mu }_1{q}_1+{\mu }_2{q}_2\frac{1}{y^{*}})x_1^{*}}{m{x}_1^{*}(1+\frac{1}{y^{*}})+({\mu }_1+{\mu }_2\frac{1}{y^{*}})x_1^{*}}=\frac{m{A}^{*}(1+\frac{1}{y^{*}})+({\mu }_1{q}_1+{\mu }_2{q}_2\frac{1}{y^{*}})}{m(1+\frac{1}{y^{*}})+({\mu }_1+{\mu }_2\frac{1}{y^{*}})}.\hfill \end{array}$$

This shows that $Q^{*}$ is unique. Finally, from Equation (14), $x_1^{*}=\frac{A_1\left(Q^{*}\right)}{{\delta }_{11}}$. It follows that $x_1^{*}$ and $x_2^{*}$ are also unique. Since ${lim}_{t\to \infty }A\left(t\right)=\frac{{\gamma }_2}{{\gamma }_1}+A_0=:A^{*}$, the existence of a unique positive equilibrium follows. ☐

The third proposition shows that when the patient is on treatment, under biologically reasonable conditions, the boundary equilibrium with the extinction of AD cells is the only equilibrium of the system. In this case, it establishes a sufficient and necessary condition for the boundary equilibrium to be globally stable. Additionally, it provides sufficient conditions for both cancer subpopulations to eventually become extinct.

Proposition 3.

In the case of $u=0$, if

$$\frac{m\frac{{\gamma }_1}{{\gamma }_2}+max\{{\mu }_1{q}_1,{\mu }_2{q}_2\}}{m+min\{{\mu }_1,{\mu }_2\}}<q_1,$$

then the system does not have a positive steady-state and $x_1$ becomes extinct as $t\to \infty$. Furthermore, $Q\left(t\right)$ approaches $Q_{*}=\frac{m{A}_{*}+{\mu }_1{q}_1}{m+{\mu }_1}$, where $A_{*}=\frac{{\gamma }_2}{{\gamma }_1}$.

In addition, if

$${\mu }_2\left(1-\frac{q_2}{Q_{*}}\right)-d_2\frac{R_2}{Q_{*}+R_2}>0,$$

then $x_2$ approaches $\frac{{\mu }_2\left(1-\frac{q_2}{Q_{*}}\right)-d_2\frac{R_2}{Q_{*}+R_2}}{{\delta }_2}$ and $E_1=(0,\frac{{\mu }_2(1-q_2/Q_{*})-D_2\left(Q_{*}\right)}{{\delta }_{22}},Q_{*},A_{*})$ is globally stable. On the other hand, if either

$${\mu }_2\left(1-\frac{q_2}{Q_{*}}\right)-d_2\frac{R_2}{Q_{*}+R_2}>0,$$

or,

$$\frac{m\frac{{\gamma }_1}{{\gamma }_2}+max\{{\mu }_1{q}_1,{\mu }_2{q}_2\}}{m+min\{{\mu }_1,{\mu }_2\}}\le q_2,$$

then both $x_1$ and $x_2$ become extinct in the limit of $t\to \infty$.

Proof. 

Similar to the previous proof, we establish that in the limit of $t\to \infty$, $A\to \frac{{\gamma }_2}{{\gamma }_1}$ and

$$\underline{Q}:=\frac{m\frac{{\gamma }_1}{{\gamma }_2}+max\{{\mu }_1{q}_1,{\mu }_2{q}_2\}}{m+min\{{\mu }_1,{\mu }_2\}}\le Q\left(t\right)\le \frac{m\frac{{\gamma }_1}{{\gamma }_2}+min\{{\mu }_1{q}_1,{\mu }_2{q}_2\}}{m+max\{{\mu }_1,{\mu }_2\}}=:\overline{Q}$$

(21)

Suppose $\overline{Q}<q_1$. This implies that ${lim}_{t\to \infty }{x}_1^{\prime }\left(t\right)<-(D_1\left(Q\right)+{\delta }_1{x}_1+\lambda \left(Q\right))x_1<0$. Thus there is no positive steady-state for $x_1\left(t\right)$ and ${lim}_{t\to \infty }{x}_1\left(t\right)=0$. Then in the limit of $x_1\to 0$ and $A\to \frac{{\gamma }_2}{{\gamma }_1}$,

$$Q^{\prime }\left(t\right)=m\left(\frac{{\gamma }_2}{{\gamma }_1}-Q\right)-{\mu }_2(Q-q_2)=\left(m\frac{{\gamma }_2}{{\gamma }_1}+{\mu }_2{q}_2\right)-(m+{\mu }_2)Q.$$

This implies that ${lim}_{t\to \infty }Q\left(t\right)=\frac{m\frac{{\gamma }_2}{{\gamma }_1}+{\mu }_2{q}_2}{m+{\mu }_2}=Q_{*}$. Furthermore, in the limit of $t\to \infty$,

$$x_2^{\prime }={\mu }_2\left(1-\frac{q_2}{Q_{*}}\right)x_2-(D_2\left(Q_{*}\right)+{\delta }_2{x}_2)x_2=\left({\mu }_2\left(1-\frac{q_2}{Q_{*}}\right)-d_2\frac{R_2}{Q_{*}+R_2}\right)x_2-{\delta }_2{x}_2^2.$$

If ${\mu }_2\left(1-\frac{q_2}{Q_{*}}\right)-d_2\frac{R_2}{Q_{*}+R_2}>0$, then $x_2$ approaches $\frac{{\mu }_2\left(1-\frac{q_2}{Q_{*}}\right)-d_2\frac{R_2}{Q_{*}+R_2}}{{\delta }_2}$ and $E_1$ is globally stable. On the other hand, if ${\mu }_2\left(1-\frac{q_2}{Q_{*}}\right)-d_2\frac{R_2}{Q_{*}+R_2}<0$, then $x_2$ becomes extinct. Alternatively, if $\overline{Q}<q_2$, then ${lim}_{t\to \infty }{x}_2^{\prime }\left(t\right)<-(D_2\left(Q\right)+{\delta }_1{x}_2)x_2<0$. This implies ${lim}_{t\to \infty }{x}_2\left(t\right)=0$. ☐

5. Discussion

Mathematical models for prostate cancer have made significant progress since the work of Jackson [25]. Consequently, recent approaches have been focused on the application aspects in clinical settings. However, there are still obvious questions without an easy answer; for example, how one would define hormonal resistance in a rigorous mathematical sense and yet still meaningful in applications, or the identifiability of the model parameters. These difficult questions, that link theoretical work and application, ask for mechanistic models that can test theories against data. To this end, we aim to build upon a series of previous works to create a model with direct links to clinical data. We study the model and explore various aspects relating to using it. In this section, we summarize our findings and point out the limitations of our work.

(A1) From Table 3, both the BK model and the new model achieved similar accuracy for fitting. Since we used a two-part fitting scheme with exponential weight, the fitting was good when PSA quickly relapsed after the patient was put off treatment; see patients 39, 77, and 79 in Figure 1. On the other hand, when PSA took a longer time to reach the peak, the accuracy of fitting was not as good as in the previous cases; for instance, in patient 28 in Figure 1. In other words, because we chose to use a fixed exponential weight for fitting, the earlier the data points, the less weight that those data points contributed in the parameter estimation process. Thus, for patients with an abnormally long first cycle, most of the earlier data were essentially not accounted for during fitting; see patient 66 in Figure 3. To resolve this problem, a possible scheme is to use a linear weight. Specifically, we would first normalize the weight contribution from the peak PSA level to be 1. Then, the weight contribution of the points before the peak is the relative height with respect to the peak. This would ensure that earlier points have a more significant contribution to the fitting. While it is well-suggested that individual patients should have their unique parameter set, we further suggest that the process of studying the patient data should be unique, in order to capture the patient’s characteristics; for example, a patient-specific weight for fitting in this case.

(A2) From Table 4, the new model slightly outperformed the BK model, in terms of prediction, which is noteworthy as the new model used fewer parameters for fitting. An interesting observation is that the new model did not overshoot forecasting, perhaps due to the parameter ranges established in Table 2. This can become a problem, if there is a stable equilibrium below the upper threshold PSA level required for putting the patient on treatment. In such a case, the model would be unrealistic for the parameter values which influence the equilibrium. While this problem can be mediated by forcing hormonal resistance within five years, as done in [6], it is perhaps better done by optimization of parameter ranges via mathematical analysis. We further note that when the data had good regularity, in terms of the similarity in the shape of data for different cycles (see patients 28, 77, and 79), the forecasting was quite accurate. However, when unforeseen changes occur in the data (patient 39), the model may fail to capture this change. Hence, the use of a stochastic model or uncertainty quantification is necessary for such applications.

(A3) Phan et al. [18] noted the problem of the sudden jump in PSA between the transition of the on- and off-treatment intervals in the fitting and forecasting of the BK model. Our result suggests that the main cause was the abnormally large value of the rate of primary androgen production (${\gamma }_1$). By adjusting this value in accordance to [6], we resolved this problem, as seen for patients 28, 39, 77, and 79 in Figure 1. Phan et al. [18] also mentioned a delay that sometimes occurs during the relapsing period of PSA; for example, in patient 77. While this can potentially be a problem with the parameter, it is more likely caused by the drug residue or the mechanism of how the patient’s body reacts to the drug. Thus, we suggest future attempts take the drug dynamics into account.

(A4) We carried out a mathematical analysis of the model, to validate its biological properties and to show that it is possible to drive the cancer cells to extinction, as seen in the limit of time approaches infinity (in an environment of sufficiently low androgen level).

The right figure in Figure 2 shows that the cancer cell subpopulations can indeed reach near-extinction, prior to the on-treatment phase. We note that, while the cause of this is likely due to setting the secondary production term to 0 (e.g., ${\gamma }_2$ = 0) in our numerical study of the new model, it suggests that if the androgen level drops below the cell quota of AI cell, the AI subpopulation can become near-extinction for the duration of on-treatment. However, this is only possible in a theoretical sense. In practice, it is difficult to find clinical studies that support this theoretical result. This is because the androgen level required for the extinction of cancer cells may be much lower than the limit of hormonal therapy. Furthermore, the result will not hold if there is a variation of the cancer cells that gives some cells near-complete independence from androgen, which would make the condition in proposition 3 impossible to achieve. To resolve this in a theoretical sense, we could replace the two cell subpopulations with N subpopulations. Taking the limit as $N\to \infty$ represents the continuous variation in cancer cells. However, such complexity resulting from adding N compartments of cancer cells is unlikely to be either insightful or practical. Instead, we suggest future work to incorporate a mechanism that takes into account the degree of androgen dependency of the tumor in a continuous spectrum, without adding unnecessary compartments. This may allow for a more useful characterization of the condition for cancer extinction under hormonal treatment.

In addition, we also studied the sensitivity of the parameters over time. While this method was one at a time, this helped to gauge the maximum effect that changing a parameter by a small percentage could have on the dynamics of the system. By doing so, we highlighted the most insensitive parameters and fixed them, which improved the robustness of the fitting and forecast. Since the model contains many parameters, the question of identifiability is of significance, especially in the context of precision medicine. An example of analysis involving parameter identifiability for cancer modeling can be found in [26]. Furthermore, the uncertainty in the data and model means that uncertainty quantification is a necessary component in clinical setting [27]. Finally, the parameter range, provided with the method used to obtain them, is not meant to be extensive or absolute; however, it serves as a unified framework for future improvement. In conclusion, future work should consider the identifiability and improve the accuracy of the model, in terms of both computational robustness and biological relevance. In the future, we will carry out comparisons of this new model across several different models by other researchers, to further advance the field. Additionally, mathematical analyses will be significant to help rigorously define concepts and propose hypotheses that can be tested to improve our understanding of prostate cancer and its treatment. If a model is identifiable (or if we know the relationship between the parameters), then we can use the fitted parameters and mathematical analysis to classify cancer types. Finally, uncertainty quantification for the prediction of the model is necessary to quantify how likely an additional cycle of treatment will be useful or not.