Associative Memories to Accelerate Approximate Nearest Neighbor Search
Abstract
1. Introduction
2. Related Work
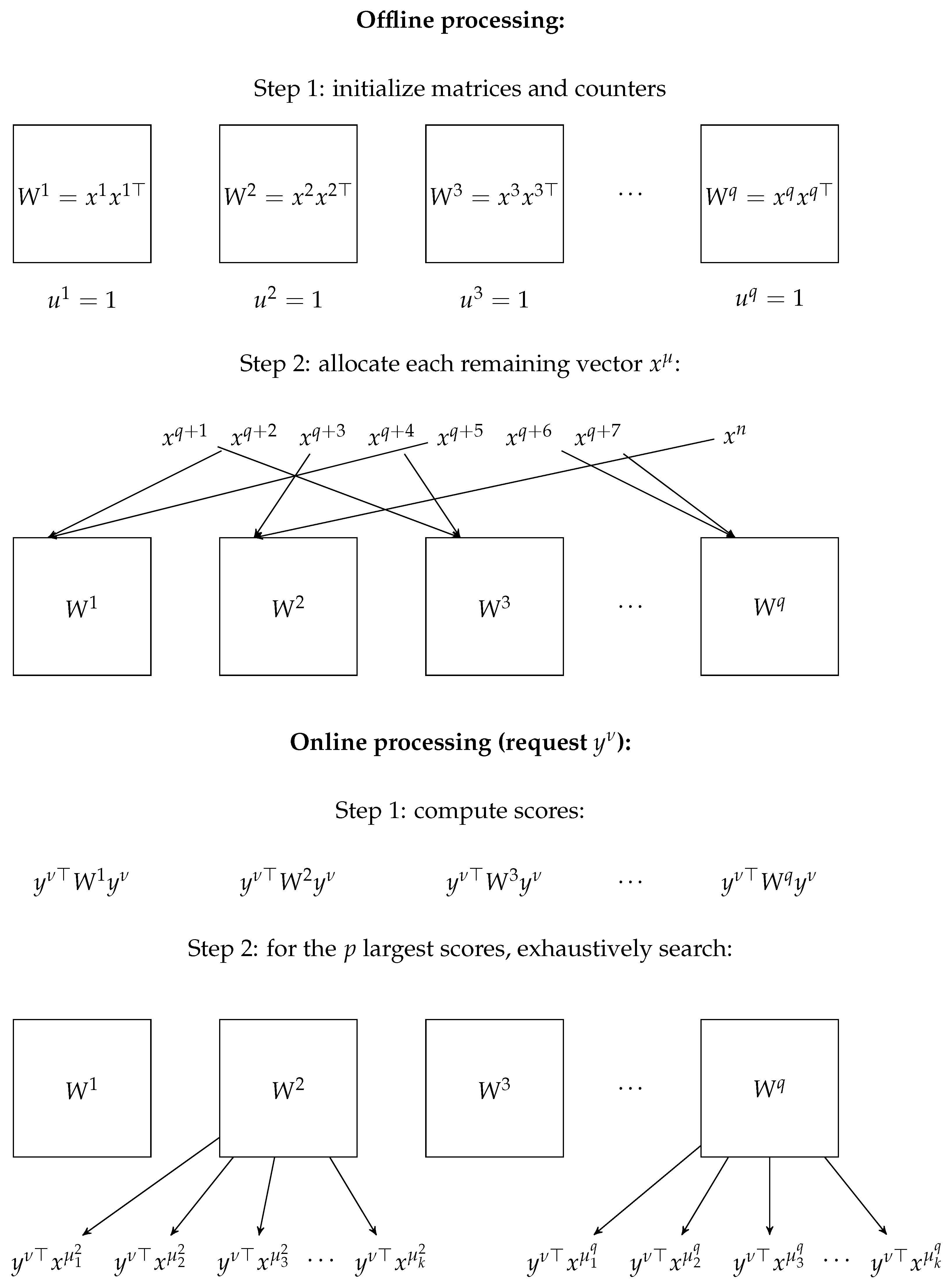
3. Search Problems with Sparse Patterns
- 1.
- , i.e., and ,
- 2.
- and
- 3.
- and .
- 1.
- ,
- 2.
- and
- 3.
- and .
4. Dense, Unbiased Patterns
- 1.
- , i.e., and , and either
- 2.
- if ,
- 3.
- or if , for some .
- 1.
- , i.e., and ,
- 2.
- and either if ,
- 3.
- or if for some .
5. Experiments
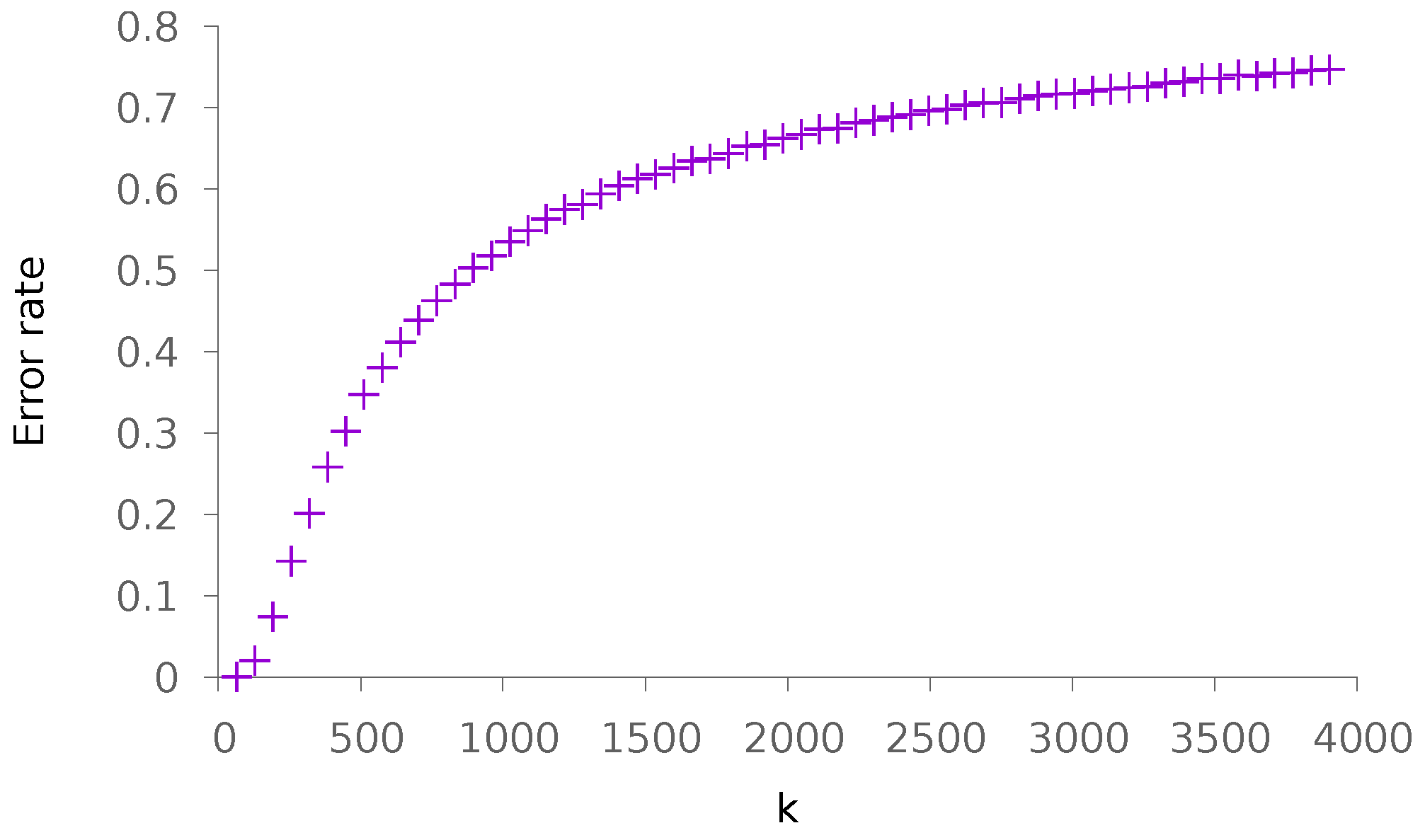
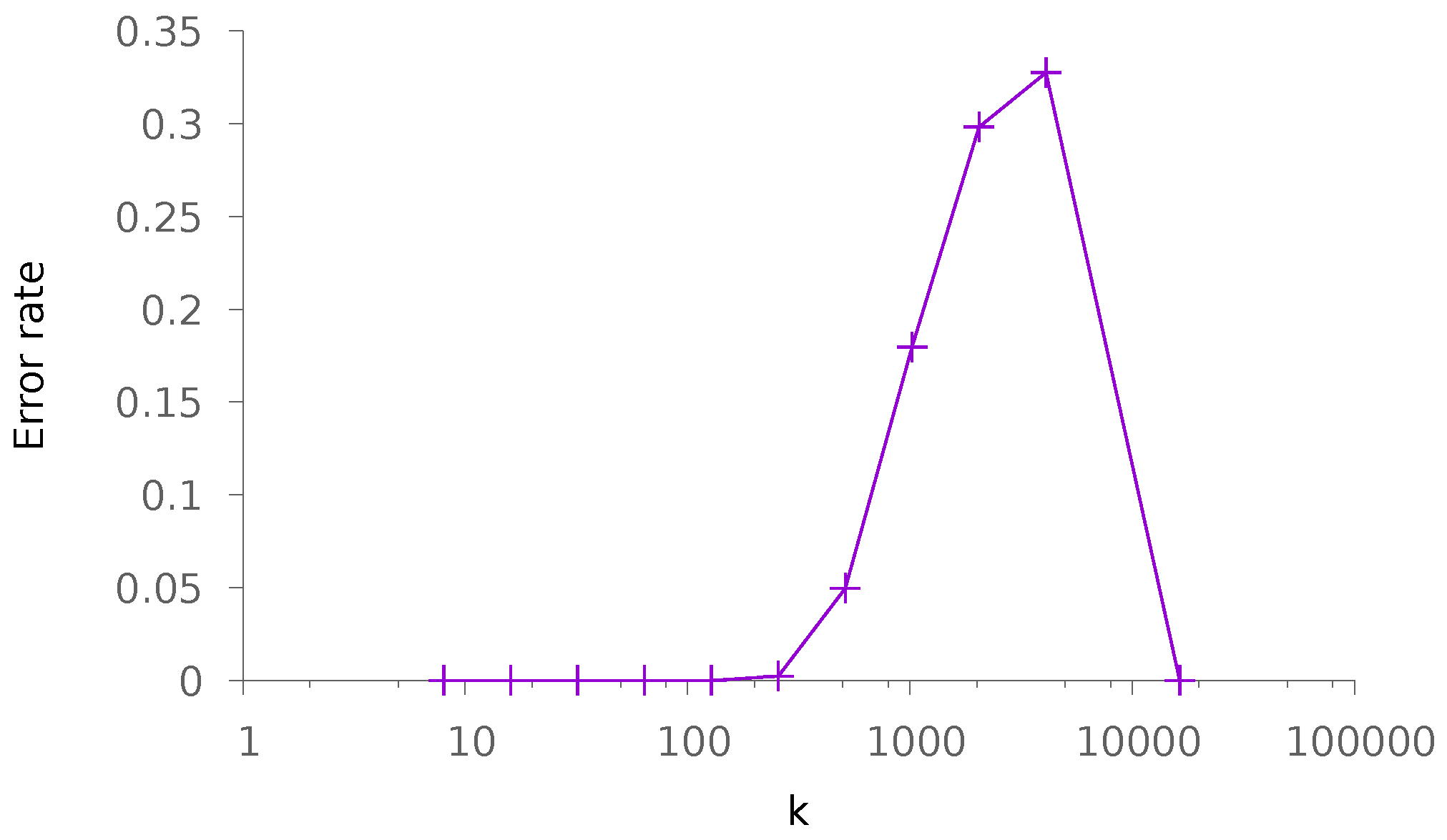
5.1. Synthetic Data
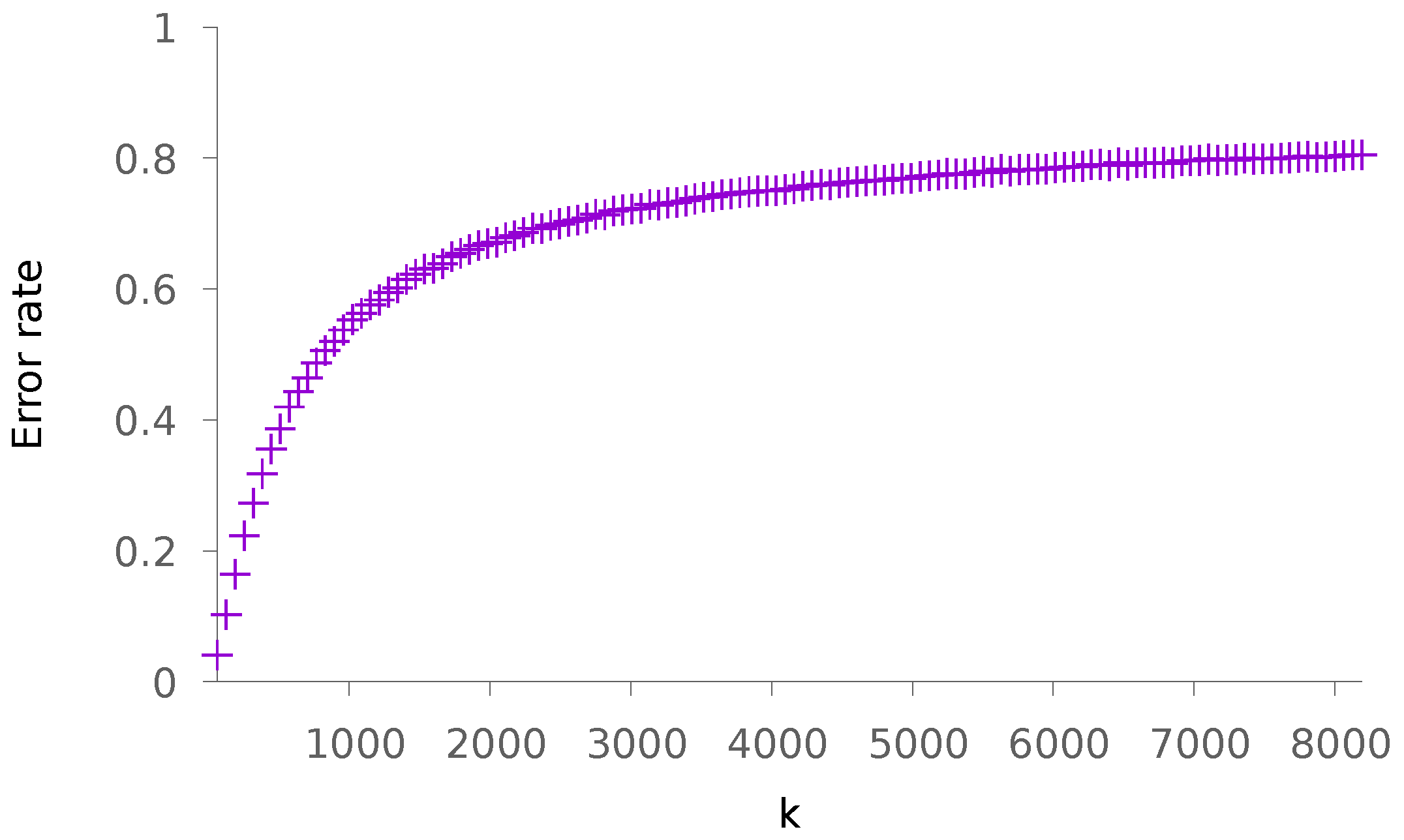
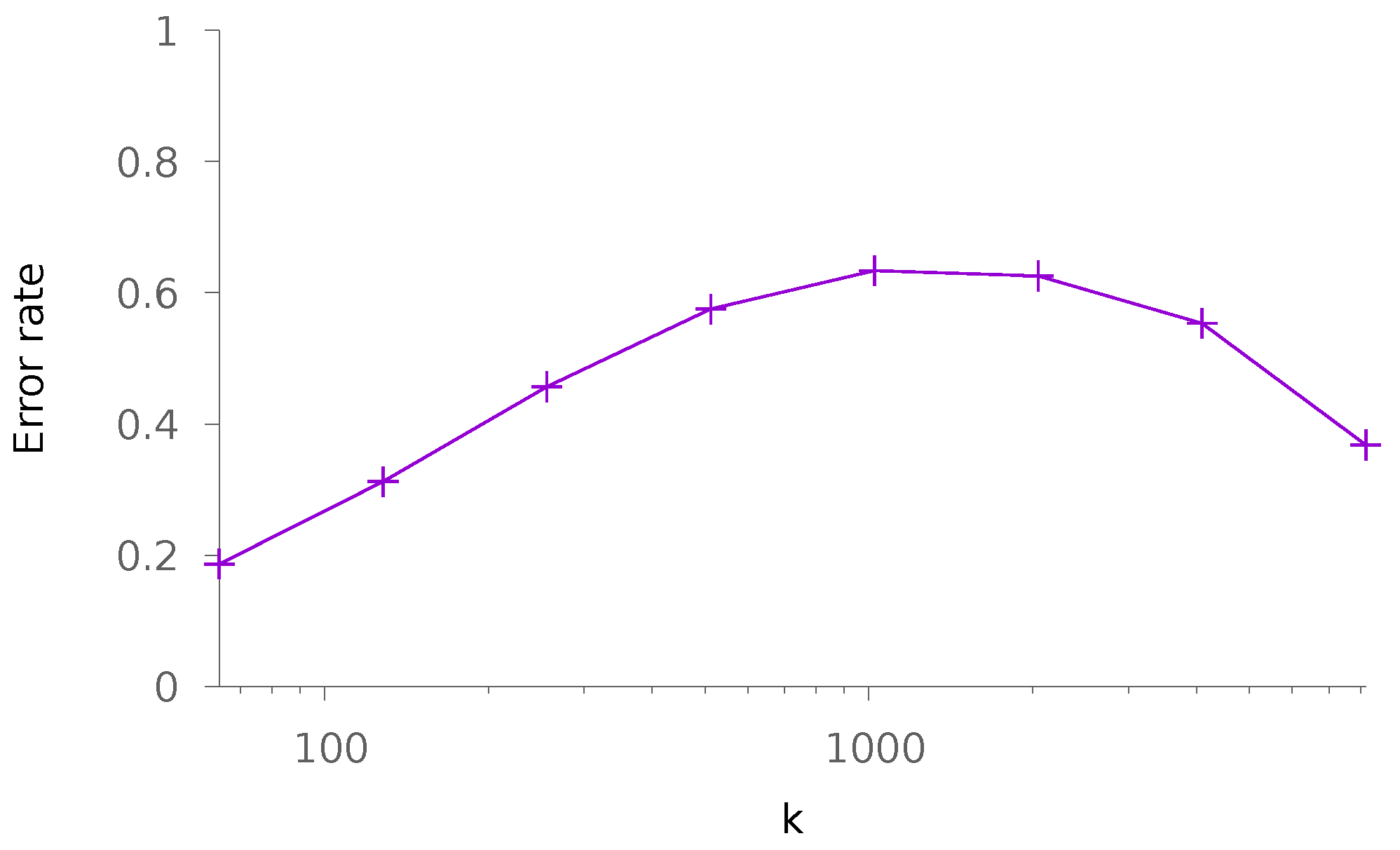
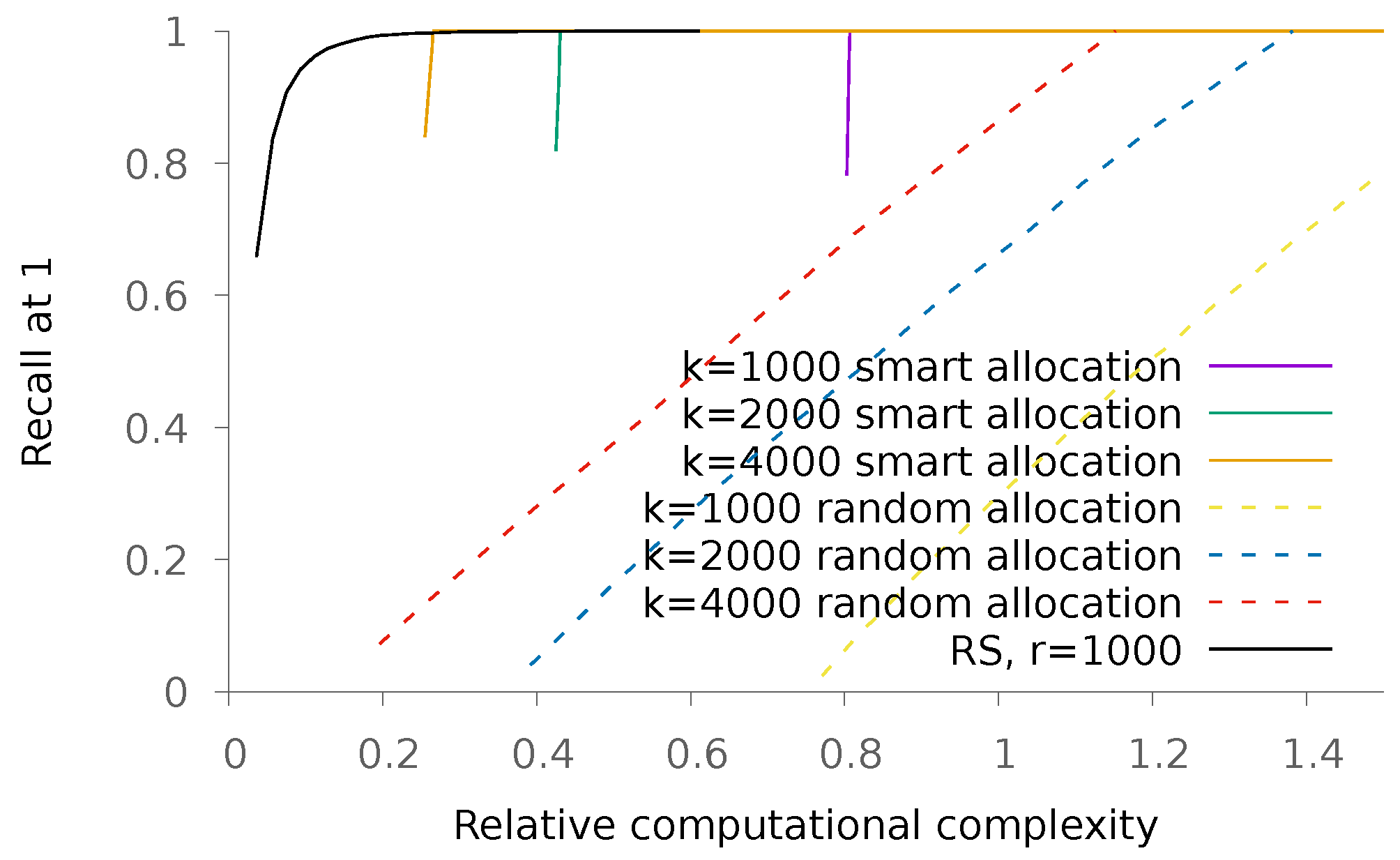
5.1.1. Sparse Patterns
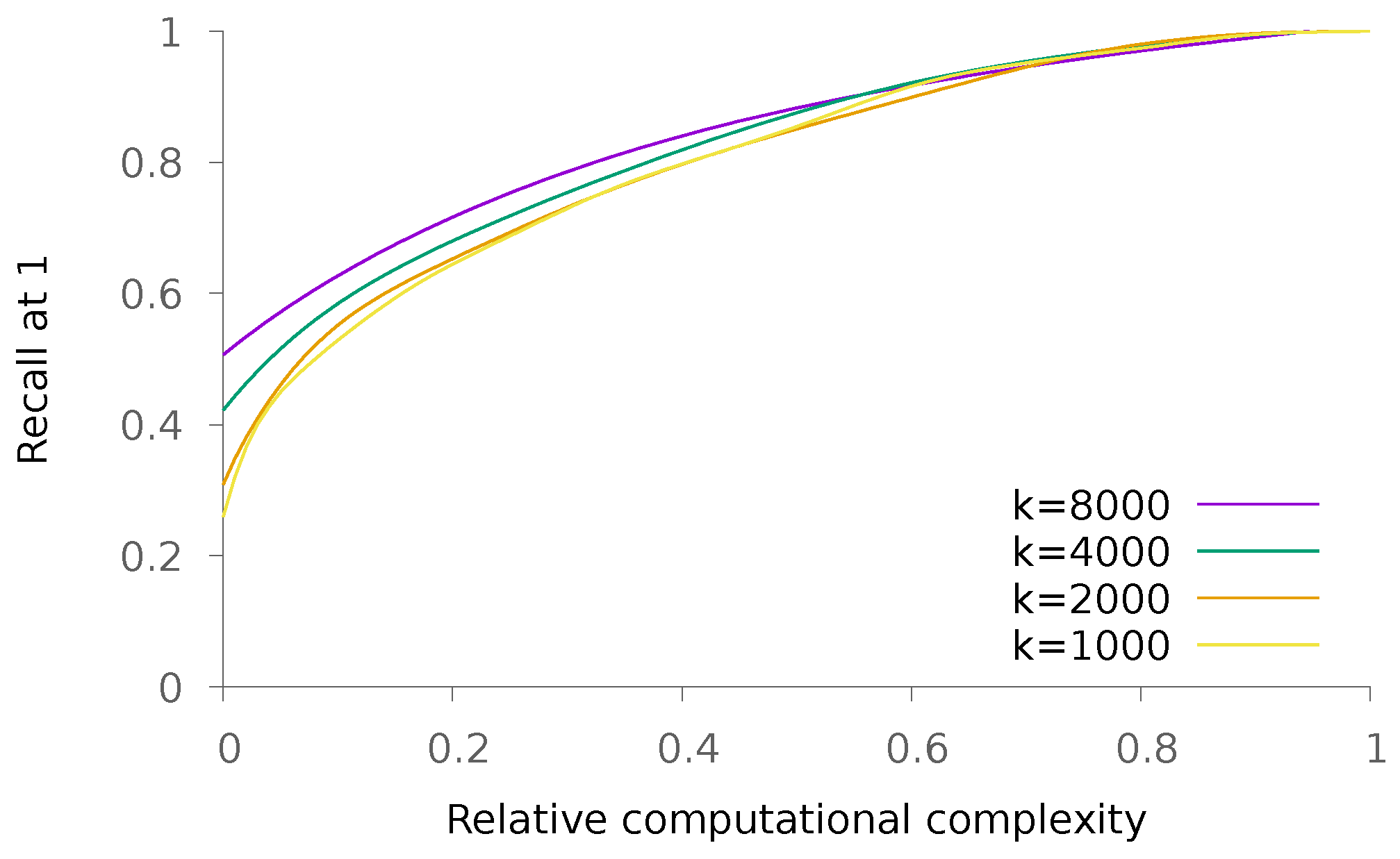
5.1.2. Dense Patterns
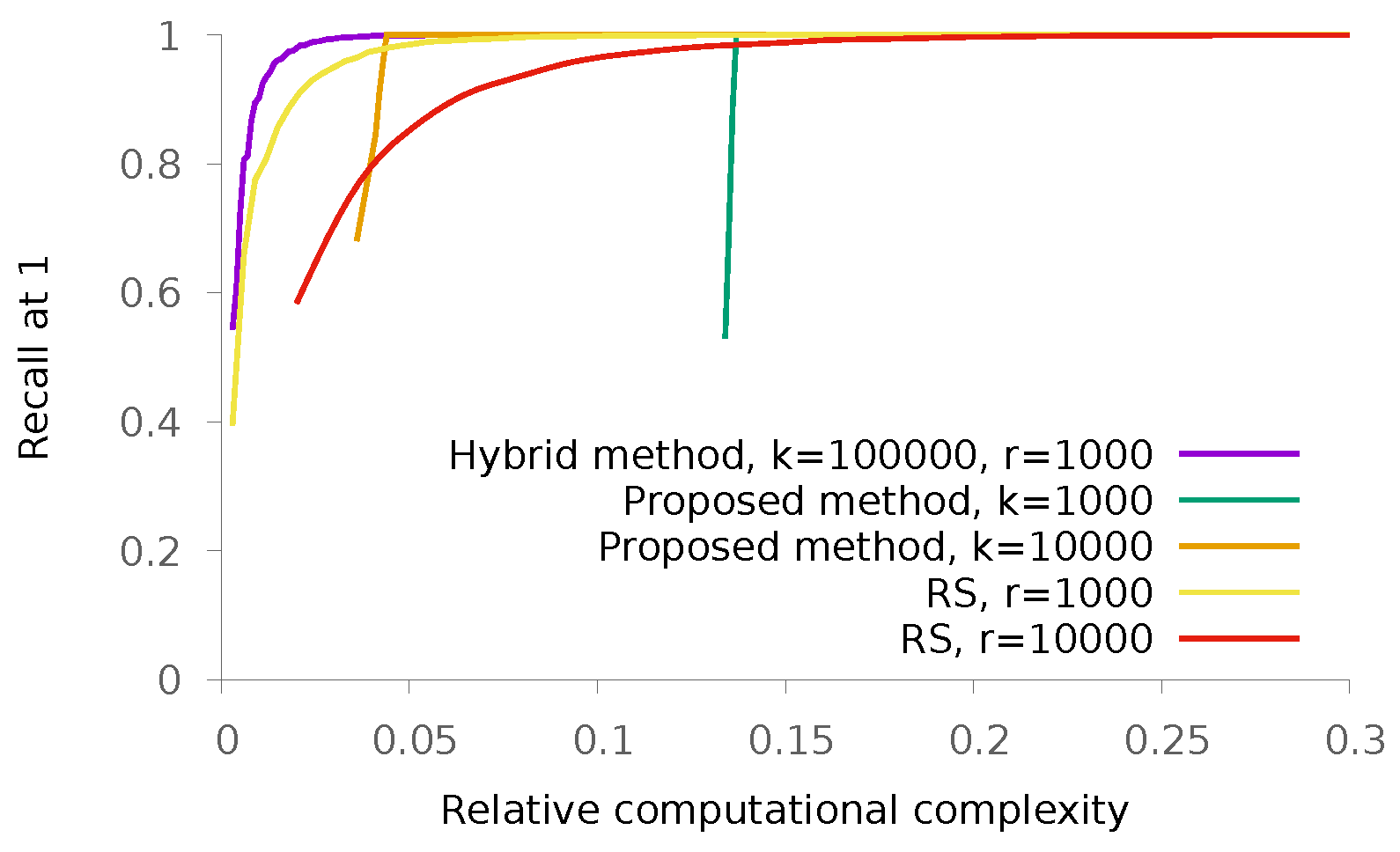
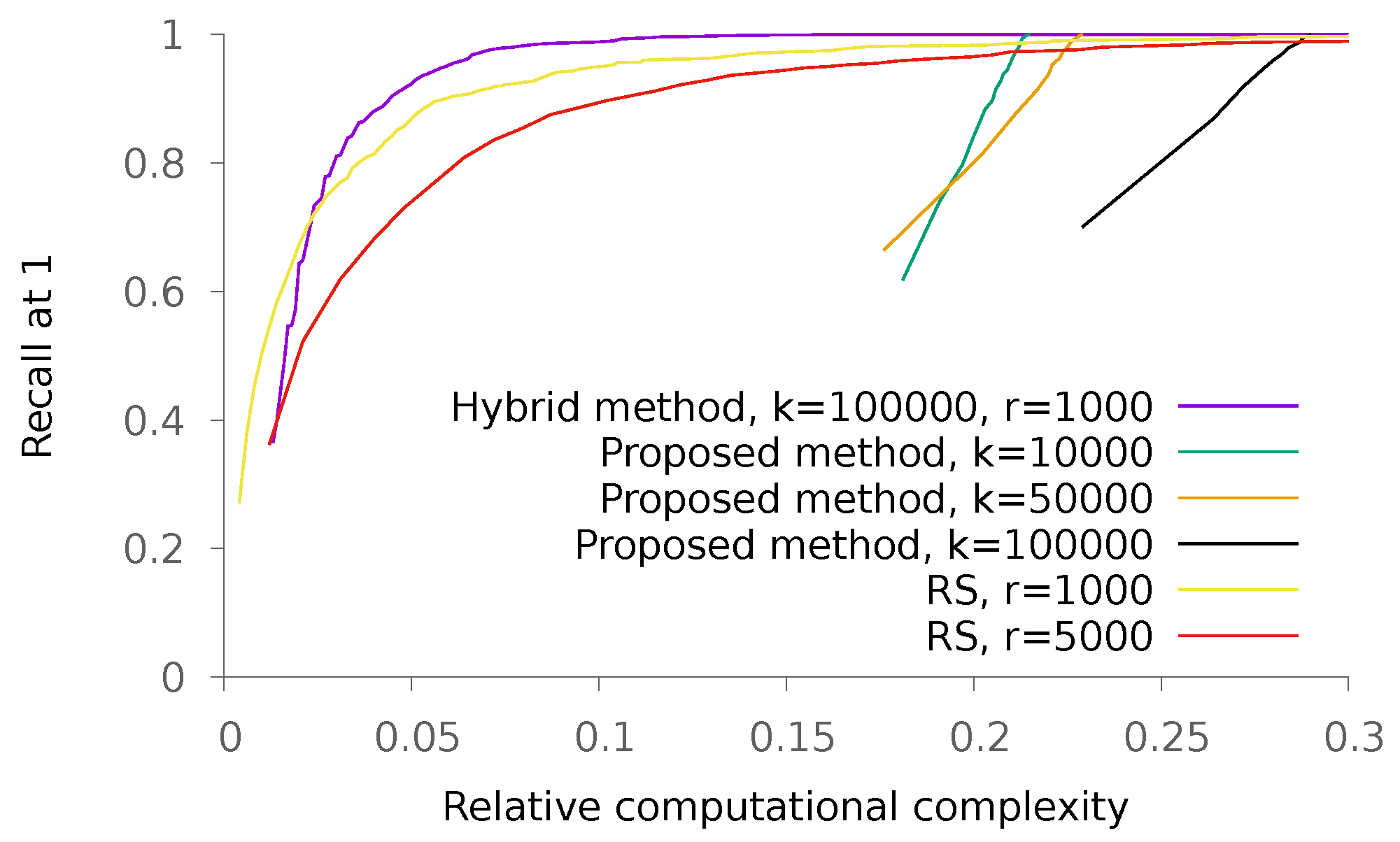
5.2. Real Data
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Muja, M.; Lowe, D.G. Scalable Nearest Neighbor Algorithms for High Dimensional Data. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 2227–2240. [Google Scholar] [CrossRef] [PubMed]
- Muja, M.; Lowe, D.G. Fast Approximate Nearest Neighbors with Automatic Algorithm Configuration. In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications (VISAPP 2009), Lisboa, Portugal, 5–8 February 2009. [Google Scholar]
- Gong, Y.; Lazebnik, S. Iterative quantization: A procrustean approach to learning binary codes. In Proceedings of the 2011 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Colorado Springs, CO, USA, 20–25 June 2011; pp. 817–824. [Google Scholar]
- Jegou, H.; Douze, M.; Schmid, C. Product quantization for nearest neighbor search. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 117–128. [Google Scholar] [CrossRef] [PubMed]
- Datar, M.; Immorlica, N.; Indyk, P.; Mirrokni, V.S. Locality-sensitive hashing scheme based on p-stable distributions. In Proceedings of the Twentieth Annual Symposium on Computational Geometry, Brooklyn, NY, USA, 8–11 June 2004; pp. 253–262. [Google Scholar]
- Iscen, A.; Furon, T.; Gripon, V.; Rabbat, M.; Jégou, H. Memory vectors for similarity search in high-dimensional spaces. IEEE Trans. Big Data 2018, 4, 65–77. [Google Scholar] [CrossRef]
- Yu, C.; Gripon, V.; Jiang, X.; Jégou, H. Neural Associative Memories as Accelerators for Binary Vector Search. In Proceedings of the COGNITIVE 2015: 7th International Conference on Advanced Cognitive Technologies and Applications, Nice, France, 22–27 March 2015; pp. 85–89. [Google Scholar]
- Hopfield, J.J. Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. USA 1982, 79, 2554–2558. [Google Scholar] [CrossRef] [PubMed]
- McEliece, R.J.; Posner, E.C.; Rodemich, E.R.; Venkatesh, S.S. The capacity of the Hopfield associative memory. IEEE Trans. Inform. Theory 1987, 33, 461–482. [Google Scholar] [CrossRef]
- Löwe, M.; Vermet, F. The storage capacity of the Hopfield model and moderate deviations. Stat. Probab. Lett. 2005, 75, 237–248. [Google Scholar] [CrossRef]
- Löwe, M.; Vermet, F. The capacity of q-state Potts neural networks with parallel retrieval dynamics. Stat. Probab. Lett. 2007, 77, 1505–1514. [Google Scholar] [CrossRef]
- Gripon, V.; Heusel, J.; Löwe, M.; Vermet, F. A comparative study of sparse associative memories. J. Stat. Phys. 2016, 164, 105–129. [Google Scholar] [CrossRef]
- Löwe, M. On the storage capacity of the Hopfield model with biased patterns. IEEE Trans. Inform. Theory 1999, 45, 314–318. [Google Scholar] [CrossRef]
- Newman, C. Memory capacity in neural network models: Rigorous lower bounds. Neural Netw. 1988, 1, 223–238. [Google Scholar] [CrossRef]
- Löwe, M.; Vermet, F. The Hopfield model on a sparse Erdos-Renyi graph. J. Stat. Phys. 2011, 143, 205–214. [Google Scholar] [CrossRef]
- Arya, S.; Mount, D.M.; Netanyahu, N.S.; Silverman, R.; Wu, A.Y. An optimal algorithm for approximate nearest neighbor searching fixed dimensions. J. ACM (JACM) 1998, 45, 891–923. [Google Scholar] [CrossRef]
- Tagami, Y. AnnexML: Approximate nearest neighbor search for extreme multi-label classification. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD ’17), Halifax, NS, Canada, 13–17 August 2017; ACM: New York, NY, USA, 2017; pp. 455–464. [Google Scholar]
- He, K.; Wen, F.; Sun, J. K-means hashing: An affinity-preserving quantization method for learning binary compact codes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 2938–2945. [Google Scholar]
- Weiss, Y.; Torralba, A.; Fergus, R.; Weiss, Y.; Torralba, A.; Fergus, R. Spectral Hashing. Available online: http://papers.nips.cc/paper/3383-spectral-hashing.pdf (accessed on 15 September 2018).
- Ge, T.; He, K.; Ke, Q.; Sun, J. Optimized product quantization for approximate nearest neighbor search. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 2946–2953. [Google Scholar]
- Norouzi, M.; Fleet, D.J. Cartesian k-means. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 3017–3024. [Google Scholar]
- Andoni, A.; Indyk, P. Near-optimal hashing algorithms for approximate nearest neighbor in high dimensions. In Proceedings of the 47th Annual IEEE Symposium on Foundations of Computer Science (FOCS’06), Berkeley, CA, USA, 21–24 October 2006; pp. 459–468. [Google Scholar]
- Norouzi, M.; Punjani, A.; Fleet, D.J. Fast search in hamming space with multi-index hashing. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Providence, RI, USA, 16–21 June 2012; pp. 3108–3115. [Google Scholar]
- Liu, Y.; Cui, J.; Huang, Z.; Li, H.; Shen, H.T. SK-LSH: An efficient index structure for approximate nearest neighbor search. Proc. VLDB Endow. 2014, 7, 745–756. [Google Scholar] [CrossRef]
- Kraska, T.; Beutel, A.; Chi, E.H.; Dean, J.; Polyzotis, N. The case for learned index structures. In Proceedings of the 2018 International Conference on Management of Data, Houston, TX, USA, 10–15 June 2018; pp. 489–504. [Google Scholar]
- Lindeberg, J.W. Über das Exponentialgesetz in der Wahrscheinlichkeitsrechnung. Ann. Acad. Sci. Fenn. 1920, 16, 1–23. [Google Scholar]
- Eichelsbacher, P.; Löwe, M. 90 Jahre Lindeberg-Methode. Math. Semesterber. 2014, 61, 7–34. [Google Scholar] [CrossRef]
- Eichelsbacher, P.; Löwe, M. Lindeberg’s method for moderate deviations and random summation. arXiv, 2017; arXiv:1705.03837. [Google Scholar]
- Demircigil, M.; Heusel, J.; Löwe, M.; Upgang, S.; Vermet, F. On a model of associative memory with huge storage capacity. J. Stat. Phys. 2017, 168, 288–299. [Google Scholar] [CrossRef]
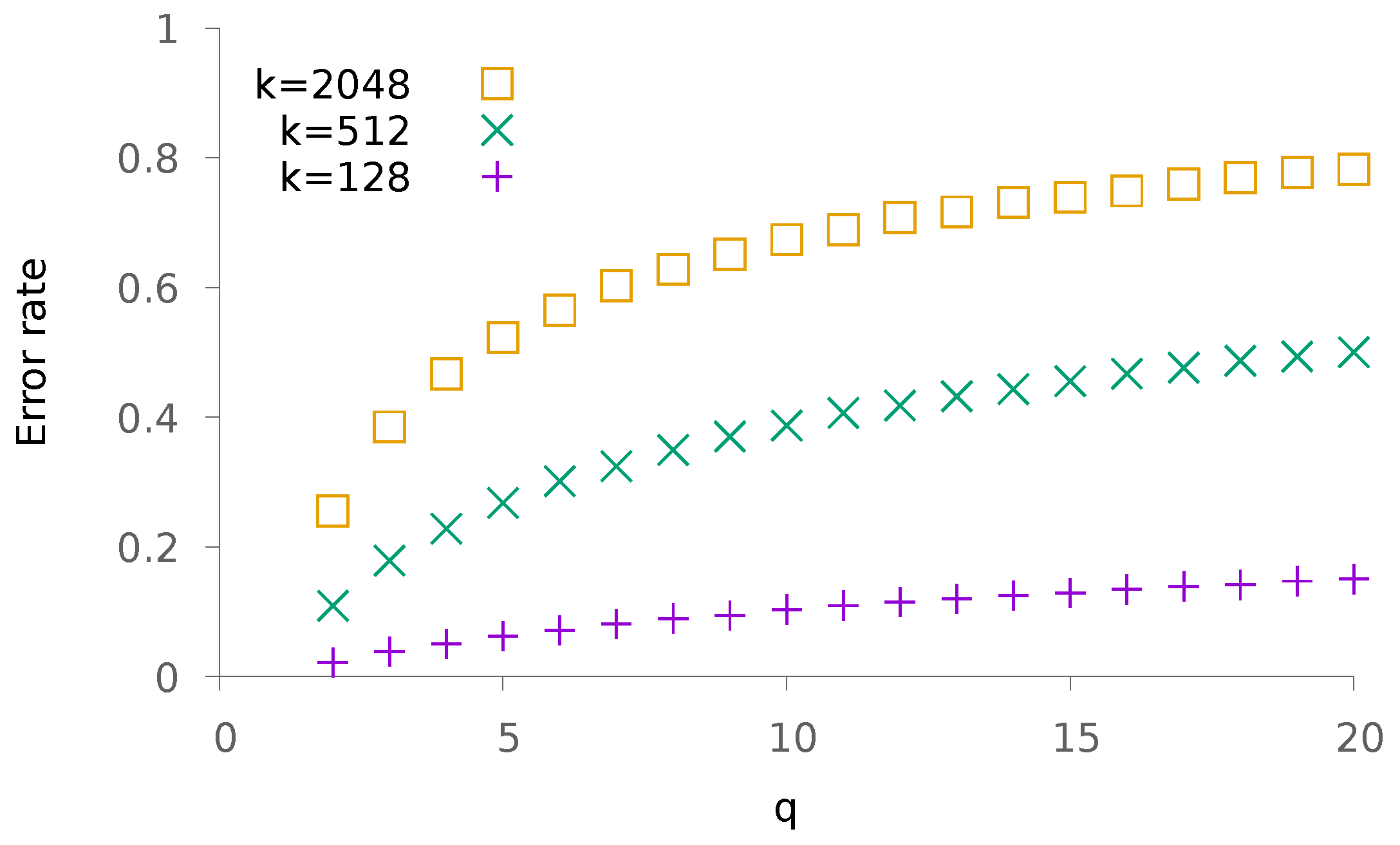
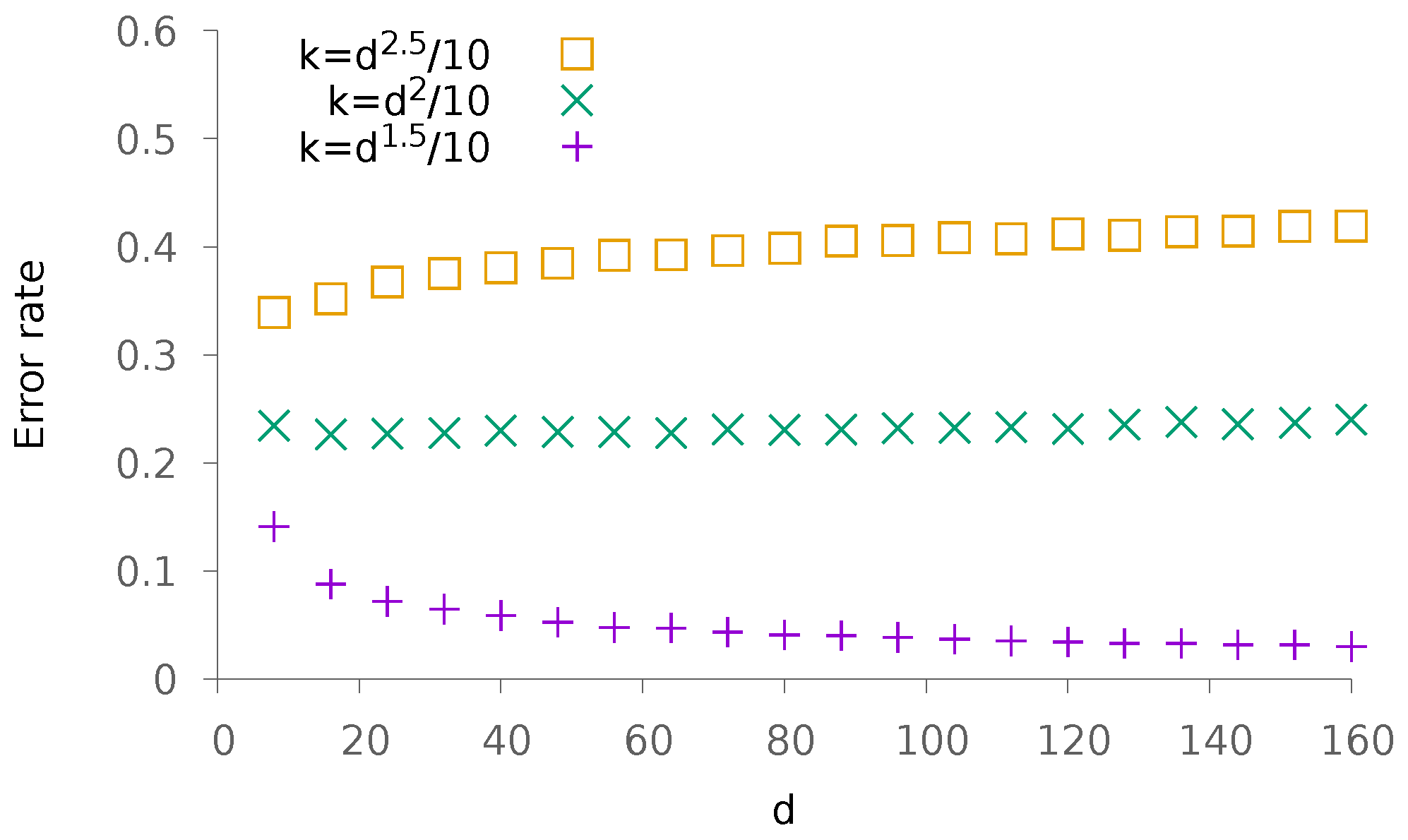
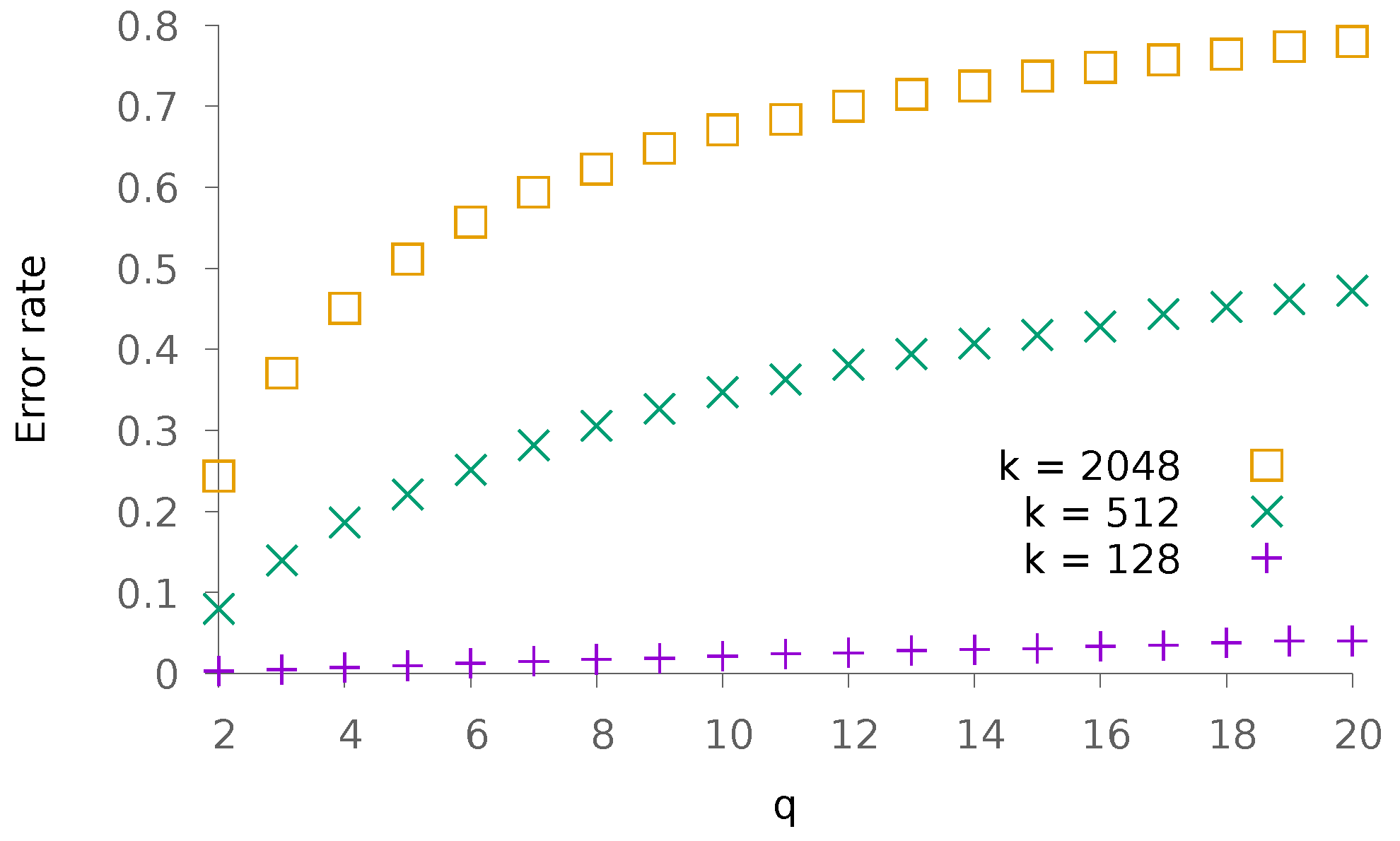
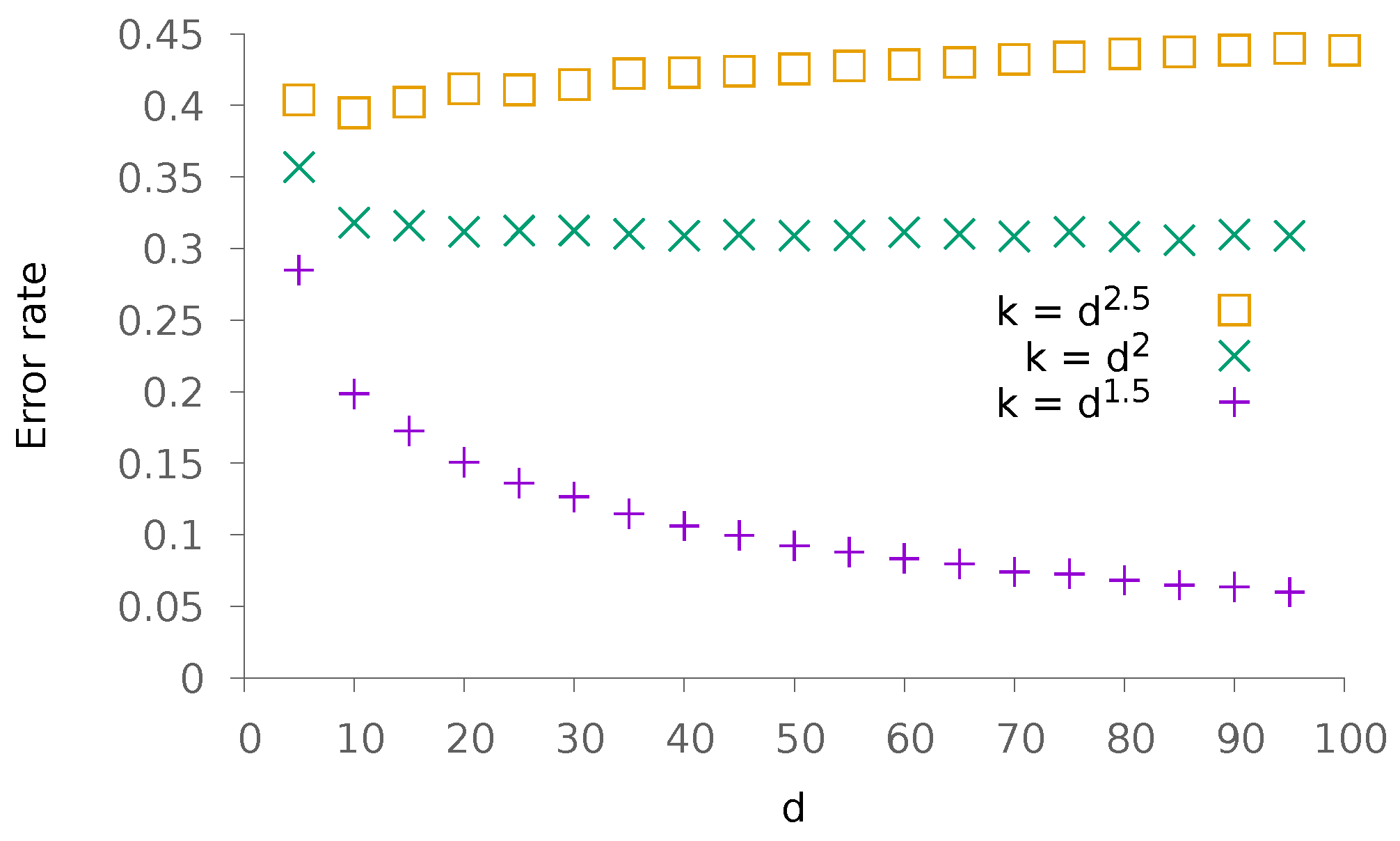
| Scan Time | Recall@1 | Scan Time | Recall@1 | Scan Time | Recall@1 | |
|---|---|---|---|---|---|---|
| Random kd-trees [1] | 0.04 | 0.6 | 0.22 | 0.8 | 3.1 | 0.95 |
| K-means trees [1] | 0.06 | 0.6 | 0.25 | 0.8 | 2.8 | 0.99 |
| Proposed method (hybrid) | 0.17 | 0.6 | 0.25 | 0.8 | 1.1 | 0.99 |
| ANN [16] | 3.7 | 0.6 | 8.2 | 0.8 | 24 | 0.95 |
| LSH [22] | 6.4 | 0.6 | 11.1 | 0.8 | 28 | 0.98 |
| Technique | Scan Complexity | ||||
|---|---|---|---|---|---|
| Quantization | |||||
| RS or K-means | |||||
| Proposed | |||||
| Hybrid scheme |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gripon, V.; Löwe, M.; Vermet, F. Associative Memories to Accelerate Approximate Nearest Neighbor Search. Appl. Sci. 2018, 8, 1676. https://doi.org/10.3390/app8091676
Gripon V, Löwe M, Vermet F. Associative Memories to Accelerate Approximate Nearest Neighbor Search. Applied Sciences. 2018; 8(9):1676. https://doi.org/10.3390/app8091676
Chicago/Turabian StyleGripon, Vincent, Matthias Löwe, and Franck Vermet. 2018. "Associative Memories to Accelerate Approximate Nearest Neighbor Search" Applied Sciences 8, no. 9: 1676. https://doi.org/10.3390/app8091676
APA StyleGripon, V., Löwe, M., & Vermet, F. (2018). Associative Memories to Accelerate Approximate Nearest Neighbor Search. Applied Sciences, 8(9), 1676. https://doi.org/10.3390/app8091676





