Pattern Recognition of Human Postures Using the Data Density Functional Method
Abstract
1. Introduction
2. Materials and Methods
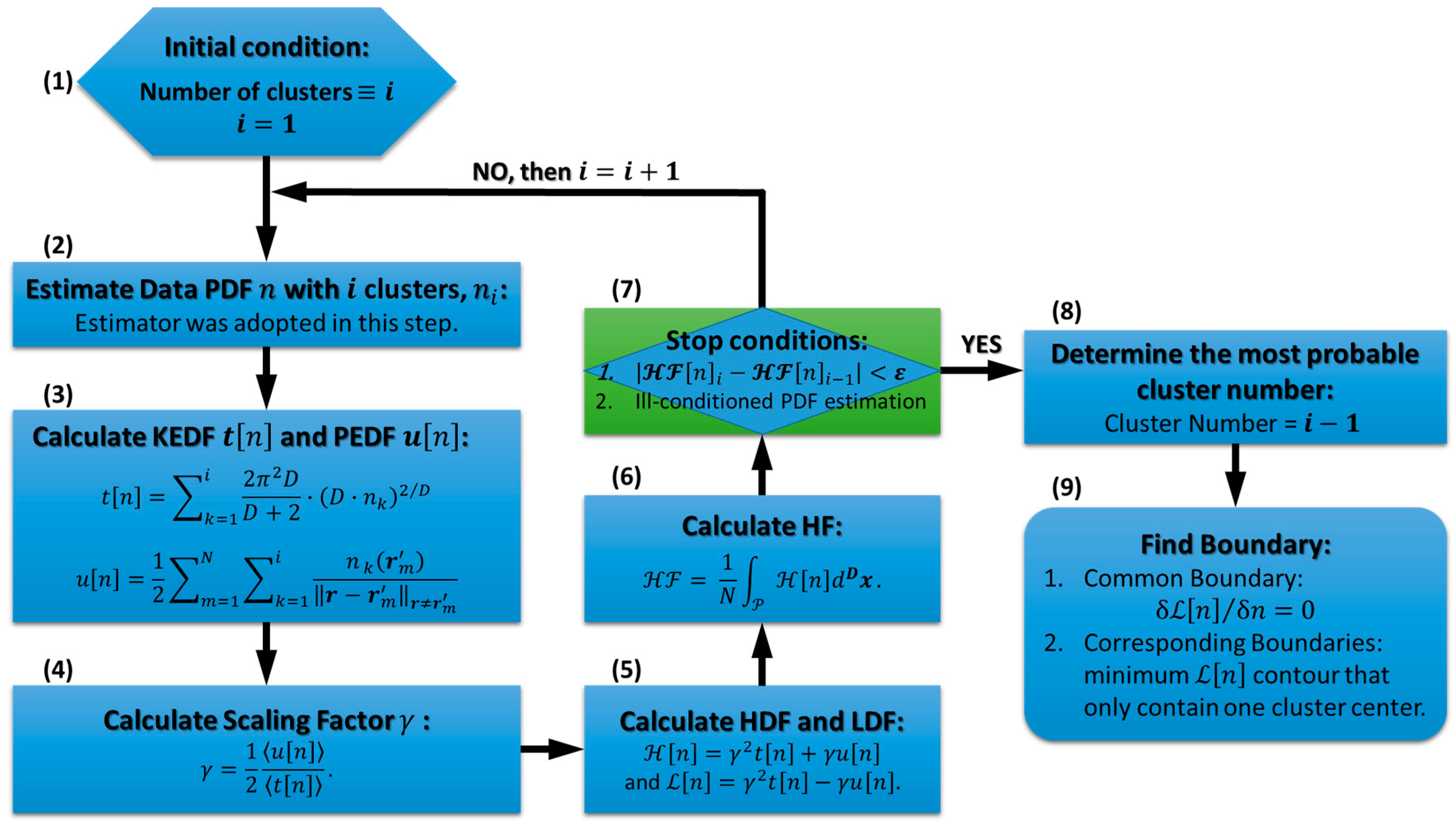
2.1. Theoretical Framework
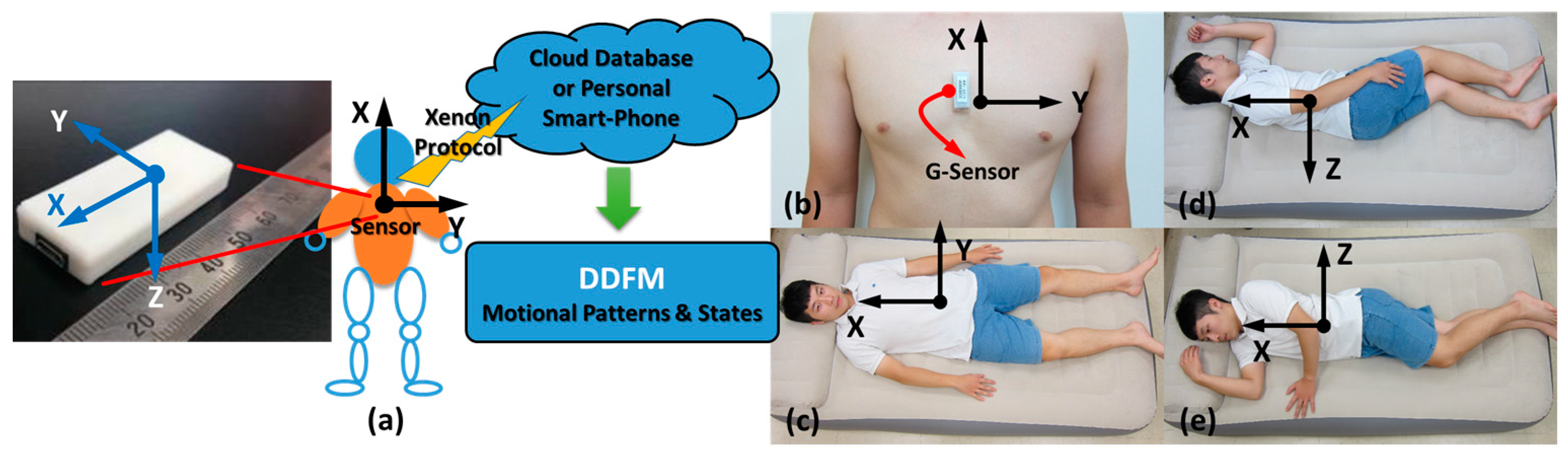
2.2. Experimental Framework
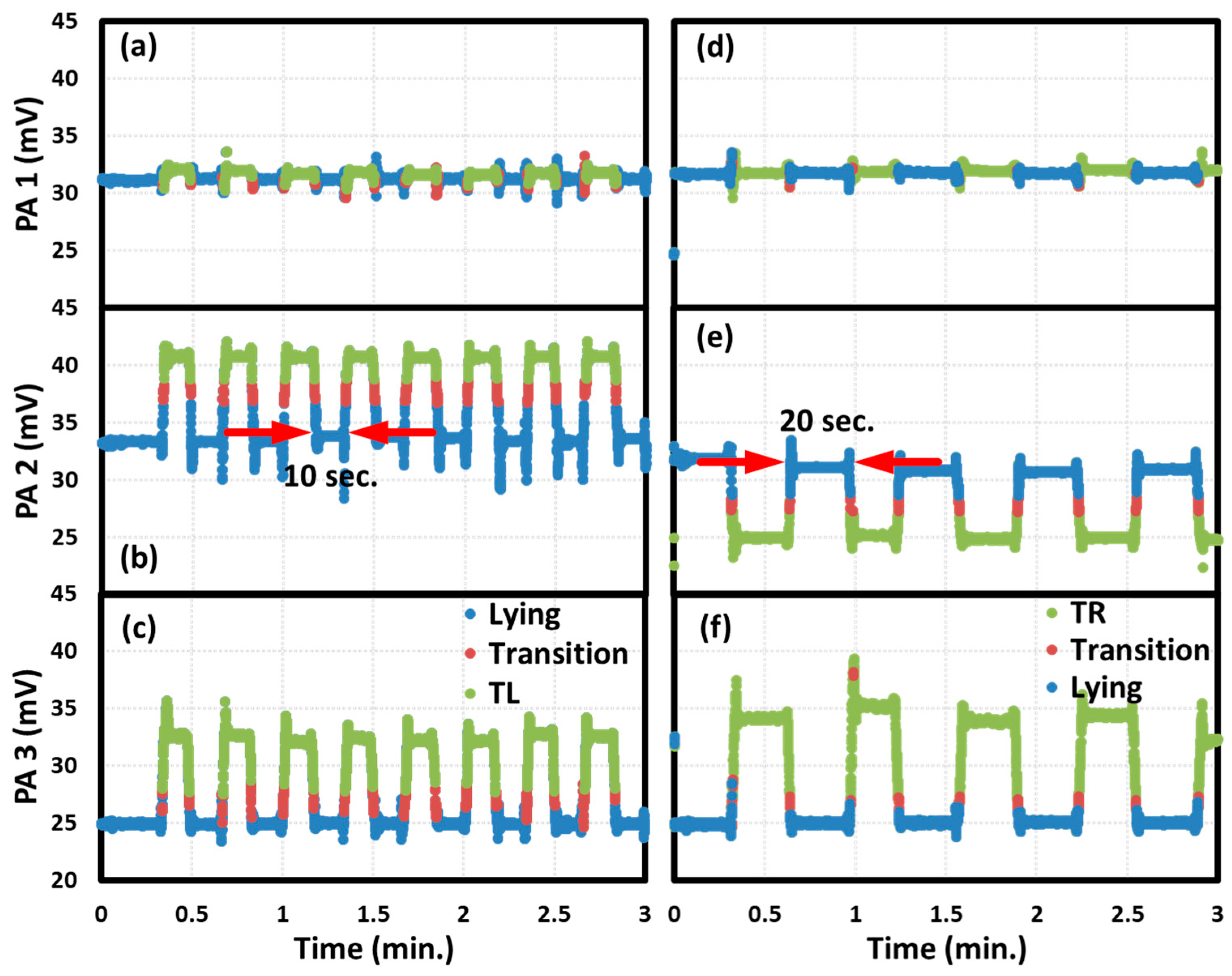
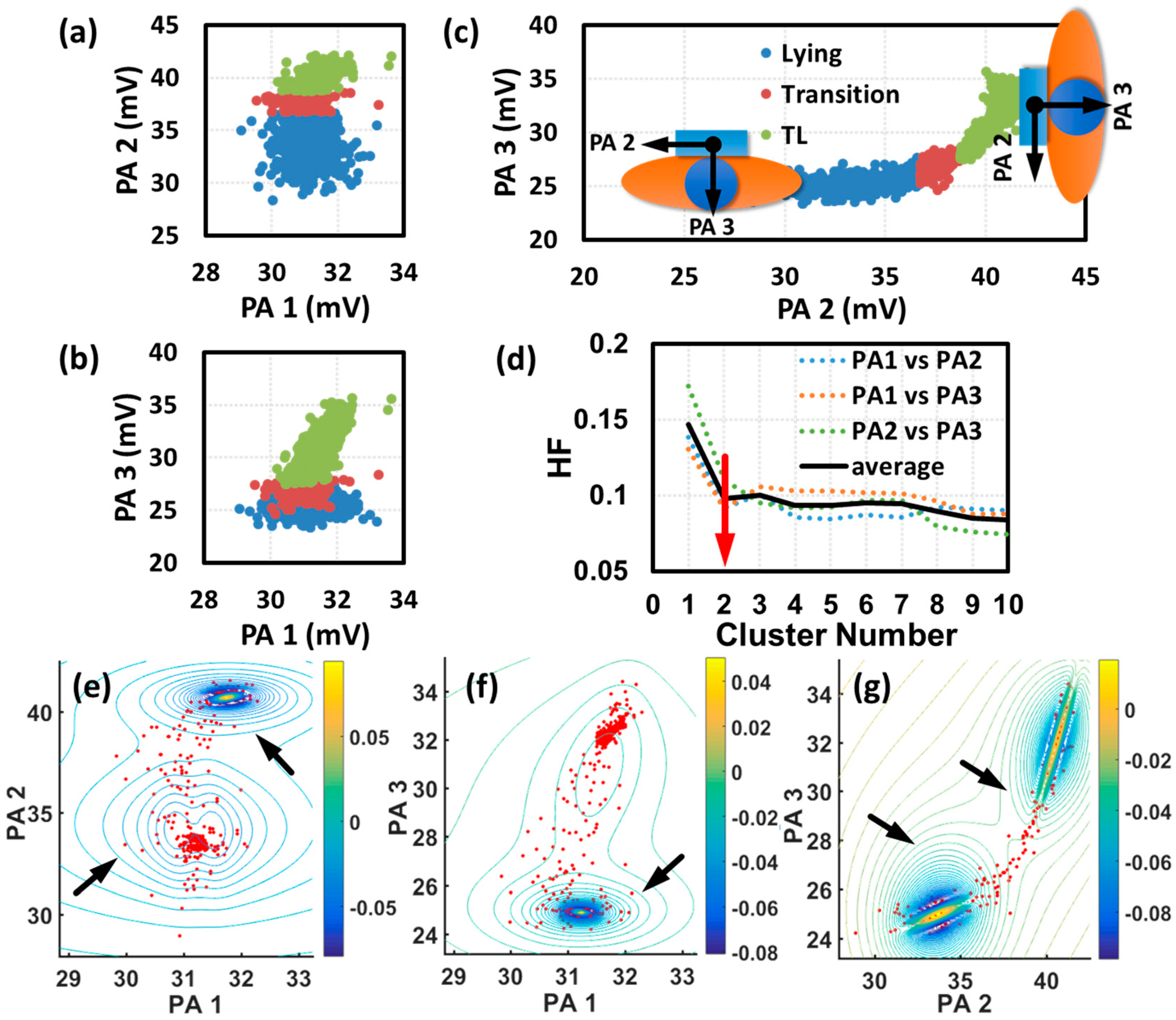
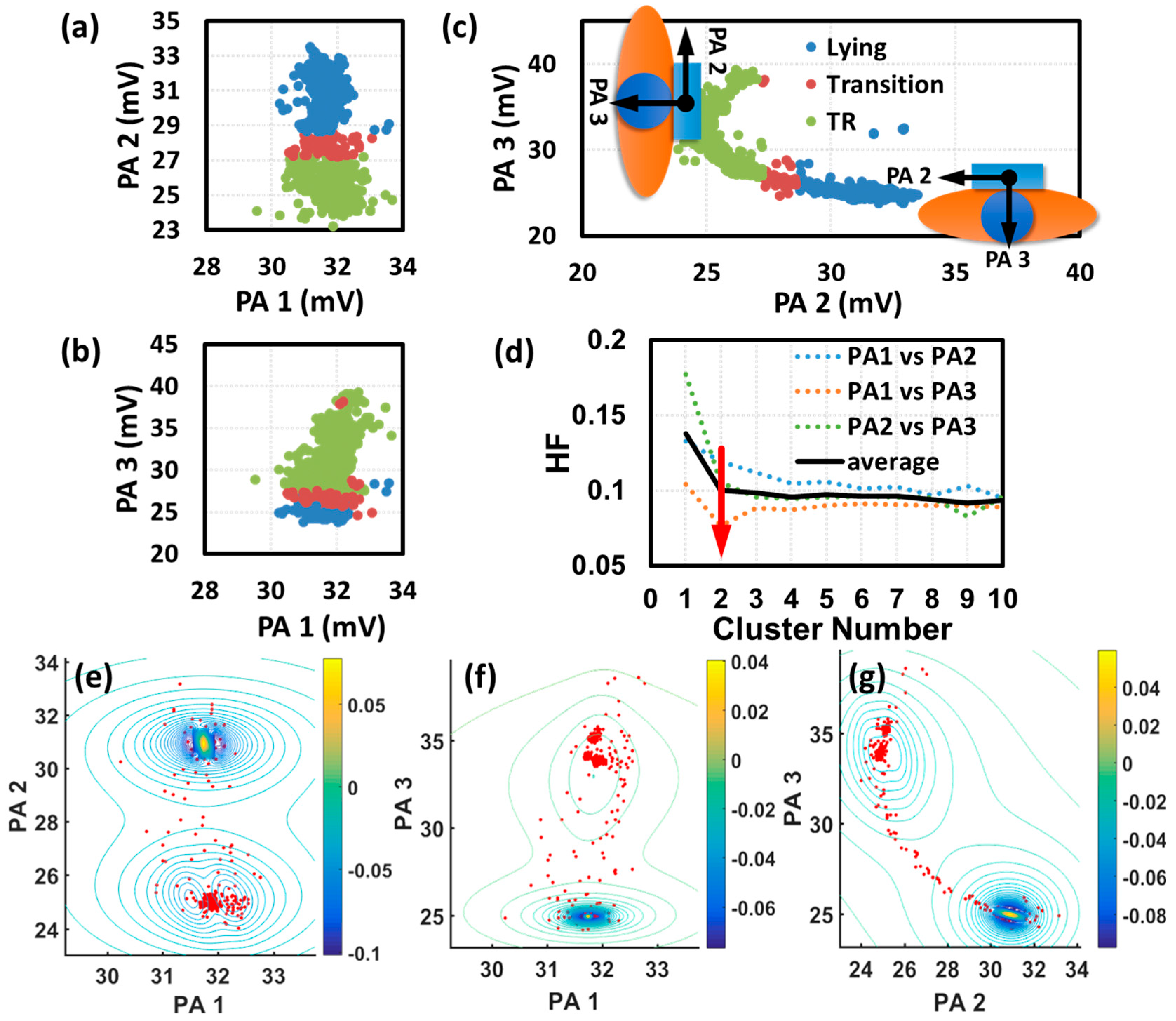
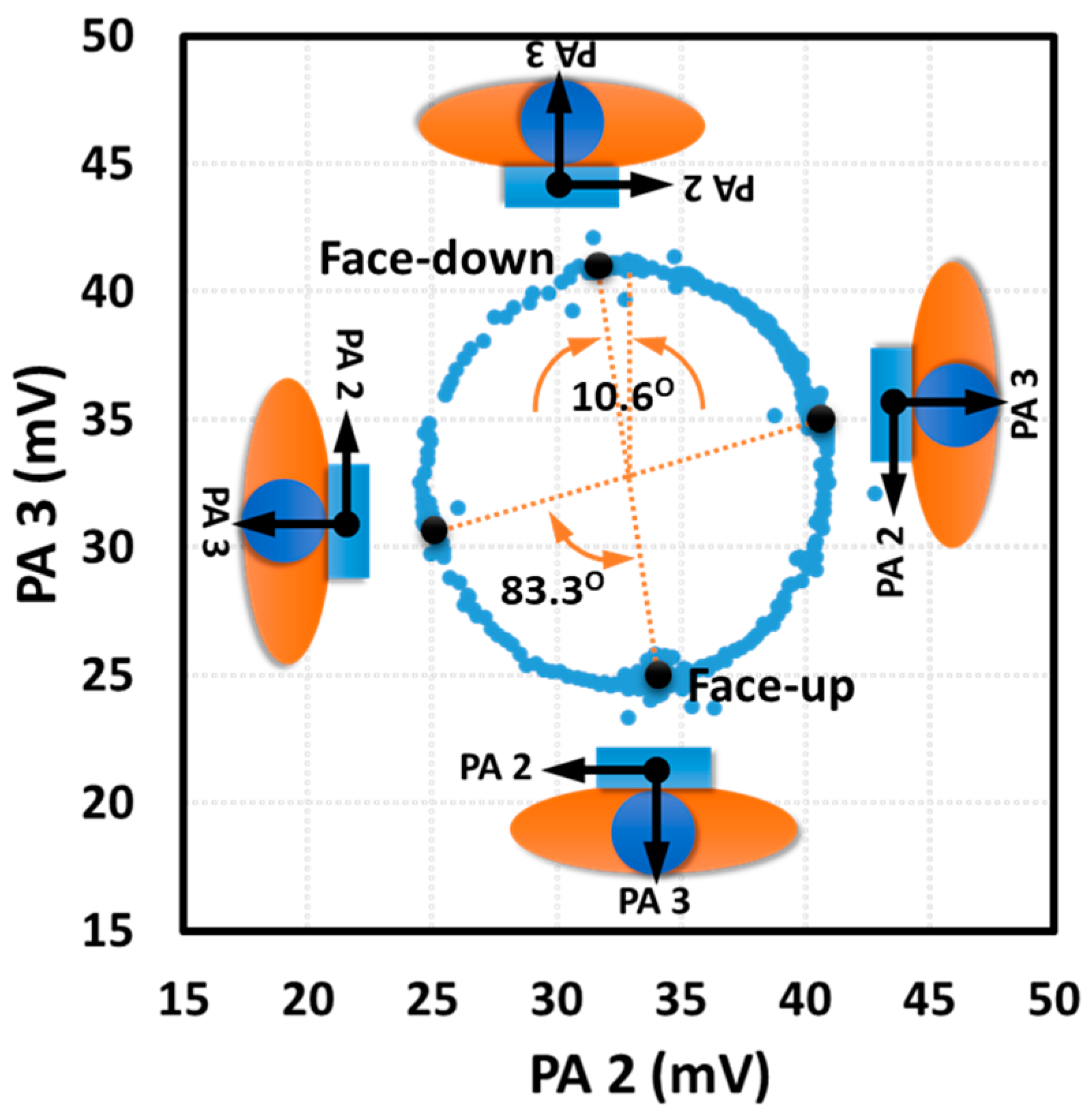
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chen, C.; Jafari, R.; Kehtarnavaz, N. A Real-Time Human Action Recognition System Using Depth and Inertial Sensor Fusion. IEEE Sens. J. 2016, 16, 773–781. [Google Scholar] [CrossRef]
- Qian, Z.; Bowden, A.E.; Zhang, D.; Wan, J.; Liu, W.; Li, X.; Baradoy, D.; Fullwood, D.T. Inverse Piezoresistive Nanocomposite Sensors for Identifying Human Sitting Posture. Sensors 2018, 18, 1745. [Google Scholar] [CrossRef] [PubMed]
- Hui, X.; Kan, E.C. Monitoring vital signs over multiplexed radio by near-field coherent sensing. Nat. Electron. 2018, 1, 74–78. [Google Scholar] [CrossRef]
- Tsai, H.J.; Kuo, T.B.; Lee, G.S.; Yang, C.C. Efficacy of paced breathing for insomnia: Enhances vagal activity and improves sleep quality. Psychophysiology 2015, 52, 388–396. [Google Scholar] [CrossRef] [PubMed]
- Kuo, T.B.; Hong, C.H.; Hsieh, I.T.; Lee, G.S.; Yang, C.C. Effects of cold exposure on autonomic changes during the last REM sleep transition and morning blood pressure surge in humans. Sleep Med. 2014, 15, 986–997. [Google Scholar] [CrossRef] [PubMed]
- Smoleń, M.; Kańtoch, E.; Augustyniak, P.; Kowalski, P. Wearable Patient Home Monitoring Based on ECG and ACC Sensors. In Proceedings of the 5th European Conference of the International Federation for Medical and Biological Engineering, Budapest, Hungary, 14–18 September 2011. [Google Scholar]
- Sagar, V.A.; Davies, E.J.; Briscoe, S.; Coats, A.J.; Dalal, H.M.; Lough, F.; Rees, K.; Singh, S.; Taylor, R.S. Exercise-based rehabilitation for heart failure: Systematic review and meta-analysis. Open Heart 2015, 28, e000163. [Google Scholar] [CrossRef] [PubMed]
- Ma, V.Y.; Chan, L.; Carruthers, K.J. Incidence, Prevalence, Costs, and Impact on Disability of Common Conditions Requiring Rehabilitation in the United States: Stroke, Spinal Cord Injury, Traumatic Brain Injury, Multiple Sclerosis, Osteoarthritis, Rheumatoid Arthritis, Limb Loss, and Back Pain. Arch. Phys. Med. Rehabil. 2014, 95, 986–995. [Google Scholar] [CrossRef] [PubMed]
- Capela, N.A.; Lemaire, E.D.; Baddour, N.; Rudolf, M.; Goljar, N.; Burger, H. Evaluation of a smartphone human activity recognition application with able-bodied and stroke participants. J. Neuroeng. Rehabil. 2016, 13, 10. [Google Scholar] [CrossRef] [PubMed]
- Shapi’i, A.; Bahari, N.N.; Arshad, H.; Zin, N.A.M.; Mahayuddin, Z.R. Rehabilitation Exercise Game Model for Post-stroke using Microsoft Kinect Camera. In Proceedings of the 2nd International Conference on Biomedical Engineering (ICoBE), Penang, Malaysia, 30–31 March 2015. [Google Scholar]
- Sin, H.; Lee, G. Additional virtual reality training using Xbox Kinect in stroke survivors with hemiplegia. Am. J. Phys. Med. Rehabil. 2013, 92, 871–880. [Google Scholar] [CrossRef] [PubMed]
- Rose, T.; Nam, C.S.; Chen, K.B. Immersion of virtual reality for rehabilitation-Review. Appl. Ergon. 2018, 69, 153–161. [Google Scholar] [CrossRef] [PubMed]
- Pfeifer, M.; Sinaki, M.; Geusens, P.; Boonen, S.; Preisinger, E.; Minne, H.W. Musculoskeletal Rehabilitation in Osteoporosis: A Review. J. Bone Miner. Res. 2004, 19, 1208–1214. [Google Scholar] [CrossRef] [PubMed]
- Chu, H.C.; Lee, T.H.; Chang, L.H.; Li, C.J. Modeling of Location Estimation for Object Tracking in WSN. J. Appl. Math. 2013, 2013, 10. [Google Scholar] [CrossRef]
- Wu, C.J.; Haung, S.J.; Chen, C.C. Method on Pattern Recognition of Various Limb Postures. J. Biomed. Syst. Emerg. Technol. 2018, 5, 118. [Google Scholar]
- Sztyler, T.; Stuckenschmidt, H. On-body Localization of Wearable Devices: An Investigation of Position-Aware Activity Recognition. In Proceedings of the IEEE International Conference on Pervasive Computing and Communications (PerCom), Sydney, Australia, 14–19 March 2016. [Google Scholar]
- Attal, F.; Mohammed, S.; Dedabrishvili, M.; Chamroukhi, F.; Oukhellou, L.; Amirat, Y. Physical Human Activity Recognition Using Wearable Sensors. Sensors 2015, 15, 31314–31338. [Google Scholar] [CrossRef] [PubMed]
- Olguin, D.O.; Pentland, A.S. Human Activity Recognition: Accuracy across Common Locations for Wearable Sensors. In Proceedings of the IEEE 10th International Symposium on Wearable Computers, Montreaux, Switzerland, 11–14 October 2006. [Google Scholar]
- Asokan, A.; Pothen, A.J.; Vijayaraj, R.K. ARMatron—A wearable gesture recognition glove, For control of robotic devices in disaster management and human Rehabilitation. In Proceedings of the International Conference on Robotics and Automation for Humanitarian Applications (RAHA), Kollam, India, 18–20 December 2016. [Google Scholar]
- Polygerinos, P.; Wang, Z.; Galloway, K.C.; Wood, R.J.; Walsh, C.J. Soft robotic glove for combined assistance and at-home rehabilitation. Robot. Auton. Syst. 2015, 73, 135–143. [Google Scholar] [CrossRef]
- Zhang, F.; Wang, X.; Yang, Y.; Fu, Y.; Wang, S. A Human-machine Interface Software Based on Android System for Hand Rehabilitation Robot. In Proceedings of the IEEE International Conference on Information and Automation, Lijiang, China, 8–10 August 2015. [Google Scholar]
- Gałka, J.; Mąsior, M.; Zaborski, M.; Barczewska, K. Inertial Motion Sensing Glove for Sign Language Gesture Acquisition and Recognition. IEEE Sens. J. 2016, 16, 6310–6316. [Google Scholar] [CrossRef]
- Maryam, S.R.D.; Payandeh, S. A novel human posture estimation using single depth image from Kinect v2 sensor. In Proceedings of the Annual IEEE International Systems Conference (SysCon), Vancouver, BC, Canada, 23–26 April 2018. [Google Scholar]
- Tarabini, M.; Marinoni, M.; Mascetti, M.; Marzaroli, P.; Corti, F.; Giberti, H.; Villa, A.; Mascagni, P. Monitoring the human posture in industrial environment: A feasibility study. In Proceedings of the IEEE Sensors Applications Symposium (SAS), Seoul, Korea, 12–14 March 2018. [Google Scholar]
- Ke, S.R.; Thuc, H.L.U.; Lee, Y.J.; Hwang, J.N.; Yoo, J.H.; Choi, K.H. A Review on Video-Based Human Activity Recognition. Computers 2013, 2, 88–131. [Google Scholar] [CrossRef]
- Chiu, C.Y.; Wu, C.C.; Wu, Y.C.; Wu, M.Y.; Chao, S.P.; Yang, S.N. Retrieval and constraint-based human posture reconstruction from a single image. J. Vis. Commun. Image Represent. 2006, 17, 892–915. [Google Scholar] [CrossRef]
- Hachaj, T.; Ogiela, M.R.; Koptyra, K. Human actions recognition from motion capture recordings using signal resampling and pattern recognition methods. Ann. Oper. Res. 2018, 265, 223–239. [Google Scholar] [CrossRef]
- Hachaj, T.; Piekarczyk, M.; Ogiela, M.R. Human Actions Analysis: Templates Generation, Matching and Visualization Applied to Motion Capture of Highly-Skilled Karate Athletes. Sensors 2017, 17, 2590. [Google Scholar] [CrossRef] [PubMed]
- Hachaj, T.; Ogiela, M.R. The adaptation of GDL motion recognition system to sport and rehabilitation techniques analysis. J. Med. Syst. 2016, 40, 137. [Google Scholar] [CrossRef] [PubMed]
- Hachaj, T.; Ogiela, M.R. Human actions recognition on multimedia hardware using angle-based and coordinate-based features and multivariate continuous hidden Markov model classifier. Multimed. Tools Appl. 2016, 75, 16265–16285. [Google Scholar] [CrossRef]
- Liu, L.; Peng, Y.; Wang, S.; Liu, M.; Huang, Z. Complex activity recognition using time series pattern dictionary learned from ubiquitous sensors. Inf. Sci. 2016, 340–341, 41–57. [Google Scholar] [CrossRef]
- Du, Y.; Wang, W.; Wang, L. Hierarchical recurrent neural network for skeleton based action recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Gaglio, S.; Giuseppe, L.R.; Morana, M. Human activity recognition process using 3-D posture data. IEEE Trans. Hum. Mach. Syst. 2015, 45, 586–597. [Google Scholar] [CrossRef]
- Jalal, A.; Kamal, S.; Kim, D. A depth video sensor-based life-logging human activity recognition system for elderly care in smart indoor environments. Sensors 2014, 14, 11735–11759. [Google Scholar] [CrossRef] [PubMed]
- Xia, L.; Chen, C.C.; Aggarwal, J.K. View invariant human action recognition using histograms of 3D joints. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops, Providence, RI, USA, 16–21 June 2012. [Google Scholar]
- Shotton, J.; Fitzgibbon, A.; Cook, M.; Sharp, T.; Finocchio, M.; Moore, R.; Kipman, A.; Blake, A. Real-time human pose recognition in parts from single depth images. Machine Learning for Computer Vision. In Studies in Computational Intelligence; Cipolla, R., Battiato, S., Farinella, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 411, pp. 119–135. ISBN 978-3-642-28660-5. [Google Scholar]
- Bonizzi, P.; Karel, J.M.H.; Meste, O.; Peeters, R.L.M. Singular Spectrum Decomposition: A New Method for Time Series Decomposition. Adv. Adapt. Data Anal. 2014, 6, 1450011. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale Entropy Analysis of Complex Physiologic Time Series. Phys. Rev. Lett. 2002, 89, 068102. [Google Scholar] [CrossRef] [PubMed]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of biological signals. Phys. Rev. E 2005, 71, 021906. [Google Scholar] [CrossRef] [PubMed]
- Costa, M.D.; Peng, C.K.; Goldberger, A.L. Multiscale Analysis of Heart Rate Dynamics: Entropy and Time Irreversibility Measures. Cardiovasc. Eng. 2008, 8, 88–93. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.C.; Juan, H.H.; Tsai, M.Y.; Lu, H.H.S. Unsupervised Learning and Pattern Recognition of Biological Data Structures with Density Functional Theory and Machine Learning. Sci. Rep. 2018, 8, 557. [Google Scholar] [CrossRef] [PubMed]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Cramer, C.J.; Truhlar, D.G. Density functional theory for transition metals and transition metal chemistry. Phys. Chem. Chem. Phys. 2009, 11, 10757–10816. [Google Scholar] [CrossRef] [PubMed]
- Wu, J. Density functional theory for chemical engineering: From capillarity to soft materials. AICHE J. 2006, 52, 1169–1193. [Google Scholar] [CrossRef]
- Daw, M.S.; Baskes, M.I. Semiempirical, quantum mechanical calculation of hydrogen embrittlement in metals. Phys. Rev. Lett. 1983, 50, 1285–1288. [Google Scholar] [CrossRef]
- Lebègue, S.; Björkman, T.; Klintenberg, M.; Nieminen, R.M.; Eriksson, O. Two-Dimensional Materials from Data Filtering and Ab Initio Calculations. Phys. Rev. X 2013, 3, 031002. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Schwabe, T.; Mück-Lichtenfeld, C. Density functional theory with dispersion corrections for supramolecular structures, aggregates, and complexes of (bio)organic molecules. Org. Biomol. Chem. 2007, 5, 741–758. [Google Scholar] [CrossRef] [PubMed]
- Riley, K.E.; Pitoňák, M.; Jurečka, P.; Hobza, P. Stabilization and Structure Calculations for Noncovalent Interactions in Extended Molecular Systems Based on Wave Function and Density Functional Theories. Chem. Rev. 2010, 110, 5023–5063. [Google Scholar] [CrossRef] [PubMed]
- Neese, F. Prediction of molecular properties and molecular spectroscopy with density functional theory: From fundamental theory to exchange-coupling. Coord. Chem. Rev. 2009, 253, 526–563. [Google Scholar] [CrossRef]
- Zupan, A.; Burke, K.; Ernzerhof, M.; Perdew, J.P. Distributions and averages of electron density parameters: Explaining the effects of gradient corrections. J. Chem. Phys. 1997, 106, 10184–10193. [Google Scholar] [CrossRef]
- Zupan, A.; Perdew, J.P.; Burke, K.; Causá, M. Density-Gradient Analysis for Density Functional Theory: Application to Atoms. Int. J. Quantum Chem. 1997, 61, 835–845. [Google Scholar] [CrossRef]
- Lin, Y.C.; Hsieh, I.T.; Lin, W.T.; Huang, W.L.; Kuo, K.L.; Lee, G.S.; Lo, M.T.; Yang, C.C.H.; Huang, N.E.; Kuo, T.B.J. Implementation of cloud computing healthcare based on xenon uploading system and Hilbert transform. In Lecture Notes on Wireless Healthcare Research; Patrick, K., Su, M.-C., Eds.; University of Taiwan System Press: Taiwan, 2013; pp. 115–124. [Google Scholar]
- Lee, G.S.; Kuo, T.B.J. Cloud computing electrocardiographic system using xenon RF & GPRS transmission Technique. In Lecture Notes on Wireless Healthcare Research; Patrick, K., Su, M.-C., Eds.; University of Taiwan System Press: Taiwan, 2013; pp. 151–156. [Google Scholar]
- Glowacz, A.; Glowacz, W.; Glowacz, Z.; Kozik, J. Early fault diagnosis of bearing and stator faults of the single-phase induction motor using acoustic signals. Measurement 2018, 113, 1–9. [Google Scholar] [CrossRef]
- Přibil, J.; Přibilová, A.; Frollo, I. Two Methods of Automatic Evaluation of Speech Signal Enhancement Recorded in the Open-Air MRI Environment. Meas. Sci. Rev. 2017, 17, 257–263. [Google Scholar] [CrossRef]
- Přibil, J.; Přibilová, A.; Frollo, I. Automatic GMM-Based evaluation of noise suppression in the speech signal recorded during phonation in the open-air MRI. In Proceedings of the 40th International Conference on Telecommunications and Signal Processing (TSP), Barcelona, Spain, 5–7 July 2017. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, S.-J.; Wu, C.-J.; Chen, C.-C. Pattern Recognition of Human Postures Using the Data Density Functional Method. Appl. Sci. 2018, 8, 1615. https://doi.org/10.3390/app8091615
Huang S-J, Wu C-J, Chen C-C. Pattern Recognition of Human Postures Using the Data Density Functional Method. Applied Sciences. 2018; 8(9):1615. https://doi.org/10.3390/app8091615
Chicago/Turabian StyleHuang, Shin-Jhe, Chi-Jui Wu, and Chien-Chang Chen. 2018. "Pattern Recognition of Human Postures Using the Data Density Functional Method" Applied Sciences 8, no. 9: 1615. https://doi.org/10.3390/app8091615
APA StyleHuang, S.-J., Wu, C.-J., & Chen, C.-C. (2018). Pattern Recognition of Human Postures Using the Data Density Functional Method. Applied Sciences, 8(9), 1615. https://doi.org/10.3390/app8091615





