Decision Support System for Medical Diagnosis Utilizing Imbalanced Clinical Data
Abstract
1. Introduction
2. Related Work
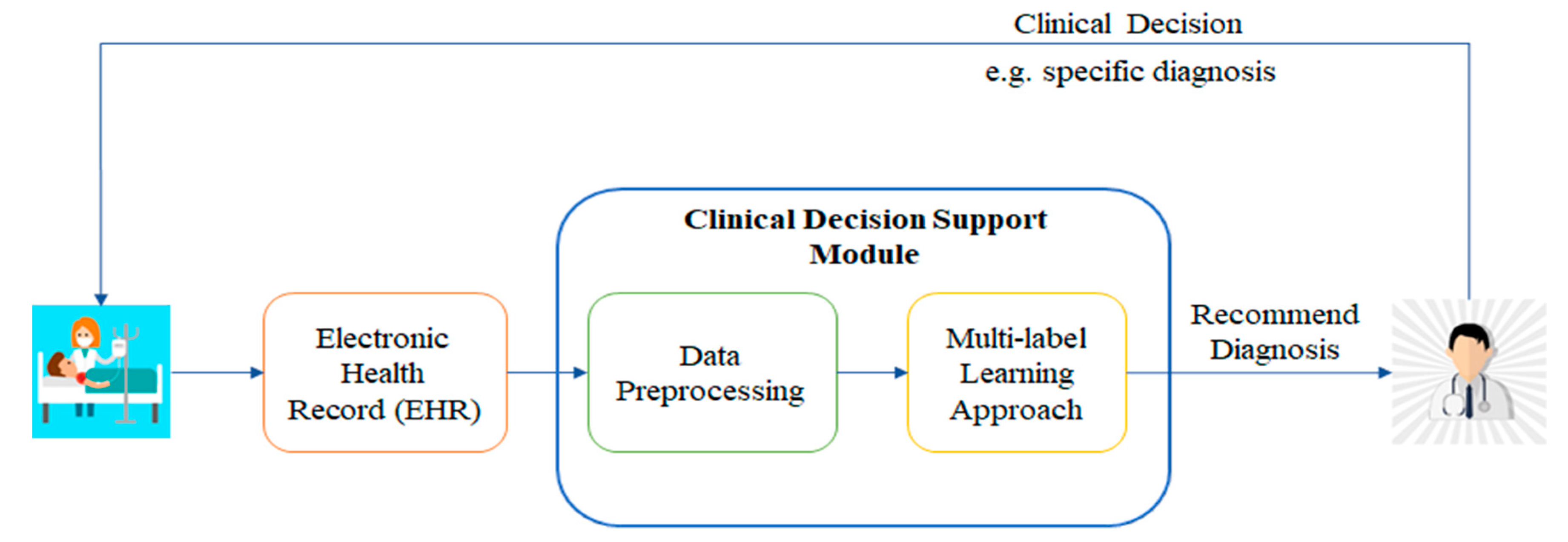
3. Proposed Methodology
3.1. Data Standardization
3.2. COCOA Method for Class-Imbalanced Data
3.3. Regularized Boosting Approach for Multi-Class Classification
3.4. COCOA Integrated with a Regularized Boosting Approach for Multi-Class Classification
4. Experiments
4.1. Data Set and Experiment Setup
4.2. Evaluation Metrics
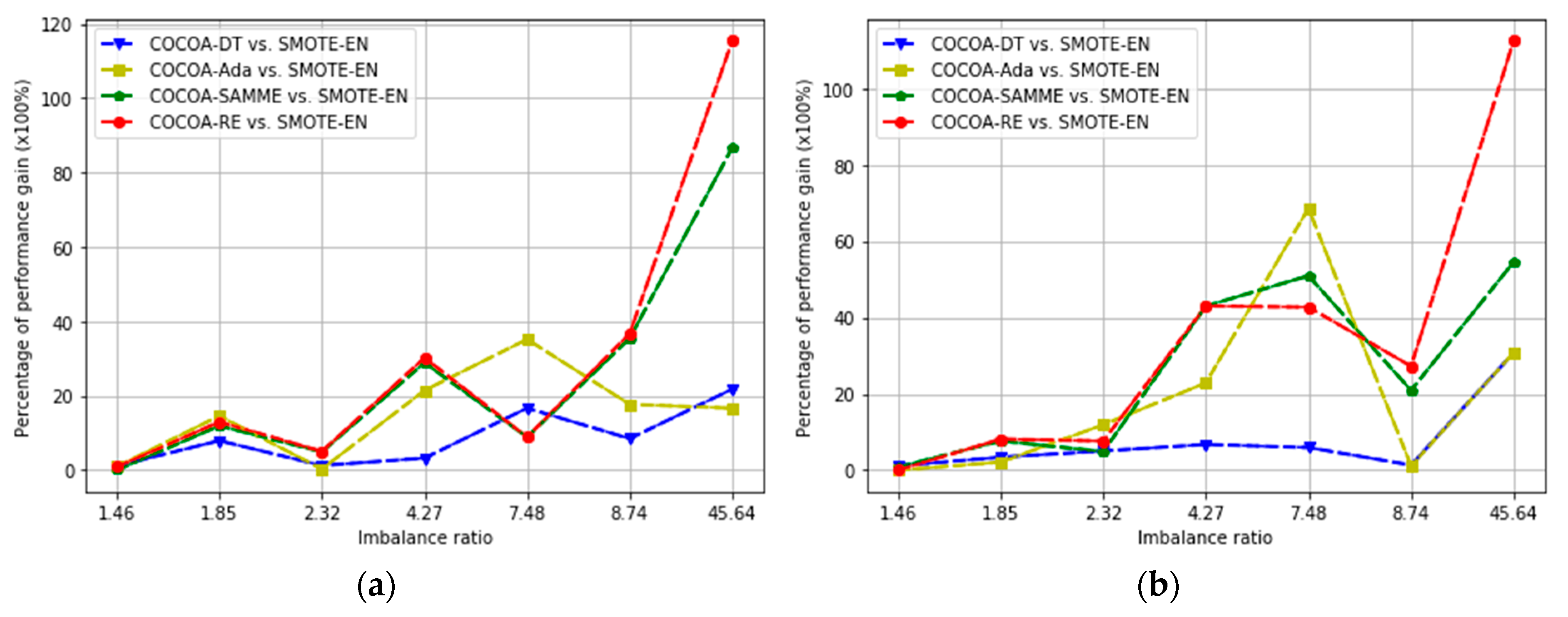
4.3. Experimental Results
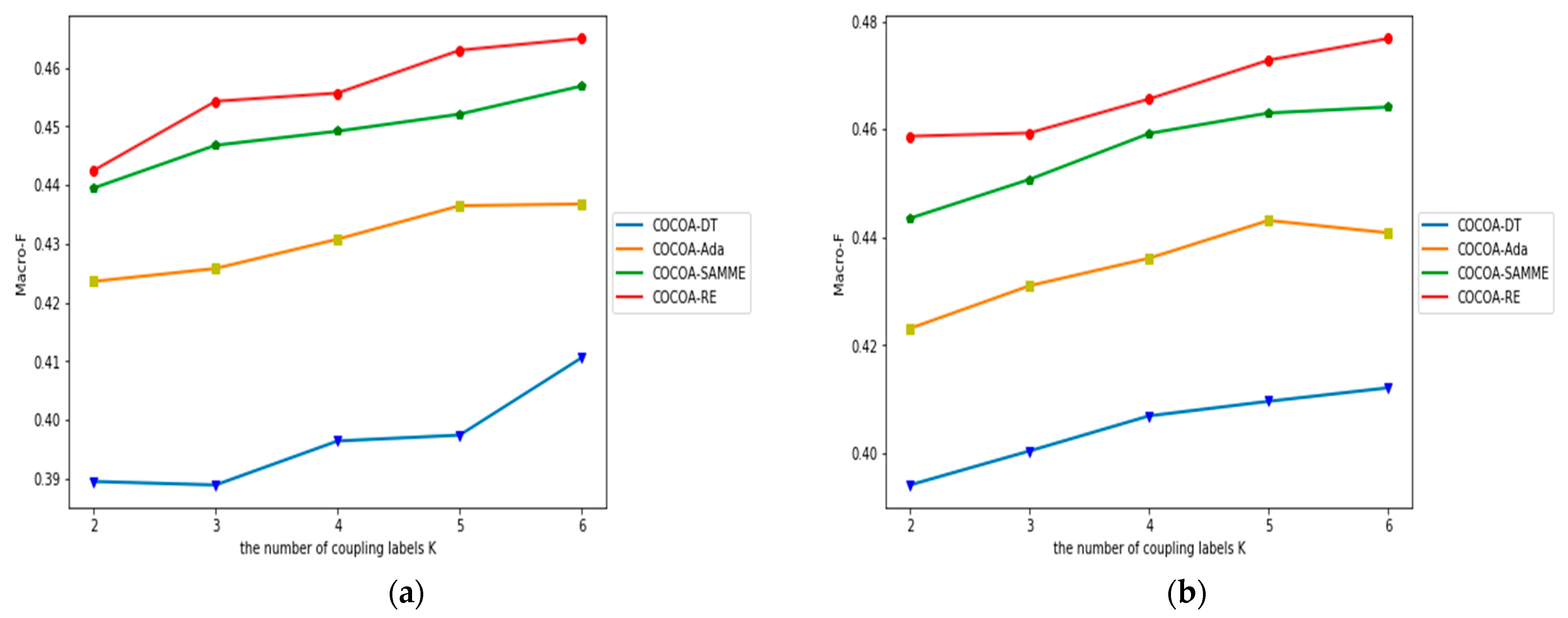
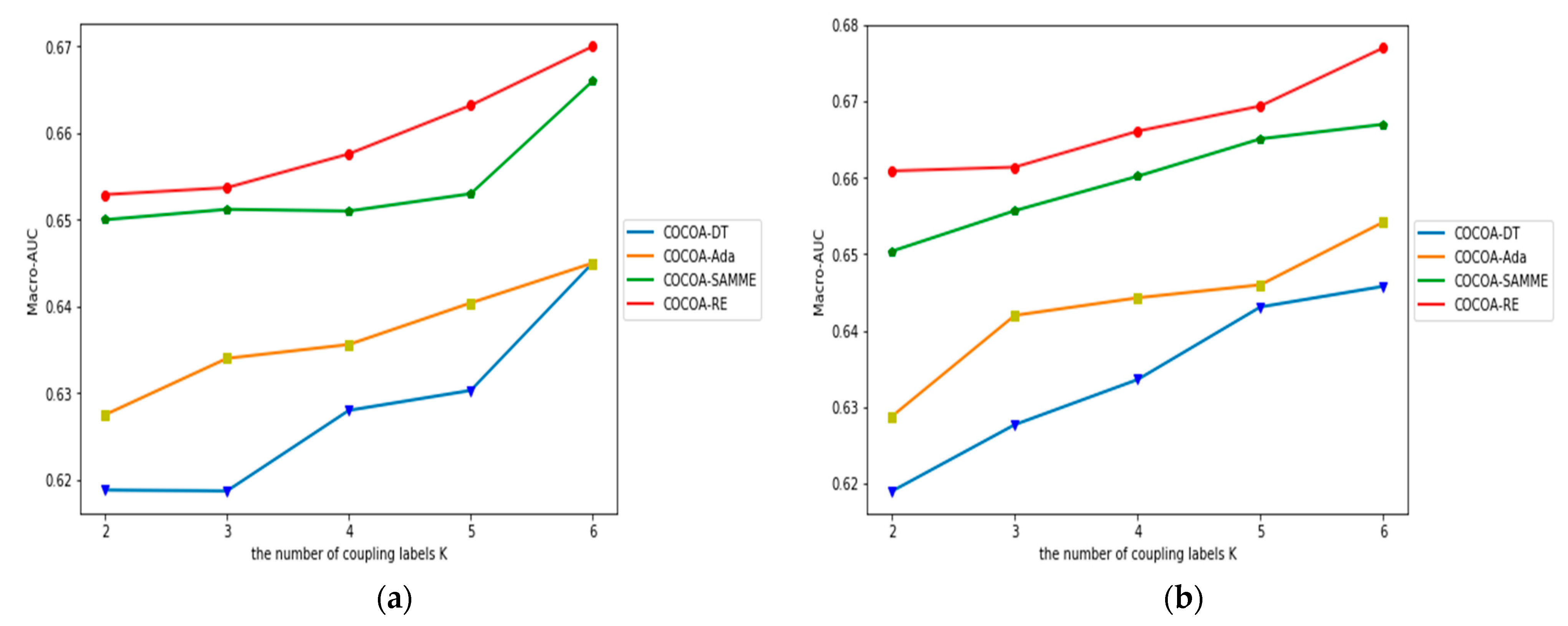
4.4. The Impact of K
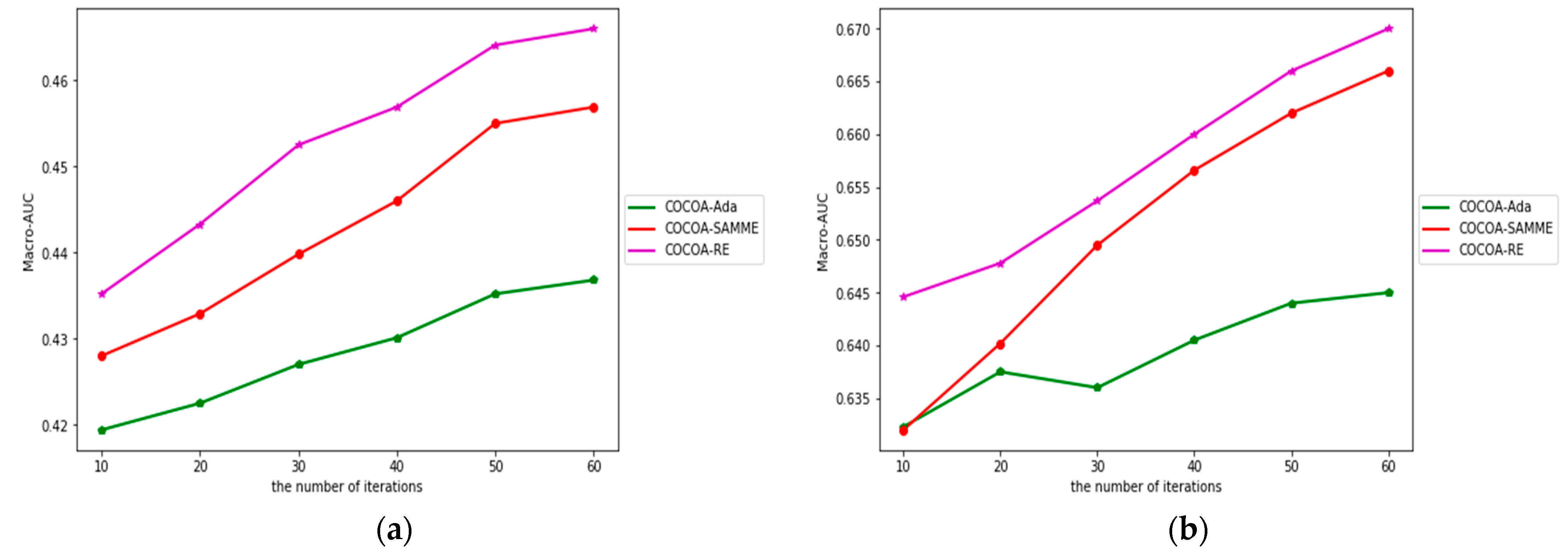
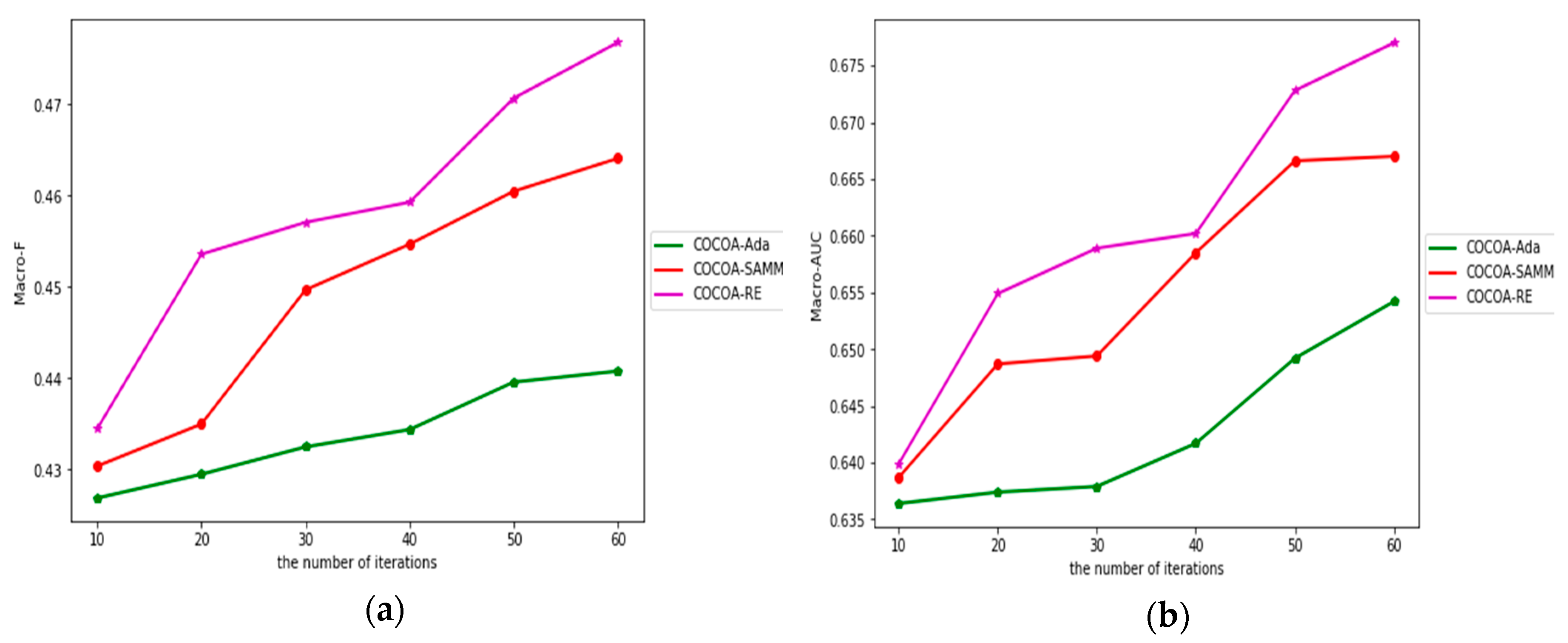
4.5. The Impact of Iterations in Ensemble Classification
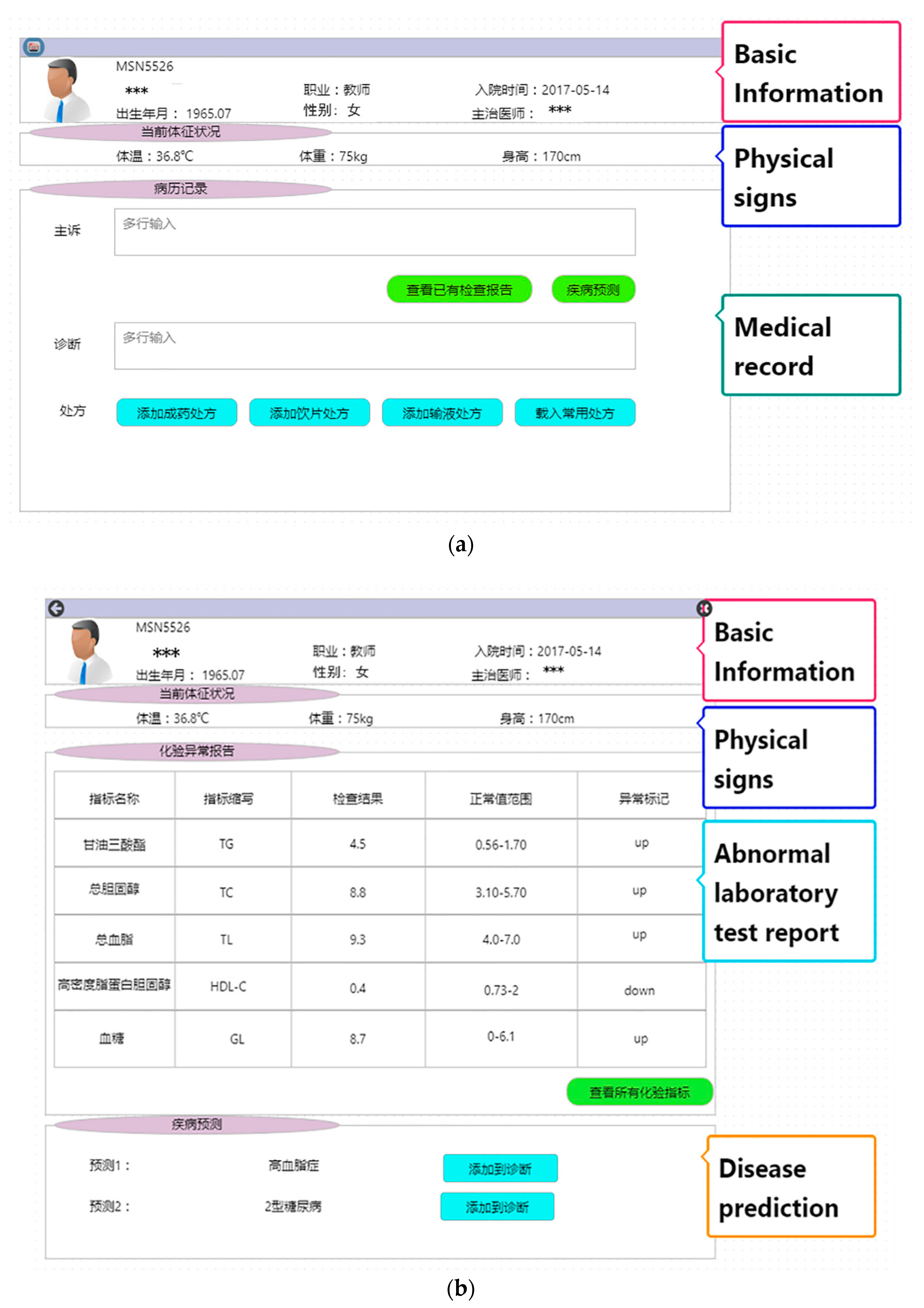
4.6. System Implementation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| List of Laboratory Testing Items | |||||
|---|---|---|---|---|---|
| Venous blood | 96 | Transferrin saturation factor | 191 | Blood glucose | |
| No. | Testing items | 97 | Serum iron | 192 | Arterial blood hemoglobin |
| 1 | Platelet counts (PCT) | 98 | Folic acid | 193 | Ionic Calcium |
| 2 | Platelet-large cell ratio(P-LCR) | 99 | The ratio of CD4 lymphocytes and CD8 lymphocyte | 194 | Chloride ion |
| 3 | Mean platelet volume (MPV) | 100 | CD3 lymphocyte count | 195 | Sodium ion |
| 4 | Platelet distribution width (PDW) | 101 | CD8 lymphocyte count | 196 | Potassium ion |
| 5 | Red blood cell volume distribution Width (RDW-SD) | 102 | CD4 lymphocyte count | 197 | Oxygen saturation |
| 6 | Coefficient of variation of red blood cell distribution width | 103 | Heart-Type fatty acid binding protein | 198 | Bicarbonate |
| 7 | Basophil | 104 | Rheumatoid | 199 | Base excess |
| 8 | Eosinophils | 105 | Anti-Streptolysin O | 200 | Partial pressure of oxygen |
| 9 | Neutrophils | 106 | Free thyroxine | 201 | Partial pressure of carbon dioxide |
| 10 | Monocytes | 107 | Free triiodothyronine | 202 | PH value |
| 11 | Lymphocytes | 108 | Antithyroglobulin antibodies | Feces | |
| 12 | Basophil ratio | 109 | Antithyroid peroxidase autoantibody | No. | Testing items |
| 13 | Eosinophils ratio | 110 | Thyrotropin | 203 | Feces with blood |
| 14 | Neutrophils ratio | 111 | Total thyroxine | 204 | Feces occult blood |
| 15 | Monocytes ratio | 112 | Total triiodothyronine | 205 | Red blood cell |
| 16 | Lymphocytes ratio | 113 | Peptide | 206 | White blood cell |
| 17 | Platelet | 114 | Insulin | 207 | Feces property |
| 18 | Mean corpuscular hemoglobin concentration | 115 | Blood sugar | 208 | Feces color |
| 19 | Mean corpuscular hemoglobin | 116 | B factor | 209 | Fungal hyphae |
| 20 | Mean corpuscular volume | 117 | Immunoglobulin G | 210 | Fungal spore |
| 21 | Hematocrit | 118 | Immunoglobulin M | 211 | Macrophage |
| 22 | Hemoglobin | 119 | Immunoglobulin A | 212 | Fat drop |
| 23 | Red blood cell | 120 | Adrenocorticotrophic | 213 | Mucus |
| 24 | White blood cell | 121 | Cortisol | 214 | Worm egg |
| 25 | Calcium | 122 | Humanepididymisprotein4 | Urine | |
| 26 | Chlorine | 123 | Carbohydrate antigen 15-3 | No. | Testing items |
| 27 | Natrium | 124 | Carbohydrate antigen 125 | 215 | Urinary albumin/creatinine ratio |
| 28 | Potassium | 125 | Alpha-fetoprotein | 216 | Microalbumin |
| 29 | Troponin I | 126 | Carcinoembryonic antigen | 217 | Microprotein |
| 30 | Myoglobin | 127 | Carbohydrate antigen 199 | 218 | Urine creatinine |
| 31 | High sensitivity C-reactive protein | 128 | Hydroxy-vitamin D | 219 | Glycosylated hemoglobin |
| 32 | Creatine kinase isoenzymes | 129 | Thyrotropin receptor antibody | 220 | Peptide |
| 33 | Creatine kinase | 130 | HCV | 221 | Insulin |
| 34 | Complement (C1q) | 131 | Enteric adenovirus | 222 | Blood sugar |
| 35 | Retinol-binding | 132 | Astrovirus | 223 | β2 micro globulin |
| 36 | Cystatin C | 133 | Norovirus | 224 | Serum β micro globulin |
| 37 | Creatinine | 134 | Duovirus | 225 | Acetaminophen glucosidase |
| 38 | Uric acid | 135 | Coxsackie virus A16-IgM | 226 | α1 micro globulin |
| 39 | Urea | 136 | Enterovirus 71-IgM | 227 | Hyaline cast |
| 40 | Pro-brain nitric peptide | 137 | Toluidine Red test | 228 | White blood cell cast |
| 41 | α-Fructosidase | 138 | Uric acid | 229 | Red blood cell cast |
| 42 | Pre-albumin | 139 | Urea | 230 | Granular cast |
| 43 | Total bile acid | 140 | Antithrombin | 231 | Waxy cast |
| 44 | Indirect bilirubin | 141 | Thrombin time | 232 | Pseudo hypha |
| 45 | Bilirubin direct | 142 | Partial-thromboplastin time | 233 | Bacteria |
| 46 | Total bilirubin | 143 | Fibrinogen | 234 | Squamous cells |
| 47 | Glutamyl transpeptidase | 144 | International normalized ratio | 235 | Non-squamous epithelium |
| 48 | Alkaline phosphatase | 145 | Prothrombin time ratio | 236 | Mucus |
| 49 | Mitochondrial-aspartate aminotransferase | 146 | Prothrombin time | 237 | Yeasts |
| 50 | Aspartate aminotransferase | 147 | D-dimer | 238 | White Blood Cell Count |
| 51 | Glutamic-pyruvic transaminase | 148 | Fibrinogen degradation product | 239 | White blood cell |
| 52 | Albumin and globulin ratio | 149 | Aldosterone-to-renin ratio | 240 | Red blood cell |
| 53 | Globulin | 150 | Renin | 241 | Vitamin C |
| 54 | Albumin | 151 | Cortisol | 242 | Bilirubin |
| 55 | Total albumin | 152 | Aldosterone | 243 | Urobilinogen |
| 56 | Lactate dehydrogenase | 153 | Angiotensin Ⅱ | 244 | Ketone body |
| 57 | Anion gap | 154 | Adrenocorticotrophic hormone | 245 | Glucose |
| 58 | Carbon dioxide | 155 | Reticulocyte absolute value | 246 | Defecate concealed blood |
| 59 | Magnesium | 156 | Reticulocyte ratio | 247 | Protein |
| 60 | Phosphorus | 157 | Middle fluorescence reticulocytes | 248 | Granulocyte esterase |
| 61 | Blood group | 158 | High fluorescence reticulocytes | 249 | Nitrite |
| 62 | Osmotic pressure | 159 | Immature reticulocytes | 250 | PH value |
| 63 | Glucose | 160 | Low fluorescence reticulocytes | 251 | Specific gravity |
| 64 | Amylase | 161 | Optical platelet | 252 | Appearance |
| 65 | Homocysteine | 162 | Erythrocyte sedimentation rate | 253 | Transparency |
| 66 | Salivary acid | 163 | Casson viscosity | 254 | Human chorionic gonadotropin |
| 67 | Free fatty acid | 164 | Red blood cell rigidity index | Cerebrospinal fluid | |
| 68 | Copper-protein | 165 | Red blood cell deformation index | No. | Testing items |
| 69 | Complement (C4) | 166 | Whole blood high shear viscosity | 255 | Glucose |
| 70 | Complement (C3) | 167 | Whole blood low shear viscosity | 256 | Chlorine |
| 71 | Lipoprotein | 168 | Red cell assembling index | 257 | β2-microglobulin |
| 72 | Apolipoprotein B | 169 | K value in blood sedimentation equation | 258 | Microalbumin |
| 73 | Apolipoprotein A1 | 170 | Whole blood low shear relative viscosity | 259 | Micro protein |
| 74 | Low density lipoprotein cholesterol | 171 | Whole blood high shear relative viscosity | 260 | Adenosine deaminase |
| 75 | High density lipoprotein cholesterol | 172 | Erythrocyte sedimentation rate (ESR) | 261 | Mononuclear white blood cell |
| 76 | Triglycerides | 173 | Plasma viscosity | 262 | Multinuclear white blood cell |
| 77 | Total cholesterol | 174 | Whole blood viscosity1(1/S) | 263 | White blood cell count |
| 78 | Procalcitonin | 175 | Whole blood viscosity50(1/S) | 264 | Pus cell |
| 79 | Hepatitis B core antibody | 176 | Whole blood viscosity200(1/S) | 265 | White Blood Cell |
| 80 | Hepatitis B e antibody | 177 | Occult blood of gastric juice | 266 | Red Blood Cell |
| 81 | Hepatitis B e antigen | 178 | Carbohydrate antigen 19-9 | 267 | Pandy test |
| 82 | Hepatitis B surface antibody | 179 | Free-beta subunit human chorionic gonadotropin | 268 | Turbidity |
| 83 | Hepatitis B surface antigen | 180 | Neuron-specific enolase | 269 | Color |
| 84 | Syphilis antibodies | 181 | Keratin 19th segment | Peritoneal dialysate | |
| 85 | C-reactive protein | 182 | Carbohydrate antigen 242 | No. | Testing items |
| 86 | Lipase | 183 | The absolute value of atypical lymphocyte | 270 | Karyocyte (single nucleus) |
| 87 | Blood ammonia | 184 | The ratio of atypical lymphocyte | 271 | Karyocyte (multiple nucleus) |
| 88 | Cardiac troponin T | Arterial blood | 272 | Karyocyte count | |
| 89 | Hydroxybutyric acid | No. | Testing items | 273 | White Blood Cell |
| 90 | Amyloid β-protein | 185 | Anion gap | 274 | Red Blood Cell |
| 91 | Unsaturated iron binding capacity | 186 | Carboxyhemoglobin | 275 | Mucin qualitative analysis |
| 92 | Transferrin | 187 | Hematocrit | 276 | Coagulability |
| 93 | Ferritin | 188 | Lactic acid | 277 | Turbidity |
| 94 | Vitamin B12 | 189 | Reduced hemoglobin | 278 | Color |
| 95 | Total iron binding capacity | 190 | Methemoglobin | ||
References
- Lindmeier, C.; Brunier, A. WHO: Number of People over 60 Years Set to Double by 2050; Major Societal Changes Required. Available online: http://www.who.int/mediacentre/news/releases/2015/older-persons-day/en/ (accessed on 25 July 2018).
- Wang, Y. Study on Clinical Decision Support Based on Electronic Health Records Data. Ph.D. Thesis, Zhejiang University, Hangzhou, China, October 2016. [Google Scholar]
- Shah, S.M.; Batool, S.; Khan, I.; Ashraf, M.U.; Abbas, S.H.; Hussain, S.A. Feature extraction through parallel probabilistic principal component analysis for heart disease diagnosis. Phys. A Stat. Mech. Appl. 2017, 482, 796–808. [Google Scholar] [CrossRef]
- Vancampfort, D.; Mugisha, J.; Hallgren, M.; De Hert, M.; Probst, M.; Monsieur, D.; Stubbs, B. The prevalence of diabetes mellitus type 2 in people with alcohol use disorders: A systematic review and large scale meta-analysis. Psychiatry Res. 2016, 246, 394–400. [Google Scholar] [CrossRef] [PubMed]
- Miller, M.; Stone, N.J.; Ballantyne, C.; Bittner, V.; Criqui, M.H.; Ginsberg, H.N.; Goldberg, A.C.; Howard, W.J.; Jacobson, M.S.; Kris-Etherton, P.M.; et al. Triglycerides and Cardiovascular Disease: A Scientific Statement from the American Heart Association. Circulation 2011, 123, 2292–2333. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Li, P.; Tian, Y.; Ren, J.J.; Li, J.S. A Shared Decision-Making System for Diabetes Medication Choice Utilizing Electronic Health Record Data. IEEE J. Biomed. Health Inform. 2017, 21, 1280–1287. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.L.; Li, Y.K.; Liu, X.Y. Towards class-imbalance aware multi-label learning. In Proceedings of the Twenty-Fourth International Joint Conference on Artificial Intelligence, Buenos Aires, Argentina, 25–31 July 2015. [Google Scholar]
- Yuan, X.; Xie, L.; Abouelenien, M. A regularized ensemble framework of deep learning for cancer detection from multi-class imbalanced training data. Pattern Recognit. 2018, 77, 160–172. [Google Scholar] [CrossRef]
- Marco-Ruiz, L.; Pedrinaci, C.; Maldonado, J.A.; Panziera, L.; Chen, R.; Bellika, J.G. Publication, discovery and interoperability of clinical decision support systems: A linked data approach. J. Biomed. Inform. 2016, 62, 243–264. [Google Scholar] [CrossRef] [PubMed]
- Suk, H.I.; Lee, S.W.; Shen, D. Deep ensemble learning of sparse regression models for brain disease diagnosis. Med. Image Anal. 2017, 37, 101–113. [Google Scholar] [CrossRef] [PubMed]
- Çomak, E.; Arslan, A.; Türkoğlu, İ. A decision support system based on support vector machines for diagnosis of the heart valve diseases. Comput. Biol. Med. 2007, 37, 21–27. [Google Scholar] [CrossRef] [PubMed]
- Molinaro, S.; Pieroni, S.; Mariani, F.; Liebman, M.N. Personalized medicine: Moving from correlation to causality in breast cancer. New Horiz. Transl. Med. 2015, 2, 59. [Google Scholar] [CrossRef]
- Song, L.; Hsu, W.; Xu, J.; van der Schaar, M. Using Contextual Learning to Improve Diagnostic Accuracy: Application in Breast Cancer Screening. IEEE J. Biomed Health Inf. 2016, 20, 902–914. [Google Scholar] [CrossRef] [PubMed]
- He, H.; Garcia, E.A. Learning from Imbalanced Data. IEEE Trans. Knowl. Data Eng. 2009, 21, 1263–1284. [Google Scholar]
- Zhang, M.; Zhou, Z. ML-KNN: A lazy learning approach to multi-label learning. Pattern Recognit. 2007, 40, 2038–2048. [Google Scholar] [CrossRef]
- Tsoumakas, G.; Katakis, I.; Taniar, D. Multi-Label Classification: An Overview. Int. J. Data Warehous. Min. 2008, 3, 1–13. [Google Scholar] [CrossRef]
- Ghamrawi, N.; Mccallum, A. Collective multi-label classification. In Proceedings of the International Conference on Information and Knowledge Management, Bremen, Germany, 31 October–5 November 2005. [Google Scholar]
- Elisseeff, A.; Weston, J. A kernel method for multi-labelled classification. In Proceedings of the International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 3–8 December 2001. [Google Scholar]
- Fürnkranz, J.; Hüllermeier, E.; Mencía, E.L.; Brinker, K. Multilabel classification via calibrated label ranking. Mach. Learn. 2008, 73, 133–153. [Google Scholar] [CrossRef]
- Tsoumakas, G.; Katakis, I.; Vlahavas, I. Random k-Labelsets for Multilabel Classification. IEEE Trans. Knowl. Data Eng. 2011, 23, 1079–1089. [Google Scholar] [CrossRef]
- Tahir, M.A.; Kittler, J.; Yan, F. Inverse random under sampling for class imbalance problem and its application to multi-label classification. Pattern Recognit. 2012, 45, 3738–3750. [Google Scholar] [CrossRef]
- Sáez, J.A.; Krawczyk, B.; Woźniak, M. Analyzing the oversampling of different classes and types of examples in multi-class imbalanced datasets. Pattern Recognit. 2016, 57, 164–178. [Google Scholar]
- Prati, R.C.; Batista, G.E.; Silva, D.F. Class imbalance revisited: A new experimental setup to assess the performance of treatment methods. Knowl. Inf. Syst. 2015, 45, 1–24. [Google Scholar] [CrossRef]
- Charte, F.; Rivera, A.J.; del Jesus, M.J.; Herrera, F. MLSMOTE: Approaching imbalanced multilabel learning through synthetic instance generation. Knowl.-Based Syst. 2015, 89, 385–397. [Google Scholar] [CrossRef]
- Xioufis, E.S.; Spiliopoulou, M.; Tsoumakas, G.; Vlahavas, I. Dealing with Concept Drift and Class Imbalance in Multi-Label Stream Classification. In Proceedings of the International Joint Conference on Artificial Intelligence (IJCAI 2011), Barcelona, Spain, 16–22 July 2011. [Google Scholar]
- Fang, M.; Xiao, Y.; Wang, C.; Xie, J. Multi-label Classification: Dealing with Imbalance by Combining Label. In Proceedings of the 26th IEEE International Conference on Tools with Artificial Intelligence, Limassol, Cyprus, 10–12 November 2014. [Google Scholar]
- Napierala, K.; Stefanowski, J. Types of minority class examples and their influence on learning classifiers from imbalanced data. J. Intell. Inf. Syst. 2016, 46, 563–597. [Google Scholar] [CrossRef]
- Krawczyk, B. Learning from imbalanced data: open challenges and future directions. Prog. Artif. Intell. 2016, 5, 1–12. [Google Scholar] [CrossRef]
- Guo, H.; Li, Y.; Li, Y.; Liu, X.; Li, J. BPSO-Adaboost-KNN ensemble learning algorithm for multi-class imbalanced data classification. Eng. Appl. Artif. Intell. 2016, 49, 176–193. [Google Scholar]
- Cao, Q.; Wang, S.Z. Applying Over-sampling Technique Based on Data Density and Cost-sensitive SVM to Imbalanced Learning. In Proceedings of the 2012 International Joint Conference on Neural Networks (IJCNN), Brisbane, Australia, 10–15 June 2012. [Google Scholar]
- Fernández, A.; López, V.; Galar, M.; Jesus, M.J.; Herrera, F. Analyzing the classification of imbalanced data-sets with multiple classes: Binarization techniques and ad-hoc approaches. Knowl.-Based Syst. 2013, 42, 91–100. [Google Scholar]
- Freund, Y.; Schapire, R.E. A desicion-theoretic generalization of on-line learning and an application to boosting. J. Comput. Syst. Sci. 1997, 13, 663–671. [Google Scholar]
- Schapire, R.E.; Singer, Y. Improved Boosting Algorithms Using Confidence-rated Predictions. Mach. Learn. 1999, 37, 297–336. [Google Scholar] [CrossRef]
- Zhu, J.; Zou, H.; Rosset, S.; Hastie, T. Multi-class AdaBoost. Stat. Interface 2009, 2, 349–360. [Google Scholar]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- López, V.; Fernández, A.; García, S.; Palade, P.; Herrera, F. An insight into classification with imbalanced data: Empirical results and current trends on using data intrinsic characteristics. Inform. Sci. 2013, 250, 113–141. [Google Scholar]
- Zhang, M.L.; Zhou, Z.H. A Review on Multi-Label Learning Algorithms. IEEE Trans. Knowl. Data Eng. 2014, 26, 1819–1837. [Google Scholar] [CrossRef]
| Algorithm: COCOA-RE |
|---|
| Inputs: : the multi-label training set : the binary-class classifier : the multi-class classifier : the number of coupling labels : the testing example Outputs: : the suggested labels for Training process: 1: For to do 2: Generate the binary training set according to Equation (3) 3: ; 4: Select a subset containing labels randomly 5: for do 6: Generate the tri-class training set according to Equation (5) 7: Initialize example weight and 8: for to do 9: Train a classifier 10: if then 11: Compute according to Equation (13) 12: end if 13: if then 14: return 15: else 16: Compute weight for classifier : 17: Compute example weight: 18: Normalize : 19: end if 20: end for 21: 22: end for 23: Set the real-valued function : 24: Set the constant thresholding function is equal to generated by Equation (7) 25: end for 26: Return according to Equation (2) |
| Input Features | Category | Number | Mean |
|---|---|---|---|
| Essential Information | |||
| Age | 62.72 | ||
| Temperature | 36.6 | ||
| Height | 168.35 | ||
| Weight | 65.47 | ||
| Gender | Male | 395 | |
| Female | 260 | ||
| Lab test results | |||
| Items | 278 |
| Labels | No. of Examples | Imbalance Ratio | Average Imbalance Ratio |
|---|---|---|---|
| Diabetes mellitus type 2 | 266 | 1.46 | 10.25 |
| Hyperlipemia | 77 | 7.48 | |
| Hyperuricemia | 14 | 45.64 | |
| Coronary illness | 197 | 2.32 | |
| Cerebral ischemic stroke | 229 | 1.85 | |
| Anemia | 124 | 4.27 | |
| Chronic kidney disease | 67 | 8.74 |
| Results | The Binary Classifier Is Decision Tree | ||||
|---|---|---|---|---|---|
| SMOTE-EN | COCOA-DT | COCOA-Ada | COCOA-SAMME | COCOA-RE | |
| Macro-F | 0.384 | 0.410 | 0.437 | 0.457 | 0.465 |
| Macro-AUC | 0.613 | 0.632 | 0.645 | 0.666 | 0.670 |
| Results | The Binary Classifier Is Neural Network | ||||
|---|---|---|---|---|---|
| SMOTE-EN | COCOA-DT | COCOA-Ada | COCOA-SAMME | COCOA-RE | |
| Macro-F | 0.392 | 0.412 | 0.441 | 0.464 | 0.477 |
| Macro-AUC | 0.620 | 0.646 | 0.654 | 0.660 | 0.671 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, H.; Huang, M.; Zhang, Y.; Liu, J. Decision Support System for Medical Diagnosis Utilizing Imbalanced Clinical Data. Appl. Sci. 2018, 8, 1597. https://doi.org/10.3390/app8091597
Han H, Huang M, Zhang Y, Liu J. Decision Support System for Medical Diagnosis Utilizing Imbalanced Clinical Data. Applied Sciences. 2018; 8(9):1597. https://doi.org/10.3390/app8091597
Chicago/Turabian StyleHan, Huirui, Mengxing Huang, Yu Zhang, and Jing Liu. 2018. "Decision Support System for Medical Diagnosis Utilizing Imbalanced Clinical Data" Applied Sciences 8, no. 9: 1597. https://doi.org/10.3390/app8091597
APA StyleHan, H., Huang, M., Zhang, Y., & Liu, J. (2018). Decision Support System for Medical Diagnosis Utilizing Imbalanced Clinical Data. Applied Sciences, 8(9), 1597. https://doi.org/10.3390/app8091597





