Towards Online Estimation of Human Joint Muscular Torque with a Lower Limb Exoskeleton Robot
Abstract
1. Introduction
2. Methods
2.1. Parameterized Model of the Human Body
2.2. Inverse Dynamics of the Human Body
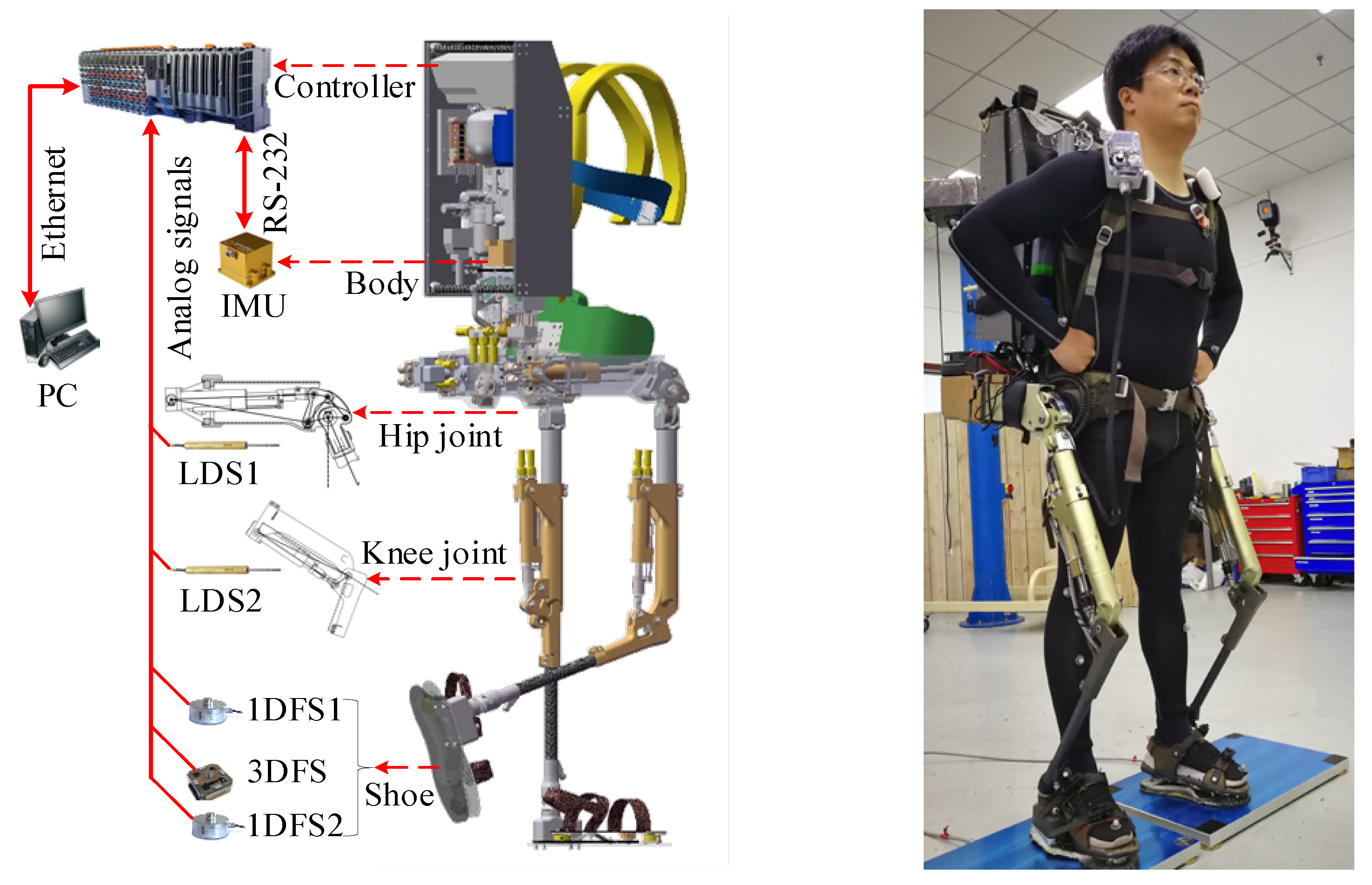
2.3. Sensing System Design
2.3.1. Overall Hardware Architecture
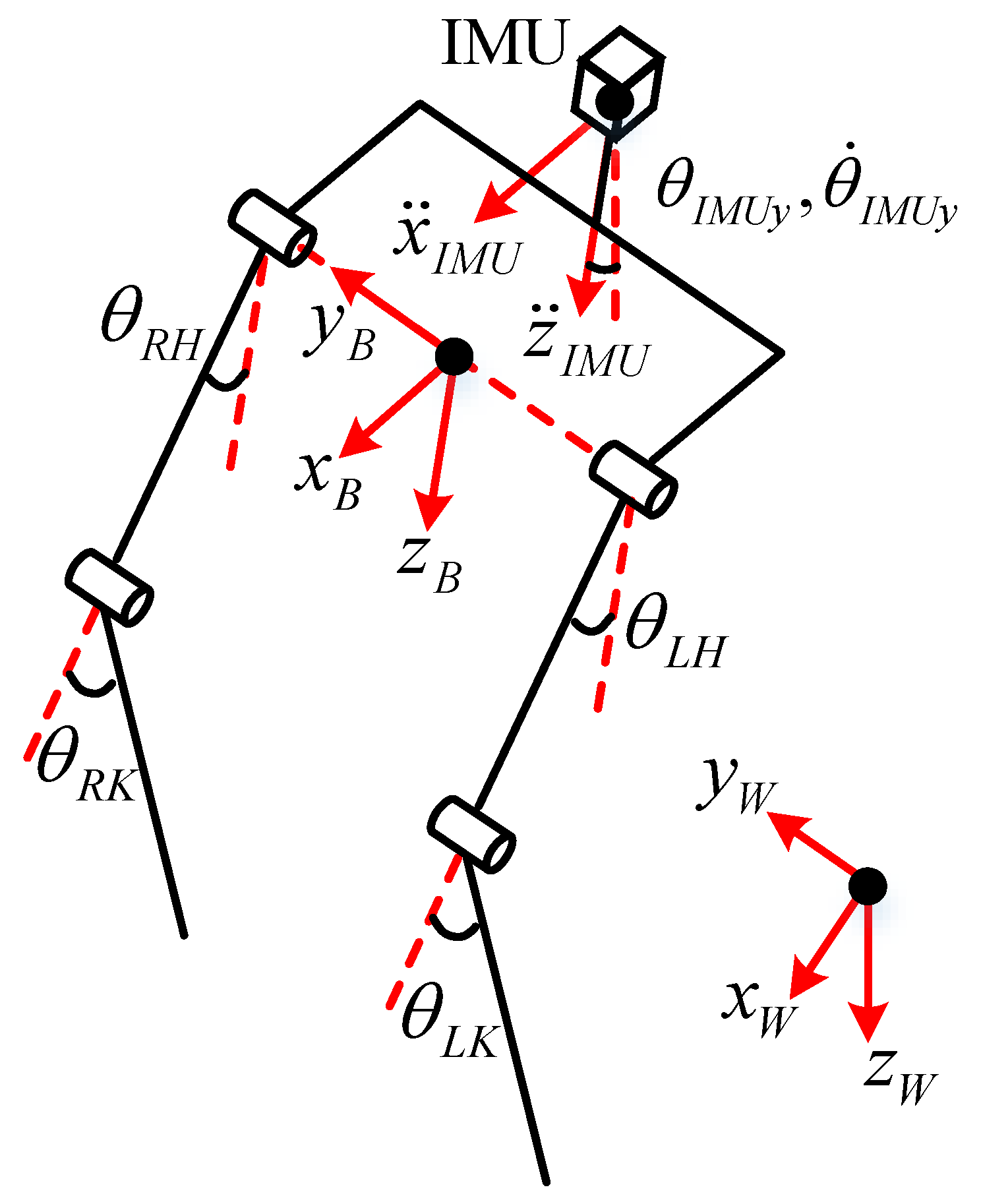
2.3.2. Trunk Posture and Hip Joint Acceleration Measurements
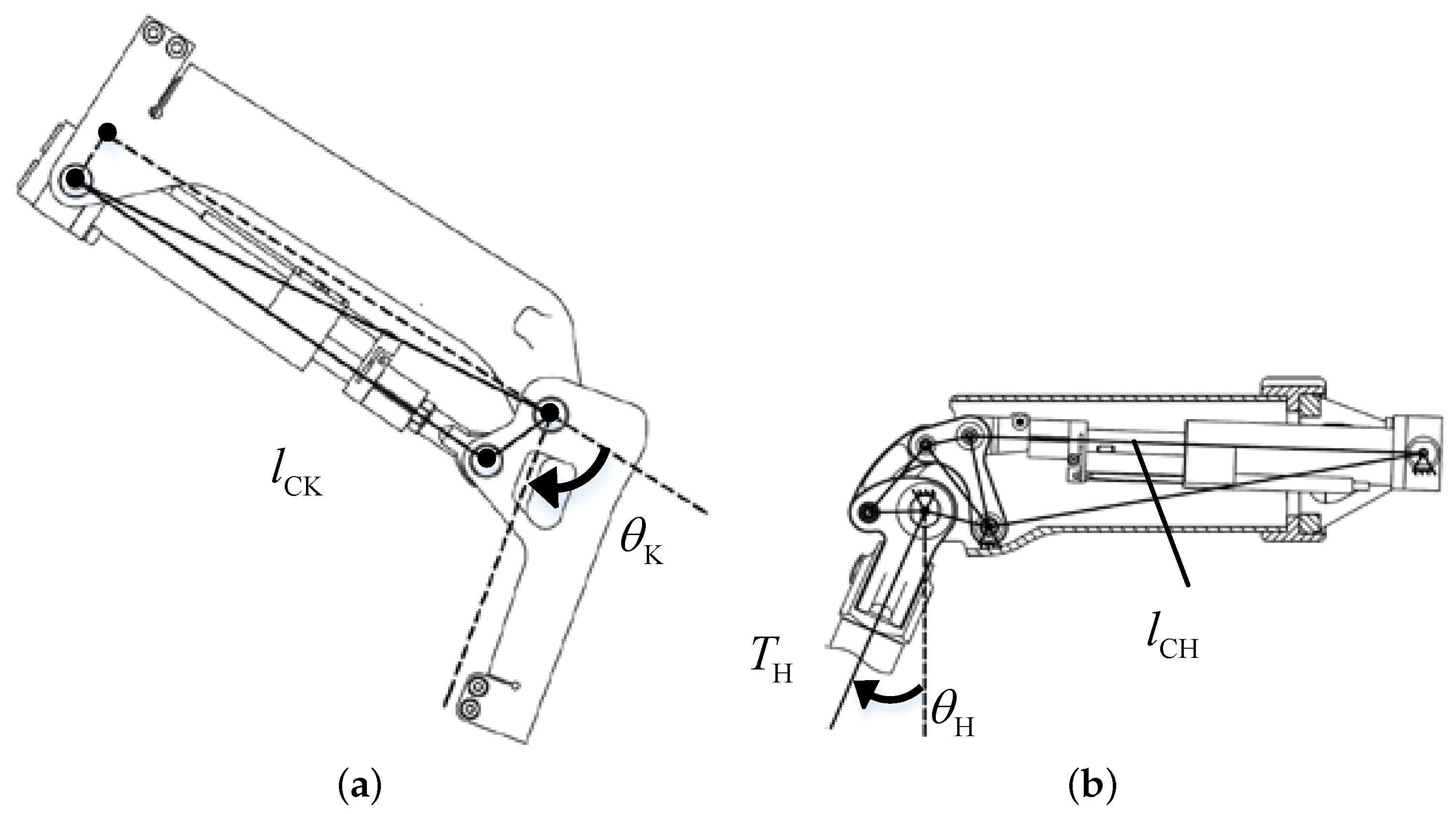
2.3.3. Hip and Knee Joint Kinematics Information Measurement
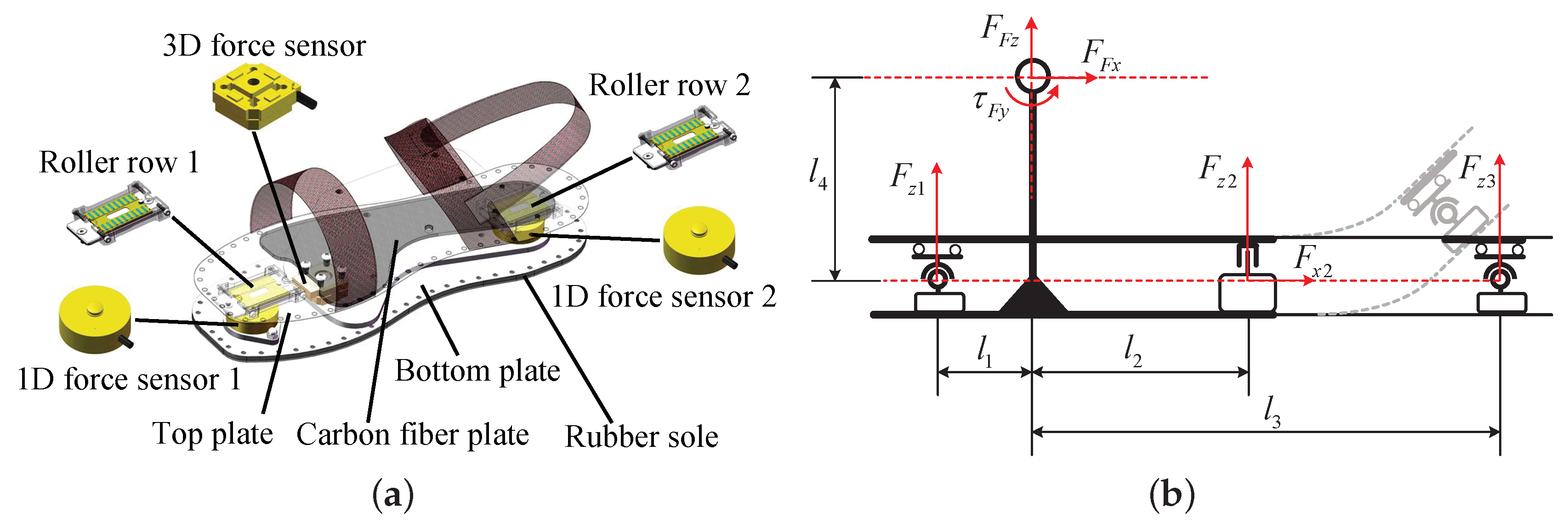
2.3.4. Foot Contact Forces (FCFs) Measurements
3. Experimental Results and Discussion
3.1. Motion Data Sampling and JMT Estimation
- (1)
- The Posture of the Trunk
- (2)
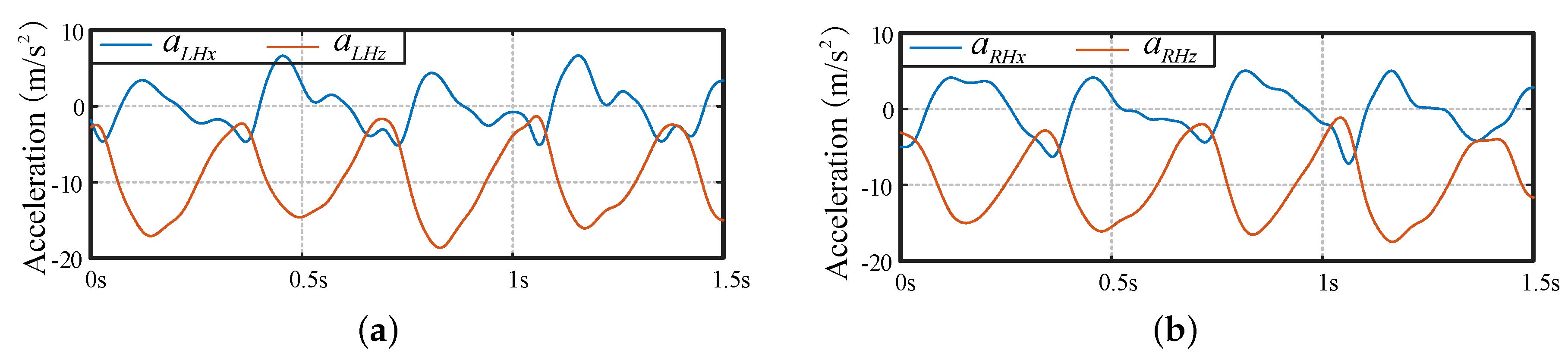
- The Acceleration of the Hip Joints
- (3)
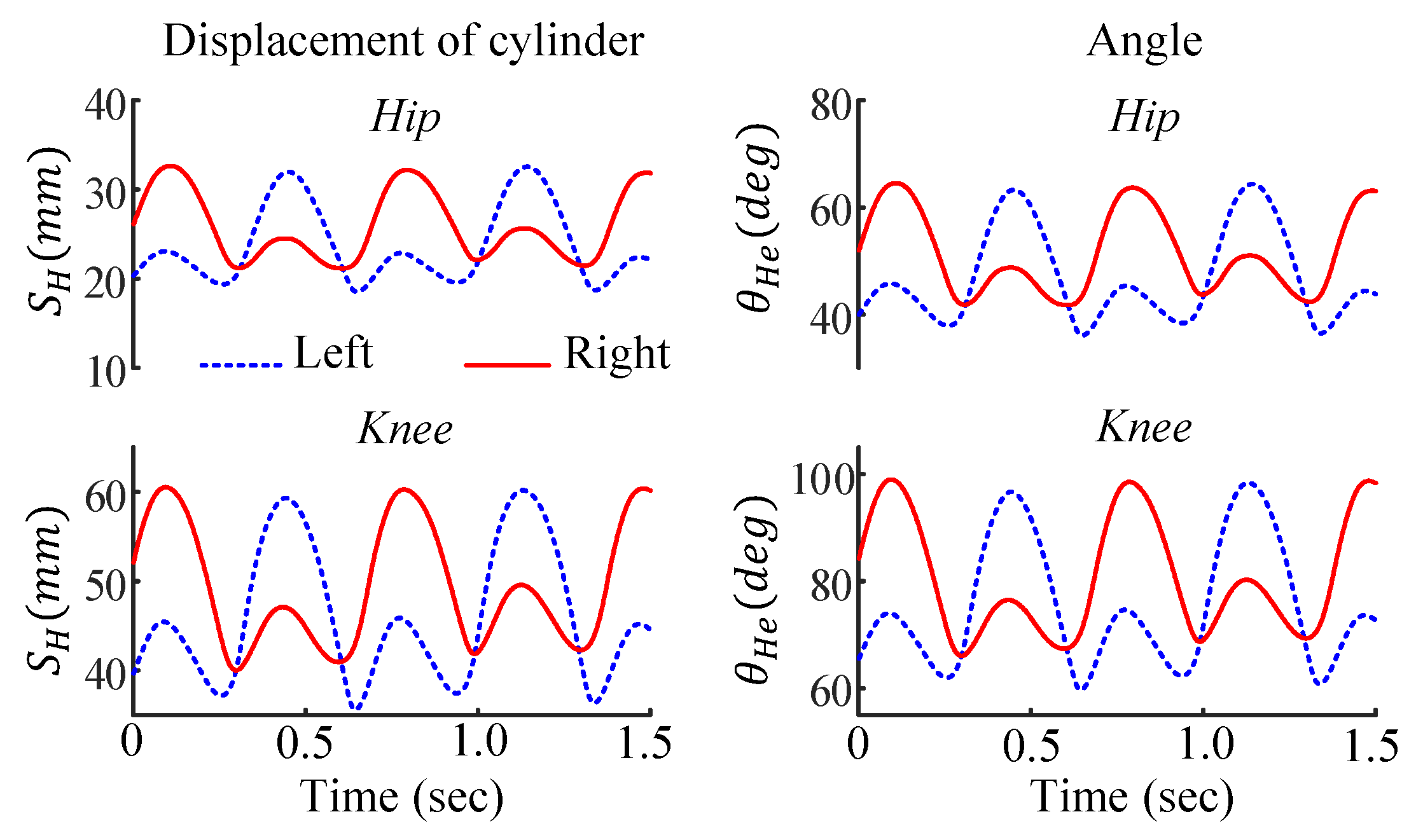
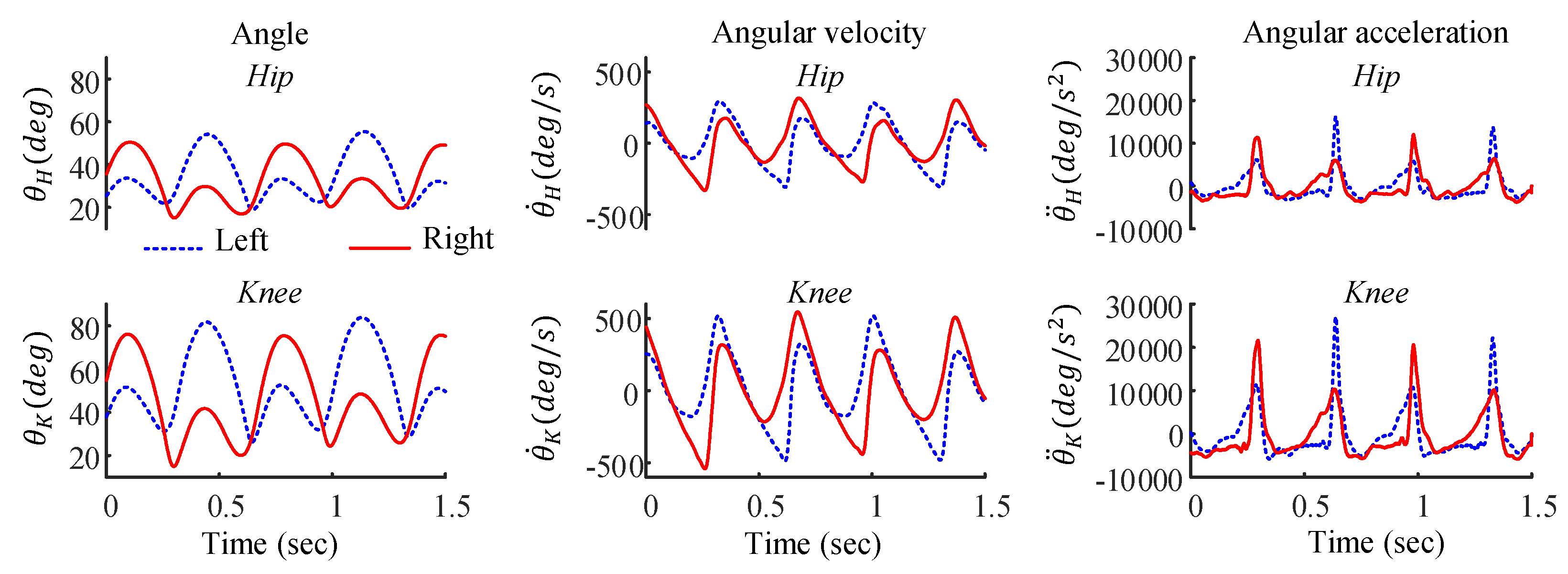
- The Joint Kinematics Information
- (4)
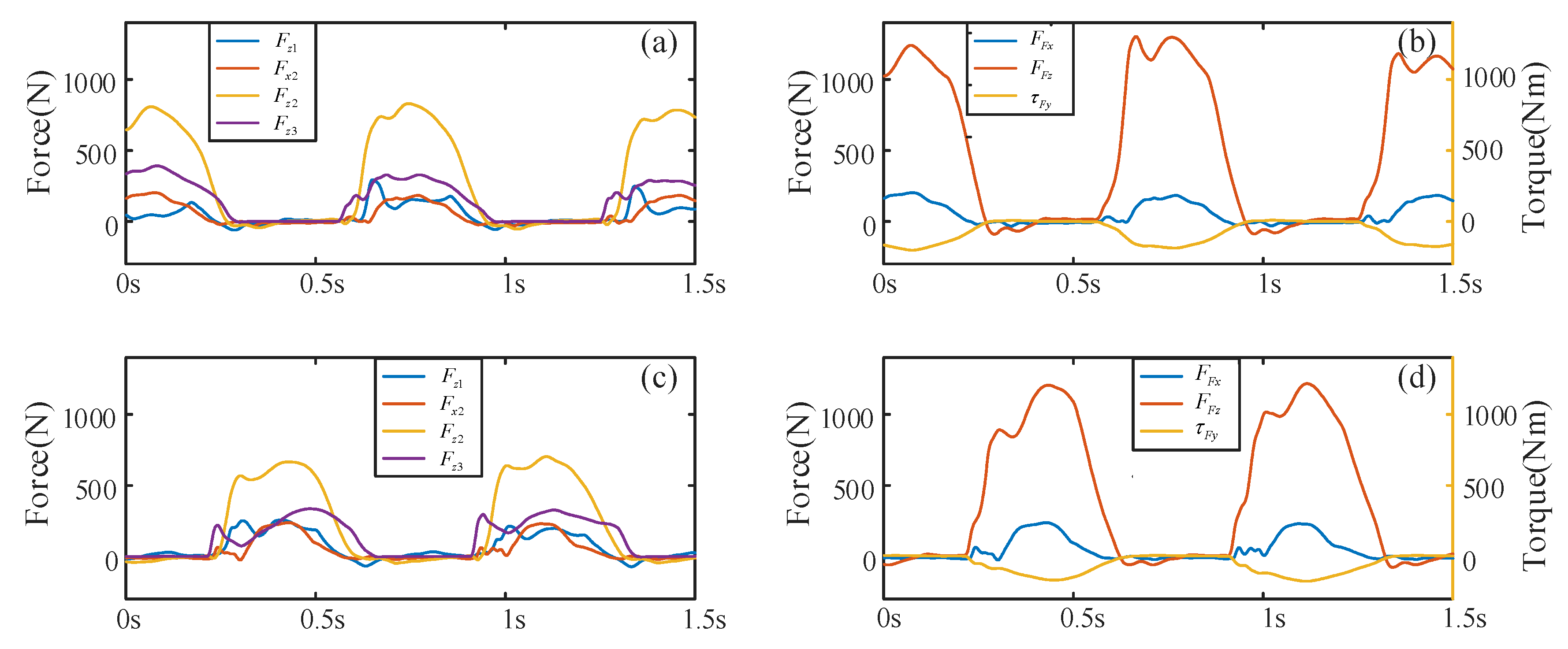
- The Foot Contact Forces
- (5)
- JMT estimation
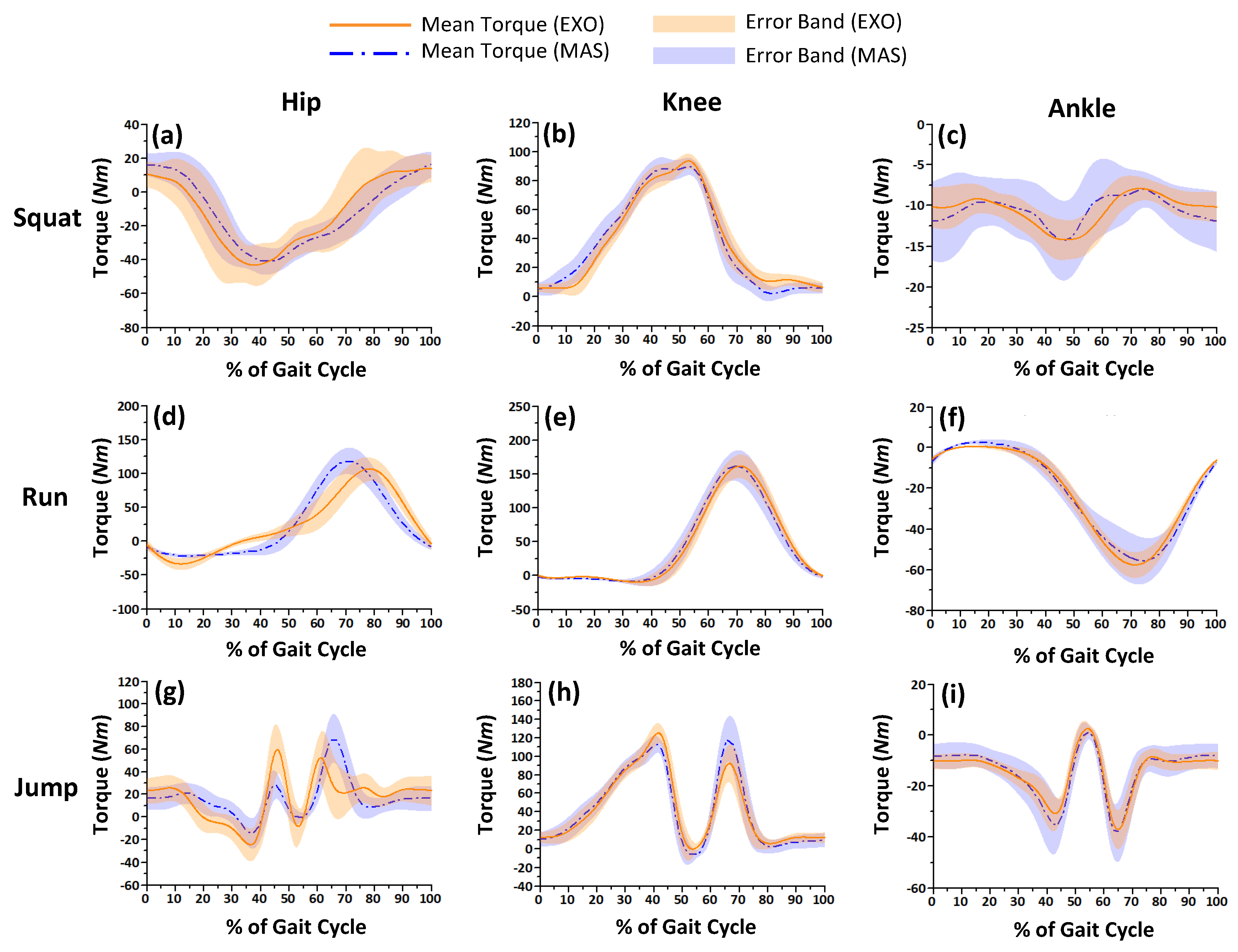
3.2. Comparison Experiments
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kazerooni, H.; Racine, J.L.; Huang, L.; Steger, R. On the control of the berkeley lower extremity exoskeleton (BLEEX). In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 4353–4360. [Google Scholar]
- Hiroaki, K.; Yoshiyuki, S. Power assist method based on Phase Sequence and muscle force condition for HAL. Adv. Robot. 2005, 19, 717–734. [Google Scholar]
- Collins, S.H.; Wiggin, M.B.; Sawicki, G.S. Reducing the energy cost of human walking using an unpowered exoskeleton. Nature 2015, 522, 212–215. [Google Scholar] [CrossRef] [PubMed]
- Asbeck, A.T.; Rossi, S.M.M.D.; Holt, K.G.; Walsh, C.J. A biologically inspired soft exosuit for walking assistance. Int. J. Robot. Res. 2015, 34, 744–762. [Google Scholar] [CrossRef]
- Khan, A.M.; Yun, D.W.; Zuhaib, K.M.; Iqbal, J.; Yan, R.J.; Khan, F.; Han, C. Estimation of Desired Motion Intention and compliance control for upper limb assist exoskeleton. Int. J. Control Autom. Syst. 2017, 15, 802–814. [Google Scholar] [CrossRef]
- Chen, C.; Wu, X.; Liu, D.X.; Feng, W.; Wang, C. Design and Voluntary Motion Intention Estimation of a Novel Wearable Full-Body Flexible Exoskeleton Robot. Mob. Inf. Syst. 2017, 2017, 1–11. [Google Scholar] [CrossRef]
- Kenta, S.; Gouji, M.; Hiroaki, K.; Yasuhisa, H.; Yoshiyuki, S. Intention-based walking support for paraplegia patients with Robot Suit HAL. Adv. Robot. 2007, 21, 1441–1469. [Google Scholar]
- Yang, C.; Wang, X.; Li, Z.; Li, Y.; Su, C.Y. Teleoperation Control Based on Combination of Wave Variable and Neural Networks. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 2125–2136. [Google Scholar] [CrossRef]
- Zhijun, L.I.; Zhao, T.; Chen, F.; Hu, Y.; Su, C.Y.; Fukuda, T. Reinforcement Learning of Manipulation and Grasping using Dynamical Movement Primitives for a Humanoid-like Mobile Manipulator. IEEE/ASME Trans. Mechatron. 2017. [Google Scholar] [CrossRef]
- Sankai, Y. HAL: Hybrid Assistive Limb Based on Cybernics. In Proceedings of the Isrr 2007 Robotics Research—The International Symposium, Hiroshima, Japan, 26–29 November 2007; pp. 25–34. [Google Scholar]
- Lloyd, D.G.; Besier, T.F. An EMG-driven musculoskeletal model to estimate muscle forces and knee joint moments in vivo. J. Biomech. 2003, 36, 765–776. [Google Scholar] [CrossRef]
- Krasin, V.; Gandhi, V.; Yang, Z.; Karamanoglu, M. EMG based elbow joint powered exoskeleton for biceps brachii strength augmentation. In Proceedings of the International Joint Conference on Neural Networks, Killarney, Ireland, 12–17 July 2015; pp. 1–6. [Google Scholar]
- Peternel, L.; Noda, T.; Petrič, T.; Ude, A.; Morimoto, J.; Babič, J. Adaptive Control of Exoskeleton Robots for Periodic Assistive Behaviours Based on EMG Feedback Minimisation. PLoS ONE 2016, 11, e0148942. [Google Scholar] [CrossRef] [PubMed]
- Cristian, C.; Marco, C.; Giuseppe, C. Design and numerical characterization of a new leg exoskeleton for motion assistance. Robotica 2015, 33, 1147–1162. [Google Scholar]
- Spring, A.N.; Kofman, J.; Lemaire, E.D. Design and evaluation of an orthotic knee-extension assist. IEEE Trans. Neural Syst. Rehabil. Eng. 2012, 20, 678–687. [Google Scholar] [CrossRef] [PubMed]
- Buchanan, T.S.; Lloyd, D.G.; Manal, K.; Besier, T.F. Estimation of muscle forces and joint moments using a forward-inverse dynamics model. Med. Sci. Sports Exerc. 2005, 37, 1911–1916. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Zeng, C.; Liang, P.; Li, Z.; Li, R.; Su, C.Y. Interface Design of a Physical Human-Robot Interaction System for Human Impedance Adaptive Skill Transfer. IEEE Trans. Autom. Sci. Eng. 2017, 1–12. [Google Scholar] [CrossRef]
- Tucker, M.R.; Olivier, J.; Pagel, A.; Bleuler, H.; Bouri, M.; Lambercy, O.; Millán, J.R.; Riener, R.; Vallery, H.; Gassert, R. Control strategies for active lower extremity prosthetics and orthotics: A review. J. Neuroeng. Rehabil. 2015, 12. [Google Scholar] [CrossRef] [PubMed]
- Pal, A.R.; Pratihar, D.K. Estimation of Joint Torque and Power Consumption During Sit-to-Stand Motion of Human-being Using a Genetic Algorithm. Procedia Comput. Sci. 2016, 96, 1497–1506. [Google Scholar] [CrossRef]
- Camomilla, V.; Cereatti, A.; Cutti, A.G.; Fantozzi, S.; Stagni, R.; Vannozzi, G. Methodological factors affecting joint moments estimation in clinical gait analysis: A systematic review. Biomed. Eng. Online 2017, 16, 106. [Google Scholar] [CrossRef] [PubMed]
- Shull, P.B.; Jirattigalachote, W.; Hunt, M.A.; Cutkosky, M.R.; Delp, S.L. Quantified self and human movement: A review on the clinical impact of wearable sensing and feedback for gait analysis and intervention. Gait Posture 2014, 40, 11–19. [Google Scholar] [CrossRef] [PubMed]
- Abdul, R.A.H.; Aladin, Z.; Begg, R.K.; Yufridin, W. Foot Plantar Pressure Measurement System: A Review. Sensors 2012, 12, 9884–9912. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Ro, K.; Bae, J. Real-time estimation of individual muscular forces of the lower limb using wearable sensors. In Proceedings of the 2015 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Busan, Korea, 7–11 July 2015; pp. 432–436. [Google Scholar]
- Liu, T.; Inoue, Y.; Shibata, K.; Shiojima, K. Three-dimensional lower limb kinematic and kinetic analysis based on a wireless sensor system. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation (ICRA), Shanghai, China, 9–13 May 2011; pp. 842–847. [Google Scholar]
- Kazerooni, H.; Steger, R.; Huang, L. Hybrid Control of the Berkeley Lower Extremity Exoskeleton (BLEEX); Sage Publications Inc.: Thousand Oaks, CA, USA, 2006; pp. 561–573. [Google Scholar]
- Yang, C.; Zeng, C.; Fang, C.; He, W.; Li, Z. A DMPs-based Framework for Robot Learning and Generalization of Human-like Variable Impedance Skills. IEEE/ASME Trans. Mechatron. 2018, 23, 1193–1203. [Google Scholar] [CrossRef]
- Saccares, L.; Brygo, A.; Sarakoglou, I.; Tsagarakis, N.G. A novel human effort estimation method for knee assistive exoskeletons. In Proceedings of the International Conference on Rehabilitation Robotics, London, UK, 17–20 July 2017; pp. 1266–1272. [Google Scholar]
- Hwang, B.; Jeon, D. A method to accurately estimate the muscular torques of human wearing exoskeletons by torque sensors. Sensors 2015, 15, 8337–8357. [Google Scholar] [CrossRef] [PubMed]
- Hwang, B.; Jeon, D. Estimation of the user’s muscular torque for an over-ground gait rehabilitation robot using torque and insole pressure sensors. Int. J. Control Autom. Syst. 2018, 16, 1–9. [Google Scholar] [CrossRef]
- Deng, J.; Wang, P.; Li, M.; Guo, W.; Zha, F.; Wang, X. Structure design of active power-assist lower limb exoskeleton APAL robot. Adv. Mech. Eng. 2017, 9. [Google Scholar] [CrossRef]
- Leva, P.D. Adjustments to Zatsiorsky-Seluyanov’s segment inertia parameters. J. Biomech. 1996, 29, 1223–1230. [Google Scholar] [CrossRef]
- Cheng, C.K.; Chen, H.H.; Chen, C.S.; Lee, C.L.; Chen, C.Y. Segment inertial properties of Chinese adults determined from magnetic resonance imaging. Clin. Biomech. 2000, 15, 559–566. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, L.; Zhu, J. Effects of toe stiffness on ankle kinetics in a robotic transtibial prosthesis during level-ground walking. Mechatronics 2014, 24, 1254–1261. [Google Scholar]




| H | M | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| (m) | (kg) | (kg) | (kg) | (kg·mm) | (kg·mm) | (mm) | (mm) | (mm) | (mm) | |
| S1 | 1.75 | 76.5 | 7.65 | 4.65 | 0.143 | 0.18 | 424 | 422 | 183 | 270 |
| S2 | 1.64 | 60.3 | 6.03 | 3.67 | 0.099 | 0.124 | 397 | 395 | 172 | 253 |
| S3 | 1.72 | 61.5 | 6.15 | 3.74 | 0.111 | 0.140 | 416 | 415 | 180 | 266 |
| S4 | 1.78 | 78.5 | 7.85 | 4.77 | 0.152 | 0.192 | 431 | 429 | 187 | 275 |
| S5 | 1.65 | 70.2 | 7.02 | 4.27 | 0.117 | 0.147 | 399 | 398 | 173 | 255 |
| Squat | Run | Jump | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Hip | Knee | Ankle | Hip | Knee | Ankle | Hip | Knee | Ankle | ||
| S1 | Left | 25.2 | 8 | 1.4 | 14.4 | 12.3 | 2.5 | 29.4 | 14.8 | 4.4 |
| Right | 22.5 | 7.8 | 1.1 | 15 | 6.9 | 2.2 | 30.1 | 15.8 | 5.5 | |
| S2 | Left | 6.8 | 5.8 | 1.1 | 21.1 | 6.9 | 2.3 | 15.5 | 9 | 2.1 |
| Right | 7.1 | 6.1 | 1.2 | 24.9 | 6.9 | 2.7 | 14.2 | 9.4 | 2.2 | |
| S3 | Left | 7.3 | 2.9 | 1 | 10.7 | 6.1 | 1.2 | 6.8 | 6.2 | 1.5 |
| Right | 10.3 | 3.2 | 0.3 | 16.5 | 3.7 | 1.3 | 7.3 | 6.2 | 1.6 | |
| S4 | Left | 12 | 2.5 | 0.7 | 14.3 | 11.9 | 3.9 | 12.6 | 5.2 | 1.3 |
| Right | 14.8 | 2.8 | 1.9 | 13.3 | 10.5 | 5.3 | 14 | 5 | 3.7 | |
| S5 | Left | 16.1 | 2.3 | 0.8 | 6.3 | 5.8 | 5 | 16.8 | 6.8 | 2.4 |
| Right | 18 | 3.6 | 1.5 | 5.3 | 3.2 | 5.5 | 16.8 | 5.4 | 4.1 | |
| Mean SD | 14 | 4.5 | 1.1 | 14.2 | 7.4 | 3.2 | 16.4 | 8.4 | 2.9 | |
| 6.5 | 2.2 | 0.5 | 6 | 3.2 | 1.6 | 7.9 | 3.9 | 1.4 | ||
| Squat | Run | Jump | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Hip | Knee | Ankle | Hip | Knee | Ankle | Hip | Knee | Ankle | ||
| S1 | Left | 0.875 | 0.985 | 0.990 | 0.928 | 0.948 | 0.998 | 0.812 | 0.958 | 0.963 |
| Right | 0.877 | 0.988 | 0.993 | 0.850 | 0.989 | 0.998 | 0.832 | 0.954 | 0.955 | |
| S2 | Left | 0.700 | 0.983 | 0.953 | 0.903 | 0.993 | 0.994 | 0.629 | 0.974 | 0.979 |
| Right | 0.891 | 0.976 | 0.965 | 0.862 | 0.993 | 0.991 | 0.732 | 0.962 | 0.982 | |
| S3 | Left | 0.932 | 0.995 | 0.982 | 0.874 | 0.978 | 0.999 | 0.896 | 0.978 | 0.986 |
| Right | 0.867 | 0.996 | 0.999 | 0.707 | 0.995 | 0.999 | 0.922 | 0.982 | 0.990 | |
| S4 | Left | 0.908 | 0.998 | 0.996 | 0.705 | 0.882 | 0.993 | 0.904 | 0.988 | 0.995 |
| Right | 0.886 | 0.997 | 0.979 | 0.710 | 0.918 | 0.989 | 0.851 | 0.985 | 0.963 | |
| S5 | Left | 0.836 | 0.998 | 0.997 | 0.839 | 0.988 | 0.99 | 0.783 | 0.973 | 0.985 |
| Right | 0.704 | 0.997 | 0.993 | 0.745 | 0.996 | 0.991 | 0.743 | 0.988 | 0.972 | |
| Mean SD | 0.848 | 0.991 | 0.985 | 0.812 | 0.968 | 0.994 | 0.810 | 0.974 | 0.977 | |
| 0.081 | 0.008 | 0.019 | 0.082 | 0.040 | 0.004 | 0.091 | 0.012 | 0.013 | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.; Deng, J.; Zha, F.; Qiu, S.; Wang, X.; Chen, F. Towards Online Estimation of Human Joint Muscular Torque with a Lower Limb Exoskeleton Robot. Appl. Sci. 2018, 8, 1610. https://doi.org/10.3390/app8091610
Li M, Deng J, Zha F, Qiu S, Wang X, Chen F. Towards Online Estimation of Human Joint Muscular Torque with a Lower Limb Exoskeleton Robot. Applied Sciences. 2018; 8(9):1610. https://doi.org/10.3390/app8091610
Chicago/Turabian StyleLi, Mantian, Jing Deng, Fusheng Zha, Shiyin Qiu, Xin Wang, and Fei Chen. 2018. "Towards Online Estimation of Human Joint Muscular Torque with a Lower Limb Exoskeleton Robot" Applied Sciences 8, no. 9: 1610. https://doi.org/10.3390/app8091610
APA StyleLi, M., Deng, J., Zha, F., Qiu, S., Wang, X., & Chen, F. (2018). Towards Online Estimation of Human Joint Muscular Torque with a Lower Limb Exoskeleton Robot. Applied Sciences, 8(9), 1610. https://doi.org/10.3390/app8091610





