Swelling Capacity and Hydraulic Conductivity of Polymer-Modified Bentonite under Saline Water Conditions

Abstract

Bentonite is widely used as a waterproof material in civil engineering. The swelling capacity and impermeability will be reduced in saline water conditions. A polymer-modified bentonite was used in this study, and the swelling characteristic and hydraulic conductivity in saline water were investigated. Results show that: the modified bentonite (MB) has good swelling characteristics and low permeability in saline water conditions; the unload swelling strain of MB in saline water conditions increased with rising swelling time; the final unload swelling strain of MB decreased with the increase of vertical pressure and increased with increasing initial dry density; and, as the swelling time increased, the swelling pressure increased rapidly at first and then decreased. Based on experimental results, this study obtained a linear relationship between the ratio of time to unload swelling strain and swelling time, a formula for load swelling strain that was related to initial dry density and vertical pressure, a linear relationship between the ratio of time to swelling pressure and swelling time, and an exponential relationship between swelling pressure and initial dry density. The MB can be used as a waterproof material in seepage-prone applications under saline environmental conditions in civil engineering works.

1. Introduction

Waterproof anti-seepage structures are important in building construction operations such as: roadway, water conservancy, house building, and landfill works. Bentonite, as a waterproof material, is widely used for seepage control applications in foundation, dike construction, hydraulic engineering, and landfill construction [1]. Bentonite is a clay mineral with high swelling properties which results in its low permeability in aqueous solution [2]. The high swelling capacity and low permeability are a result of its main component [3]: montmorillonite. The swelling process and mechanism of montmorillonite crystals have been examined by many scholars [4,5,6,7,8].

The swelling capacity is an important property of bentonite as it affects the self-healing and crack-filling ability of waterproof materials [9,10]. When bentonite is used as a waterproof material, owing to the complexity of most geological structures, seepage-prone structures may be destroyed and bentonite can swell and fill cracks to prevent water penetration of the structure. On the other hand, if the swelling pressure is too strong, then the protective structure is extruded; therefore, the swelling capacity of bentonite is essential to its use as a waterproof material in civil engineering [11].

Disadvantages such as a low swelling capacity and high permeability will be evident when bentonite is used in saline conditions [12,13,14,15]. A low hydraulic conductivity and high swelling capacity are prominent characteristics of bentonite, which always depend on the salinity of the contact solution and can change the microstructure of the bentonite [16]. Saline water can increase the hydraulic conductivity of bentonite and thus reduce its swelling capacity and sealing performance [17,18,19]. Karnland [20] found that the swelling pressure of bentonite was reduced in saline conditions and the pressure reduction increased with increasing bentonite density. Owing to the concentration gradient between the pore water and external salt solution, osmotic flow from the lower salinity solution to the higher salinity solution would cause a reduction in the swelling pressure of bentonite under saline conditions [21].

Modified bentonite (MB) has been developed to improve bentonite’s performance in saline conditions [22]. Hu [23] found that salt tolerance could be enhanced when adding some types of high-molecular-weight polymer to bentonite. The MB solved the leakage problems in agricultural irrigation and led to a significant water-saving. In Camillis’ study, bentonite was treated with 2% and 8% polymer (carboxymethyl cellulose) by weight of bentonite, and the swelling ability increased as the polymer content increased, which has implications for bentonite barrier resistance in seawater [24]. Di Enudio [25] developed a superior clay with enhanced hydraulic performance. The treatment with an anionic polymer can improve the sealing, hydraulic, and membrane properties of clays. Polymer addition can enhance the solution viscosity and decrease the hydraulic conductivity of bentonite-aggregate mixtures [26]. Thus, such polymer-improved bentonite mixtures can be effectively used as barrier layers [27]. Different from other previous studies, guar gum was selected as an additive for bentonite modification. Guar gum has a higher hydrophilicity than other polymers, therefore it dissolves easily in water and combines with bentonite molecules to form MB [28]. Due to the high stability and relatively low price of guar gum, it has much potential as an additive in MB that can be used in hydraulic barrier materials for civil engineering applications [29].

In this research, bentonite was modified with guar gum and a MB was developed for anti-seepage projects under saline water conditions. To investigate the hydraulic performance, hydraulic conductivity testing of the MB was carried out. To study the swelling characteristics of MB, swelling strain tests (load/unload conditions) and swelling pressure tests were conducted in saline water conditions. In addition, unload swelling strain tests of MB under fresh water conditions were performed as a control. Based on the test results, relationships between initial dry density, swelling time, swelling strain (load/unload), and swelling pressure were separately established.

2. Materials

2.1. Bentonite

Natural sodium bentonite (NB) mined in India was used in the current research. The MB was developed by attaching the polymer (guar gum) to the surface of the NB. The mixing ratio of NB and guar gum was 95:5. The modification process mainly consists of dissolving the polymer in distilled water and then mixing it with the NB. The mixture was put in a mechanical stirrer for 1 h to ensure full mixing, then the slurries containing polymer solution and NB were oven-dried at 105 °C for 24 h. Thereafter, the dried mixture was ground using a mortar and pestle: MB powder was sieved through a No. 200 sieve. The physical and chemical properties of NB and MB are summarized in

Table 1. Physical properties of NB (Nature sodium bentonite) and MB (Modified bentonite) as used in this study.

Physical Properties	NB	MB
Specific gravity	2.7	2.65
Liquid limit (%)	397	344.2
Plastic index (%)	360	313
Unified Soil Classification System	CH	CH
Percentage passing the sieve No. 200	100%	100%
Specific surface area (m2/g)	40–50	50–60
Cation exchange capacity (meq/100 g)	100–130	100–130

and

Table 2. Chemical compositions of NB and MB: XRF (X-ray fluorescence spectrometer) data; L.O.I. (Loss on ignition).

Compounds	NB (%)	MB (%)
SiO2	61.30	56.39
MgO	1.64	3.55
Al2O3	14.62	12.62
Na2O	2.54	2.43
K2O	0.28	0.27
Fe2O3	3.8	3.47
TiO2	0.52	0.52
MnO	0.07	0.07
CaO	4.13	7.34
P2O5	0.01	0.01
L.O.I	11.09	13.33
Total	100	100

. Tests for measuring the classification, proportions and liquid-plastic limit of NB and MB were separately conducted using ASTM D2487, ASTM D854 and ASTM D4318 standard methods [30,31,32]. The chemical compositions of the bentonite were analyzed by X-ray fluorescence spectrometer (XRF). Figure 1 shows the microstructure of the NB as captured by scanning electron microscope (SEM). As the NB has a plate-like structure, a large amount of water can penetrate the void spaces therein, which causes a change from a plate-like structure to a house-of-cards structure which exacerbates the volumetric expansion of the NB.

2.2. Guar Gum

Guar gum powders mined in India were used in this research. The pH value of guar gum was 5.8 and it had a density of 1.492 g/cm³. Guar gum can be completely dissolved in water to form a viscous liquid which has typical entangled biopolymer properties in aqueous solution, resulting in the wrapping up of bentonite to prevent the ions contacting with bentonite molecules in saline water. The chemical compositions of guar gum are shown in

Table 3. Chemical compositions of guar gum.

Moisture (%)	Ash (%)	Protein (%)	Crude Fiber (%)	Galactomannan (%)
10	0.66	3.10	1.9	84.34

.

2.3. Permeant Solutions

To observe the properties of MB under fresh and saline conditions, distilled water and artificial sea water were used in this research. The artificial sea water was prepared based on ASTM D 1141-98 [33] which represents standard practice for preparing substitute ocean water. There are four main components in artificial sea water compared with natural sea water in Inchon sea in Korea. Based on ASTM method, artificial sea water was prepared by dissolving NaCl (24.5%), MgCl₂ (0.52%), Na₂SO₄ (0.41%), and CaCl₂ (0.12%) in distilled water to simulate sea water. A comparison of the compositions of artificial and natural sea water is shown in

Table 4. Comparison of the compositions of artificial sea water and natural sea water.

Compounds	Artificial Sea Water (g/L)	Natural Sea Water (g/L)
NaCl	24.5	24.32
MgCl2	5.2	5.12
Na2SO4	4.1	4.09
CaCl2	1.2	1.11
KCl	0	0.162
NaHCO3	0	0.081
KBr	0	0.063
H3BO3	0	0.026
SrCl2	0	0.025
NaF	0	0.003

. The properties of the artificial sea water used in this study were follows: pH of 8.2, a salinity of 3.5%, electrical conductivity of 4.3 Ω·m and an ionic strength of 0.66 mol/L.

3. Methods

3.1. Specimen Preparation

To investigate the improvement effect of MB, the NB and MB specimens with its optimum water content of 19% and compacted initial dry density of 1.7 g/cm³ were, respectively, made for unloaded swelling strain testing. The optimum water content of bentonite was determined using a compaction test based on ASTM D 1557 standard methods [34]. To investigate the effects of compacted initial dry density of MB on the swelling strain and swelling pressure, specimens of different compacted initial dry densities (1.25, 1.40, 1.55, 1.70, and 1.85 g/cm³) were made for swelling strain testing and swelling pressure testing.

The natural moisture content of the MB powder was obtained by oven-drying; the required amount of water was calculated based on the weight of the MB (or bentonite) and the optimum moisture content of MB (19%), then water was added to the MB (or NB) material; the wet MB (or NB) sample was agitated and then placed in a sealed bag for 48 h to equilibrate. MB (or NB) specimens with a height of 10 mm and diameter of 61.8 mm were used for swelling tests; a certain amount of wet MB (or NB) was weighed according to the volume of the specimen and the required initial dry density; and then, this was evenly layered into a mold and compacted under a static force applied via hydraulic jack. The specimen was stood under load until the pressure plate would no longer rebound and the height of the specimen was 10 mm. After that, demolding was carried out by hydraulic jack to obtain the MB (or NB) specimen.

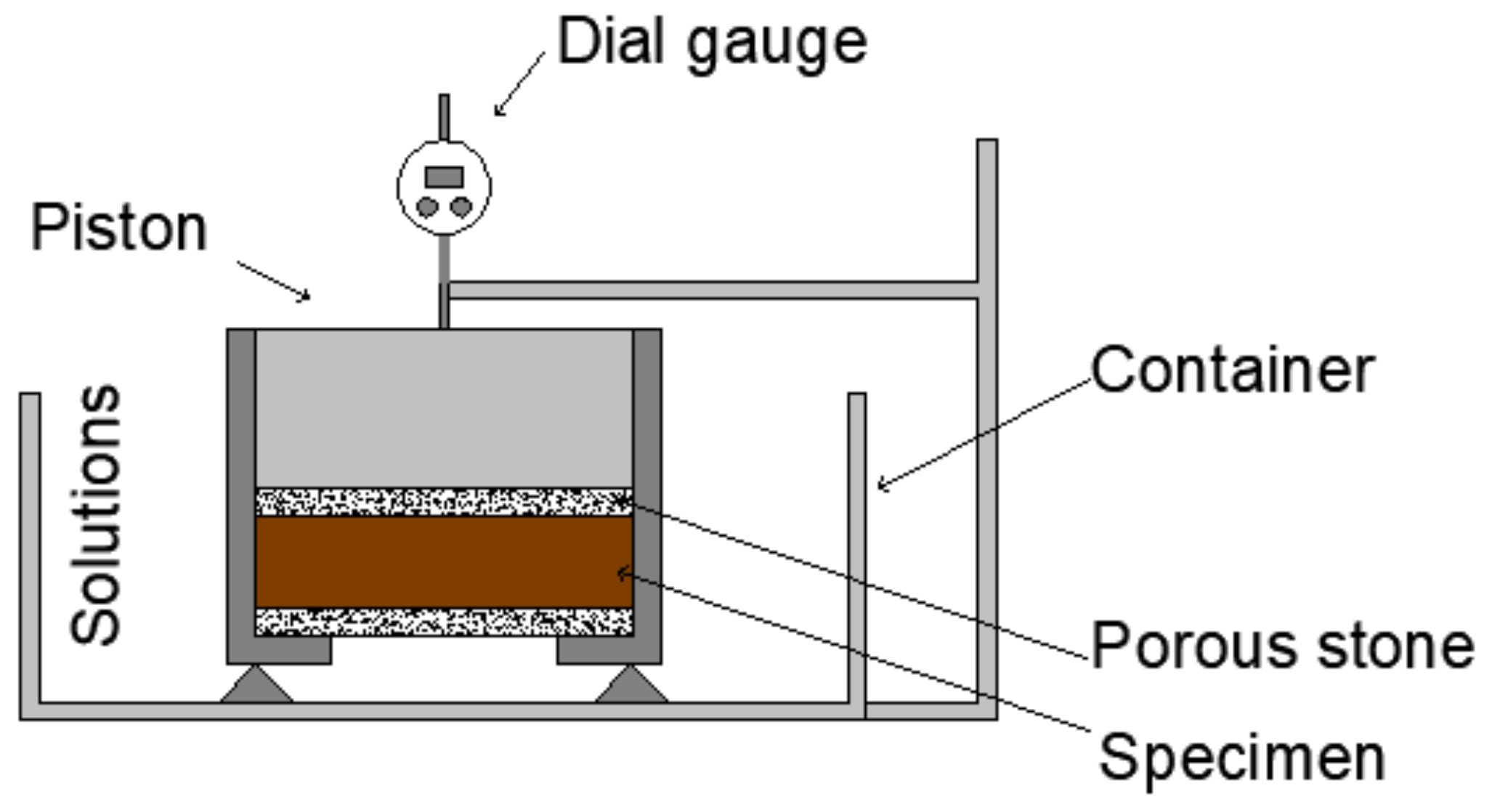
3.2. Unloaded Swelling Strain Test

Self-designed test apparatus was used for determining the swelling deformation of MB specimens as shown in Figure 2. The apparatus consists of a rigid specimen tube (61.8 mm in diameter and 10 mm in height) that is open at the lower end, two porous stones, a piston, a dial gauge, and a sink. The porous stone, filter paper, specimen, filter paper, porous stone, and piston were placed in the test specimen tube in turn, the dial gauge was then installed above the piston and the dial gauge was adjusted to zero to measure the vertical swelling strain of each MB specimen. Fresh water or saline water, respectively, was then injected into the different sinks; at the same time, silicon oil was added above the water to nullify the influence of change in the salinity and volume of the seawater solution caused by evaporation on the test specimen swelling. Vertical swelling deformation was recorded by the dial gauge. In the initial stage, the change in swelling strain was relatively rapid and the value was recorded once every five minutes; and then, the swelling strain decelerated and its value was recorded every two hours. The swelling strain was deemed stable when the value remained unchanged for 24 h. After the swelling process was completed, the test specimen was removed from the equipment and weighed. Additionally, the water content was calculated. The entire swelling process was conducted at room temperature (24 ± 1 °C).

3.3. Loaded Swelling Strain Test

The loaded swelling strain test was performed in an oedometer (Figure 3). To study the changes in swelling strain during the gradual stabilization process for each MB specimen with a certain initial dry density and under a certain vertical load, load swelling strain tests of MB specimens with a certain water content (19%), different dry densities (1.25, 1.40, 1.55, 1.70, and 1.85 g/cm³) and different vertical stresses (25, 50, 100, 150, 200, 300, and 400 kPa) were conducted under saline water conditions. The spacer disk filter paper, specimen, filter paper, spacer disk, and pressurizing upper cover were put into the oedometer in turn. The upper cover was aligned with the center of the pressurization frame, then dial gauge was installed. To ensure full contact between the specimen and the instrument, the pressure was pre-set to 1 kPa and the dial gauge was set to zero before testing. The required load was then applied to the specimen and saline water was added to the sink. We measured, and recorded, the vertical swelling deformation of the specimen using the same method as described for the unload swelling strain test.

The swelling strain (ε) in the experiment under both unloading and loading conditions is given by Equation (1):

$$\epsilon =\frac{\Delta H}{H_0}=\frac{H_{\mathrm{t}}-H_0}{H_0}\times 100\%$$

(1)

where ε is the swelling strain in the MB specimen; H₀ represents the initial height of the MB specimen (mm); and H_t is the final height of MB specimen after the swelling process was completed (mm).

3.4. Vertical Swelling Pressure Test

The swelling pressure test of MB specimens under saline water condition was performed with the aid of a consolidation instrument. The specimen was installed according to the installation method used in the load swelling strain test. Saline water was injected into the sink, the change of dial gauge value (< 0.01 mm) indicted that the swelling of the MB specimen had occurred. An appropriate load should be applied immediately as the dial gauge indicator moved to ensure that the swelling strain value remained zero. The load was increased to prevent swelling strain in the MB specimen and the sample finally stabilized at a certain value. The final applied pressure would be regarded as the swelling pressure when the specimen swelling strain was constant for 2 h under a constant pressure. The swelling pressure can be expressed as Equation (2):

$$P=\frac{W}{A}\times 10$$

(2)

where P is swelling pressure (kPa); W is the total load on the MB specimen in the equilibrium condition (N); and A denotes the cross-sectional area of the MB specimen (cm²).

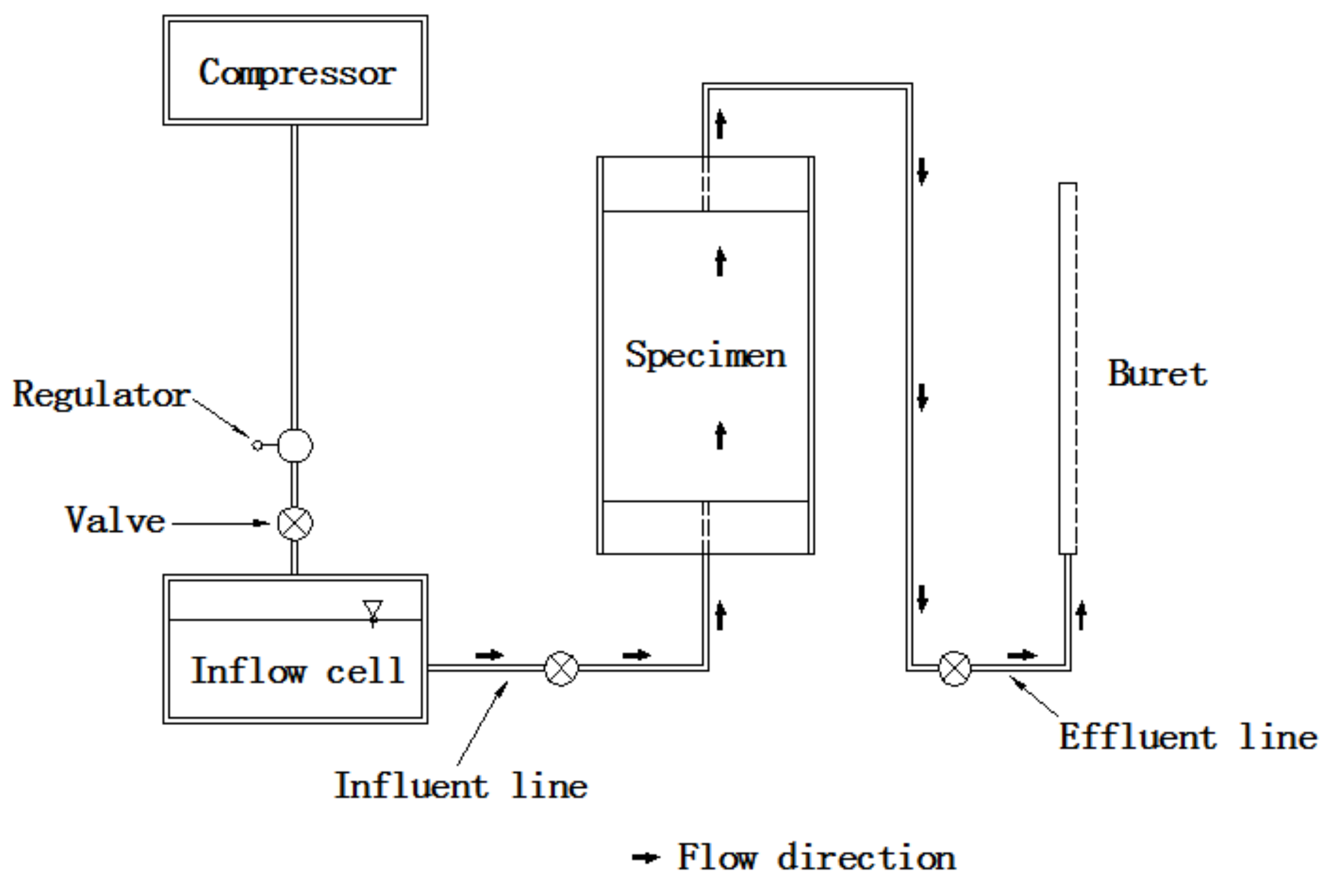
3.5. Hydraulic Conductivity Test

In fresh and saline water conditions, hydraulic conductivity tests were performed on NB and MB samples. The hydraulic conductivity test was carried out using a rigid wall permeameter and the falling head method was used in both cases. The bentonite has a low hydraulic conductivity and therefore it is difficult to measure the hydraulic conductivity by ordinary constant- or falling-head methods. By modifying the equipment used in variable head testing and pressurizing the solution influx to the bentonite specimen (using nitrogen), the test time was shortened to reduce the influence of the environmental change on the test results. The hydraulic conductivity test was performed in accordance with ASTM D5856 [35] and the test equipment is illustrated in Figure 4. The cylinder is 34 mm in diameter and 72 mm in height. Moreover, a pressure of 34.5 kPa was imposed on the solution and pressure measuring devices were separately installed at the inlet and outlet to measure the pressure drop across the flow path and the hydraulic gradient was 21.9. All the tests were carried out at a constant temperature of 24 °C.

4. Results and Discussion

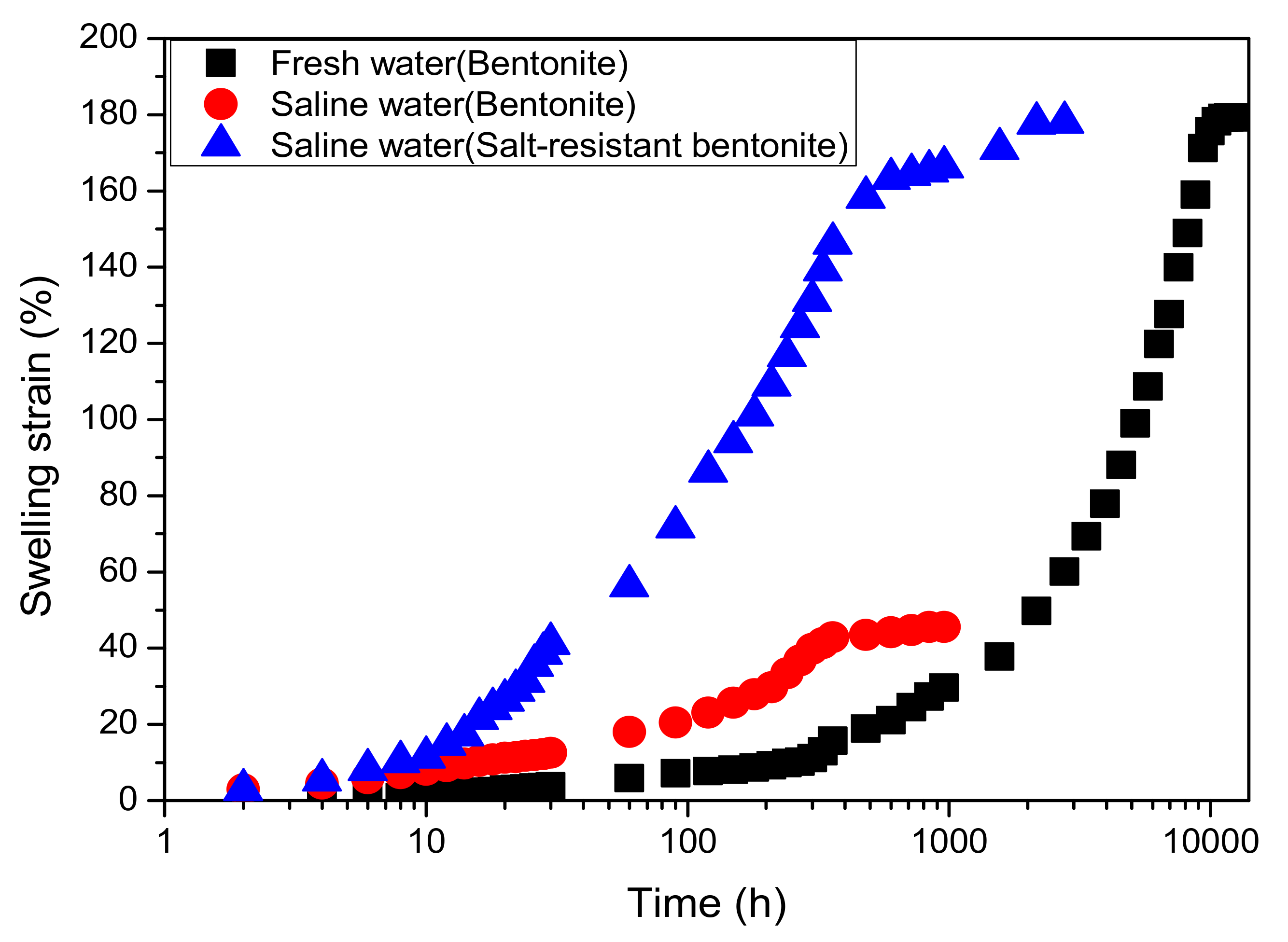
4.1. Unloaded Swelling Deformation

4.1.1. Improvement Effect of MB

To investigate the improvement effect of MB, the swelling strains of NB specimens under fresh and saline water conditions, and the swelling strains of MB specimens under saline water conditions were compared. Figure 5 shows the relationships between the unloading swelling strain and swelling time for these three conditions. For the NB, the swelling strain in saline water (45.5%) was about four times smaller than that in fresh water (179.3%). The swelling strain of MB under saline water conditions was 178%, which was almost identical to the swelling strain of NB in fresh water. The results indicate that the improvement efficiency was remarkable and MB exhibited high salt tolerance.

In addition, it can be seen in Figure 5 that the swelling speed of NB in saline water is greater than that in fresh water. This can be attributed to the higher concentration difference (gradient) in saline water conditions [36,37]. Large quantities of saline water can percolate rapidly through the bentonite and cause the rapid swelling of the specimen, as a result, the bentonite specimen has greater rate of swelling in saline water conditions [38].

Saline water conditions had a significant effect on the swelling capacity of NB that can be explained by the diffuse electric double layer. Due to high ion concentrations in saline water, the thickness of the diffuse electric double layer of NB decreased, further affecting changes in the molecular structure of NB. The structure of NB changed from being dispersed to flocculated structure at high ion concentrations. In addition, the swelling capacity of NB decreased and hydraulic conductivity increased with changes in structure [39]. Using polymer (guar gum) to modify bentonite can effectively prevent ions affecting structural changes in NB. When the NB and guar gum dissolve in water, the guar gum can surround the NB, therefore ions in saline water are prevented from making contact with the NB molecules and structural changes cannot occur. The MB can maintain a high swelling capacity and low hydraulic conductivity under saline water conditions. Hydraulic conductivity changes of NB and MB in saline water conditions are discussed in the following section.

4.1.2. Unloaded Swelling Deformation of MB

The unloaded swelling strain is an important indicator of the waterproofing performance of bentonite, which can reflect the capacity of it to fill cracks. The unloading swelling deformation tests on MB specimens with five different initial dry densities and the same initial moisture content were conducted under saline water conditions. The relationships between the unloaded swelling strains of MB specimens and swelling times were obtained (Figure 6). The swelling strain of different MB specimens exhibited similar changes with increasing swelling time. At the beginning of the test, the swelling strain in the MB specimen increased rapidly over time. After that, the swelling strain increased slowly and reached a stable final value, which indicated that the swelling deformation was complete. This occurred because montmorillonite is the main component of bentonite: in the initial stage of the swelling process, due to the small thickness of water film around the montmorillonite, a large amount of space was available for swollen minerals to adsorb water and swell [40]. With increasing water absorption, the arrangement of montmorillonite wafers gradually developed from the initial anisotropic arrangement into an aligned arrangement. The thickness of the water film between the montmorillonite wafers increased stepwise, thus the speed of the water absorption process decreased and the rate of change in the swelling strain decreased. The thickness of the water film finally reached its maximum value, and swelling strain remained unchanged thereafter.

Furthermore, curves of swelling strain to swelling time always follow a rectangular hyperbolic relationship [41]. Linear relationships between the ratio of time to swelling strain and swelling time for the MB specimens under five different dry densities (Figure 7) can be fitted by Equation (3):

$$\frac{t}{\epsilon }=a+bt$$

(3)

where ε is the unloading swelling strain of an MB specimen; t represents the swelling time (h); and a and b are fitting parameters.

Since a and b are related to the initial dry density, their values under each corresponding initial dry density of MB specimen were discussed and fitting equations for the linear relationships between a and b, and dry density were obtained (Equations (4) and (5)). The correlation coefficient values (R²) are 0.97 for a and 0.95 for b.

$$a=0.016{\rho }_d-0.015$$

(4)

$$b=-0.014{\rho }_d+0.03$$

(5)

where a and b refer to fitting parameters; and ρ_d is the initial dry density of the MB specimen (g/cm³).

Based on Equations (3)–(5), relationship between the ratio of time to unloaded swelling strain and swelling time for MB specimens can be further fitted by Equation (6), which was related to the initial dry density of MB specimen and swelling time:

$$\frac{t}{\epsilon }=0.016{\rho }_d-0.014{\rho }_{d}t+0.03t-0.015$$

(6)

where ε is the unload swelling strain of an MB specimen; ρ_d denotes the initial dry density (g/cm³); and t is the swelling time (h).

The initial dry density is the main control index in the engineering application of bentonite. The relationship between the final swelling strain and initial dry density was obtained through the swelling strain testing of MB specimens with different initial dry densities under saline water conditions (Figure 8). The relationship between final swelling strain and initial dry density can be fitted by Equation (7). The correlation coefficient (R²) is 0.98:

$${\epsilon }_{\max }=209.13{\rho }_d-188.23$$

(7)

where ε_max is the final unload swelling strain of MB specimen, and ρ_d denotes the initial dry density of the MB specimen (g/cm³).

4.2. Loaded Swelling Deformation

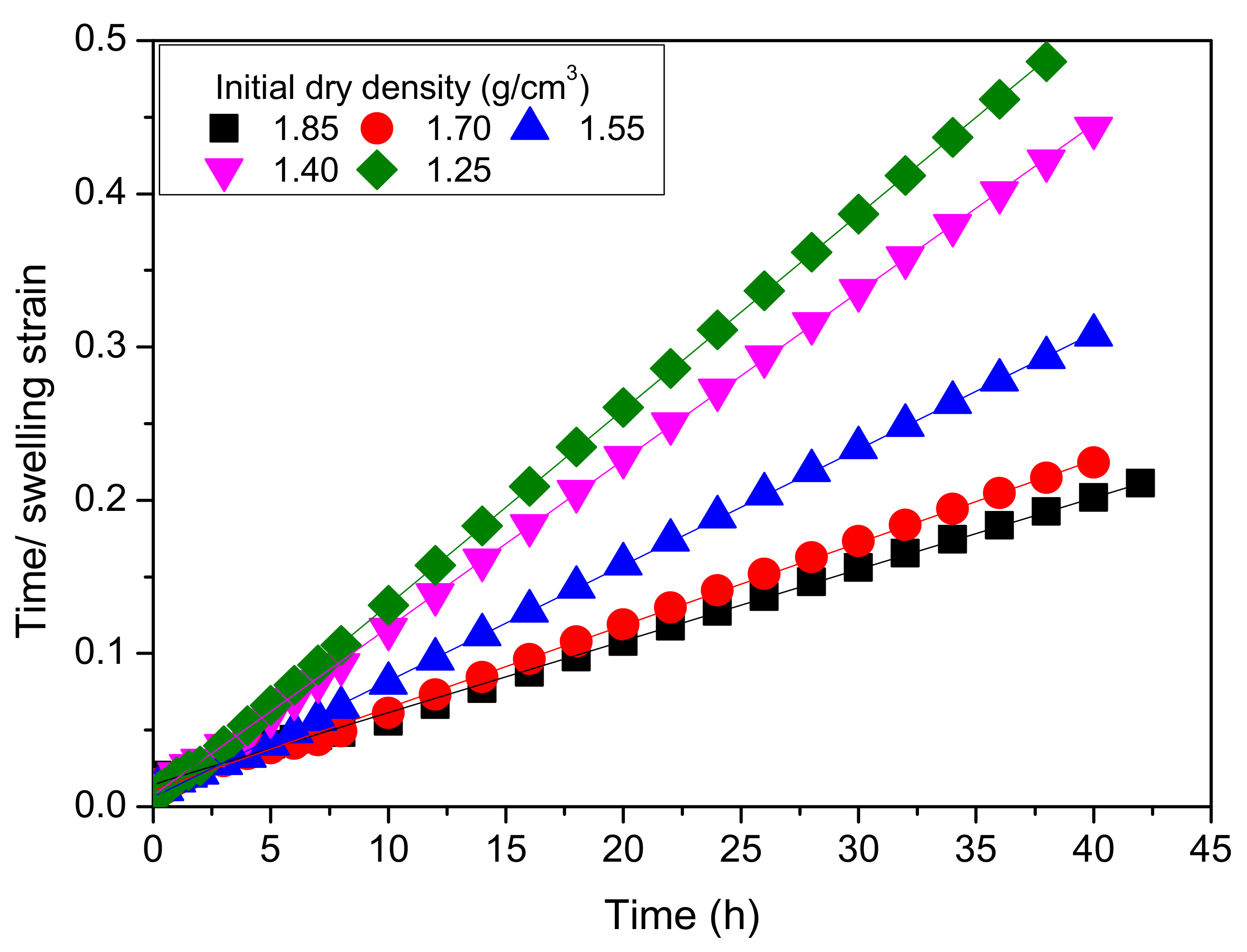
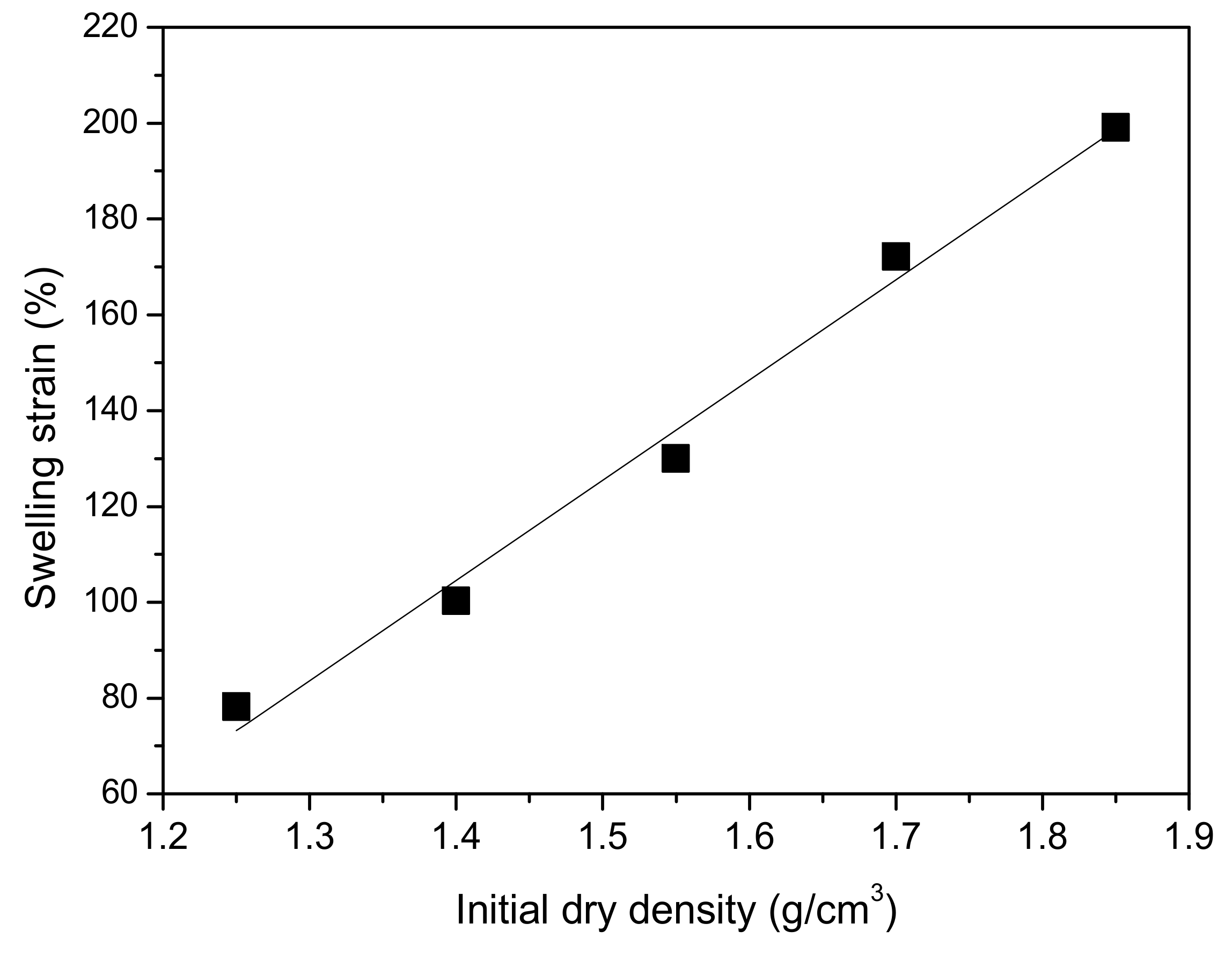
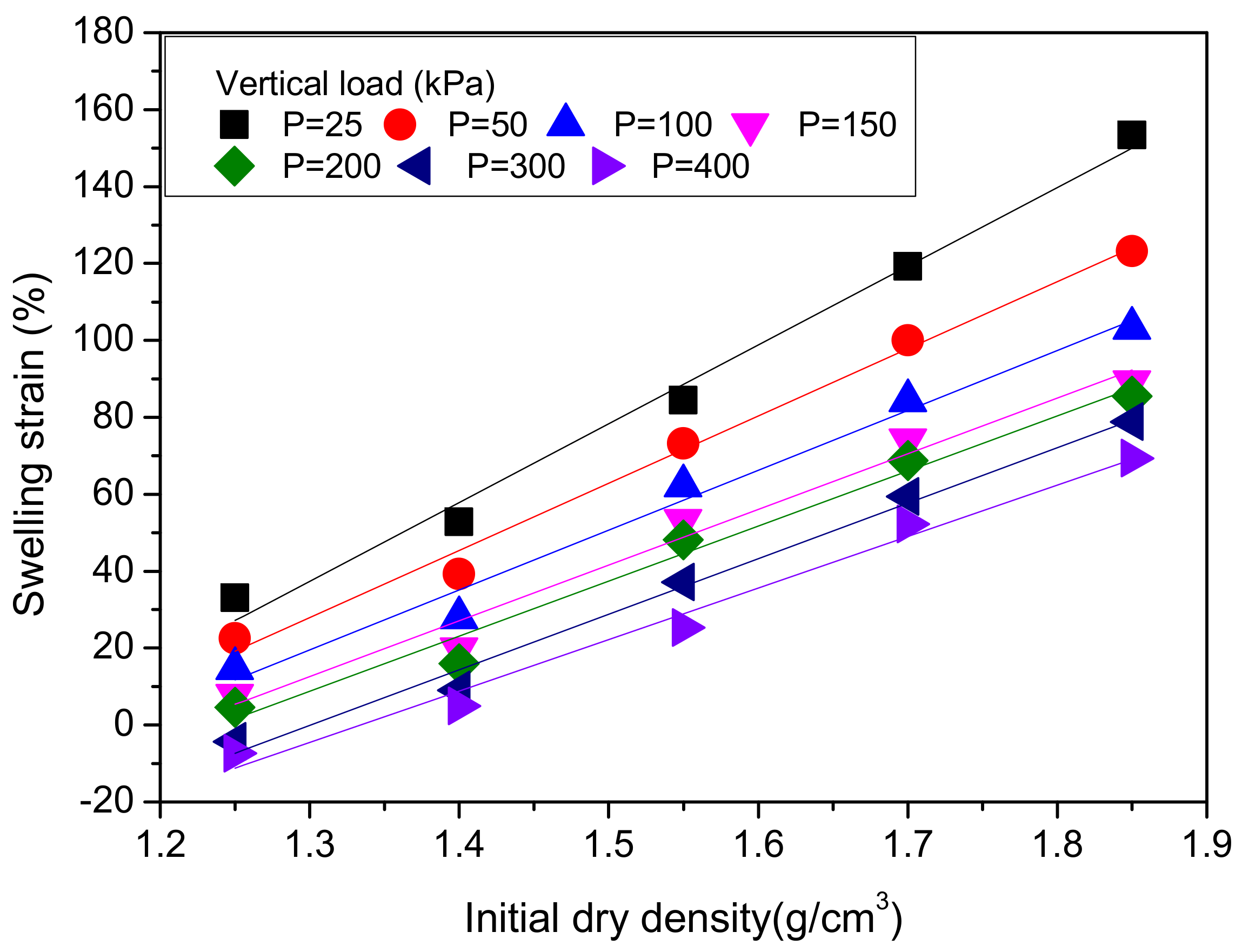
4.2.1. Effect of Initial Dry Density

The relationships between the final swelling strains and initial dry densities of MB specimens under different vertical loads are shown in Figure 9. Under identical vertical pressure conditions, the final swelling strain of MB specimens increased with the initial dry density [42]. The greater is the vertical load, the smaller is the increase in swelling strain change with increasing initial dry density. The linear best-fit relationship between the swelling strain and initial dry density of MB specimens can be expressed by Equation (8):

$${\epsilon }_P=a{\rho }_d-b$$

(8)

where ε_P is the load swelling strain of an MB specimen under load P; ρ_d is the initial dry density of an MB specimen (g/cm³); and a and b are linear fitting parameters related to the vertical pressure on the MB specimen (

Table 5. Parameters relating to the relationship between swelling strain and initial dry density.

Vertical Load (kPa)	a	b
25	204.8	228.8
50	174.8	199.3
100	155.6	182.7
150	144.7	175.5
200	144.4	187.8
300	143.1	177.2
400	133.9	178.6

).

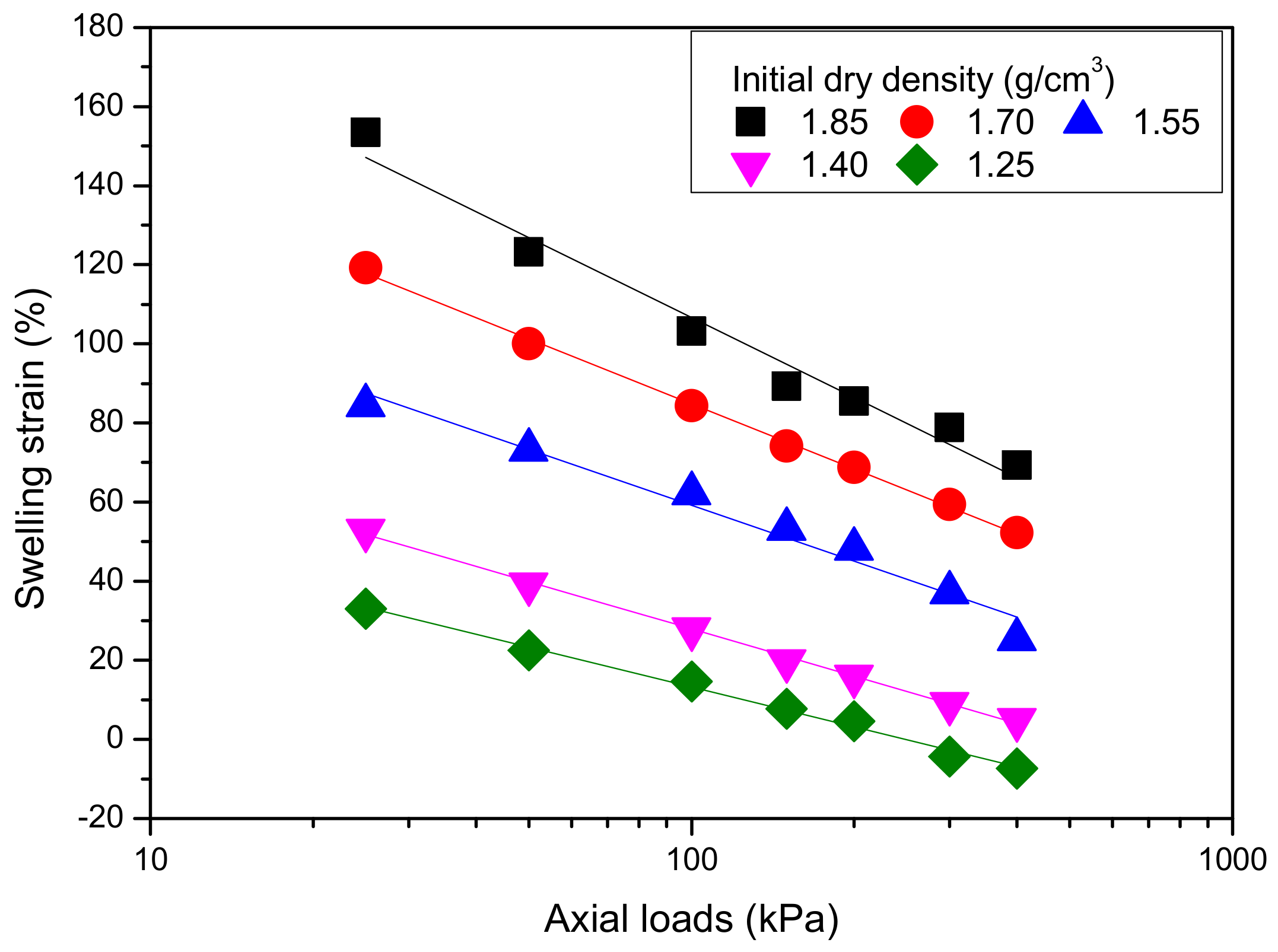
4.2.2. Effect of Vertical Pressure

As an impermeable material in engineering application, vertical swelling strain is an important factor for MB. The vertical swelling strain of MB represents the corresponding vertical load causing expansion to the same strain under the same load [43]. Hence, the relationship between vertical swelling strain of MB specimen and vertical pressure levels could express the constitutive relationship between vertical swelling strain and vertical swelling stress. Figure 10 demonstrates the final vertical swelling strain of MB specimens with different initial dry densities and the logarithm of vertical swelling pressures under saline water conditions. The final swelling strain decreased with the increase of vertical pressure for the MB specimens under all initial dry densities. With the increase of vertical pressure, the effective vertical stress on MB specimens increased, which could hinder water adsorption thereon and prevent the thickening of the water film on the surface of the soil particles. As a result, the swelling deformation of MB specimens was suppressed.

Figure 10 shows the linear relationship between swelling strain (E_P) and the logarithm of swelling pressure (lnP). The relationship between the final swelling strain and vertical load can be expressed as Equation (9):

$${\epsilon }_P=a-b\ln P$$

(9)

where ε_P is the vertical swelling strain of an MB specimen under vertical pressure P; P denotes the vertical pressure (kPa); and a and b are fitting parameters related to the initial dry density of the MB specimen and represent the swelling characteristics of MB.

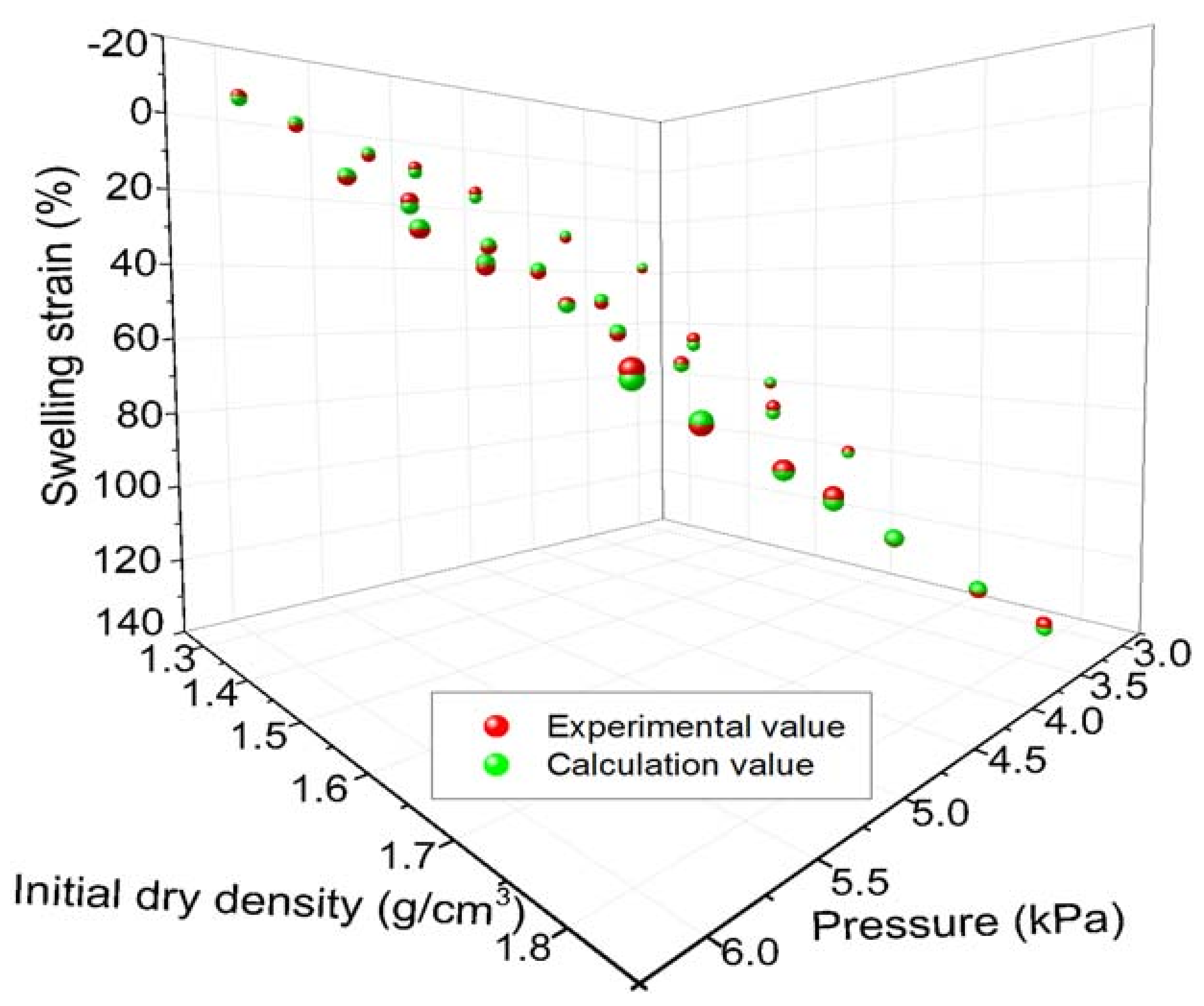
4.2.3. Calculation of Loaded Swelling Strain

Parameters a and b in Equation (9) are different for MB specimens with different initial dry densities. Equations (10) and (11) reflected linear relationships between the parameters and initial dry density of the MB specimen, and the best-fit plots showing the linear relationship between parameters a and b and initial dry density are shown in Figure 11.

$$a=272.25{\rho }_d-266.77$$

(10)

$$b=54.89{\rho }_d-36.65$$

(11)

where a and b are fitting parameters related to the swelling characteristics of MB, and ρ_d is the initial dry density of the MB specimen (g/cm³).

Based on Equations (9)–(11), a formula for swelling strain, as related to initial dry density and vertical load, was obtained as given by Equation (12):

$${\epsilon }_P=-54.89\ln P{\rho }_d+36.65\ln P+272.25{\rho }_d-266.77$$

(12)

where ε_P is the swelling strain in the MB specimen under vertical pressure P; P represents the vertical pressure (kPa); and ρ_d is the initial dry density of the MB specimen (g/cm³).

To verify the accuracy of Equation (12), the load swelling strain test of MB specimens with other initial dry densities (1.3, 1.5, 1.6, and 1.8 g/cm³) was conducted under different vertical pressures (25, 50, 100, 150, 200, 300, and 400 kPa). The difference between the calculated, and experimental, values is shown to be small (Figure 12) indicating the efficacy of Equation (12) when expressing the load swelling characteristics.

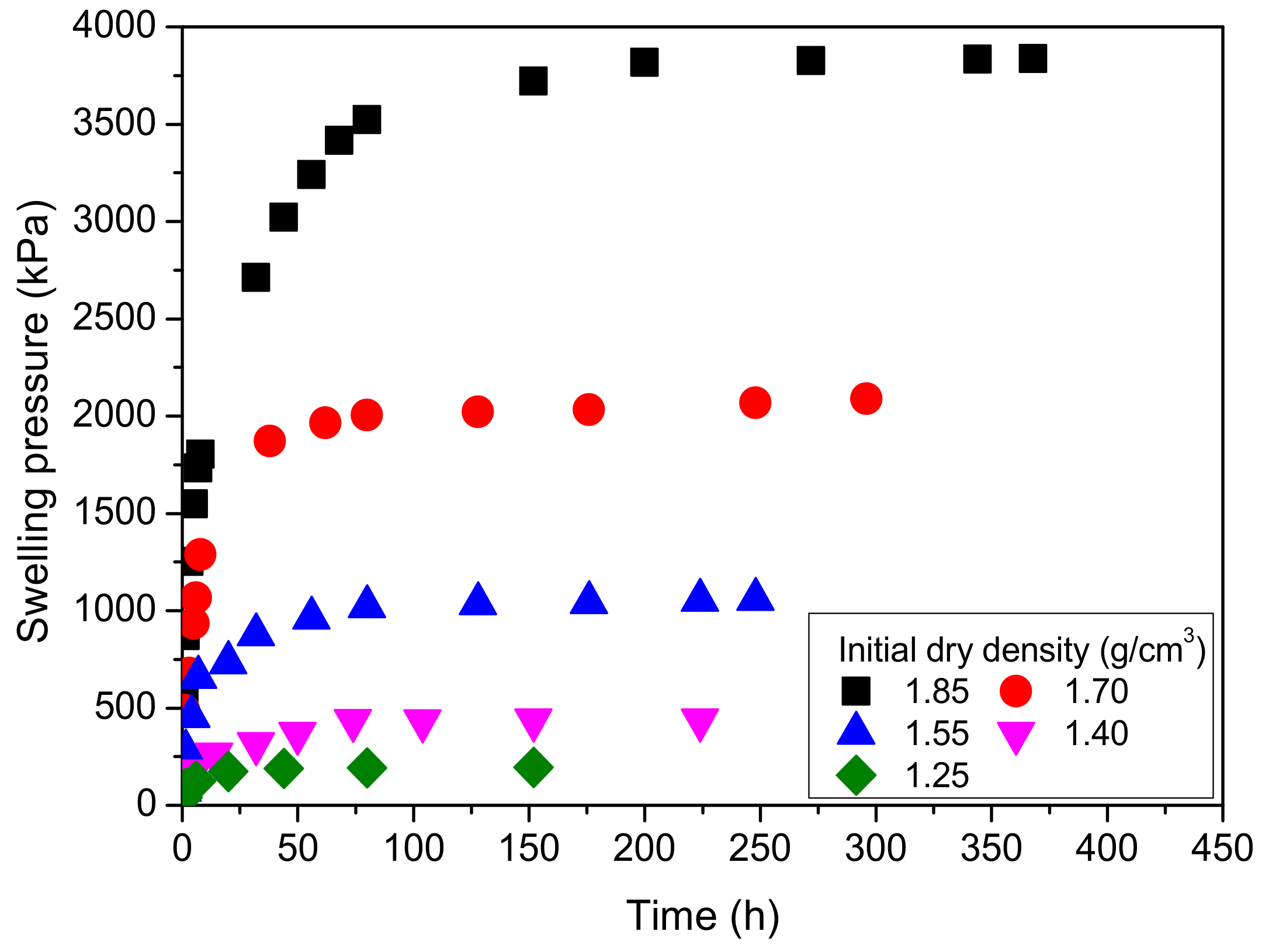
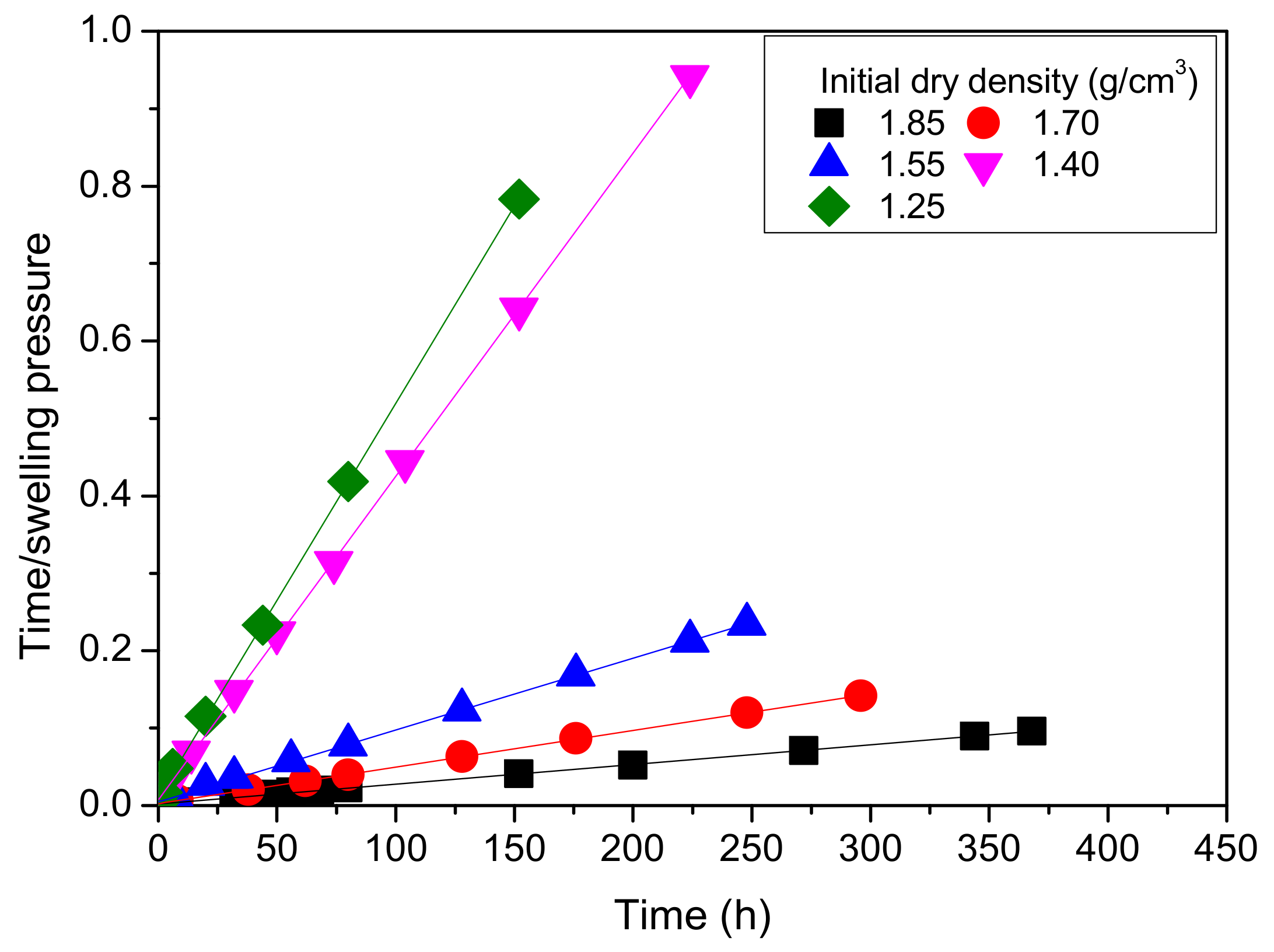
4.3. Vertical Swelling Pressure

4.3.1. Effect of Swelling Time

Figure 13 shows the relationships between vertical swelling pressure and swelling time under different initial dry densities for MB specimens. At the beginning of the test, the structure of the MB specimen gradually changed with the infiltration of saline water, at the same time, the specimen was restricted by the rigid wall and this produced a vertical swelling pressure. In the initial stage, the swelling accelerated, and the vertical swelling pressure increased rapidly. Over time, the sample entered a slow swelling stage, when the swelling pressure reached a certain value, the rate of change of vertical swelling pressure decreased, the MB specimen tended to be saturated and the corresponding vertical swelling pressure stabilized. The experimental results showed that the vertical swelling pressure of MB specimens presented stage-changing characteristics over time, as found elsewhere by studies exploring the relationship between swelling pressure of NB and swelling time under fresh water [44,45].

By further analysis of the change in swelling pressure with swelling time for MB specimens under different initial dry densities, it was found that the ratio of time to vertical swelling pressure showed a linear relationship with swelling time (Figure 14):

$$\frac{t}{P}=a+b\times t$$

(13)

where P is the swelling pressure (kPa), and fitting parameters a and b are listed in

Table 6. Relationship between the initial dry density and time/swelling pressure.

Initial Dry Density (g/cm3)	a	b
1.25	0.0023	0.00025
1.40	0.0024	0.00047
1.55	0.0048	0.00093
1.75	0.0077	0.00418
1.85	0.0106	0.00509

.

4.3.2. Effect of Initial Dry Density

For a certain water content, there is a power function relationship between the vertical pressure on compacted bentonite without experiencing deformation, and the initial dry density [46,47]. Figure 15 shows the relationship between the initial dry density of MB specimens and the corresponding final swelling pressure under saline water conditions (Equation (14)). The correlation coefficient (R²) is 0.98.

$$P_{final}=25.25{\rho }_d{}^{8.11}$$

(14)

where P_final is the swelling pressure (kPa), and ρ_d represents the initial dry density of the MB specimen (g/cm³).

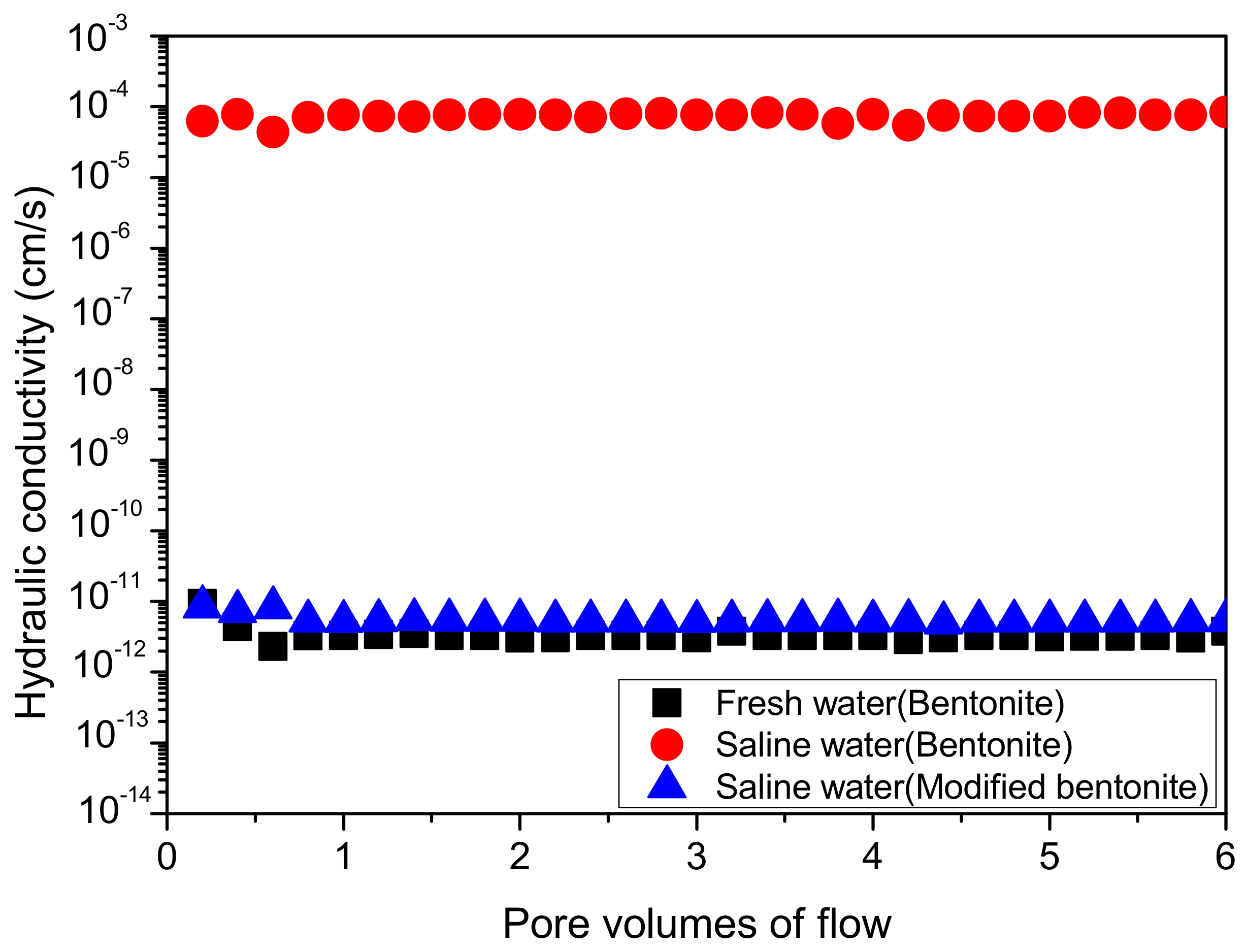
4.4. Hydraulic Conductivity

A low hydraulic conductivity is an important characteristic for NB as an impermeable material in civil engineering applications; however, the impermeability will be restricted when NB is used in saline water conditions. Figure 16 shows the hydraulic conductivity of NB in fresh water conditions, and that of MB in fresh and saline water conditions. The hydraulic conductivity of NB in saline water conditions was much higher than that in fresh water conditions. After polymer modification, the hydraulic conductivity of MB in saline water conditions was identical to that of NB in fresh water conditions. The hydraulic conductivities of modified bentonite were smaller than 1.0 × 10⁻⁷ cm/s under saline conditions. This satisfied the permeability standard requirements for waterproof materials for use in civil engineering works. As has been mentioned, the improvement efficiency was significant and MB exhibited high salt tolerance with the polymer effectively preventing contacting between salt ions and bentonite molecules. The hydraulic conductivity of MB in saline water was similar to that of NB in fresh water.

5. Conclusions

The swelling characteristics of MB specimens after different swelling times at different initial dry densities and under different loads were studied. The hydraulic conductivity testing of MB was carried out in both fresh and saline water conditions. The following conclusions are drawn:

(1)

The improvement efficiency of MB is remarkable, the MB material exhibits good swelling characteristic and a low permeability in saline water, and the hydraulic conductivity of MB is less than 3 × 10⁻¹² cm/s.

(2)

The unloading swelling strain on MB in saline water increases over time and there is a linear relationship between the ratio of time to swelling strain and swelling time; the final unloading swelling strain of MB increases linearly with increasing initial dry density.

(3)

The loading swelling strain of MB decreases with the increase of vertical pressure and increases with the initial dry density; a formula for the loading swelling strain that was related to initial dry density and vertical pressure was obtained.

(4)

With increasing swelling time, the swelling pressure increases rapidly at first and then decreases, the ratio of time to swelling pressure has a linear relationship with swelling time, and the relationship between swelling pressure and initial dry density of MB specimens is exponential and increasing.

(5)

Relationship affecting the swelling capacity of bentonite was deduced, and all such equations can provide a theoretical basis for the use of modified bentonite as an impermeable material in civil engineering practice.

(6)

The empirical relationships obtained above are only applicable to the specific conditions of this study. Swelling capacity can be influenced by other factors, for example, mixing of polymer and bentonite, and chemical compositions of the permeant. In future studies, these factors will be explored to facilitate the characterization of universal empirical relationships.