Realization of the Zone Length Measurement during Zone Refining Process via Implementation of an Infrared Camera
Abstract
1. Introduction
2. Experimental Assessment
2.1. Zone Refining Equipment and Infrared Camera Setup
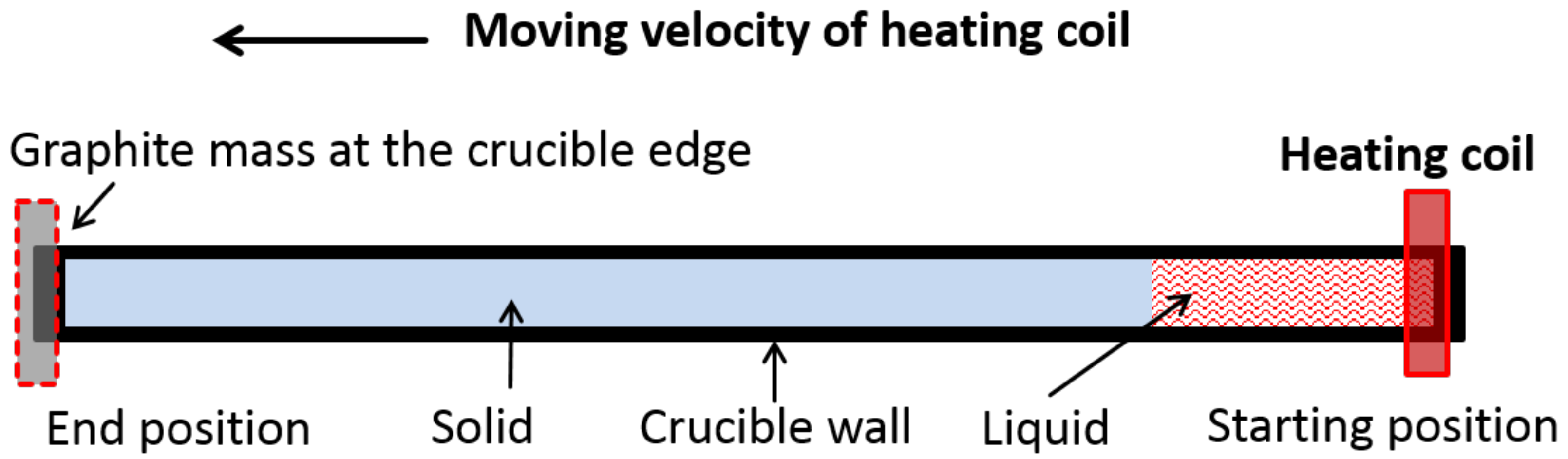
2.2. Zone Refining Trial
3. Results and Discussion
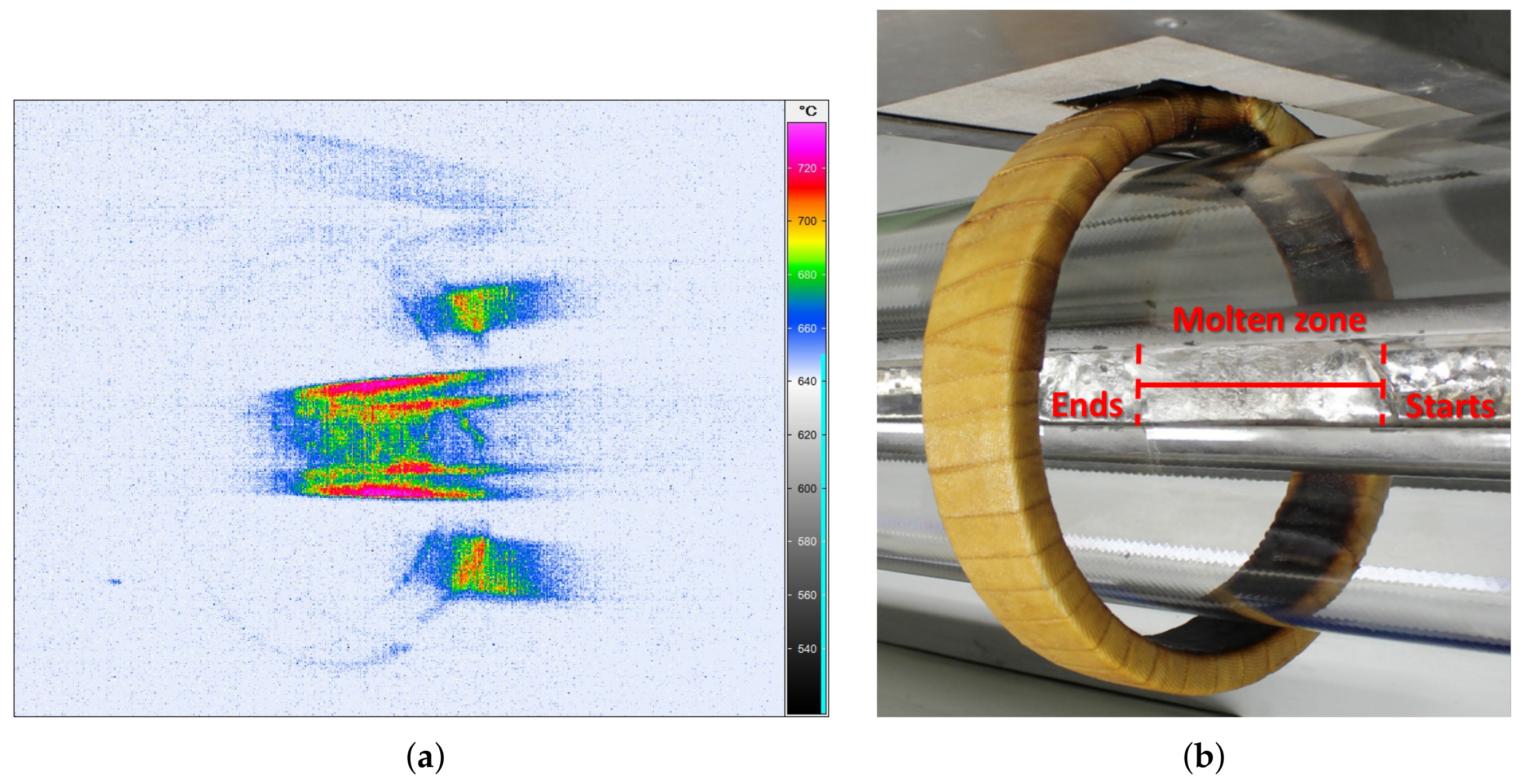
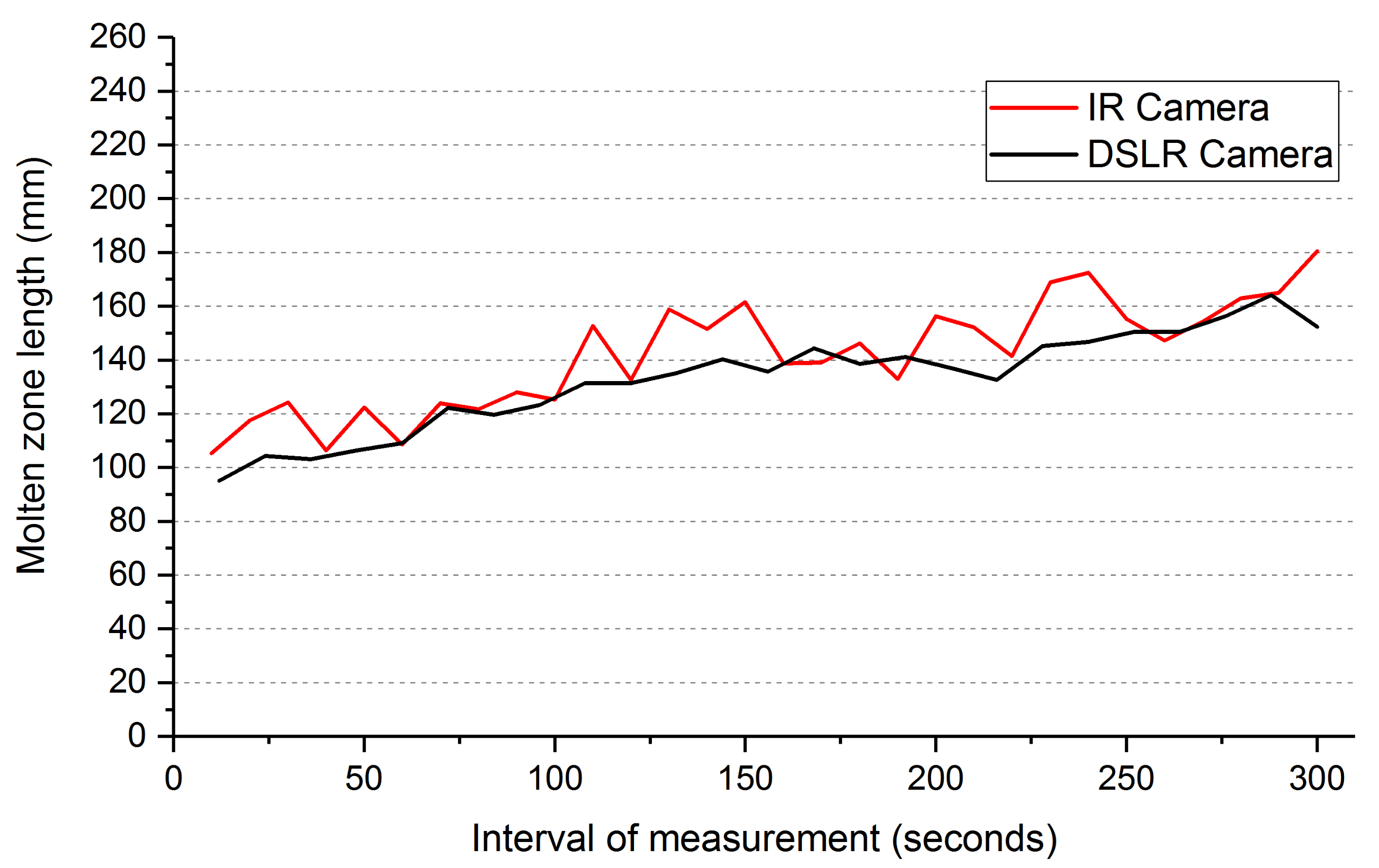
3.1. Correlation between an IR and a DSLR Camera to Determine the Zone Length
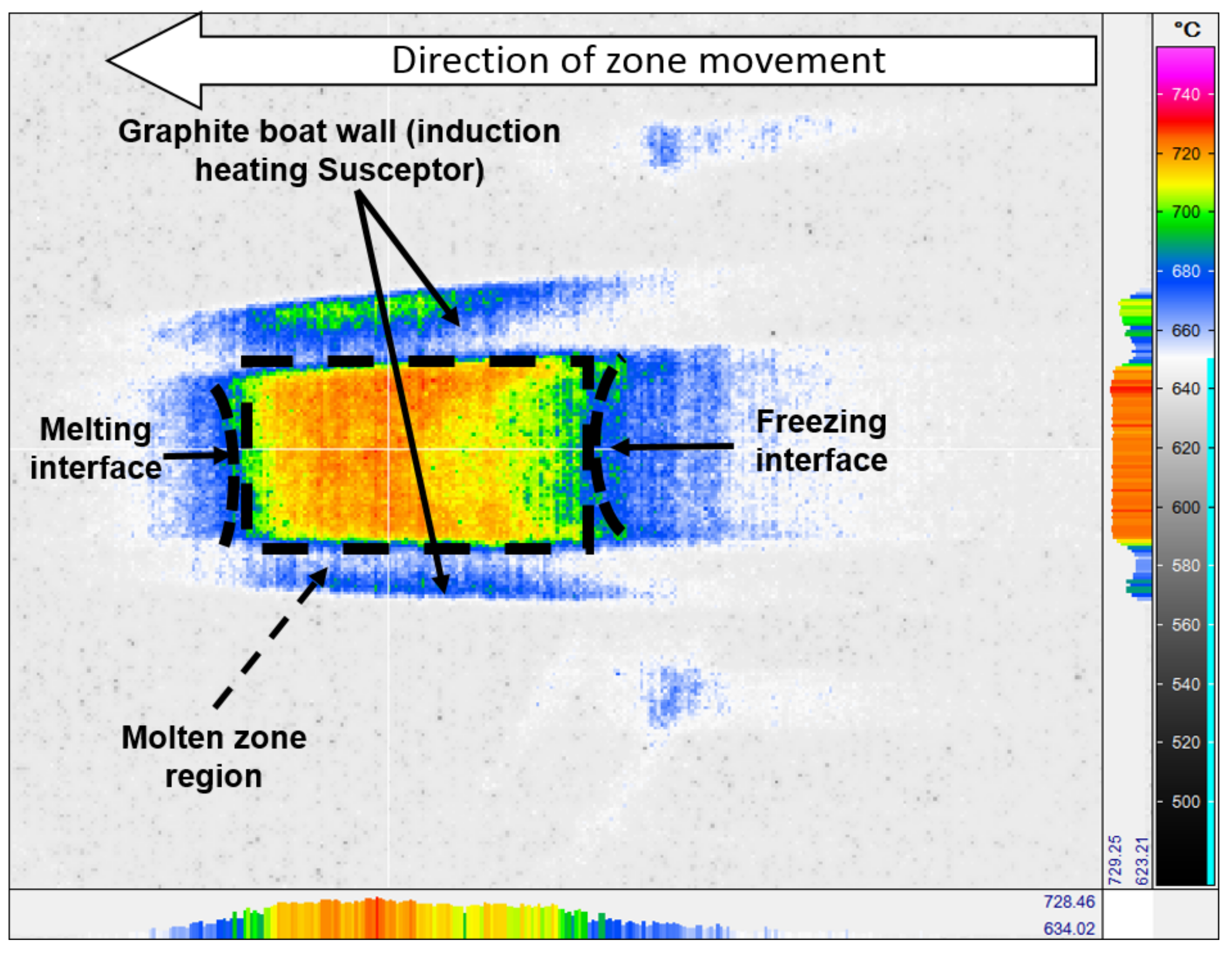
3.2. Infrared Image Analysis and Calculations
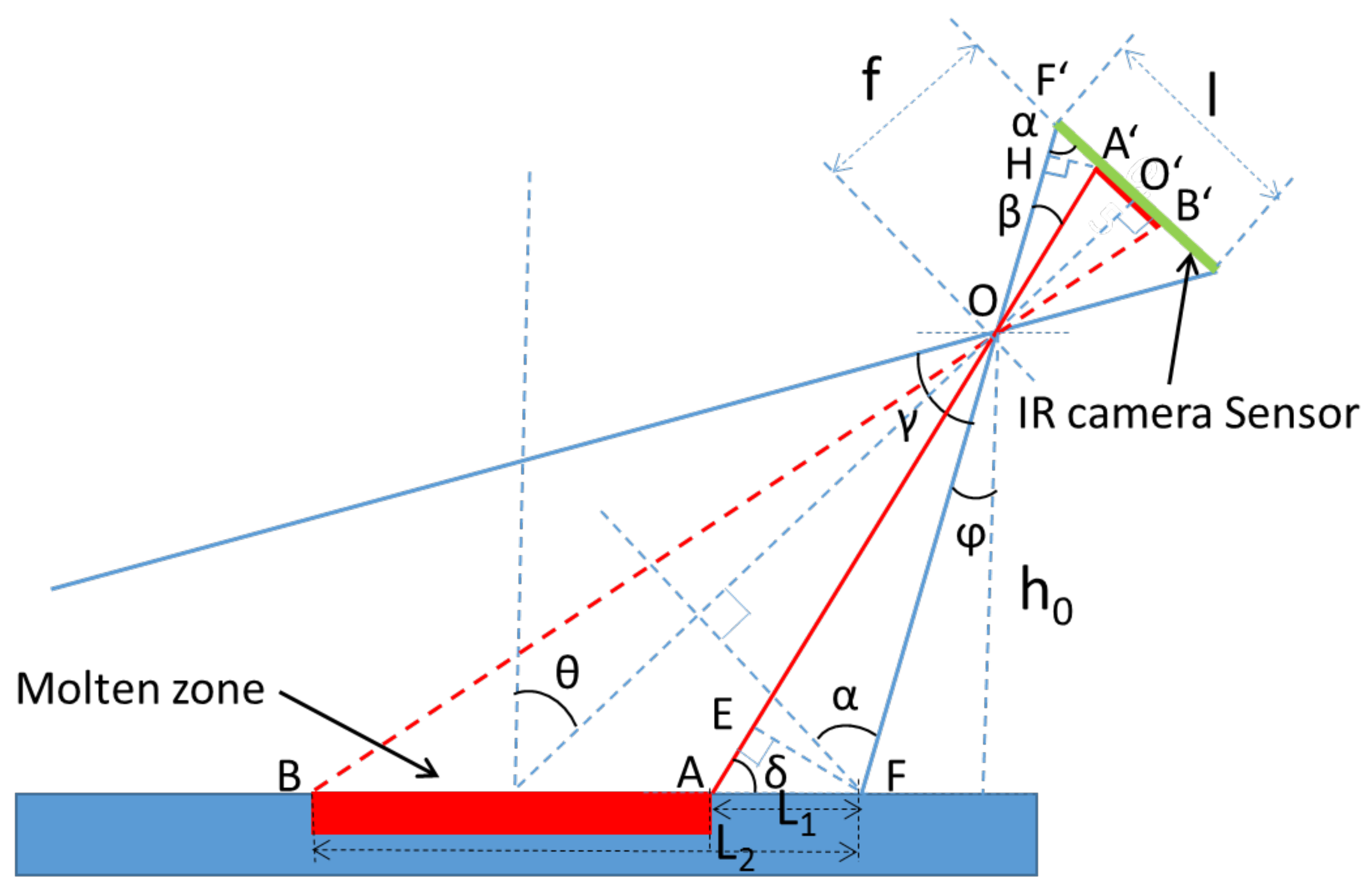
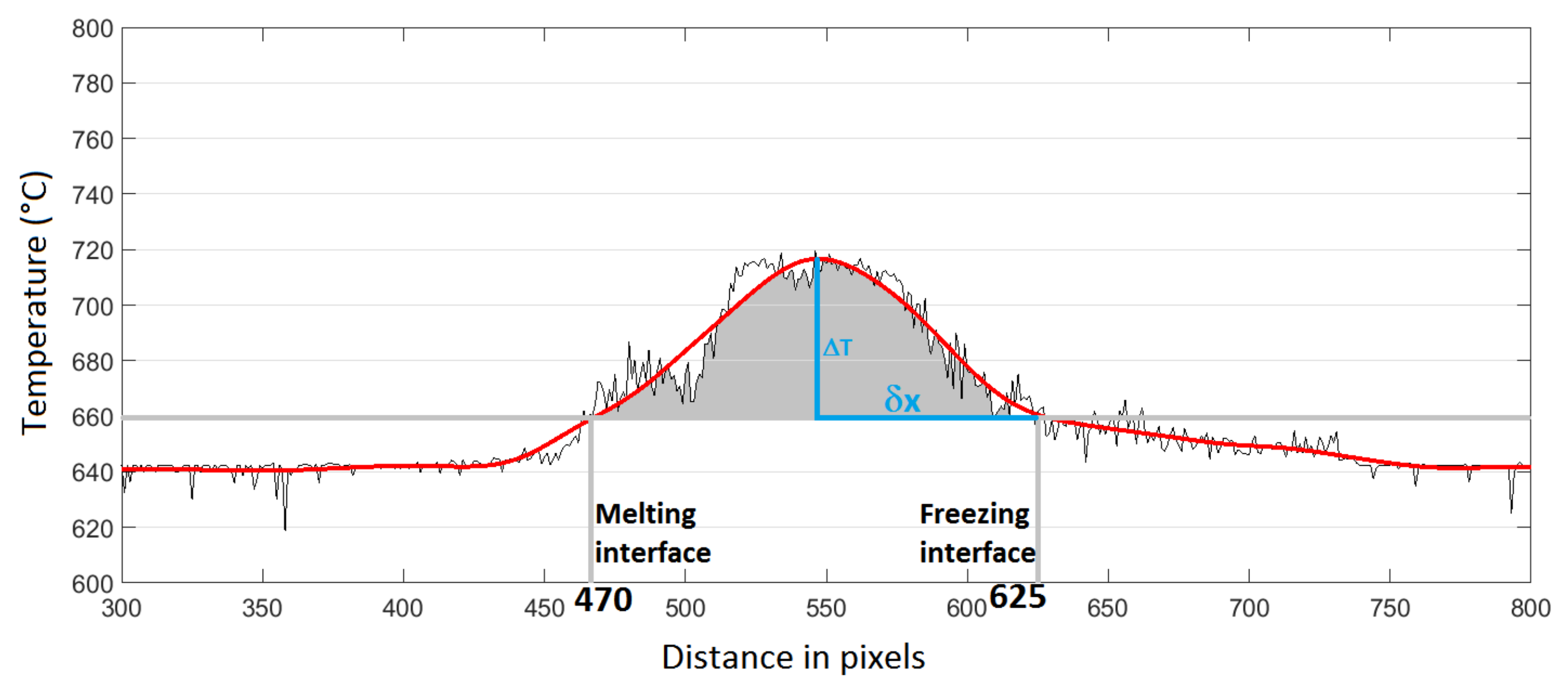
3.2.1. Calculation of Zone Length and Molten Zone Thermal Gradient
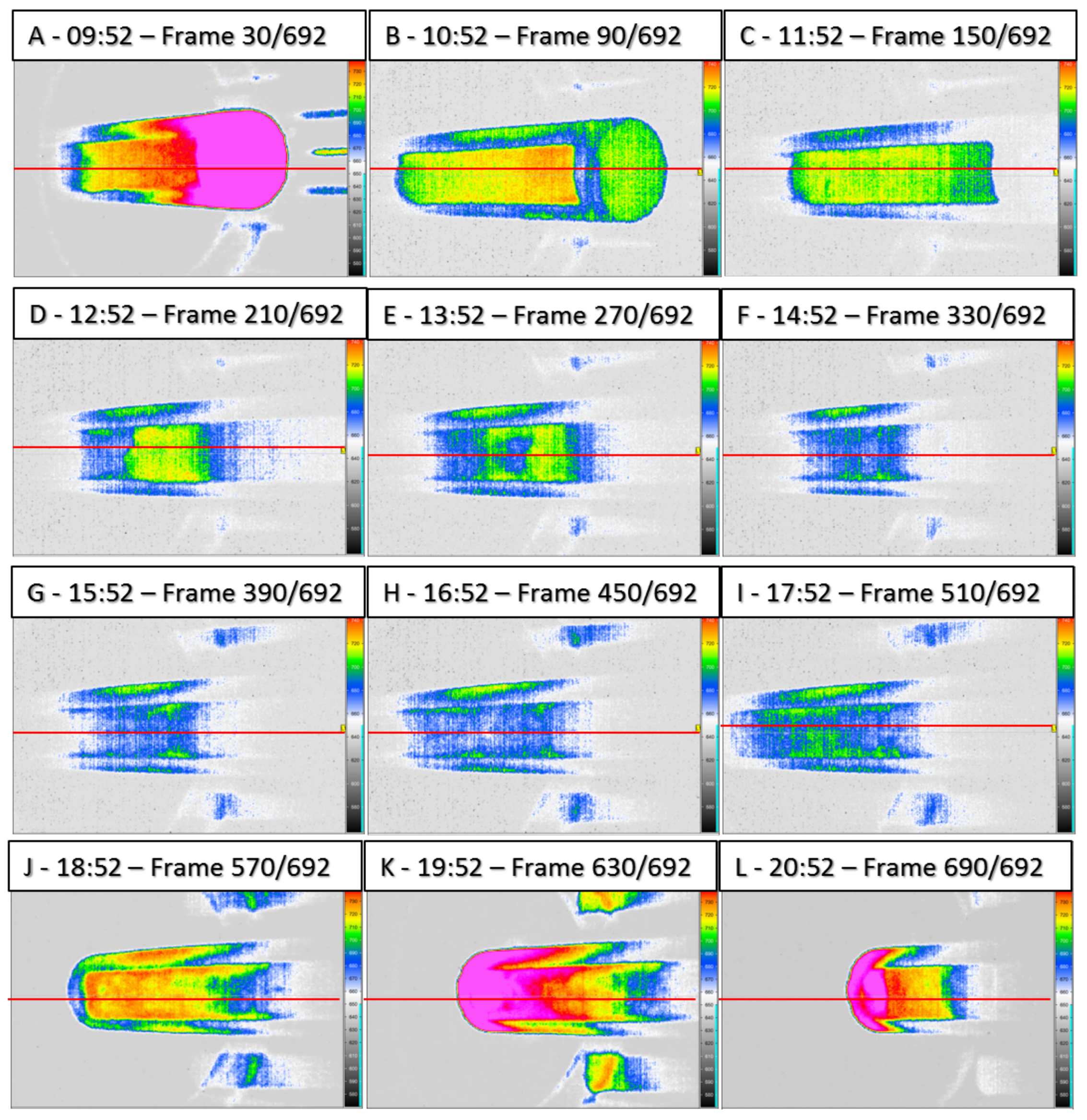
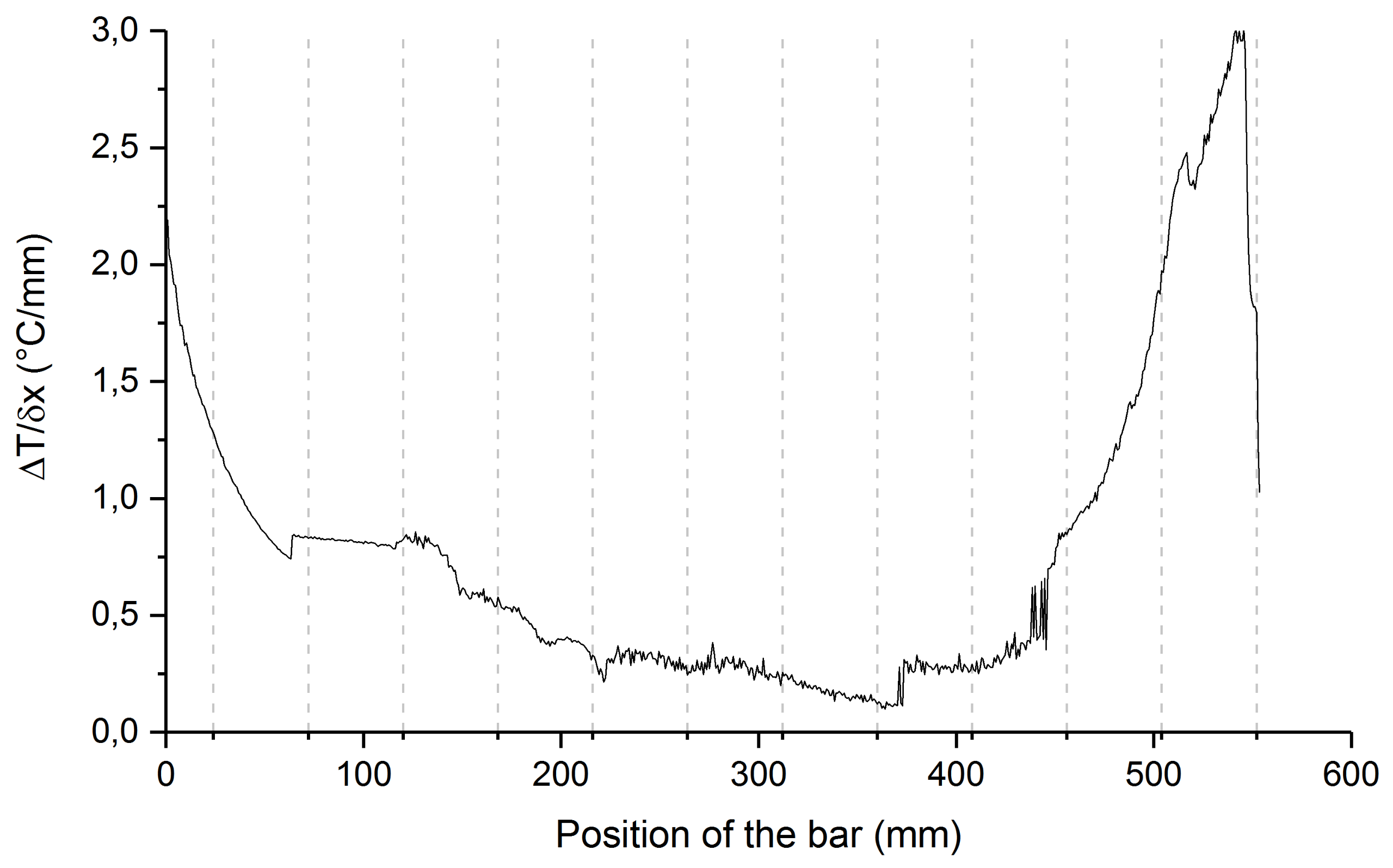
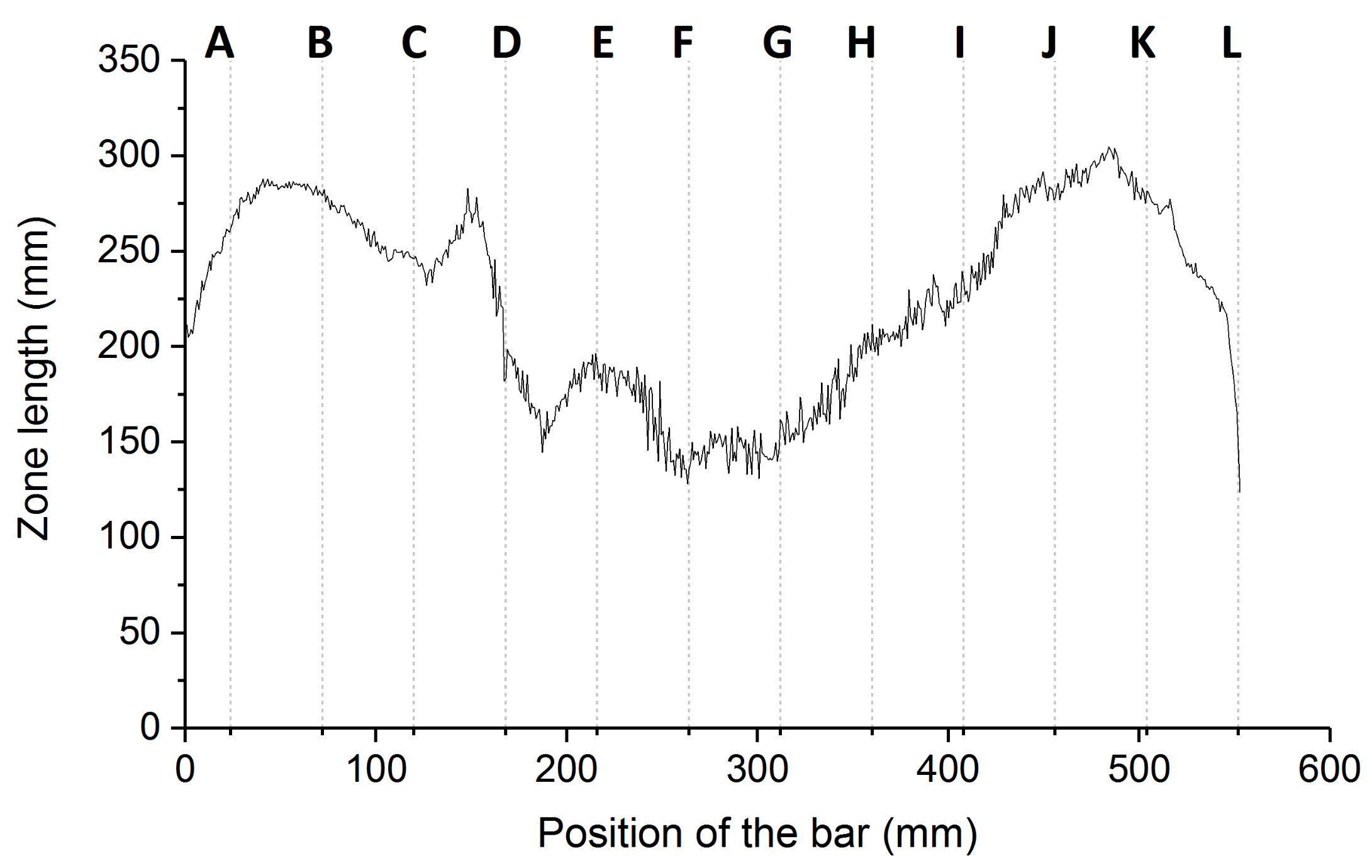
3.2.2. Calculation of the Zone Length Variation over the Bar Length
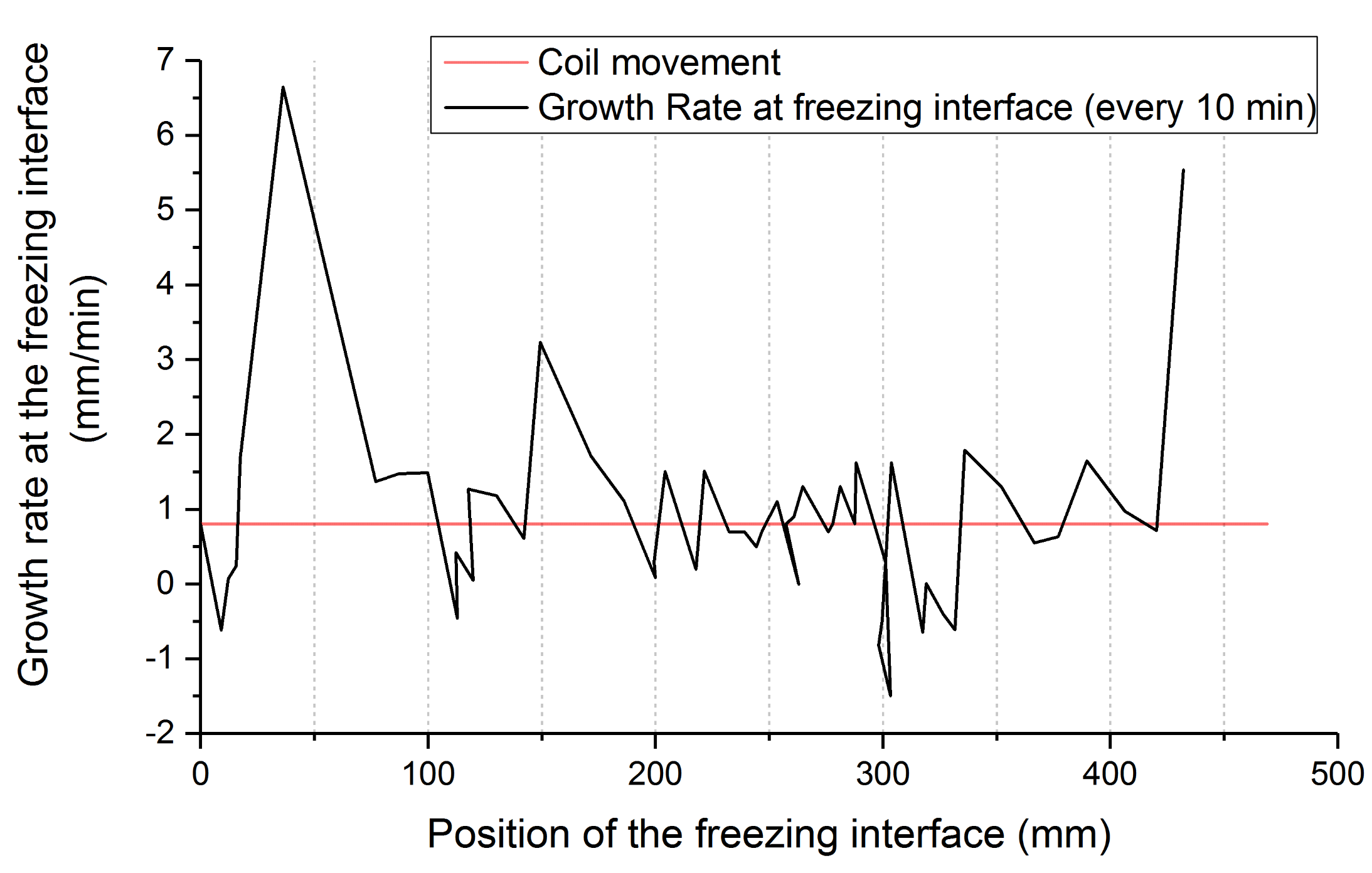
3.3. Calculation of the Growth Rate Variation
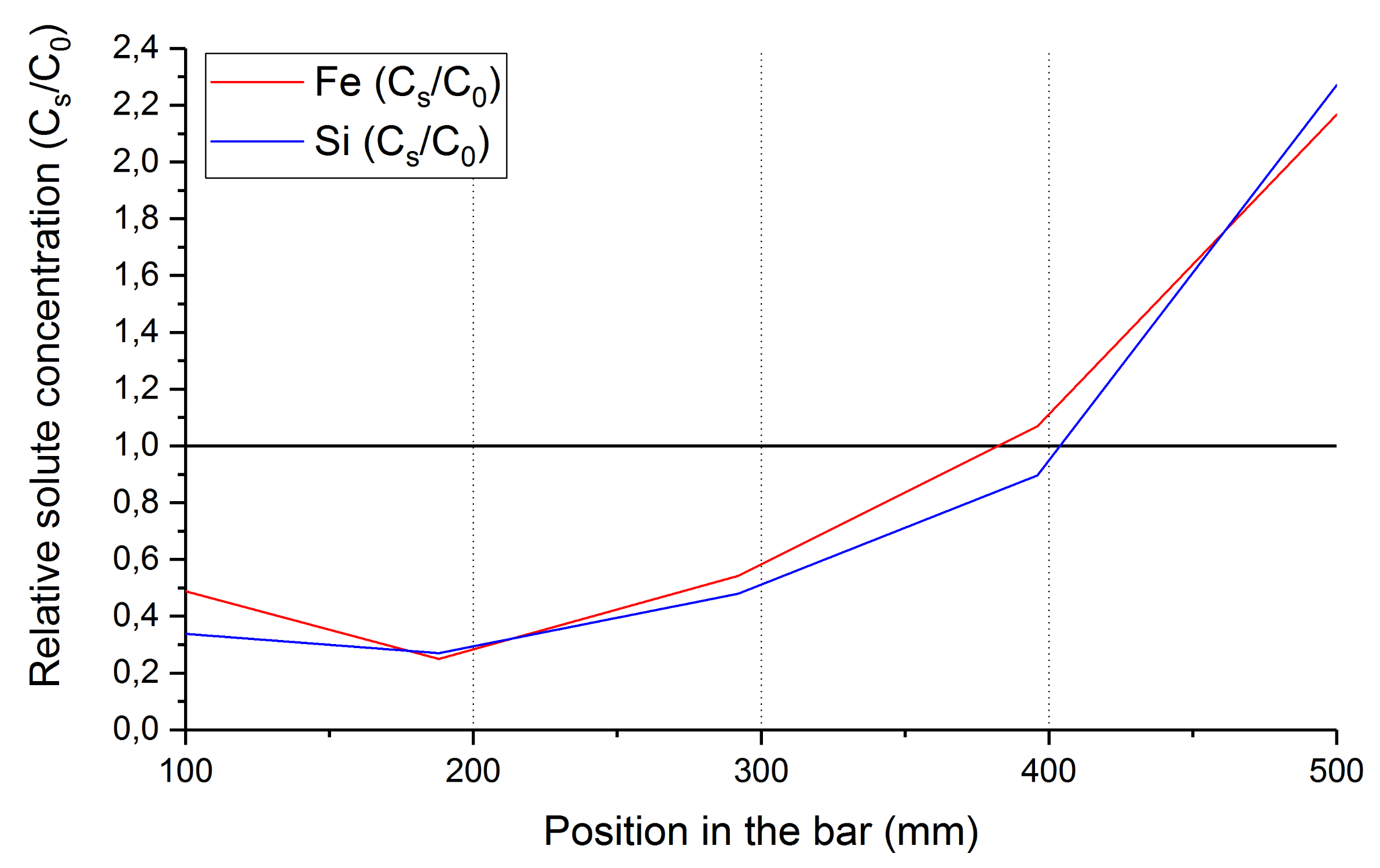
3.4. Impurity Concentration Profile
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A. Function for the Conversion of the Zone Length from Pixels to Millimeters
References
- Pfann, W.G. Principles of Zone-Melting. JOM 1952, 4, 747–753. [Google Scholar] [CrossRef]
- Spim, J.; Bernadou, M.; Garcia, A. Numerical modeling and optimization of zone refining. J. Alloys Compd. 2000, 298, 299–305. [Google Scholar] [CrossRef]
- Burris, L.; Stockman, C.H.; Dillon, I.G. Contribution to Mathematics of Zone Melting. JOM 1955, 7, 1017–1023. [Google Scholar] [CrossRef]
- Pfann, W.G. Zone Melting: This technique offers unique advantages in purification and in control of composition in various substances. Science 1962, 135, 1101–1109. [Google Scholar] [CrossRef] [PubMed]
- Rodway, G.; Hunt, J. Optimizing zone refining. J. Cryst. Growth 1989, 97, 680–688. [Google Scholar] [CrossRef]
- Ho, C.d.; Yeh, H.M.; Yeh, T.l. Numerical analysis on optimal zone lengths for each pass in multipass zone-refining processes. Can. J. Chem. Eng. 1998, 76, 113–119. [Google Scholar] [CrossRef]
- Zhang, X.; Friedrich, S.; Friedrich, B. Investigation of Influencing Parameters on Zone Melting Refining of Aluminium, Part One Impurities: Iron and Silicon. In Proceedings of the 2017 European Metallurgical Conference, Düsseldorf, Germany, 23–26 June 2017; pp. 1–8. [Google Scholar]
- Munirathnam, N.R.; Prasad, D.S.; Sudheer, C.; Rao, J.V.; Prakash, T.L. Zone refining of cadmium and related characterization. Bull. Mater. Sci. 2005, 28, 209–212. [Google Scholar] [CrossRef]
- Kobayashi, N. Power required to form a floating zone and the zone shape. J. Cryst. Growth 1978, 43, 417–424. [Google Scholar] [CrossRef]
- Louchev, O.A. The influence of natural convection on the formation of a molten zone under optical heating. J. Cryst. Growth 1993, 133, 261–266. [Google Scholar] [CrossRef]
- Wang, J.H.; Kim, D.H. Numerical analysis of melt/solid interface shape in zone melting recrystallization process. J. Cryst. Growthh 1997, 173, 201–209. [Google Scholar] [CrossRef]
- Roussopoulos, G.; Rubini, P. A thermal analysis of the horizontal zone refining of indium antimonide. J. Cryst. Growth 2004, 271, 333–340. [Google Scholar] [CrossRef]
- Zhang, X.; Friedrich, S.; Friedrich, B. Production of High Purity Metals: A Review on Zone Refining Process. J. Cryst. Process. Technol. 2018, 8, 33–55. [Google Scholar] [CrossRef]




| Temperature (C) | 650 | 668 | 674 | 683 | 692 | 699 |
| Emissivity () | 0.47 | 0.42 | 0.41 | 0.39 | 0.36 | 0.32 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Curtolo, D.C.; Zhang, X.; Rojas, M.J.R.; Friedrich, S.; Friedrich, B. Realization of the Zone Length Measurement during Zone Refining Process via Implementation of an Infrared Camera. Appl. Sci. 2018, 8, 875. https://doi.org/10.3390/app8060875
Curtolo DC, Zhang X, Rojas MJR, Friedrich S, Friedrich B. Realization of the Zone Length Measurement during Zone Refining Process via Implementation of an Infrared Camera. Applied Sciences. 2018; 8(6):875. https://doi.org/10.3390/app8060875
Chicago/Turabian StyleCurtolo, Danilo C., Xiaoxin Zhang, Martin J. R. Rojas, Semiramis Friedrich, and Bernd Friedrich. 2018. "Realization of the Zone Length Measurement during Zone Refining Process via Implementation of an Infrared Camera" Applied Sciences 8, no. 6: 875. https://doi.org/10.3390/app8060875
APA StyleCurtolo, D. C., Zhang, X., Rojas, M. J. R., Friedrich, S., & Friedrich, B. (2018). Realization of the Zone Length Measurement during Zone Refining Process via Implementation of an Infrared Camera. Applied Sciences, 8(6), 875. https://doi.org/10.3390/app8060875






