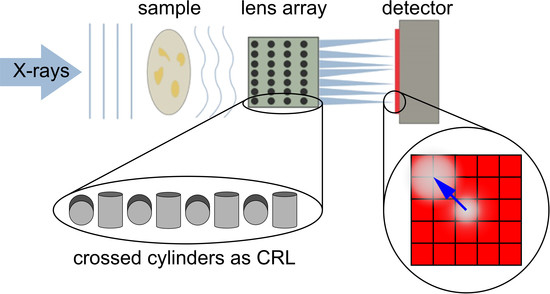
A Shack-Hartmann Sensor for Single-Shot Multi-Contrast Imaging with Hard X-rays
Abstract
1. Introduction
2. Material and Methods
2.1. Fabrication of the 2D Lens Array
2.2. Image Formation
2.3. Retrieval of The Contrasts: Amplitude, Phase and Diffraction
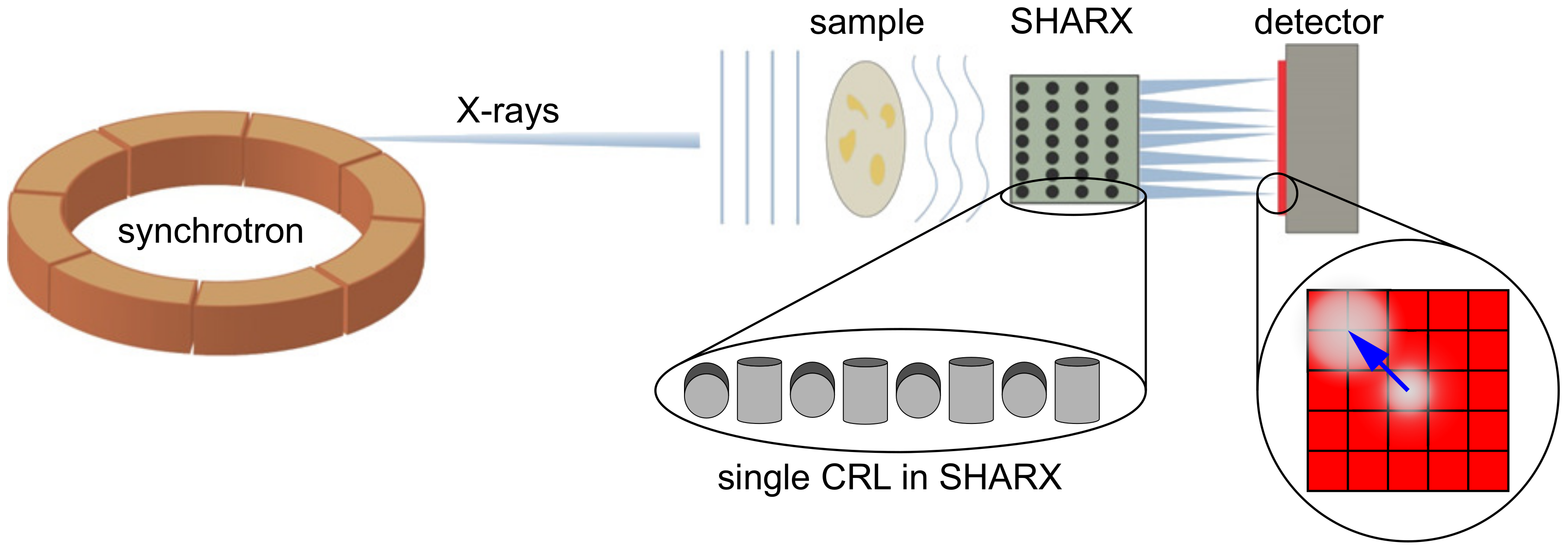
2.4. Experimental setup
- (i)
- The internal microstructure of the SHARX was examined by means of micro-tomography acquired in filtered white beam (central energy 15 keV) with a 7 cm distance between the SHARX and the scintillator, which is much smaller than the focal distance of the lens array. A PCO.dimax (PCO AG, Kelheim, Germany) camera was used to image a 10 m thick LSO:Tb scintillator by a 10× objective (Mitutoyo LWD 10X 0.28 (Mitutoyo Deutschland GmbH, Neuss, Germany)) and a 180 mm tube lens, resulting in a ninefold optical magnification. The effective pixel size was 1.22 m. Projections were continuously recorded while rotating the sample with constant angular velocity around an axis perpendicular to the beam propagation directions [39].
- (ii)
- The focal distance of the SHARX was characterized in monochromatic beam (double-multilayer monochromator with 2% bandwidth at 9 keV). As detector an Andor Neo (Andor Technology Ltd., Belfast, Northern Ireland) camera coupled to a 200 m LuAG:Ce scintillator via a single objective lens (Nikon Nikkor 85/1.4 (Nikon GmbH, Düsseldorf, Germany)) was used. The optical magnification was 3.6x, resulting in an effective pixel size of 1.8 m.
- (iii)
- The phase-front reconstruction of the diamond lens was performed in monochromatic beam (8.5 keV). The camera used was the Andor Neo using the same optics as in setup (i) resulting in an effective pixel size of 0.72 m. The distance between the detector and the SHARX was 16 cm and the diamond lens was placed before the SHARX.
- (iv)
- The fast multi-contrast imaging during the ablation process was performed in filtered white beam (central energy 15 keV). The camera was a PCO.dimax, lens-coupled with twofold magnification to a 50 m thick LuAG:Ce scintillator. The effective pixel size was 5.5 m. The ablation process was measured in a pump-record mode. For each laser pulse a complete image sequence was recorded with a frame rate of 15 kHz and an exposure time of 33 s to limit motion blurring [27]. This image sequence started before the laser impact (used for flat correction) and lasted longer than the final cavitation bubble collapse. For statistical reasons images sequences from 700 subsequent laser shots were averaged. The ablation process occurred in an in situ chamber, which was placed behind the SHARX close to the scintillator (7 cm distance). The ablation, in brief, was performed on a silver wire target (0.7 mm diameter) continuously transported through a sealed chamber of 0.4 cm volume and flushed continuously by a water flow to avoid laser shielding by nanoparticles produced at predecessing laser pulses. Pulses from a nanosecond laser (Continuum Minilite I (Continuum, San Jose, USA), 1064 nm, 10 mJ) entered the chamber via a lens (38 mm effective focal length in water) to be focused onto the target (for more details see [27,40,41]).
3. Results and Discussion
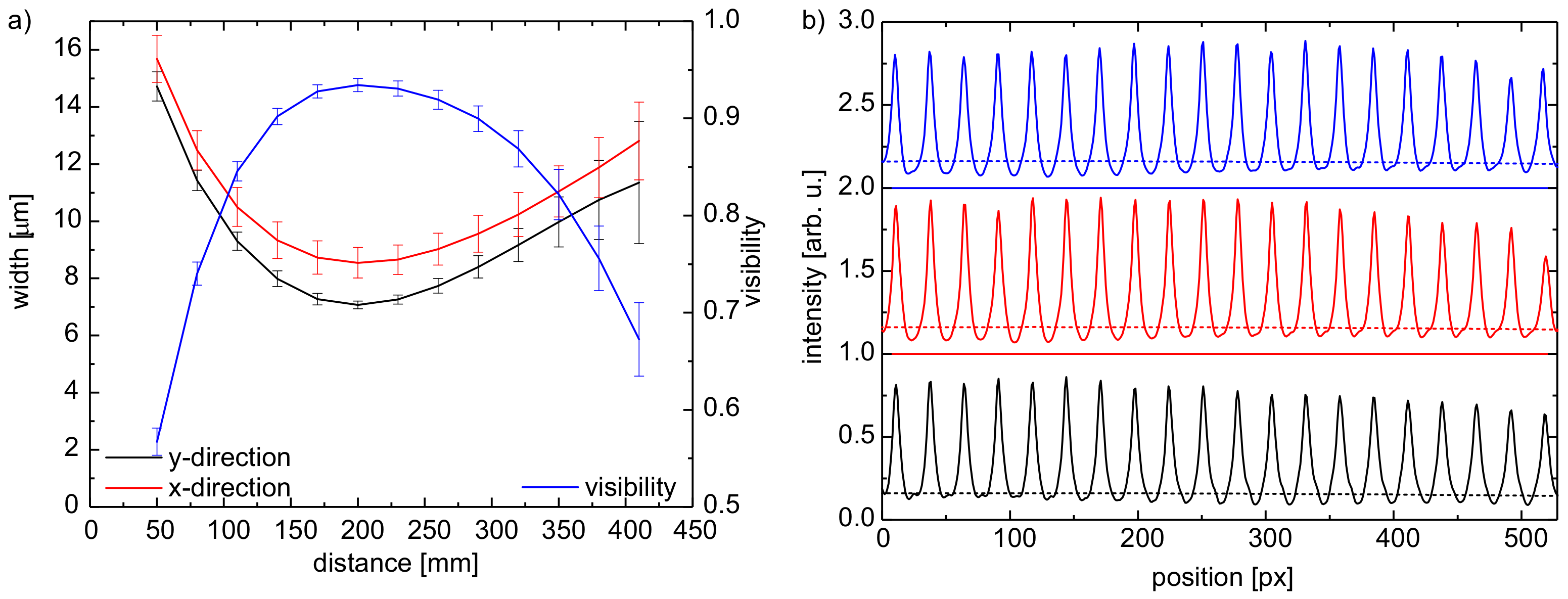
3.1. Lens Array Characterization
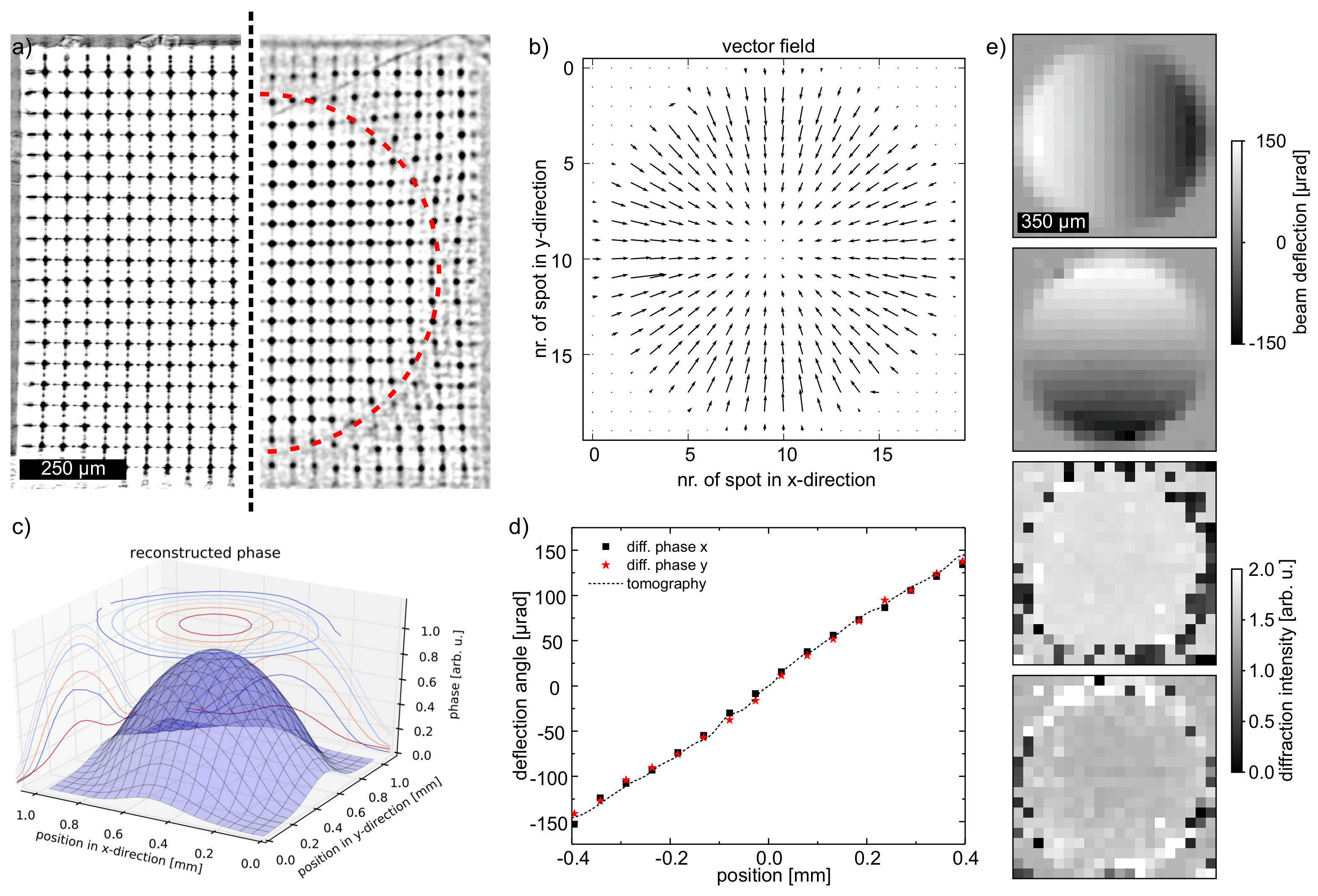
3.2. Reconstruction of The Phase Shift of a Diamond Lens
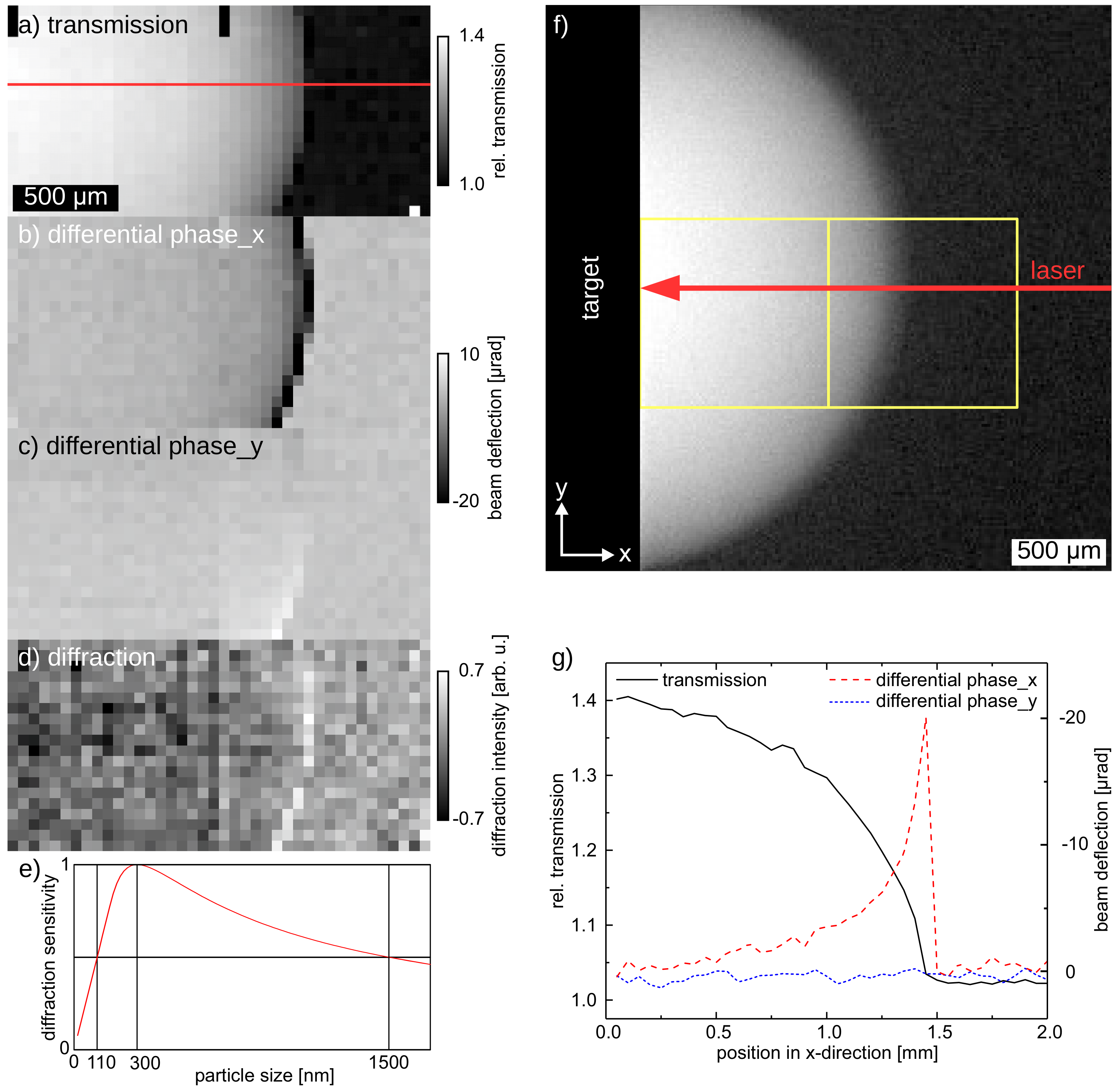
3.3. In-Situ Imaging of Laser-Induced Cavitation Bubble
4. Summary and Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Wilkins, S.W.; Gureyev, T.E.; Gao, D.; Pogany, A.; Stevenson, A.W. Phase-contrast imaging using polychromatic hard X-rays. Nature 1996, 384, 335–338. [Google Scholar] [CrossRef]
- Diemoz, P.; Bravin, A.; Coan, P. Theoretical comparison of three X-ray phase-contrast imaging techniques: propagation-based imaging, analyzer-based imaging and grating interferometry. Opt. Express 2012, 20, 2789–2805. [Google Scholar] [CrossRef] [PubMed]
- Cloetens, P.; Barrett, R.; Baruchel, J.; Guigay, J.P.; Schlenker, M. Phase objects in synchrotron radiation hard X-ray imaging. J. Phys. D Appl. Phys. 1996, 29, 133–146. [Google Scholar] [CrossRef]
- Bonse, U.; Hart, M. An X-ray Interferometer. Appl. Phys. Lett. 1965, 6, 155–156. [Google Scholar] [CrossRef]
- Endrizzi, M.; Diemoz, P.C.; Millard, T.P.; Louise Jones, J.; Speller, R.D.; Robinson, I.K.; Olivo, A. Hard X-ray dark-field imaging with incoherent sample illumination. Appl. Phys. Lett. 2014, 104, 024106. [Google Scholar] [CrossRef]
- Momose, A.; Kawamoto, S.; Koyama, I.; Hamaishi, Y.; Takai, K.; Suzuki, Y. Demonstration of X-ray Talbot Interferometry. Jpn. J. Appl. Phys. 2003, 42, L866–L868. [Google Scholar] [CrossRef]
- Weitkamp, T.; Diaz, A.; David, C.; Pfeiffer, F.; Stampanoni, M.; Cloetens, P.; Ziegler, E. X-ray phase imaging with a grating interferometer. Opt. Express 2005, 13, 6296–6304. [Google Scholar] [CrossRef] [PubMed]
- Pfeiffer, F.; Weitkamp, T.; Bunk, O.; David, C. Phase retrieval and differential phase-contrast imaging with low-brilliance X-ray sources. Nat. Phys. 2006, 2, 258–261. [Google Scholar] [CrossRef]
- Momose, A.; Yashiro, W.; Maikusa, H.; Takeda, Y. High-speed X-ray phase imaging and X-ray phase tomography with Talbot interferometer and white synchrotron radiation. Opt. Express 2009, 17, 12540. [Google Scholar] [CrossRef] [PubMed]
- Pfeiffer, F.; Bech, M.; Bunk, O.; Kraft, P.; Eikenberry, E.F.; Brönnimann, C.; Grünzweig, C.; David, C. Hard-X-ray dark-field imaging using a grating interferometer. Nat. Mater. 2008, 7, 134–137. [Google Scholar] [CrossRef] [PubMed]
- Kagias, M.; Wang, Z.; Jefimovs, K.; Stampanoni, M. Dual phase grating interferometer for tunable dark-field sensitivity. Appl. Phys. Lett. 2017, 110, 014105. [Google Scholar] [CrossRef]
- McDonald, S.A.; Marone, F.; Hintermüller, C.; Mikuljan, G.; David, C.; Pfeiffer, F.; Stampanoni, M. Advanced phase-contrast imaging using a grating interferometer. J. Synchrotron Radiat. 2009, 16, 562–572. [Google Scholar] [CrossRef] [PubMed]
- Momose, A.; Yashiro, W.; Harasse, S.; Kuwabara, H. Four-dimensional X-ray phase tomography with Talbot interferometry and white synchrotron radiation: dynamic observation of a living worm. Opt. Express 2011, 19, 8423–8432. [Google Scholar] [CrossRef] [PubMed]
- Wen, H.H.; Bennett, E.E.; Kopace, R.; Stein, A.F.; Pai, V. Single-shot X-ray differential phase-contrast and diffraction imaging using two-dimensional transmission gratings. Opt. Lett. 2010, 35, 1932–1934. [Google Scholar] [CrossRef] [PubMed]
- Morgan, K.S.; Paganin, D.M.; Siu, K.K.W. Quantitative single-exposure X-ray phase contrast imaging using a single attenuation grid. Opt. Express 2011, 19, 19781–19789. [Google Scholar] [CrossRef] [PubMed]
- Rutishauser, S.; Samoylova, L.; Krzywinski, J.; Bunk, O.; Grünert, J.; Sinn, H.; Cammarata, M.; Fritz, D.M.; David, C. Exploring the wavefront of hard X-ray free-electron laser radiation. Nat. Commun. 2012, 3, 947. [Google Scholar] [CrossRef] [PubMed]
- Rand, D.; Ortiz, V.; Liu, Y.; Derdak, Z.; Wands, J.R.; Tatíček, M.; Rose-Petruck, C. Nanomaterials for X-ray Imaging: Gold Nanoparticle Enhancement of X-ray Scatter Imaging of Hepatocellular Carcinoma. Nano Lett. 2011, 11, 2678–2683. [Google Scholar] [CrossRef] [PubMed]
- Vittoria, F.A.; Endrizzi, M.; Diemoz, P.C.; Zamir, A.; Wagner, U.H.; Rau, C.; Robinson, I.K.; Olivo, A. X-ray absorption, phase and dark-field tomography through a beam tracking approach. Sci. Rep. 2015, 5, 16318. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Kashyap, Y.; Sawhney, K. Hard-X-ray Directional Dark-Field Imaging Using the Speckle Scanning Technique. Phys. Rev. Lett. 2015, 114, 103901. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Kashyap, Y.; Sawhney, K. Quantitative X-ray dark-field and phase tomography using single directional speckle scanning technique. Appl. Phys. Lett. 2016, 108, 124102. [Google Scholar] [CrossRef]
- Kagias, M.; Wang, Z.; Villanueva-Perez, P.; Jefimovs, K.; Stampanoni, M. 2D-Omnidirectional Hard-X-ray Scattering Sensitivity in a Single Shot. Phys. Rev. Lett. 2016, 116, 093902. [Google Scholar] [CrossRef] [PubMed]
- Snigirev, A.; Kohn, V.; Snigireva, I.; Lengeler, B. A compound refractive lens for focusing high-energy X-rays. Nature 1996, 384, 49–51. [Google Scholar] [CrossRef]
- Lengeler, B.; Tümmler, J.; Snigirev, A.; Snigireva, I.; Raven, C. Transmission and gain of singly and doubly focusing refractive X-ray lenses. J. Appl. Phys. 1998, 84, 5855–5861. [Google Scholar] [CrossRef]
- Lyubomirskiy, M.; Snigireva, I.; Kohn, V.; Kuznetsov, S.; Yunkin, V.; Vaughan, G.; Snigirev, A. 30-Lens interferometer for high-energy X-rays. J. Synchrotron Rad. 2016, 23, 1104–1109. [Google Scholar] [CrossRef] [PubMed]
- Lynch, S.K.; Pai, V.; Auxier, J.; Stein, A.F.; Bennett, E.E.; Kemble, C.K.; Xiao, X.; Lee, W.K.; Morgan, N.Y.; Wen, H.H. Interpretation of dark-field contrast and particle-size selectivity in grating interferometers. Appl. Opt. 2011, 50, 4310–4319. [Google Scholar] [CrossRef] [PubMed]
- Strobl, M. General solution for quantitative dark-field contrast imaging with grating interferometers. Sci. Rep. 2014, 4, 7243. [Google Scholar] [CrossRef] [PubMed]
- Ibrahimkutty, S.; Wagener, P.; dos Santos Rolo, T.; Karpov, D.; Menzel, A.; Baumbach, T.; Barcikowski, S.; Plech, A. A hierarchical view on material formation during pulsed-laser synthesis of nanoparticles in liquid. Sci. Rep. 2015, 5, 16313. [Google Scholar] [CrossRef] [PubMed]
- Von Freymann, G.; Ledermann, A.; Thiel, M.; Staude, I.; Essig, S.; Busch, K.; Wegener, M. Three-dimensional nanostructures for photonics. Adv. Funct. Mater. 2010, 20, 1038–1052. [Google Scholar] [CrossRef]
- Maruo, S.; Nakamura, O.; Kawata, S. Three-dimensional microfabrication with two-photon-absorbed photopolymerization. Opt. Lett. 1997, 22, 132–134. [Google Scholar] [CrossRef] [PubMed]
- Goodman, J.W. Introduction to Fourier Optics; Roberts and Company: Atlanta, GA, USA, 2005. [Google Scholar]
- Malecki, A.; Potdevin, G.; Pfeiffer, F. Quantitative wave-optical numerical analysis of the dark-field signal in grating-based X-ray interferometry. EPL 2012, 99, 48001. [Google Scholar] [CrossRef]
- Wen, H.; Bennett, E.E.; Hegedus, M.M.; Rapacchi, S. Fourier X-ray Scattering Radiography Yields Bone Structural Information. Radiology 2009, 251, 910–918. [Google Scholar] [CrossRef] [PubMed]
- Koenig, T.; Zuber, M.; Trimborn, B.; Farago, T.; Meyer, P.; Kunka, D.; Albrecht, F.; Kreuer, S.; Volk, T.; Fiederle, M.; et al. On the origin and nature of the grating interferometric dark-field contrast obtained with low-brilliance X-ray sources. Phys. Med. Biol. 2016, 61, 3427–3442. [Google Scholar] [CrossRef] [PubMed]
- Artzner, G.E. Microlens arrays for Shack-Hartmann wavefront sensors. Opt. Eng. 1992, 31, 1311. [Google Scholar] [CrossRef]
- Reich, S.; Plech, A. Shack-Hartman Sensor Wavefront Reconstruction Software; Karlsruhe Institute of Technology (KIT): Karlsruhe, Germany, 2018. [Google Scholar]
- Vittoria, F.A.; Kallon, G.K.N.; Basta, D.; Diemoz, P.C.; Robinson, I.K.; Olivo, A.; Endrizzi, M. Beam tracking approach for single-shot retrieval of absorption, refraction, and dark-field signals with laboratory X-ray sources. Appl. Phys. Lett. 2015, 106, 224102. [Google Scholar] [CrossRef]
- Southwell, W. Wave-front estimation from wave-front slope measurements. J. Opt. Soc. Am. 1980, 70, 998. [Google Scholar] [CrossRef]
- Pathak, B.; Boruah, B.R. Improved wavefront reconstruction algorithm for Shack-Hartmann type wavefront sensors. J. Opt. 2014, 16, 055403. [Google Scholar] [CrossRef]
- Dos Santos Rolo, T.; Ershov, A.; van de Kamp, T.; Baumbach, T. In vivo X-ray cine-tomography for tracking morphological dynamics. Proc. Natl. Acad. Sci. USA 2014, 111, 3921–3926. [Google Scholar] [CrossRef] [PubMed]
- Reich, S.; Schönfeld, P.; Wagener, P.; Letzel, A.; Ibrahimkutty, S.; Gökce, B.; Barcikowski, S.; Menzel, A.; dos Santos Rolo, T.; Plech, A. Pulsed laser ablation in liquids: Impact of the bubble dynamics on particle formation. J. Colloid Interface Sci. 2017, 489, 106–113. [Google Scholar] [CrossRef] [PubMed]
- Reich, S.; Schönfeld, P.; Letzel, A.; Kohsakowski, S.; Olbinado, M.; Gökce, B.; Barcikowski, S.; Plech, A. Fluence Threshold Behaviour on Ablation and Bubble Formation in Pulsed Laser Ablation in Liquids. ChemPhysChem 2017, 18, 1084–1090. [Google Scholar] [CrossRef] [PubMed]
- David, C.; Nöhammer, B.; Solak, H.H.; Ziegler, E. Differential X-ray phase contrast imaging using a shearing interferometer. Appl. Phys. Lett. 2002, 81, 3287–3289. [Google Scholar] [CrossRef]
- Polyakov, S.N.; Zholudev, S.I.; Gasilov, S.V.; Martyushov, S.Y.; Denisov, V.N.; Terentiev, S.A.; Blank, V.D. Resolution of X-ray parabolic compound refractive diamond lens defined at the home laboratory. Proc. SPIE 2017, 10243, 102430X. [Google Scholar] [CrossRef]
- Gasilov, S.; dos Santos Rolo, T.; Mittone, A.; Polyakov, S.; Terentyev, S.; Farago, T.; Blank, V.; Bravin, A.; Baumbach, T. Generalized pupil function of a compound X-ray refractive lens. Opt. Express 2017, 25, 25090–25097. [Google Scholar] [CrossRef] [PubMed]
- Gasilov, S.; Mittone, A.; dos Santos Rolo, T.; Polyakov, S.; Zholudev, S.; Terentyev, S.; Blank, V.; Bravin, A.; Baumbach, T. Refraction and ultra-small-angle scattering of X-rays in a single-crystal diamond compound refractive lens. J. Synchrotron Radiat. 2017, 24, 1137–1145. [Google Scholar] [CrossRef] [PubMed]
- Yashiro, W.; Momose, A. Effects of unresolvable edges in grating-based X-ray differential phase imaging. Opt. Express 2015, 23, 9233. [Google Scholar] [CrossRef] [PubMed]
- Zeng, H.; Du, X.W.; Singh, S.C.; Kulinich, S.A.; Yang, S.; He, J.; Cai, W. Nanomaterials via laser ablation/irradiation in liquid: A review. Adv. Funct. Mater. 2012, 22, 1333–1353. [Google Scholar] [CrossRef]
- Zhang, D.; Gökce, B.; Barcikowski, S. Laser Synthesis and Processing of Colloids: Fundamentals and Applications. Chem. Rev. 2017, 117, 3990–4103. [Google Scholar] [CrossRef] [PubMed]
- Reich, S.; Göttlicher, J.; Letzel, A.; Gökce, B.; Barcikowski, S.; dos Santos Rolo, T.; Baumbach, T.; Plech, A. X-ray spectroscopic and stroboscopic analysis of pulsed-laser ablation of Zn and its oxidation. Appl. Phys. A 2018, 124, 71. [Google Scholar] [CrossRef]
- Ibrahimkutty, S.; Wagener, P.; Menzel, A.; Plech, A.; Barcikowski, S. Nanoparticle formation in a cavitation bubble after pulsed laser ablation in liquid studied with high time resolution small angle X-ray scattering. Appl. Phys. Lett. 2012, 101, 103104. [Google Scholar] [CrossRef]
- Letzel, A.; Gökce, B.; Wagener, P.; Ibrahimkutty, S.; Menzel, A.; Plech, A.; Barcikowski, S. Size Quenching during Laser Synthesis of Colloids Happens Already in the Vapor Phase of the Cavitation Bubble. J. Phys. Chem. C 2017, 121, 5356–5365. [Google Scholar] [CrossRef]
- Kaeppler, S.; Bayer, F.; Weber, T.; Maier, A.; Anton, G.; Hornegger, J.; Beckmann, M.; Fasching, P.A.; Hartmann, A.; Heindl, F.; et al. Signal Decomposition for X-ray Dark-Field Imaging. In MICCAI 2014, Part I; Golland, P., Hata, N., Barillot, C., Hornegger, J., Howe, R., Eds.; Springer International Publishing: Berlin, Germany, 2014; pp. 170–177. [Google Scholar]
- Reich, S.; dos Santos Rolo, T.; Letzel, A.; Baumbach, T.; Plech, A. Scalable, large area compound array refractive lens for hard X-rays. Appl. Phys. Lett. 2018, 112, 151903. [Google Scholar] [CrossRef]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dos Santos Rolo, T.; Reich, S.; Karpov, D.; Gasilov, S.; Kunka, D.; Fohtung, E.; Baumbach, T.; Plech, A. A Shack-Hartmann Sensor for Single-Shot Multi-Contrast Imaging with Hard X-rays. Appl. Sci. 2018, 8, 737. https://doi.org/10.3390/app8050737
Dos Santos Rolo T, Reich S, Karpov D, Gasilov S, Kunka D, Fohtung E, Baumbach T, Plech A. A Shack-Hartmann Sensor for Single-Shot Multi-Contrast Imaging with Hard X-rays. Applied Sciences. 2018; 8(5):737. https://doi.org/10.3390/app8050737
Chicago/Turabian StyleDos Santos Rolo, Tomy, Stefan Reich, Dmitry Karpov, Sergey Gasilov, Danays Kunka, Edwin Fohtung, Tilo Baumbach, and Anton Plech. 2018. "A Shack-Hartmann Sensor for Single-Shot Multi-Contrast Imaging with Hard X-rays" Applied Sciences 8, no. 5: 737. https://doi.org/10.3390/app8050737
APA StyleDos Santos Rolo, T., Reich, S., Karpov, D., Gasilov, S., Kunka, D., Fohtung, E., Baumbach, T., & Plech, A. (2018). A Shack-Hartmann Sensor for Single-Shot Multi-Contrast Imaging with Hard X-rays. Applied Sciences, 8(5), 737. https://doi.org/10.3390/app8050737