Prediction of HIFU Propagation in a Dispersive Medium via Khokhlov–Zabolotskaya–Kuznetsov Model Combined with a Fractional Order Derivative
Abstract
:1. Introduction
2. Theory and Experiments
2.1. The KZK Equation
2.2. The Modified KZK Model
2.3. The Numerical Algorithm
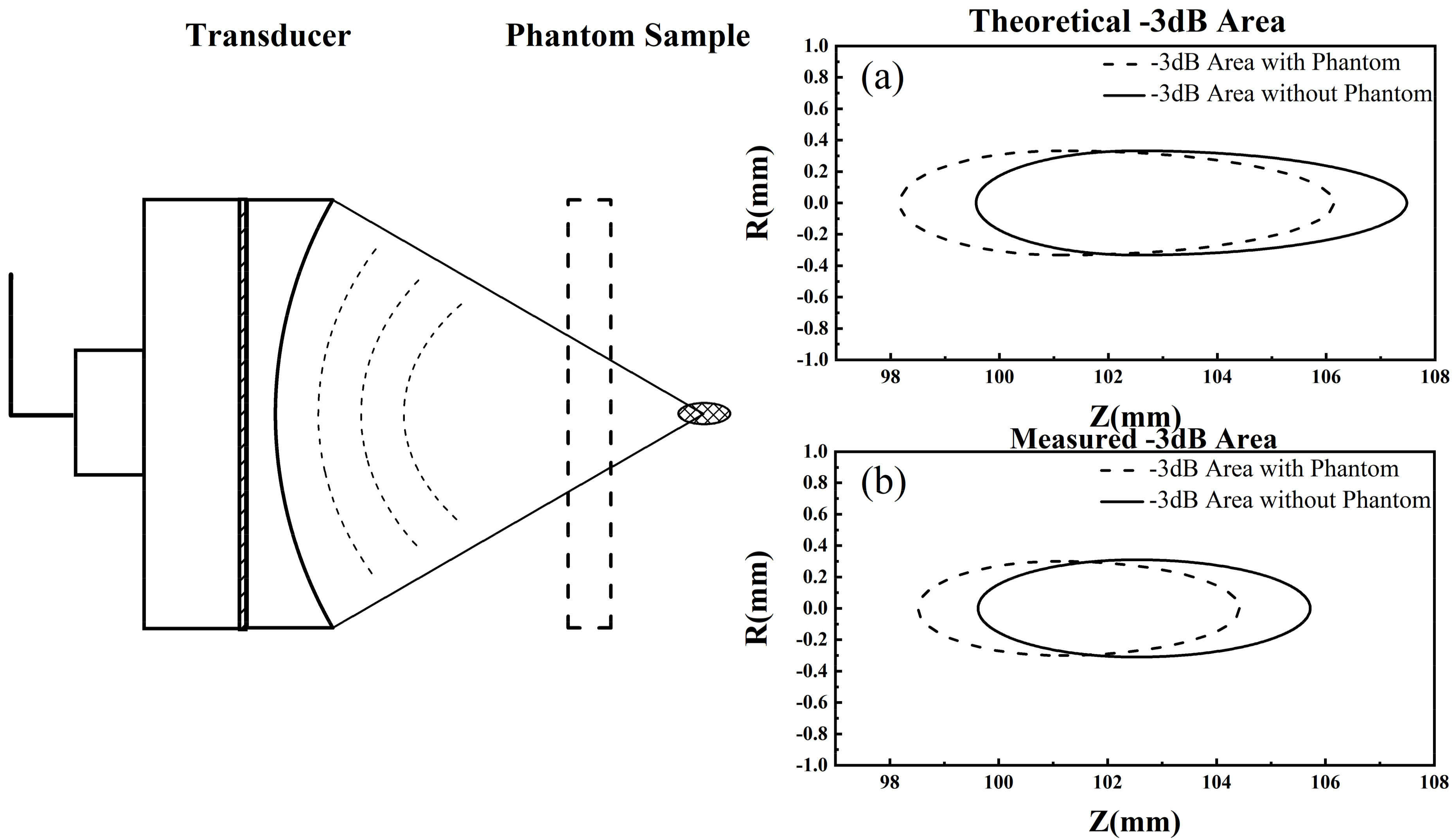
2.4. Experimental Methods
2.4.1. Phantom Preparation
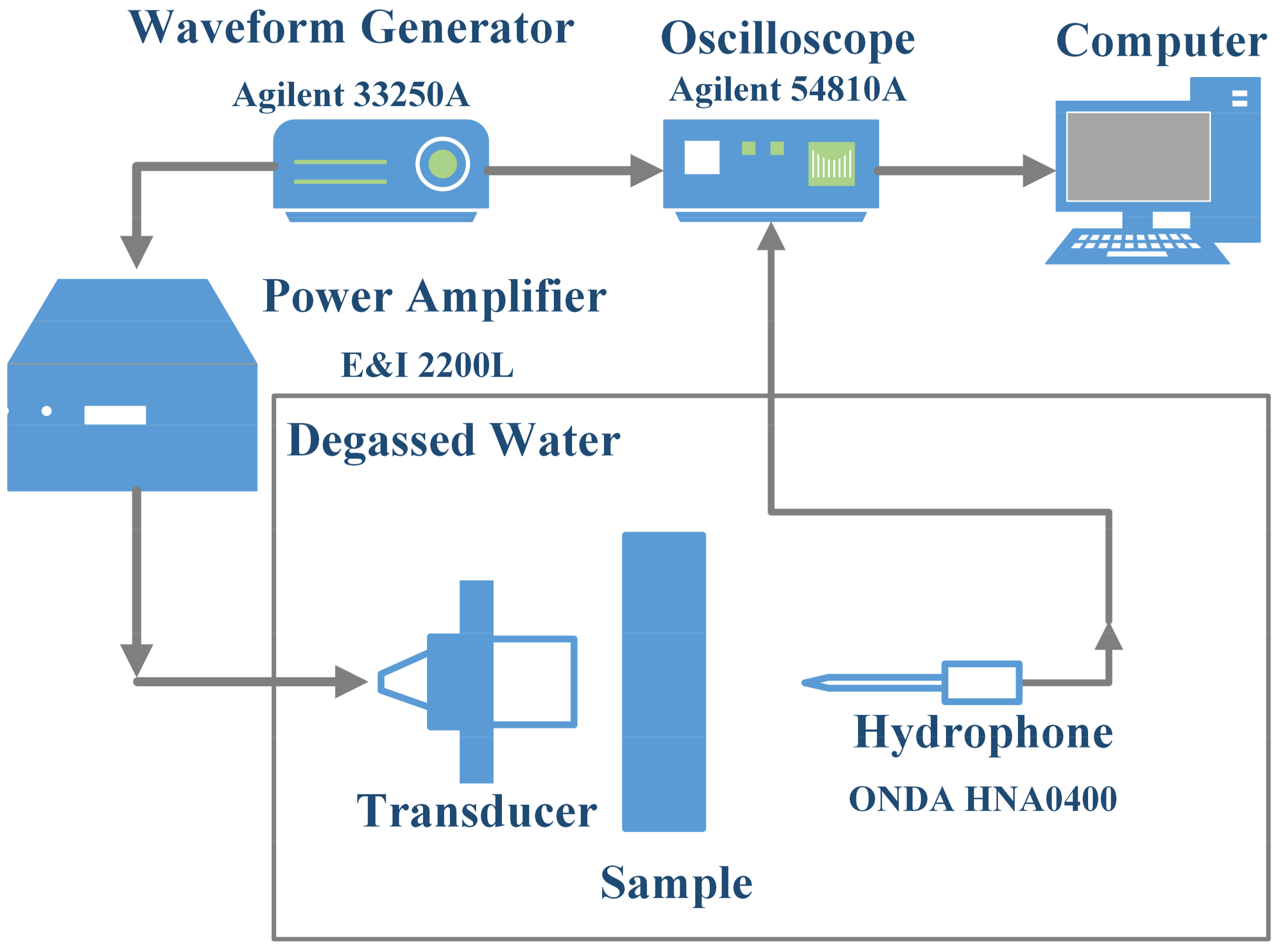
2.4.2. Experimental Setup
3. Results and Discussions
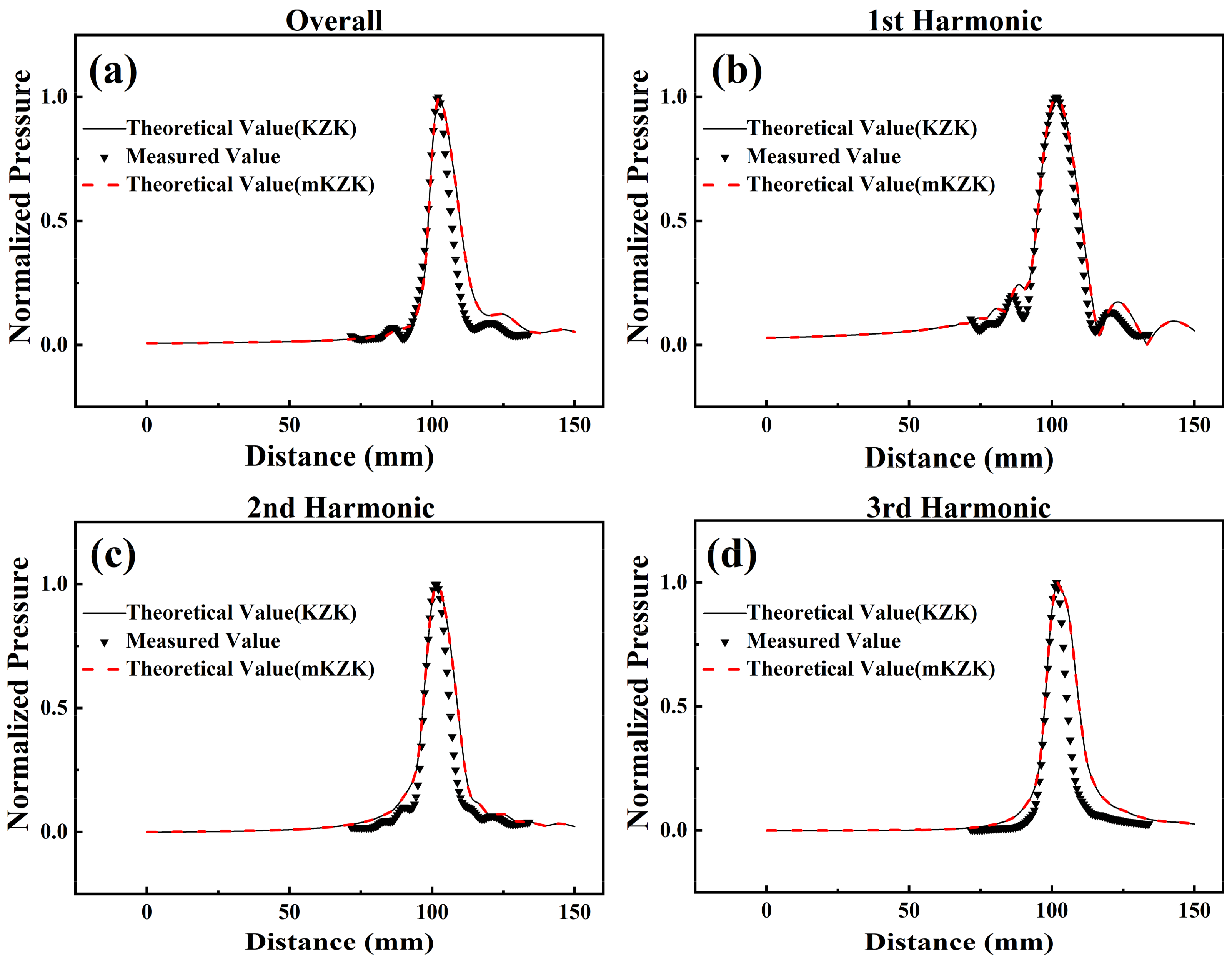
3.1. Non-Dispersive Water
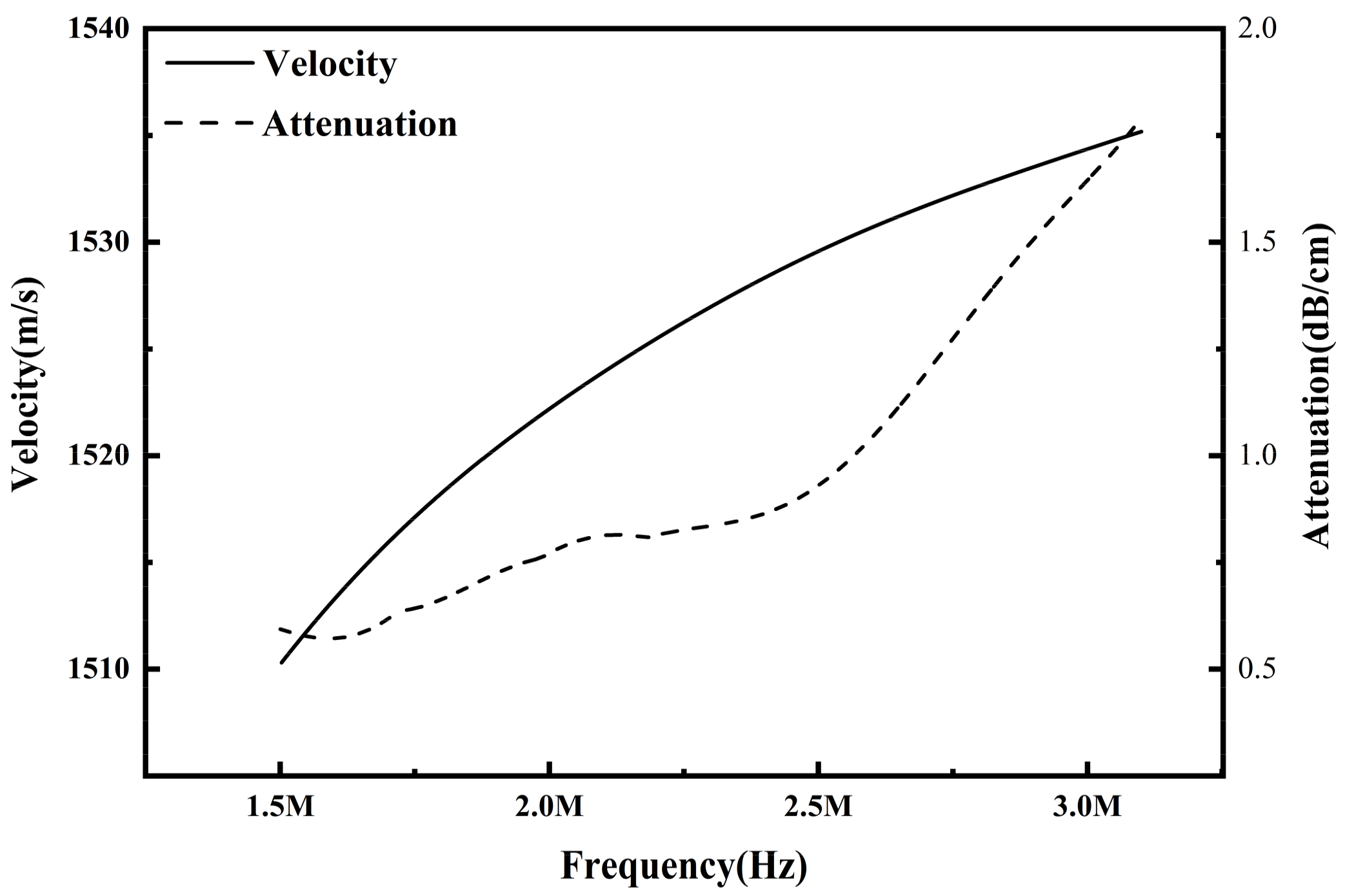
3.2. Dispersive Phantom
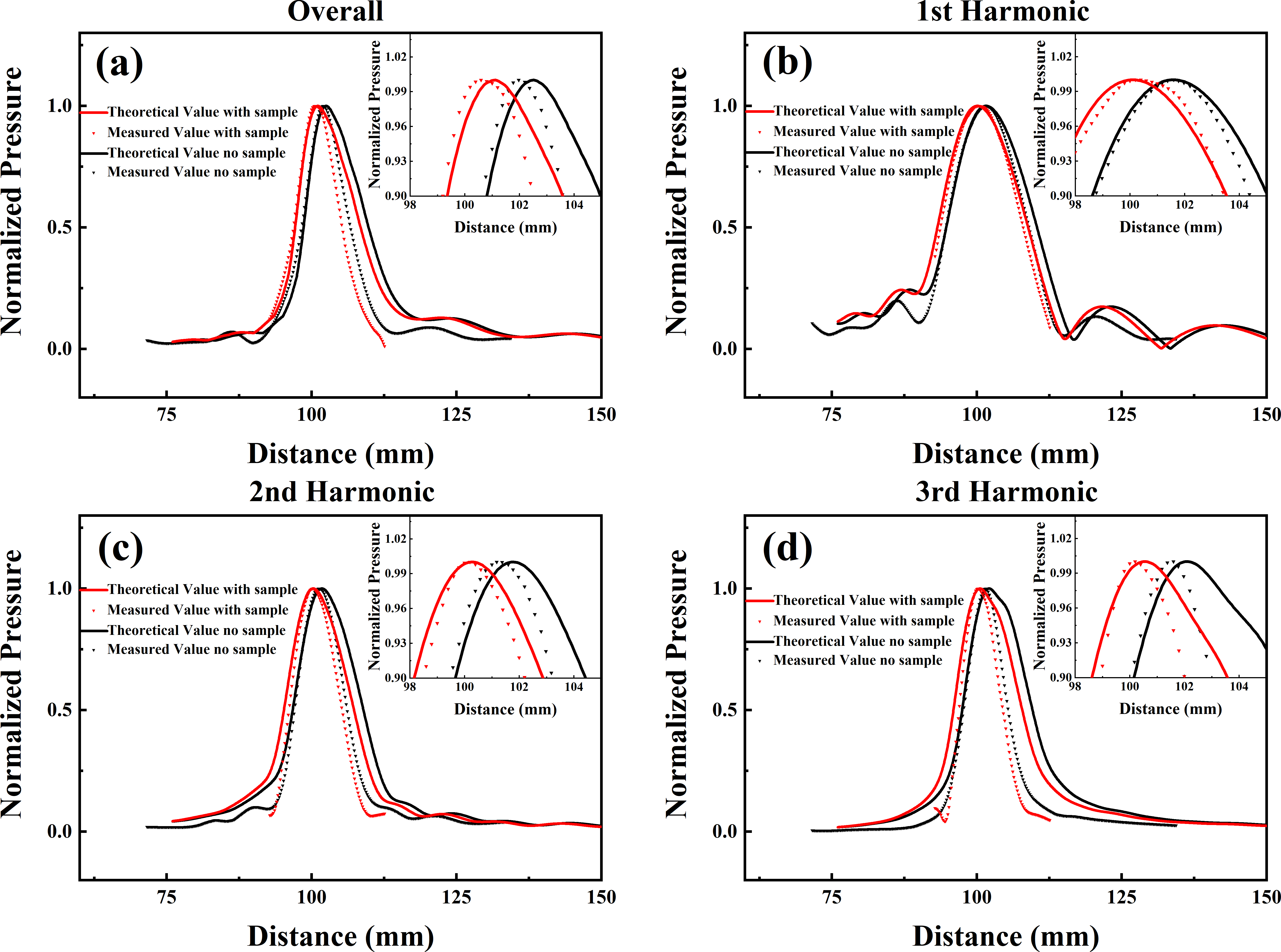
3.3. Dispersion-Induced Focus Shift
3.4. Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lynn, J.G.; Zwemer, R.L.; Chick, A.J.; Miller, A.E. A new method for the generation and use of focused ultrasound in experimental biology. J. Gen. Physiol. 1942, 26, 179. [Google Scholar] [CrossRef] [PubMed]
- Fry, W.J.; Fry, F.; Barnard, J.; Krumins, R.; Brennan, J. Ultrasonic lesions in mammalian central nervous system. Science 1955, 122, 1091. [Google Scholar] [CrossRef]
- Westervelt, P.J. Parametric acoustic array. J. Acoust. Soc. Am. 1963, 35, 535–537. [Google Scholar] [CrossRef]
- Hallaj, I.M.; Cleveland, R.O. FDTD simulation of finite-amplitude pressure and temperature fields for biomedical ultrasound. J. Acoust. Soc. Am. 1999, 105, L7–L12. [Google Scholar] [CrossRef] [PubMed]
- Zabolotskaya, E. Quasi-plane waves in the nonlinear acoustics of confined beams. Sov. Phys. Acoust. 1969, 15, 35–40. [Google Scholar]
- Kuznetsov, V. Equation of nonlinear acoustics. Sov. Phys. Acoust. 1971, 16, 467–470. [Google Scholar]
- Tjotta, J.N.; Tjotta, S.; Vefring, E.H. Effects of focusing on the nonlinear interaction between two collinear finite amplitude sound beams. J. Acoust. Soc. Am. 1991, 89, 1017–1027. [Google Scholar] [CrossRef]
- Kamakura, T.; Ishiwata, T.; Matsuda, K. Model equation for strongly focused finite-amplitude sound beams. J. Acoust. Soc. Am. 2000, 107, 3035–3046. [Google Scholar] [CrossRef] [PubMed]
- Kamakura, T.; Ishiwata, T.; Matsuda, K. A new theoretical approach to the analysis of nonlinear sound beams using the oblate spheroidal coordinate system. J. Acoust. Soc. Am. 1999, 105, 3083–3086. [Google Scholar] [CrossRef]
- ter Haar, G. Biological effects of ultrasound in clinical applications. In Ultrasound: Its Chemical, Physical and Biological Effects; VCH Publishers: New York, NY, USA, 1988. [Google Scholar]
- ter Haar, G. Turning up the power: High intensity focused ultrasound (HIFU) for the treatment of cancer. Ultrasound 2007, 15, 73–77. [Google Scholar] [CrossRef]
- Wu, F.; Chen, W.-Z.; Bai, J.; Zou, J.-Z.; Wang, Z.-L.; Zhu, H.; Wang, Z.-B. Pathological changes in human malignant carcinoma treated with high-intensity focused ultrasound. Ultrasound Med. Biol. 2001, 27, 1099–1106. [Google Scholar] [CrossRef]
- Gelet, A.; Chapelon, J.; Bouvier, R.; Rouviere, O.; Lasne, Y.; Lyonnet, D.; Dubernard, J. Transrectal high-intensity focused ultrasound: Minimally invasive therapy of localized prostate cancer. J. Endourol. 2000, 14, 519–528. [Google Scholar] [CrossRef] [PubMed]
- Orsi, F.; Arnone, P.; Chen, W.; Zhang, L. High intensity focused ultrasound ablation: A new therapeutic option for solid tumors. J. Cancer Res. Ther. 2010, 6, 414. [Google Scholar] [CrossRef] [PubMed]
- Illing, R.; Kennedy, J.; Wu, F.; ter Haar, G.; Protheroe, A.; Friend, P.; Gleeson, F.; Cranston, D.; Phillips, R.; Middleton, M. The safety and feasibility of extracorporeal High-Intensity Focused Ultrasound (HIFU) for the treatment of liver and kidney tumours in a Western population. Br. J. Cancer 2005, 93, 890. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.-F. High intensity focused ultrasound in clinical tumor ablation. World J. Clin. Oncol. 2011, 2, 8. [Google Scholar] [CrossRef] [PubMed]
- Gudur, M.S.R.; Kumon, R.E.; Zhou, Y.; Deng, C.X. High-frequency rapid B-mode ultrasound imaging for real-time monitoring of lesion formation and gas body activity during high-intensity focused ultrasound ablation. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2012, 59, 1687–1699. [Google Scholar] [CrossRef] [PubMed]
- Kemmerer, J.; Ghoshal, G.; Oelze, M. Quantitative ultrasound assessment of HIFU induced lesions in rodent liver. In Proceedings of the 2010 IEEE International Ultrasonics Symposium, San Diego, CA, USA, 11–14 October 2010; pp. 1396–1399. [Google Scholar]
- Wijlemans, J.; Bartels, L.; Deckers, R.; Ries, M.; Mali, W.T.M.; Moonen, C.; Van Den Bosch, M. Magnetic resonance-guided high-intensity focused ultrasound (MR-HIFU) ablation of liver tumours. Cancer Imaging 2012, 12, 387. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Chen, W.; Liu, Y.; Hu, X.; Zhou, K.; Chen, L.; Peng, S.; Zhu, H.; Zou, H.; Bai, J. Feasibility of magnetic resonance imaging-guided high intensity focused ultrasound therapy for ablating uterine fibroids in patients with bowel lies anterior to uterus. Eur. J. Radiol. 2010, 73, 396–403. [Google Scholar] [CrossRef] [PubMed]
- Petrusca, L.; Viallon, M.; Breguet, R.; Terraz, S.; Manasseh, G.; Auboiroux, V.; Goget, T.; Baboi, L.; Gross, P.; Sekins, K.M. An experimental model to investigate the targeting accuracy of MR-guided focused ultrasound ablation in liver. J. Transl. Med. 2014, 12, 12. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Shen, G.; Bai, J.; Chen, Y. Focus shift and phase correction in soft tissues during focused ultrasound surgery. IEEE Trans. Biomed. Eng. 2011, 58, 1621–1628. [Google Scholar] [CrossRef] [PubMed]
- Connor, C.W.; Hynynen, K. Bio-acoustic thermal lensing and nonlinear propagation in focused ultrasound surgery using large focal spots: A parametric study. Phys. Med. Biol. 2002, 47, 1911. [Google Scholar] [CrossRef] [PubMed]
- Meaney, P.M.; Cahill, M.D.; ter Haar, G. The intensity dependence of lesion position shift during focused ultrasound surgery. Ultrasound Med. Biol. 2000, 26, 441–450. [Google Scholar] [CrossRef]
- Zderic, V.; Foley, J.; Luo, W.; Vaezy, S. Prevention of post-focal thermal damage by formation of bubbles at the focus during high intensity focused ultrasound therapy. Med. Phys. 2008, 35, 4292–4299. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Wilson Gao, X. Variations of bubble cavitation and temperature elevation during lesion formation by high-intensity focused ultrasound. J. Acoust. Soc. Am. 2013, 134, 1683–1694. [Google Scholar] [CrossRef] [PubMed]
- Laughner, J.I.; Sulkin, M.S.; Wu, Z.; Deng, C.X.; Efimov, I.R. Three potential mechanisms for failure of high intensity focused ultrasound ablation in cardiac tissue. Circulation 2012, 5, 409–416. [Google Scholar] [CrossRef] [PubMed]
- Bobkova, S.; Gavrilov, L.; Khokhlova, V.; Shaw, A.; Hand, J. Focusing of high-intensity ultrasound through the rib cage using a therapeutic random phased array. Ultrasound Med. Biol. 2010, 36, 888–906. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Fan, T.; Zhang, D.; Gong, X. Influence of the abdominal wall on the nonlinear propagation of focused therapeutic ultrasound. Chin. Phys. B 2009, 18, 4932–4937. [Google Scholar]
- Rosnitskiy, P.B.; Yuldashev, P.V.; Sapozhnikov, O.A.; Maxwell, A.D.; Kreider, W.; Bailey, M.R.; Khokhlova, V.A. Design of HIFU Transducers for Generating Specified Nonlinear Ultrasound Fields. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2017, 64, 374–390. [Google Scholar] [CrossRef] [PubMed]
- Soneson, J.E. A parametric study of error in the parabolic approximation of focused axisymmetric ultrasound beams. J. Acoust. Soc. Am. 2012, 131, EL481–EL486. [Google Scholar] [CrossRef] [PubMed]
- O’Donnell, M.; Jaynes, E.; Miller, J. Kramers-Kronig relationship between ultrasonic attenuation and phase velocity. J. Acoust. Soc. Am. 1981, 69, 696–701. [Google Scholar] [CrossRef]
- Kudo, N.; Kamataki, T.; Yamamoto, K.; Onozuka, H.; Mikami, T.; Kitabatake, A.; Ito, Y.; Kanda, H. Ultrasound attenuation measurement of tissue in frequency range 2.5–40 MHz using a multi-resonance transducer. In Proceedings of the Ultrasonics Symposium, Toronto, ON, Canada, 5–8 October 1997; pp. 1181–1184. [Google Scholar]
- Wojcik, G.; Mould, J.; Abboud, N.; Ostromogilsky, M.; Vaughan, D. Nonlinear modeling of therapeutic ultrasound. In Proceedings of the Ultrasonics Symposium, Seattle, WA, USA, 7–10 November 1995; pp. 1617–1622. [Google Scholar]
- Makris, N.; Constantinou, M. Fractional-derivative Maxwell model for viscous dampers. J. Struct. Eng. 1991, 117, 2708–2724. [Google Scholar] [CrossRef]
- Szabo, T.L. Time domain wave equations for lossy media obeying a frequency power law. J. Acoust. Soc. Am. 1994, 96, 491–500. [Google Scholar] [CrossRef]
- Szabo, T.L. Causal theories and data for acoustic attenuation obeying a frequency power law. J. Acoust. Soc. Am. 1995, 97, 14–24. [Google Scholar] [CrossRef]
- Szabo, T.L.; Wu, J. A model for longitudinal and shear wave propagation in viscoelastic media. J. Acoust. Soc. Am. 2000, 107, 2437–2446. [Google Scholar] [CrossRef] [PubMed]
- Treeby, B.E.; Jaros, J.; Rendell, A.P.; Cox, B.T. Modeling nonlinear ultrasound propagation in heterogeneous media with power law absorption using a k-space pseudospectral method. J. Acoust. Soc. Am. 2012, 131, 4324–4336. [Google Scholar] [CrossRef] [PubMed]
- Prieur, F.; Holm, S. Nonlinear acoustic wave equations with fractional loss operators. J. Acoust. Soc. Am. 2011, 130, 1125–1132. [Google Scholar] [CrossRef] [PubMed]
- Rosnitskiy, P.B.; Yuldashev, P.V.; Vysokanov, B.A.; Khokhlova, V.A. Setting boundary conditions on the Khokhlov-Zabolotskaya equation for modeling ultrasound fields generated by strongly focused transducers. Acoust. Phys. 2016, 62, 151–159. [Google Scholar] [CrossRef]
- Heymans, N.; Podlubny, I. Physical interpretation of initial conditions for fractional differential equations with Riemann-Liouville fractional derivatives. Rheol. Acta 2006, 45, 765–771. [Google Scholar] [CrossRef]
- Zhao, X.; McGough, R.J. The Khokhlov-Zabolotskaya-Kuznetsov (KZK) equation with power law attenuation. In Proceedings of the IEEE International Ultrasonics Symposium, Chicago, IL, USA, 3–6 September 2014; pp. 2225–2228. [Google Scholar]
- Kelly, J.F.; McGough, R.J.; Meerschaert, M.M. Analytical time-domain Green’s functions for power-law media. J. Acoust. Soc. Am. 2008, 124, 2861–2872. [Google Scholar] [CrossRef] [PubMed]
- Fan, T.; Liu, Z.; Zhang, D.; Tang, M. Comparative study of lesions created by high-intensity focused ultrasound using sequential discrete and continuous scanning strategies. IEEE Trans. Biomed. Eng. 2013, 60, 763–769. [Google Scholar] [CrossRef] [PubMed]
- Fan, T.; Zhang, D.; Gong, X. Estimation of the tissue lesion induced by a transmitter with aluminium lens. J. Phys. 2011, 279, 012020. [Google Scholar] [CrossRef]
- Lafon, C.; Zderic, V.; Noble, M.L.; Yuen, J.C.; Kaczkowski, P.J.; Sapozhnikov, O.A.; Chavrier, F.; Crum, L.A.; Vaezy, S. Gel phantom for use in high-intensity focused ultrasound dosimetry. Ultrasound Med. Biol. 2005, 31, 1383–1389. [Google Scholar] [CrossRef] [PubMed]
- He, P. Measurement of acoustic dispersion using both transmitted and reflected pulses. J. Acoust. Soc. Am. 2000, 107, 801–807. [Google Scholar] [CrossRef] [PubMed]
- He, P.; Zheng, J. Acoustic dispersion and attenuation measurement using both transmitted and reflected pulses. Ultrasonics 2001, 39, 27–32. [Google Scholar] [CrossRef]
- Fan, T.; Zhang, D.; Zhang, Z.; Ma, Y.; Gong, X. Effects of vapour bubbles on acoustic and temperature distributions of therapeutic ultrasound. Chin. Phys. B 2008, 17, 3372–3377. [Google Scholar] [CrossRef]
- Camarena, F.; Adrián-Martínez, S.; Jiménez, N.; Sánchez-Morcillo, V. Nonlinear focal shift beyond the geometrical focus in moderately focused acoustic beams. J. Acoust. Soc. Am. 2013, 134, 1463–1472. [Google Scholar] [CrossRef] [PubMed]

| Method | Overall | Fundamental | 2nd Harmonic | 3rd Harmonic |
|---|---|---|---|---|
| mKZK | 1.47 | 1.41 | 1.51 | 1.62 |
| Experiment | 1.42 ± 0.04 | 1.40 ± 0.03 | 1.45 ± 0.04 | 1.51 ± 0.04 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Yang, Y.; Li, C.; Guo, X.; Tu, J.; Zhang, D. Prediction of HIFU Propagation in a Dispersive Medium via Khokhlov–Zabolotskaya–Kuznetsov Model Combined with a Fractional Order Derivative. Appl. Sci. 2018, 8, 609. https://doi.org/10.3390/app8040609
Liu S, Yang Y, Li C, Guo X, Tu J, Zhang D. Prediction of HIFU Propagation in a Dispersive Medium via Khokhlov–Zabolotskaya–Kuznetsov Model Combined with a Fractional Order Derivative. Applied Sciences. 2018; 8(4):609. https://doi.org/10.3390/app8040609
Chicago/Turabian StyleLiu, Shilei, Yanye Yang, Chenghai Li, Xiasheng Guo, Juan Tu, and Dong Zhang. 2018. "Prediction of HIFU Propagation in a Dispersive Medium via Khokhlov–Zabolotskaya–Kuznetsov Model Combined with a Fractional Order Derivative" Applied Sciences 8, no. 4: 609. https://doi.org/10.3390/app8040609
APA StyleLiu, S., Yang, Y., Li, C., Guo, X., Tu, J., & Zhang, D. (2018). Prediction of HIFU Propagation in a Dispersive Medium via Khokhlov–Zabolotskaya–Kuznetsov Model Combined with a Fractional Order Derivative. Applied Sciences, 8(4), 609. https://doi.org/10.3390/app8040609





