Fault Studies and Distance Protection of Transmission Lines Connected to DFIG-Based Wind Farms
Abstract
:Featured Application
Abstract
1. Introduction
2. Fault Analysis of DFIG-Based Wind Farm and Its Verification
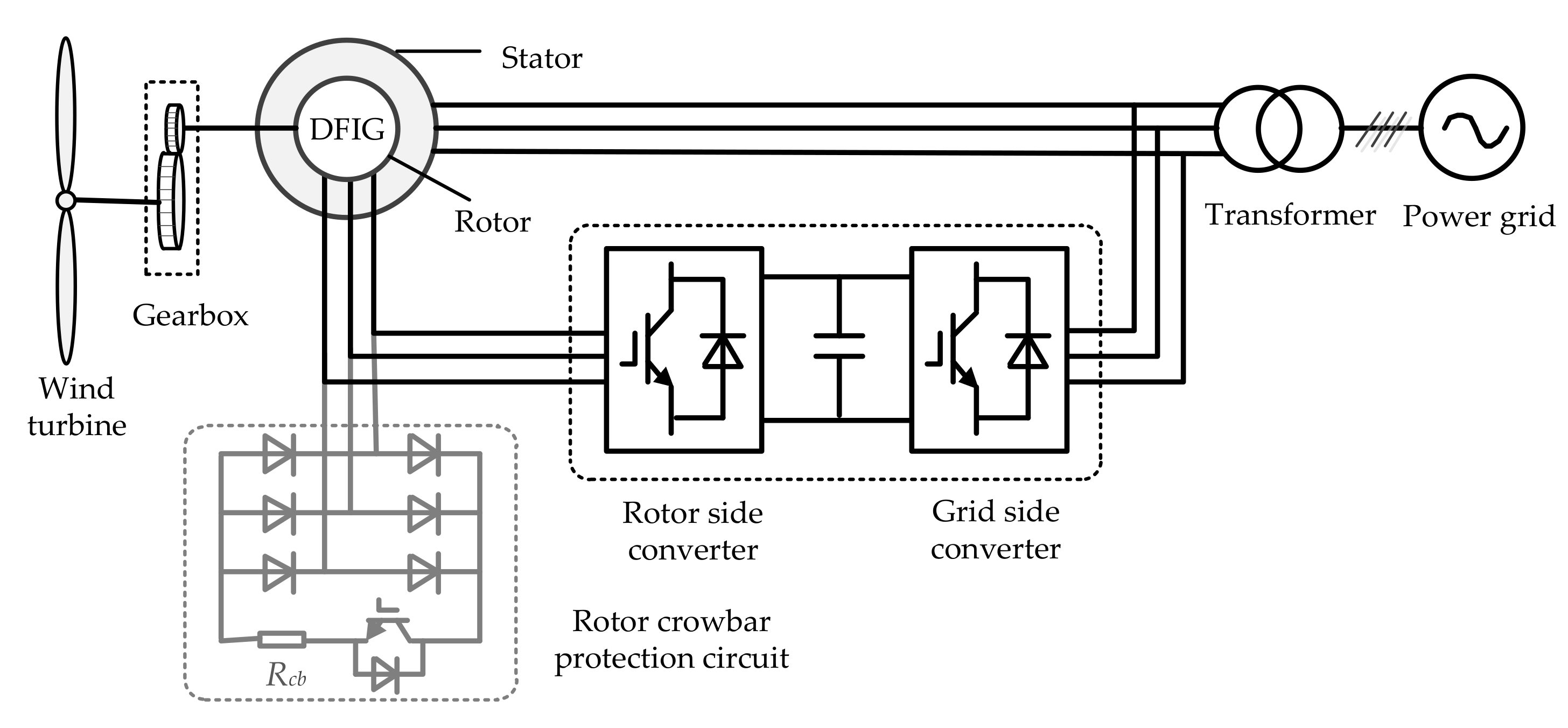
2.1. DFIG Short Circuit Current
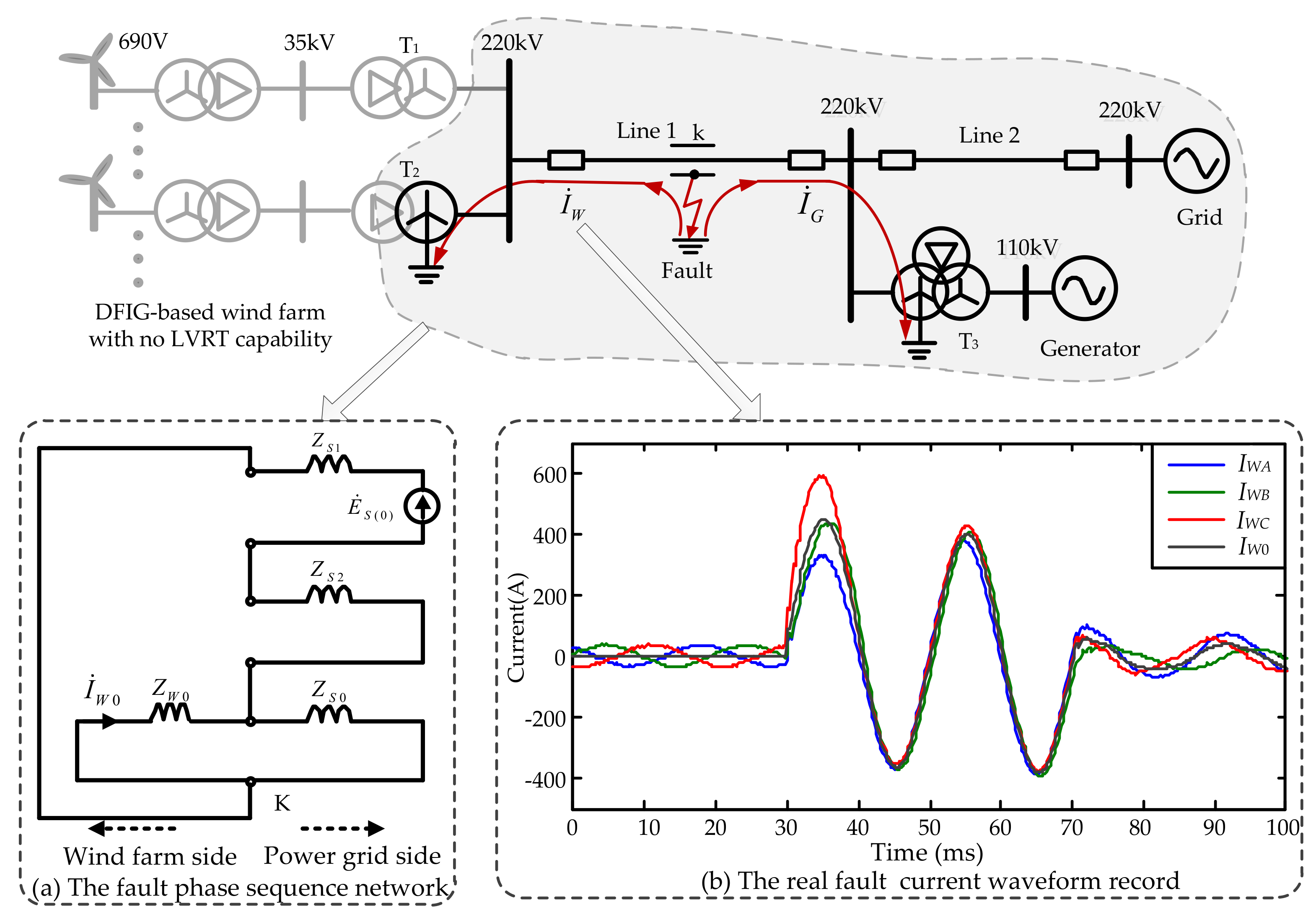
2.2. Fault Analysis of the DFIG-Based Wind Farm without LVRT Capability
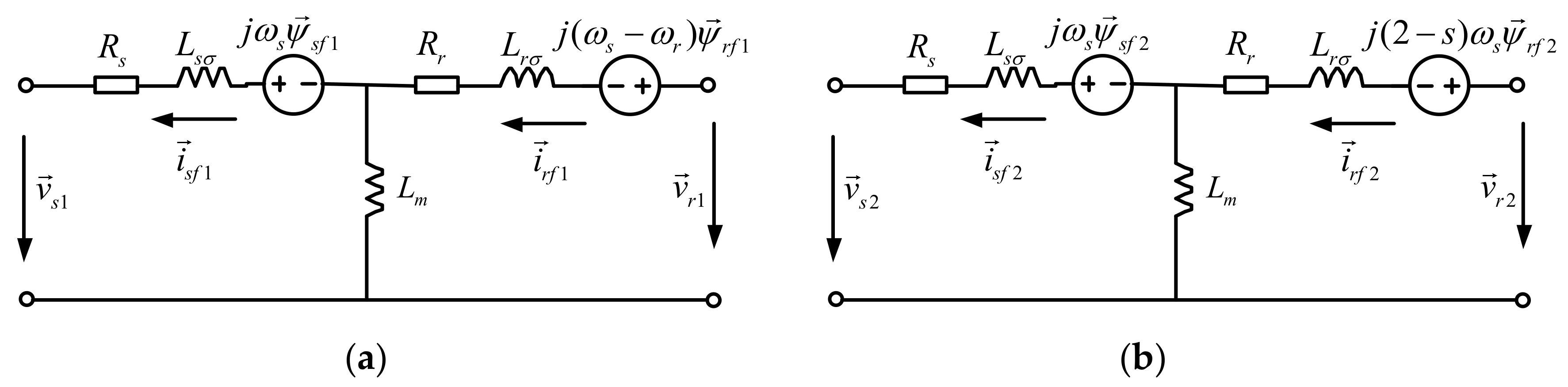
2.3. Fault Analysis of the DFIG-Based Wind Farm with LVRT Capability
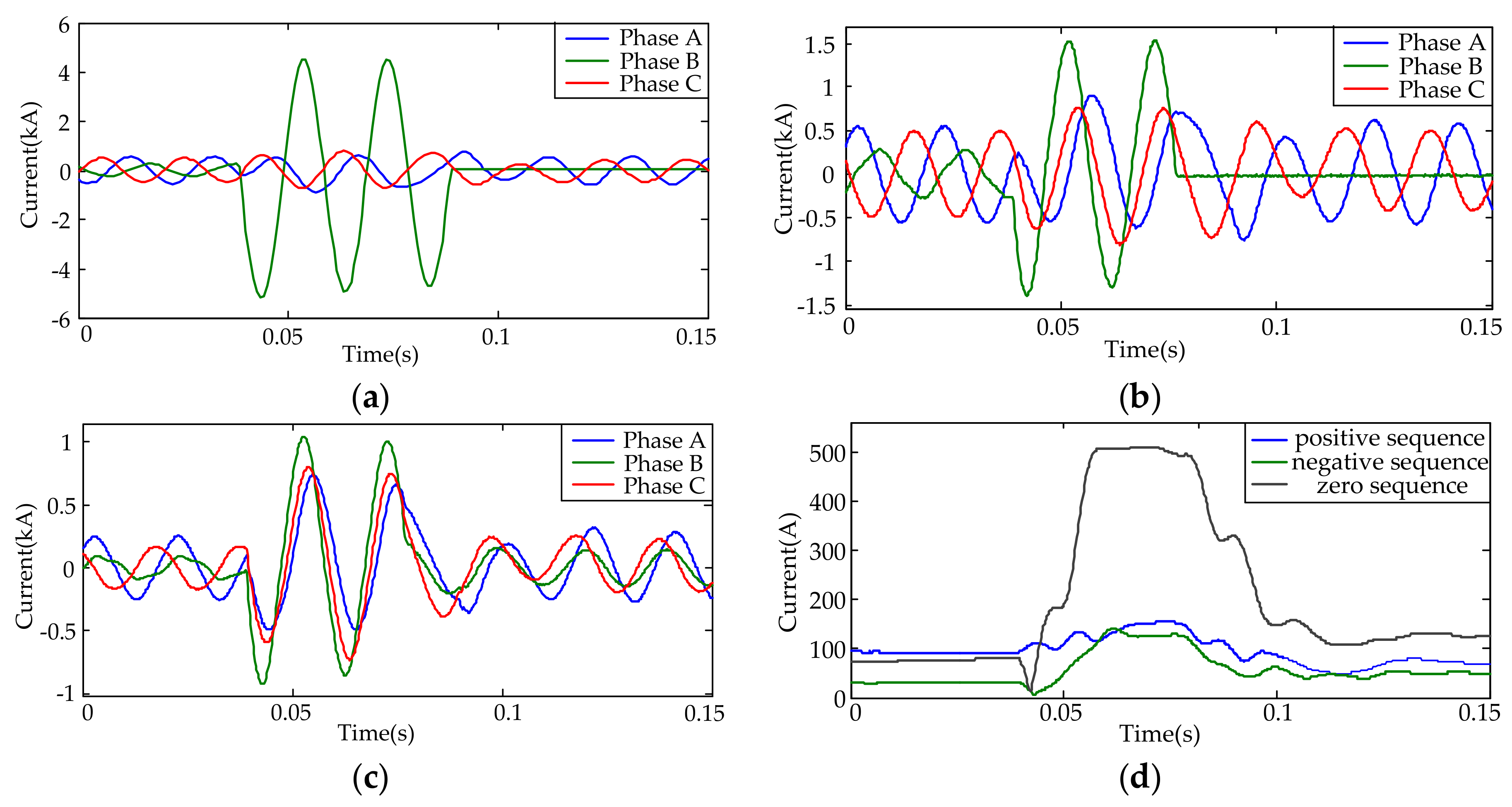
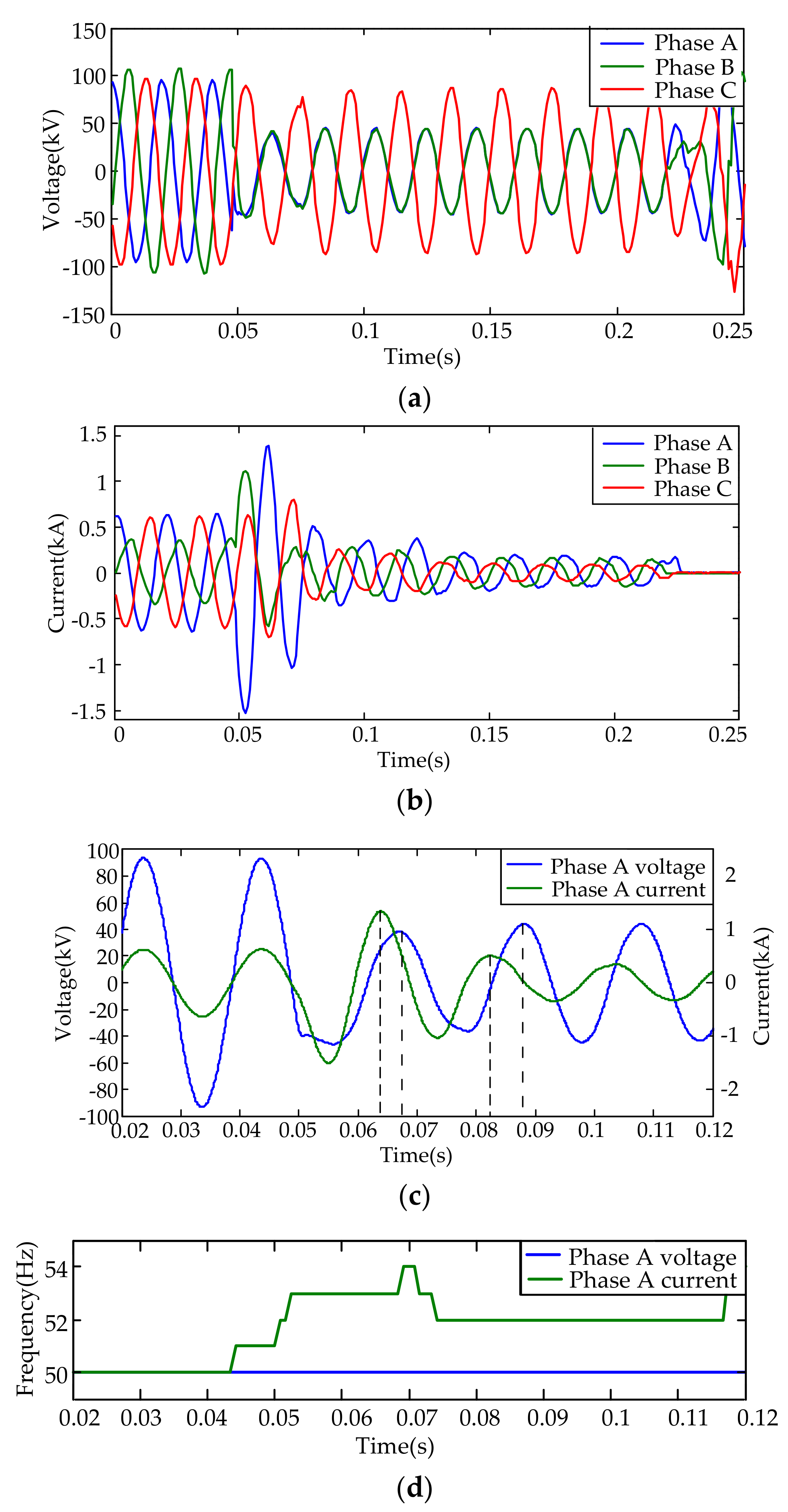
2.3.1. The Single-Phase Ground Fault Case
2.3.2. The Phase-to-Phase Short Circuit Fault Case
3. Distance Protection and Its Improvement Method for the Transmission Line Connected to DFIG-Based Wind Farms
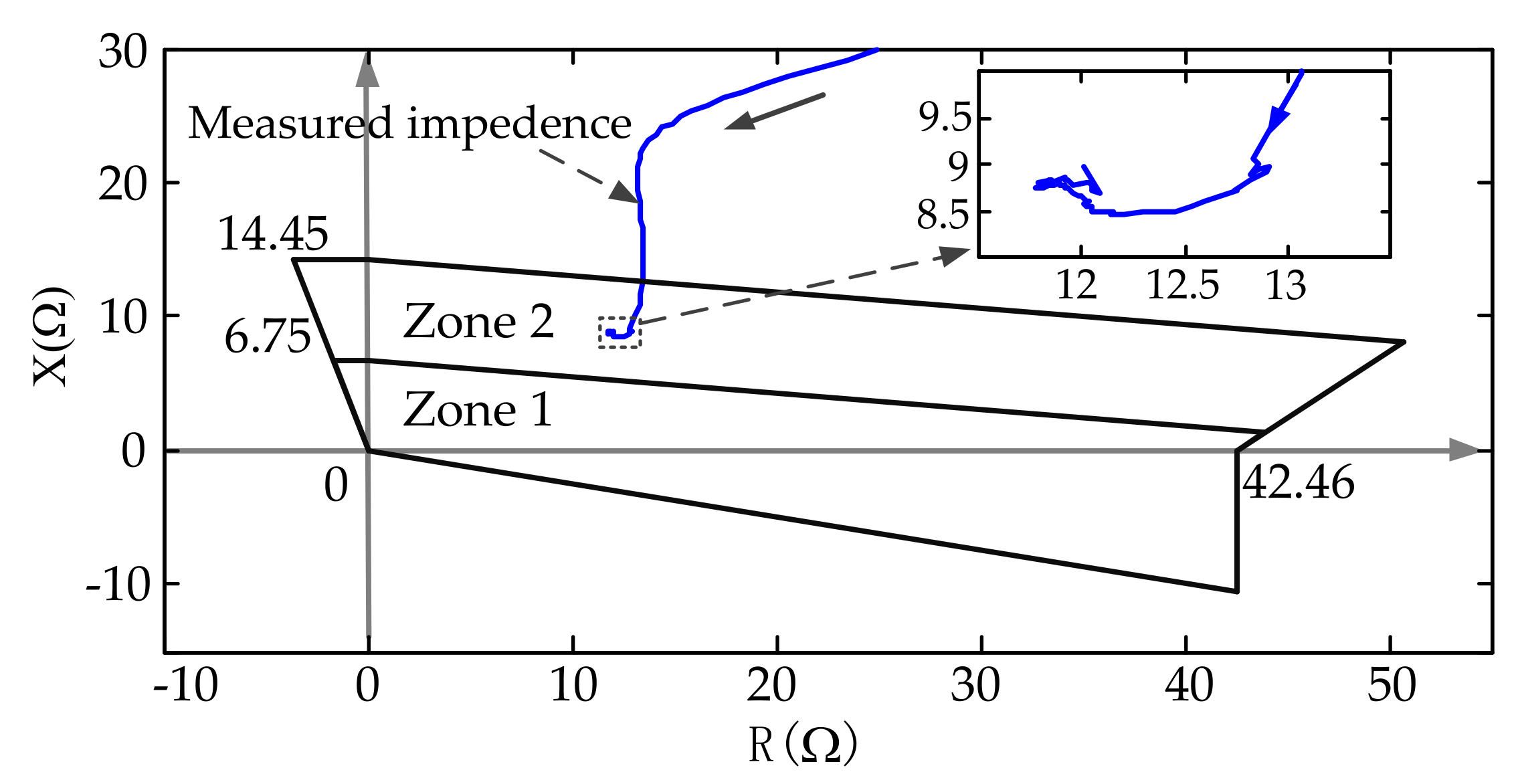
3.1. Application of Conventional Distance Protection
3.1.1. Phase-to-Ground Fault
3.1.2. Phase-to-Phase Fault
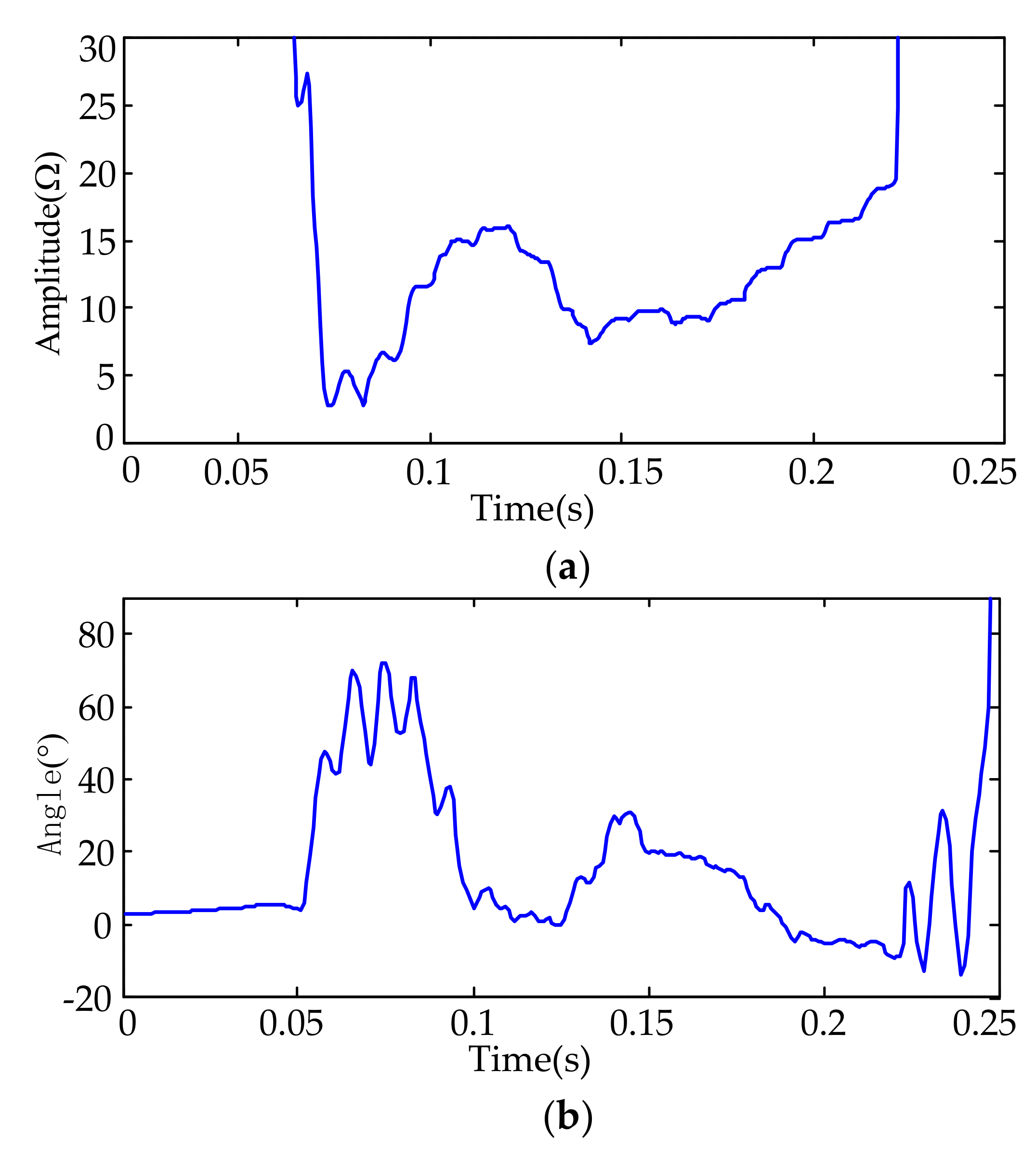
3.2. Time-Domain Distance Protection Based on the R-L Model
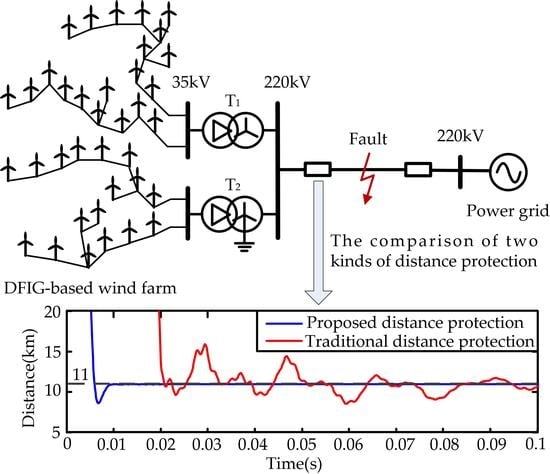
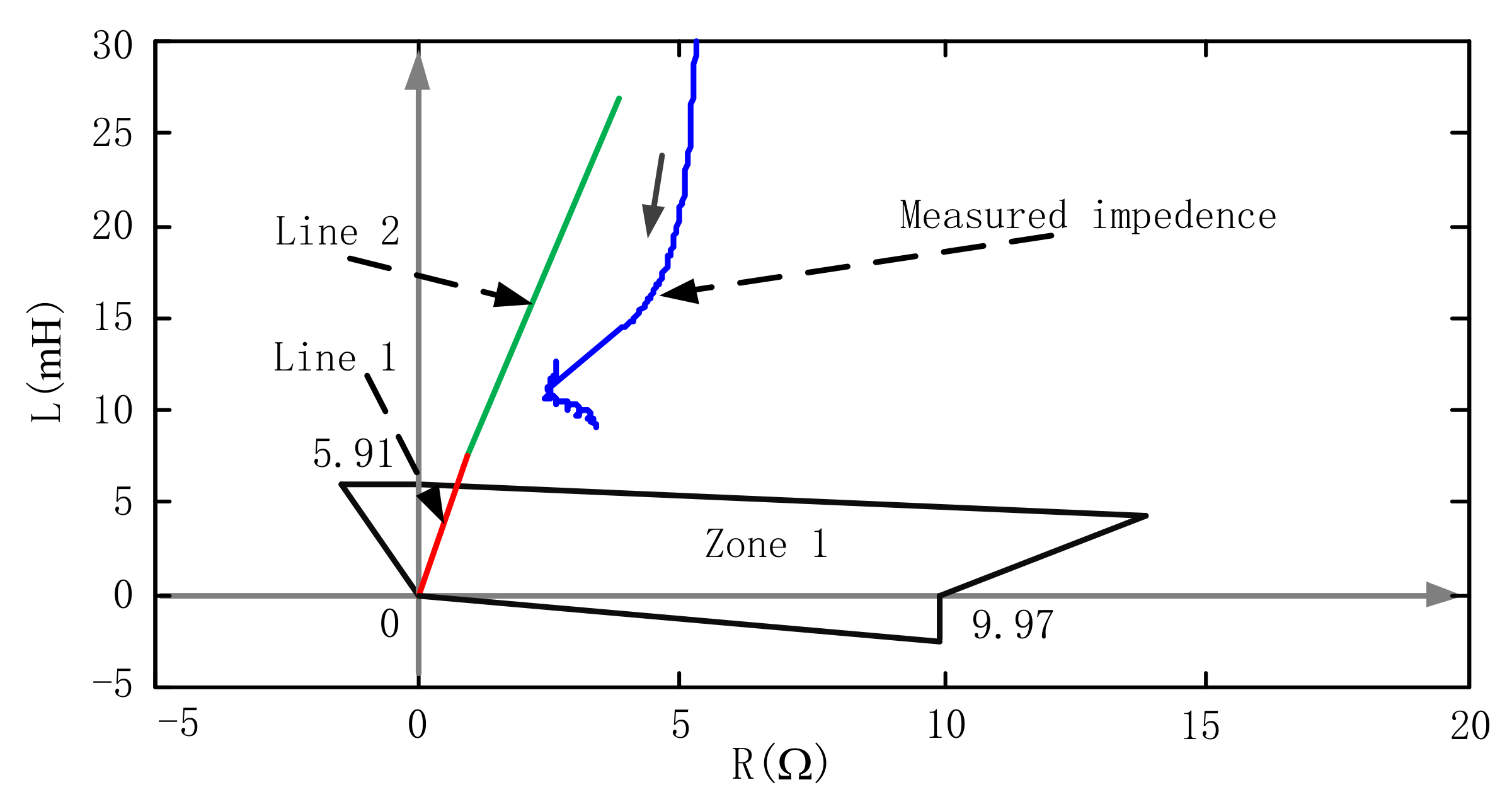
3.3. Case Studies
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
Appendix A.1. The Derivation of Pre-Fault Rotor Flux Linkage
Appendix A.2. The Derivation of Post-Fault Rotor Flux Linkage
Appendix B
| Parameter Name | Line 1 | Line 2 |
|---|---|---|
| Length (km) | 22.018 | 70.202 |
| Z1 (Ω/km) | 0.080 + j0.430 | 0.048 + j0.320 |
| Z0 (Ω/km) | 0.360 + j1.000 | 0.317 + j1.000 |
| Parameter Name | Line 1 | Line 2 |
|---|---|---|
| Length (km) | 5.325 | 16.168 |
| Z1 (Ω/km) | 0.113 + j0.419 | 0.154 + j0.407 |
| Z0 (Ω/km) | 0.871 + j1.085 | 0.593 + j1.216 |
| Parameter Name | Value | Parameter Name | Value (p.u.) |
|---|---|---|---|
| Nominal capacity | Stator resistance | ||
| Rated stator voltage | Stator leakage inductance | ||
| System frequency | Rotor resistance | ||
| Rated voltage of DC-link | Rotor leakage inductance | ||
| Pairs of poles | Mutual inductance | ||
| Nominal wind speed | Crowbar resistance |
References
- Hossain, M.M.; Ali, M.H. Future research directions for the wind turbine generator system. Renew. Sustain. Energy Rev. 2015, 49, 481–489. [Google Scholar] [CrossRef]
- Li, H.; Chen, Z. Overview of different wind generator systems and their comparisons. IET Renew. Power Gener. 2008, 2, 123–138. [Google Scholar] [CrossRef]
- Muller, S.; Deicke, M.; De Doncker, R.W. Doubly fed induction generator systems for wind turbines. IEEE Trans. Ind. Appl. Mag. 2002, 8, 26–33. [Google Scholar] [CrossRef]
- Hughes, F.M.; Anaya-Lara, O.; Jenkins, N.; Strbac, G. Control of DFIG based wind generation for power network support. IEEE Trans. Power Syst. 2005, 20, 1958–1966. [Google Scholar] [CrossRef]
- Iwanski, G.; Koczara, W. DFIG-based power generation system with UPS function for variable-speed applications. IEEE Trans. Ind. Electron. 2008, 55, 3047–3054. [Google Scholar] [CrossRef]
- Marques, G.D.; Sousa, D.M. Understanding the doubly fed induction generator during voltage dips. IEEE Trans. Energy Convers. 2012, 27, 421–461. [Google Scholar] [CrossRef]
- Ling, Y.; Cai, X.; Wang, N. Rotor current transient analysis of DFIG-based wind turbines during symmetrical voltage faults. Energy Convers Manag. 2013, 76, 910–917. [Google Scholar] [CrossRef]
- The Grid Code 3. Available online: http//www.nationalgrid.com/uk/Electricity/Codes/gridcode (accessed on 1 January 2006).
- Transmission Code 2007—Network and System Rules of the German Transmission System Operators. Available online: https://www.bdew.de/ (accessed on 1 August 2007).
- Inspection and Quarantine of China. Technical Rule for Connecting Wind Farm to Power System; Technical Report for Inspection and Quarantine of China; Inspection and Quarantine of China: Beijing, China, 2011.
- Rahim, A.H.M.A.; Nowicki, E.P. Supercapacitor energy storage system for fault ride through of a DFIG wind generation system. Energy Convers. Manag. 2012, 59, 96–102. [Google Scholar] [CrossRef]
- Cardenas, R.; Pena, R.; Alepuz, S.; Asher, G. Overview of control systems for the operation of DFIGs in wind energy applications. IEEE Trans. Ind. Electron. 2013, 60, 2776–2798. [Google Scholar] [CrossRef]
- Akhmatov, V. Induction Generators for Wind Power; Multi-Science Publishing Company Ltd.: Brentwood, UK, 2005. [Google Scholar]
- Morren, J.; de Haan, S.W.H. Ride through of wind turbines with doubly-fed induction generator during a voltage dip. IEEE Trans. Energy Convers. 2005, 20, 435–441. [Google Scholar] [CrossRef]
- Lopez, J.; Sanchis, P.; Roboam, X.; Marroyo, L. Dynamic behavior of the doubly-fed induction generator during three-phase voltage dips. IEEE Trans. Energy Convers. 2007, 22, 709–717. [Google Scholar] [CrossRef]
- Pannell, G.; Atkinson, D.J.; Zahawi, B. Analytical study of grid-fault response of wind turbine doubly fed induction generator. IEEE Trans. Energy Convers. 2010, 25, 1081–1091. [Google Scholar] [CrossRef]
- Sulla, F.; Svensson, J.; Samuelsson, O. Symmetrical and unsymmetrical short-circuit current of squirrel-cage and doubly-fed induction generators. Electr. Power Syst. Res. 2011, 81, 1610–1618. [Google Scholar] [CrossRef]
- Morren, J.; de Haan, S.W.H. Short-circuit current of wind turbines with doubly fed induction generator. IEEE Trans. Energy Convers. 2007, 22, 174–180. [Google Scholar] [CrossRef]
- Lopez, J.; Gubia, E.; Sanchis, P.; Roboam, X.; Marroyo, L. Wind turbines based on doubly fed induction generator under asymmetrical voltage dips. IEEE Trans. Energy Convers. 2008, 23, 321–330. [Google Scholar] [CrossRef]
- Kong, X.; Zhang, Z.; Yin, X.; Wen, M. Study of fault current characteristics of the DFIG considering dynamic response of the RSC. IEEE Trans. Energy Convers. 2014, 29, 278–287. [Google Scholar]
- Ouyang, J.; Xiong, X. Dynamic behavior of the excitation circuit of a doubly-fed induction generator under a symmetrical voltage drop. Renew. Energy 2014, 71, 629–638. [Google Scholar] [CrossRef]
- Xiao, F.; Zhang, Z.; Yin, X. Fault Current Characteristics of the DFIG under Asymmetrical Fault Conditions. Energies 2015, 8, 10971–10992. [Google Scholar] [CrossRef]
- Naggar, A.E.; Erlich, I. Fault current contribution analysis of doubly fed induction generator-based wind turbines. IEEE Trans. Energy Convers. 2015, 30, 874–883. [Google Scholar] [CrossRef]
- El-Naggar, A.; Erlich, I. Short-circuit current reduction techniques of the doubly-fed induction generator based wind turbines for fault ride through enhancement. IET Renew. Power Gener. 2017, 11, 1033–1040. [Google Scholar] [CrossRef]
- Pannell, G.; Atkinson, D.J.; Zahawi, B. Minimum-threshold crowbar for a fault-ride-through grid-code-compliant DFIG wind turbine. IEEE Trans. Energy Convers. 2010, 25, 750–759. [Google Scholar] [CrossRef]
- Xiao, S.; Yang, G.; Zhou, H.; Geng, H. An LVRT Control Strategy Based on Flux Linkage Tracking for DFIG-Based WECS. IEEE Trans. Ind. Electron. 2013, 60, 2820–2832. [Google Scholar] [CrossRef]
- Piwko, R.; Miller, N.; Sanchez-Gasca, J.; Yuan, X.; Dai, R.; Lyons, J. Integrating large wind farms into weak power grids with long transmission lines. In Proceedings of the Transmission and Distribution Conference and Exposition: Asia and Pacific, Dalian, China, 18–18 August 2005; pp. 1–7. [Google Scholar]
- Hooshyar, A.; Azzous, M.A.; El-Saadany, E.F. Distance protection of lines connected to induction generator-based wind farms during balanced faults. IEEE Trans. Sustain. Energy 2014, 5, 1193–1203. [Google Scholar] [CrossRef]
- Hooshyar, A.; Azzous, M.A.; El-Saadany, E.F. Three-Phase Fault Direction Identification for Distribution Systems with DFIG-Based Wind DG. IEEE Trans. Sustain. Energy 2014, 5, 747–756. [Google Scholar] [CrossRef]
- Saleh, S.A.; Aljankawey, A.S.; Meng, R. Impacts of grounding configurations on responses of ground protective relays for DFIG-Based WECSs-Part I: Solid ground faults. IEEE Trans. Ind. Appl. 2015, 51, 2804–2818. [Google Scholar] [CrossRef]
- Saleh, S.A.; Aljankawey, A.S.; Meng, R. Impacts of grounding configurations on responses of ground protective relays for DFIG-Based WECSs-Part II: High-Impedance Ground Faults. IEEE Trans. Ind. Appl. 2016, 52, 1204–1214. [Google Scholar]
- Arachchige, L.N.W.; Rajapakse, A.D.; Muthumuni, D. Implementation, Comparison and Application of an Average Simulation Model of a Wind Turbine Driven Doubly Fed Induction Generator. Energies 2017, 10, 1726. [Google Scholar] [CrossRef]
- Zheng, Z.; Yang, G.; Geng, H. Short circuit current analysis of DFIG-type WG with crowbar protection under grid faults. In Proceedings of the International Symposium on Industrial Electronics, Hangzhou, China, 28–31 May 2012; pp. 1072–1079. [Google Scholar]
- Smith, J.C.; Milligan, M.R.; DeMeo, E.A.; Parsons, B. Utility wind integration and operating impact state of the art. IEEE Trans. Power Syst. 2007, 22, 900–908. [Google Scholar] [CrossRef]
- Li, B.; Duan, Z.; Wang, X.; Wu, J. Loss-of-excitation analysis and protection for pumped-storage machines during starting. IET Renew. Power Gener. 2016, 10, 71–78. [Google Scholar] [CrossRef]
- Yin, M.; Li, G.; Zhou, M.; Liu, G.; Zhao, C. Study on the Control of DFIG and Its Responses to Grid Disturbances. In Proceedings of the Power Engineering Society General Meeting, Montreal, QC, Canada, 18–22 June 2006; pp. 1–6. [Google Scholar]
- Abad, G.; Rodriguez, M.A.; Iwanski, G.; Poza, J. Direct Power Control of Doubly Fed Induction Generator Based Wind Turbines under Unbalanced Grid Voltage. IEEE Trans. Power Electron. 2010, 25, 442–452. [Google Scholar] [CrossRef]



| Fault Type | The Error of Fault Distance Measurement Result | ||
|---|---|---|---|
| 5 km | 10 km | 15 km | |
| Single-phase ground | 0.17% | 0.20% | 0.22% |
| Two-phase ground | 0.23% | 0.16% | 0.30% |
| Phase-to-phase short circuit | 0.04% | 0.63% | 0.03% |
| Three-phase short circuit | 0.07% | 0.18% | 0.03% |
| Fault Type | The Error of Fault Distance Measurement Result | ||
|---|---|---|---|
| 5 km | 10 km | 15 km | |
| Single-phase ground | 3.67% | 3.38% | 3.11% |
| Two-phase ground | 3.27% | 3.13% | 2.94% |
| Phase-to-phase short circuit | 7.24% | 7.64% | 7.29% |
| Three-phase short circuit | 26.39% | 26.07% | 25.71% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, B.; Liu, J.; Wang, X.; Zhao, L. Fault Studies and Distance Protection of Transmission Lines Connected to DFIG-Based Wind Farms. Appl. Sci. 2018, 8, 562. https://doi.org/10.3390/app8040562
Li B, Liu J, Wang X, Zhao L. Fault Studies and Distance Protection of Transmission Lines Connected to DFIG-Based Wind Farms. Applied Sciences. 2018; 8(4):562. https://doi.org/10.3390/app8040562
Chicago/Turabian StyleLi, Bin, Junyu Liu, Xin Wang, and Lili Zhao. 2018. "Fault Studies and Distance Protection of Transmission Lines Connected to DFIG-Based Wind Farms" Applied Sciences 8, no. 4: 562. https://doi.org/10.3390/app8040562
APA StyleLi, B., Liu, J., Wang, X., & Zhao, L. (2018). Fault Studies and Distance Protection of Transmission Lines Connected to DFIG-Based Wind Farms. Applied Sciences, 8(4), 562. https://doi.org/10.3390/app8040562