Heat Transfer in Non-Newtonian Flows by a Hybrid Immersed Boundary–Lattice Boltzmann and Finite Difference Method
Abstract
1. Introduction
2. Numerical Method
2.1. Fluid Solver
2.2. Heat Transfer Solver
2.3. Structural Solver
2.4. The IB Method for Fluid–Structure Interaction and Heat Transfer
3. Validations
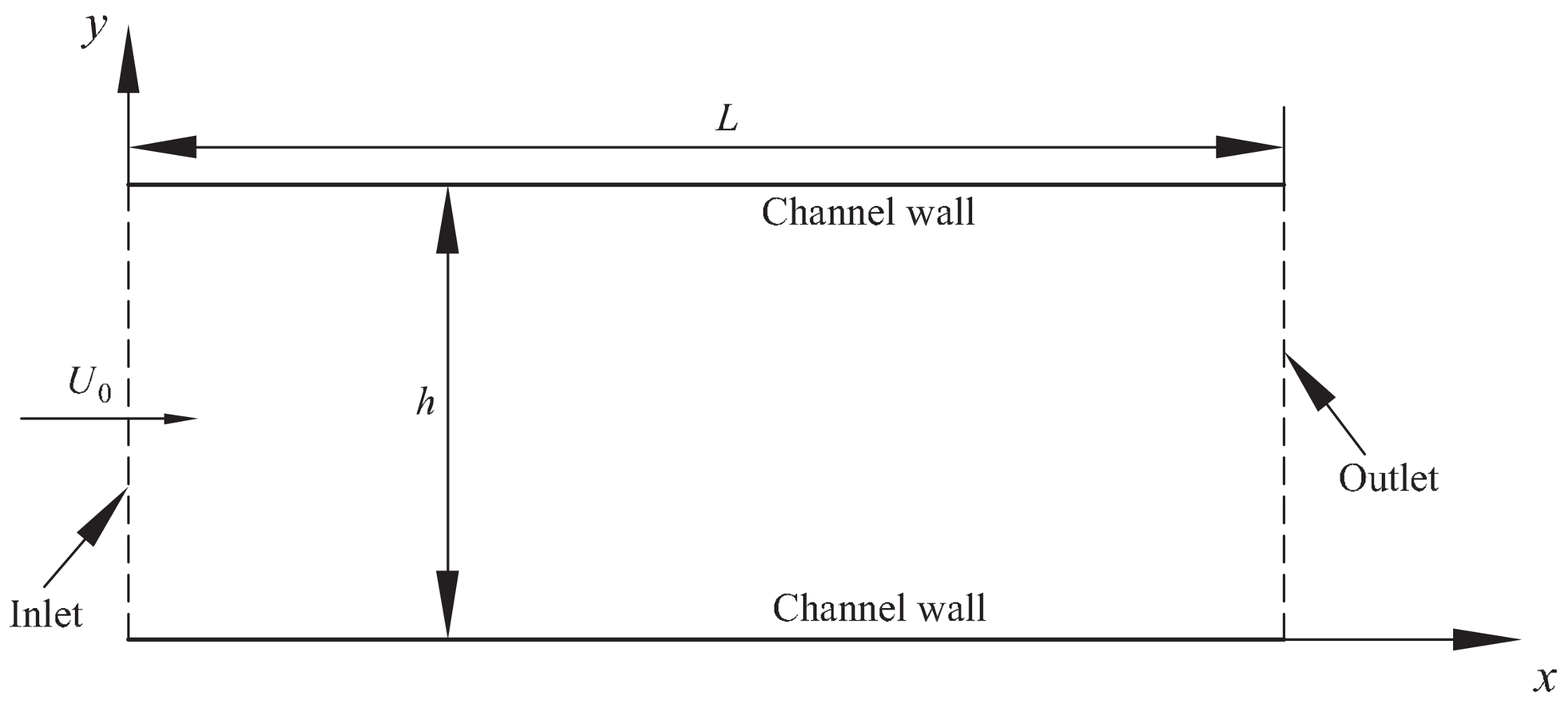
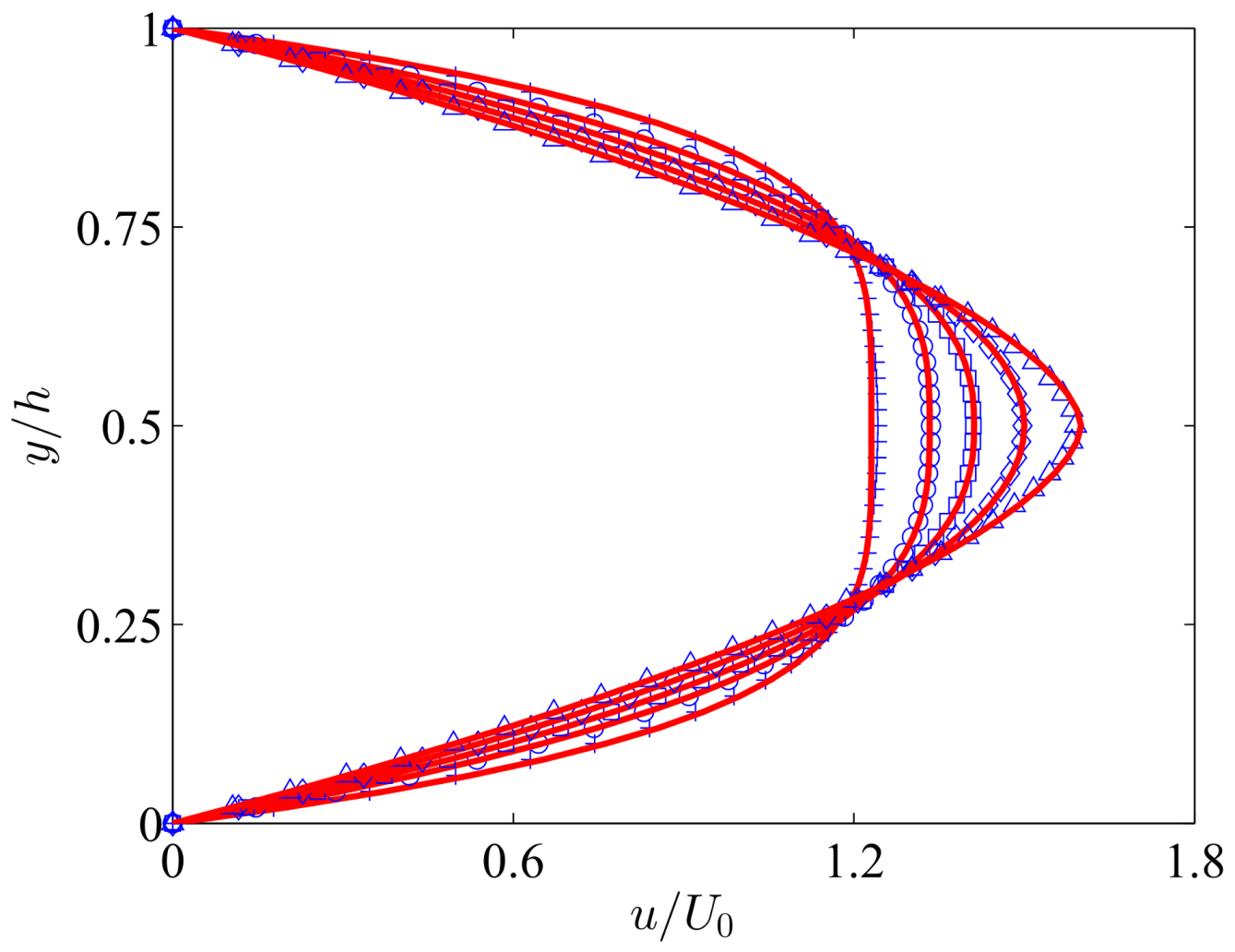
3.1. The Developing Flow of Non-Newtonian Power-Law Fluid in a Channel
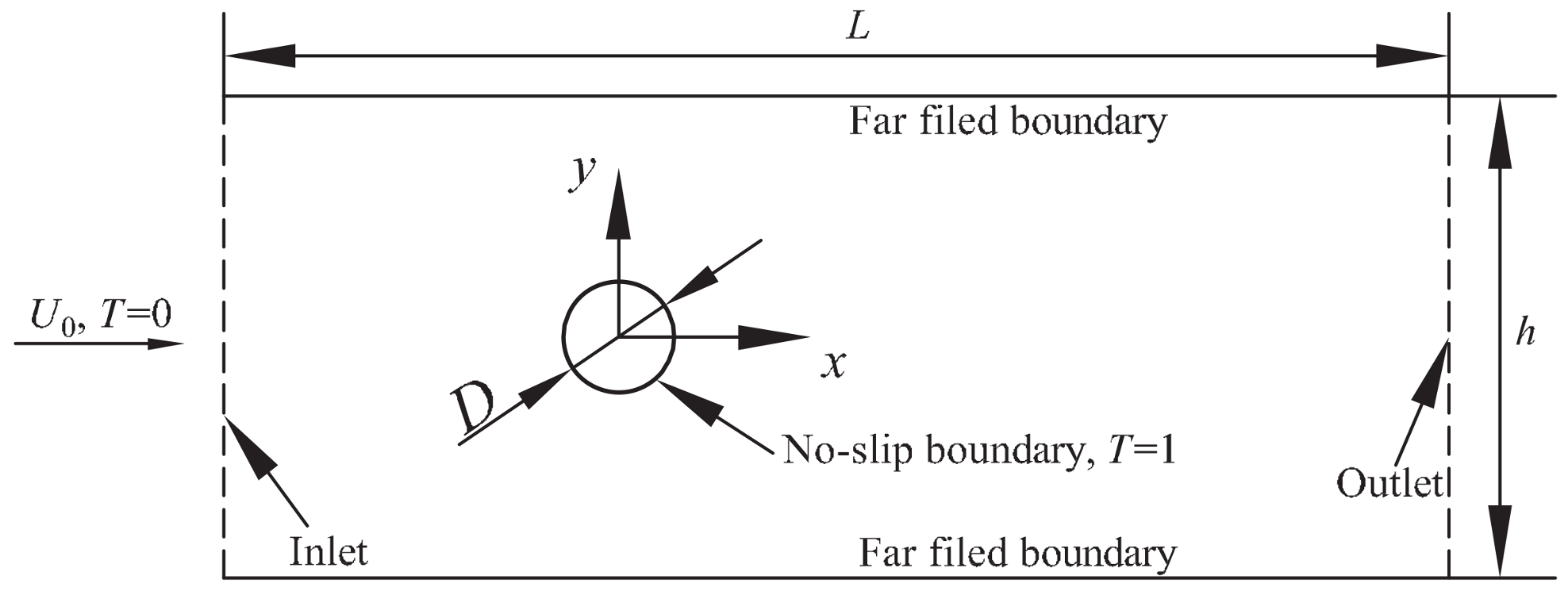
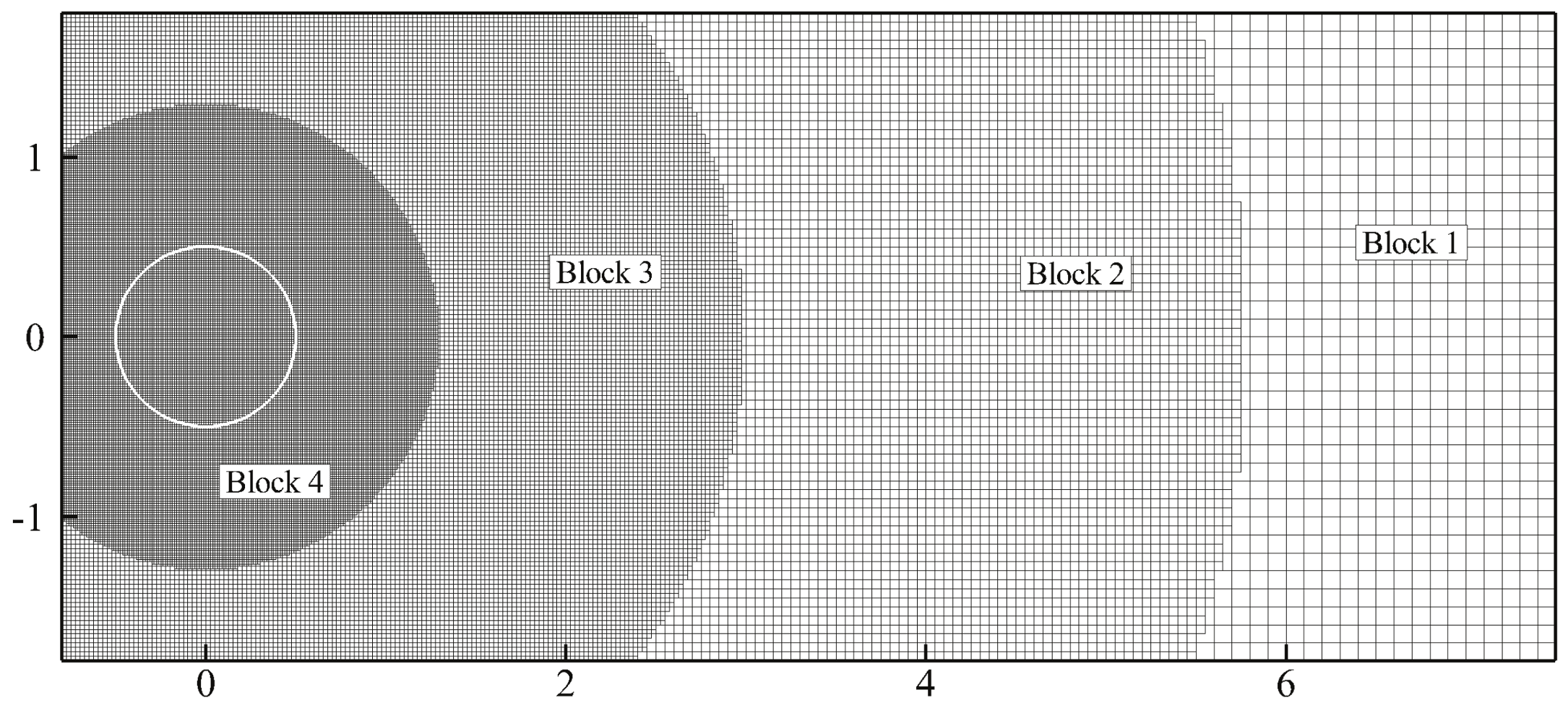
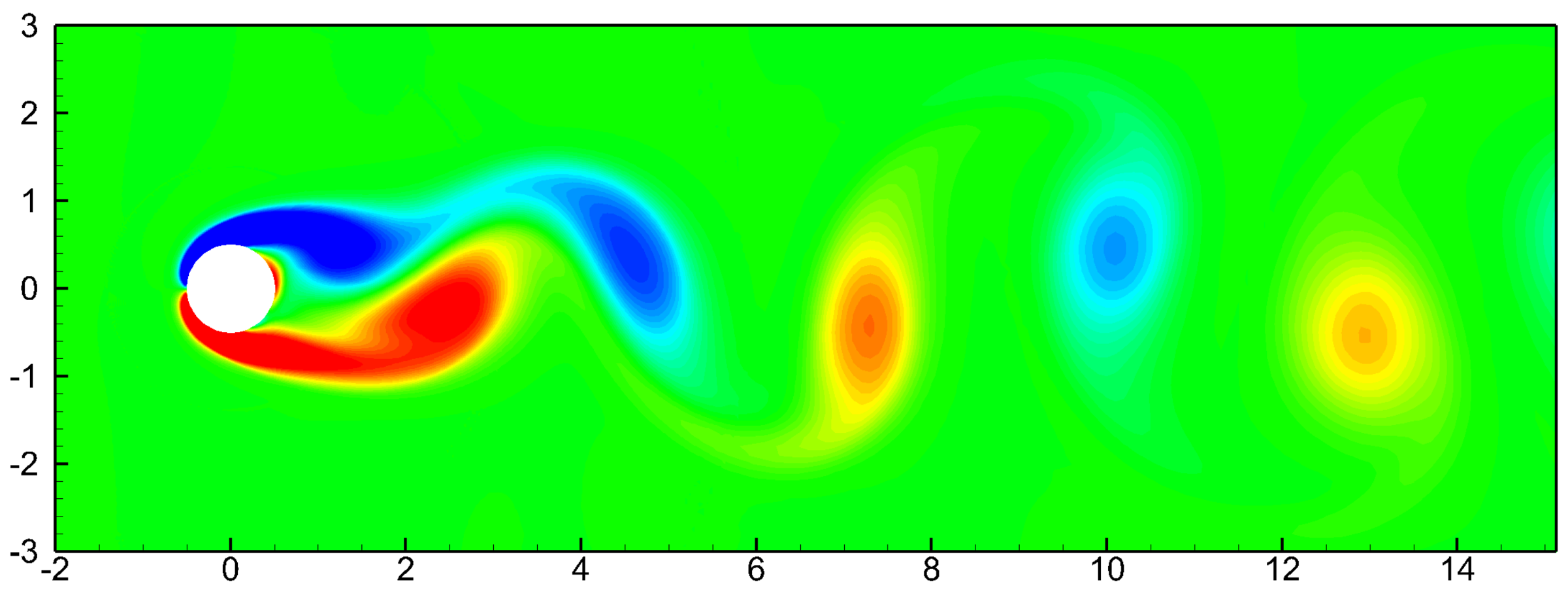
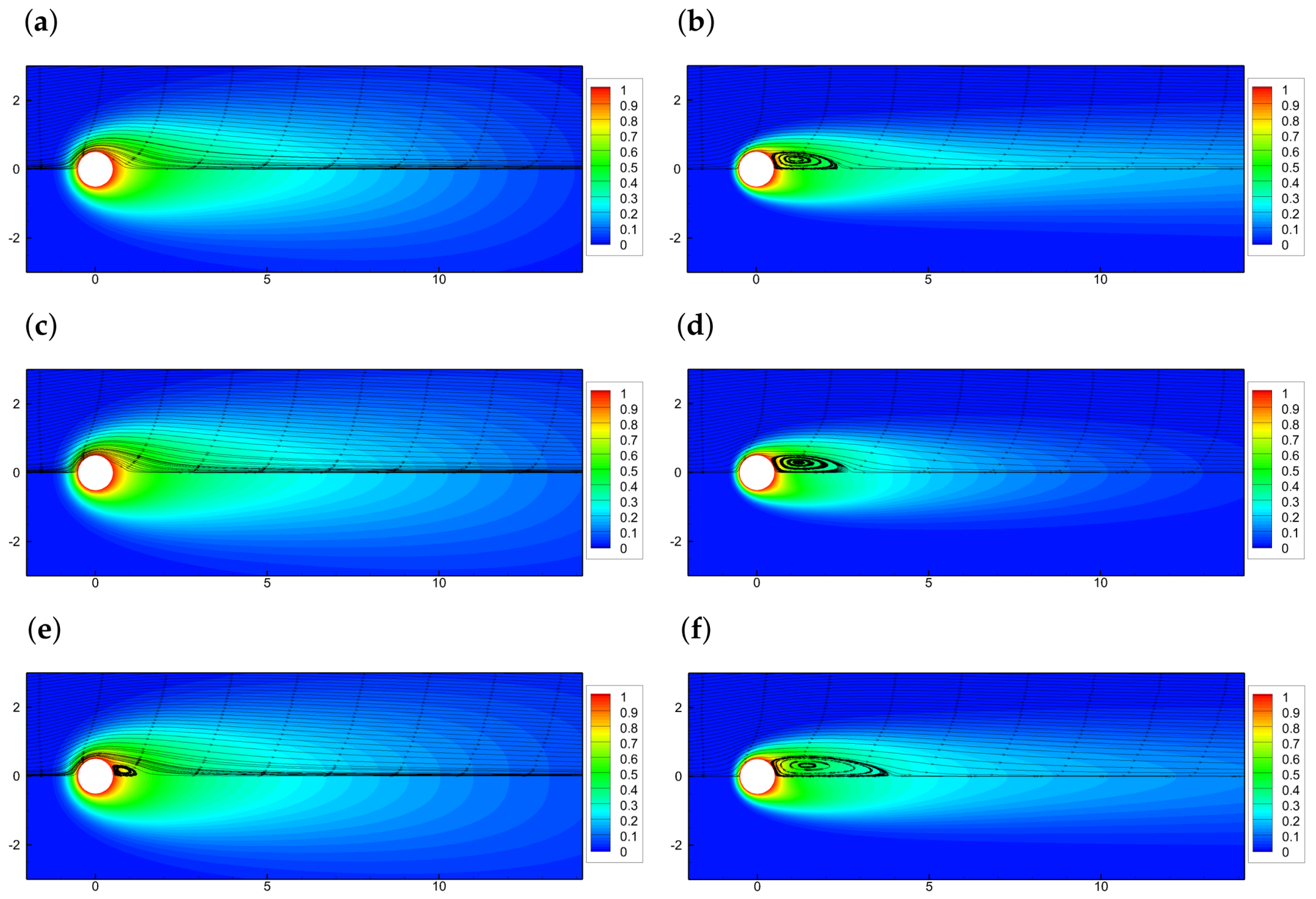
3.2. Non-Newtonian Power-Law Fluid Flow and Heat Transfer around a Stationary Cylinder
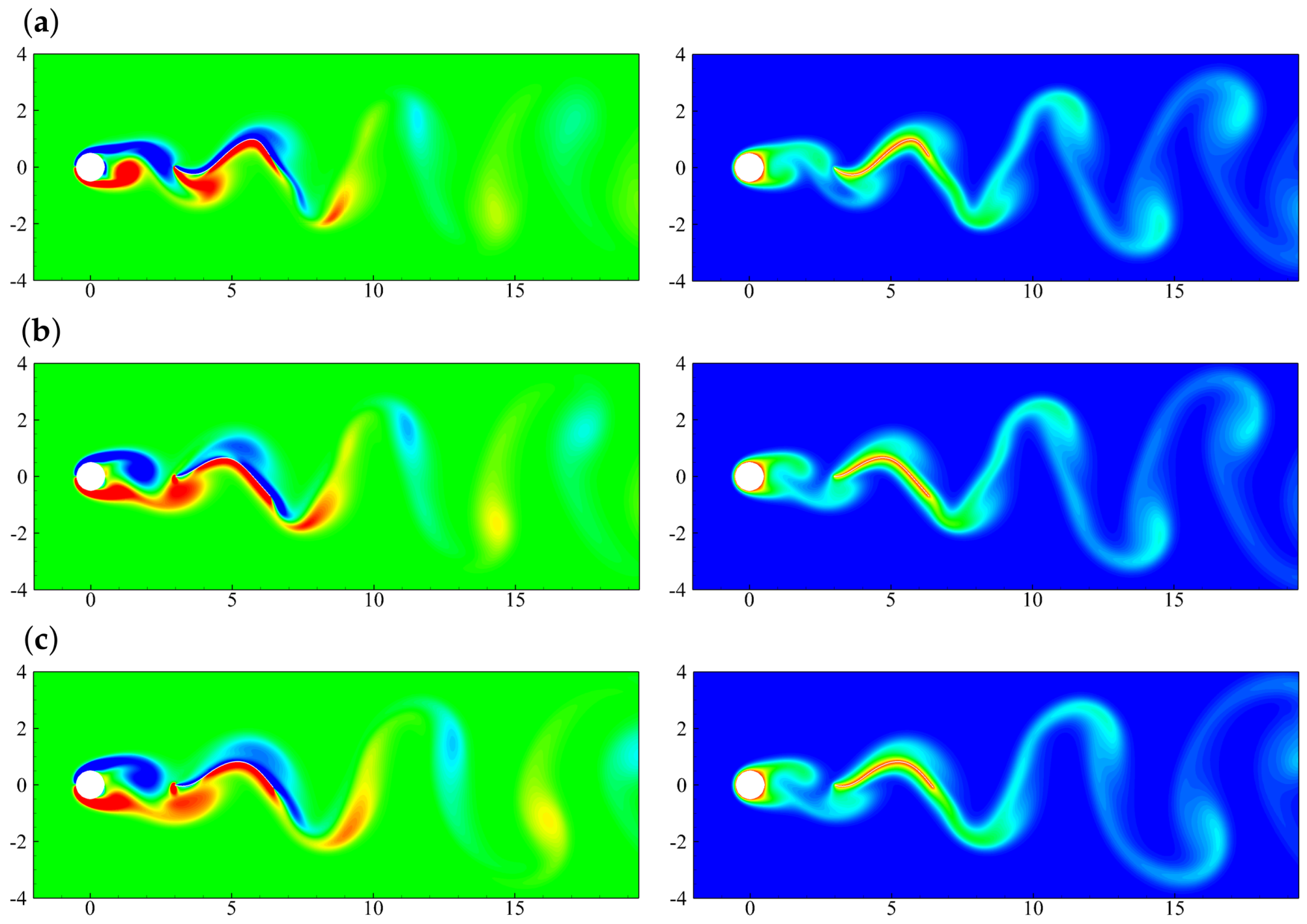
4. Heat Transfer around a Stationary Cylinder with a Detached Filament
5. Heat Transfer around an Oscillating Cylinder in Non-Newtonian Fluid Flow
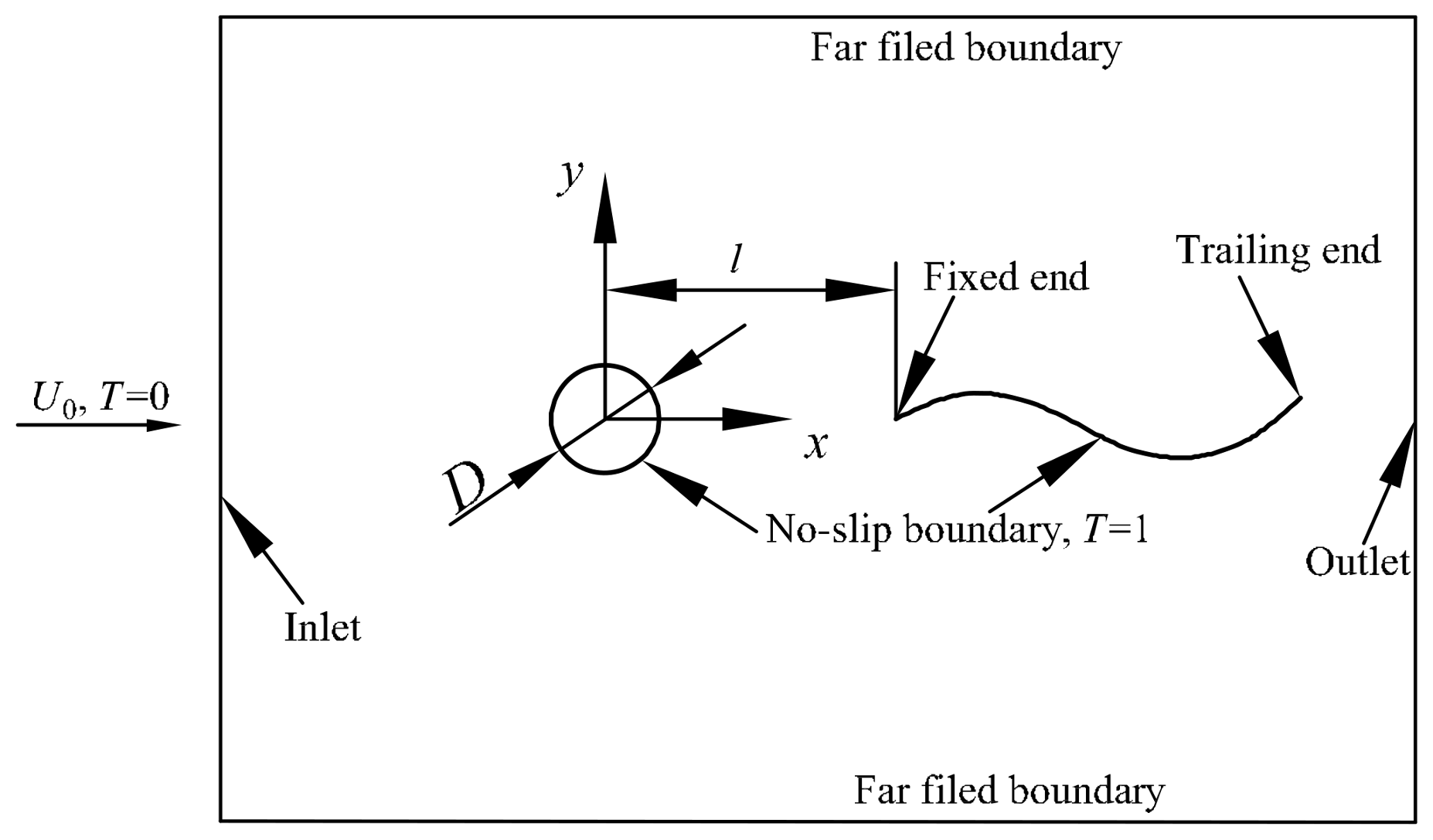
5.1. Physical Problem
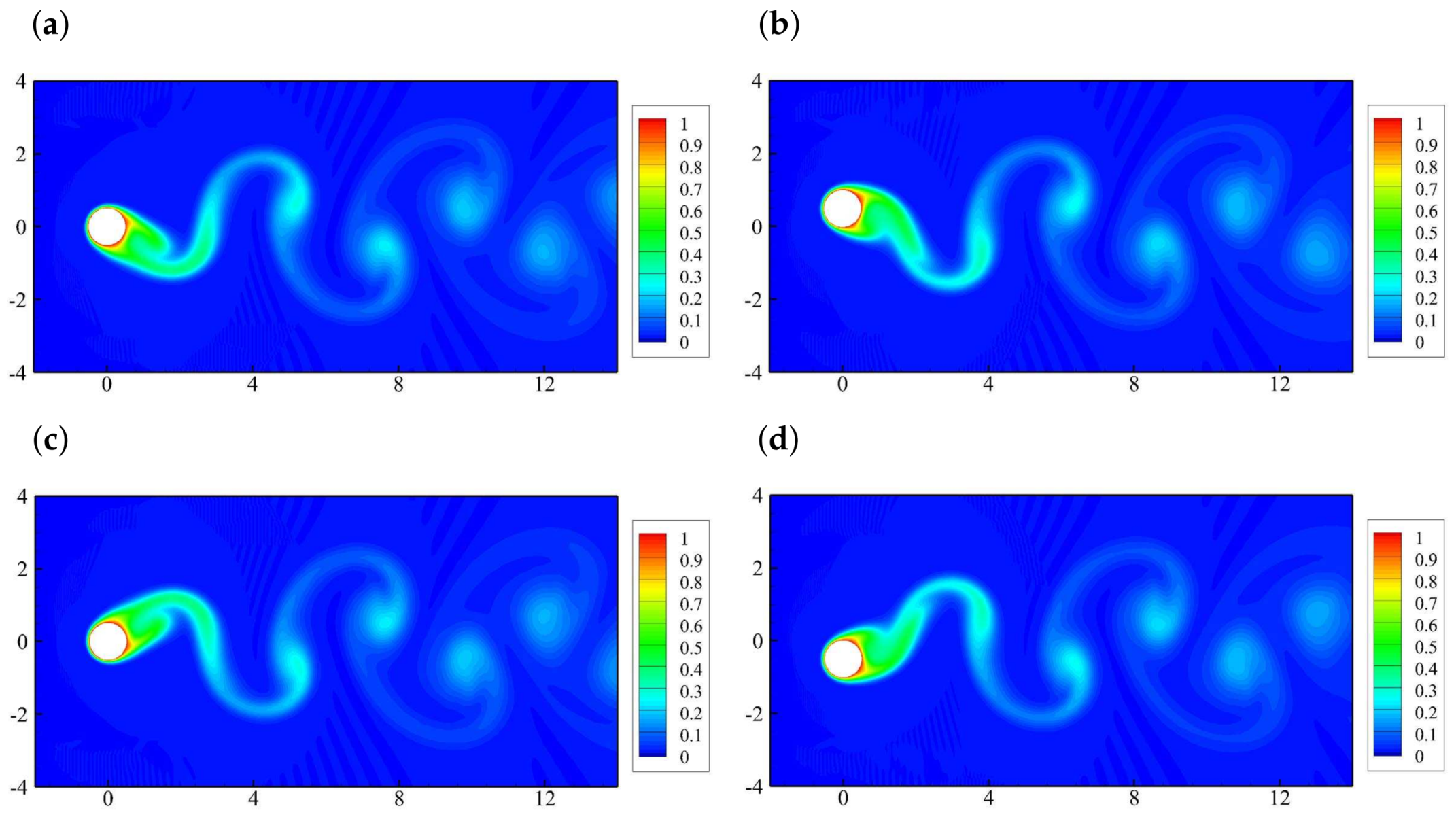
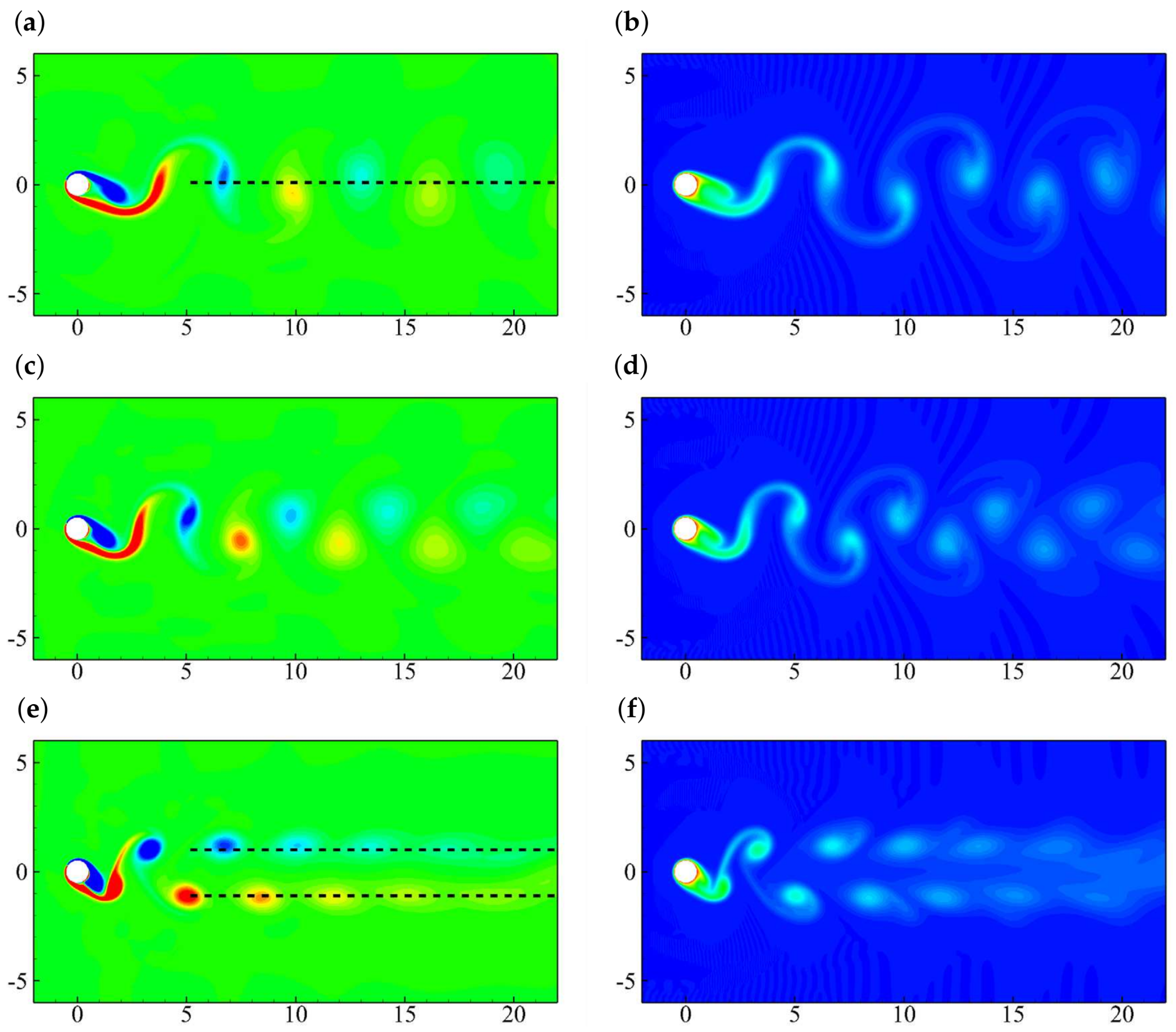
5.2. Effects of the Oscillating Amplitude
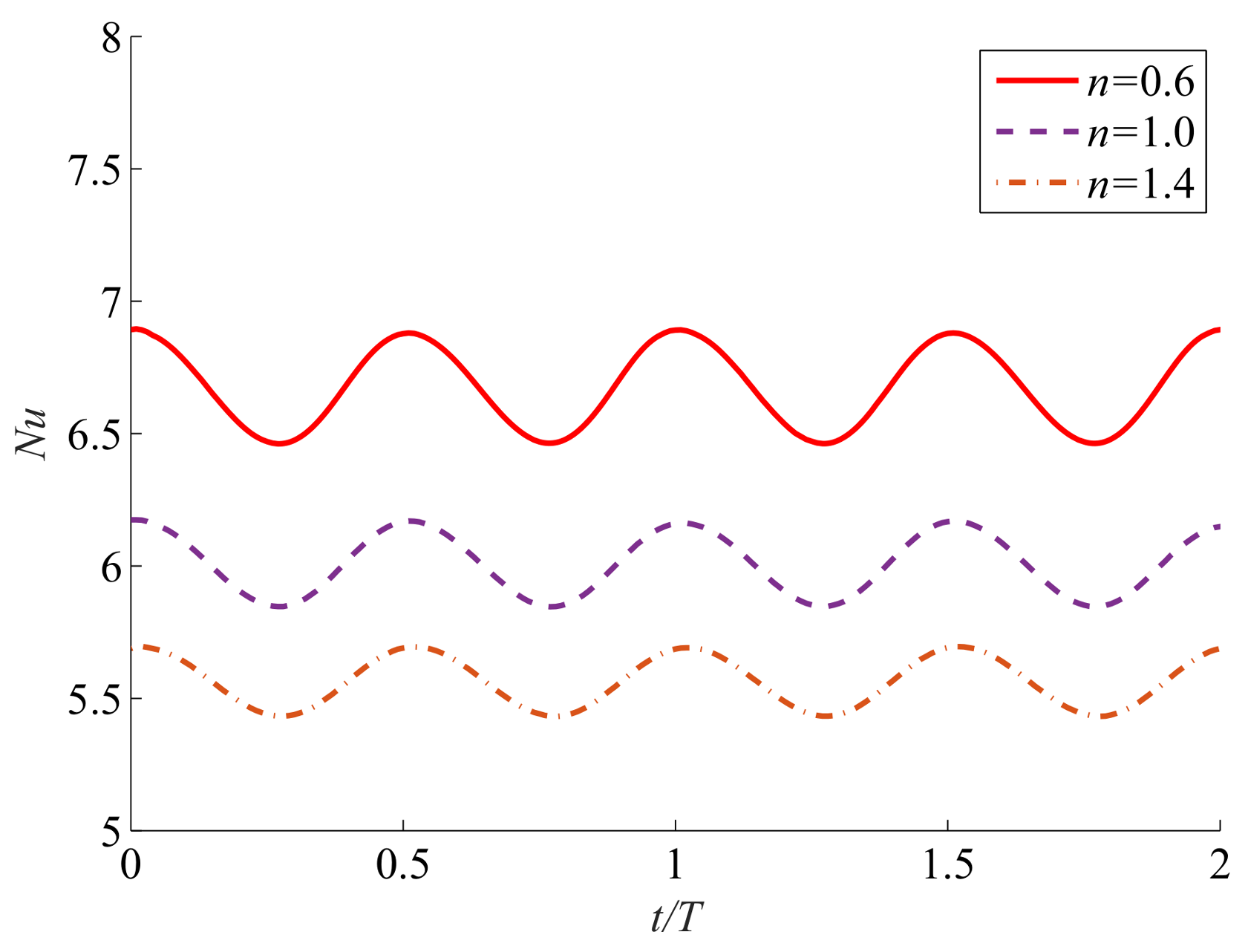
5.3. Effects of the Oscillating Frequency
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| CFD | computational fluid dynamics |
| LBM | lattice Boltzmann method |
| IBM | immersed boundary method |
| BGK | Bhatnagar-Gross-Krook |
| TRT | two-relaxation time |
| MRT | multi-relaxation time |
| FSI | fluid–structure interaction |
References
- Bazilevs, Y.; Takizawa, K.; Tezduyar, T.E. Computational Fluid-Structure Interaction: Methods and Applications; John Wiley & Sons: New York, NY, USA, 2013. [Google Scholar]
- Chen, S.; Doolen, G.D. Lattice Boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef]
- Guo, Z.; Shu, C. Lattice Boltzmann Method and Its Applications in Engineering; World Scientific: Singapore, 2013. [Google Scholar]
- McCracken, M.E.; Abraham, J. Multiple-relaxation-time lattice-Boltzmann model for multiphase flow. Phys. Rev. E 2005, 71, 036701. [Google Scholar] [CrossRef] [PubMed]
- Zheng, H.; Shu, C.; Chew, Y.-T. A lattice Boltzmann model for multiphase flows with large density ratio. J. Comput. Phys. 2006, 218, 353–371. [Google Scholar] [CrossRef]
- Wang, Y.; Shu, C.; Huang, H.; Teo, C. Multiphase lattice Boltzmann flux solver for incompressible multiphase flows with large density ratio. J. Comput. Phys. 2015, 280, 404–423. [Google Scholar] [CrossRef]
- Wang, Y.; Shu, C.; Yang, L. An improved multiphase lattice Boltzmann flux solver for three-dimensional flows with large density ratio and high reynolds number. J. Comput. Phys. 2015, 302, 41–58. [Google Scholar] [CrossRef]
- Spaid, M.A.; Phelan, F.R., Jr. Lattice Boltzmann methods for modeling microscale flow in fibrous porous media. Phys. Fluids 1997, 9, 2468–2474. [Google Scholar] [CrossRef]
- Gabbanelli, S.; Drazer, G.; Koplik, J. Lattice Boltzmann method for non-newtonian (power-law) fluids. Phys. Rev. E 2005, 72, 046312. [Google Scholar] [CrossRef] [PubMed]
- Tian, F.-B. Deformation of a capsule in a power-law shear flow. Comput. Math. Methods Med. 2016, 2016, 7981386. [Google Scholar] [CrossRef] [PubMed]
- Boghosian, B.M.; Yepez, J.; Coveney, P.V.; Wager, A. Entropic lattice Boltzmann methods. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 2001, 457, 717–766. [Google Scholar] [CrossRef]
- Ansumali, S.; Karlin, I.V. Single relaxation time model for entropic lattice Boltzmann methods. Phys. Rev. E 2002, 65, 056312. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Shu, C. A solution-adaptive lattice Boltzmann method for two-dimensional incompressible viscous flows. J. Comput. Phys. 2011, 230, 2246–2269. [Google Scholar] [CrossRef]
- Yu, D.; Mei, R.; Shyy, W. A multi-block lattice Boltzmann method for viscous fluid flows. Int. J. Numer. Methods Fluids 2002, 39, 99–120. [Google Scholar] [CrossRef]
- Guo, Z.; Zheng, C.; Shi, B. Discrete lattice effects on the forcing term in the lattice Boltzmann method. Phys. Rev. E 2002, 65, 046308. [Google Scholar] [CrossRef] [PubMed]
- Feng, Z.-G.; Michaelides, E.E. The immersed boundary-lattice Boltzmann method for solving fluid–particles interaction problems. J. Comput. Phys. 2004, 195, 602–628. [Google Scholar] [CrossRef]
- Tian, F.-B.; Luo, H.; Zhu, L.; Liao, J.C.; Lu, X.-Y. An efficient immersed boundary-lattice Boltzmann method for the hydrodynamic interaction of elastic filaments. J. Comput. Phys. 2011, 230, 7266–7283. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Shu, C.; Teo, C.; Wu, J. An immersed boundary-lattice Boltzmann flux solver and its applications to fluid–structure interaction problems. J. Fluids Struct. 2015, 54, 440–465. [Google Scholar] [CrossRef]
- Wu, J.; Shu, C. Implicit velocity correction-based immersed boundary-lattice Boltzmann method and its applications. J. Comput. Phys. 2009, 228, 1963–1979. [Google Scholar] [CrossRef]
- Shu, C.; Liu, N.; Chew, Y.-T. A novel immersed boundary velocity correction–lattice Boltzmann method and its application to simulate flow past a circular cylinder. J. Comput. Phys. 2007, 226, 1607–1622. [Google Scholar] [CrossRef]
- Zhang, J.; Johnson, P.C.; Popel, A.S. An immersed boundary lattice Boltzmann approach to simulate deformable liquid capsules and its application to microscopic blood flows. Phys. Biol. 2007, 4, 285. [Google Scholar] [CrossRef] [PubMed]
- Tian, F.-B.; Luo, H.; Zhu, L.; Lu, X.Y. Interaction between a flexible filament and a downstream rigid body. Phys. Rev. E 2010, 82, 026301. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.Q.; Tian, F.B.; Li, H.; Deng, Y. Red blood cell partitioning and blood flux redistribution in microvascular bifurcation. Theor. Appl. Mech. Lett. 2012, 2, 024001. [Google Scholar] [CrossRef][Green Version]
- Xu, Y.Q.; Tian, F.B.; Deng, Y.L. An efficient red blood cell model in the frame of IB–LBM and its application. Int. J. Biomath. 2013, 6, 1250061. [Google Scholar] [CrossRef]
- Liu, Z.; Lai, J.C.; Young, J.; Tian, F.B. Discrete vortex method with flow separation corrections for flapping-foil power generators. AIAA J. 2016, 55, 410–418. [Google Scholar] [CrossRef]
- Liu, Z.; Tian, F.B.; Lai, J.C.; Young, J. Flapping foil power generator performance enhanced with a spring-connected tail. Phys. Fluids 2017, 29, 123601. [Google Scholar] [CrossRef]
- Tian, F.-B.; Bharti, R.P.; Xu, Y.-Q. Deforming-spatial-domain/stabilized space–time (DSD/SST) method in computation of non-newtonian fluid flow and heat transfer with moving boundaries. Comput. Mech. 2014, 53, 257–271. [Google Scholar] [CrossRef]
- Tian, F.-B.; Zhu, L.; Fok, P.W.; Lu, X.Y. Simulation of a pulsatile non-Newtonian flow past a stenosed 2D artery with atherosclerosis. Comput. Biol. Med. 2013, 53, 1098–1113. [Google Scholar] [CrossRef] [PubMed]
- Behr, M.A.; Franca, L.P.; Tezduyar, T.E. Stabilized finite element methods for the velocity-pressure-stress formulation of incompressible flows. Comput. Methods Appl. Mech. Eng. 1993, 104, 31–48. [Google Scholar] [CrossRef]
- Alexander, F.J.; Chen, S.; Sterling, J. Lattice Boltzmann thermohydrodynamics. Phys. Rev. E 1993, 47, R2249. [Google Scholar] [CrossRef]
- Qian, Y. Simulating thermohydrodynamics with lattice BGK models. J. Sci. Comput. 1993, 8, 231–242. [Google Scholar] [CrossRef]
- Chen, Y.; Ohashi, H.; Akiyama, M. Two-parameter thermal lattice BGK model with a controllable prandtl number. J. Sci. Comput. 1997, 12, 169–185. [Google Scholar] [CrossRef]
- Inamuro, T.; Yoshino, M.; Inoue, H.; Mizuno, R.; Ogino, F. A lattice Boltzmann method for a binary miscible fluid mixture and its application to a heat-transfer problem. J. Comput. Phys. 2002, 179, 201–215. [Google Scholar] [CrossRef]
- Peng, Y.; Shu, C.; Chew, Y. Simplified thermal lattice Boltzmann model for incompressible thermal flows. Phys. Rev. E 2003, 68, 026701. [Google Scholar] [CrossRef] [PubMed]
- Guo, Z.; Zheng, C. Analysis of lattice Boltzmann equation for microscale gas flows: Relaxation times, boundary conditions and the knudsen layer. Int. J. Comput. Fluid Dyn. 2008, 22, 465–473. [Google Scholar] [CrossRef]
- Peng, Y.; Shu, C.; Chew, Y.; Niu, X.; Lu, X. Application of multi-block approach in the immersed boundary–lattice Boltzmann method for viscous fluid flows. J. Comput. Phys. 2006, 218, 460–478. [Google Scholar] [CrossRef]
- Abel, S.; Prasad, K.; Mahaboob, A. Buoyancy force and thermal radiation effects in MHD boundary layer visco-elastic fluid flow over continuously moving stretching surface. Int. J. Therm. Sci. 2005, 44, 465–476. [Google Scholar] [CrossRef]
- Wu, J.; Shu, C.; Zhao, N.; Tian, F.B. Numerical study on the power extraction performance of a flapping foil with a flexible tail. Phys. Fluids 2015, 27, 013602. [Google Scholar] [CrossRef]
- Tian, F.B.; Wang, Y.; Young, J.; Lai, J.C. An FSI solution technique based on the DSD/SST method and its applications. Math. Models Methods Appl. Sci. 2015, 25, 2257–2285. [Google Scholar] [CrossRef]
- Tian, F.B. FSI modeling with the DSD/SST method for the fluid and finite difference method for the structure. Comput. Mech. 2014, 54, 581–589. [Google Scholar] [CrossRef]
- Wu, J.; Wu, J.; Tian, F.B.; Zhao, N.; Li, Y.D. How a flexible tail improves the power extraction efficiency of a semi-activated flapping foil system: A numerical study. J. Fluids Struct. 2015, 54, 886–899. [Google Scholar] [CrossRef]
- Tian, F.B.; Young, J.; Lai, J.C.S. Improving power-extraction efficiency of a flapping plate: From passive deformation to active control. J. Fluids Struct. 2014, 51, 384–392. [Google Scholar] [CrossRef]
- Tian, F.B.; Luo, H.; Song, J.; Lu, X.Y. Force production and asymmetric deformation of a flexible flapping wing in forward flight. J. Fluids Struct. 2013, 36, 149–161. [Google Scholar] [CrossRef]
- Zhu, L.; Peskin, C.S. Simulation of a flapping flexible filament in a flowing soap film by the immersed boundary method. J. Comput. Phys. 2002, 179, 452–468. [Google Scholar] [CrossRef]
- Kim, Y.; Peskin, C.S. Penalty immersed boundary method for an elastic boundary with mass. Phys. Fluids 2007, 19, 053103. [Google Scholar] [CrossRef]
- Deng, H.B.; Chen, D.D.; Dai, H.; Wu, J.; Tian, F.B. On numerical modeling of animal swimming and flight. Comput. Mech. 2013, 52, 1221–1242. [Google Scholar] [CrossRef]
- Tian, F.-B.; Dai, H.; Luo, H.; Doyle, J.F.; Rousseau, B. Fluid–structure interaction involving large deformations: 3D simulations and applications to biological systems. J. Comput. Phys. 2014, 258, 451–469. [Google Scholar] [CrossRef] [PubMed]
- Tian, F.-B.; Lu, X.Y.; Luo, H. Onset of instability of a flag in uniform flow. Theor. Appl. Mech. Lett. 2012, 2, 022005. [Google Scholar] [CrossRef][Green Version]
- Shahzad, A.; Tian, F.B.; Young, J.; Lai, J.C.S. Effects of wing shape, aspect ratio and deviation angle on aerodynamic performance of flapping wings in hover. Phys. Fluids 2016, 28, 111901. [Google Scholar] [CrossRef]
- Mittal, R.; Dong, H.; Bozkurttas, M.; Najjar, F.M.; Vargas, A.; von Loebbecke, A. A versatile sharp interface immersed boundary method for incompressible flows with complex boundaries. J. Comput. Phys. 2008, 227, 4825–4852. [Google Scholar] [CrossRef] [PubMed]
- Peskin, C.S. The immersed boundary method. Acta Numer. 2002, 11, 479–517. [Google Scholar] [CrossRef]
- Ren, W.; Shu, C.; Wu, J.; Yang, W. Boundary condition-enforced immersed boundary method for thermal flow problems with dirichlet temperature condition and its applications. Comput. Fluids 2012, 57, 40–51. [Google Scholar] [CrossRef]
- Guo, Z.; Zheng, C.; Shi, B. An extrapolation method for boundary conditions in lattice Boltzmann method. Phys. Fluids 2002, 14, 2007–2010. [Google Scholar] [CrossRef]
- Patnana, V.K.; Bharti, R.P.; Chhabra, R.P. Two-dimensional unsteady flow of power-law fluids over a cylinder. Chem. Eng. Sci. 2009, 64, 2978–2999. [Google Scholar] [CrossRef]
- Wang, L.; Currao, G.M.; Han, F.; Neely, A.J.; Young, J.; Tian, F.-B. An immersed boundary method for fluid–structure interaction with compressible multiphase flows. J. Comput. Phys. 2017, 341, 131–151. [Google Scholar] [CrossRef]
- Xu, S.; Wang, Z.J. An immersed interface method for simulating the interaction of a fluid with moving boundaries. J. Comput. Phys. 2006, 216, 454–493. [Google Scholar] [CrossRef]
- Bharti, R.; Sivakumar, P.; Chhabra, R. Forced convection heat transfer from an elliptical cylinder to power-law fluids. Int. J. Heat Mass Transf. 2008, 51, 1838–1853. [Google Scholar] [CrossRef]
- Soares, A.; Ferreira, J.; Chhabra, R. Flow and forced convection heat transfer in crossflow of non-newtonian fluids over a circular cylinder. Ind. Eng. Chem. Res. 2005, 44, 5815–5827. [Google Scholar] [CrossRef]
- Alben, S. Simulating the dynamics of flexible bodies and vortex sheets. J. Comput. Phys. 2009, 228, 2587–2603. [Google Scholar] [CrossRef]
- Sui, Y.; Chew, Y.T.; Roy, P.; Low, H.T. A hybrid immersed-boundary and multi-block lattice Boltzmann method for simulating fluid and moving-boundaries interactions. Int. J. Numer. Methods Fluids 2007, 53, 1727–1754. [Google Scholar] [CrossRef]
- Stewart, W.J.; Tian, F.B.; Akanyeti, O.; Walker, C.J.; Liao, J.C. Refuging rainbow trout selectively exploit flows behind tandem cylinders. J. Exp. Biol. 2016, 219, 2182–2191. [Google Scholar] [CrossRef] [PubMed]
| Sources | |||||
|---|---|---|---|---|---|
| Present | 1.242 | 1.333 | 1.411 | 1.501 | 1.591 |
| Analytical | 1.231 | 1.333 | 1.412 | 1.500 | 1.600 |
| n | Sources | St | ||
|---|---|---|---|---|
| 0.6 | Present | 0.182 | 1.258 | 0.375 |
| Patnana et al. [54] | 0.180 | 1.180 | – | |
| Tian et al. [27] | 0.188 | 1.179 | 0.367 | |
| 1.0 | Present | 0.164 | 1.415 | 0.349 |
| Patnana et al. [54] | 0.164 | 1.341 | 0.325 | |
| Tian et al. [27] | 0.160 | 1.430 | 0.360 | |
| Wang et al. [55] | 0.161 | 1.450 | 0.310 | |
| Xu and Wang [56] | 0.171 | 1.423 | 0.340 | |
| Tian et al. [17] | 0.166 | 1.43 | – | |
| 1.4 | Present | 0.159 | 1.546 | 0.345 |
| Patnana et al. [54] | 0.150 | 1.497 | – | |
| Tian et al. [27] | 0.161 | 1.523 | 0.356 | |
| 1.8 | Present result | 0.152 | 1.661 | 0.327 |
| Patnana et al. [54] | 0.139 | 1.630 | – | |
| Tian et al. [27] | 0.155 | 1.657 | 0.356 |
| Re | Sources | |||
|---|---|---|---|---|
| 10 | Present | 2.089 | 2.038 | 1.973 |
| Bharti et al. [57] | 2.123 | 2.060 | 1.973 | |
| Tian et al. [27] | 2.208 | 2.150 | 2.075 | |
| Soares et al. [58] | 2.116 | 2.058 | 1.973 | |
| 40 | Present | 3.714 | 3.588 | 3.401 |
| Bharti et al. [57] | 3.830 | 3.653 | 3.400 | |
| Tian et al. [27] | 3.923 | 3.769 | 3.554 | |
| Soares et al. [58] | 3.736 | 3.570 | 3.325 |
| Sources | n | |||||
|---|---|---|---|---|---|---|
| Present | 0.6 | 2.5 | 1.25 | 0.175 | 5.881 | 1.10 |
| 4.0 | 1.24 | 0.175 | 5.872 | 1.28 | ||
| Present | 1.0 | 2.5 | 1.38 | 0.156 | 5.407 | 1.11 |
| Sui et al. [60] | 2.5 | 1.41 | 0.156 | – | 1.14 | |
| Present | 4.0 | 1.37 | 0.152 | 5.401 | 1.30 | |
| Tian et al. [17] | 4.0 | 1.39 | 0.153 | – | 1.34 | |
| Present | 1.4 | 2.5 | 1.51 | 0.143 | 5.077 | 1.10 |
| 4.0 | 1.48 | 0.141 | 5.069 | 1.30 |
| 1.0 | 6.677, 0.431 | 5.993, 0.295 | 5.563, 0.262 |
| 0.5 | 6.368, 0.115 | 5.786, 0.086 | 5.394, 0.067 |
| 0.25 | 6.296, – | 5.683, – | 5.312, – |
| 0.8 | 6.326, 0.283 | 5.776, 0.224 | 5.408, 0.163 |
| 1.0 | 6.677, 0.431 | 5.993, 0.295 | 5.563, 0.262 |
| 1.2 | 6.901, 0.591 | 6.152, 0.421 | 5.567, 0.351 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Tian, F.-B. Heat Transfer in Non-Newtonian Flows by a Hybrid Immersed Boundary–Lattice Boltzmann and Finite Difference Method. Appl. Sci. 2018, 8, 559. https://doi.org/10.3390/app8040559
Wang L, Tian F-B. Heat Transfer in Non-Newtonian Flows by a Hybrid Immersed Boundary–Lattice Boltzmann and Finite Difference Method. Applied Sciences. 2018; 8(4):559. https://doi.org/10.3390/app8040559
Chicago/Turabian StyleWang, Li, and Fang-Bao Tian. 2018. "Heat Transfer in Non-Newtonian Flows by a Hybrid Immersed Boundary–Lattice Boltzmann and Finite Difference Method" Applied Sciences 8, no. 4: 559. https://doi.org/10.3390/app8040559
APA StyleWang, L., & Tian, F.-B. (2018). Heat Transfer in Non-Newtonian Flows by a Hybrid Immersed Boundary–Lattice Boltzmann and Finite Difference Method. Applied Sciences, 8(4), 559. https://doi.org/10.3390/app8040559






