A Lattice Boltzmann Method and Asynchronous Model Coupling for Viscoelastic Fluids
Abstract
1. Introduction
2. The Descriptions of Mathematical Models
3. The Coupled LBM of Viscoelastic Fluids
3.1. Incompressible LBGK Model with the Extra Force
3.2. Solving the Oldroyd-B Constitutive Model
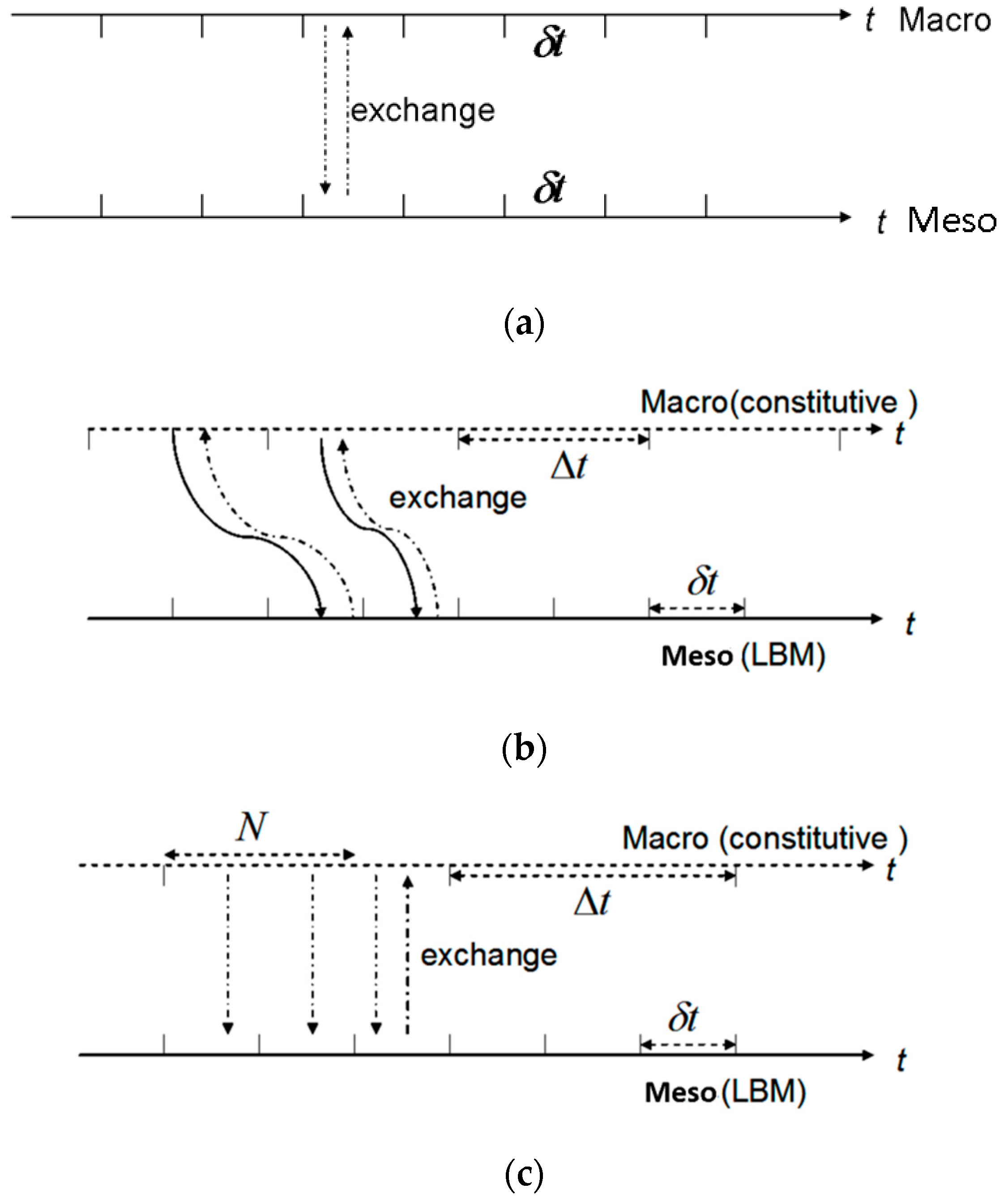
3.3. The Temporal Marching of Coupled Solvers
| Algorithm 1. The coupled algorithm using a homogeneous time step. |
| Require: , , , , (is a dimension less terminal time) |
| Do |
| ; |
| ; |
| ; |
| ; |
| ; |
| ; |
| While |
| Algorithm 2. Generalized asynchronously coupling method. |
| Require: , , , , (is a dimension less terminal time) |
| Do |
| For (k = 1; k++; k ≤ N) |
| { |
| ; |
| } |
| ; |
| ; |
| ; |
| ; |
| While |
4. Numerical Results and Discussions
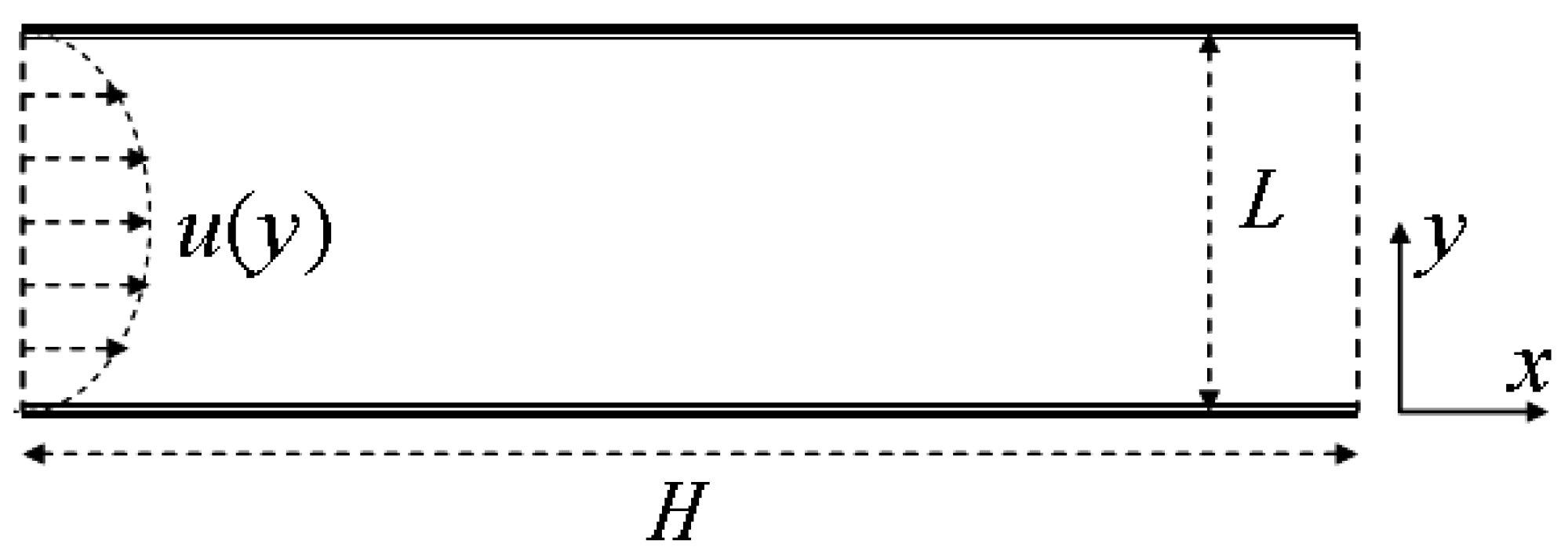
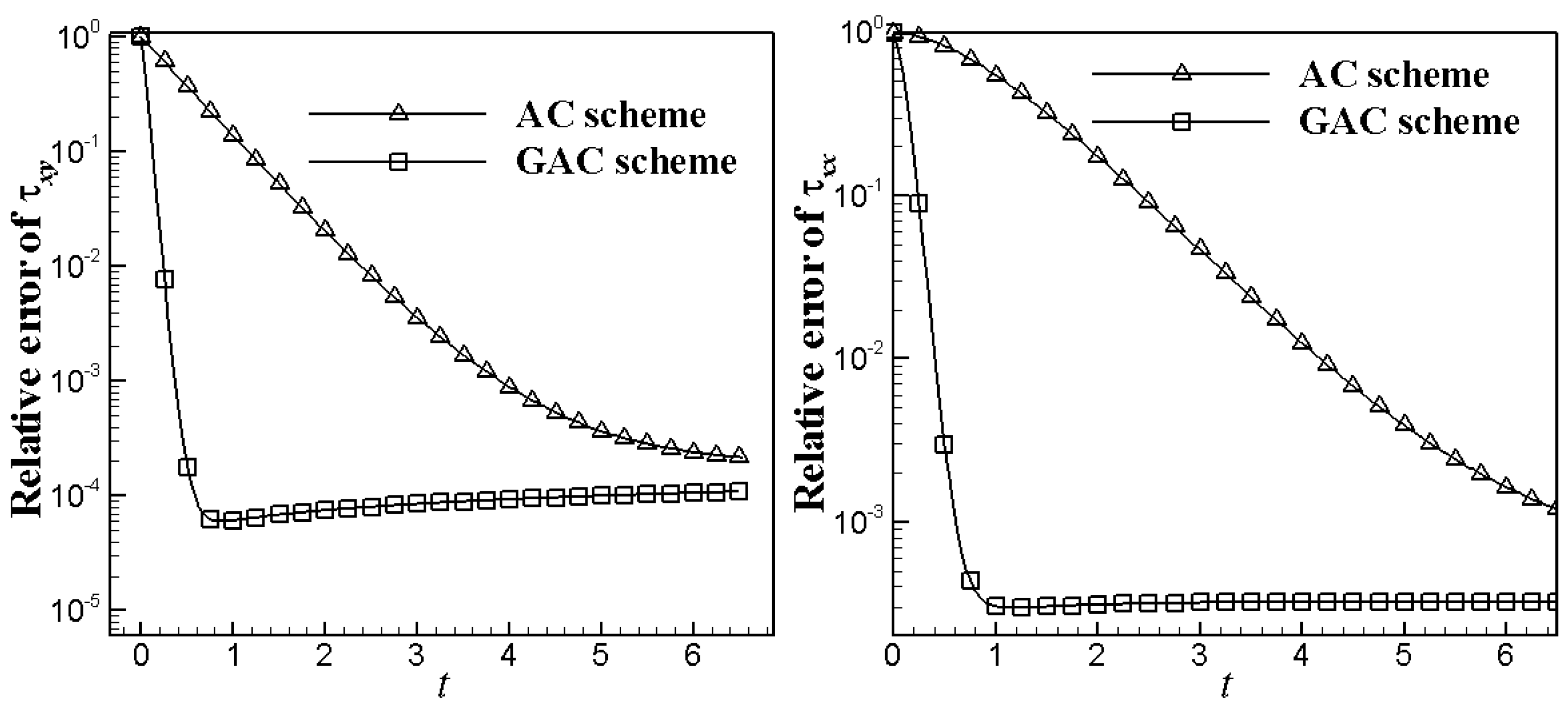
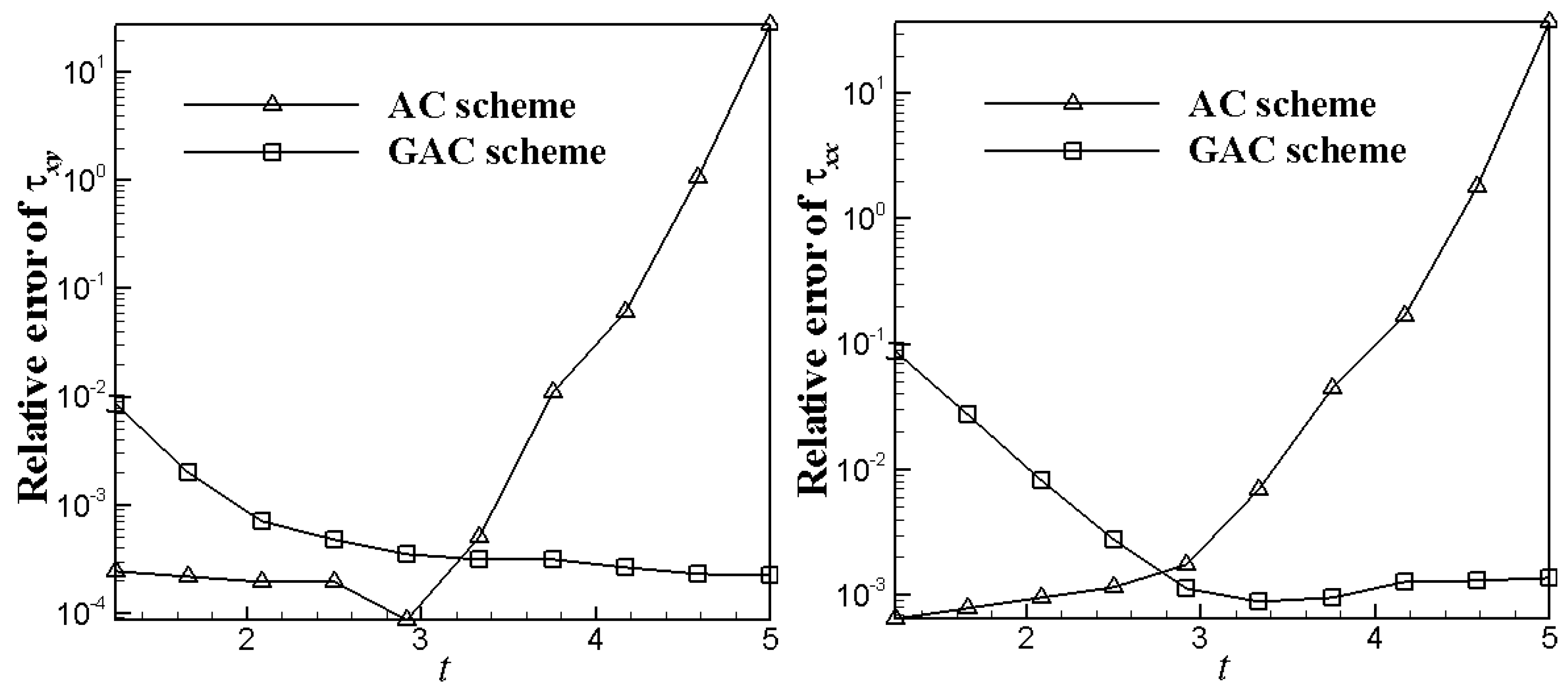
4.1. 2D Channel Flows
4.2. Contraction Flows
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Recovering Incompressible Naveier-Stokes Equation with Elastic Force
References
- Keunings, R. On the high Weissenberg number problem. J. Non-Newton. Fluid Mech. 1986, 20, 209–226. [Google Scholar] [CrossRef]
- Walters, K.; Webster, M.F. The distinctive CFD challenges of computational rheology. Int. J. Numer. Methods Fluids 2003, 43, 577–596. [Google Scholar] [CrossRef]
- Renardy, M. Current issues in non-Newtonian flows: A mathematical perspective. J. Non-Newton. Fluid Mech. 2000, 90, 243–259. [Google Scholar] [CrossRef]
- Mirzakhalili, E.; Nejat, A. High-order solution of viscoelastic fluids using the discontinuous Galerk in method. J. Fluids Eng. 2015, 137, 031205. [Google Scholar] [CrossRef]
- Comminal, R.; Hattel, J.H.; Alves, M.A.; Spangenberg, J. Vortex behavior of the Oldroyd-B fluid in the 4-1 planar contraction simulated with the stream function–log-conformation formulation. J. Non-Newton. Fluid Mech. 2016, 237, 1–15. [Google Scholar] [CrossRef]
- Niethammer, M.; Marschall, H.; Kunkelmann, C.; Bothe, D. A numerical stabilization framework for viscoelastic fluid flow using the finite volume method on general unstructured meshes. Int. J. Number. Methods Fluids 2017, 86, 131–166. [Google Scholar] [CrossRef]
- Pimenta, F.; Alves, M.A. Stabilization of an open-source finite-volume solver for viscoelastic fluid flows. J. Non-Newton. Fluid Mech. 2017, 239, 85–104. [Google Scholar] [CrossRef]
- Chen, S.; Doolen, G.D. Lattice Boltzmann method for fluid flows. Ann. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef]
- Qian, Y.H.; d’Humières, D.; Lallemand, P. Lattice BGK Models for Navier-Stokes Equation. Europhys. Lett. 1992, 17, 479–484. [Google Scholar] [CrossRef]
- Succi, S. The Lattice Boltzmann Equation for Fluid Dynamics and Beyond; Oxford University Press: Oxford, MS, USA, 2001. [Google Scholar]
- Qian, Y.H.; Deng, Y.F. A lattice BGK model for viscoelastic media. Phys. Rev. Lett. 1997, 79, 2742–2745. [Google Scholar] [CrossRef]
- Giraud, L.; d’Humières, D.; Lallemand, P. A lattice Boltzmann model for Jeffreys viscoelastic fluid. Euro Phys. Lett. 1998, 42, 625–630. [Google Scholar] [CrossRef]
- Ammar, A. Lattice Boltzmann method for polymer kinetic theory. J. Non-Newton. Fluid Mech. 2010, 165, 1082–1092. [Google Scholar] [CrossRef]
- Gupta, A.; Sbragaglia, M.; Scagliarini, A. Hybrid Lattice Boltzmann/Finite Difference simulations of viscoelastic multicomponent flows in confined geometries. J. Comput. Phys. 2015, 291, 177–197. [Google Scholar] [CrossRef]
- Su, J.; Ouyang, J.; Wang, X. Lattice Boltzmann method for the simulation of viscoelastic fluid flows over a large range of Weissenberg numbers. J. Non-Newton. Fluid Mech. 2013, 194, 42–59. [Google Scholar] [CrossRef]
- Zou, S.; Yuan, X.F.; Yang, X. An integrated lattice Boltzmann and finite volume method for the simulation of viscoelastic fluid flows. J. Non-Newton. Fluid Mech. 2014, 211, 99–113. [Google Scholar] [CrossRef]
- Phillips, T.N.; Roberts, G.W. Lattice Boltzmann models for non-Newtonian flows. J. Appl. Math. 2011, 76, 790–816. [Google Scholar] [CrossRef]
- Papenkort, S.; Voigtmann, T. Lattice Boltzmann simulations of a viscoelastic shear-thinning fluid. J. Chem. Phys. 2015, 143, 044512. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Shu, C.; Yang, L.M.; Yuan, H.Z. A decoupling multiple-relaxation-time lattice Boltzmann flux solver for non-Newtonian power-law fluid flows. J. Non-Newton. Fluid Mech. 2016, 235, 20–28. [Google Scholar] [CrossRef]
- Xie, C.; Zhang, J.; Bertola, V.; Wang, M. Lattice Boltzmann modeling for multiphase viscoplastic fluid flow. J. Non-Newton. Fluid Mech. 2016, 234, 118–128. [Google Scholar] [CrossRef]
- Su, J.; Ouyang, J.; Wang, X. Lattice Boltzmann method coupled with Oldroyd-B constitutive model for a viscoelastic fluid. Phys. Rev. E 2013, 88, 053304. [Google Scholar] [CrossRef] [PubMed]
- Weinan, E.; Ren, W.Q.; Vanden-Eijnden, E. A general strategy for designing seamless multiscale methods. J. Comput. Phys. 2009, 228, 5437–5453. [Google Scholar] [CrossRef]
- Ren, W. Seamless multiscale modeling of complex fluids using fiber bundle dynamics. Commun. Math. Sci. 2007, 5, 1027–1037. [Google Scholar] [CrossRef]
- Bird, R.; Curtiss, C.; Armstrong, R. Dynamics of Polymeric Liquids; Wiley: New York, NY, USA, 1987; Volume 1 and 2. [Google Scholar]
- Guo, Z.L.; Shi, B.C.; Wang, N.C. Lattice BGK model for incompressible Navier–Stokes equation. J. Comput. Phys. 2000, 165, 288–306. [Google Scholar] [CrossRef]
- Guo, Z.L.; Zheng, C.G.; Shi, B.C. Discrete lattice effects on the forcing term in the lattice Boltzmann method. Phys. Rev. E 2002, 65, 046308. [Google Scholar] [CrossRef] [PubMed]
- Lockerby, D.A.; Duque-Daza, C.A.; Borg, M.K. Time-step coupling for hybrid simulations of multiscale flows. J. Comput. Phys. 2013, 237, 344–365. [Google Scholar] [CrossRef]
- Hassager, O. Working group on numerical techniques. J. Non-Newton. Fluid Mech. 1988, 29, 2–5. [Google Scholar]
- Afonso, A.; Oliveira, P.J.; Pinho, F.T. Dynamics of high-Deborah number entry flows: A numerical study. J. Fluid Mech. 2011, 677, 272–304. [Google Scholar] [CrossRef]


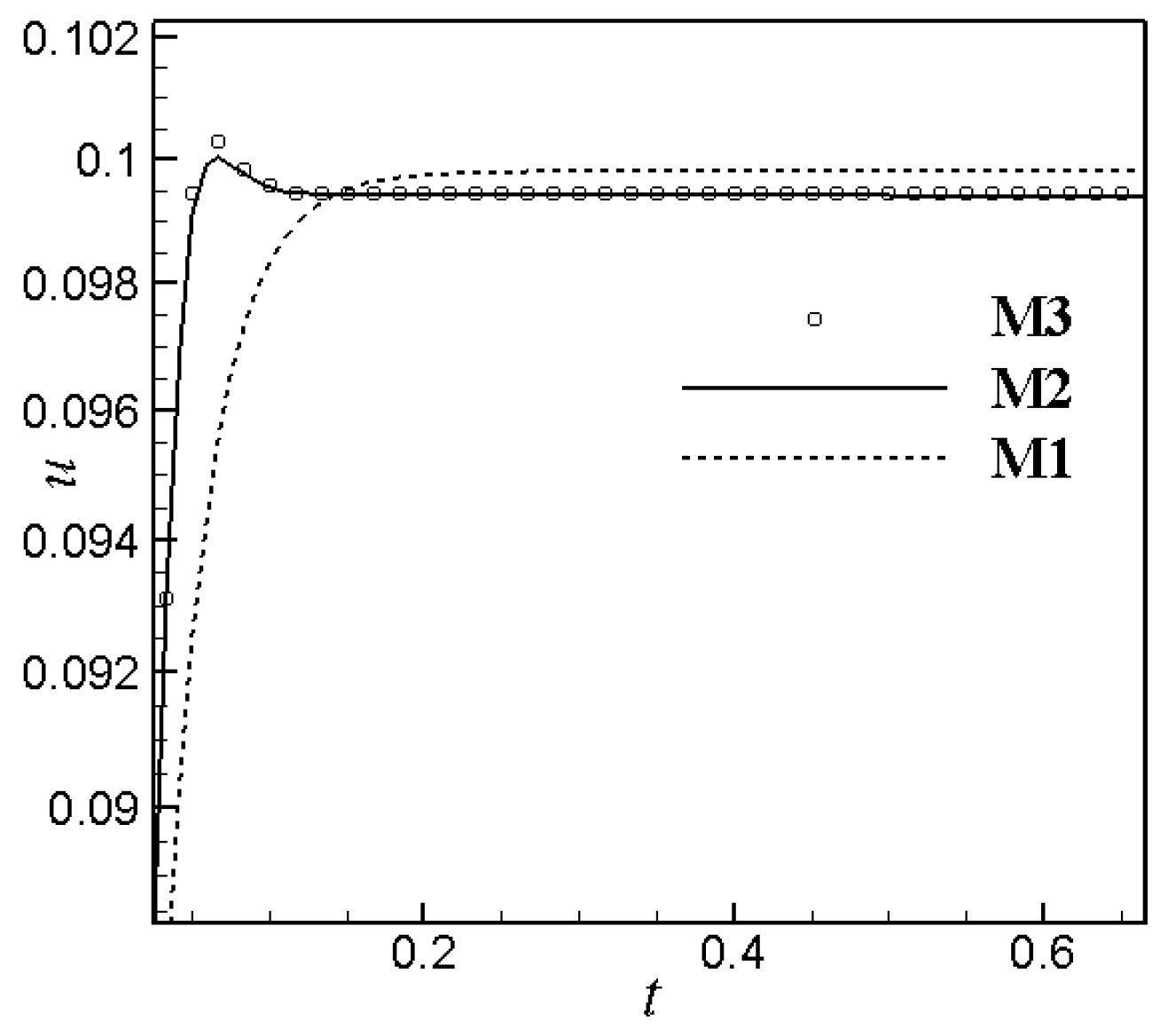


| Mesh | Total Cell | (x/L) |
|---|---|---|
| M1 | 120,000 | 0.05 |
| M2 | 392,000 | 0.0142 |
| M3 | 512,000 | 0.0125 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, J.; Ouyang, J.; Lu, J. A Lattice Boltzmann Method and Asynchronous Model Coupling for Viscoelastic Fluids. Appl. Sci. 2018, 8, 352. https://doi.org/10.3390/app8030352
Su J, Ouyang J, Lu J. A Lattice Boltzmann Method and Asynchronous Model Coupling for Viscoelastic Fluids. Applied Sciences. 2018; 8(3):352. https://doi.org/10.3390/app8030352
Chicago/Turabian StyleSu, Jin, Jie Ouyang, and Junxiang Lu. 2018. "A Lattice Boltzmann Method and Asynchronous Model Coupling for Viscoelastic Fluids" Applied Sciences 8, no. 3: 352. https://doi.org/10.3390/app8030352
APA StyleSu, J., Ouyang, J., & Lu, J. (2018). A Lattice Boltzmann Method and Asynchronous Model Coupling for Viscoelastic Fluids. Applied Sciences, 8(3), 352. https://doi.org/10.3390/app8030352





