Mathematical Models of Electro-Magnetohydrodynamic Multiphase Flows Synthesis with Nano-Sized Hafnium Particles
Abstract
:Featured Application
Abstract
1. Introduction
2. Mathematical Model
- (i)
- For the fluid phase:
- (ii)
- For the particle phase:
3. Solution of the Problem
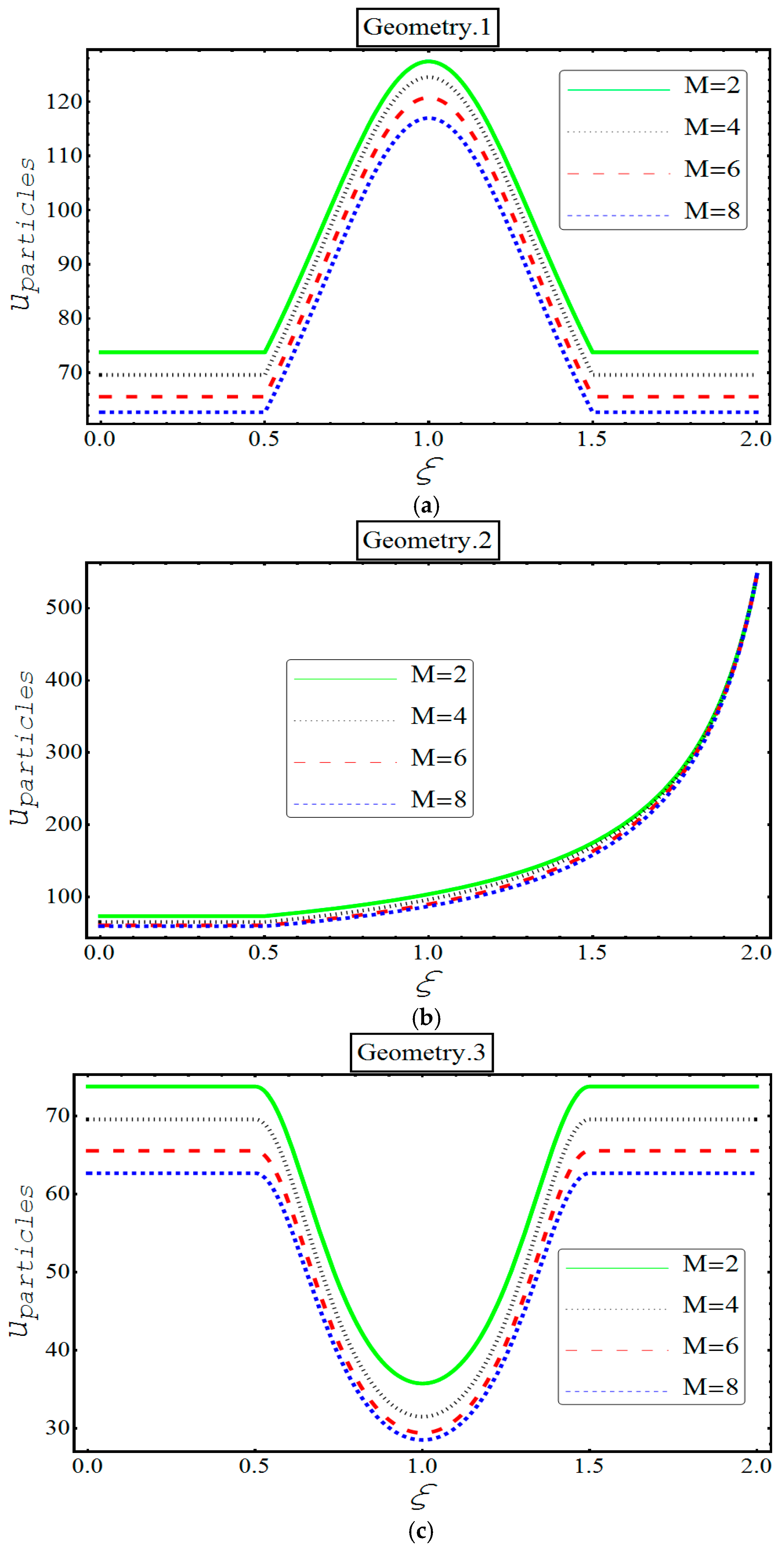
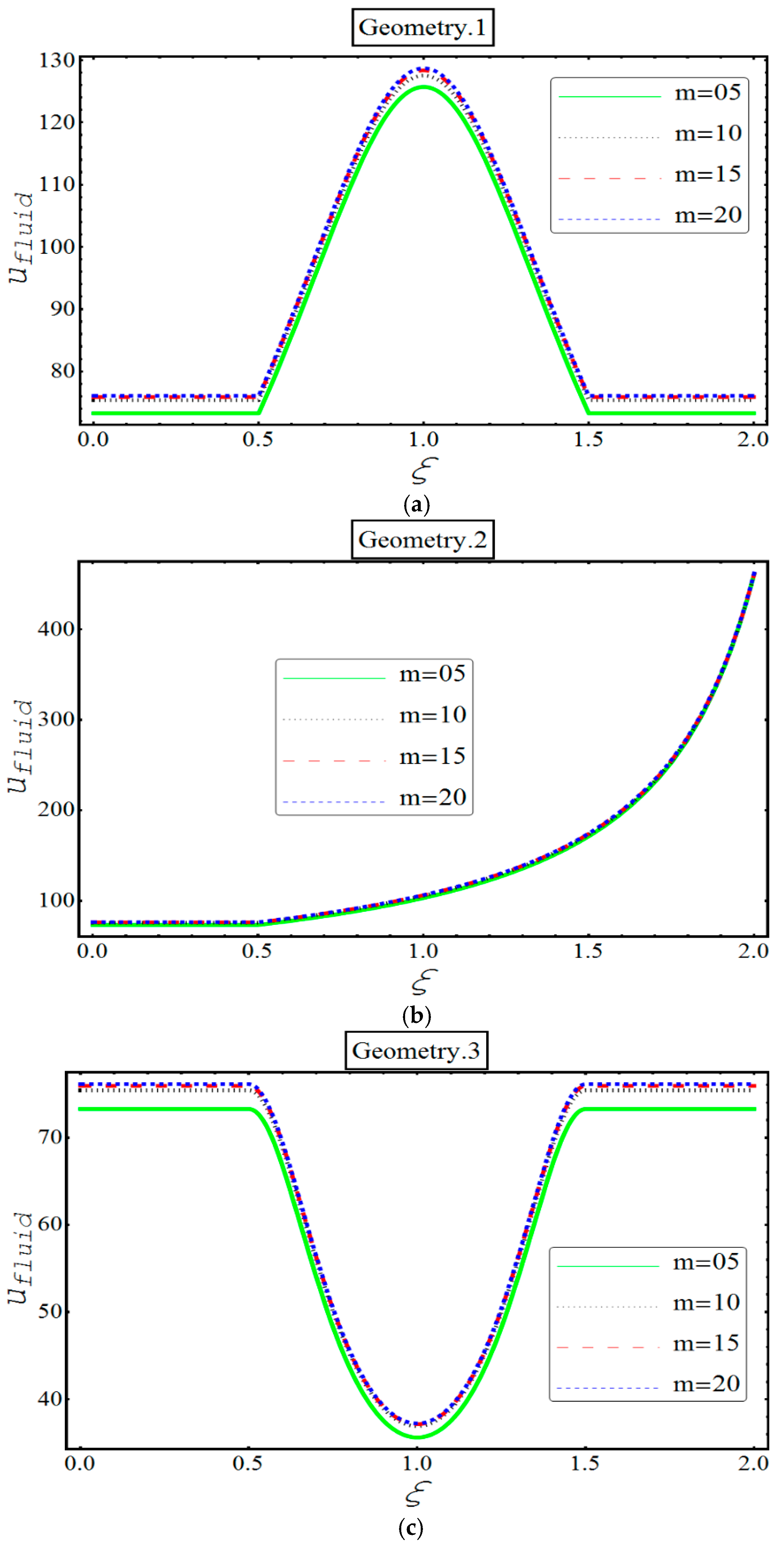
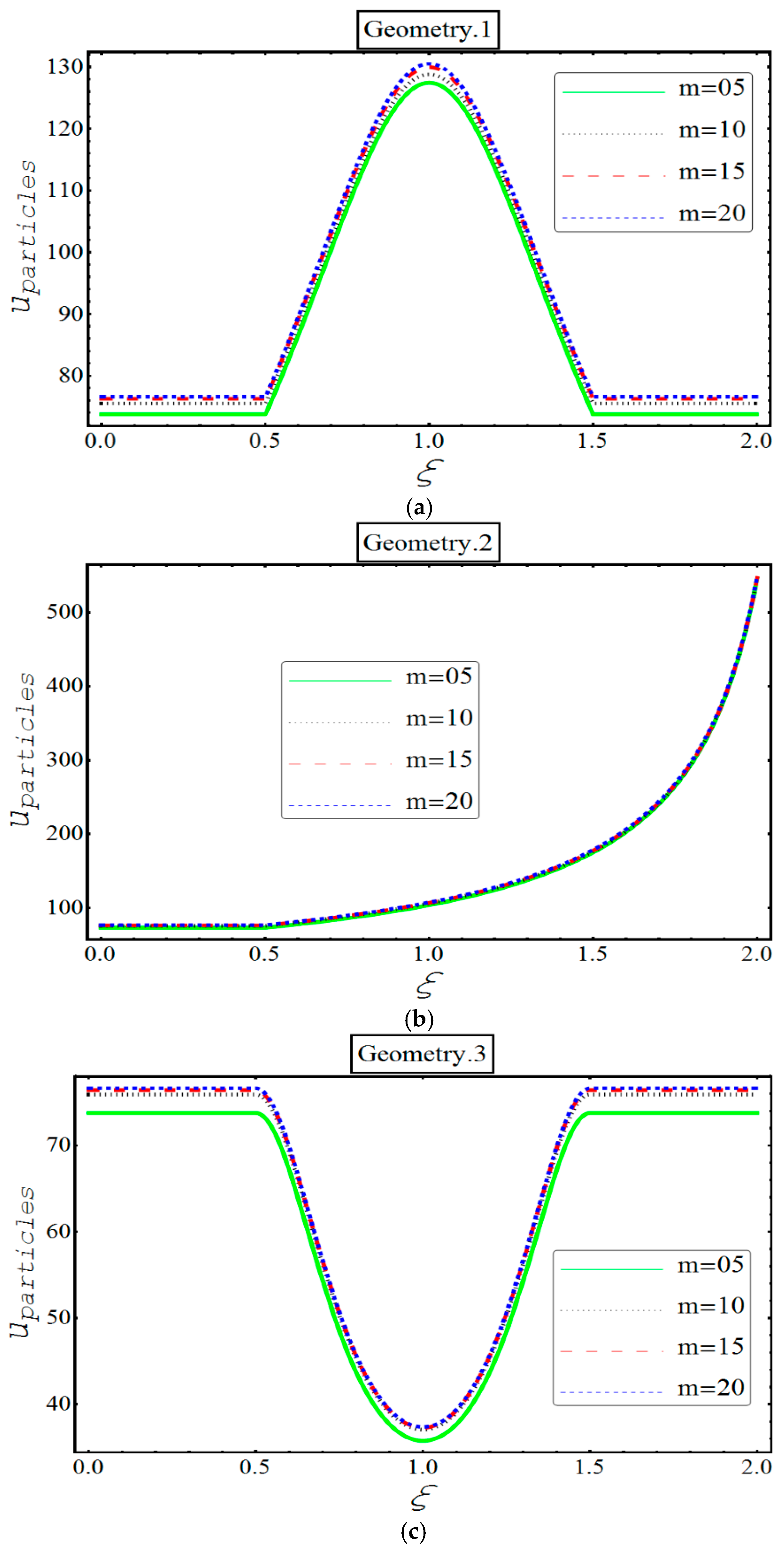
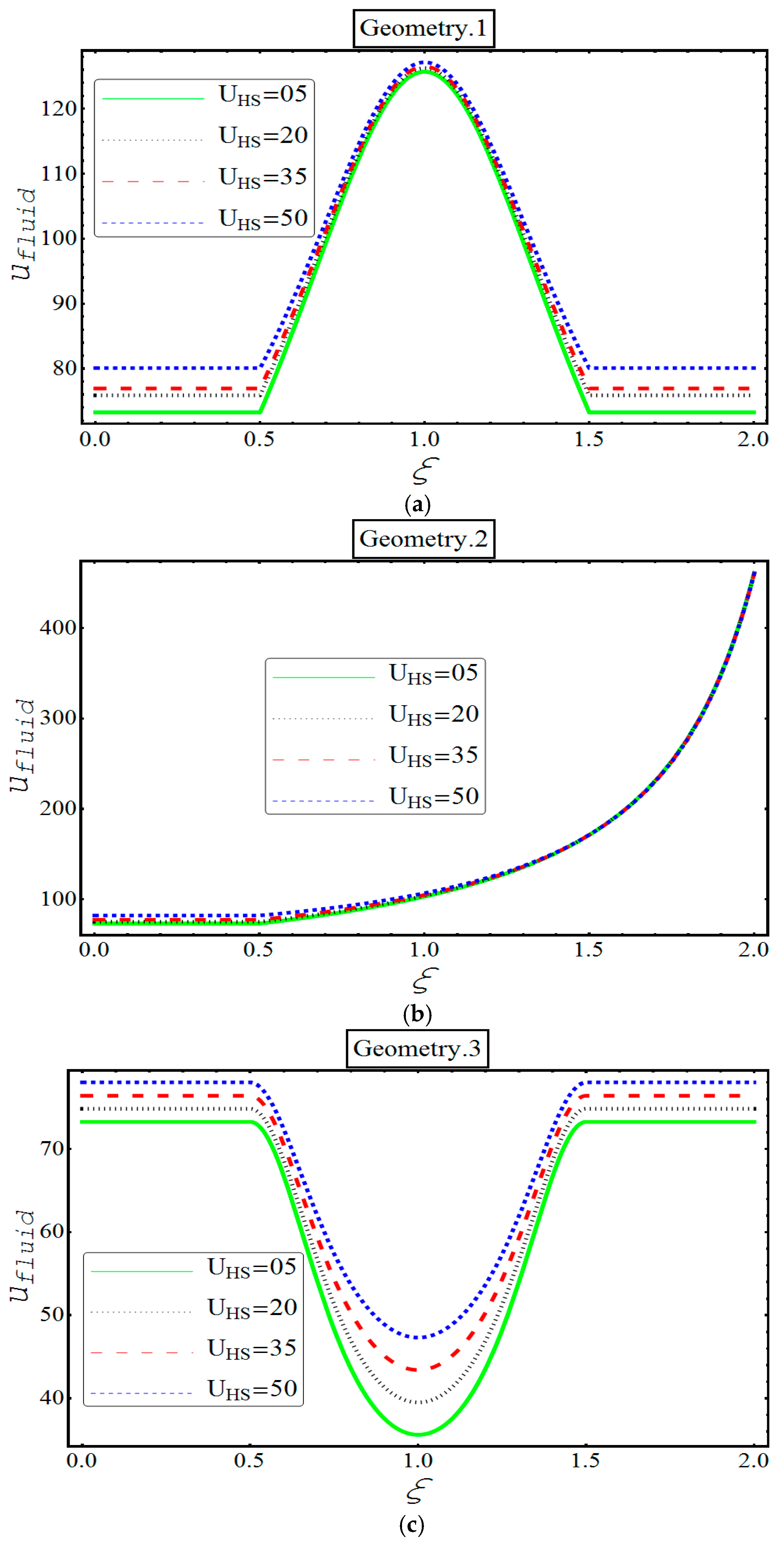
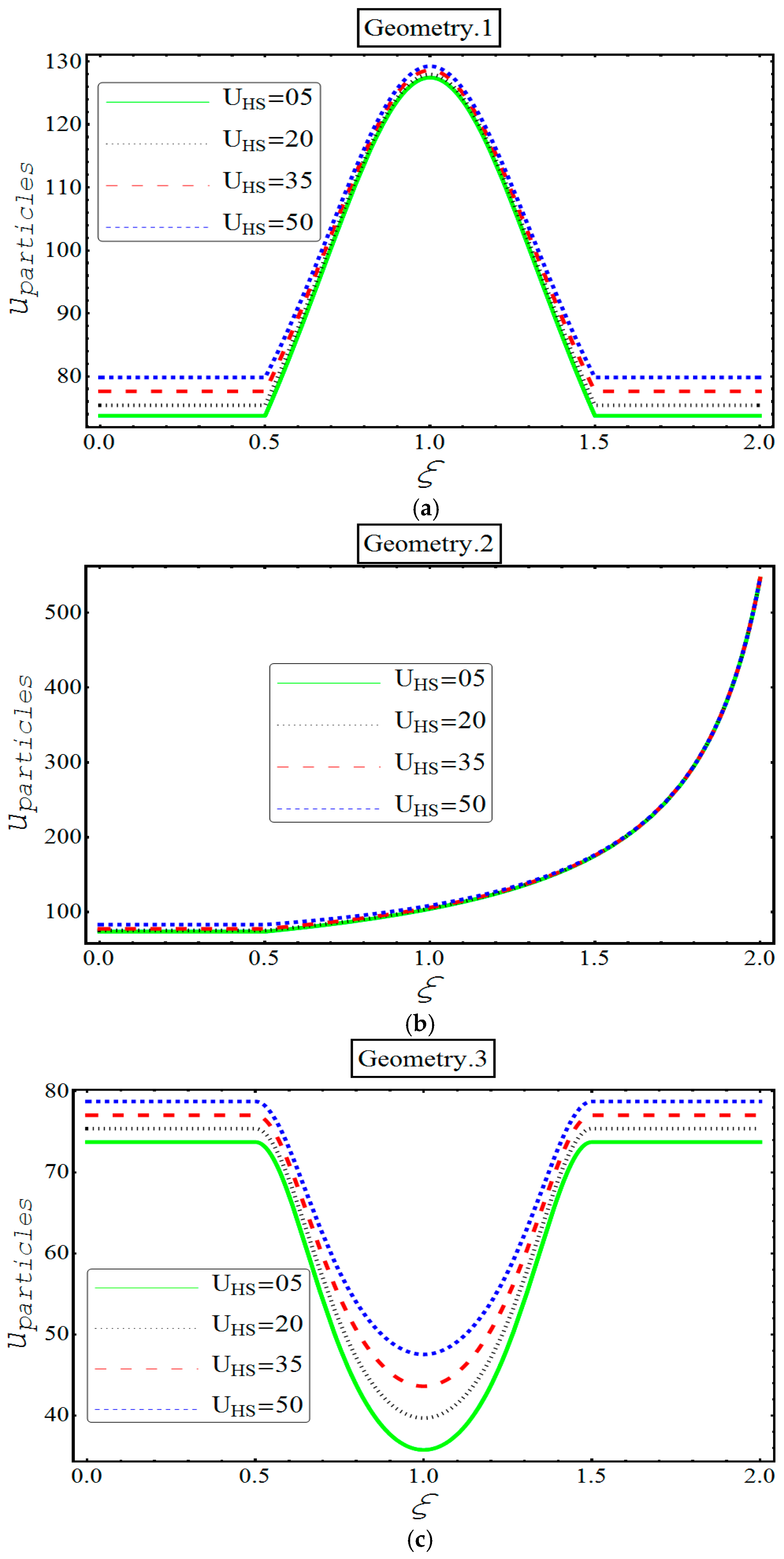
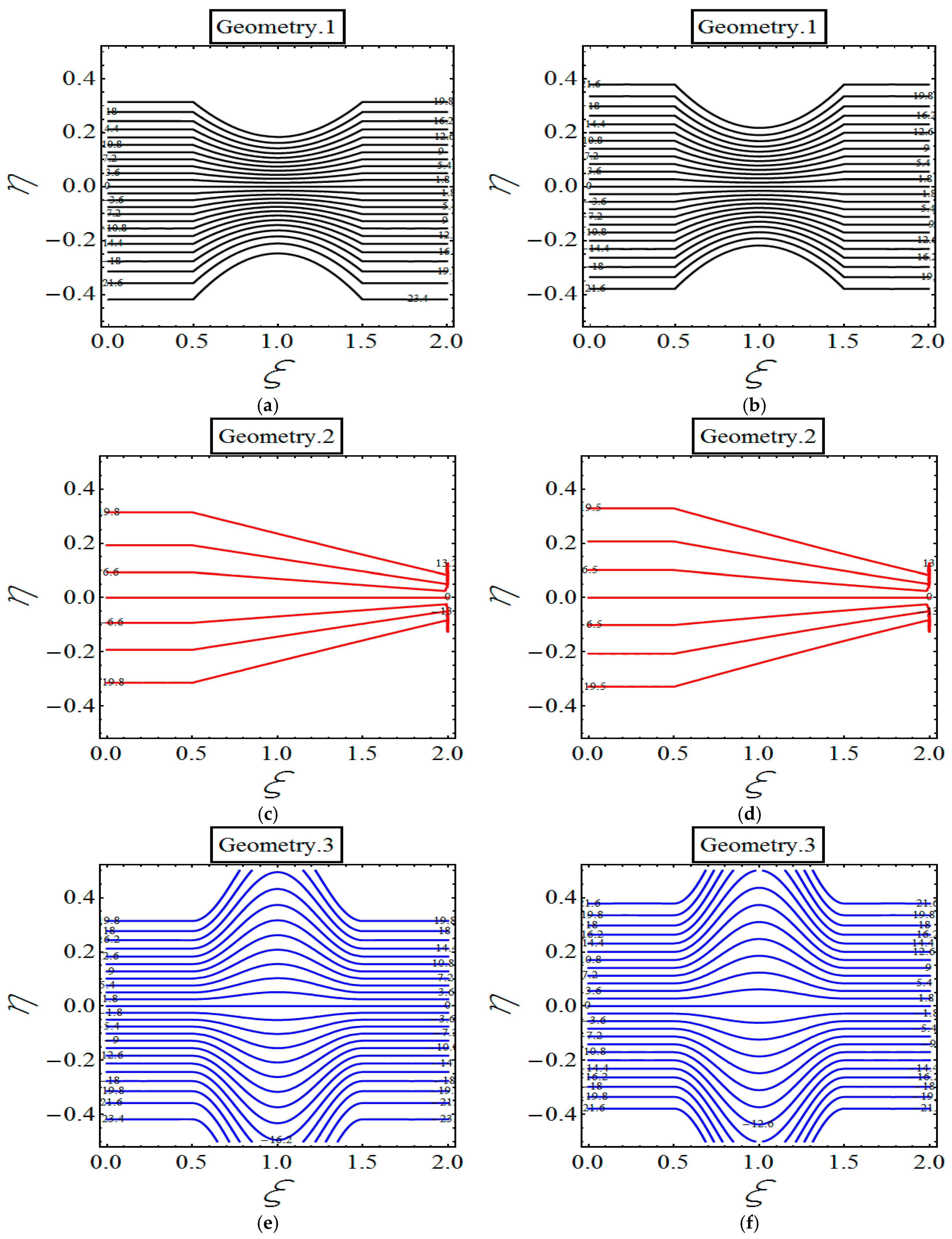
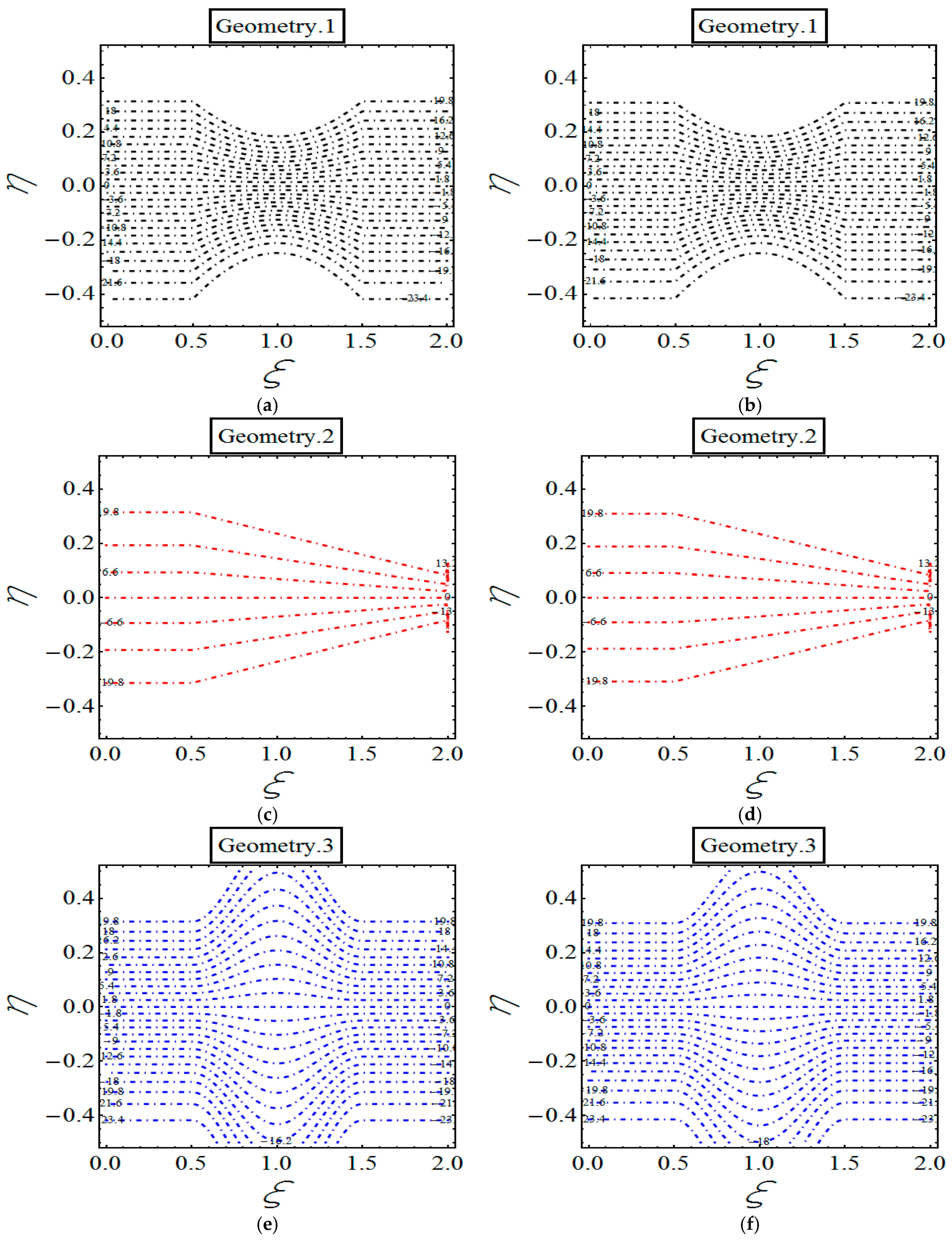
4. Results and Discussion
5. Conclusions
- ➢
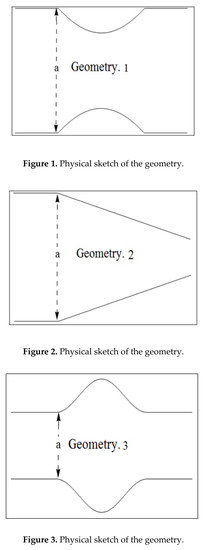
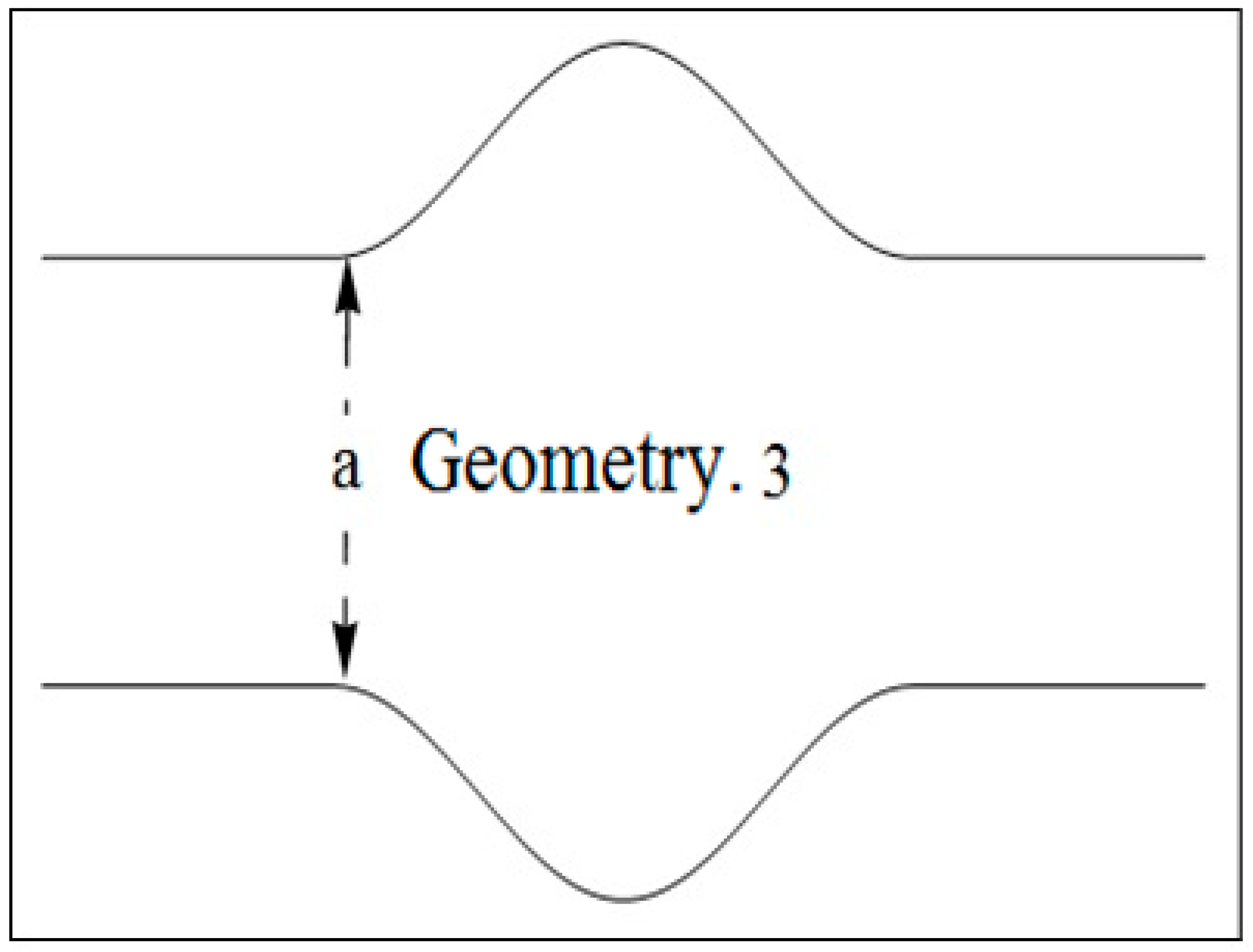
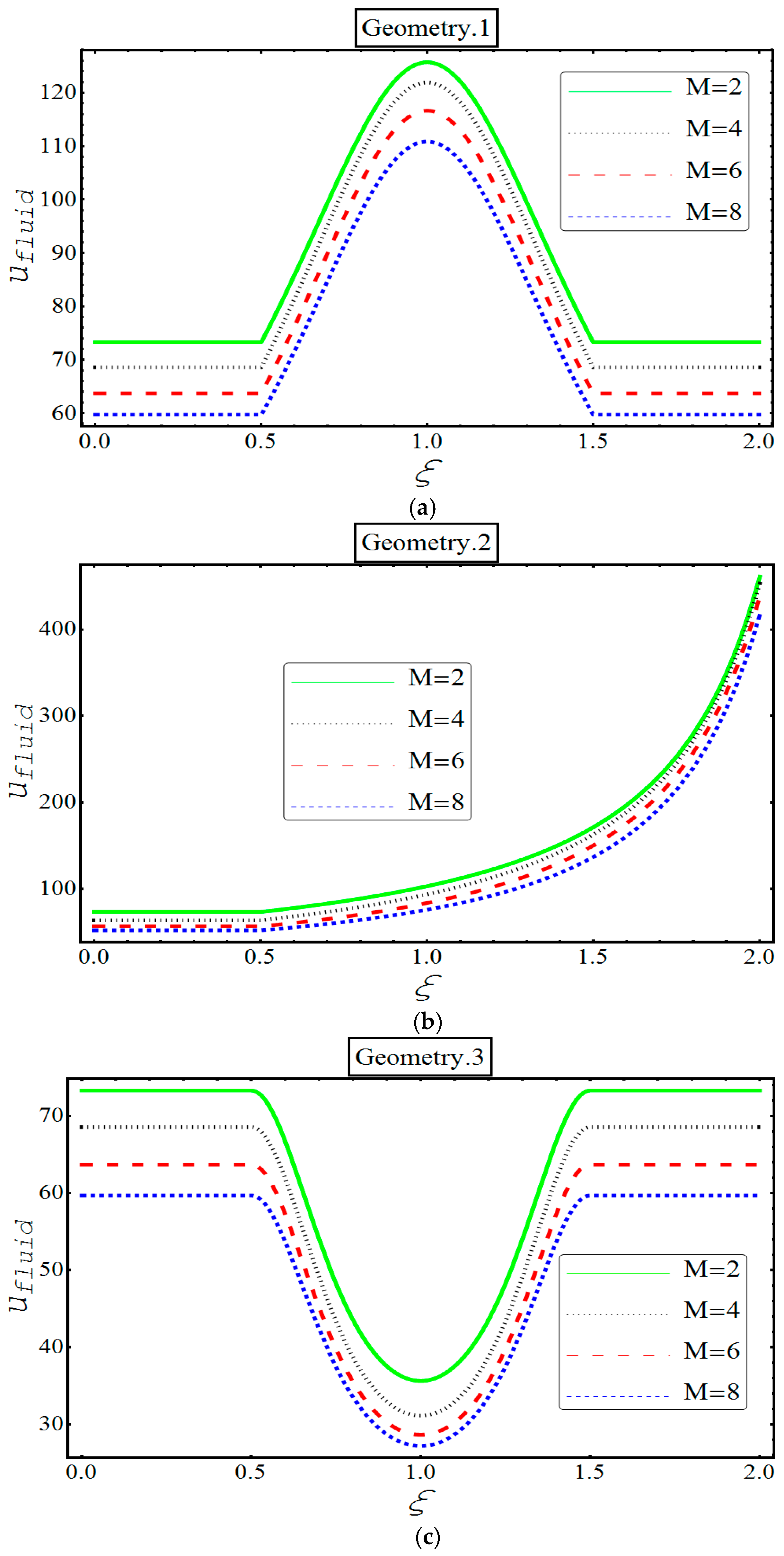
- Decrease in the behavior of both fluid and particle velocity, is found in third geometry and it is because of central ‘bulging out’ corrugation.
- ➢
- Velocity of each phase loses its strength for different values of Hartmann number in all geometries.
- ➢
- An apparent incline in the velocity of both phases is observed in all three geometries for various values of and .
- ➢
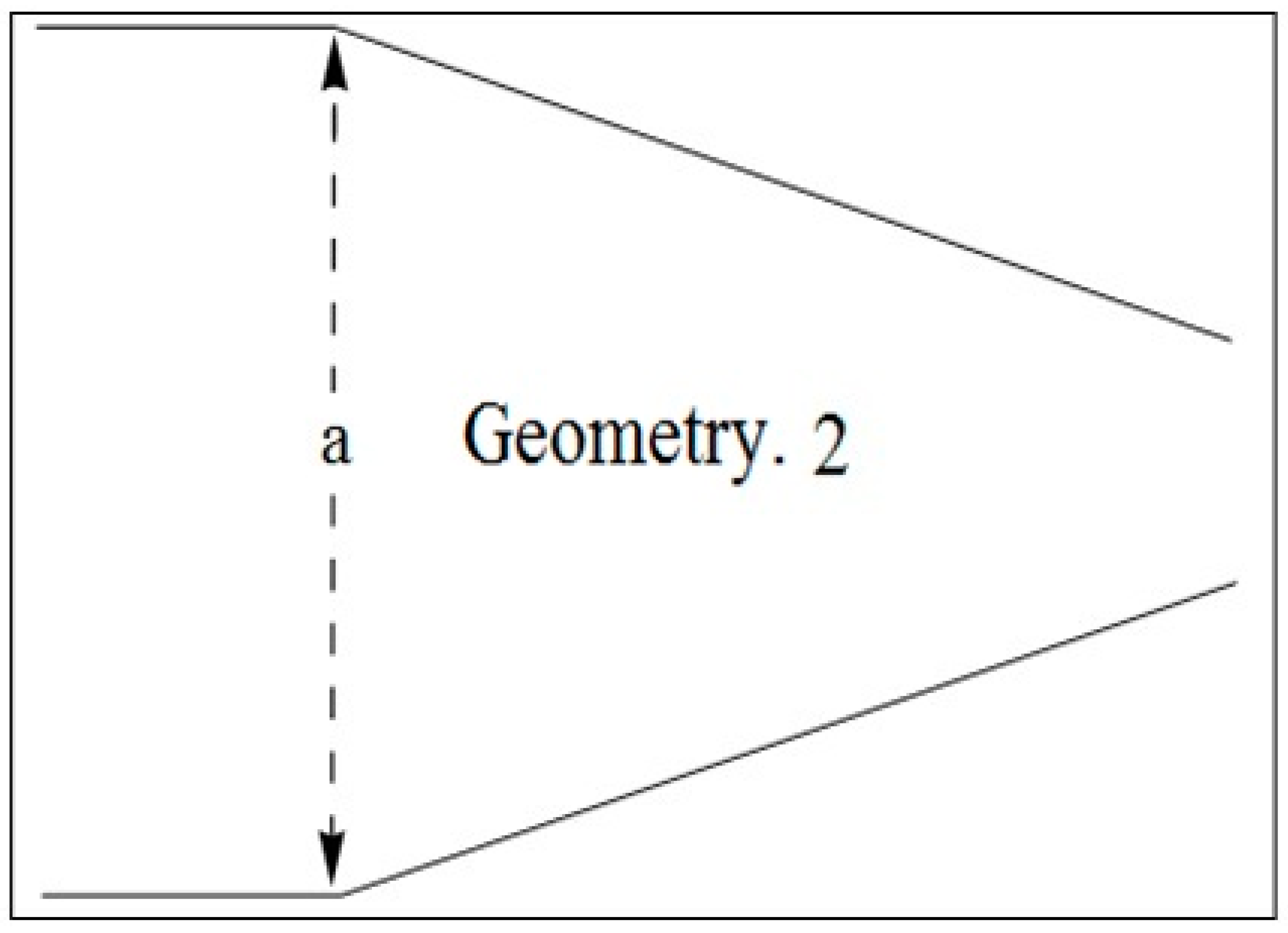
- Unlike in other geometries, only in second geometry, the velocity of each phase keeps on increasing indefinitely. This unique feature can be termed because of the bent ‘bellows’ structure of the channel.
- ➢
- Emergence of extra stream lines in all geometries in response of strengthening the magnetic field.
- ➢
- Reduction in stream lines for solely observed in first geometry.
- ➢
- In the case of , flow patterns in all geometries remain same.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chamkha, A.J. Solutions for fluid-particle flow and heat transfer in a porous channel. Int. J. Eng. Sci. 1996, 34, 1423–1439. [Google Scholar] [CrossRef]
- Khan, U.; Adnan, M.; Ahmed, N. Soret and Dufour effects on Jeffery-Hamel flow of second-grade fluid between convergent/divergent channel with stretchable walls. Results Phys. 2017, 7, 361–372. [Google Scholar] [CrossRef]
- Malvandi, A.; Ghasemi, A.; Ganji, D. Thermal performance analysis of hydromagnetic Al2O3-water nanofluid flows inside a concentric micro annulus considering nanoparticle migration and asymmetric heating. Int. J. Therm. Sci. 2016, 109, 10–22. [Google Scholar] [CrossRef]
- Misra, J.C.; Chandra, S. Electro-osmotic flow of a second-grade fluid in a porous microchannel subject to an AC electric field. J. Hydrodyn. 2013, 25, 309–316. [Google Scholar] [CrossRef]
- Nadeem, S.; Akram, S. Influence of inclined magnetic field on peristaltic flow of a Williamson fluid model in an inclined symmetric or asymmetric channel. Math. Comput. Model. 2010, 52, 107–119. [Google Scholar] [CrossRef]
- Chamkha, A.J. Hydromagnetic two-phase flow in a channel. Int. J. Eng. Sci. 1995, 33, 437–446. [Google Scholar] [CrossRef]
- Hank, S.; Favrie, N.; Massoni, J. Modeling hyperelasticity in non-equilibrium multiphase flows. J. Comput. Phys. 2017, 330, 65–91. [Google Scholar] [CrossRef]
- Dong, S. Wall-bounded multiphase flows of immiscible incompressible fluids: Consistency and contact-angle boundary condition. J. Comput. Phys. 2017, 338, 21–67. [Google Scholar] [CrossRef]
- Hayat, T.; Sajjad, R.; Ellahi, R.; Alsaedi, A.; Muhammad, T. Homogeneous-heterogeneous reactions in MHD flow of micropolar fluid by a curved stretching surface. J. Mol. Liq. 2017, 240, 209–220. [Google Scholar] [CrossRef]
- Awais, M.; Aqsa; Malik, M.Y.; Awan, S.E. Generalized magnetic effects in a Sakiadis flow of polymeric Nano-liquids: Analytic and numerical solutions. J. Mol. Liq. 2017, 241, 570–576. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Bhatti, M.M. Active method for nanofluid heat transfer enhancement by means of EHD. Int. J. Heat Mass Transf. 2017, 109, 115–122. [Google Scholar] [CrossRef]
- Hassan, M.; Zeeshan, A.; Majeed, A.; Ellahi, R. Particle shape effects on ferro fluid flow and heat transfer under influence of low oscillating magnetic field. J. Magn. Magn. Mater. 2017, 443, 36–44. [Google Scholar] [CrossRef]
- Khan, M.; Hashim; Hussain, M.; Azam, M. Magnetohydrodynamic flow of Carreau fluid over a convectively heated surface in the presence of non-linear radiation. J. Magn. Magn. Mater. 2016, 412, 63–68. [Google Scholar] [CrossRef]
- Hayat, T.; Muhammad, T.; Ahmad, B.; Shehzad, S. Impact of magnetic field in three-dimensional flow of Sisko nanofluid with convective condition. J. Magn. Magn. Mater. 2016, 413, 1–8. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Abbas, T.; Rashidi, M.M.; Ali, M.E.; Yang, Z. Entropy generation on MHD Eyring-Powell nanofluid through a permeable stretching surface. Entropy 2016, 18, 224. [Google Scholar] [CrossRef]
- Daskiran, C.; Liu, I.; Oztekin, A. Computational study of multiphase flows over ventilated translating blades. Int. J. Heat Mass Transf. 2017, 110, 262–275. [Google Scholar] [CrossRef]
- Raza, J.; Rohni, A.M.; Omar, Z.; Awais, M. Heat and mass transfer analysis of MHD nanofluid flow in a rotating channel with slip effects. J. Mol. Liq. 2016, 219, 703–708. [Google Scholar] [CrossRef]
- Haq, R.U.; Kazmi, S.N.; Mekkaoui, T. Thermal management of water based SWCNTs enclosed in a partially heated trapezoidal cavity via FEM. Int. J. Heat Mass Transf. 2017, 112, 972–982. [Google Scholar] [CrossRef]
- Raza, J.; Rohni, A.M.; Omar, Z.; Awais, M. Rheology of the Cu-H2O nanofluid in porous channel with heat transfer: Multiple solutions. Phys. E Low Dimens. Syst. Nanostruct. 2017, 86, 248–252. [Google Scholar] [CrossRef]
- Haq, R.U.; Rashid, I.; Khan, Z.H. Effects of aligned magnetic field and CNTs in two different base fluids over a moving slip surface. J. Mol. Liq. 2017, 243, 682–688. [Google Scholar] [CrossRef]
- Tripathi, D.; Bhushan, S.; Anwar Beg, O. Transverse magnetic field driven modification in unsteady peristaltic transport with electrical double layer effects. Colloids Surf. A Physicochem. Eng. Asp. 2016, 506, 32–39. [Google Scholar] [CrossRef]
- Mohyud-Din, S.T.; Khan, U.; Ahmed, N.; Hassan, S.M. Magnetohydrodynamic flow and heat transfer of nanofluids in stretchable convergent/divergent channels. Appl. Sci. 2015, 5, 1639–1664. [Google Scholar] [CrossRef]
- Khan, W.G.; Idrees, T.; Islam, M.; Khan, S.; Dennis, L.C. Thin film Williamson nanofluid flow with varying viscosity and thermal conductivity on a time-dependent stretching sheet. Appl. Sci. 2016, 6, 334. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ellahi, R. Electrohydrodynamic nanofluid hydrothermal treatment in an enclosure with sinusoidal upper wall. Appl. Sci. 2015, 5, 294–306. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Zia, Q.M.; Ellahi, R. Influence of induced magnetic field on free convection of nanofluid considering Koo-Kleinstreuer-Li (KKL) correlation. Appl. Sci. 2016, 6, 324. [Google Scholar] [CrossRef]
- Sekrani, G.; Poncet, S. Further investigation on laminar forced convection of nanofluid flows in a uniformly heated pipe using direct numerical simulations. Appl. Sci. 2016, 6, 332. [Google Scholar] [CrossRef]
- Rashidi, S.; Esfahani, J.A.; Ellahi, R. Convective heat transfer and particle motion in an obstructed duct with two side by side obstacles by means of DPM model. Appl. Sci. 2017, 7, 431. [Google Scholar] [CrossRef]
- Ellahi, R. Special issue on recent developments of nanofluids. Appl. Sci. 2018, 8, 192. [Google Scholar] [CrossRef]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hussain, F.; Ellahi, R.; Zeeshan, A. Mathematical Models of Electro-Magnetohydrodynamic Multiphase Flows Synthesis with Nano-Sized Hafnium Particles. Appl. Sci. 2018, 8, 275. https://doi.org/10.3390/app8020275
Hussain F, Ellahi R, Zeeshan A. Mathematical Models of Electro-Magnetohydrodynamic Multiphase Flows Synthesis with Nano-Sized Hafnium Particles. Applied Sciences. 2018; 8(2):275. https://doi.org/10.3390/app8020275
Chicago/Turabian StyleHussain, Farooq, Rahmat Ellahi, and Ahmad Zeeshan. 2018. "Mathematical Models of Electro-Magnetohydrodynamic Multiphase Flows Synthesis with Nano-Sized Hafnium Particles" Applied Sciences 8, no. 2: 275. https://doi.org/10.3390/app8020275
APA StyleHussain, F., Ellahi, R., & Zeeshan, A. (2018). Mathematical Models of Electro-Magnetohydrodynamic Multiphase Flows Synthesis with Nano-Sized Hafnium Particles. Applied Sciences, 8(2), 275. https://doi.org/10.3390/app8020275