Topology Optimisation Using MPBILs and Multi-Grid Ground Element
Abstract
:1. Introduction
2. Topological Designs with Single-and Multi-Ground Design Approaches
2.1. Topological Designs with Ground Element Filtering
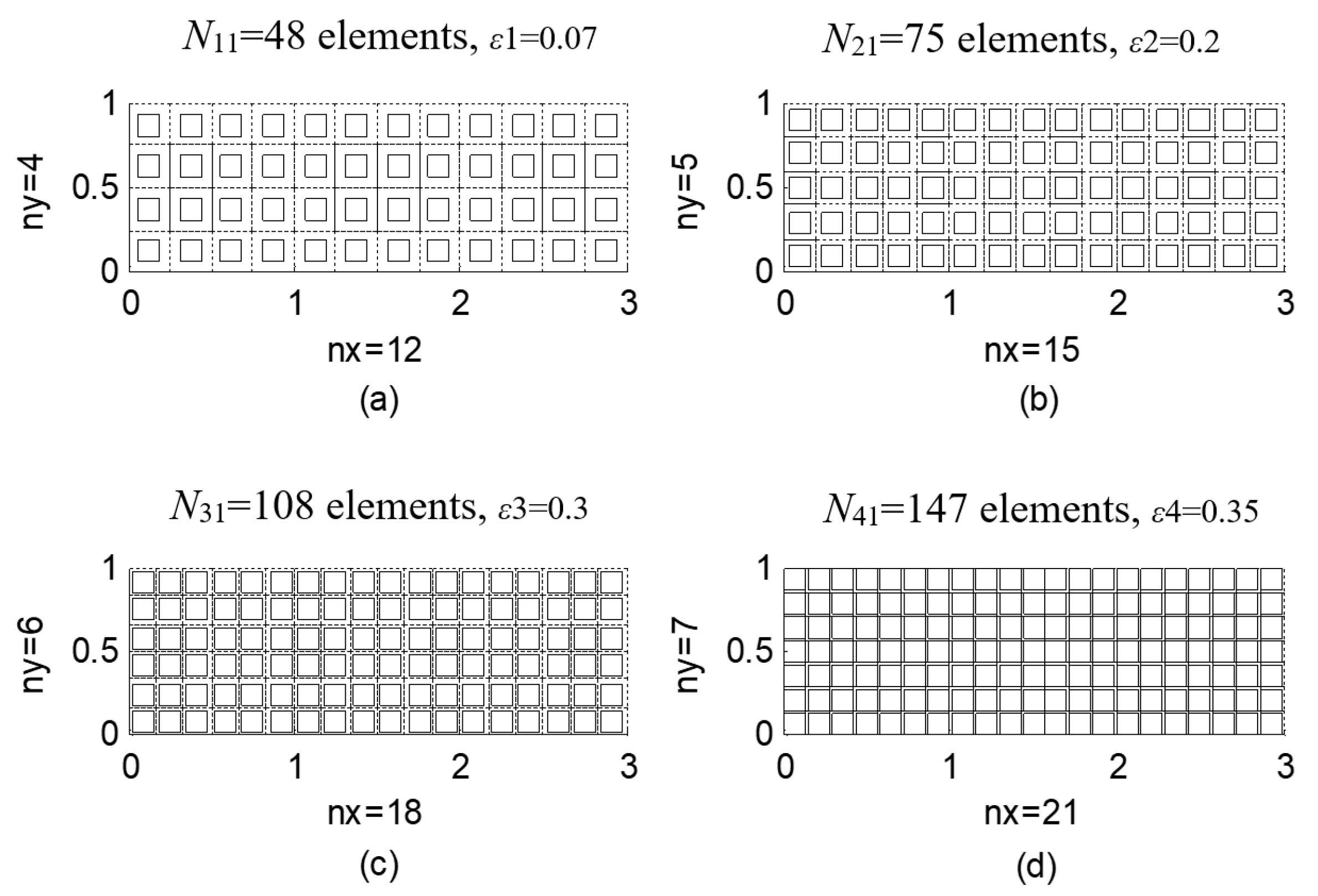
2.2. Single-and Multi-Grid Ground Elements
| Algorithm 1. Encoding and decoding scheme for a MG approach. |
| Initialization: Generate four sets of ground elements and define the threshold value of ε for each set. Inputx sized (N41 + 1) × 1. Output: Thicknesses of ground elements. Encoding x1 ∈ [1, 4] is used for selecting a set of ground elements. x2 to are used for element thicknesses. Decoding 1: Find n = round(x1) where round(.) is a round-off operator. 2: If n = 1: x2 to are set as N11 element thicknesses and ε = ε1. 3: If n = 2: x2 to are set as N21 element thicknesses and ε = ε2. 4: If n = 3: x2 to are set as N31 element thicknesses and ε = ε3. 5: If n = 4: x2 to are set as N41 element thicknesses and ε = ε4. |
3. Performance Enhancements of Multi-Objective, Population-Based Incremental Learning
3.1. Multi-Objective, Population-Based Incremental Learning
3.2. Opposite-Based MPBIL
3.3. Multi-Learning Rate
| Algorithm 2. MPBIL with multi-learning rate. |
| Initialization Probability matrix P = [0.5]l×nb, Probability matrix Pi = [0.5]l/M×nb where i = 1, …, M = 3, external Pareto archive Pareto = {}. 1: Generate a binary population B from P. 2: Decode the binary population to be xn×Np and find the objective values fm×Np. 3: Update Pareto by replacing it with non-dominated solutions of union set Pareto ∪ x. 4: If the number of members in Pareto exceeds the predefined archive size NA, remove some of them by using an archiving technique. 5: If the termination criterion is fulfilled, stop the procedure. Otherwise, go to step 6: 6: Update P and create a binary population 6.1: Set a binary population B = {}. 6.2: For i = 1 to l/M. 6.2.1: Select n0 binary solutions from Pareto randomly. 6.2.2: Use LRk = 0.25, 0.5, 0.75, for each k = 1, …, M. (For this research M = 3) 6.2.3: Update the ith row of P by using (1). 6.2.4: Generate the ith row of probability matrix Pi using (2) and each LRk. 6.2.5: Generate rand ∈ [0, 1] a uniform random number. 6.2.6: If rand < the predefined mutation probability, update the ith row of P1, P2 and P3 using similar equation in [3]. 6.2.7: Generate binary subpopulations SB1, SB2 and SB3 from the ith row of P1, P2 and P3, respectively. 6.2.8: Set B = B∪SB1∪SB2∪SB3 6.3: Next i. 7: Go to step 2. |
3.4. Adaptive Learning Rate
| Algorithm 3. MPBIL with adaptive learning rate. |
| Initialization probability matrix P = [0.5]l×nb, external Pareto archive Pareto = {}. 1: Generate a binary population B from P. 2: Decode the binary population to be xn×Np and find the objective values fm×Np. 3: Update Pareto by replacing it with non-dominated solutions of union set Pareto∪x. 4: If the number of members in Pareto exceeds the predefined archive size NA, remove some of them by using an archiving technique. 5: If the termination criterion is fulfilled, stop the procedure. Otherwise, go to step 6: 6: Update P. 6.1: For i = 1 to l. 6.1.1: Select n0 binary solutions from Pareto randomly. 6.1.2: Generate LR using (3). 6.1.3: Update the ith row of P by using (1). 6.1.4: Generate rand ∈ [0, 1] a uniform random number. 6.1.5: If rand <the predefined mutation probability, update the ith row of P using similar equation in [3]. 6.2: Next i. 7: Go to step 1. |
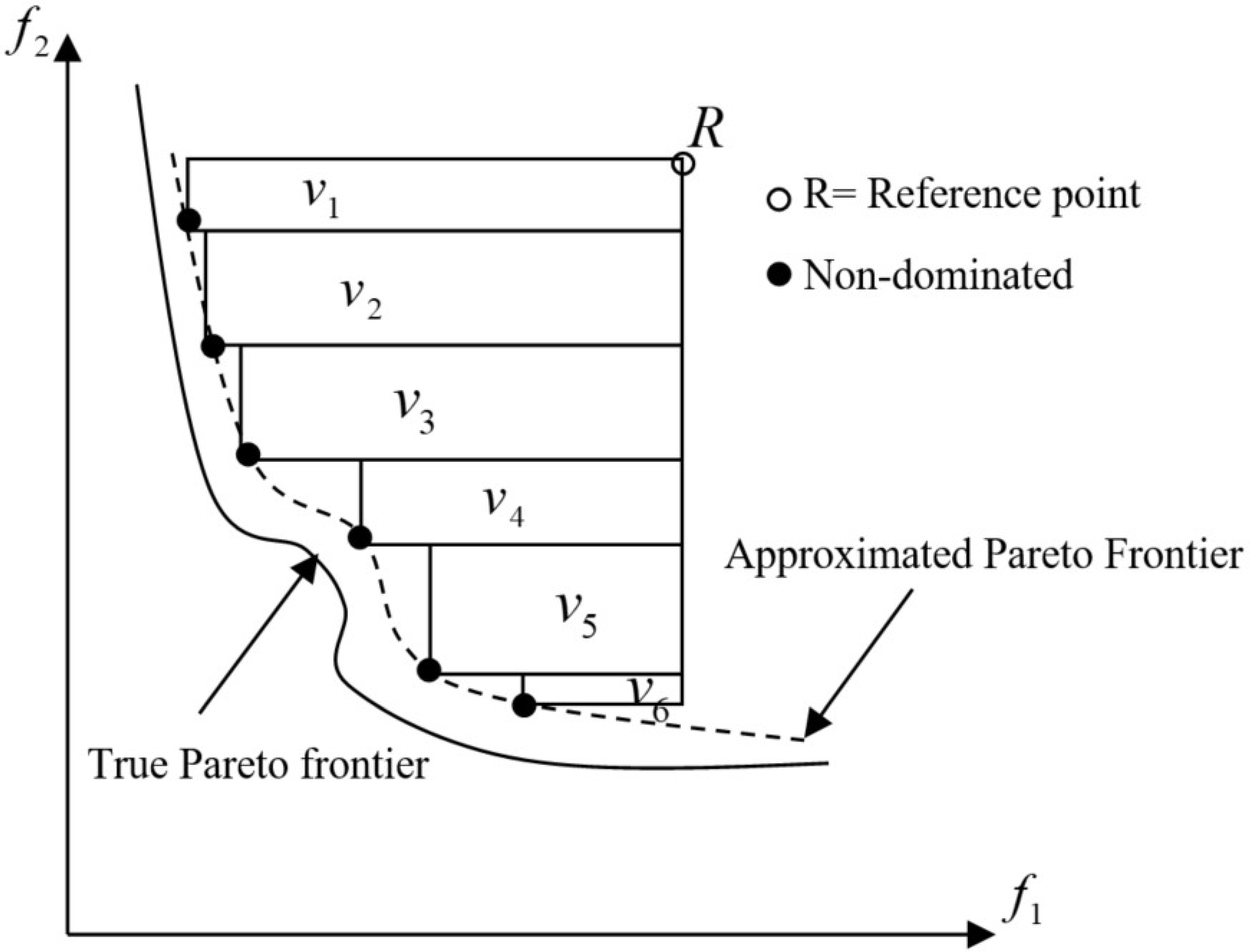
3.5. The Performance Index and Non-Parametric Statistical Test
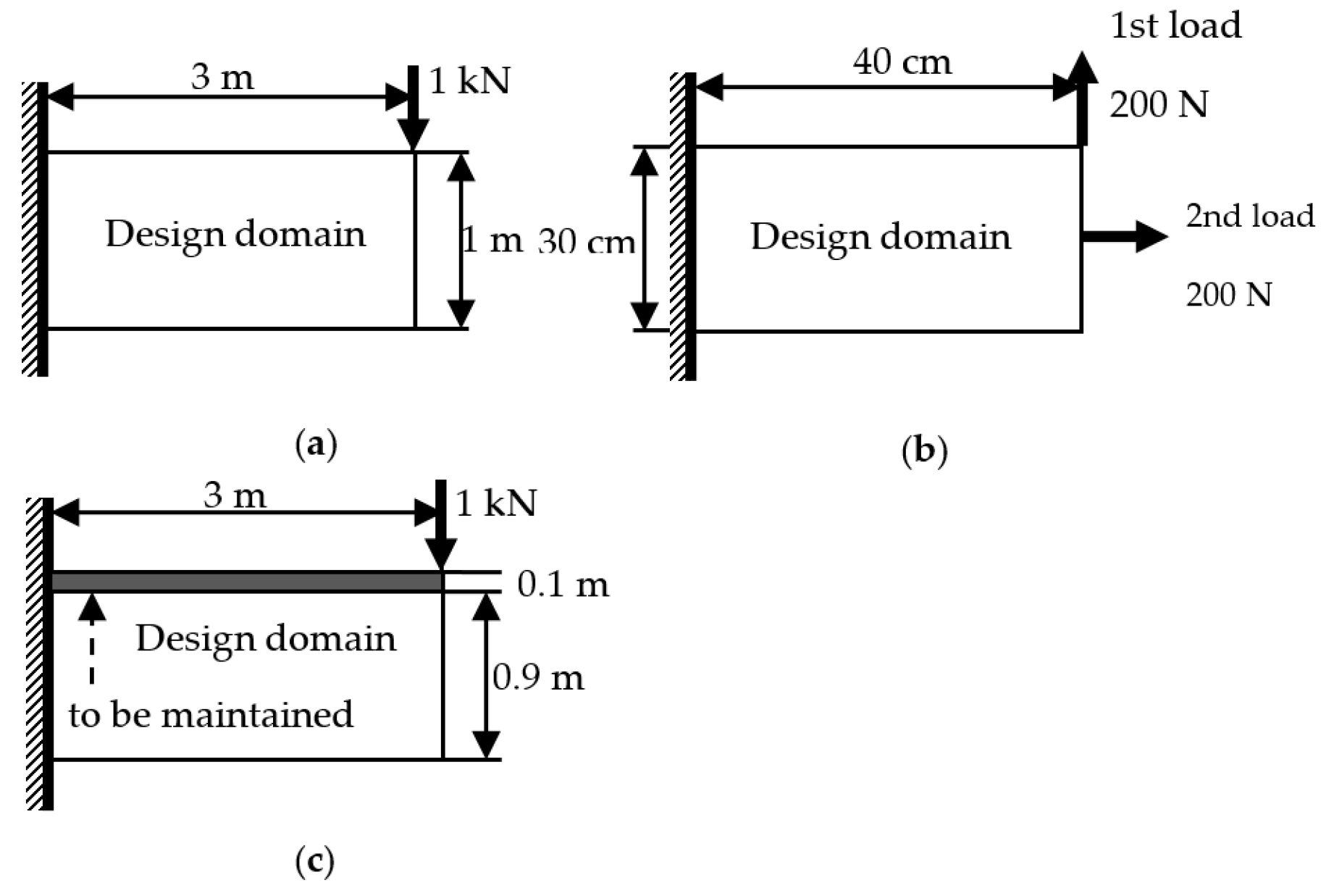
4. Numerical Experiment
0.2 ≤ r ≤ 0.8
ρi ∈ {0.0001, 1}
c2 ≤ 5c2,min
0.2 ≤ r ≤ 0.8
ρi ∈ {0.0001, 1}
5. Design Results
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Noilublao, N.; Bureerat, S. Topology and sizing optimization of trusses with adaptive ground finite elements using Multiobjective PBIL. Adv. Mater. Res. 2011, 308, 1116–1121. [Google Scholar] [CrossRef]
- Noilublao, N.; Bureerat, S. Simultaneous topology, shape, and sizing optimisation of plane trusses with adaptive ground finite elements using MOEAs. Math. Probl. Eng. 2013, 2013, 838102. [Google Scholar] [CrossRef]
- Sleesongsom, S.; Bureerat, S. Morphing wing structural optimization using opposite-based population-based incremental learning and multigrid Ground elements. Math. Probl. Eng. 2015, 2015, 730626. [Google Scholar] [CrossRef]
- Rahnamayan, S.; Tizhoosh, H.R.; Salama, M.M.A. A novel population initialization method for accelerating evolutionary algorithms. Comput. Math. Appl. 2007, 53, 1605–1614. [Google Scholar] [CrossRef]
- Gao, X.Z.; Wang, X.; Ovaska, S.J. A hybrid harmony search method based on OBL. In Proceedings of the 13th IEEE International Conference on Computational Science and Engineering, Hong Kong, China, 11–13 December 2010; Kellenberger, P., Ed.; IEEE Computer Society Conference Publishing Services: Piscataway, NJ, USA, 2010. [Google Scholar]
- Wang, H.; Wu, Z.; Rahnamayan, S.; Liu, Y.; Ventresca, M. Enhancing particle swarm optimization using generalized opposition-based learning. Inform. Sci. 2011, 181, 4699–4714. [Google Scholar] [CrossRef]
- Xu, Q.; Wang, L.; Wang, N.; Hei, H.; Zhao, L. A review of opposition-based learning from 2005 to 2012. Eng. Appl. Artif. Intell. 2014, 29, 1–12. [Google Scholar] [CrossRef]
- Kunakote, T.; Bureerat, S. Multi-objective topology optimization using evolutionary algorithms. Eng. Optim. 2011, 43, 541–557. [Google Scholar] [CrossRef]
- Ventresca, M.; Tizhoosh, H.R. A diversity maintaining population-based incremental learning algorithm. Inform. Sci. 2008, 178, 4038–4056. [Google Scholar] [CrossRef]
- Gao, S.C.; Cao, Q.; Ishii, M.; Tang, Z. Local search with probabilistic modeling for learning multiple-valued logic networks. IEICE Trans. Fund. Electron. Commun. Comput. Sci. 2011, 94-A, 795–805. [Google Scholar] [CrossRef]
- Xu, Z.; Wang, Y.; Li, S.; Liu, Y.; Todo, Y.; Gao, S. Immune algorithm combined with estimation of distribution for traveling salesman problem. IEEJ Trans. Electr. Electron. Eng. 2016, 11, S142–S154. [Google Scholar] [CrossRef]
- Karshenas, H.; Santana, R.; Bielza, C.; Larranaga, P. Multiobjective estimation of distribution algorithm based on joint modeling of objectives and variables. IEEE Trans. Evol. Comput. 2014, 18, 519–542. [Google Scholar] [CrossRef]
- Shim, V.A.; Tan, K.C.; Cheong, C.Y.; Chia, J.Y. Enhancing the scalability of muti-objective optimization via restricted Bolzmann machine-based estimation of distribution algorithm. Inform. Sci. 2013, 248, 191–213. [Google Scholar] [CrossRef]
- Folly, K.A.; Venayagamoothy, G.K. Effects of learning rate on the performance of the population based incremental learning algorithm. In Proceedings of the 2009 International Joint Conference on Neural Networks, Atlanta, GA, USA, 14–19 June 2009. [Google Scholar]
- Yang, S.Y.; Ho, S.L.; Ni, G.Z.; Machado, J.M.; Wong, K.F. A new implementation of population based incremental learning method for optimizations in electromagnetic. IEEE Trans. Magn. 2007, 43, 1601–1604. [Google Scholar] [CrossRef]
- Sleesongsom, S.; Bureerat, S. New conceptual design of aeroelastic wing structures by multi-objective optimization. Eng. Optim. 2013, 45, 107–122. [Google Scholar] [CrossRef]
- Sleesongsom, S.; Bureerat, S.; Tai, K. Aircraft morphing wing design by using partial topology optimization. Struct. Multidiscip. Optim. 2013, 48, 1109–1128. [Google Scholar] [CrossRef]
- Bureerat, S.; Limtragool, J. Performance enhancement of evolutionary search for topology optimization. Finite Elem. Anal. Des. 2006, 42, 547–566. [Google Scholar] [CrossRef]
- Bureerat, S.; Limtragool, J. Structural topology optimization using simulated annealing with multiresolution design variables. Finite Elem. Anal. Des. 2008, 44, 738–747. [Google Scholar] [CrossRef]
- Guirguis, D.; Aly, M.F. A derivative-free level-set method for topology optimization. Finite Elem. Anal. Des. 2016, 120, 41–56. [Google Scholar] [CrossRef]
- Ram, L.; Sharma, D. Evolutionary and GPU computing for topology optimization of structures. Swarm Evol.Comput. 2017, 35, 1–13. [Google Scholar] [CrossRef]
- Guirguis, D. Commentson“Evolutionary and GPU computing for topology optimization of structures”. Swarm Evol. Comput. 2017, 35, 111–113. [Google Scholar] [CrossRef]
- Guirguis, D.; Aly, M.; Hamza, K.; Hegazi, H.; Saitou, K. Multi-objective topologyoptimization of multi-component continuum structures via a Kriging interpolated level set approach. Struct. Multidiscip. Optim. 2015, 51, 733–748. [Google Scholar] [CrossRef]
- Bin, X.; Ding, H.; Min, X.Y. Optimal design of material microstructure for maximizing damping dissipation velocity of piezoelectric composite beam. Int. J. Mech. Sci. 2017, 128–129, 527–540. [Google Scholar]
- Xie, L.; Xia, B.; Liu, J.; Huang, G.; Lei, J. An improved fast plane wave expansion method for topology optimization of phononic crystals. Int. J. Mech. Sci. 2017, 120, 171–181. [Google Scholar] [CrossRef]
- Hu, J.; Zhao, M.; Zou, J.; Li, Y. Comparative study of stator configurations of a permanent magnet linear oscillating actuator for orbital friction vibration actuator. Appl. Sci. 2017, 7, 630. [Google Scholar] [CrossRef]
- Hagen, M.T.; Demuth, H.B.; Beale, M. Neural Network Design; PWS Publishing Company: Boston, MA, USA, 1996. [Google Scholar]
- Yuan, B.; Gallagher, M. Playing in continuous spaces: Some analysis and extension of population-based incremental learning. In Proceedings of the IEEE Congress on Evolutionary Computation, CEC 2003, Canberra, Australia, 8–12 December 2003. [Google Scholar]
- While, L.; Hingston, P.; Barone, L.; Huband, S. A faster algorithm for calculating hypervolume. IEEE Trans. Evol. Comput. 2006, 10, 29–38. [Google Scholar] [CrossRef]
- Sleesongsom, S.; Bureerat, S. Four-bar linkage path generation through self-adaptive population size teaching-learning based optimization. Knowl. Based Syst. 2017, 135, 180–191. [Google Scholar] [CrossRef]
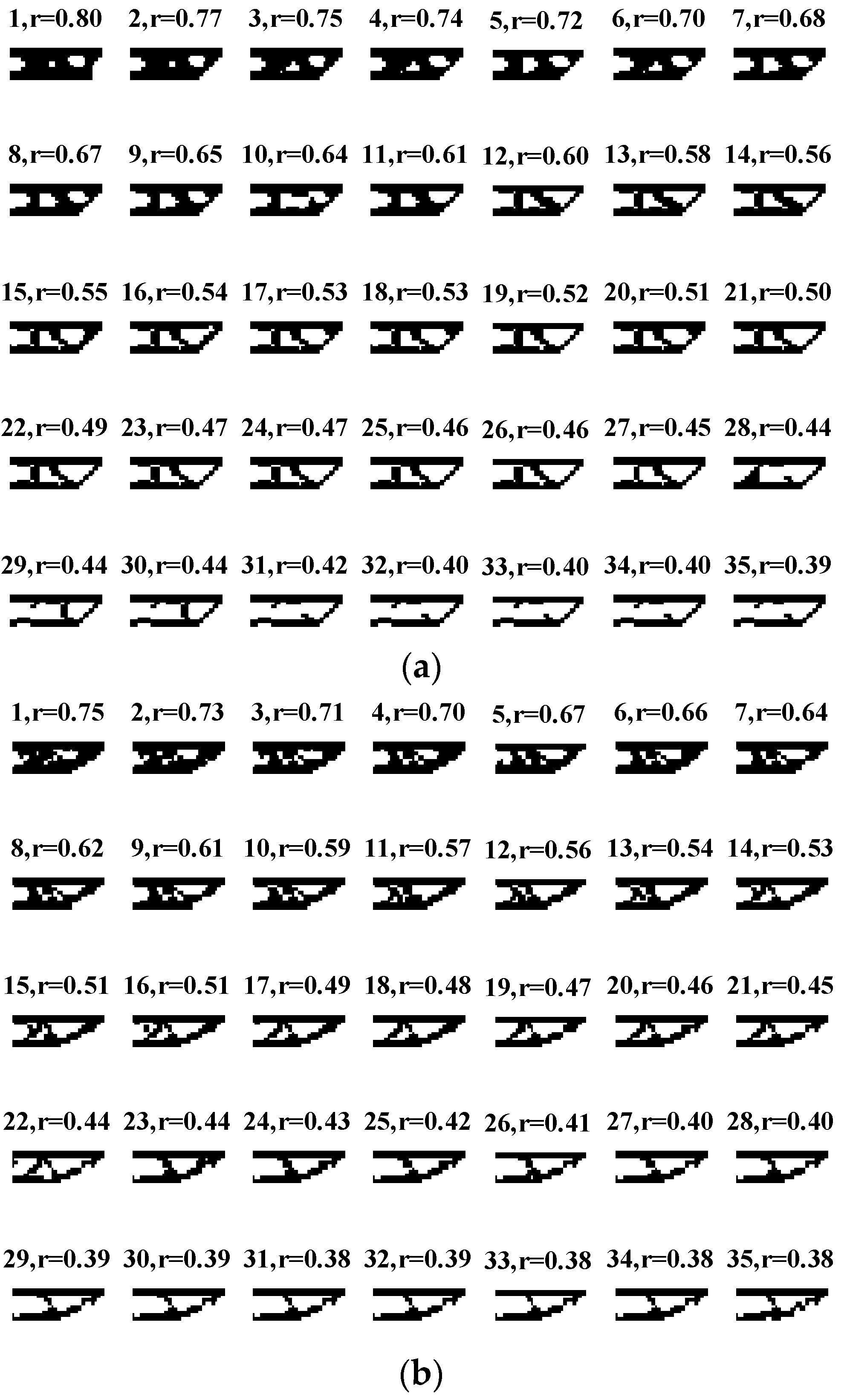




| MOP1 | MOP2 | MOP3 | MOP4 | |||||
|---|---|---|---|---|---|---|---|---|
| WMG | WOMG | WMG | WOMG | WMG | WOMG | WMG | WOMG | |
| MPBIL | 0.8553 | 0.8255 | 0.7255 | 0.6420 | 0.7951 | 0.7229 | 0.7195 | 0.6219 |
| OMPBIL | 0.8556 | 0.8426 | 0.7259 | 0.6430 | 0.7968 | 0.7438 | 0.6723 | 0.6403 |
| MPBILMLR | 0.8115 | 0.7739 | 0.7212 | 0.6285 | 0.7016 | 0.5976 | 0.6167 | 0.5651 |
| MPBILADLR | 0.8543 | 0.8371 | 0.7240 | 0.6385 | 0.7954 | 0.7407 | 0.6404 | 0.6292 |
| Average Ranking of Each AlgorithmFriedman | p-Value | |||
|---|---|---|---|---|
| MPBIL | OMPBIL | MPBILMLR | MPBILADLR | |
| 2.6250 | 3.8750 | 1 | 2.5000 | 0.0002 |
| (2) | (1) | (4) | (3) | |
| Design Problems | Average Hypervolume | |
|---|---|---|
| WMG | WOMG | |
| MOP1 | 0.8442 | 0.8198 |
| MOP2 | 0.7242 | 0.6380 |
| MOP3 | 0.7722 | 0.7013 |
| MOP4 | 0.6622 | 0.6141 |
| Average Ranking (p-value = 0.0455) | 2 (1) | 1 (2) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sleesongsom, S.; Bureerat, S. Topology Optimisation Using MPBILs and Multi-Grid Ground Element. Appl. Sci. 2018, 8, 271. https://doi.org/10.3390/app8020271
Sleesongsom S, Bureerat S. Topology Optimisation Using MPBILs and Multi-Grid Ground Element. Applied Sciences. 2018; 8(2):271. https://doi.org/10.3390/app8020271
Chicago/Turabian StyleSleesongsom, Suwin, and Sujin Bureerat. 2018. "Topology Optimisation Using MPBILs and Multi-Grid Ground Element" Applied Sciences 8, no. 2: 271. https://doi.org/10.3390/app8020271
APA StyleSleesongsom, S., & Bureerat, S. (2018). Topology Optimisation Using MPBILs and Multi-Grid Ground Element. Applied Sciences, 8(2), 271. https://doi.org/10.3390/app8020271







