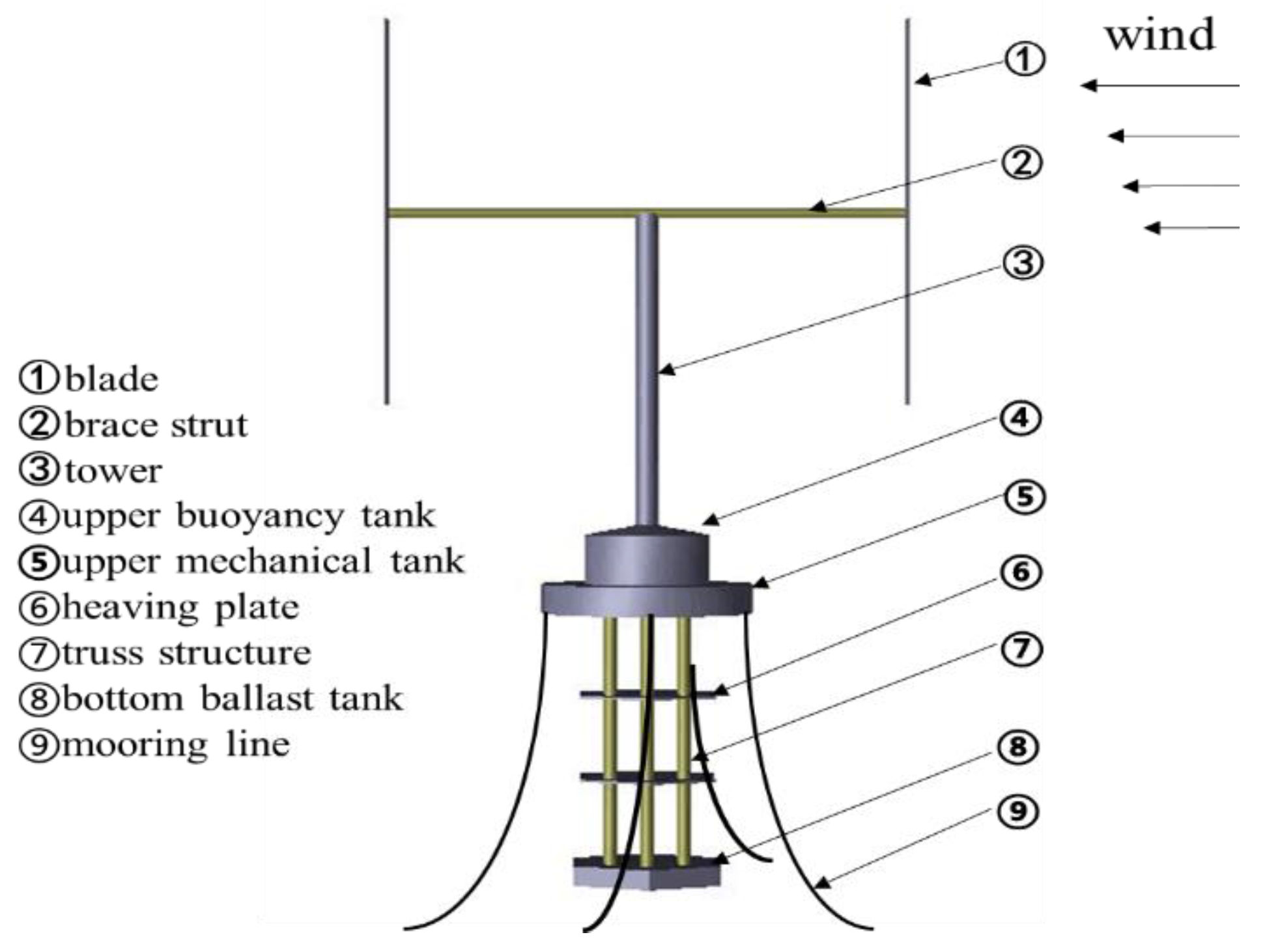
1. Introduction
With the increase of unit capacity, size of the offshore wind turbine is getting bigger and bigger. The instability of floating horizontal axis wind turbine (HAWT) may become obvious as the huge drive system is placed on the top of the high tower [
1]. The drive system of Vertical Axis Wind Turbine (VAWT) is installed on the bottom, which has little effect on the dynamic behavior of the tower. This makes floating VAWT more advantageous in the development of large-scale offshore wind power [
2].
Darrieus wind turbine is the earliest lift type VAWT, and it has the higher power coefficient comparing with other VAWT [
1]. According to the form of the blade, the Darrieus wind turbine includes curved blade and straight blade, withib which the Φ-type and the H-type are the most common. With the development of the offshore wind farm, the feasibility of the Darrieus wind turbine is assessed to be used in deep water and supported by the floating foundation.
The research on the floating VAWT has been carried out, including the aerodynamic load calculations of the floating VAWT, the motion comparison of the VAWT supported by different floating foundations, the influences between aerodynamic and hydrodynamic loads, and so on. Some methods and codes were developed to calculate the floating VAWT, including the FloVAWT code [
3], the enhanced Hawc2 code [
4], Simo-Riflex-DMS (AC) code [
5,
6], and a rigid-flexible coupling code [
7]. The motion performances of the floating VAWT were investigated by these codes. Vita studied the feasibility of a 5 MW Φ-type wind turbine supported by a rotating spar type foundation by using the enhanced Hawc2 code [
4]. Borg and Collu calculated the responses of vertical wind turbines supported by different floating foundations by using the FloVAWT code [
8]. Cheng et al. implemented the AC method in the Simo-Reflex to conduct the fully coupled aero-hydro-servo-elastic simulation of the floating VAWT [
6,
9]. Cahay et al. put forward the concept of a three-blade H-type wind turbine installed on a semi-submersible floating foundation [
10].
In the above research, the form of the floating foundations mainly includes Spar type, Semi-submersible type, and TLP type. Liu et al. studied the motion performance of a 5 MW VAWT supported by the truss Spar platform [
11], which had shorter length than the existent spar type foundation [
12,
13,
14] and can be used in the moderate water depth with good motion performance, and had lighter weight than the existing semi-submersible type foundation [
15]. The above codes cannot be used to calculate the truss Spar type VAWT, as the nonlinear coupling between the heave and pitch of truss Spar foundation is important, similar to the deep see Spar platform [
16,
17], and this is not considered in the above methods.
Compared with Φ-type, H-type is easier to manufacture and has higher power output [
18]. In this paper, we studied the motion performances of the H-type VAWT supported by a truss Spar type floating foundation. The aerodynamic loads were calculated considering the dynamic stall and motions of the floating foundation. The surge–heave–pitch coupling nonlinear motion equations of the floating VAWT were established, and the motions of the floating VAWT were assessed.
2. The Aerodynamic Loads of H-Type Floating VAWT
Based on the double multiple stream tube (DMST) theory, the aerodynamic loads acting on the blades were calculated considering dynamic stall, tip losses, aspect ratio, tower shadow effect and the influence of the surge–heave–pitch motions of the floater. The whole floating VAWT was dealt with as a rigid body.
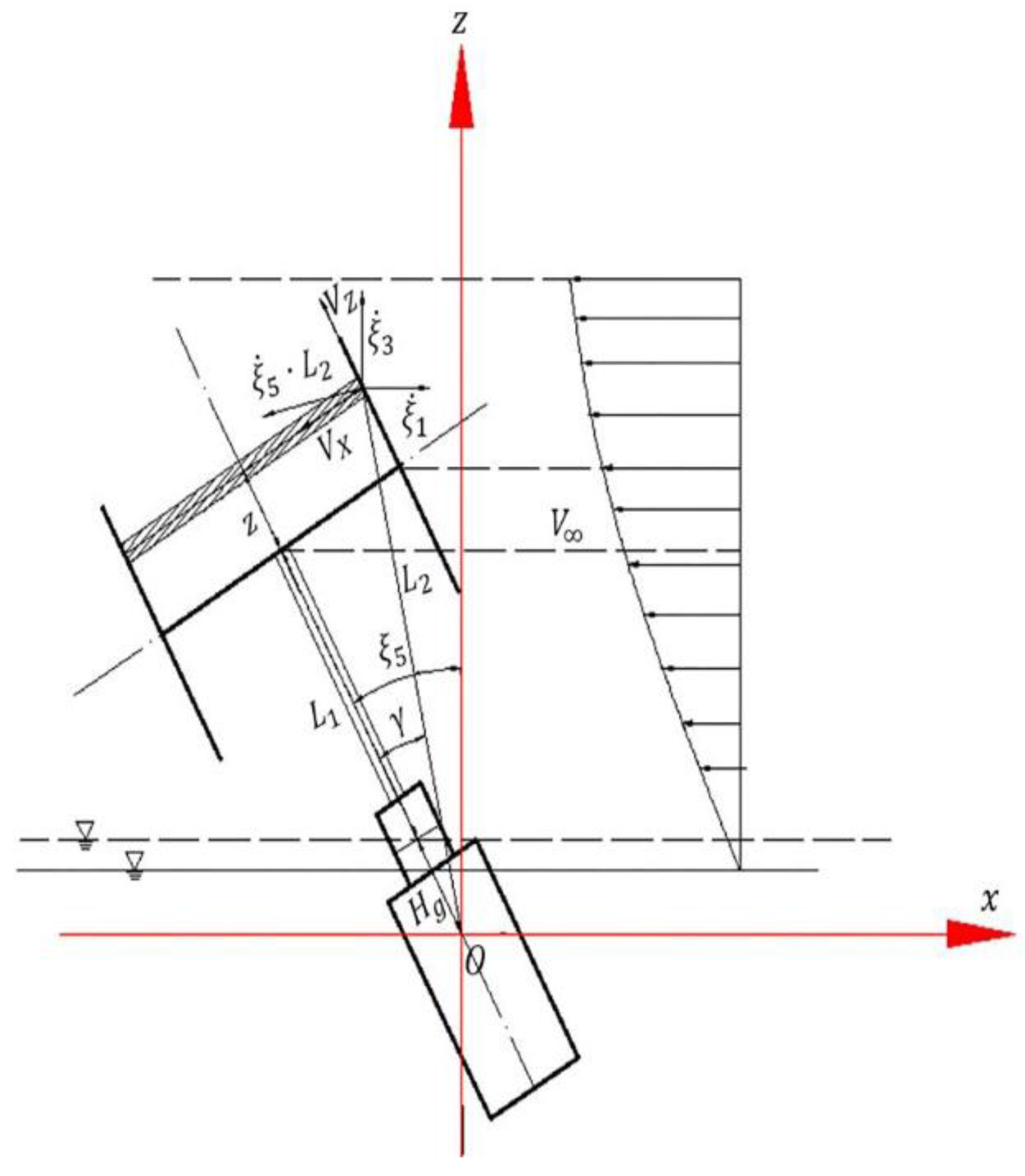
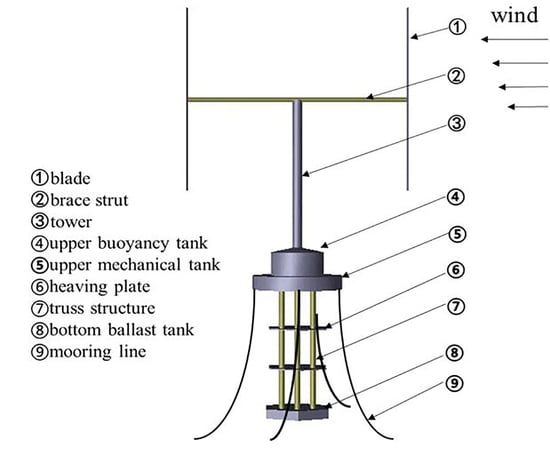
The stream tubes were divided into upwind and downwind sectors, respectively. Coordinate system is shown in
Figure 1, where the coordinate origin
is in the center of gravity of the floating VAWT, and
,
, and
are the displacements of surge, heave and pitch of the floating VAWT, respectively. The positive directions of the surge and heave motions are along the positive directions of the
axis and
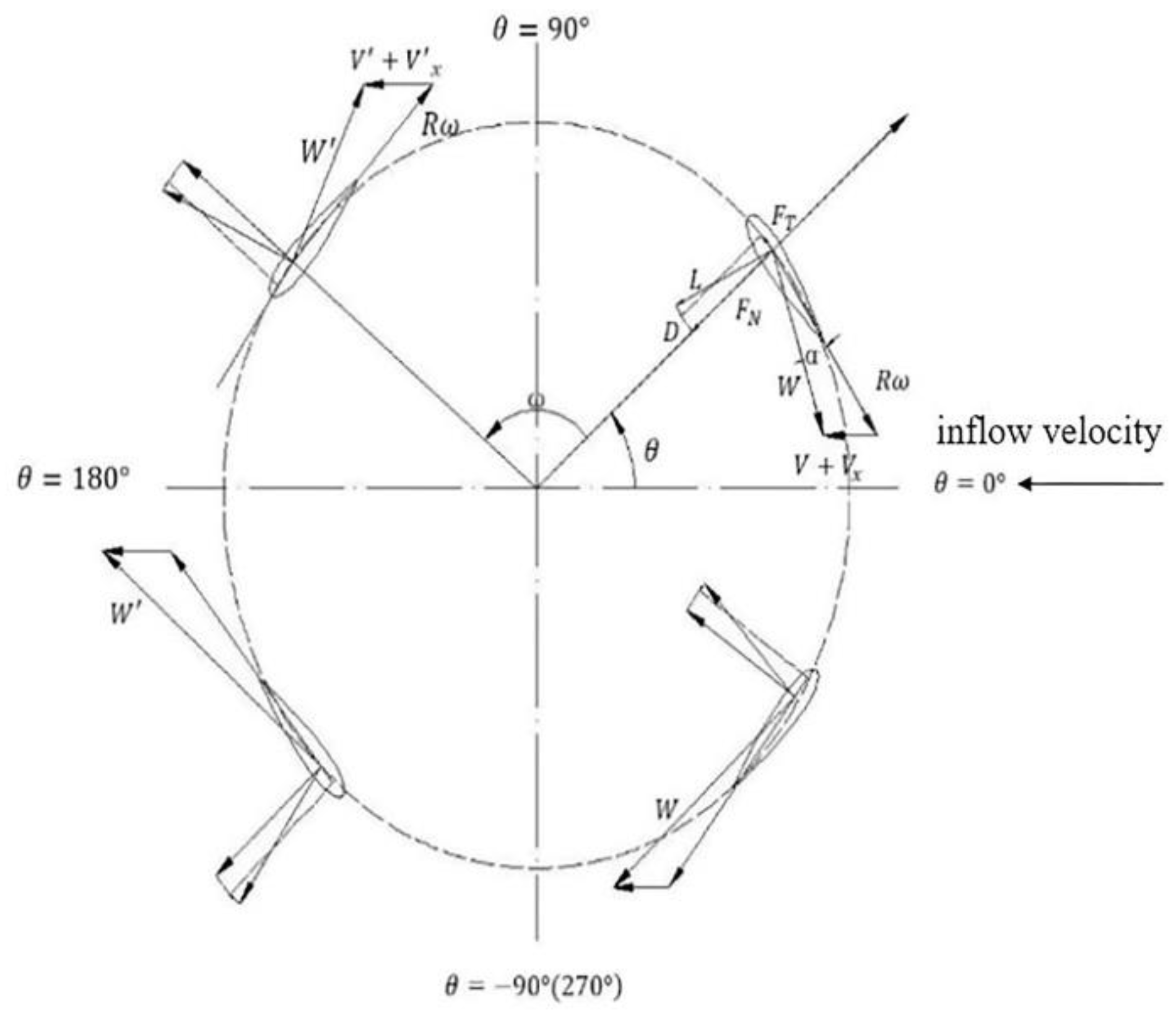
axis, respectively; the positive direction of the pitch motion is clockwise. The vector relations of the wind turbine are shown in
Figure 2.
The steady wind was considered here, it was a function of the height above the water level, and for a local height
, the wind speed can be written as follow,
where
is the average wind velocity at a reference height
, the vertical distance from the center of the blades to the water level is taken as the reference height in this paper, and with power
[
19].
Assuming the velocity parallel to the direction of the steam tube affects the induced velocities and the velocity perpendicular to the direction of the steam tube only affects the local relative velocities, the coordinate and the velocity of each stream tube were deduced considering the motions of the floating foundation in the following parts.
Induced velocities at the upwind and downwind sectors
and
, and the induced equilibrium velocity
are given by [
20],
where
is the interference factor, and
is the second interference factor.
For the upwind sector, the distance from local blades to the gravity center of floating wind turbine system is expressed as,
where
is the radius of rotor,
is the azimuth of rotor,
is the distance from each stream tube to equator (below equator is negative direction),
is the distance from equator to still water level, and
is the distance from still water level to the gravity center of floating wind system when the system is in a state of stillness. The angle between the local position of the blade and the tower is written as
Then, the local wind velocity of the blade is given by,
where
is the half-height of rotor. The velocities of local blades can be derived from the surge, heave and pitch velocities of floater by using transformation matrix. Then, the resultant velocities, which are caused by the motion of the floating foundation, parallel to the direction of the steam tube for the local position can be written as,
Using a similar deducing progress, we get the resultant velocities parallel to and vertical to the direction of the steam tube for the downwind sector, as follows,
For the rotor of upwind sector, namely, the range of azimuth
is
, and the local relative velocity of the rotor can be written as,
where
is the rotation velocity of the blade.
The local attack of angle is derived as,
The azimuthal angle of upwind sector of the rotor is divided into several angular tubes, and the angle of each tube is
. Assuming the induced velocity for each angular tube is a constant, the interference factor of each angular tube is a constant, it can be presented as,
where
,
and
can be given by following expressions,
where
is the number of blade,
is the chord length, and
and
are the normal force and tangential force coefficients, respectively, they can be given by,
where
and
are the lift coefficient and the drag coefficient, respectively. 2D static coefficient
and
can be obtained by interpolation of the experimental data [
21] considering the local Reynolds number and the local attack angle
, and 3D static coefficient
and
can be derived by taking into account the influence of tip losses and finite aspect ratio [
22]. Finally, the coefficients can be corrected by the Gormont–Berg method about the dynamic stall [
23].
The local Reynolds number is presented as,
where
is the coefficient of kinematic viscosity.
For the given the geometric lines of rotor, rotational speed and wind speed of each stream tube, the final induced factor can be derived by iteration of Equations (2)–(18). Furthermore, the normal force and tangential force coefficients can be obtained.
The normal force
and tangential force
of the blade at different
are further calculated by the following formulae,
where
is local height of the stream tube to equator plane of the rotor.
The thrust force
and side force
of the blade are calculated as following,
The power coefficient is presented as following,
Similarly, the normal force
and the tangential force
can be calculated for the downwind sector, and obtain the power coefficient
. The power coefficient for one cycle can be written as,
In this paper, the steady wind speed was used to calculate the aerodynamics loads. The lift and thrust forces acting on the heave and surge of the floating VAWT can be obtained by decomposing the normal and tangential forces. Calculating the moment of the thrust force about the center of gravity of the floating VAWT, the pitch moment of the aerodynamics acting of the pitch motions of the floating VAWT can be obtained.
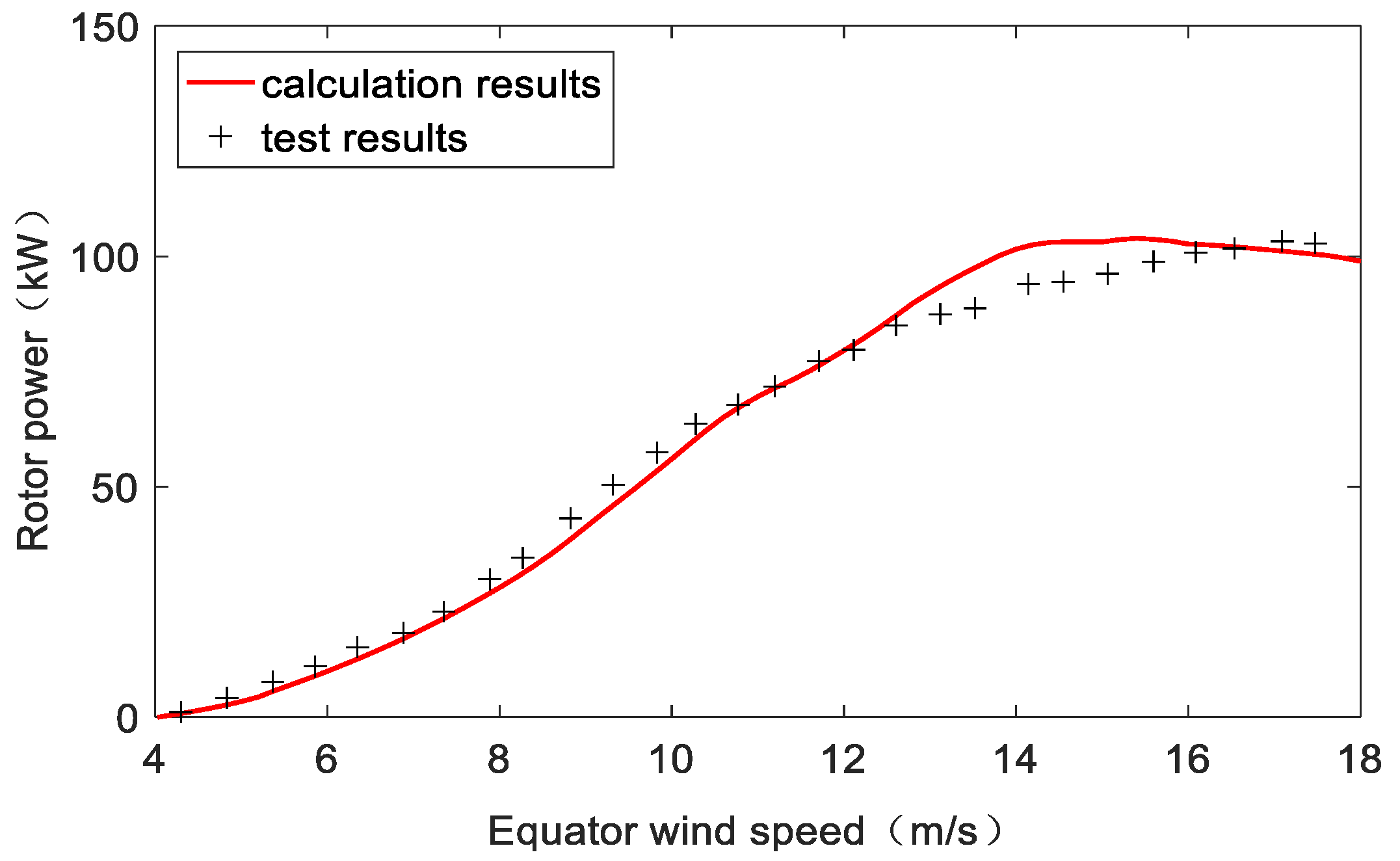
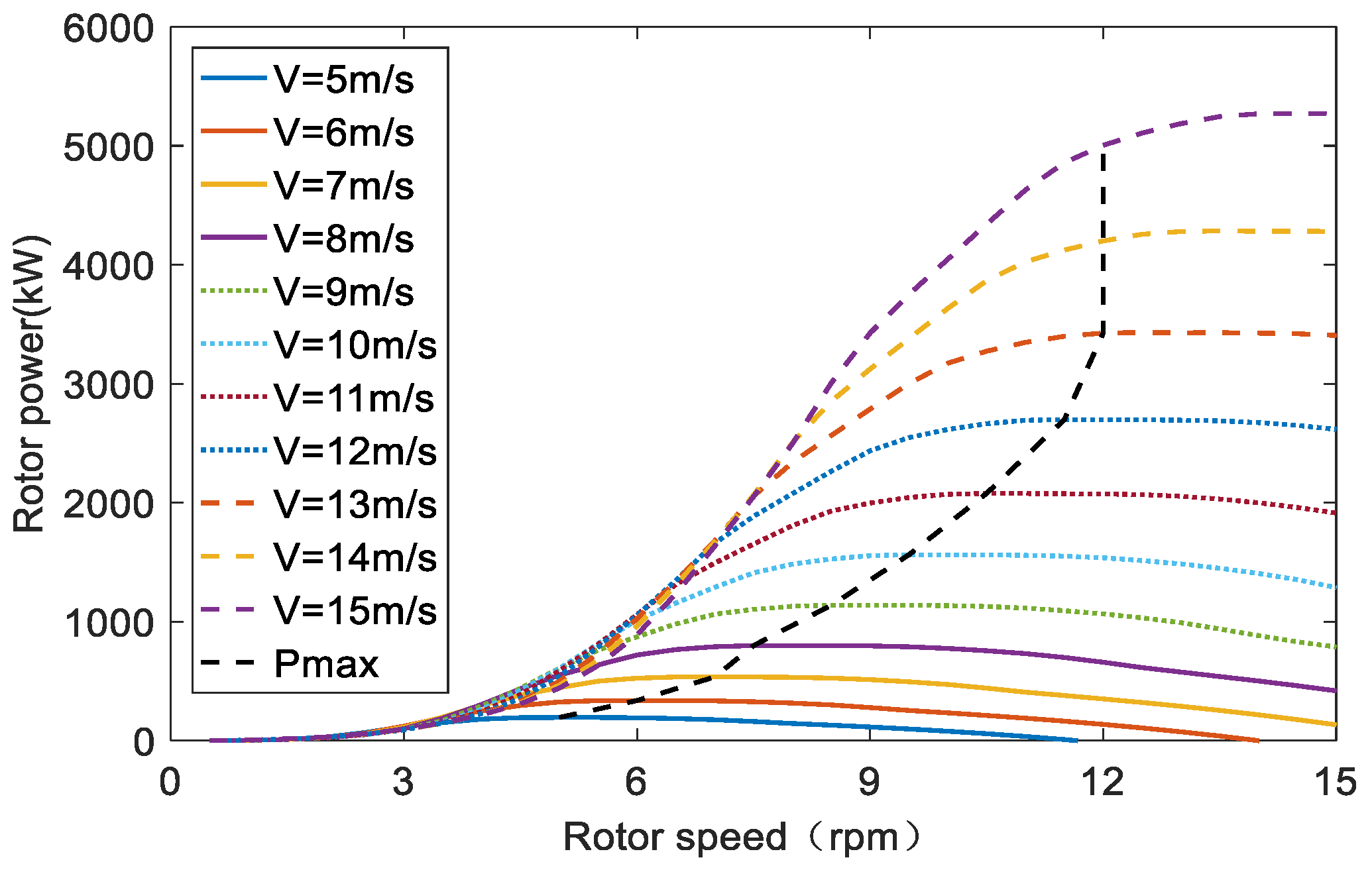
Taking a fixed H-type wind turbine VAWT260 [
24] as an example, the rotor power was calculated (the coupling of aerodynamics and hydrodynamics was not considered in this part). The VAWT260 H-rotor has two blades with chord length of 1.02 cm and airfoil of NACA0018. The lift and drag coefficients used in this paper are from static test, and iteration residual standard is set to
. The results of rotor power obtained by the numerical simulation were compared with those of model experiment [
24], as shown in
Figure 3.
It can be seen in
Figure 3 that the rotor power obtained by the numerical simulation agrees well with the results of the experiment.
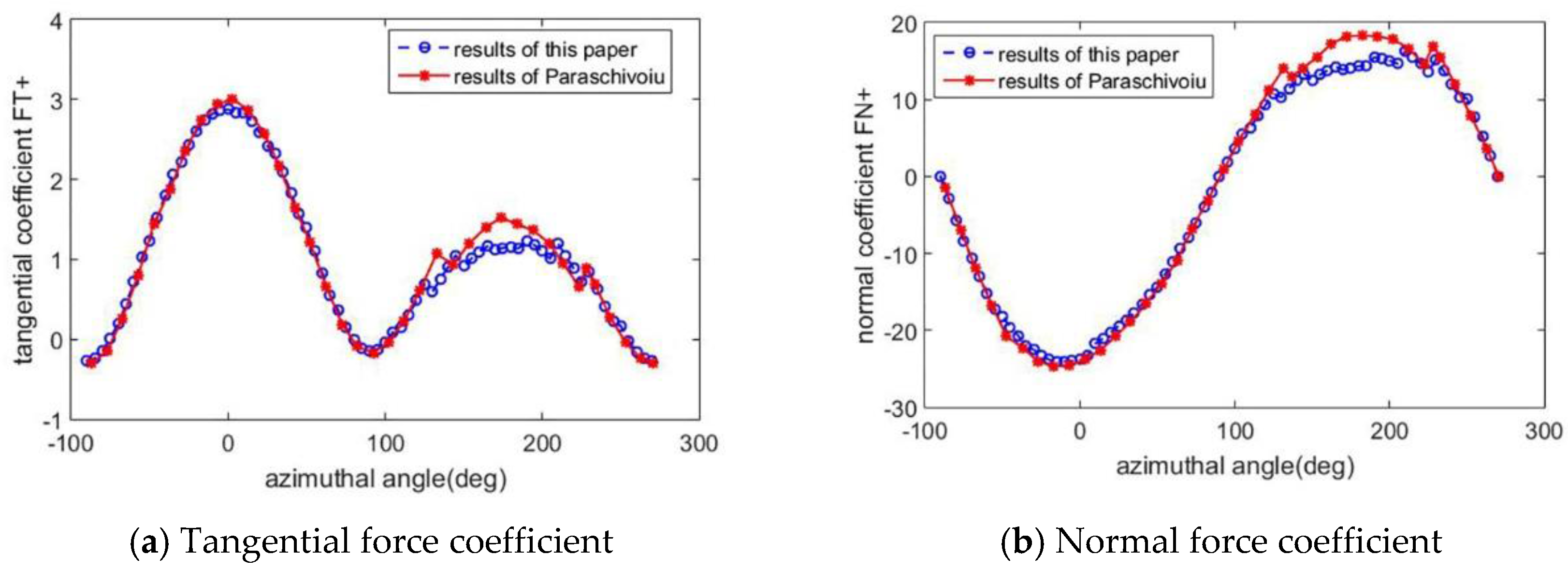
To verify the aerodynamic loads, comparisons of tangential and normal force coefficients with the calculation results of Paraschivoiu [
25] are presented in
Figure 4. A NACA0015 blade profile, a chord of 0.2 m and 6 m high H-type blade is used here. The rotational speed is 125 rpm, and the tip speed ratio is 5.2. The double multiple stream tube method with considering finite aspect ratio is used in [
25].
Figure 4 shows that the aerodynamic load coefficients mainly agree well with the results of Paraschivoiu. The reason for the relatively obvious differences appearing downwind is that the tower effect is ignored in Paraschivoiu’s calculation. The thrust force and side force used in the dynamical equation in
Section 3 can be checked by Equations (21) and (22).