An Efficient Method to Learn Overcomplete Multi-Scale Dictionaries of ECG Signals
Abstract
1. Introduction
2. Problem Formulation
- Which is the optimal dictionary to model external ECG signals and how can we construct it?
- Given an overcomplete dictionary, how can we obtain the optimal set of coefficients that represent only the relevant signal components?
3. Multi-Scale Dictionary Derivation
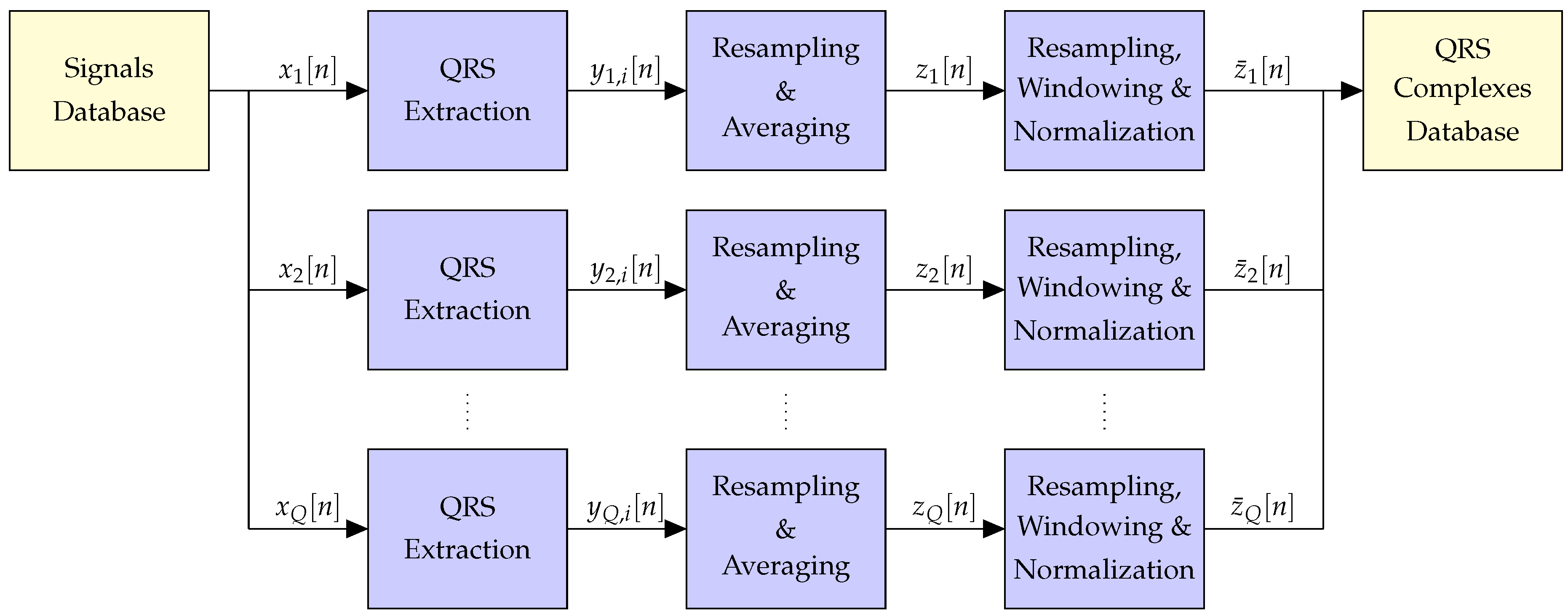
3.1. Database
3.2. Pre-Processing
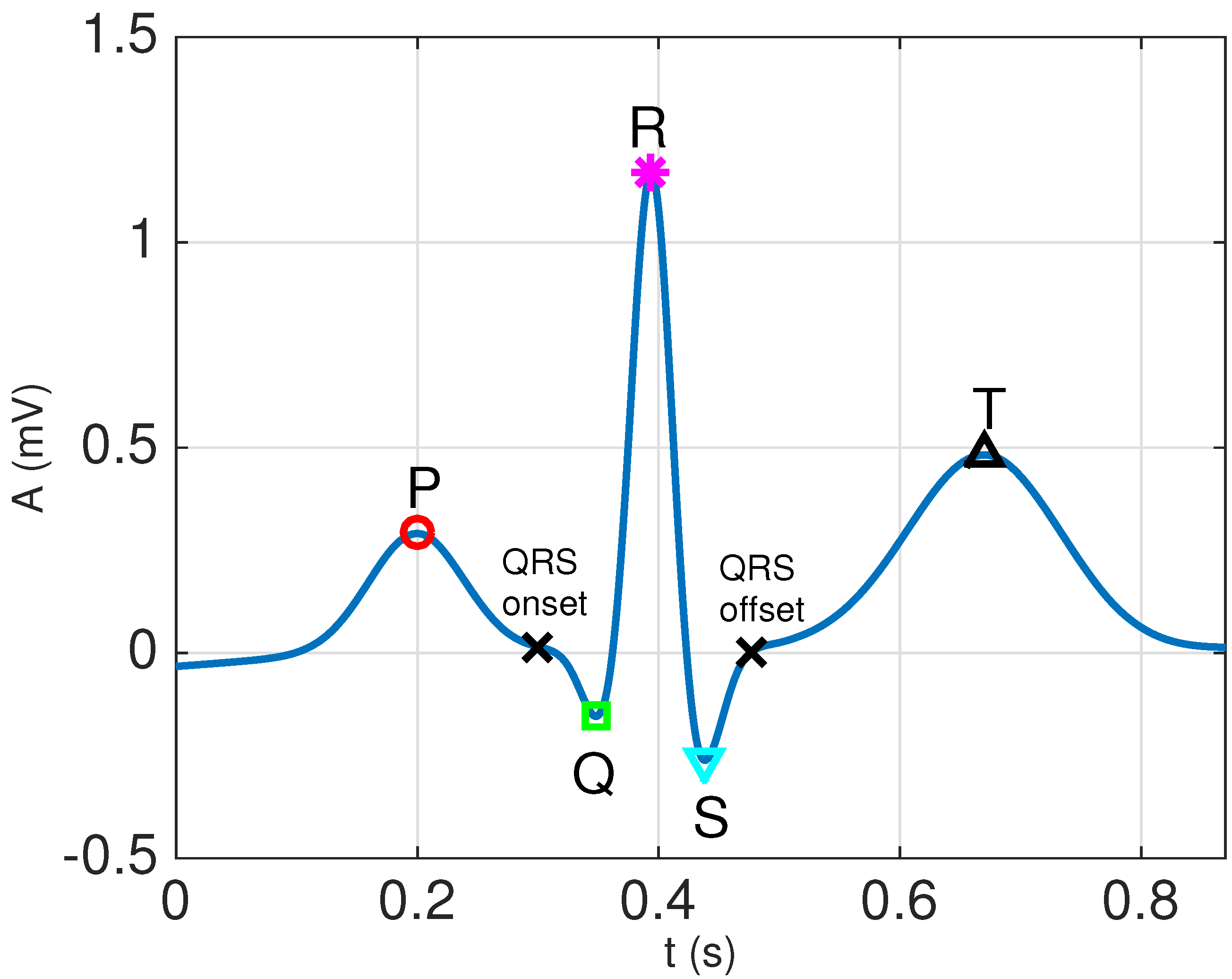
3.2.1. QRS Extraction
- Apply a 4th order Butterworth bandpass filter with cut-off frequencies Hz and Hz to remove noise and interferences. Forward–backward filtering, with an appropriate choice of the initial state to remove transients [31], is used to avoid phase distortion.
- Locate the positions of the R waveforms using the Pan–Tompkins QRS detector [32].
- Determine the fiducial points that mark the beginning and end of the QRS complexes by tracking backwards and forward from the R peaks, estimating the QRS onset and offset points using the minimum radius of curvature technique, as described in Section 4.2 of [30].
3.2.2. Resampling and Averaging
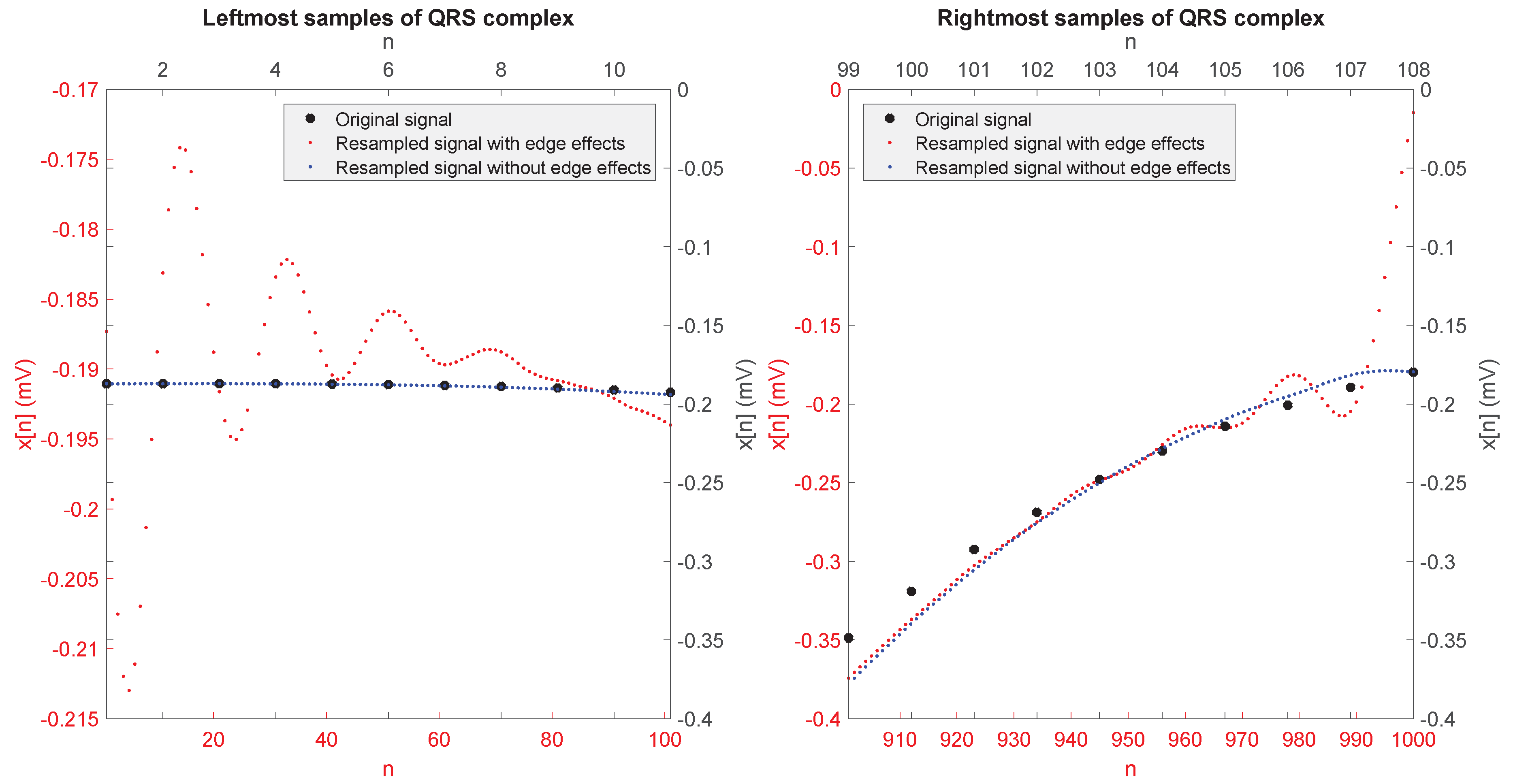
- From the ith QRS complex signal, for , we first constructed the following two sequences:which are not likely to be affected by the edge effect on their leftmost and rightmost samples, respectively.
- We performed the resampling by the factor separately on and , obtaining two resampled sequences and .
- The desired resampled sequence is finally given by
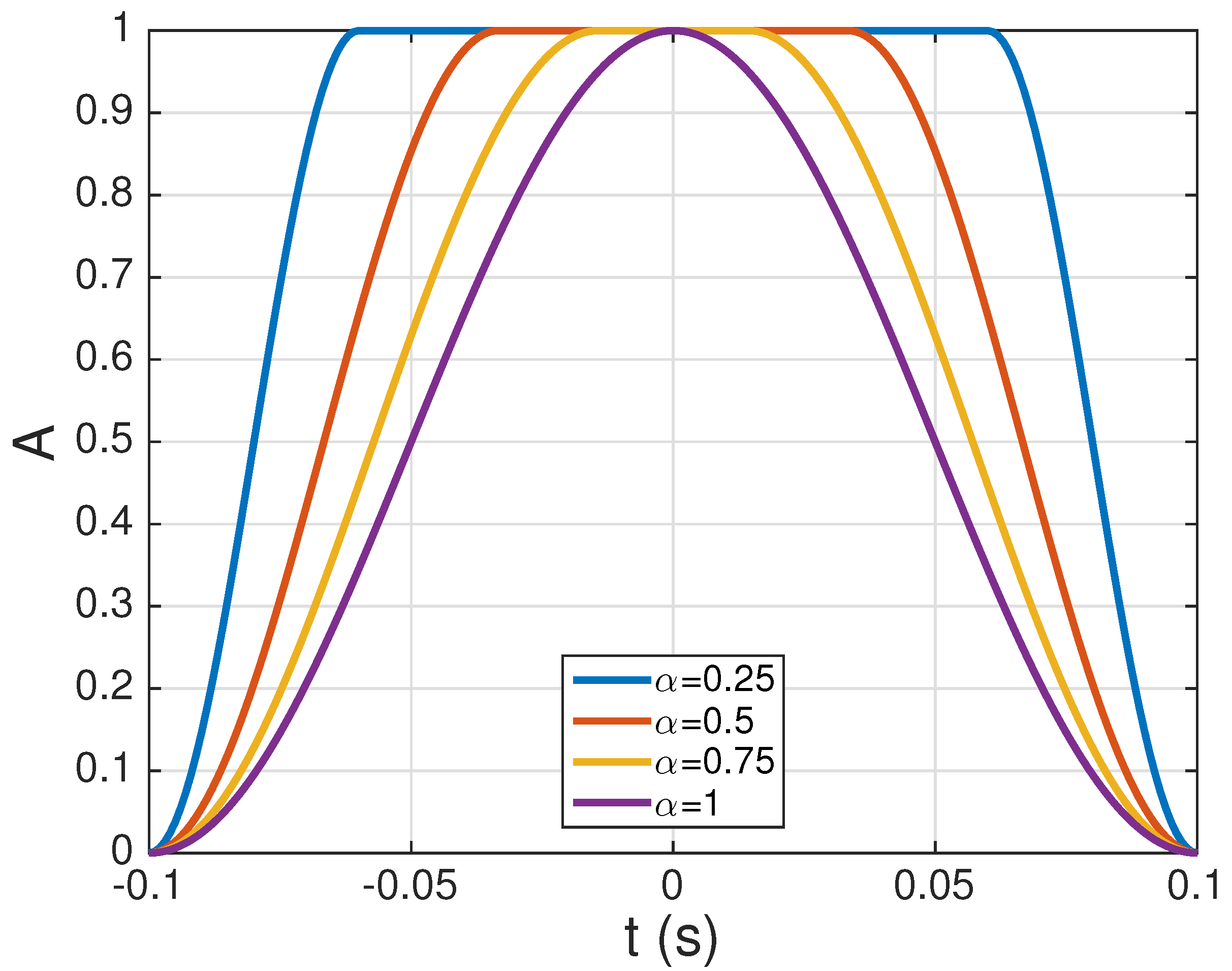
3.2.3. Windowing and Normalization
3.3. Dictionary Construction
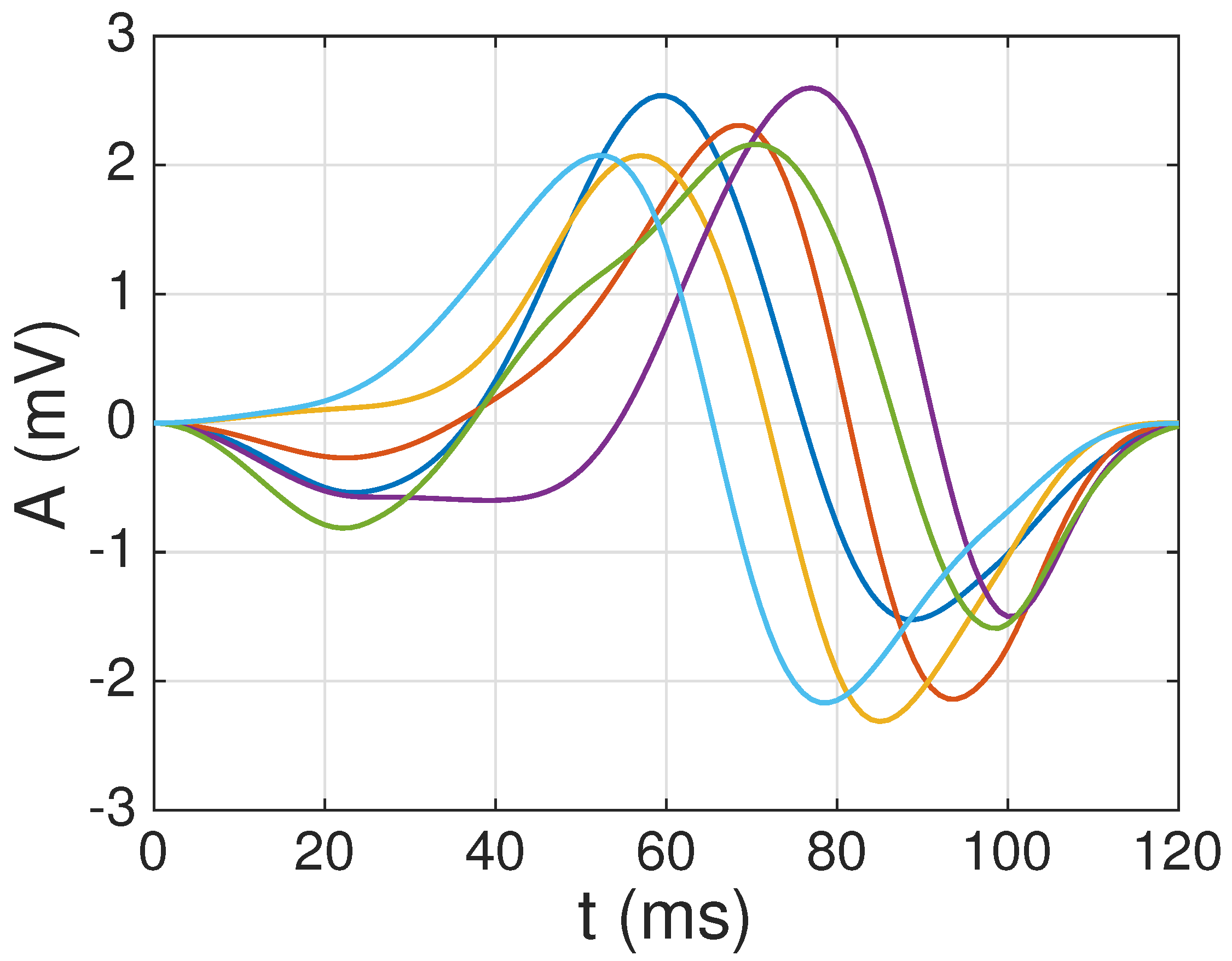
3.3.1. Selection of the First Atom
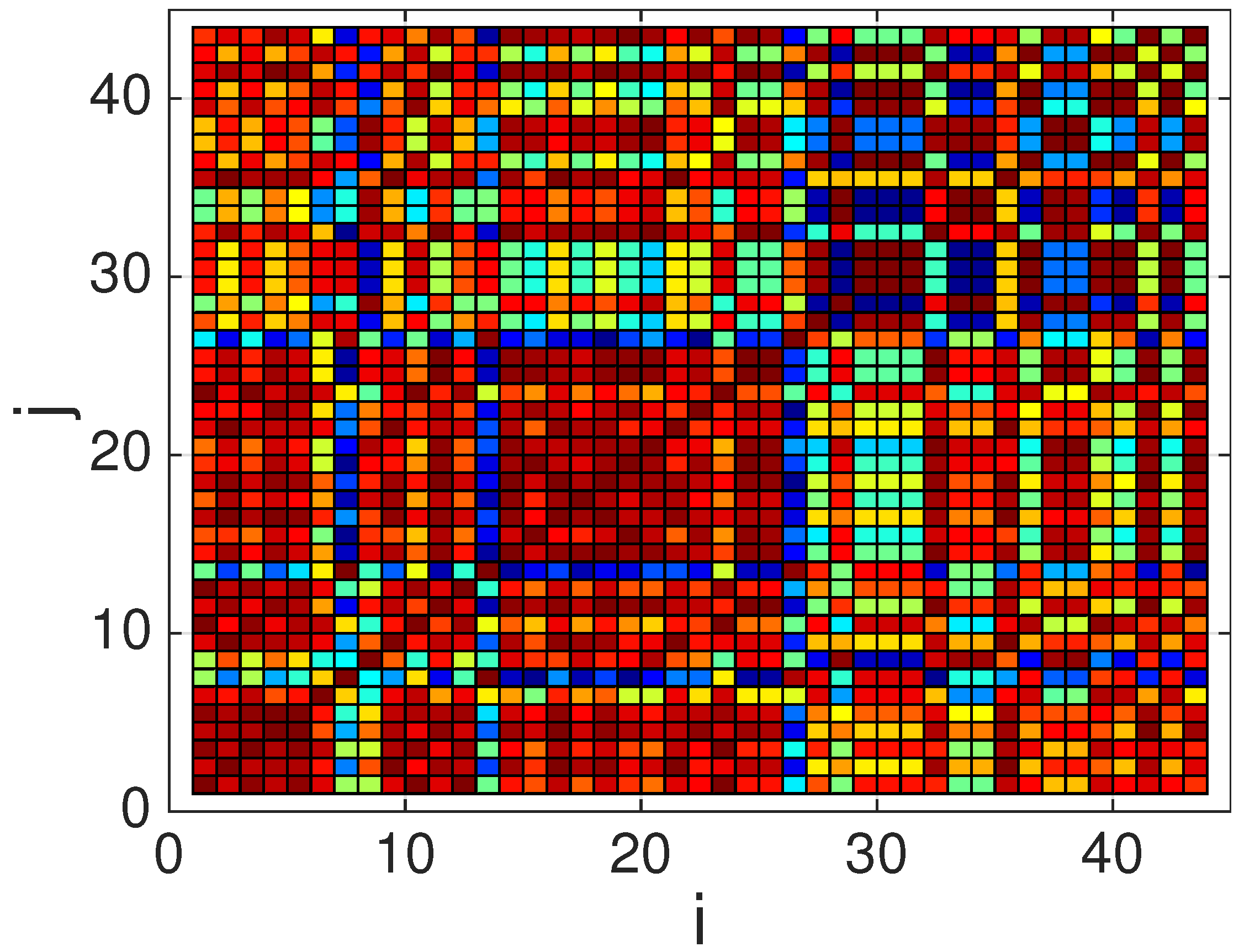
- Compute a correlation matrix , whose elements correspond to Pearson’s correlation coefficient among each pair of waveforms in the QRS complexes database (in practice, only coefficients have to be computed, since and ).where denotes the cross-covariance between the ith and jth waveforms at lag 0 (i.e., without any time shift), and the last expression () is due to the energy normalization described in Section 3.2.3, which implies that .
- Select the waveform with the highest average correlation (in absolute value) with respect to all the other candidate waveforms, i.e.,which corresponds to the most representative waveform of all the candidate waveforms.
3.3.2. Selection of Additional Atoms
- Set the number of accepted atoms equal to one (), the pool of candidate waveforms as (i.e., all the waveforms except for the one selected for the first atom), the pool of accepted waveforms as , and construct a reduced correlation matrix by removing the row and column corresponding to the first atom selected from the global correlation matrix :
- WHILE:
- (a)
- Select, from the remaining waveforms in the pool of candidates, the one with the highest average correlation (in absolute value) with respect to all the other candidate waveforms in the pool, i.e.,and obtain the associated index, , in the original set of candidate waveforms.
- (b)
- Compute the maximum correlation (in absolute value) between the selected candidate and all the already accepted atoms,
- (c)
- Remove the th waveform from the pool of candidates (i.e., set ), and construct a new reduced matrix () by removing the th row and column from the current .
- (d)
- IF (with denoting a pre-defined maximum correlation threshold), THEN add the selected waveform to the pool of accepted atoms (i.e., ), and set .
END
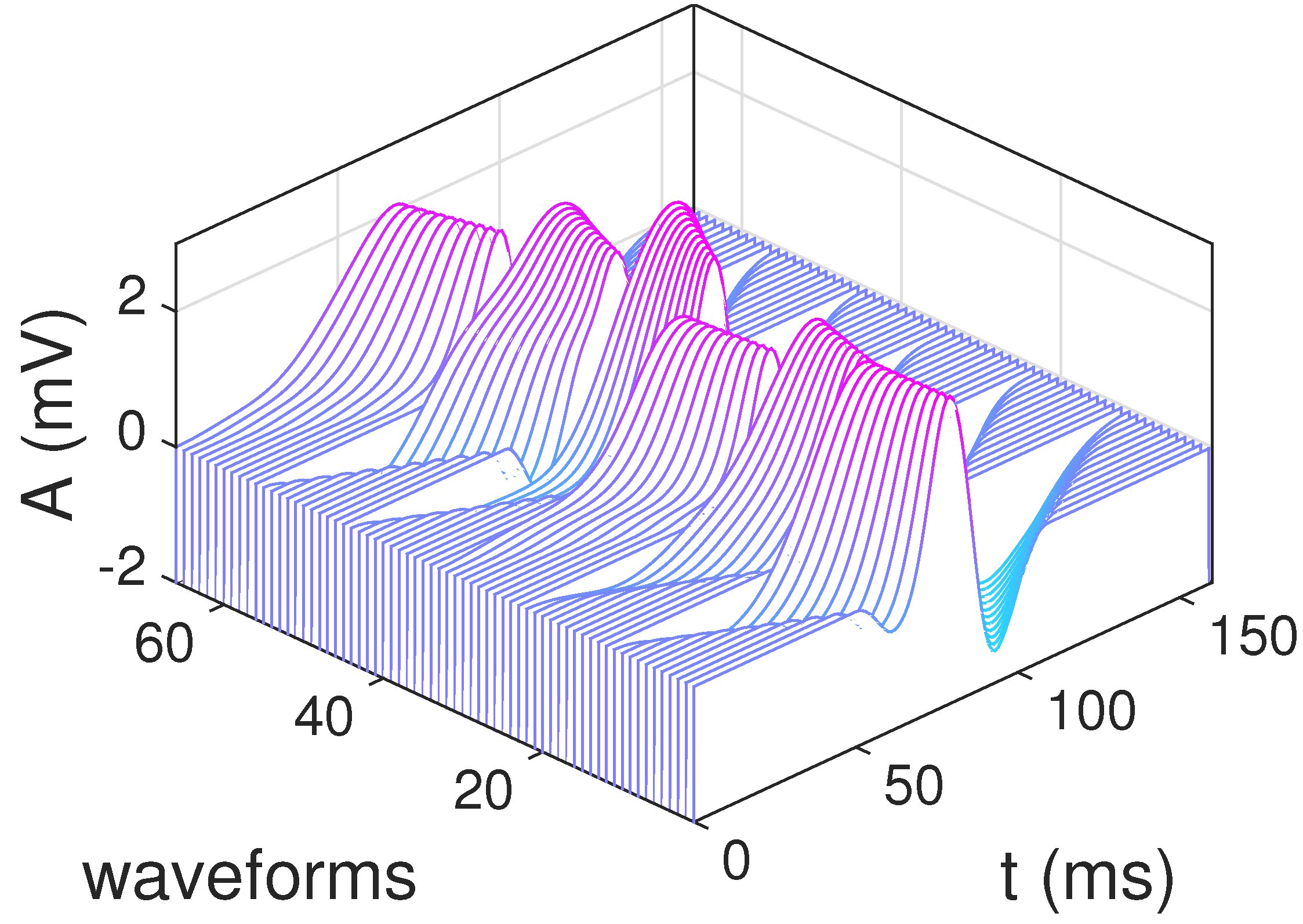
3.3.3. Construction of the Multi-Scale Dictionary
4. Numerical Results
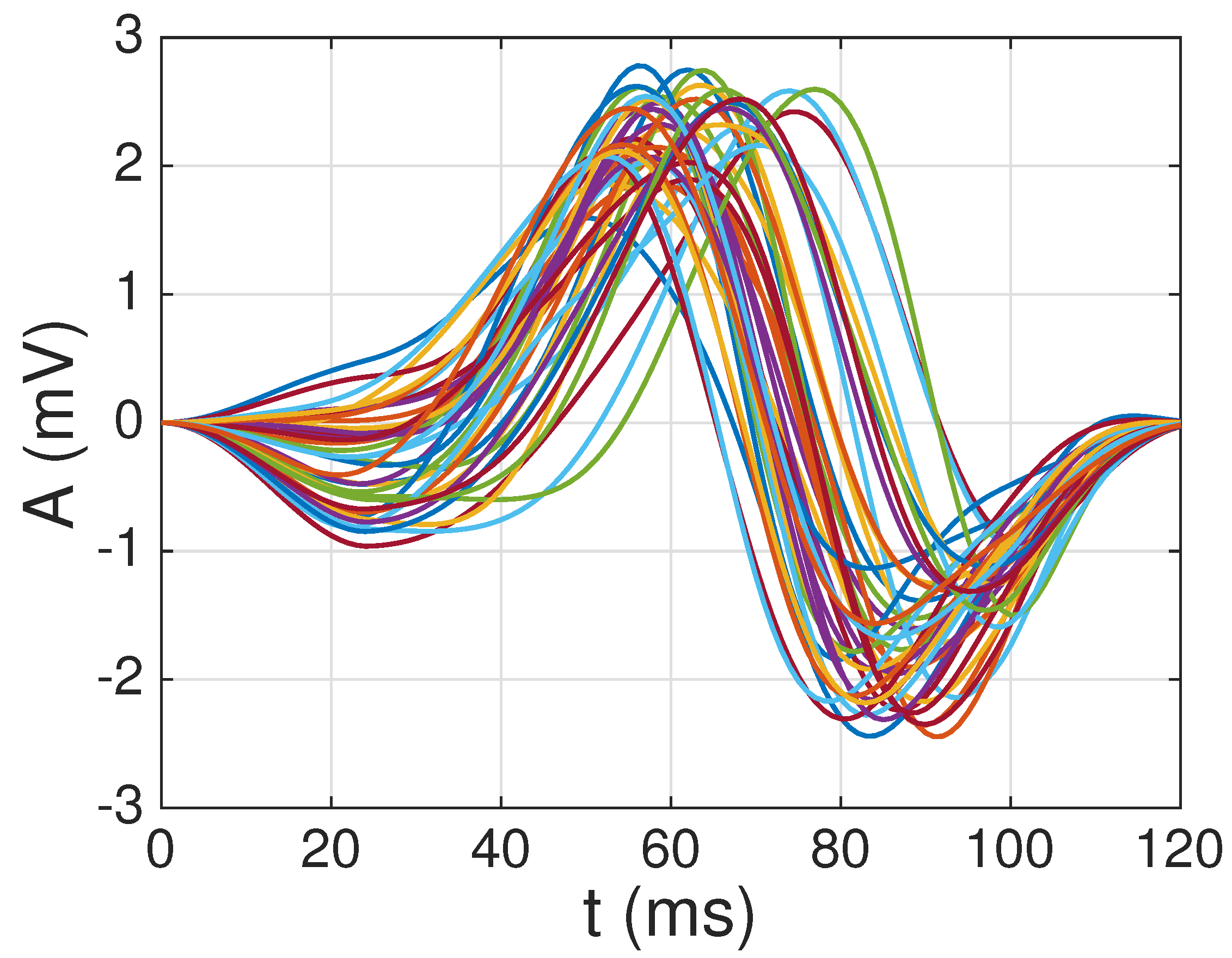
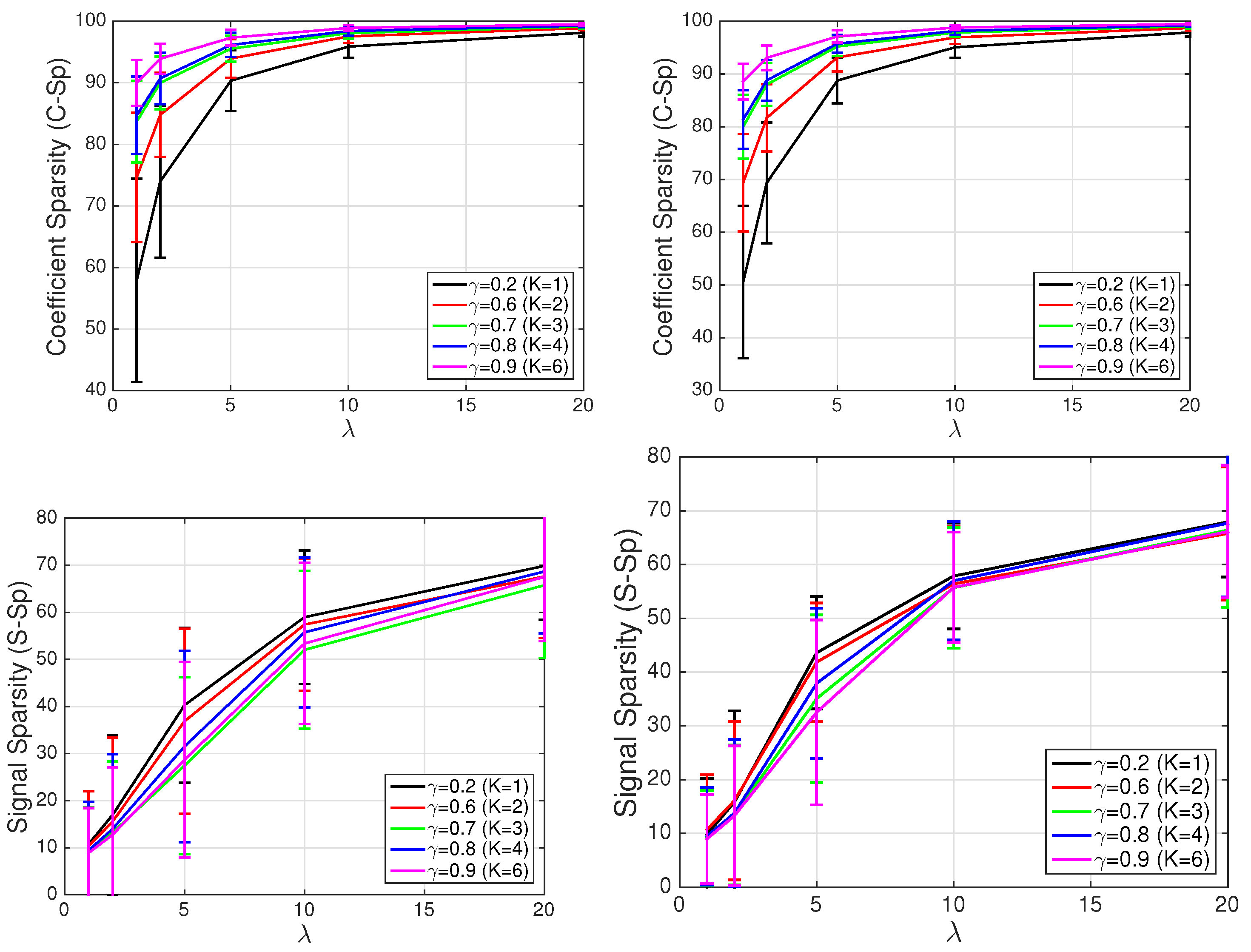
4.1. Dictionary Construction
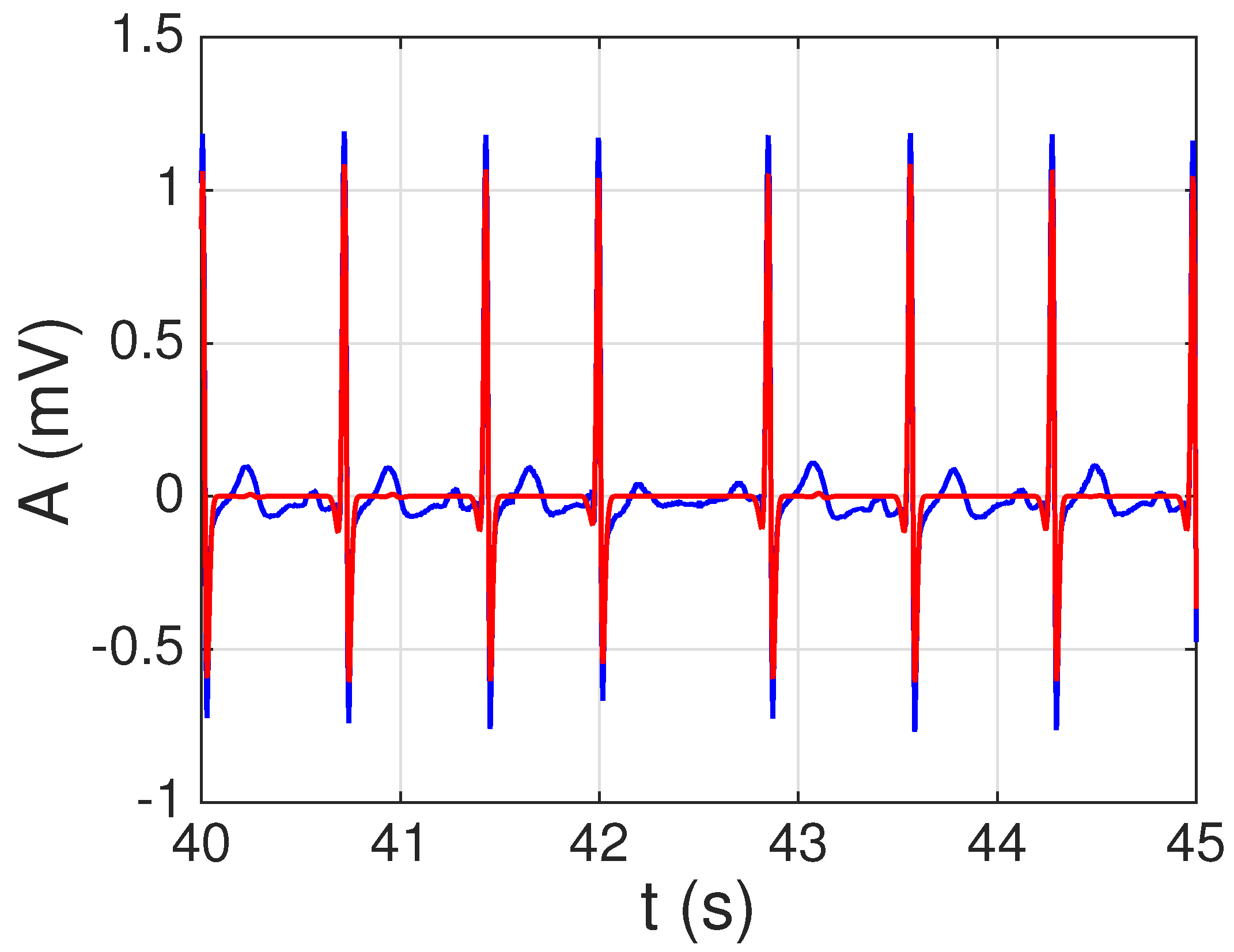
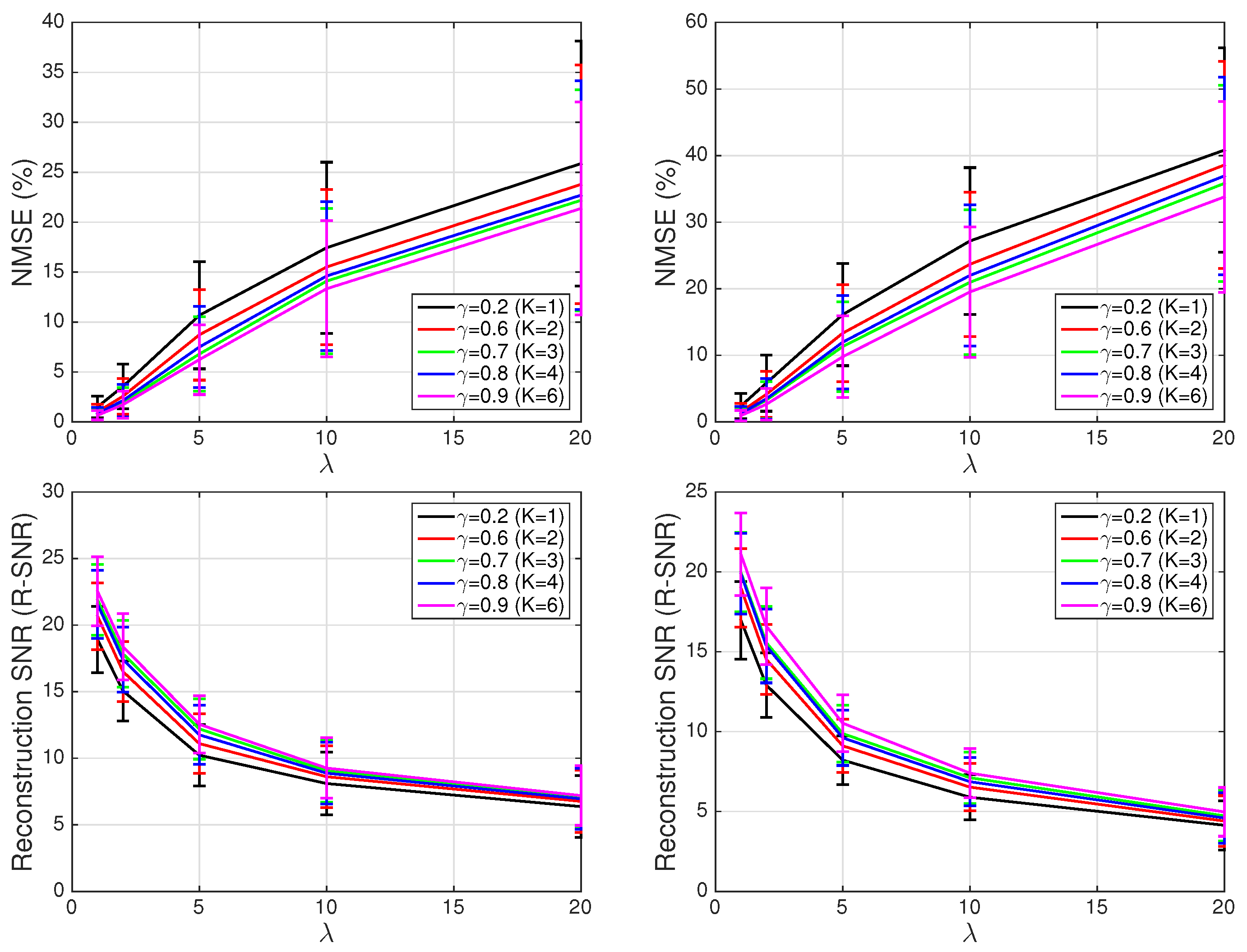
4.2. Sparse ECG Representation
4.3. Sparse ECG Representation of Other Channels
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sörnmo, L.; Laguna, P. Bioelectrical Signal Processing in Cardiac and Neurological Applications; Academic Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Clifford, G.; Azuaje, F.; McSharry, P. (Eds.) Advanced Methods and Tools for ECG Data Analysis; Artech House: Norwood, MA, USA, 2009. [Google Scholar]
- Tibshirani, R. Regression shrinkage and selection via the Lasso. J. R. Stat. Soc. Ser. B (Methodol.) 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Elad, M. Sparse and Redundant Representations: From Theory to Applications in Signal and Image Processing; Springer: Berlin, Germany, 2010. [Google Scholar]
- Kreutz-Delgado, K.; Murray, J.F.; Rao, B.D.; Engan, K.; Lee, T.W.; Sejnowski, T.J. Dictionary learning algorithms for sparse representation. Neural Comput. 2003, 15, 349–396. [Google Scholar] [CrossRef] [PubMed]
- Rubinstein, R.; Bruckstein, A.M.; Elad, M. Dictionaries for sparse representation modeling. Proc. IEEE 2010, 98, 1045–1057. [Google Scholar] [CrossRef]
- Tosic, I.; Frossard, P. Dictionary learning. IEEE Signal Process. Mag. 2011, 28, 27–38. [Google Scholar] [CrossRef]
- Billah, M.; Mahmud, T.; Snigdha, F.; Arafat, M. A novel method to model ECG beats using Gaussian functions. In Proceedings of the 2011 4th International Conference on Biomedical Engineering and Informatics (BMEI), Shanghai, China, 15–17 October 2011; Volume 2, pp. 612–616. [Google Scholar]
- Monzón, S.; Trigano, T.; Luengo, D.; Artés-Rodríguez, A. Sparse spectral analysis of atrial fibrillation electrograms. In Proceedings of the 2012 IEEE International Workshop on Machine Learning for Signal Processing, Santander, Spain, 23–26 September 2012; pp. 1–6. [Google Scholar]
- Trigano, T.; Kolesnikov, V.; Luengo, D.; Artés-Rodríguez, A. Grouped sparsity algorithm for multichannel intracardiac ECG synchronization. In Proceedings of the 2014 22nd European Signal Processing Conference (EUSIPCO), Lisbon, Portugal, 1–5 September 2014; pp. 1537–1541. [Google Scholar]
- Divorra-Escoda, O.; Granai, L.; Lemay, M.; Hernandez, J.M.; Vandergheynst, P.; Vesin, J.M. Ventricular and atrial activity estimation through sparse ECG signal decompositions. In Proceedings of the 2006 IEEE International Conference on Acoustics Speech and Signal Processing Proceedings, Toulouse, France, 14–19 May 2006; Volume II, pp. 1060–1063. [Google Scholar]
- Fira, M.; Goras, L.; Barabasa, C.; Cleju, N. On ECG compressed sensing using specific overcomplete dictionaries. Adv. Electr. Comput. Eng. 2010, 10, 23–28. [Google Scholar] [CrossRef]
- Luengo, D.; Monzón, S.; Trigano, T.; Vía, J.; Artés-Rodríguez, A. Blind analysis of atrial fibrillation electrograms: A sparsity-aware formulation. Integr. Comput.-Aided Eng. 2015, 22, 71–85. [Google Scholar] [CrossRef]
- Luengo, D.; Vía, J.; Monzón, S.; Trigano, T.; Artés-Rodríguez, A. Cross-products LASSO. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 6118–6122. [Google Scholar]
- Wang, C.; Liu, J.; Sun, J. Compression algorithm for electrocardiograms based on sparse decomposition. Front. Electr. Electron. Eng. China 2009, 4, 10–14. [Google Scholar] [CrossRef]
- Mailhé, B.; Gribonval, R.; Bimbot, F.; Lemay, M.; Vandergheynst, P.; Vesin, J.M. Dictionary learning for the sparse modelling of atrial fibrillation in ECG signals. In Proceedings of the 2009 IEEE International Conference on Acoustics, Speech and Signal Processing, Taipei, Taiwan, 19–24 April 2009; pp. 465–468. [Google Scholar]
- Polania, L.F.; Barner, K.E. Multi-scale dictionary learning for compressive sensing ECG. In Proceedings of the IEEE Digital Signal Processing and Signal Processing Education Meeting (DSP/SPE), Napa, CA, USA, 11–14 August 2013; pp. 36–41. [Google Scholar]
- Fira, M.; Goras, L.; Barabasa, C.; Cleju, N. ECG compressed sensing based on classification in compressed space and specified dictionaries. In Proceedings of the 19th European Signal Processing Conference (EUSIPCO), Barcelona, Spain, 29 August–2 September 2011; pp. 1573–1577. [Google Scholar]
- Fira, M.; Goras, L.; Barabasa, C. Reconstruction of compressed sensed ECG signals using patient specific dictionaries. In Proceedings of the International Symposium on Signals, Circuits and Systems ISSCS2013, Iasi, Romania, 11–12 July 2013; pp. 1–4. [Google Scholar]
- Fira, M.; Goras, L. On projection matrices and dictionaries in ECG compressive sensing— A comparative study. In Proceedings of the 12th Symposium on Neural Network Applications in Electrical Engineering (NEUREL), Belgrade, Serbia, 25–27 November 2014; pp. 3–8. [Google Scholar]
- Trigano, T.; Shevtsov, I.; Luengo, D. CoSA: An accelerated ISTA algorithm for dictionaries based on translated waveforms. Signal Process. 2017, 139, 131–135. [Google Scholar] [CrossRef]
- Luengo, D.; Meltzer, D.; Trigano, T. Sparse ECG Representation with a Multi-Scale Dictionary Derived from Real-World Signals. In Proceedings of the 41st International Conference on Telecommunications and Signal Processing (TSP), Athens, Greece, 4–6 July 2018; pp. 1–5. [Google Scholar]
- Satija, U.; Ramkumar, B.; Manikandan, M.S. Noise-aware dictionary-learning-based sparse representation framework for detection and removal of single and combined noises from ECG signal. Healthc. Technol. Lett. 2017, 4, 2–12. [Google Scholar] [CrossRef] [PubMed]
- Faust, O.; Acharya, U.R.; Ma, J.; Min, L.C.; Tamura, T. Compressed sampling for heart rate monitoring. Comput. Methods Prog. Biomed. 2012, 108, 1191–1198. [Google Scholar] [CrossRef] [PubMed]
- Whitaker, B.M.; Rizwan, M.; Aydemir, V.B.; Rehg, J.M.; Anderson, D.V. AF classification from ECG recording using feature ensemble and sparse coding. Computing 2017, 44, 1. [Google Scholar]
- McSharry, P.E.; Clifford, G.D.; Tarassenko, L.; Smith, L.A. A dynamical model for generating synthetic electrocardiogram signals. IEEE Trans. Biomed. Eng. 2003, 50, 289–294. [Google Scholar] [CrossRef] [PubMed]
- Goldberger, A.; Amaral, L.A.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.B.; Peng, C.K.; Stanley, H.E. Physiobank, physiotoolkit, and physionet. Circulation 2000, 101, e215–e220. [Google Scholar] [CrossRef] [PubMed]
- Hu, X.; Liu, J.; Wang, J.; Xiao, Z. Detection of onset and offset of QRS complex based a modified triangle morphology. In Frontier and Future Development of Information Technology in Medicine and Education; Springer: Berlin, Germany, 2014; pp. 2893–2901. [Google Scholar]
- Bousseljot, R.; Kreiseler, D.; Schnabel, A. Nutzung der EKG-Signaldatenbank CARDIODAT der PTB über das Internet. Biomed. Tech./Biomed. Eng. 1995, 40, 317–318. [Google Scholar] [CrossRef]
- Israel, S.; Irvine, J.M.; Cheng, A.; Wiederhold, M.D.; Wiederhold, B.K. ECG to identify individuals. Pattern Recognit. 2005, 38, 133–142. [Google Scholar] [CrossRef]
- Gustafsson, F. Determining the initial states in forward–backward filtering. IEEE Trans. Signal Process. 1996, 44, 988–992. [Google Scholar] [CrossRef]
- Pan, J.; Tompkins, W.J. A real-time QRS detection algorithm. IEEE Trans. Biomed. Eng. 1985, 32, 230–236. [Google Scholar] [CrossRef] [PubMed]
- Oppenheim, A.V.; Schafer, R.W. Discrete-Time Signal Processing; Pearson Education: London, UK, 2014. [Google Scholar]
- Proakis, J.G. Digital Communications; McGraw-Hill: New York, NY, USA, 1995. [Google Scholar]
| Channel | Lead | C-Sp (%) | S-Sp (%) | NMSE (%) | R-SNR (dB) |
|---|---|---|---|---|---|
| 1 | I | 86.5245 | 11.0095 | 4.1476 | 13.8220 |
| 2 | II | 83.6901 | 5.1302 | 1.8310 | 17.3732 |
| 3 | III | 92.0191 | 38.1580 | 5.1706 | 12.8646 |
| 4 | aVR | 85.4093 | 6.0408 | 2.5404 | 15.9510 |
| 5 | aVL | 92.9162 | 61.9314 | 10.2057 | 9.9116 |
| 6 | aVF | 88.1383 | 12.0894 | 3.0323 | 15.1823 |
| 7 | V1 | 87.4629 | 5.5182 | 3.1652 | 14.9960 |
| 8 | V2 | 90.7240 | 51.0356 | 3.0689 | 15.1302 |
| 9 | V3 | 86.5196 | 40.1319 | 2.3935 | 16.2097 |
| 10 | V4 | 83.1699 | 26.8689 | 2.9814 | 15.2557 |
| 11 | V5 | 80.9004 | 5.1181 | 2.1296 | 16.7170 |
| 12 | V6 | 81.0859 | 3.4931 | 1.6270 | 17.8862 |
| 13 | Vx | 80.1663 | 4.3333 | 1.7768 | 17.5037 |
| 14 | Vy | 93.0671 | 62.7804 | 11.4420 | 9.4150 |
| 15 | Vz | 94.0583 | 69.9991 | 5.8457 | 12.3316 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luengo, D.; Meltzer, D.; Trigano, T. An Efficient Method to Learn Overcomplete Multi-Scale Dictionaries of ECG Signals. Appl. Sci. 2018, 8, 2569. https://doi.org/10.3390/app8122569
Luengo D, Meltzer D, Trigano T. An Efficient Method to Learn Overcomplete Multi-Scale Dictionaries of ECG Signals. Applied Sciences. 2018; 8(12):2569. https://doi.org/10.3390/app8122569
Chicago/Turabian StyleLuengo, David, David Meltzer, and Tom Trigano. 2018. "An Efficient Method to Learn Overcomplete Multi-Scale Dictionaries of ECG Signals" Applied Sciences 8, no. 12: 2569. https://doi.org/10.3390/app8122569
APA StyleLuengo, D., Meltzer, D., & Trigano, T. (2018). An Efficient Method to Learn Overcomplete Multi-Scale Dictionaries of ECG Signals. Applied Sciences, 8(12), 2569. https://doi.org/10.3390/app8122569






