1. Introduction
As a second most common neurodegenerative disorder, Parkinson’s disease (PD) is expected to impose an increasing social and economic burden on societies as populations age [
1]. Its prevalence rate is estimated to approximately 1.5% for people aged over 65 years [
2]. The risk of being affected by PD strongly increases with age, and, in the next 15 years, the incidence of PD is expected to be doubled [
3,
4]. The rapid degeneration of dopaminergic cells in the substantia nigra pars compacta [
5] arose as the most significant biological finding associated with the disease, but the exact pathophysiological cause of PD has not yet been discovered. PD cardinal motor symptoms involve bradykinesia (slowness of movement), tremor at rest, rigidity, gait impairment, and postural instability [
6,
7,
8]. A variety of non-motor symptoms may emerge as well—for instance, cognitive impairment, dementia, depression, sleep disorders, or anxiety [
6,
9,
10].
Handwriting requires cognitive, perceptual, and fine motor abilities. In conjunction with motor dysfunctions in people suffering from PD, it has been proven that disrupted handwriting may be used as a significant biomarker for PD diagnosis [
11,
12]. Micrographia, which is associated with the progressive decrease in letters’ amplitude, is the most commonly observed handwriting abnormality in patients with PD [
13,
14]. Moreover, according to McLennan et al. [
14], in approximately 5% of PD patients, micrographia may be observed even before the onset of the cardinal motor symptoms.
The recent advantage of new technologies coming hand-in-hand with Health 4.0 systems enables the acquisition of online handwriting signals, where temporal information is added to the
x and
y position. Therefore, by using a digitizing tablet, the analysis is not limited to spatial features which mainly quantify PD micrographia. In addition, we are able to quantify temporal, kinematic, and dynamic manifestations of PD dysgraphia, such as hesitations, pauses, and slow movement [
7], which cannot be studied objectively using a classical paper-and-pen method. Due to this complexity, Letanneux et al. [
15] started to refer to these manifestations using the generalized term PD dysgraphia.
Several research teams have explored the impact of quantitative PD dysgraphia analysis utilizing simple handwriting/drawing tasks (e.g., separate characters, a combination of two or three characters, repetitive loops, circles), as well as more complex ones (e.g., words, sentences, figures, 3D objects, and the Archimedean spiral) [
8,
16,
17,
18,
19,
20]. An overview of recent related works (2015–present) can be seen in
Table 1. Most of them confirm the irreplaceability of kinematic features in PD dysgraphia analysis. Additionally, the researchers usually employ temporal, spatial, and dynamic features. Some more advanced parameters are reported too. For instance, Drotar et al. [
8,
16,
17] demonstrated a combination of kinematic, pressure, energy, or empirical mode decomposition (EMD)-based features that resulted in a classification accuracy of up to 89% using several handwriting tasks. Kotsavasilogloua et al. [
21] achieved an average prediction accuracy of 91% using simple horizontal lines and features describing the variability in the pen tip’s velocity, a deviation from the horizontal plane, and the trajectory’s entropy. Other works report even higher classification accuracies (approximately 97%), e.g., Loconsole et al. [
18], who used computer vision and electromyography signal processing techniques, or Taleb et al. [
22], who used a combination of features related to the correlation between kinematic and pressure characteristics (but, in this case, applied to a very small dataset). Another promising approach was published by Moetesum et al. [
23], who reached an 83% classification accuracy by employing convolutional neural networks (CNN) that were used to extract discriminating visual features from handwriting data transformed into the offline mode. In 2018, Impedovo et al. reported the results of a study focused only on the early stages of PD; the best accuracy was 74.76% for a combination of three handwriting tasks. Finally, in our previous work [
20], we proposed a new approach of advanced kinematic feature extraction that utilizes fractional-order derivatives (FD). This approach increased the classification accuracy by 10% (72.39%) for Archimedean spiral tasks in comparison with the baseline [
20].
Although the authors of the previously mentioned studies reported high classification accuracies, further signal processing and machine learning pipeline improvements are expected to make the differential analysis even more accurate. One possible approach could involve an advanced feature extraction methodology based on fractional calculus (FC) [
29,
30], which enables the use of an arbitrary order of derivatives and/or integrals. Generally, FC has many applications in different fields of science [
31,
32,
33]. For instance, it has been advantageously used during the modeling of different diseases, such as human immunodeficiency virus (HIV) [
34] and malaria [
35]. In addition, FC-based analytical tools have outperformed classical techniques in geology [
36,
37], economics and finance [
38,
39], etc. Moreover, in our recent paper [
20], we identified a high potential for the use of FC in the kinematic analysis of PD drawings. Based on these preliminary results, we assume that FD-based handwriting features may bring improvements to PD diagnosis and assessment. In the frame of this article, we would like to go further and deeply explore the impact of FD on the PD dysgraphia diagnosis and its monitoring. More specifically, we aim to:
investigate the relationship between newly designed FD handwriting features and a patient’s clinical data and compare these results with a baseline (i.e., results based on conventional parameters),
evaluate the discrimination power of the FD features in terms of binary classification accuracy and compare the results to the baseline,
use the newly designed features to establish regression models that will estimate the severity of PD and compare its performance to that of a baseline.
The rest of this paper is organized as follows:
Section 2 describes the cohort of patients and the methodology, and
Section 3 includes the results. A discussion is presented in
Section 4, and, finally, conclusions are drawn in
Section 5.
3. Results
In
Table 5, the results of partial correlation analysis between the handwriting features (FD-based features, conventional features) and patients’ clinical characteristics (UPDRS V, PD duration) are summarized. The table shows the five best features according to Spearman’s correlation coefficient for each movement (on-surface, in-air).
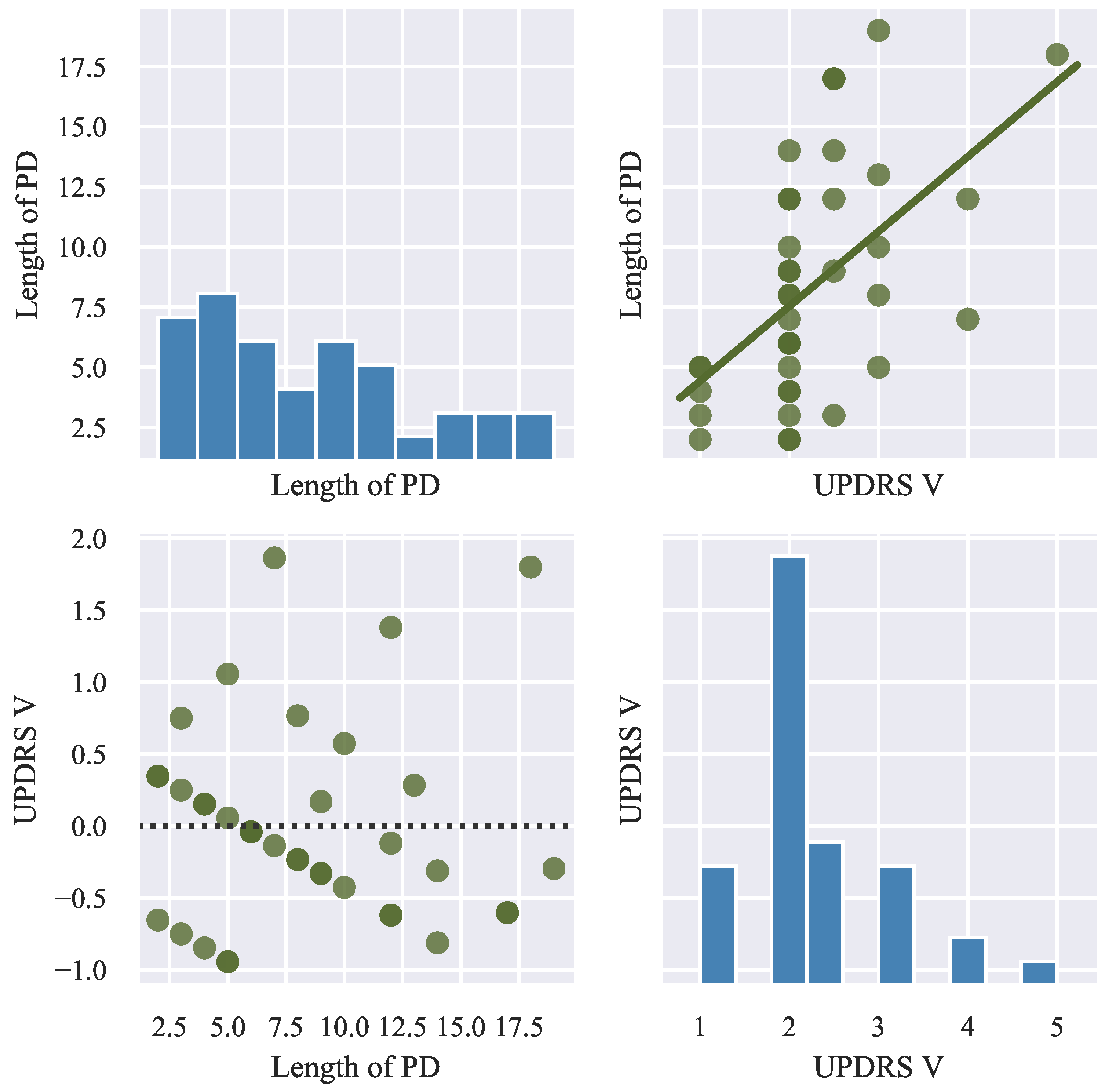
In the case of UPDRS V (on-surface movement), the following FD-based features achieved a statistical significance of correlation: the median of jerk (, ) and horizontal velocity ( = 0.1) for the repetitive letter l, the mean of vertical acceleration () for repetitive loops, and the standard deviation of the vertical velocity () for the sentence. The following conventional features achieved a statistical significance of correlation (p-value of only one of the coefficients was below the threshold): the maximum of horizontal jerk and velocity for the repetitive letters le, the maximum of horizontal jerk and horizontal velocity for the repetitive letter l, and the maximum of horizontal velocity for the letter l. Regarding UPDRS V (in-air movement), the following FD-based features achieved a statistical significance of correlation: the median of vertical velocity (, , ) for the sentence and the median of horizontal velocity () and vertical jerk () for the repetitive letters le. The following conventional features achieved a statistical significance of correlation (p-value of only one of the coefficients was below the threshold): the mean of acceleration for the repetitive word lektorka, the maximum of horizontal jerk for the word porovnat, the median of the vertical velocity for the repetitive letter l, and the median of the horizontal velocity of the repetitive letters le.
For PD duration (on-surface movement), the following FD-based features achieved a statistical significance of correlation (of note: all of these features satisfied the stronger threshold for statistical significance of correlation ): the maximum of the velocity () and acceleration (, , , ) for the Archimedean spiral. The following conventional features achieved a statistical significance of correlation (p-value of only one of the coefficients was below the threshold): the maximum of horizontal velocity, horizontal jerk, and velocity for the repetitive letter l; the mean of the vertical velocity for the Archimedean spiral; and the mean of horizontal acceleration for repetitive loops. For PD duration (in-air movement), the following FD-based features achieved a statistical significance of correlation: the median of jerk () for sentence, the maximum of jerk (, , ) and velocity () for repetitive word les. The following conventional features achieved a statistical significance of correlation (p-value of only one of the coefficients was below the threshold): the median and mean of horizontal jerk for the word lektorka, the maximum of the velocity for the word nepopadnout, and the mean of horizontal velocity for the repetitive word lektorka and the word nepopadnout.
The results of the multivariate binary classification analysis are summarized in
Table 6. In total, we built and evaluated nine different classification models. These models were selected according to the following criteria: movement type (on-surface, in-air, all), feature type (FD features, conventional features, all). We built models based on the combinations of these criteria as well. For more information, see
Table 4.
With respect to the classification performance, the highest MCC achieved was 0.95 was for eight out of the total nine feature sets (with the exception being the feature set composed of conventional handwriting features computed for the on-surface movements). An interesting fact to note is that for all models based on conventional handwriting features, only a single feature was capable of providing the classification models with such a high discrimination power. In terms of the specific features important for the trained models, the following feature importances were returned by the models (feature importance quantifies the relative importance of the features in the ensemble of the trained XGBoost model [
49]; therefore, the higher the value of the feature importance, the more important the feature for the prediction of the dependent variable): conventional on-surface (horizontal jerk (median) of repetitive loops), conventional in-air (horizontal velocity (median) of the sentence), conventional together (horizontal velocity (median) of the sentence), FD on-surface (jerk (max)
of the letters
le), FD in-air (vertical acceleration (mean)
of the word
nepopadnout (
), horizontal jerk (mean)
of the word
nepopadnout (
), horizontal jerk (mean)
of the repetitive word
lektorka (
)), FD together (jerk (max)
of the letters
le (on-surface;
), horizontal jerk (mean)
of the word
nepopadnout (in-air;
)), all on-surface (horizontal jerk (median) of repetitive loops (
), jerk (max)
of the letters
le (
)), all in-air (horizontal velocity (median) of the sentence), and all together (horizontal velocity (median) of the sentence (in-air)).
The results of multivariate regression analysis are summarized in
Table 7. For this purpose, we used UPDRS V and PD duration as our target variables. As in the case of binary classification, we built and evaluated nine different regression models according to the same criteria. For each of the rating scales, the table shows the results achieved using the trained models and the associated feature importance values. All obtained results are discussed in the following section.
Considering EER as our performance evaluation metric, the following results are worth pointing out. In the case of UPDRS V, the lowest EER was achieved using a single FD-based feature—specifically, the standard deviation of vertical velocity () computed for the on-surface movements (). The same feature was selected when both FD and conventional features were considered while building the model. In general, all models achieved an EER of around 12–13%. In comparison with the conventional features, the FD-based features performed better, with a difference of about 1%. In terms of the specific features important for the trained models, the following feature importances were returned by the models: conventional on-surface (vertical normalized jerk (mean) of the repetitive word lektorka), conventional in-air (vertical velocity (mean) of the sentence), conventional together (vertical velocity (mean) of the sentence), FD on-surface (vertical velocity (std) of the sentence), FD in-air (vertical velocity (median) of the sentence), FD together (vertical velocity (std) of the sentence (on-surface; ), vertical velocity (median) of the sentence (in-air; )), all on-surface (vertical velocity (std) of the sentence), all in-air (vertical velocity (median) of the sentence), and all together (vertical velocity (std) of the sentence (on-surface; ), vertical velocity (median) of the sentence (in-air; )). With respect to PD duration, the lowest EER was achieved using conventional handwriting features computed for both on-surface as well as in-air movements ().
4. Discussion
To the best of our knowledge, except for our pilot work [
20], there are no prior studies which integrate FD into a handwriting parameterization for quantitative PD dysgraphia analysis. Therefore, the results published in this paper are exploratory in nature.
In comparison with the conventional kinematic features, FD-based ones correlate more significantly with the clinical characteristics (UPDRS V and PD duration). We observed especially strong correlations for handwriting tasks based on the periodic repetition of specific movements (Archimedean spiral; repetitive letter
l, syllable
le, or word
les). Although the levels of significance based on the conventional handwriting parameters are lower, similar handwriting tasks are involved in the most significant results. We hypothesize that this is due to their ability to highlight or better quantify the cardinal motor symptoms of PD. For example, the most significant relationship between handwriting performance and PD duration was identified in acceleration extracted from the Archimedean spiral. Rigidity combined with tremor and/or bradykinesia makes a PD patient’s handwriting/drawing less fluent (increased changes in velocity and higher acceleration). This is highlighted in a task such as the spiral, where the proper coordination of the fingers, wrist, and arm is required. Generally, the observed problems with coordination are in line with the work of Dounskaia et al. [
51] and Teulings et al. [
52]. To better illustrate these manifestations,
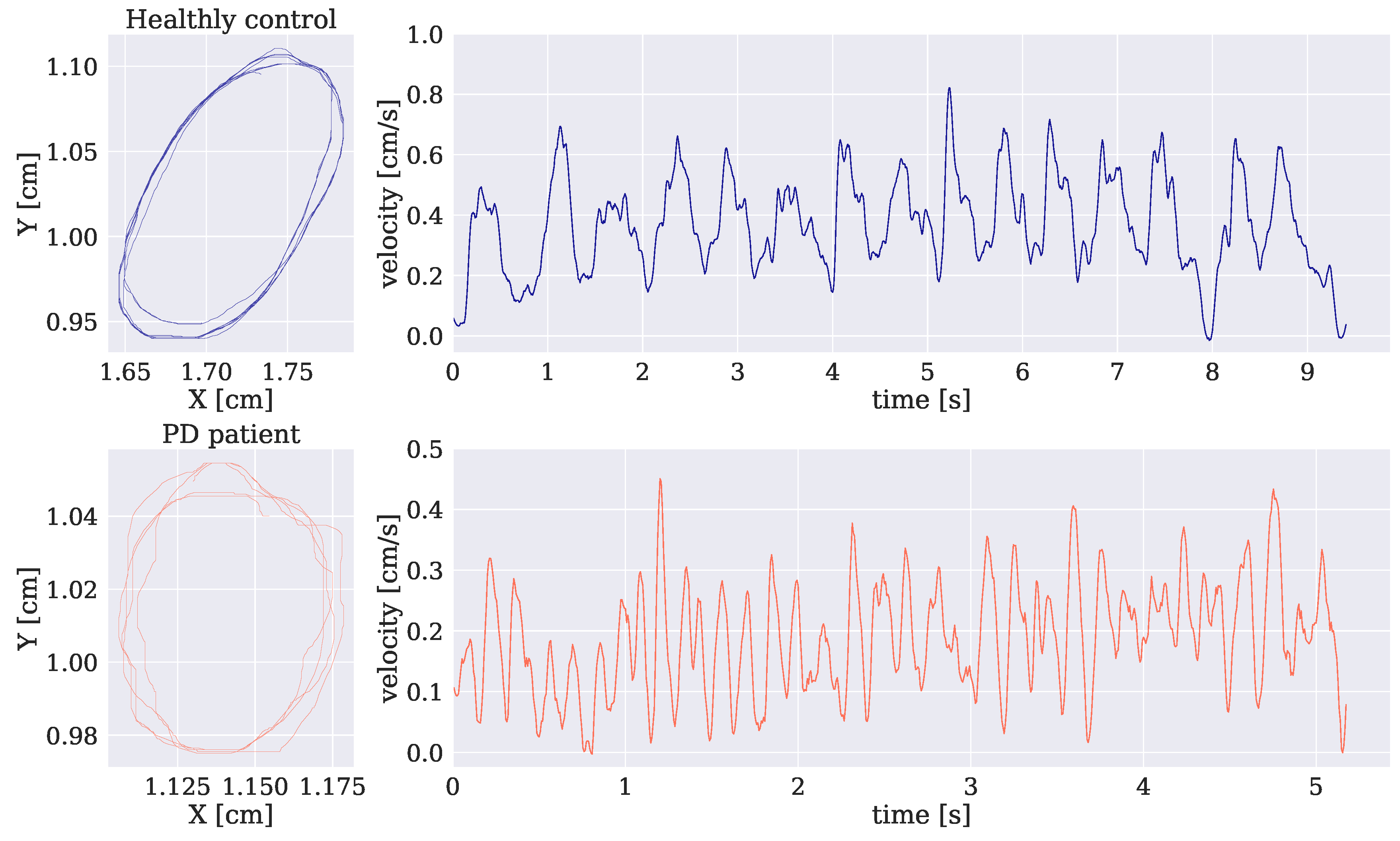
Figure 3 plots the velocity profiles of repetitive loops for a healthy control and a PD patient. As can be seen, the patient introduced more changes in velocity, and their drawing became much more non-fluent. To summarize these findings, FD features in combination with properly selected tasks provide a stronger relationship with the severity and progress of PD.
On the other hand, in terms of binary classification, the conventional parameters provided the best results. The classification performance is remarkable:
,
, and
. In fact, our results represent the highest classification accuracy that has ever been reported based on the PaHaW database (see
Table 1). We hypothesize that the improvement was caused by the inclusion of the state-of-the-art XGBoost algorithm into our machine learning pipelines. As already mentioned, the result is based on one in-air feature: median horizontal velocity of a sentence. In comparison with the HC cohort, the PD patients exhibited much lower values of this measure, i.e., while writing the sentence, the PD patients were not able to perform horizontal transitions (movement between neighboring letters or words) as quickly as the HC could. This finding is in line with the work of Ma et al. [
53], who observed that wrist extension stiffness in PD patients makes the handwriting in the horizontal direction more problematic. Therefore, scientists started to use the term
horizontal dysgraphia [
13]. Generally, vertical or horizontal dysgraphia may be considered a presymptomatic neurobehavioral biomarker of PD with possible significance in early PD diagnosis [
13].
In [
20], we proved that the FD features improved the accuracy of PD dysgraphia diagnosis in the Archimedean spiral drawing task by 10%. Contrary to our pilot results, in the frame of this work, these features did not lead to any improvements. After a deeper analysis, we found that this was caused by a combined task approach. Performance of the Archimedean spiral is a quasiparticle and continuous task with some repetitive patterns. It looks as though the FD features work especially well in these specific cases. Nevertheless, when combining these tasks with a complex handwriting task (such as a sentence), the measures quantifying in-air movement tend to be more discriminative (in our case, the median in-air horizontal velocity of a sentence). This brings us to the same conclusion that was given during the correlation analysis—the FD features advance the PD dysgraphia diagnosis only in some specific cases.
The best regression model, estimating the UPDRS V score with a 12.51% error, is based only on the standard deviation of on-surface vertical velocity (
) extracted from the sentence. This FD-based parameter was selected from the feature set combining all on-surface measures; therefore, we can confirm the positive influence of FC on the regression analysis performance. In fact, the FD features outperformed the conventional ones in all scenarios. To better understand this result, we plotted vertical velocity patterns of the sentence task for different orders of FD (see
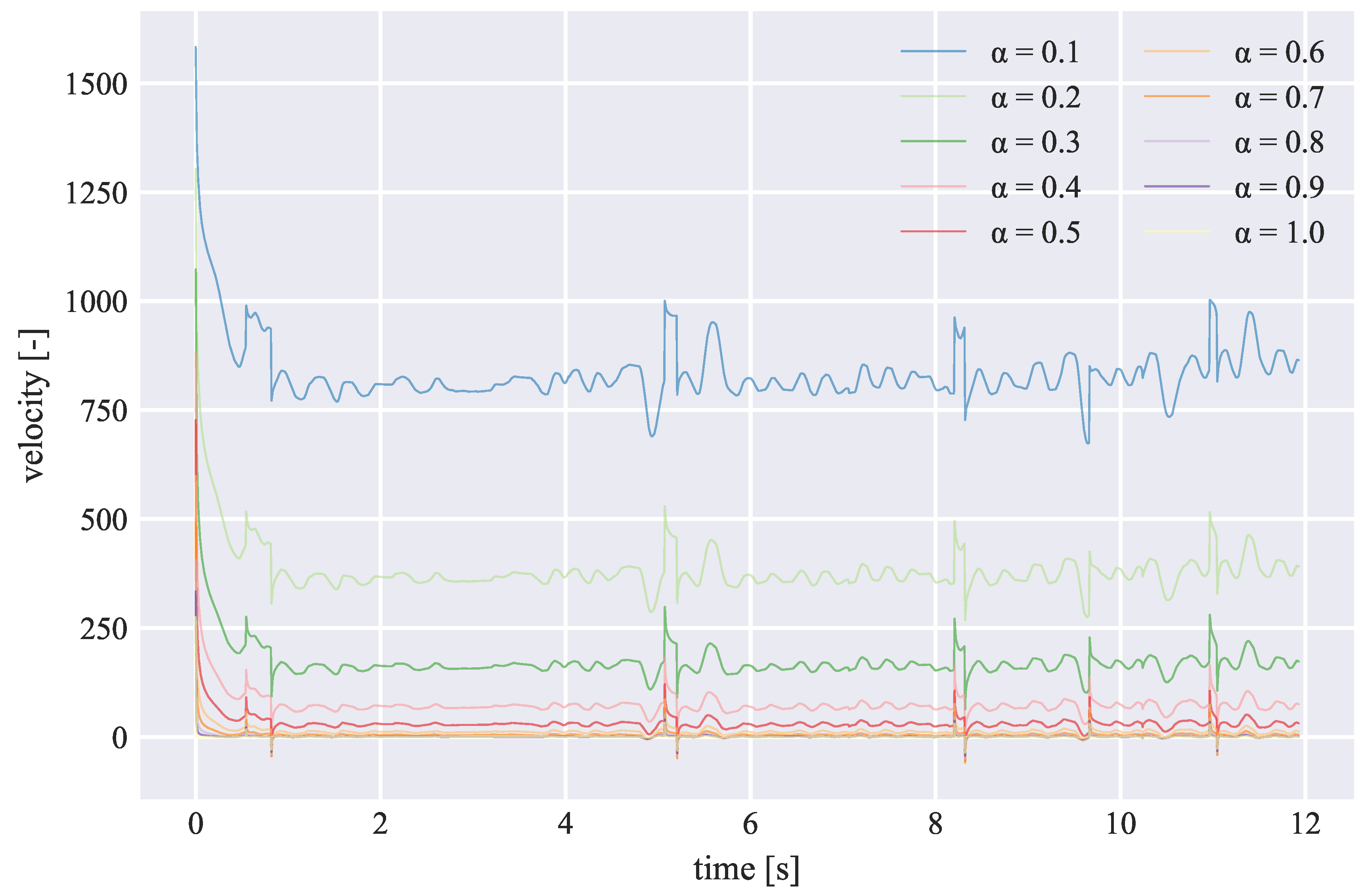
Figure 4). We can observe a big difference between
and the rest of the orders, including the full derivative. This large distance means that we are working with completely new information that is far from that contained in the full derivative. Although it is difficult to clinically interpret this information, it is clear that FC opens new possibilities for monitoring PD severity.
Regarding the PD duration estimation results, the most successful model (
) consists of 16 conventional on-surface/in-air features (all features’ importance values can be found in
Supplementary Table S1). The most frequent feature with the highest feature importance is the jerk extracted from several handwriting tasks. This probably means that as PD progresses, handwriting becomes more jerky and irregular. Vertical velocity is the second most frequent feature involved in the models, which is probably linked with micrographia. Generally, in the case of PD duration estimation, the FD-based features did not yield any improvement.
In conclusion, the FD-based features are better for modeling PD severity (in terms of UPDRS V score estimation), but they do not lead to an improvement in PD duration modeling. The progress of PD is nonlinear and very individual. This means that patients with the same PD duration can be in different stages of the disease. This fact supports our results: the estimation error of PD duration was generally much worse than the estimation error of the UPDRS V score. Since PD duration estimation is a difficult task with poor results, fine improvements based on FD parameters play no role.
5. Conclusions
This study deals with advanced approaches to PD dysgraphia diagnosis and monitoring based on FC integrated with online handwriting/drawing parameterization. To the best of our knowledge, it is the first work that performs a complex investigation into the possibilities for FC in online handwriting processing and proposes new advances in kinematic analyses based on FD. Although the conventional features provided better and very high classification accuracy, which is at the top of the state-of-the-art analyses based on the PaHaW database (, , and ), the newly designed parameters were proven to work better for specific tasks (continuous and/or repetitive, such as the Archimedean spiral) and for specific applications, i.e., PD severity estimation (EER = 12.51%). However, our results need to be confirmed by subsequent scientific research.
This study has several limitations and suggestions for further improvements. Since the dataset is small, to be able to generalize the results, bigger databases should be involved. On the other hand, it is common to have such small numbers of PD patients and HC samples in PD dysgraphia analysis, e.g., see our review in
Table 1. Next, we considered only the kinematic measures. To better evaluate the discrimination power of the FD features and better evaluate their ability to estimate PD severity or progress, other feature types, such as temporal, spatial, and dynamic, should be included in future comparisons. Finally, the FD-based parameters could be further explored. For instance, we can consider other approximations (e.g., Caputo) or employ FC for other measures (e.g., entropies).