Towards Quantitative Acoustic Emission by Finite Element Modelling: Contribution of Modal Analysis and Identification of Pertinent Descriptors
Abstract
1. Introduction
2. Numerical Methods and Experimental Procedure
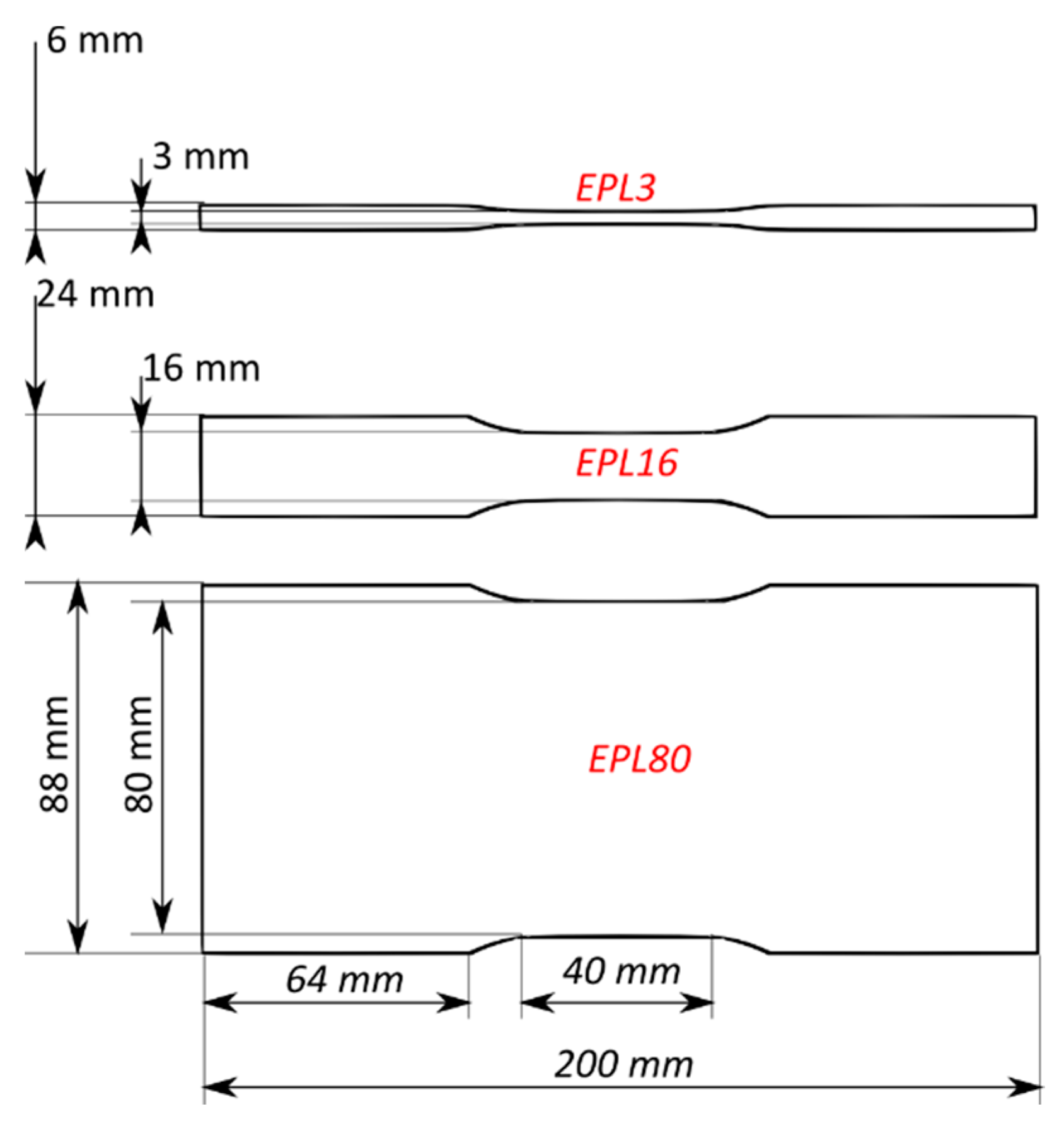
2.1. Sample Geometry
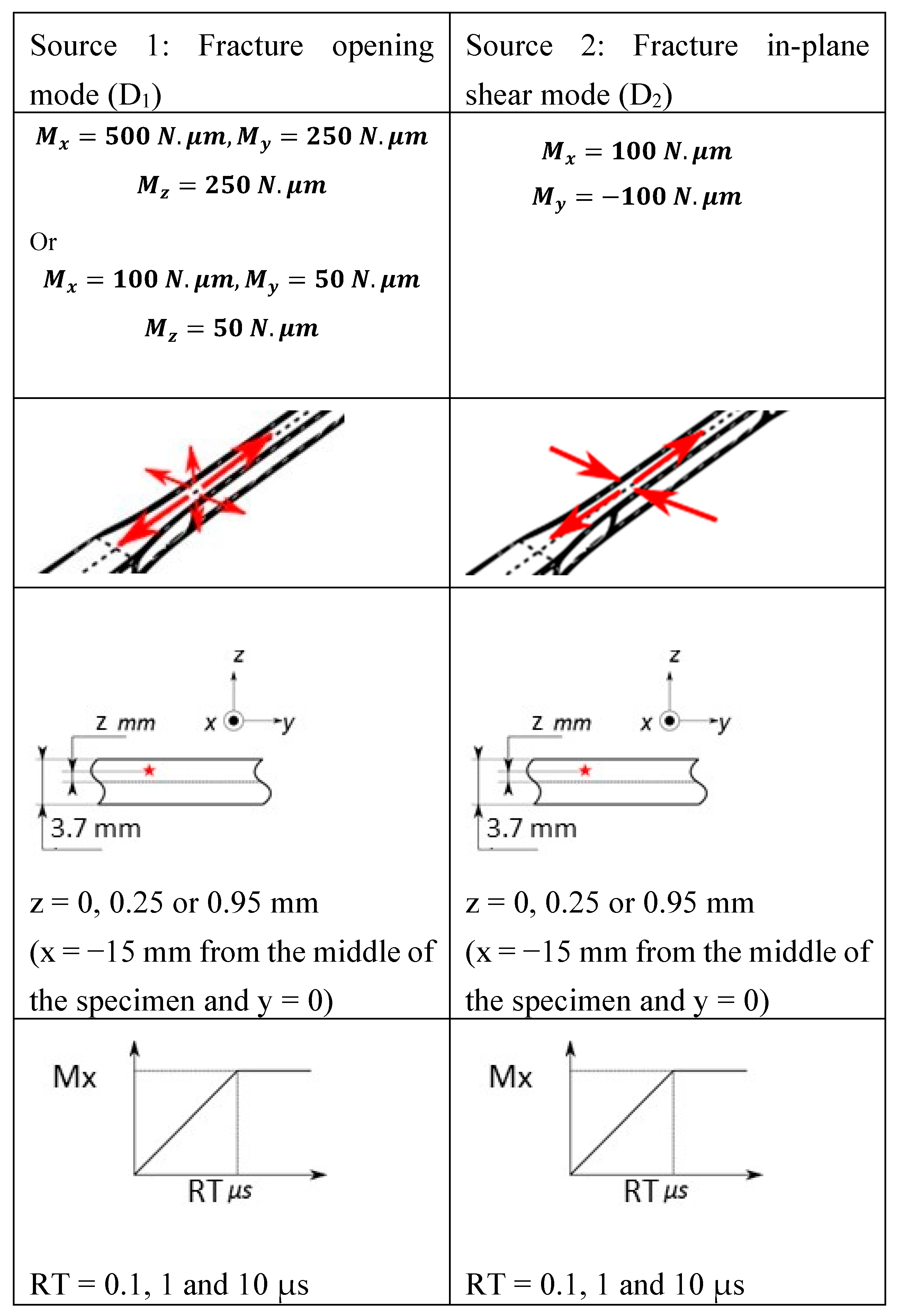
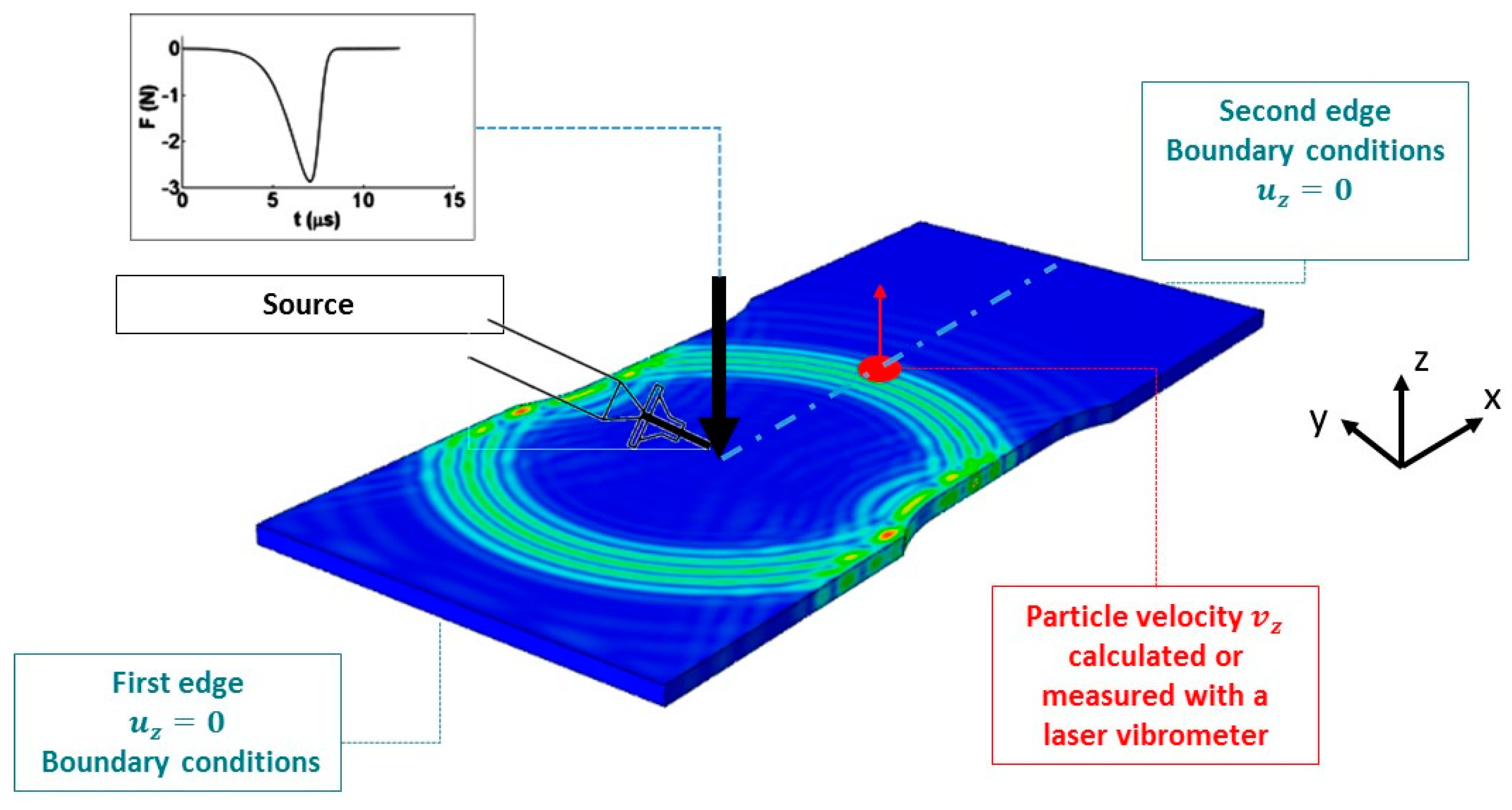
2.2. Source Modelling
2.3. Propagation and Attenuation
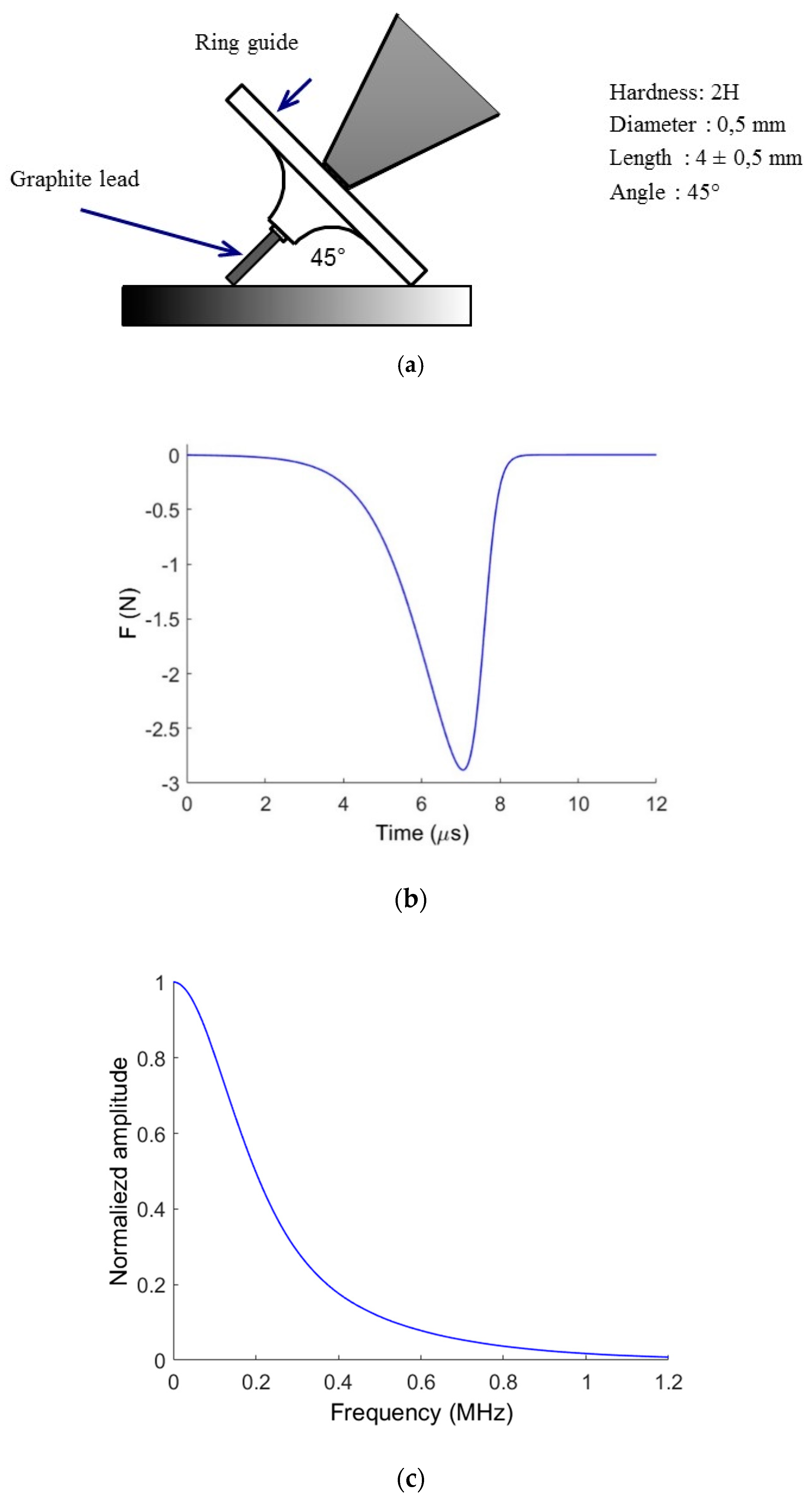
2.4. Experimental Procedure
2.5. Sensor Effect
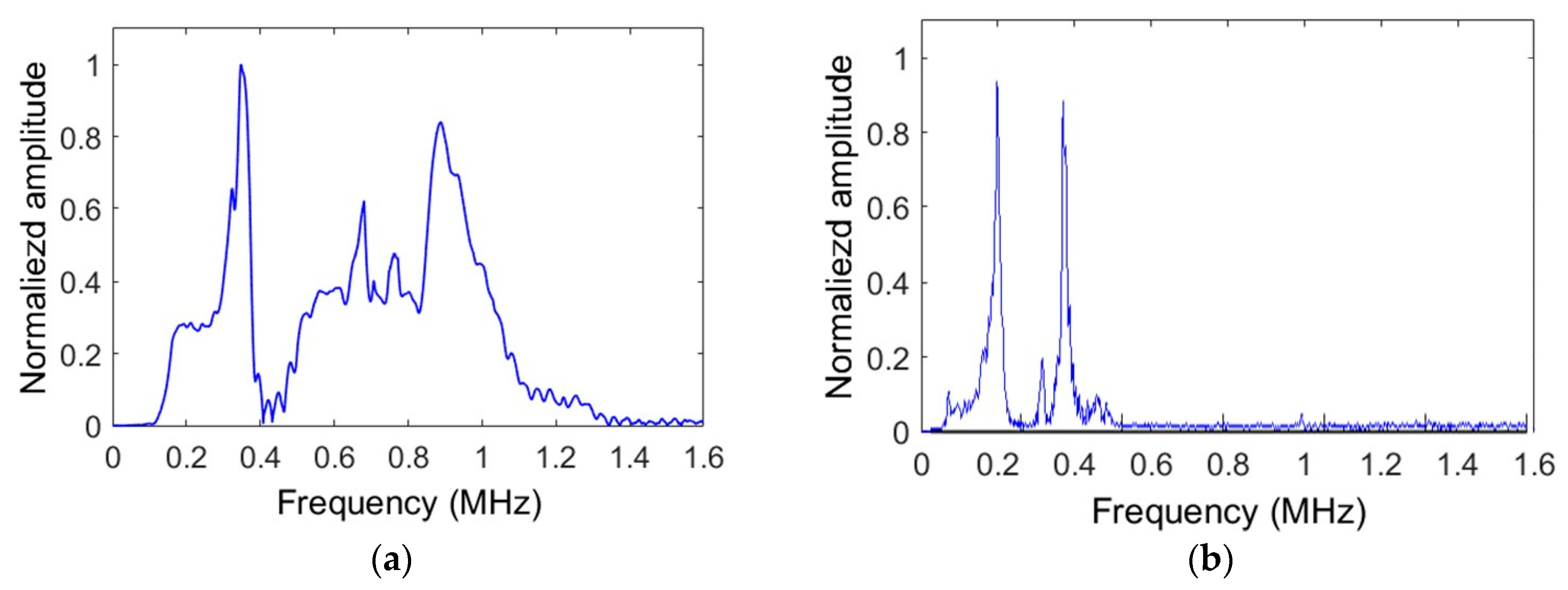
2.6. Signal Analysis
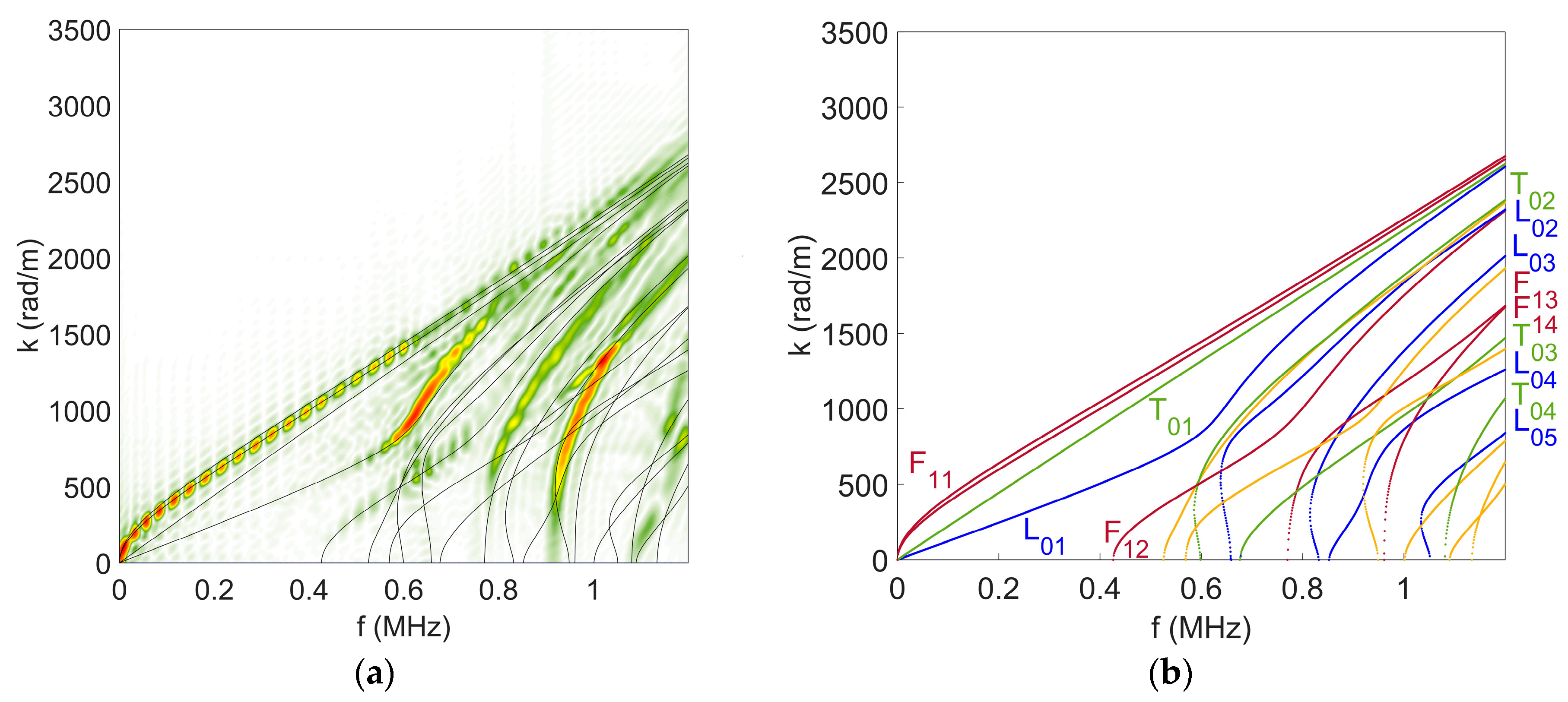
2.6.1. Modal Analysis
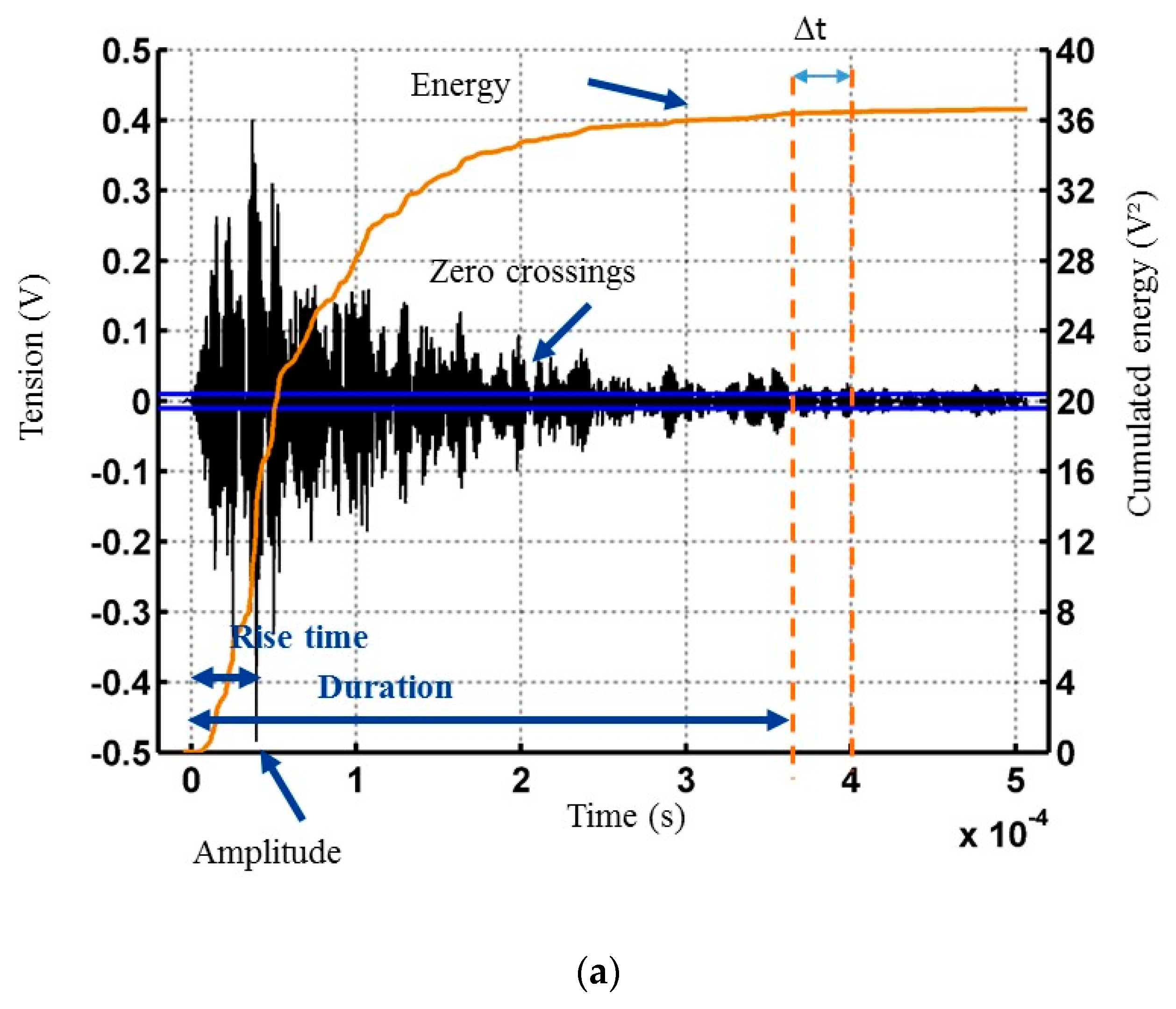
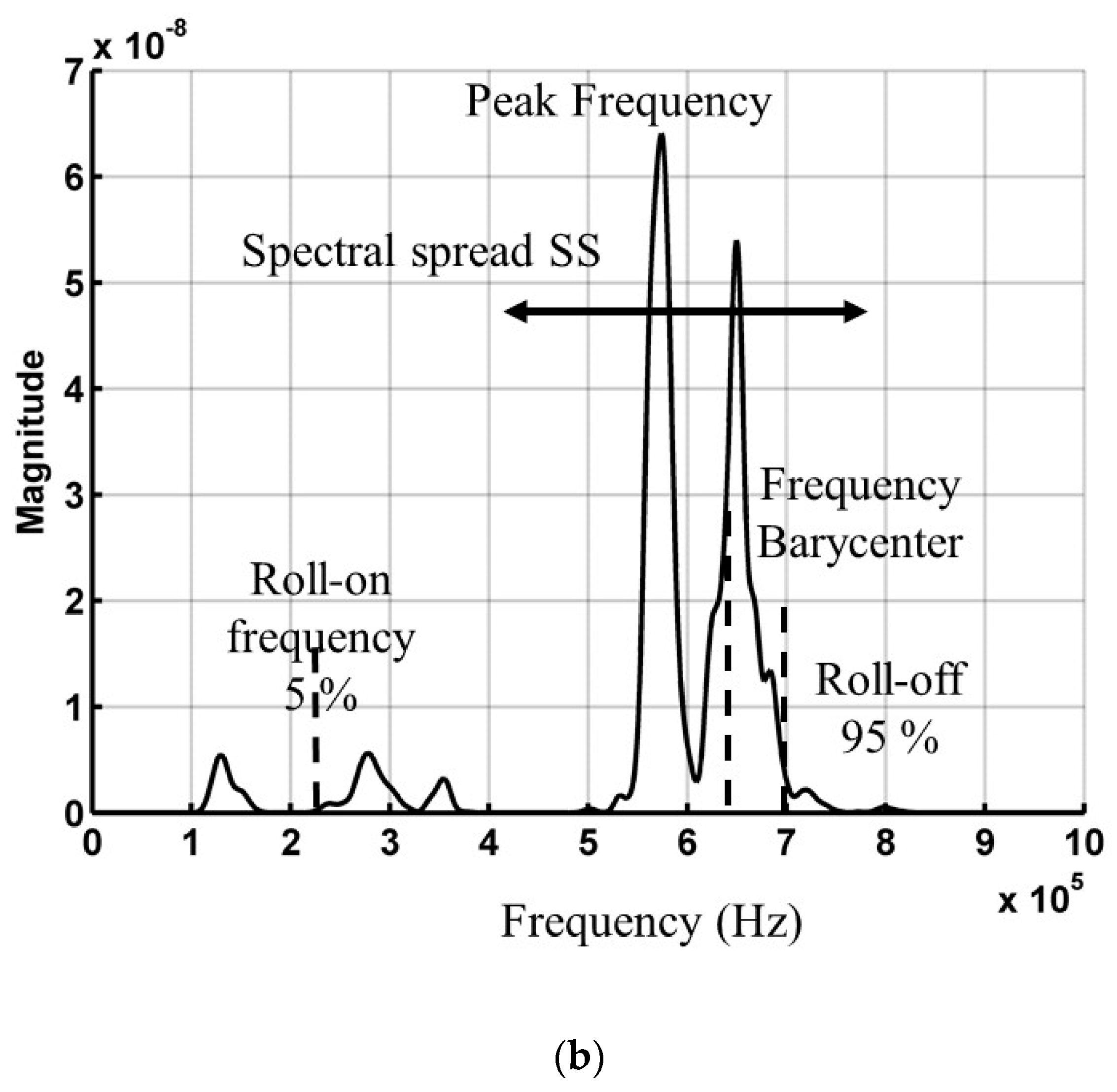
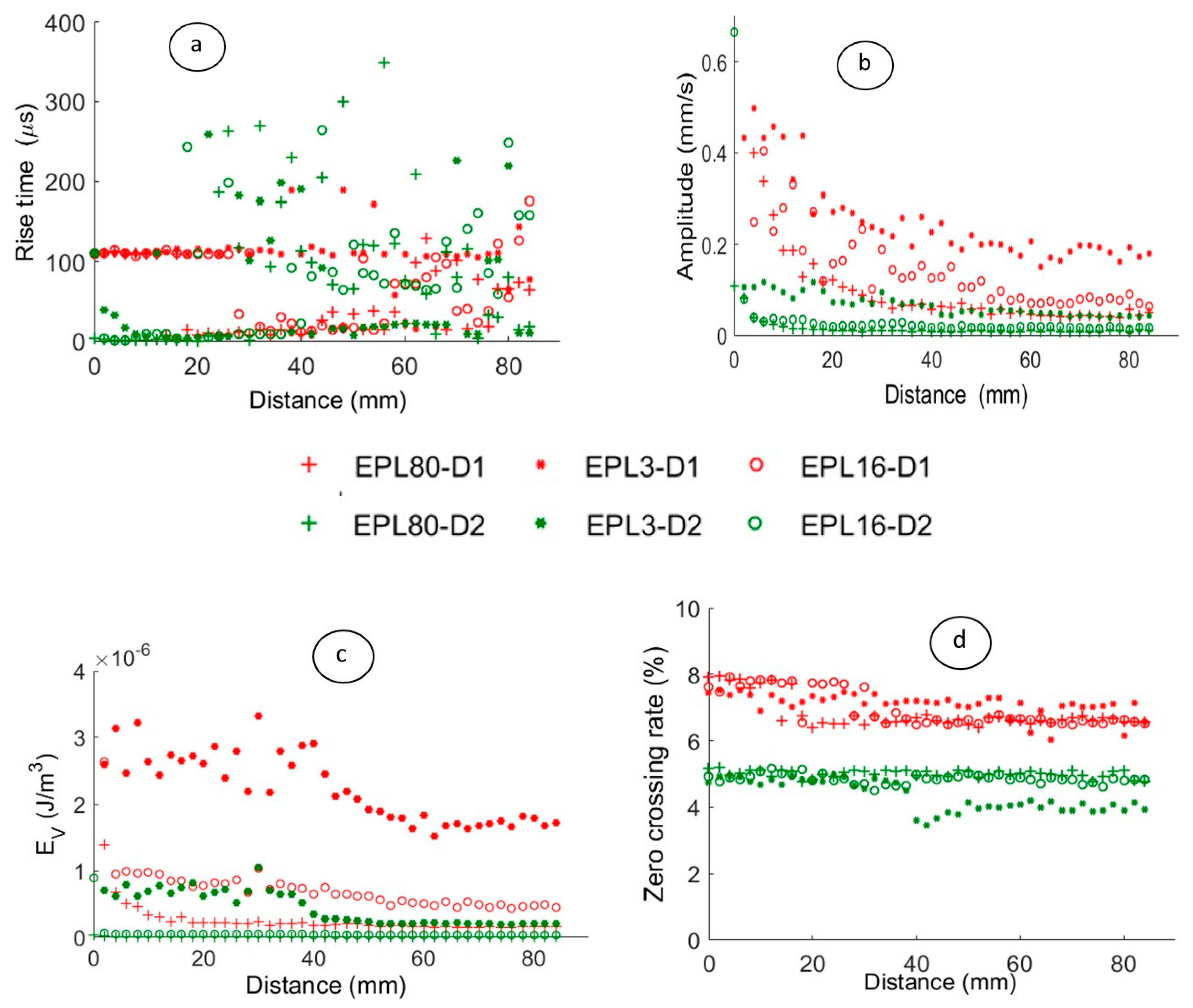
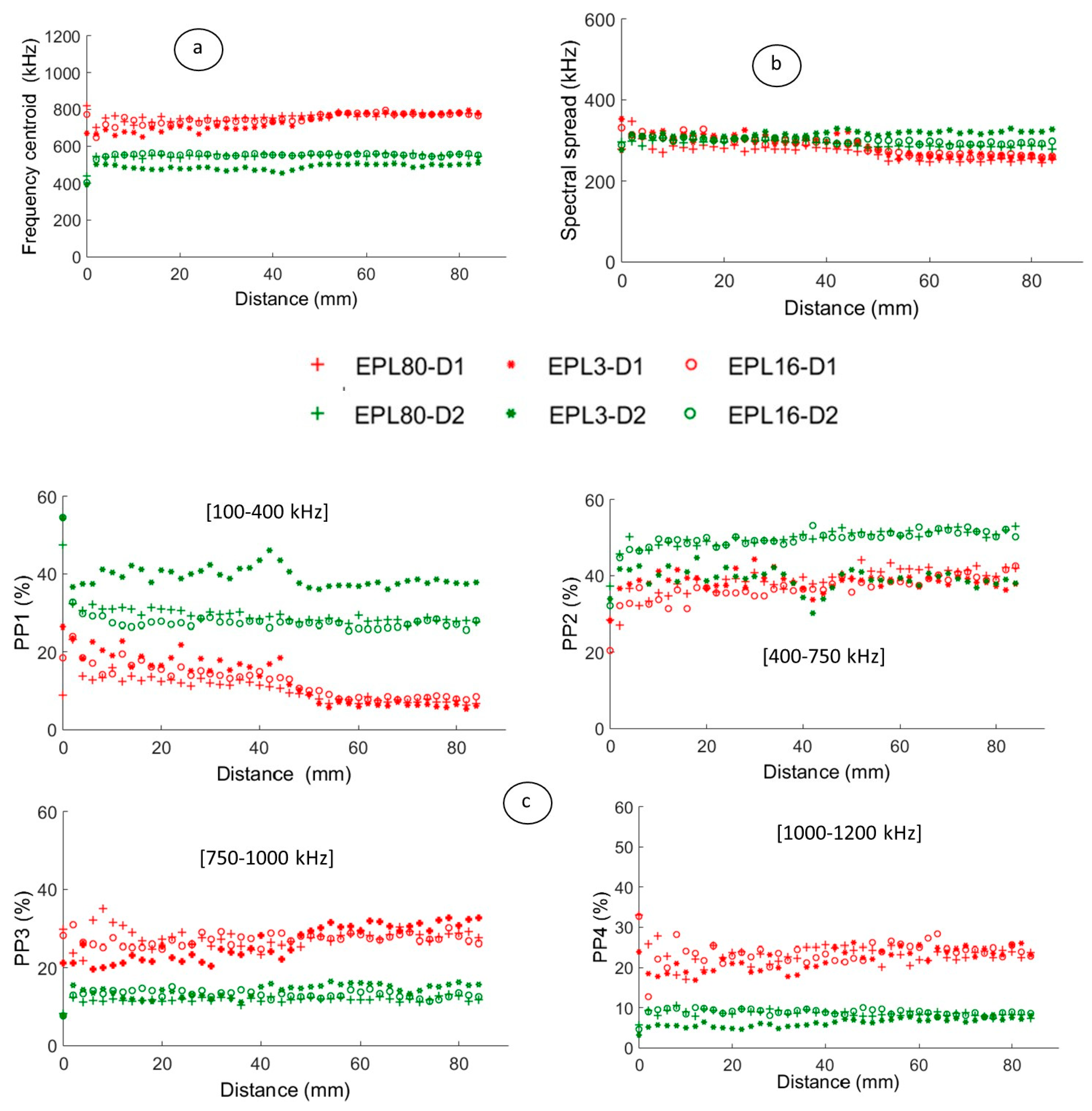
2.6.2. Acoustic Emission Parameters
3. Experimental Validation of the Finite Element Method
4. Results and Discussion
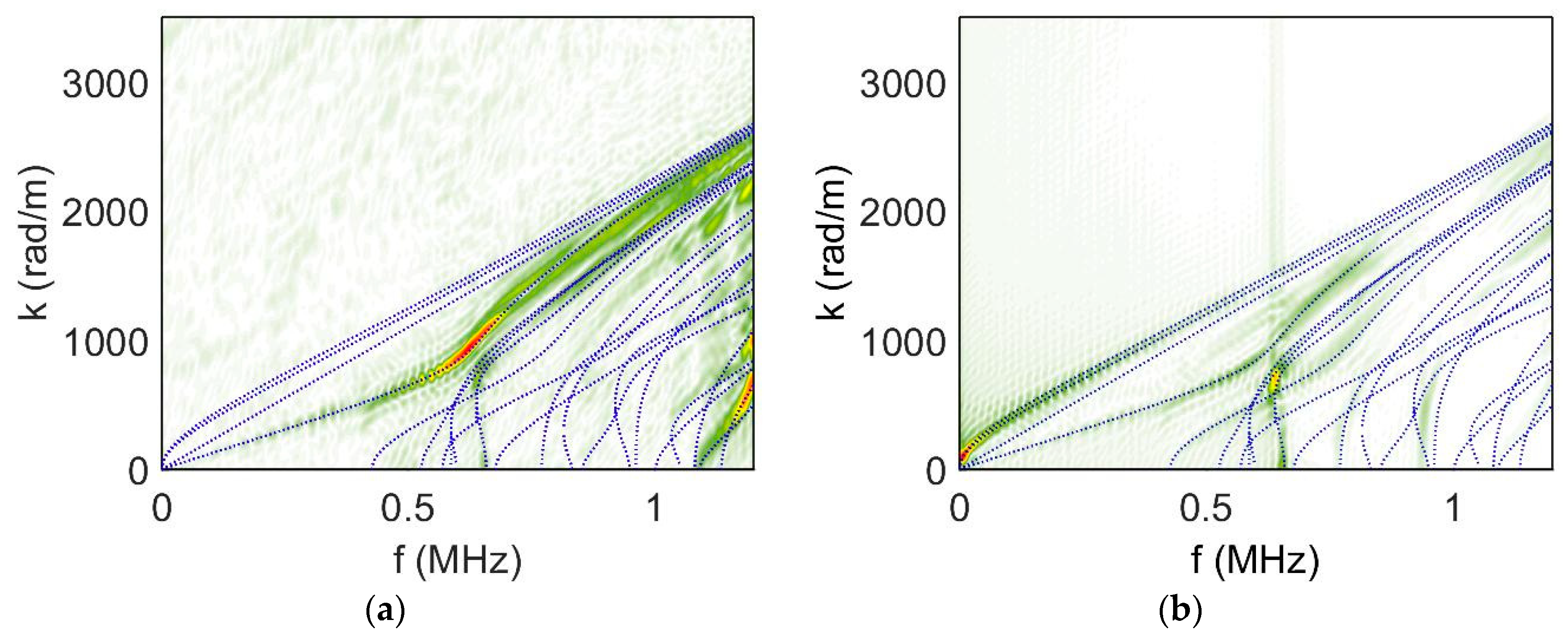
4.1. Modal Analysis of Numerical Results: Identification of the Excited Modes
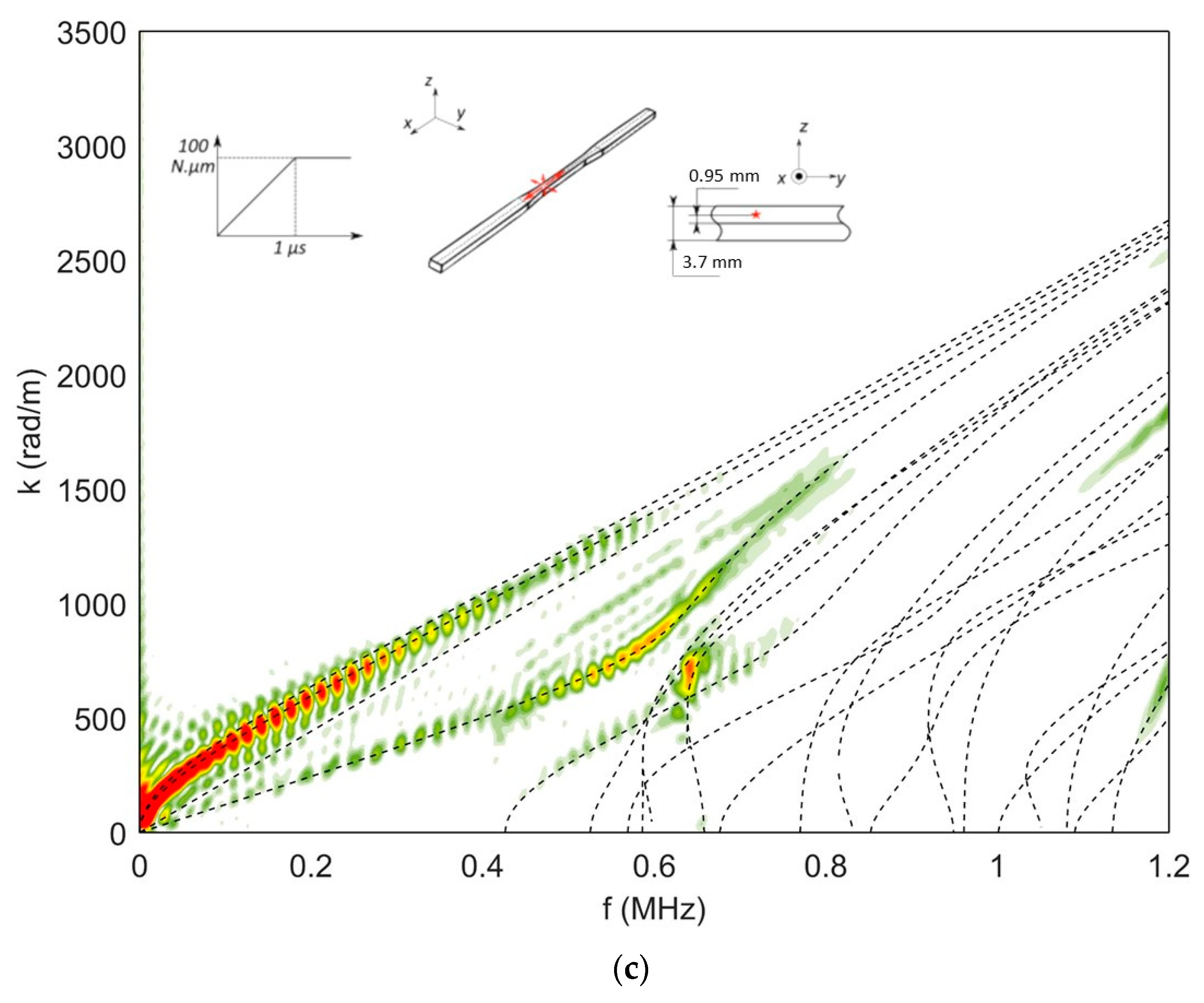
4.1.1. Influence of the Geometry on the Excited Waves
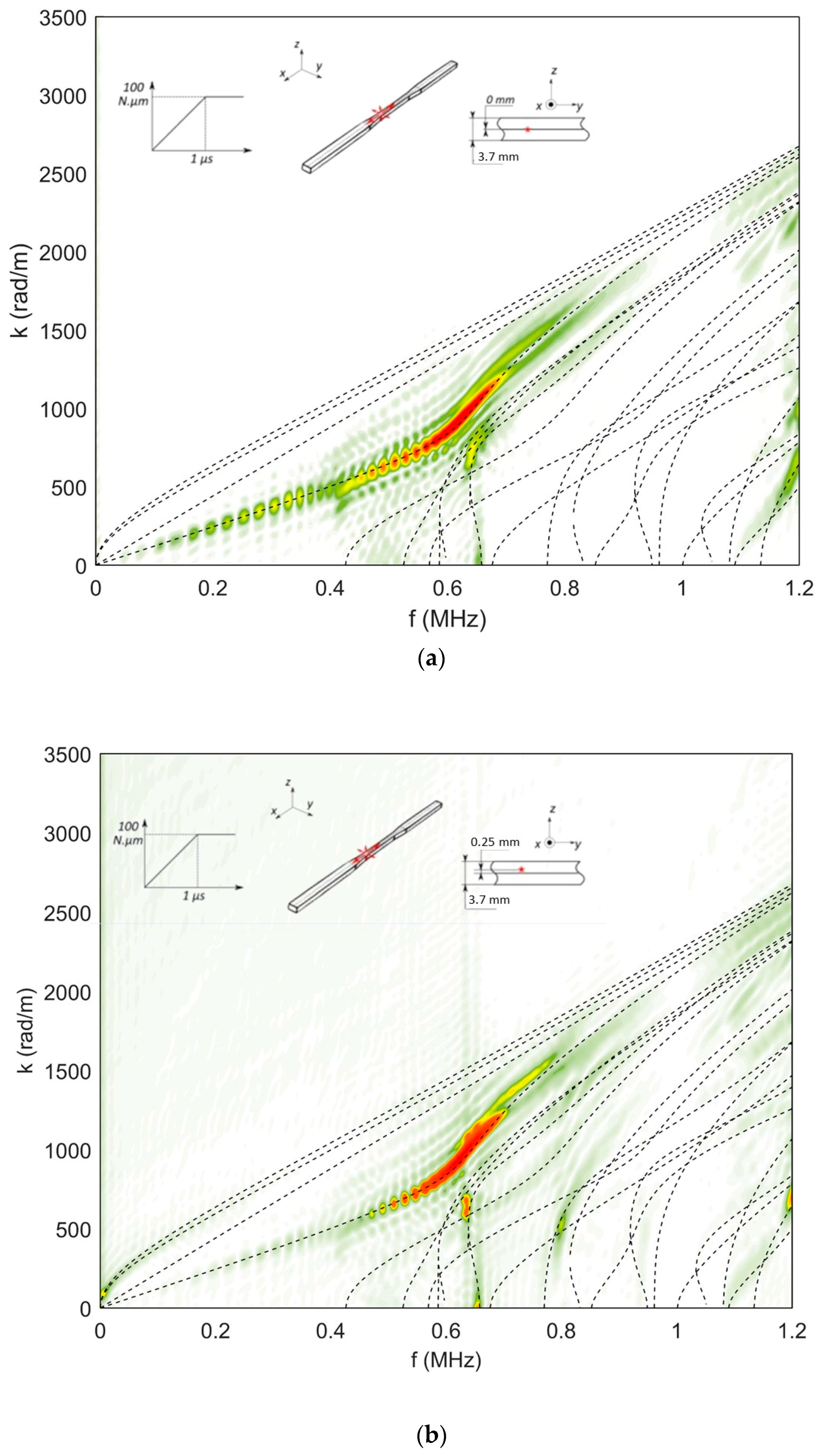
4.1.2. Effect of the Depth of the Source
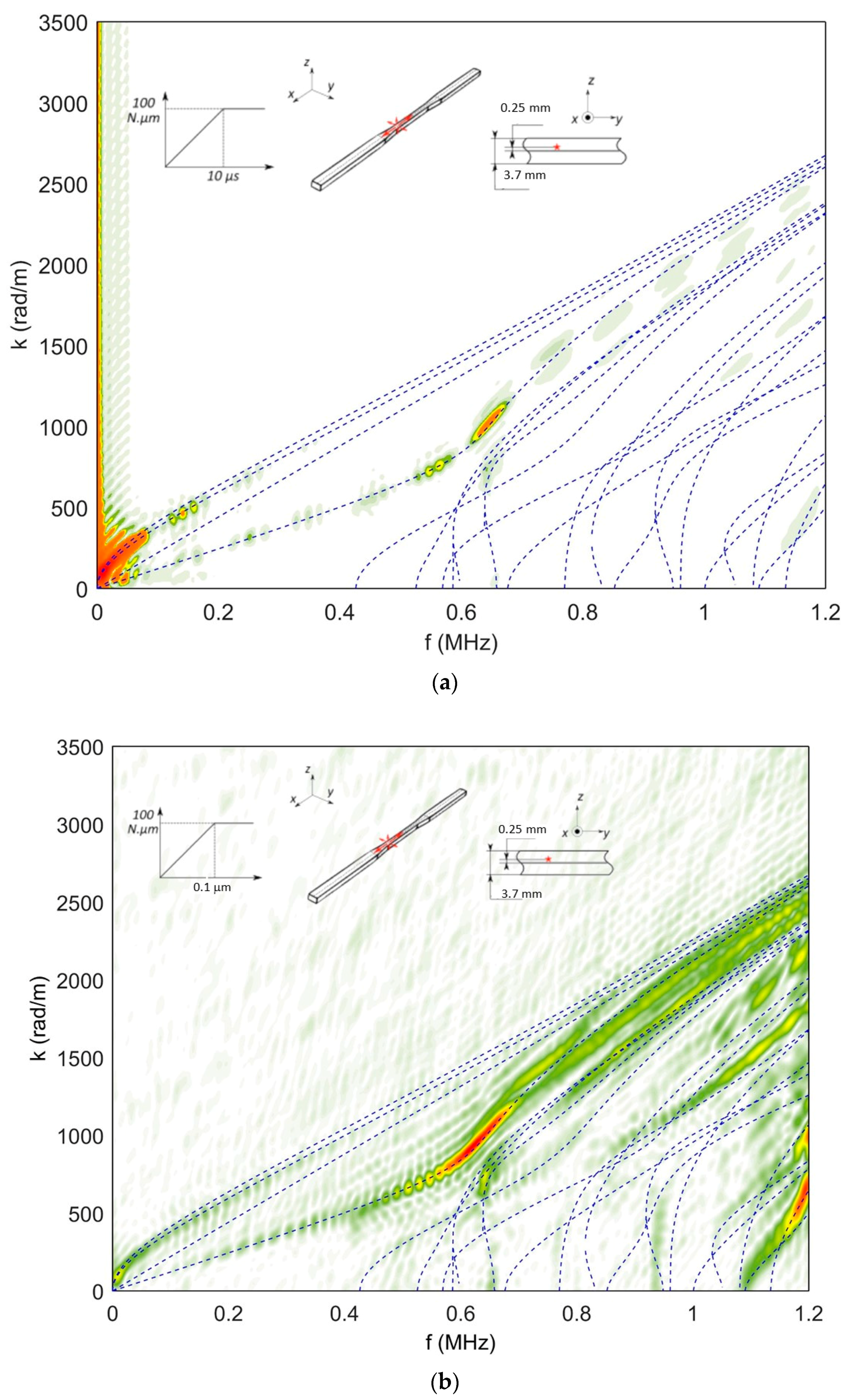
4.1.3. Effect of Source Rise Time
4.2. Numerical Modelling as a Tool to Improve the AE Clustering: Effect of the Sensor
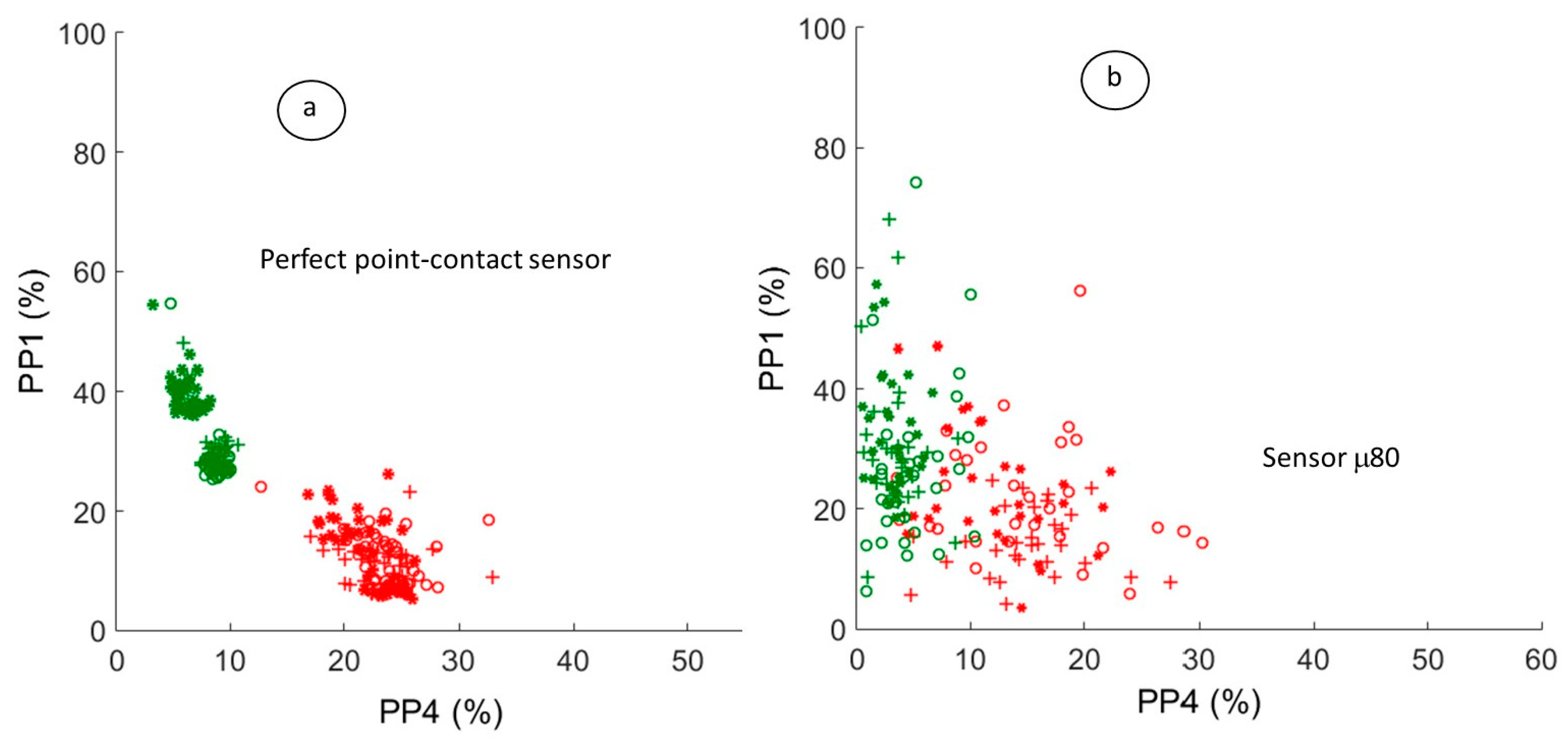
4.2.1. Relevant Parameters on the Surface with a Perfect Point Contact-Sensor
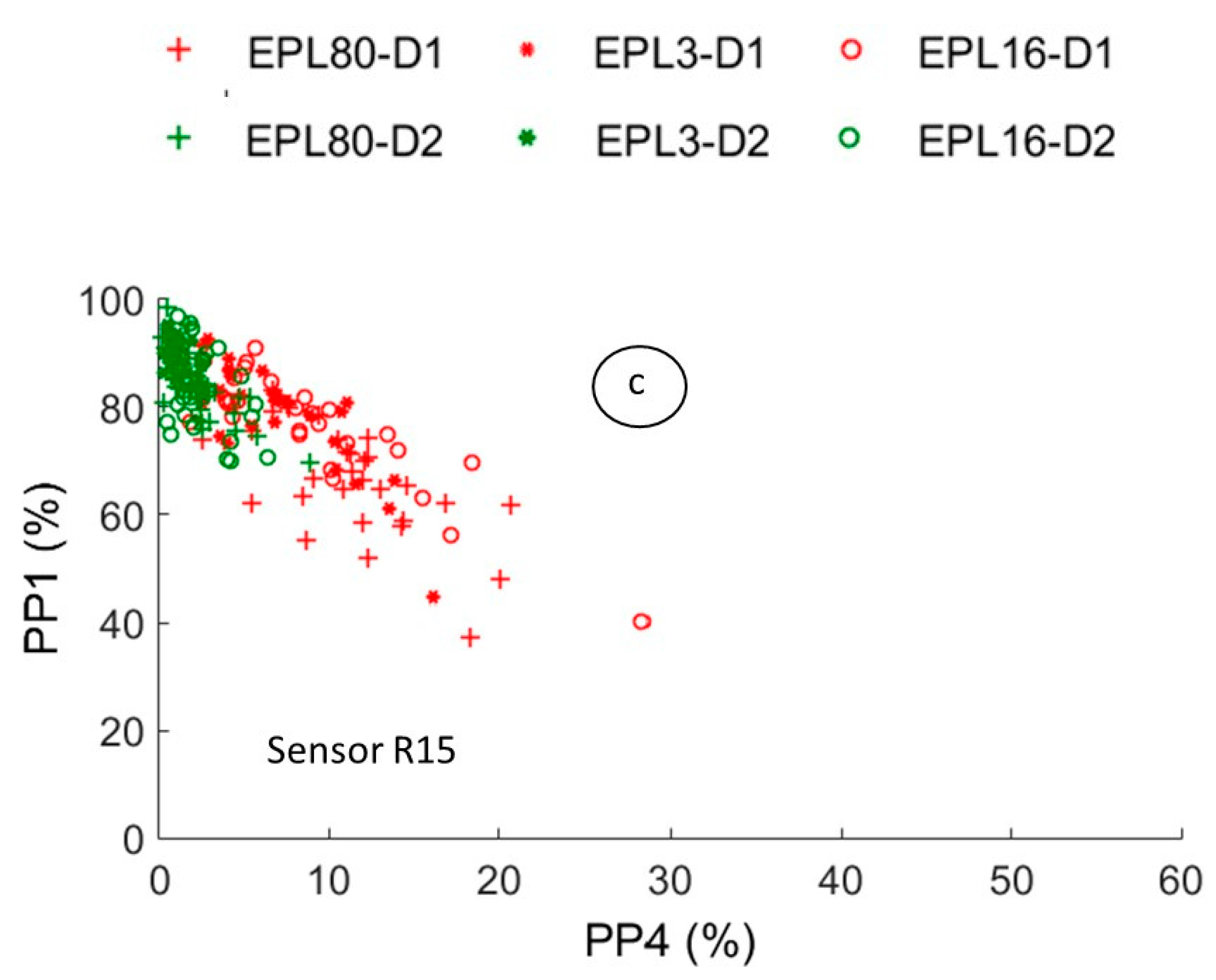
4.2.2. Effect of the Piezoelectric Sensor on the Pertinent Descriptors
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Anastassopoulos, A.; Philippidis, T. Clustering methodology for the evaluation of acoustic emission from composites. J. Acoust. Emiss. 1995, 13, 11–12. [Google Scholar]
- Huguet, S.; Godin, N.; Gaertner, R.; Salmon, L.; Villard, D. Use of acoustic emission to identify damages modes in glass fibre reinforced polyester. Compos. Sci. Technol. 2002, 62, 1433–1444. [Google Scholar] [CrossRef]
- Kostopoulos, V.; Loutas, T.; Kontsos, A.; Sotiriadis, G.; Pappas, Y. On the identification of the failure machanisms in oxide/oxide composites using acoustic emission. NDT E Int. 2003, 36, 571–580. [Google Scholar] [CrossRef]
- Maillet, E.; Godin, N.; R’Mili, M.; Reynaud, P.; Lamon, J.; Fantozzi, G. Analysis of Acoustic Emission energy release during static fatigue tests at intermediate temperatures on Ceramic Matrix Composites: Towards rutpure time prediction. Compos. Sci. Technol. 2012, 72, 1001–1007. [Google Scholar] [CrossRef]
- Ramasso, E.; Placet, V.; Boubakar, L. Unsupervised Consensus Clustering of Acoustic Emission Time-Series for Robust Damage Sequence Estimation in Composites. IEEE Trans. Instrum. Meas. 2015, 64, 3297–3307. [Google Scholar] [CrossRef]
- Marec, A.; Thomas, J.-H.; El Guerjouma, R. Damage characterization of polymer-based composite materials: Multivariable analysis and wavelet transform for clustering acoustic emission data. Mech. Syst. Signal Process. 2008, 22, 1441–1464. [Google Scholar] [CrossRef]
- Li, L.; Lomov, S.V.; Yan, X. Correlation of acoustic emission with optically observed damage in a glass/epoxy woven laminate under tensile loading. Compos. Struct. 2015, 123, 45–53. [Google Scholar] [CrossRef]
- Bhuiyan, M.Y.; Giurgiutiu, V. The signatures of acoustic emission waveforms from fatigue crack advancing in thin metallic plates. Smart Mater. Struct. 2017, 27, 015019. [Google Scholar] [CrossRef]
- Aggelis, D.G.; Shiotani, T.; Papacharalampopoulos, A.; Polyzos, D. The Influence of propagation path on elastic waves as measured by acoustic emission parameters. Struct. Health Monit. 2011, 11, 359–366. [Google Scholar] [CrossRef]
- Aggelis, D.G.; Matikas, T. Effect of plate wave dispersion on the acoustic emission parameters in metals. Comput. Struct. 2012, 98–99, 17–22. [Google Scholar] [CrossRef]
- Bhuiyan, M.Y.; Giurgiutiu, V. Multiphysics simulation of Low-Amplitude acoustic wave detection by piezoelectric wafer active sensors validated by in-situ AE-Fatigue experiment. Materials 2017, 10, 962. [Google Scholar] [CrossRef] [PubMed]
- Breckenridge, F.; Tschiegg, C.; Greenspan, M. Acoustic emission—Some applications of Lamb’s problem. J. Acoust. Soc. Am. 1975, 57, 626–631. [Google Scholar] [CrossRef]
- Ohtsu, M.; Ono, K. A generalized theory of acoustic emission and Green’s functions in a half space. J. Acoust. Emiss. 1984, 3, 27–40. [Google Scholar]
- Ohtsu, M.; Ono, K. A generalized theory of acoustic emission and source representations of acoustic emission. J. Acoust. Emiss. 1986, 5, 124–133. [Google Scholar]
- Scruby, C. Quantitative acoustic emission techniques. Nondestruct. Test. 1984, 8, 141–208. [Google Scholar]
- Scruby, C.; Wadley, H.; Hill, J. Dynamic elastic displacements at the surface of an elastic half-space due to defect sources. J. Phys. D Appl. Phys. 1983, 16, 1069–1083. [Google Scholar] [CrossRef]
- Scruby, C.; Baldwin, G.; Stacey, K. Characterization of fatigue crack extension by quantitative acoustic emission. Int. J. Fract. 1985, 28, 201–222. [Google Scholar]
- Rice, J. Elastic wave emission from damage processes. J. Nondestruct. Eval. 1980, 1, 215–224. [Google Scholar] [CrossRef]
- Andreykiv, O.; Skalsky, V.; Serhiyenko, O.; Rudavsky, D. Acoustic emission estimation of crack formation in aluminum alloys. Eng. Fract. Mech. 2010, 77, 759–767. [Google Scholar] [CrossRef]
- Sause, M. Investigation of pencil-lead breaks as acoustic emission sources. J. Acoust. Emiss. 2011, 29, 184–196. [Google Scholar]
- Sause, M.; Horn, S. Simulation of Acoustic Emission in Planar Carbon Fiber Reinforced Plastic Specimens. J. Nondestruct. Eval. 2010, 29, 123–142. [Google Scholar] [CrossRef]
- Zelenyak, A.M.; Hamstad, M.A.; Sause, M. Modeling of acoustic emission signal propagation in waveguides. Sens. J. 2015, 15, 11805–11822. [Google Scholar] [CrossRef] [PubMed]
- Hora, P.; Cervena, O. Acoustic emission source modeling. Appl. Comput. Mech. 2010, 4, 25–36. [Google Scholar]
- Åberg, M. Numerical modeling of acoustic emission in laminated tensile test specimens. Int. J. Solids Struct. 2001, 38, 6643–6663. [Google Scholar] [CrossRef]
- Achenbach, J.D. Ray method for elastodynamic radiation from a slip zone of arbitrary shape. J. Geophys. Res. 1978, 83, 2283–2291. [Google Scholar] [CrossRef]
- Achenbach, J.D. Acoustic Emission from a Brief Crack Propagation Event. J. Appl. Mech. 1979, 46, 107–112. [Google Scholar] [CrossRef]
- Achenbach, J.D. Ray Methods for Waves in Elastic Solids; Pitman Advanced Publishing Program: Boston, MA, USA, 1982. [Google Scholar]
- Rose, L. The stress-wave radiation from growing cracks. Int. J. Fract. 1981, 17, 45–60. [Google Scholar]
- Pekeris, C. Solution of an integral equation occuring in impulsive wave propagation problems. Proc. Natl. Acad. Sci. USA 1956, 42, 439–443. [Google Scholar] [CrossRef]
- Ben Khalifa, W.; Jezzine, K.; Hello, G.; Grondel, S. Analytical modelling of acoustic emission from buried or surface-breaking cracks under stress. J. Phys. Conf. Ser. 2012, 353, 012016. [Google Scholar] [CrossRef]
- Giordano, M.; Condelli, L.; Nicolais, L. Acoustic emission wave propagation in a viscoelastic plate. Compos. Sci. Technol. 1999, 59, 1735–1743. [Google Scholar] [CrossRef]
- Gary, J.; Hamstad, M. On the far-field structure of waves generated by a pencil lead break on a thin plate. J. Acoust. Emiss. 1994, 12, 157–170. [Google Scholar]
- Hamstad, M.; Gary, J.; O’Gallagher, A. Wideband acoustic emission displacement signals as a function of source rise-time and plate thickness. J. Acoust. Emiss. 1998, 16, 251–260. [Google Scholar]
- Sause, M.G.R.; Müller, T.; Horoschenkoff, A.; Horn, S. Quantification of failure mechanisms in mode-I loading of fiber reinforced plastics utilizing acoustic emission analysis. Compos. Sci. Technol. 2012, 72, 167–174. [Google Scholar] [CrossRef]
- Sause, M.G.R.; Hamstad, M. Acoustic Emission Analysis. In Comprehensive Composite Materials II; Beaumont, P.W.R., Zweben, C.H., Eds.; Academic Press: Cambridge, MA, USA, 2017; pp. 291–326. [Google Scholar]
- Sych, T.; Gerasimov, S.; Kuleshov, V. Simulation of the Propagation of Acoustic Waves by the Finite Element Method. Russ. J. Nondestruct. Test. 2012, 48, 147–152. [Google Scholar] [CrossRef]
- Hamstad, M. On Lamb modes as a function of acoustic emission source rise time. J. Acoust. Emiss. 2010, 28, 41–58. [Google Scholar]
- Prosser, W.; Seale, M.; Smith, B. Time-frequency analysis of the dispersion of Lamb modes. J. Acoust. Soc. Am. 1999, 105, 2669–2676. [Google Scholar] [CrossRef]
- Hamstad, M.; O’Gallagher, A.; Gary, J. Effects of lateral plate dimensions on acoustic emission signals from dipole sources. J. Acoust. Emiss. 2001, 19, 258–274. [Google Scholar]
- Gorman, M. Some connections between AE testing of large structures and small samples. Nondestruct. Test. Eval. 1998, 14, 89–104. [Google Scholar] [CrossRef]
- Cuadra, J.; Vanniamparambil, P.; Servansky, D.; Bartoli, I.; Kontsos, A. Acoustic emission source modeling using a data-driven approach. J. Sound Vib. 2015, 341, 222–236. [Google Scholar] [CrossRef]
- Wilcox, P.; Lee, C.; Scholey, J.; Friswell, M.I.; Winsom, M.; Drinkwater, B. Progress Towards a Forward Model of the Complete Acoustic Emission Process. Adv. Mater. Res. 2006, 13–14, 69–76. [Google Scholar] [CrossRef]
- Bracewell, R. The Two-Dimensional Fourier Transform. In Fourier Analysis and Imaging; Springer: Boston, MA, USA, 2003; pp. 140–173. [Google Scholar]
- Brigham, E. Fast Fourier Transform and Its Applications; Pearson: London, UK, 1988. [Google Scholar]
- Hsu, N.; Breckenridge, F. Characterization and calibration of acoustic emission sensors. Mater. Eval. 1981, 39, 60–68. [Google Scholar]
- Dia, S.; Monnier, T.; Godin, N.; Zhang, F. Primary Calibration of Acoustic Emission Sensors by the Method of Reciprocity, Theoretical and Experimental Considerations. J. Acoust. Emiss. 2012, 30, 152–166. [Google Scholar]
- Hatano, H.; Mori, E. Acoustic-emission transducer and its absolute calibration. J. Acoust. Soc. Am. 1976, 59, 344–349. [Google Scholar] [CrossRef]
- Goujon, L.; Baboux, J.C. Behaviour of acoustic emission sensors using broadband calibration techniques. Meas. Sci. Technol. 2003, 14, 903–908. [Google Scholar] [CrossRef]
- McLaskey Gregory, C.; Glaser Steven, D. Acoustic Emission Sensor Calibration for Absolute Source Measurements. J. Nondestruct. Eval. 2012, 31, 157–168. [Google Scholar] [CrossRef]
- Morizet, N.; Godin, N.; Tang, J.; Maillet, E.; Fregonese, M.; Normand, B. Classification of acoustic emission signals using wavelets and Random Forests: Application to localized corrosion. Mech. Syst. Signal Process. 2016, 70–71, 1026–1037. [Google Scholar] [CrossRef]
- Godin, N.; Reynaud, P.; Fantozzi, G. Acoustic Emission and Durability of Composites Materials; John Wiley & Sons: Hoboken, NJ, USA, 2018; ISBN 9781786300195. [Google Scholar]
- Miklowitz, J. The Theory of Elastic Waves and Waveguides; North Holland Publishing Company: Amsterdam, The Netherlands, 2015; Volume 22. [Google Scholar]
- Hebaz, S.E.; Benmeddour, F.; Moulin, E.; Assaad, J. Semi-analytical discontinuous Galerkin finite element method for the calculation of dispersion properties of guided waves in plates. J. Acoust. Soc. Am. 2018, 143, 460–469. [Google Scholar] [CrossRef]
- Hamstad, M.A.; Gallagher, A.O.; Gary, J. A wavelet transform applied to acoustic emission signals: Part 1 source identification. J. Acoust. Emiss. 2002, 20, 39–61. [Google Scholar]



| Young’s modulus (E) | 72 Gpa |
| Poisson’s coefficient (ν) | 0.34 |
| Density (ρ) | 2700 kg/m3 |
| Loss factor (κ) at 500 kHz | 2 × 10−4 |
| ) | 6407 m/s |
| ) | 3154 m/s |
| ) | 2944 m/s |
| Parameter | |||||
|---|---|---|---|---|---|
| Value |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Le Gall, T.; Monnier, T.; Fusco, C.; Godin, N.; Hebaz, S.-E. Towards Quantitative Acoustic Emission by Finite Element Modelling: Contribution of Modal Analysis and Identification of Pertinent Descriptors. Appl. Sci. 2018, 8, 2557. https://doi.org/10.3390/app8122557
Le Gall T, Monnier T, Fusco C, Godin N, Hebaz S-E. Towards Quantitative Acoustic Emission by Finite Element Modelling: Contribution of Modal Analysis and Identification of Pertinent Descriptors. Applied Sciences. 2018; 8(12):2557. https://doi.org/10.3390/app8122557
Chicago/Turabian StyleLe Gall, Thomas, Thomas Monnier, Claudio Fusco, Nathalie Godin, and Salah-Eddine Hebaz. 2018. "Towards Quantitative Acoustic Emission by Finite Element Modelling: Contribution of Modal Analysis and Identification of Pertinent Descriptors" Applied Sciences 8, no. 12: 2557. https://doi.org/10.3390/app8122557
APA StyleLe Gall, T., Monnier, T., Fusco, C., Godin, N., & Hebaz, S.-E. (2018). Towards Quantitative Acoustic Emission by Finite Element Modelling: Contribution of Modal Analysis and Identification of Pertinent Descriptors. Applied Sciences, 8(12), 2557. https://doi.org/10.3390/app8122557





