Towards Quantitative Acoustic Emission by Finite Element Modelling: Contribution of Modal Analysis and Identification of Pertinent Descriptors

Abstract

Acoustic emission (AE) is used for damage monitoring and health diagnosis of materials. Several experimental investigations have shown the aptitude of AE to identify signatures of damage mechanisms. Nevertheless, there is a lack of numerical modelling or simulation to understand the link between the source and the AE signals. Since the interpretation of data of AE measurements mainly relies on empirical correlation between the signal and the mechanical source, a detailed description of the effects of the different stages of the acquisition chain is still lacking. Moreover, the geometry of the specimen can strongly influence the propagation modes. In this study, we propose to model AE with the Finite Element Method, in order to investigate the effect of the type of damage, the geometry of the specimen and the piezoelectric sensor on the waves and on the AE parameters. After validating the model with an experimental pencil lead break, we perform a modal analysis on the numerical signals. This consists of identifying the excited modes for several sources using a 2D Fast Fourier Transform. The last part is devoted to the identification of pertinent descriptors with a perfect point contact sensor and with a resonant sensor.

1. Introduction

When a material undergoes stress, it can release transient elastic sound waves named Acoustic Emission (AE) events. AE, as a non-destructive testing technique, monitors damage in materials and structures, usually thanks to piezoelectric sensors directly applied on the sample surface in order to capture these elastic waves. In the conventional approach (phenomenological approach), the interpretation of data measured by AE is established through empirical correlations between the source (the damage mechanism) and the measured signal. The possibility of identifying the signatures of damage mechanisms is customary in the field of conventional AE [1,2,3,4,5,6,7]. For example, in a recent work, Bhuiyan et al. [8] classified AE signals, recorded during fatigue cracking in a metallic plate, into 4 groups. The signals were coordinated to the load level during cyclic fatigue and attributed to a damage mechanism. This approach often uses classification algorithms to gather signals into classes as a function of parameter values measured on the signals: each class is then associated with a specific damage mechanism. The attribution of each class to a specific damage mechanism is mainly based on empirical approaches, and the validation of this labelling remains difficult and is still a challenge. Extracting the coding parameters from signals outputted by the AE system as a whole thus ignores the modifications of the AE source signal due to the propagation medium and the acquisition chain. Wave propagation in the material, sensor measurements and signal treatments made by the acquisition system modify the signal and the information it carries. Moreover, AE signals are elastic waves subjected to attenuation, as well as dispersion. The specific values of the AE parameters are very sensitive to the experimental set up, as well as conditions like geometries. Comparisons should be done carefully and only for exactly the same experimental conditions. In this context, the acoustic signature of a damage mechanism is not generalizable. Consequently, identification of the source and comparison with results from other tests performed under different conditions are difficult. Aggelis [9,10] shows that the separation distance of the sensors is of paramount importance, and it should be taken into account when crack mode estimation is attempted with experimental data. Moreover, since the effect of the sensor on the AE signal is crucial, the sensor should be explicitly included in the AE acquisition chain. For example, Bhuyan et al. [11] modelled Piezoelectric Wafer Active Sensors using Multiphysics Finite Element simulations, validating their model with an in situ AE-fatigue experiment.

To address these problems, one should consider the different steps of the whole acquisition chain. This is the goal of Quantitative Acoustic Emission (QAE). This approach, which began four decades ago, depends on modelling techniques to evaluate the impact of each step of the acquisition chain on the AE signal. In 1975, Breckenridge et al. initiated these works by comparing the theoretical displacement of a seismic surface pulse in a half space with experimental signals emitted by the breaking of glass capillary on a block of aluminium alloy [12]. Other works placed more emphasis on the modelling of the damage mechanism at the origin of the AE event. Otsu and Ono [13,14] developed a generalised theory of AE by using the integral formulation of the elastodynamics and proposed a source representation for the tensile and shear cracks. In the works of Scruby et al., the source is modelled as a point source, where dipoles of force are used to generate a stress field [15,16,17]. This model is used by the same author to study micro-cracking during the propagation of a fatigue fracture in aluminium, and also by Rice [18] to study the acoustic waves emitted by tensile opening and slip events. Other authors considered alternative models for artificial AE sources, such as penny-shaped cracks in aluminium alloys under tensile and twisting loading, introduced by Andreykiv et al. [19], who obtained the displacement vectors as a function of time and coordinates for arbitrary distances from the centre of the crack. Sause used a pencil lead-break model implemented through Finite Element analysis [20]. The same author [21] found a new AE source model, which takes into account the microscopic elastic properties near the source. A pencil lead-break model was also used by Zelenyak et al. [22] to validate Finite Element Analysis used to evaluate the influence of waveguides on the AE signals. Hora [23], in order to build representative sources, investigated the difference between nodal sources, line sources and cylindrical sources. In the work of Åberg [24], sources are described as time-dependent displacement discontinuities which are translated to volume forces, and the transient waves are computed using a finite element model of the specimen’s cross-section. There are also wave propagation models based on the analytical or numerical resolution of the elastodynamic equations. Analytical methods are adapted to simple geometries. Achenbach et al. proposed a ray method in the context of geophysics [25] and for AE [26,27]. Thereafter, Rose used it to describe the response of an infinite space to the propagation of a crack [28]. Pekeris calculated the analytical solution of the surface displacement of a half-space due to buried and surface pulses using Green functions [29], and Ben Khalifa used the reciprocity theorem to combine a quasi-static crack propagation model and Rayleigh waves Green functions in a half-space [30]. Giordano [31] represented a microfailure event as a point source and used the ray theory to develop a physical model of wave propagation. To resolve the problem in complex geometries, the Finite Element Method (FEM) is the one of the most commonly used numerical method. It has been applied and experimentally validated on plates [32,33] and composite materials [34,35,36]. Gary and Hamstad [33] were the first to show that the explicit finite elements are effective and efficient to compute the far-field structure of wave mode propagation. Sause [21] realised such capabilities by using an implicit three-dimensional finite element code to determine the spectral content of signals originating from the most common damage in composite material. Some scientific works interpreted AE signals through modal analysis [37,38]. However, only few of the studies performed on laboratory samples took into account the influence of reflections on the AE signals. Hamstad showed that the presence of reflections modifies the frequency content of the signal [39] and Gorman concluded that it is necessary to reduce or cut out reflections in laboratory specimens in order to better simulate the test field conditions on larger specimens [40]. A recent study [41] investigated AE by a combination of experimental, analytical and computational methods. Using full field experimental data obtained from crack initiation, it constructed a phenomenological mechanical law and implemented it in a FEM simulation. This work emphasised the influence of the geometry and of the material properties on the wave propagation. Wilcox et al. [42] also proposed a modular framework for quantitative forward modelling of the complete AE process. To interpret AE signals in terms of their relevance to the material failure, one needs a worthy knowledge of the AE signal propagation from the source to the surface of the sample and of detection. Modal analysis [43,44] is a judicious way of analysing AE signals, but the modes used to interpret the signals are often plate modes.

The aim of this work is to better understand the relationship between the AE sources and the detected signal by unravelling the effect of the different stages of the acquisition chain, namely the propagation medium and the detection system. For this purpose, we carried out FEM modelling of AE for aluminium samples at different scales. We validated our model with experimental pencil lead break procedures performed on aluminium specimens. We organised the present paper as follows. In Section 2, we first detail the model, the numerical method, and the experimental setup used to validate them. Section 3 presents the validation of the numerical method. The validated FEM model enables to calculate the out-of-plane velocities corresponding to two different sources in each aluminium sample. Point multi-dipoles located at different depths mimic the AE sources. In Section 4, we discuss our results. These results concern the modal analysis on the signals generated by various sources using 2D Fourier Transforms on three different specimens and the identification of relevant parameters to characterise AE sources. The strategy is to initially study the numerical AE signals without considering the sensor, and then to add the sensor effect and compare the results. Finally, Section 5 provides our conclusions.

2. Numerical Methods and Experimental Procedure

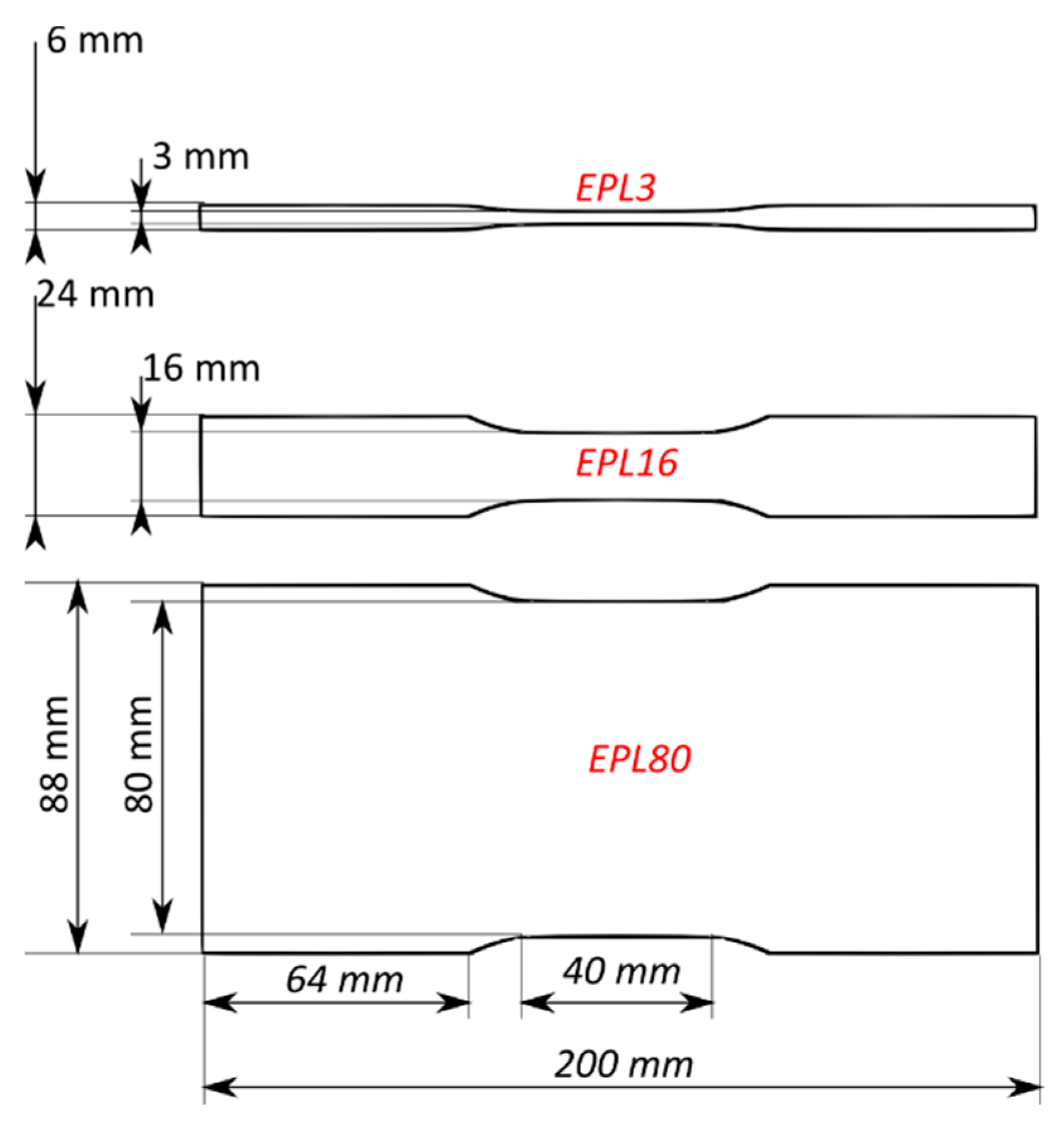
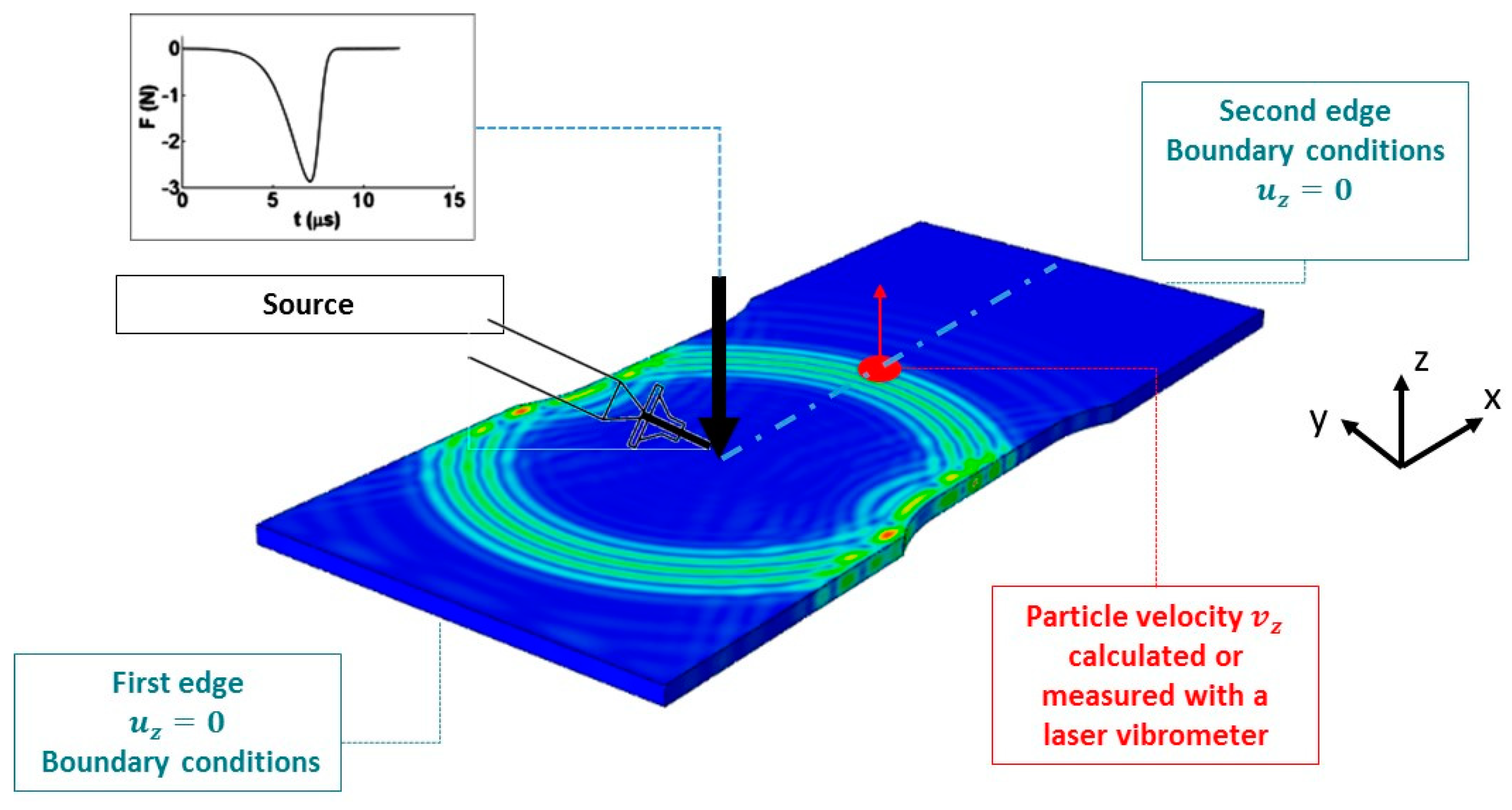
2.1. Sample Geometry

We consider a homogeneous and isotropic material, aluminium, whose properties are summarised in

Table 1. Properties of aluminium used in the study.

Young’s modulus (E)	72 Gpa
Poisson’s coefficient (ν)	0.34
Density (ρ)	2700 kg/m3
Loss factor (κ) at 500 kHz	2 × 10−4
$\mathrm{Compressive}\mathrm{wave}\mathrm{speed}(c_P$)	6407 m/s
$\mathrm{Shear}\mathrm{wave}\mathrm{speed}(c_S$)	3154 m/s
$\mathrm{Rayleigh}\mathrm{wave}\mathrm{speed}(c_R$)	2944 m/s

. The simulations and experiments involve tensile samples with three different widths of the neck (Figure 1). The thickness of the samples is equal to 3.7 mm, and their total length is 200 mm. These three tensile samples represent three different scales for materials. For the narrowest sample (denoted EPL3), the width and thickness are of the same order of magnitude and shorter than the length. The largest sample (EPL80) represents a structural component. Its width and length are far greater than its thickness. Finally, the last sample (EPL16) represents the classical laboratory test sample.

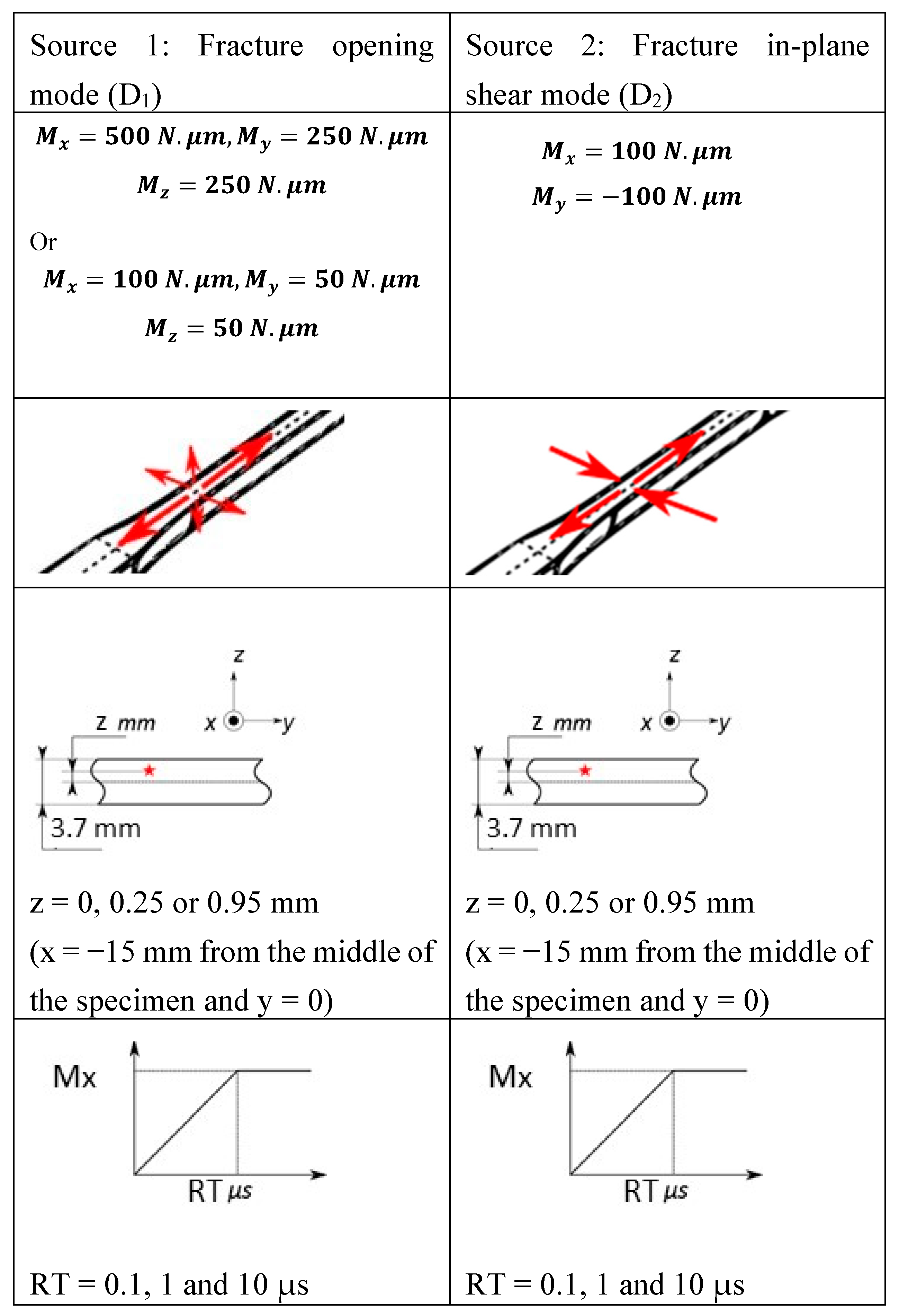
2.2. Source Modelling

For the validation of the FEM calculations, we simulated a pencil lead break, PLB (Hsu-Nielsen source), on the surface of the sample (Figure 2a) [45]. Figure 2b shows the temporal evolution of the point force used to simulate the lead break according to the work of Sause [20]. Figure 2c represents the frequency content of the source. The modes are excited using a monopole point source located on the surface of the specimen, acting in the out-of-plane direction in the centre of the specimen surface at following location (x = −36 mm, y = 0, z = 1.85 mm). The origin of the coordinate system is situated at the centre of the specimen.

For the modal analysis, in order to identify the excited modes, we used a chirp signal (Figure 3a), which rather equally stimulates all frequencies up to 1.2 MHz, as shown by its frequency content (Figure 3b). The chirp is applied as a point force on the surface of the material (x = −36 mm, y = 0 mm, z = 1.85 mm).

Assuming that the physical dimensions of the AE sources are much smaller than the distance to the point of observation, we chose a point source. In contrast to complex models, force dipoles are computationally more efficient to investigate the effect of propagation. According to Scruby [15,16,17], we model two sources corresponding to two different damage mechanisms as buried point sources. To model buried sources in the continuous mesh domain, two closely spaced, self-equilibrating monopoles are simultaneously applied along opposite directions. The distance between monopoles, 800 μm, is assumed to be as small as possible, considering the element size in the FEM calculation. Sources are denoted by D_i (M_α, z, RT)), where i = 1, 2, $\alpha =x,y,z$, M_α is the intensity of the force dipole (in N.µm) in the α-direction, z is the distance from the midplane (xoy) of the specimen, and RT is the source rise time. The two sources shown in Figure 4 represent the fracture-opening mode (D₁) and the fracture in-plane shear mode (D₂). For the source D₁, the strongest dipole is in plane and aligned along the x-direction. The source D₂ represents a slip, which occurs in a direction in the plane (x, y) at 45° to the x-axis. The dipole moments are determined based on the literature [17]. The order of magnitude of the dipole moments is 100 N.μm. The dipole moment for the source D₁ is assumed to be 5 times larger. The source rise times are 0.1 µs, 1 µs and 10 µs. These values are also determined based on the literature [16,21]. The temporal shape of the source rise functions considered are linear. The dipole forces reach their maximum value after the rise time and persist at a constant value. The sources are located in the gauge section at three different values of z (z = 0 mm, 0.25 mm, 0.95 mm) and at (x = −15 mm, y = 0).

2.3. Propagation and Attenuation

We use 3D FEM to solve the dynamic equation, and derive the displacement field due to the wave propagation. We used an explicit integration scheme because it requires less memory space that an implicit scheme. It is faster and better suited to problems such as the present study, where the frequency band of interest necessitates a huge number of elements to discretise the geometries. Moreover, temporal increments need to be small for the explicit scheme to be stable. Consequently, it is well suited to modelling transient waves. To calculate signals as close as possible to the experimental signals, we have to consider damping. In the present study, we use Rayleigh damping, for which the damping matrix is a linear combination of mass and stiffness matrices:

$$\left[C\right]= \alpha \left[M\right]+\beta \left[K\right]$$

(1)

The Rayleigh coefficients $\alpha$ and $\beta$ are linked to the loss factor $\kappa$ and the damping coefficient $\xi$ as follows:

$$\kappa =2\xi =\frac{\alpha }{\omega }+\beta \omega$$

(2)

Table 1 shows a numerical value of the loss factor for aluminium for a specific frequency (500 kHz). We do not have access to values of $\kappa$ at several frequencies, so it not possible to deduce a value of $\alpha$ and $\beta$. We thus choose to use only $\alpha$, which is set to 700, as it gives a less frequency-dependent damping.

The FEM simulations are implemented with the commercial software ABAQUS© (Dassault Systèmes Simulia Corp., Providence, RI, USA) using first order hexahedral elements with reduced integration (C3D8R). The validity of the results with the model demands a careful choice of the size of the elements and the time step of the simulation. The typical size of an element ($l_e$) is:

$$l_e=\frac{{\lambda }_{min}}{R}$$

(3)

where ${\lambda }_{min}$ is the minimum wavelength of interest and $R$ a resolution parameter that must be between 5 and 20. The minimum wavelength is:

$${\lambda }_{min}=\frac{c_R}{f_{max}}$$

(4)

with $f_{max}$ the maximum frequency of interest and $c_R$ the Rayleigh wave velocity.

If damping is considered, the critical time step is:

$$\Delta t_{lim}=\frac{2}{\pi f_{max}}\left(\sqrt{1+{\xi }_{max}^2}-{\xi }_{max}\right)$$

(5)

where $f_{max}$ is the highest eigen frequency of the system and ${\xi }_{max}$ the damping coefficient at the highest eigen frequency. Therefore, one should know the highest eigen frequency in order to calculate the critical time step, which, in practice, is not trivial. However, considering the time needed by the fastest wave (compressive wave) to cross a single element, an approximate value of the critical time step is:

$$\Delta t_{lim}\simeq \frac{l_e}{c_P}$$

(6)

where $c_P$ is the compressive wave speed.

The ABAQUS software automatically calculates the time-step, which is inferior to the critical time step:

$$\Delta t_{lim}\simeq \frac{l_e}{c_P}=\frac{{400.10}^{-6}}{6407}={\mathrm{1.62.10}}^{-6}s$$

(7)

Table 2. Parameters of the finite element calculation.

Parameter	${\mathit{f}}_{\mathit{m}\mathit{a}\mathit{x}}$	$\mathit{R}$	${\mathit{\lambda }}_{\mathit{m}\mathit{i}\mathit{n}}$	${\mathit{l}}_{\mathit{e}}$	$\mathbf{\Delta }{\mathit{t}}_{\mathit{l}\mathit{i}\mathit{m}}$
Value	$1 \mathrm{MHz}$	$8$	$3\mathrm{mm}$	$400\mathsf{\mu }\mathrm{m}$	$1.35\times {10}^{-7}\mathrm{s}$

shows the values used for spatial and temporal discretisation in the present study. The total simulation window is 100 µs.

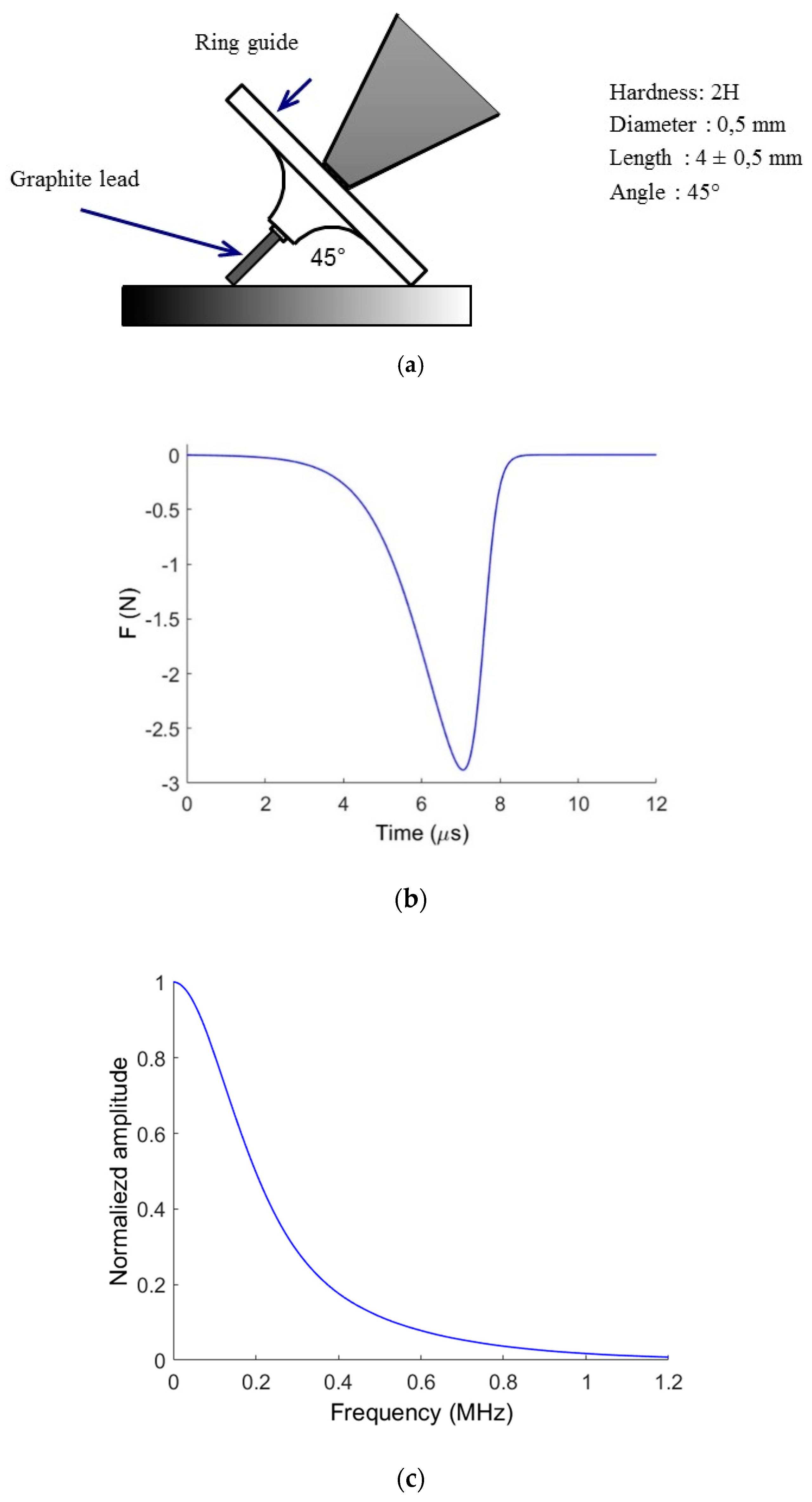
2.4. Experimental Procedure

To validate the simulation conditions, the experimental setup consists of a PLB procedure, repeated ten times, on a sample of each of the three geometries. The lead used is a 2H lead of 0.5 mm diameter and 4.0 mm length and is broken on the sample surface at a 45° angle (Figure 2a). The PLB is positioned at the centre width of the sample and at x = −36 mm. The LASER vibrometer (POLYTEC, Châtillon, France), whose head is positioned 50 cm above the samples, measures the particle velocity on the surface 21 mm and 60 mm from the source. To minimise the influence of boundary conditions, each sample stands on the extremities of two steel bars. To acquire the signals, an oscilloscope is used. Once the acquisition is over, the signals are post-treated using MATLAB Software. First, they are resampled in time and space. After resampling, the signals are smoothed to improve the signal/noise ratio. Finally, they are filtered with a 1kHz–1MHz Butterworth bandpass filter.

2.5. Sensor Effect

The AE numerical signals from a single node provide the out-of-plane top surface displacement or velocity corresponding to a perfect point-contact sensor. We assume that the sensors are only sensitive to displacement normal to the surface of the sample. Reception wave sensitivity was measured on a steel block [46,47,48]. The sensor is taken into account with respect to its transfer function, which is experimentally determined by the reciprocity method. The post-processing phase accounts for this transfer function in the Fourier domain, following Equation (8):

$$S_{sensor}\left(f\right)=M\left(f\right)\times S_{surf}\left(f\right)$$

(8)

where $S_{sensor}\left(f\right)$ is the Fourier Transform of the signal, $M\left(f\right)$ is the reception sensitivity function, and $S_{surf}\left(f\right)$ is the Fourier Transform of the simulated signal recorded on a single node at the sensor position. If we assume that the sensor is a point receiver, this implies that the sensor acts on regions that are small compared to the wavelengths of interest. In this study, we do not take into account the aperture effect of the sensor and the coupling medium. The aperture effect is certainly most evident for the sensor R15, for which the diameter of the piezoelectric element is large [46,49]. Figure 5 shows the sensitivity of reception obtained for the two sensors used in this study (R15 and µ80) with the reciprocity method.

2.6. Signal Analysis

2.6.1. Modal Analysis

Having a very long width and length in comparison to the thickness, and a thickness on the order of magnitude of the wavelength, EPL80 can be considered to be a plate. In a plate, two kinds of so-called Lamb waves can propagate, i.e., symmetric (Sn) and antisymmetric (An) modes, with n being the index of the mode. Having both its width and its thickness on the order of magnitude of the wavelength, EPL3 can be considered to be a bar. This means that the propagating modes can be longitudinal (L_0n), flexural (F_mn), or torsional modes (T_0n). We used the two-dimensional Fourier Transform (2DFT) [43] to analyse the modal content of the propagating waves and compared it to the theoretical modes. The 2DFT enables to visualise 2D matrix signals, of size N × M, in the frequency domain. One dimension of the matrix is time (t), and the other dimension is the distance to the source (x). The 2DFT shows the evolution of the wave number k (which is a spatial frequency) as a function of the temporal frequency. For a discrete signal matrix v_z(t, x), the 2DFT is given by:

$$\left|V_z\left(k,f\right)\right|= \left|{{\displaystyle \sum }}_{t=0}^{N-1}{{\displaystyle \sum }}_{x=0}^{M-1}{v}_z\left(t,x\right)e^{-j2\pi \left(k\frac{t}{N}+f\frac{x}{M}\right)}\right|$$

(9)

where k the spatial frequency in x-direction and f the temporal frequency. The 2DFT are calculated using the particle velocity (v_z) of every node of the finite element mesh along the median line of the upper face of each sample, from the source to a distance of 85 mm (Figure 6). The signal duration taken for the 2DFT calculations is 70 μs. This duration discards the reflections on the two extremities of the samples without any loss of information contained in the signal directly propagated from the source. We chose this signal-processing tool because it shows information on the source but also on the geometry of the propagating medium.

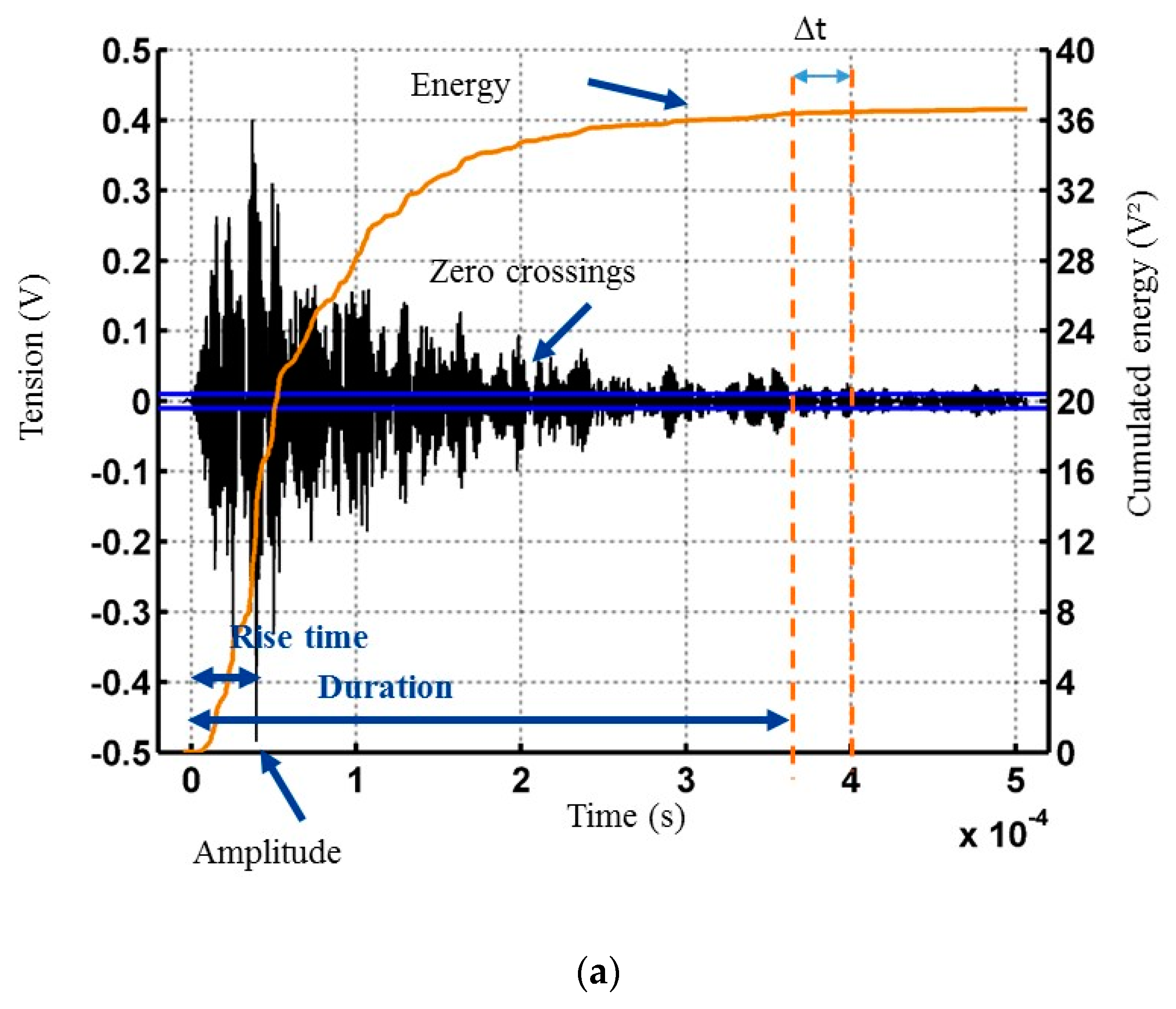
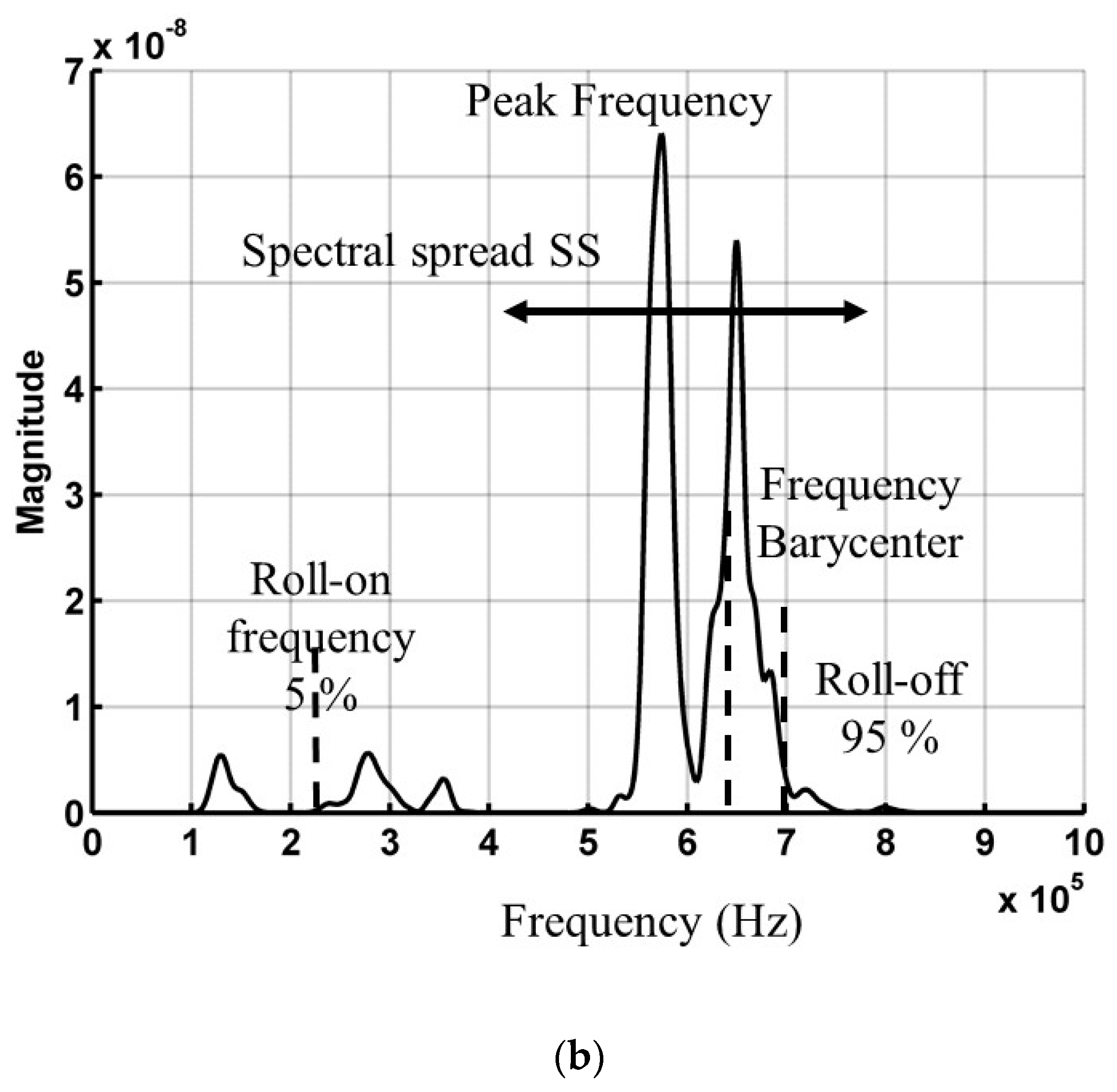
2.6.2. Acoustic Emission Parameters

In traditional AE, many different features are extracted [50,51] from the signals to structure them using classification algorithms and to associate each signal class with a specific damage mechanism. These features are the so-called “AE features or descriptors”. Figure 7 shows a typical experimental AE signal to illustrate these parameters. The beginning of the signal used to calculate a descriptor is determined as the point where a fixed threshold is exceeded. The threshold values are chosen with respect to the experimental signals and are fixed as 10⁻⁷ m/s for the particle velocity. To determine the end of the signal, we employ an energetic criterion (Figure 7a). For each point in the waveform, the cumulative energy computed from the first threshold crossing is compared to the energy contained in a time interval (10 µs) following that point. If this energy is less than 0.5% of the cumulative energy, then the corresponding point represents the end of the signal. We calculated more than 20 parameters [50] for each AE signal (Figure 7), but only several of them are presented here for the sake of clarity. Among the temporal features derived from the evolution of the signal with time, one can cite the amplitude, the duration, the rise time, etc. The rise time (RT) is the time between the first threshold crossing and the time of the maximum peak. Zero crossing rate (ZCR) shows how many times the signal crosses the temporal axis with respect to signal duration. One can also extract features from the Fourier Transform of the signal. FC is the Fourier Transform centroid of the signal given by [44].

$$FC=\frac{{{\displaystyle \sum }}_{i=1}^{max}{f}_i{A}_i}{{{\displaystyle \sum }}_{i=1}^{max}{A}_i}$$

(10)

with A being the numerical particle velocity. The spectral spread, denoted SS, gives an indication of the bandwidth of the spectral content of a signal. This is actually the standard deviation of the FT, and is given by:

$$SS=\sqrt{\frac{{{\displaystyle \sum }}_{i=1}^{max}{\left(f_i-FC\right)}^2{A}_i}{{{\displaystyle \sum }}_{i=1}^{max}{A}_i}}$$

(11)

The partial powers PPi represent the percentage of energy contained in each frequency interval. The partial power begins at 100 kHz due to the interest domain of AE.

3. Experimental Validation of the Finite Element Method

In this section, we compare the experimental and numerical results in order to validate the FEM model before extending this numerical approach to different AE sources. In the experimental setup, pencil lead break is carried out on the three specimens, and the signals are detected by means of a laser vibrometer. The pencil lead break is modelled as a displacement source [15]. The simulation intended to validate the use of FEM and the chosen parameters consists of a PLB (Figure 2) on the surface of each sample: EPL3, EPL16 and EPL80. The simulated lead break is applied on the upper surface of the sample (Figure 6). The vertical displacements (z) of the lower extremities’ nodes are blocked. Vertical particle velocity v(z) on the surface is calculated at 21 mm and at 60 mm from the source (PLB). Simulated signals are then filtered between 1 kHz and 1 MHz by a Butterworth bandpass filter, which is the frequency range of interest in AE. Figure 8 shows a comparison between the measured velocity and the simulated out-of-plane velocity for each case. The green lines indicate the time at which oscillations of simulated signals start, while the black lines indicate the time up to which experimental and simulated signals are similar. The part of the signal before the green line is called Section 1, the part between the green and black line is called Section 2, and the part after the black line is called Section 3. Cross-correlation coefficients (CC) between simulated and measured signals are larger than 0.6 for each geometry, especially if they are computed only on Section 2 (CC = 0.77 and CC = 0.80 in EPL16 at 21 mm and 60 mm). This indicates a good resemblance between signals. In some cases (Figure 8c), oscillations are visible before the green line on the experimental waveforms. The intrinsic noise of the laser vibrometer can cause these oscillations. Despite the signal processing made to discard the noise, some of it could not be avoided. At longer times, there is some discrepancy between the signals in Section 3, due to the reflections on the endings of the samples. In each sample, the arrival time of the reflections corresponds to the beginning of Section 3. The boundary conditions are not exactly the same for the two methods. Moreover, the comparison between the frequency spectrum of the numerical and experimental signals shows similar cross-correlation coefficients. Overall, we find a good agreement between the experimental results and the numerical simulations, allowing us to validate the FEM model. Consequently, we can conclude that the numerical approach is able to describe AE signal propagation.

4. Results and Discussion

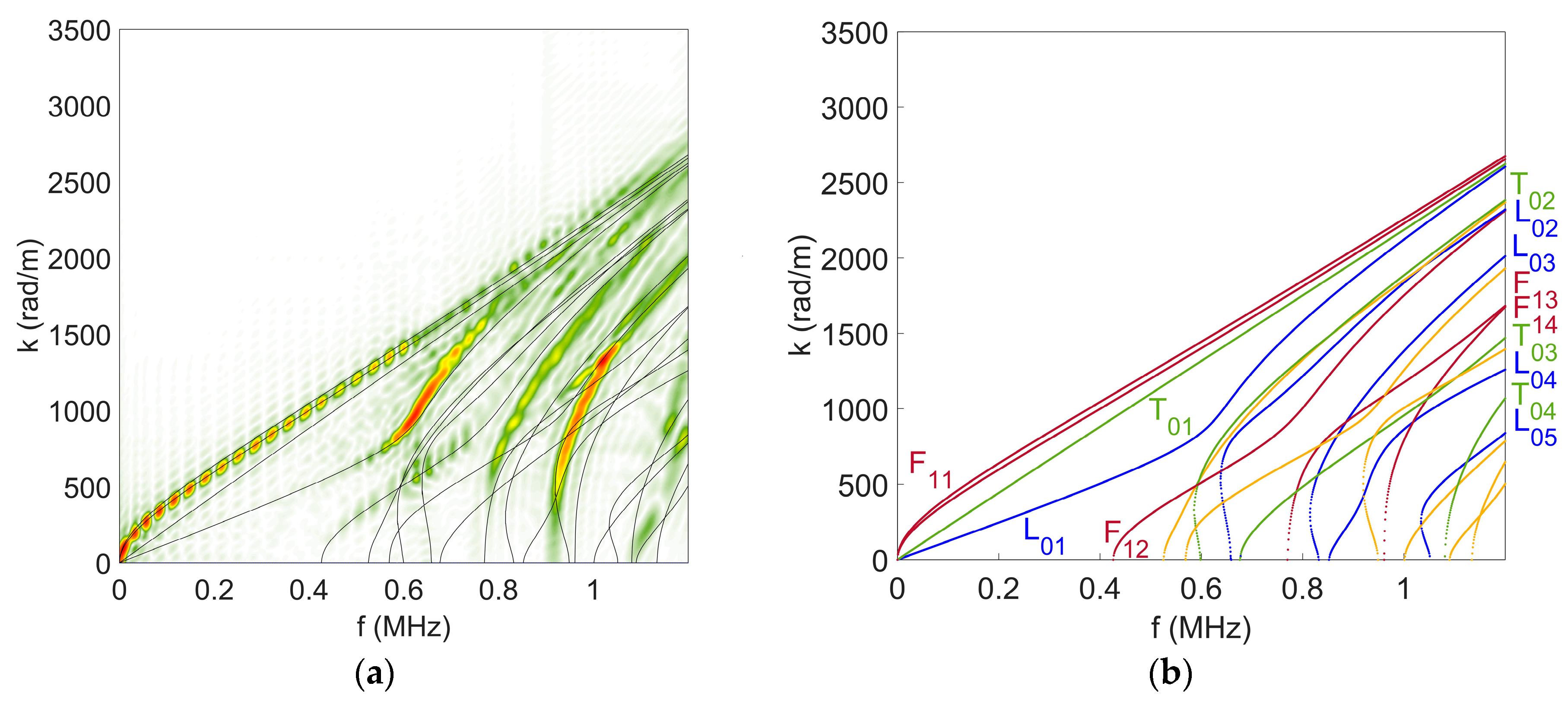
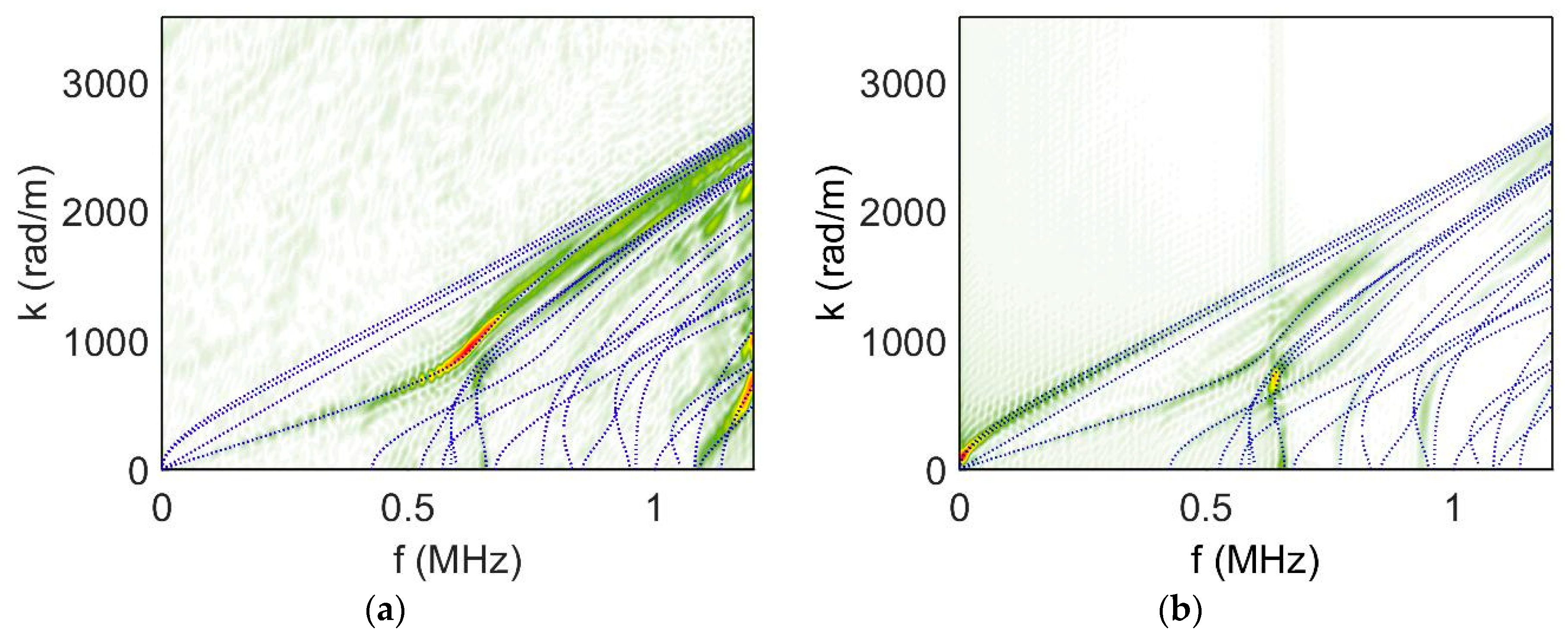
4.1. Modal Analysis of Numerical Results: Identification of the Excited Modes

The use of 2D Fourier Transform makes it possible to visualise the modal content of propagating waves in each sample and compare it to the theoretical dispersion curves in order to ascertain which modes are excited by the source [52,53,54]. However, the large number of signals required to calculate the 2DFT represent a difficulty in experimental conditions, especially because of the insufficient reproducibility of pencil lead ruptures. The 2DFT is calculated only on the basis of numerical results, which are filtered between 1 kHz and 1.2 MHz by a Butterworth bandpass filter.

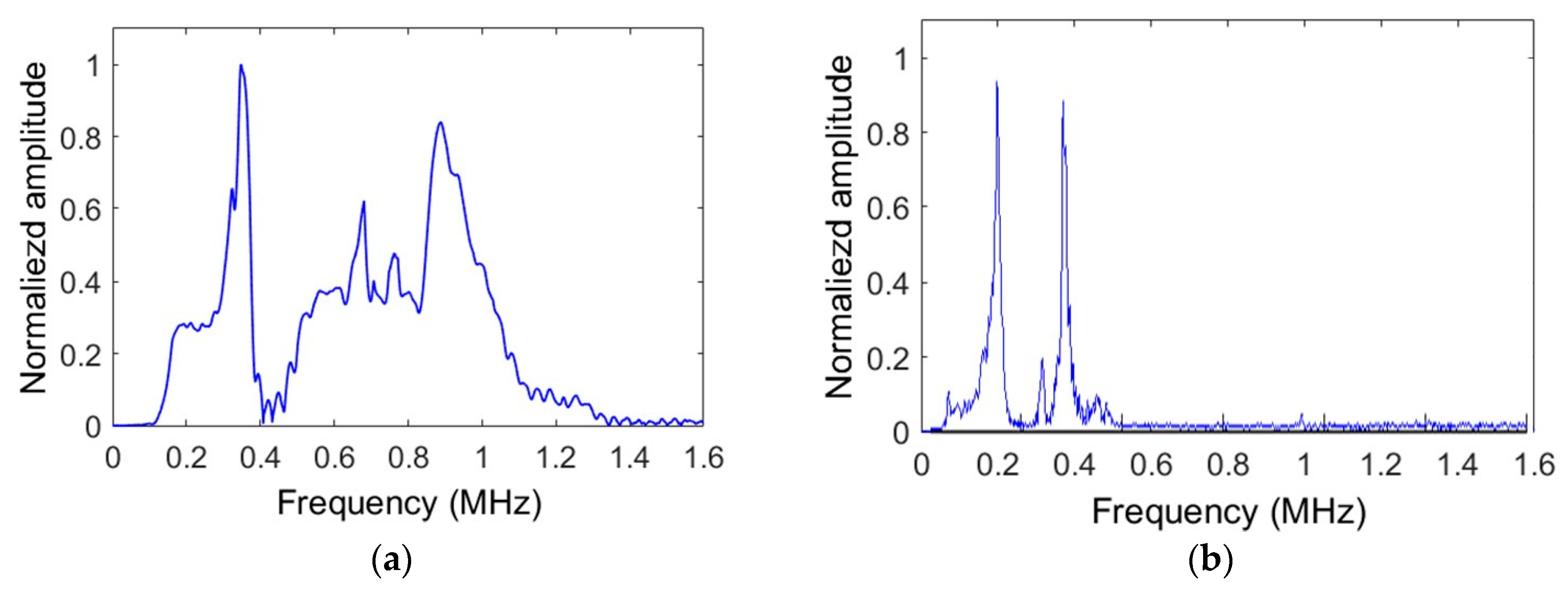
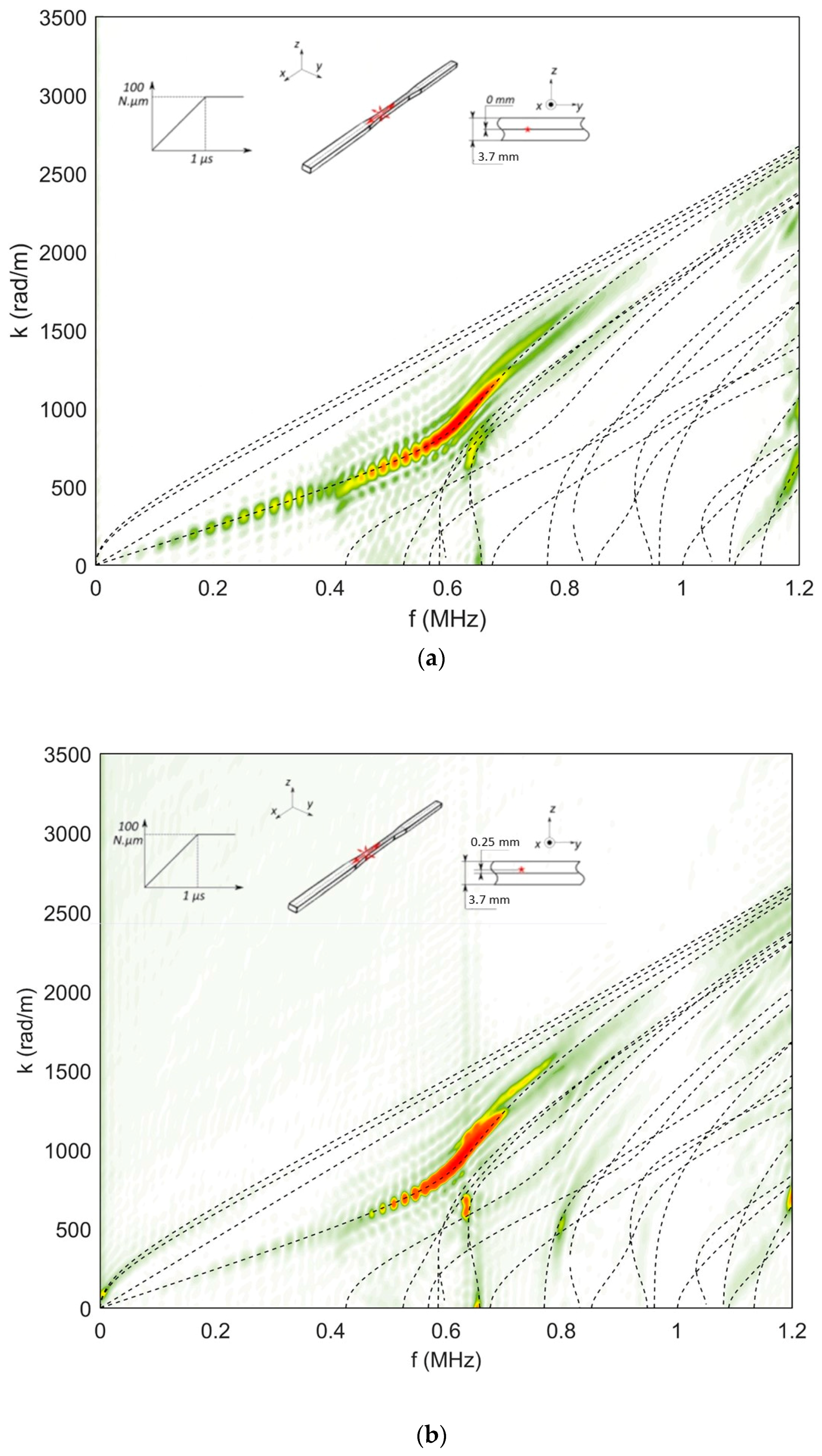
4.1.1. Influence of the Geometry on the Excited Waves

In the three geometries (EPL3, EPL16 and EPL80), we simulate a chirp signal (Figure 3) on the surface of each sample as a point force. The numerical signals calculated from the close vicinity of the source to the end of the specimen allow us to identify the different propagating modes through the 2D Fourier Transform (2DFT). The results are the dispersion curves, i.e., the wave number as a function of frequency. The simulated dispersion curves represented on the left hand side, e.g., Figure 9a,c,e, are obtained from the simulated signal when applying a point force source (chirp) on the surface of each sample. These are compared to the theoretical semi-analytical ones (on the right hand side, e.g., Figure 9b,d,f). The theoretical semi-analytical curves are calculated for infinite waveguides of arbitrary cross section, e.g., plate, beam and bar in the cases of the EPL80, EPL16 and EPL3 samples, respectively, with a dedicated resolution algorithm using the semi-analytical discontinuous Galerkin method [53]. All the semi-analytical curves displayed in Figure 9b,d,f consist of black dots. However, for Figure 9b, we superimposed on the black dots the pure modes of torsion, flexion and the longitudinal modes of a beam in three different colours, while for Figure 9f, we superimposed the Lamb modes corresponding to the analytical solutions of the Lamb modes of an infinite plate in red and blue.

The results show that the sample geometry evidently affects the propagated signals. For the thin sample (EPL3), bar modes are excited (Figure 9a,b). A good agreement is observed between the simulated modes and the theoretical modes, with the exception of the high wavenumber domain, i.e., above 1500 rad/m for the EPL3 and EPL16 specimens, and even more pronounced above 1000 rad/m for EPL80. This is easy to explain, since the discretisation of the FEM simulation would never be sufficiently sharp for the wideband chirp used as a source. Such chirp excitation is chosen to generate a large number of modes. However, some modes are not excited (resp. not measurable) on particular frequency bands (for instance $S_0$ at low frequencies for EPL80) or not excited at all (for instance, $S_1$). This is because the chirp applies a point force on the surface. This asymmetry of the applied force favours Antisymmetric/Flexural modes. In the case of EPL16 (Figure 9c), the 2DFT is more complex, and the identification of modes is more complicated due to the intermediate nature of the EPL16 geometry, half way between plate and bar. In this case, it is not possible to superimpose the theoretical modes on Figure 9d.

For the large one (EPL80), very numerous plate modes can theoretically be excited (Figure 9e,f), and are indeed observed. Nevertheless, one can observe that these waves are predominantly excited close to Lamb modes, which strengthens the hypothesis of the EPL80 specimen being large enough to mimic a quasi-infinite plate.

The excited modes are different from a geometry to another even if the source is the same. This study shows that AE tests done on a classical sample, e.g., EPL16 (Figure 9c), in the laboratory cannot replace an industrial case from a perspective of geometry. This observation leads to the conclusion that AE classification results obtained during a laboratory test on a laboratory sample cannot be directly applied to a structure whose geometry is completely different. In the following part, we examine the effect of the characteristics of the source on the recorded signal.

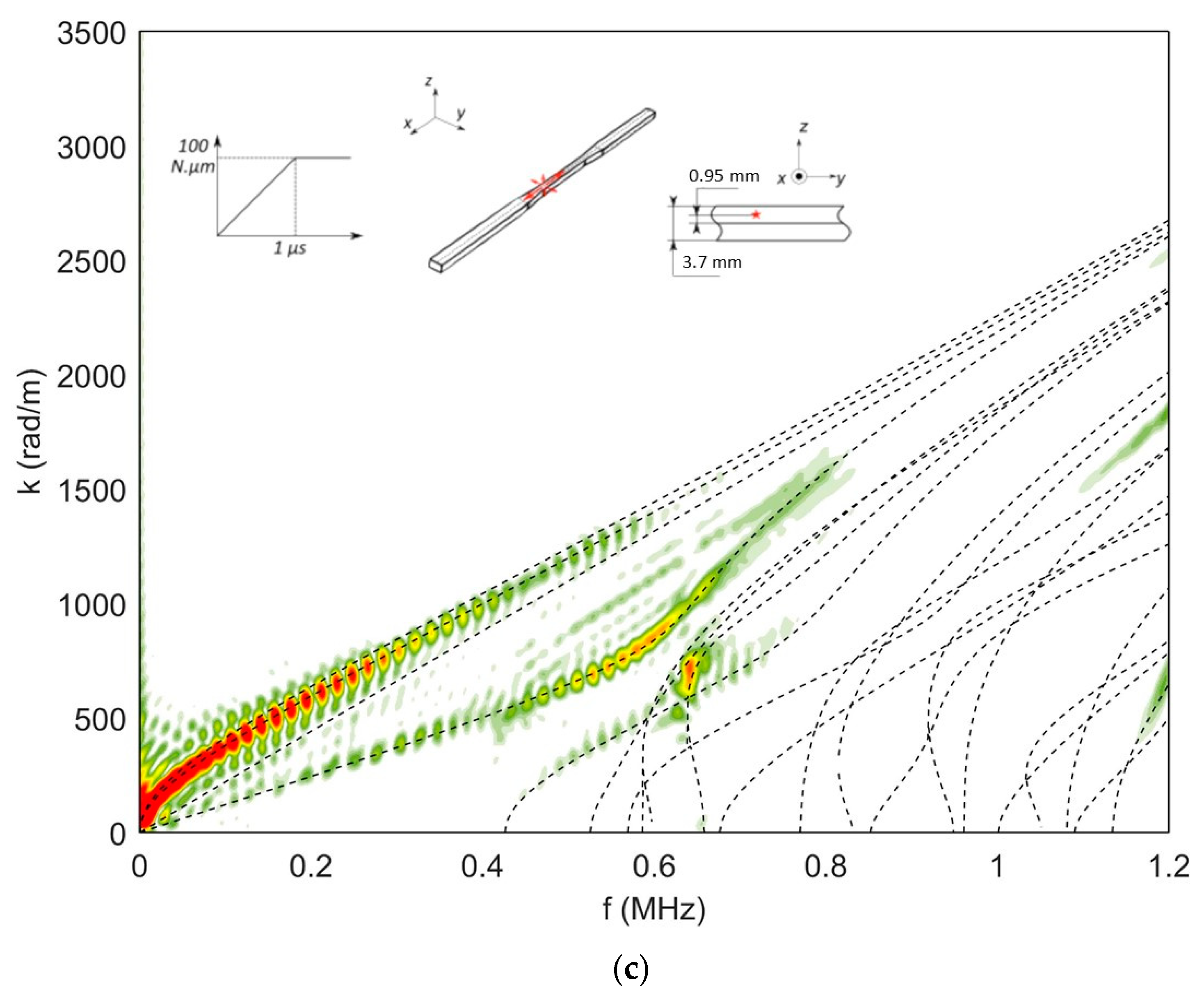
4.1.2. Effect of the Depth of the Source

In this part, a point source modelling a crack-opening mode 1 (source D₁) is located on the midplane and at two different distances, 0.25 mm and 0.95 mm, away from the midplane of the EPL3 sample. Figure 10 shows the 2DFT of the signals. When the source is located on the midplane, only the longitudinal modes are excited (Figure 10a). However, when the source is located away from the midplane, the external load ceases to be symmetric and a flexural mode (F₁₁) starts to be stimulated (Figure 10b). When the source is located further away from the midplane, close to the surface (Figure 10c), the longitudinal modes are very attenuated, and the flexural mode F₁₁ is predominant. The further the source is away from the midplane and the closer to the surface, the more flexural modes are stimulated in comparison to longitudinal modes for the same source. As already pointed out by Hamstad [54], the z-position of AE sources influences the ratio of simulated modes and therefore the spectral content of the signal.

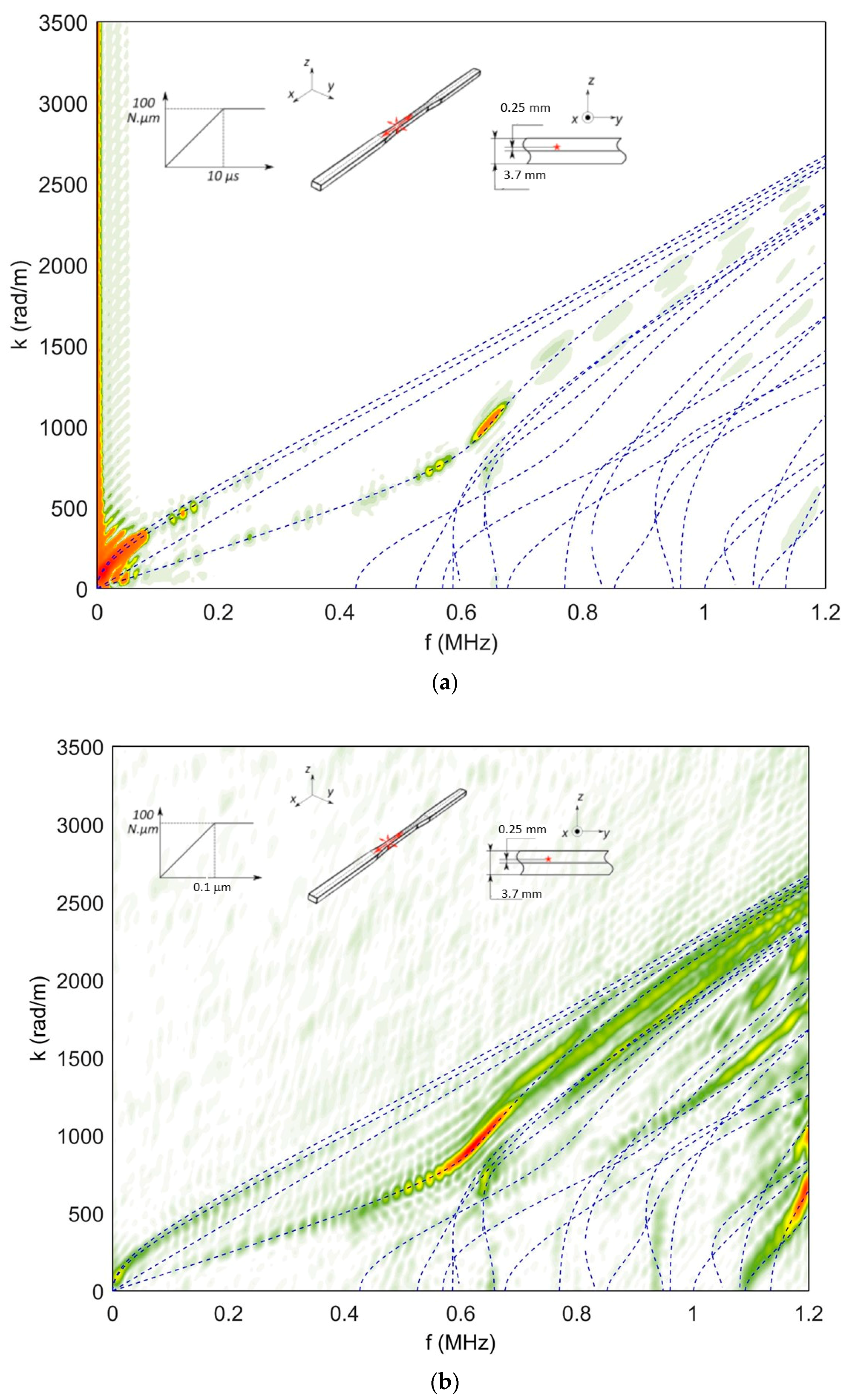
4.1.3. Effect of Source Rise Time

We study the influence of the source rise time in order to evaluate the consequences of a rapid or slow event on the 2DFT. Three sources with three different rise time: 0.1 μs, 1 μs and 10 μs, modelling a mode I crack opening D₁, are placed 0.25 mm from the midplane of the sample in the gauge section.

A source with a long rise time represents a ductile event, whereas a source with a short rise time can be associated with a brittle event. Figure 11a shows the 2DFT of signals generated by the 10 μs rise time source. It is clear that the frequency band stimulated by the source is narrow and the stimulated frequencies are low frequencies. As already seen in Figure 10b, the 2DFT calculated for the 1 μs rise time source shows a wider frequency band with higher frequencies. In that case, the L₀₁ mode is excited between 400 and 700 kHz, which is not the case for the 10 μs-rise time source. The 2DFT calculated for the 0.1 μs-rise time source (Figure 11b) shows an even wider frequency band. L₀₁ mode is stimulated between 400 and 1200 kHz and F₁₃, L₀₅ and F₁₅ modes are also stimulated. When the rise time decreases, the frequency band stimulated by the source gets wider and the 2DFT exhibits modes with higher frequencies. Certainly, as the rise time increases significantly, it becomes more difficult to detect the waves.

Each sample can be seen as a propagation medium with a finite number of excitable modes. These modes will be stimulated in a different way if the source’s characteristics are different. As was emphasised earlier, various parameters can affect the signals generated by the source and thus the 2DFT, such as preferential directions of the stress field generated by the source, source position in the sample thickness and source rise time. The results of the simulations represent a useful tool to analyse the effects of the nature of the source, of its position and of the geometry of the specimen. When it comes to AE testing and classification, parameters are extracted from the measured signals, and as it is almost impossible to measure as many signals as requested to calculate the 2DFT, this tool cannot be used to analyse the data. However, useful information can be extracted from the results presented in the above studies, especially to emphasise relevant parameters to identify AE sources.

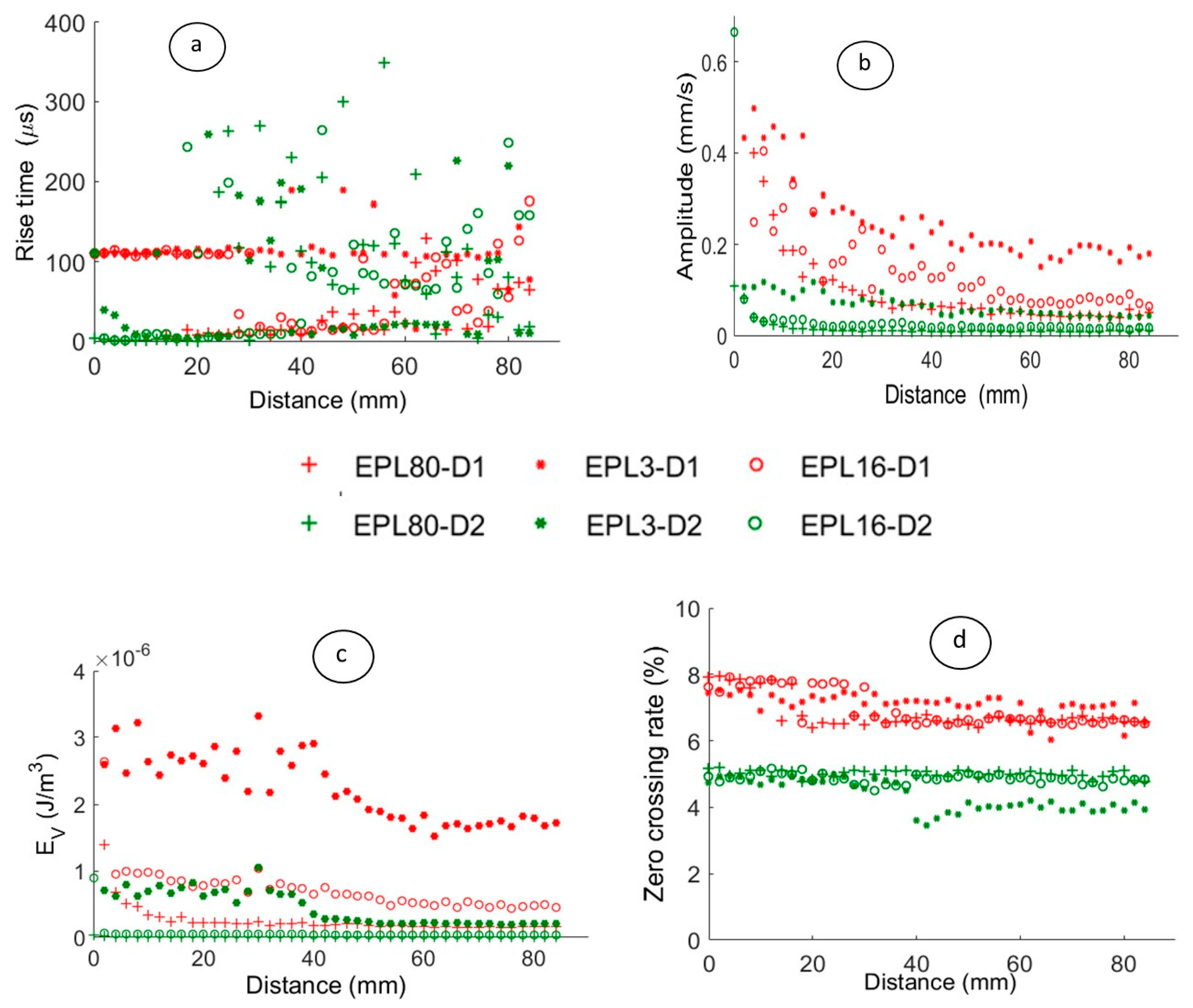
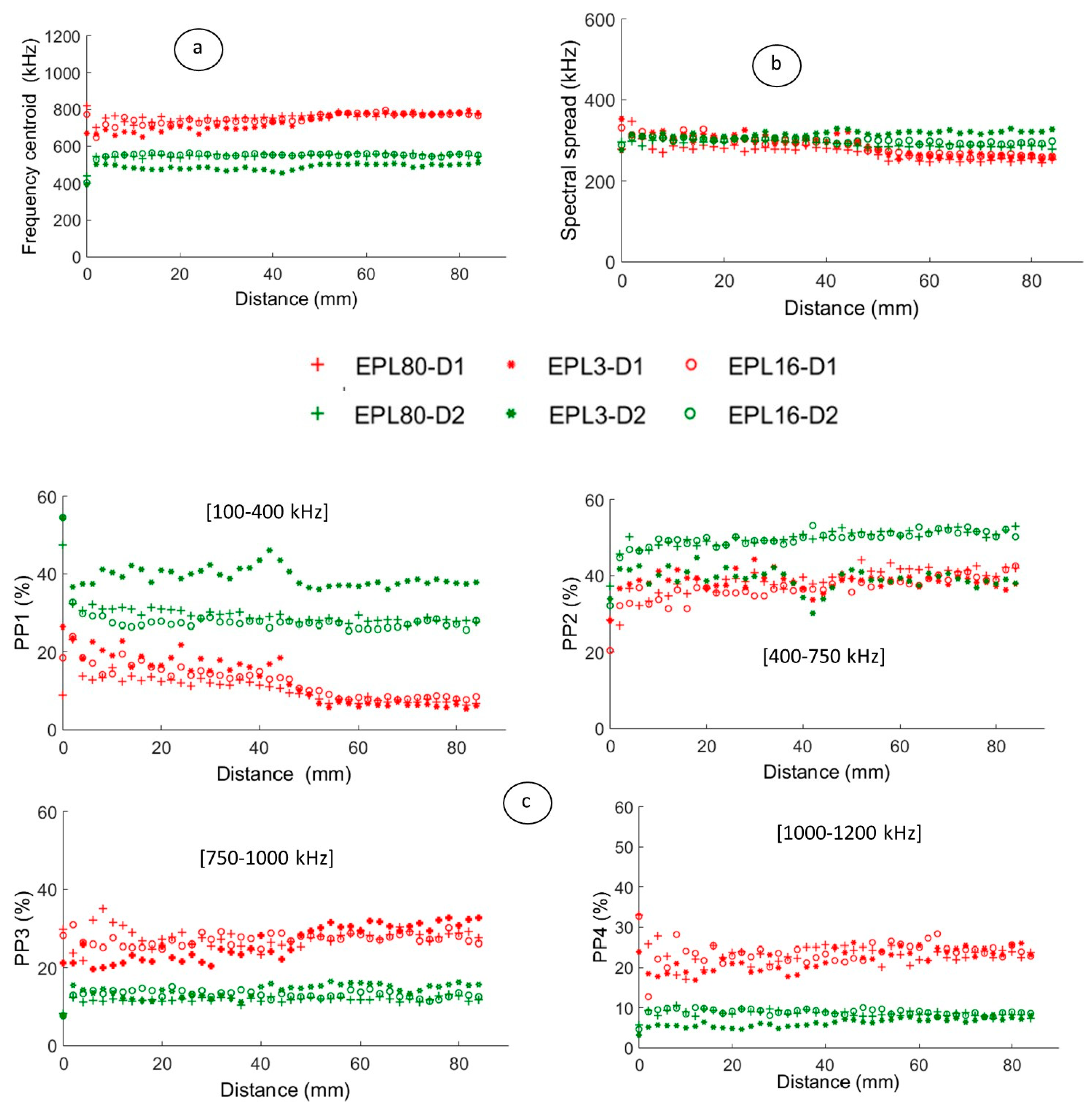
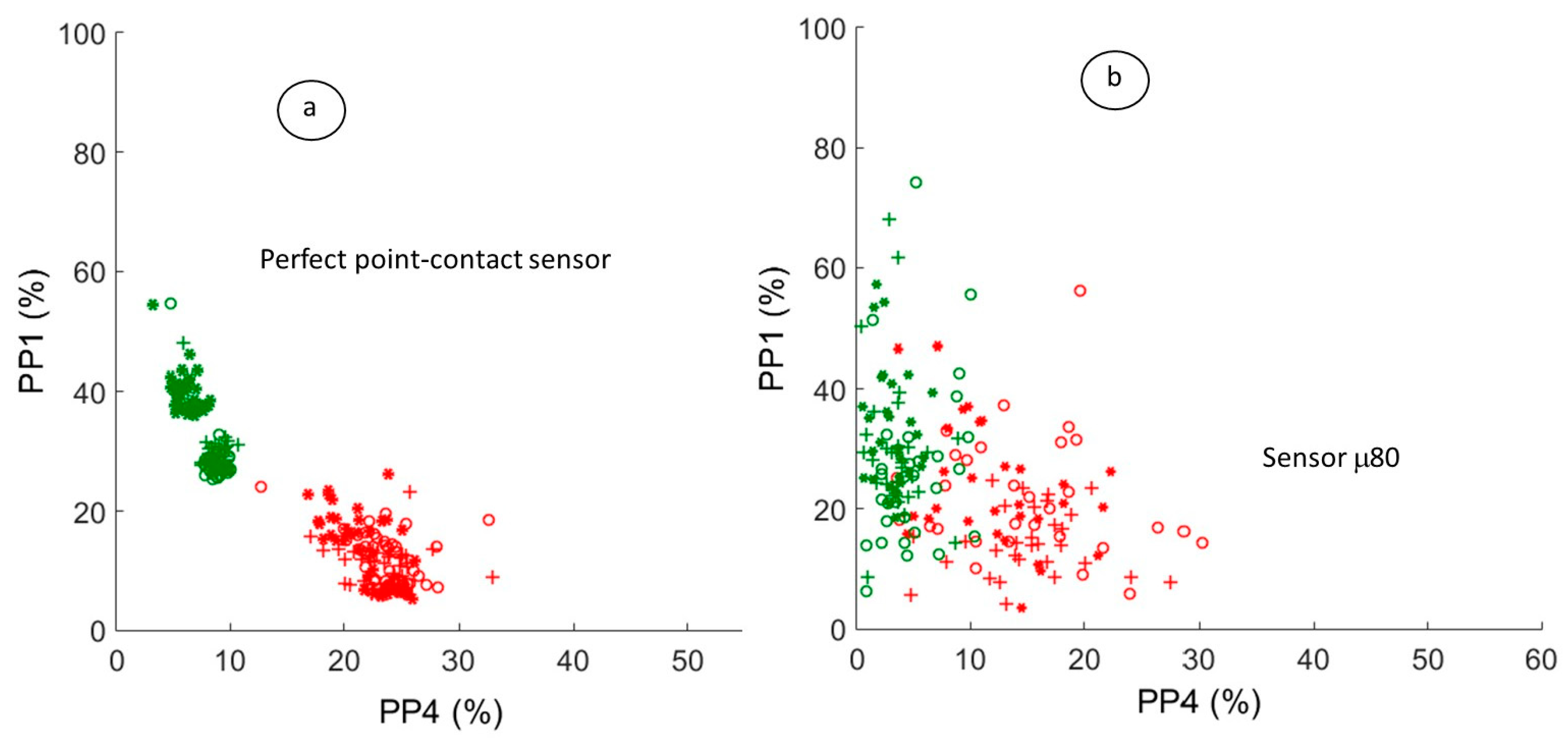
4.2. Numerical Modelling as a Tool to Improve the AE Clustering: Effect of the Sensor

4.2.1. Relevant Parameters on the Surface with a Perfect Point Contact-Sensor

In this work, a parameter is defined as relevant if: (1) its value is constant whatever the distance from the source, (2) it is independent of sample geometry, (3) its value depends on the source’s characteristics. To identify relevant parameters, two distinct sources are placed in the gauge section of the sample. The first one simulates a mode I cracking placed at the midplane of the sample with a 0.1 μs rise time and M_x = 500 N∙μm (D₁ (M_x = 500 N∙μm, 0 mm, 0.1 μs)). The second one models a mode II cracking placed 0.95 mm away from the midplane towards the surface with a 1 μs rise time and M_x = 100 N∙μm (D₂ (M_x = 100 N∙μm,0.95 mm,1 μs)). Figure 12 shows the 2DFT results for the two types of damage. Neither the stimulated modes nor the stimulated frequency ranges are the same in the two cases. As expected, the higher frequencies are not present in the AE sources as the source rise time is increased. The further the source is from the midplane, the more the modes of flexion are requested, to the detriment of the longitudinal modes. These results highlight the acoustic signature of each kind of source. The signals generated by each source are calculated for each geometry, and several descriptors are presented: rise time (RT), zero crossing rate (ZCR), frequency centroid (FC), spectral spread (SS), peak amplitude, energy, and the partial powers PPi.

Figure 13 shows the evolution of several parameters as a function of distance from the source for each source and each geometry. These parameters are calculated based on the numerical signals extracted from the nodes. Figure 13a suggests that the RT cannot be considered to be a relevant parameter, as it is not constant with distance; it depends on the sample geometry, and it seems difficult to relate its value to a source characteristic. Moreover, this parameter does not exhibit a specific trend with the distance of propagation. Despite some fluctuations, there is a decreasing trend of peak amplitude with distance. There are relatively large losses in the peak amplitude and energy of the signal over the propagation distance from 0 mm to 20 mm. Moreover, Figure 13b shows that the signal in the thin sample (EPL3) has a higher amplitude than those in EPL16 or EPL80. This parameter is not relevant for classifications such as energy (Figure 13c).

The feature ZCR (Figure 13d) is constant with distance, independent of geometry, and ZCR values calculated for source D₁ are higher than ZCR values calculated for source D₂. This last observation seems logical, as source D₁ varies faster than source D₂, so it is more likely to generate signals with a higher number of oscillations. Concerning frequency features (Figure 14), the frequency centroid does not exhibit large fluctuations with distance, like the spectral spread. The feature FC (Figure 14a) is pertinent. The SS (Figure 14b) is constant as a function of distance and independent of geometry, but is the same for the two sources. Consequently, it cannot be considered to be a relevant parameter for the identification of sources. The partial powers are calculated in the range of [100; 400] kHz for PP1, [400; 750] kHz for PP2, [750; 1000] kHz for PP3 and [1000; 1200] kHz for PP4. The last interval is situated in frequency range that is generally little-studied in EA. The partial powers seem to be a relevant except for PP2 (Figure 14c).

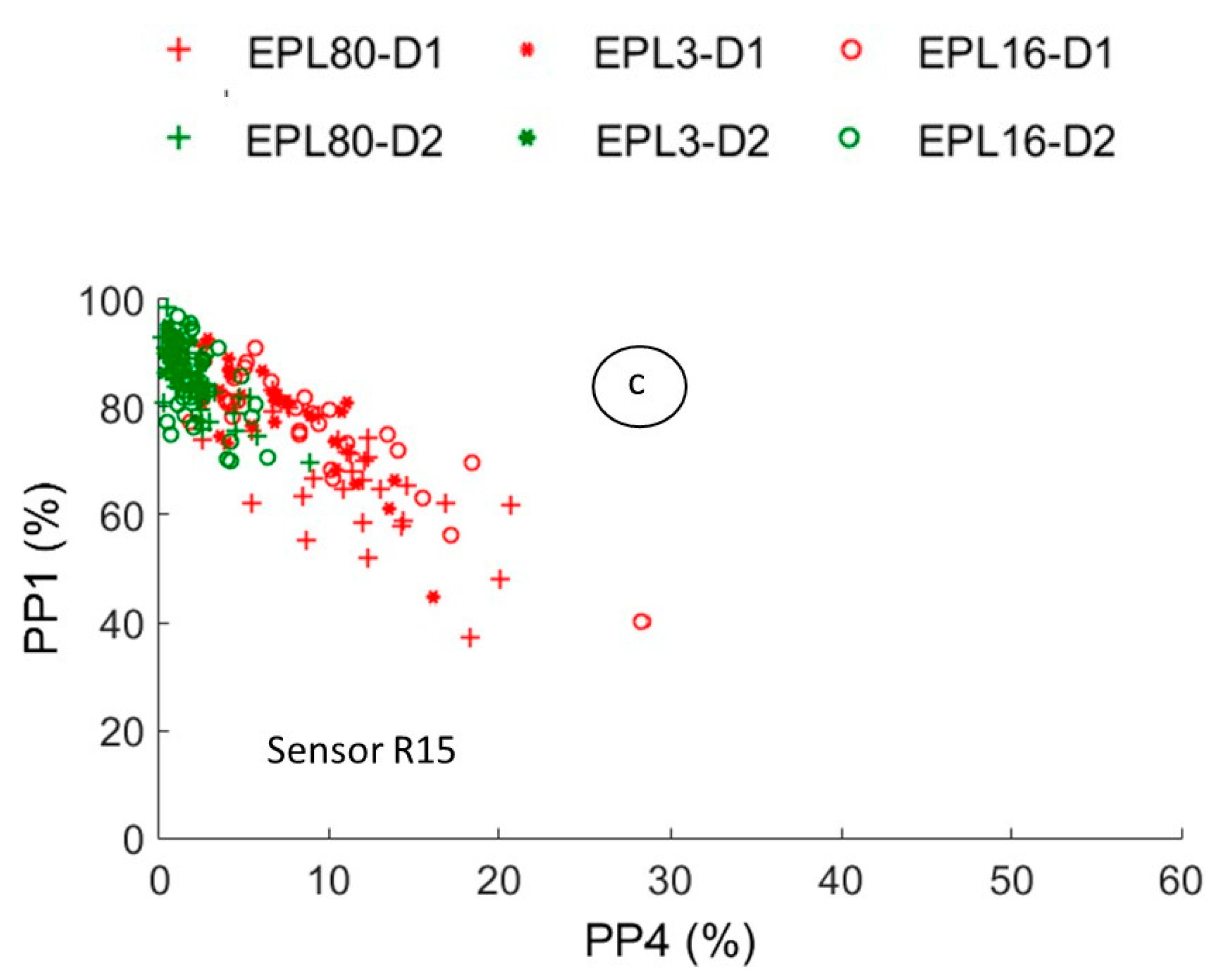
4.2.2. Effect of the Piezoelectric Sensor on the Pertinent Descriptors

With the numerical model, we identify relevant parameters such as ZCR and FC or PP1 and PP4, in order to plot a correlation diagram. Without any doubt, two classes of signals can be observed on the diagram (Figure 15a and Figure 16a) independently of the specimen’s size: one class with higher FC and ZCR that is more likely to be related to the signals generated by source D₁ (varying more rapidly), and another class with lower FC and ZCR that is more likely to be associated with the signals generated by source D₂ (varying less rapidly). This observation was made without the aid of any kind of classification algorithm and using only two parameters, which were identified with model work. However, all studies above were performed without considering the piezoelectric AE sensor. Therefore, in the last part, we will take into account the sensor effect on the recorded signals. We will consider typical commercial PAC μ80 and R15 sensors from MISTRAS Group France (Sucy-en-Brie, France). Once the signal on the surface of the material is known by modelling, we can determine the signal of sensor responses by multiplying the signal on the surface by the transfer function (Equation (8)) in the frequency domain. After considering the sensor, we observe an overlapping of two classes in the plane ZCR/FC or in the plane PP1/PP4, which highlights the crucial influence of the piezoelectric sensor on the AE features (Figure 15 and Figure 16). The values of the pertinent descriptors are strongly affected by the sensor, mainly by the R15 sensor. Nevertheless, even if the pertinent descriptors are affected by the sensor effect, they also contain information on the source. This result shows the requirement to take into account several descriptors. Therefore, it would be very useful to know the pertinent descriptors on the surface of the material in order to choose the most pertinent descriptors for the unsupervised classification. The results of the modelling work will improve the robustness of the segmentation of AE signals.

5. Conclusions

In this paper, we used FEM to model wave propagation in aluminium samples with different geometries. Initially, we validated the use of FEM on a pencil lead break experiment by comparing the simulated and experimental signal. This experimental validation shows that FEM is a suitable method to model wave propagation in the frequency band typically used in AE. We then showed how the sample’s geometry, modifying the reflections, affects the propagated signal. When the sample dimensions are large enough, it can be considered to be a plate, and the modes stimulated by the source will be close to plate modes (Lamb waves). When the sample is narrow, it can be considered a bar. In that case, the propagation modes will be close to bar modes. Finally, when the sample has the dimensions of a laboratory sample, the propagation modes are more complicated, making their interpretation more difficult.

To correlate the damage mechanisms with the characteristics of the AE signal, numerical simulations are necessary in order to define pertinent descriptors. The novelty of this study is mainly the use of 2DFT for the modal analysis, showing that source parameters could be seen and interpreted using these 2DFT. To link these results to more traditional AE analysis using relevant parameters, the 2DFT also showed that information related to the frequency content of the signal could give useful information about the source for this study, thus providing a useful methodology to define relevant parameters. The knowledge of the pertinent descriptors at the surface of the material without the sensor effect will be very useful in order to improve the results of the unsupervised classification. It may be fruitful to choose the most pertinent descriptors in order to give robustness to the classification. It is important to differentiate what is characteristic of the source from what comes from transformations related to propagation and acquisition. The modelling of the entire AE chain from the source to the analysed signal seems essential. This fundamental aspect is important for the good use of AE data, choice of sensors and needs to be developed in order to make this technique more reliable. Future work will consist of estimating the influence of the damage on the propagation and on AE signals.