The Effect of Isomorphic Pitch Layouts on the Transfer of Musical Learning †
Abstract
Featured Application
Abstract
1. Introduction
Current Study
2. Materials and Methods
2.1. Participants
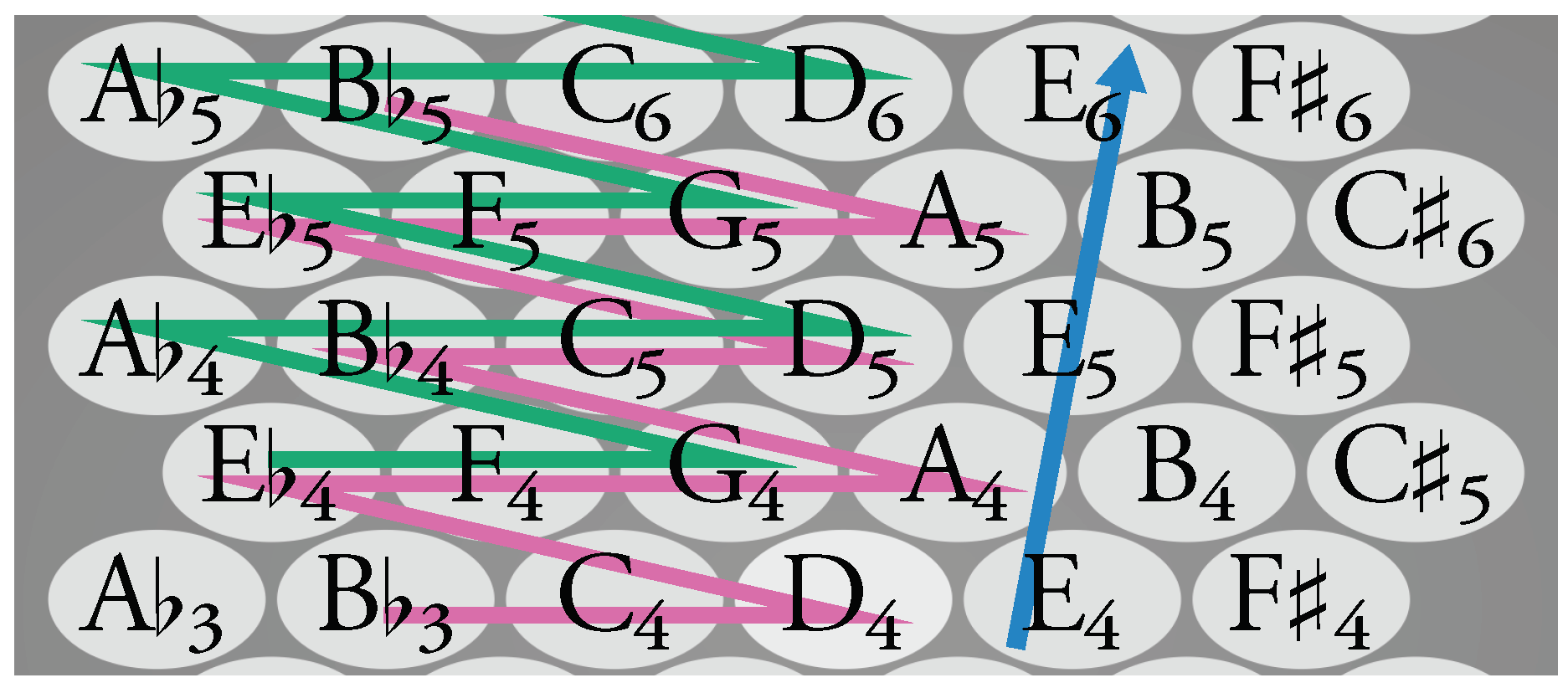
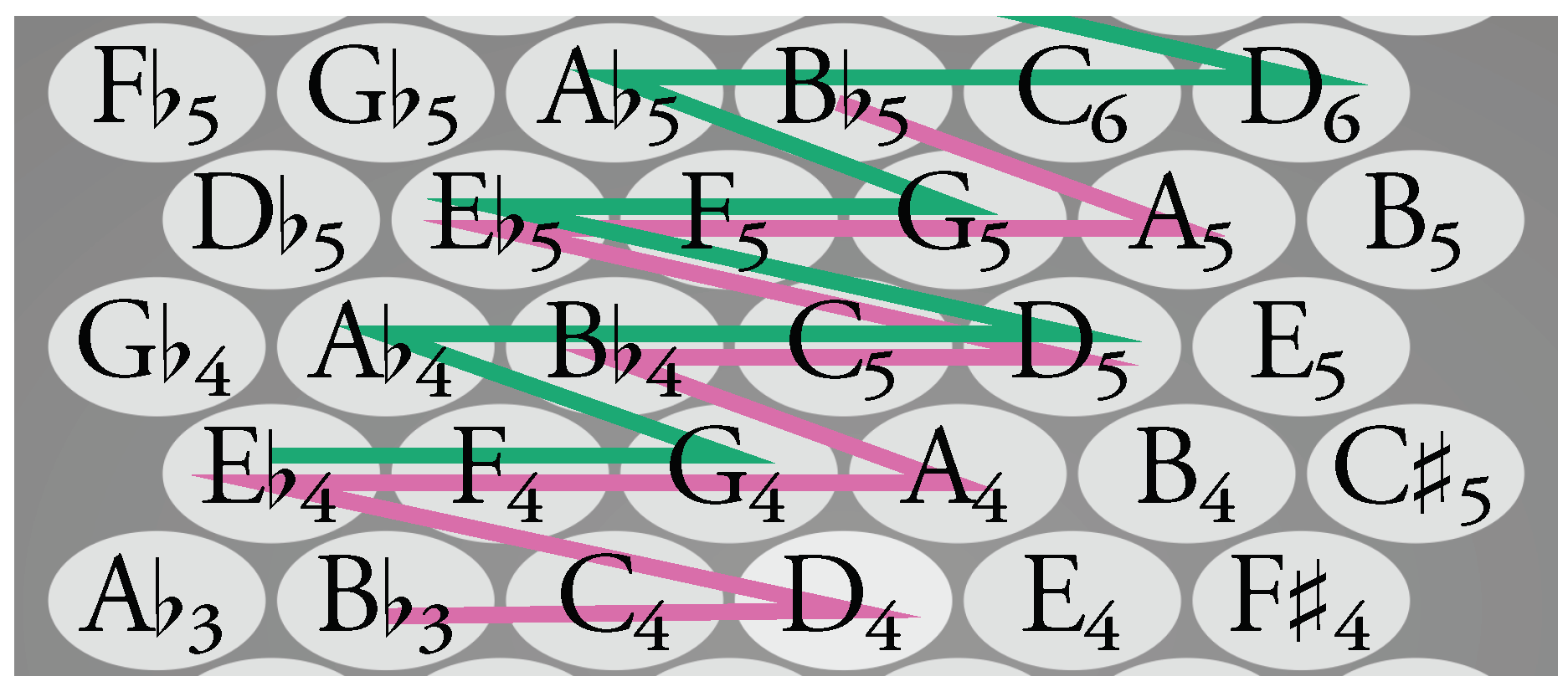
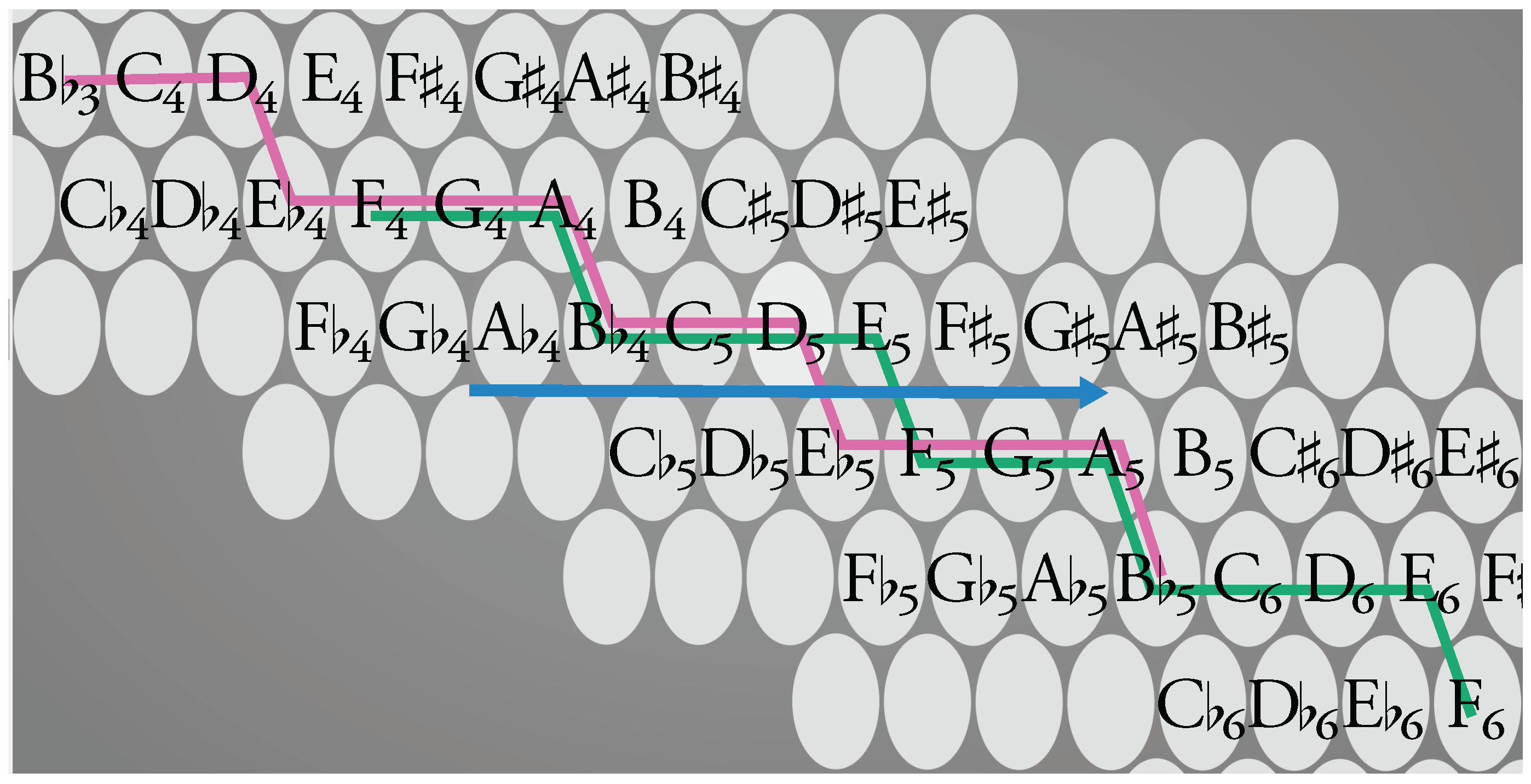
2.2. Materials
2.3. Procedure
- Did you have a preference for either layout?
- What did you prefer about that layout?
- Do you have any other comments about the layouts or the tasks?
2.4. Data Analysis
2.4.1. Accuracy: Training Tasks
- N is the total number of notes in the target sequence
- is the time in milliseconds of nth target note
- is the time in milliseconds of first performed note within the time window that matches the pitch of the target note.
2.4.2. Accuracy: Retention and Transfer Tasks
- N is the total number of notes in the target sequence.
- C is the total number of notes in the corrected performance.
- is the time in milliseconds of the cth note in the corrected performance.
- is the time of the metronome beat closest to the performed note .
- E is the number of “first errors” calculated.
2.4.3. Semi-Structured Interviews
2.5. Statistical Approach
2.5.1. Bayesian Regression
2.5.2. Priors
3. Results
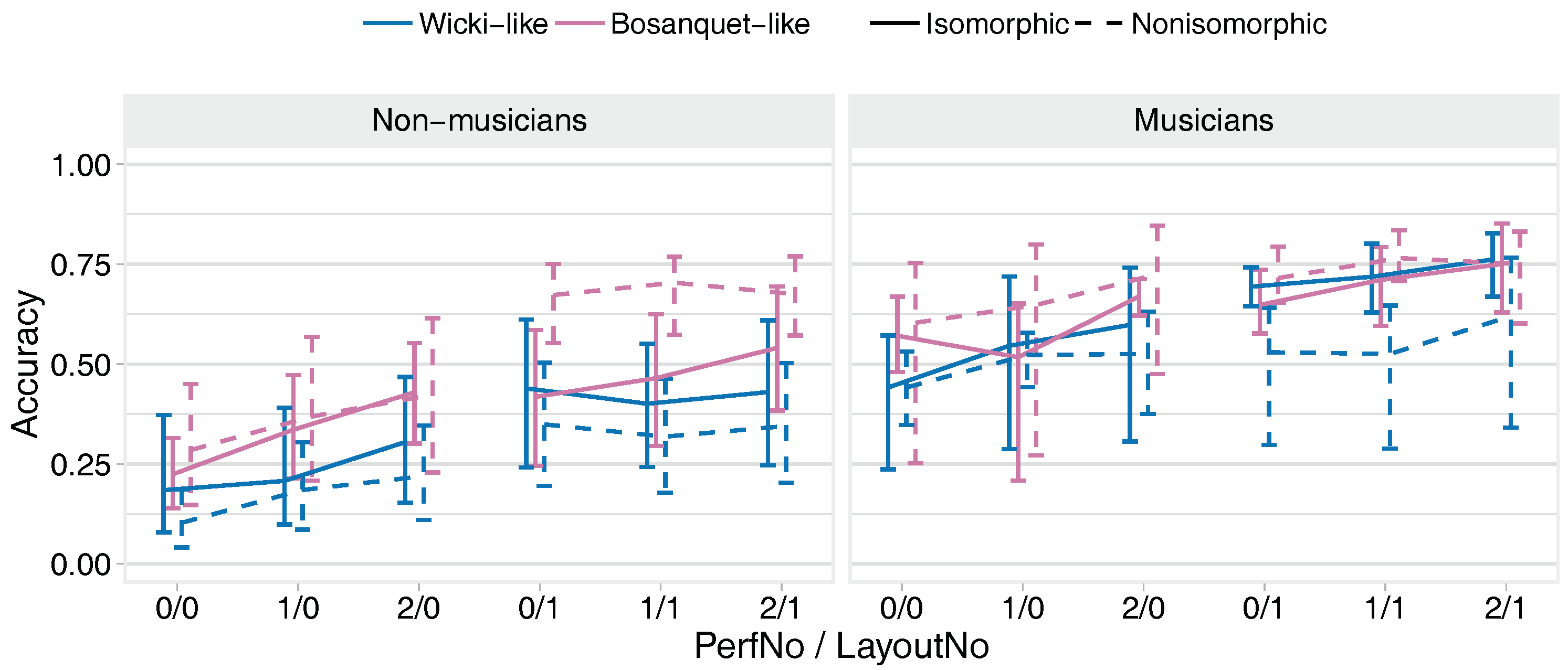
3.1. Confirmatory Analysis
3.2. Exploratory Analysis
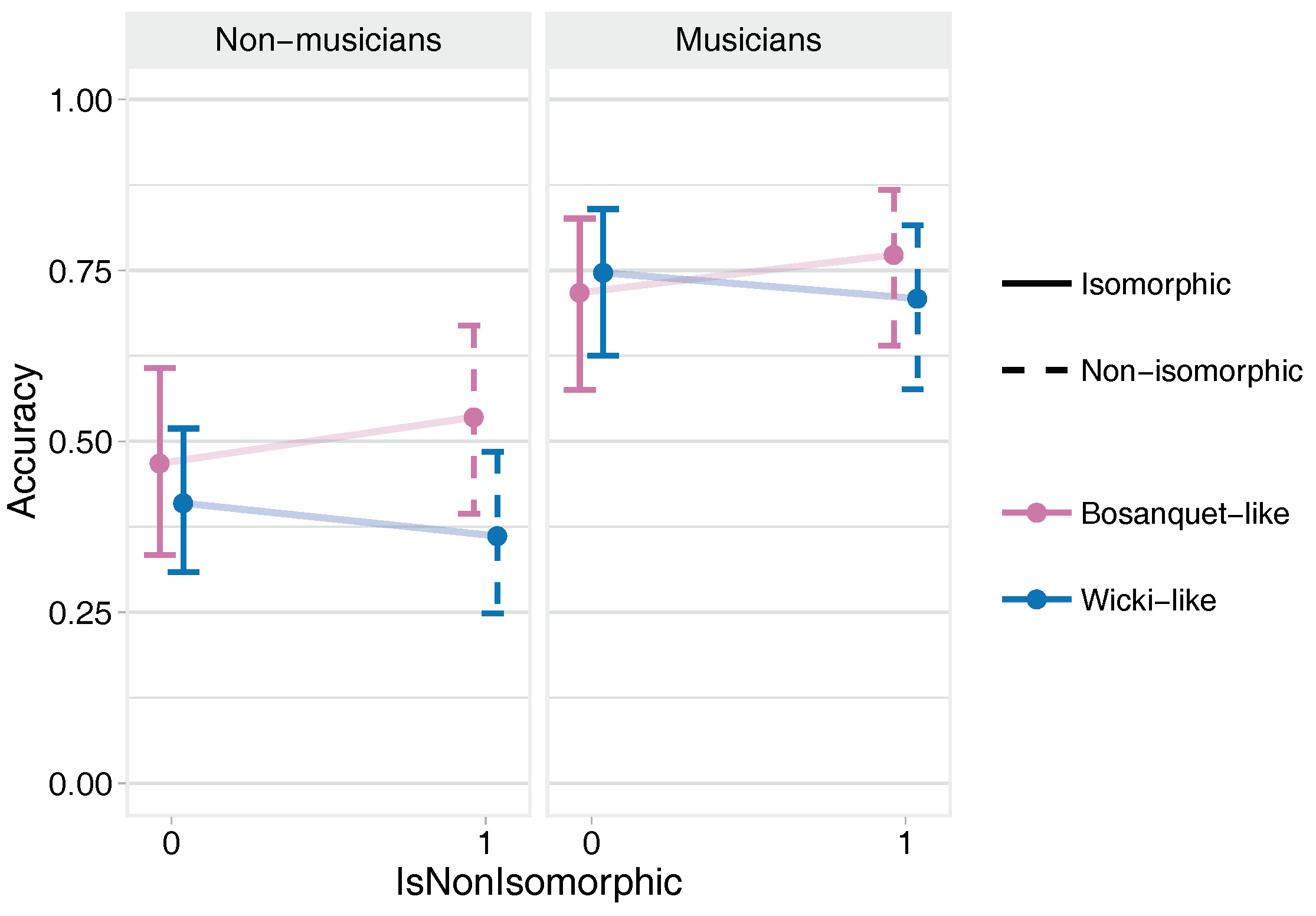
3.2.1. Scale Training Task
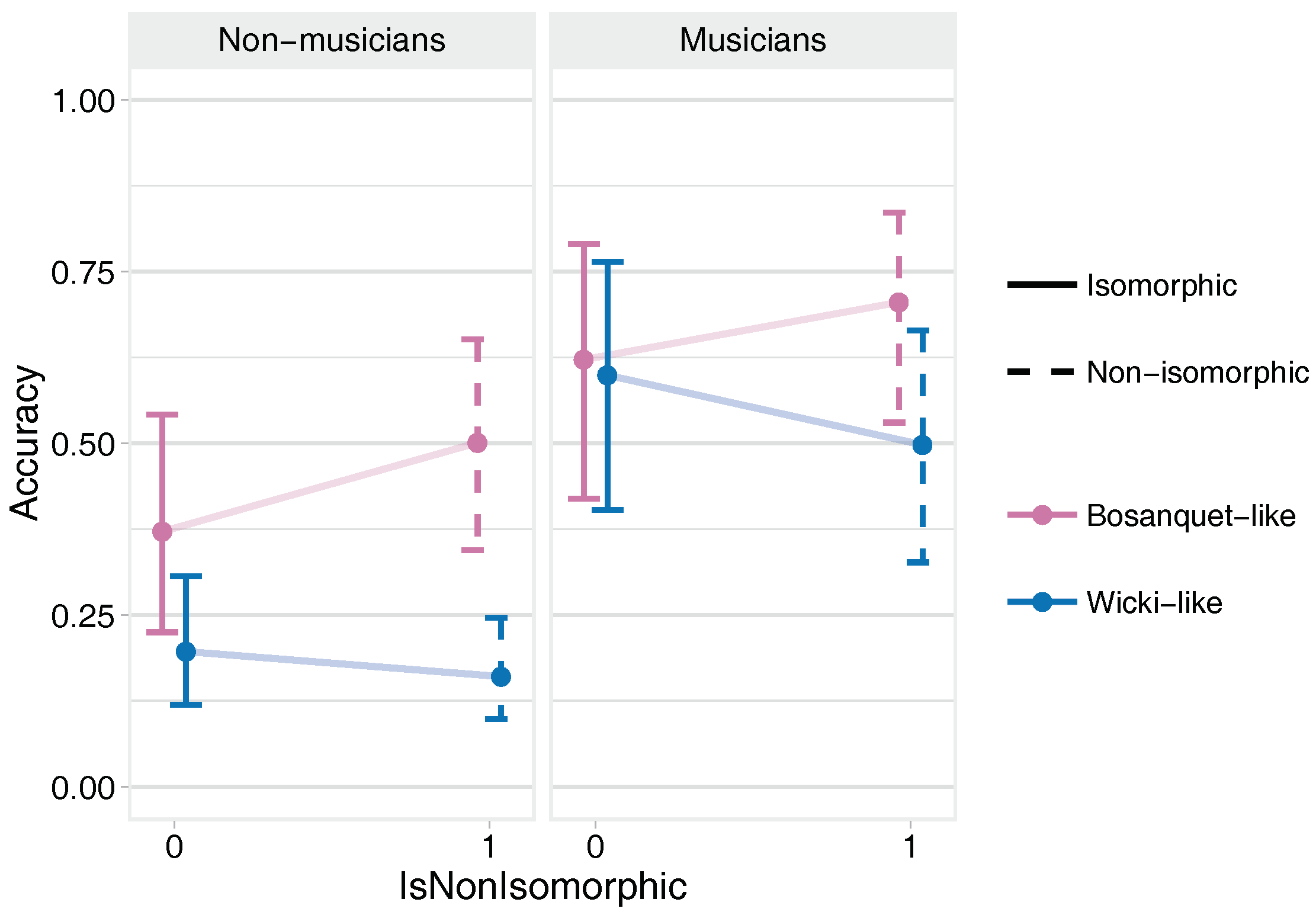
- Strong evidence that, on the Wicki-like layouts, non-musicians and musicians performed better on the isomorphic versions; conversely, on the Bosanquet layouts, non-musicians and musicians performed better on the non-isomorphic versions.
- Strong evidence that performances were better on Bosanquet-like layouts than on Wicki-like layouts in all cases except for musicians playing the isomorphic layout (mean effect across all conditions was 0.88).
- Very strong evidence that musicians performed substantially better than non-musicians under all conditions (mean effect across all conditions was 1.84).
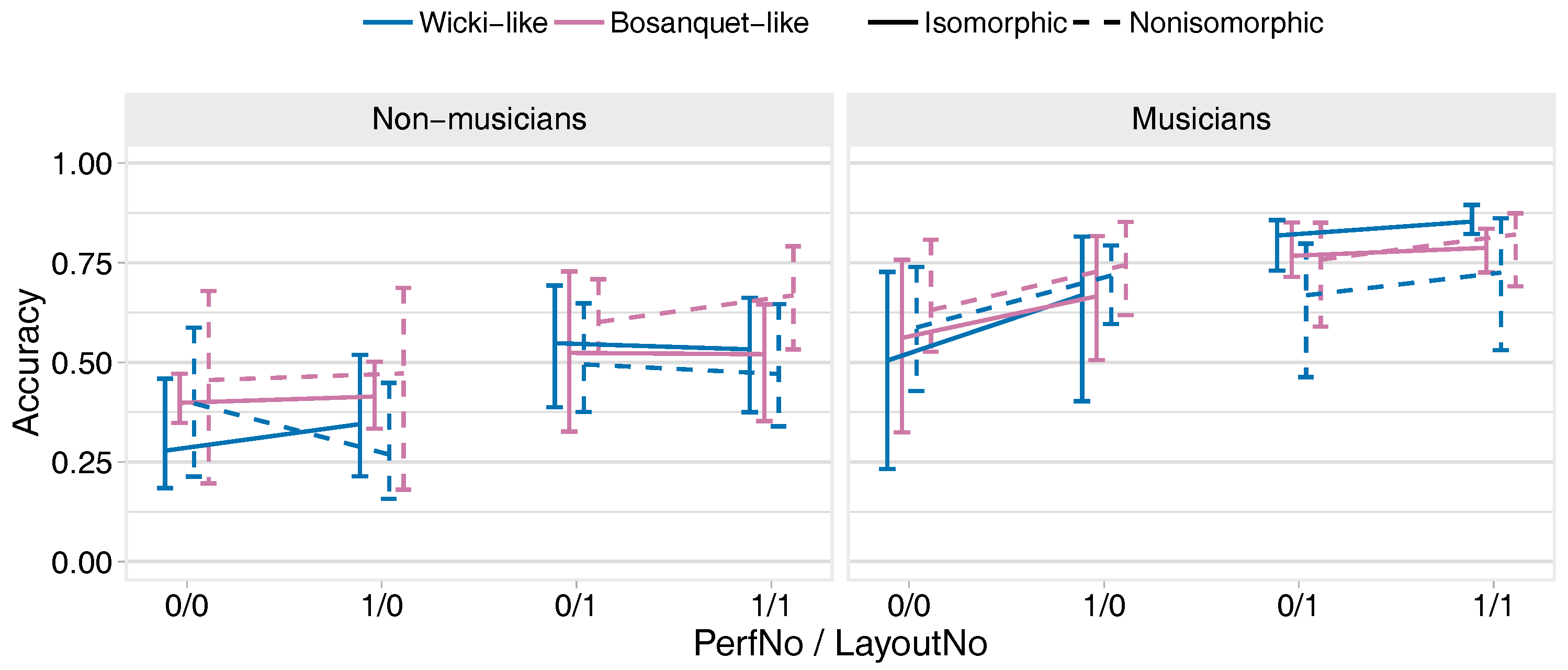
- Very strong evidence that accuracy improved across successive performances of the task and in the second-played layout, although the improvement was smaller for non-musicians when both were high.
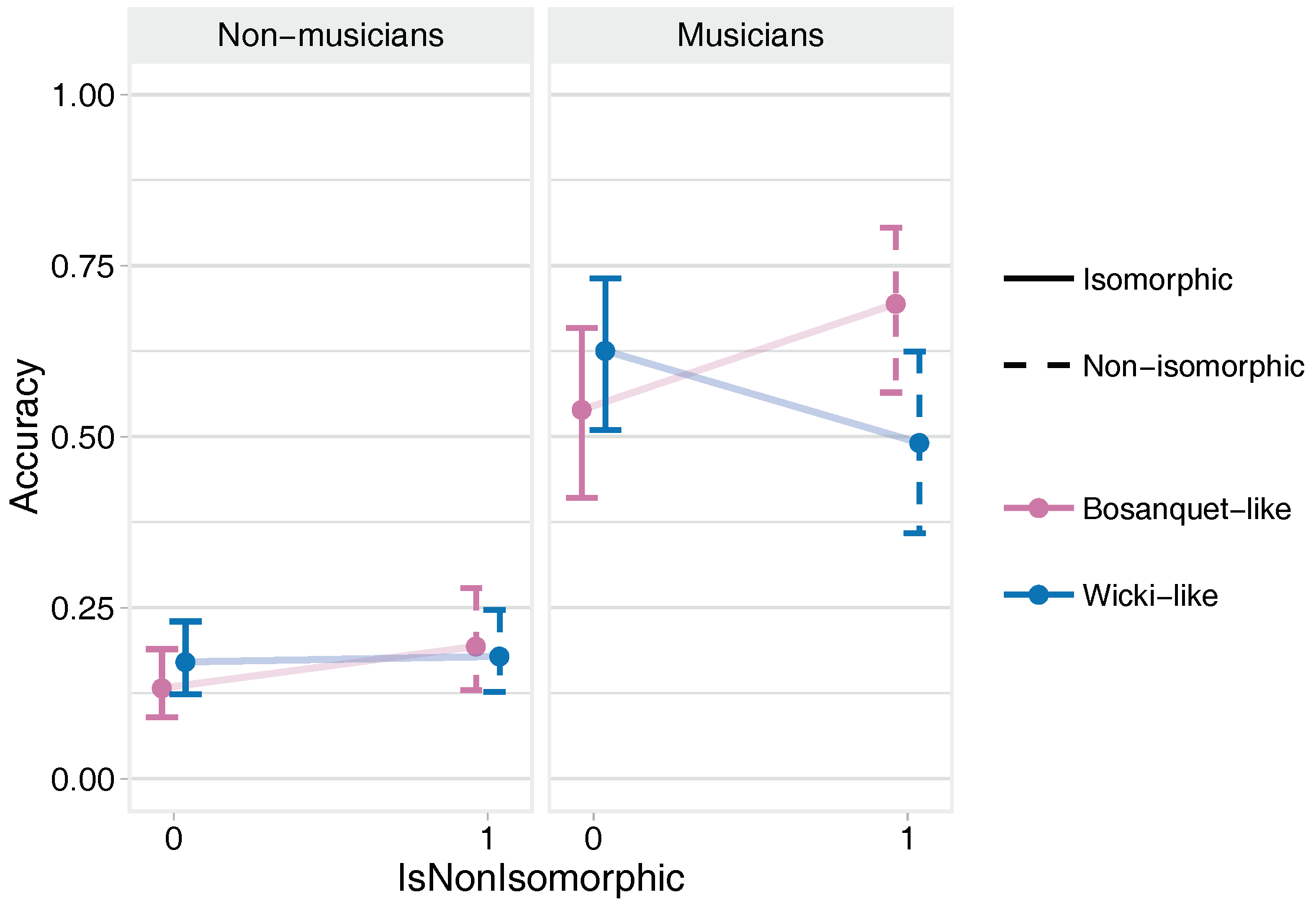
3.2.2. Scale Immediate Retention Task
- No strong evidence for any impact of isomorphism on accuracy.
- Strong evidence that non-musicians performed better on the non-isomorphic Bosanquet-like layout than on the non-isomorphic Wicki-like layout.
- Very strong evidence that musicians performed substantially better than non-musicians under all conditions (mean effect across all conditions was 1.08).
- Very strong evidence that accuracy improved in the second-played layout. However, only musicians improved with successive performances, and the improvements for musicians reduced for their second-played layout.
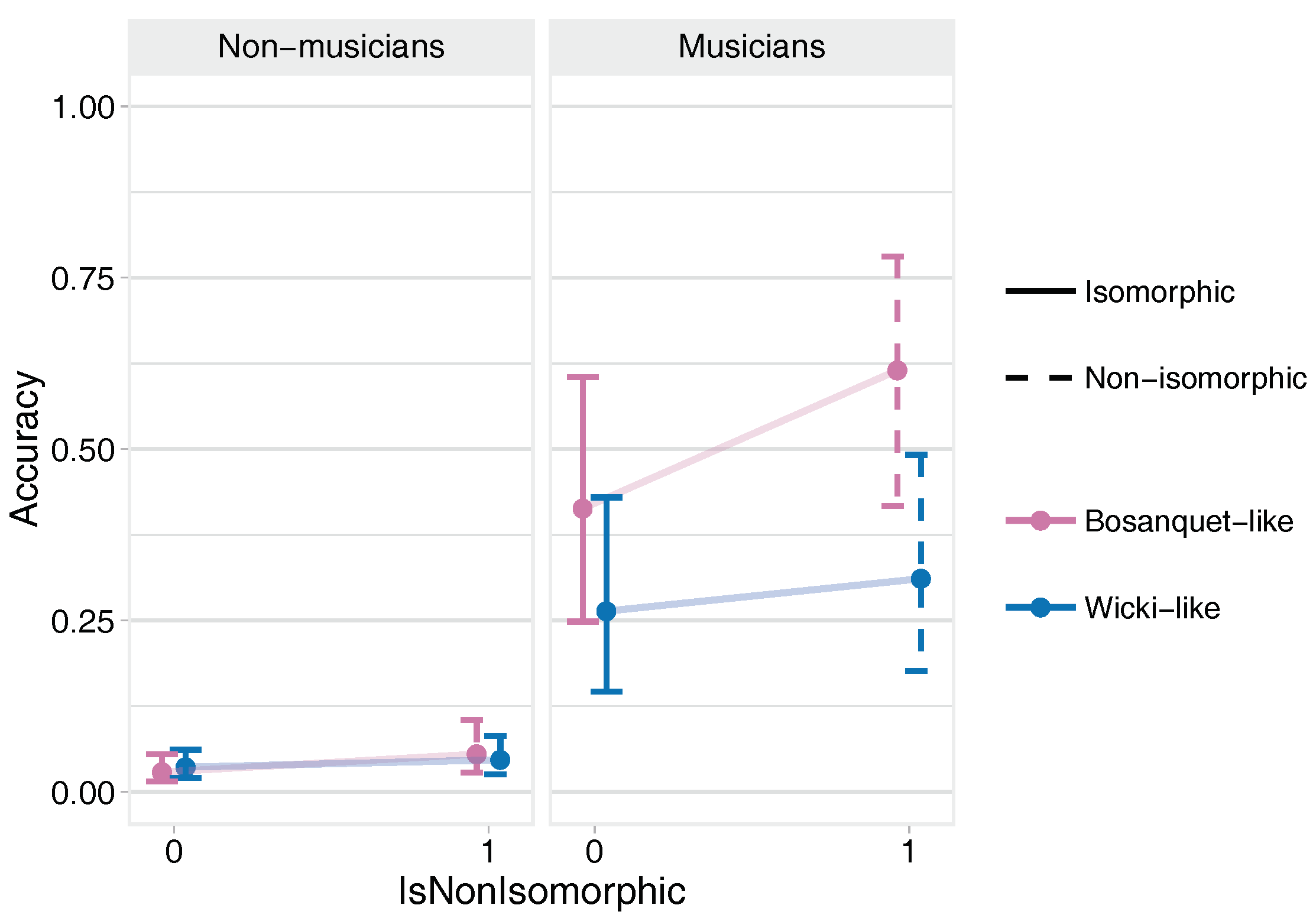
3.2.3. Arpeggio Training Task
- Strong evidence that, for the Bosanquet layouts, non-musicians and musicians performed better on the non-isomorphic versions.
- Very strong evidence that musicians performed better on the non-isomorphic Bosanquet-like layout than on the non-isomorphic Wicki-like layout.
- Very strong evidence that musicians performed substantially better than non-musicians under all conditions (mean effect across all conditions is 2.41).
- Very strong evidence that accuracy improved across successive performances of the task and in the second-played layout.
3.2.4. Arpeggio Immediate Retention Task
- Strong evidence that, for the Wicki-like layouts, musicians performed better on the isomorphic version; for the Bosanquet-like layouts, non-musicians and musicians both performed better on the non-isomorphic versions.
- Very strong evidence that musicians performed better on the non-isomorphic Bosanquet-like layout than on the non-isomorphic Wicki layout.
- Strong evidence that musicians performed substantially better than non-musicians under all conditions (mean effect across all conditions is 1.58).
- Very strong evidence that accuracy improved for the second-played layout. For musicians only, performance also improved with successive performances of the task but less so on the second layout.
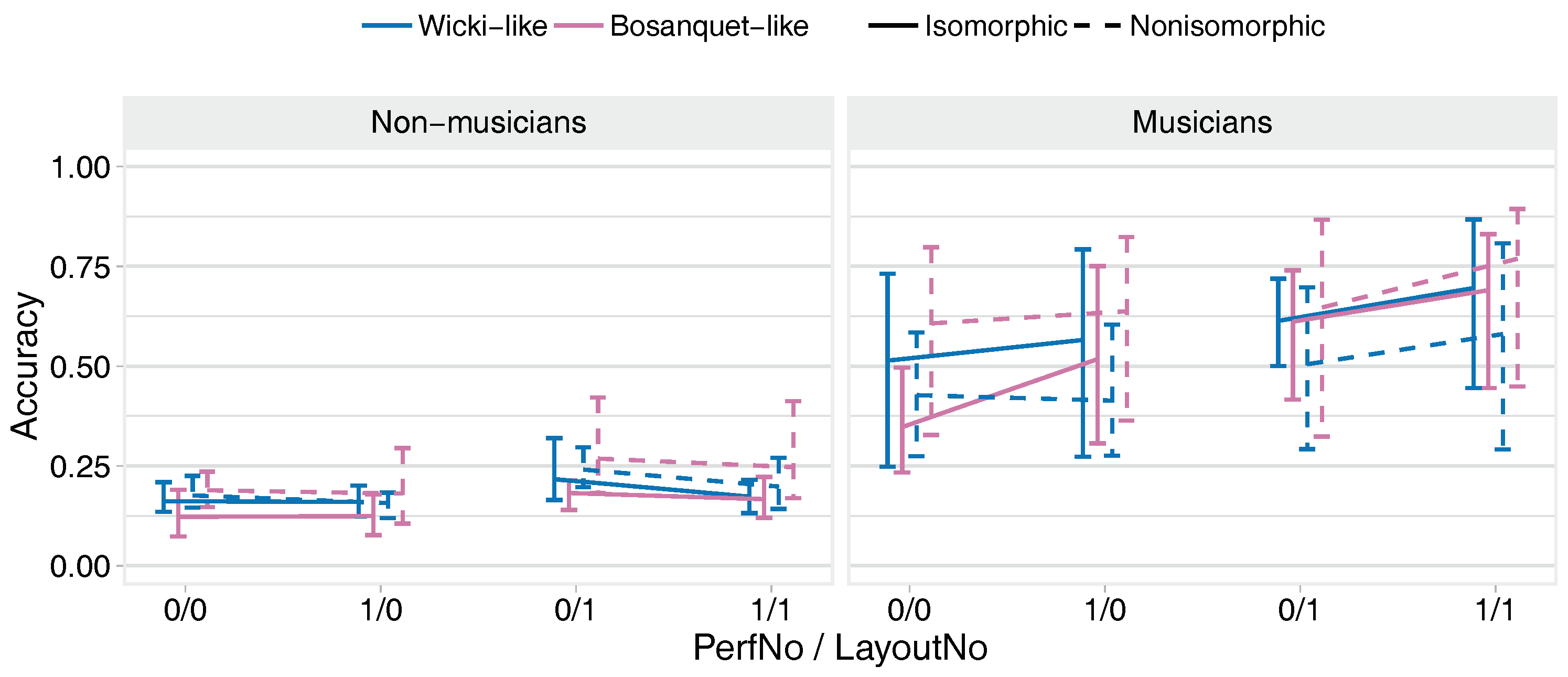
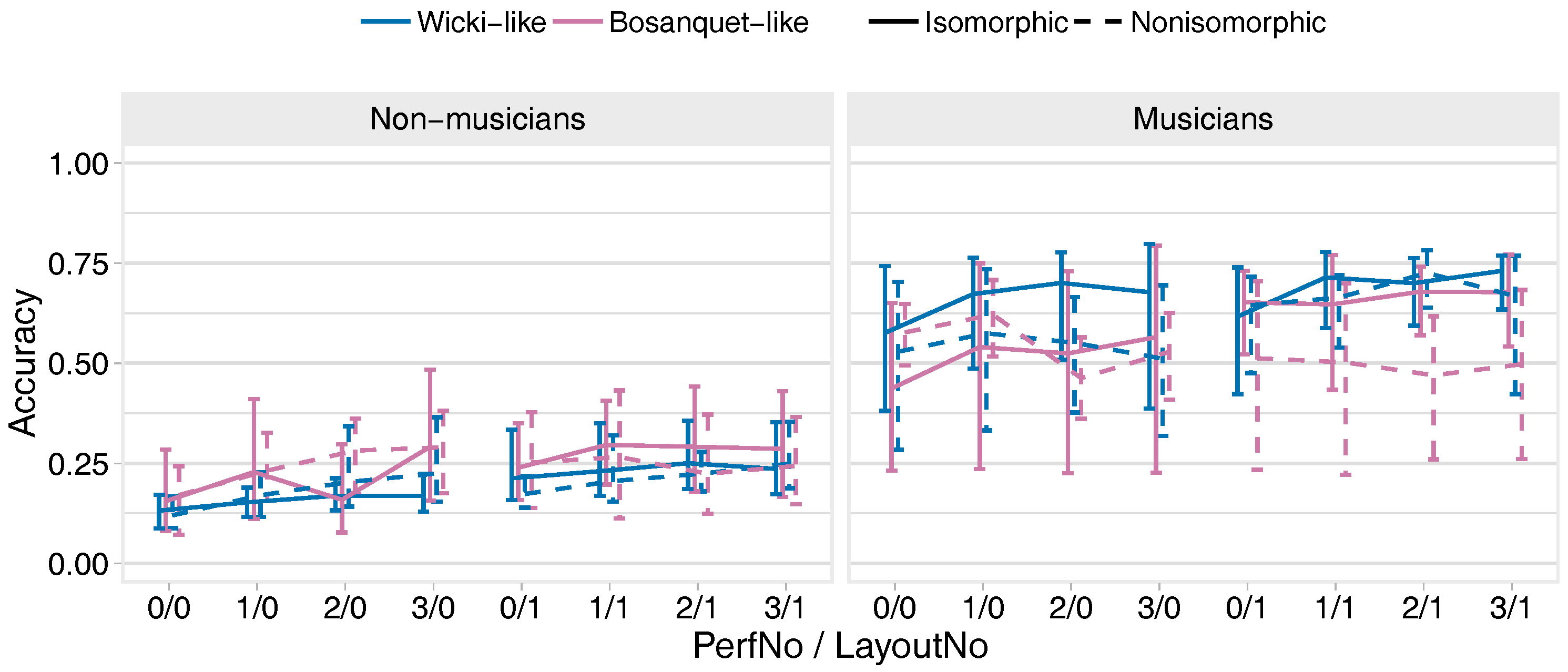
3.2.5. Melody Transfer Task
- Strong evidence that non-musicians’ performances in the trained key were better on the isomorphic Wicki layout compared with the non-isomorphic version; strong evidence that musicians’ performances in the trained key were better using the isomorphic Bosanquet layout than using the non-isomorphic version.
- Strong evidence that non-musicians’ performances in the untrained key were worse on the isomorphic Bosanquet than the non-isomorphic Bosanquet layout; very strong evidence that musicians’ performances in the untrained key were better on the isomorphic versions of both types of layout (mean effect of 0.79).
- Strong evidence that musicians’ performances in the trained key were better on the non-isomorphic Bosanquet than the non-isomorphic Wicki layout.
- Very strong evidence that musicians performed better than non-musicians across all conditions (mean effect was 2.05).
- Very strong evidence that performance improved with the second layout and with successive performances, although for non-musicians this reduced on the second layout.
3.3. Qualitative Content Analysis
3.3.1. Layout Preference
3.3.2. Reason for Layout Preference
3.3.3. Challenging Aspects
4. Discussion
4.1. Melody Transfer Task
4.2. Training and Immediate Retention Tasks
4.3. Summary of All Tasks
4.4. Semi-Structured Interviews
4.5. Limitations and Future Directions
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
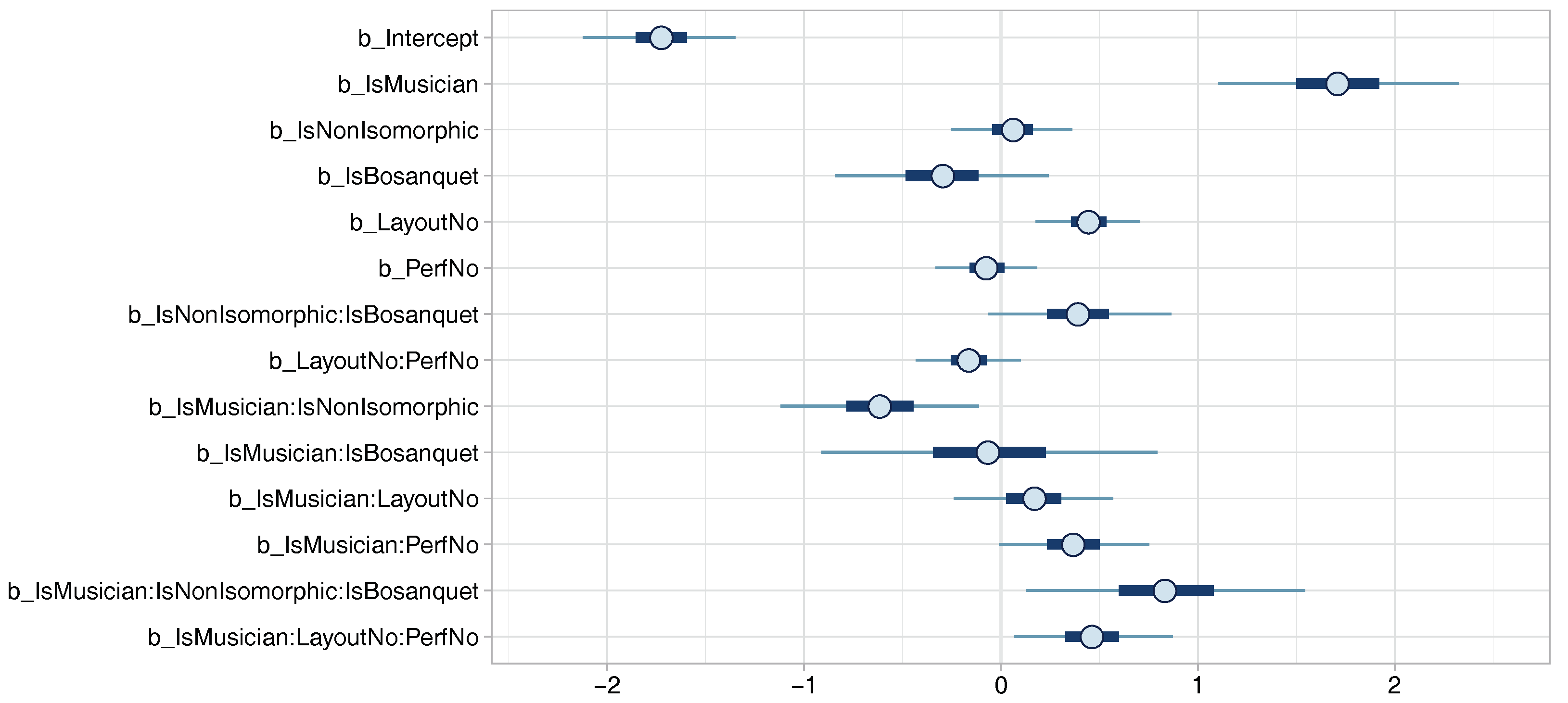
Appendix A. Exploratory Model Summaries
| Family: | beta | |||||||
| Links: | mu = logit; phi = identity | |||||||
| Formula: | Accuracy ~ IsMusician * (IsNonIsomorphic * IsBosanquet + LayoutNo * PerfNo) + (IsNonIsomorphic + LayoutNo * PerfNo | ID) | |||||||
| Data: | PitchLayoutsDataTask0 (Number of observations: 399) | |||||||
| Samples: | 4 chains, each with iter = 4000; warmup = 2000; thin = 1; total post-warmup samples = 8000 | |||||||
| Group-Level Effects: | ||||||||
| ID (Number of Levels: 67) | Estimate | Est.Error | l-95% CI | u-95% CI | Eff.Sample | Rhat | ||
| sd(Intercept) | 1.56 | 0.16 | 1.26 | 1.90 | 2460 | 1.00 | ||
| sd(IsNonIsomorphic) | 0.44 | 0.22 | 0.04 | 0.85 | 325 | 1.03 | ||
| sd(LayoutNo) | 0.60 | 0.21 | 0.13 | 0.96 | 336 | 1.02 | ||
| sd(PerfNo) | 0.12 | 0.08 | 0.01 | 0.30 | 811 | 1.01 | ||
| sd(LayoutNo:PerfNo) | 0.10 | 0.08 | 0.00 | 0.33 | 1068 | 1.01 | ||
| cor(Intercept,IsNonIsomorphic) | −0.38 | 0.26 | −0.77 | 0.29 | 2910 | 1.00 | ||
| cor(Intercept,LayoutNo) | −0.42 | 0.21 | −0.73 | 0.08 | 2281 | 1.00 | ||
| cor(IsNonIsomorphic,LayoutNo) | −0.22 | 0.28 | −0.70 | 0.39 | 1600 | 1.00 | ||
| cor(Intercept,PerfNo) | −0.05 | 0.34 | −0.67 | 0.65 | 9137 | 1.00 | ||
| cor(IsNonIsomorphic,PerfNo) | −0.12 | 0.37 | −0.78 | 0.63 | 3236 | 1.00 | ||
| cor(LayoutNo,PerfNo) | 0.38 | 0.37 | −0.51 | 0.89 | 1601 | 1.00 | ||
| cor(Intercept,LayoutNo:PerfNo) | −0.06 | 0.38 | −0.74 | 0.69 | 10760 | 1.00 | ||
| cor(IsNonIsomorphic,LayoutNo:PerfNo) | −0.01 | 0.40 | −0.75 | 0.74 | 6739 | 1.00 | ||
| cor(LayoutNo,LayoutNo:PerfNo) | −0.09 | 0.41 | −0.79 | 0.71 | 3019 | 1.00 | ||
| cor(PerfNo,LayoutNo:PerfNo) | −0.24 | 0.44 | −0.91 | 0.68 | 2168 | 1.00 | ||
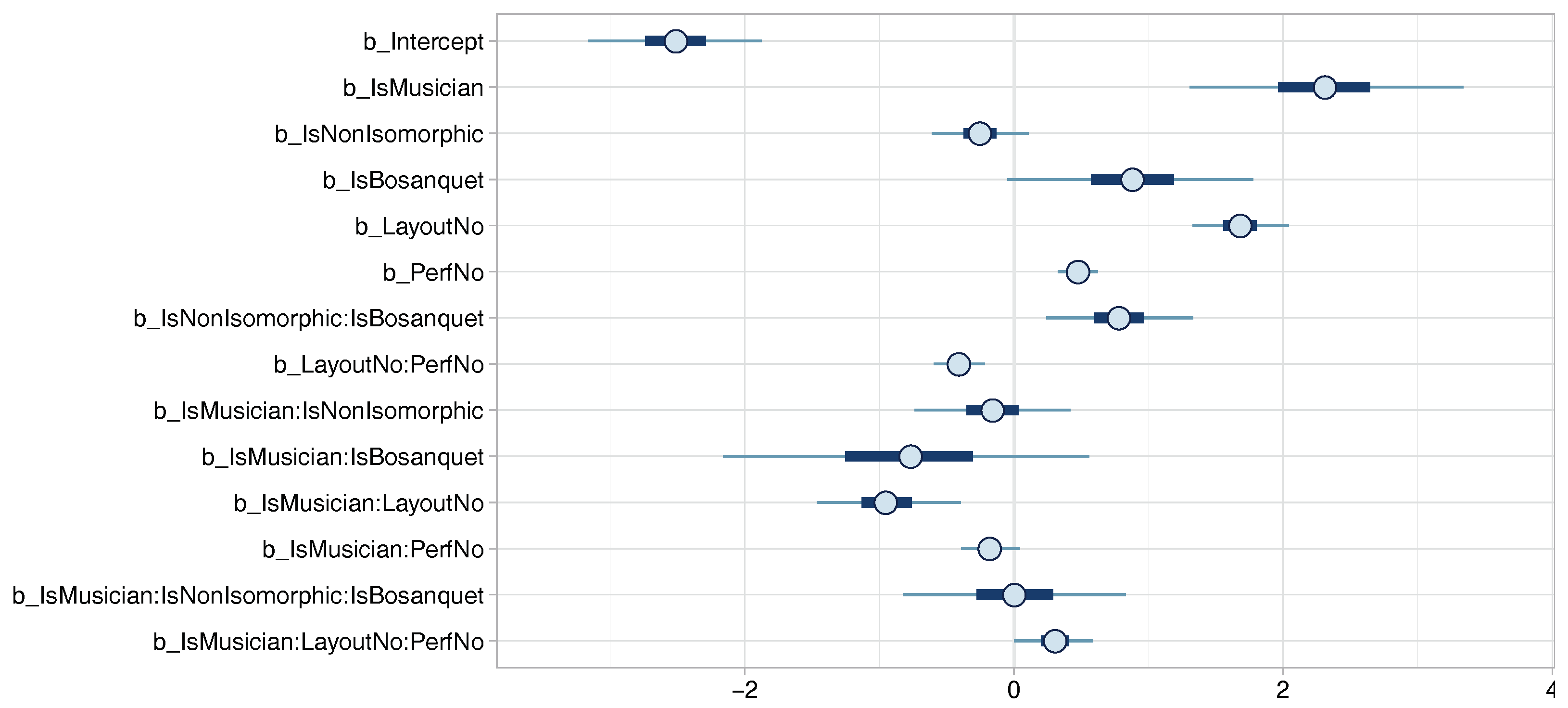
| Population-Level Effects: | Estimate | Est.Error | l-95% CI | u-95% CI | Eff.Sample | Rhat | Eff.Fact | |
| Intercept | −2.51 | 0.33 | −3.17 | −1.88 | 1720 | 1.00 | 0.08 | |
| IsMusician | 2.31 | 0.52 | 1.30 | 3.34 | 1675 | 1.00 | 10.07 | |
| IsNonIsomorphic | −0.25 | 0.18 | −0.61 | 0.11 | 4119 | 1.00 | 0.78 | |
| IsBosanquet | 0.88 | 0.46 | −0.05 | 1.78 | 1643 | 1.00 | 2.41 | |
| LayoutNo | 1.68 | 0.18 | 1.33 | 2.04 | 3420 | 1.00 | 5.37 | |
| PerfNo | 0.48 | 0.08 | 0.33 | 0.62 | 4898 | 1.00 | 1.62 | |
| IsNonIsomorphic:IsBosanquet | 0.78 | 0.28 | 0.24 | 1.33 | 3639 | 1.00 | 2.18 | |
| LayoutNo:PerfNo | −0.41 | 0.10 | −0.60 | −0.22 | 5131 | 1.00 | 0.66 | |
| IsMusician:IsNonIsomorphic | −0.16 | 0.29 | −0.74 | 0.42 | 3720 | 1.00 | 0.85 | |
| IsMusician:IsBosanquet | −0.78 | 0.70 | −2.16 | 0.56 | 1823 | 1.00 | 0.46 | |
| IsMusician:LayoutNo | −0.95 | 0.27 | −1.46 | −0.40 | 3189 | 1.00 | 0.39 | |
| IsMusician:PerfNo | −0.18 | 0.11 | −0.39 | 0.04 | 4203 | 1.00 | 0.84 | |
| IsMusician:IsNonIsomorphic:IsBosanquet | 0.01 | 0.43 | −0.82 | 0.83 | 4019 | 1.00 | 1.01 | |
| IsMusician:LayoutNo:PerfNo | 0.30 | 0.15 | 0.00 | 0.59 | 4699 | 1.00 | 1.35 | |
| Family Specific Parameters: | Estimate | Est.Error | l-95% CI | u-95% CI | Eff.Sample | Rhat | ||
| phi | 15.93 | 1.61 | 13.10 | 19.37 | 1863 | 1.01 | ||
| Model fit: | Estimate | Est.Error | l-95% CI | u-95% CI | ||||
| BayesR2 | 0.89 | 0.01 | 0.87 | 0.90 | ||||
| Family: | beta | |||||||
| Links: | mu = logit; phi = identity | |||||||
| Formula: | Accuracy ~ IsMusician * (IsNonIsomorphic * IsBosanquet + LayoutNo * PerfNo) + (IsNonIsomorphic + LayoutNo * PerfNo | ID) | |||||||
| Data: | PitchLayoutsDataTask1 (Number of observations: 230) | |||||||
| Samples: | 4 chains, each with iter = 4000; warmup = 2000; thin = 1; total post-warmup samples = 8000 | |||||||
| Group-Level Effects: | ||||||||
| ID (Number of Levels: 65) | Estimate | Est.Error | l-95% CI | u-95% CI | Eff.Sample | Rhat | ||
| sd(Intercept) | 1.14 | 0.14 | 0.89 | 1.44 | 1709 | 1.00 | ||
| sd(IsNonIsomorphic) | 0.53 | 0.33 | 0.02 | 1.08 | 216 | 1.02 | ||
| sd(LayoutNo) | 0.66 | 0.31 | 0.04 | 1.14 | 243 | 1.01 | ||
| sd(PerfNo) | 0.18 | 0.12 | 0.01 | 0.46 | 1154 | 1.01 | ||
| sd(LayoutNo:PerfNo) | 0.23 | 0.17 | 0.01 | 0.62 | 687 | 1.01 | ||
| cor(Intercept,IsNonIsomorphic) | −0.18 | 0.31 | −0.65 | 0.57 | 831 | 1.00 | ||
| cor(Intercept,LayoutNo) | −0.49 | 0.25 | −0.82 | 0.24 | 989 | 1.00 | ||
| cor(IsNonIsomorphic,LayoutNo) | 0.02 | 0.33 | −0.64 | 0.68 | 1054 | 1.00 | ||
| cor(Intercept,PerfNo) | −0.28 | 0.35 | −0.83 | 0.50 | 5662 | 1.00 | ||
| cor(IsNonIsomorphic,PerfNo) | 0.11 | 0.38 | −0.66 | 0.78 | 3327 | 1.00 | ||
| cor(LayoutNo,PerfNo) | 0.09 | 0.37 | −0.66 | 0.77 | 5364 | 1.00 | ||
| cor(Intercept,LayoutNo:PerfNo) | −0.01 | 0.36 | −0.71 | 0.68 | 6300 | 1.00 | ||
| cor(IsNonIsomorphic,LayoutNo:PerfNo) | 0.11 | 0.38 | −0.65 | 0.78 | 3576 | 1.00 | ||
| cor(LayoutNo,LayoutNo:PerfNo) | −0.09 | 0.39 | −0.77 | 0.69 | 2559 | 1.00 | ||
| cor(PerfNo,LayoutNo:PerfNo) | −0.12 | 0.41 | −0.81 | 0.69 | 2321 | 1.00 | ||
| Population-Level Effects: | Estimate | Est.Error | l-95% CI | u-95% CI | Eff.Sample | Rhat | Eff.Fact | |
| Intercept | −0.88 | 0.26 | −1.40 | −0.36 | 1525 | 1.00 | 0.41 | |
| IsMusician | 1.26 | 0.41 | 0.45 | 2.06 | 2076 | 1.00 | 3.53 | |
| IsNonIsomorphic | −0.21 | 0.25 | −0.71 | 0.30 | 3468 | 1.00 | 0.81 | |
| IsBosanquet | 0.24 | 0.36 | −0.45 | 0.95 | 1907 | 1.00 | 1.27 | |
| LayoutNo | 0.96 | 0.21 | 0.54 | 1.36 | 3205 | 1.00 | 2.61 | |
| PerfNo | −0.01 | 0.13 | −0.27 | 0.25 | 5080 | 1.00 | 0.99 | |
| IsNonIsomorphic:IsBosanquet | 0.47 | 0.38 | −0.28 | 1.19 | 3035 | 1.00 | 1.60 | |
| LayoutNo:PerfNo | 0.04 | 0.17 | −0.29 | 0.37 | 4957 | 1.00 | 1.04 | |
| IsMusician:IsNonIsomorphic | 0.02 | 0.37 | −0.72 | 0.74 | 3497 | 1.00 | 1.02 | |
| IsMusician:IsBosanquet | −0.38 | 0.54 | −1.44 | 0.67 | 2127 | 1.00 | 0.68 | |
| IsMusician:LayoutNo | −0.07 | 0.31 | −0.66 | 0.55 | 3291 | 1.00 | 0.93 | |
| IsMusician:PerfNo | 0.66 | 0.19 | 0.29 | 1.04 | 4882 | 1.00 | 1.93 | |
| IsMusician:IsNonIsomorphic:IsBosanquet | 0.00 | 0.54 | −1.06 | 1.08 | 3060 | 1.00 | 1.00 | |
| IsMusician:LayoutNo:PerfNo | −0.41 | 0.26 | −0.94 | 0.09 | 5254 | 1.00 | 0.66 | |
| Family Specific Parameters: | Estimate | Est.Error | l-95% CI | u-95% CI | Eff.Sample | Rhat | ||
| phi | 25.62 | 5.21 | 18.05 | 37.59 | 694 | 1.01 | ||
| Model fit: | Estimate | Est.Error | l-95% CI | u-95% CI | ||||
| BayesR2 | 0.89 | 0.02 | 0.85 | 0.93 | ||||
| Family: | beta | |||||||
| Links: | mu = logit; phi = identity | |||||||
| Formula: | Accuracy ~ IsMusician * (IsNonIsomorphic * IsBosanquet + LayoutNo * PerfNo) + (IsNonIsomorphic + LayoutNo * PerfNo | ID) | |||||||
| Data: | PitchLayoutsDataTask2 (Number of observations: 393) | |||||||
| Samples: | 4 chains, each with iter = 4000; warmup = 2000; thin = 1; total post-warmup samples = 8000 | |||||||
| Group-Level Effects: | ||||||||
| ID (Number of levels: 67) | Estimate | Est.Error | l-95% CI | u-95% CI | Eff.Sample | Rhat | ||
| sd(Intercept) | 1.32 | 0.15 | 1.05 | 1.65 | 2481 | 1.00 | ||
| sd(IsNonIsomorphic) | 0.43 | 0.31 | 0.02 | 1.04 | 195 | 1.03 | ||
| sd(LayoutNo) | 0.86 | 0.29 | 0.17 | 1.31 | 243 | 1.02 | ||
| sd(PerfNo) | 0.09 | 0.07 | 0.00 | 0.25 | 2316 | 1.00 | ||
| sd(LayoutNo:PerfNo) | 0.50 | 0.09 | 0.35 | 0.70 | 1631 | 1.00 | ||
| cor(Intercept,IsNonIsomorphic) | −0.00 | 0.33 | −0.57 | 0.70 | 1200 | 1.00 | ||
| cor(Intercept,LayoutNo) | −0.18 | 0.23 | −0.53 | 0.43 | 649 | 1.01 | ||
| cor(IsNonIsomorphic,LayoutNo) | −0.25 | 0.32 | −0.80 | 0.47 | 708 | 1.00 | ||
| cor(Intercept,PerfNo) | 0.05 | 0.37 | −0.66 | 0.74 | 9924 | 1.00 | ||
| cor(IsNonIsomorphic,PerfNo) | −0.03 | 0.41 | −0.77 | 0.73 | 4734 | 1.00 | ||
| cor(LayoutNo,PerfNo) | 0.13 | 0.40 | −0.69 | 0.79 | 5507 | 1.00 | ||
| cor(Intercept,LayoutNo:PerfNo) | −0.06 | 0.19 | −0.44 | 0.31 | 1530 | 1.00 | ||
| cor(IsNonIsomorphic,LayoutNo:PerfNo) | 0.20 | 0.34 | −0.56 | 0.78 | 718 | 1.01 | ||
| cor(LayoutNo,LayoutNo:PerfNo) | −0.47 | 0.22 | −0.83 | 0.05 | 1047 | 1.00 | ||
| cor(PerfNo,LayoutNo:PerfNo) | −0.25 | 0.39 | −0.84 | 0.60 | 979 | 1.00 | ||
| Population-Level Effects: | Estimate | Est.Error | l-95% CI | u-95% CI | Eff.Sample | Rhat | Eff.Fact | |
| Intercept | −3.96 | 0.32 | −4.59 | −3.35 | 2230 | 1.00 | 0.02 | |
| IsMusician | 1.92 | 0.49 | 0.97 | 2.91 | 1895 | 1.00 | 6.82 | |
| IsNonIsomorphic | 0.27 | 0.24 | −0.22 | 0.74 | 3960 | 1.00 | 1.31 | |
| IsBosanquet | −0.23 | 0.44 | −1.10 | 0.62 | 2127 | 1.00 | 0.79 | |
| LayoutNo | 0.69 | 0.23 | 0.22 | 1.14 | 4098 | 1.00 | 1.99 | |
| PerfNo | 0.29 | 0.09 | 0.10 | 0.47 | 5072 | 1.00 | 1.34 | |
| IsNonIsomorphic:IsBosanquet | 0.40 | 0.38 | −0.33 | 1.14 | 3215 | 1.00 | 1.49 | |
| LayoutNo:PerfNo | 0.08 | 0.15 | −0.20 | 0.37 | 4216 | 1.00 | 1.08 | |
| IsMusician:IsNonIsomorphic | −0.03 | 0.36 | −0.74 | 0.67 | 3769 | 1.00 | 0.97 | |
| IsMusician:IsBosanquet | 0.92 | 0.69 | −0.45 | 2.29 | 2000 | 1.00 | 2.51 | |
| IsMusician:LayoutNo | 0.41 | 0.33 | −0.25 | 1.06 | 3571 | 1.00 | 1.51 | |
| IsMusician:PerfNo | 0.24 | 0.12 | 0.01 | 0.48 | 5147 | 1.00 | 1.27 | |
| IsMusician:IsNonIsomorphic:IsBosanquet | 0.18 | 0.54 | −0.87 | 1.25 | 3166 | 1.00 | 1.20 | |
| IsMusician:LayoutNo:PerfNo | −0.21 | 0.21 | −0.61 | 0.21 | 4207 | 1.00 | 0.81 | |
| Family Specific Parameters: | Estimate | Est.Error | l-95% CI | u-95% CI | Eff.Sample | Rhat | ||
| phi | 23.37 | 2.65 | 18.61 | 28.91 | 2732 | 1.00 | ||
| Model fit: | Estimate | Est.Error | l-95% CI | u-95% CI | ||||
| BayesR2 | 0.95 | 0.01 | 0.93 | 0.96 | ||||
| Family: | beta | |||||||
| Links: | mu = logit; phi = identity | |||||||
| Formula: | Accuracy ~ IsMusician * (IsNonIsomorphic * IsBosanquet + LayoutNo * PerfNo) + (IsNonIsomorphic + LayoutNo + PerfNo | ID) | |||||||
| Data: | PitchLayoutsDataTask3 (Number of observations: 258) | |||||||
| Samples: | 4 chains, each with iter = 4000; warmup = 2000; thin = 1; total post-warmup samples = 8000 | |||||||
| Group-Level Effects: | ||||||||
| ID (Number of levels: 66) | Estimate | Est.Error | l-95% CI | u-95% CI | Eff.Sample | Rhat | ||
| sd(Intercept) | 0.80 | 0.10 | 0.63 | 1.01 | 2676 | 1.00 | ||
| sd(IsNonIsomorphic) | 0.55 | 0.14 | 0.15 | 0.77 | 401 | 1.01 | ||
| sd(LayoutNo) | 0.21 | 0.17 | 0.01 | 0.61 | 347 | 1.01 | ||
| sd(PerfNo) | 0.50 | 0.08 | 0.36 | 0.67 | 2796 | 1.00 | ||
| cor(Intercept,IsNonIsomorphic) | −0.06 | 0.21 | −0.43 | 0.42 | 1892 | 1.00 | ||
| cor(Intercept,LayoutNo) | −0.20 | 0.38 | −0.82 | 0.67 | 4250 | 1.00 | ||
| cor(IsNonIsomorphic,LayoutNo) | 0.13 | 0.37 | −0.68 | 0.80 | 5372 | 1.00 | ||
| cor(Intercept,PerfNo) | 0.21 | 0.18 | −0.14 | 0.56 | 3269 | 1.00 | ||
| cor(IsNonIsomorphic,PerfNo) | −0.38 | 0.21 | −0.77 | 0.06 | 1433 | 1.00 | ||
| cor(LayoutNo,PerfNo) | 0.01 | 0.40 | −0.76 | 0.77 | 576 | 1.00 | ||
| Population-Level Effects: | Estimate | Est.Error | l-95% CI | u-95% CI | Eff.Sample | Rhat | Eff.Fact | |
| Intercept | −1.73 | 0.20 | −2.12 | −1.35 | 3321 | 1.00 | 0.18 | |
| IsMusician | 1.71 | 0.31 | 1.10 | 2.33 | 3244 | 1.00 | 5.53 | |
| IsNonIsomorphic | 0.06 | 0.16 | −0.26 | 0.36 | 5171 | 1.00 | 1.06 | |
| IsBosanquet | −0.30 | 0.28 | −0.84 | 0.24 | 3427 | 1.00 | 0.74 | |
| LayoutNo | 0.44 | 0.13 | 0.18 | 0.71 | 6494 | 1.00 | 1.55 | |
| PerfNo | −0.07 | 0.13 | −0.33 | 0.18 | 6423 | 1.00 | 0.93 | |
| IsNonIsomorphic:IsBosanquet | 0.39 | 0.24 | −0.07 | 0.86 | 5406 | 1.00 | 1.48 | |
| LayoutNo:PerfNo | −0.16 | 0.14 | −0.43 | 0.10 | 7867 | 1.00 | 0.85 | |
| IsMusician:IsNonIsomorphic | −0.61 | 0.25 | −1.12 | −0.11 | 5376 | 1.00 | 0.54 | |
| IsMusician:IsBosanquet | −0.06 | 0.43 | −0.91 | 0.79 | 3027 | 1.00 | 0.94 | |
| IsMusician:LayoutNo | 0.17 | 0.21 | −0.24 | 0.57 | 5870 | 1.00 | 1.19 | |
| IsMusician:PerfNo | 0.37 | 0.20 | −0.01 | 0.75 | 6526 | 1.00 | 1.45 | |
| IsMusician:IsNonIsomorphic:IsBosanquet | 0.84 | 0.36 | 0.13 | 1.54 | 5611 | 1.00 | 2.32 | |
| IsMusician:LayoutNo:PerfNo | 0.46 | 0.20 | 0.07 | 0.87 | 7973 | 1.00 | 1.58 | |
| Family Specific Parameters: | Estimate | Est.Error | l-95% CI | u-95% CI | Eff.Sample | Rhat | ||
| phi | 39.56 | 6.38 | 28.30 | 53.03 | 1467 | 1.00 | ||
| Model fit: | Estimate | Est.Error | l-95% CI | u-95% CI | ||||
| BayesR2 | 0.94 | 0.01 | 0.92 | 0.96 | ||||
| Family: | beta | |||||||
| Links: | mu = logit; phi = identity | |||||||
| Formula: | Accuracy ~ IsMusician * (IsNonIsomorphic * IsBosanquet + LayoutNo * PerfNo) + (IsNonIsomorphic + LayoutNo * PerfNo | ID) | |||||||
| Data: | PitchLayoutsDataTask4 (Number of observations: 472) | |||||||
| Samples: | 4 chains, each with iter = 4000; warmup = 2000; thin = 1; total post-warmup samples = 8000 | |||||||
| Group-Level Effects: | ||||||||
| ID (Number of levels: 67) | Estimate | Est.Error | l-95% CI | u-95% CI | Eff.Sample | Rhat | ||
| sd(Intercept) | 0.87 | 0.10 | 0.69 | 1.07 | 3694 | 1.00 | ||
| sd(IsNonIsomorphic) | 0.20 | 0.12 | 0.01 | 0.43 | 635 | 1.01 | ||
| sd(IsUntrained) | 0.47 | 0.08 | 0.33 | 0.63 | 2538 | 1.00 | ||
| sd(LayoutNo) | 0.15 | 0.09 | 0.01 | 0.34 | 866 | 1.00 | ||
| sd(PerfNo) | 0.06 | 0.04 | 0.00 | 0.15 | 1290 | 1.00 | ||
| sd(IsNonIsomorphic:IsUntrained) | 0.47 | 0.14 | 0.17 | 0.74 | 908 | 1.00 | ||
| sd(LayoutNo:PerfNo) | 0.13 | 0.05 | 0.02 | 0.22 | 1126 | 1.00 | ||
| cor(Intercept,IsNonIsomorphic) | 0.00 | 0.27 | −0.51 | 0.56 | 7607 | 1.00 | ||
| cor(Intercept,IsUntrained) | −0.27 | 0.16 | −0.56 | 0.05 | 5732 | 1.00 | ||
| cor(IsNonIsomorphic,IsUntrained) | 0.08 | 0.29 | −0.53 | 0.59 | 1183 | 1.00 | ||
| cor(Intercept,LayoutNo) | −0.25 | 0.31 | −0.75 | 0.45 | 3873 | 1.00 | ||
| cor(IsNonIsomorphic,LayoutNo) | 0.06 | 0.34 | −0.61 | 0.69 | 3639 | 1.00 | ||
| cor(IsUntrained,LayoutNo) | 0.17 | 0.31 | −0.48 | 0.72 | 6179 | 1.00 | ||
| cor(Intercept,PerfNo) | 0.15 | 0.31 | −0.50 | 0.70 | 8226 | 1.00 | ||
| cor(IsNonIsomorphic,PerfNo) | 0.13 | 0.34 | −0.58 | 0.73 | 3640 | 1.00 | ||
| cor(IsUntrained,PerfNo) | −0.04 | 0.32 | −0.63 | 0.60 | 6247 | 1.00 | ||
| cor(LayoutNo,PerfNo) | 0.19 | 0.36 | −0.55 | 0.79 | 1933 | 1.00 | ||
| cor(Intercept,IsNonIsomorphic:IsUntrained) | 0.03 | 0.20 | −0.37 | 0.40 | 4819 | 1.00 | ||
| cor(IsNonIsomorphic,IsNonIsomorphic:IsUntrained) | −0.42 | 0.33 | −0.87 | 0.40 | 834 | 1.00 | ||
| cor(IsUntrained,IsNonIsomorphic:IsUntrained) | −0.47 | 0.20 | −0.78 | 0.01 | 2176 | 1.00 | ||
| cor(LayoutNo,IsNonIsomorphic:IsUntrained) | −0.13 | 0.32 | −0.71 | 0.53 | 2279 | 1.00 | ||
| cor(PerfNo,IsNonIsomorphic:IsUntrained) | −0.12 | 0.32 | −0.70 | 0.53 | 2183 | 1.00 | ||
| cor(Intercept,LayoutNo:PerfNo) | −0.23 | 0.24 | −0.66 | 0.27 | 5751 | 1.00 | ||
| cor(IsNonIsomorphic,LayoutNo:PerfNo) | −0.10 | 0.31 | −0.67 | 0.52 | 1690 | 1.00 | ||
| cor(IsUntrained,LayoutNo:PerfNo) | −0.00 | 0.26 | −0.52 | 0.50 | 4117 | 1.00 | ||
| cor(LayoutNo,LayoutNo:PerfNo) | 0.07 | 0.33 | −0.58 | 0.69 | 1602 | 1.00 | ||
| cor(PerfNo,LayoutNo:PerfNo) | −0.06 | 0.34 | −0.67 | 0.61 | 2378 | 1.00 | ||
| cor(IsNonIsomorphic:IsUntrained,LayoutNo:PerfNo) | 0.10 | 0.27 | −0.43 | 0.61 | 3710 | 1.00 | ||
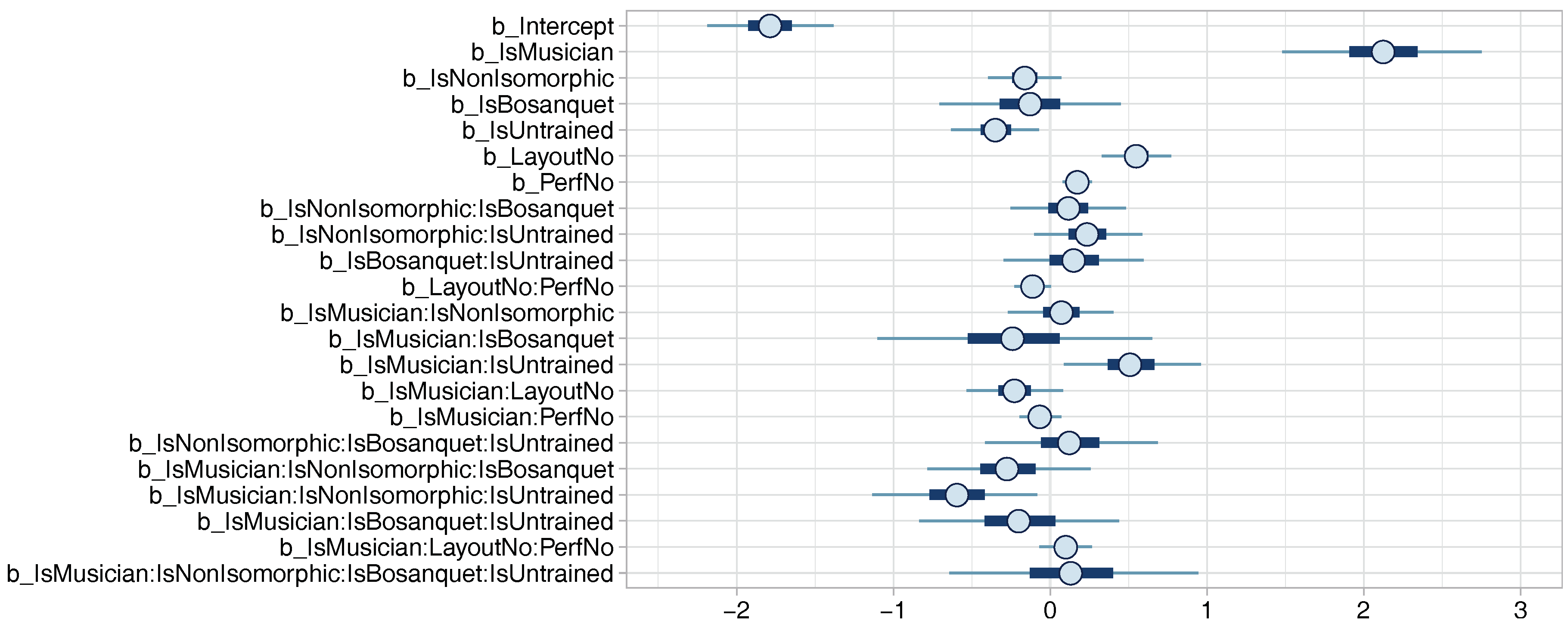
| Population-Level Effects: | Estimate | Est.Error | l-95% CI | u-95% CI | Eff.Sample | Rhat | Eff.Fact | |
| Intercept | −1.79 | 0.20 | −2.19 | −1.38 | 1703 | 1.00 | 0.17 | |
| IsMusician | 2.12 | 0.32 | 1.48 | 2.75 | 2006 | 1.00 | 8.33 | |
| IsNonIsomorphic | −0.16 | 0.12 | −0.40 | 0.07 | 3349 | 1.00 | 0.85 | |
| IsBosanquet | −0.13 | 0.29 | −0.71 | 0.45 | 2037 | 1.00 | 0.88 | |
| IsUntrained | −0.35 | 0.14 | −0.63 | −0.07 | 3204 | 1.00 | 0.70 | |
| LayoutNo | 0.55 | 0.11 | 0.33 | 0.77 | 4136 | 1.00 | 1.73 | |
| PerfNo | 0.17 | 0.05 | 0.08 | 0.26 | 4276 | 1.00 | 1.19 | |
| IsNonIsomorphic:IsBosanquet | 0.11 | 0.19 | −0.25 | 0.48 | 3347 | 1.00 | 1.12 | |
| IsNonIsomorphic:IsUntrained | 0.24 | 0.18 | −0.10 | 0.59 | 3176 | 1.00 | 1.27 | |
| IsBosanquet:IsUntrained | 0.15 | 0.23 | −0.30 | 0.60 | 2980 | 1.00 | 1.16 | |
| LayoutNo:PerfNo | −0.11 | 0.06 | −0.23 | 0.00 | 3994 | 1.00 | 0.90 | |
| IsMusician:IsNonIsomorphic | 0.07 | 0.17 | −0.27 | 0.40 | 3187 | 1.00 | 1.07 | |
| IsMusician:IsBosanquet | −0.24 | 0.44 | −1.10 | 0.65 | 2145 | 1.00 | 0.79 | |
| IsMusician:IsUntrained | 0.51 | 0.22 | 0.09 | 0.96 | 3361 | 1.00 | 1.67 | |
| IsMusician:LayoutNo | −0.23 | 0.16 | −0.53 | 0.08 | 4164 | 1.00 | 0.79 | |
| IsMusician:PerfNo | −0.07 | 0.07 | −0.20 | 0.07 | 4143 | 1.00 | 0.93 | |
| IsNonIsomorphic:IsBosanquet:IsUntrained | 0.13 | 0.28 | −0.42 | 0.69 | 3051 | 1.00 | 1.14 | |
| IsMusician:IsNonIsomorphic:IsBosanquet | −0.27 | 0.26 | −0.78 | 0.26 | 3335 | 1.00 | 0.76 | |
| IsMusician:IsNonIsomorphic:IsUntrained | −0.60 | 0.27 | −1.13 | −0.08 | 3400 | 1.00 | 0.55 | |
| IsMusician:IsBosanquet:IsUntrained | −0.20 | 0.33 | −0.84 | 0.44 | 3277 | 1.00 | 0.82 | |
| IsMusician:LayoutNo:PerfNo | 0.10 | 0.09 | −0.07 | 0.27 | 4239 | 1.00 | 1.11 | |
| IsMusician:IsNonIsomorphic:IsBosanquet:IsUntrained | 0.14 | 0.40 | −0.64 | 0.94 | 3010 | 1.00 | 1.15 | |
| Family Specific Parameters: | Estimate | Est.Error | l-95% CI | u-95% CI | Eff.Sample | Rhat | ||
| phi | 42.62 | 4.33 | 34.55 | 51.55 | 1635 | 1.00 | ||
| Model fit: | Estimate | Est.Error | l-95% CI | u-95% CI | ||||
| BayesR2 | 0.94 | 0.01 | 0.93 | 0.95 | ||||
Appendix B. Confirmatory Model Summaries
| Family: | beta | |||||||
| Links: | mu = logit; phi = identity | |||||||
| Formula: | Accuracy ~ IsNonIsomorphic * IsUntrained + IsBosanquet + LayoutNo * PerfNo + IsMusician + (IsNonIsomorphic * IsUntrained + LayoutNo * PerfNo | ID) | |||||||
| Data: | PitchLayoutsDataTask4 (Number of observations: 472) | |||||||
| Samples: | 4 chains, each with iter = 4000; warmup = 2000; thin = 1; total post-warmup samples = 8000 | |||||||
| Group-Level Effects: | ||||||||
| ID (Number of levels: 66) | Estimate | Est.Error | l-95% CI | u-95% CI | Eff.Sample | Rhat | ||
| sd(Intercept) | 0.85 | 0.10 | 0.68 | 1.06 | 2450 | 1.00 | ||
| sd(IsNonIsomorphic) | 0.18 | 0.11 | 0.01 | 0.40 | 619 | 1.00 | ||
| sd(IsUntrained) | 0.50 | 0.08 | 0.36 | 0.65 | 2207 | 1.00 | ||
| sd(LayoutNo) | 0.18 | 0.10 | 0.01 | 0.37 | 615 | 1.00 | ||
| sd(PerfNo) | 0.08 | 0.04 | 0.00 | 0.17 | 804 | 1.01 | ||
| sd(IsNonIsomorphic:IsUntrained) | 0.51 | 0.13 | 0.25 | 0.75 | 867 | 1.00 | ||
| sd(LayoutNo:PerfNo) | 0.12 | 0.05 | 0.02 | 0.21 | 851 | 1.00 | ||
| cor(Intercept,IsNonIsomorphic) | 0.05 | 0.29 | −0.51 | 0.62 | 4894 | 1.00 | ||
| cor(Intercept,IsUntrained) | −0.28 | 0.16 | −0.56 | 0.06 | 3004 | 1.00 | ||
| cor(IsNonIsomorphic,IsUntrained) | 0.03 | 0.30 | −0.57 | 0.61 | 680 | 1.01 | ||
| cor(Intercept,LayoutNo) | −0.28 | 0.28 | −0.73 | 0.38 | 3007 | 1.00 | ||
| cor(IsNonIsomorphic,LayoutNo) | 0.04 | 0.33 | −0.61 | 0.65 | 2150 | 1.00 | ||
| cor(IsUntrained,LayoutNo) | 0.12 | 0.29 | −0.47 | 0.65 | 4789 | 1.00 | ||
| cor(Intercept,PerfNo) | 0.21 | 0.29 | −0.38 | 0.72 | 4566 | 1.00 | ||
| cor(IsNonIsomorphic,PerfNo) | 0.15 | 0.34 | −0.54 | 0.73 | 1524 | 1.00 | ||
| cor(IsUntrained,PerfNo) | −0.10 | 0.30 | −0.65 | 0.53 | 4385 | 1.00 | ||
| cor(LayoutNo,PerfNo) | 0.20 | 0.35 | −0.55 | 0.76 | 1144 | 1.00 | ||
| cor(Intercept,IsNonIsomorphic:IsUntrained) | 0.09 | 0.19 | −0.30 | 0.46 | 2864 | 1.00 | ||
| cor(IsNonIsomorphic,IsNonIsomorphic:IsUntrained) | −0.33 | 0.33 | −0.81 | 0.45 | 677 | 1.01 | ||
| cor(IsUntrained,IsNonIsomorphic:IsUntrained) | −0.54 | 0.17 | −0.80 | −0.14 | 1965 | 1.00 | ||
| cor(LayoutNo,IsNonIsomorphic:IsUntrained) | 0.01 | 0.30 | −0.60 | 0.57 | 1704 | 1.00 | ||
| cor(PerfNo,IsNonIsomorphic:IsUntrained) | −0.13 | 0.31 | −0.69 | 0.52 | 1426 | 1.00 | ||
| cor(Intercept,LayoutNo:PerfNo) | −0.23 | 0.24 | −0.66 | 0.27 | 4646 | 1.00 | ||
| cor(IsNonIsomorphic,LayoutNo:PerfNo) | −0.06 | 0.31 | −0.64 | 0.55 | 1899 | 1.00 | ||
| cor(IsUntrained,LayoutNo:PerfNo) | −0.04 | 0.26 | −0.54 | 0.50 | 4078 | 1.00 | ||
| cor(LayoutNo,LayoutNo:PerfNo) | 0.13 | 0.32 | −0.53 | 0.71 | 1288 | 1.00 | ||
| cor(PerfNo,LayoutNo:PerfNo) | −0.10 | 0.33 | −0.67 | 0.57 | 1898 | 1.00 | ||
| cor(IsNonIsomorphic:IsUntrained,LayoutNo:PerfNo) | 0.11 | 0.27 | −0.41 | 0.61 | 3204 | 1.00 | ||
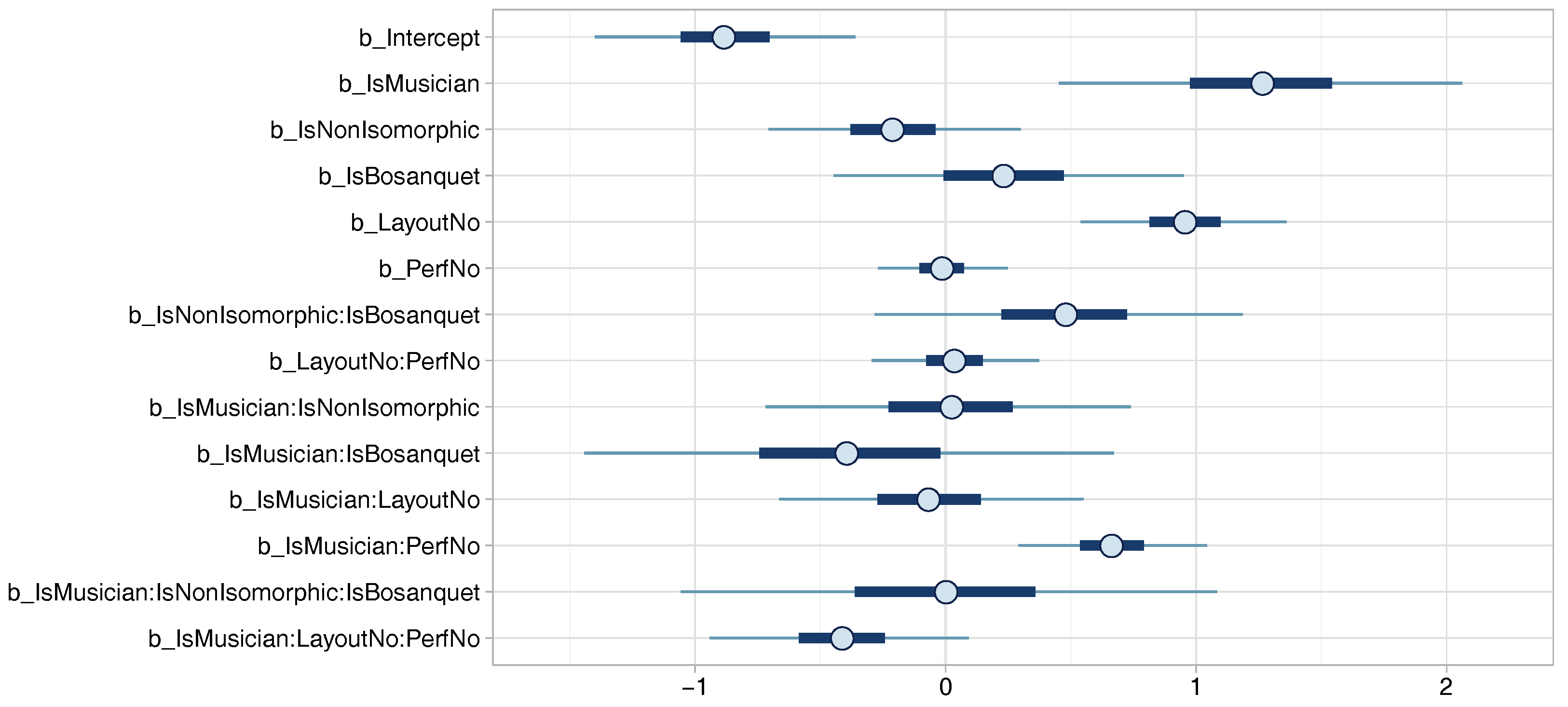
| Population-Level Effects: | Estimate | Est.Error | l-95% CI | u-95% CI | Eff.Sample | Rhat | Eff.Fact | |
| Intercept | −1.76 | 0.17 | −2.10 | −1.43 | 1742 | 1.00 | 0.17 | |
| IsNonIsomorphic | −0.13 | 0.07 | −0.26 | −0.00 | 4155 | 1.00 | 0.88 | |
| IsUntrained | −0.09 | 0.09 | −0.26 | 0.08 | 3182 | 1.00 | 0.91 | |
| IsBosanquet | −0.13 | 0.20 | −0.51 | 0.27 | 1745 | 1.00 | 0.88 | |
| LayoutNo | 0.43 | 0.08 | 0.28 | 0.58 | 4387 | 1.00 | 1.54 | |
| PerfNo | 0.13 | 0.04 | 0.06 | 0.20 | 3522 | 1.00 | 1.14 | |
| IsMusician | 1.98 | 0.22 | 1.54 | 2.39 | 1280 | 1.00 | 7.24 | |
| IsNonIsomorphic:IsUntrained | 0.02 | 0.10 | −0.19 | 0.22 | 4211 | 1.00 | 1.02 | |
| LayoutNo:PerfNo | −0.05 | 0.04 | −0.14 | 0.03 | 3909 | 1.00 | 0.95 | |
| Family Specific Parameters: | Estimate | Est.Error | l-95% CI | u-95% CI | Eff.Sample | Rhat | ||
| phi | 342.76 | 4.30 | 34.73 | 51.57 | 1381 | 1.00 | ||
| Model fit: | Estimate | Est.Error | l-95% CI | u-95% CI | ||||
| BayesR2 | 0.94 | 0.01 | 0.93 | 0.95 | ||||
| Hypothesis | Estimate | Est.Error | CI.Lower | CI.Upper | Evid.Ratio | Post.Prob | Star |
|---|---|---|---|---|---|---|---|
| IsNonIso (IsUnTra = 0) < 0 | −0.13 | 0.07 | −Inf | −0.02 | 39.00 | 0.98 | * |
| IsNonIso (IsUnTra = 1) < 0 | −0.11 | 0.09 | −Inf | 0.04 | 8.50 | 0.89 | |
| IsBos < 0 | −0.13 | 0.20 | −Inf | 0.20 | 2.96 | 0.75 | |
| LayoutNo > 0 | 0.43 | 0.08 | 0.30 | Inf | Inf | 1.00 | * |
| PerfNo > 0 | 0.13 | 0.04 | 0.08 | Inf | 2665.67 | 1.00 | * |
| IsMus > 0 | 1.98 | 0.22 | 1.62 | Inf | Inf | 1.00 | * |
| IsUntra < 0 | −0.09 | 0.09 | −Inf | 0.06 | 5.41 | 0.84 | |
| LayoutNo:PerfNo < 0 | −0.05 | 0.04 | −Inf | 0.02 | 8.03 | 0.89 |
References
- Rickard, N.S.; Appelman, P.; James, R.; Murphy, F.; Gill, A.; Bambrick, C. Orchestrating life skills: The effect of increased school-based music classes on children’s social competence and self-esteem. Int. J. Music Educ. 2013, 31, 292–309. [Google Scholar] [CrossRef]
- Costa-Giomi, E. Effects of three years of piano instruction on children’s academic achievement, school performance and self-esteem. Psychol. Music 2004, 32, 139–152. [Google Scholar] [CrossRef]
- North, A.C.; Hargreaves, D.J.; O’Neill, S.A. The importance of music to adolescents. Br. J. Educ. Psychol. 2000, 70, 255–272. [Google Scholar] [CrossRef] [PubMed]
- Tarrant, M.; North, A.C.; Hargreaves, D.J. Social categorization, self-esteem, and the estimated musical preferences of male adolescents. J. Soc. Psychol. 2001, 141, 565–581. [Google Scholar] [CrossRef] [PubMed]
- Hallam, S.; Creech, A.; Varvarigou, M.; McQueen, H. Perceived benefits of active engagement with making music in community settings. Int. J. Community Music 2012, 5, 155–174. [Google Scholar] [CrossRef]
- Oechslin, M.S.; Descloux, C.; Croquelois, A.; Chanal, J.; Van De Ville, D.; Lazeyras, F.; James, C.E. Hippocampal volume predicts fluid intelligence in musically trained people. Hippocampus 2013, 23, 552–558. [Google Scholar] [CrossRef] [PubMed]
- Schellenberg, E.G. Long-term positive associations between music lessons and IQ. J. Educ. Psychol. 2006, 98, 457–468. [Google Scholar] [CrossRef]
- Mansens, D.; Deeg, D.J.; Comijs, H.C. The association between singing and/or playing a musical instrument and cognitive functions in older adults. Aging Ment. Health 2017, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Seinfeld, S.; Figueroa, H.; Ortiz-Gil, J.; Sanchez-Vives, M.V. Effects of music learning and piano practice on cognitive function, mood and quality of life in older adults. Front. Psychol. 2013, 4, 1–13. [Google Scholar] [CrossRef]
- Paine, G.; Stevenson, I.; Pearce, A. The Thummer Mapping Project (ThuMP). In Proceedings of the 2007 Conference on New Interfaces for Musical Expression (NIME07), New York, NY, USA, 6–10 June 2007; pp. 70–77. [Google Scholar] [CrossRef]
- C-Thru Music. The AXiS-49 USB Music Interface. Available online: http://www.c-thru-music.com/cgi/?page=prod_axis-49 (accessed on 14 November 2018).
- Roger Linn Design. LinnStrument: A Revolutionary Expressive Musical Performance Controller. Available online: http://www.rogerlinndesign.com/linnstrument.html (accessed on 14 November 2018).
- ROLI. ROLI|BLOCKS. Available online: https://roli.com/products/blocks (accessed on 14 November 2017).
- Paine, G. Towards unified design guidelines for new interfaces for musical expression. Organ. Sound 2009, 14, 142–155. [Google Scholar] [CrossRef]
- MacRitchie, J.; Milne, A. Exploring the Effects of Pitch Layout on Learning a New Musical Instrument. Appl. Sci. 2017, 7, 1218. [Google Scholar] [CrossRef]
- Schmidt, R.A.; Lee, T.D. Motor Control and Learning. A Behavioural Emphasis; Human Kinetics: Champaign, IL, USA, 2011. [Google Scholar]
- Milne, A.J.; Sethares, W.A.; Plamondon, J. Tuning continua and keyboard layouts. J. Math. Music 2008, 2, 1–19. [Google Scholar] [CrossRef]
- Prechtl, A.; Milne, A.J.; Holland, S.; Laney, R.; Sharp, D.B. A MIDI sequencer that widens access to the compositional possibilities of novel tunings. Comput. Music J. 2012, 36, 42–54. [Google Scholar] [CrossRef]
- Milne, A.; Sethares, W.; Plamondon, J. Isomorphic controllers and dynamic tuning: Invariant fingering over a tuning continuum. Comput. Music J. 2007, 31, 15–32. [Google Scholar] [CrossRef]
- Wicki, K. Tastatur für Musikinstrumente. Switzerland Patent Nr. CH13329, 30 October 1896. [Google Scholar]
- Helmholtz, H.L.F. On the Sensations of Tone as a Physiological Basis for the Theory of Music; Dover: New York, NY, USA, 1877. [Google Scholar]
- Keislar, D. History and Principles of Microtonal Keyboards. Comput. Music J. 1987, 11, 18–28. [Google Scholar] [CrossRef]
- Array Instruments. The Array Mbira. Available online: http://www.arraymbira.com (accessed on 14 November 2018).
- Park, B.; Gerhard, D. Rainboard and Musix: Building dynamic isomorphic interfaces. In Proceedings of the International Conference on New Interfaces for Musical Expression, Daejeon, Korea, 27–30 May 2013; pp. 319–324. [Google Scholar]
- Terpstra, S.; Horvath, D. Terpstra Keyboard. Available online: http://terpstrakeyboard.com (accessed on 14 November 2017).
- Bosanquet, R.H.M. Elementary Treatise on Musical Intervals and Temperament; Macmillan: London, UK, 1877. [Google Scholar]
- Rusconi, E.; Kwana, B.; Giordano, B.L.; Umilta, C.; Butterworth, B. Spatial representation of pitch height: The SMARC effect. Cognition 2006, 99, 113–129. [Google Scholar] [CrossRef]
- Dehaene, S.; Bossini, S.; Giraux, P. The mental representation of parity and number magnitude. J. Exp. Psychol. Gener. 1993, 122, 371–396. [Google Scholar] [CrossRef]
- MacRitchie, J.; Milne, A.J. Evaluation of the learnability and playability of pitch layouts in new musical instruments. In Proceedings of the 14th Sound and Music Computing Conference, Espoo, Finland, 5–8 July 2017; Lokki, T., Pätynen, J., Välimäki, V., Eds.; Aalto University: Helsinki, Finland, 2017; pp. 450–457. [Google Scholar]
- Bürkner, P.C. brms: An R Package for Bayesian Multilevel Models Using Stan. J. Stat. Softw. 2017, 80, 1–28. [Google Scholar] [CrossRef]
- Bürkner, P.C. Advanced Bayesian Multilevel Modeling with the R Package brms. R J. 2018, 10, 395–411. [Google Scholar]
- Jayanthakumar, J.; Schubert, E.; de Graaf, D.L.E. NTPP (Note Time Playing Path) MIDI Performance Analyser (Version 0.1); Empirical Musicology Laboratory, University of New South Wales: Sydney, Australia.
- Verkuilen, M.S.J. A better lemon squeezer? Maximum-likelihood regression with beta-distributed dependent variables. Psychol. Methods 2006, 11, 54–71. [Google Scholar] [CrossRef]
- Barr, D.J.; Levy, R.; Scheepers, C.; Tilyc, H.J. Random effects structure for confirmatory hypothesis testing: Keep it maximal. J. Mem. Lang. 2013, 68, 255–278. [Google Scholar] [CrossRef] [PubMed]
- Kruschke, J.K.; Liddell, T.M. Bayesian data analysis for newcomers. Psychon. Bull. Rev. 2018, 25, 155–177. [Google Scholar] [CrossRef] [PubMed]
- Dienes, Z.; McLatchie, N. Four reasons to prefer Bayesian analyses over significance testing. Psychon. Bull. Rev. 2018, 25, 207–218. [Google Scholar] [CrossRef] [PubMed]
- Gelman, A.; Goodrich, B.; Gabry, J.; Ali, I. R-squared for Bayesian regression models. Available online: http://www.stat.columbia.edu/~gelman/research/unpublished/ (accessed on 14 November 2018).
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Dunson, D.B.; Vehtari, A.; Rubin, D.B. Bayesian Data Analysis, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]

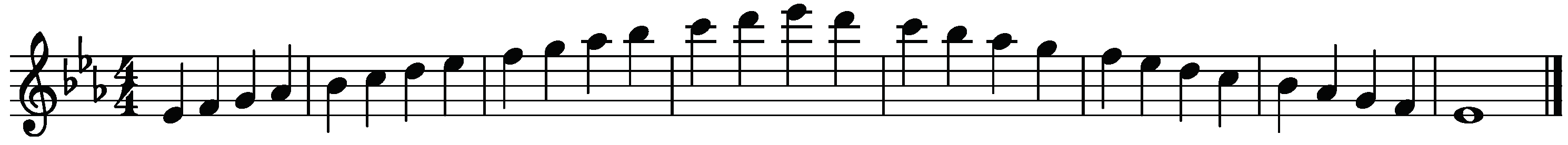
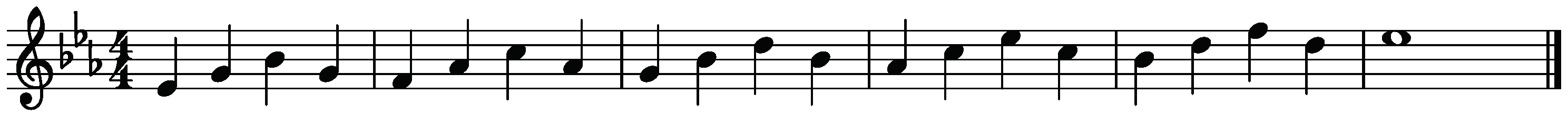
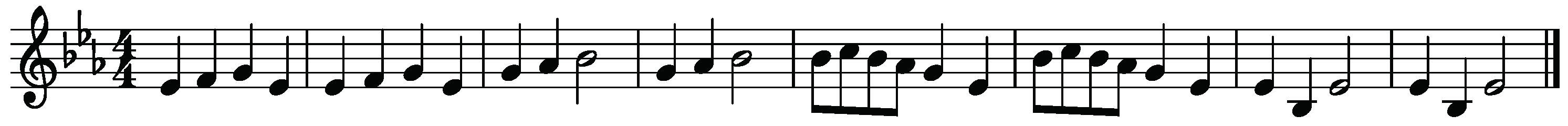
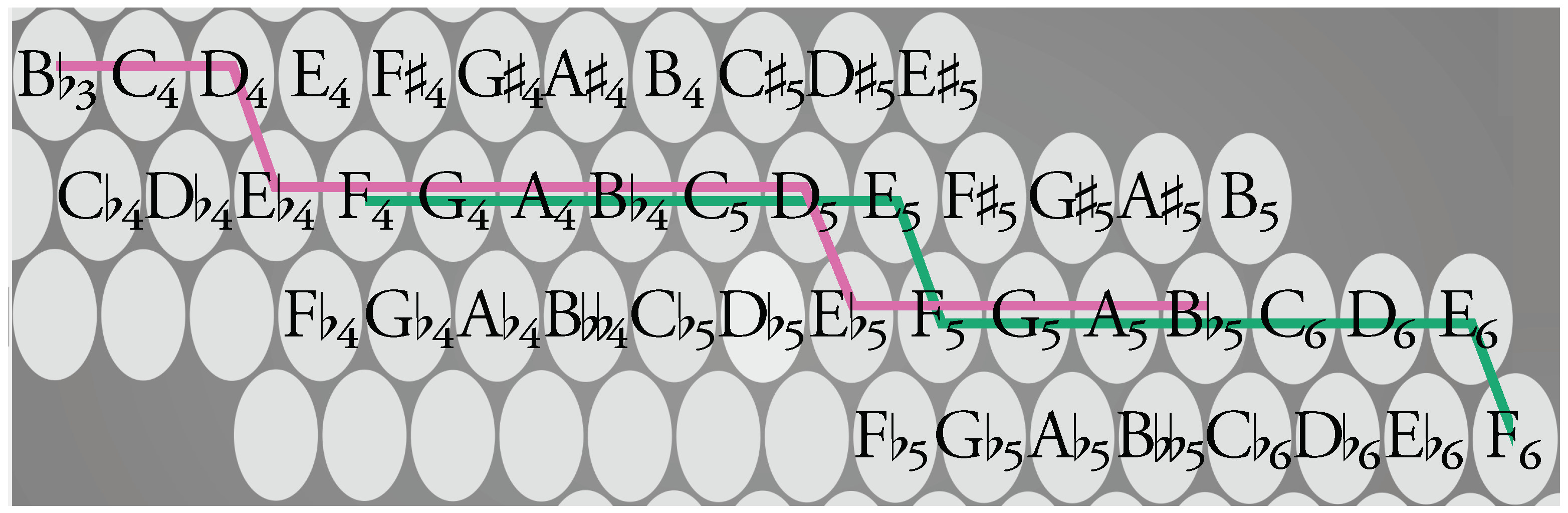


| Hypothesis | Estimate | Est.Error | CI.Lower | CI.Upper | Evid.Ratio | Post.Prob | Star |
|---|---|---|---|---|---|---|---|
| IsNonIso (IsMus = 0, IsBos = 0) < 0 | −0.25 | 0.18 | −Inf | 0.05 | 10.76 | 0.92 | |
| IsNonIso (IsMus = 0, IsBos = 1) > 0 | 0.53 | 0.22 | 0.18 | Inf | 155.86 | 0.99 | * |
| IsNonIso (IsMus = 1, IsBos = 0) < 0 | −0.41 | 0.23 | −Inf | −0.05 | 27.47 | 0.96 | * |
| IsNonIso (IsMus = 1, IsBos = 1) > 0 | 0.38 | 0.25 | −0.03 | Inf | 14.66 | 0.94 | |
| IsBos (IsMus = 0, IsNonIso = 0) > 0 | 0.88 | 0.46 | 0.11 | Inf | 30.87 | 0.97 | * |
| IsBos (IsMus = 0, IsNonIso = 1) > 0 | 1.66 | 0.42 | 0.96 | Inf | Inf | 1.00 | * |
| IsBos (IsMus = 1, IsNonIso = 0) > 0 | 0.09 | 0.56 | −0.81 | Inf | 1.27 | 0.56 | |
| IsBos (IsMus = 1, IsNonIso = 1) > 0 | 0.88 | 0.51 | 0.05 | Inf | 25.06 | 0.96 | * |
| IsMus (IsNonIso = 0, IsBos = 0) > 0 | 2.31 | 0.52 | 1.46 | Inf | 7999.00 | 1.00 | * |
| IsMus (IsNonIso = 0, IsBos = 1) > 0 | 2.15 | 0.49 | 1.35 | Inf | 7999.00 | 1.00 | * |
| IsMus (IsNonIso = 1, IsBos = 0) > 0 | 1.52 | 0.57 | 0.59 | Inf | 209.53 | 1.00 | * |
| IsMus (IsNonIso = 1, IsBos = 1) > 0 | 1.37 | 0.54 | 0.49 | Inf | 199.00 | 1.00 | * |
| LayoutNo (IsMus = 0) > 0 | 1.68 | 0.18 | 1.38 | Inf | Inf | 1.00 | * |
| LayoutNo (IsMus = 1) > 0 | 0.74 | 0.21 | 0.39 | Inf | 7999.00 | 1.00 | * |
| PerfNo (IsMus = 0) > 0 | 0.48 | 0.08 | 0.35 | Inf | Inf | 1.00 | * |
| PerfNo (IsMus = 1) > 0 | 0.30 | 0.08 | 0.16 | Inf | 3999.00 | 1.00 | * |
| LayoutNo:PerfNo (IsMus = 0) < 0 | −0.41 | 0.10 | −Inf | −0.25 | Inf | 1.00 | * |
| LayoutNo:PerfNo (IsMus = 1) < 0 | −0.11 | 0.11 | −Inf | 0.08 | 4.69 | 0.82 |
| Hypothesis | Estimate | Est.Error | CI.Lower | CI.Upper | Evid.Ratio | Post.Prob | Star |
|---|---|---|---|---|---|---|---|
| IsNonIso (IsMus = 0, IsBos = 0) < 0 | −0.21 | 0.25 | −Inf | 0.22 | 3.98 | 0.80 | |
| IsNonIso (IsMus = 0, IsBos = 1) > 0 | 0.27 | 0.28 | −0.21 | Inf | 4.70 | 0.82 | |
| IsNonIso (IsMus = 1, IsBos = 0) < 0 | −0.19 | 0.28 | −Inf | 0.27 | 3.11 | 0.76 | |
| IsNonIso (IsMus = 1, IsBos = 1) > 0 | 0.29 | 0.31 | −0.22 | Inf | 4.69 | 0.82 | |
| IsBos (IsMus = 0, IsNonIso = 0) > 0 | 0.24 | 0.36 | −0.35 | Inf | 2.92 | 0.74 | |
| IsBos (IsMus = 0, IsNonIso = 1) > 0 | 0.71 | 0.39 | 0.07 | Inf | 28.52 | 0.97 | * |
| IsBos (IsMus = 1, IsNonIso = 0) > 0 | −0.15 | 0.43 | −0.84 | Inf | 0.57 | 0.36 | |
| IsBos (IsMus = 1, IsNonIso = 1) > 0 | 0.33 | 0.44 | −0.39 | Inf | 3.47 | 0.78 | |
| IsMus (IsNonIso = 0, IsBos = 0) > 0 | 1.26 | 0.41 | 0.59 | Inf | 399.00 | 1.00 | * |
| IsMus (IsNonIso = 0, IsBos = 1) > 0 | 1.28 | 0.45 | 0.55 | Inf | 499.00 | 1.00 | * |
| IsMus (IsNonIso = 1, IsBos = 0) > 0 | 0.88 | 0.47 | 0.12 | Inf | 32.20 | 0.97 | * |
| IsMus (IsNonIso = 1, IsBos = 1) > 0 | 0.90 | 0.48 | 0.10 | Inf | 30.37 | 0.97 | * |
| LayoutNo (IsMus = 0) > 0 | 0.96 | 0.21 | 0.61 | Inf | Inf | 1.00 | * |
| LayoutNo (IsMus = 1) > 0 | 0.89 | 0.23 | 0.51 | Inf | 7999.00 | 1.00 | * |
| PerfNo (IsMus = 0) < 0 | −0.01 | 0.13 | −Inf | 0.20 | 1.18 | 0.54 | |
| PerfNo (IsMus = 1) > 0 | 0.65 | 0.14 | 0.42 | Inf | Inf | 1.00 | * |
| LayoutNo:PerfNo (IsMus = 0) > 0 | 0.04 | 0.17 | −0.24 | Inf | 1.39 | 0.58 | |
| LayoutNo:PerfNo (IsMus = 1) < 0 | −0.38 | 0.20 | −Inf | −0.05 | 32.47 | 0.97 | * |
| Hypothesis | Estimate | Est.Error | CI.Lower | CI.Upper | Evid.Ratio | Post.Prob | Star |
|---|---|---|---|---|---|---|---|
| IsNonIso (IsMus = 0, IsBos = 0) > 0 | 0.27 | 0.24 | −0.13 | Inf | 6.98 | 0.87 | |
| IsNonIso (IsMus = 0, IsBos = 1) > 0 | 0.68 | 0.29 | 0.20 | Inf | 99.00 | 0.99 | * |
| IsNonIso (IsMus = 1, IsBos = 0) > 0 | 0.24 | 0.28 | −0.21 | Inf | 4.25 | 0.81 | |
| IsNonIso (IsMus = 1, IsBos = 1) > 0 | 0.82 | 0.31 | 0.32 | Inf | 204.13 | 1.00 | * |
| IsBos (IsMus = 0, IsNonIso = 0) < 0 | −0.23 | 0.44 | −Inf | 0.49 | 2.32 | 0.70 | |
| IsBos (IsMus = 0, IsNonIso = 1) > 0 | 0.17 | 0.47 | −0.60 | Inf | 1.83 | 0.65 | |
| IsBos (IsMus = 1, IsNonIso = 0) > 0 | 0.69 | 0.54 | −0.20 | Inf | 8.80 | 0.90 | |
| IsBos (IsMus = 1, IsNonIso = 1) > 0 | 1.26 | 0.56 | 0.36 | Inf | 83.21 | 0.99 | * |
| IsMus (IsNonIso = 0, IsBos = 0) > 0 | 1.92 | 0.49 | 1.13 | Inf | Inf | 1.00 | * |
| IsMus (IsNonIso = 0, IsBos = 1) > 0 | 1.89 | 0.52 | 1.06 | Inf | Inf | 1.00 | * |
| IsMus (IsNonIso = 1, IsBos = 0) > 0 | 2.84 | 0.55 | 1.93 | Inf | Inf | 1.00 | * |
| IsMus (IsNonIso = 1, IsBos = 1) > 0 | 2.98 | 0.57 | 2.02 | Inf | Inf | 1.00 | * |
| LayoutNo (IsMus = 0) > 0 | 0.69 | 0.23 | 0.30 | Inf | 570.43 | 1.00 | * |
| LayoutNo (IsMus = 1) > 0 | 1.09 | 0.25 | 0.68 | Inf | Inf | 1.00 | * |
| PerfNo (IsMus = 0) > 0 | 0.29 | 0.09 | 0.13 | Inf | 1332.33 | 1.00 | * |
| PerfNo (IsMus = 1) > 0 | 0.53 | 0.07 | 0.41 | Inf | Inf | 1.00 | * |
| LayoutNo:PerfNo (IsMus = 0) > 0 | 0.08 | 0.15 | −0.15 | Inf | 2.53 | 0.72 | |
| LayoutNo:PerfNo (IsMus = 1) < 0 | −0.12 | 0.15 | −Inf | 0.12 | 4.15 | 0.81 |
| Hypothesis | Estimate | Est.Error | CI.Lower | CI.Upper | Evid.Ratio | Post.Prob | Star |
|---|---|---|---|---|---|---|---|
| IsNonIso (IsMus = 0, IsBos = 0) > 0 | 0.06 | 0.16 | −0.20 | Inf | 1.87 | 0.65 | |
| IsNonIso (IsMus = 0, IsBos = 1) > 0 | 0.45 | 0.19 | 0.14 | Inf | 116.65 | 0.99 | * |
| IsNonIso (IsMus = 1, IsBos = 0) < 0 | −0.56 | 0.20 | −Inf | −0.23 | 295.30 | 1.00 | * |
| IsNonIso (IsMus = 1, IsBos = 1) > 0 | 0.67 | 0.21 | 0.33 | Inf | 2665.67 | 1.00 | * |
| IsBos (IsMus = 0, IsNonIso = 0) < 0 | −0.30 | 0.28 | −Inf | 0.16 | 5.97 | 0.86 | |
| IsBos (IsMus = 0, IsNonIso = 1) > 0 | 0.10 | 0.31 | −0.41 | Inf | 1.65 | 0.62 | |
| IsBos (IsMus = 1, IsNonIso = 0) < 0 | −0.36 | 0.34 | −Inf | 0.20 | 6.17 | 0.86 | |
| IsBos (IsMus = 1, IsNonIso = 1) > 0 | 0.87 | 0.40 | 0.21 | Inf | 58.26 | 0.98 | * |
| IsMus (IsNonIso = 0, IsBos = 0) > 0 | 1.71 | 0.31 | 1.21 | Inf | Inf | 1.00 | * |
| IsMus (IsNonIso = 0, IsBos = 1) > 0 | 1.10 | 0.35 | 0.52 | Inf | 1332.33 | 1.00 | * |
| IsMus (IsNonIso = 1, IsBos = 0) > 0 | 1.65 | 0.34 | 1.09 | Inf | Inf | 1.00 | * |
| IsMus (IsNonIso = 1, IsBos = 1) > 0 | 1.87 | 0.39 | 1.23 | Inf | Inf | 1.00 | * |
| LayoutNo (IsMus = 0) > 0 | 0.44 | 0.13 | 0.22 | Inf | 3999.00 | 1.00 | * |
| LayoutNo (IsMus = 1) > 0 | 0.61 | 0.16 | 0.36 | Inf | Inf | 1.00 | * |
| PerfNo (IsMus = 0) < 0 | −0.07 | 0.13 | −Inf | 0.14 | 2.44 | 0.71 | |
| PerfNo (IsMus = 1) > 0 | 0.29 | 0.15 | 0.06 | Inf | 47.78 | 0.98 | * |
| LayoutNo:PerfNo (IsMus = 0) < 0 | −0.16 | 0.14 | −Inf | 0.06 | 7.76 | 0.89 | |
| LayoutNo:PerfNo (IsMus = 1) > 0 | 0.30 | 0.15 | 0.05 | Inf | 40.03 | 0.98 | * |
| Hypothesis | Estimate | Est.Error | CI.Lower | CI.Upper | Evid.Ratio | Post.Prob | Star |
|---|---|---|---|---|---|---|---|
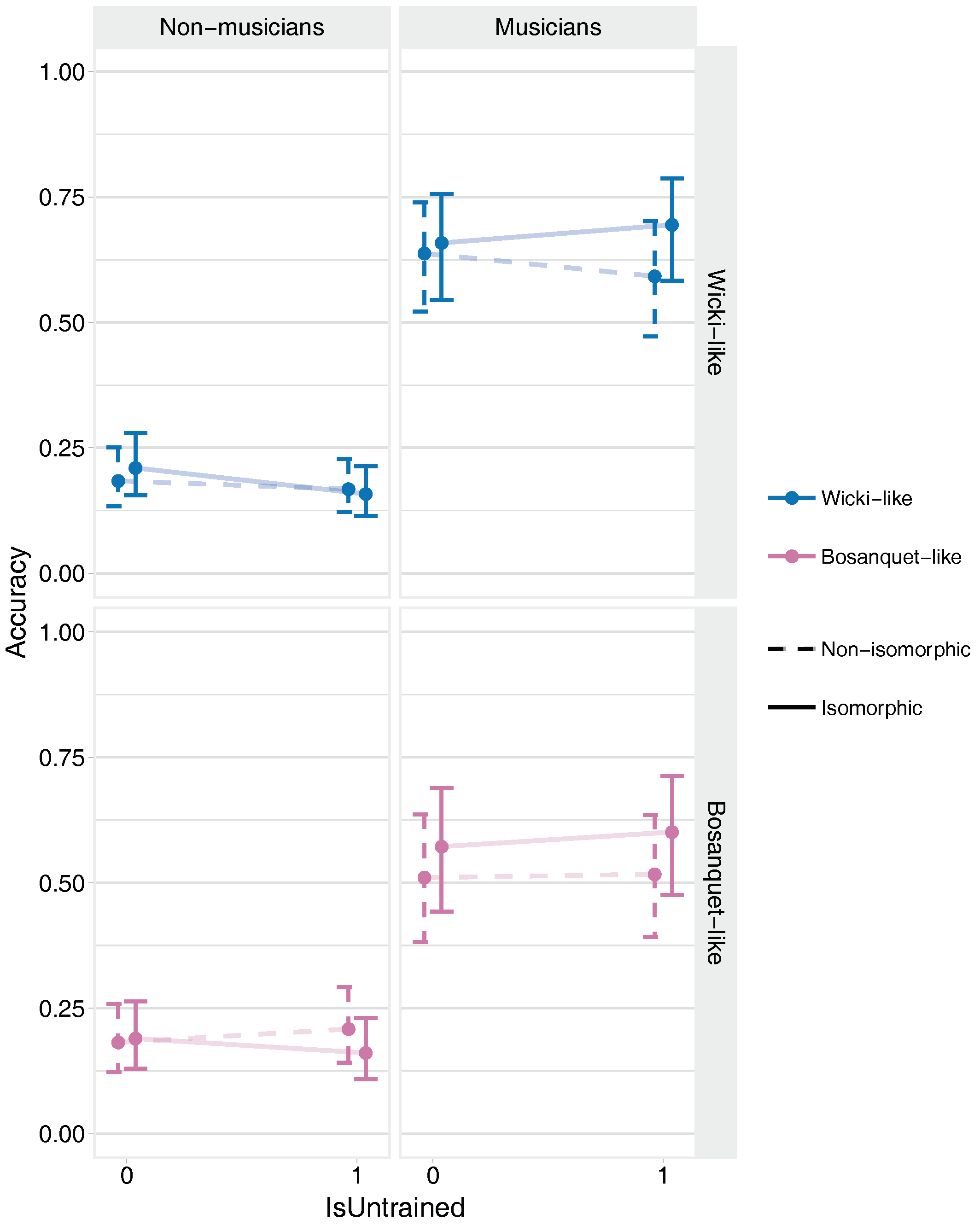
| IsNonIso (IsMus = 0, IsBos = 0, IsUnTra = 0) < 0 | −0.16 | 0.12 | −Inf | 0.03 | 10.61 | 0.91 | |
| IsNonIso (IsMus = 0, IsBos = 1, IsUnTra = 0) < 0 | −0.05 | 0.15 | −Inf | 0.19 | 1.70 | 0.63 | |
| IsNonIso (IsMus = 1, IsBos = 0, IsUnTra = 0) < 0 | −0.09 | 0.13 | −Inf | 0.11 | 3.18 | 0.76 | |
| IsNonIso (IsMus = 1, IsBos = 1, IsUnTra = 0) < 0 | −0.25 | 0.14 | −Inf | −0.01 | 23.10 | 0.96 | * |
| IsNonIso (IsMus = 0, IsBos = 0, IsUnTra = 1) > 0 | 0.08 | 0.14 | −0.16 | Inf | 2.36 | 0.70 | |
| IsNonIso (IsMus = 0, IsBos = 1, IsUnTra = 1) > 0 | 0.32 | 0.19 | 0.01 | Inf | 21.04 | 0.95 | * |
| IsNonIso (IsMus = 1, IsBos = 0, IsUnTra = 1) < 0 | −0.45 | 0.17 | −Inf | −0.17 | 209.53 | 1.00 | * |
| IsNonIso (IsMus = 1, IsBos = 1, IsUnTra = 1) < 0 | −0.34 | 0.18 | −Inf | −0.05 | 31.52 | 0.97 | * |
| IsBos (IsMus = 0, IsNonIso = 0, IsUnTra = 0) < 0 | −0.13 | 0.29 | −Inf | 0.35 | 2.07 | 0.67 | |
| IsBos (IsMus = 0, IsNonIso = 1, IsUnTra = 0) < 0 | −0.02 | 0.30 | −Inf | 0.48 | 1.08 | 0.52 | |
| IsBos (IsMus = 1, IsNonIso = 0, IsUnTra = 0) < 0 | −0.36 | 0.35 | −Inf | 0.20 | 5.76 | 0.85 | |
| IsBos (IsMus = 1, IsNonIso = 1, IsUnTra = 0) < 0 | −0.52 | 0.35 | −Inf | 0.06 | 13.39 | 0.93 | |
| IsBos (IsMus = 0, IsNonIso = 0, IsUnTra = 1) > 0 | 0.02 | 0.29 | −0.47 | Inf | 1.14 | 0.53 | |
| IsBos (IsMus = 0, IsNonIso = 1, IsUnTra = 1) > 0 | 0.26 | 0.30 | −0.24 | Inf | 4.33 | 0.81 | |
| IsBos (IsMus = 1, IsNonIso = 0, IsUnTra = 1) < 0 | −0.09 | 0.41 | −Inf | 0.59 | 1.39 | 0.58 | |
| IsBos (IsMus = 1, IsNonIso = 1, IsUnTra = 1) < 0 | −0.30 | 0.35 | −Inf | 0.27 | 4.24 | 0.81 | |
| IsMus (IsNonIso = 0, IsBos = 0, IsUnTra = 0) > 0 | 2.12 | 0.32 | 1.59 | Inf | Inf | 1.00 | * |
| IsMus (IsNonIso = 0, IsBos = 1, IsUnTra = 0) > 0 | 2.19 | 0.33 | 1.65 | Inf | Inf | 1.00 | * |
| IsMus (IsNonIso = 1, IsBos = 0, IsUnTra = 0) > 0 | 1.89 | 0.36 | 1.30 | Inf | Inf | 1.00 | * |
| IsMus (IsNonIso = 1, IsBos = 1, IsUnTra = 0) > 0 | 1.69 | 0.37 | 1.09 | Inf | Inf | 1.00 | * |
| IsMus (IsNonIso = 0, IsBos = 0, IsUnTra = 1) > 0 | 2.64 | 0.34 | 2.09 | Inf | Inf | 1.00 | * |
| IsMus (IsNonIso = 0, IsBos = 1, IsUnTra = 1) > 0 | 2.11 | 0.33 | 1.56 | Inf | Inf | 1.00 | * |
| IsMus (IsNonIso = 1, IsBos = 0, IsUnTra = 1) > 0 | 2.20 | 0.36 | 1.59 | Inf | Inf | 1.00 | * |
| IsMus (IsNonIso = 1, IsBos = 1, IsUnTra = 1) > 0 | 1.54 | 0.37 | 0.93 | Inf | Inf | 1.00 | * |
| LayoutNo (IsMus = 0) > 0 | 0.55 | 0.11 | 0.37 | Inf | Inf | 1.00 | * |
| LayoutNo (IsMus = 1) > 0 | 0.32 | 0.11 | 0.14 | Inf | 379.95 | 1.00 | * |
| PerfNo (IsMus = 0) > 0 | 0.17 | 0.05 | 0.09 | Inf | 7999.00 | 1.00 | * |
| PerfNo (IsMus = 1) > 0 | 0.11 | 0.05 | 0.03 | Inf | 70.43 | 0.99 | * |
| LayoutNo:PerfNo (IsMus = 0) < 0 | −0.11 | 0.06 | −Inf | −0.01 | 33.48 | 0.97 | * |
| LayoutNo:PerfNo (IsMus = 1) < 0 | −0.01 | 0.06 | −Inf | 0.09 | 1.42 | 0.59 |
| Layout Type | Number of Participants | ||
|---|---|---|---|
| Musicians | Non-Musicians | ||
| Isomorphic | Wicki-like | 9 | 12 |
| Bosanquet-like | 4 | 4 | |
| Non-isomorphic | Wicki-like | 0 | 2 |
| Bosanquet-like | 3 | 8 | |
| No preference | 8 | 8 | |
| No specification made | 1 | 7 | |
| Sub-Theme | Example Statement | Number of Statements | |
|---|---|---|---|
| Mus | Non-Mus | ||
| Layout structure | “I found it’s more structured as to the rows 4 and then 3 and 4 before you change into the next note.” (ID1). | 15 | 8 |
| Intuitiveness | “I felt like I could feel the notes better in this layout…Like the way my brain put together like playing the notes and the sounds—it felt easier to do in this layout basically.” (ID14). | 4 | 5 |
| Similarity to piano | “It was kind of like the piano, so it was easier to remember I guess because I could do it with my fingers in the same way as for scales.” (ID22). | 2 | 0 |
| Identifying reference note | “Well for the first one [Wicki-like non-isomorphic],…I couldn’t find the reference note. For the second one [Wicki-like isomorphic] it was easier to know where the C was I guess or whatever the tonic was.” (ID7). | 2 | 3 |
| Practice effects | “I think because I did it the first time, so the second time was like kinda the same thing but I had more practice. I guess I was more familiar with it by then.” (ID44). | 5 | 15 |
| Sub-Theme | Isomorphic | Non-Isomorphic | No Preference | ||
|---|---|---|---|---|---|
| Wicki-Like | Bosanquet-Like | Wicki-Like | Bosanquet-Like | ||
| Layout structure | 10 | 3 | 0 | 5 | 5 |
| Practice effects | 6 | 4 | 2 | 6 | 2 |
| Intuitiveness | 3 | 4 | 0 | 2 | 0 |
| Similarity to piano | 1 | 1 | 0 | 0 | 0 |
| Identifying reference note | 4 | 0 | 0 | 1 | 0 |
| Sub-Theme | Example Statement | Number of Statements |
|---|---|---|
| Layout structure | But just trying to figure out where all the notes were at, it was more of a challenge of making something work. Like where the intervals were.” (ID24). | 20 |
| Familiarity of interface | But umm for this sort of task and especially when it’s an interface that I’m not familiar with…because it’s so alien to me, it’s not as simple to pick up.” (ID15). | 8 |
| Pace of AV demonstration | I think sometimes the keys, with the highlighting, it flashed a little fast, like you’re trying to catch up with it.” (ID2). | 2 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stanford, S.; Milne, A.J.; MacRitchie, J. The Effect of Isomorphic Pitch Layouts on the Transfer of Musical Learning †. Appl. Sci. 2018, 8, 2514. https://doi.org/10.3390/app8122514
Stanford S, Milne AJ, MacRitchie J. The Effect of Isomorphic Pitch Layouts on the Transfer of Musical Learning †. Applied Sciences. 2018; 8(12):2514. https://doi.org/10.3390/app8122514
Chicago/Turabian StyleStanford, Sophia, Andrew J. Milne, and Jennifer MacRitchie. 2018. "The Effect of Isomorphic Pitch Layouts on the Transfer of Musical Learning †" Applied Sciences 8, no. 12: 2514. https://doi.org/10.3390/app8122514
APA StyleStanford, S., Milne, A. J., & MacRitchie, J. (2018). The Effect of Isomorphic Pitch Layouts on the Transfer of Musical Learning †. Applied Sciences, 8(12), 2514. https://doi.org/10.3390/app8122514





