Improvement of Mechanical Performance of Bioresorbable Magnesium Alloy Coronary Artery Stents through Stent Pattern Redesign
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials and Methods
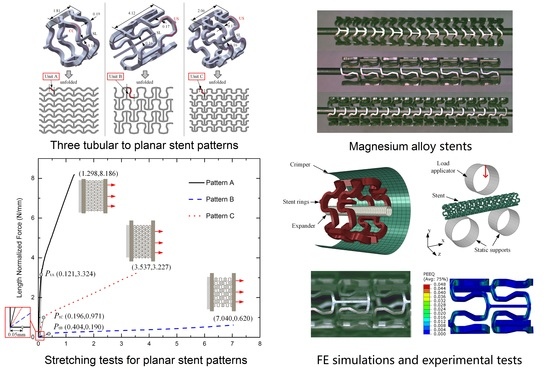
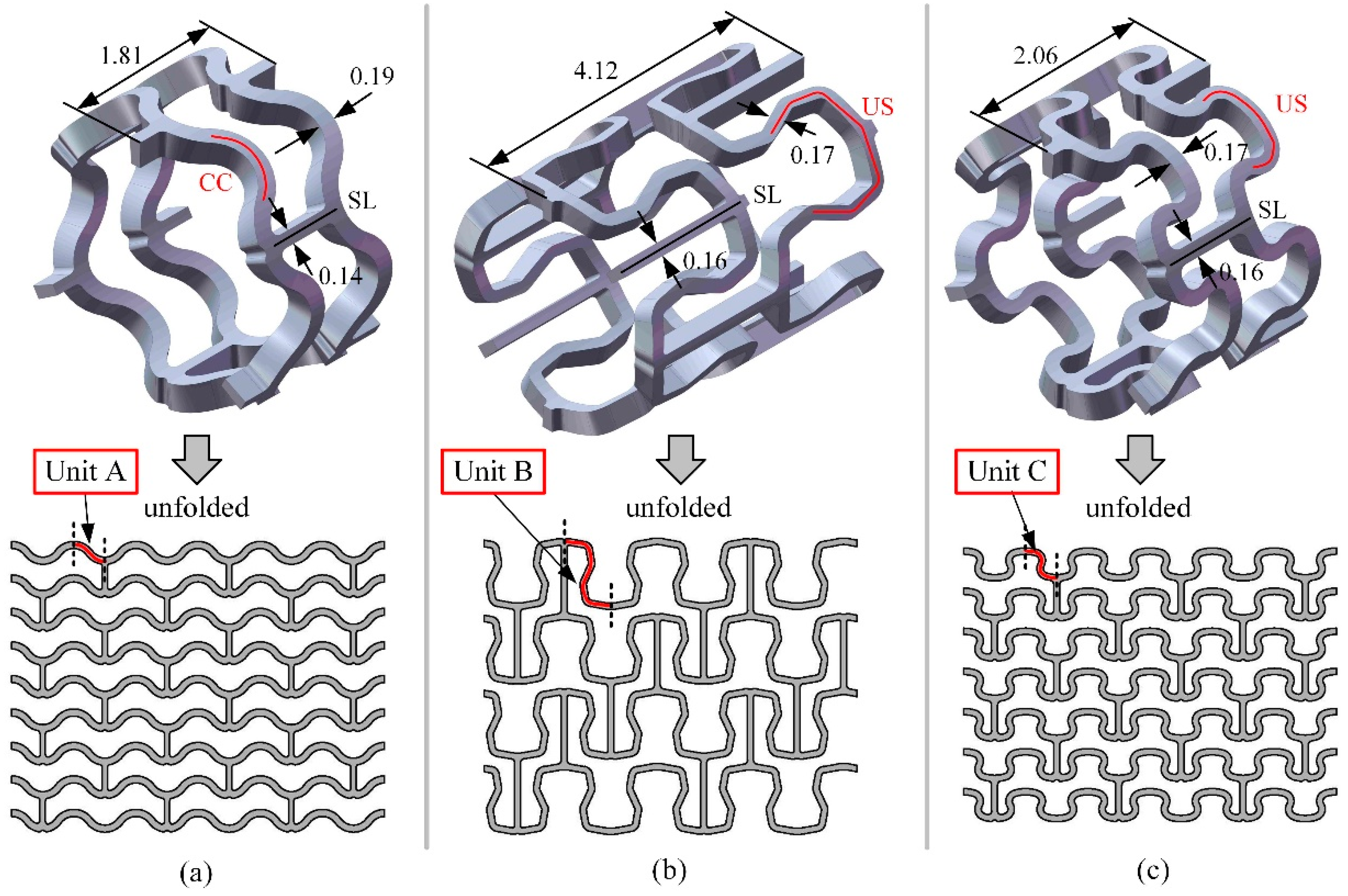
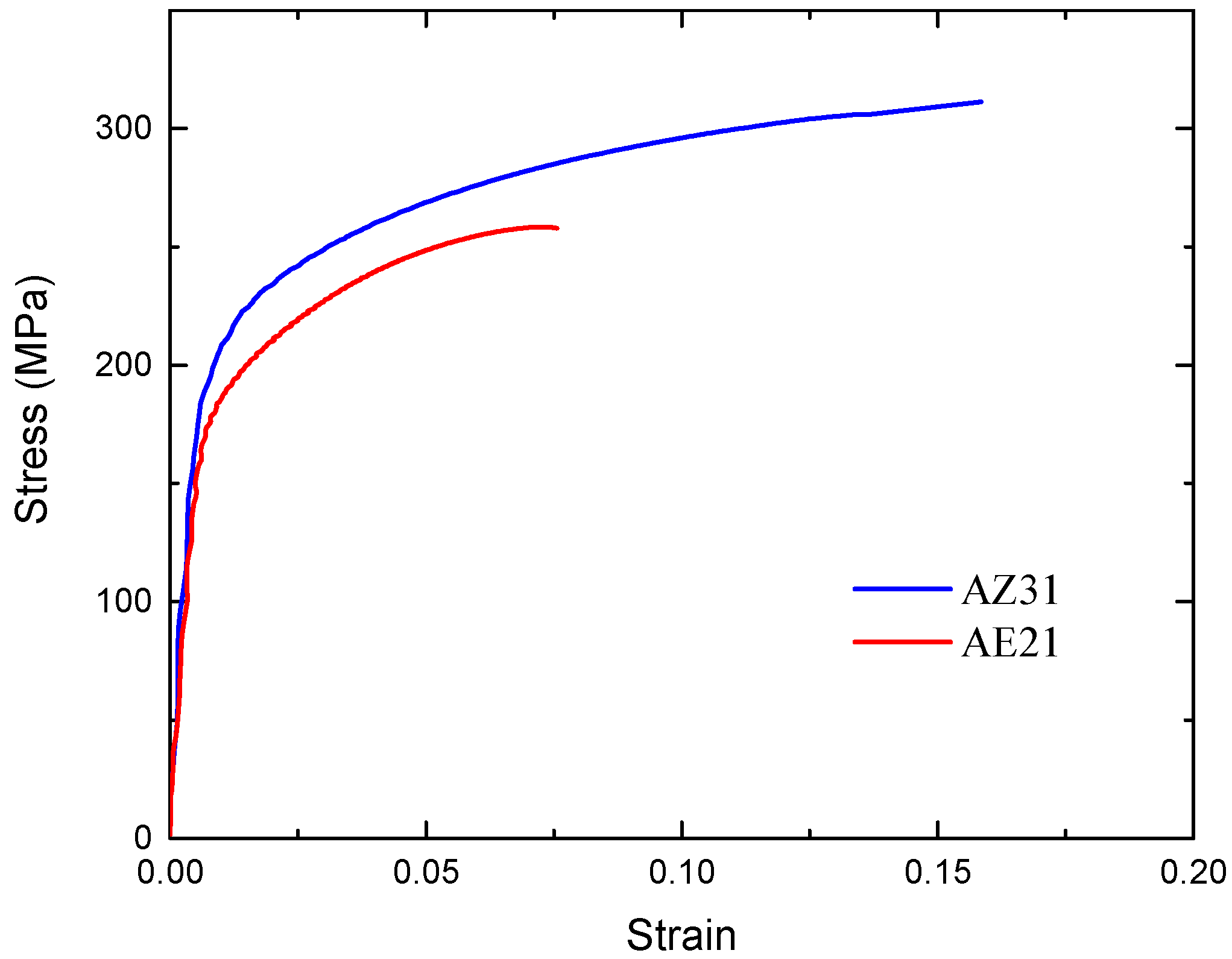
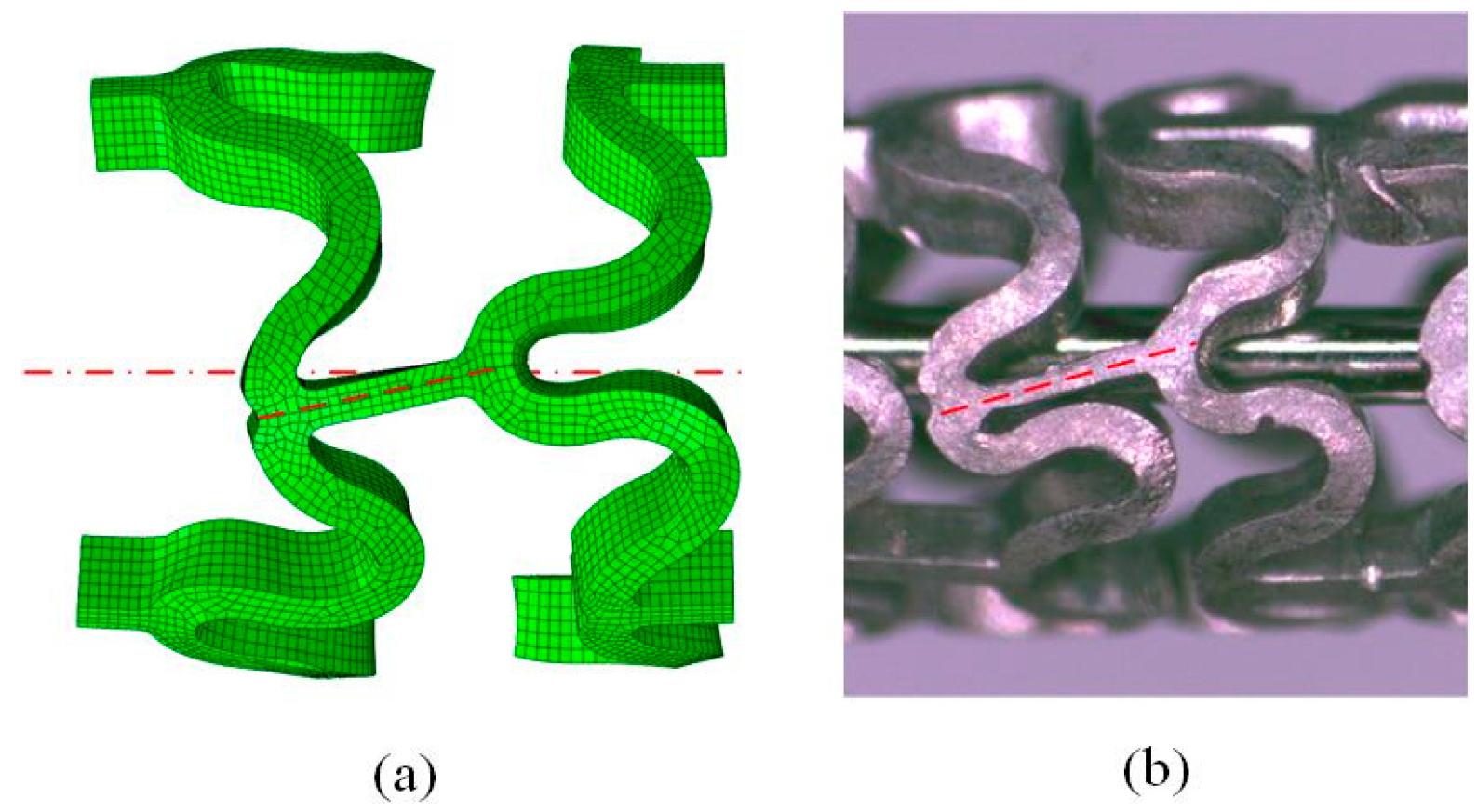
2.1. Stent Geometry and Materials
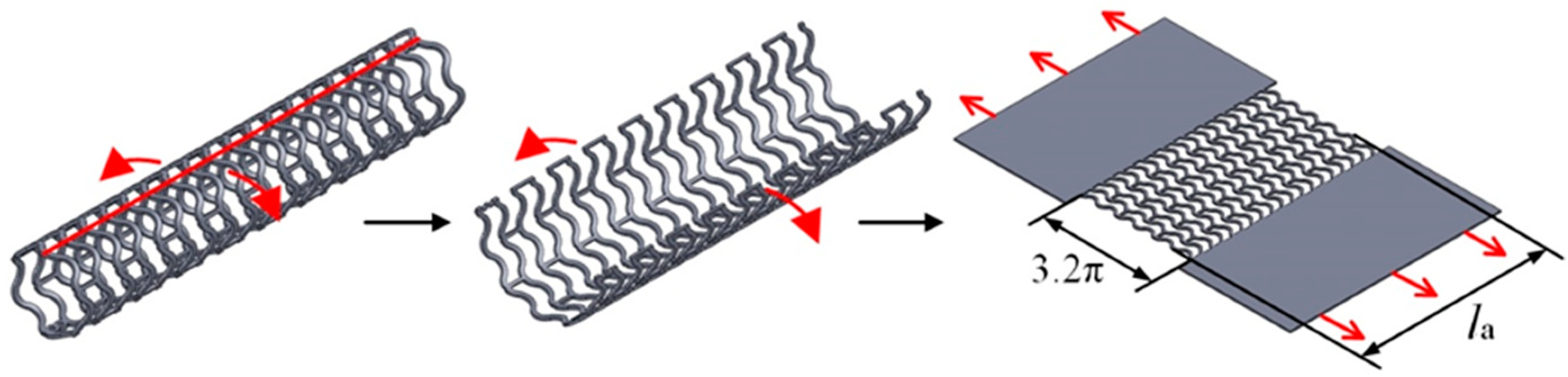
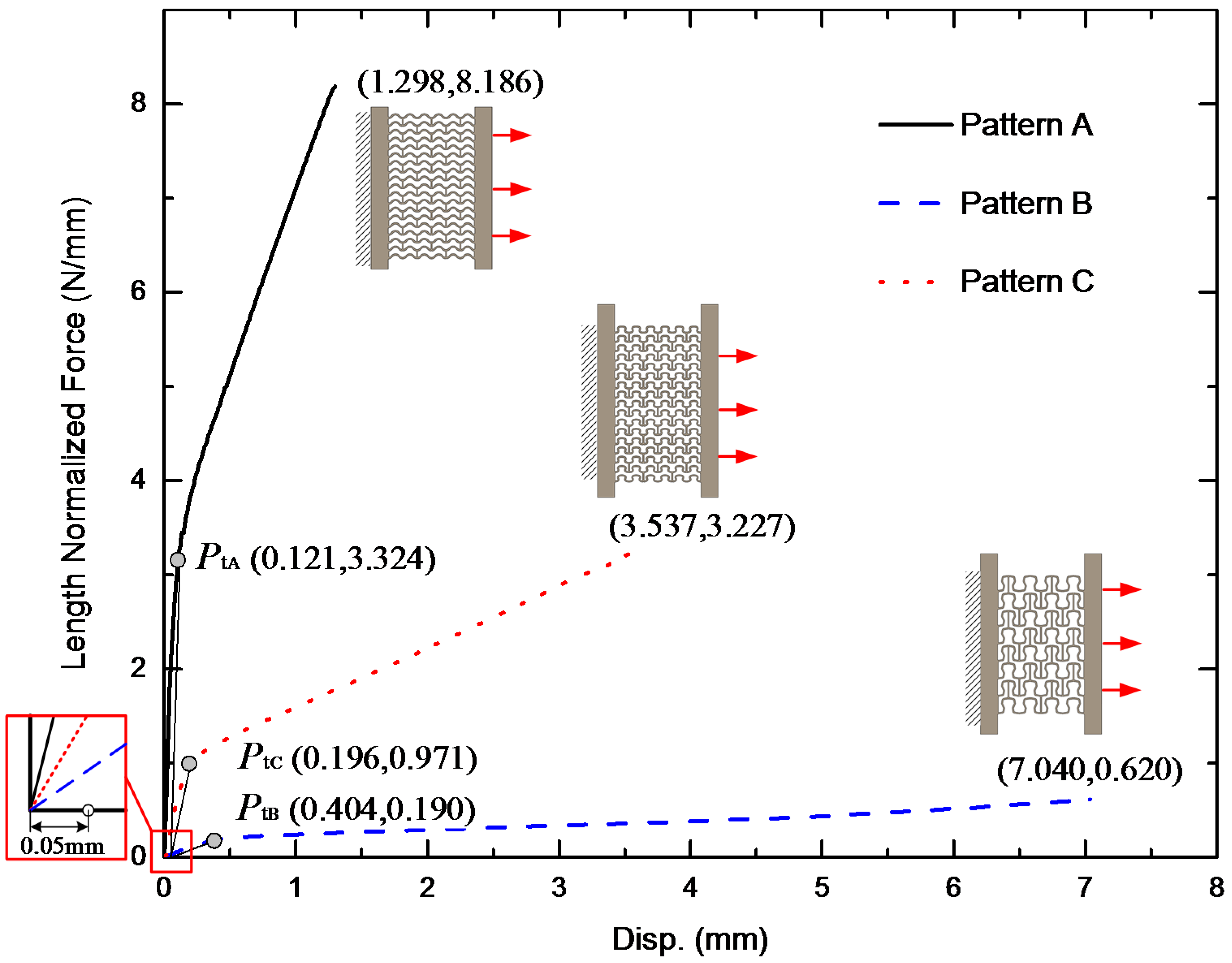
2.2. Analysis of Stretching Behavior of the Planar Specimens
2.3. Experimental Evaluation of Stretching Behavior of the Planar Specimens
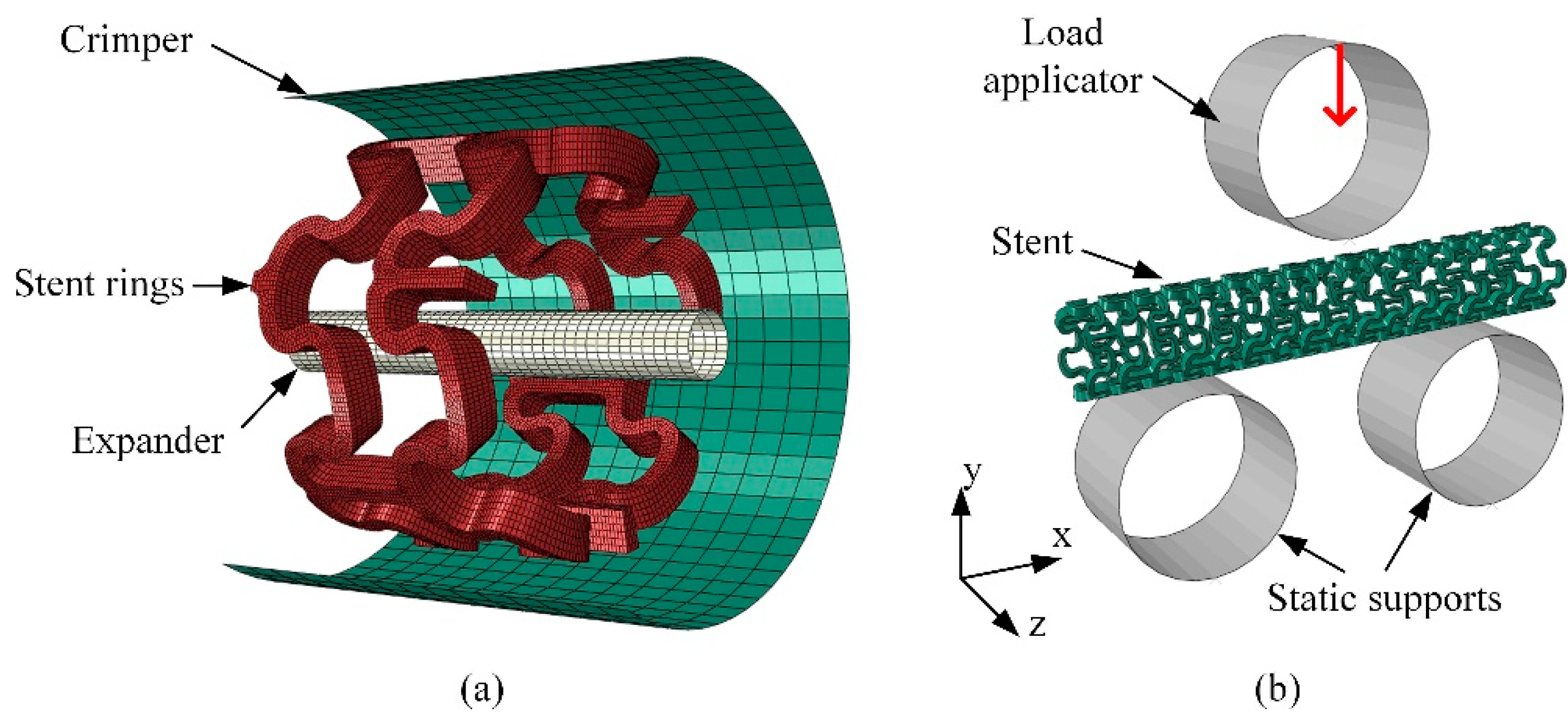
2.4. FEA of Deformation Behaviors of the Tubular Stents
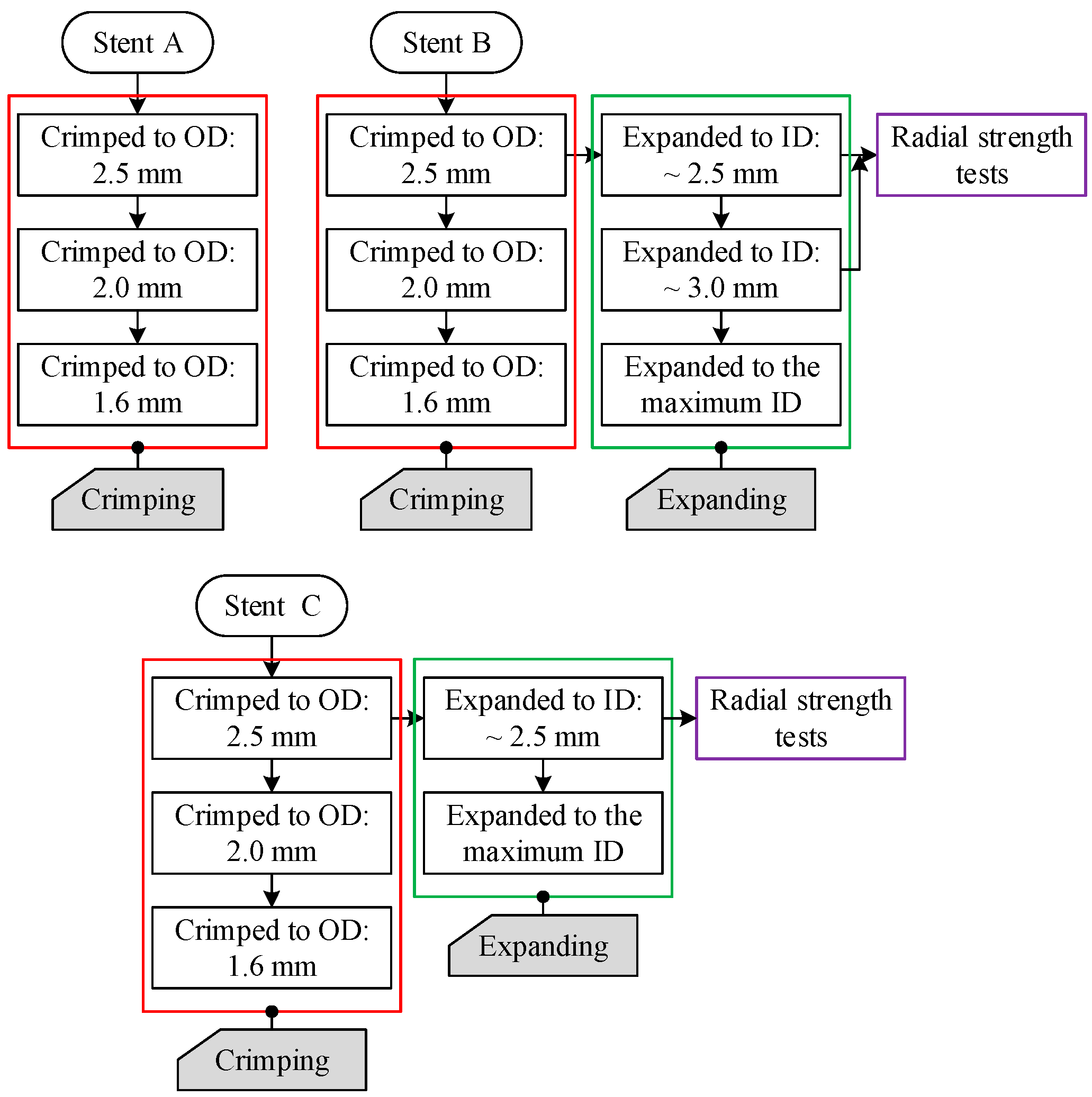
- Step 1.
- Crimp the stent specimen to an outside diameter of 2.5 mm;
- Step 2.
- Release the crimper and let the stent specimen recoil;
- Step 3.
- Expand the stent specimen to a specific inside diameter (2.67 mm for Stent B and 2.52 mm for Stent C);
- Step 4.
- Release the expander and let the stent specimen recoil.
- Step 1.
- Move the upper load applicator downwards and bend the stent specimen to a deflection of 1.4 mm;
- Step 2.
- Retract the upper load applicator and release the stent specimen to let the spring-back of the bent stent occur.
2.5. Experimental Evaluation of Deformation Behaviors of the Tubular Stents
3. Results
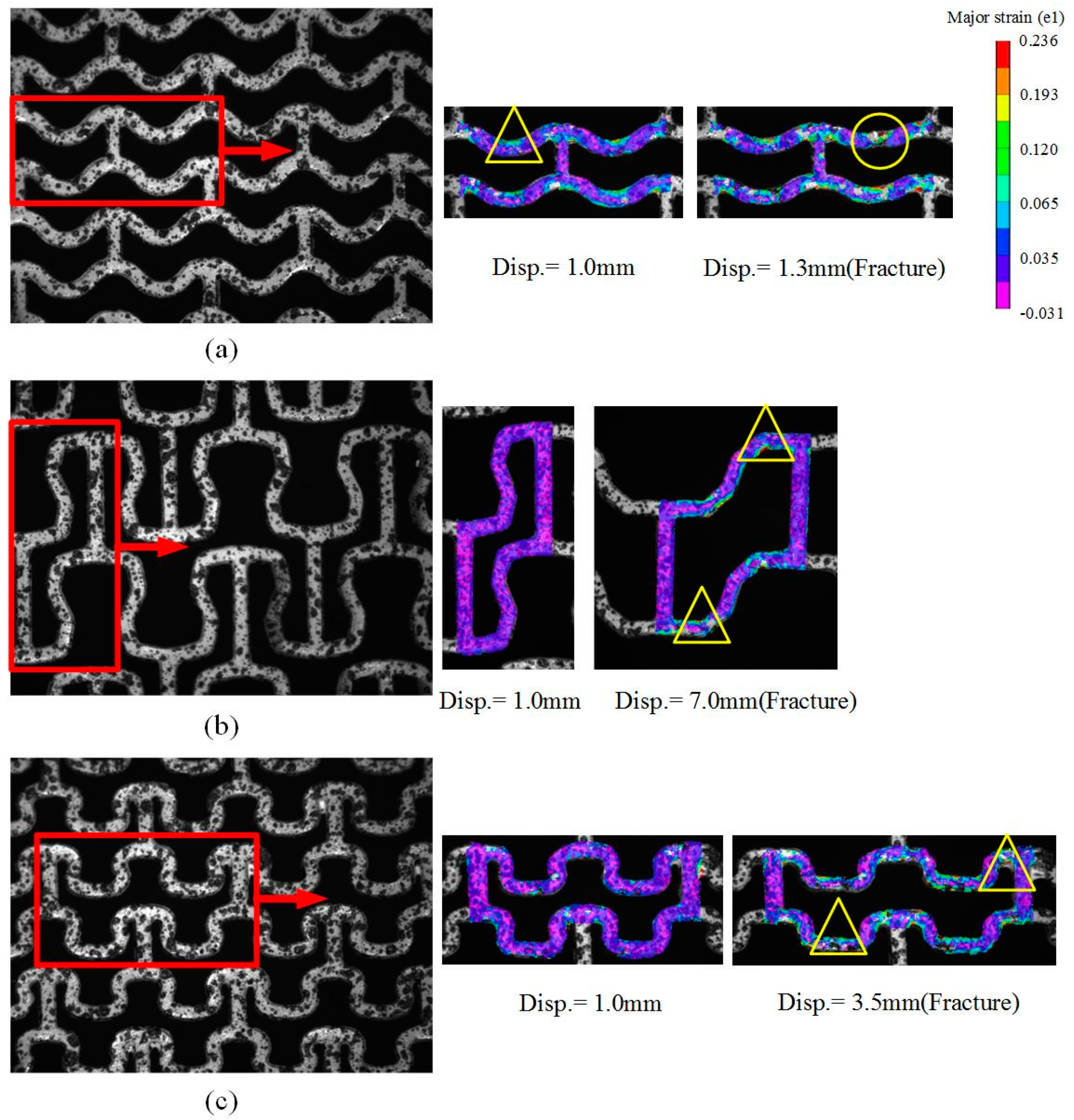
3.1. Stretching Behavior of the Planar Specimens
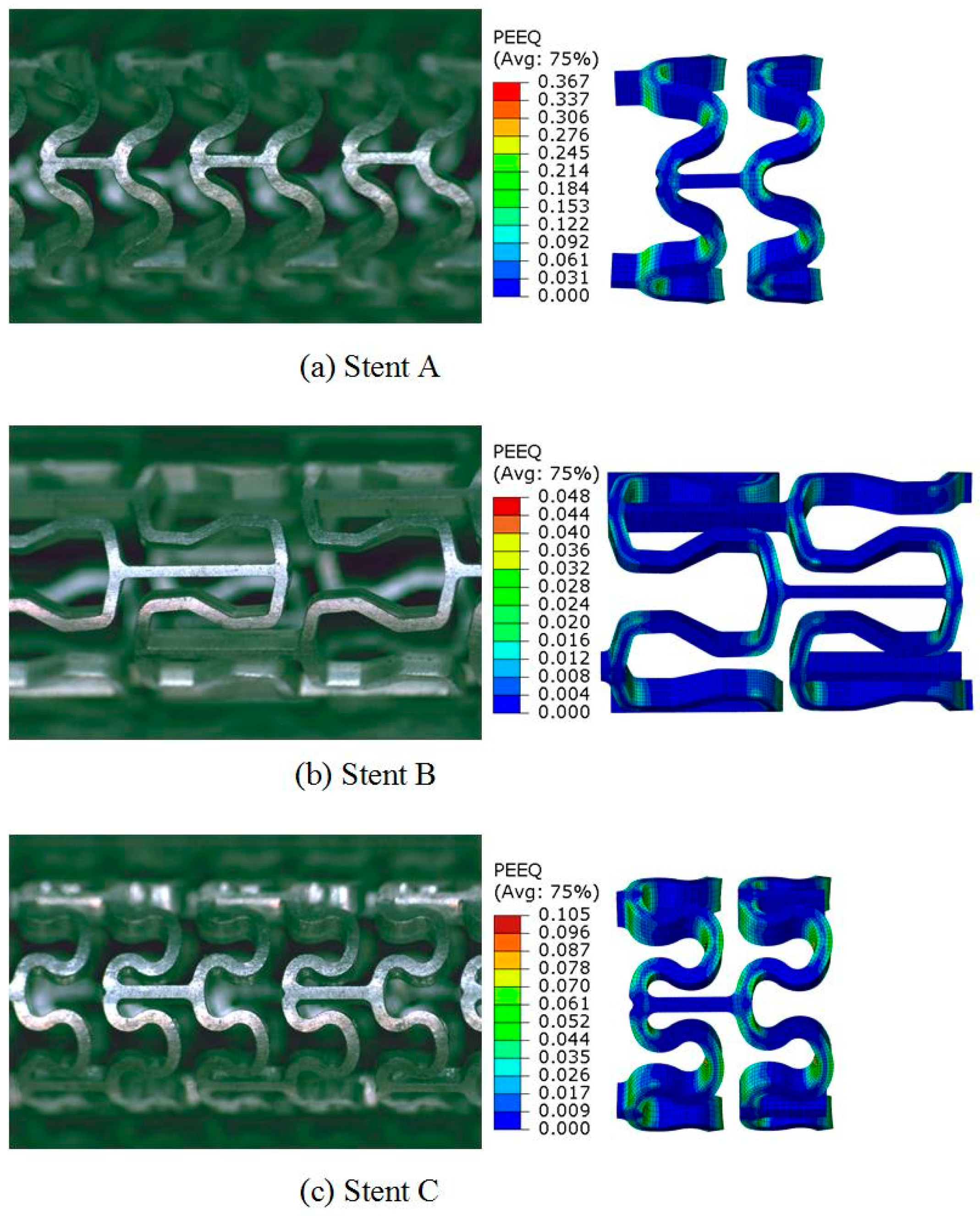
3.2. Crimping Behavior of the Tubular Stents
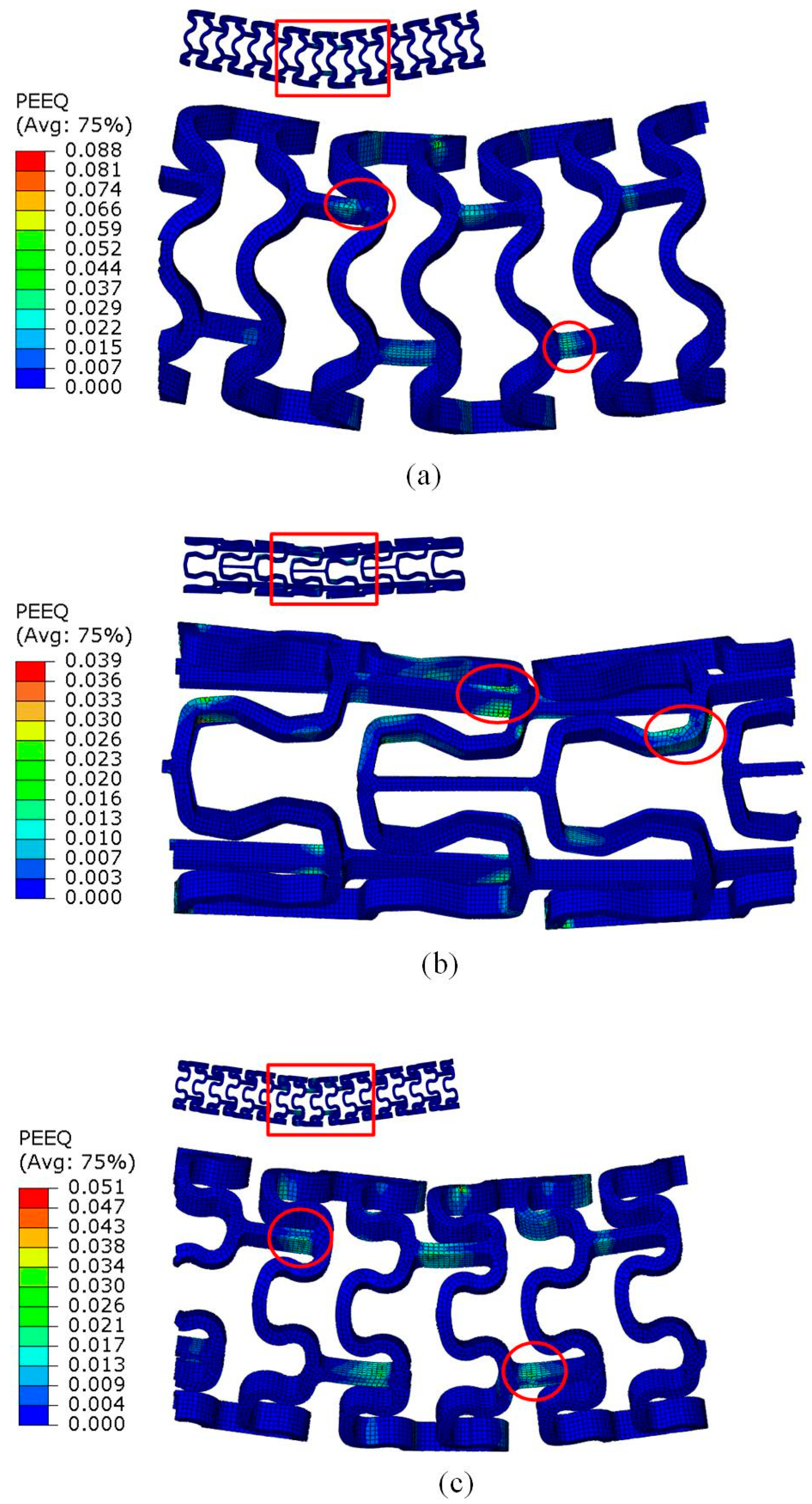
3.3. Expanding Behavior of the Tubular Stents
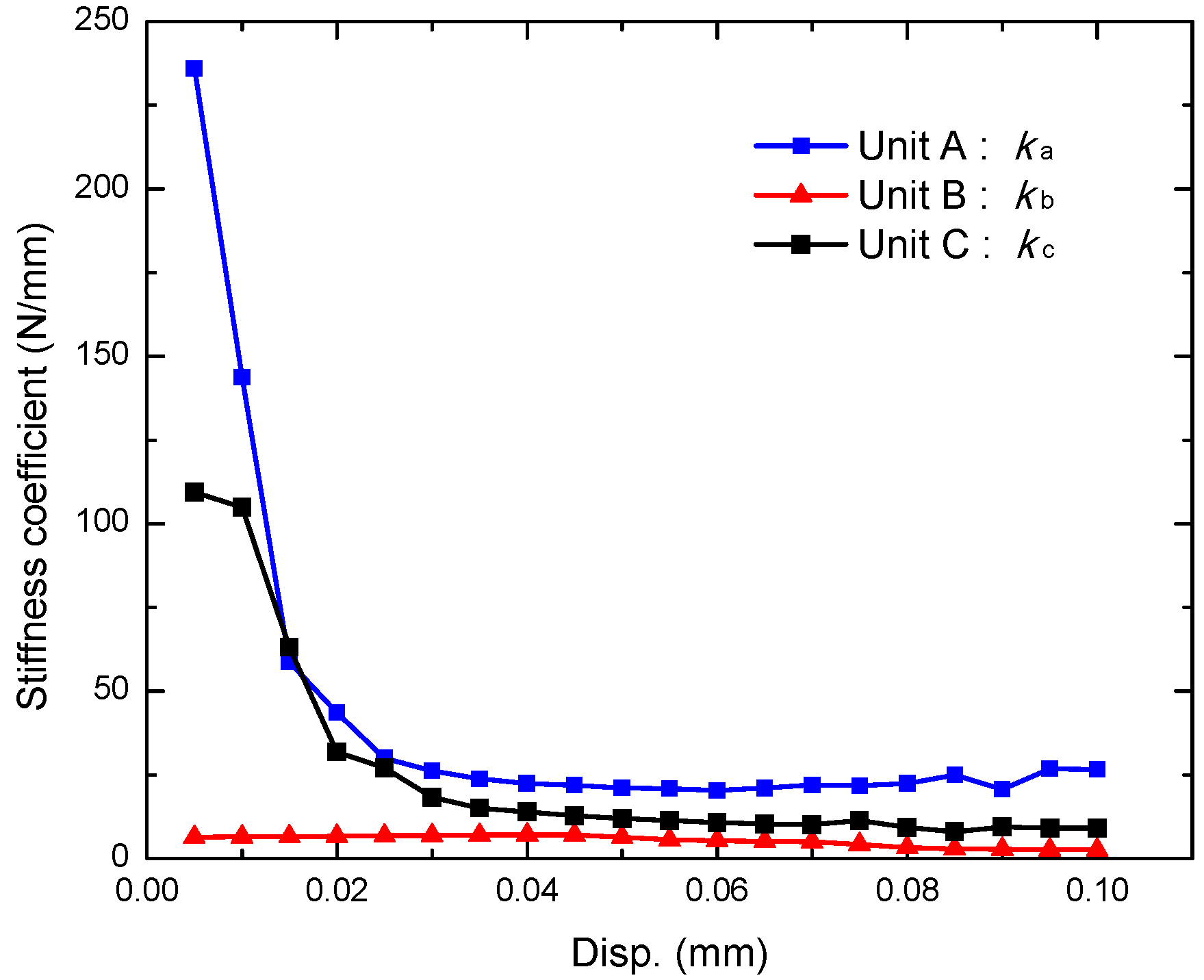
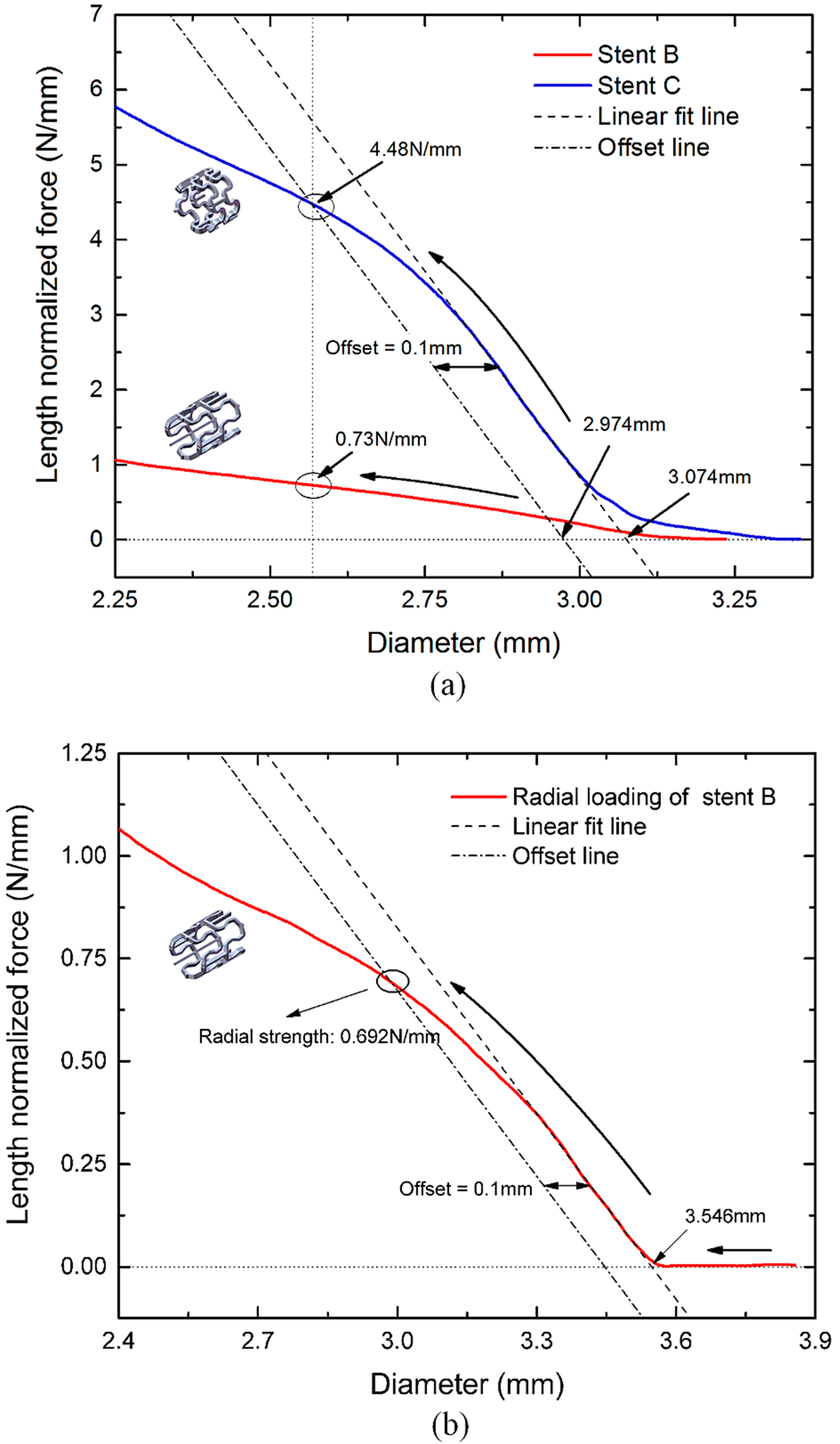
3.4. Radial Strength of the Tubular Stents
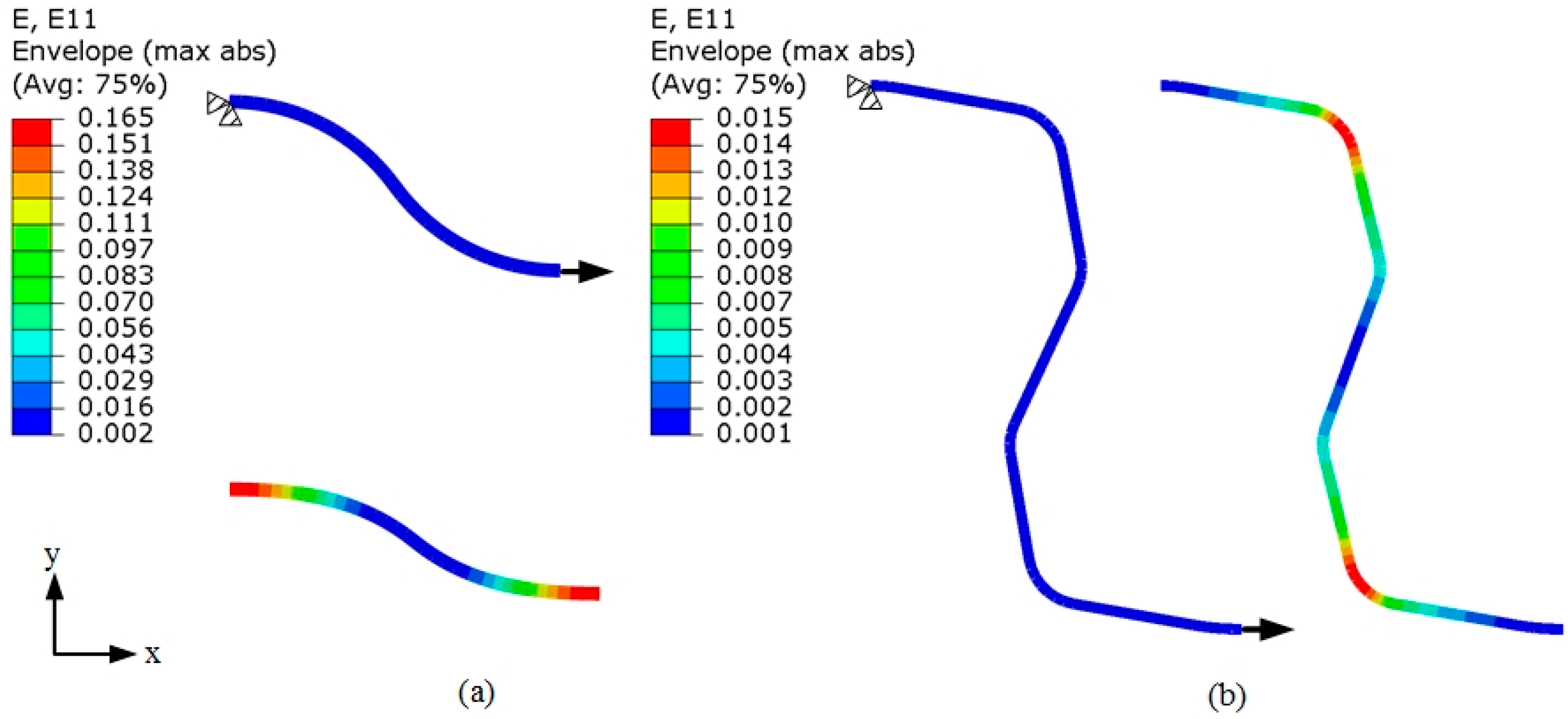
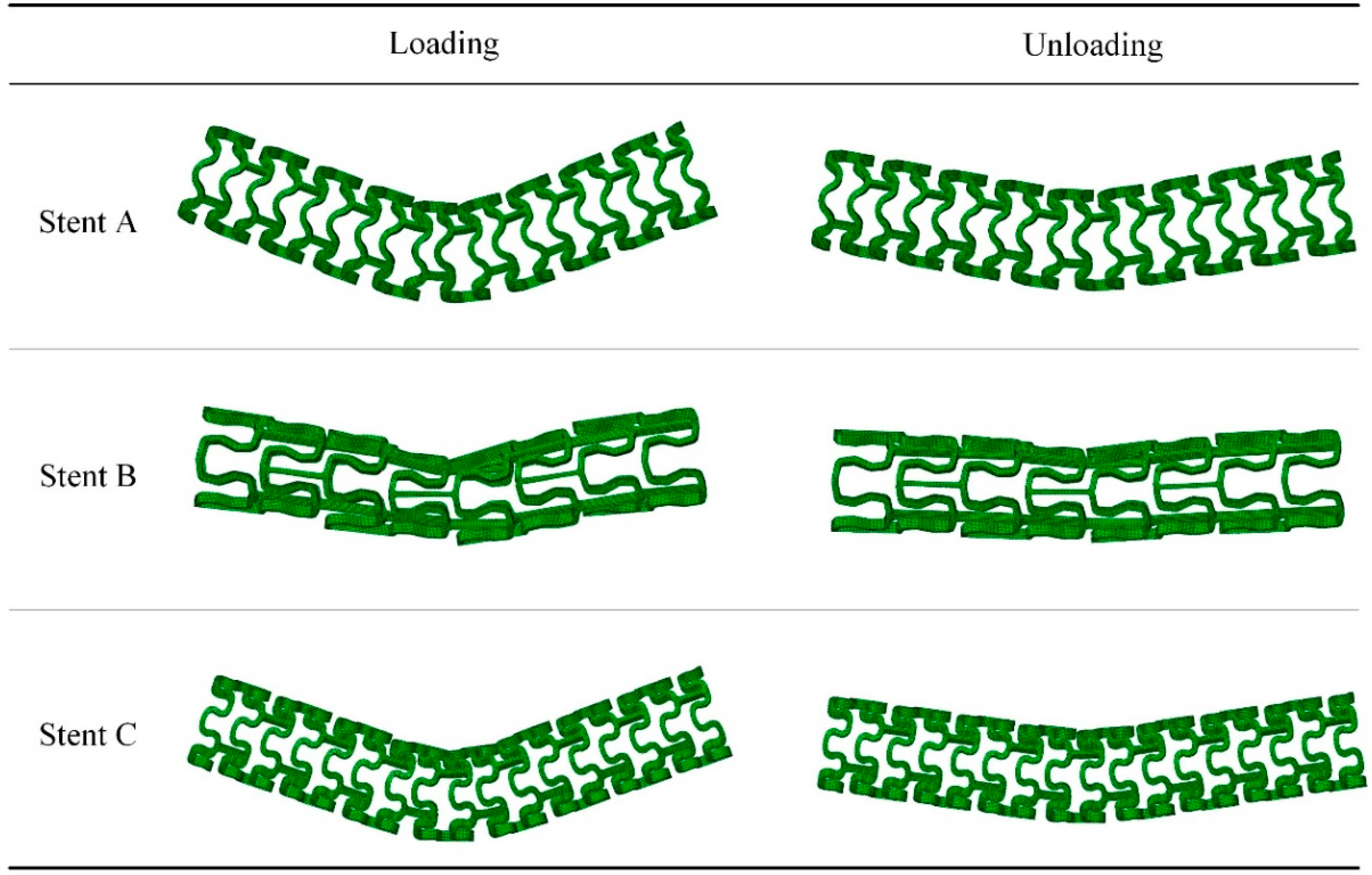
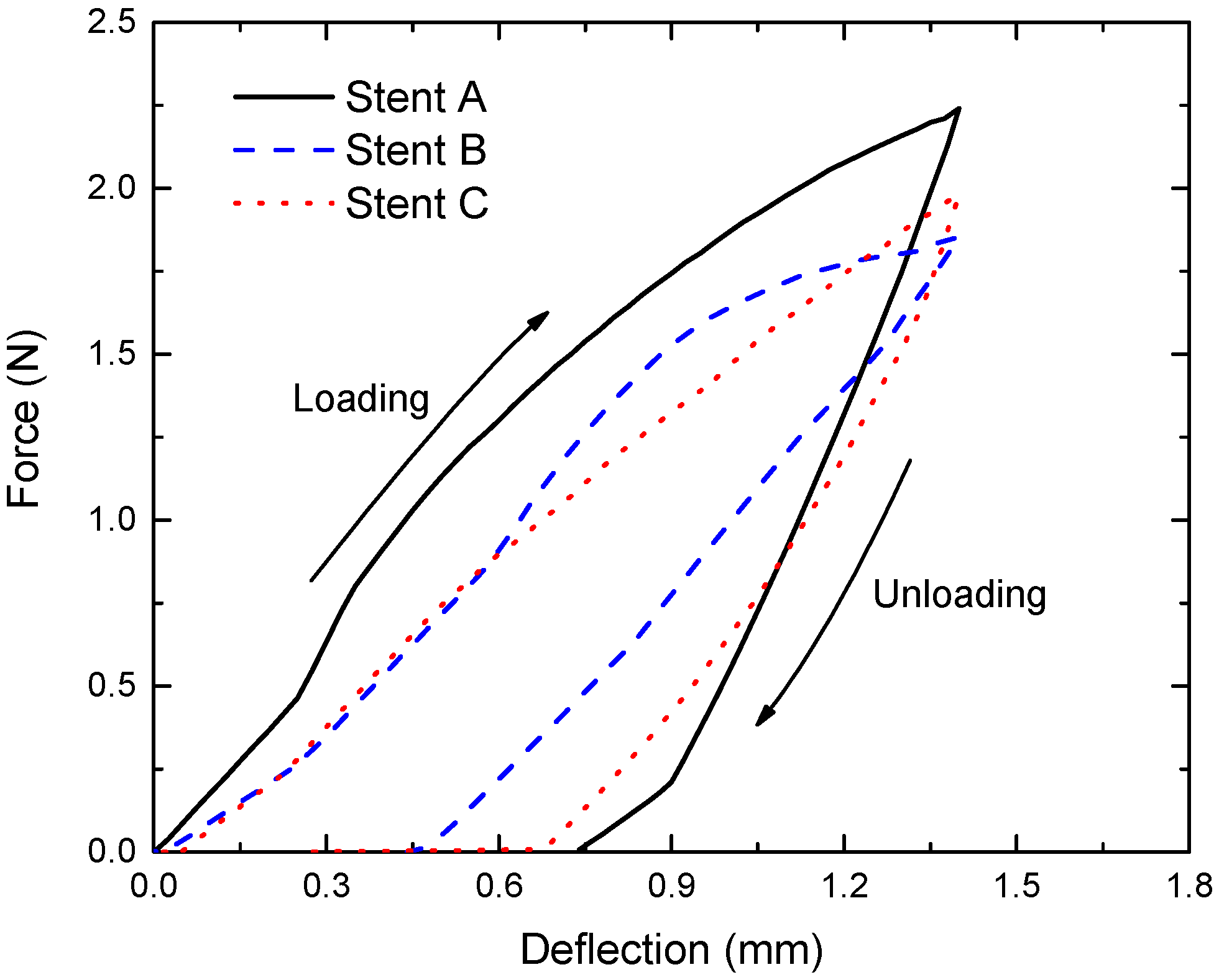
3.5. Flexibility of the Tubular Stents
4. Discussion
5. Conclusions
- (1)
- In terms of scaffolding capacity and radial recoil, the performance of Pattern C was better than that of Pattern B.
- (2)
- A new stent design pattern proposed for magnesium alloys (Stent C) exhibited balanced radial strength and deformability. In comparison with the existing stent pattern designs (Stents A and B), Stent C had a compromised overall mechanical performance in expanding deformability, radial strength, and radial recoil. However, the expanding capacity of Stent C would need to be improved.
- (3)
- The crimping deformability of Pattern C was comparable with that of Pattern B, and better than that of Pattern A. Stent A exhibited non-uniform shrinkage and rotated axial links during crimping, and then cracking and fracture occurred. Thus, this design pattern would not be suitable for magnesium alloy stents.
- (4)
- Stent C had bending flexibility comparable with Stent B at low deflections and it had far better bending flexibility than Stent A. The advantage of Stent C over Stent B became apparent when the bending deflection exceeded 0.6 mm. Stent B had poor consistencies at large deflections due to the squashing of the stent circular rings, where Stent A and C performed much better.
- (5)
- Stent pattern redesign could open up new possibilities for magnesium alloy stents to meet the performance requirements of bioresorbable coronary artery stents, despite the low ductility of magnesium alloys at normal body temperature.
Author Contributions
Funding
Conflicts of Interest
References
- Kossuth, B.M.; Perkins, L.E.; Rapoza, R.J. Design principles of bioresorbable polymeric scaffolds. Interv. Cardiol. Clin. 2016, 5, 349–355. [Google Scholar] [CrossRef] [PubMed]
- Liao, L.; Peng, C.; Li, S.; Lu, Z.; Fan, Z. Evaluation of bioresorbable polymers as potential stent material—In vivo degradation behavior and histocompatibility. J. Appl. Polym. Sci. 2017, 134. [Google Scholar] [CrossRef]
- Geller, J. Food and Drug Administration Approves Plethora of Medical Devices. J. Clin. Eng. 2017, 42, 4–10. [Google Scholar] [CrossRef]
- Giacchi, G.; Ortega-Paz, L.; Brugaletta, S.; Ishida, K.; Sabaté, M. Bioresorbable vascular scaffolds technology: Current use and future developments. Med. Devices 2016, 9, 185. [Google Scholar] [CrossRef] [PubMed]
- Aunoble, S.; Clément, D.; Frayssinet, P.; Harmand, M.F.; le Huec, J.C. Biological performance of a new β-TCP/PLLA composite material for applications in spine surgery: In vitro and in vivo studies. J. Biomed. Mater. Res. A 2006, 78, 416–422. [Google Scholar] [CrossRef]
- Tenekecioglu, E.; Bourantas, C.; Abdelghani, M.; Zeng, Y.; Silva, R.C.; Tateishi, H.; Sotomi, Y.; Onuma, Y.; Yılmaz, M.; Serruys, P.W. From drug eluting stents to bioresorbable scaffolds; to new horizons in PCI. Expert Rev. Med. Devices 2016, 13, 271–286. [Google Scholar] [CrossRef] [PubMed]
- Waksman, R.; Pakala, R.; Kuchulakanti, P.K.; Baffour, R.; Hellinga, D.; Seabron, R.; Tio, F.O.; Wittchow, E.; Hartwig, S.; Harder, C. Safety and efficacy of bioabsorbable magnesium alloy stents in porcine coronary arteries. Catheter. Cardiovasc. Interv. 2006, 68, 607–617. [Google Scholar] [CrossRef] [PubMed]
- Waksman, R. Promise and challenges of bioabsorbable stents. Catheter. Cardiovasc. Interv. 2007, 70, 407–414. [Google Scholar] [CrossRef]
- Atan, M.B.A.; Taib, I.; Lazim, Z. A review on fracture prevention of stent in femoropopliteal artery. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2017; Volume 165. [Google Scholar]
- Wu, W.; Petrini, L.; Gastaldi, D.; Villa, T.; Vedani, M.; Lesma, E.; Previtali, B.; Migliavacca, F. Finite element shape optimization for biodegradable magnesium alloy stents. Ann. Biomed. Eng. 2010, 38, 2829–2840. [Google Scholar] [CrossRef]
- Grogan, A.J.; Leen, S.B.; McHugh, P.E. Optimizing the design of a bioabsorbable metal stent using computer simulation methods. Biomaterials 2013, 34, 8049–8060. [Google Scholar] [CrossRef]
- Li, J.; Zheng, F.; Qiu, X.; Wan, P.; Tan, L.; Yang, K. Finite element analyses for optimization design of biodegradable magnesium alloy stent. Mater. Sci. Eng. C 2014, 42, 705–714. [Google Scholar] [CrossRef] [PubMed]
- Limon, T.A. Stents with High Radial Strength and Methods of Manufacturing Same. U.S. Patent US8002817B2, 23 August 2011. [Google Scholar]
- Lootz, D.; Surber, B.; Wintsch, D.; Riedmuller, J. Stent Having Radially Expandable Main Body. U.S. Patent US 2008/0243230 A1, 2 October 2008. [Google Scholar]
- Bedoya, J.; Meyer, C.A.; Timmins, L.H.; Moreno, M.R.; Moore, J.E. Effects of stent design parameters on normal artery wall mechanics. J. Biomech. Eng. 2006, 128, 757–765. [Google Scholar] [CrossRef] [PubMed]
- Stoeckel, D.; Bonsignore, C.; Duda, S. A survey of stent designs. Minim. Invasiv. Ther. 2002, 11, 137–147. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Fang, G.; Qian, L.; Leeflang, S.; Duszczyk, J.; Zhou, J. Forming of magnesium alloy microtubes in the fabrication of biodegradable stents. Prog. Nat. Sci. Mater. Int. 2014, 24, 500–506. [Google Scholar] [CrossRef]
- Zhao, J.; Zeng, P.; Pan, B.; Lei, L.; Du, H.; He, W.; Liu, Y.; Xu, Y. Improved Hermite finite element smoothing method for full-field strain measurement over arbitrary region of interest in digital image correlation. Opt. Laser Eng. 2012, 50, 1662–1671. [Google Scholar] [CrossRef]
- Wang, Q.; Fang, G.; Zhao, Y.; Wang, G.; Cai, T. Computational and experimental investigation into mechanical performances of Poly-L-Lactide Acid (PLLA) coronary stents. J. Mech. Behav. Biomed. 2017, 65, 415–427. [Google Scholar] [CrossRef] [PubMed]
- Imani, M.; Goudarzi, A.M.; Ganji, D.D.; Aghili, A.L. The comprehensive finite element model for stenting: The influence of stent design on the outcome after coronary stent placement. J. Theor. Appl. Mech.-Pol. 2013, 51, 639–648. [Google Scholar]
- Schmidt, W.; Behrens, P.; Schmitz, K. Biomechanical aspects of potential stent malapposition at coronary stent implantation. In Proceedings of the World Congress on Medical Physics and Biomedical Engineering, Munich, Germany, 7–12 September 2009; pp. 136–139. [Google Scholar]
- Schmidt, W.; Lanzer, P. Instrumentation. In Catheter-Based Cardiovascular Interventions; Springer: Berlin, Germany, 2013; pp. 445–472. [Google Scholar]
- ASTM International Standards F2606-08 (Reapproved in 2014). Standard Guide for Three-Point Bending of Balloon Expandable Vascular Stents and Stent Systems; ASTM: West Conshohocken, PA, USA, 2008. [Google Scholar]
- Rittersma, Z.S.; de Winter, R.J.; Koch, K.T.; Bax, M.; Schotborgh, C.E.; Mulder, K.J.; Tijssen, J.G.; Piek, J.J. Impact of strut thickness on late luminal loss after coronary artery stent placement. Am. J. Cardiol. 2004, 93, 477–480. [Google Scholar] [CrossRef]
- Schmidt, W.; Behrens, P.; Brandt-Wunderlich, C.; Siewert, S.; Grabow, N.; Schmitz, K. In vitro performance investigation of bioresorbable scaffolds–Standard tests for vascular stents and beyond. Cardiovasc. Revasc. Med. 2016, 17, 375–383. [Google Scholar] [CrossRef]
- Paryab, N.; Cronin, D.; Lee-Sullivan, P.; Ying, X.; Boey, F.Y.; Venkatraman, S. Uniform expansion of a polymeric helical stent. J. Med. Devices 2012, 6, 021012. [Google Scholar] [CrossRef]
- Lanzer, P.; Strupp, G.; Schmidt, W.; Topoleski, L.D. The need for stent–lesion matching to optimize outcomes of intracoronary stent implantation. J. Biomed. Mater. Res. B Appl. Biomater. 2013, 101, 1560–1570. [Google Scholar] [CrossRef] [PubMed]






| Stent A | Stent B | Stent C | PLLA Stent [19] | |
|---|---|---|---|---|
| Bending stiffness (Nmm2) | 60.1 | 42.1 | 41.5 | 2.9 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Fang, G.; Zhao, Y.-H.; Zhou, J. Improvement of Mechanical Performance of Bioresorbable Magnesium Alloy Coronary Artery Stents through Stent Pattern Redesign. Appl. Sci. 2018, 8, 2461. https://doi.org/10.3390/app8122461
Wang Q, Fang G, Zhao Y-H, Zhou J. Improvement of Mechanical Performance of Bioresorbable Magnesium Alloy Coronary Artery Stents through Stent Pattern Redesign. Applied Sciences. 2018; 8(12):2461. https://doi.org/10.3390/app8122461
Chicago/Turabian StyleWang, Qian, Gang Fang, Ying-Hong Zhao, and Jie Zhou. 2018. "Improvement of Mechanical Performance of Bioresorbable Magnesium Alloy Coronary Artery Stents through Stent Pattern Redesign" Applied Sciences 8, no. 12: 2461. https://doi.org/10.3390/app8122461
APA StyleWang, Q., Fang, G., Zhao, Y.-H., & Zhou, J. (2018). Improvement of Mechanical Performance of Bioresorbable Magnesium Alloy Coronary Artery Stents through Stent Pattern Redesign. Applied Sciences, 8(12), 2461. https://doi.org/10.3390/app8122461