Dam-Break Flows: Comparison between Flow-3D, MIKE 3 FM, and Analytical Solutions with Experimental Data
Abstract
1. Introduction
2. Materials and Methods
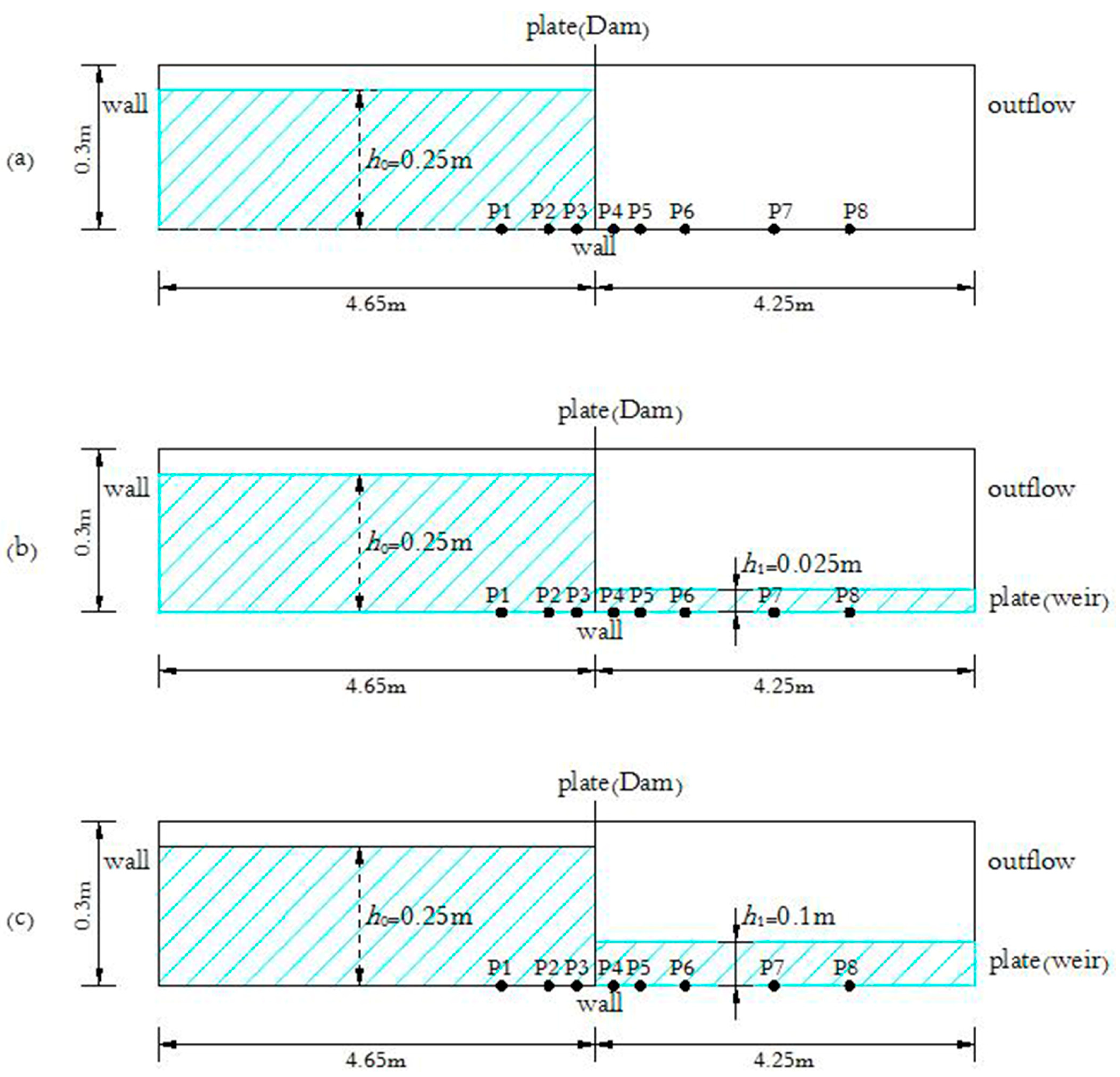
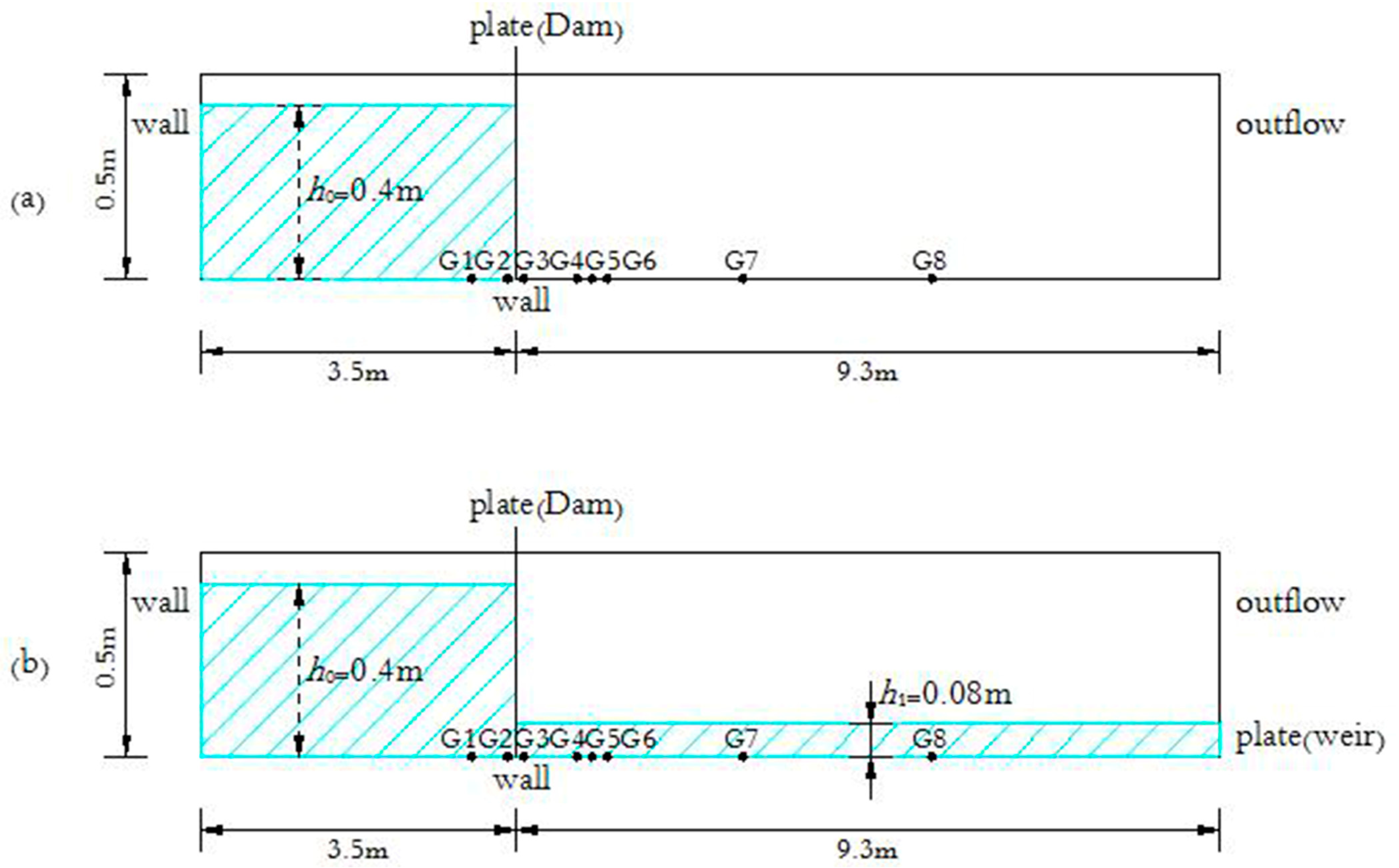
2.1. Data
2.2. Model Performance Criteria
2.3. Analytical Solution
2.4. Numerical Model and Simulation Setup
2.4.1. Flow-3D
2.4.2. MIKE 3 FM
3. Comparison between Flow-3D, MIKE 3 FM, and 1D Exact Riemann Solver Predictions
3.1. Free Surface
3.1.1. Free Surface during the Early Stage
3.1.2. Free Surface during the Late Stage ()
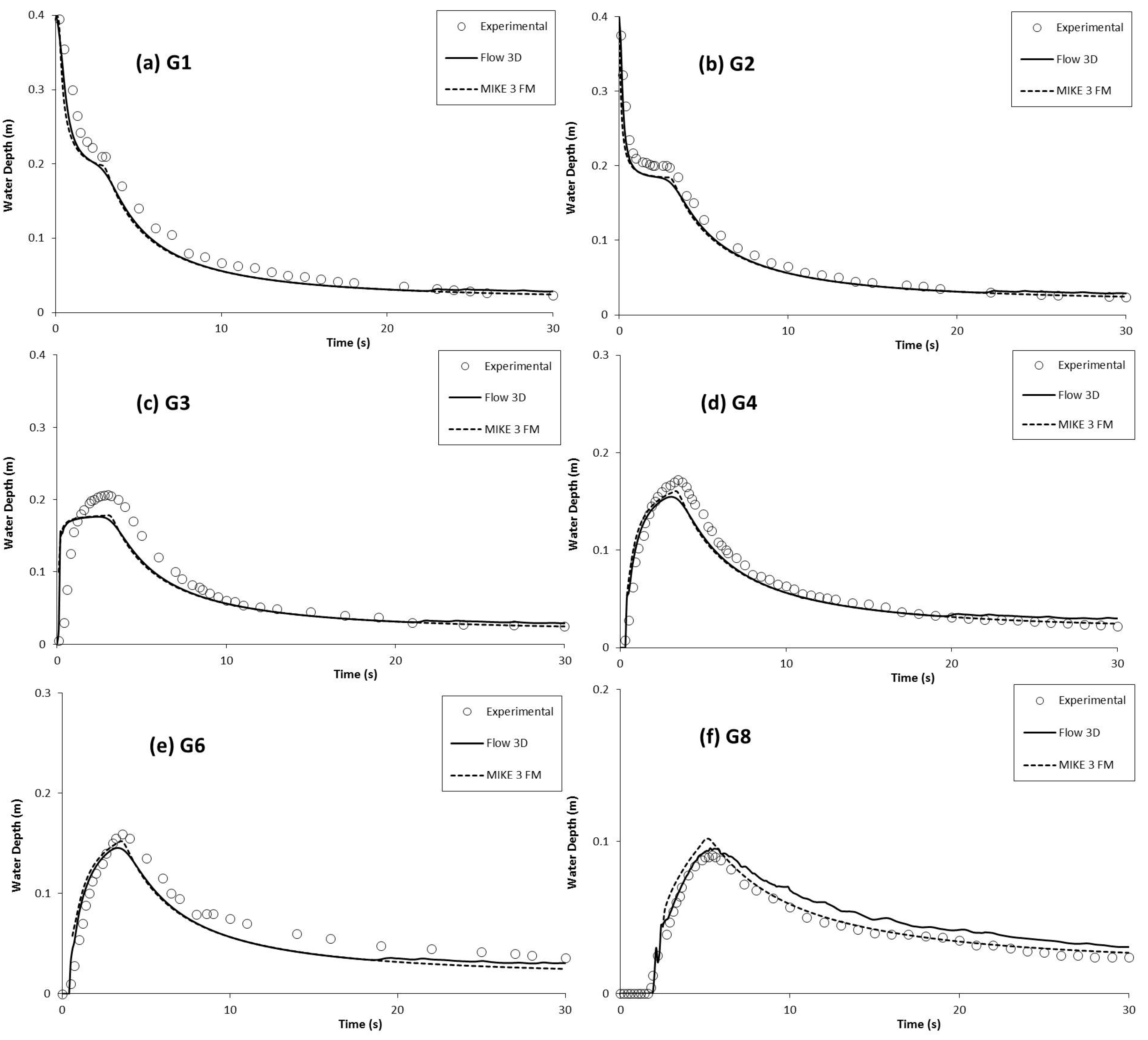
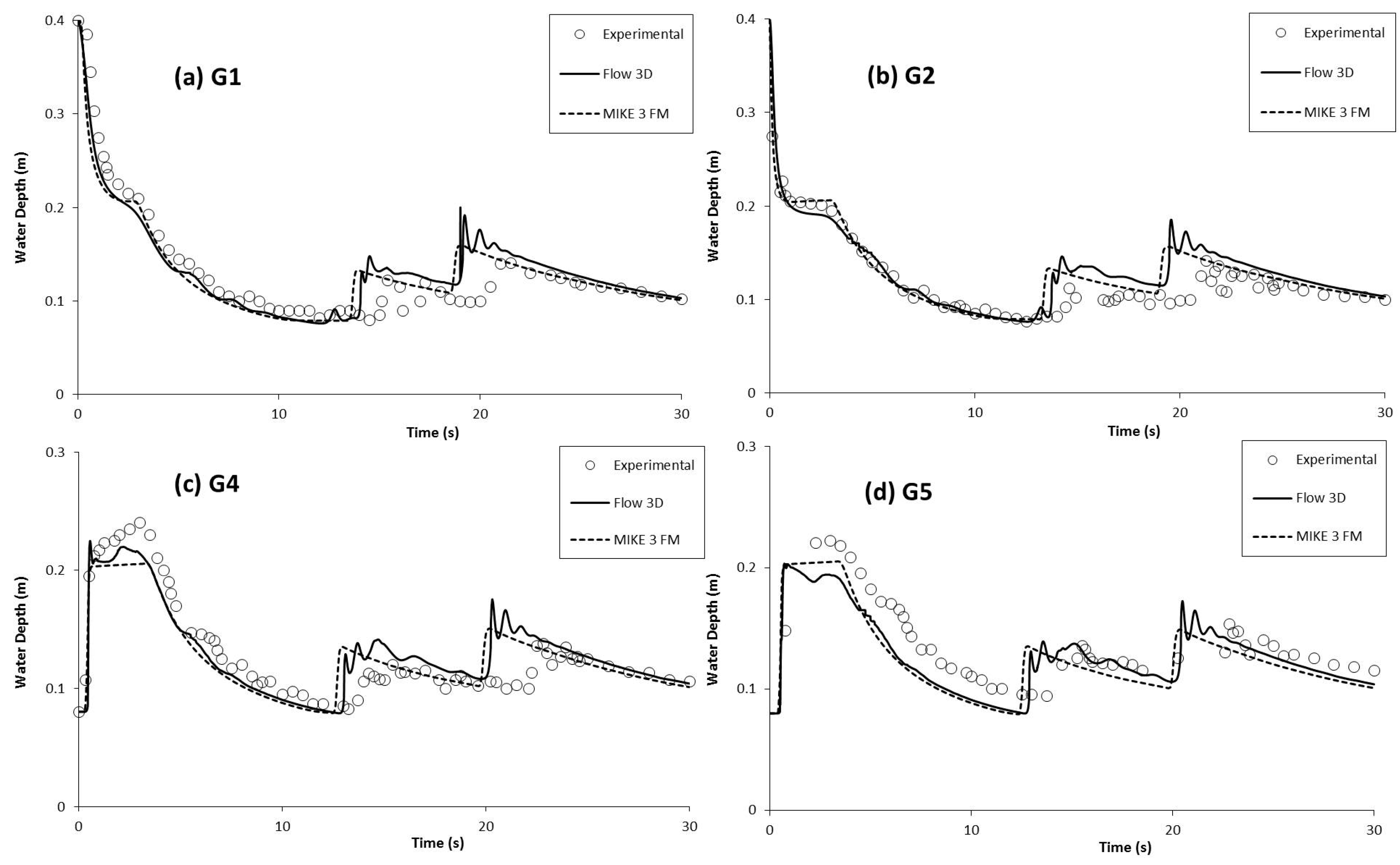
3.2. Water Depth Variations
3.3. Velocity
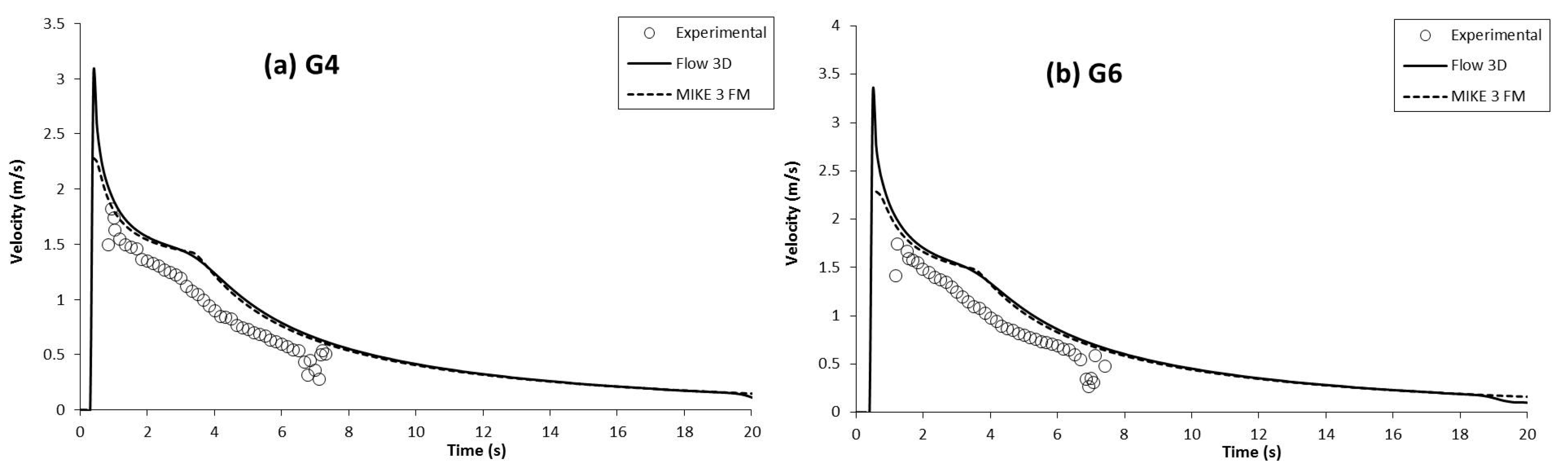
3.3.1. Averaged Velocity Evolution
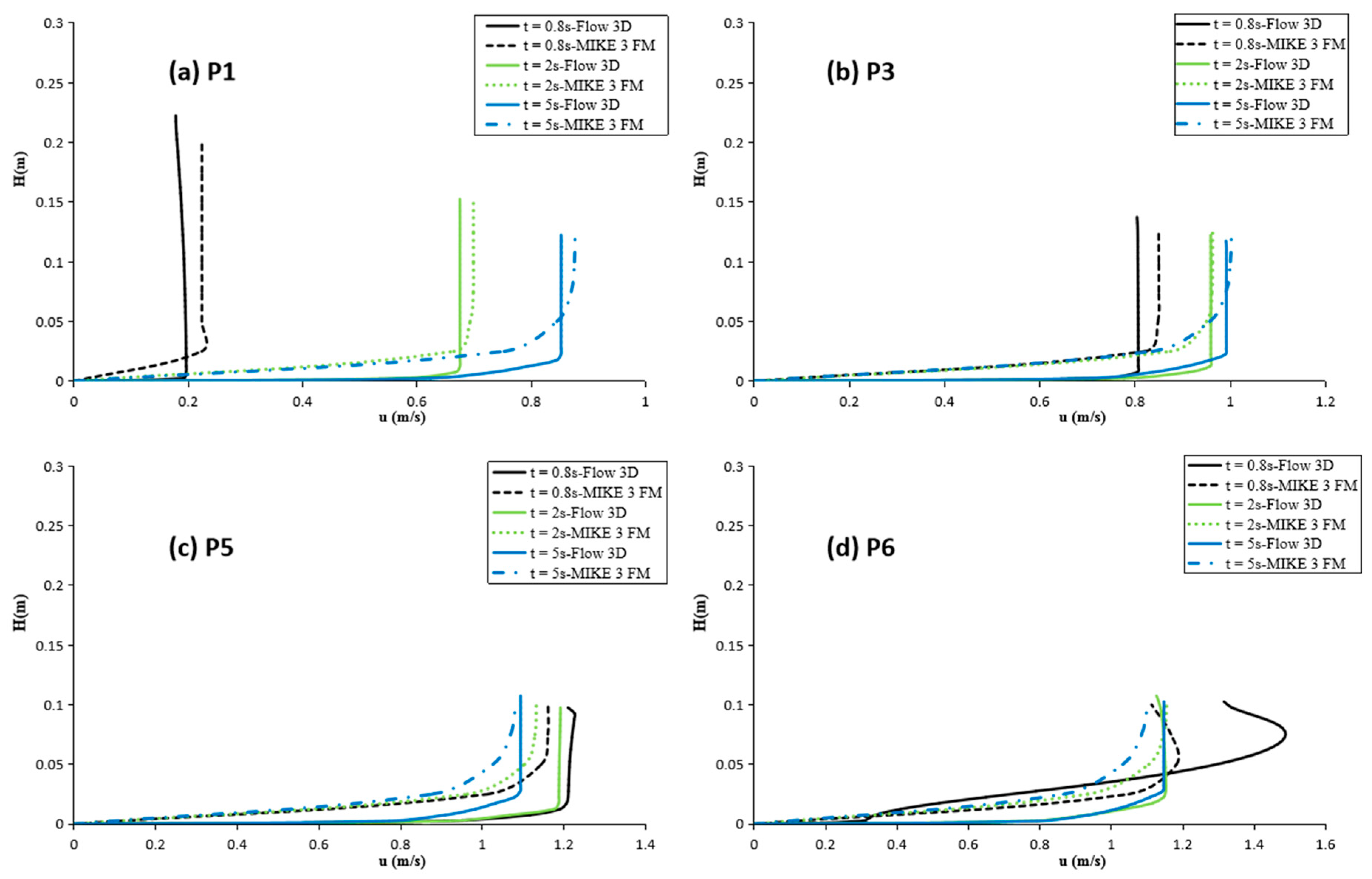
3.3.2. Vertical Velocity Profiles
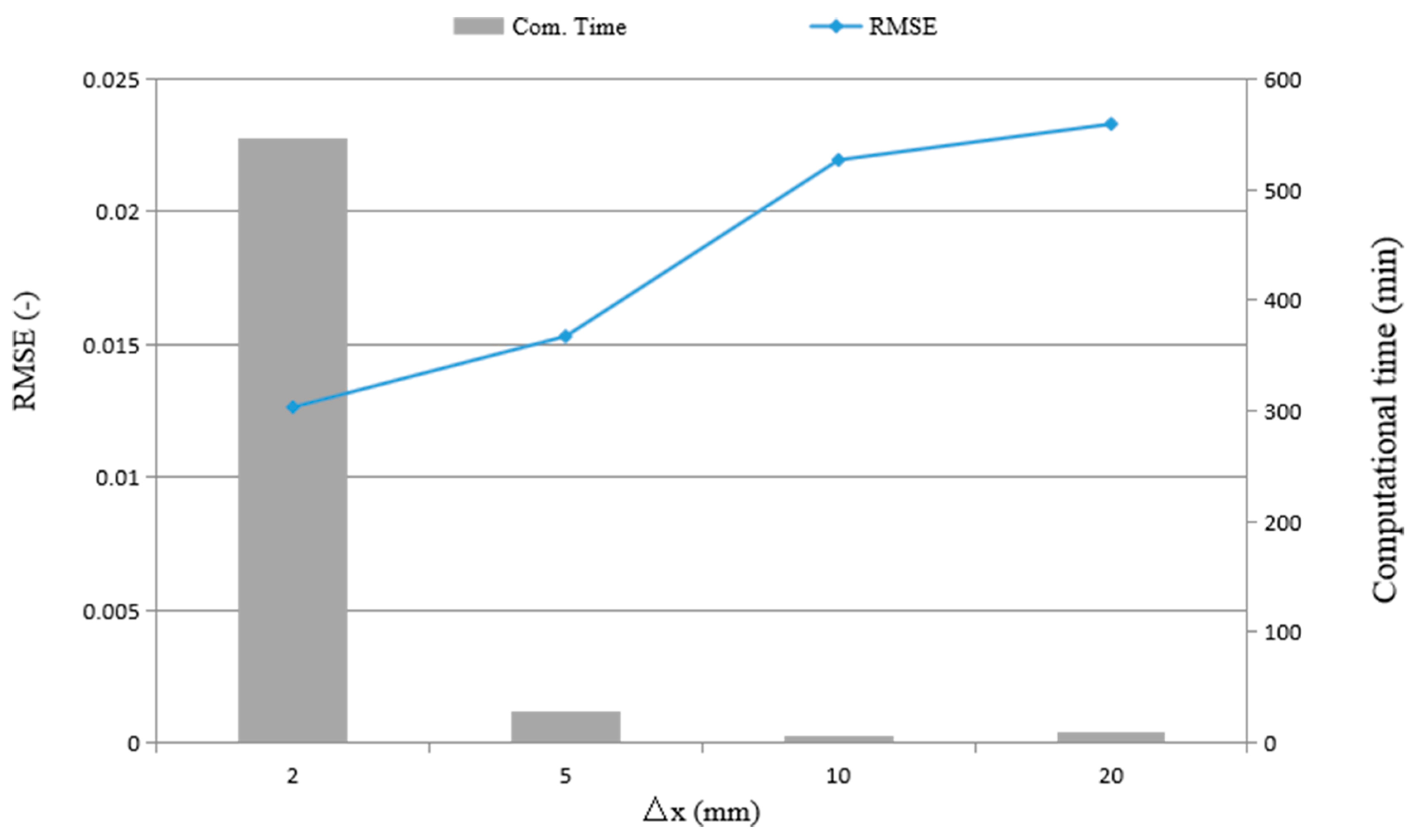
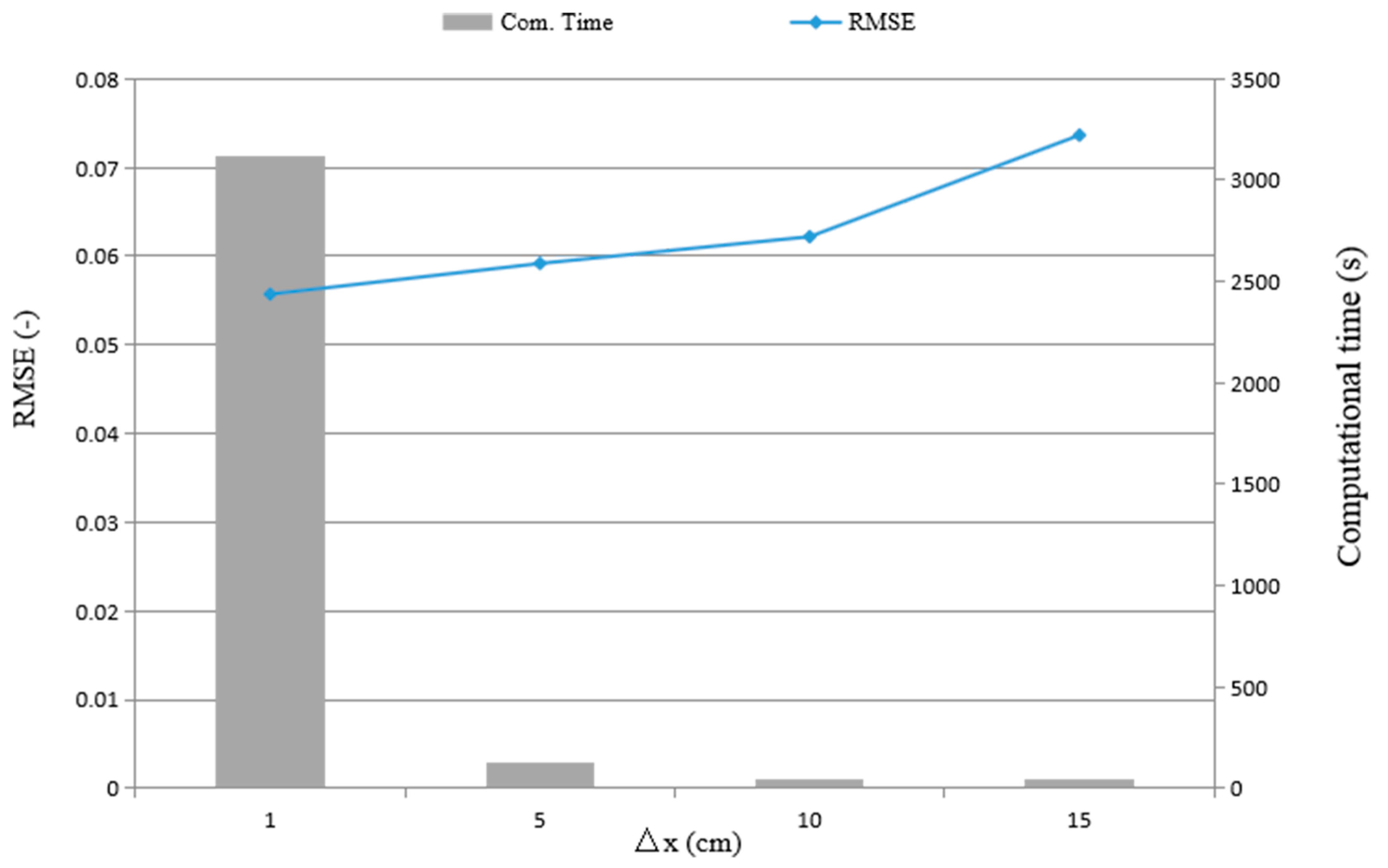
3.4. Computational Costs
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gallegos, H.A.; Schubert, J.E.; Sanders, B.F. Two-dimensional high-resolution modeling of urban dam-break flooding: A case study of Baldwin Hills, California. Adv. Water Resour. 2009, 32, 1323–1335. [Google Scholar] [CrossRef]
- Kim, K.S. A Mesh-Free Particle Method for Simulation of Mobile-Bed Behavior Induced by Dam Break. Appl. Sci. 2018, 8, 1070. [Google Scholar] [CrossRef]
- Robb, D.M.; Vasquez, J.A. Numerical simulation of dam-break flows using depth-averaged hydrodynamic and three-dimensional CFD models. In Proceedings of the Canadian Society for Civil Engineering Hydrotechnical Conference, Québec, QC, Canada, 21–24 July 2015. [Google Scholar]
- LaRocque, L.A.; Imran, J.; Chaudhry, M.H. 3D numerical simulation of partial breach dam-break flow using the LES and k-ε. J. Hydraul. Res. 2013, 51, 145–157. [Google Scholar] [CrossRef]
- Ritter, A. Die Fortpflanzung der Wasserwellen (The propagation of water waves). Z. Ver. Dtsch. Ing. 1892, 36, 947–954. [Google Scholar]
- Dressler, R.F. Hydraulic resistance effect upon the dam-break functions. J. Res. Nat. Bur. Stand. 1952, 49, 217–225. [Google Scholar] [CrossRef]
- Dressler, R.F. Comparison of theories and experiments for the hydraulic dam-break wave. Int. Assoc. Sci. Hydrol. 1954, 38, 319–328. [Google Scholar]
- Whitham, G.B. The effects of hydraulic resistance in the dam-break problem. Proc. R. Soc. Lond. 1955, 227A, 399–407. [Google Scholar] [CrossRef]
- Stoker, J.J. Water Waves: The Mathematical Theory with Applications; Wiley and Sons: New York, NY, USA, 1957; ISBN 0-471-57034-6. [Google Scholar]
- Marshall, G.; Méndez, R. Computational Aspects of the Random Choice Method for Shallow Water Equations. J. Comput. Phys. 1981, 39, 1–21. [Google Scholar] [CrossRef]
- Godunov, S.K. Finite Difference Methods for the Computation of Discontinuous Solutions of the Equations of Fluid Dynamics. Math. Sb. 1959, 47, 271–306. [Google Scholar]
- Toro, E.F. Shock-Capturing Methods for Free-Surface Shallow Flows; Wiley and Sons Ltd.: New York, NY, USA, 2001. [Google Scholar]
- Chanson, H. Application of the method of characteristics to the dam break wave problem. J. Hydraul. Res. 2009, 47, 41–49. [Google Scholar] [CrossRef]
- Cagatay, H.; Kocaman, S. Experimental Study of Tail Water Level Effects on Dam-Break Flood Wave Propagation; 2008 Kubaba Congress Department and Travel Services: Ankara, Turkey, 2008; pp. 635–644. [Google Scholar]
- Stansby, P.K.; Chegini, A.; Barnes, T.C.D. The initial stages of dam-break flow. J. Fluid Mech. 1998, 374, 407–424. [Google Scholar] [CrossRef]
- Soares-Frazao, S.; Zech, Y. Dam Break in Channels with 90° Bend. J. Hydraul. Eng. 2002, 128, 956–968. [Google Scholar] [CrossRef]
- Zolghadr, M.; Hashemi, M.R.; Zomorodian, S.M.A. Assessment of MIKE21 model in dam and dike-break simulation. IJST-Trans. Mech. Eng. 2011, 35, 247–262. [Google Scholar]
- Bukreev, V.I.; Gusev, A.V. Initial stage of the generation of dam-break waves. Dokl. Phys. 2005, 50, 200–203. [Google Scholar] [CrossRef]
- Soares-Frazao, S.; Noel, B.; Zech, Y. Experiments of dam-break flow in the presence of obstacles. Proc. River Flow 2004, 2, 911–918. [Google Scholar]
- Aureli, F.; Maranzoni, A.; Mignosa, P.; Ziveri, C. Dambreak flows: Acquisition of experimental data through an imaging technique and 2D numerical modelling. J. Hydraul. Eng. 2008, 134, 1089–1101. [Google Scholar] [CrossRef]
- Rehman, K.; Cho, Y.S. Bed Evolution under Rapidly Varying Flows by a New Method for Wave Speed Estimation. Water 2016, 8, 212. [Google Scholar] [CrossRef]
- Wu, G.F.; Yang, Z.H.; Zhang, K.F.; Dong, P.; Lin, Y.T. A Non-Equilibrium Sediment Transport Model for Dam Break Flow over Moveable Bed Based on Non-Uniform Rectangular Mesh. Water 2018, 10, 616. [Google Scholar] [CrossRef]
- Ferrari, A.; Fraccarollo, L.; Dumbser, M.; Toro, E.F.; Armanini, A. Three-dimensional flow evolution after a dam break. J. Fluid Mech. 2010, 663, 456–477. [Google Scholar] [CrossRef]
- Liang, D. Evaluating shallow water assumptions in dam-break flows. Proc. Inst. Civ. Eng. Water Manag. 2010, 163, 227–237. [Google Scholar] [CrossRef]
- Biscarini, C.; Francesco, S.D.; Manciola, P. CFD modelling approach for dam break flow studies. Hydrol. Earth Syst. Sci. 2010, 14, 705–718. [Google Scholar] [CrossRef]
- Oertel, M.; Bung, D.B. Initial stage of two-dimensional dam-break waves: Laboratory versus VOF. J. Hydraul. Res. 2012, 50, 89–97. [Google Scholar] [CrossRef]
- Quecedo, M.; Pastor, M.; Herreros, M.I.; Merodo, J.A.F.; Zhang, Q. Comparison of two mathematical models for solving the dam break problem using the FEM method. Comput. Method Appl. Mech. Eng. 2005, 194, 3984–4005. [Google Scholar] [CrossRef]
- Shigematsu, T.; Liu, P.L.F.; Oda, K. Numerical modeling of the initial stages of dam-break waves. J. Hydraul. Res. 2004, 42, 183–195. [Google Scholar] [CrossRef]
- Soares-Frazao, S. Experiments of dam-break wave over a triangular bottom sill. J. Hydraul. Res. 2007, 45, 19–26. [Google Scholar] [CrossRef]
- Ozmen-Cagatay, H.; Kocaman, S. Dam-break flows during initial stage using SWE and RANS approaches. J. Hydraul. Res. 2010, 48, 603–611. [Google Scholar] [CrossRef]
- Vasquez, J.; Roncal, J. Testing River2D and FLOW-3D for Sudden Dam-Break Flow Simulations. In Proceedings of the Canadian Dam Association’s 2009 Annual Conference: Protecting People, Property and the Environment, Whistler, BC, Canada, 3–8 October 2009. [Google Scholar]
- Ozmen-Cagatay, H.; Kocaman, S. Dam-break flow in the presence of obstacle: Experiment and CFD simulation. Eng. Appl. Comput. Fluid 2011, 5, 541–552. [Google Scholar] [CrossRef]
- Ozmen-Cagatay, H.; Kocaman, S.; Guzel, H. Investigation of dam-break flood waves in a dry channel with a hump. J. Hydro-Environ. Res. 2014, 8, 304–315. [Google Scholar] [CrossRef]
- Gu, S.L.; Zheng, S.P.; Ren, L.Q.; Xie, H.W.; Huang, Y.F.; Wei, J.H.; Shao, S.D. SWE-SPHysics Simulation of Dam Break Flows at South-Gate Gorges Reservoir. Water 2017, 9, 387. [Google Scholar] [CrossRef]
- Evangelista, S. Experiments and Numerical Simulations of Dike Erosion due to a Wave Impact. Water 2015, 7, 5831–5848. [Google Scholar] [CrossRef]
- Bocci, M.; Chiarlo, R.; De Nat, L.; Fanelli, A.; Petersen, O.; Sorensen, J.T.; Friss-Christensen, A. Modelling of impacts from a long sea outfall outside of the Venice Lagoon (Italy). In Proceedings of the MWWD—IEMES 2006 Conference, Antalya, Turkey, 6–10 November 2006; MWWD Organization: Antalya, Turkey, 2006. [Google Scholar]
- Nikolaos, T.F.; Georgios, M.H. Three-dimensional numerical simulation of wind-induced barotropic circulation in the Gulf of Patras. Ocean Eng. 2010, 37, 355–364. [Google Scholar]
- Goyal, R.; Rathod, P. Hydrodynamic Modelling for Salinity of Singapore Strait and Johor Strait using MIKE 3FM. In Proceedings of the 2011 2nd International Conference on Environmental Science and Development, Singapore, 26–28 February 2011. [Google Scholar]
- Khankandi, A.F.; Tahershamsi, A.; Soares-Frazão, S. Experimental investigation of reservoir geometry effect on dam-break flow. J. Hydraul. Res. 2012, 50, 376–387. [Google Scholar] [CrossRef]
- Flow Science Inc. FLOW-3D User’s Manuals; Flow Science Inc.: Santa Fe, NM, USA, 2007. [Google Scholar]
- Danish Hydraulic Institute (DHI). MIKE 3 Flow Model FM. Hydrodynamic Module-User Guide; DHI: Horsholm, Denmark, 2014. [Google Scholar]
- Pilotti, M.; Tomirotti, M.; Valerio, G. Simplified Method for the Characterization of the Hydrograph following a Sudden Partial Dam Break. J. Hydraul. Eng. 2010, 136, 693–704. [Google Scholar] [CrossRef]
- Hooshyaripor, F.; Tahershamsi, A.; Razi, S. Dam break flood wave under different reservoir’s capacities and lengths. Sādhanā 2017, 42, 1557–1569. [Google Scholar] [CrossRef]
- Kocaman, S.; Ozmen-Cagatay, H. Investigation of dam-break induced shock waves impact on a vertical Wall. J. Hydrol. 2015, 525, 1–12. [Google Scholar] [CrossRef]
- Liu, H.; Liu, H.J.; Guo, L.H.; Lu, S.X. Experimental Study on the Dam-Break Hydrographs at the Gate Location. J. Ocean Univ. China 2017, 16, 697–702. [Google Scholar] [CrossRef]
- Marra, D.; Earl, T.; Ancey, C. Experimental Investigations of Dam Break Flows down an Inclined Channel. In Proceedings of the 34th World Congress of the International Association for Hydro- Environment Research and Engineering: 33rd Hydrology and Water Resources Symposium and 10th Conference on Hydraulics in Water Engineering, Brisbane, Australia, 26 June–1 July 2011. [Google Scholar]
- Wang, J.; Liang, D.F.; Zhang, J.X.; Xiao, Y. Comparison between shallow water and Boussinesq models for predicting cascading dam-break flows. Nat. Hazards 2016, 83, 327–343. [Google Scholar] [CrossRef]
- Yang, C.; Lin, B.L.; Jiang, C.B.; Liu, Y. Predicting near-field dam-break flow and impact force using a 3D model. J. Hydraul. Res. 2010, 48, 784–792. [Google Scholar] [CrossRef]

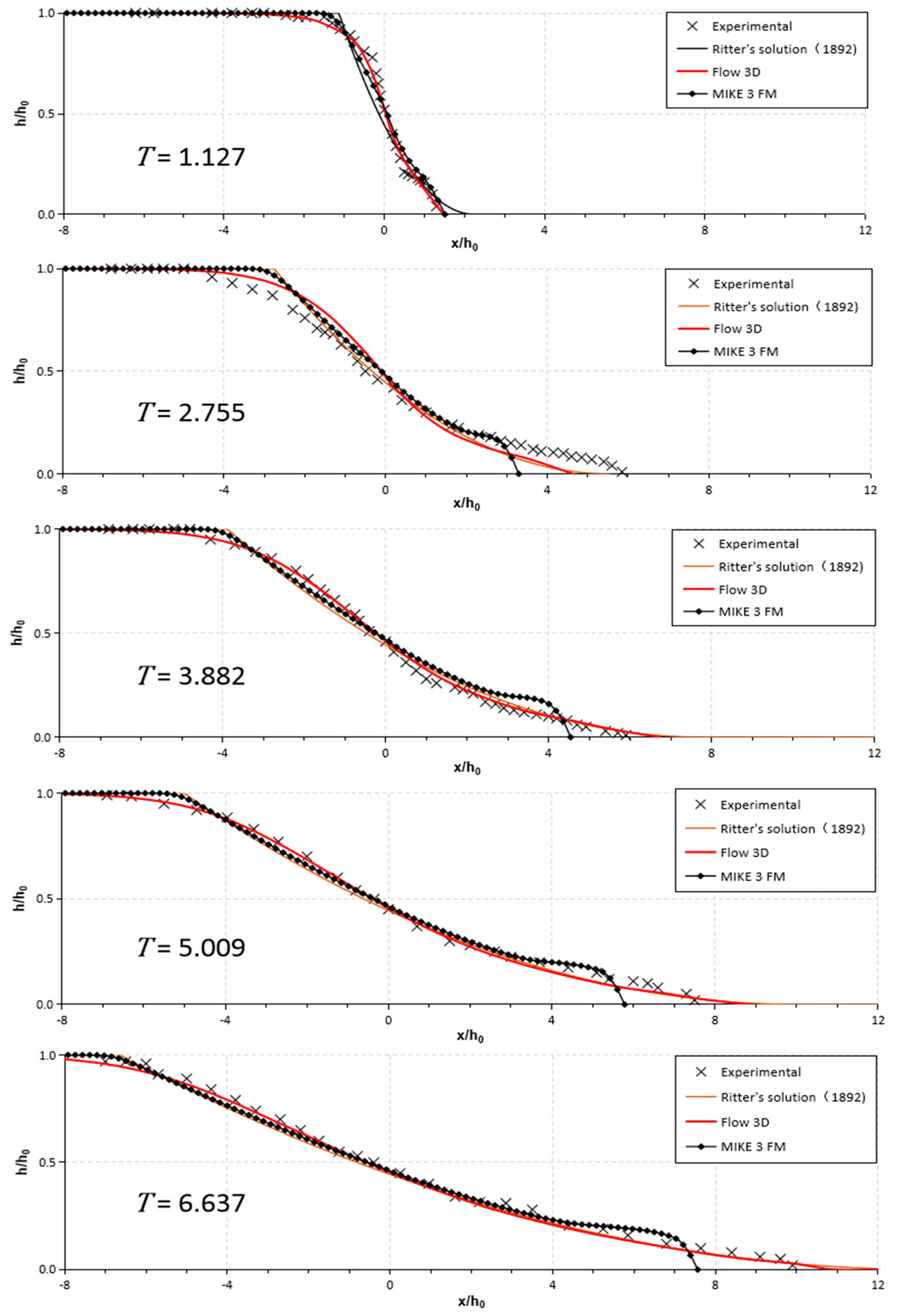
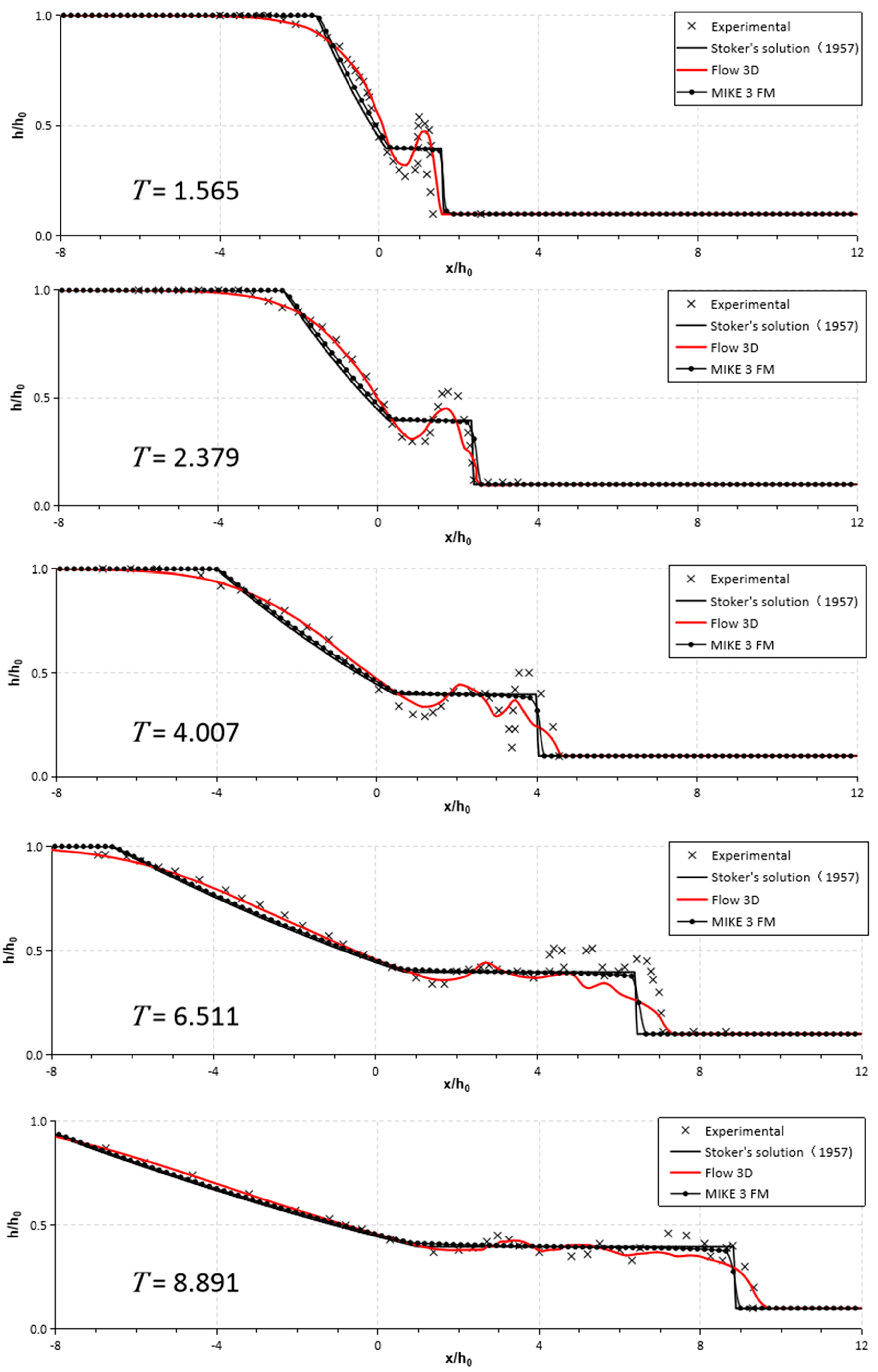
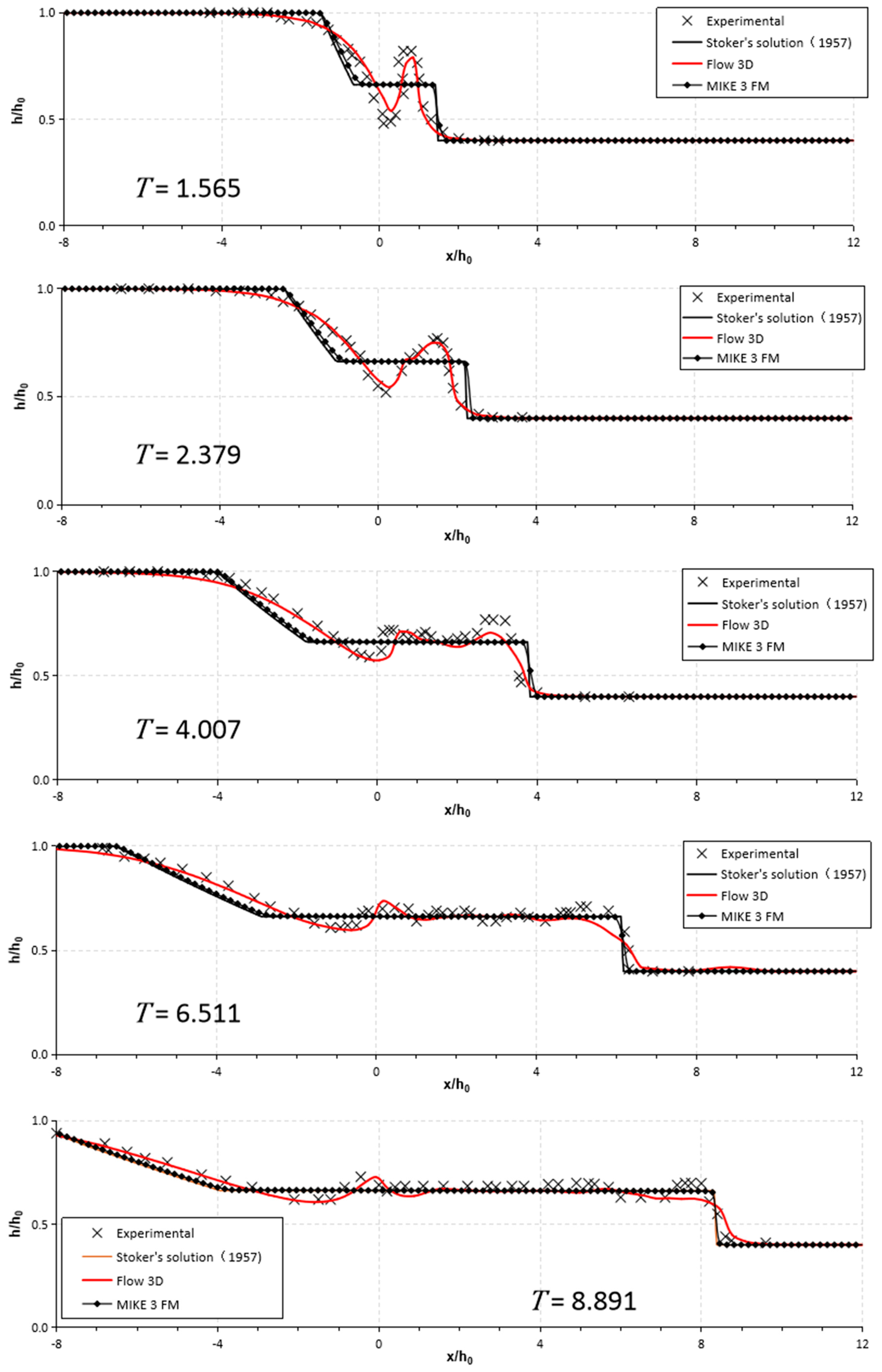
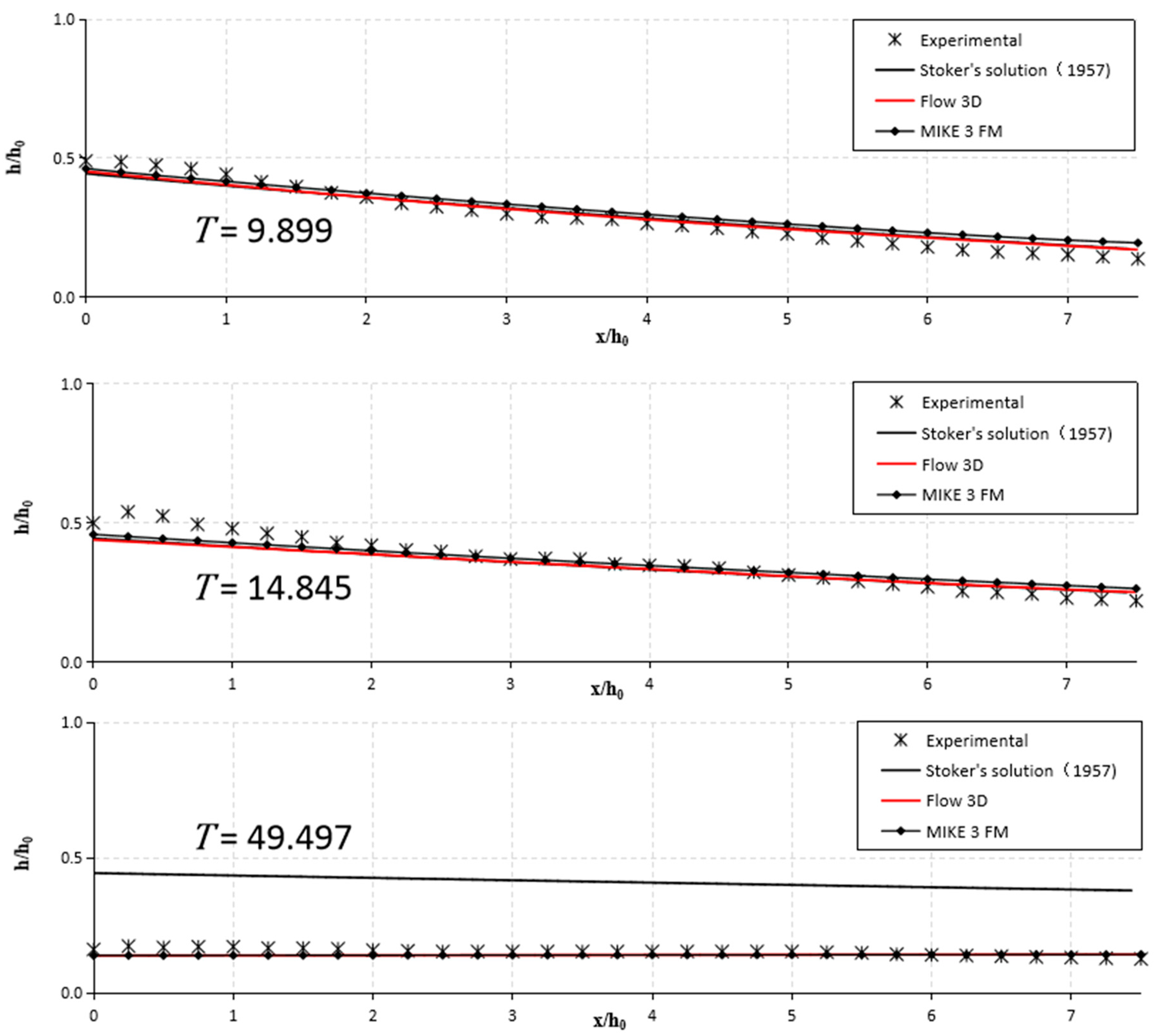
| Water Depth Ratios | Time T (-) | RMSE | ||
|---|---|---|---|---|
| Analytical Solution | Flow 3D | MIKE 3 FM | ||
| 0 | 1.127 | 0.07 | 0.04 | 0.05 |
| 2.755 | 0.05 | 0.06 | 0.06 | |
| 3.882 | 0.04 | 0.02 | 0.04 | |
| 5.009 | 0.03 | 0.02 | 0.04 | |
| 6.637 | 0.03 | 0.02 | 0.04 | |
| 0.1 | 1.565 | 0.10 | 0.09 | 0.09 |
| 2.379 | 0.07 | 0.05 | 0.07 | |
| 4.007 | 0.10 | 0.08 | 0.09 | |
| 6.511 | 0.10 | 0.08 | 0.10 | |
| 8.891 | 0.05 | 0.04 | 0.05 | |
| 0.4 | 1.565 | 0.09 | 0.06 | 0.09 |
| 2.379 | 0.08 | 0.02 | 0.07 | |
| 4.007 | 0.07 | 0.05 | 0.06 | |
| 6.511 | 0.05 | 0.03 | 0.04 | |
| 8.891 | 0.04 | 0.04 | 0.03 | |
| Water Depth Ratios | Time T (-) | RMSE | ||
|---|---|---|---|---|
| Analytical Solution | Flow 3D | MIKE 3 FM | ||
| 0 | 9.899 | 0.03 | 0.03 | 0.04 |
| 14.845 | 0.04 | 0.04 | 0.04 | |
| 49.497 | 0.26 | 0.02 | 0.02 | |
| Water Depth Ratios | Probe | RMSE | |
|---|---|---|---|
| Flow 3D | MIKE 3 FM | ||
| 0 | G1 | 0.02 | 0.02 |
| G2 | 0.01 | 0.02 | |
| G3 | 0.03 | 0.04 | |
| G4 | 0.01 | 0.01 | |
| G6 | 0.02 | 0.02 | |
| G8 | 0.01 | 0.01 | |
| 0.1 | G1 | 0.02 | 0.03 |
| G2 | 0.04 | 0.03 | |
| G4 | 0.02 | 0.02 | |
| G5 | 0.02 | 0.02 | |
| Water Depth Ratios | Probe | RMSE | |
|---|---|---|---|
| Flow 3D | MIKE 3 FM | ||
| 0 | G4 | 0.26 | 0.23 |
| G6 | 0.29 | 0.26 | |
| Experimental Group | No. of Grids | Computation Time (s) | ||
|---|---|---|---|---|
| MIKE 3 FM | Flow-3D | MIKE 3 FM | Flow-3D | |
| Test 1 ( | 267 | 106,800 | 5 min | 120 min |
| Test 2 ( | 267 | 106,800 | 5 min | 120 min |
| Test 3 ( | 267 | 106,800 | 5 min | 120 min |
| Test 4 ( | 2860 | 256,000 | 9 min | 480 min |
| Test 5 ( | 2860 | 256,000 | 9 min | 480 min |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, H.; Zhang, J.; Li, T. Dam-Break Flows: Comparison between Flow-3D, MIKE 3 FM, and Analytical Solutions with Experimental Data. Appl. Sci. 2018, 8, 2456. https://doi.org/10.3390/app8122456
Hu H, Zhang J, Li T. Dam-Break Flows: Comparison between Flow-3D, MIKE 3 FM, and Analytical Solutions with Experimental Data. Applied Sciences. 2018; 8(12):2456. https://doi.org/10.3390/app8122456
Chicago/Turabian StyleHu, Hui, Jianfeng Zhang, and Tao Li. 2018. "Dam-Break Flows: Comparison between Flow-3D, MIKE 3 FM, and Analytical Solutions with Experimental Data" Applied Sciences 8, no. 12: 2456. https://doi.org/10.3390/app8122456
APA StyleHu, H., Zhang, J., & Li, T. (2018). Dam-Break Flows: Comparison between Flow-3D, MIKE 3 FM, and Analytical Solutions with Experimental Data. Applied Sciences, 8(12), 2456. https://doi.org/10.3390/app8122456





