MIM_SLAM: A Multi-Level ICP Matching Method for Mobile Robot in Large-Scale and Sparse Scenes
Abstract
1. Introduction
- ▪
- In sparse environments, due to the scarce environmental information perceived by a 3D LIDAR sensor and the non-flat road, data association is easy to fall into a local minimum. Liu [14] proposes a LiDAR SLAM method in natural terrains which fuses multiple sensors including two 3D LiDAR. Therefore, the robustness of data associated with a lower accumulated error should be strengthened.
- ▪
- In large-scale environments, it is difficult to obtain a reasonable pose estimation when the robot returns to a region it has previously explored and then generates an inconsistent map. Liang [15] addresses the laser-based loop closure problem by fusing visual information. Hess [16] can achieve real-time mapping in indoor scenes, and it may fail in the closing loop due to the incremental computation in large-scale outdoor scenes. How to reduce the computational complexity of graph optimization is also a problem that needs to be improved.
2. Algorithm Overview
3. Algorithm Description
3.1. SLAM as an Incremental Optimization Problem
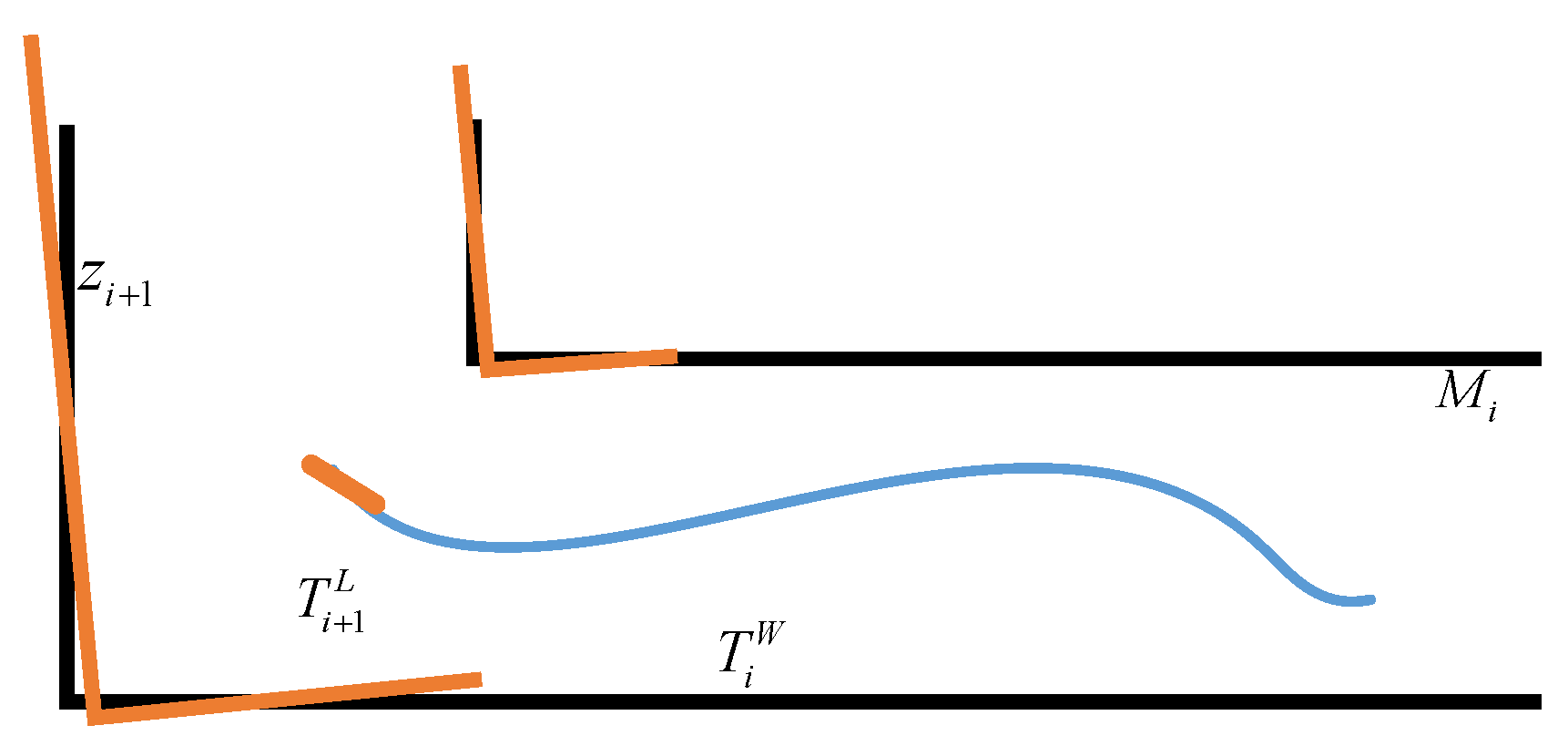
3.2. The Multi-Level ICP Matching Method
| Algorithm 1: Point-to-plane ICP. |
| Input: Two point cloud: , ; An initial transformation: Output: Transformation which aligns and ; Fitness Score: |
| 1: |
| 2: while not converged do |
| 3: for do |
| 4: |
| 5: if then |
| 6: else |
| 7: end |
| 8: end |
| 9: |
| 10: end |
| 11: |
| 12: |
- ▪
- Finding the nearest neighbor in for each point in , and saving it as . We use the combination of octree and approximate nearest neighbor algorithm in PCL [23] for speeding up.
- ▪
- Taking and as the input of Algorithm 1, the transformation matrix can be obtained after registering the two point clouds.
- ▪
- The pose of the robot at time is .
| Algorithm 2: Matching the current frame with an area-neighbor keyframe. |
| Input: Current pose and observation: Output: Transformation which aligns and |
| 1: calculate |
| 2: if then |
| 3: return null |
| 4: end |
| 5: foreach in do |
| 6: if then |
| 7: if then |
| 8: put and into Algorithm 1, get and |
| 9: if then |
| 10: |
| 11: return |
| 12: end |
| 13: end |
| 14: end |
| 15: end |
| 16: |
| 17: return null |
3.3. Uncertainty Estimation
4. Experimental Results and Analysis
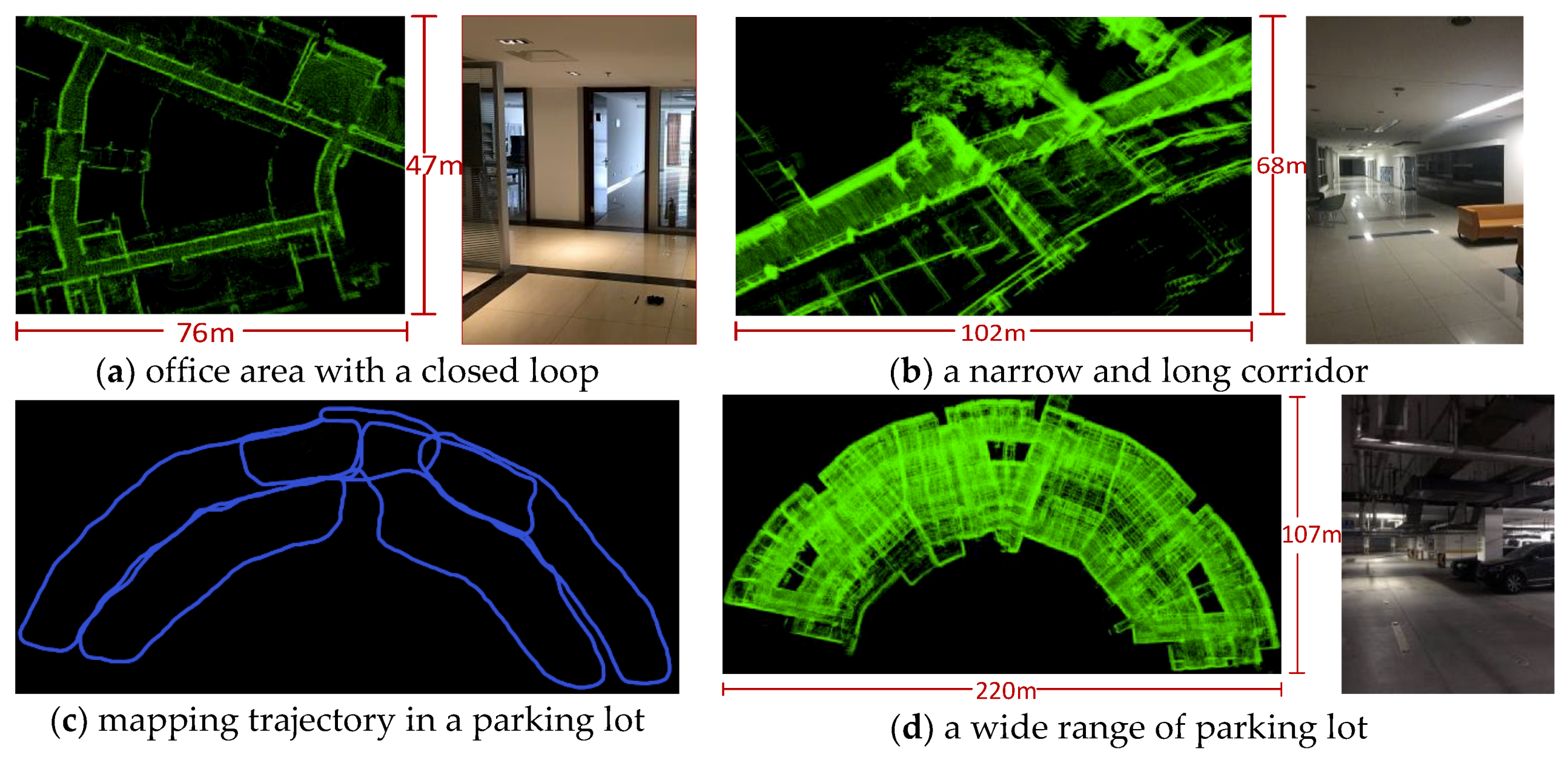
4.1. Indoor and Outdoor Mapping Test
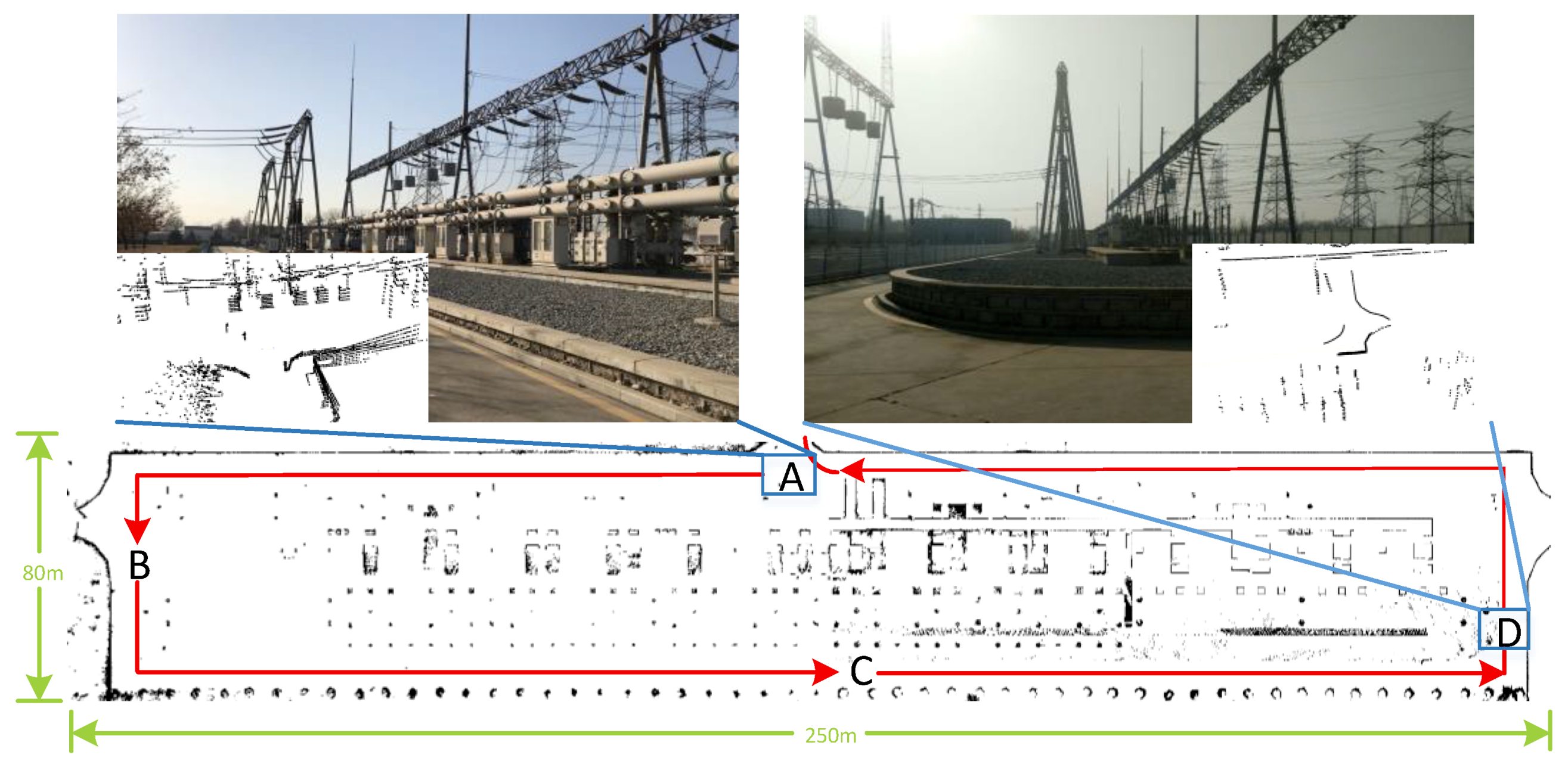
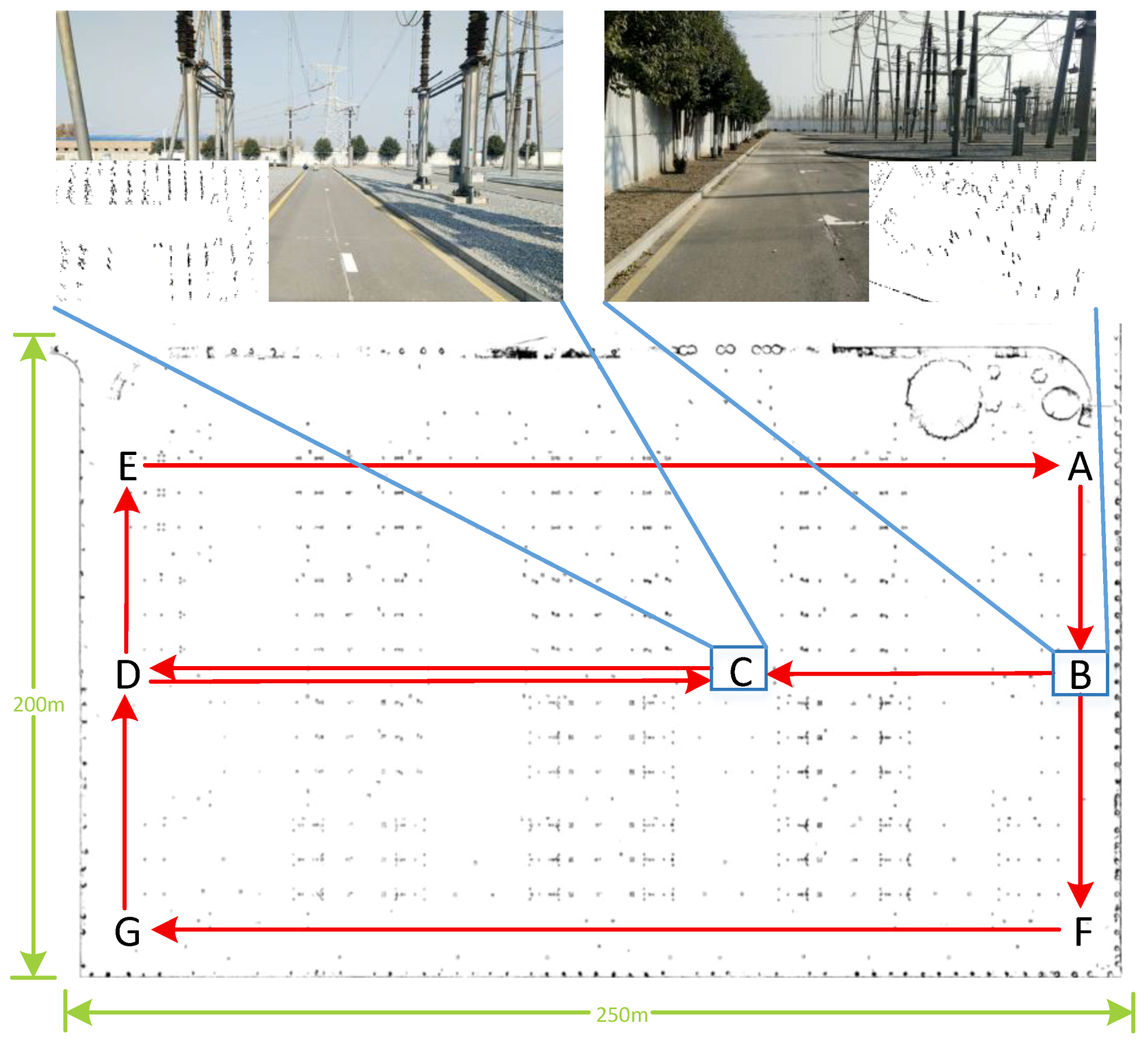
4.2. Large-Scale and Sparse Scenes Test
4.3. Mapping Accuracy Test
4.4. Benchmarking Datasets Test
- (1)
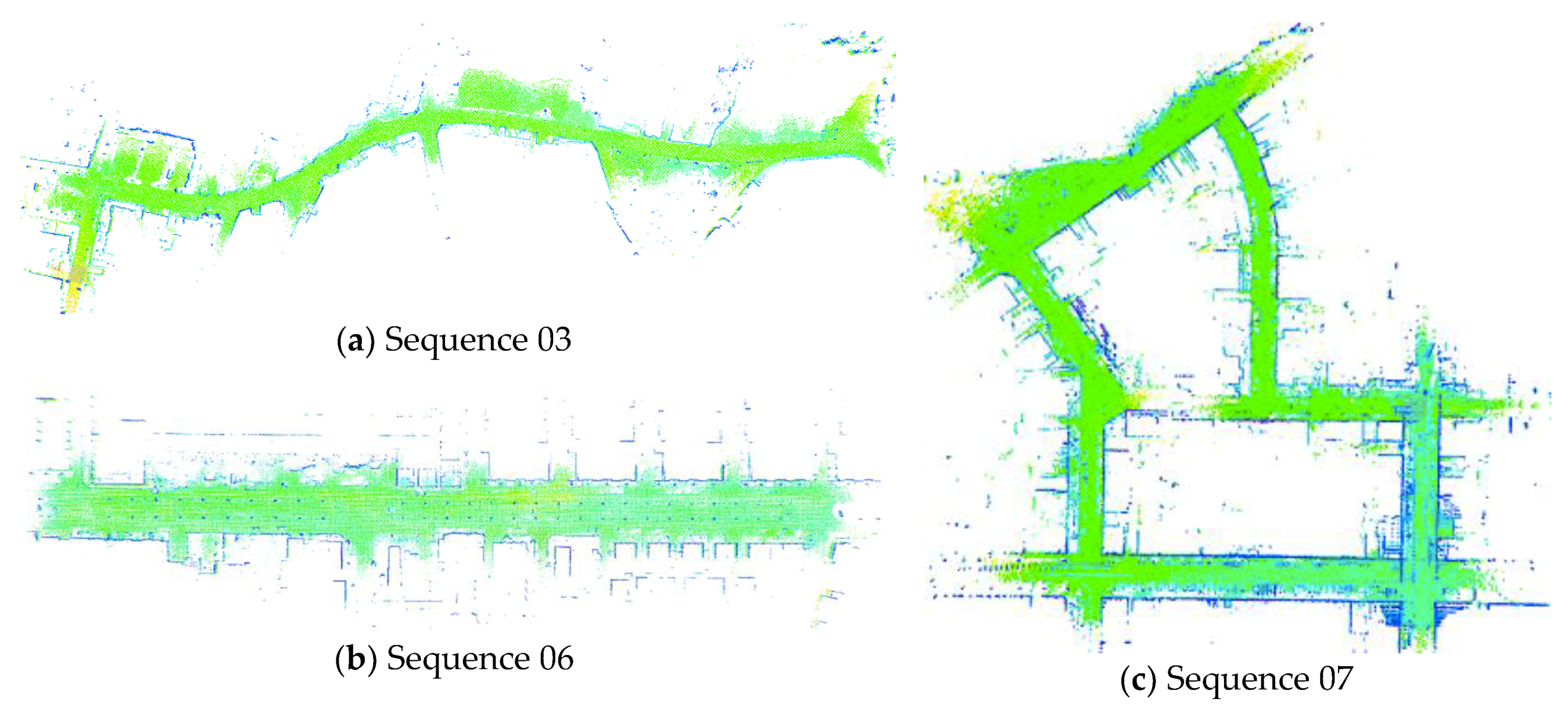
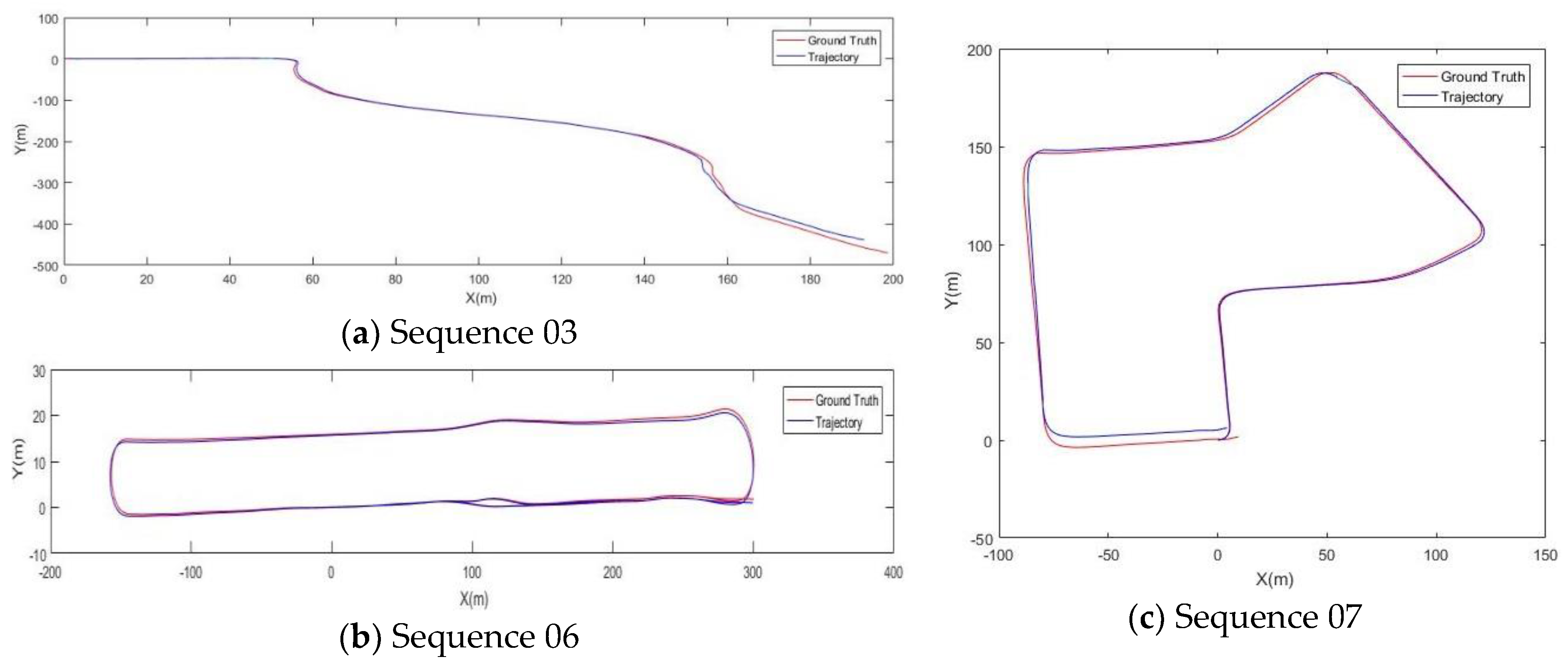
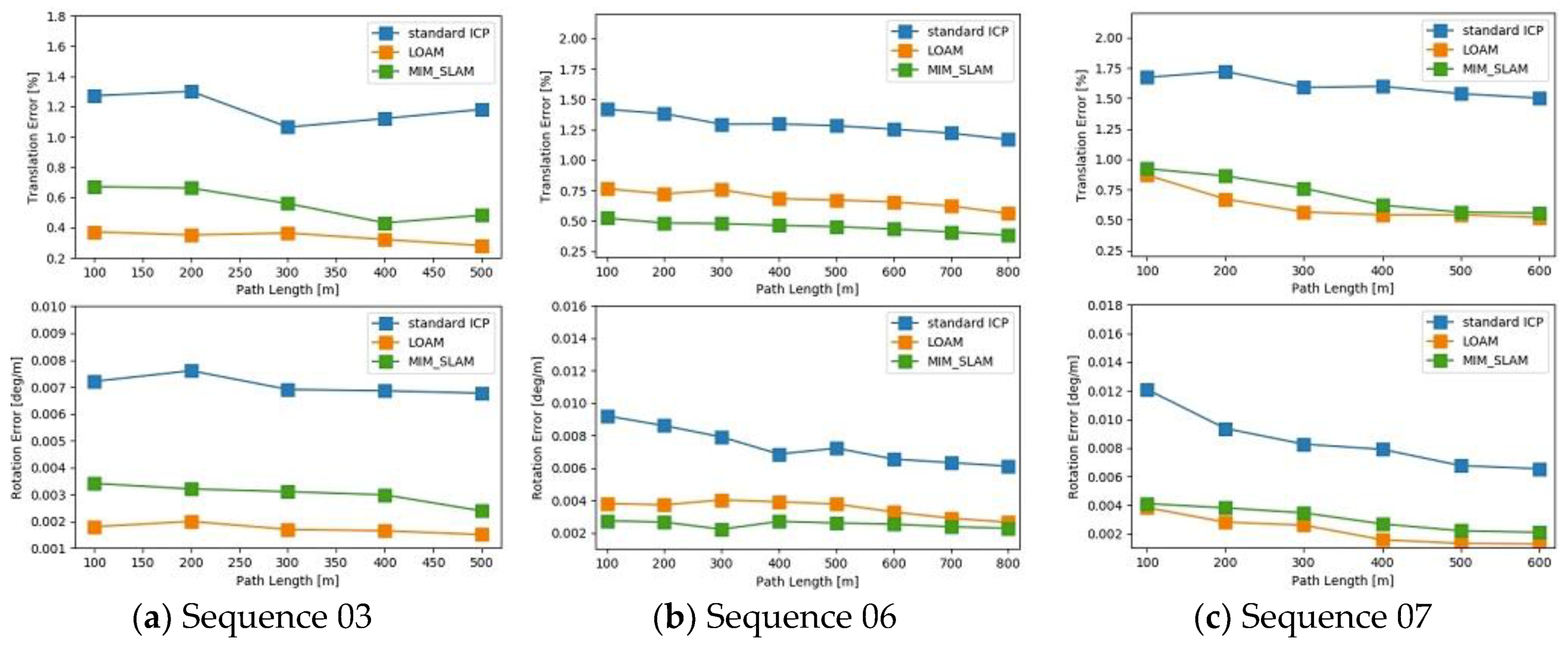
- Sequence 03: This dataset is designed to verify that MIM_SLAM can achieve a low drift pose estimation in sparse vegetation environment. The mapping result is shown in Figure 10a and the trajectory and the ground truth are shown in Figure 11a. Due to the scarce stable features in this scene, there is a bit of position deviation after 420 m of traveling compared with the ground truth in Figure 11a. To evaluate the pose estimation accuracy, we use the evaluation method in the KITTI odometry benchmark which calculated the translational and rotational errors for all possible subsequences of length (100, 200, …, 800) meters. As is shown in Figure 12a, both LOAM and MIM_SLAM achieve lower drift values compared with the standard ICP method, and MIM_SLAM is slightly worse than LOAM.
- (2)
- Sequence 06: We use this dataset to verify that MIM_SLAM can effectively process the data association of the closed-loop area shown in Figure 10b and Figure 11b. From Figure 12b, it can be seen that the translational and rotational errors are lower compared to the standard ICP, and slightly better than LOAM.
- (3)
- Sequence 07: This urban road scene is highly dynamic and large-scale. The vehicle travels approximately 660 m at a speed of 6.2 m/s. The mapping result is shown in Figure 10c and the trajectory and the ground truth are shown in Figure 11c. Intuitively, the details of the point cloud map are clear. The estimated pose and the ground truth are almost overlapping. The pose estimation error is shown in Figure 12c quantitatively.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Martínez, J.L.; Morán, M.; Morales, J.; Reina, A.J.; Zafra, M. Field Navigation Using Fuzzy Elevation Maps Built with Local 3D Laser Scans. Appl. Sci. 2018, 8, 397. [Google Scholar] [CrossRef]
- Smith, R.; Cheeseman, P. On the Estimation and Representations of Spatial Uncertainty. Int. J. Robot. Res. 1987, 5, 56–68. [Google Scholar] [CrossRef]
- Shinsuke, M.M.D.; Noboru, I.M.D.; Yoshito, I.M.D. Estimating Uncertain Spatial Relationships in Robotics. Mach. Intell. Pattern Recognit. 2013, 5, 435–461. [Google Scholar]
- Thrun, S.; Liu, Y.; Koller, D.; Ng, A.Y.; Ghahramani, Z.; Durrant-Whyte, H. Simultaneous localization and mapping with sparse extended information filters. Int. J. Robot. Res. 2004, 23, 693–716. [Google Scholar] [CrossRef]
- Montemerlo, M.S. Fastslam: A factored solution to the simultaneous localization and mapping problem with unknown data association. Arch. Environ. Contam. Toxicol. 2015, 50, 240–248. [Google Scholar]
- Gutmann, J.S.; Konolige, K. Incremental mapping of large cyclic environments. In Proceedings of the 1999 IEEE International Symposium on Computational Intelligence in Robotics and Automation (CIRA ’99), Monterey, CA, USA, 8–9 November 2002; pp. 318–325. [Google Scholar]
- Zlot, R.; Bosse, M. Efficient large-scale 3D mobile mapping and surface reconstruction of an underground mine. In Field and Service Robotics; Springer: Berlin/Heidelberg, Germany, 2014; pp. 479–493. [Google Scholar]
- Olufs, S.; Vincze, M. An efficient area-based observation model for monte-carlo robot localization. In Proceedings of the 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2009), St. Louis, MO, USA, 10–15 October 2009; pp. 13–20. [Google Scholar]
- Huang, S.; Wang, Z.; Dissanayake, G. Sparse local submap joining filter for building large-scale maps. IEEE Trans. Robot. 2008, 24, 1121–1130. [Google Scholar] [CrossRef]
- Moosmann, F.; Stiller, C. Velodyne slam. In Proceedings of the 2011 IEEE Intelligent Vehicles Symposium (IV), Baden, Germany, 5–9 June 2011; pp. 393–398. [Google Scholar]
- Nüchter, A.; Lingemann, K.; Hertzberg, J.; Surmann, H. 6D SLAM-3D mapping outdoor environments. J. Field Robot. 2007, 24, 699–722. [Google Scholar] [CrossRef]
- Zhang, J.; Singh, S. LOAM: Lidar Odometry and Mapping in Real-time. In Proceedings of the 2014 Robotics: Science and Systems, Berkeley, CA, USA, 12–16 July2014; Volume 2. [Google Scholar]
- Wang, J.; Li, L.; Zhe, L.; Weidong, C. Multilayer matching SLAM for large-scale and spacious environments. Int. J. Adv. Robot. Syst. 2015, 12, 124. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, H.; Di, H.; Tao, Y.; Gong, J.; Xiong, G.; Qi, J. Real-Time 6D Lidar SLAM in Large Scale Natural Terrains for UGV. In Proceedings of the 2018 IEEE Intelligent Vehicles Symposium (IV), Changshu, China, 26–30 June 2018; pp. 662–667. [Google Scholar]
- Liang, X.; Chen, H.; Li, Y.; Liu, Y. Visual laser-SLAM in large-scale indoor environments. In Proceedings of the IEEE International Conference on Robotics and Biomimetics, Qingdao, China, 3–7 December 2017; pp. 19–24. [Google Scholar]
- Hess, W.; Kohler, D.; Rapp, H.; Andor, D. Real-time loop closure in 2D LIDAR SLAM. In Proceedings of the IEEE International Conference on Robotics and Automation, Stockholm, Sweden, 16–21 May 2016; pp. 1271–1278. [Google Scholar]
- Kaess, M.; Ranganathan, A.; Dellaert, F. iSAM: Incremental smoothing and mapping. IEEE Trans. Robot. 2008, 24, 1365–1378. [Google Scholar] [CrossRef]
- Hartley, H.O. The modified Gauss-Newton method for the fitting of non-linear regression functions by least squares. Technometrics 1961, 3, 269–280. [Google Scholar] [CrossRef]
- Moré, J.J. The Levenberg-Marquardt algorithm: Implementation and theory. In Numerical Analysis; Springer: Berlin/Heidelberg, Germany, 1978; pp. 105–116. [Google Scholar]
- Besl, P.J.; Mckay, N.D. Method for registration of 3-D shapes. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 14, 239–256. [Google Scholar] [CrossRef]
- Li, L.; Liu, J.; Zuo, X.; Zhu, H. An Improved MbICP Algorithm for Mobile Robot Pose Estimation. Appl. Sci. 2018, 8, 272. [Google Scholar] [CrossRef]
- Chen, Y.; Medioni, G. Object modelling by registration of multiple range images. Image Vis. Comput. 1992, 10, 145–155. [Google Scholar] [CrossRef]
- Rusu, R.B.; Cousins, S. 3D is here: Point Cloud Library (PCL). In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 1–4. [Google Scholar]
- Liu, Z.; Chen, W.; Wang, Y.; Wang, J. Localizability estimation for mobile robots based on probabilistic grid map and its applications to localization. In Proceedings of the 2012 IEEE Conference on Multisensor Fusion and Integration for Intelligent Systems (MFI), Hamburg, Germany, 13–15 September 2015; pp. 46–51. [Google Scholar]
- Wang, Y.; Chen, W.; Wang, J.; Wang, H. Active global localization based on localizability for mobile robots. Robotica 2015, 33, 1609–1627. [Google Scholar] [CrossRef]
- Bobrovsky, B.; Zakai, M. A lower bound on the estimation error for certain diffusion processes. IEEE Trans. Inf. Theory 1976, 22, 45–52. [Google Scholar] [CrossRef]
- Wang, B.; Guo, R.; Li, B.; Han, L.; Sun, Y.; Wang, M. SmartGuard: An autonomous robotic system for inspecting substation equipment. J. Field Robot. 2012, 29, 123–137. [Google Scholar] [CrossRef]
- Burgard, W.; Stachniss, C.; Grisetti, G.; Steder, B.; Kümmerle, R.; Dornhege, C.; Ruhnke, M.; Kleiner, A.; Tardös, J.D. A comparison of SLAM algorithms based on a graph of relations. In Proceedings of the 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2009), St. Louis, MO, USA, 10–15 October 2009; pp. 2089–2095. [Google Scholar]
- Geiger, A. Are we ready for autonomous driving? The KITTI vision benchmark suite. In Proceedings of the 2012 Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 3354–3361. [Google Scholar]





| Standard ICP | LOAM | MIM_SALM | |
|---|---|---|---|
| Trans. Error (unit: m) | |||
| A | 0.213 ± 0.148 | 0.064 ± 0.057 | 0.052 ± 0.043 |
| B | 0.282 ± 0.177 | 0.075 ± 0.066 | 0.066 ± 0.062 |
| Rot. Error (unit: deg) | |||
| A | 2.5 ± 1.9 | 1.8 ± 1.2 | 1.6 ± 1.4 |
| B | 3.1 ± 2.2 | 2.5 ± 2.1 | 2.2 ± 1.8 |
| Standard ICP | LOAM | MIM_SALM | |
|---|---|---|---|
| Processing Time (unit: s) | |||
| A | 0.0405 | 0.1036 | 0.0886 |
| B | 0.0416 | 0.1067 | 0.0932 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Zhao, M.; Chen, W. MIM_SLAM: A Multi-Level ICP Matching Method for Mobile Robot in Large-Scale and Sparse Scenes. Appl. Sci. 2018, 8, 2432. https://doi.org/10.3390/app8122432
Wang J, Zhao M, Chen W. MIM_SLAM: A Multi-Level ICP Matching Method for Mobile Robot in Large-Scale and Sparse Scenes. Applied Sciences. 2018; 8(12):2432. https://doi.org/10.3390/app8122432
Chicago/Turabian StyleWang, Jingchuan, Ming Zhao, and Weidong Chen. 2018. "MIM_SLAM: A Multi-Level ICP Matching Method for Mobile Robot in Large-Scale and Sparse Scenes" Applied Sciences 8, no. 12: 2432. https://doi.org/10.3390/app8122432
APA StyleWang, J., Zhao, M., & Chen, W. (2018). MIM_SLAM: A Multi-Level ICP Matching Method for Mobile Robot in Large-Scale and Sparse Scenes. Applied Sciences, 8(12), 2432. https://doi.org/10.3390/app8122432





