Magnetic Field Effect on the Double Diffusive Natural Convection in Three-Dimensional Cavity Filled with Micropolar Nanofluid

Abstract

This article presents a three-dimensional numerical investigation of heat and mass transfers and fluid flow in a cavity filled with an Al₂O₃/water micropolar fluid under uniform magnetic field. To solve the governing non-dimensional equations, Finite Volume Method (FVM) based on 3-D vorticity-vector potential formulation has been employed. The effects of various parameters such as buoyancy ratio (−2 ≤ N ≤ 0), Rayleigh number (10³ ≤ Ra ≤ 10⁵), Hartmann number (0≤ Ha≤ 60), nanoparticles volume fraction (0 ≤ φ ≤ 0.06) and micropolar material parameter (0≤ K≤ 5) on flow structure and on heat and mass transfers are presented. The results illustrate that for the micropolar nanofluid model, both heat and mass transfer rates and three-dimensional character of the flow are smaller when compared with the pure nanofluid model. It is also observed that increase and decrease in heat and mass transfer rates is experienced due to increase in Rayleigh number and Hartmann number, respectively. It is also noted that increase in vortex viscosity parameter reduces the average heat and mass transfer rates and is more evident when the magnetic field is imposed. Combined effects of magnetic field and nanoparticles volume fraction on heat and mass transfers are also explored.

1. Introduction

In recent years, nanotechnology has attracted the research community through which an innovative technique is developed to enhance heat transfer by adding nanoparticles to pure fluid. The term ‘nanofluid’ was originally coined by Choi [1] to refer to the fluids with nanoparticle suspensions. The heat transfer characteristic of a nanofluid depends mainly on thermo-physical properties of the base fluid and the nanoparticles, along with nanoparticle’s shape, size and solid volume fraction [2,3,4]. It is clear that the addition of high thermal conductive nanoparticles to base fluid enhances thermal performance of the resultant mixtures. However, experimental investigations reveal that heat transfer is deteriorated with high nanoparticle volume fraction. Putra et al. [5] demonstrated experimentally that the Nusselt number reduces by enhancing a nanoparticle’s volume fraction for Al₂O₃/water and CuO/water. Wen and Ding [6,7] and Hwang et al. [8] confirmed similar results toPutra et al. [5]. On the other hand, the majority of computational studies reported an enhancement in heat transfer by adding nanoparticles. Khanafer et al. [9] critically analyzed the diverse models of nanofluids by measuring density, thermal expansion coefficients and viscosity. His findings establish that the heat transfer rate is amplified due to suspended nanoparticles. Jou and Tzeng [10] worked on Khanafer’s model and remarked that as the nanoparticle’s volume fraction increases, the average heat transfer coefficient enhances. Oztop and Abu-Nada [11] numerically investigated the natural convection in nanofluids by using FVM inpartially heated enclosures with different aspect ratios and established that the Nusselt numberwas augmented with an increase inthe nanoparticle’s volume fraction and Rayleigh number. Ho et al. [12] also observed the heat transfer rate enhancement with the addition of nanoparticles. Bouhalleb and Abbassi [13] carried out numerical investigation of natural convection in CuO–Water nanofluid within rectangular enclosures and ascertained that addition of CuO nanoparticles enhanced the heat transfer. Mahfoud and Bendjaghloli [14] used FVM to employ numerical investigation of natural convection in a truncated cone and found an heat transfer characteristics of cooling device by adding Cu–water nanofluid. In addition, the heat source length and inclined sidewalls’ angle influence the maximum temperature and the heat transfer rate.

Most researchers predicted an enhancement in heat transfer by the addition of nanoparticles. On the contrary, some researchers reported the deterioration in heat transfer. The mitigation or enhancement in heat transfer of nanofluid may be because of the hypothesis employed in the theoretical models used for their thermal properties. Hence, most of the numerical works assume that nanoparticles are in thermal equilibrium with the fluid and there is no slip between the nanoparticles and fluid molecules. Polidori et al. [15] given theoretical prediction for the experimental results of natural convection in an Al₂O₃–water nanofluid an external boundary layer and concluded that the models used for nanofluid viscosity and effective thermal conductivity model influenced the heat transfer rate. Ahuja [16] claimed from his experimental works that the augmentation in heat transfer may be due to the rotation of nanoparticles about their own axis due to the shear stress effect, and subsequently a three-dimensional hydrodynamic boundary layer was also observed.

The rotating micro-constituents’ effects in nanofluids should be considered to understand the fluid flow behavior in a better way and hence the micropolar theory explains the difference between experimental and numerical observations. This theory was originally proposed by Eringen [17] to elucidate fluid particles’ micro-motions which cannot be explained by the classical models. The aforementioned subject has been recently reviewed by Ariman et al. [18] and Lukaszewics [19]. The micropolar fluids have many engineering applications, such as the polymer fluids extrusion, animal bloods, exotic lubricants, colloidal and suspension solutions and liquid crystals solidification.

A few investigators have studied micropolar fluid natural convection in enclosures (Aydin and Pop [20], Zadravec et al. [21], Saleem et al. [22]). Jena et al. [23] has recently investigated transient micropolar double diffusive natural convection for buoyancy-opposing ratio and noticed that a monotonic decrease in the flow strength and heat and mass transfer ratesoccurs due to the vortex viscosity parameter. It should be noted that major researches in literature for the three-dimensional flow of micropolar fluids concerned numerical and/or analytical study of a flow due to stagnation point or stretching flat surface (Agarwal and et al. [24], Takhar and al. [25], Chamkha and et al. [26]).

With the wide use of a non-Newtonian fluids model with suspended particles in modern technology and industries, the extension to micropolar nanofluid model is desirable. In this context, Bourantas and Loukopoulos [27] introduced a micropolar nanofluid model to carry out theoretical investigation of natural convection in nanofluids and compared the nanofluidic suspensions with the micropolar theory. It is observed that the average Nusselt number increases with increase Rayleigh number when the microrotation number is kept constant. Hashemi et al. [28] investigated natural convection in Cu–water micropolar nanofluid with a heat-generated source in a porous medium. They found that as the material parameter increased, rotational strength of vortices and the particles micro-rotation increase and decrease, respectively. Hussanan et al. [29] explored the transient natural convection in micropolar nanofluid on a vertical plate using five types of oxide nanoparticles. They established that the temperature of nanofluid based on graphene oxide is much higher than the other nanofluids.

Magneto-convection research has been of extensive interest due to its vast engineering applications such as microelectronic mechanical devices, electronic packaging, and crystal growth in liquids [30]. Most of the researchers considered an electrically conducting fluid with low thermal conductivity which, in turn, restricts the heat-transfer enhancement in the cavity, and the use of nanofluid is a better option to improve the mechanism of heat transfer. Ghasemi et al. [31] considered the magnetic field impact on an Al₂O₃ water-nanofluid natural convection flow in square cavity and found that the heat transfer deteriorated with increased Hartmann number. Teamaha and El-Maghlany [32] investigated, numerically, nanofluid natural convection flow in a square enclosure in the presence of uniform generation and absorption of heat and magnetic field. They concluded that heat transfer is enhanced with solid nanoparticles’ volume fraction but decreased when the Hartmann number increased. Mahmoudi et al. [33] examined the natural convection in a two-dimensional triangular enclosure filled with nanofluid under the influence of magnetic field and noticed that the nanoparticles are more efficient once the Raleigh number is as high as 10⁴. Mahmoudi and Abu-Nada [34] conducted numerical investigation of natural convection in CuO-water nanofluid to understand the impact of hydromagnetic heat transfer on. They analyzed the combined impact of both high magnetic field and nanofluids in heat transfer enhancement. Sheikholeslami et al. [35] studied the magnetic field impact on natural convection in Cu–water nanofluid and claimed that increase in nanoparticle volume fraction and Rayleigh number increases the average Nusselt number; however, it diminishes as the Hartmann number increases. Similar finding are reported by Zhou and Yan [36]. Abbassi et al. [37] carried out the lattice Boltzmann method based numerical investigation of natural convection in nanofluid with nanoparticle’s Brownian motion in open cavity under the influence of magnetic field. The authors found that heat transfer was reduced due to the addition of nanoparticles. Furthermore, the Brownian motion significantly affects the heat transfer rate according to the Rayleigh number, Hartmann number, and nanoparticle volume fraction. Al Kalbani et al. [38] experimented with different types of nanofluids with various shapes of nanoparticles and analyzed the oriented magnetic field effect on natural convection in an inclined square enclosure. They established that an increase in Rayleigh number and the nanoparticles’ volume fraction enhance the heat transfer, whereas the increase in Hartmann number reduced by the same. Javed et al. [39] carried out numerical investigation of flow of Cu-water nanofluid flow inside an isosceles triangular cavity under uniform magnetic field and illustrated that the flow strength enhanced as Rayleigh number increases and deteriorated as the Hartman number increases. Using the lattice Boltzmann method, Abbassi et al. [40] considered the nanofluid (water-Al2O3) flow in an incinerator-shaped enclosure with a heated source situated at the bottom. They found that the Rayleigh number, the nanoparticles volume fraction and the heat source height enhanced the heat transfer and influenced the flow and thermal structures. Bourantas and Loukopoulos [41] studied the effect of magnetic field on natural convection in micropolar nanofluid inside an inclined rectangular cavity and remarked that the thermal properties of the base fluid are altered by the presence of nanoparticles.

It is worth mentioning that very few papers have investigated the magnetic field effect on double diffusive convection in nanofluid. Akbar et al. [42] used Buongiorno mode and examined the effect of magnetic field on nanofluid double-diffusive natural convection on a linearly stretching sheet, and they identified that buoyancy ratio and magnetic field enhance the skin friction but decrease the heat and mass transfer rates.

On the basis of the aforementioned literature review, the authors’ understand that the three-dimensional double-diffusive natural convection in micropolar nanofluid filled cavity under the influence of uniform magnetic field has not been explored so far and hence is the topic of research of this article. The influences of relevant parameters such as Rayleigh number, Hartmann number, buoyancy ratio, nanoparticles’ volume fraction, and vortex viscosity parameter on flow structure and heat are elaborately analyzed.

2. Mathematical Formulation

Consider three-dimensional double diffusive convection inside a cubical enclosure filled with incompressible viscous electrically conducting micropolar nanofluid Al₂O₃/water as shown in Figure 1. The uniform magnetic field is applied perpendicularly to the differentially heated cavity walls. The fluid thermo-physical properties are supposed to be constant except the density in the buoyancy force term which is modeled by Boussinesq approximation. The base fluid (i.e., water) and nanoparticles are assumed to be in thermal equilibrium state. The thermo-physical properties of the nanofluid are listed in

Table 1. Thermo-physical properties of pure water and Alumina (Al₂O₃) [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41].

	Pure Water	Alumina (Al2O3)
Pr	6.2
ρ (kg/m3)	997.1	8933
Cp (J/kg·K)	4179	385
k (W/m.K)	0.613	401
β (K−1)	21.10−5	1.67.10−5
σ (Ω·m)−1	0.05	1.10−10

.

The viscous dissipation, radiation and Joules heating effects are judiciously neglected.

It is also assumed that the magnetic Reynolds number is as small as the induced magnetic field is neglected.

Using the dimensionless variables below: $\mathrm{x}=\frac{{\mathrm{x}}^{\prime }}{\mathrm{L}}$, $\mathrm{y}=\frac{{\mathrm{y}}^{\prime }}{\mathrm{L}}$, $\mathrm{z}=\frac{{\mathrm{z}}^{\prime }}{\mathrm{L}}$, $\mathrm{t}=\frac{\mathsf{\alpha }{\mathrm{t}}^{\prime }}{{\mathrm{L}}^2}$ $({\mathrm{U}}_1,{\mathrm{U}}_2,{\mathrm{U}}_3)=\frac{({{\mathrm{U}}^{\prime }}_1,{{\mathrm{U}}^{\prime }}_2,{{\mathrm{U}}^{\prime }}_3)\mathrm{L}}{\mathsf{\alpha }}$, $\mathrm{T}=\frac{{\mathrm{T}}^{\prime }-{{\mathrm{T}}^{\prime }}_{\mathrm{c}}}{{{\mathrm{T}}^{\prime }}_{\mathrm{h}}-{{\mathrm{T}}^{\prime }}_{\mathrm{c}}}$, $\mathrm{C}=\frac{{\mathrm{C}}^{\prime }-{{\mathrm{C}}^{\prime }}_{\mathrm{l}}}{{{\mathrm{C}}^{\prime }}_{\mathrm{h}}-{{\mathrm{C}}^{\prime }}_{\mathrm{l}}}$, and $\left({\mathrm{h}}_1,{\mathrm{h}}_2,0\right)=\frac{\left({\mathrm{h}}_1{}^{\prime },{\mathrm{h}}_2{}^{\prime },0\right){\mathrm{L}}^2}{\mathsf{\alpha }}$.

The microrotation vector $\overrightarrow{{\mathrm{h}}^{\prime }}$ can be expressed as $\overrightarrow{{\mathrm{h}}^{\prime }}=({{\mathrm{h}}^{\prime }}_1,{{\mathrm{h}}^{\prime }}_2,0)$ ([24,25,26]).

The vorticity–vector potential formulation is employed in order to eliminate the pressure term which is delicate to treat. The $\overrightarrow{\omega }$ and $\overrightarrow{\mathsf{\psi }}$ are, respectively, defined by the following relations: $\overrightarrow{\mathsf{\omega }}=\nabla \times \overrightarrow{\mathrm{U}}$ and $\overrightarrow{\mathrm{U}}=\nabla \times \overrightarrow{\mathsf{\psi }}$.

Using the above hypothesis, the dimensionless governing equations [23,41,43] are:

$${\nabla }^2\overrightarrow{\psi }=-\overrightarrow{\omega }$$

(1)

$$\begin{array}{l}\frac{\partial \overrightarrow{\mathsf{\omega }}}{\partial \mathrm{t}}+\left(\overrightarrow{\mathrm{U}}·\nabla \right)\overrightarrow{\mathsf{\omega }}-\left(\overrightarrow{\mathsf{\omega }}·\nabla \right)\overrightarrow{\mathrm{U}}=\mathrm{Pr}\left(\frac{{\mathsf{\mu }}_{\mathrm{nf}}}{{\mathsf{\mu }}_{\mathrm{f}}}+\mathrm{K}\right)\left(\frac{{\mathsf{\rho }}_{\mathrm{f}}}{{\mathsf{\rho }}_{\mathrm{nf}}}\right){\nabla }^2\overrightarrow{\mathsf{\omega }}-\mathrm{Pr}·\mathrm{K}\left(\frac{{\mathsf{\rho }}_{\mathrm{f}}}{{\mathsf{\rho }}_{\mathrm{nf}}}\right){\nabla }^2\overrightarrow{\mathrm{h}}+\\ \mathrm{RaPr}\left(\frac{{\left(\mathsf{\rho }\mathsf{\beta }\right)}_{\mathrm{nf}}}{{\left(\mathsf{\rho }\mathsf{\beta }\right)}_{\mathrm{f}}}\right)\left(\frac{{\mathsf{\rho }}_{\mathrm{f}}}{{\mathsf{\rho }}_{\mathrm{nf}}}\right)\left(\left[\frac{\partial \mathrm{T}}{\partial \mathrm{z}},0,-\frac{\partial \mathrm{T}}{\partial \mathrm{x}}\right]-\mathrm{N}\left[\frac{\partial \mathrm{C}}{\partial \mathrm{z}},0,-\frac{\partial \mathrm{C}}{\partial \mathrm{x}}\right]\right)+\mathrm{Pr} {\mathrm{Ha}}^2\left(\frac{{\mathsf{\rho }}_{\mathrm{f}}}{{\mathsf{\rho }}_{\mathrm{nf}}}\right)\left(\frac{{\mathsf{\sigma }}_{\mathrm{nf}}}{{\mathsf{\sigma }}_{\mathrm{f}}}\right)\left(\overrightarrow{\nabla }\times \left(\overrightarrow{\mathrm{J}}\times \overrightarrow{{\mathrm{e}}_{\mathrm{B}}}\right)\right)\end{array}$$

(2)

$$\frac{\partial \mathrm{T}}{\partial \mathrm{t}}+\left(\overrightarrow{\mathrm{U}}·\nabla \right)\mathrm{T}=\left(\frac{{\left({\mathsf{\rho }\mathrm{C}}_{\mathrm{p}}\right)}_{\mathrm{f}}}{{\left({\mathsf{\rho }\mathrm{C}}_{\mathrm{p}}\right)}_{\mathrm{nf}}}\right)\left(\frac{{\mathrm{k}}_{\mathrm{nf}}}{{\mathrm{k}}_{\mathrm{f}}}\right){\nabla }^2\mathrm{T}$$

(3)

$$\frac{\partial \mathrm{C}}{\partial \mathrm{t}}+\left(\overrightarrow{\mathrm{U}}·\nabla \right)\mathrm{C}=\frac{1}{\mathrm{L}\mathrm{e}}\left(\frac{{\left({\mathsf{\rho }\mathrm{C}}_{\mathrm{p}}\right)}_{\mathrm{nf}}}{{\left({\mathsf{\rho }\mathrm{C}}_{\mathrm{p}}\right)}_{\mathrm{f}}}\right)\left(\frac{{\mathrm{k}}_{\mathrm{f}}}{{\mathrm{k}}_{\mathrm{nf}}}\right){\nabla }^2\mathrm{C}$$

(4)

$$\frac{\partial \overrightarrow{\mathrm{h}}}{\partial \mathrm{t}}+\left(\overrightarrow{\mathrm{U}}·\nabla \right)\overrightarrow{\mathrm{h}}=\mathrm{Pr}\left(\frac{{\mathsf{\mu }}_{\mathrm{nf}}}{{\mathsf{\mu }}_{\mathrm{f}}}+\frac{\mathrm{K}}{2}\right)\left(\frac{{\mathsf{\rho }}_{\mathrm{f}}}{{\mathsf{\rho }}_{\mathrm{nf}}}\right){\nabla }^2\overrightarrow{\mathrm{h}}+\mathrm{Pr}·\mathrm{K}\left(\frac{{\mathsf{\rho }}_{\mathrm{f}}}{{\mathsf{\rho }}_{\mathrm{nf}}}\right)\left(\overrightarrow{\mathsf{\omega }}-2·\overrightarrow{\mathrm{h}}\right)$$

(5)

$$\overrightarrow{\mathrm{J}}=-\overrightarrow{\nabla }\mathsf{\Phi }+\overrightarrow{\mathrm{U}}\times \overrightarrow{{\mathrm{e}}_{\mathrm{B}}}$$

(6)

$${\overrightarrow{\nabla }}^2\mathsf{\Phi }=\overrightarrow{\nabla }\left(\overrightarrow{\mathrm{U}}\times \overrightarrow{\mathrm{B}}\right)=-\overrightarrow{{\mathrm{e}}_{\mathrm{B}}}·\overrightarrow{\mathsf{\omega }}$$

(7)

With: $\mathrm{Pr}=\frac{\mathsf{\nu }}{\mathsf{\alpha }}$, $\mathrm{R}\mathrm{a}=\frac{\mathrm{g}{\mathsf{\beta }}_{\mathrm{T}}\left({\mathrm{T}}_{\mathrm{h}}-{\mathrm{T}}_c\right){\mathrm{L}}^3}{\mathsf{\nu }\mathsf{\alpha }}$, $\mathrm{L}\mathrm{e}=\frac{\mathsf{\alpha }}{\mathrm{D}}$, $\mathrm{N}=\frac{{\mathsf{\beta }}_{\mathrm{C}}\left({\mathrm{C}}_{\mathrm{h}}-{\mathrm{C}}_{\mathrm{l}}\right)}{{\mathsf{\beta }}_{\mathrm{T}}\left({\mathrm{T}}_{\mathrm{h}}-{\mathrm{T}}_{\mathrm{c}}\right)}$, $\mathrm{H}\mathrm{a}={\mathrm{B}}_0\mathrm{L}\sqrt{\frac{\mathsf{\sigma }}{{\mathsf{\rho }}_{\mathrm{f}}{\mathsf{\upsilon }}_{\mathrm{f}}}}$ and $\mathrm{K}=\frac{\mathrm{k}}{\mathsf{\mu }}$.

The effective density, the heat capacitance, the thermal expansion coefficient and the thermal diffusivity of nanofluid are given respectively by ([9,10,11]):

$${\mathsf{\rho }}_{\mathrm{n}\mathrm{f}}=(1-\mathsf{\varphi }){\mathsf{\rho }}_{\mathrm{f}}+\mathsf{\varphi }{\mathsf{\rho }}_{\mathrm{p}}$$

$${(\mathsf{\rho }\mathrm{C}\mathrm{p})}_{\mathrm{n}\mathrm{f}}=(1-\mathsf{\varphi }){(\mathsf{\rho }\mathrm{C}\mathrm{p})}_{\mathrm{f}}+\mathsf{\varphi }{(\mathsf{\rho }\mathrm{C}\mathrm{p})}_{\mathrm{p}}$$

$${(\mathsf{\rho }\mathsf{\beta })}_{\mathrm{n}\mathrm{f}}=(1-\mathsf{\varphi }){(\mathsf{\rho }\mathsf{\beta })}_{\mathrm{f}}+\mathsf{\varphi }{(\mathsf{\rho }\mathsf{\beta })}_{\mathrm{p}}$$

$${\mathsf{\alpha }}_{\mathrm{n}\mathrm{f}}=\frac{{\mathrm{k}}_{\mathrm{n}\mathrm{f}}}{{\left(\mathsf{\rho }\mathrm{C}\mathrm{p}\right)}_{\mathrm{n}\mathrm{f}}}$$

The thermal conductivity and the effective dynamic viscosity of the nanofluid have been calculated experimentally ([44,45]) and is given as follows:

$$k_{nf}=k_f(1+7.47\varphi )$$

$${\mathsf{\mu }}_{\mathrm{n}\mathrm{f}}={\mathsf{\mu }}_{\mathrm{f}}(1+39.11\mathsf{\varphi }+533.9{\mathsf{\varphi }}^2)$$

The nanofluid electrical conductivity is given by ([33]):

$${\sigma }_{nf}={\sigma }_f\left[1+\frac{3\varphi (\frac{{\sigma }_s}{{\sigma }_f}-1)}{(\frac{{\sigma }_s}{{\sigma }_f}+2)-\varphi (\frac{{\sigma }_s}{{\sigma }_f}-1)}\right]$$

Boundary conditions are given as follows:

Temperature and Concentration:

$$\mathrm{T}(1, \mathrm{y}, \mathrm{z})=1, \mathrm{C}(1, \mathrm{y}, \mathrm{z})=1$$

$$\mathrm{T}(0, \mathrm{y}, \mathrm{z})=0,\mathrm{C}(0, \mathrm{y}, \mathrm{z})=0$$

$${\frac{\partial \mathrm{T}}{\partial \mathrm{z}})}_{\mathrm{z}=0}=0 \mathrm{and} {\frac{\partial \mathrm{C}}{\partial \mathrm{z}})}_{\mathrm{z}=0}=0$$

$${\frac{\partial \mathrm{T}}{\partial \mathrm{z}})}_{\mathrm{z}=1}=0 \mathrm{and} {\frac{\partial \mathrm{C}}{\partial \mathrm{z}})}_{\mathrm{z}=1}=0$$

Vorticity:

$$\mathrm{At} \mathrm{x} = 0 \mathrm{and} \mathrm{x} = 1: {\mathsf{\omega }}_1=0,{\mathsf{\omega }}_2=-\frac{\partial {\mathrm{U}}_3}{\partial \mathrm{x}},{\mathsf{\omega }}_3=\frac{\partial {\mathrm{U}}_2}{\partial \mathrm{x}}$$

$$\mathrm{At} \mathrm{y} = 0 \mathrm{and} \mathrm{y} = 1:{\mathsf{\omega }}_1=\frac{\partial {\mathrm{U}}_3}{\partial \mathrm{y}},{\mathsf{\omega }}_2=0,{\mathsf{\omega }}_3=-\frac{\partial {\mathrm{U}}_1}{\partial \mathrm{y}}$$

$$\mathrm{At} \mathrm{z} = 0 \mathrm{and} \mathrm{z} = 1:{\mathsf{\omega }}_1=-\frac{\partial {\mathrm{U}}_2}{\partial \mathrm{z}},{\mathsf{\omega }}_2=\frac{\partial {\mathrm{U}}_1}{\partial \mathrm{z}},{\mathsf{\omega }}_3=0$$

Vector potential:

$$\mathrm{At} \mathrm{x} = 0 \mathrm{and} \mathrm{x} = 1:\frac{\partial {\mathsf{\psi }}_1}{\partial \mathrm{x}}={\mathsf{\psi }}_2={\mathsf{\psi }}_3=0$$

$$\mathrm{At} \mathrm{y} = 0 \mathrm{and} \mathrm{y} = 1:{\mathsf{\psi }}_1=\frac{\partial {\mathsf{\psi }}_2}{\partial \mathrm{y}}={\mathsf{\psi }}_3=0$$

$$\mathrm{At} \mathrm{z} = 0 \mathrm{and} \mathrm{z} = 1:{\mathsf{\psi }}_1={\mathsf{\psi }}_2=\frac{\partial {\mathsf{\psi }}_3}{\partial \mathrm{z}}=0$$

Velocity, on all walls:

$${\mathrm{U}}_1={\mathrm{U}}_2={\mathrm{U}}_3=0$$

Calculations are performed for strong concentrated suspensions ([46]). These characterize the case in which the microelements near to the wall surface are unable to rotate. Thus, the micro-rotation vector boundary condition is defined as:

$$\mathrm{At} \mathrm{x}=0,1 ; \mathrm{y}= 0,1 \mathrm{and} \mathrm{z} = 0,1 : \overrightarrow{\mathrm{h}}=0$$

It is worth citing that the equations of vorticity (Equation (2)) and microrotation (Equation (5)) become uncoupled when K = 0, thus the flow is independent of the microrotation, and the governing equations depict the classical problem of Newtonian nanofluid natural convection in differentially heated enclosure.

The local Nusselt and Sherwood numbers are defined by:

$$\mathrm{N}\mathrm{U}={\frac{{\mathrm{k}}_{\mathrm{n}\mathrm{f}}\frac{\partial {\mathrm{T}}^{\prime }}{\partial {\mathrm{x}}^{\prime }}}{{\mathrm{k}}_{\mathrm{f}}\frac{{\mathrm{T}}_{\mathrm{h}}^{\prime }-{\mathrm{T}}_{\mathrm{c}}^{\prime }}{\mathrm{L}}})}_{{\mathrm{x}}^{\prime }=0,\mathrm{L}}=\frac{{\mathrm{k}}_{\mathrm{n}\mathrm{f}}}{{\mathrm{k}}_{\mathrm{f}}}{\frac{\partial {\mathrm{T}}^{}}{\partial {\mathrm{x}}^{}})}_{{\mathrm{x}}^{}=0,1}$$

(8)

$$\mathrm{S}\mathrm{h}={\frac{\mathrm{D}\frac{\partial {\mathrm{C}}^{\prime }}{\partial {\mathrm{x}}^{\prime }}}{\mathrm{D}\frac{{\mathrm{C}}_{\mathrm{h}}^{\prime }-{\mathrm{C}}_{\mathrm{l}}^{\prime }}{\mathrm{L}}})}_{{\mathrm{x}}^{\prime }=0,\mathrm{L}}={\frac{\partial {\mathrm{C}}^{}}{\partial \mathrm{x}})}_{\mathrm{x}=0,1}$$

(9)

The average Nusselt and Sherwood numbers, on the isothermal walls are defined as:

$$\overline{\mathrm{N}}\mathrm{u}=\underset{0}{\overset{1}{\int }}\underset{0}{\overset{1}{\int }}\mathrm{N}\mathrm{u}\partial \mathrm{y}\partial \mathrm{z}$$

(10)

and

$$\overline{\mathrm{S}}\mathrm{h}=\underset{0}{\overset{1}{\int }}\underset{0}{\overset{1}{\int }}\mathrm{S}\mathrm{h}\partial \mathrm{y}\partial \mathrm{z}$$

(11)

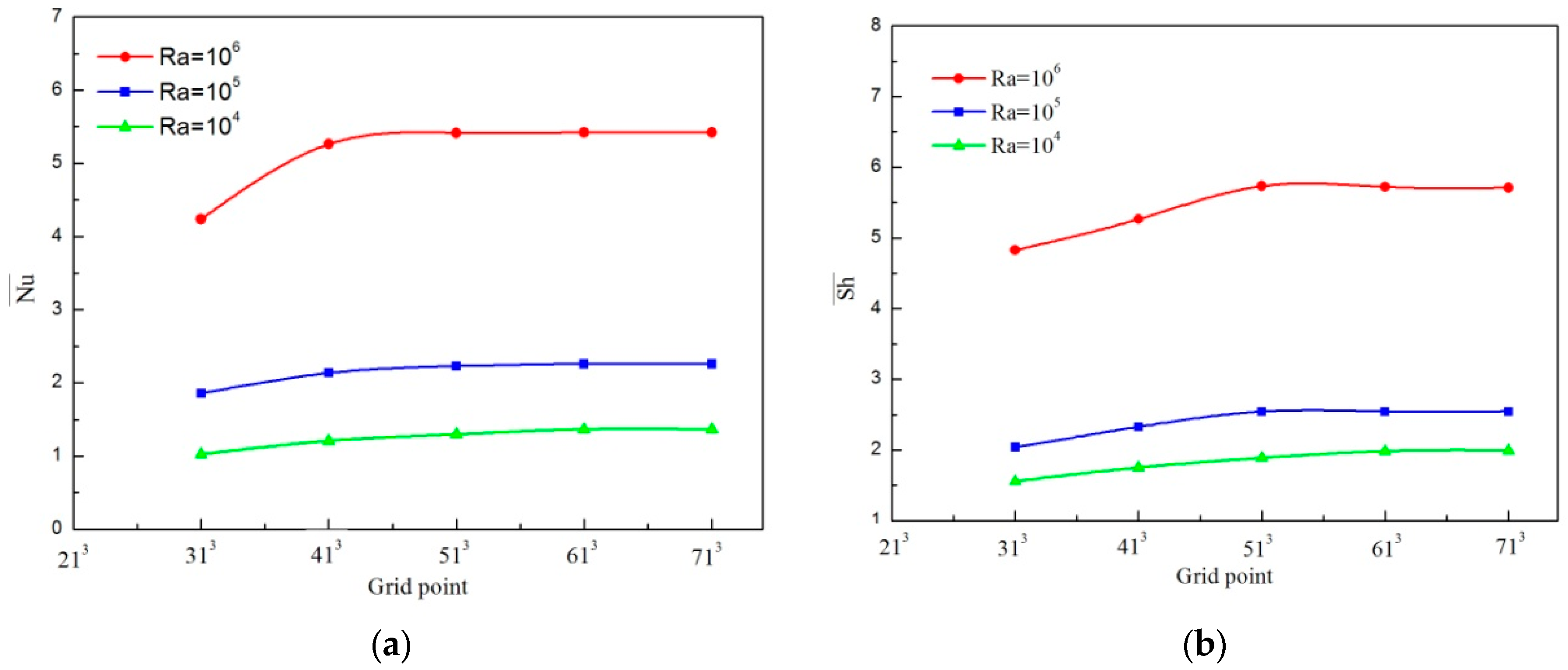
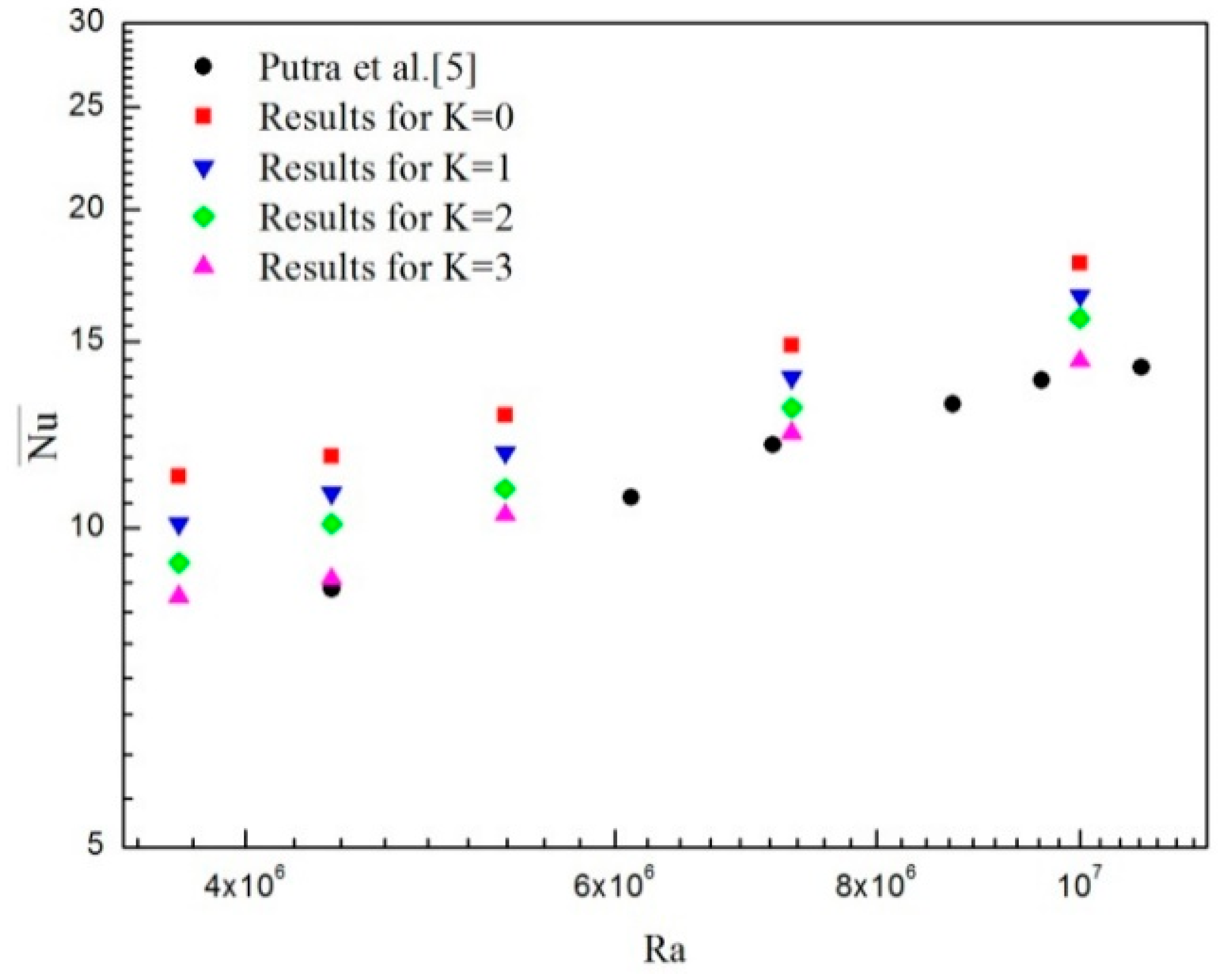
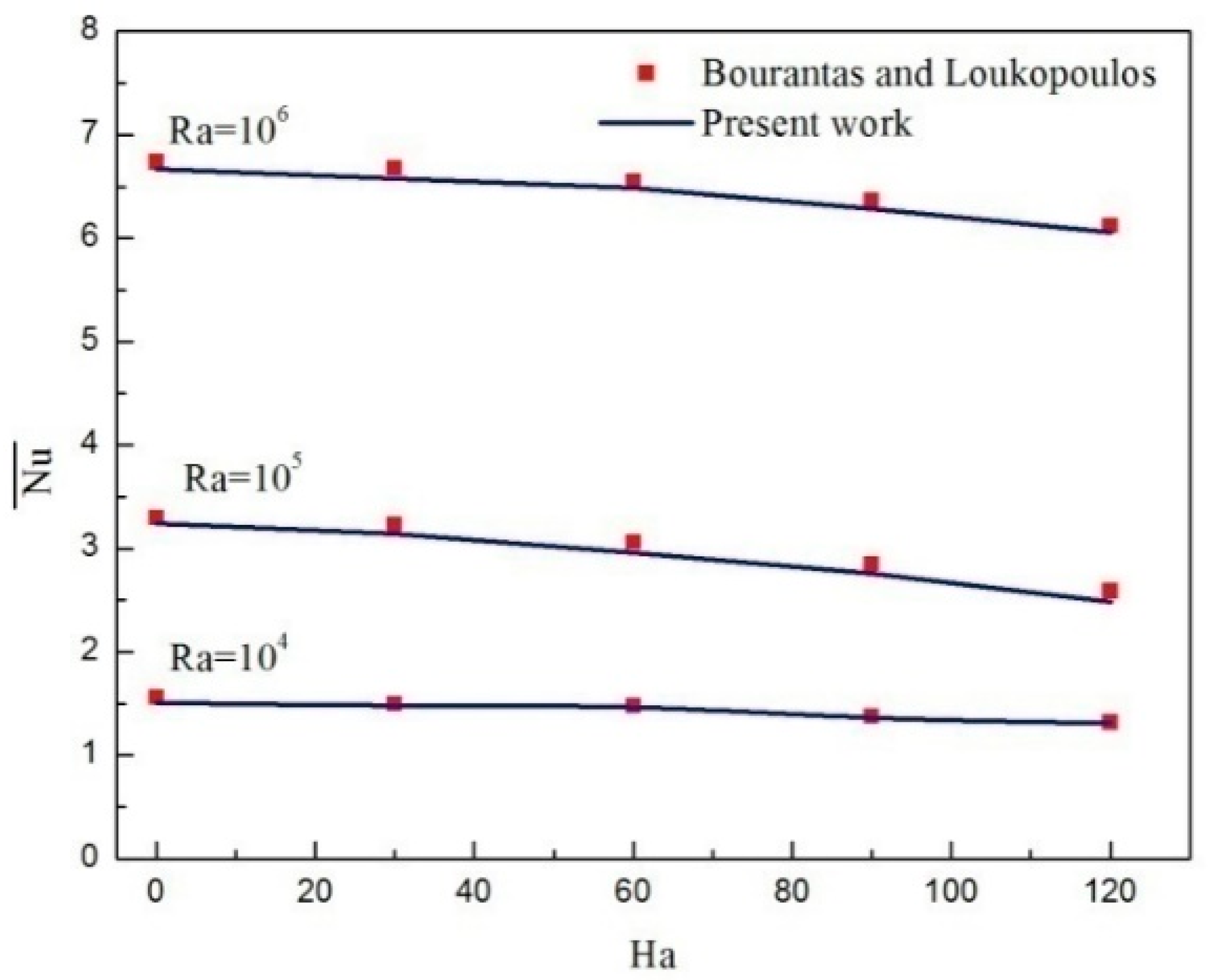
3. Numerical Approach and Benchmarking of the Code

The dimensionless governing equations are written in the scalar form as:

$${\mathsf{\omega }}_1=-\left[\frac{{\partial }^2{\mathsf{\psi }}_1}{\partial {\mathrm{x}}^2}+\frac{{\partial }^2{\mathsf{\psi }}_1}{\partial {\mathrm{y}}^2}+\frac{{\partial }^2{\mathsf{\psi }}_1}{\partial {\mathrm{z}}^2}\right],{\mathsf{\omega }}_2=-\left[\frac{{\partial }^2{\mathsf{\psi }}_2}{\partial {\mathrm{x}}^2}+\frac{{\partial }^2{\mathsf{\psi }}_2}{\partial {\mathrm{y}}^2}+\frac{{\partial }^2{\mathsf{\psi }}_2}{\partial {\mathrm{z}}^2}\right] \mathrm{and} {\mathsf{\omega }}_3=-\left[\frac{{\partial }^2{\mathsf{\psi }}_3}{\partial {\mathrm{x}}^2}+\frac{{\partial }^2{\mathsf{\psi }}_3}{\partial {\mathrm{y}}^2}+\frac{{\partial }^2{\mathsf{\psi }}_3}{\partial {\mathrm{z}}^2}\right]$$

(12)

$$\begin{array}{l}\frac{\partial {\mathsf{\omega }}_1}{\partial \mathrm{t}}+\frac{\partial }{\partial \mathrm{x}}\left[{\mathrm{U}}_1{\mathsf{\omega }}_1-{\mathsf{\Gamma }}_{\mathsf{\omega }}\frac{\partial {\mathsf{\omega }}_1}{\partial \mathrm{x}}\right]+\frac{\partial }{\partial \mathrm{y}}\left[{\mathrm{U}}_2{\mathsf{\omega }}_1-{\mathsf{\Gamma }}_{\mathsf{\omega }}\frac{\partial {\mathsf{\omega }}_1}{\partial \mathrm{y}}\right]+\frac{\partial }{\partial \mathrm{z}}\left[{\mathrm{U}}_3{\mathsf{\omega }}_1-{\mathsf{\Gamma }}_{\mathsf{\omega }}\frac{\partial {\mathsf{\omega }}_1}{\partial \mathrm{z}}\right]={\mathsf{\omega }}_1\frac{\partial {\mathrm{U}}_1}{\partial \mathrm{x}}+{\mathsf{\omega }}_2\frac{\partial {\mathrm{U}}_1}{\partial \mathrm{y}}+{\mathsf{\omega }}_3\frac{\partial {\mathrm{U}}_1}{\partial \mathrm{z}}\\ - \mathrm{Pr}·\mathrm{K}\left(\frac{{\mathsf{\rho }}_{\mathrm{f}}}{{\mathsf{\rho }}_{\mathrm{nf}}}\right)\left(\frac{{\partial }^2{\mathrm{h}}_1}{\partial {\mathrm{x}}^2}+\frac{{\partial }^2{\mathrm{h}}_1}{\partial {\mathrm{y}}^2}+\frac{{\partial }^2{\mathrm{h}}_1}{\partial {\mathrm{z}}^2}\right)+\mathrm{RaPr}\left(\frac{{\left(\mathsf{\rho }\mathsf{\beta }\right)}_{\mathrm{nf}}}{{\left(\mathsf{\rho }\mathsf{\beta }\right)}_{\mathrm{f}}}\right)\left(\frac{{\mathsf{\rho }}_{\mathrm{f}}}{{\mathsf{\rho }}_{\mathrm{nf}}}\right)\left(\frac{\partial \mathrm{T}}{\partial \mathrm{z}}-\mathrm{N}\frac{\partial \mathrm{C}}{\partial \mathrm{z}}\right)+\mathrm{Pr} {\mathrm{Ha}}^2\left(\frac{{\mathsf{\rho }}_{\mathrm{f}}}{{\mathsf{\rho }}_{\mathrm{nf}}}\right)\left(\frac{{\mathsf{\sigma }}_{\mathrm{nf}}}{{\mathsf{\sigma }}_{\mathrm{f}}}\right)\left(\frac{\partial {\mathrm{U}}_1}{\partial \mathrm{x}}\right)\end{array}$$

(13)

$$\begin{array}{l}\frac{\partial {\mathsf{\omega }}_2}{\partial \mathrm{t}}+\frac{\partial }{\partial \mathrm{x}}\left[{\mathrm{U}}_1{\mathsf{\omega }}_2-{\mathsf{\Gamma }}_{\mathsf{\omega }}\frac{\partial {\mathsf{\omega }}_2}{\partial \mathrm{x}}\right]+\frac{\partial }{\partial \mathrm{y}}\left[{\mathrm{U}}_2{\mathsf{\omega }}_2-{\mathsf{\Gamma }}_{\mathsf{\omega }}\frac{\partial {\mathsf{\omega }}_2}{\partial \mathrm{y}}\right]+\frac{\partial }{\partial \mathrm{z}}\left[{\mathrm{U}}_3{\mathsf{\omega }}_2-{\mathsf{\Gamma }}_{\mathsf{\omega }}\frac{\partial {\mathsf{\omega }}_2}{\partial \mathrm{z}}\right]={\mathsf{\omega }}_1\frac{\partial {\mathrm{U}}_2}{\partial \mathrm{x}}+{\mathsf{\omega }}_2\frac{\partial {\mathrm{U}}_2}{\partial \mathrm{y}}+{\mathsf{\omega }}_3\frac{\partial {\mathrm{U}}_2}{\partial \mathrm{z}}\\ -\mathrm{Pr}·\mathrm{K}\left(\frac{{\mathsf{\rho }}_{\mathrm{f}}}{{\mathsf{\rho }}_{\mathrm{nf}}}\right)\left(\frac{{\partial }^2{\mathrm{h}}_2}{\partial {\mathrm{x}}^2}+\frac{{\partial }^2{\mathrm{h}}_2}{\partial {\mathrm{y}}^2}+\frac{{\partial }^2{\mathrm{h}}_2}{\partial {\mathrm{z}}^2}\right)+\mathrm{Pr} {\mathrm{Ha}}^2\left(\frac{{\mathsf{\rho }}_{\mathrm{f}}}{{\mathsf{\rho }}_{\mathrm{nf}}}\right)\left(\frac{{\mathsf{\sigma }}_{\mathrm{nf}}}{{\mathsf{\sigma }}_{\mathrm{f}}}\right)\left(\frac{\partial {\mathrm{U}}_2}{\partial \mathrm{x}}\right)\end{array}$$

(14)

$$\begin{array}{l}\frac{\partial {\mathsf{\omega }}_3}{\partial \mathrm{t}}+\frac{\partial }{\partial \mathrm{x}}\left[{\mathrm{U}}_1{\mathsf{\omega }}_3-{\mathsf{\Gamma }}_{\mathsf{\omega }}\frac{\partial {\mathsf{\omega }}_3}{\partial \mathrm{x}}\right]+\frac{\partial }{\partial \mathrm{y}}\left[{\mathrm{U}}_2{\mathsf{\omega }}_3-{\mathsf{\Gamma }}_{\mathsf{\omega }}\frac{\partial {\mathsf{\omega }}_3}{\partial \mathrm{y}}\right]+\frac{\partial }{\partial \mathrm{z}}\left[{\mathrm{U}}_3{\mathsf{\omega }}_3-{\mathsf{\Gamma }}_{\mathsf{\omega }}\frac{\partial {\mathsf{\omega }}_3}{\partial \mathrm{z}}\right]={\mathsf{\omega }}_1\frac{\partial {\mathrm{U}}_3}{\partial \mathrm{x}}+{\mathsf{\omega }}_2\frac{\partial {\mathrm{U}}_3}{\partial \mathrm{y}}+{\mathsf{\omega }}_3\frac{\partial {\mathrm{U}}_3}{\partial \mathrm{z}}\\ -\mathrm{Pr}·\mathrm{K}\left(\frac{{\mathsf{\rho }}_{\mathrm{f}}}{{\mathsf{\rho }}_{\mathrm{nf}}}\right)\left(\frac{{\partial }^2{\mathrm{h}}_1}{\partial {\mathrm{x}}^2}+\frac{{\partial }^2{\mathrm{h}}_1}{\partial {\mathrm{y}}^2}+\frac{{\partial }^2{\mathrm{h}}_1}{\partial {\mathrm{z}}^2}\right)+\mathrm{RaPr}\left(\frac{{\left(\mathsf{\rho }\mathsf{\beta }\right)}_{\mathrm{nf}}}{{\left(\mathsf{\rho }\mathsf{\beta }\right)}_{\mathrm{f}}}\right)\left(\frac{{\mathsf{\rho }}_{\mathrm{f}}}{{\mathsf{\rho }}_{\mathrm{nf}}}\right)\left(\frac{\partial \mathrm{T}}{\partial \mathrm{x}}+\mathrm{N}\frac{\partial \mathrm{C}}{\partial \mathrm{x}}\right)+\mathrm{Pr} {\mathrm{Ha}}^2\left(\frac{{\mathsf{\rho }}_{\mathrm{f}}}{{\mathsf{\rho }}_{\mathrm{nf}}}\right)\left(\frac{{\mathsf{\sigma }}_{\mathrm{nf}}}{{\mathsf{\sigma }}_{\mathrm{f}}}\right)\left(\frac{\partial {\mathrm{U}}_3}{\partial \mathrm{x}}\right)\end{array}$$

(15)

$$\frac{\partial \mathrm{T}}{\partial \mathrm{t}}+\frac{\partial }{\partial \mathrm{x}}\left[{\mathrm{U}}_1-{\mathsf{\Gamma }}_{\mathrm{T}}\frac{\partial \mathrm{T}}{\partial \mathrm{x}}\right]+\frac{\partial }{\partial \mathrm{y}}\left[{\mathrm{U}}_2-{\mathsf{\Gamma }}_{\mathrm{T}}\frac{\partial \mathrm{T}}{\partial \mathrm{y}}\right]+\frac{\partial }{\partial \mathrm{z}}\left[{\mathrm{U}}_3-{\mathsf{\Gamma }}_{\mathrm{T}}\frac{\partial \mathrm{T}}{\partial \mathrm{z}}\right]=0$$

(16)

$$\frac{\partial \mathrm{C}}{\partial \mathrm{t}}+\frac{\partial }{\partial \mathrm{x}}\left[{\mathrm{U}}_1-{\mathsf{\Gamma }}_{\mathrm{C}}\frac{\partial \mathrm{C}}{\partial \mathrm{x}}\right]+\frac{\partial }{\partial \mathrm{y}}\left[{\mathrm{U}}_2-{\mathsf{\Gamma }}_{\mathrm{C}}\frac{\partial \mathrm{C}}{\partial \mathrm{y}}\right]+\frac{\partial }{\partial \mathrm{z}}\left[{\mathrm{U}}_3-{\mathsf{\Gamma }}_{\mathrm{C}}\frac{\partial \mathrm{C}}{\partial \mathrm{z}}\right]=0$$

(17)

$$\frac{\partial {\mathrm{h}}_1}{\partial \mathrm{t}}+\frac{\partial }{\partial \mathrm{x}}\left[{\mathrm{U}}_1-{\mathsf{\Gamma }}_{\mathrm{h}}\frac{\partial {\mathrm{h}}_1}{\partial \mathrm{x}}\right]+\frac{\partial }{\partial \mathrm{y}}\left[{\mathrm{U}}_2-{\mathsf{\Gamma }}_{\mathrm{h}}\frac{\partial {\mathrm{h}}_1}{\partial \mathrm{y}}\right]+\frac{\partial }{\partial \mathrm{z}}\left[{\mathrm{U}}_3-{\mathsf{\Gamma }}_{\mathrm{h}}\frac{\partial {\mathrm{h}}_1}{\partial \mathrm{z}}\right]=\mathrm{Pr}·\mathrm{K}\left(\frac{{\mathsf{\rho }}_{\mathrm{f}}}{{\mathsf{\rho }}_{\mathrm{nf}}}\right)\left({\mathsf{\omega }}_1-{\mathrm{h}}_1\right)$$

(18)

$$\frac{\partial {\mathrm{h}}_2}{\partial \mathrm{t}}+\frac{\partial }{\partial \mathrm{x}}\left[{\mathrm{U}}_1-{\mathsf{\Gamma }}_{\mathrm{h}}\frac{\partial {\mathrm{h}}_2}{\partial \mathrm{x}}\right]+\frac{\partial }{\partial \mathrm{y}}\left[{\mathrm{U}}_2-{\mathsf{\Gamma }}_{\mathrm{h}}\frac{\partial {\mathrm{h}}_2}{\partial \mathrm{y}}\right]+\frac{\partial }{\partial \mathrm{z}}\left[{\mathrm{U}}_3-{\mathsf{\Gamma }}_{\mathrm{h}}\frac{\partial {\mathrm{h}}_2}{\partial \mathrm{z}}\right]=\mathrm{Pr}·\mathrm{K}\left(\frac{{\mathsf{\rho }}_{\mathrm{f}}}{{\mathsf{\rho }}_{\mathrm{nf}}}\right)\left({\mathsf{\omega }}_2-{\mathrm{h}}_2\right)$$

(19)

One notes that the above equations can be written in the following general form:

$$\frac{\partial \mathsf{\Phi }}{\partial \mathrm{t}}+\frac{\partial }{\partial \mathrm{x}}\left[{\mathrm{U}}_1\mathsf{\Phi }-{\mathsf{\Gamma }}_{\mathsf{\Phi }}\frac{\partial \mathsf{\Phi }}{\partial \mathrm{x}}\right]+\frac{\partial }{\partial \mathrm{y}}\left[{\mathrm{U}}_2\mathsf{\Phi }-{\mathsf{\Gamma }}_{\mathsf{\Phi }}\frac{\partial \mathsf{\Phi }}{\partial \mathrm{y}}\right]+\frac{\partial }{\partial \mathrm{z}}\left[{\mathrm{U}}_3\mathsf{\Phi }-{\mathsf{\Gamma }}_{\mathsf{\Phi }}\frac{\partial \mathsf{\Phi }}{\partial \mathrm{z}}\right]={\mathrm{S}}_{\mathsf{\Phi }}$$

(20)

With:

• $\mathsf{\Phi }$: ${\mathsf{\omega }}_1, {\mathsf{\omega }}_2, {\mathsf{\omega }}_3, {\mathrm{h}}_1, {\mathrm{h}}_2, \mathrm{T} \mathrm{and} \mathrm{C}$
• ${\mathsf{\Gamma }}_{\mathsf{\Phi }}$: dimensionless coefficient
• ${\mathrm{S}}_{\mathsf{\Phi }}$: source term

Using the following expressions:

$${\mathrm{L}}_1={\mathrm{U}}_1\mathsf{\Phi }-{\mathsf{\Gamma }}_{\mathsf{\Phi }}\frac{\partial \mathsf{\Phi }}{\partial \mathrm{x}},{\mathrm{L}}_2={\mathrm{U}}_2\mathsf{\Phi }-{\mathsf{\Gamma }}_{\mathsf{\Phi }}\frac{\partial \mathsf{\Phi }}{\partial \mathrm{x}} \mathrm{and} {\mathrm{L}}_3={\mathrm{U}}_3\mathsf{\Phi }-{\mathsf{\Gamma }}_{\mathsf{\Phi }}\frac{\partial \mathsf{\Phi }}{\partial \mathrm{x}}$$

The general equation can be written as:

$$\frac{\partial \mathsf{\Phi }}{\partial \mathrm{t}}+\frac{\partial {\mathrm{L}}_1}{\partial \mathrm{x}}+\frac{\partial {\mathrm{L}}_2}{\partial \mathrm{y}}+\frac{\partial {\mathrm{L}}_3}{\partial \mathrm{z}}={\mathrm{S}}_{\mathsf{\Phi }}$$

The integration of the previous equation on a control volume leads to (Patankar [47]):

$$({\mathsf{\Phi }}_p-{\mathsf{\Phi }}_p^0)\Delta x\Delta y\Delta z+(L_{1e}-L_{1w})\Delta y\Delta z\Delta t+(L_{2n}-L_{2s})\Delta x\Delta z\Delta t+(L_{3f}-L_{3b})\Delta x\Delta y\Delta t=\overline{S}\Delta x\Delta y\Delta z\Delta t$$

(21)

e, w, n, s, b and f represent the faces of control volume centered in P.

E, W, N, S, B and F refer to the node around the nodal point P.

The governing equations are developed as follows (Patankar [47])

Energy equation ($\mathsf{\Phi }=\mathrm{T}$):

$${\mathrm{a}}_{\mathrm{p}}{\mathrm{T}}_{\mathrm{p}}={\mathrm{a}}_{\mathrm{E}}{\mathrm{T}}_{\mathrm{E}}+{\mathrm{a}}_{\mathrm{w}}{\mathrm{T}}_{\mathrm{w}}+{\mathrm{a}}_{\mathrm{N}}{\mathrm{T}}_{\mathrm{N}}+{\mathrm{a}}_{\mathrm{S}}{\mathrm{T}}_{\mathrm{S}}+{\mathrm{a}}_{\mathrm{F}}{\mathrm{T}}_{\mathrm{F}}+{\mathrm{a}}_{\mathrm{B}}{\mathrm{T}}_{\mathrm{B}}+{\mathrm{b}}_{\mathrm{p}}$$

(22)

With ${\mathrm{b}}_{\mathrm{p}}={\mathrm{T}}_{\mathrm{p}}^0\frac{\Delta \mathrm{x}\Delta \mathrm{y}\Delta \mathrm{z}}{\Delta \mathrm{t}}$

Concentration equation ($\mathsf{\Phi }=\mathrm{C}$):

$${\mathrm{a}}_{\mathrm{p}}{\mathrm{C}}_{\mathrm{p}}={\mathrm{a}}_{\mathrm{E}}{\mathrm{C}}_{\mathrm{E}}+{\mathrm{a}}_{\mathrm{w}}{\mathrm{C}}_{\mathrm{w}}+{\mathrm{a}}_{\mathrm{N}}{\mathrm{C}}_{\mathrm{N}}+{\mathrm{a}}_{\mathrm{S}}{\mathrm{C}}_{\mathrm{S}}+{\mathrm{a}}_{\mathrm{F}}{\mathrm{C}}_{\mathrm{F}}+{\mathrm{a}}_{\mathrm{B}}{\mathrm{C}}_{\mathrm{B}}+{\mathrm{b}}_{\mathrm{p}}$$

(23)

With ${\mathrm{b}}_{\mathrm{p}}={\mathrm{C}}_{\mathrm{p}}^0\frac{\Delta \mathrm{x}\Delta \mathrm{y}\Delta \mathrm{z}}{\Delta \mathrm{t}}$

Vorticity equation: x-component ($\mathsf{\Phi }={\mathsf{\omega }}_1$):

$$a_p{\omega }_{1p}=a_E{\omega }_{1E}+a_w{\omega }_{1w}+a_N{\omega }_{1N}+a_S{\omega }_{1S}+a_F{\omega }_{1F}+a_B{\omega }_{1B}+b_p$$

(24)

With:

$$\begin{array}{l}{\mathrm{b}}_{\mathrm{p}}={\mathsf{\omega }}_{1\mathrm{p}}^0\frac{\Delta \mathrm{x}\Delta \mathrm{y}\Delta \mathrm{z}}{\Delta \mathrm{t}}+{\mathsf{\omega }}_{1\mathrm{p}}\left(\frac{{\mathrm{U}}_{1\mathrm{E}}-{\mathrm{U}}_{1\mathrm{W}}}{2}\right)\Delta \mathrm{y}\Delta \mathrm{z}+{\mathsf{\omega }}_{2\mathrm{p}}\left(\frac{{\mathrm{U}}_{1\mathrm{S}}-{\mathrm{U}}_{1\mathrm{N}}}{2}\right)\Delta \mathrm{x}\Delta \mathrm{z}+{\mathsf{\omega }}_{3\mathrm{p}}\left(\frac{{\mathrm{U}}_{1\mathrm{F}}-{\mathrm{U}}_{1\mathrm{B}}}{2}\right)\Delta \mathrm{x}\Delta \mathrm{y}\\ -\mathrm{Pr}·\mathrm{K}\left(\frac{{\mathsf{\rho }}_{\mathrm{f}}}{{\mathsf{\rho }}_{\mathrm{nf}}}\right)\left(\frac{{\mathrm{h}}_{1\mathrm{E}}+{\mathrm{h}}_{1\mathrm{w}}}{\Delta \mathrm{x}²}+\frac{{\mathrm{h}}_{1\mathrm{N}}+{\mathrm{h}}_{1\mathrm{S}}}{\Delta \mathrm{y}²}+\frac{{\mathrm{h}}_{1\mathrm{F}}+{\mathrm{h}}_{1\mathrm{B}}}{\Delta \mathrm{z}²}\right)\Delta \mathrm{x}\Delta \mathrm{y}\Delta \mathrm{z}+\mathrm{RaPr}\left(\frac{{\left(\mathsf{\rho }\mathsf{\beta }\right)}_{\mathrm{nf}}}{{\left(\mathsf{\rho }\mathsf{\beta }\right)}_{\mathrm{f}}}\right)\left(\frac{{\mathsf{\rho }}_{\mathrm{f}}}{{\mathsf{\rho }}_{\mathrm{nf}}}\right){\left(\frac{{\mathrm{T}}_{\mathrm{F}}-{\mathrm{T}}_{\mathrm{B}}}{2}-\mathrm{N}\frac{{\mathrm{C}}_{\mathrm{F}}-{\mathrm{C}}_{\mathrm{B}}}{2}\right)}_{\mathrm{p}}\Delta \mathrm{x}\Delta \mathrm{y}\\ -\mathrm{Pr} {\mathrm{Ha}}^2\left(\frac{{\mathsf{\rho }}_{\mathrm{f}}}{{\mathsf{\rho }}_{\mathrm{nf}}}\right)\left(\frac{{\mathsf{\sigma }}_{\mathrm{nf}}}{{\mathsf{\sigma }}_{\mathrm{f}}}\right)\left(\frac{{\mathrm{U}}_{1\mathrm{E}-}{\mathrm{U}}_{1\mathrm{W}}}{2}\right)\Delta \mathrm{y}\Delta \mathrm{z}\end{array}$$

Vorticity equation: y-component ($\mathsf{\Phi } ={\mathsf{\omega }}_2$):

$$a_p{\omega }_{2p}=a_E{\omega }_{2E}+a_w{\omega }_{2w}+a_N{\omega }_{2N}+a_S{\omega }_{2S}+a_F{\omega }_{2F}+a_B{\omega }_{2B}+b_p$$

(25)

With:

$$\begin{array}{l}{\mathrm{b}}_{\mathrm{p}}={\mathsf{\omega }}_{2\mathrm{p}}^0\frac{\Delta \mathrm{x}\Delta \mathrm{y}\Delta \mathrm{z}}{\Delta \mathrm{t}}+{\mathsf{\omega }}_{1\mathrm{p}}\left(\frac{{\mathrm{U}}_{2\mathrm{E}}-{\mathrm{U}}_{2\mathrm{W}}}{2}\right)\Delta \mathrm{y}\Delta \mathrm{z}+{\mathsf{\omega }}_{2\mathrm{p}}\left(\frac{{\mathrm{U}}_{2\mathrm{S}}-{\mathrm{U}}_{2\mathrm{N}}}{2}\right)\Delta \mathrm{x}\Delta \mathrm{z}+{\mathsf{\omega }}_{3\mathrm{p}}\left(\frac{{\mathrm{U}}_{2\mathrm{F}}-{\mathrm{U}}_{2\mathrm{B}}}{2}\right)\Delta \mathrm{x}\Delta \mathrm{y}\\ -\mathrm{Pr}·\mathrm{K}\left(\frac{{\mathsf{\rho }}_{\mathrm{f}}}{{\mathsf{\rho }}_{\mathrm{nf}}}\right)\left(\frac{{\mathrm{h}}_{2\mathrm{E}}+{\mathrm{h}}_{2\mathrm{w}}}{\Delta \mathrm{x}²}+\frac{{\mathrm{h}}_{2\mathrm{N}}+{\mathrm{h}}_{2\mathrm{S}}}{\Delta \mathrm{y}²}+\frac{{\mathrm{h}}_{2\mathrm{f}}+{\mathrm{h}}_{2\mathrm{B}}}{\Delta \mathrm{z}²}\right)\Delta \mathrm{x}\Delta \mathrm{y}\Delta \mathrm{z}-\mathrm{Pr} {\mathrm{Ha}}^2\left(\frac{{\mathsf{\rho }}_{\mathrm{f}}}{{\mathsf{\rho }}_{\mathrm{nf}}}\right)\left(\frac{{\mathsf{\sigma }}_{\mathrm{nf}}}{{\mathsf{\sigma }}_{\mathrm{f}}}\right)\left(\frac{{\mathrm{U}}_{2\mathrm{E}-}{\mathrm{U}}_{2\mathrm{W}}}{2}\right)\Delta \mathrm{y}\Delta \mathrm{z}\end{array}$$

Vorticity equation: z-component ($\mathsf{\Phi }={\omega }_3$):

$$a_p{\omega }_{3p}=a_E{\omega }_{3E}+a_w{\omega }_{3w}+a_N{\omega }_{3N}+a_S{\omega }_{3S}+a_F{\omega }_{3F}+a_B{\omega }_{3B}+b_p$$

(26)

$$\begin{array}{l}{\mathrm{b}}_{\mathrm{p}}={\mathsf{\omega }}_{1\mathrm{p}}^0\frac{\Delta \mathrm{x}\Delta \mathrm{y}\Delta \mathrm{z}}{\Delta \mathrm{t}}+{\mathsf{\omega }}_{1\mathrm{p}}\left(\frac{{\mathrm{U}}_{1\mathrm{E}}-{\mathrm{U}}_{1\mathrm{W}}}{2}\right)\Delta \mathrm{y}\Delta \mathrm{z}+{\mathsf{\omega }}_{2\mathrm{p}}\left(\frac{{\mathrm{U}}_{1\mathrm{S}}-{\mathrm{U}}_{1\mathrm{N}}}{2}\right)\Delta \mathrm{x}\Delta \mathrm{z}+{\mathsf{\omega }}_{3\mathrm{p}}\left(\frac{{\mathrm{U}}_{1\mathrm{F}}-{\mathrm{U}}_{1\mathrm{B}}}{2}\right)\Delta \mathrm{x}\Delta \mathrm{y}\\ -\mathrm{Pr}·\mathrm{K}\left(\frac{{\mathsf{\rho }}_{\mathrm{f}}}{{\mathsf{\rho }}_{\mathrm{nf}}}\right)\left(\frac{{\mathrm{h}}_{1\mathrm{E}}+{\mathrm{h}}_{1\mathrm{w}}}{\Delta \mathrm{x}²}+\frac{{\mathrm{h}}_{1\mathrm{N}}+{\mathrm{h}}_{1\mathrm{S}}}{\Delta \mathrm{y}²}+\frac{{\mathrm{h}}_{1\mathrm{F}}+{\mathrm{h}}_{1\mathrm{B}}}{\Delta \mathrm{z}²}\right)\Delta \mathrm{x}\Delta \mathrm{y}\Delta \mathrm{z}+\mathrm{RaPr}\left(\frac{{\left(\mathsf{\rho }\mathsf{\beta }\right)}_{\mathrm{nf}}}{{\left(\mathsf{\rho }\mathsf{\beta }\right)}_{\mathrm{f}}}\right)\left(\frac{{\mathsf{\rho }}_{\mathrm{f}}}{{\mathsf{\rho }}_{\mathrm{nf}}}\right){\left(\frac{{\mathrm{T}}_{\mathrm{F}}-{\mathrm{T}}_{\mathrm{B}}}{2}-\mathrm{N}\frac{{\mathrm{C}}_{\mathrm{F}}-{\mathrm{C}}_{\mathrm{B}}}{2}\right)}_{\mathrm{p}}\Delta \mathrm{x}\Delta \mathrm{y}\\ -\mathrm{Pr}{\mathrm{Ha}}^2\left(\frac{{\mathsf{\rho }}_{\mathrm{f}}}{{\mathsf{\rho }}_{\mathrm{nf}}}\right)\left(\frac{{\mathsf{\sigma }}_{\mathrm{nf}}}{{\mathsf{\sigma }}_{\mathrm{f}}}\right)\left(\frac{{\mathrm{U}}_{1\mathrm{E}-}{\mathrm{U}}_{1\mathrm{W}}}{2}\right)\Delta \mathrm{y}\Delta \mathrm{z}\end{array}$$

Microrotation equation: x-component ($\mathsf{\Phi }={\mathrm{h}}_1$):

$${\mathrm{a}}_{\mathrm{p}}{\mathrm{h}}_{1\mathrm{p}}={\mathrm{a}}_{\mathrm{E}}{\mathrm{h}}_{1\mathrm{E}}+{\mathrm{a}}_{\mathrm{w}}{\mathrm{h}}_{1\mathrm{w}}+{\mathrm{a}}_{\mathrm{N}}{\mathrm{h}}_{1\mathrm{N}}+{\mathrm{a}}_{\mathrm{S}}{\mathrm{h}}_{1\mathrm{S}}+{\mathrm{a}}_{\mathrm{F}}{\mathrm{h}}_{1\mathrm{F}}+{\mathrm{a}}_{\mathrm{B}}{\mathrm{h}}_{1\mathrm{B}}+{\mathrm{b}}_{\mathrm{p}}$$

(27)

With ${\mathrm{b}}_{\mathrm{p}}={\mathrm{h}}_{1\mathrm{p}}^0\frac{\Delta \mathrm{x}\Delta \mathrm{y}\Delta \mathrm{z}}{\Delta \mathrm{t}}+\mathrm{Pr}·\mathrm{K}\left(\frac{{\mathsf{\rho }}_{\mathrm{f}}}{{\mathsf{\rho }}_{\mathrm{nf}}}\right)\left({\mathsf{\omega }}_{1\mathrm{p}}-{\mathrm{h}}_{1\mathrm{p}}\right)$

Microrotation equation: y-component ($\mathsf{\Phi }={\mathrm{h}}_2$):

$${\mathrm{a}}_{\mathrm{p}}{\mathrm{h}}_{2\mathrm{p}}={\mathrm{a}}_{\mathrm{E}}{\mathrm{h}}_{2\mathrm{E}}+{\mathrm{a}}_{\mathrm{w}}{\mathrm{h}}_{2\mathrm{w}}+{\mathrm{a}}_{\mathrm{N}}{\mathrm{h}}_{2\mathrm{N}}+{\mathrm{a}}_{\mathrm{S}}{\mathrm{h}}_{2\mathrm{S}}+{\mathrm{a}}_{\mathrm{F}}{\mathrm{h}}_{2\mathrm{F}}+{\mathrm{a}}_{\mathrm{B}}{\mathrm{h}}_{2\mathrm{B}}+{\mathrm{b}}_{\mathrm{p}}$$

(28)

With ${\mathrm{b}}_{\mathrm{p}}={\mathrm{h}}_{2\mathrm{p}}^0\frac{\Delta \mathrm{x}\Delta \mathrm{y}\Delta \mathrm{z}}{\Delta \mathrm{t}}+\mathrm{Pr}·\mathrm{K}\left(\frac{{\mathsf{\rho }}_{\mathrm{f}}}{{\mathsf{\rho }}_{\mathrm{nf}}}\right)\left({\mathsf{\omega }}_{2\mathrm{p}}-{\mathrm{h}}_{2\mathrm{p}}\right)$

Vector potential equations:

$${\mathsf{\psi }}_{1\mathrm{p}}=\frac{1}{2}{\left[\frac{1}{\Delta \mathrm{x}²}+\frac{1}{\Delta \mathrm{y}²}+\frac{1}{\Delta \mathrm{z}²}\right]}^{-1}\left({\mathsf{\omega }}_{1\mathrm{p}}++\frac{{\mathsf{\psi }}_{1\mathrm{E}}+{\mathsf{\psi }}_{1\mathrm{w}}}{\Delta \mathrm{x}²}+\frac{{\mathsf{\psi }}_{1\mathrm{N}}+{\mathsf{\psi }}_{1\mathrm{S}}}{\Delta \mathrm{y}²}+\frac{{\mathsf{\psi }}_{1\mathrm{F}}+{\mathsf{\psi }}_{1\mathrm{B}}}{\Delta \mathrm{z}²}\right)$$

(29)

$${\mathsf{\psi }}_{2\mathrm{p}}=\frac{1}{2}{\left[\frac{1}{\Delta \mathrm{x}²}+\frac{1}{\Delta \mathrm{y}²}+\frac{1}{\Delta \mathrm{z}²}\right]}^{-1}\left({\mathsf{\omega }}_{2\mathrm{p}}++\frac{{\mathsf{\psi }}_{2\mathrm{E}}+{\mathsf{\psi }}_{2\mathrm{w}}}{\Delta \mathrm{x}²}+\frac{{\mathsf{\psi }}_{2\mathrm{N}}+{\mathsf{\psi }}_{2\mathrm{S}}}{\Delta \mathrm{y}²}+\frac{{\mathsf{\psi }}_{2\mathrm{F}}+{\mathsf{\psi }}_{2\mathrm{B}}}{\Delta \mathrm{z}²}\right)$$

(30)

$${\mathsf{\psi }}_{3\mathrm{p}}=\frac{1}{2}{\left[\frac{1}{\Delta \mathrm{x}²}+\frac{1}{\Delta \mathrm{y}²}+\frac{1}{\Delta \mathrm{z}²}\right]}^{-1}\left({\mathsf{\omega }}_{3\mathrm{p}}++\frac{{\mathsf{\psi }}_{3\mathrm{E}}+{\mathsf{\psi }}_{3\mathrm{w}}}{\Delta \mathrm{x}²}+\frac{{\mathsf{\psi }}_{3\mathrm{N}}+{\mathsf{\psi }}_{3\mathrm{S}}}{\Delta \mathrm{y}²}+\frac{{\mathsf{\psi }}_{3\mathrm{F}}+{\mathsf{\psi }}_{3\mathrm{B}}}{\Delta \mathrm{z}²}\right)$$

(31)

The equations governing the problem are discretized by applying the control volume method. The power laws scheme is used to treat the convective terms. To discretize the temporal derivatives, the fully implicit procedure is retained to ensure the stability of computational scheme. The grids are considered uniform in all directions with additional nodes on boundaries. The successive relaxation-iterating scheme is employed in solving the resulting algebraic equations.

The solution is considered as acceptable as the next convergence criterion is satisfied for every time step:

$$\sum _{\mathrm{i}}^{1,2,3}\frac{\max \left|{\mathsf{\psi }}_{\mathrm{i}}{}^{\mathrm{n}}-{\mathsf{\psi }}_{\mathrm{i}}{}^{\mathrm{n}-1}\right|}{\max \left|{\mathsf{\psi }}_{\mathrm{i}}{}^{\mathrm{n}}\right|}+\max \left|{\mathrm{T}}^{\mathrm{n}}-{\mathrm{T}}^{\mathrm{n}-1}\right|+\max \left|{\mathrm{C}}^{\mathrm{n}}-{\mathrm{C}}^{\mathrm{n}-1}\right|\le {10}_{}^{-5}$$

(32)

The superscript n corresponds to the iteration number. The solution is regarded as a steady state if the following criterion is satisfied:

$$\frac{\max \left|{\mathsf{\psi }}^{\mathrm{m}}-{\mathsf{\psi }}^{\mathrm{m}-1}\right|}{\max \left|{\mathsf{\psi }}^{\mathrm{m}}\right|}\le {10}_{}^{-5}$$

(33)

where m denotes the number of the time step.

To determine an appropriate grid for numerical simulations, a grid independence study has been undertaken first. A dimensionless time step equal to 10⁻⁴ is retained. Figure 2 presents the effect of grid size on the average Nusselt and the average Sherwood numbers on the hot wall for N = −0.5, φ = 0.04 and K =1 for different Rayleigh numbers. Hence, the (51 × 51 × 51) grid was estimated to be convenient for the present work at least for Ra ≤ 10⁵ because it allows a good compromise between the computational cost (a significant reduction of the execution time) and the accuracy of the results obtained.

To prove the precision of the present code, comparisons with previously published results are necessary. But due to the lack of availability of data on the particular problems of three-dimensional double diffusive convection in micropolar nanofluid investigated in this research, the validation of our three-dimensional code was made in different stages:

First, the 3-D double diffusive convection code for a Newtonian fluid is compared with the numerical results of Sezai and Mohamad [48]. The validation which is reported in a previous work (Abidi et al. [49]) shows good agreement.

Second, the proposed three-dimensional nanofluid model that takes into account the nanoparticles microrotation is validated against experimental data of Putra et al. [5]. Figure 3 demonstrates that the experimental data and the present numerical results reveal similar trends. Apparently, as the microrotation parameter K augments our numerical results are closer to the experimental data. The proposed model is consistent with the assumptions describing that the nanoparticles microrotation must be taken into account.

The third validation concerns the model of micropolar nanofluid under a magnetic field. To that end, a 2-D version of our code is derived and the results are verified against the numerical solutions reported by Bourantas and Loukopoulos [41]. As revealed in Figure 4, a very good agreement is found.

The results of the present investigation are in good agreement with the results of the models used [5,41,48]. Hence, the developed computer code can be effectively and reliably used to simulate the problem under consideration.

4. Results and Discussion

The numerical investigations are performed to explore the double-diffusive natural convection in a cubic cavity filled with Al₂O₃/water micropolar nanofluid with the influence of horizontal magnetic field.The present numerical simulation assume pure water as the base fluid with Pr = 6.2 and Le = 1.The computations are performed for the range of Rayleigh numbers (10³ ≤ Ra ≤ 10⁶), vortex viscosity parameter K (0 ≤ K ≤ 5) and buoyancy ratio N(−2 ≤ N ≤ 0), nanoparticle volume fractions of (0–6%)and Hartmann numbers (0–60). The influences of these parameters on flow dynamics and heat and mass transfers are detailed.

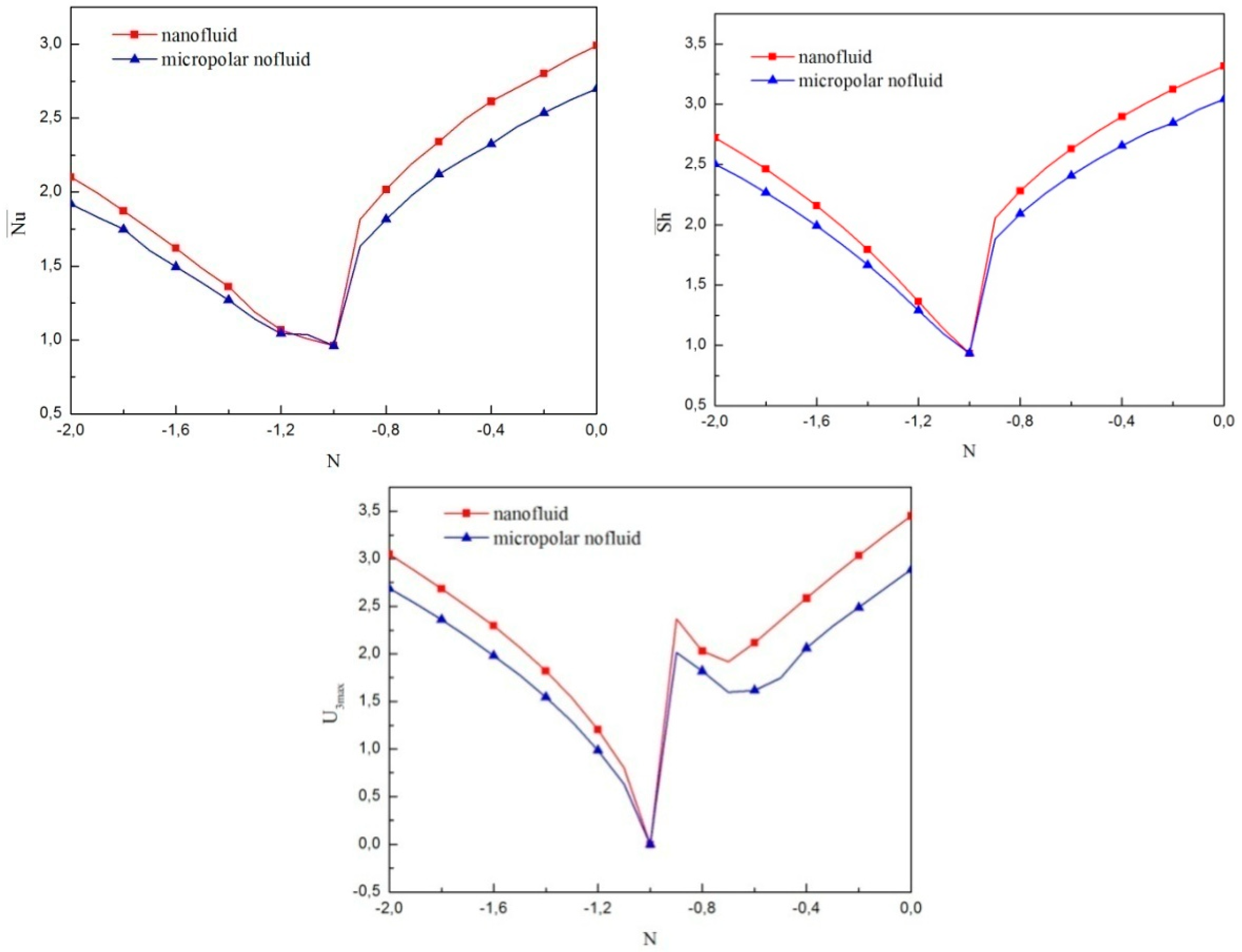
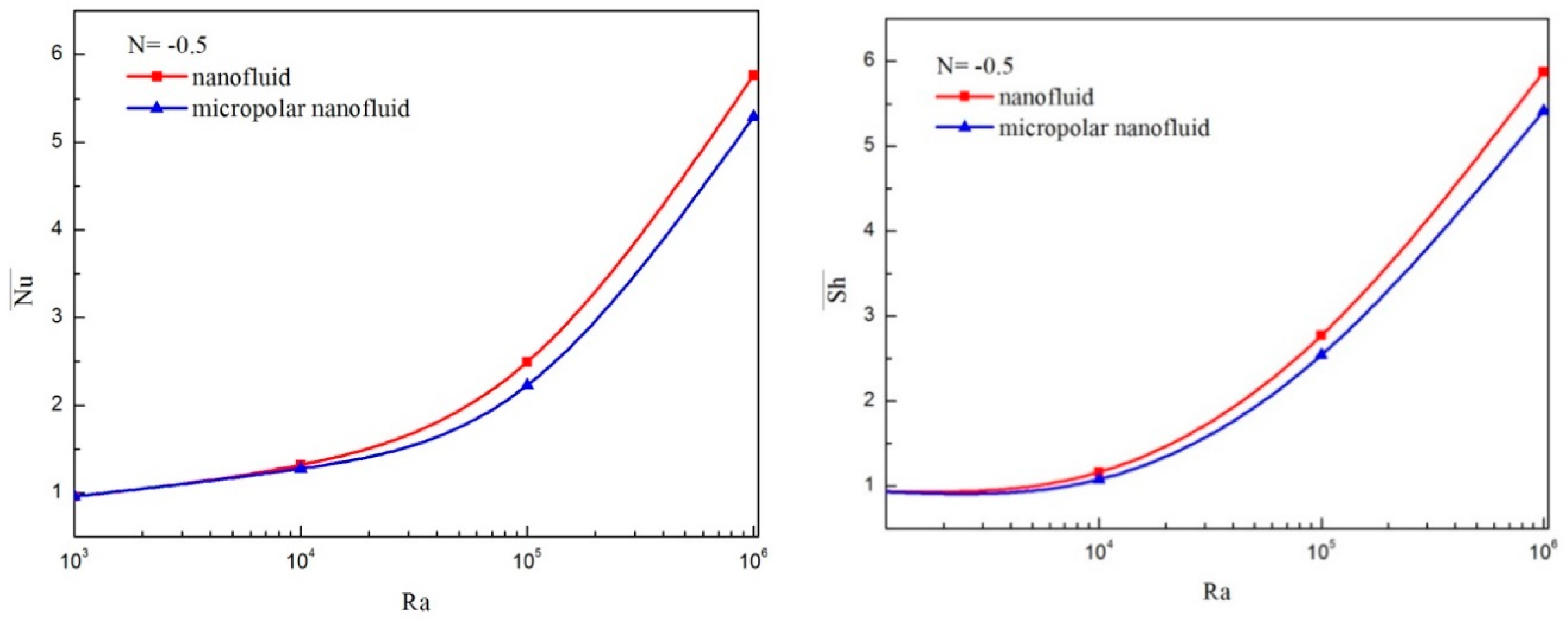
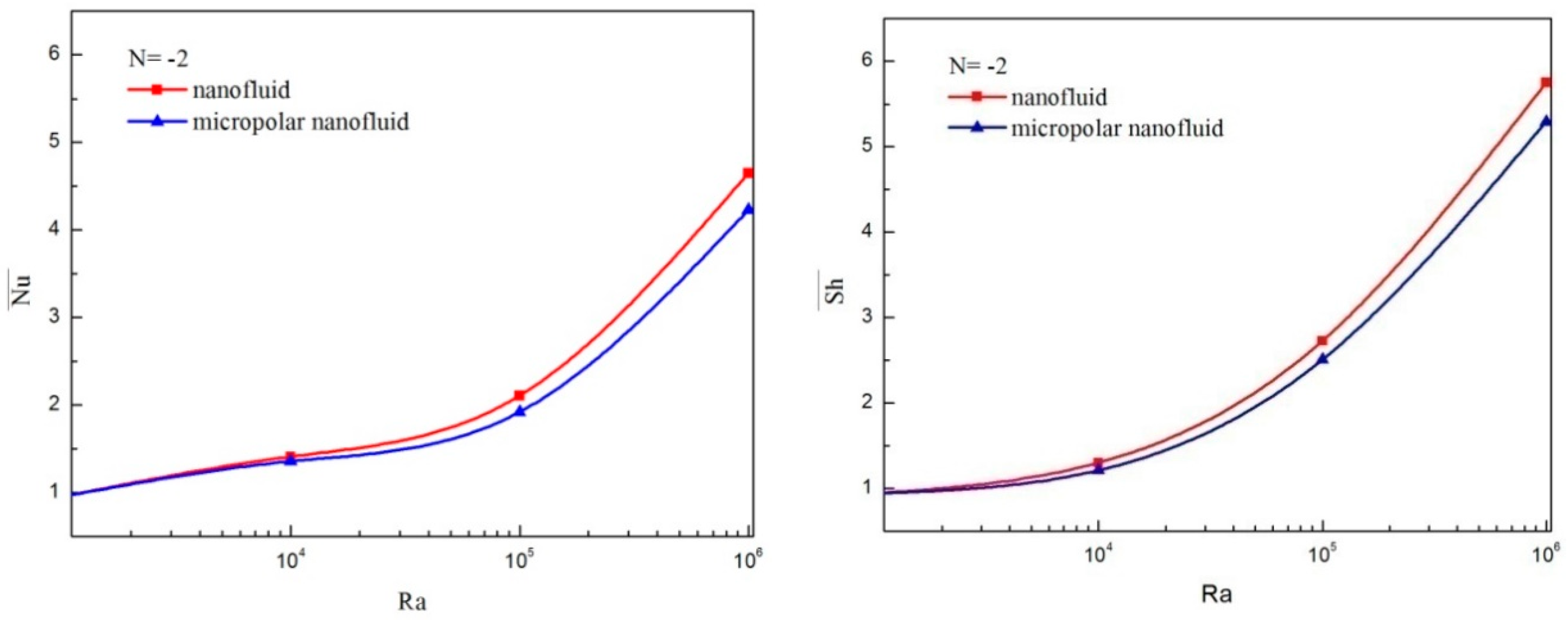
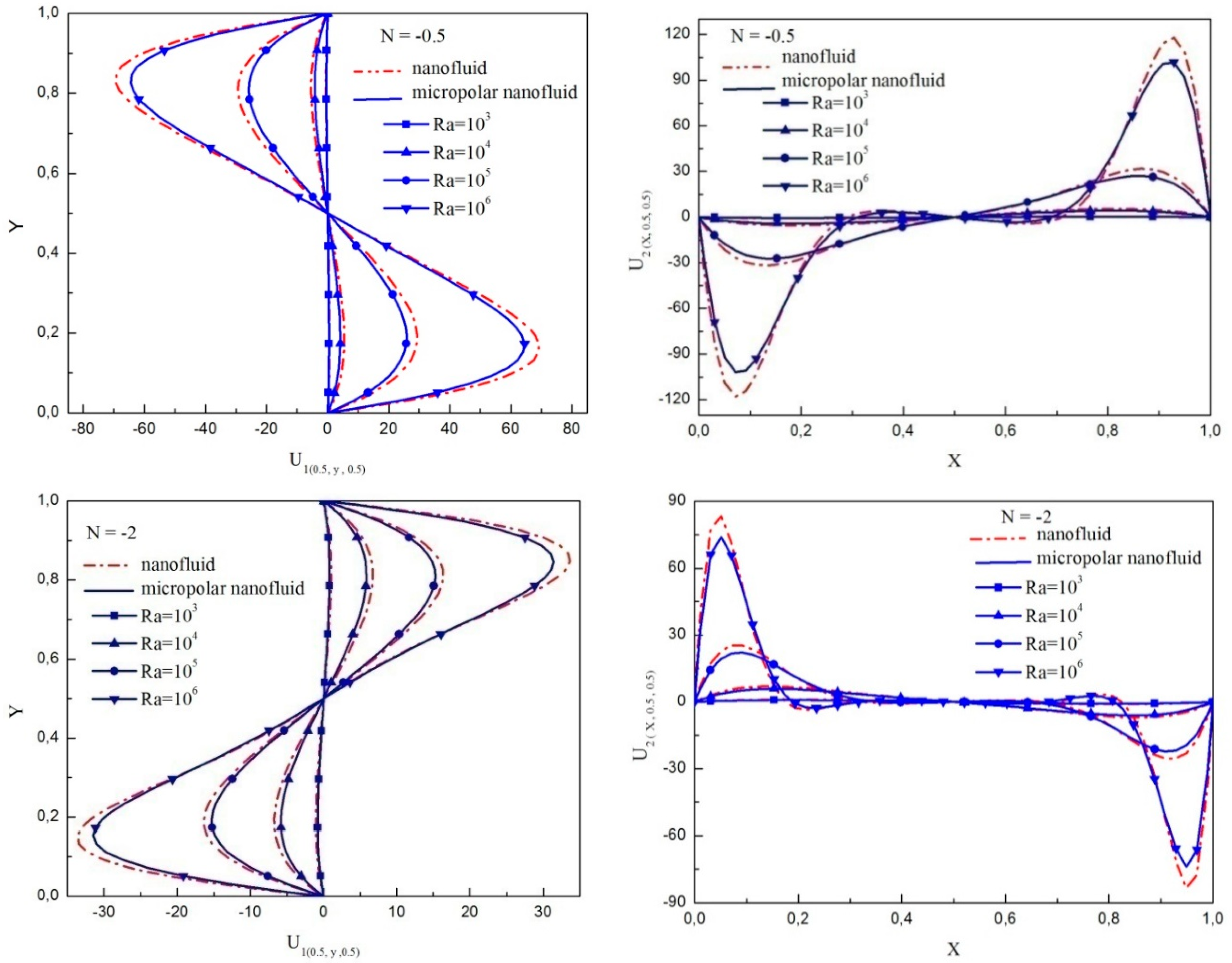
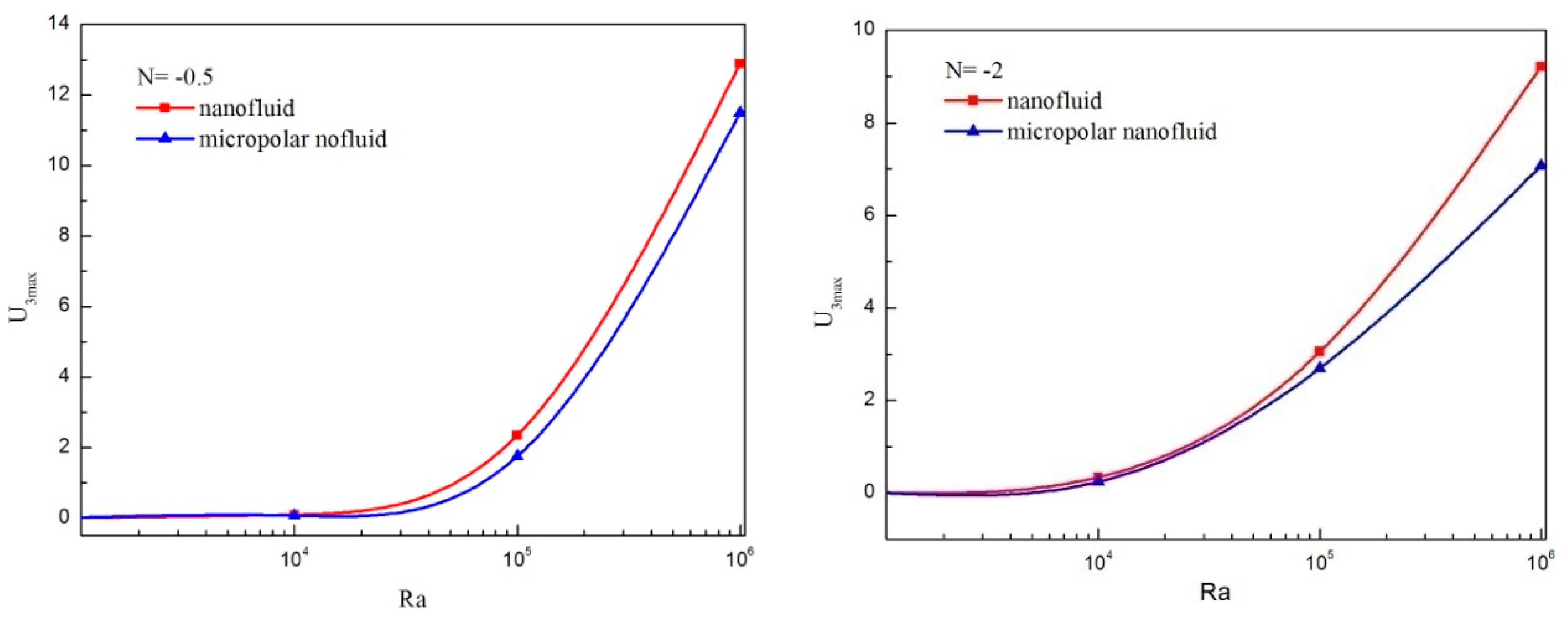
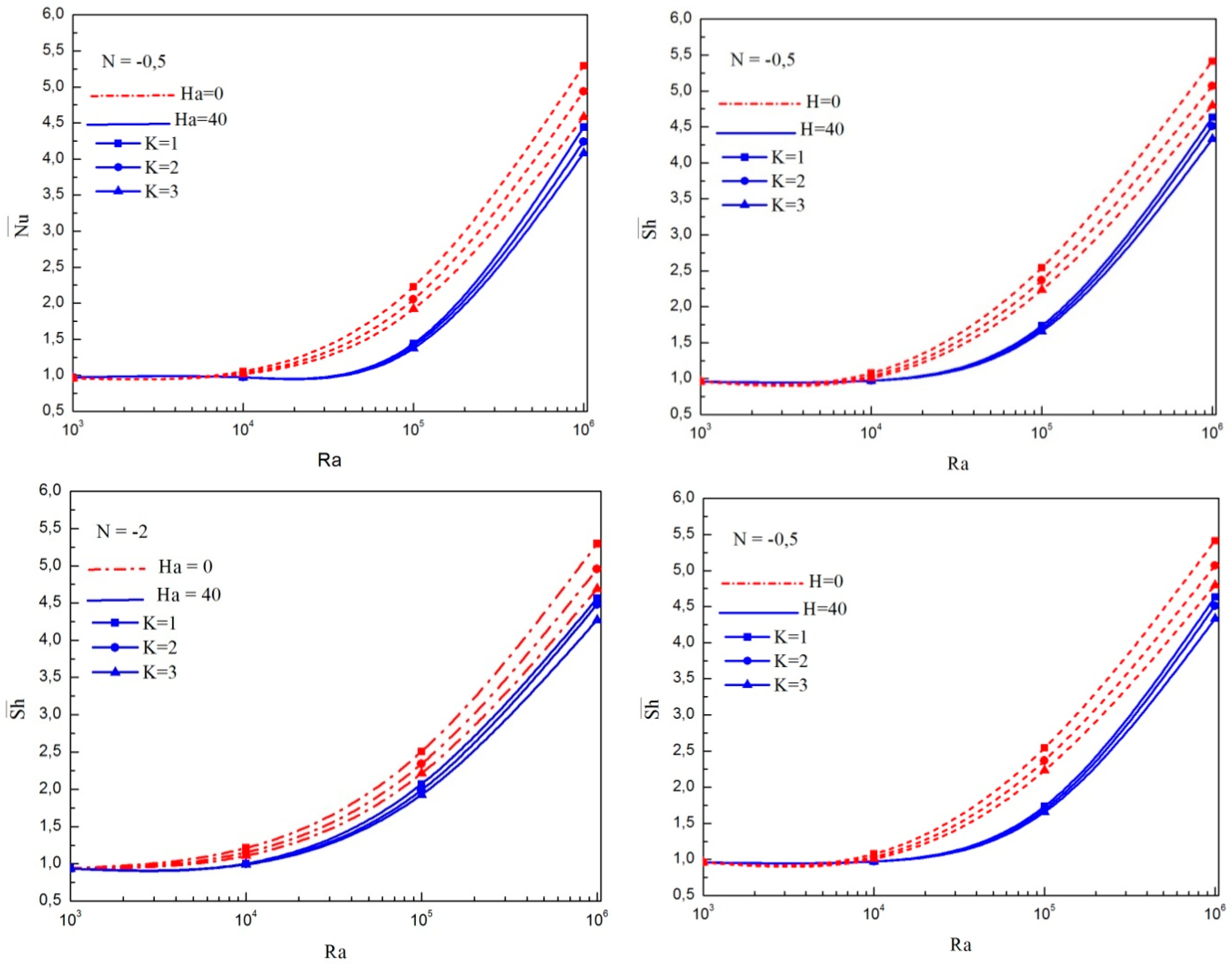
4.1. Comparison between the Micropolar Nanofluid and Nanofluid Models

Comparison between micropolar and non-micropolar nanofluid models are made in terms of $\overline{\mathrm{Nu}}$, $\overline{\mathrm{Sh}}$ and U_3max as per the buoyancy ratio illustrated in Figure 5. It can be observed for a micropolar nanofluid model that all of $\overline{\mathrm{Nu}}$, $\overline{\mathrm{Sh}}$ and U_3max are smaller than that of a pure nanofluid model regardless the value of N considered. This gap is minimized adjacent to the transition value of N = −1 and the disparity is more significant for the thermal buoyancy-dominated zone.

Variation of $\overline{\mathrm{Nu}}$ and $\overline{\mathrm{Sh}}$ against the Rayleigh is shown in Figure 6. Both micropolar and non-micropolar nanofluid models are considered with N = 0.5 in the thermal buoyancy-dominated regime and N = 2 in the solutal buoyancy-dominated regime. Both $\overline{\mathrm{Nu}}$ and $\overline{\mathrm{Sh}}$ are smaller than when considering the micropolar theory regardless of the value of Ra for both values of buoyancy ratio. However, the gap is more prominent when the Rayleigh numbers are enhanced. The current observations are in good agreement with the results of Bourantas and Loukopoulos [41] for two-dimensional flow by considering only the thermal gradient.

Figure 7 elucidates the variations of the horizontal and vertical velocity components at the Z = 0.5 plane according to the Rayleigh numbers for N = −0.5 and N = −2. Regardless of the modelconsidered, it is noticed that with increase in Rayleigh numbers, the flow regime is intensified and the magnitude of each component of velocity is increased. However, their magnitudes are higher in the case of ordinary nanofluid than in that of micropolar nanofluid. This difference becomes more significant for Ra up to 10⁴ and implies that the insertion of the vortex viscosity parameter decelerates the principal flow strength for both regimes.

Figure 8 shows the maximum of the transverse velocity for various Rayleigh number applying the micropolar and non-micropolar nanofluid models in the absence microrotation for N = −0.5 and N = −2. For both cases, U_3max is smaller without considering the micropolar theory and the gap is more noticeable when Ra outdoes 10⁴. Hence, the consideration of micropolar material parameter weakens the three-dimensional character of the flow.

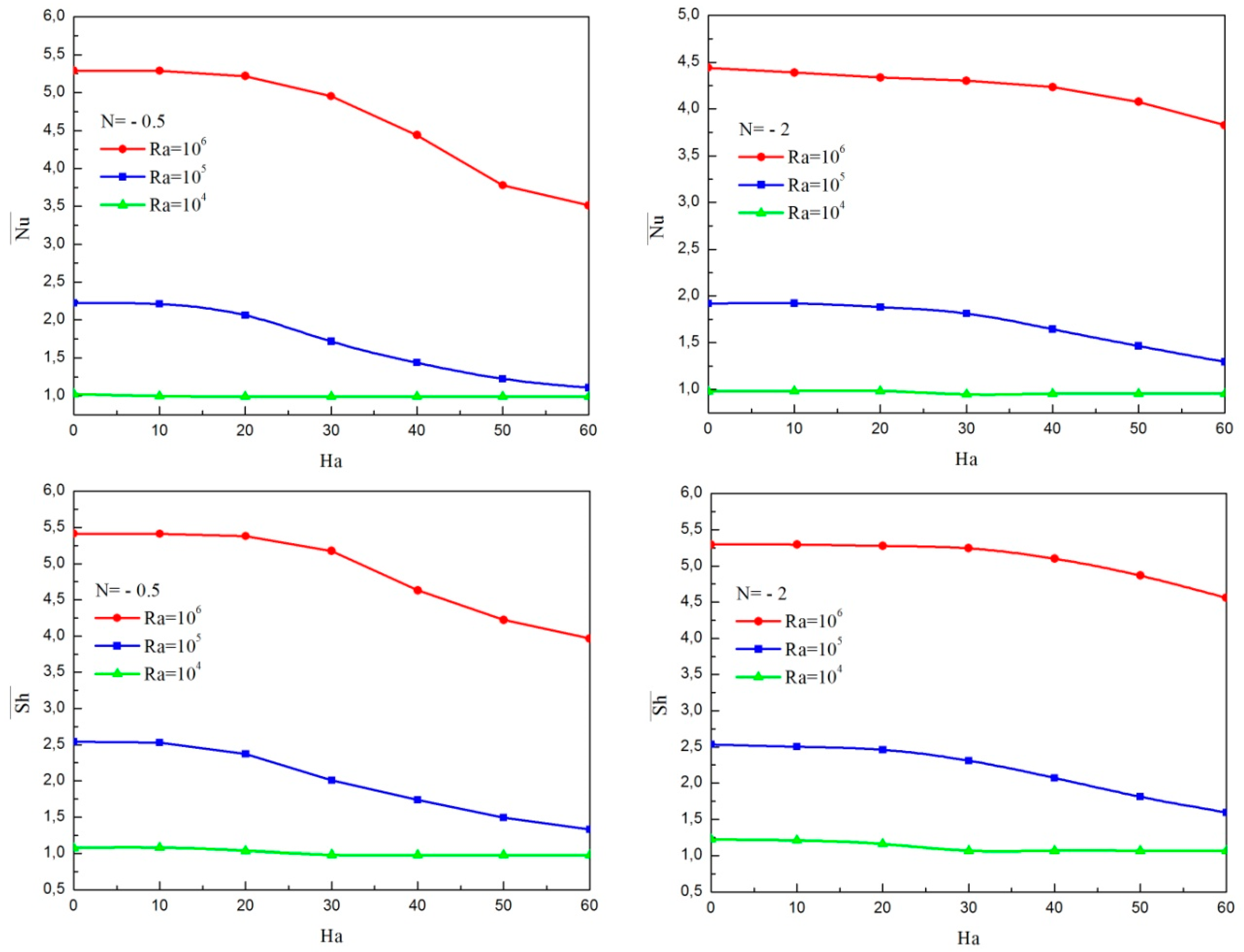
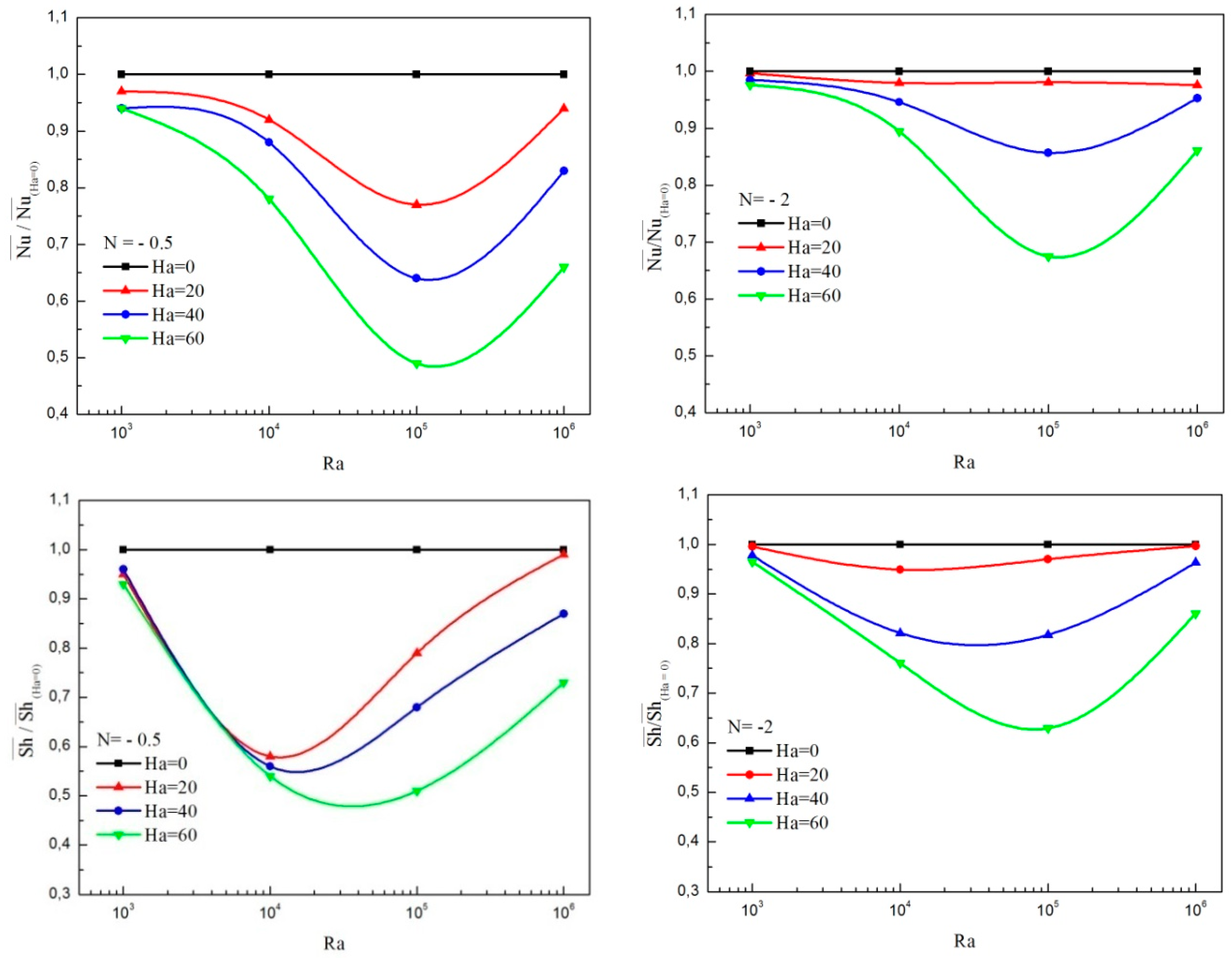
4.2. Effect of Magnetic Field

To study the impacts of uniform magnetic field, comparisons of isotherms, isoconcentrations, and projections of the flow lines in the mid (X–Y) plane are undertaken for thermally dominated (N = −0.5) and compositionally dominated (N = −2) regimes. The results for the average Nusselt and Sherwood numbers are also presented and analyzed.

Figure 9 shows projections of flow lines, isotherms and isoconcentrations in the main plan Z = 0.5 for various combinations of Ra and Ha with φ = 4% for N = −0.5. In this case, the flow is mainly initiated by thermal volume forces so that the main flow direction is clockwise in the X–Y plane.

In absence of magnetic field (Ha=0), when the Rayleigh number enhances, the convection mechanism is more noticeable. The rotation cells become larger near the isothermal and the insulated walls indicating the strength of motion of the fluid. The projections of the flow lines on the mid X–Y plane are not closed but have a spiral form. Normally, the flow structure shows with two inner vortexes at high Rayleigh number (Ra= 10⁵) but in the presence of magnetic field these two inner vortexes are initiated with lower Ra=10⁴ and are moving towards the isothermal walls as the Rayleigh number increases.

When Ha = 0, an increase in Ra changes the direction of isotherms from almost vertical to the horizontal in the core and are stacked near the active walls. An isoconcentrations central zone is created and extended to the upper and lower regions of the enclosure as Ra increases. Once Ha = 40, both the thermal and solutal gradients diminish near the active walls. Furthermore, the temperature and concentration contours become inclined and parallel to each other within the core of the cavity as Ra increases and these changes in direction is an indication of weakness in convection flow due to the magnetic field.

Figure 10 displays similar results as shown in Figure 9 except for N = −2. For this specific value of N, the main flow direction is reversed due to the enhancement in solutal effect. In the presence of magnetic field, the flow involves a counter-clockwise rotating main cell with two inner vortexes slightly titled to the hot wall and move towards the isothermal walls as the Rayleigh number increases.

When the influence of magnetic field is negligible (Ha = 0), both isotherms and isoconcentrations became inclined and parallel to each other within the cavity center with the increase in Rayleigh number. On the contrary, as the Rayleigh number remains constant both isotherms and isoconcentrations seem to be insensitive to the magnetic field.

To assess the magnetic field effect on the three-dimensional flow, the variation of the maximum of the transverse velocity versus the buoyancy ratio for two cases, Ha = 0 and Ha = 40 are illustrated in Figure 11. The presence of magnetic field causes an enhancement in the transverse velocity for both regimes regardless of the buoyancy ratio. However, its effect is more obvious for thermally-dominated zone than for the solutal-dominated one. The maximum of the transverse velocity has a minimum for N ≈ −1.

The variations of U_3max according to the Rayleigh number without (Ha = 0) and with (Ha = 40) magnetic field for both thermally-dominated flow (N = −0.5) and solutal-dominated flow (N = −2) are presented in Figure 12. When the magnetic field is absent, U_3max increases slightly with increase in Rayleigh number for both value of N. However, U_3max enhanced considerably due to the influence of the magnetic field and is more prominent for the thermally dominated flow (N = −0.5).

Figure 13 shows the effects of the Hartmann number on U_3max with the Rayleigh number for both thermally-dominated flow (N = −0.5) and solutal-dominated flow (N = −2). As seen from the figure, the velocity is augmented for Hartmann numbers lower than the critical value of Ha and decreased by increasing the Hartmann number once more. Indeed, by increasing the Ha numbers, Lorentz force becomes stronger and overcomes the buoyancy force, which causes a considerable reduction in the three-dimensional character of the flow. The 3-D flow behavior against the Hartmann number is already discussed by Ozoe and Okada [43] and by Kolsi et al. [50] for three-dimensional natural convection of pure fluid. It is interesting to detect the existence of peak at which U_3max is maximized regardless of the value of Ra. This peak value moves towards the highest value of Ha as an increase in Ra. In fact, for high Rayleigh number, convection is the dominant mechanism of heat transfer and the three-dimensional character of the flow is more prominent. Thus, to act against the convection mechanism, a stronger magnetic field must be applied and hence the Hartmann number should be higher. Therefore, the critical value of Ha is influenced by the values of Ra.

Also, the magnitude of U_3max is greater for thermally-dominated flow (N = −0.5) than for solutal-dominated flow (N = −2). Besides, it should be mentioned that the minimum values of U_3max occur when magnetic field is removed (Ha = 0) for both thermally-dominated flow (N = −0.5) and solutal-dominated flow (N = −2).

To highlight the effect of magnetic field on heat and mass transfers, the variations of $\overline{\mathrm{Nu}}$ and $\overline{\mathrm{Sh}}$ versus the buoyancy ratio for both cases, Ha = 0 and Ha = 40 are shown in Figure 14. It is clear that both $\overline{\mathrm{Nu}}$ and $\overline{\mathrm{Sh}}$ have a quasi-similar profile for both Ha = 0 and Ha = 40.

It is noticed that for both cases $\overline{\mathrm{Nu}}$ and $\overline{\mathrm{Sh}}$ have a decreasing trend upon increasing N in the negative sense. Beyond N = −1, $\overline{\mathrm{Nu}}$ and $\overline{\mathrm{Sh}}$ increase as N increases. The presence of a magnetic field decreased both $\overline{\mathrm{Nu}}$ and $\overline{\mathrm{Sh}}$ regardless of the buoyancy ratio. The magnetic field effect is more prominent for thermally-dominated regimes compared to solutal-dominated regimes.

Figure 15 illustrates the variations of $\overline{\mathrm{Nu}}$ and $\overline{\mathrm{Sh}}$ with the Hartmann number for different Rayleigh numbers for both thermally-dominated regime (N = −0.5) and compositionally dominated regime. (N = −2). As revealed from the figure for both cases N = −0.5 and N = −2, increase in Ra number produces a heat and mass transfer enhancement. However, in contradiction, both $\overline{\mathrm{Nu}}$ and $\overline{\mathrm{Sh}}$ decrease with increase in the Hartmann number. Thus, the magnetic field suppress the heat and mass transfer within the cavity by reducing the average Nusselt and Sherwood numbers. Also, it can be noticed that the magnetic field effect is more significant for a high Ra number. Moreover, it should be mentioned that, the maximum values of $\overline{\mathrm{Nu}}$ and $\overline{\mathrm{Sh}}$ occur when the magnetic field is removed (Ha = 0) for both thermally dominated flow (N = −0.5) and solutal dominated flow (N = −2).

A closer examination of the average Nusselt and Sherwood ratios reveal the impacts of magnetic field on the cavity heat and mass transfer performances.

Figure 16 present respectively the variations of the average Nusselt number ratio $\overline{\mathrm{Nu}/}\overline{\mathrm{Nu}}\left(\mathrm{Ha}=0\right)$ and the average Sherwood ratio $\overline{\mathrm{Sh}/}\overline{\mathrm{Sh}}\left(\mathrm{Ha}=0\right)$ versus Rayleigh number at different values of the Hartmann number for both thermally-dominated regime (N = −0.5) and solutal-dominated one (N = −2). The average Nusselt and Sherwood number ratios at Ha = 0 are considered as reference values. The nanoparticles volume fraction is kept constant (φ = 0.04). The results show that a critical Rayleigh number minimizes both the average Nusselt number ratio and the average Sherwood number ratio regardless of the Hartmann number value. These minimums move towards higher Ra number as the Ha number increases.

Figure 17 presents the variations of $\overline{\mathrm{Nu}}$ and $\overline{\mathrm{Sh}}$ with nanoparticles volume fraction at Ra = 10⁵ for various Hartmann numbers. As seen from the figure, for lower value of Ha, both $\overline{\mathrm{Nu}}$ and $\overline{\mathrm{Sh}}$ are decreased with increase in the nanoparticles volume fraction. In fact, adding nanoparticles to base fluid increase not only the thermal conductivity but also the viscosity of the fluid which results in the reduction of heat transfer rate. However, addition of nanoparticles enhances the heat and mass transfer for Ha more than 30.

Indeed, by increasing the Hartmann number, the rotation of the particles remains without intensive mixing in the fluid. At higher nanoparticles volume fraction, the effect of thermal conductivity exceeds the opposite effect of the viscosity. So, an increase in Hartmann number may lessen the deterioration in the heat transfer brought about by the effect of the viscosity. These results demonstrate the effectiveness of using magnetic field in enhancing the heat transfer by adding nanoparticles. In fact, one can control the magnetic field intensity and nanoparticles volume fraction to find an optimum heat transfer enhancement using nanoparticles.

Figure 18a,b are plotted to explore the effect the Rayleigh number Ra for different vortex viscosity parameter K on the average Nusselt and Sherwood numbers without (Ha = 0) and with (Ha = 40) magnetic field. Irrespective of the Hartmann number, by keeping the vortex viscosity parameter K constant, $\overline{\mathrm{Nu}}$ improves when increasing the Rayleigh number whereas the converse occurs when the Rayleigh number remains constant that is, the $\overline{\mathrm{Nu}}$ reduces by increasing the vortex viscosity parameter. It can be observed also that there is a reduction in the heat transfer rate by enhancing the Ha number regardless of the vortex viscosity parameter value and this diminution became more significant for Ra up to 10⁴. Furthermore, results for N = −2 shows similar tends for the impact of Rayleigh number and vortex viscosity parameter on $\overline{\mathrm{Sh}}$ number. The vital difference is that the $\overline{\mathrm{Sh}}$ number generally takes higher values than the $\overline{\mathrm{Nu}}$ number.

5. Conclusions

A numerical investigation has been carried out to explore the magnetic field effects on 3-D double diffusive natural convection in a cavity filled with an Al₂O₃/water micropolar nanofluid. The principal conclusions are listed as follows:

-

For a micropolar nanofluid model, both heat and mass transfer rates are smaller than those of a pure nanofluid model.

-

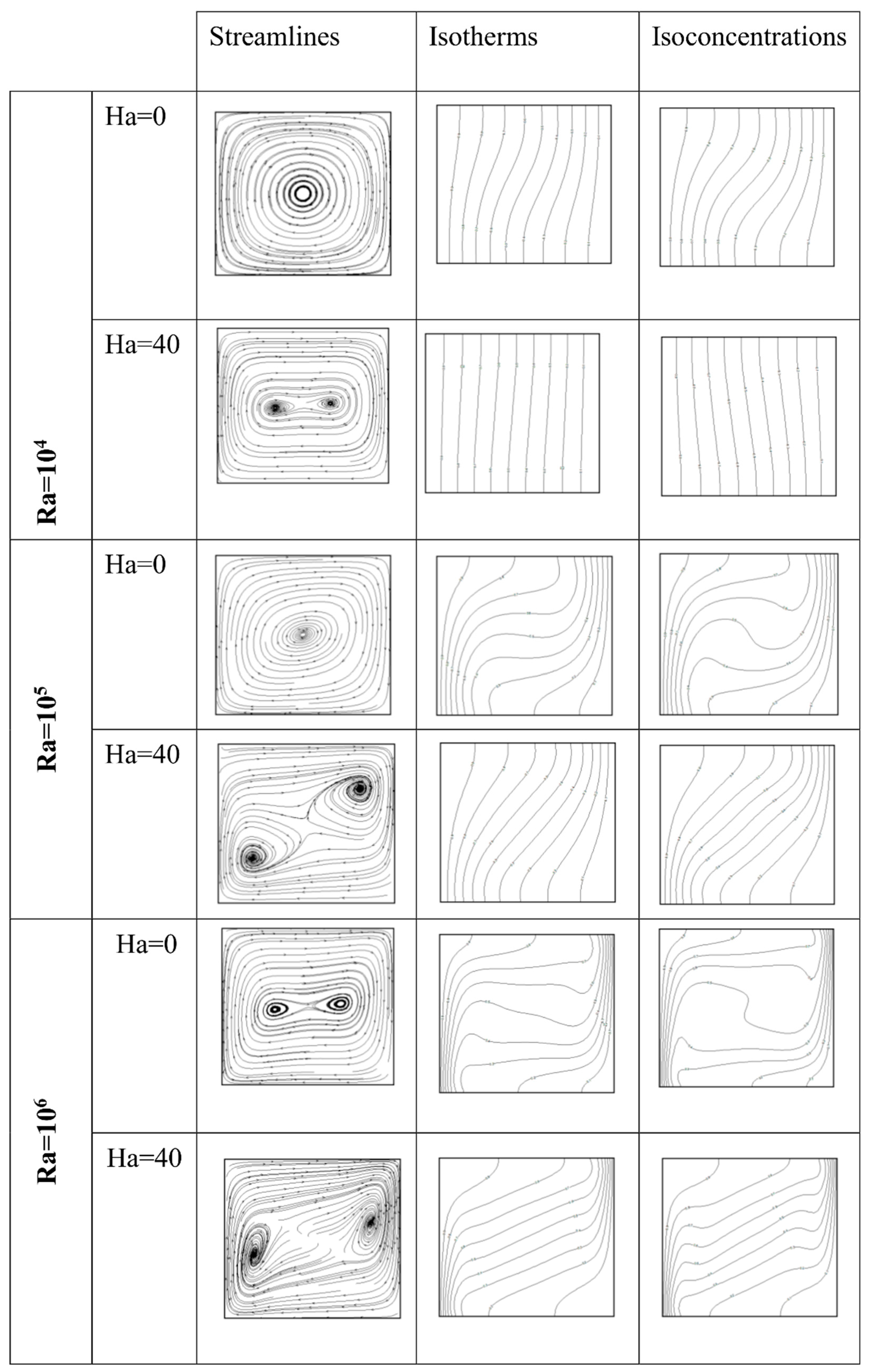
Taking in to account particle microrotation, the three-dimensional flow character is weakened.

-

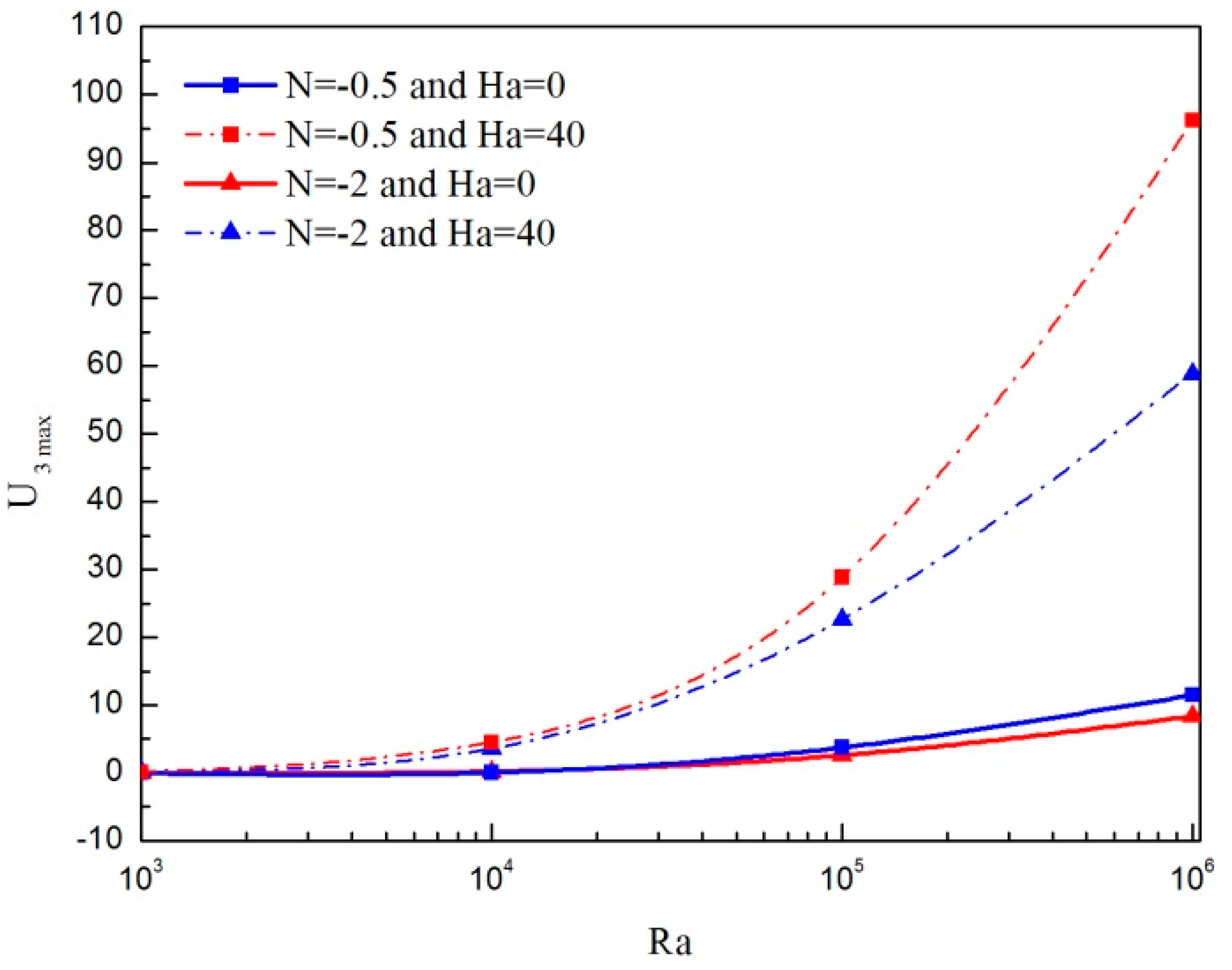
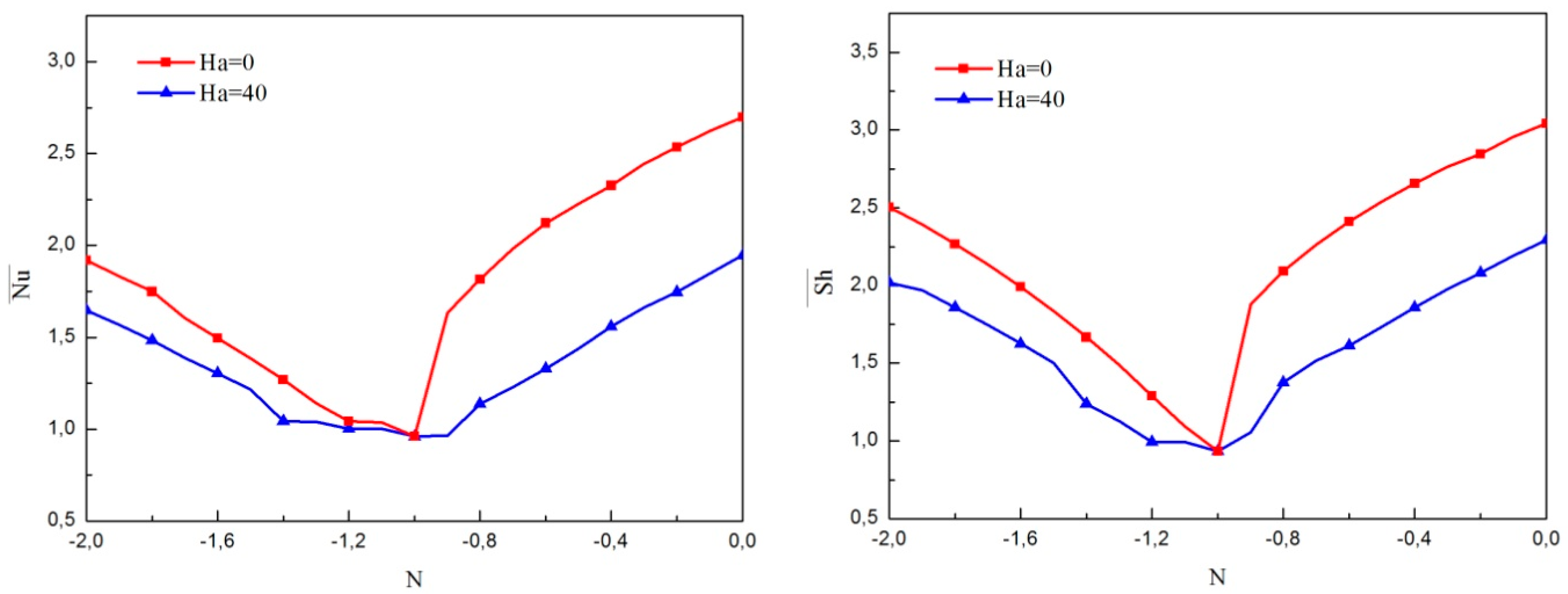
For a fixed value of nanoparticle volume fraction with a wide range Rayleigh number, the heat and mass transfer rates are reduced due to increase in the Hartman number.

-

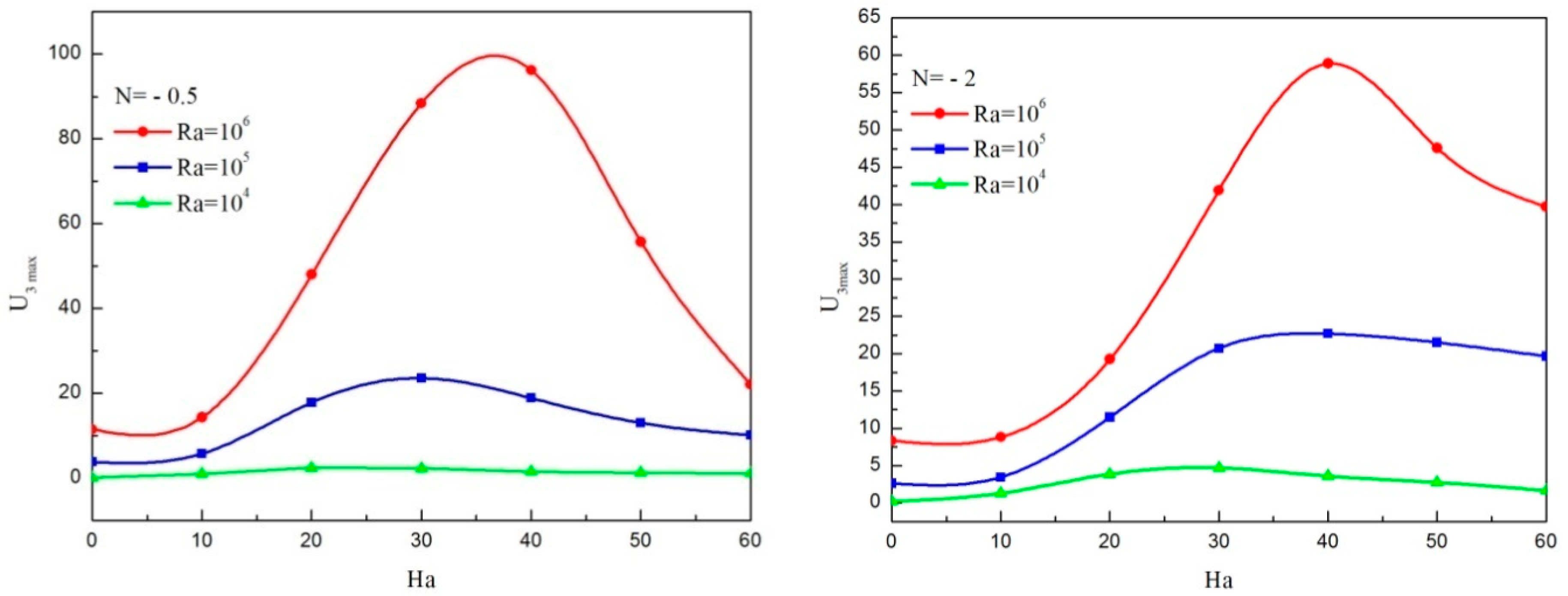
For various Rayleigh numbers, the maximum of the transverse velocity enhances for Hartmann numbers lower than a critical value and diminishes as the Hartmann number increases. This critical value moves towards the highest value of the Ha number as increasing the Ra number.

-

In the absence of magnetic field, the increase in nanoparticles volume fraction deteriorates the heat and mass transfer. However, for Ha greater than 30, the enhancement of nanoparticle volume fraction increases the heat and mass transfer rates.

-

During non-existence of a magnetic field, an increase in vortex viscosity parameter diminishes the average heat and mass transfer rates and is more pronounced when the magnetic field is enforced. However, for Ha greater than 30, the enhancement of nanoparticle volume fraction increases heat and mass transfer rates.