Magnetic Field Effect on the Double Diffusive Natural Convection in Three-Dimensional Cavity Filled with Micropolar Nanofluid
Abstract
1. Introduction
2. Mathematical Formulation
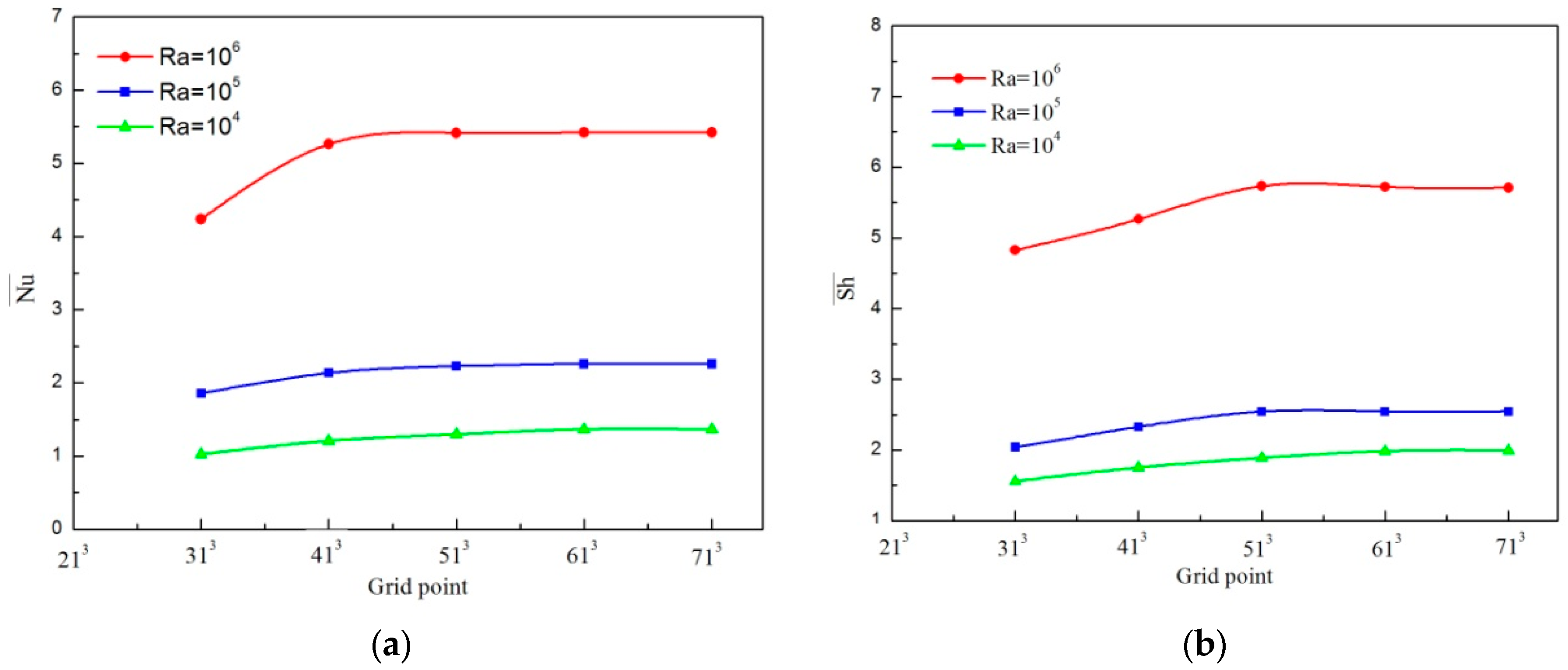
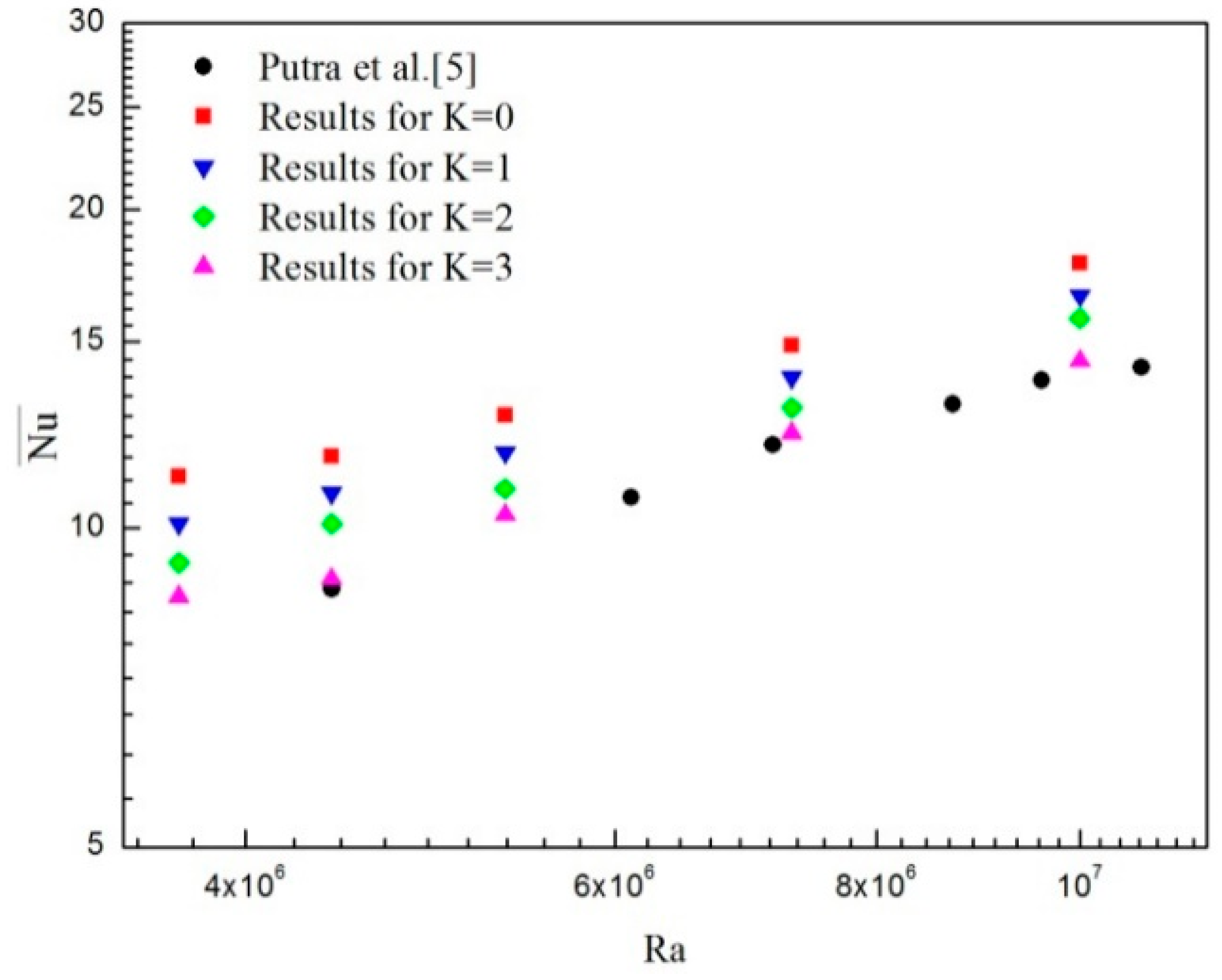
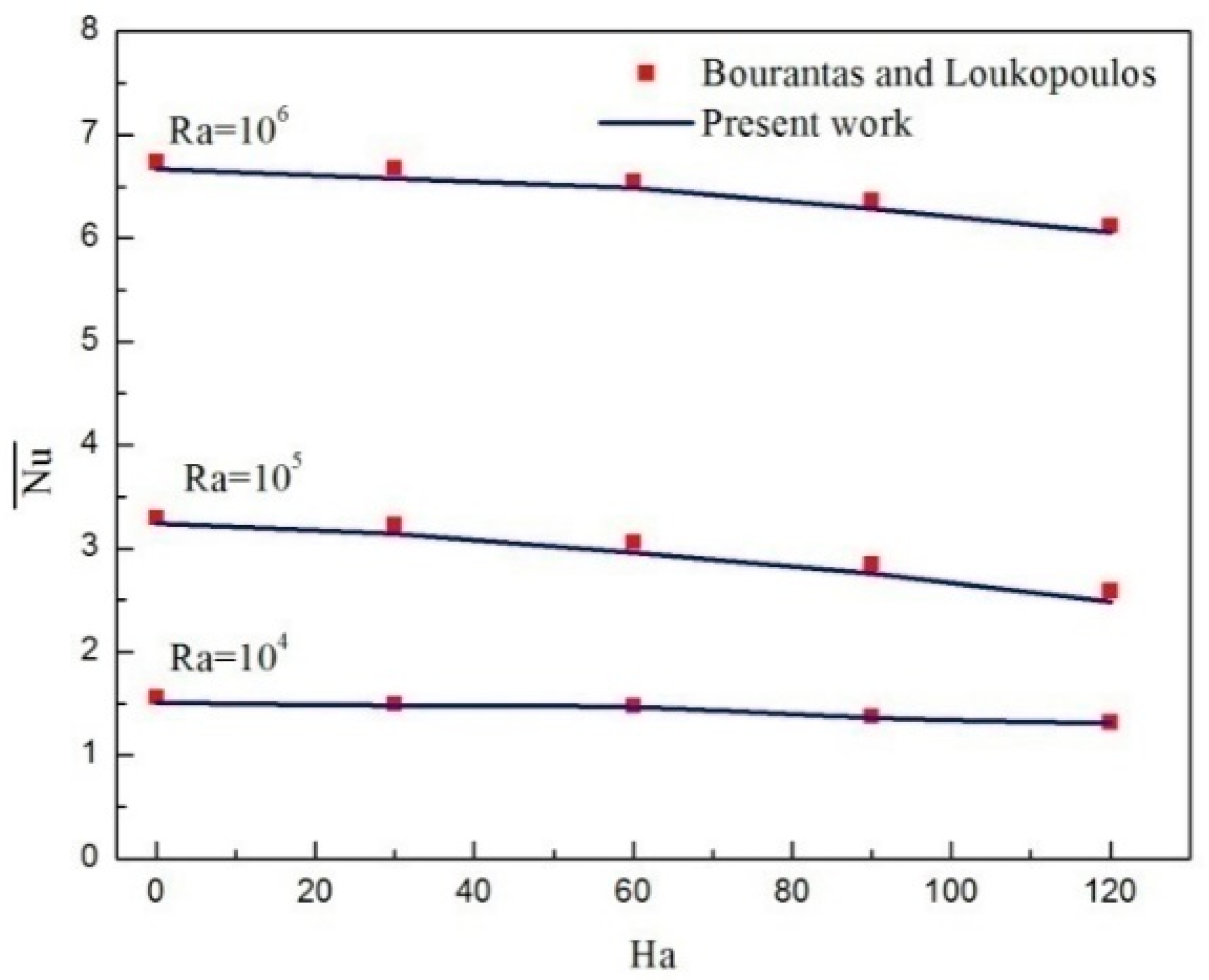
3. Numerical Approach and Benchmarking of the Code
- :
- : dimensionless coefficient
- : source term
4. Results and Discussion
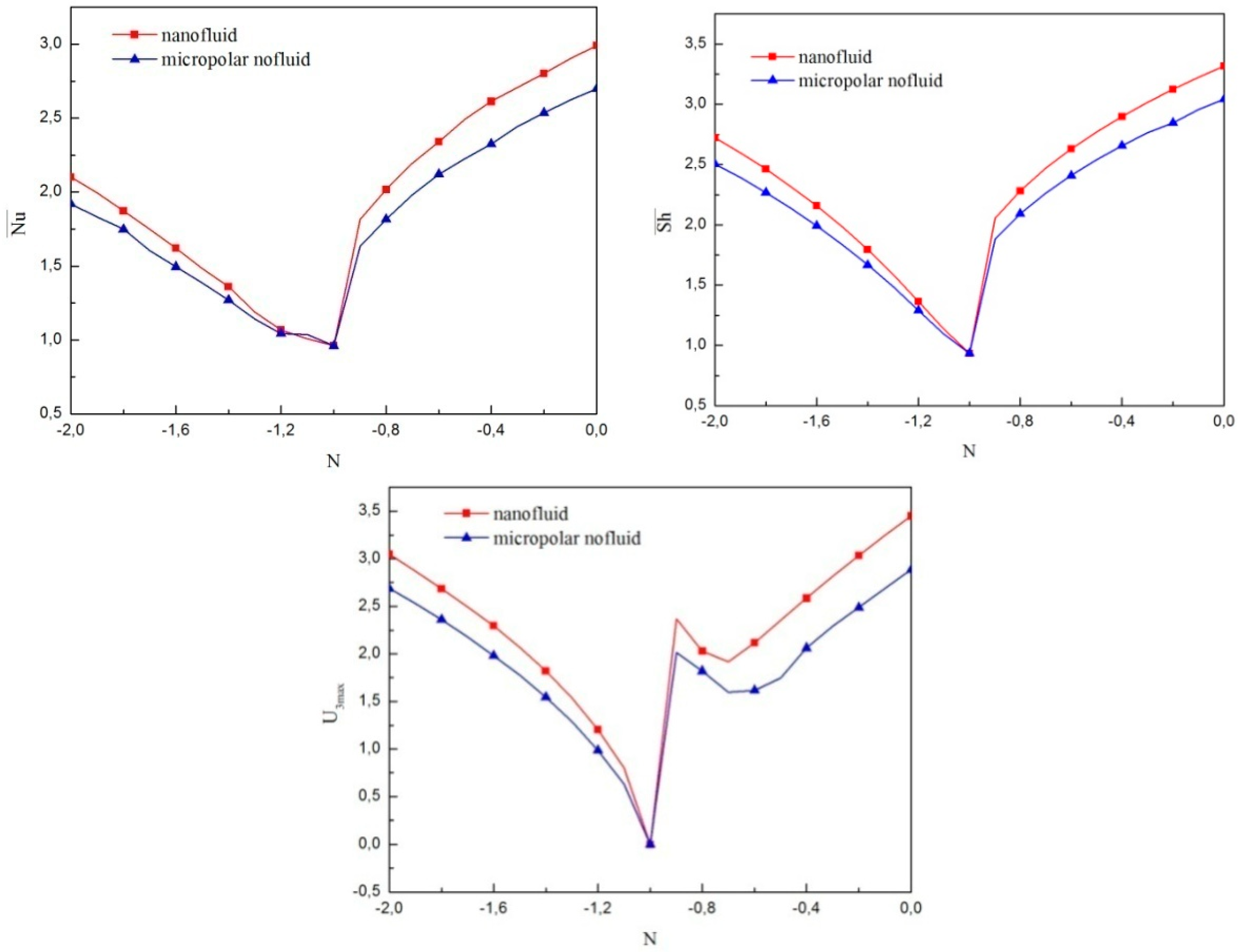
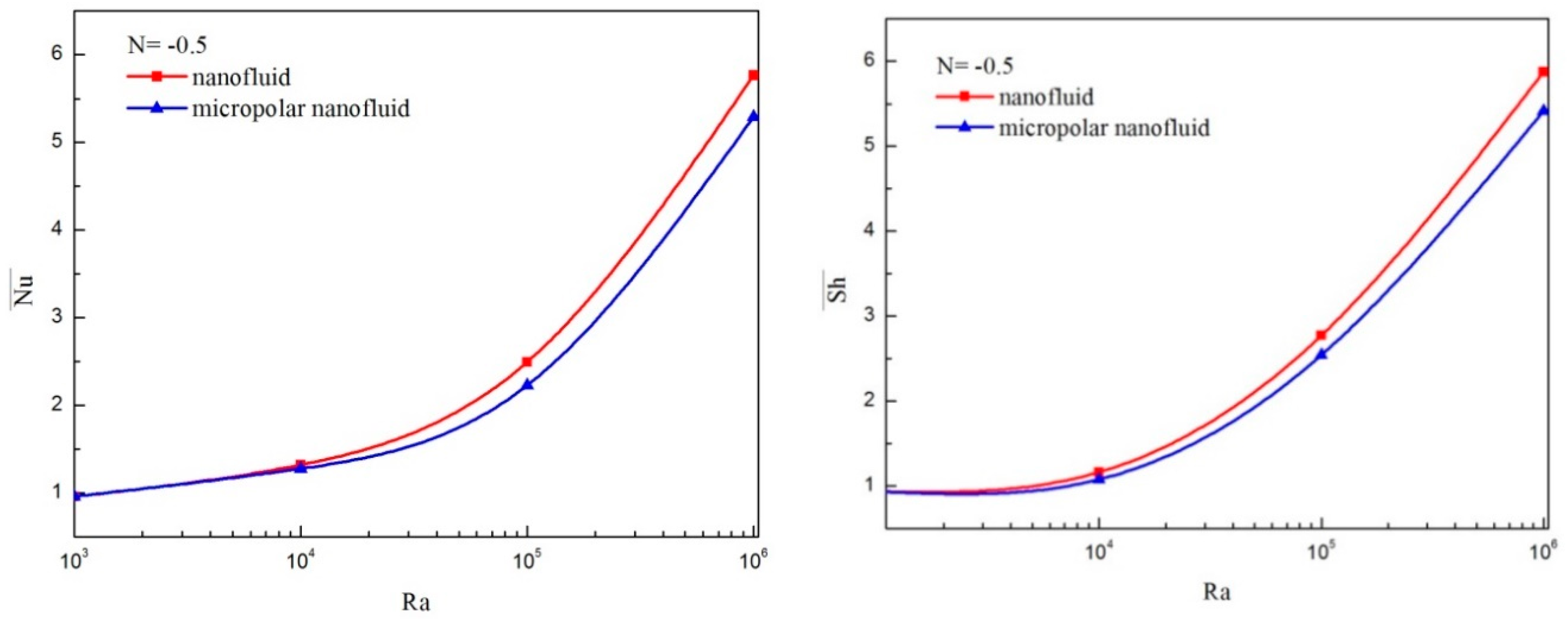
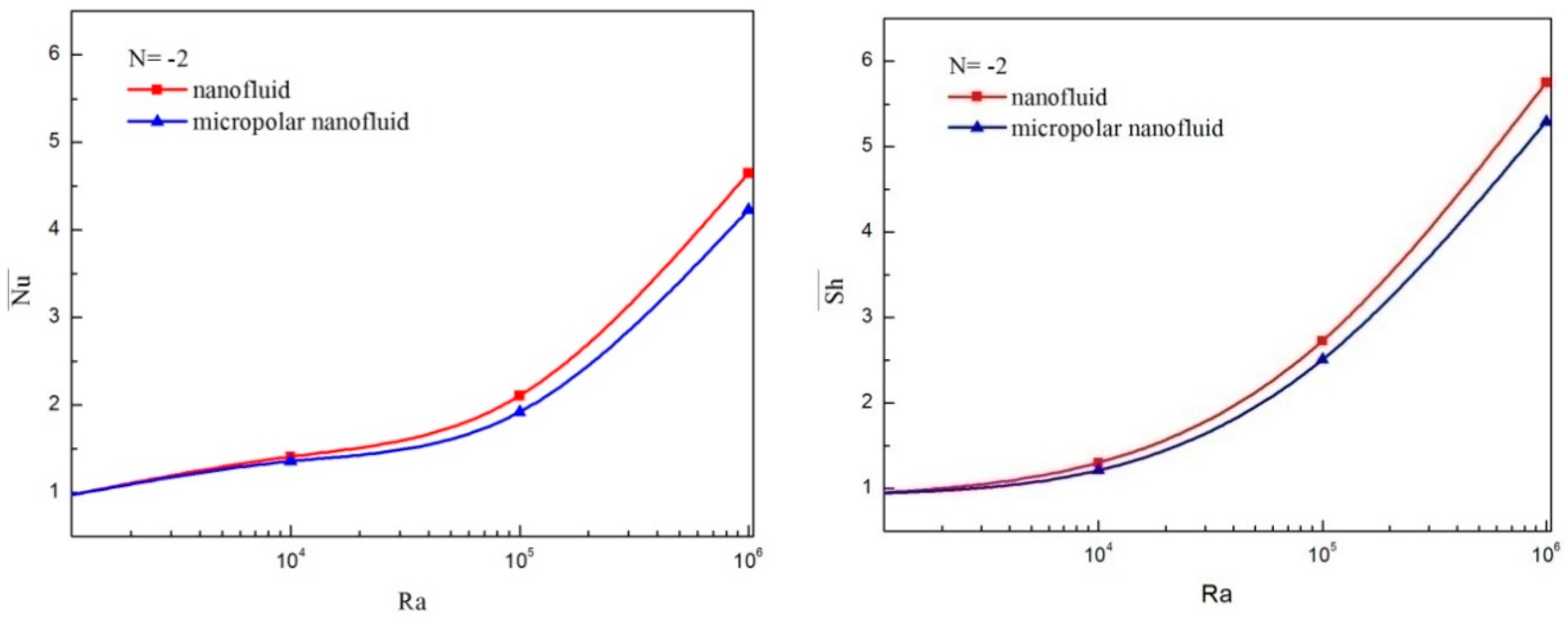
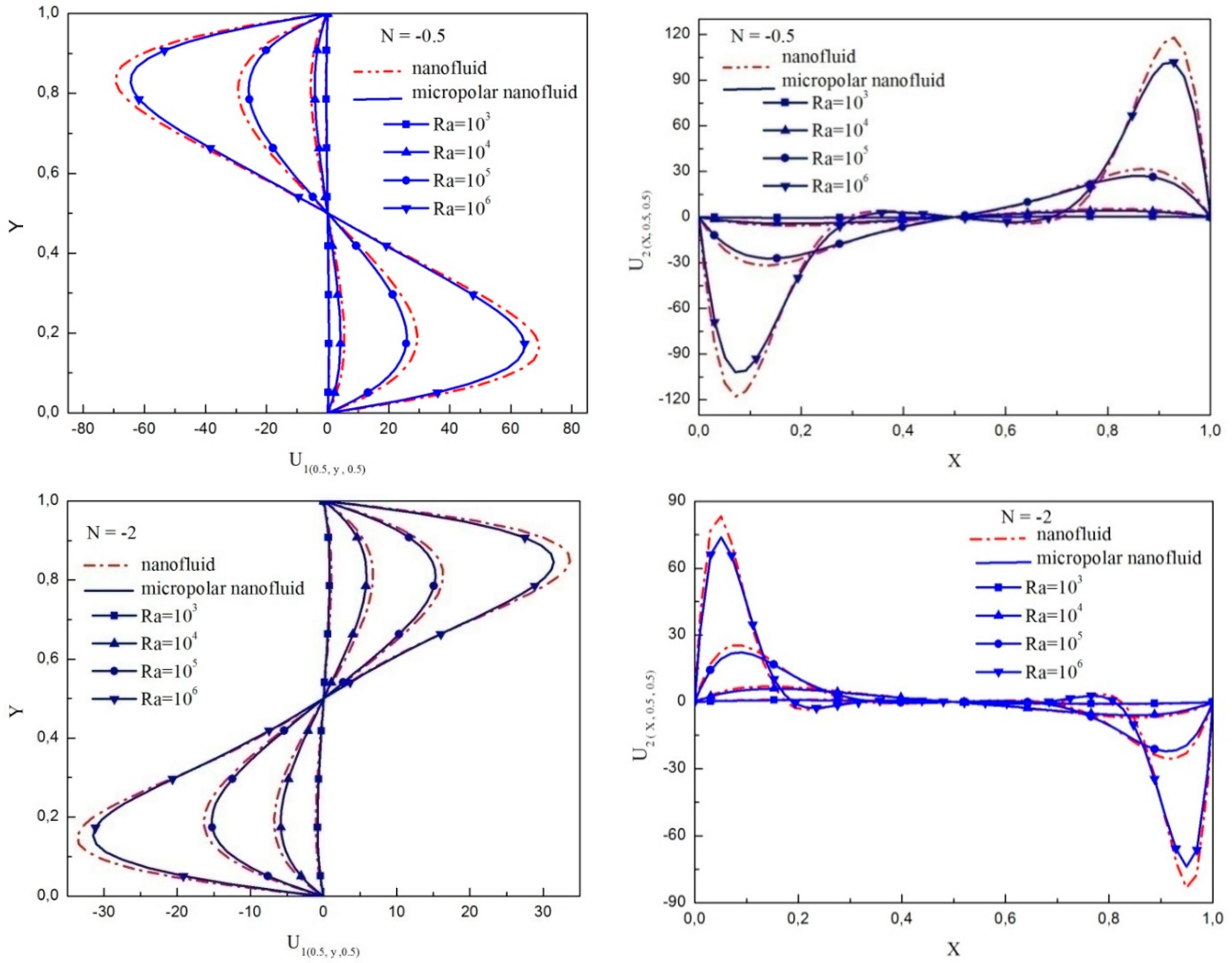
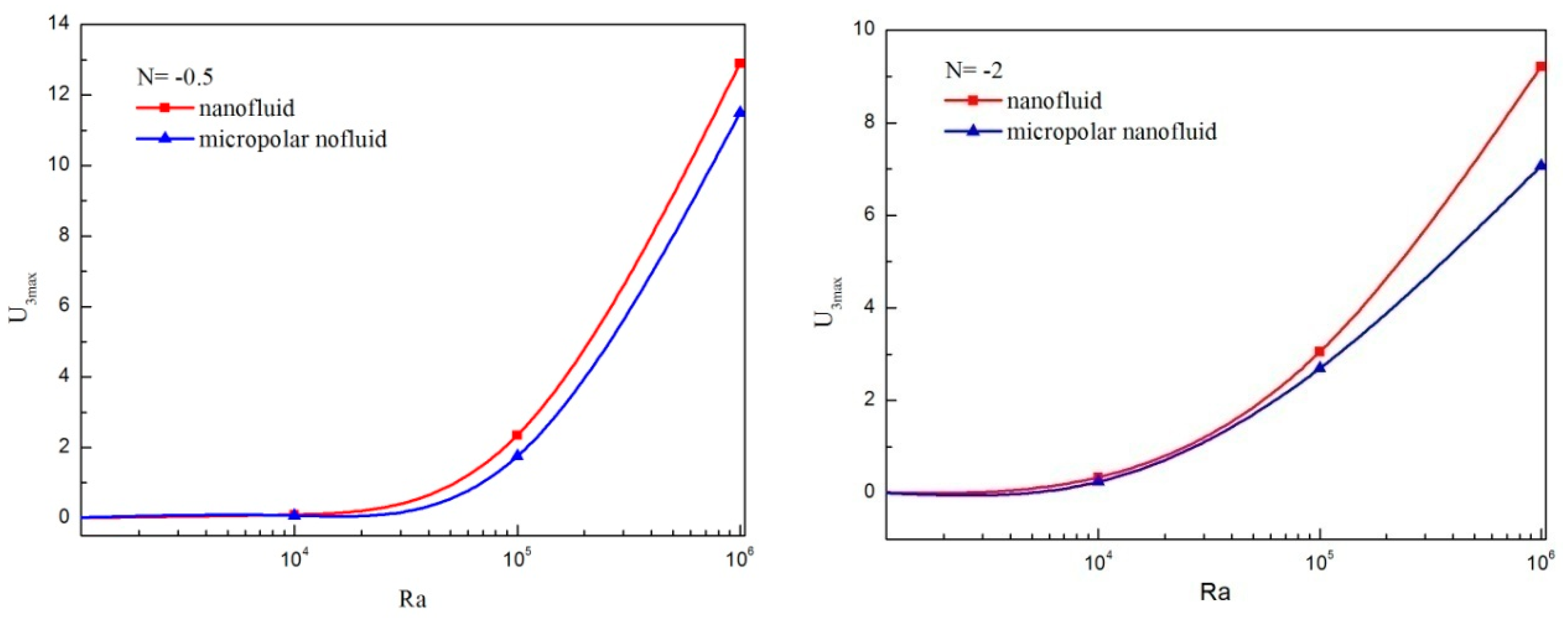
4.1. Comparison between the Micropolar Nanofluid and Nanofluid Models
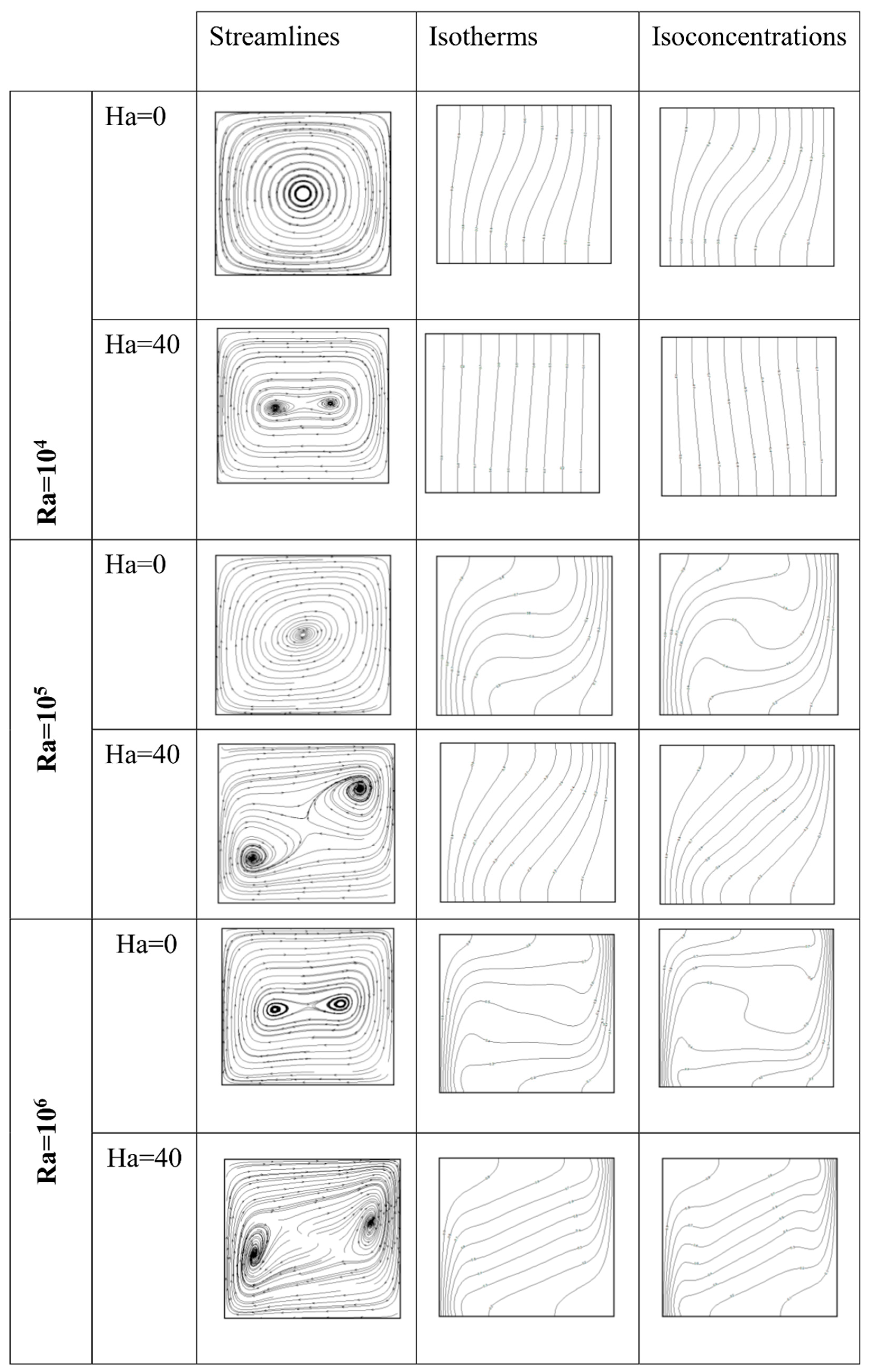
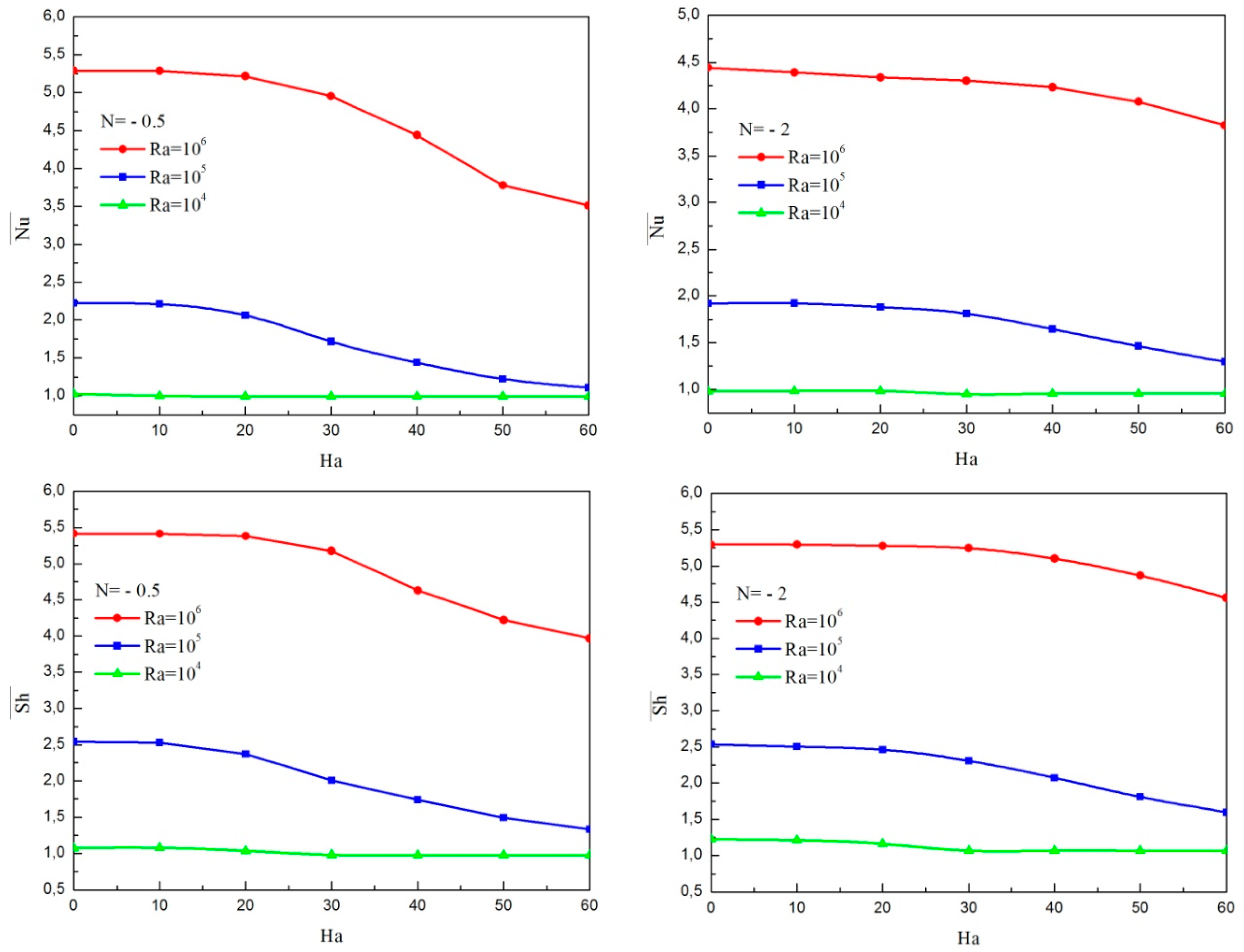
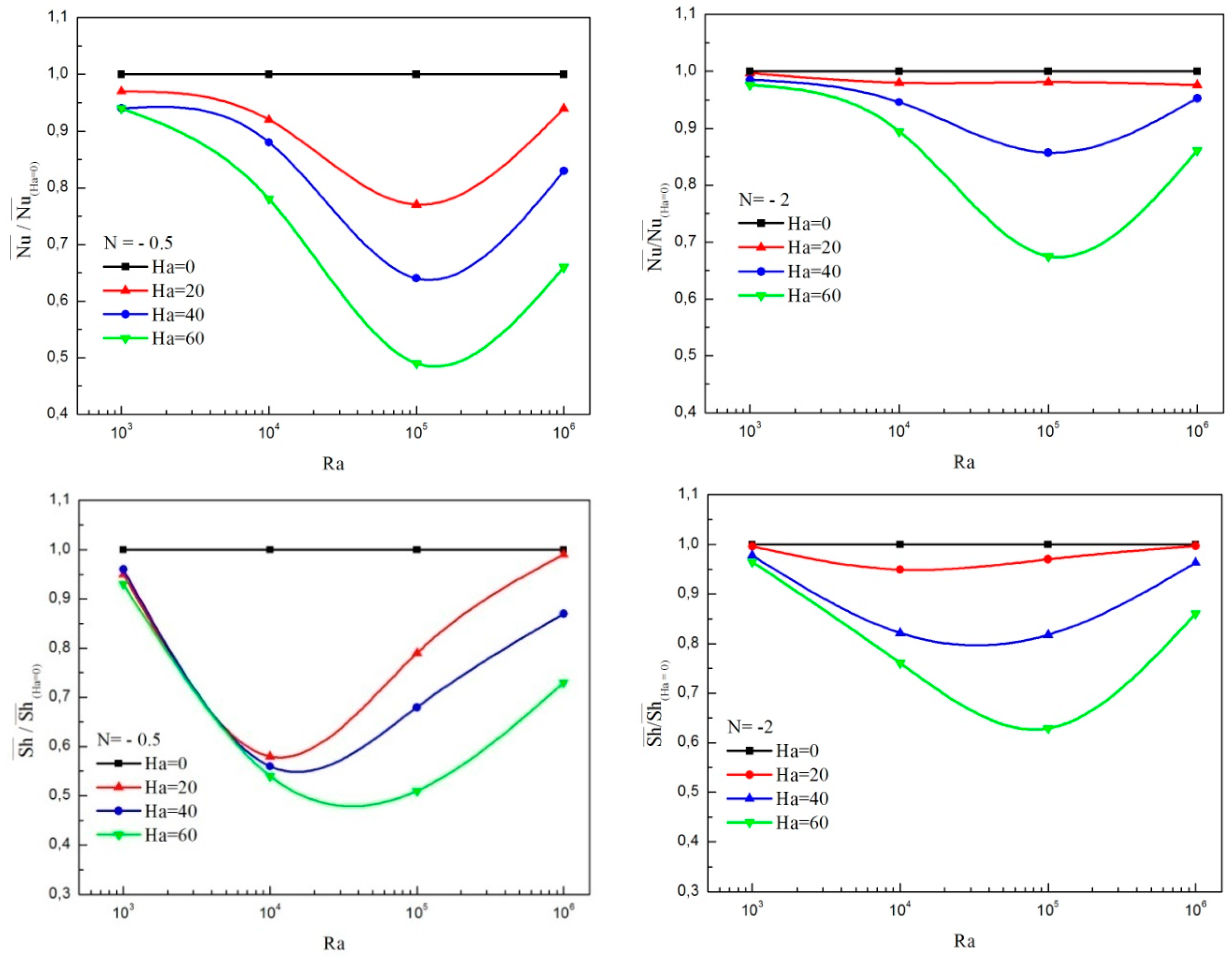
4.2. Effect of Magnetic Field
5. Conclusions
- -
- For a micropolar nanofluid model, both heat and mass transfer rates are smaller than those of a pure nanofluid model.
- -
- Taking in to account particle microrotation, the three-dimensional flow character is weakened.
- -
- For a fixed value of nanoparticle volume fraction with a wide range Rayleigh number, the heat and mass transfer rates are reduced due to increase in the Hartman number.
- -
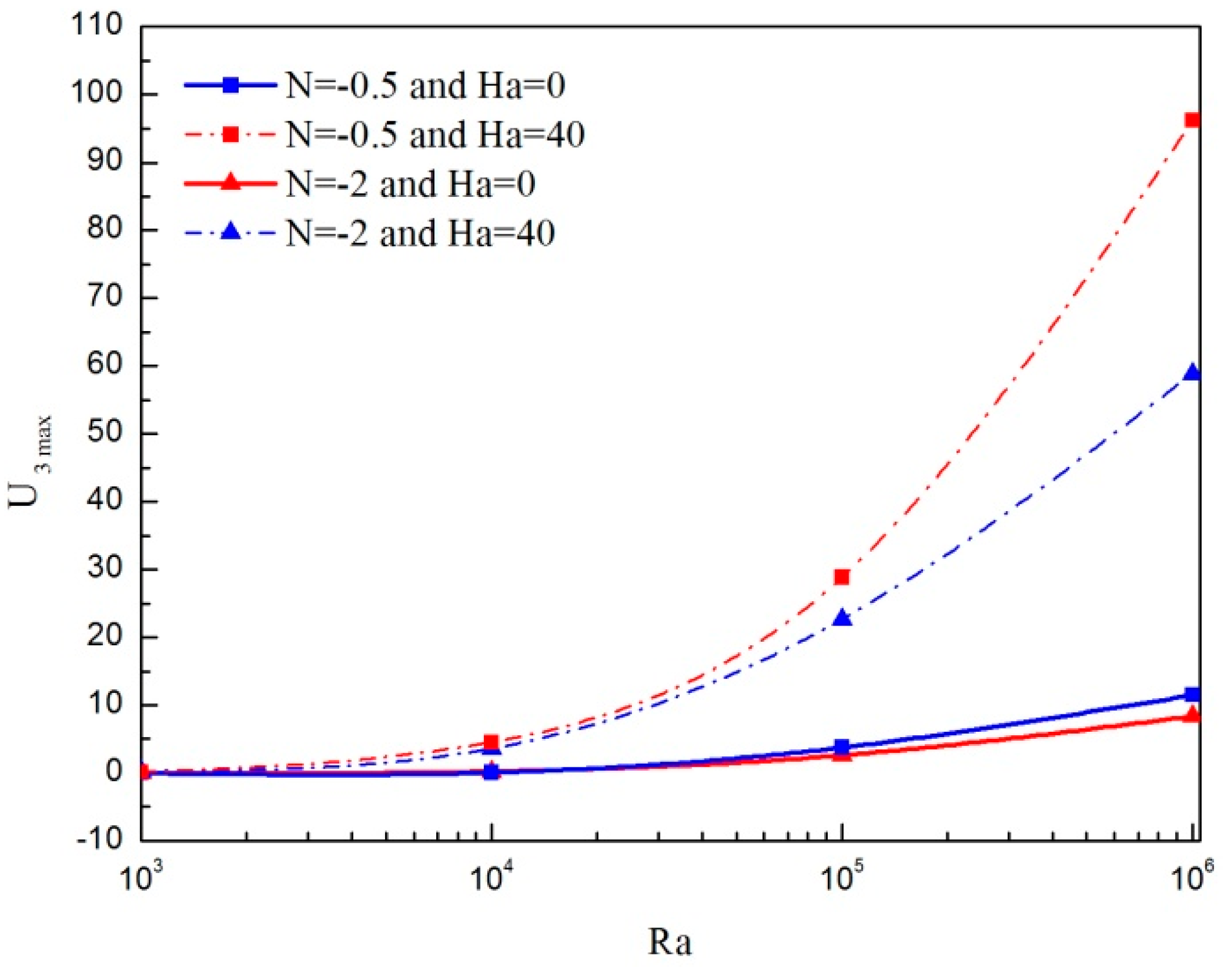
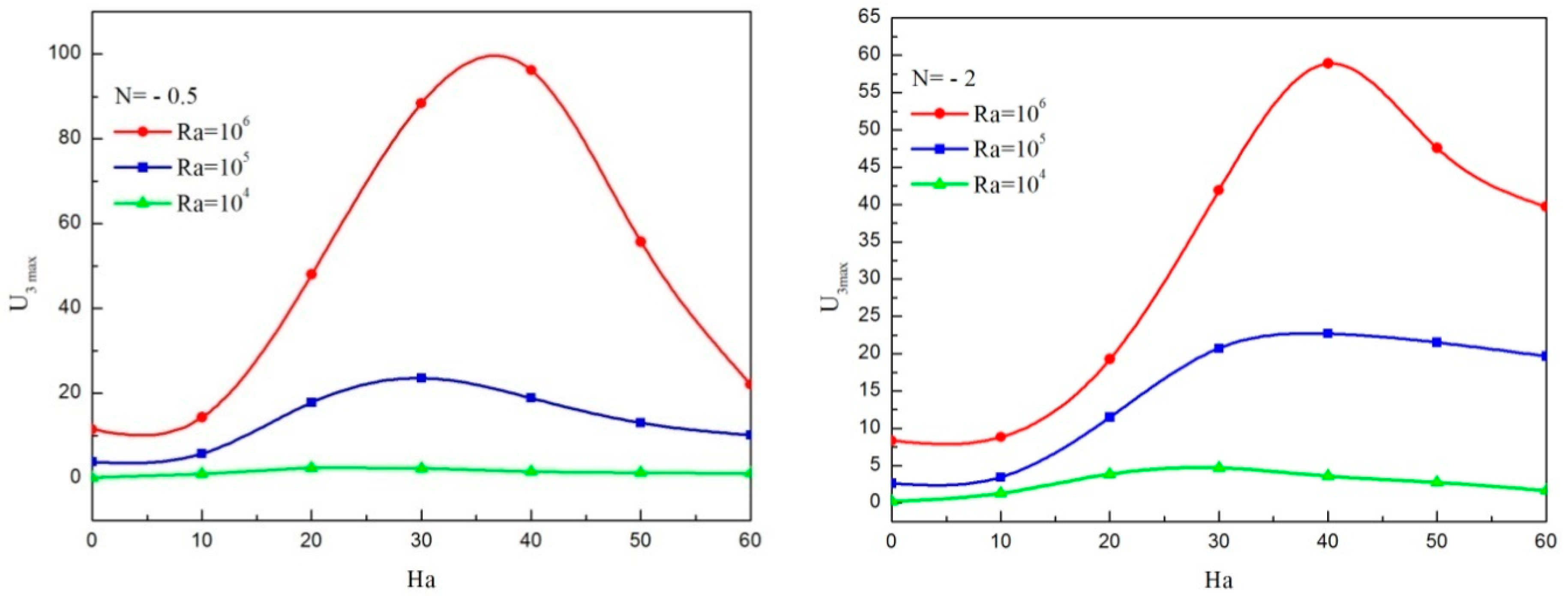
- For various Rayleigh numbers, the maximum of the transverse velocity enhances for Hartmann numbers lower than a critical value and diminishes as the Hartmann number increases. This critical value moves towards the highest value of the Ha number as increasing the Ra number.
- -
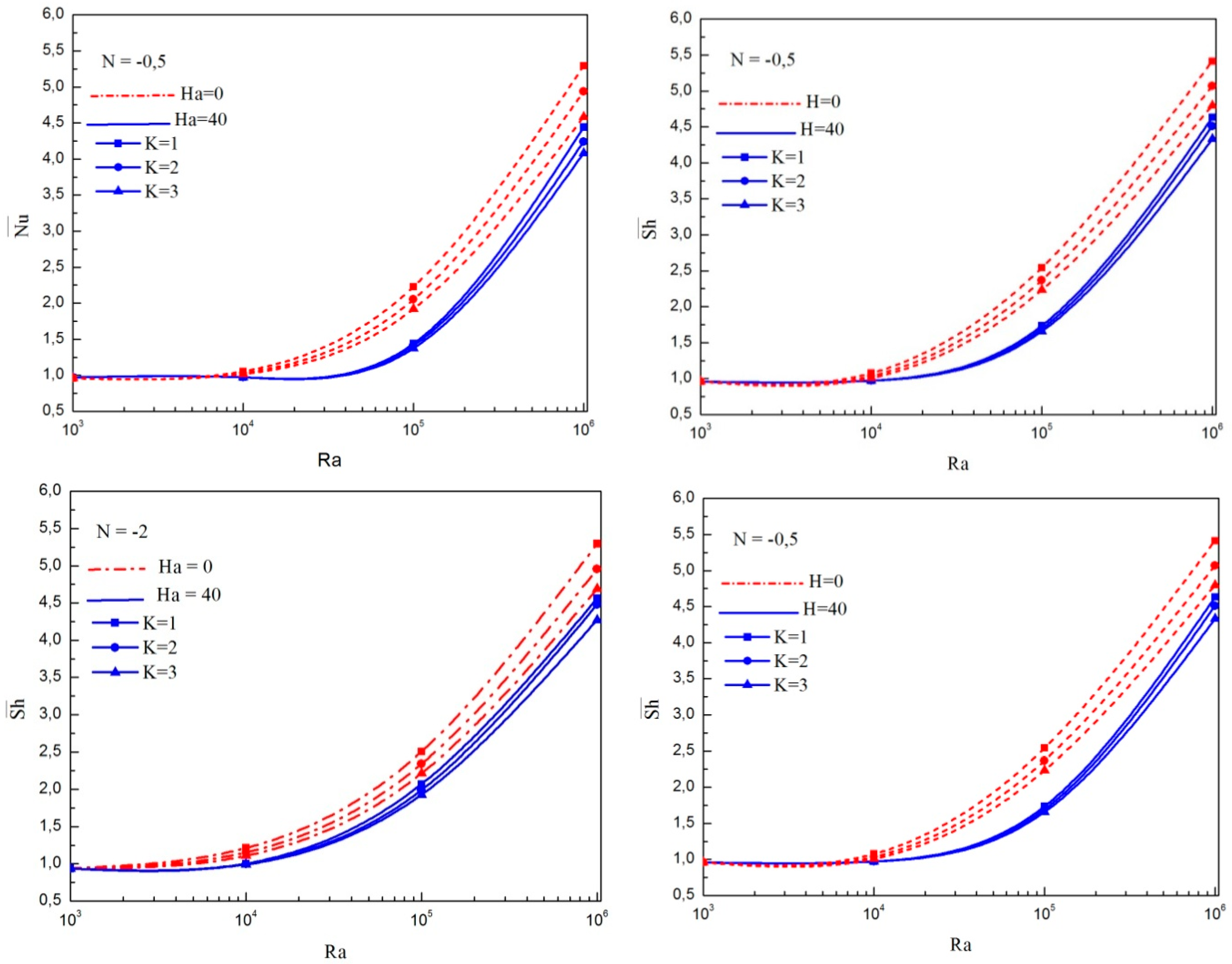
- In the absence of magnetic field, the increase in nanoparticles volume fraction deteriorates the heat and mass transfer. However, for Ha greater than 30, the enhancement of nanoparticle volume fraction increases the heat and mass transfer rates.
- -
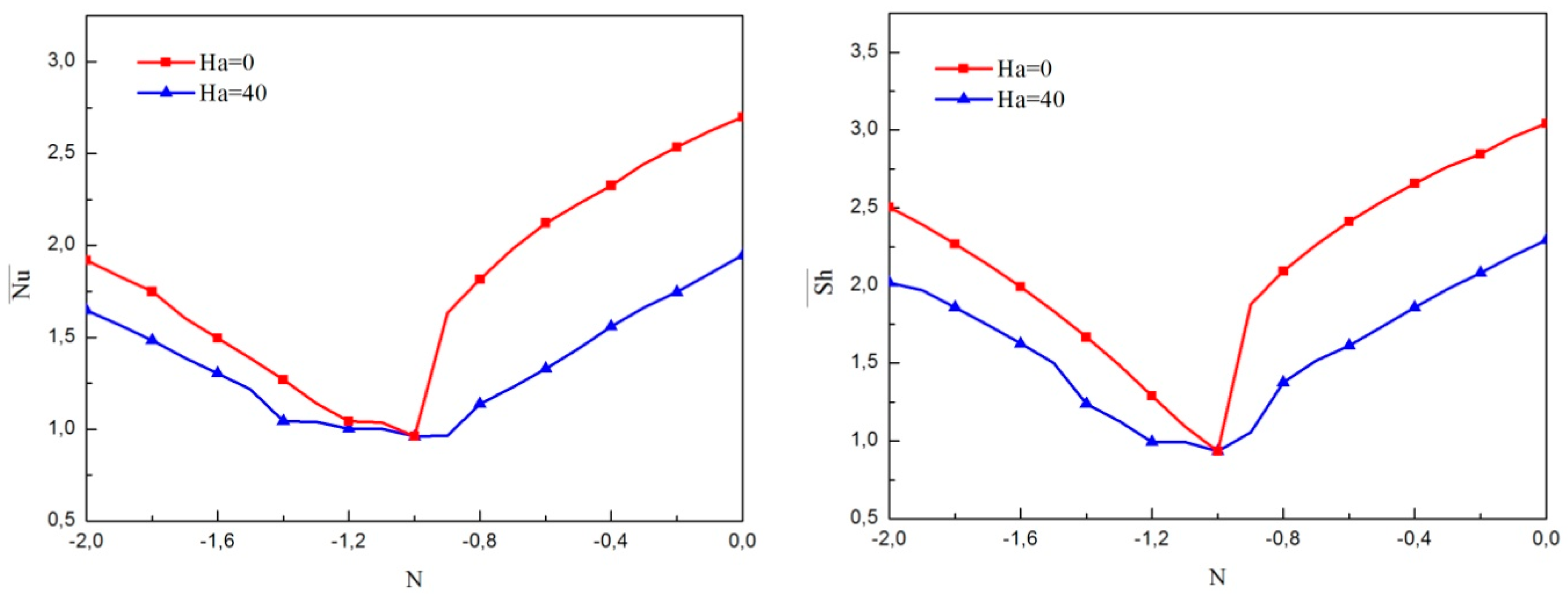
- During non-existence of a magnetic field, an increase in vortex viscosity parameter diminishes the average heat and mass transfer rates and is more pronounced when the magnetic field is enforced. However, for Ha greater than 30, the enhancement of nanoparticle volume fraction increases heat and mass transfer rates.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| B0 | Magnetic field strength, N·m−1·A−1 |
| C | Dimensionless species concentration, |
| D | Species diffusivity, m2/s |
| g | Acceleration of gravity, m/s2 |
| Dimensionless microrotation vector | |
| The microrotation vector, m/s | |
| Ha | Hartmann number, dimensionless |
| K | Micropolar vortex parameter |
| k | Vortex viscosity, kg. m−1·s−1 |
| L | Enclosure height, m |
| Le | Lewis number, |
| N | Buoyancy ratio, |
| Average Nusselt number | |
| Pr | Prandtl number, |
| Ra | Thermal Rayleigh number, |
| Average Sherwood number | |
| t | Dimensionless time, |
| T | Dimensionless temperature, |
| Dimensionless velocity | |
| x, y, z | Dimensionless Cartesian coordinates, x = x’/L, y = y’/L, z = z’/L |
| Greek symbols | |
| Thermal diffusivity, m2s−1 | |
| βC | Coefficient of compositional expansion, m3kg−1 |
| βT | Coefficient of thermal expansion, K−1 |
| φ | Solid volume fraction |
| λ | Thermal conductivity, Wm−1K−1 |
| μ | Dynamic viscosity of the fluid, kg m−1 s−1 |
| υ | Kinematic viscosity, m2s−1 |
| ρ | Density, kgm−3 |
| σ | Electrical conductivity, Ω−1m−1 |
| Dimensionless vorticity, | |
| Dimensionless vector potential of velocity, | |
| Subscripts | |
| c | cold |
| f | fluid |
| h | hot |
| l | low |
| nf | Al2O3/water nanofluid |
| s | solid |
| Superscript | |
| ‘ | dimensional variables |
| 1 | x-component |
| 2 | y-component |
| 3 | z-component |
References
- Choi, U. Enhancing thermal conductivity of fluids with nanoparticles. In Developments and Applications of Non-Newtonian Flows, FED231; Siginer, D.A., Wang, H.P., Eds.; ASME: New York, NY, USA, 1995; pp. 99–105. [Google Scholar]
- Abu-Nada, E.; Ziyad, M.; Oztop, H.F.; Campo, A. Effect of nanofluid variable properties on natural convection in enclosures. Int. J. Therm. Sci. 2010, 49, 479–491. [Google Scholar] [CrossRef]
- Das, S.K.; Choi, S.U.S.; Patel, H.E. Heat Transfer in Nanofluids—A Review. Heat Transf. Eng. 2006, 27, 3–19. [Google Scholar] [CrossRef]
- Aybar, H.Ş.; Sharifpur, M.; Azizian, M.R.; Mehrabi, M.; Meyer, J.P. A Review of Thermal Conductivity Models for Nanofluids. Heat Transf. Eng. 2015, 36, 1085–1110. [Google Scholar] [CrossRef]
- Putra, N.; Roetzel, W.; Das, S.K. Natural convection of nano-fluids. Heat Mass Transf. 2003, 39, 775–784. [Google Scholar] [CrossRef]
- Wen, D.; Ding, Y. Natural convective heat transfer of suspensions of titanium dioxide nanoparticles (nanofluids). IEEE Trans. Nanotech. 2006, 5, 220–227. [Google Scholar]
- Wen, D.; Ding, Y. Formulation of nanofluids for natural convective heat transfer applications. Int. J. Heat Fluid Flow 2005, 26, 855–864. [Google Scholar] [CrossRef]
- Hwang, K.S.; Jang, S.P.; Choi, S.U.S. Flow and convective heat transfer characteristics of water-based Al2O3 nanofluids in fully developed laminar flow regime. Int. J. Heat Mass Transf. 2009, 52, 193–199. [Google Scholar] [CrossRef]
- Khanafer, K.; Vafai, K.; Lightstone, M. Buoyancy-driven heat transfer enhancement in a two-dimensional enclosure utilizing nanofluids. Int. J. Heat Mass Transf. 2003, 46, 3639–3653. [Google Scholar] [CrossRef]
- Jou, R.; Tzeng, S. Numerical research of nature convective heat transfer enhancement filled with nanofluids in rectangular enclosures. Int. Comm. J. Heat Mass Transf. 2006, 33, 727–736. [Google Scholar] [CrossRef]
- Oztop, H.F.; Abu-Nada, E. Numerical study of natural convection in partially heated rectangular enclosure filled with nanofluids. Int. J. Heat Fluid Flow 2008, 29, 1326–1336. [Google Scholar] [CrossRef]
- Ho, C.J.; Chen, M.W.; Li, Z.W. Numerical simulation of natural convection of nanofluid in a square enclosure: Effects due to uncertainties of viscosity and thermal conductivity. Int. J. Heat Mass Transf. 2008, 51, 4506–4516. [Google Scholar] [CrossRef]
- Bouhalleb, M.; Abbassi, H. Numerical Investigation of Heat Transfer by CuO–Water Nanofluid in Rectangular Enclosures. Heat Transf. Eng. 2016, 37, 13–23. [Google Scholar] [CrossRef]
- Mahfoud, B.; Bendjaghlouli, A. Natural Convection of a Nanofluid in a Conical Container. J. Ther. Eng. 2018, 4, 1713–1723. [Google Scholar] [CrossRef]
- Polidori, G.; Fohanno, S.; Nguyen, C.T. A note on heat transfer modeling of Newtonian nanofluids in laminar free convection. Int. J. Therm. Sci. 2007, 46, 739–774. [Google Scholar] [CrossRef]
- Ahuja, A.S. Augmentation of heat transport in laminar flow of polystyrene suspensions. I. Experiments and results. J. App. Phys. 1975, 46, 3408–3425. [Google Scholar] [CrossRef]
- Eringen, A.C. Theory of micropolar fluids. J. Math. Mech. 1966, 16, 1–18. [Google Scholar] [CrossRef]
- Ariman, T.; Turk, M.A.; Sylvester, N.D. Application of Micro continuum Fluid Mechanics. Int. J. Eng. Sci. 1974, 12, 273–293. [Google Scholar] [CrossRef]
- Łukaszewicz, G. Micropolar Fluids: Theory and Application; Birkhauser: Basel, Switzerland, 1999. [Google Scholar]
- Aydin, O.; Pop, I. Natural convection in a differentially heated enclosure filled with a micropolar fluids. Int. J. Therm. Sci. 2007, 46, 963–969. [Google Scholar] [CrossRef]
- Zadravec, M.; Hriberšek, M.; Škerget, L. Natural convection of micropolar fluidsin an enclosure with boundary element method. Eng. Anal. Bound. Elem. 2009, 33, 485–492. [Google Scholar] [CrossRef]
- Saleem, M.; Asghar, S.; Hossain, M.A. Natural convection flow of micropolar fluid in a rectangular cavity heated from below with cold sidewalls. Math. Comput. Model. 2011, 54, 508–518. [Google Scholar] [CrossRef]
- Jena, S.K.; Malla, L.K.; Mahapatra, S.K.; Chamkha, A.J. Transient buoyancy-opposed double diffusive convection of micropolar fluids in a square enclosure. Int. J. Heat Mass Transf. 2015, 81, 681–694. [Google Scholar] [CrossRef]
- Agrawal, R.S.; Bhargava, R.; Balaji, A.V.S. Finite element solution of non-steady three dimensional micropolar fluid flow at a stagnante point. Int. J. Eng. Sci. 1990, 28, 851–857. [Google Scholar] [CrossRef]
- Takhar, H.S.; Agarwal, R.S.; Bhargava, R.; Jain, S. Mixed convective non-steady 3-dimensional micropolar fluid flow at a stagnation point. Heat Mass Transf. 1998, 33, 443–448. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Jaradat, M.; Pop, I. Three-dimensional micropolar flow due to a stretching flat surface. Int. J. Fluid Mech. Res. 2003, 30, 357–366. [Google Scholar] [CrossRef]
- Bourantas, G.C.; Loukopoulos, V.C. Modeling the natural convective flow of micropolarnano fluids. Int. J. Heat Mass Transf. 2014, 68, 35–41. [Google Scholar] [CrossRef]
- Hashemi, H.; Namazian, Z.; Mehryan, S.A.M. Cu-water micropolar nanofluid natural convection within a porous enclosure with heat generation. J. Mol. Liq. 2017, 236, 48–60. [Google Scholar] [CrossRef]
- Hussanan, A.; Salleh, Z.M.; Khan, I.; Sharidan, S. Convection heat transfer in micropolar nanofluids with oxide nanoparticles in water, kerosene and engine oil. J. Mol. Liq. 2017, 229, 482–488. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Roknib, H.B. Simulation of nanofluid heat transfer in presence of magnetic field: A review. J. Heat Mass Transf. 2017, 115, 1203–1233. [Google Scholar] [CrossRef]
- Ghasemi, B.; Aminossadati, S.M.; Raisi, A. Magnetic field effect on natural convection in a nanofluid field square enclosure. Int. J. Therm. Sci. 2011, 50, 1748–1756. [Google Scholar] [CrossRef]
- Teamah, M.A.; El-Maghlany, W.M. Augmentation of Natural Convective Heat Transfer in Square Cavity by Utilizing Nanofluids in the Presence of Magnetic Field and Uniform Heat generation absorption. Int. J. Therm. Sci. 2012, 58, 130–142. [Google Scholar] [CrossRef]
- Mahmoudi, A.H.; Pop, I.; Shahi, M. Effect of magnetic field on natural convection in a triangular enclosure filled with nanofluid. Int. J. Therm. Sci. 2012, 59, 126–140. [Google Scholar] [CrossRef]
- Mahmoudi, A.H.; Abu-Nada, E. Combined effect of magnetic field and nanofluid variable properties on heat transfer enhancement in natural convection. Numer. Heat Transf. Part A 2013, 63, 452–472. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Bandpy, M.G.; Ellahi, R.; Hassan, M.; Soleimani, S. Effects of MHD on Cu–water nanofluid flow and heat transfer by means of CVFEM. J. Magn. Magn. Mater. 2014, 349, 188–200. [Google Scholar] [CrossRef]
- Zhou, W.N.; Yan, Y.Y. numerical investigation of the effects of a magnetic field on nanofluid flow and heat transfer by the lattice boltzmann method. Numer. Heat Transf. Part A 2015, 68, 1–16. [Google Scholar] [CrossRef]
- Abbassi, M.A.; Mliki, B.; Djebali, R. Lattice Boltzmann Method for simulation of nanoparticle Brownian motion and magnetic field effects on free convection in a nanofluid-filled open cavity with heat generation/absorption and non uniform heating on the left solid vertical wall. Fluid Dyn. Mater. Proc. 2017, 13, 59–83. [Google Scholar]
- Al Kalbani, K.S.; Rahman, M.M.; Alam, M.S.; Al-Salti, N.; Eltayeb, I.A. Buoyancy Induced Heat Transfer Flow Inside a Tilted Square Enclosure Filled with Nanofluids in the Presence of Oriented Magnetic Field. Heat Transf. Eng. 2018, 39, 511–525. [Google Scholar] [CrossRef]
- Javed, T.; Mehmood, Z.; Siddiqui, M.A.; Pop, I. Effects of uniform magnetic field on the natural convection of Cu–water nanofluid in a triangular cavity. Int. J. Num. Meth. Heat Fluid Flow 2017, 27, 334–357. [Google Scholar] [CrossRef]
- Abbassi, M.A.; Safaei, M.R.; Djebali, R.; Guedri, K.; Zeghmati, B.; Alrashed, A.A.A. LBM simulation of free convection in a nanofluid filled incinerator containing a hot block. Int. J. Mech. Sci. 2018, 144, 172–185. [Google Scholar] [CrossRef]
- Bourantas, G.C.; Loukopoulos, V.C. MHD natural-convection flow in an inclined square enclosure filledwith a micropolar-nanofluid. Int. J. Heat Mass Transf. 2014, 79, 930–944. [Google Scholar] [CrossRef]
- Akbar, N.; Khan, Z.; Nadeem, S.; Khan, W. Double-diffusive natural convective boundary-layer flow of a nanofluid over a stretching sheet with magnetic field. Int. J. Num. Meth. Heat Fluid Flow 2016, 26, 108–121. [Google Scholar] [CrossRef]
- Ozoe, H.; Okada, K. Experimental heat transfer rates of natural convection of Molten Gallium supressed under an external magnetic field in either x, y or z direction. Int. J. Heat Mass Transf. 1992, 114, 107–114. [Google Scholar]
- Godson, L.; Raja, B.; Mohan, L.D.; Wongwises, S. Experimental investigation on the thermal conductivity and viscosity of silver-deionized water nanofluid. Exp. Heat Transf. 2010, 23, 317–332. [Google Scholar] [CrossRef]
- Pak, B.; Cho, Y. Hydrodynamic and heat transfer study of dispersed fluid with submicron metallic oxide particles. Exp. Heat Transf. 1998, 11, 151–170. [Google Scholar] [CrossRef]
- Guram, G.S.; Smith, C. Stagnation flows of micropolar fluids with strong and weak interactions. Comput. Math. Appl. 1980, 6, 213–233. [Google Scholar] [CrossRef]
- Patankar, S.V. Numerical Heat Transfer and Fluid Flow; McGraw Hill: New York, NY, USA, 1980. [Google Scholar]
- Sezai, I.; Mohamad, A.A. Double diffusive convection in a cubic enclosure with opposing temperature and concentration gradient. Phys. Fluids 2000, 12, 2210–2223. [Google Scholar] [CrossRef]
- Abidi, A.; Kolsi, L.; Borjini, M.N.; Ben Aissia, H. Effect of radiative heat transfer on three-dimensional double diffusive natural convection. Numer. Heat Transf. Part A 2011, 60, 785–809. [Google Scholar] [CrossRef]
- Kolsi, L.; Abidi, A.; Borjini, M.N.; Daous, N.; Ben Aïssia, H. Effect of an External Magnetic Field on the 3-D Un steady Natural convection in a cubical enclosure. Numer. Heat Transf. Part A 2007, 51, 1003–1021. [Google Scholar] [CrossRef]




| Pure Water | Alumina (Al2O3) | |
|---|---|---|
| Pr | 6.2 | |
| ρ (kg/m3) | 997.1 | 8933 |
| Cp (J/kg·K) | 4179 | 385 |
| k (W/m.K) | 0.613 | 401 |
| β (K−1) | 21.10−5 | 1.67.10−5 |
| σ (Ω·m)−1 | 0.05 | 1.10−10 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abidi, A.; Raizah, Z.; Madiouli, J. Magnetic Field Effect on the Double Diffusive Natural Convection in Three-Dimensional Cavity Filled with Micropolar Nanofluid. Appl. Sci. 2018, 8, 2342. https://doi.org/10.3390/app8122342
Abidi A, Raizah Z, Madiouli J. Magnetic Field Effect on the Double Diffusive Natural Convection in Three-Dimensional Cavity Filled with Micropolar Nanofluid. Applied Sciences. 2018; 8(12):2342. https://doi.org/10.3390/app8122342
Chicago/Turabian StyleAbidi, Awatef, Zehba Raizah, and Jamel Madiouli. 2018. "Magnetic Field Effect on the Double Diffusive Natural Convection in Three-Dimensional Cavity Filled with Micropolar Nanofluid" Applied Sciences 8, no. 12: 2342. https://doi.org/10.3390/app8122342
APA StyleAbidi, A., Raizah, Z., & Madiouli, J. (2018). Magnetic Field Effect on the Double Diffusive Natural Convection in Three-Dimensional Cavity Filled with Micropolar Nanofluid. Applied Sciences, 8(12), 2342. https://doi.org/10.3390/app8122342





