Pursuing High Quality Phase-Only Liquid Crystal on Silicon (LCoS) Devices
Abstract
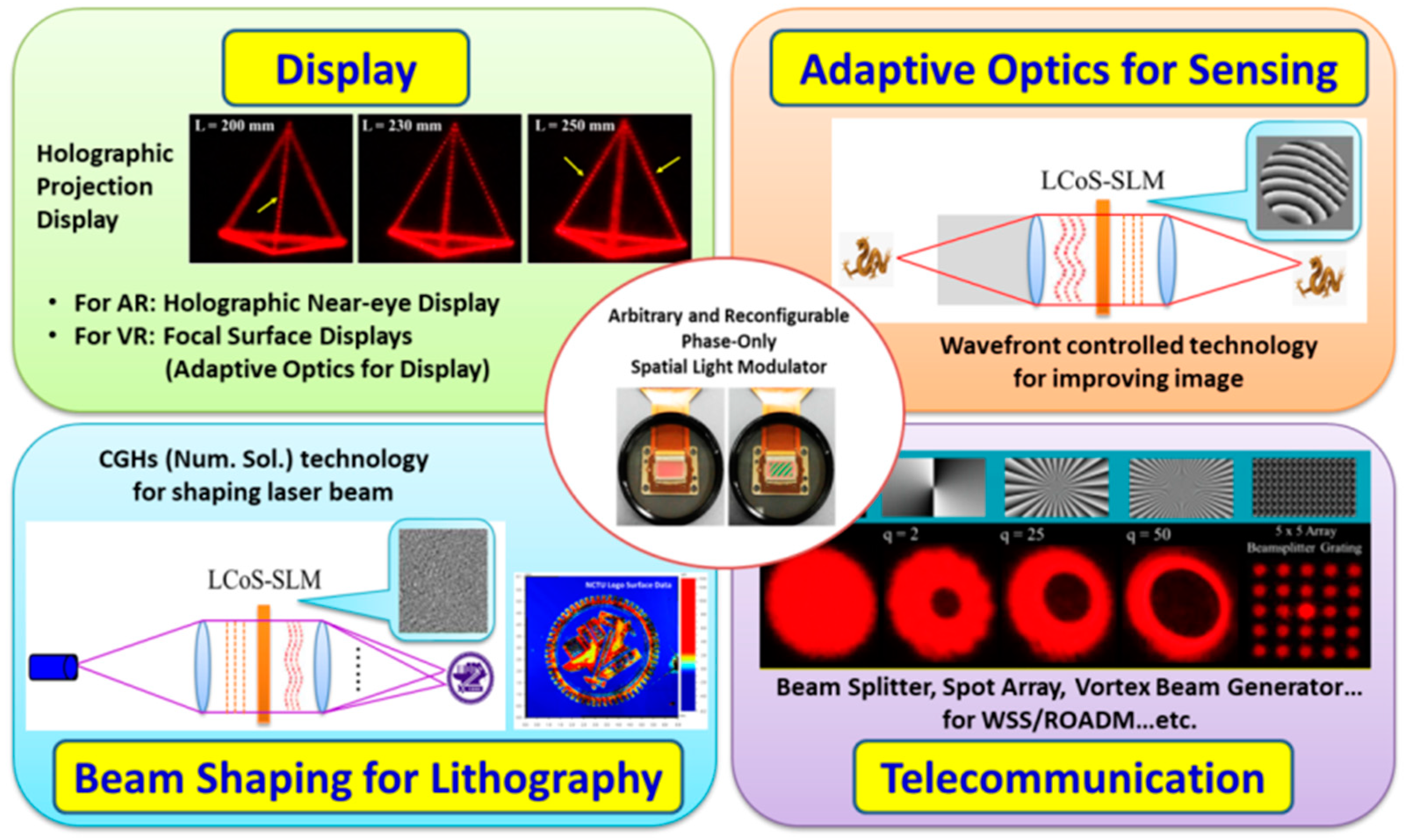
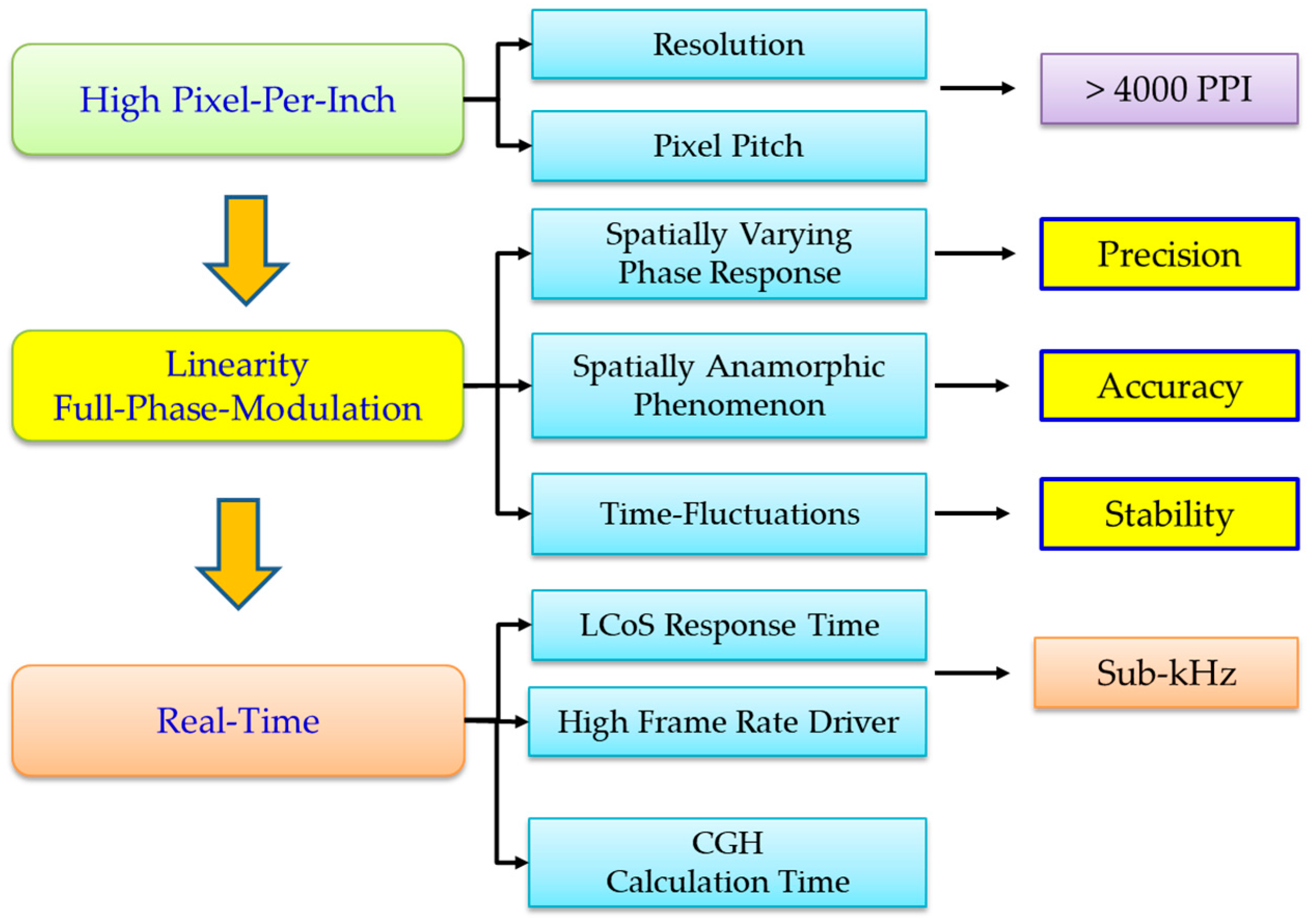
1. Introduction
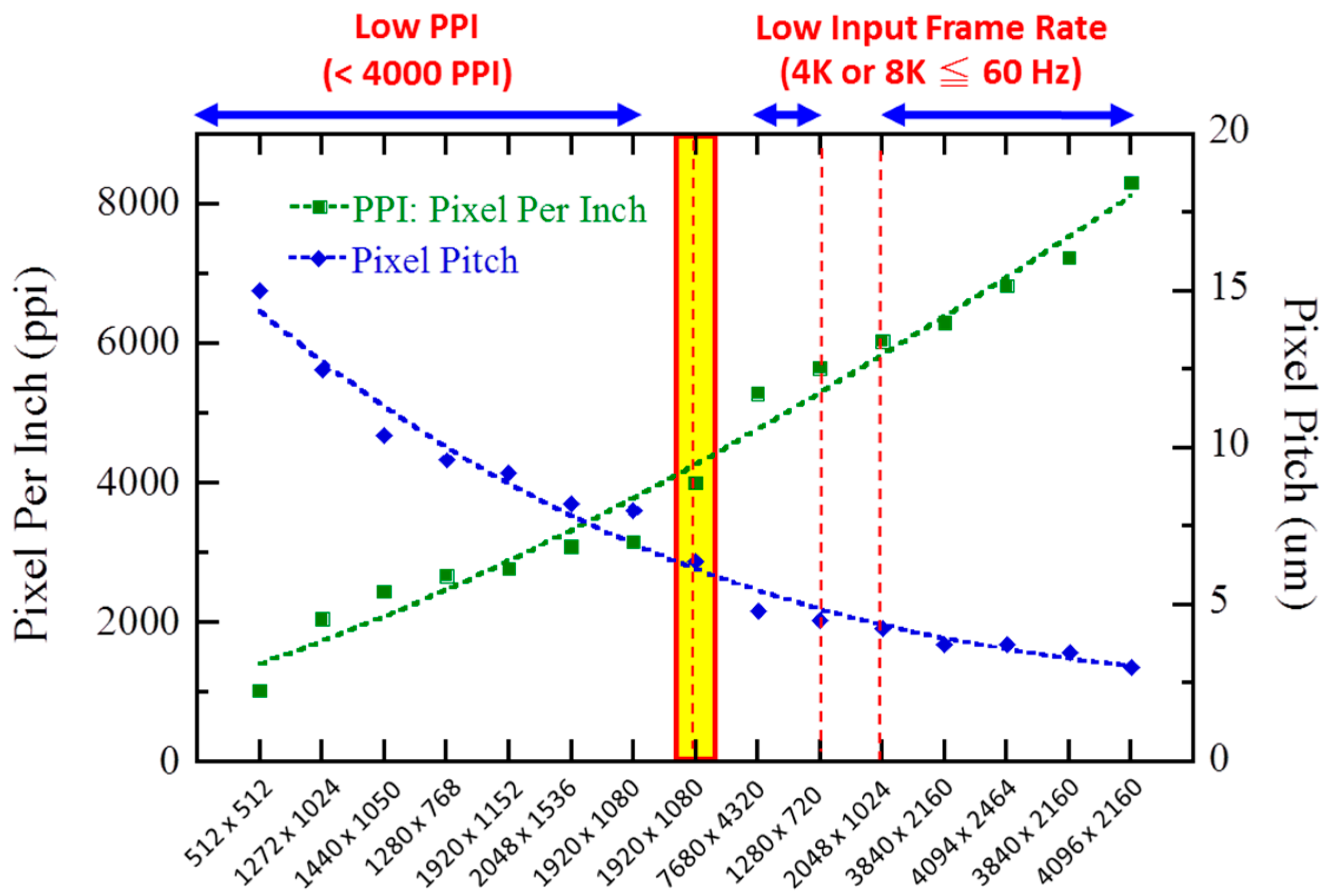
2. High Resolution and High Pixel-Per-Inch (PPI)
3. Switching Time for Phase Modulation
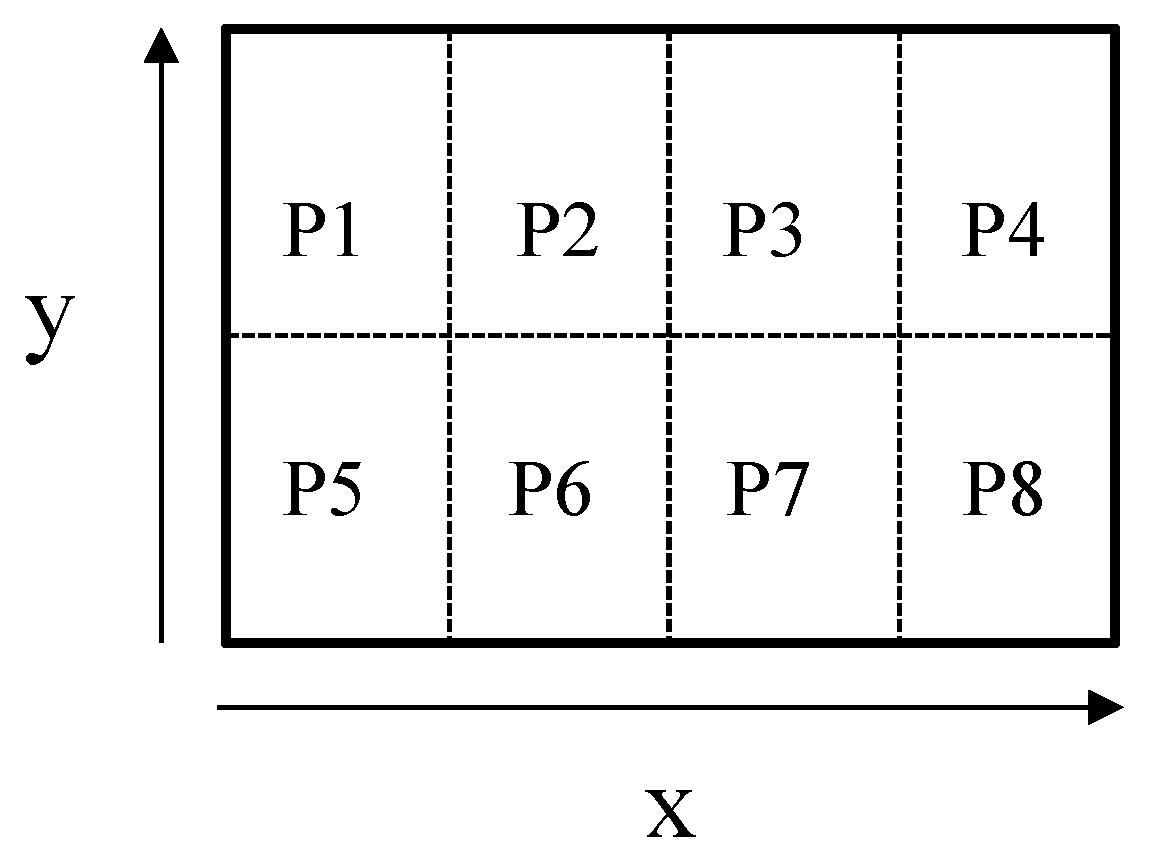
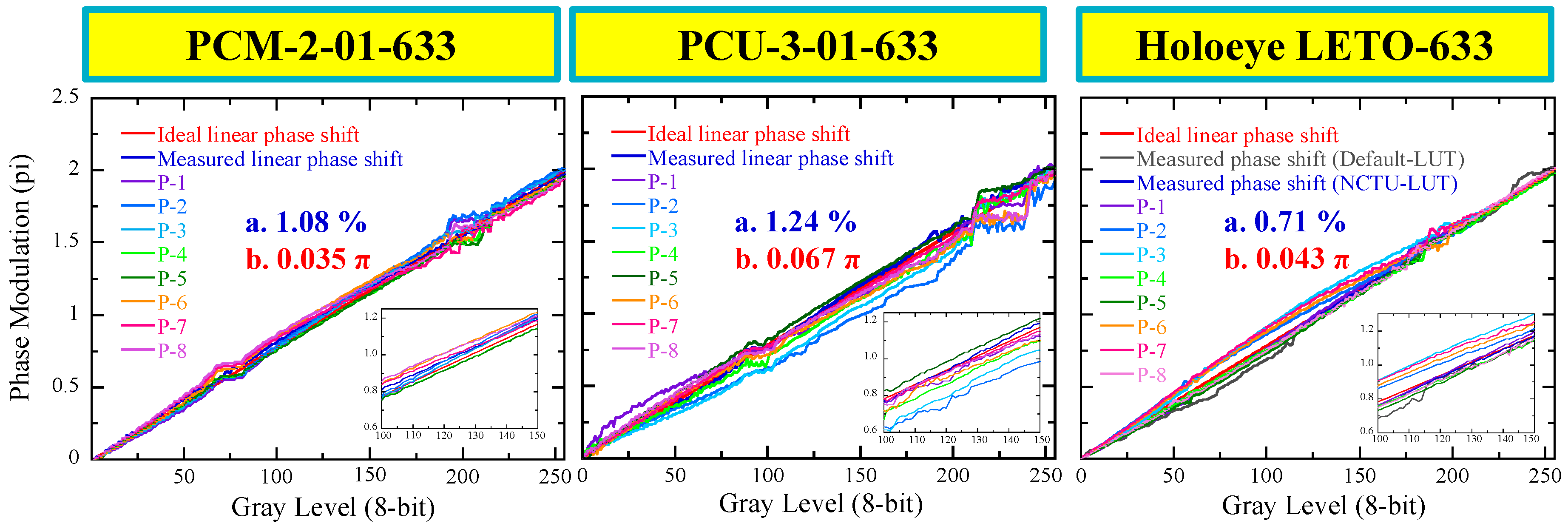
4. Phase Linearity
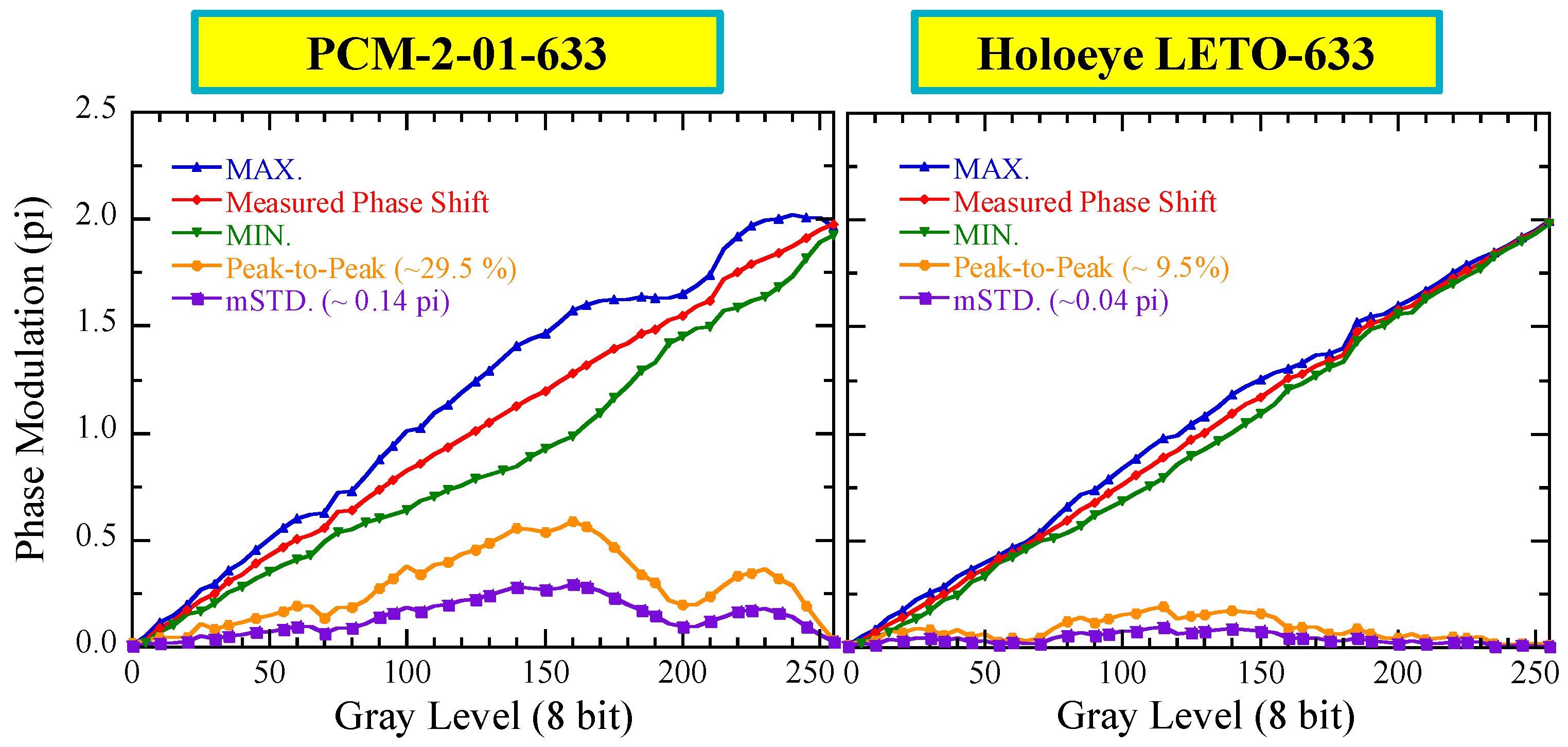
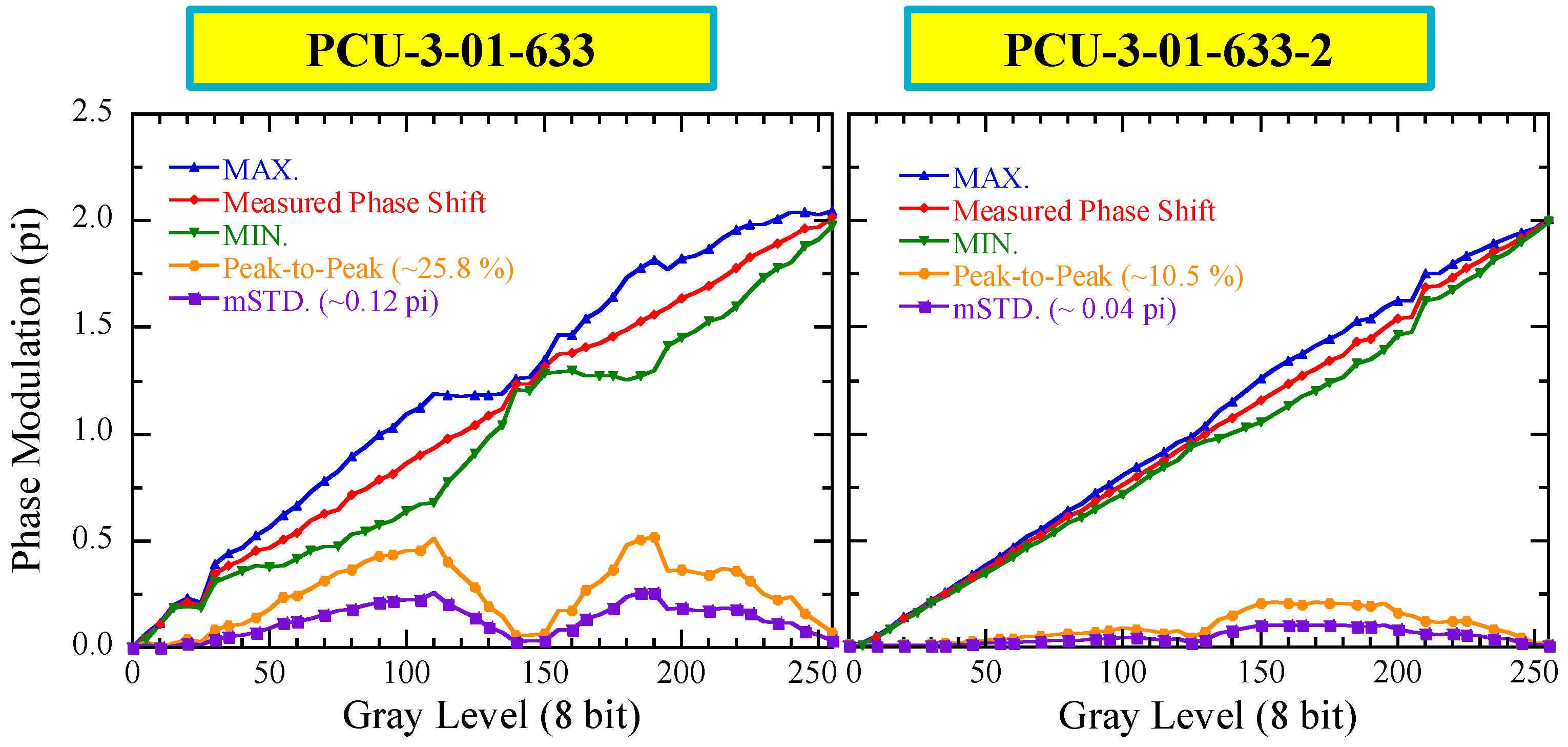
5. Phase Precision
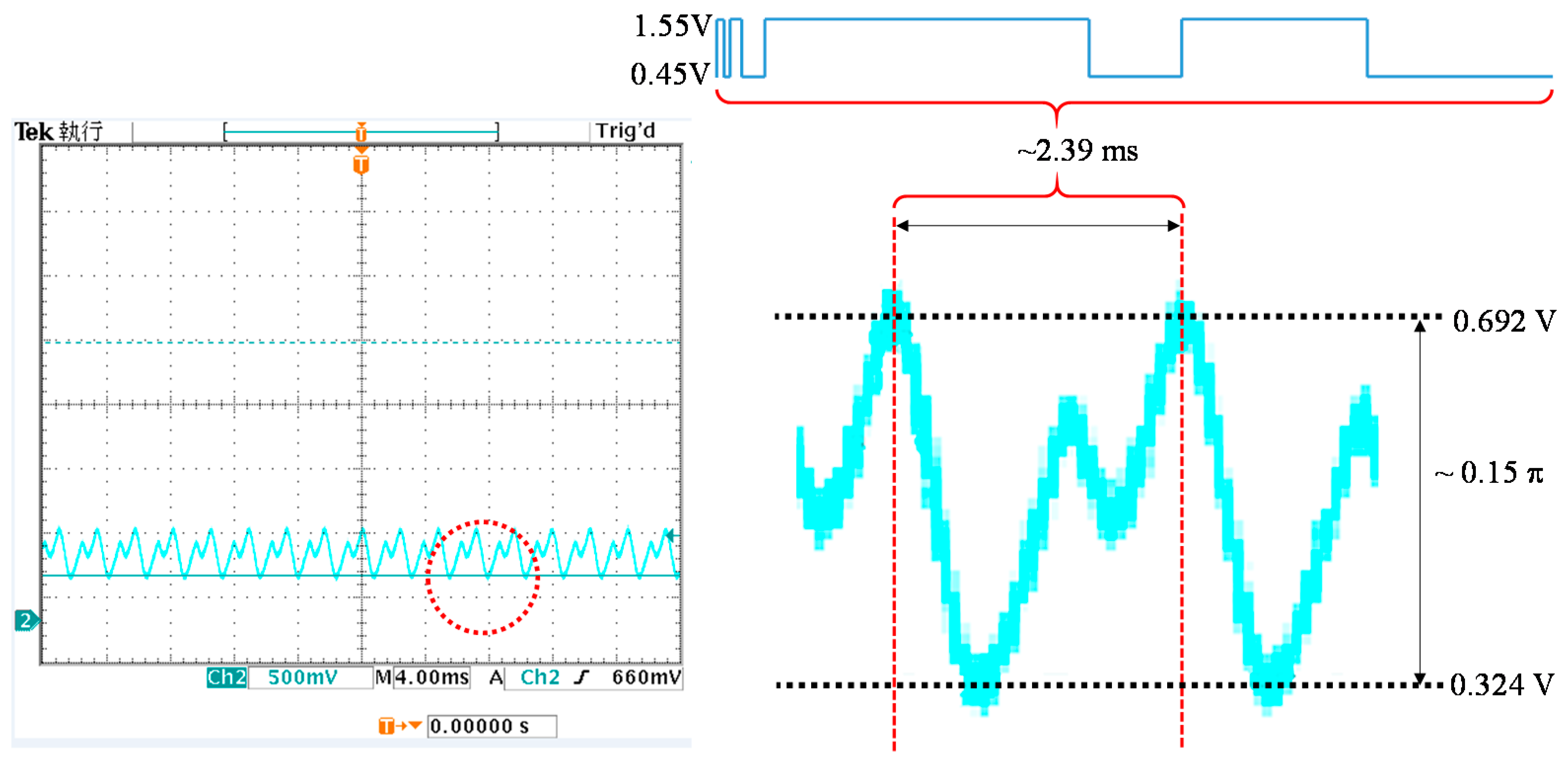
6. Phase Stability
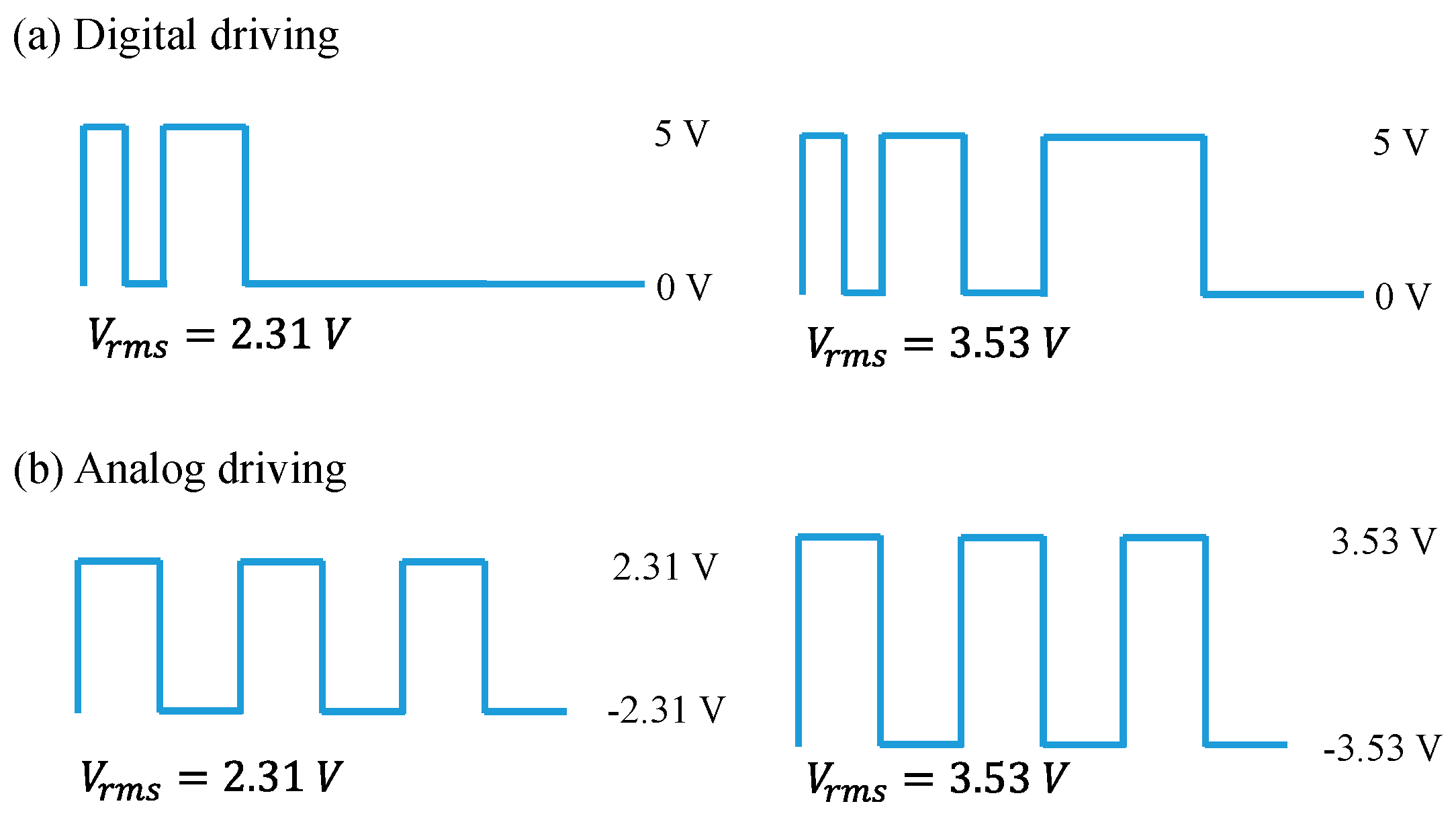
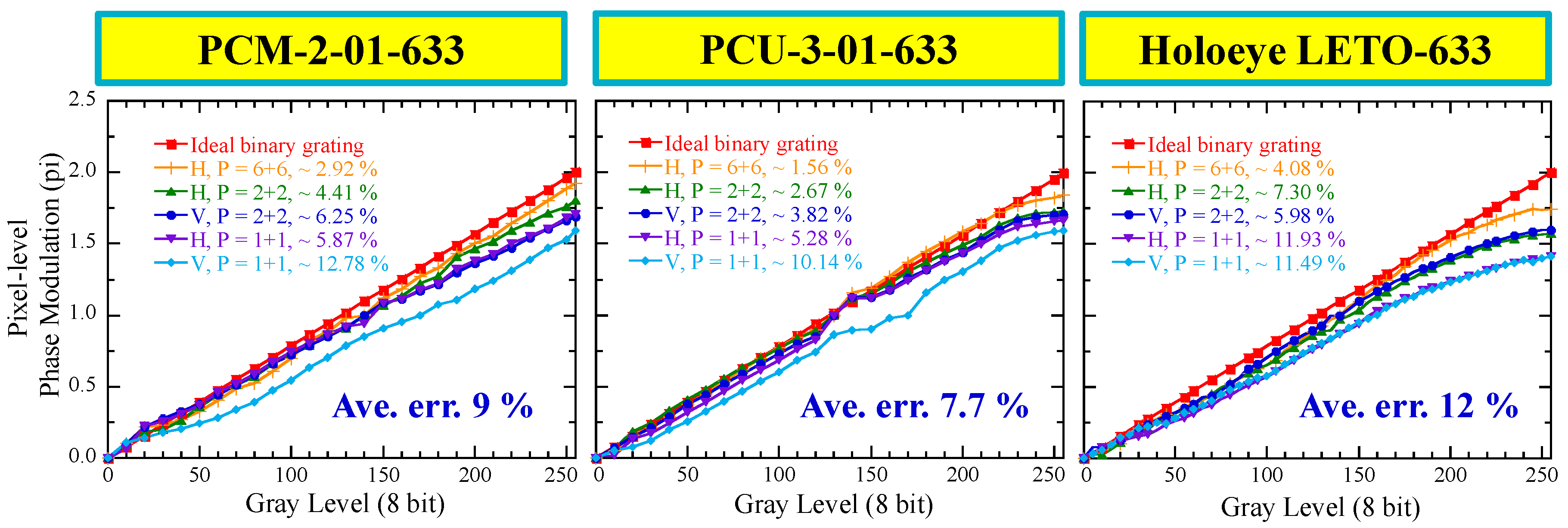
7. Phase Accuracy
8. Conclusions
Author Contributions
Funding
Acknowledgments
References
- Margerum, J.D.; Nimoy, J.; Wong, S.-Y. Reversible ultraviolet imaging with liquid crystals. Appl. Phys. Lett. 1970, 17, 51–53. [Google Scholar] [CrossRef]
- Beard, T.D.; Bleha, W.P.; Wong, S.-Y. Ac liquid-crystal light valve. Appl. Phys. Lett. 1973, 22, 90–92. [Google Scholar] [CrossRef]
- Ernstoff, M.N.; Leupp, A.M.; Little, M.J.; Peterson, H.T. Liquid crystal pictorial display. Int. Electron. Devices Meet. 1973, 548–551. [Google Scholar] [CrossRef]
- Efron, U.; Braatz, P.O.; Little, M.J.; Schwartz, R.N.; Grinberg, J. Silicon liquid crystal light valves: Status and issues. Opt. Eng. 1983, 22, 682–686. [Google Scholar] [CrossRef]
- Efron, U.; Wu, S.T.; Bates, T.D. Nematic liquid crystals for spatial light modulators: Recent studies. J. Opt. Soc. Am. B. 1986, 3, 247–252. [Google Scholar] [CrossRef]
- Johnson, K.M.; McKnight, D.J.; Underwood, I. Smart Spatial Light Modulators Using Liquid Crystals on Silicon. IEEE J. Quantum Electron. 1993, 29, 699–714. [Google Scholar] [CrossRef]
- Vettese, D. Liquid crystal on silicon. Nat. Photonics 2010, 4, 752–754. [Google Scholar] [CrossRef]
- Maimone, A.; Georgiou, A.; Kollin, J.S. Holographic Near-Eye Displays for Virtual and Augmented Reality. ACM Trans. Graph. 2017, 36, 85. [Google Scholar] [CrossRef]
- Matsuda, N.; Fix, A.; Lanman, D. Focal Surface Displays. ACM Trans. Graph. 2017, 36, 86. [Google Scholar] [CrossRef]
- Lazarev, G.; Gädekea, F.; Luberek, J. Ultrahigh-resolution phase-only LCOS spatial light modulator. In Proceedings of the Emerging Liquid Crystal Technologies XII, San Francisco, CA, USA, 28 January–2 February 2017. [Google Scholar]
- Inoue, T.; Tanaka, H.; Fukuchi, N.; Takumi, M.; Matsumotoa, N.; Hara, T.; Yoshida, N.; Igasaki, Y.; Kobayashi, Y. LCOS spatial light modulator controlled by 12-bit signals for optical phase-only modulation. In Proceedings of the Emerging Liquid Crystal Technologies II, San Jose, CA, USA, 9 February 2007. [Google Scholar]
- Linnenberger, A. Advanced SLMs for Microscopy. Proc. SPIE 2018, 10502, 1050204. [Google Scholar]
- Santec. Available online: http://www.santec.com/en/products/components/slm (accessed on 29 October 2018).
- Wang, M.; Zong, L.; Mao, L.; Marquez, A.; Ye, Y.; Zhao, H.; Vaquero, F.J. LCoS SLM Study and Its Application in Wavelength Selective Switch. Photonics 2017, 4, 22. [Google Scholar] [CrossRef]
- Vizsnyiczai, G.; Kelemen, L.; Ormos, P. Holographic multi-focus 3D two-photon polymerization with real-time calculated holograms. Opt. Express 2014, 22, 24217–24223. [Google Scholar] [CrossRef] [PubMed]
- Beck, R.J.; Parry, J.P.; Shephard, J.D.; Hand, D.P. Compensation for time fluctuations of phase modulation in a liquid-crystal-on-silicon display by process synchronization in laser materials processing. Appl. Opt. 2011, 50, 2899–2905. [Google Scholar] [CrossRef] [PubMed]
- Toyoda, H.; Inoue, T.; Mukozaka, N.; Hara, T.; Wu, M.H. Advances in Application of Liquid Crystal on Silicon Spatial Light Modulator (LCOS-SLM). SID Int. Symp. Dig. Tech. 2014, 45, 559–562. [Google Scholar] [CrossRef]
- Vieri, C.; Lee, G.; Balram, N.; Jung, S.H.; Yang, J.Y.; Yoon, S.Y.; Kang, I.B. An 18 megapixel 4.3” 1443 ppi 120 Hz OLED display for wide field of view high acuity head mounted displays. J. Soc. Inf. Disp. 2018, 26, 314–324. [Google Scholar] [CrossRef]
- Lee, H.S.; Jang, S.; Jeon, H.; Choi, B.S.; Cho, S.H.; Kim, W.T.; Song, K.; Chu, H.Y.; Kim, S.; Jo, S.C.; et al. Large-area Ultra-high Density 5.36” 10Kx6K 2250 ppi Display. Proc. SID Symp. Dig. Tech. 2018, 49, 607–609. [Google Scholar] [CrossRef]
- Wakunami, K.; Hsieh, P.Y.; Oi, R.; Senoh, T.; Sasaki, H.; Ichihashi, Y.; Okui, M.; Huang, Y.P.; Yamamoto, K. Projection-type see-through holographic three-dimensional display. Nat. Commun. 2016, 7, 12954. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.H.; Hwang, C.Y.; Choi, J.H.; Pi, J.E.; Yang, J.H.; Cho, S.M.; Cheon, S.H.; Kim, G.H.; Choi, K.; Kim, H.O.; et al. Development of high-resolution active matrix spatial light modulator. Opt. Eng. 2018, 57, 061606. [Google Scholar] [CrossRef]
- Holoeye. Available online: https://holoeye.com/spatial-light-modulators/gaea-4k-phase-only-spatial-light-modulator/ (accessed on 29 October 2018).
- Yang, J.P.; Chen, H.M.P.; Huang, Y.; Wu, S.T.; Hsu, C.; Ting, L.; Hsu, R. Sub-KHz 4000-PPI LCoS Phase Modulator for Holographic Displays. Proc. SID Symp. Dig. Tech. 2018, 49, 772–775. [Google Scholar] [CrossRef]
- Abeeluck, A.K.; Iverson, A.; Goetz, H.; Passon, E. High-Performance Displays for Wearable and HUD Applications. Proc. SID Symp. Dig. Tech. 2018, 49, 768–771. [Google Scholar] [CrossRef]
- Zeng, Z.; Zheng, H.; Yu, Y.; Asund, A.K.; Valyukh, S. Full-color holographic display with increased-viewing-angle. Appl. Opt. 2017, 56, F112–F120. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.P.; Chen, H.M.P. A 3-msec Response-Time Full-Phase-Modulation 1080p LCoS-SLM for Dynamic 3D Holographic Displays. Proc. SID Symp. Dig. Tech. 2017, 48, 1073–1076. [Google Scholar] [CrossRef]
- Inoue, T.; Takaki, Y. Table screen 360-degree holographic display using circular viewing-zone scanning. Opt. Express 2015, 23, 6533–6542. [Google Scholar] [CrossRef] [PubMed]
- Ko, S.B.; Park, J.H. Speckle reduction using angular spectrum interleaving for triangular mesh based computer generated hologram. Opt. Express 2017, 25, 29788–29797. [Google Scholar] [CrossRef] [PubMed]
- Fourth Dimension Displays. Available online: https://www.forthdd.com/products/spatial-light-modulators/ (accessed on 29 October 2018).
- Lin, C.W.; Chen, H.M.P. Defect-free half-V-mode ferroelectric liquid-crystal device. J. Soc. Inf. Disp. 2010, 18, 976–980. [Google Scholar] [CrossRef]
- Turtaev, S.; Leite, I.T.; Mitchell, K.J.; Padgett, M.J.; Phillips, D.B.; Čižmár, T. Comparison of nematic liquid-crystal and DMD based spatial light modulation in complex photonics. Opt. Express 2017, 25, 29874–29884. [Google Scholar] [CrossRef] [PubMed]
- Xianyu, H.; Wu, S.T.; Lin, C.L. Dual frequency liquid crystals: A review. Liq. Cryst. 2009, 36, 717–726. [Google Scholar] [CrossRef]
- Peng, F.; Xu, D.; Chen, H.; Wu, S.T. Low voltage polymer network liquid crystal for infrared spatial light modulators. Opt. Express 2015, 23, 2361–2368. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Chen, Y.; Wu, S.T. Submillisecond-response and scattering-free infrared liquid crystal phase modulators. Opt. Express 2012, 20, 20124–20129. [Google Scholar] [CrossRef] [PubMed]
- Peng, F.; Lee, Y.H.; Luo, Z.; Wu, S.T. Low voltage blue phase liquid crystal for spatial light modulators. Opt. Lett. 2015, 40, 5097–5100. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; He, Z.; Wu, S.T. Fast-response liquid crystal phase modulators for augmented reality displays. Opt. Express 2017, 25, 32757–32766. [Google Scholar] [CrossRef]
- Chen, R.; Huang, Y.; Li, J.; Hu, M.; Li, J.; Wu, S.T.; An, Z. High-frame-rate liquid crystal phase modulator for augmented reality displays. Liq. Cryst. 2018. [Google Scholar] [CrossRef]
- Wu, S.T.; Efron, U. Optical properties of thin nematic liquid crystal cells. Appl. Phys. Lett. 1986, 48, 624–626. [Google Scholar] [CrossRef]
- Thalhammer, G.; Bowman, R.W.; Love, G.D.; Padgett, M.J.; Ritsch-Marte, M. Speeding up liquid crystal SLMs using overdrive with phase change reduction. Opt. Express 2013, 21, 1779–1797. [Google Scholar] [CrossRef] [PubMed]
- Lazarev, G.; Bonifer, S.; Engel, P.; Höhne, D.; Notni, G. High-resolution LCOS microdisplay with sub-kHz frame rate for high performance, high precision 3D sensor. Proc. SPIE Dig. Opt. Technol. 2017, 10335. [Google Scholar] [CrossRef]
- Meadowlark Optics. Available online: https://www.meadowlark.com/1920-1152-spatial-light-modulator-p-119?mid=18#.W34yX84zYdU (accessed on 29 October 2018).
- Xiao, K.D.; Fu, C.Y.; Dimosthenis, K.; Wuerger, S. Visual gamma correction for LCD displays. Displays 2011, 32, 17–23. [Google Scholar] [CrossRef]
- Yang, L.; Xia, J.; Chang, C.; Zhang, X.; Yang, Z.; Chen, J. Nonlinear dynamic phase response calibration by digital holographic microscopy. Appl. Opt. 2015, 54, 7799–7806. [Google Scholar] [CrossRef] [PubMed]
- Strauß, J.; Häfner, T.; Dobler, M.; Heberle, J.; Schmidt, M. Evaluation and calibration of LCoS SLM for direct laser structuring with tailored intensity distributions. Phys. Procedia 2016, 83, 1160–1169. [Google Scholar] [CrossRef]
- Zhang, H.; Zhou, H.; Li, J.; Qiao, Y.J.; Si, J.; Gao, W. Compensation of phase nonlinearity of liquid crystal spatial light modulator for high-resolution wavefront correction. J. Eur. Opt. Soc.-Rapid 2015, 10, 15036. [Google Scholar] [CrossRef]
- Engström, D.; Persson, M.; Bengtsson, J.; Goksör, M. Calibration of spatial light modulators suffering from spatially varying phase response. Opt. Express 2013, 21, 16086–16103. [Google Scholar] [CrossRef] [PubMed]
- Reichelt, S. Spatially resolved phase-response calibration of liquid-crystal-based spatial light modulators. Appl. Opt. 2013, 52, 2610–2618. [Google Scholar] [CrossRef] [PubMed]
- Otón, J.; Ambs, P.; Millán, M.S.; Cabré1, E.P. Multipoint phase calibration for improved compensation of inherent wavefront distortion in parallel aligned liquid crystal on silicon displays. Appl. Opt. 2007, 46, 5667–5679. [Google Scholar] [CrossRef] [PubMed]
- Otón, J.; Ambs, P.; Millán, M.S.; Cabré1, E.P. Dynamic calibration for improving the speed of a parallel-aligned liquid-crystal-on-silicon display. Appl. Opt. 2009, 48, 4616–4624. [Google Scholar] [CrossRef] [PubMed]
- Lu, Q.; Sheng, L.; Zeng, F.; Gao, S.; Qiao, Y. Improved method to fully compensate the spatial phase nonuniformity of LCoS devices with a Fizeau interferometer. Appl. Opt. 2016, 55, 7796–7802. [Google Scholar] [CrossRef] [PubMed]
- Xia, J.; Chang, C.; Chen, Z.; Zhu, Z.; Zeng, T.; Liang, P.Y.; Ding, J. Pixel-addressable phase calibration of spatial light modulators: A common-path phase-shifting interferometric microscopy approach. J. Opt. 2017, 19, 125701. [Google Scholar] [CrossRef]
- Gelder, R.V.; Melnik, G. Uniformity metrology in ultra-thin LCoS LCDs. J. Soc. Inf. Disp. 2006, 14, 233–239. [Google Scholar] [CrossRef]
- Zhang, Z.; Chapman, A.M.J.; Collings, N.; Pivnenko, M.; Moore, J.; Crossland, B.; Chu, D.P.; Milne, B. High Quality Assembly of Phase-Only Liquid Crystal on Silicon (LCOS) Devices. J. Disp. Technol. 2011, 7, 120–126. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, H.; Robertson, B.; Redmond, M.; Pivnenko, M.; Collings, N.; Crossland, W.A.; Chu, D.P. Diffraction based phase compensation method for phase-only liquid crystal on silicon devices in operation. Appl. Opt. 2012, 51, 3837–3846. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Pivnenko, M.; Salazar, I.M.; You, Z.; Chu, D.P. Advanced die-level assembly techniques and quality analysis for phase-only liquid crystal on silicon devices. Proc IMechE Part B J Eng. Manuf. 2016, 230, 1659–1664. [Google Scholar] [CrossRef]
- Čižmár, T.; Mazilu, M.; Dholakia, K. In situ wavefront correction and its application to micromanipulation. Nat. Photonics 2010, 4, 388–394. [Google Scholar] [CrossRef]
- Serati, S.; Xia, X.; Mughal, O.; Linnenberger, A. High-resolution phase-only spatial light modulators with submillisecond response. In Proceedings of the Optical Pattern Recognition XIV, Orlando, FL, USA, 6 August 2003. [Google Scholar]
- Harriman, J.; Linnenberger, A.; Serati, S. Improving spatial light modulator performance through phase compensation. In Proceedings of the Advanced Wavefront Control: Methods, Devices, and Applications II, Denver, CO, USA, 12 October 2004. [Google Scholar]
- Xu, J.; Qin, S.; Liu, C.; Fu, S.; Liu, D. Precise calibration of spatial phase response nonuniformity arising in liquid crystal on silicon. Opt. Lett. 2018, 43, 2993–2996. [Google Scholar] [CrossRef] [PubMed]
- Collings, N.; Christmas, J.L. Real-Time Phase-Only Spatial Light Modulators for 2D Holographic Display. J. Disp. Technol. 2015, 11, 278–284. [Google Scholar] [CrossRef]
- Lizana, A.; Márquez, A.; Lobato, L.; Rodange, Y.; Moreno, I.; Iemmi, C.; Campos, J. The minimum Euclidean distance principle applied to improve the modulation diffraction efficiency in digitally controlled spatial light modulators. Opt. Express 2010, 18, 10581–10593. [Google Scholar] [CrossRef] [PubMed]
- Márquez, J.G.; López, V.; Vega, A.G.; Noé1, E. Flicker minimization in an LCoS spatial light modulator. Opt. Express 2012, 20, 8431–8441. [Google Scholar] [CrossRef] [PubMed]
- Moore, J.R.; Collings, N.; Crossland, W.A.; Davey, A.B.; Evans, M.; Jeziorska, A.M.; Komarˇcevic´, M.; Parker, R.J.; Wilkinson, T.D.; Xu, H. The Silicon Backplane Design for an LCOS Polarization-Insensitive Phase Hologram SLM. IEEE Photonics Technol. Lett. 2008, 20, 60–62. [Google Scholar] [CrossRef]
- Bouvier, M.; Scharf, T. Analysis of nematic-liquid-crystal binary gratings with high spatial frequency. Opt. Eng. 2000, 39, 2129–2137. [Google Scholar] [CrossRef]
- Márquez, A.; Iemmi, C.; Moreno, I.; Campos, J.; Yzuel, M.J. Anamorphic and spatial frequency dependent phase modulation on liquid crystal displays. Optimization of the modulation diffraction efficiency. Opt. Express 2005, 13, 2111–2119. [Google Scholar] [CrossRef] [PubMed]
- Cuypers, D.; Smet, H.D.; Calster, A.V. Electronic Compensation for Fringe-Field Effects in VAN LCOS Microdisplays. SID Symp. Dig. Tech. 2008, Papers 39, 228–231. [Google Scholar] [CrossRef]
- Lobato, L.; Lizana, A.; M´arquez, A.; Moreno, I.; Iemmi, C.; Campos, J.; Yzuel, M.J. Characterization of the anamorphic and spatial frequency dependent phenomenon in liquid crystal on silicon displays. J. Eur. Opt. Soc. 2011, 6, 11012S. [Google Scholar] [CrossRef]
- Francés, J.; Márquez, A.; Martínez-Guardiola, F.J.; Bleda, S.; Gallego, S.; Neipp, C.; Pascual, I.; Beléndez, A. Simplified physical modeling of parallel-aligned liquid crystal devices at highly non-linear tilt angle profiles. Opt. Express 2018, 26, 12723–12741. [Google Scholar] [CrossRef] [PubMed]
- Martínez, F.J.; Márquez, A.; Gallego, S.; Francés, J.; Pascual, I.; Beléndez, A. Effective angular and wavelength modeling of parallel aligned liquid crystal devices. Opt. Laser Eng. 2015, 74, 114–121. [Google Scholar] [CrossRef]
- Martínez, F.J.; Márquez, A.; Gallego, S.; Francés, J.; Ortuño, M.; Francés, J.; Beléndez, A.; Pascual, I. Electrical dependencies of optical modulation capabilities in digitally addressed parallel aligned liquid crystal on silicon devices. Opt. Eng. 2014, 53, 067104. [Google Scholar]

| HOLOEYE Photonics AG | Hamamatsu Photonic | Meadowlark Optics | Santec Corp. |
|---|---|---|---|
| Products | Products | Products | Products |
| 1. PLUTO-2: VIS-014, VIS-016, VIS-020, VIS-056 2. LETO: LETO-only 3. GAEA-2: VIS-036 | 1. X-10468: -01, -02, -03 2. X-13138:-01, -02, -03 | 1. P512: P-, PDM-, HSP-, HSPDM-, ODP-, ODPDM 2. P1920: P-, HSP- | 1. SLM-100: -01 2. SLM-200: -01 |
| Features | Features | Features | Features |
| 1. UHD 4K-Panel (7000 ppi) 2. Driver Interface Up to 600 MHz(HDMI 2.0) 3. SDK Solution | 1. Pure, Linear and Precise Phase Control 2. High-Power-Use | 1. Analogy Driving Scheme 2. Fast LC Response Time 3. Sub-KHz PCIe Interface | 1. Super Flatness Available: λ/40 2. 10-bit LUT |
| * Only List for VIS Light-Region-Use LCoS-SLM (Top. = 35 °C) * BNS LCoS-SLM is acquired by Meadowlark Optics in 2014 | |||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.-M.P.; Yang, J.-P.; Yen, H.-T.; Hsu, Z.-N.; Huang, Y.; Wu, S.-T. Pursuing High Quality Phase-Only Liquid Crystal on Silicon (LCoS) Devices. Appl. Sci. 2018, 8, 2323. https://doi.org/10.3390/app8112323
Chen H-MP, Yang J-P, Yen H-T, Hsu Z-N, Huang Y, Wu S-T. Pursuing High Quality Phase-Only Liquid Crystal on Silicon (LCoS) Devices. Applied Sciences. 2018; 8(11):2323. https://doi.org/10.3390/app8112323
Chicago/Turabian StyleChen, Huang-Ming Philip, Jhou-Pu Yang, Hao-Ting Yen, Zheng-Ning Hsu, Yuge Huang, and Shin-Tson Wu. 2018. "Pursuing High Quality Phase-Only Liquid Crystal on Silicon (LCoS) Devices" Applied Sciences 8, no. 11: 2323. https://doi.org/10.3390/app8112323
APA StyleChen, H.-M. P., Yang, J.-P., Yen, H.-T., Hsu, Z.-N., Huang, Y., & Wu, S.-T. (2018). Pursuing High Quality Phase-Only Liquid Crystal on Silicon (LCoS) Devices. Applied Sciences, 8(11), 2323. https://doi.org/10.3390/app8112323






