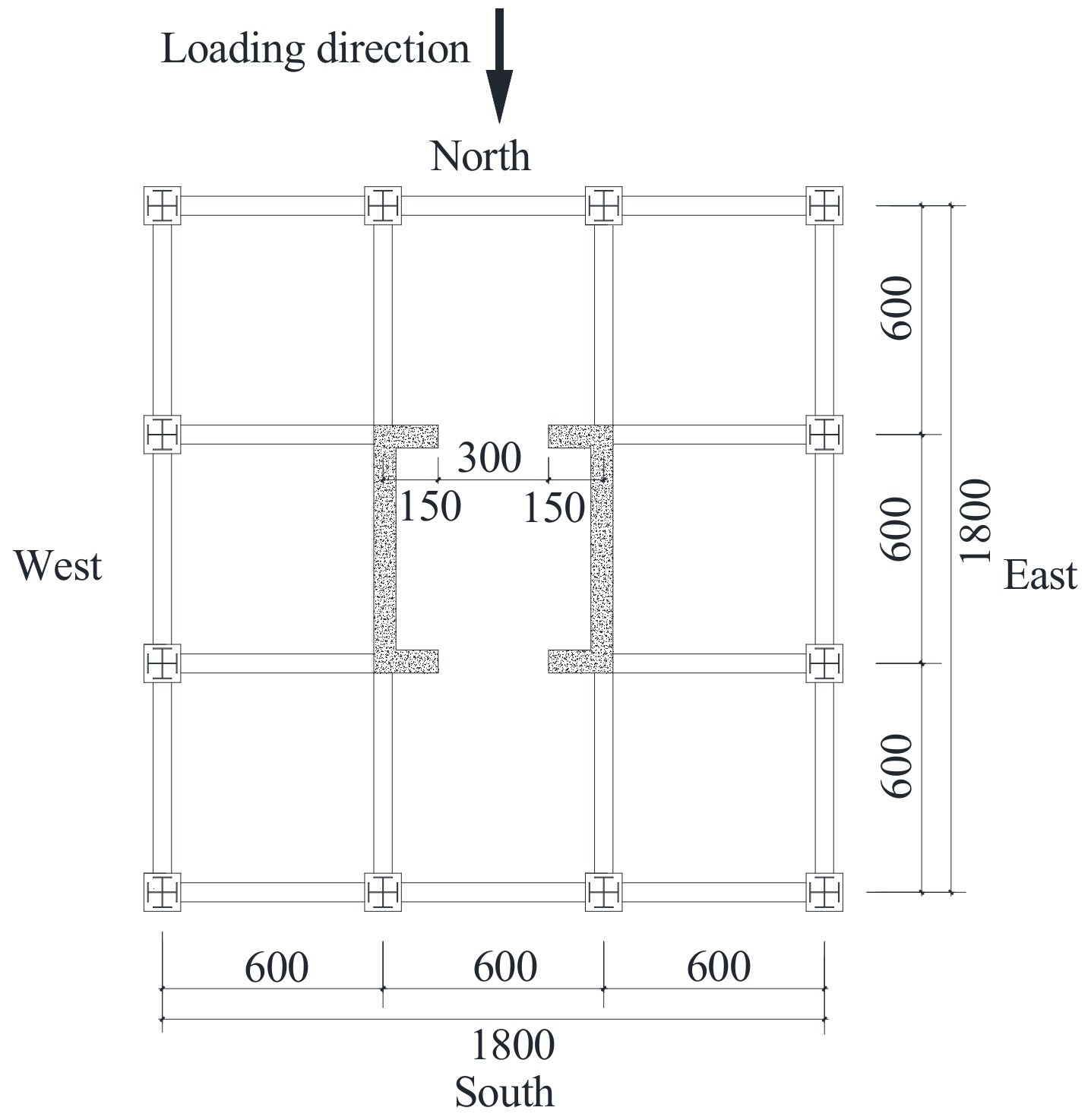
Figure 1.
Plan arrangement (units: mm).
Figure 1.
Plan arrangement (units: mm).
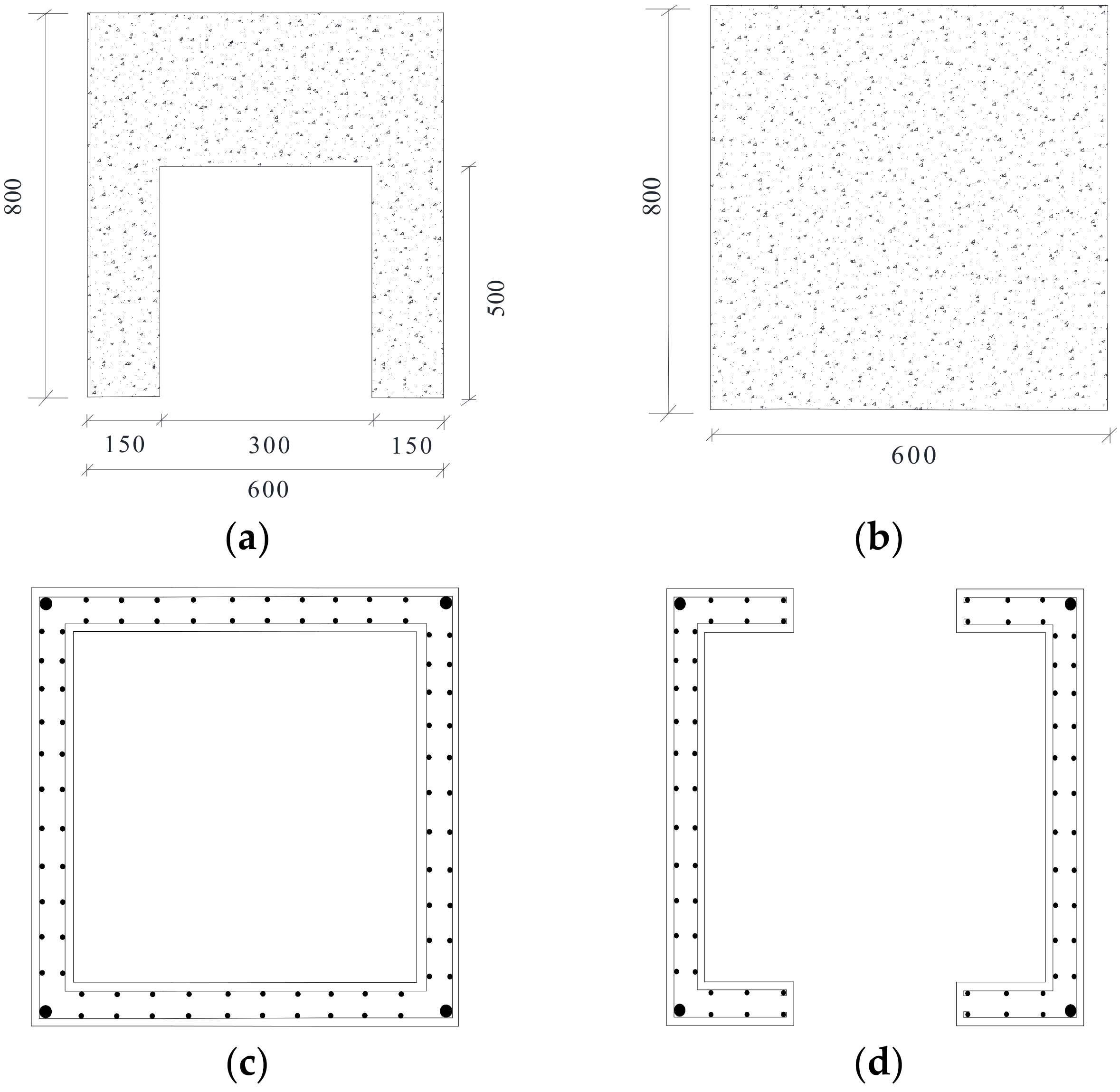
Figure 2.
Details of core tube: (a) the south and north shear wall, (b) the west and east shear wall, (c) the reinforcement in the shear wall and (d) the reinforcement in the opening. (units: mm).
Figure 2.
Details of core tube: (a) the south and north shear wall, (b) the west and east shear wall, (c) the reinforcement in the shear wall and (d) the reinforcement in the opening. (units: mm).
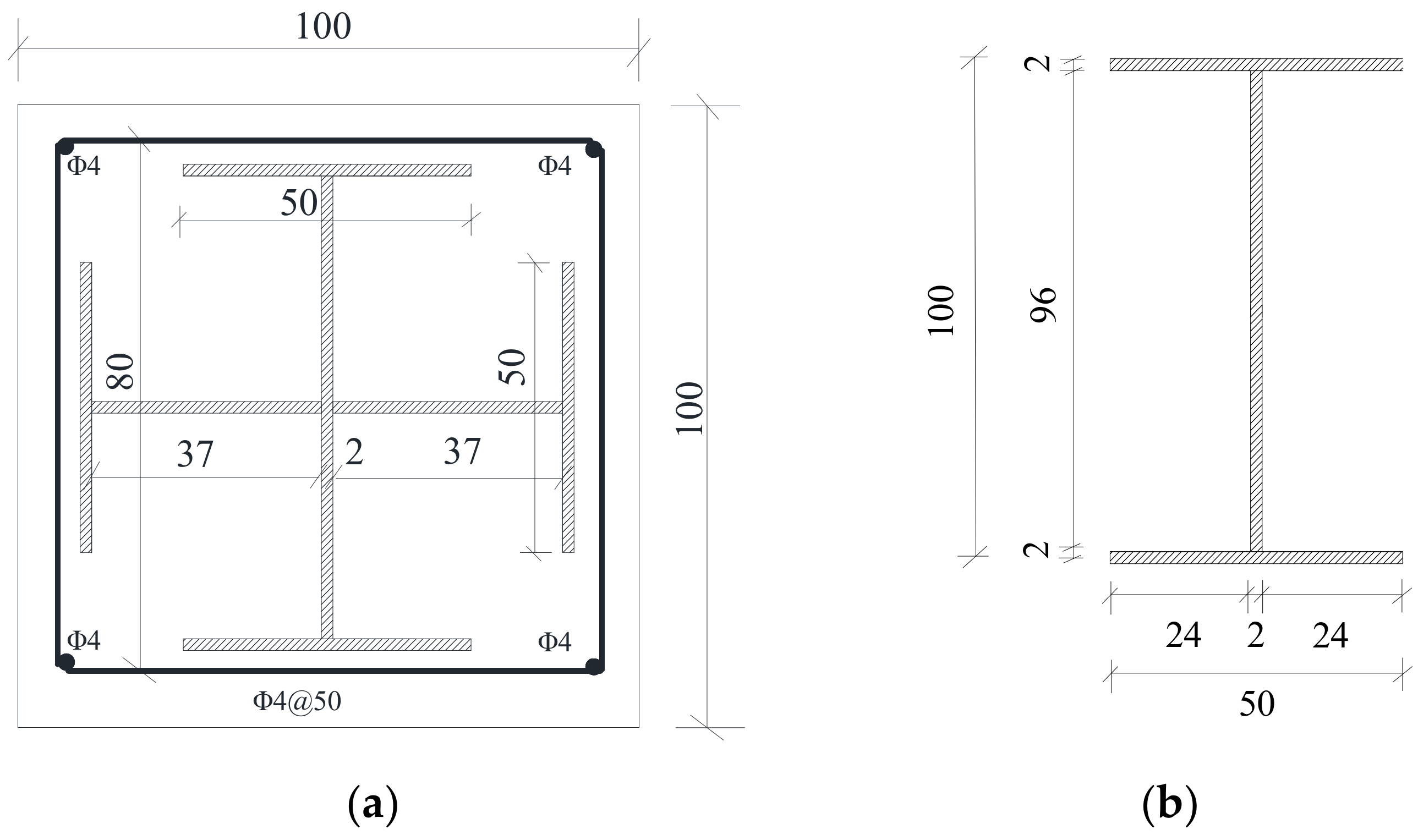
Figure 3.
Details of components: (a) steel reinforced concrete (SRC) column and (b) steel beam. (units: mm).
Figure 3.
Details of components: (a) steel reinforced concrete (SRC) column and (b) steel beam. (units: mm).
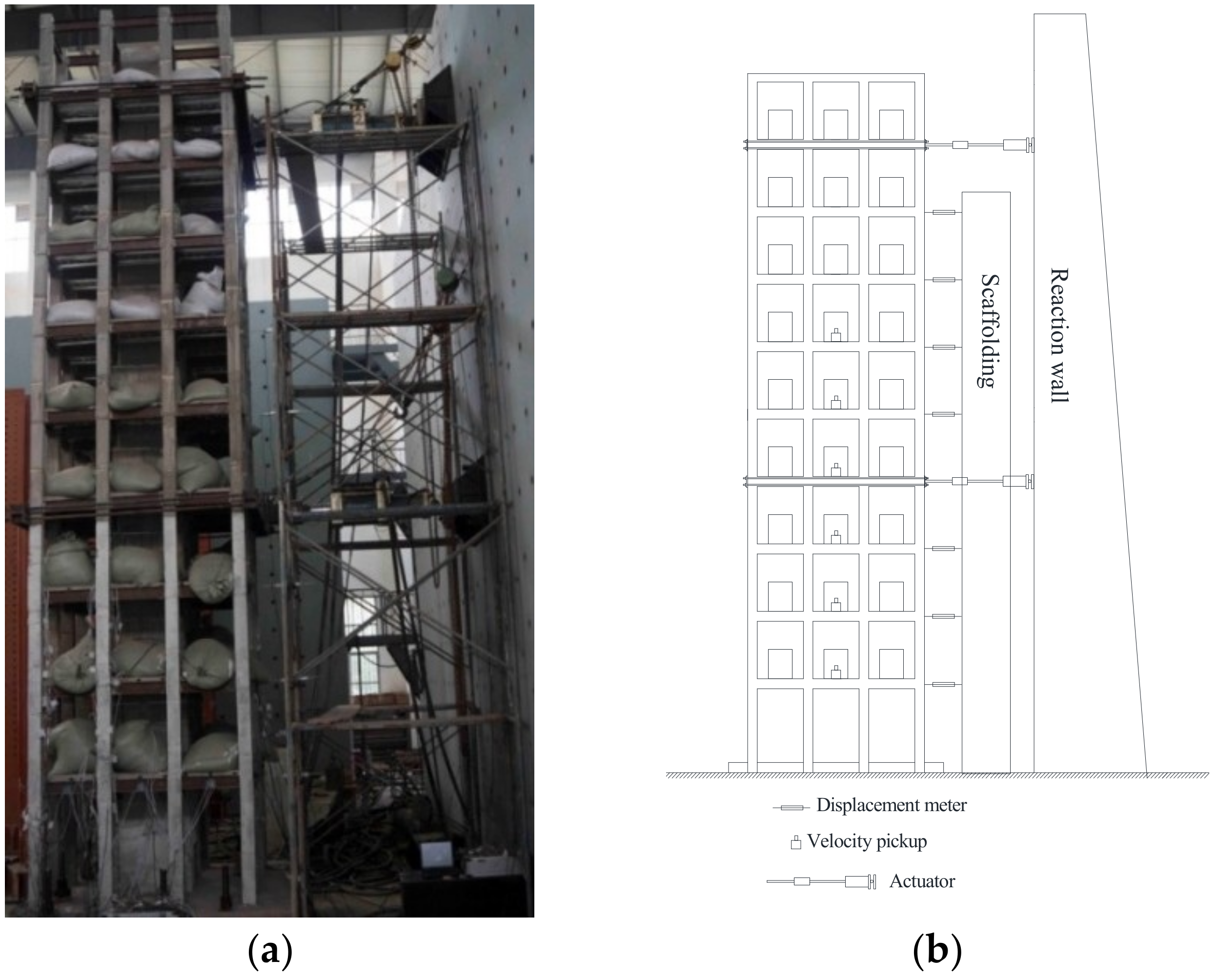
Figure 4.
Test setup: (a) Test specimen and (b) Arrangement of instruments.
Figure 4.
Test setup: (a) Test specimen and (b) Arrangement of instruments.
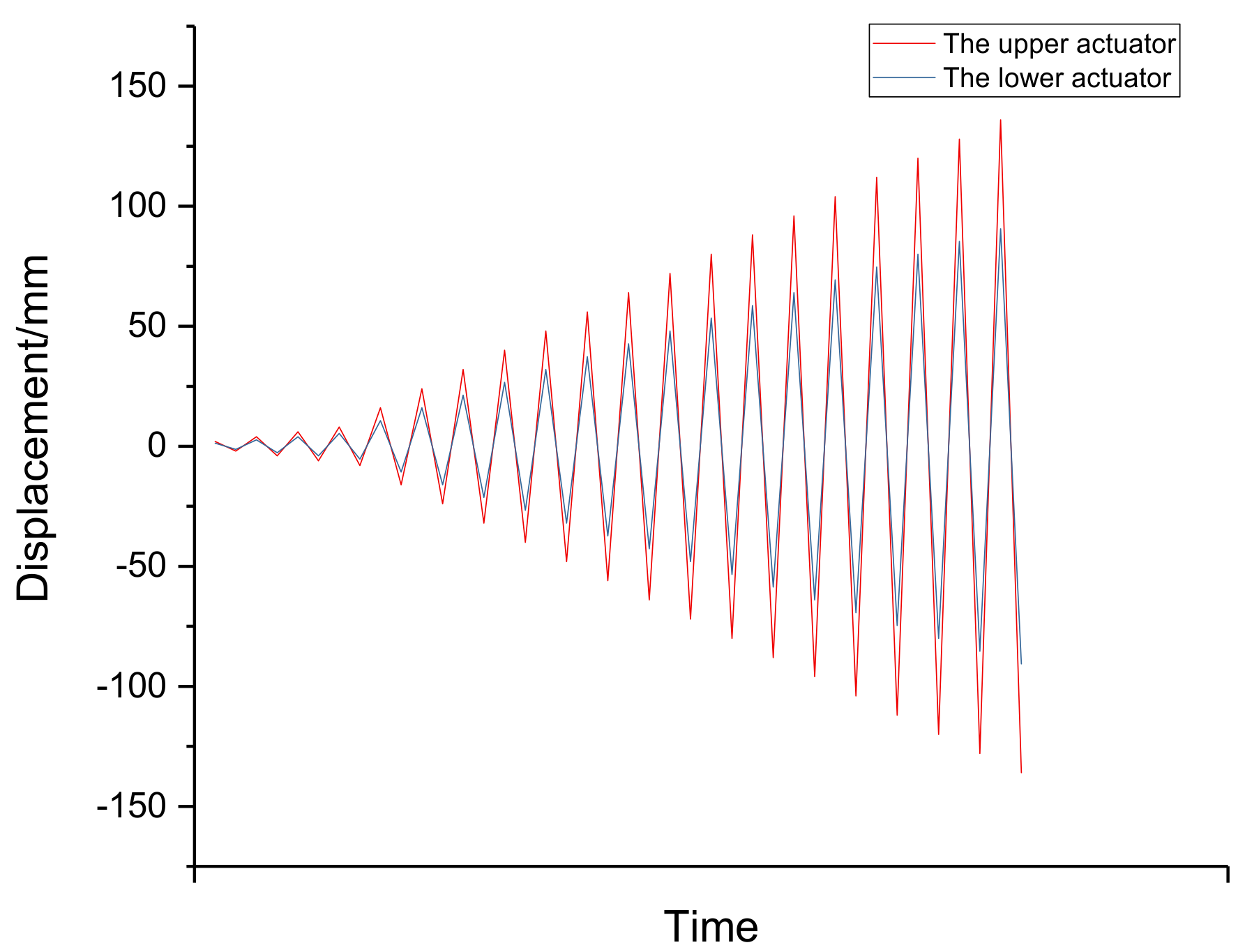
Figure 5.
History of loading program.
Figure 5.
History of loading program.
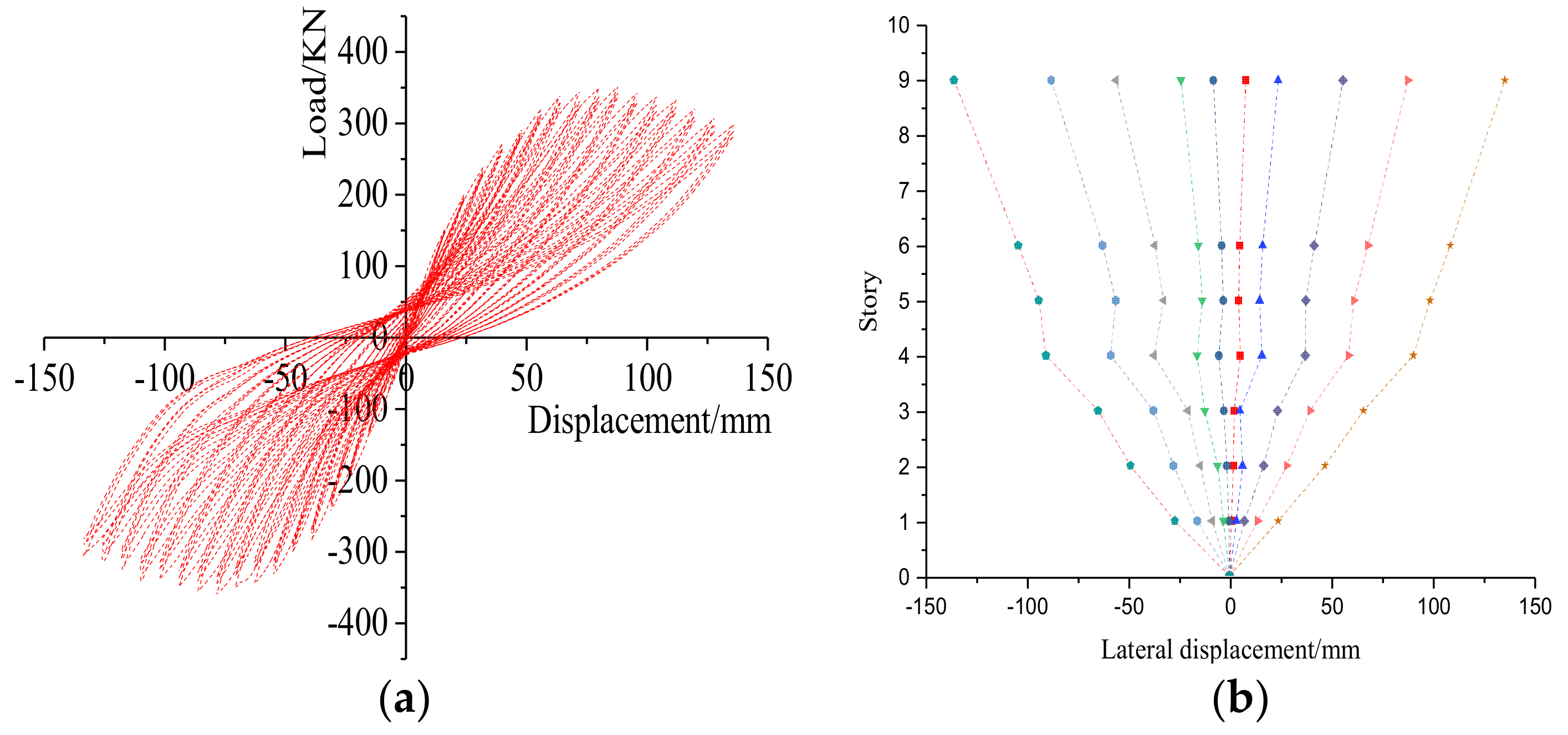
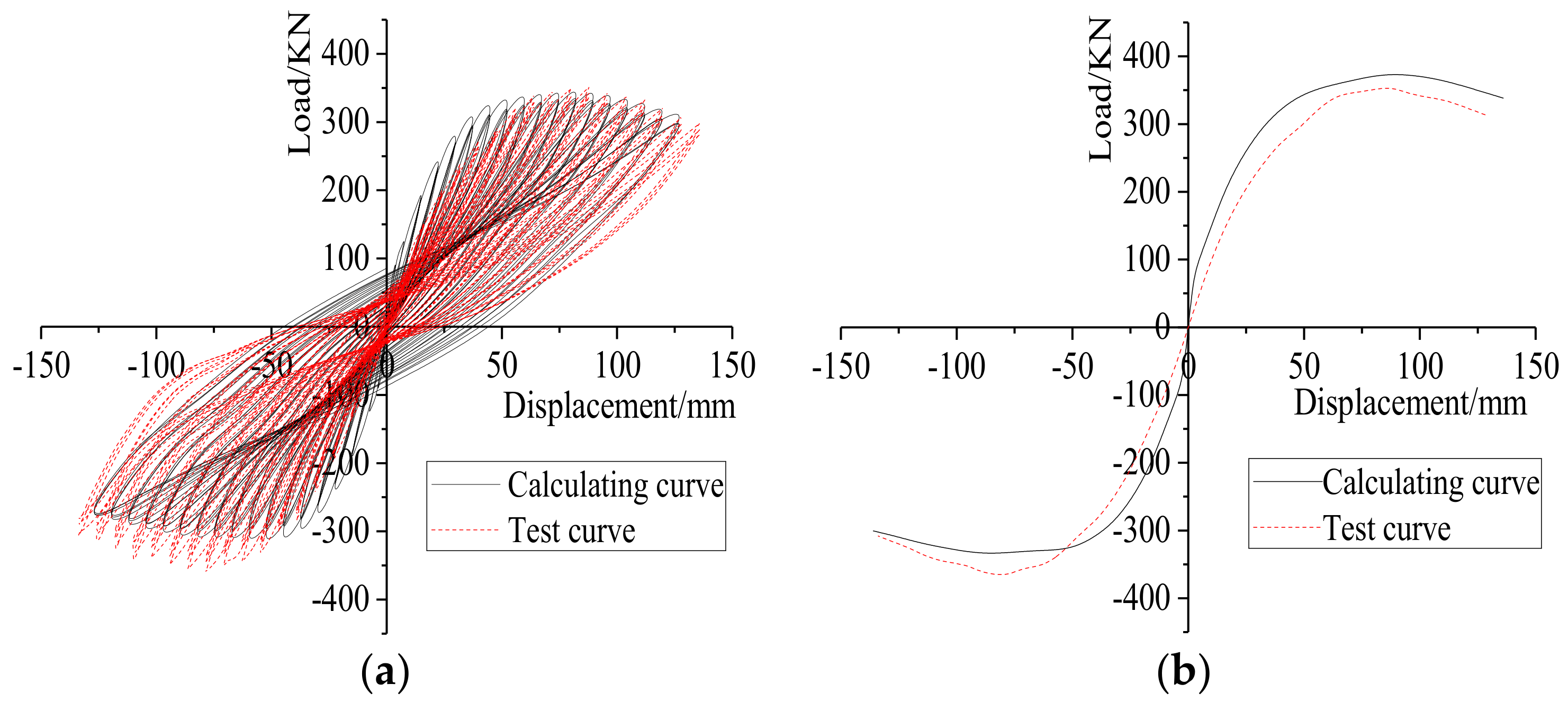
Figure 6.
Test results: (a) The hysteretic curve and (b) lateral displacement.
Figure 6.
Test results: (a) The hysteretic curve and (b) lateral displacement.
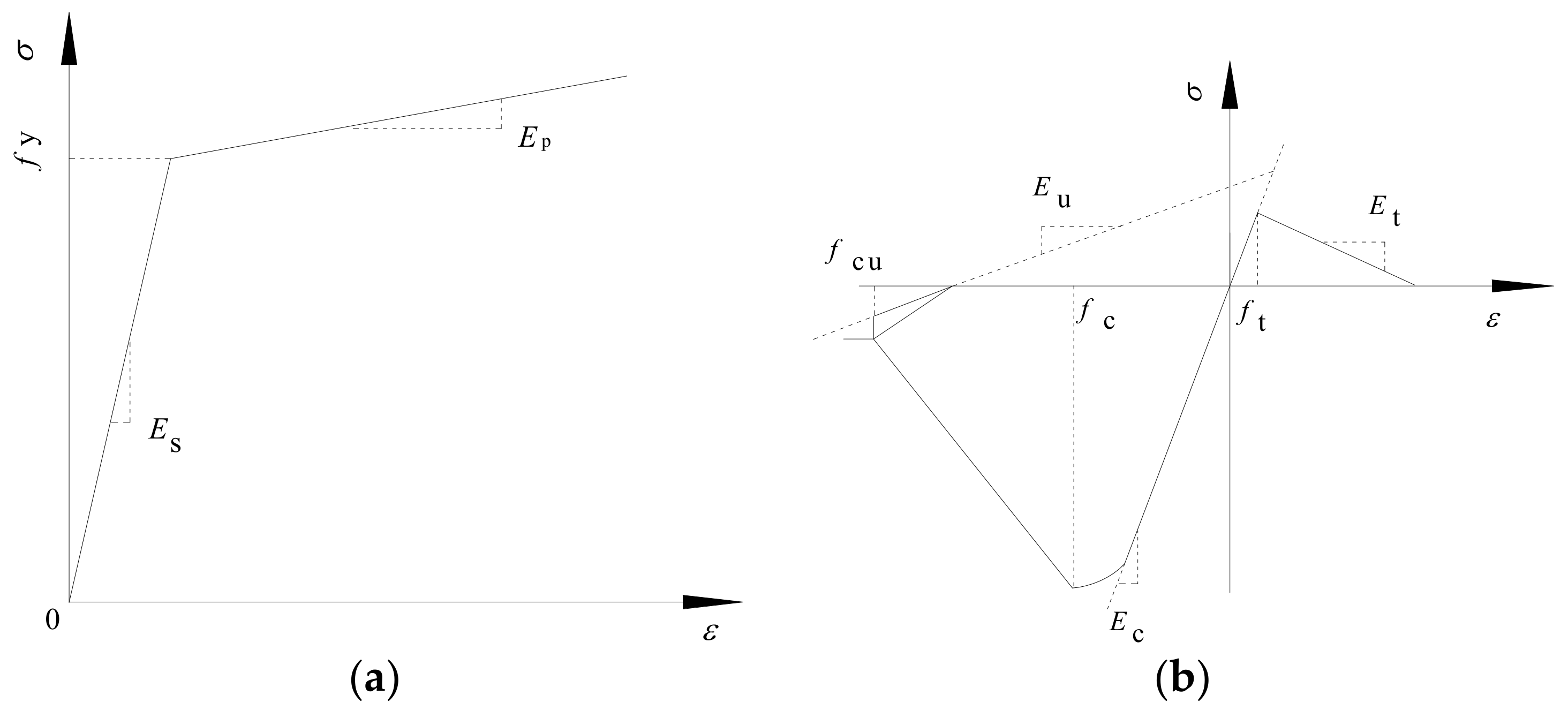
Figure 7.
Constitutive model of materials: (a) constitutive model of steel and (b) constitutive model of concrete.
Figure 7.
Constitutive model of materials: (a) constitutive model of steel and (b) constitutive model of concrete.
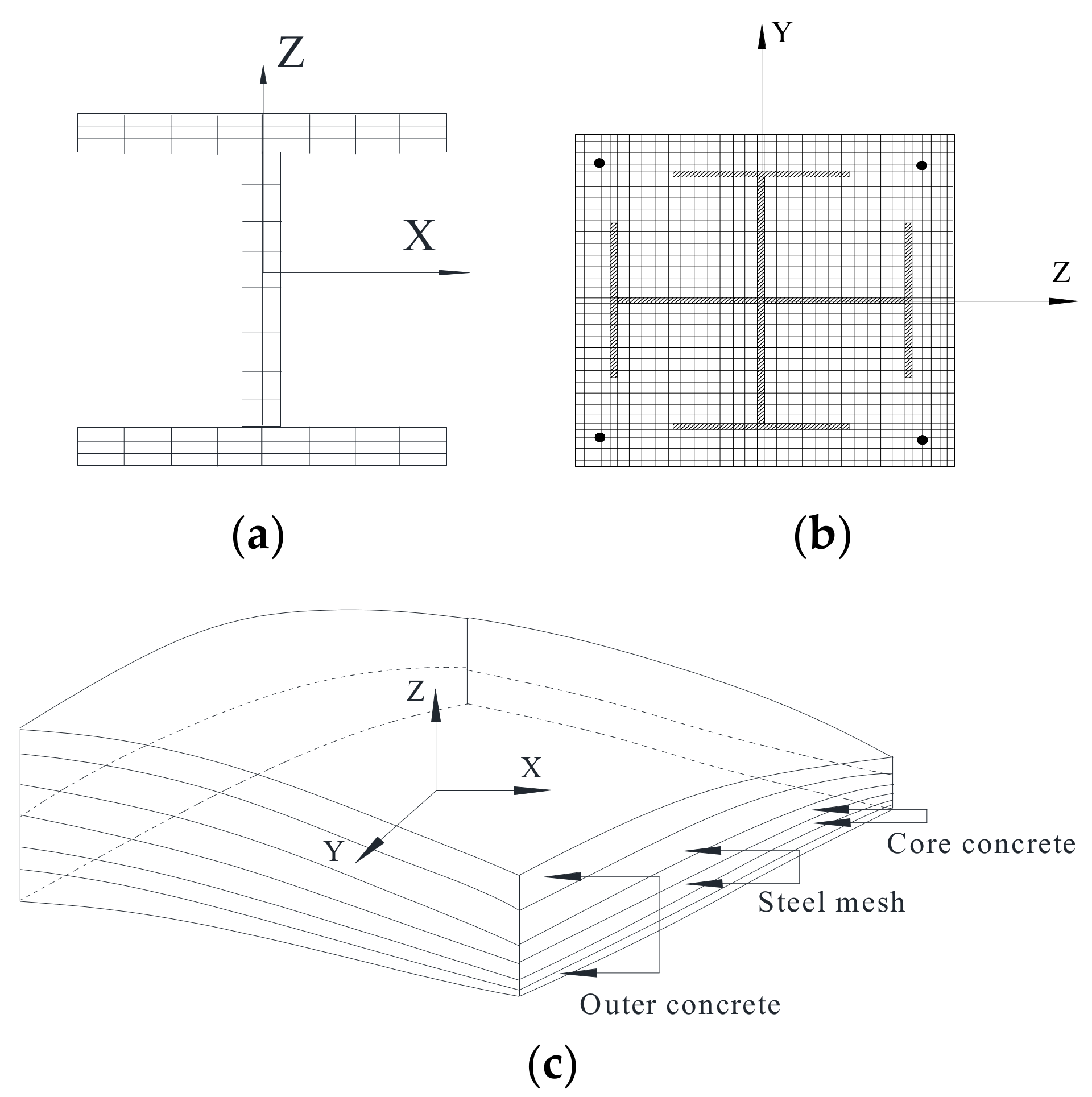
Figure 8.
Fiber sections: (a) beam, (b) column and (c) wall and floor.
Figure 8.
Fiber sections: (a) beam, (b) column and (c) wall and floor.
Figure 9.
The finite element (FE) model.
Figure 9.
The finite element (FE) model.
Figure 10.
Comparison of hysteretic and skeleton curves: (a) Hysteretic curve and (b) Skeleton curve.
Figure 10.
Comparison of hysteretic and skeleton curves: (a) Hysteretic curve and (b) Skeleton curve.
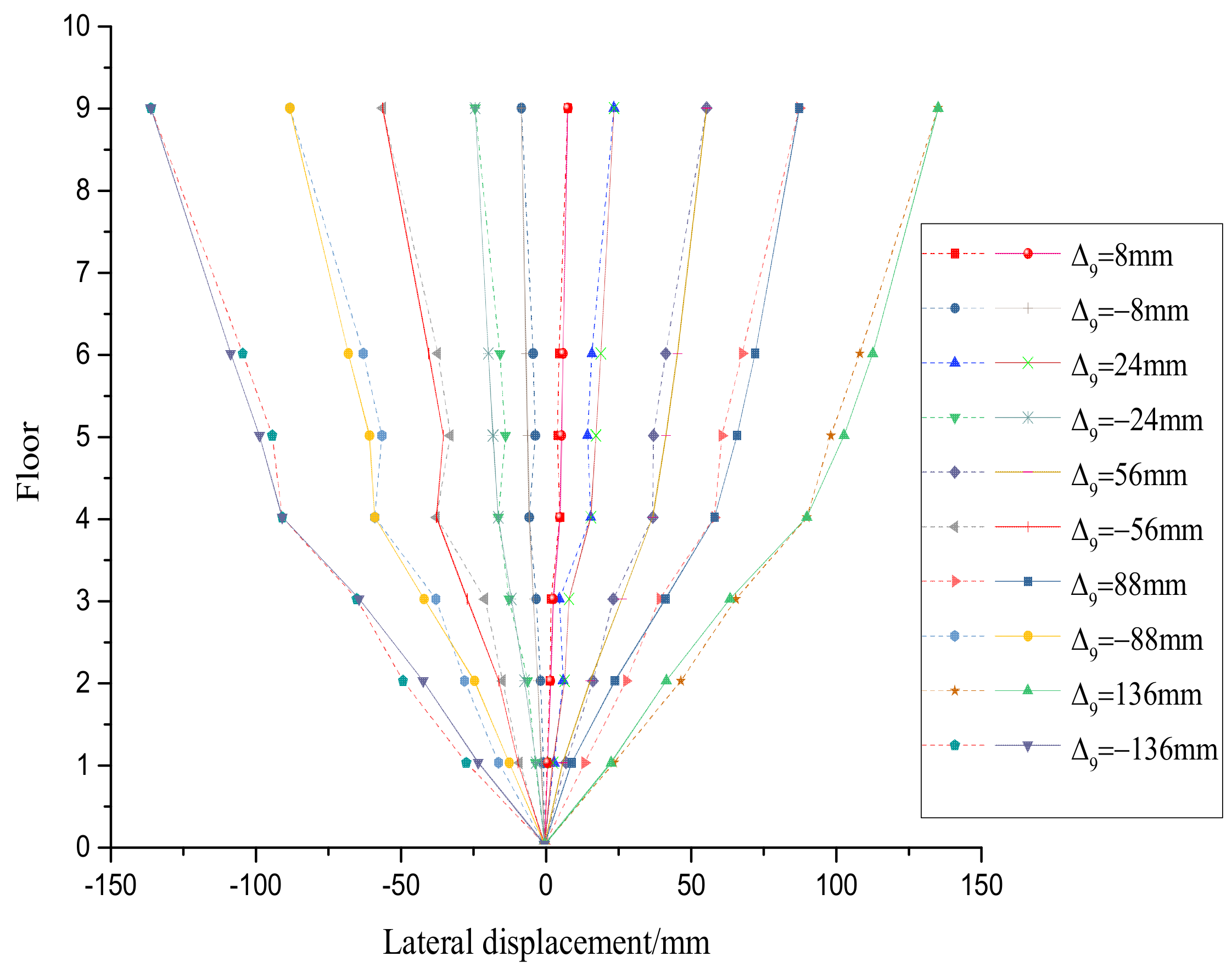
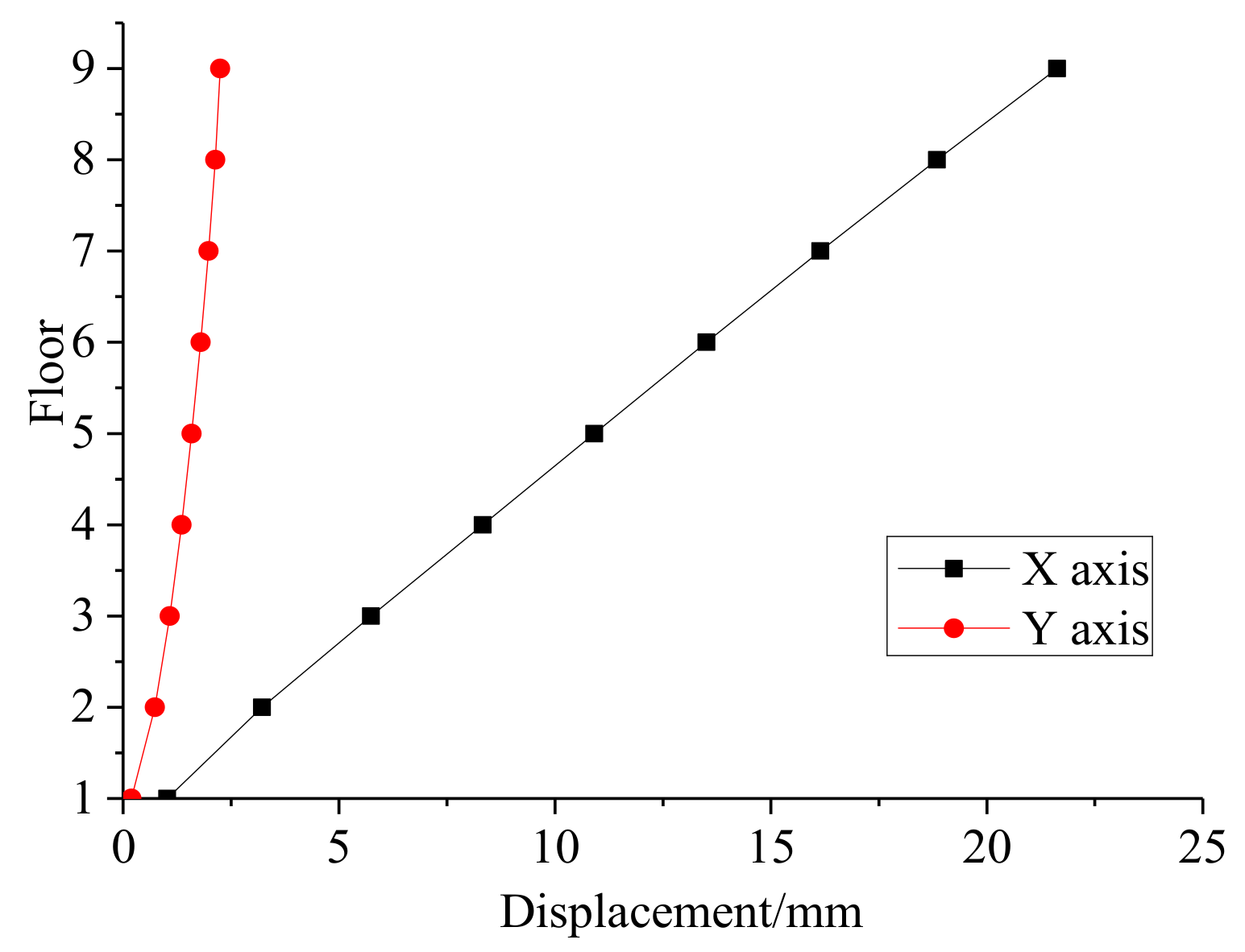
Figure 11.
Comparison of lateral displacement.
Figure 11.
Comparison of lateral displacement.
Figure 12.
Acceleration-time curves: (a) HOLLYWOOD, (b) ELCENTRO, (c) NRIGDE and (d) artificial wave.
Figure 12.
Acceleration-time curves: (a) HOLLYWOOD, (b) ELCENTRO, (c) NRIGDE and (d) artificial wave.
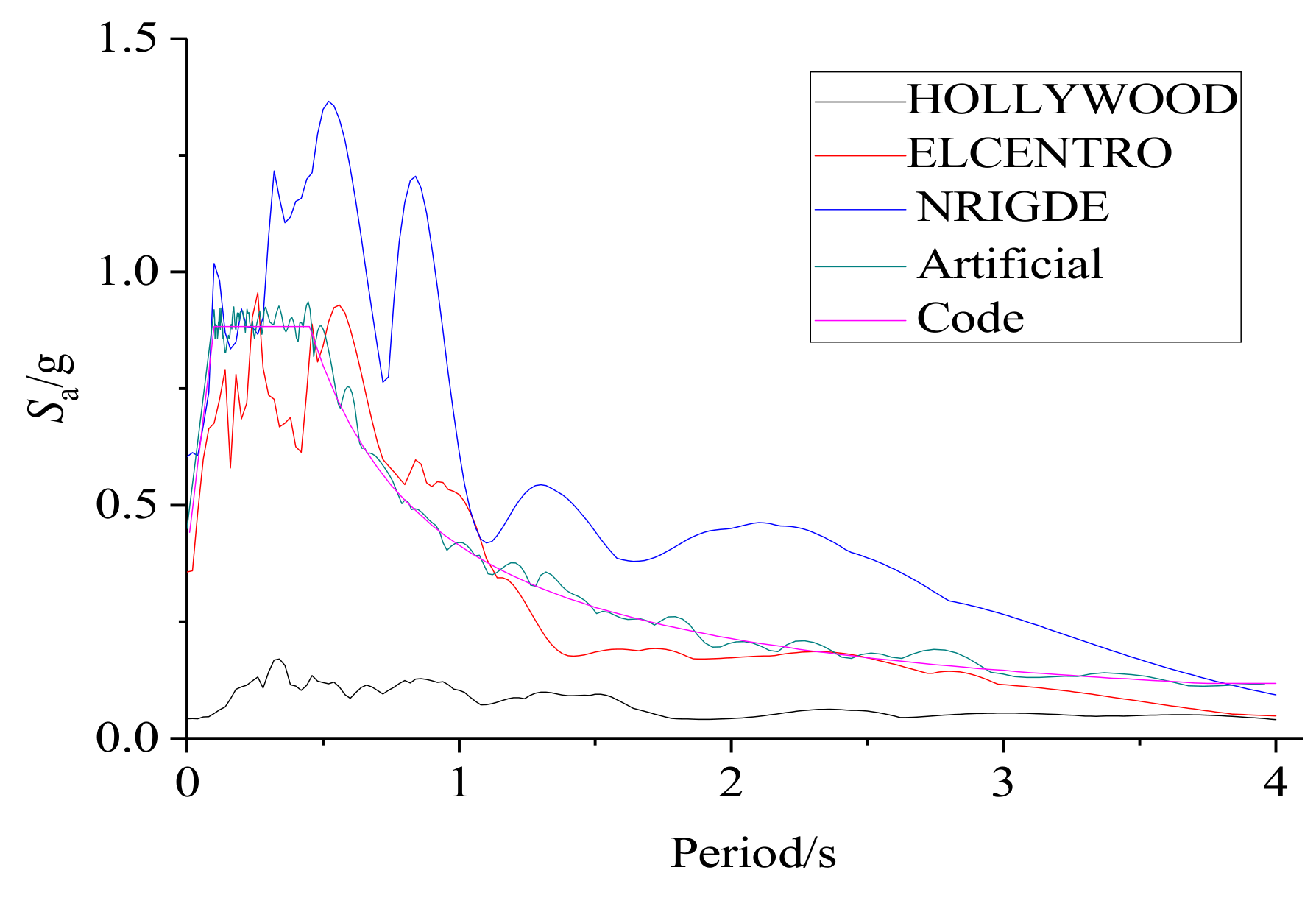
Figure 13.
Response spectra of seismic waves.
Figure 13.
Response spectra of seismic waves.
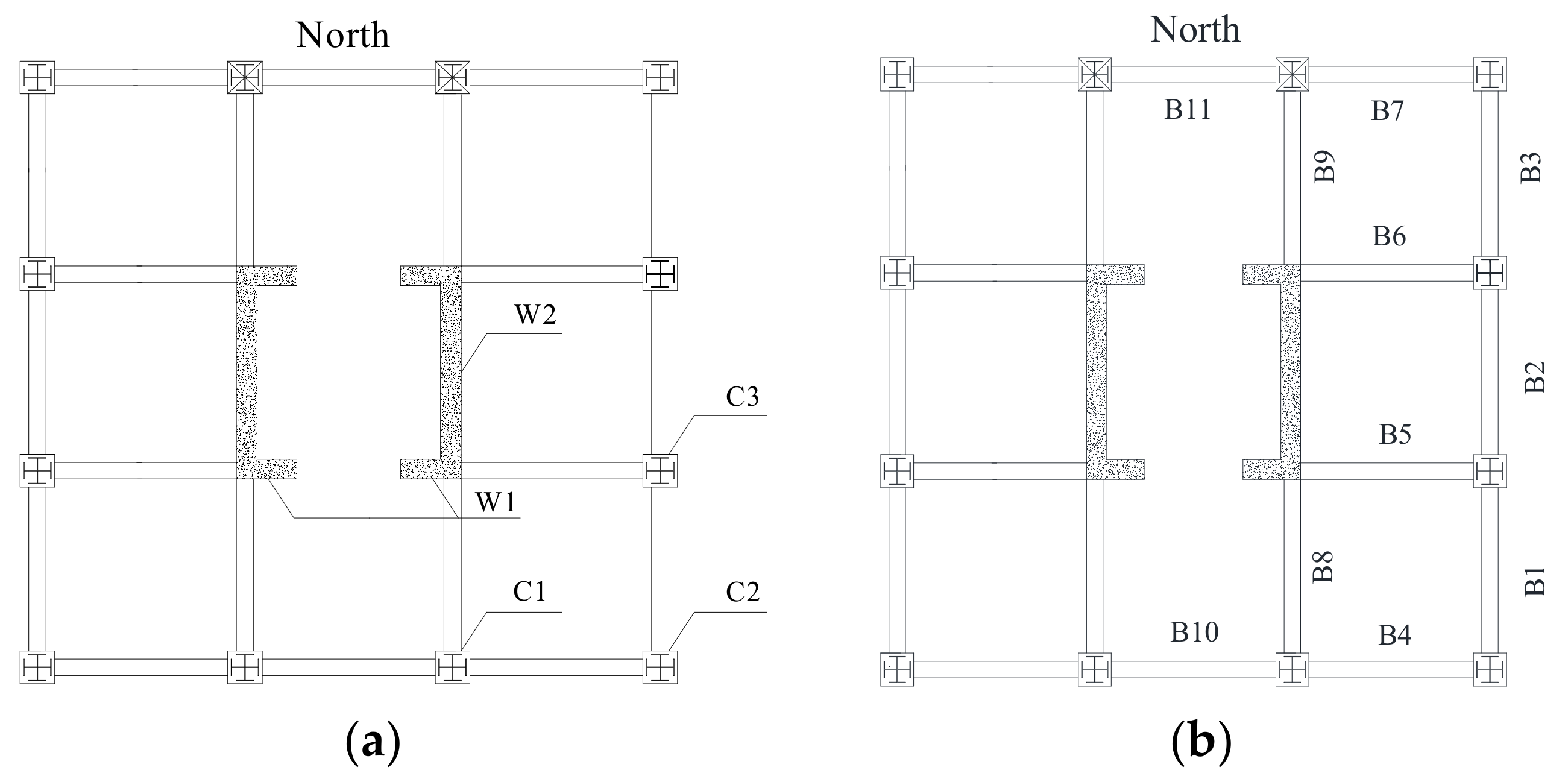
Figure 14.
Location of members at the first floor: (a) location of key components and (b) location of the adjacent beams.
Figure 14.
Location of members at the first floor: (a) location of key components and (b) location of the adjacent beams.
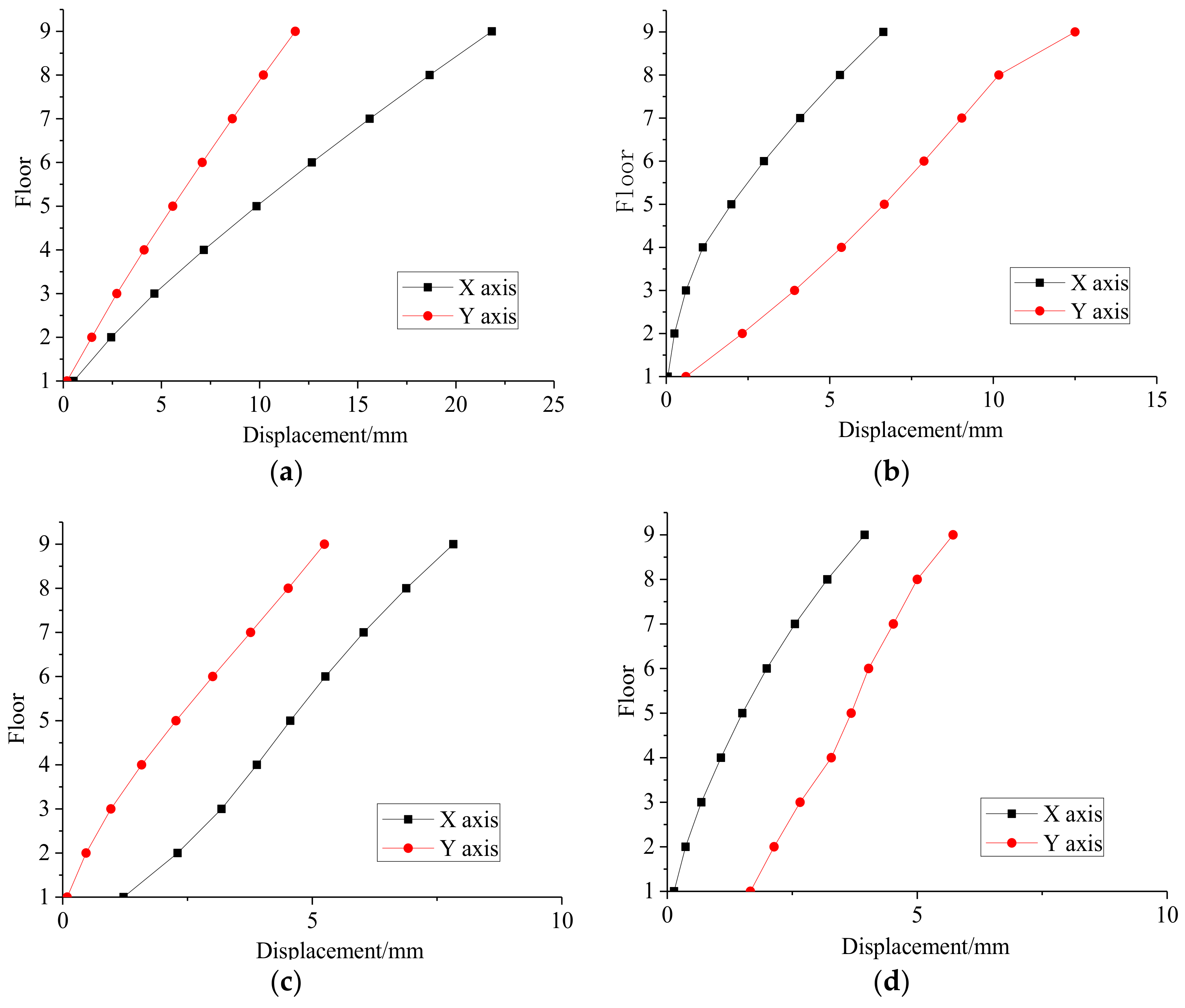
Figure 15.
Displacement of structure in case 1.
Figure 15.
Displacement of structure in case 1.
Figure 16.
Displacement of structure in (a) case 2, (b) case 3, (c) case 4 and (d) case 5.
Figure 16.
Displacement of structure in (a) case 2, (b) case 3, (c) case 4 and (d) case 5.
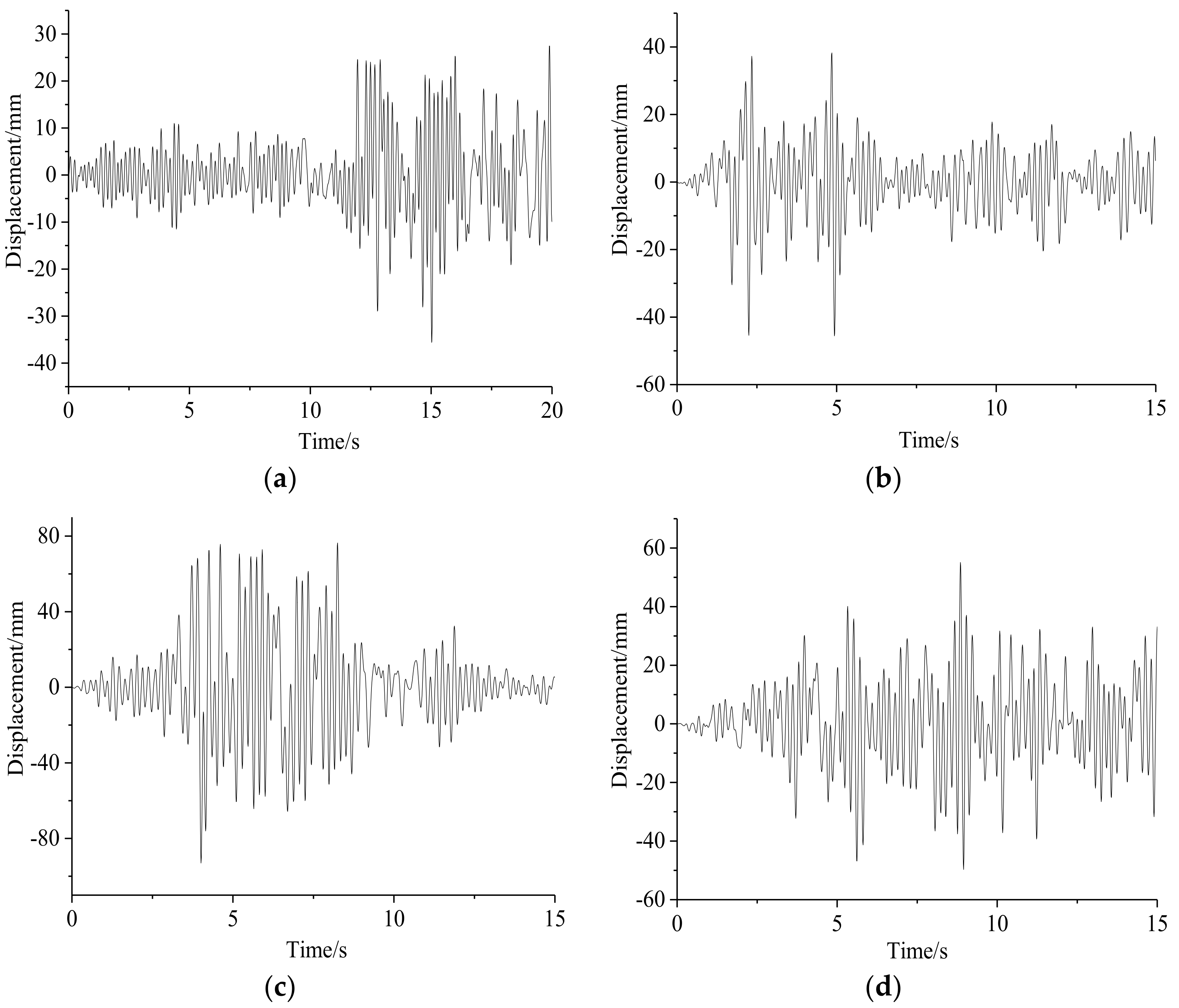
Figure 17.
Displacement-time curve of top under different seismic wave in case 1: (a) HOLLYWOOD, (b) ELCENTRO, (c) NRIGDE and (d) Artificial wave.
Figure 17.
Displacement-time curve of top under different seismic wave in case 1: (a) HOLLYWOOD, (b) ELCENTRO, (c) NRIGDE and (d) Artificial wave.
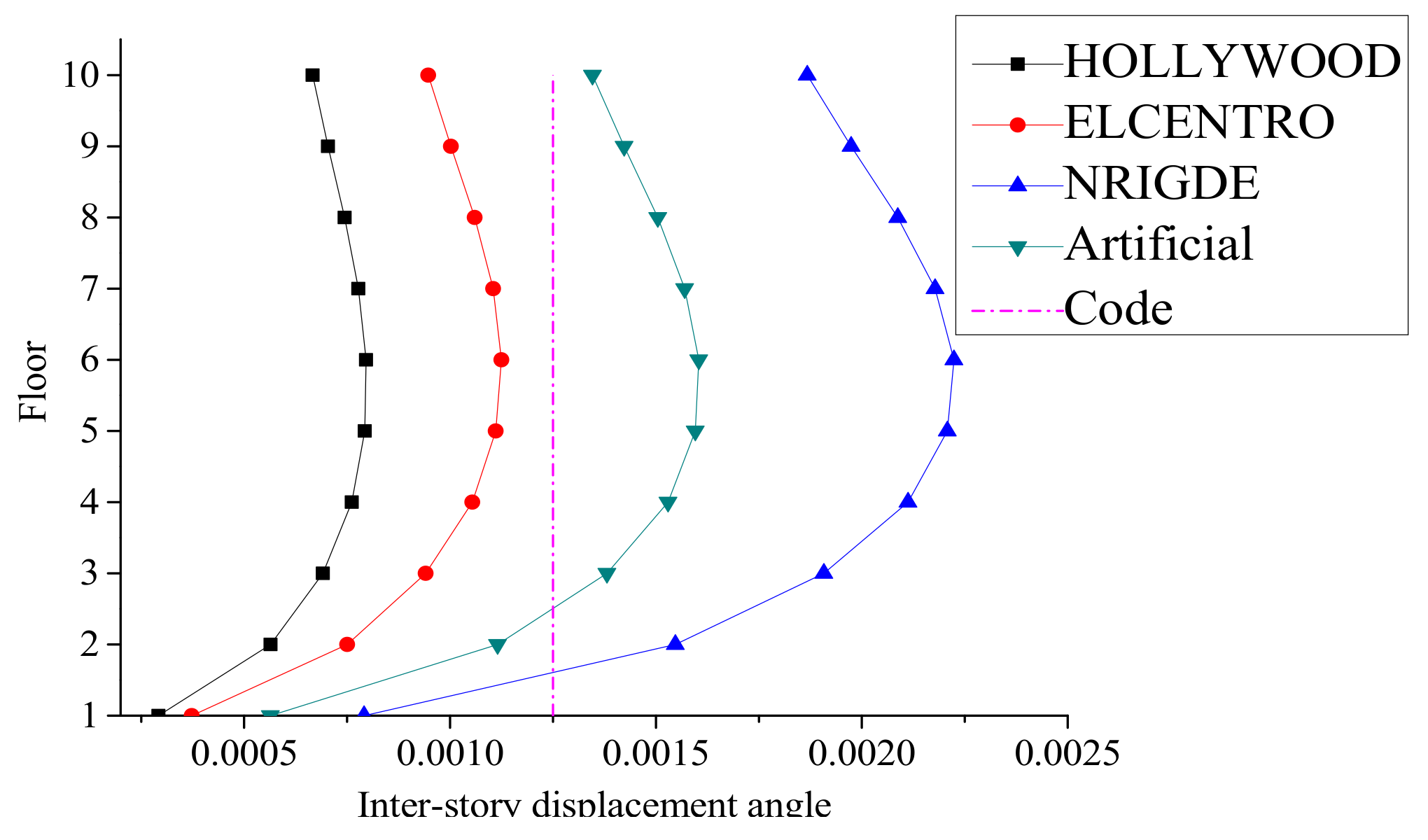
Figure 18.
Inter-story displacement angle in case 1.
Figure 18.
Inter-story displacement angle in case 1.
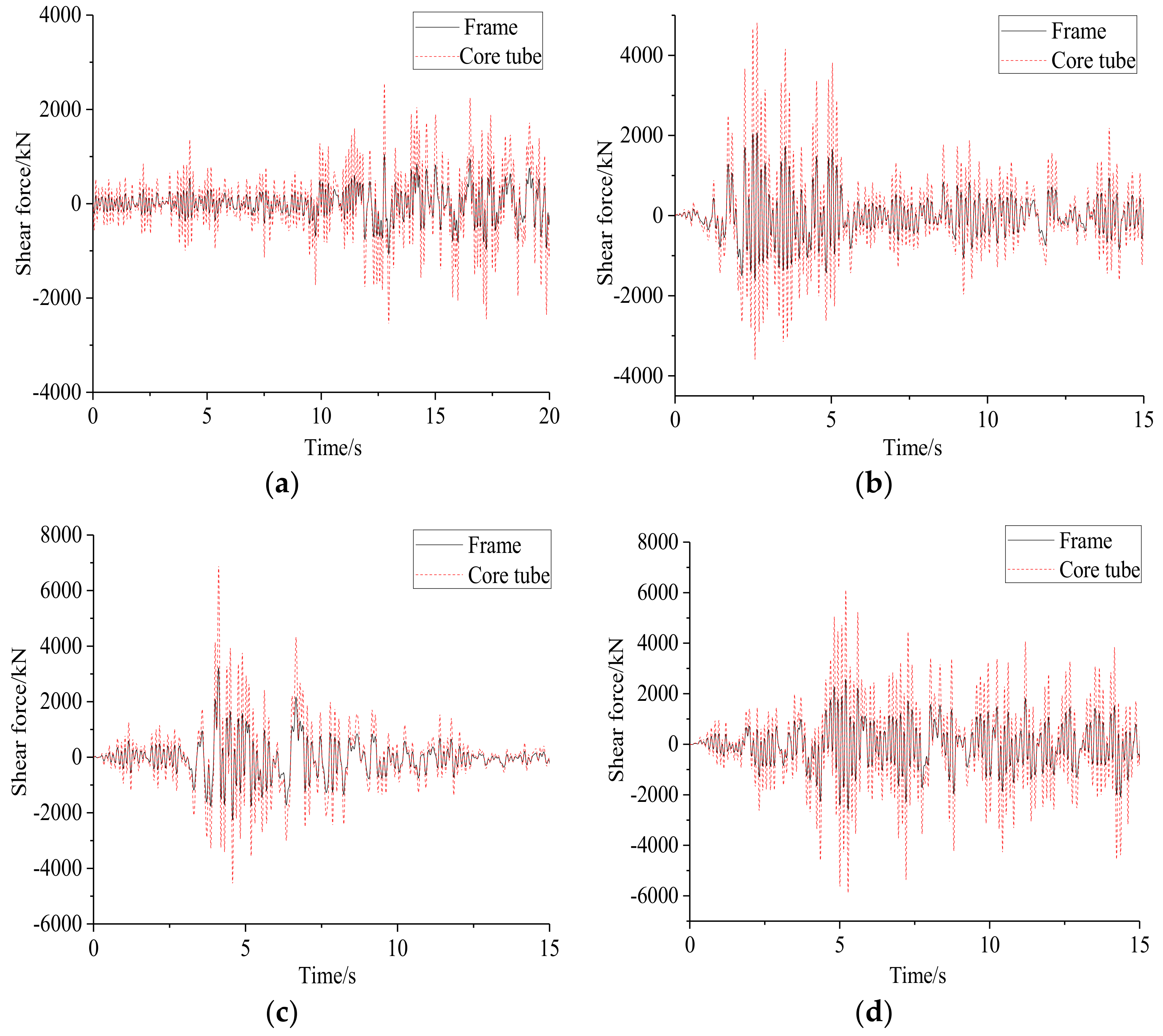
Figure 19.
Shear distribution of bottom under different seismic wave in case 1: (a) HOLLYWOOD, (b) ELCENTRO, (c) NRIGDE and (d) Artificial wave.
Figure 19.
Shear distribution of bottom under different seismic wave in case 1: (a) HOLLYWOOD, (b) ELCENTRO, (c) NRIGDE and (d) Artificial wave.
Table 1.
Properties of Concrete.
Table 1.
Properties of Concrete.
| Concrete Strength Grade | Concrete Compressive Strength/MPa | Elastic Modulus/MPa |
|---|
| C40 | 41.5 | 3.03 × 104 |
Table 2.
Properties of steel.
Table 2.
Properties of steel.
| Material | Yield Strength/MPa | Ultimate Strength/MPa | Elastic Modulus/MPa |
|---|
| Φ4 bar | 305 | 424 | 2.1 × 105 |
| Steel plate | 327 | 463 | 2.0 × 105 |
Table 3.
Test value of frequencies.
Table 3.
Test value of frequencies.
| Vibration Modes | Initial State | Failure State |
|---|
| Test Value/Hz | Test Value/Hz |
|---|
| 1 | 5.94 | 3.26 |
| 2 | 18.98 | 6.22 |
| 3 | 25.13 | 15.96 |
| 4 | 37.93 | 31.82 |
| 5 | 50.03 | 42.01 |
Table 4.
Comparison of characteristic value.
Table 4.
Comparison of characteristic value.
| Load | Direction | Test Value/kN | Calculating Value/kN | Absolute Error/% |
|---|
| Py | Positive | 238.49 | 256.72 | 7.64 |
| Negative | −243.52 | −251.89 | 3.43 |
| Pmax | Positive | 351.72 | 373.69 | 6.24 |
| Negative | −356.12 | −333.91 | 6.23 |
| Pu | Positive | 308.47 | 338.44 | 9.72 |
| Negative | −304.96 | −300.55 | 1.44 |
Table 5.
Comparison of frequencies.
Table 5.
Comparison of frequencies.
| Vibration Modes | Initial State | Failure State |
|---|
| Test Value/Hz | Calculating Value/Hz | Absolute Error/% | Test Value/Hz | Calculating Value/Hz | Absolute Error/% |
|---|
| 1 | 5.94 | 5.86 | 1.31 | 3.26 | 3.35 | 2.73 |
| 2 | 18.98 | 18.13 | 4.50 | 6.22 | 6.01 | 3.23 |
| 3 | 25.13 | 23.97 | 4.60 | 15.96 | 15.25 | 4.47 |
| 4 | 37.93 | 36.47 | 3.87 | 31.82 | 32.47 | 2.06 |
| 5 | 50.03 | 48.43 | 3.20 | 42.01 | 40.85 | 2.76 |
Table 6.
PGA of seismic waves.
Table 6.
PGA of seismic waves.
| Number | Seismic Wave | PGA/g |
|---|
| 1 | HOLLYWOOD | 0.041 |
| 2 | ELCENTRO | 0.278 |
| 3 | NRIGDE | 0.603 |
| 4 | Artificial wave | 0.540 |
Table 7.
/Gal of seismic waves.
Table 7.
/Gal of seismic waves.
| Earthquake Intensity | 7 | 8 | 9 |
|---|
| Frequently occurring | 35 | 70 | 140 |
| Moderate | 107 | 215 | 429 |
| Rarely expected | 220 | 400 | 620 |
Table 8.
Progressive analysis cases.
Table 8.
Progressive analysis cases.
| Case | 1 | 2 | 3 | 4 | 5 |
|---|
| Removed component | C1 | C2 | C3 | W1 | W2 |
Table 9.
Force condition of beams in case 1.
Table 9.
Force condition of beams in case 1.
| Case | Beam Number | Direction | Bending Moment/kN·m | Portion (%) | Average Value (%) | DCR |
|---|
| 1 (C1) | B4 | Positive | 110.00 | 15.69 | 20.06 | 0.23 |
| Negative | −202.50 | 24.43 | 0.42 |
| B8 | Positive | 280.00 | 39.92 | 45.23 | 0.58 |
| Negative | −418.75 | 50.53 | 0.86 |
| B10 | Positive | 311.25 | 44.39 | 34.71 | 0.64 |
| Negative | −207.50 | 25.04 | 0.43 |
Table 10.
Force condition of beams in cases 2, 3, 4 and 5.
Table 10.
Force condition of beams in cases 2, 3, 4 and 5.
| Case | Beam Number | Direction | Bending Moment/kN·m | Portion (%) | Average Value (%) | DCR |
|---|
| 2 (C2) | B1 | Positive | 213.75 | 33.79 | 50 | 0.44 |
| Negative | −428.75 | 66.21 | 0.88 |
| B4 | Positive | 418.75 | 67.39 | 50 | 0.86 |
| Negative | −207.50 | 32.61 | 0.43 |
| 3 (C3) | B1 | Positive | 206.25 | 22.39 | 20.02 | 0.42 |
| Negative | −88.75 | 17.66 | 0.18 |
| B2 | Positive | 313.75 | 34.06 | 32.21 | 0.64 |
| Negative | −142.50 | 28.36 | 0.29 |
| B5 | Positive | 401.25 | 43.55 | 48.77 | 0.82 |
| Negative | −271.25 | 53.98 | 0.55 |
| 4 (W1) | B5 | Positive | 347.50 | 46.41 | 47.10 | 0.71 |
| Negative | −380.00 | 47.80 | 0.78 |
| B8 | Positive | 401.25 | 53.59 | 52.90 | 0.82 |
| Negative | −415.00 | 52.20 | 0.85 |
| 5 (W2) | B5 | Positive | 497.50 | 55.43 | 56.59 | 1.02 |
| Negative | −440.00 | 57.74 | 0.90 |
| B8 | Positive | 400.00 | 44.57 | 43.41 | 0.82 |
| Negative | −322.50 | 42.26 | 0.66 |
Table 11.
Force condition of beams in case 1.
Table 11.
Force condition of beams in case 1.
| Case | Beam Number | Seismic Wave | Average Bending Moment/kN·m | Portion (%) | DCR |
|---|
| 1 (C1) | B4 | HOLLYWOOD | 457.50 | 27.98 | 0.94 |
| ELCENTRO | 558.75 | 23.99 | 1.15 |
| NRIGDE | 885.00 | 23.30 | 1.82 |
| Artificial wave | 763.75 | 22.36 | 1.57 |
| B8 | HOLLYWOOD | 555.00 | 33.95 | 1.14 |
| ELCENTRO | 900.00 | 38.65 | 1.79 |
| NRIGDE | 1440.00 | 37.91 | 2.92 |
| Artificial wave | 1347.50 | 39.46 | 2.77 |
| B10 | HOLLYWOOD | 622.50 | 38.07 | 1.28 |
| ELCENTRO | 870.00 | 37.36 | 1.87 |
| NRIGDE | 1473.75 | 38.79 | 3.04 |
| Artificial wave | 1303.75 | 38.18 | 2.68 |
Table 12.
The maximum inter-story displacement angle in cases 2, 3, 4 and 5.
Table 12.
The maximum inter-story displacement angle in cases 2, 3, 4 and 5.
| Case | Seismic Wave | θmax |
|---|
| 2 (C2) | HOLLYWOOD | 0.00078 |
| ELCENTRO | 0.00108 |
| NRIGDE | 0.00206 |
| Artificial wave | 0.00149 |
| 3 (C3) | HOLLYWOOD | 0.00076 |
| ELCENTRO | 0.00105 |
| NRIGDE | 0.00199 |
| Artificial wave | 0.00142 |
| 4 (W1) | HOLLYWOOD | 0.00077 |
| ELCENTRO | 0.00101 |
| NRIGDE | 0.00209 |
| Artificial wave | 0.00151 |
| 5 (W2) | HOLLYWOOD | 0.00074 |
| ELCENTRO | 0.00093 |
| NRIGDE | 0.00192 |
| Artificial wave | 0.00136 |
Table 13.
Shear distribution in cases 2, 3, 4 and 5.
Table 13.
Shear distribution in cases 2, 3, 4 and 5.
| Case | Seismic Wave | Shear Distribution |
|---|
| 2 (C2) | HOLLYWOOD | 1:1.76 |
| ELCENTRO | 1:2.19 |
| NRIGDE | 1:2.01 |
| Artificial wave | 1:2.17 |
| 3 (C3) | HOLLYWOOD | 1:1.81 |
| ELCENTRO | 1:2.03 |
| NRIGDE | 1:2.05 |
| Artificial wave | 1:2.19 |
| 4 (W1) | HOLLYWOOD | 1:1.37 |
| ELCENTRO | 1:1.61 |
| NRIGDE | 1:1.47 |
| Artificial wave | 1:1.59 |
| 5 (W2) | HOLLYWOOD | 1:1.23 |
| ELCENTRO | 1:1.58 |
| NRIGDE | 1:1.44 |
| Artificial wave | 1:1.56 |
Table 14.
Force condition of beams in cases 2, 3, 4 and 5.
Table 14.
Force condition of beams in cases 2, 3, 4 and 5.
| Case | Beam Number | Seismic Wave | Average Bending Moment/kN·m | Portion (%) | DCR |
|---|
| 2 (C2) | B1 | HOLLYWOOD | 748.75 | 48.74 | 1.54 |
| ELCENTRO | 885.00 | 51.12 | 1.82 |
| NRIGDE | 1576.25 | 49.03 | 3.24 |
| Artificial wave | 1445.00 | 48.31 | 2.97 |
| B4 | HOLLYWOOD | 787.50 | 51.26 | 1.62 |
| ELCENTRO | 846.25 | 48.88 | 1.74 |
| NRIGDE | 1638.75 | 50.97 | 3.37 |
| Artificial wave | 1546.25 | 51.69 | 3.18 |
| 3 (C3) | B1 | HOLLYWOOD | 365.00 | 25.44 | 0.75 |
| ELCENTRO | 447.50 | 22.13 | 0.92 |
| NRIGDE | 730.00 | 23.86 | 1.5 |
| Artificial wave | 627.50 | 22.70 | 1.29 |
| B2 | HOLLYWOOD | 622.50 | 43.38 | 1.28 |
| ELCENTRO | 870.00 | 43.02 | 1.79 |
| NRIGDE | 1245.00 | 40.69 | 2.56 |
| Artificial wave | 1090.00 | 39.44 | 2.24 |
| B5 | HOLLYWOOD | 447.50 | 31.18 | 0.92 |
| ELCENTRO | 705.00 | 34.86 | 1.45 |
| NRIGDE | 1085.00 | 35.46 | 2.23 |
| Artificial wave | 1046.25 | 37.86 | 2.15 |
| 4 (W1) | B5 | HOLLYWOOD | 602.50 | 48.20 | 1.24 |
| ELCENTRO | 782.50 | 40.94 | 1.61 |
| NRIGDE | 1426.25 | 47.90 | 2.93 |
| Artificial wave | 1196.25 | 46.68 | 2.46 |
| B8 | HOLLYWOOD | 647.50 | 51.80 | 1.33 |
| ELCENTRO | 1128.75 | 59.06 | 2.32 |
| NRIGDE | 1551.25 | 52.10 | 3.19 |
| Artificial wave | 1366.25 | 53.32 | 2.81 |
| 5 (W2) | B5 | HOLLYWOOD | 715.00 | 47.59 | 1.47 |
| ELCENTRO | 1026.25 | 44.52 | 2.11 |
| NRIGDE | 1502.50 | 46.33 | 3.09 |
| Artificial wave | 1430.00 | 50.87 | 2.94 |
| B8 | HOLLYWOOD | 787.50 | 52.41 | 1.62 |
| ELCENTRO | 1278.75 | 55.48 | 2.63 |
| NRIGDE | 1740.00 | 53.67 | 3.58 |
| Artificial wave | 1381.25 | 49.13 | 2.84 |