Ethylene- and Propylene-Glycol Based Nanofluids: A Litterature Review on Their Thermophysical Properties and Thermal Performances
Abstract
1. Introduction
2. Thermophysical Properties
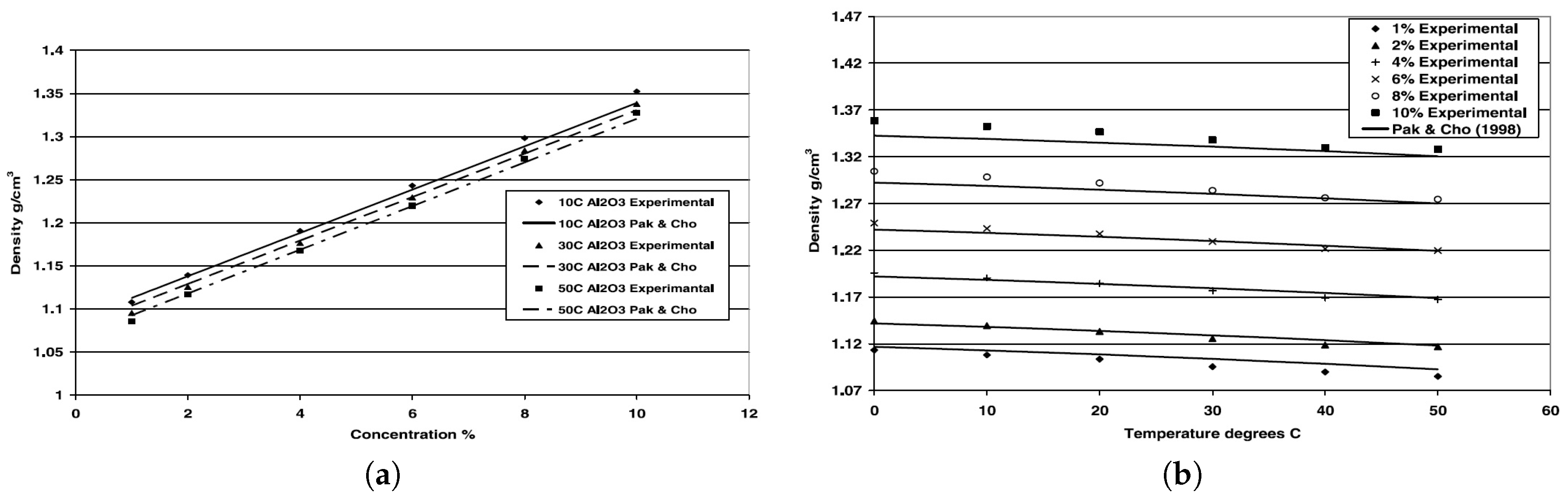
2.1. Density
2.2. Specific Heat
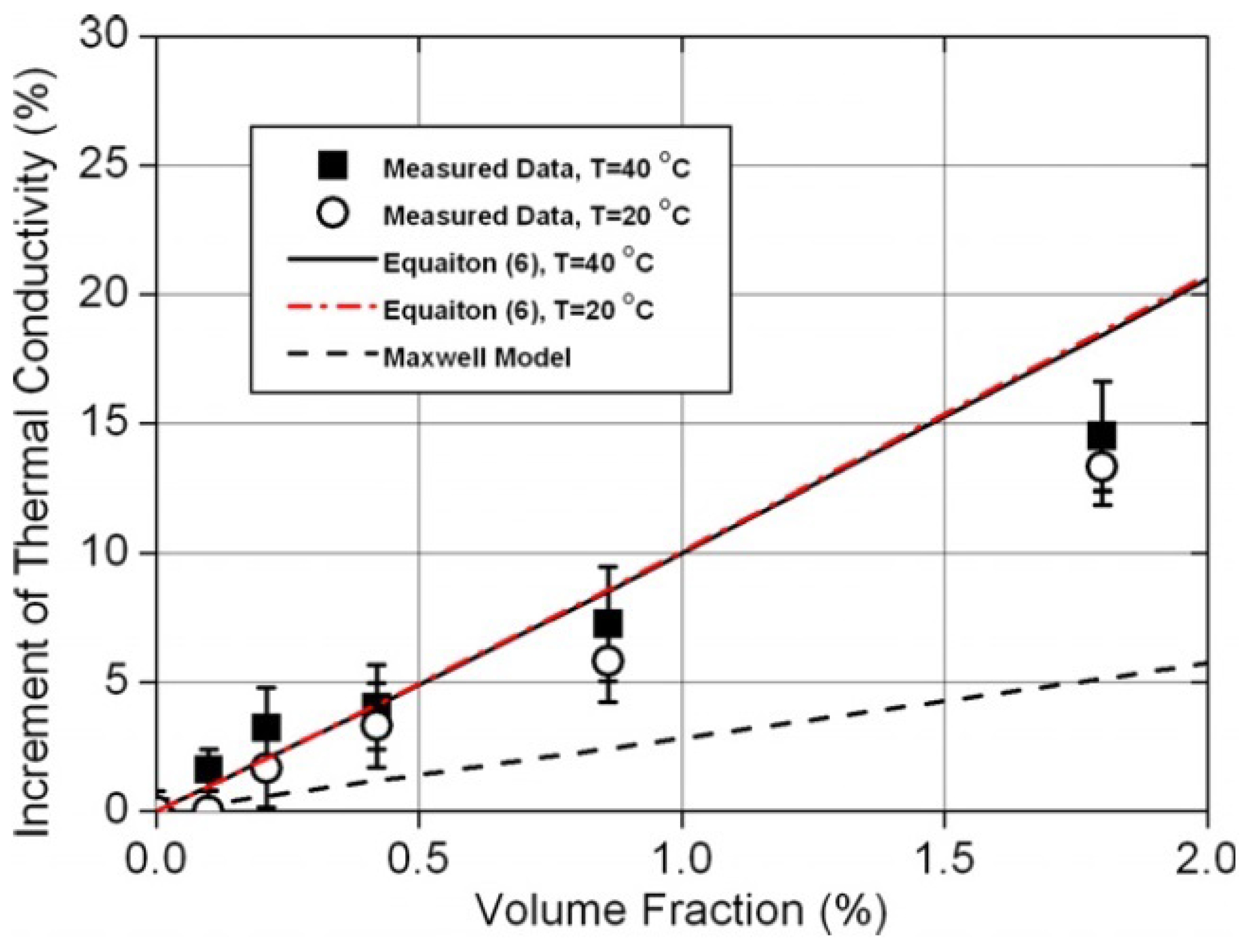
2.3. Thermal Conductivity
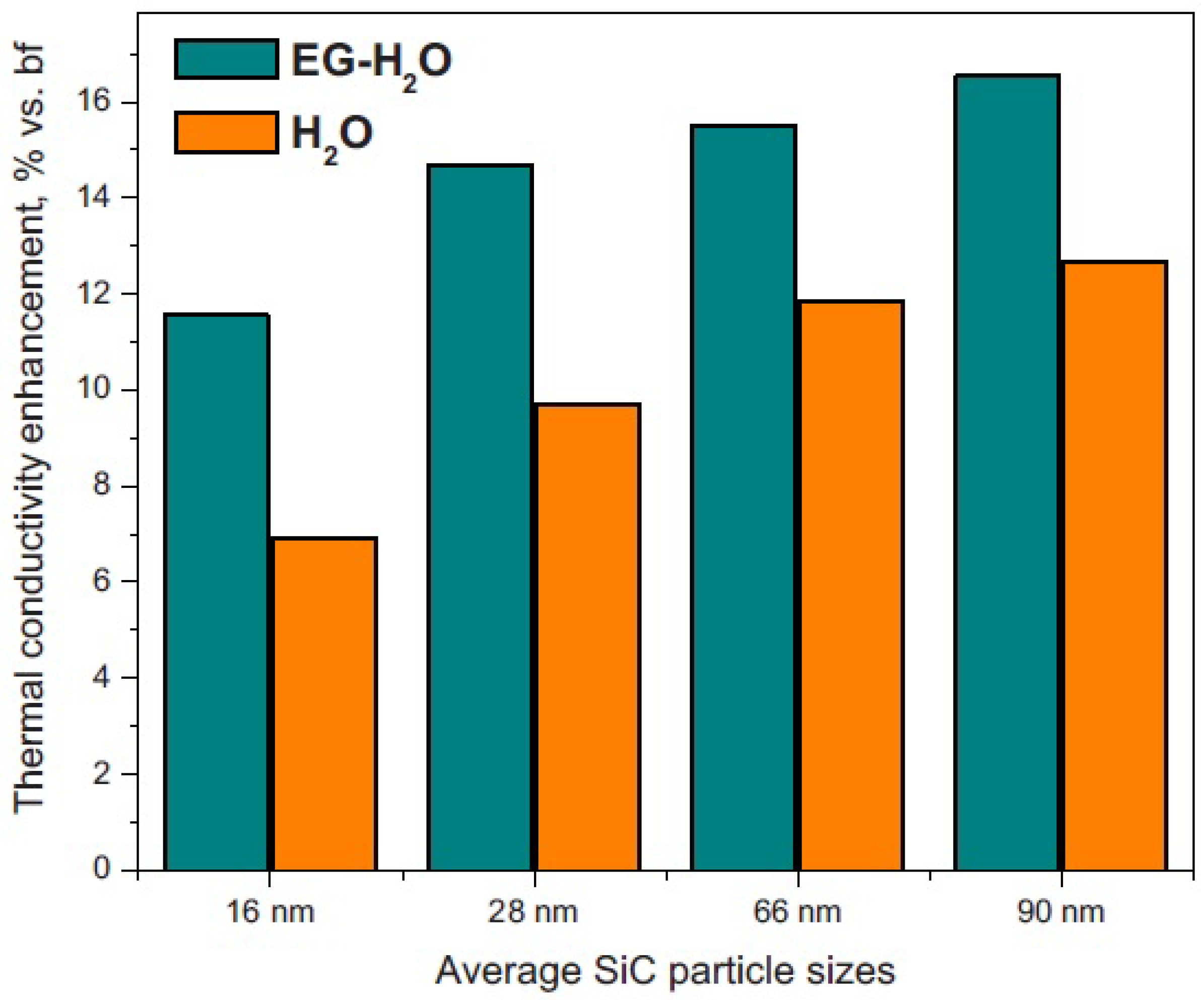
2.3.1. Ethylene-Glycol-Based Nanofluids
2.3.2. Propylene-Glycol-Based Nanofluids
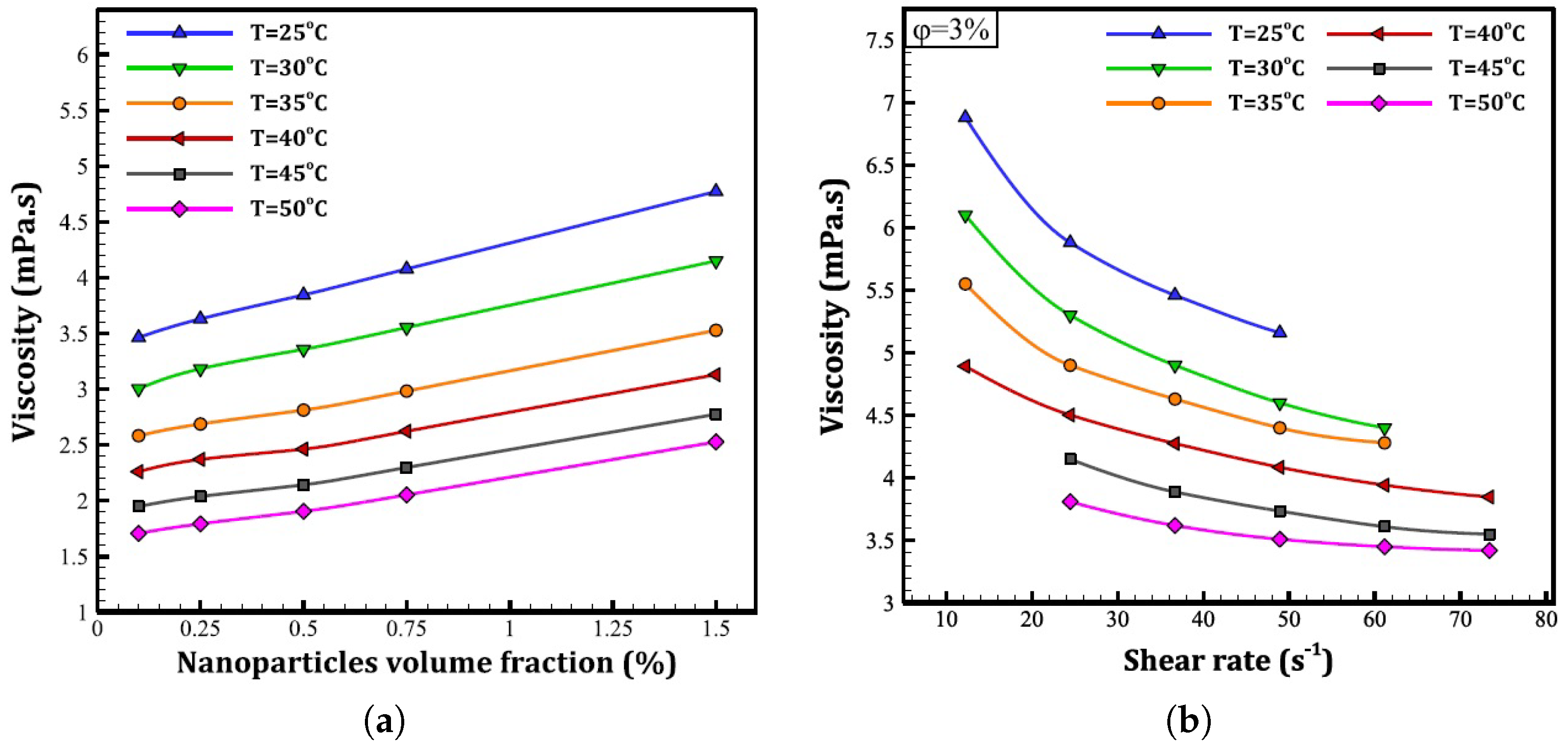
2.4. Rheological Behaviour of Nanofluids
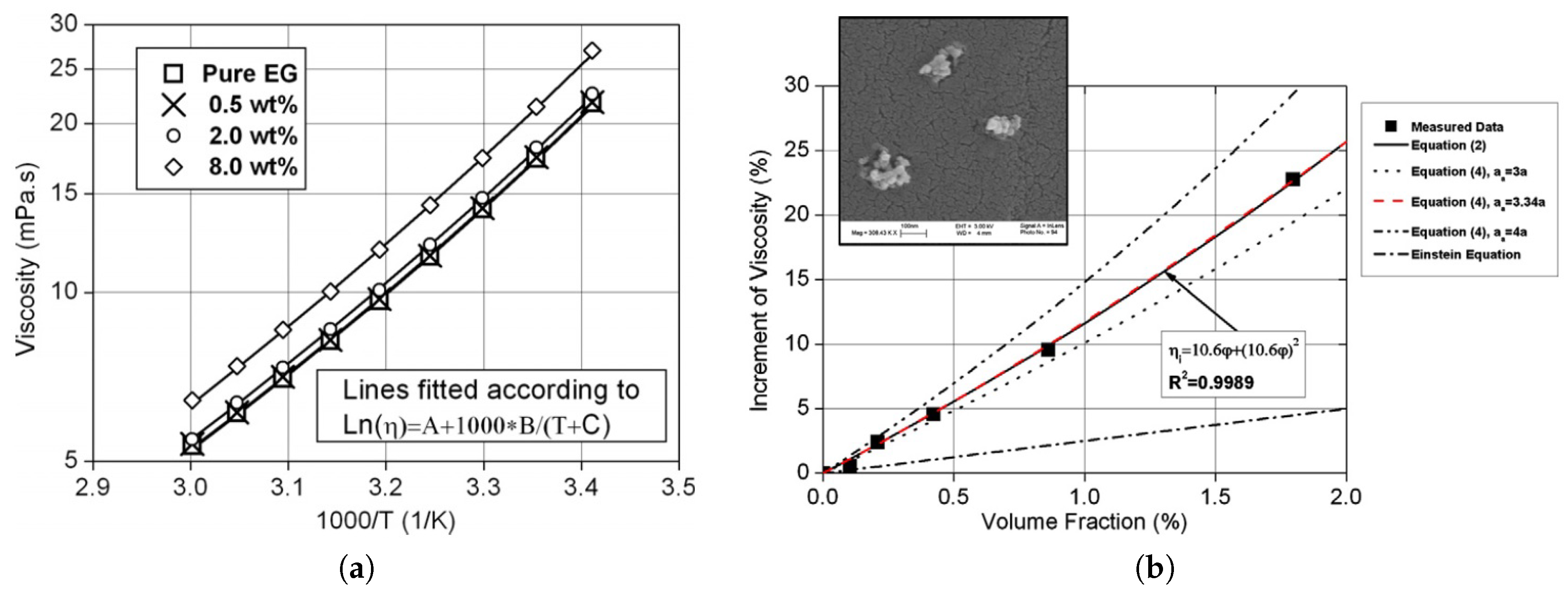
2.4.1. Ethylene-Glycol-Based Nanofluids
2.4.2. Propylene-Glycol-Based Nanofluids
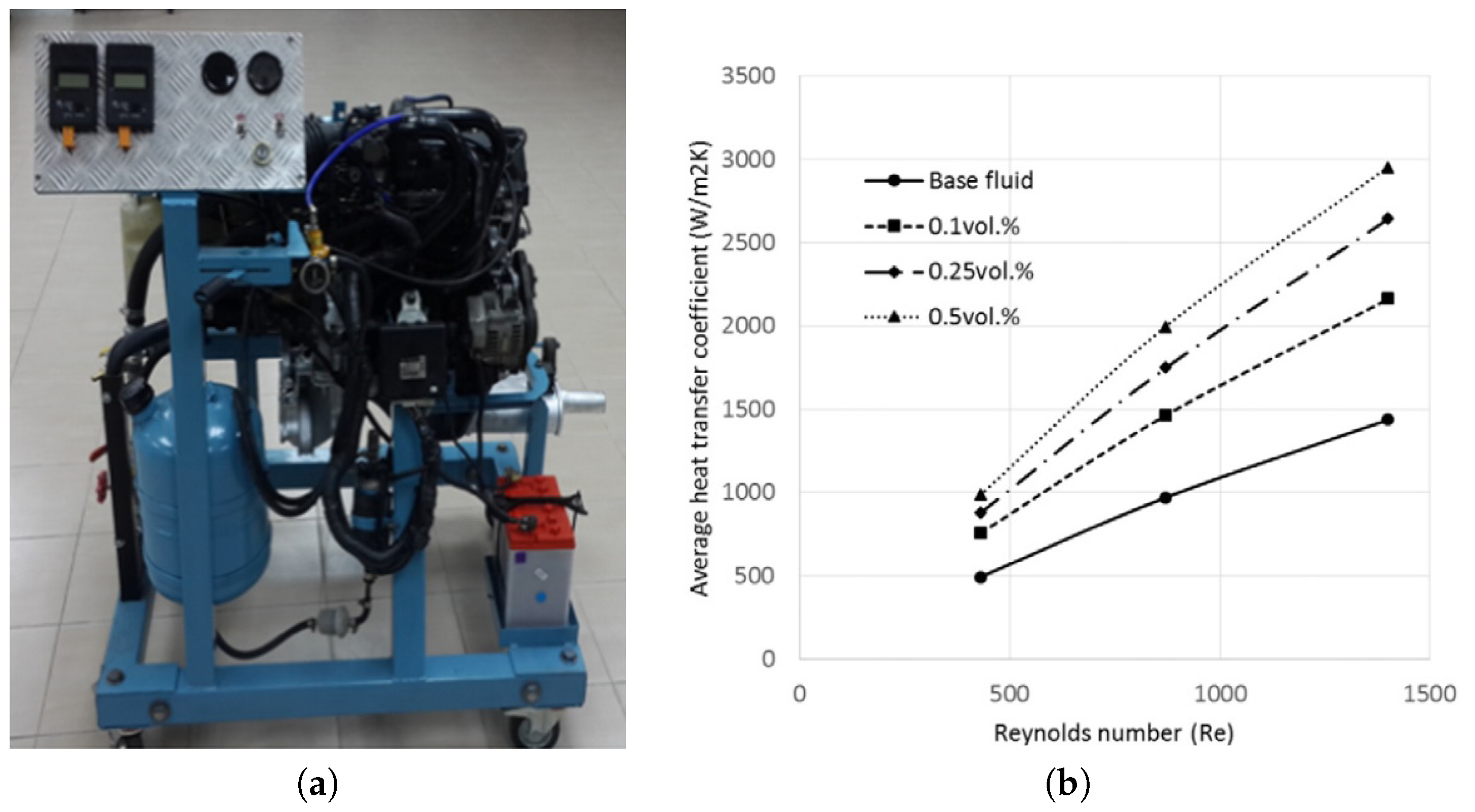
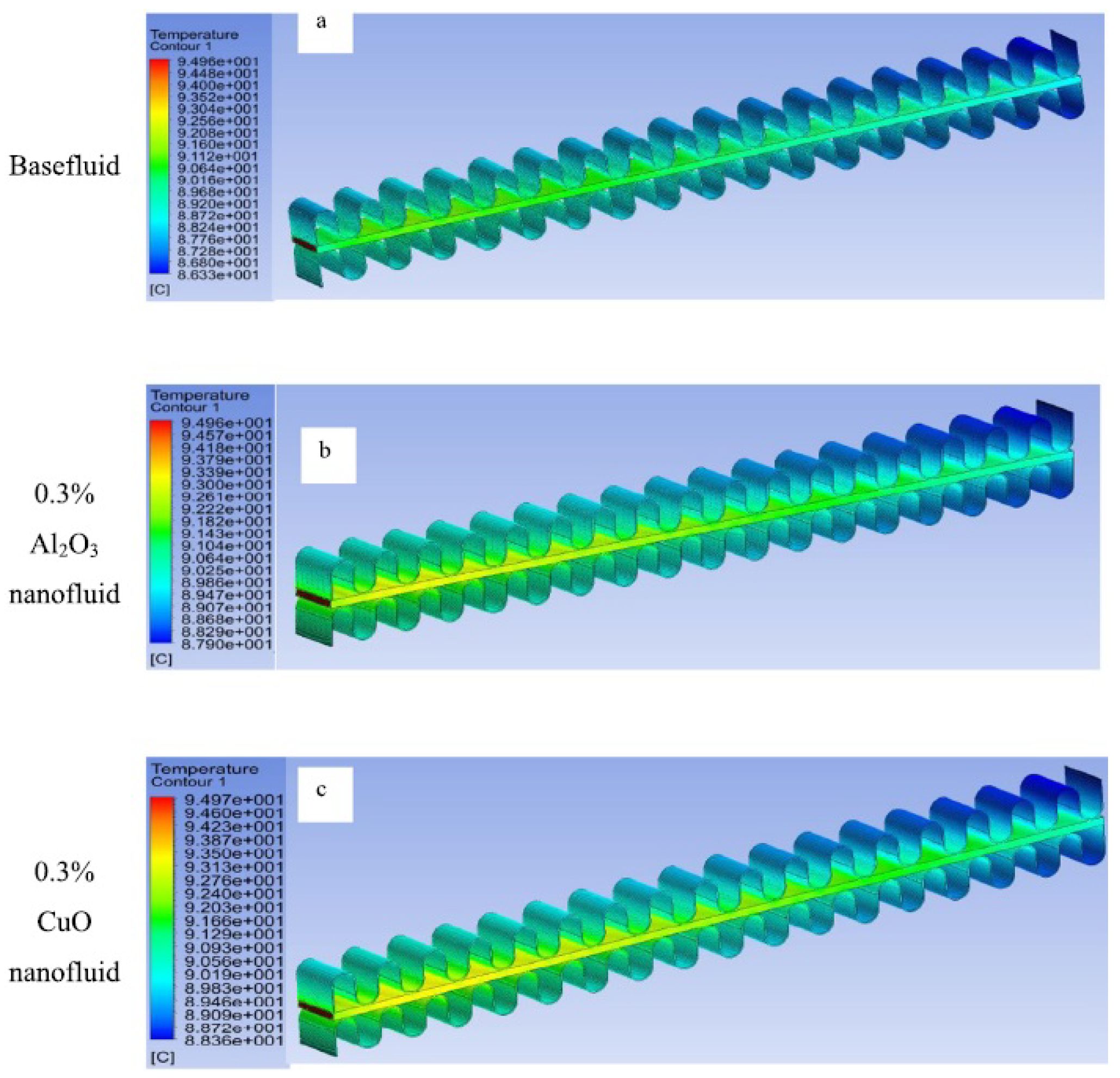
3. Heat Transfer Enhancement
3.1. Experimental Results
3.2. Numerical Simulations
4. Research Perspectives
- the ratio introduced by Prasher et al. [79], which gathers the thermal conductivity and dynamic viscosity of the nanofluid.
- the Mouromtseff number , which gathers the four main thermophysical properties and where the exponents a, b, c, and d take on values appropriate for the heat transfer mode of interest and the corresponding heat transfer correlation, as proposed by Simons [80].
- the performance evaluation criterion introduced by Ferrouillat et al. [81], which is based on the ratio of heat transferred to the requiring pumping. , , , and are the mass flow rate, temperature difference, volumetric flow rate, and pressure drop, respectively.
- the overall efficiency , where represents the Nusselt number.
- the efficiency of nanofluids based on the first and the second laws of thermodynamics can be tackled by considering the performance parameter proposed by Siavashi and Jamali [82]: , where is the dimensionless entropy generation.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| specific heat, J·K·kg | |
| coefficients related to the dynamic viscosity and thermal conductivity, respectively, − | |
| average nanoparticle diameter, nm | |
| h | heat transfer coefficient, W·m·K |
| k | thermal conductivity, W·m·K |
| , | mass and volumetric flow rates, kg·s and m·s |
| Mouromtseff number, − | |
| dimensionless entropy generation, − | |
| Nusselt number, − | |
| performance parameter, − | |
| Reynolds number, − | |
| T | temperature, K |
| , | pressure drop (Pa) and temperature difference (K) |
| overall efficiency, − | |
| volume fraction, − | |
| dynamic viscosity, Pa·s | |
| density, kg·m | |
| base fluid | |
| nanofluid | |
| nanoparticles | |
| ANN | artificial neural network |
| EG | ethylene-glycol |
| MWCNT, SWCNT | multi-, single-wall carbon nanotube |
| PEC | performance evaluation criterion, − |
| PG | propylene-glycol |
| vol. | refers to proportions in terms of volume |
| W | water |
| wt. | refers to proportions in terms of mass |
References
- Handbook, A.F. American Society of Heating, Refrigerating and Air-Conditioning Engineers; ASHRAE Inc.: Atlanta, GA, USA, 2009. [Google Scholar]
- Engineeringtoolbox. Ethylene Glycol Heat-Transfer Fluid. 2018. Available online: https://www.engineeringtoolbox.com/ethylene-glycol-d_146.html (accessed on 15 November 2018).
- Kulkarni, D.P.; Das, D.K.; Patil, S.L. Effect of temperature on rheological properties of copper oxide nanoparticles dispersed in propylene-glycol and water mixture. J. Nanosci. Nanotechnol. 2007, 7, 2318–2322. [Google Scholar] [CrossRef] [PubMed]
- Naik, M.; Janardhana, G.R.; Reddy, K.V.K.; Reddy, B.S. Experimental investigation into rheological property of copper oxide nanoparticles suspended in propylene-glycol–water based fluids. ARPN J. Eng. Appl. Sci. 2010, 5, 29–34. [Google Scholar]
- Palabiyik, I.; Musina, Z.; Witharana, S.; Ding, Y. Dispersion stability and thermal conductivity of propylene glycol-based nanofluids. J. Nanopart. Res. 2011, 13, 5049–5055. [Google Scholar] [CrossRef]
- Satti, J.R.; Das, D.K.; Ray, D. Investigation of the thermal conductivity of propylene-glycol nanofluids and comparison with correlations. Int. J. Heat Mass Transf. 2017, 107, 871–881. [Google Scholar] [CrossRef]
- Vallejo, J.P.; Gómez-Barreiro, S.; Cabaleiro, D.; Gracia-Fernández, C.; Fernández-Seara, J.; Lugo, L. Flow behaviour of suspensions of functionalized graphene nanoplatelets in propylene-glycol–water mixtures. Int. Commun. Heat Mass Transf. 2018, 91, 150–157. [Google Scholar] [CrossRef]
- Rashidi, S.; Eskandarian, M.; Mahian, O.; Poncet, S. Combination of nanofluid and inserts for heat transfer enhancement-Gaps and challenges. J. Ther. Anal. Calorim. 2018, 1–24. [Google Scholar] [CrossRef]
- Vajjha, R.S.; Das, D.K.; Namburu, P.K. Numerical study of fluid dynamic and heat transfer performance of Al2O3 and CuO nanofluids in the flat tubes of a radiator. Int. J. Heat Fluid Flow 2010, 31, 613–621. [Google Scholar] [CrossRef]
- Leong, K.; Saidur, R.; Kazi, S.; Mamun, A. Performance investigation of an automotive car radiator operated with nanofluid-based coolants (nanofluid as a coolant in a radiator). Appl. Ther. Eng. 2010, 30, 2685–2692. [Google Scholar] [CrossRef]
- Peyghambarzadeh, S.; Hashemabadi, S.; Hoseini, S.; Jamnani, M.S. Experimental study of heat transfer enhancement using water/ethylene glycol-based nanofluids as a new coolant for car radiators. Int. Commun. Heat Mass Transf. 2011, 38, 1283–1290. [Google Scholar] [CrossRef]
- Peyghambarzadeh, S.M.; Hashemabadi, S.H.; Jamnani, M.S.; Hoseini, S.M. Improving the cooling performance of automobile radiator with Al2O3/water nanofluid. Appl. Ther. Eng. 2011, 31, 1833–1838. [Google Scholar] [CrossRef]
- Teng, T.P.; Yu, C.C. Heat dissipation performance of MWCNTs nano-coolant for vehicle. Exp. Ther. Fluid Sci. 2013, 49, 22–30. [Google Scholar] [CrossRef]
- Chavan, D.; Pise, A.T. Performance investigation of an automotive car radiator operated with nanofluid as a coolant. J. Ther. Sci. Eng. Appl. 2014, 6. [Google Scholar] [CrossRef]
- Heris, S.Z.; Shokrgozar, M.; Poorpharhang, S.; Shanbedi, M.; Noie, S. Experimental study of heat transfer of a car radiator with CuO/ethylene-glycol-water as a coolant. J. Dispers. Sci. Technol. 2014, 35, 677–684. [Google Scholar] [CrossRef]
- Ali, M.; El-Leathy, A.; Al-Sofyany, Z. The effect of nanofluid concentration on the cooling system of vehicles radiator. Adv. Mech. Eng. 2014, 6, 962510. [Google Scholar] [CrossRef]
- M’hamed, B.; Sidik, N.A.C.; Akhbar, M.F.A.; Mamat, R.; Najafi, G. Experimental study on thermal performance of MWCNT nano-coolant in Perodua Kelisa 1000cc radiator system. Int. Commun. Heat Mass Transf. 2016, 76, 156–161. [Google Scholar] [CrossRef]
- Devireddy, S.; Mekala, C.S.R.; Veeredhi, V.R. Improving the cooling performance of automobile radiator with ethylene-glycol water based TiO2 nanofluids. Int. Commun. Heat Mass Transf. 2016, 78, 121–126. [Google Scholar] [CrossRef]
- Salamon, V.; Senthil Kumar, D.; Thirumalin, S. Experimental investigation of heat transfer characteristics of automobile radiator using TiO2-nanofluid coolant. Mater. Sci. Eng. 2017, 225, 012101. [Google Scholar] [CrossRef]
- Subhedar, D.G.; Ramani, B.M.; Gupta, A. Experimental investigation of heat transfer potential of Al2O3/Water-Mono Ethylene Glycol nanofluids as a car radiator coolant. Case Stud. Ther. Eng. 2018, 11, 26–34. [Google Scholar] [CrossRef]
- Tijani, A.S.; bin Sudirman, A.S. Thermos-physical properties and heat transfer characteristics of water/anti-freezing and Al2O3/CuO based nanofluid as a coolant for car radiator. Int. J. Heat Mass Transf. 2018, 118, 48–57. [Google Scholar] [CrossRef]
- Kulkarni, D.P.; Vajjha, R.S.; Das, D.K.; Oliva, D. Application of aluminium oxide nanofluids in diesel electric generator as jacket water coolant. Appl. Ther. Eng. 2008, 28, 1774–1781. [Google Scholar] [CrossRef]
- Zamzamian, A.; Oskouie, S.N.; Doosthoseini, A.; Joneidi, A.; Pazouki, M. Experimental investigation of forced convective heat transfer coefficient in nanofluids of Al2O3/EG and CuO/EG in a double pipe and plate heat exchangers under turbulent flow. Exp. Ther. Fluid Sci. 2011, 35, 495–502. [Google Scholar] [CrossRef]
- Selvakumar, P.; Suresh, S. Thermal performance of ethylene-glycol-based nanofluids in an electronic heat sink. J. Nanosci. Nanotechnol. 2014, 14, 2325–2333. [Google Scholar] [CrossRef] [PubMed]
- Kleinstreuer, C.; Xu, Z. Mathematical Modeling and Computer Simulations of Nanofluid Flow with Applications to Cooling and Lubrication. Fluids 2016, 1, 16. [Google Scholar] [CrossRef]
- Yu, W.; Xie, H. A review on nanofluids: Preparation, stability mechanisms, and applications. J. Nanomater. 2012, 2012, 1. [Google Scholar] [CrossRef]
- Ali, H.M.; Babar, H.; Shah, T.R.; Sajid, M.U.; Qasim, M.A.; Javed, S. Preparation Techniques of TiO2 Nanofluids and Challenges: A Review. Appl. Sci. 2018, 8, 587. [Google Scholar] [CrossRef]
- Patil, M.S.; Seo, J.H.; Kang, S.J.; Lee, M.Y. Review on Synthesis, Thermo-Physical Property, and Heat Transfer Mechanism of Nanofluids. Energies 2016, 9, 840. [Google Scholar] [CrossRef]
- Huminic, G.; Huminic, A. Application of nanofluids in heat exchangers: a review. Renew. Sustain. Energy Rev. 2012, 16, 5625–5638. [Google Scholar] [CrossRef]
- Wang, X.Q.; Mujumdar, A.S. A review on nanofluids-part I: theoretical and numerical investigations. Braz. J. Chem. Eng. 2008, 25, 613–630. [Google Scholar] [CrossRef]
- Patil, M.S.; Kim, S.C.; Seo, J.H.; Lee, M.Y. Review of the Thermo-Physical Properties and Performance Characteristics of a Refrigeration System Using Refrigerant-Based Nanofluids. Energies 2016, 9, 22. [Google Scholar] [CrossRef]
- Bianco, V.; Manca, O.; Nardini, S.; Vafai, K. Heat Transfer Enhancement with Nanofluids; CRC Press, Taylor & Francis: London, UK, 2015. [Google Scholar]
- Kakac, S.; Pramuanjaroenkij, A. Review of convective heat transfer enhancement with nanofluids. Int. J. Heat Mass Transf. 2009, 52, 3187–3196. [Google Scholar] [CrossRef]
- Pinto, R.V.; Fiorelli, F.A.S. Review of the mechanisms responsible for heat transfer enhancement using nanofluids. Appl. Ther. Eng. 2016, 108, 720–739. [Google Scholar] [CrossRef]
- Riazi, H.; Murphy, T.; Webber, G.B.; Atkin, R.; Mostafavi Tehrani, S.S.; Taylor, R.A. Specific heat control of nanofluids: A critical review. Int. J. Ther. Sci. 2016, 107, 25–38. [Google Scholar] [CrossRef]
- Vajjha, R.; Das, D.; Mahagaonkar, B. Density measurement of different nanofluids and their comparison with theory. Pet. Sci. Technol. 2009, 27, 612–624. [Google Scholar] [CrossRef]
- Pak, B.C.; Cho, Y.I. Hydrodynamic and heat transfer study of dispersed fluids with submicron metallic oxide particles. Exp. Heat Transf. Int. J. 1998, 11, 151–170. [Google Scholar] [CrossRef]
- Satti, J.R.; Das, D.K.; Ray, D.R. Measurements of Densities of Propylene Glycol-Based Nanofluids and Comparison With Theory. J. Ther. Sci. Eng. Appl. 2016, 8, 021021. [Google Scholar] [CrossRef]
- Xuan, Y.; Roetzel, W. Conceptions for heat transfer correlation of nanofluids. Int. J. Heat Mass Transf. 2000, 43, 3701–3707. [Google Scholar] [CrossRef]
- Lee, J.; Mudawar, I. Assessment of the effectiveness of nanofluids for single-phase and two-phase heat transfer in micro-channels. Int. J. Heat Mass Transf. 2007, 50, 452–463. [Google Scholar] [CrossRef]
- Moraveji, M.K.; Ardehali, R.M. CFD modeling (comparing single and two-phase approaches) on thermal performance of Al2O3/water nanofluid in mini-channel heat sink. Int. Commun. Heat Mass Transf. 2013, 44, 157–164. [Google Scholar] [CrossRef]
- Behzadmehr, A.; Saffar-Avval, M.; Galanis, N. Prediction of turbulent forced convection of a nanofluid in a tube with uniform heat flux using a two phase approach. Int. J. Heat Fluid Flow 2007, 28, 211–219. [Google Scholar] [CrossRef]
- Sekrani, G.; Poncet, S. Further Investigation on Laminar Forced Convection of Nanofluid Flows in a Uniformly Heated Pipe Using Direct Numerical Simulations. Appl. Sci. 2016, 6, 332. [Google Scholar] [CrossRef]
- Sekrani, G.; Poncet, S.; Proulx, P. Modeling of convective turbulent heat transfer of water-based Al2O3 nanofluids in an uniformly heated pipe. Chem. Eng. Sci. 2018, 176, 205–219. [Google Scholar] [CrossRef]
- Vajjha, R.S.; Das, D.K. Experimental determination of thermal conductivity of three nanofluids and development of new correlations. Int. J. Heat Mass Transf. 2009, 52, 4675–4682. [Google Scholar] [CrossRef]
- Pal, R. A Novel Method to Determine the Thermal Conductivity of Interfacial Layers Surrounding the Nanoparticles of a Nanofluid. Nanomaterials 2014, 4, 844–855. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.; Choi, S.U.S.; Li, S.; Eastman, J.A. Measuring thermal conductivity of fluids containing oxide nanoparticles. J. Heat Transf. 1999, 121, 280–289. [Google Scholar] [CrossRef]
- Wang, X.; Xu, X.; Choi, S.U.S. Thermal conductivity of nanoparticle-fluid mixture. J. Thermophys. Heat Transf. 1999, 13, 474–480. [Google Scholar] [CrossRef]
- Reddy, M.C.S.; Rao, V.V. Experimental studies on thermal conductivity of blends of ethylene glycol-water-based TiO2 nanofluids. Int. Commun. Heat Mass Transf. 2013, 46, 31–36. [Google Scholar] [CrossRef]
- Sundar, L.S.; Farooky, M.H.; Sarada, S.N.; Singh, M. Experimental thermal conductivity of ethylene-glycol and water mixture based low volume concentration of Al2O3 and CuO nanofluids. Int. Commun. Heat Mass Transf. 2013, 41, 41–46. [Google Scholar] [CrossRef]
- Usri, N.; Azmi, W.; Mamat, R.; Abdul Hamid, K.; Najafi, G. Thermal Conductivity Enhancement of Al2O3 Nanofluid in Ethylene Glycol and Water Mixture. Energy Procedia 2015, 79, 397–402. [Google Scholar] [CrossRef]
- Chen, H.; Ding, Y.; He, Y.; Tan, C. Rheological behaviour of ethylene-glycol-based titania nanofluids. Chem. Phys. Lett. 2007, 444, 333–337. [Google Scholar] [CrossRef]
- Xie, H.; Yu, W.; Li, Y. Thermal performance enhancement in nanofluids containing diamond nanoparticles. J. Phys. D Appl. Phys. 2009, 42, 095413. [Google Scholar] [CrossRef]
- Eastman, J.A.; Choi, S.U.S.; Li, S.; Yu, W.; Thompson, L. Anomalously increased effective thermal conductivities of ethylene glycol-based nanofluids containing copper nanoparticles. Appl. Phys. Lett. 2001, 78, 718–720. [Google Scholar] [CrossRef]
- Hong, T.K.; Yang, H.S.; Choi, C. Study of the enhanced thermal conductivity of Fe nanofluids. J. Appl. Phys. 2005, 97. [Google Scholar] [CrossRef]
- Zhu, H.T.; Zhang, C.Y.; Yin, Y.S. Rapid synthesis of copper nanoparticles by sodium hypophosphite reduction in ethylene-glycol under microwave irradiation. J. Cryst. Growth 2004, 270, 722–728. [Google Scholar] [CrossRef]
- Xie, H.; Yu, W.; Chen, W. MgO nanofluids: Higher thermal conductivity and lower viscosity among ethylene-glycol-based nanofluids containing oxide nanoparticles. J. Exp. Nanosci. 2010, 5, 463–472. [Google Scholar] [CrossRef]
- Xie, H.; Wang, J.; Xi, T.; Liu, Y. Thermal conductivity of suspensions containing nanosized SiC particles. Int. J. Thermophys. 2002, 23, 571–580. [Google Scholar] [CrossRef]
- Timofeeva, E.V.; Yu, W.; France, D.M.; Singh, D.; Routbort, J.L. Base fluid and temperature effects on the heat transfer characteristics of SiC in ethylene-glycol/H2O and H2O nanofluids. J. Appl. Phys. 2011, 109, 014914. [Google Scholar] [CrossRef]
- Xie, H.; Lee, H.; Youn, W.; Choi, M. Nanofluids containing multiwalled carbon nanotubes and their enhanced thermal conductivities. J. Appl. Phys. 2003, 94, 4967–4971. [Google Scholar] [CrossRef]
- Liu, M.S.; Lin, M.C.C.; Huang, I.T.; Wang, C.C. Enhancement of thermal conductivity with carbon nanotube for nanofluids. Int. Commun. Heat Mass Transf. 2005, 32, 1202–1210. [Google Scholar] [CrossRef]
- Harish, S.; Ishikawa, K.; Einarsson, E.; Aikawa, S.; Chiashi, S.; Shiomi, J.; Maruyama, S. Enhanced thermal conductivity of ethylene-glycol with single-walled carbon nanotube inclusions. Int. J. Heat Mass Transf. 2012, 55, 3885–3890. [Google Scholar] [CrossRef]
- Puliti, G.; Paolucci, S.; Sen, M. Nanofluids and Their Properties. Appl. Mech. Rev. 2012, 64, 030803. [Google Scholar] [CrossRef]
- Prasher, R.; Bhattacharya, P.; Phelan, P.E. Brownian-Motion-Based Convective-Conductive Model for the Effective Thermal Conductivity of Nanofluids. J. Heat Transf. 2006, 128, 588–595. [Google Scholar] [CrossRef]
- Prasher, R.; Evans, W.; Meakin, P.; Fish, J.; Phelan, P.; Keblinski, P. Effect of aggregation on thermal conduction in colloidal nanofluids. Appl. Phys. Lett. 2006, 89, 143119. [Google Scholar] [CrossRef]
- Leena, M.; Srinivasan, S. Experimental Investigation of the Thermophysical Properties of TiO2/Propylene Glycol-Water Nanofluids for Heat-Transfer Applications. J. Eng. Phys. Thermophys. 2018, 91, 498–506. [Google Scholar] [CrossRef]
- Garg, J.; Poudel, B.; Chiesa, M.; Gordon, J.; Ma, J.; Wang, J.; Ren, Z.; Kang, Y.; Ohtani, H.; Nanda, J.; et al. Enhanced thermal conductivity and viscosity of copper nanoparticles in ethylene-glycol nanofluid. J. Appl. Phys. 2008, 103, 074301. [Google Scholar] [CrossRef]
- Chopkar, M.; Kumar, S.; Bhandari, D.; Das, P.K.; Manna, I. Development and characterization of Al2Cu and Ag2Al nanoparticle dispersed water and ethylene-glycol-based nanofluid. Mater. Sci. Eng. B 2007, 139, 141–148. [Google Scholar] [CrossRef]
- Akbari, M.; Afrand, M.; Arshi, A.; Karimipour, A. An experimental study on rheological behaviour of ethylene-glycol based nanofluid: proposing a new correlation as a function of silica concentration and temperature. J. Mol. Liq. 2017, 233, 352–357. [Google Scholar] [CrossRef]
- Namburu, P.K.; Kulkarni, D.P.; Misra, D.; Das, D.K. Viscosity of copper oxide nanoparticles dispersed in ethylene-glycol and water mixture. Exp. Ther. Fluid Sci. 2007, 32, 397–402. [Google Scholar] [CrossRef]
- Kumar, M.; Sawhney, N.; Sharma, A.K.; Sharma, M. Thermo-physical profile of zinc oxide nanoparticles dispersed in aqueous solution of propylene-glycol. J. Mol. Liq. 2018, 249, 650–658. [Google Scholar] [CrossRef]
- Afrand, M.; Abedini, E.; Teimouri, H. How the dispersion of magnesium oxide nanoparticles effects on the viscosity of water-ethylene-glycol mixture: experimental evaluation and correlation development. Phys. E Low-Dimens. Syst. Nanostruct. 2017, 87, 273–280. [Google Scholar] [CrossRef]
- Namburu, P.K.; Das, D.K.; Tanguturi, K.M.; Vajjha, R.S. Numerical study of turbulent flow and heat transfer characteristics of nanofluids considering variable properties. Int. J. Ther. Sci. 2009, 48, 290–302. [Google Scholar] [CrossRef]
- Bahiraei, M. A Comprehensive Review on Different Numerical Approaches for Simulation in Nanofluids: Traditional and Novel Techniques. J. Dispers. Sci. Technol. 2014, 35, 984–996. [Google Scholar] [CrossRef]
- Strandberg, R.; Das, D.K. Finned tube performance evaluation with nanofluids and conventional heat transfer fluids. Int. J. Ther. Sci. 2010, 49, 580–588. [Google Scholar] [CrossRef]
- Bouguerra, N.; Poncet, S.; Elkoun, S. Dispersion regimes in alumina/water-based nanofluids: simultaneous measurements of thermal conductivity and dynamic viscosity. Int. Commun. Heat Mass Transf. 2018, 92, 51–55. [Google Scholar] [CrossRef]
- Bouguerra, N. Caractérisation des propriétés thermiques et rhéologiques des nanofluides eau-alumine: compréhension des mécanismes physicochimiques et études paramétriques. Ph.D. Thesis, Université de Sherbrooke, Longueuil, QC, Canada, 2018. [Google Scholar]
- Sekrani, G.; Poncet, S.; Proulx, P. Conjugated heat transfer and entropy generation of Al2O3-water nanofluid flows over a heated wall-mounted obstacle. J. Ther. Anal. Calorim. 2018. [Google Scholar] [CrossRef]
- Prasher, R.; Song, D.; Phelan, J.W. Measurements of nanofluid viscosity and its implications for thermal applications. App. Phys. Lett. 2006, 89. [Google Scholar] [CrossRef]
- Simons, R.E. Comparing heat transfer rates of liquid coolants using the Mouromtseff number. Calcul. Corner 2006, 12, 10. [Google Scholar]
- Ferrouillat, S.; Bontemps, A.; Ribeiro, J.; Gruss, J.; Soriano, O. Hydraulic and heat transfer study of SiO2/water nanofluids in horizontal tubes with imposed wall temperature boundary conditions. Int. J. Heat Fluid Flow 2011, 32, 424–439. [Google Scholar] [CrossRef]
- Siavashi, M.; Jamali, M. Heat transfer and entropy generation analysis of turbulent flow of TiO2-water nanofluid inside annuli with different radius ratios using two-phase mixture model. Appl. Ther. Eng. 2016, 100, 1149–1160. [Google Scholar] [CrossRef]
- Esfe, M.H.; Rejvani, M.; Karimpour, R.; Arani, A.A.A. Estimation of thermal conductivity of ethylene-glycol-based nanofluid with hybrid suspensions of SWCNT-Al2O3 nanoparticles by correlation and ANN methods using experimental data. J. Ther. Anal. Calorim. 2017, 128, 1359–1371. [Google Scholar] [CrossRef]
- Esfe, M.H.; Razi, P.; Hajmohammad, M.H.; Rostamian, S.H.; Sarsam, W.S.; Arani, A.A.A.; Dahari, M. Optimization, modeling and accurate prediction of thermal conductivity and dynamic viscosity of stabilized ethylene-glycol and water mixture Al2O3 nanofluids by NSGA-II using ANN. Int. Commun. Heat Mass Transf. 2017, 82, 154–160. [Google Scholar] [CrossRef]
| Ethylene Glycol Solution (% by Volume) | 0 | 10 | 20 | 30 | 40 | 50 | 60 |
| Temperature (C) | 0 | −3.4 | −7.9 | −13.7 | −23.5 | −36.8 | −52.8 |
| Propylene-glycol solution (% by volume) | 0 | 10 | 20 | 30 | 40 | 50 | 60 |
| Temperature (C) | 0 | −3 | −8 | −14 | −22 | −34 | −48 |
| Ethylene Glycol Solution (% by Volume) | 0 | 10 | 20 | 30 | 40 | 50 | 60 |
| Temperature (C) | 100 | 101.1 | 102.2 | 104.4 | 104.4 | 107.2 | 111.1 |
| Propylene-glycol solution (% by volume) | 0 | 10 | 20 | 30 | 40 | 50 | 60 |
| Temperature (C) | 100 | 100 | 100.5 | 102.2 | 103.8 | 105.5 | 107.2 |
| Properties | (kg·m) | (J·kg·K) | k (W·m·K) | (Pa·s) |
|---|---|---|---|---|
| Ethylene-glycol | 1126 | 2354 | ||
| Propylene-glycol | 2479 | |||
| Water | 999 | 4185 |
| Authors | Nanofluid | Nanoparticle Concentration | Particle Size (nm) | Increase in k (%) | Temperature Range (C) |
|---|---|---|---|---|---|
| Eastman et al. [54] | Cu/EG | 0.3 vol.% | 10 | 40 | 17–37 |
| Lee et al. [47] | CuO/EG | 1–4 vol.% | 24 | 4–20 | 17–37 |
| /EG | 1–4 vol.% | 38 | 2–14 | 17–37 | |
| Wang and Choi [48] | /EG | 6–10 vol.% | 28 | 26–40 | 20 |
| CuO/EG | 5–15 vol.% | 23 | 20–55 | 20 | |
| Hong and Yang [55] | Fe/EG | 10 vol.% | 0.55 | 18 | 20 |
| Xie et al. [60] | CNTs/EG | 1 vol.% | 15 × 3 | 12.6 | 20 |
| Xie et al. [58] | SiC/EG | 4.2 vol.% | 26 | 15.8 | 4 |
| (spherical shape) | |||||
| SiC/EG | 4 vol.% | 600 | 22.9 | 4 | |
| (cylindrical shape) | |||||
| Chen et al. [52] | /EG | ≤1.8 vol.% | 25 | ≤14.5 | 20, 40 |
| Garg et al. [67] | Cu/EG | 0.04–2 vol.% | 200 | 2–12.6 | 25 |
| Xie et al. [57] | MgO/EG | 5 vol.% | 20 | 40.6 | 10–60 |
| /EG | 5 vol.% | 20 | 28.2 | 10–60 | |
| /EG | 5 vol.% | 20 | 27.2 | 10–60 | |
| ZnO/EG | 5 vol.% | 20 | 26.8 | 10–60 | |
| /EG | 5 vol.% | 20 | 25.3 | 10–60 | |
| Chopkar et al. [68] | /EG | 0.2–2.5 vol.% | 15 | 6–220 | 20 |
| /EG | 0.2–2.5 vol.% | 18 | 8–250 | 20 | |
| Palabiyik et al. [5] | /PG | 1–9 wt.% | 70–100 | 3.6–11 | 20–80 |
| /PG | 1–9 wt.% | 100–140 | 1.4–9 | 20–80 | |
| Harish et al. [62] | SWCNT/EG | 0.2 vol.% | 1.6 × 150 | 14.8 | 27–57 |
| Xie et al. [53] | Diamond/EG-W(45:55) | 0.5–2 vol.% | 10 | 6–18 | 10–60 |
| Timofeeva et al. [59] | SiC/EG-W(50:50) | 4 vol.% | 16, 29, 66 and 90 | 11.5–17 | 15-85 |
| Vajjha and Das [45] | /EG-W(60:40) | 1–10 vol.% | 53 | 8–69 | 25–90 |
| CuO/EG-W(60:40) | 1–6 vol.% | 29 | 14–60 | 25–90 | |
| ZnO/EG-W(60:40) | 1–7 vol.% | 29 and 77 | 9.8–48.5 | 25–90 | |
| Sundar et al. [50] | /EG-W(50:50) | 0.2–0.8 vol.% | 36.5 | 9.8–17.89 | 15–50 |
| CuO/EG-W(50:50) | 0.2–0.8 vol.% | 27 | 15.6–24.56 | 15–50 | |
| Reddy and Rao [49] | /EG-W(40:60) | 0.2–1 vol.% | 21 | 1.94–4.3 | 30–70 |
| /EG-W(50:50) | 0.2–1 vol.% | 21 | 10.64–14.2 | 30–70 | |
| Satti et al. [6] | /PG-W(60:40) | 0.5–6 vol.% | 15–45 | 2–12.2 | −30–90 |
| ZnO/PG-W(60:40) | 0.5–6 vol.% | 36–76 | 1.6–21.36 | −30–90 | |
| CuO/PG-W(60:40) | 0.5–6 vol.% | 30 | 2.3–15.6 | −30–90 | |
| /PG-W(60:40) | 6 vol.% | 30 | 4.7–7.2 | −30–90 | |
| /PG-W(60:40) | 0.5–1.5 vol.% | 15 | 1–7.3 | −30–90 |
| Authors | Nanofluid | Nanoparticle Concentration | Particle Size (nm) | Increase in (%) | Temperature Range (C) |
|---|---|---|---|---|---|
| Chen et al. [52] | /EG | 0.5–8 wt.% | 70–100 | 0.55–22.75 | 20–60 |
| Wang and Choi [48] | /EG | 1.2–3.5 vol.% | 28 | 8–40 | 20 |
| Garg et al. [67] | Cu/EG | 0.04–2 vol.% | 200 | 4.7–23.8 | 25 |
| Xie et al. [57] | MgO/EG | 5 vol.% | 20 | 17.4 | 10–60 |
| /EG | 5 vol.% | 20 | 28.2 | 10–60 | |
| /EG | 5 vol.% | 20 | 31.2 | 10–60 | |
| ZnO/EG | 5 vol.% | 20 | 129.2 | 10–60 | |
| /EG | 5 vol.% | 20 | 31.5 | 10–60 | |
| Akbari et al. [69] | /EG | 0.1–3 vol.% | 25 | 8–116 | 30–50 |
| Namburu et al. [70] | CuO/EG-W(60:40) | 1–6.12 vol.% | 29 | 12.25-45.6 | −35–50 |
| Timofeeva et al. [59] | SiC/EG-W(50:50) | 4 vol.% | 16–90 | 48–14 | 15–85 |
| Kulkarni et al. [3] | CuO/PG-W(60:40) | 1–5.9 vol.% | 29 | 100 | −35–50 |
| Naik et al. [4] | CuO/PG-W(60:40) | 0.025–1.2 vol.% | 50 | 0.2–5 | −15–60 |
| Kumar et al. [71] | ZnO/PG-W(10:90) | 0.02–0.1 wt.% | 30 | 1.69–3.48 | 30–40 |
| Afrand et al. [72] | MgO/EG-W(50:50) | 0.1–1.5 vol.% | 40 | 2.15–52.72 | 25–50 |
| Vallejo et al. [7] | f-GnPs/PG-W(10:90) | 0.25–0.5 wt.% | - | 60–110 | 5–50 |
| f-GnPs/PG-W(30:70) | 0.25–1 wt.% | - | 40–222 | 5–50 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sekrani, G.; Poncet, S. Ethylene- and Propylene-Glycol Based Nanofluids: A Litterature Review on Their Thermophysical Properties and Thermal Performances. Appl. Sci. 2018, 8, 2311. https://doi.org/10.3390/app8112311
Sekrani G, Poncet S. Ethylene- and Propylene-Glycol Based Nanofluids: A Litterature Review on Their Thermophysical Properties and Thermal Performances. Applied Sciences. 2018; 8(11):2311. https://doi.org/10.3390/app8112311
Chicago/Turabian StyleSekrani, Ghofrane, and Sébastien Poncet. 2018. "Ethylene- and Propylene-Glycol Based Nanofluids: A Litterature Review on Their Thermophysical Properties and Thermal Performances" Applied Sciences 8, no. 11: 2311. https://doi.org/10.3390/app8112311
APA StyleSekrani, G., & Poncet, S. (2018). Ethylene- and Propylene-Glycol Based Nanofluids: A Litterature Review on Their Thermophysical Properties and Thermal Performances. Applied Sciences, 8(11), 2311. https://doi.org/10.3390/app8112311






