Quadrotor Formation Strategies Based on Distributed Consensus and Model Predictive Controls
Abstract
:1. Introduction
2. Background
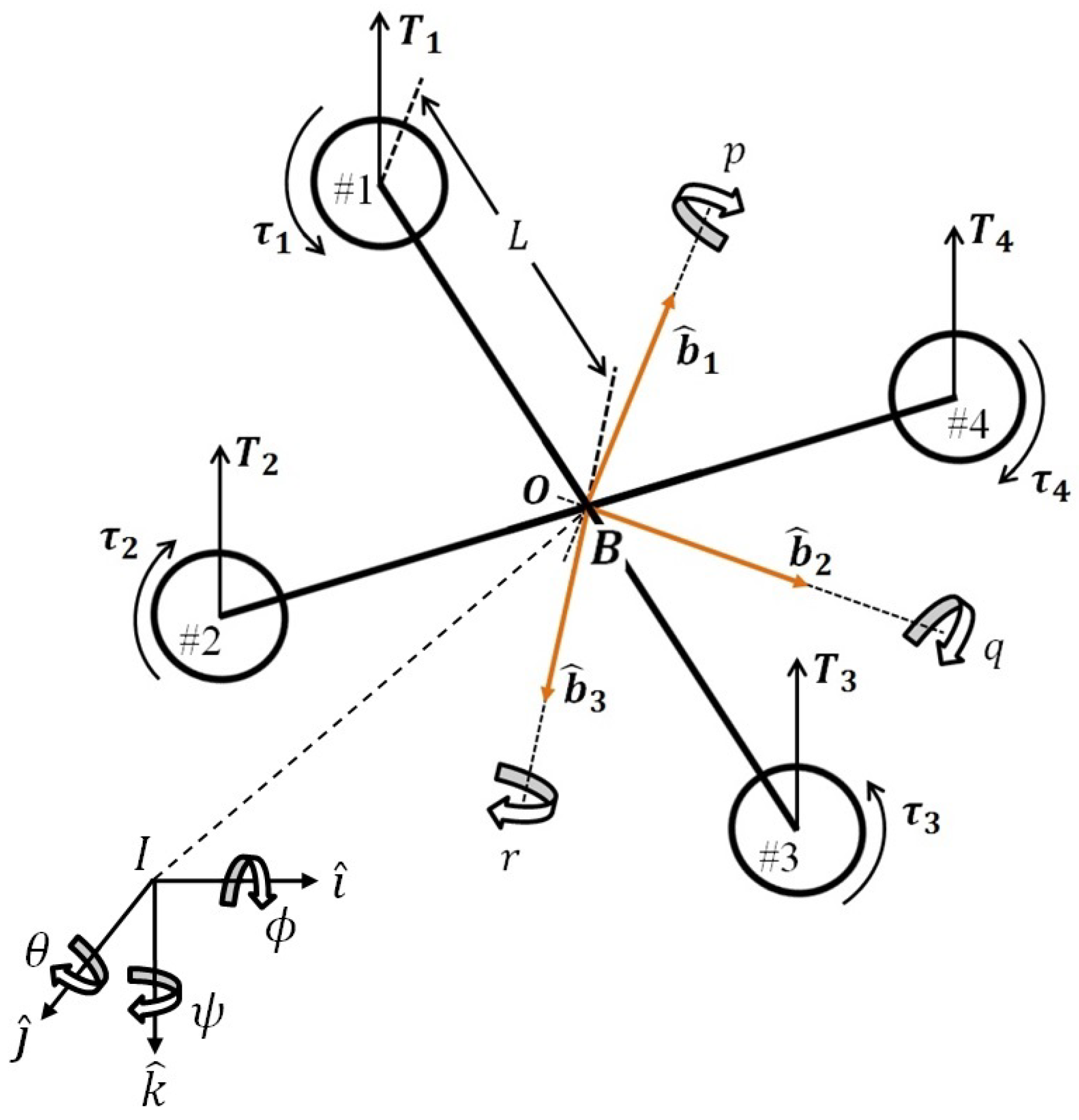
3. Dynamic Model of a Quadrotor
3.1. EOM of the Quadrotor
3.2. Linearization of the EOMs
4. Control Law Preliminaries
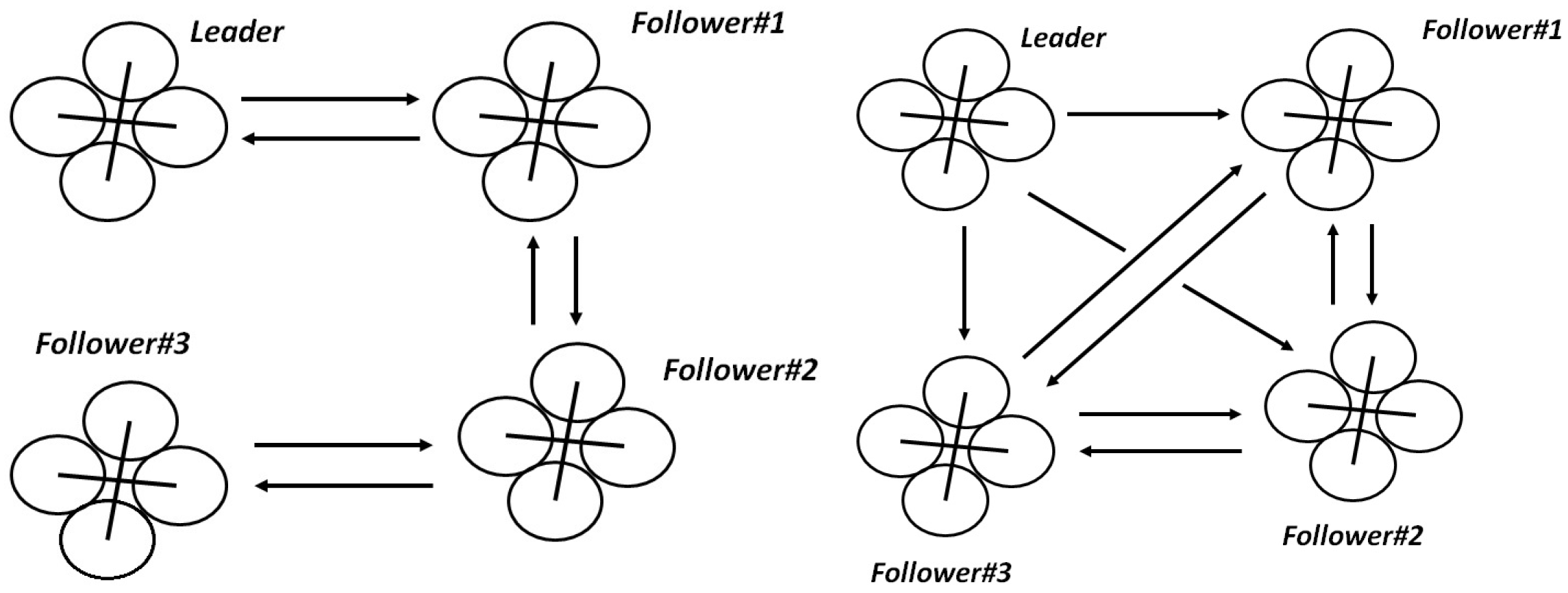
4.1. Consensus Control
4.2. Model Predictive Control
4.2.1. Linear Quadratic Tracker
4.2.2. Unconstrained Quadratic Programming Problem
5. Formation Strategies
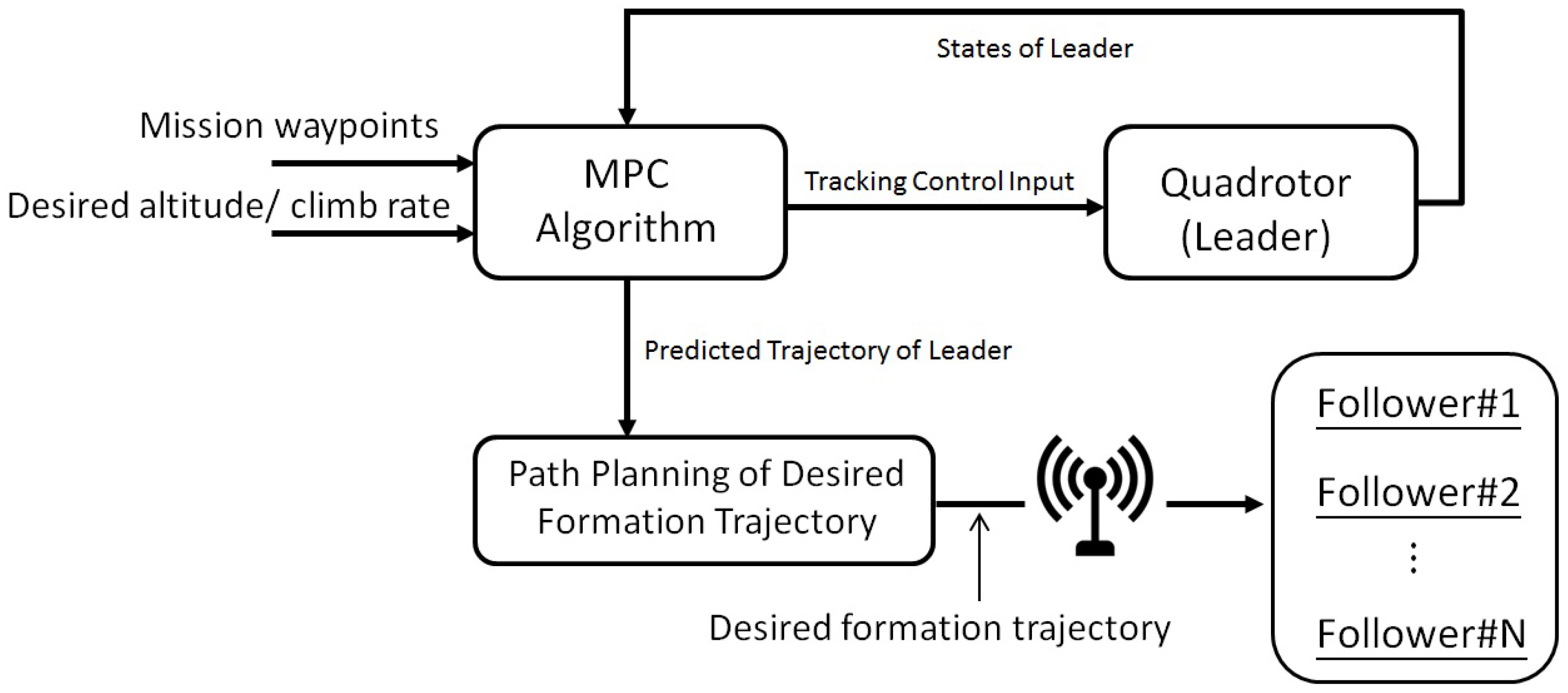
5.1. Formation Strategy: Leader
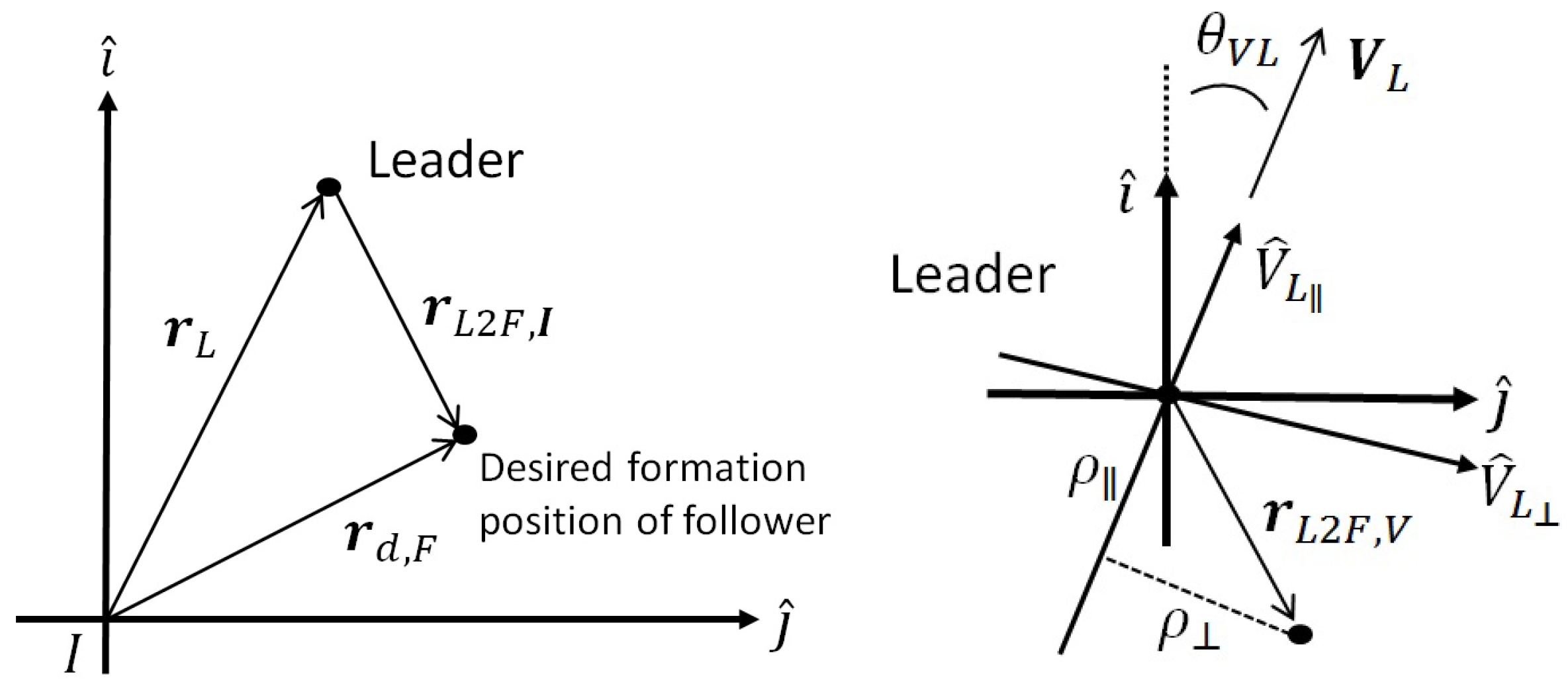
5.1.1. Generation of the Desired Formation Trajectory in the Horizontal Motion
5.1.2. Generation of the Desired Formation Trajectory in the Vertical Motion
- Case I: maintain the current altitude.In this case, the leader is designated to maintain the altitude. Thus, the reference trajectories of and over the predicted time horizon are equal to zero.
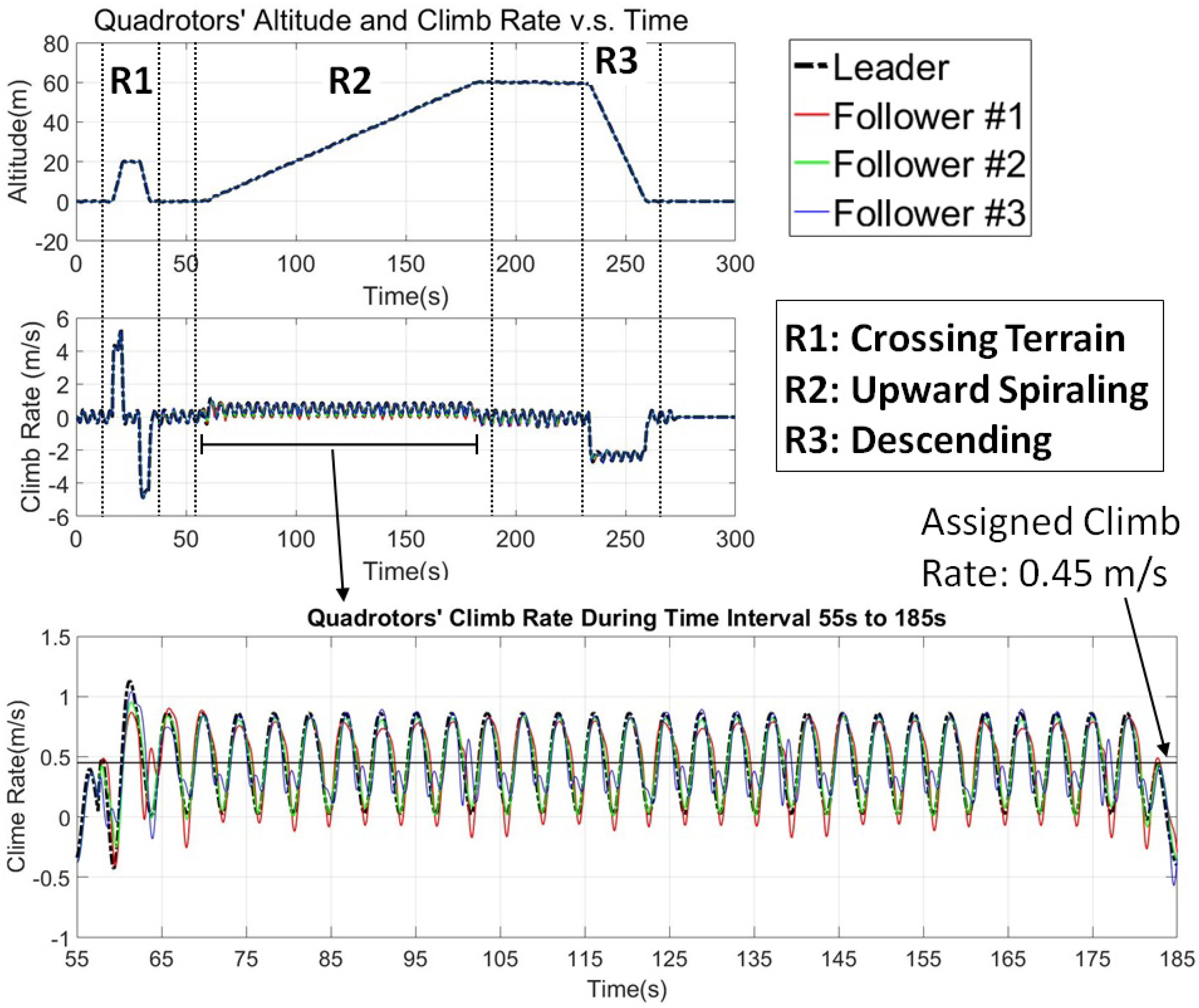
- Case II: climb to the desired altitude.If the desired altitude is given but not the climb rate, the leader is designated to climb to the desired altitude with the default climb rate. The reference for is the negative default climb rate and the reference trajectory of is computed bywhere denotes the reference altitude at time step k, which is equal to the leader’s current altitude plus the default climb rate times the time step k and the interval of the time step . Time step k is defined over the predicted time horizon considered by the MPC with the interval of .A deceleration action is taken as the leader is approaching the desired altitude. If the distance between the leader’s current position and the desired altitude is smaller than the altitude that can increase/decrease according to the climb rate within one second, then the reference of the altitude is set to the desired altitude and the reference of the climb rate will be set to zero.
- Case III: continuous climbing with the given climb rate.In this case, the reference trajectory of the altitude is generated by Equation (39) as well, but is replaced by the given climb rate. No deceleration action is taken.
- Case IV: climb to desired altitude with the given rate.In this case, the reference trajectory of the altitude is generated by Equation (39) as well, but is replaced by the given climb rate. This is the same if the statement in Case II is taken into consideration as the leader is approaching the desired altitude.
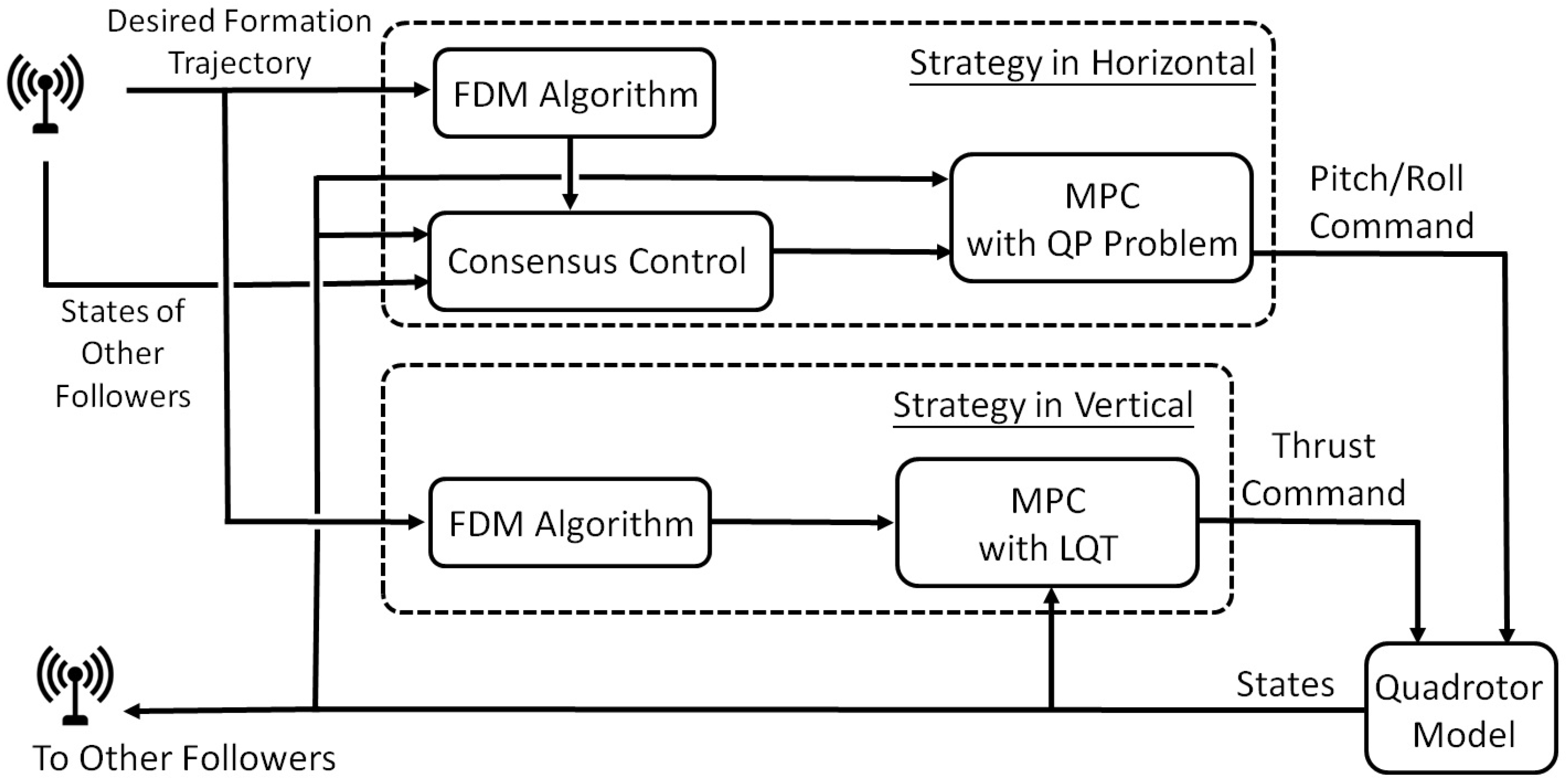
5.2. Formation Strategy: Follower
5.2.1. Formation Strategy in the Horizontal Motion
5.2.2. Formation Strategy in the Vertical Motion
6. Simulation Preparation
6.1. Transformation of the Variable of the Discrete State-Space Model
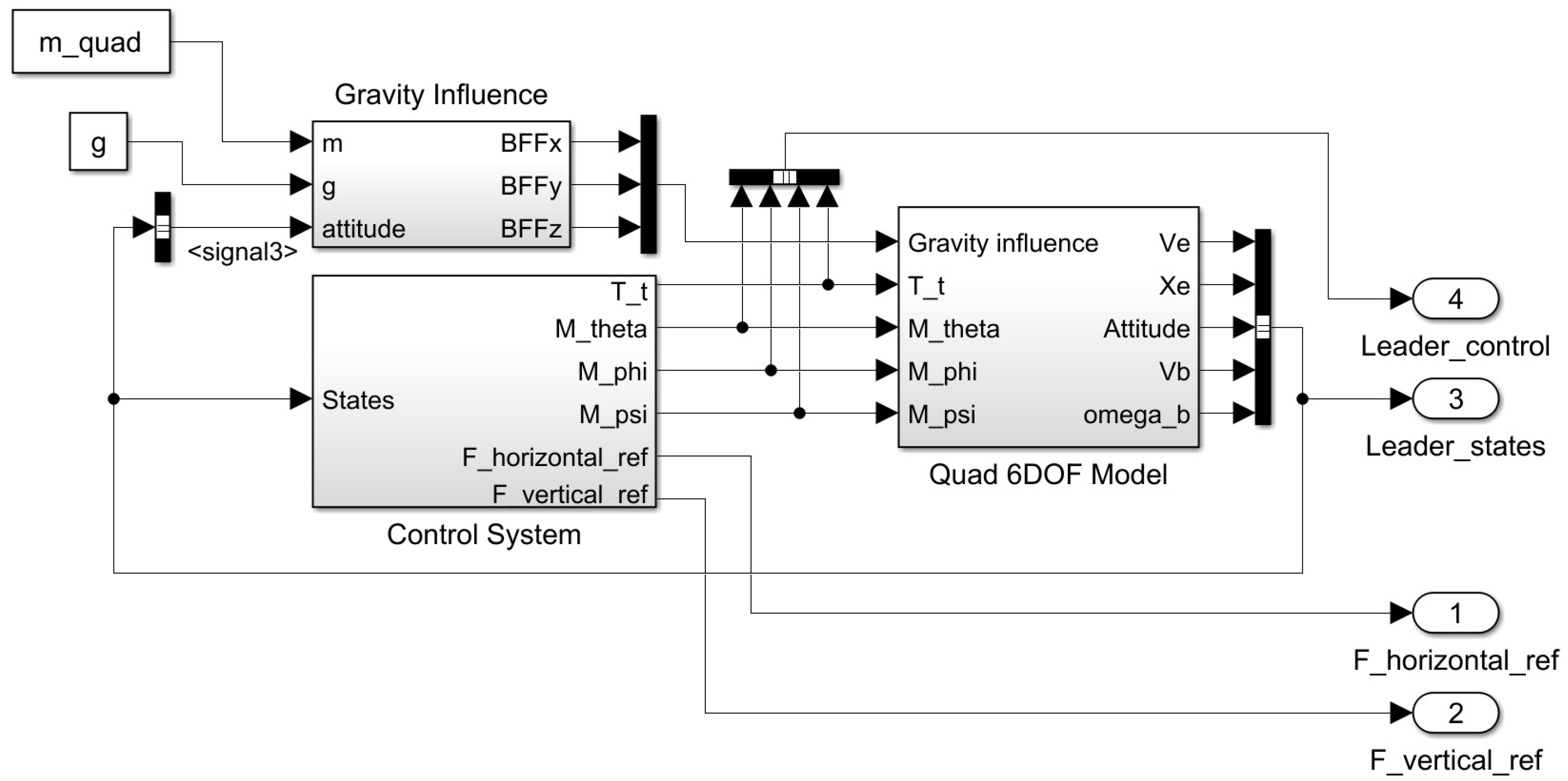
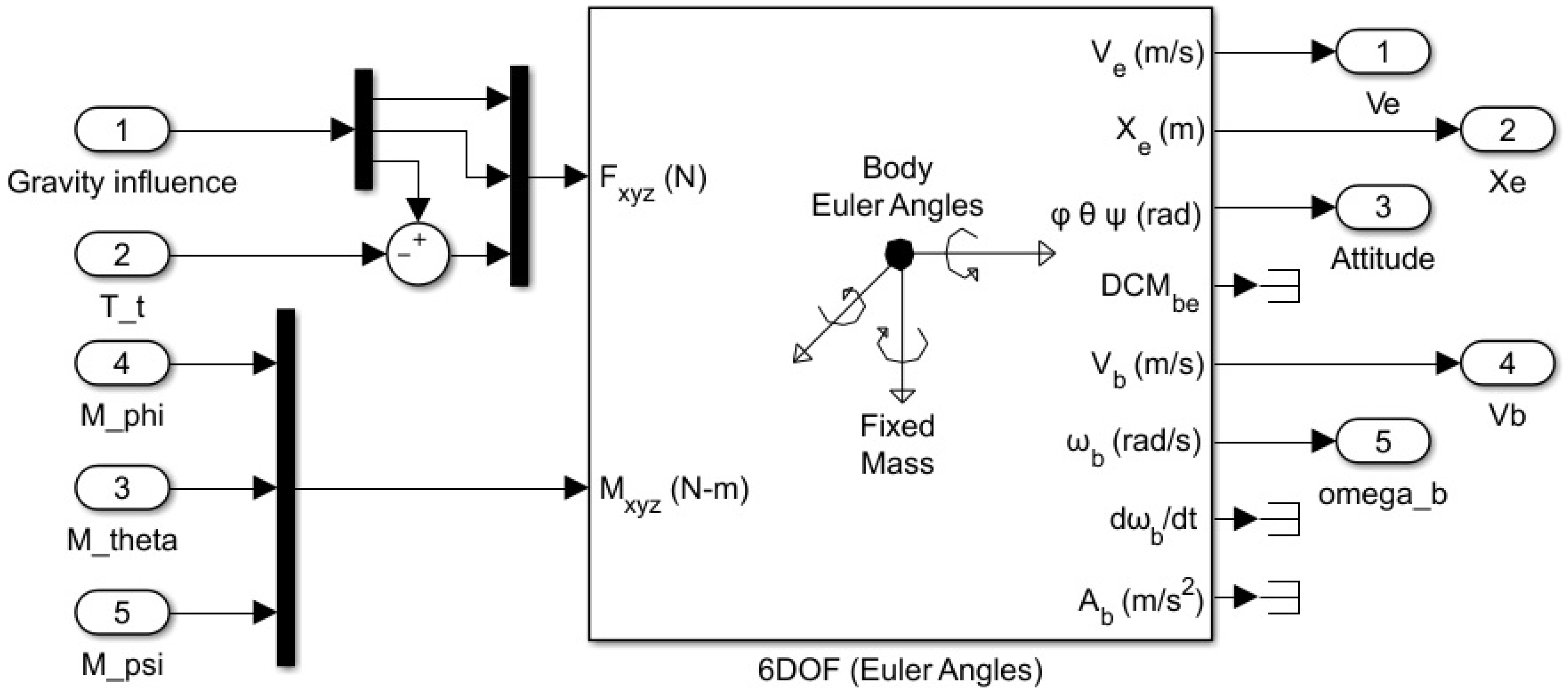
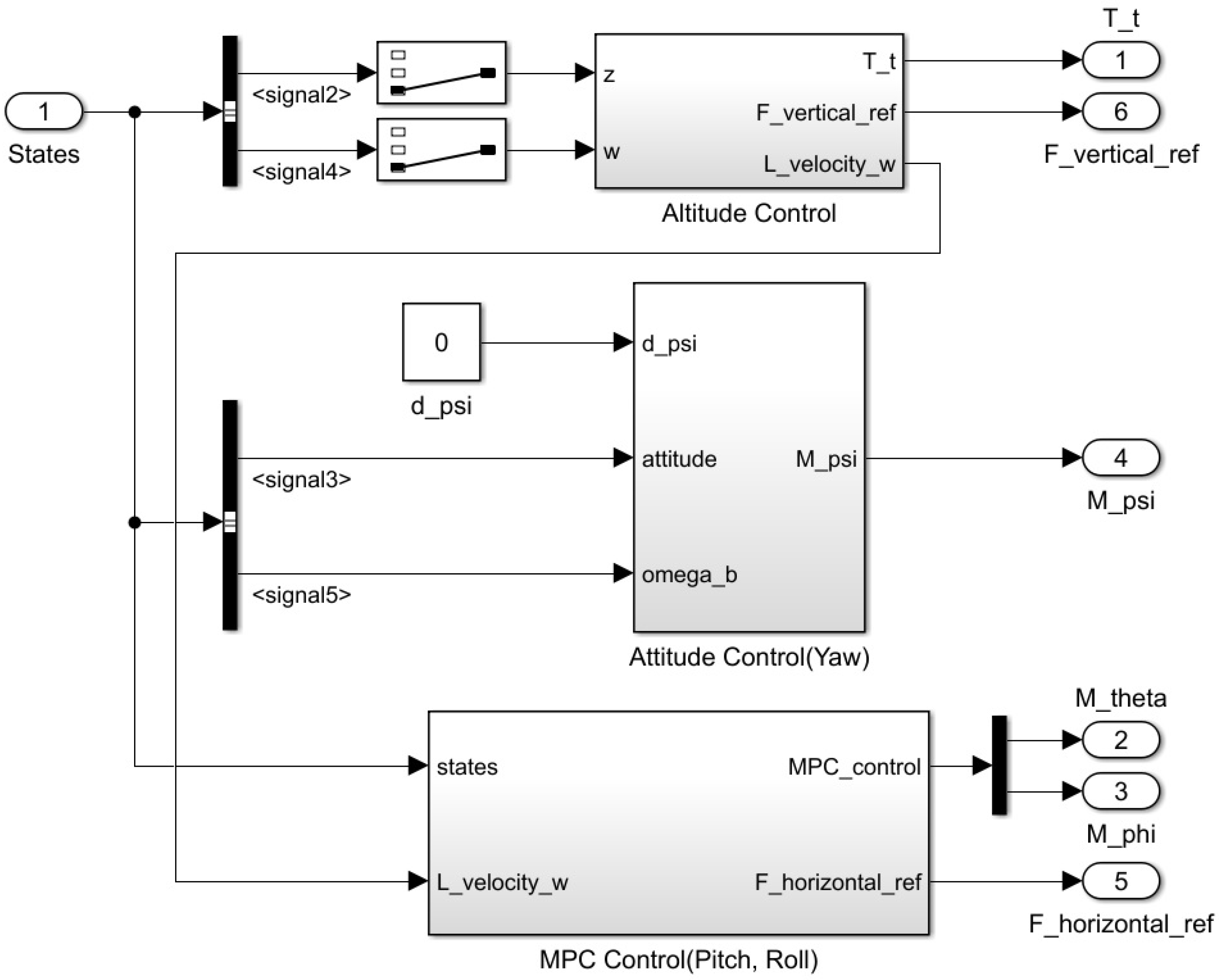
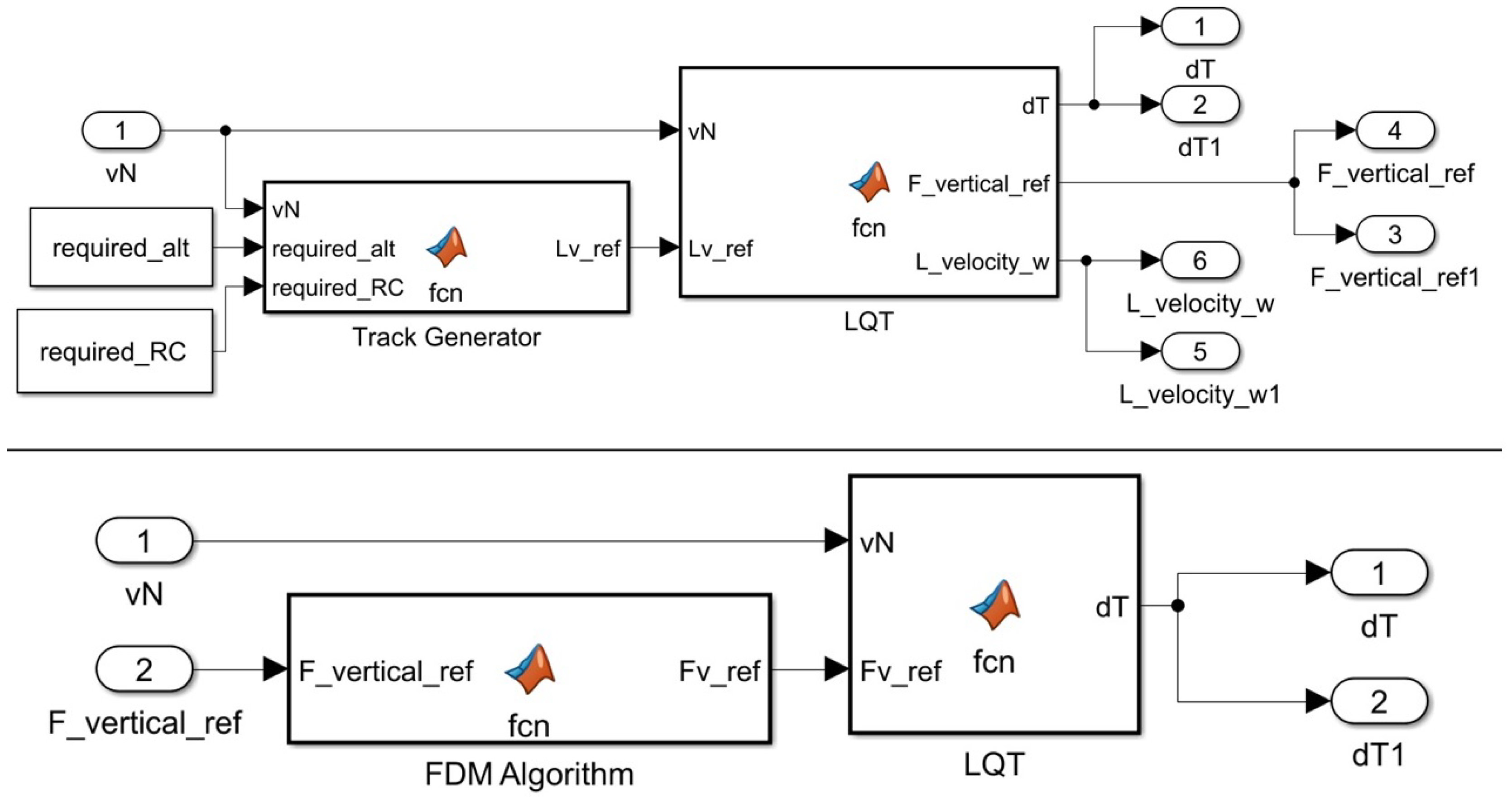
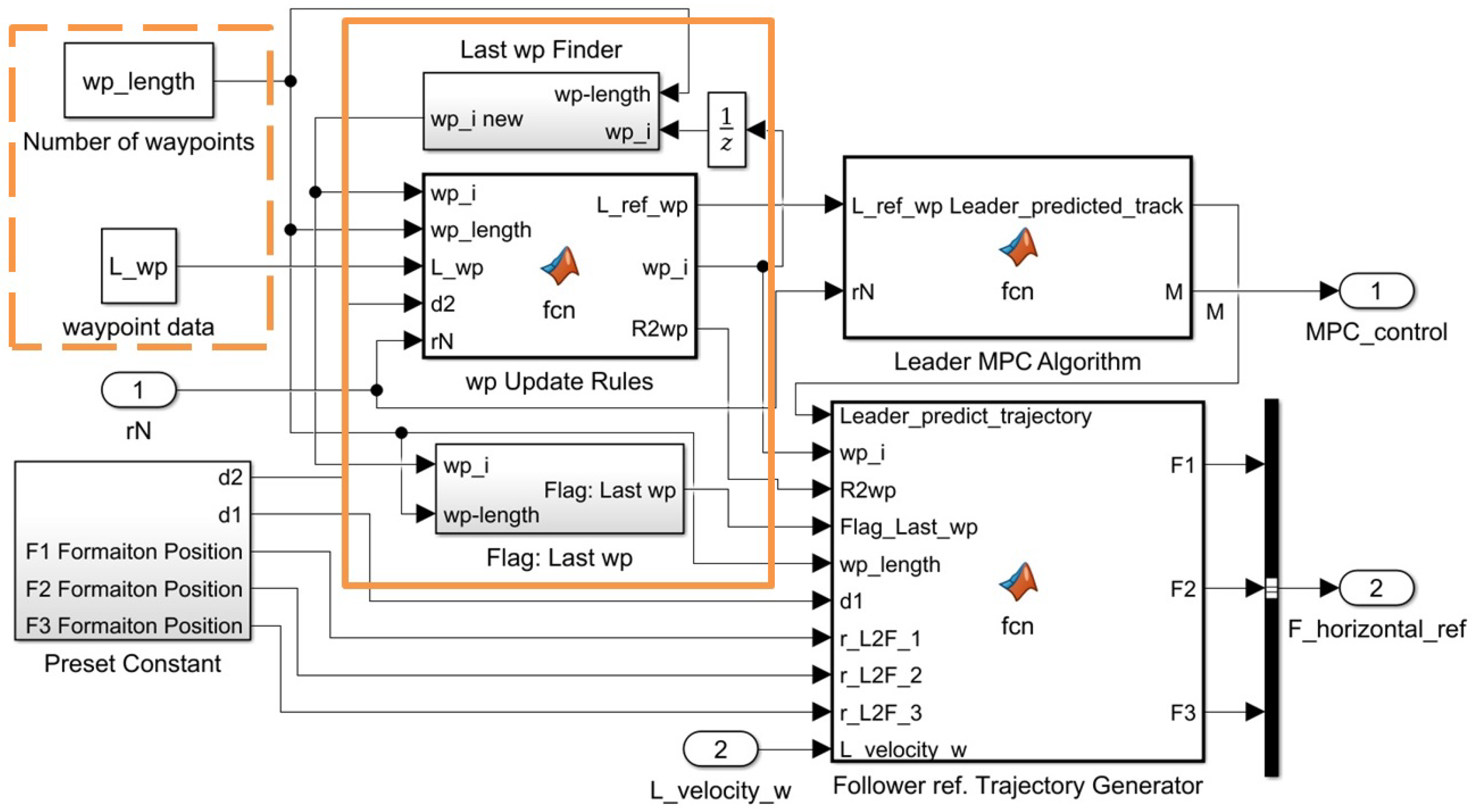
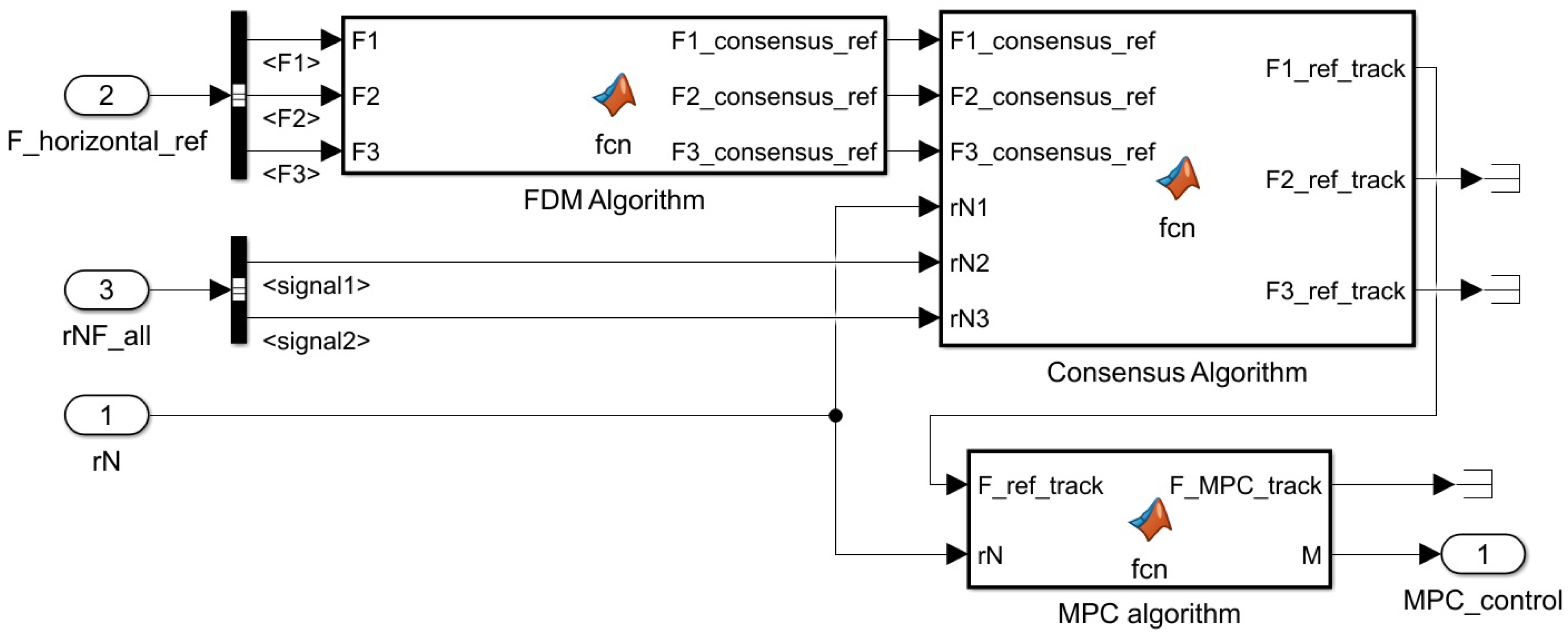
6.2. Simulink Environment Setup for the Formation Simulation
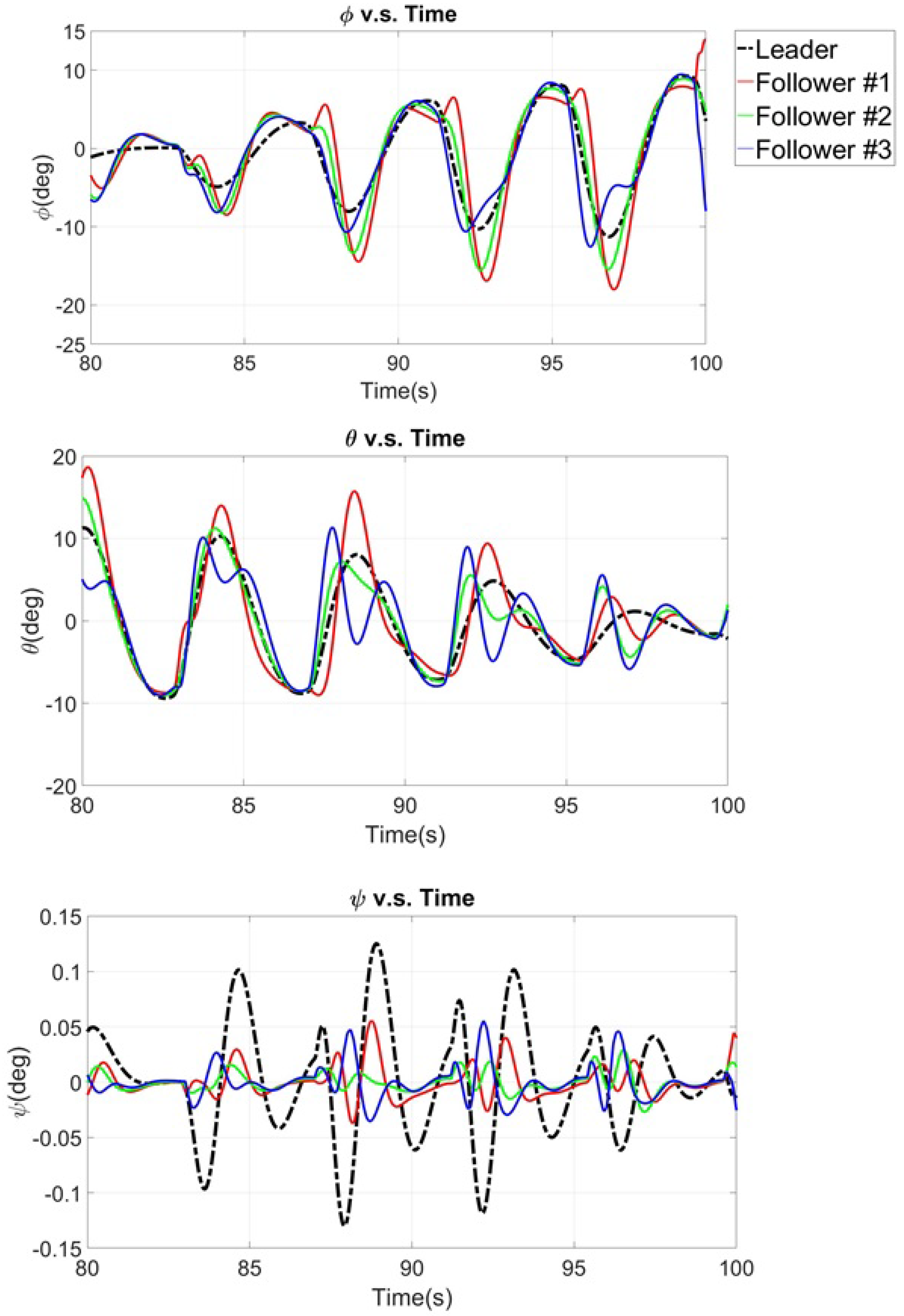
7. Simulation Results
7.1. Quadrotor Parameter, Control Gain, and Weighting Matrices
- Weighting matrices P, Q, and R of the unconstrained QP problem coded in simulink function Leader MPC Algorithm in Figure 10 for the leader’s horizontal motion control are given as follows:
- Weighting matrices P, Q, and R for the LQT coded in the simulink function LQT in Figure 9 for the leader’s altitude control are given as follows:
- Weighting matrices P, Q, and R of the unconstrained QP problem coded in simulink function MPC Algorithm in Figure 11 for the follower’s horizontal motion control are given as follows:
- Weighting matrices P, Q, and R for the LQT coded in simulink function LQT in Figure 9 for the follower’s altitude control are given as follows:
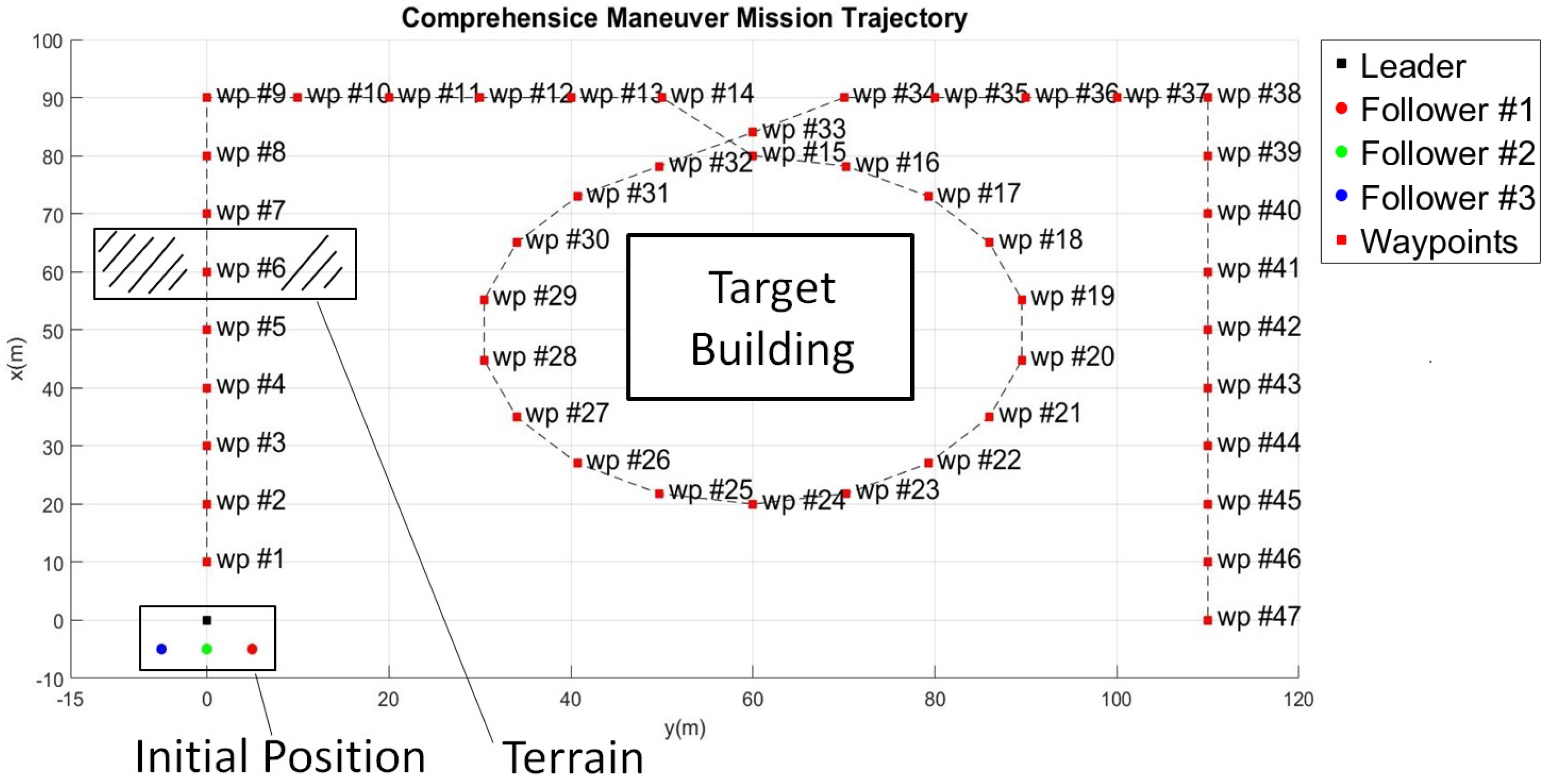
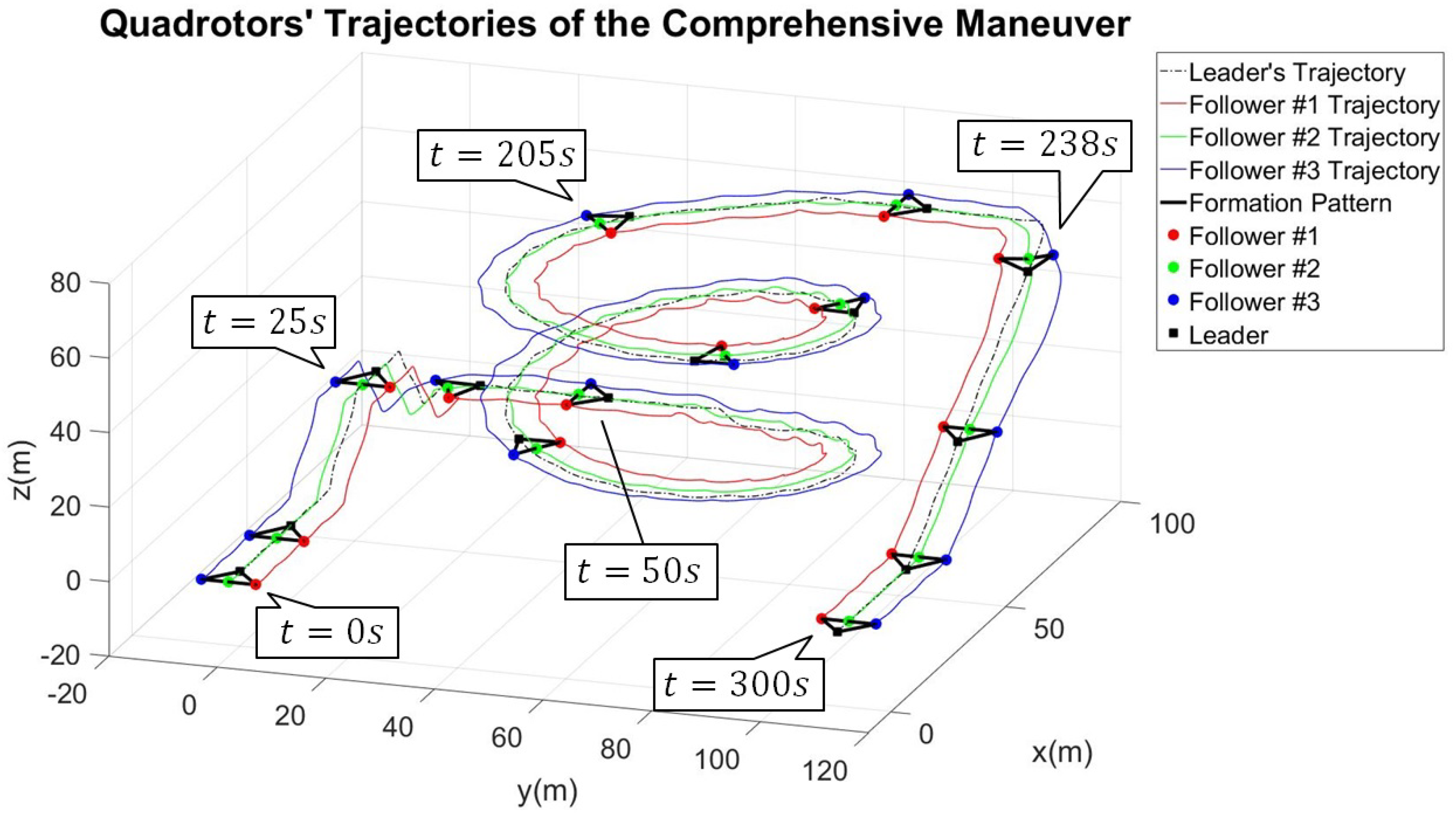
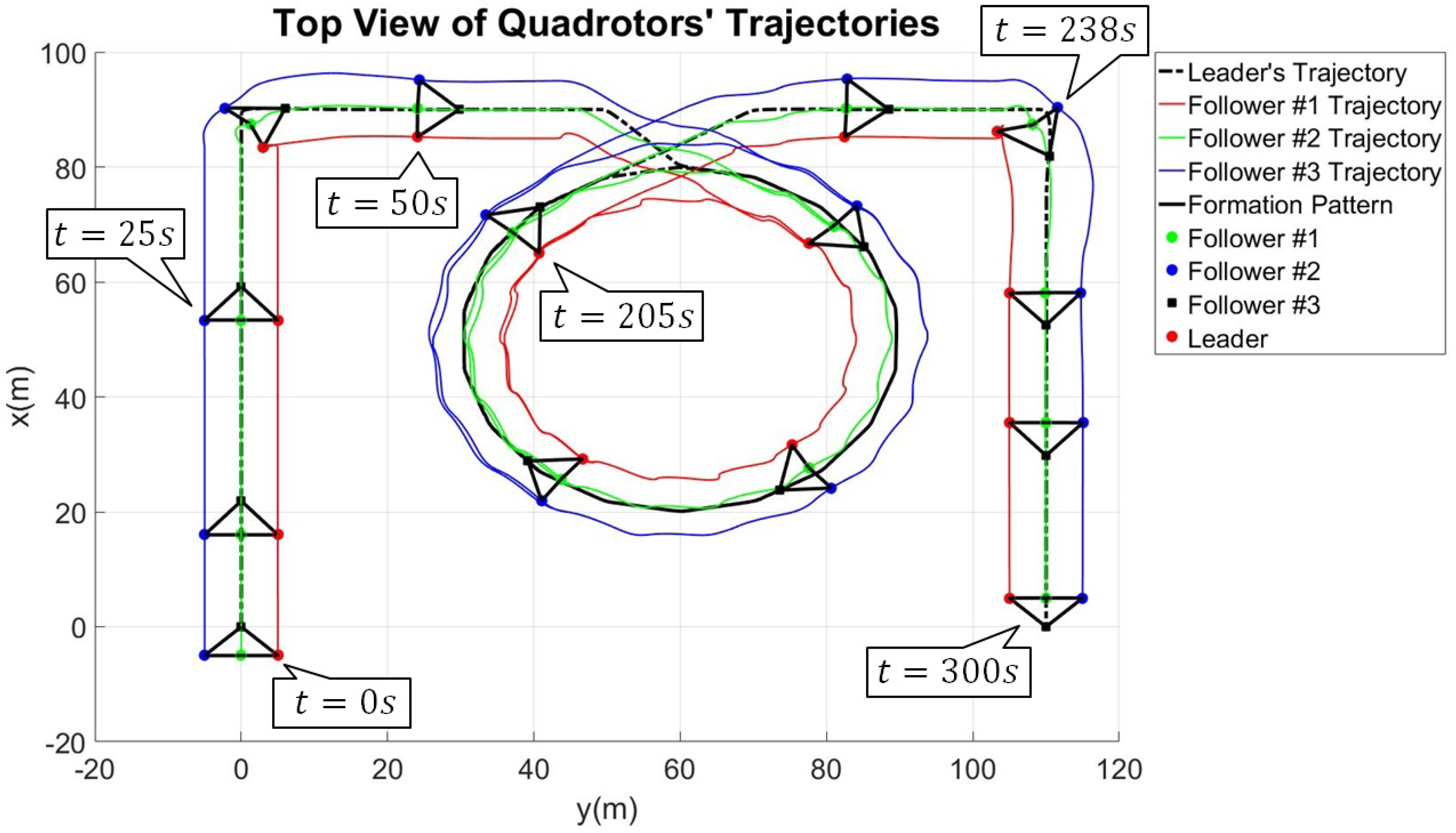
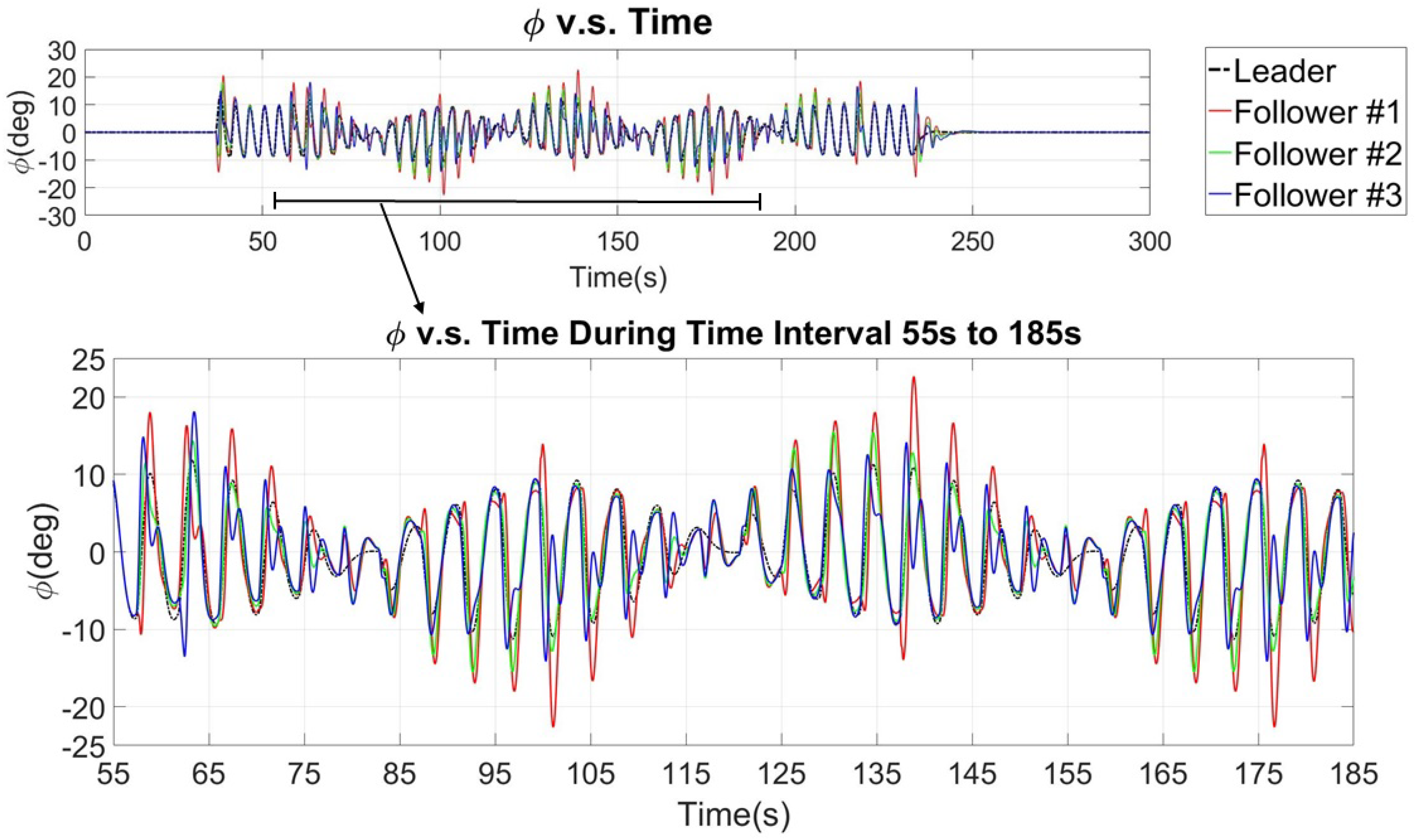
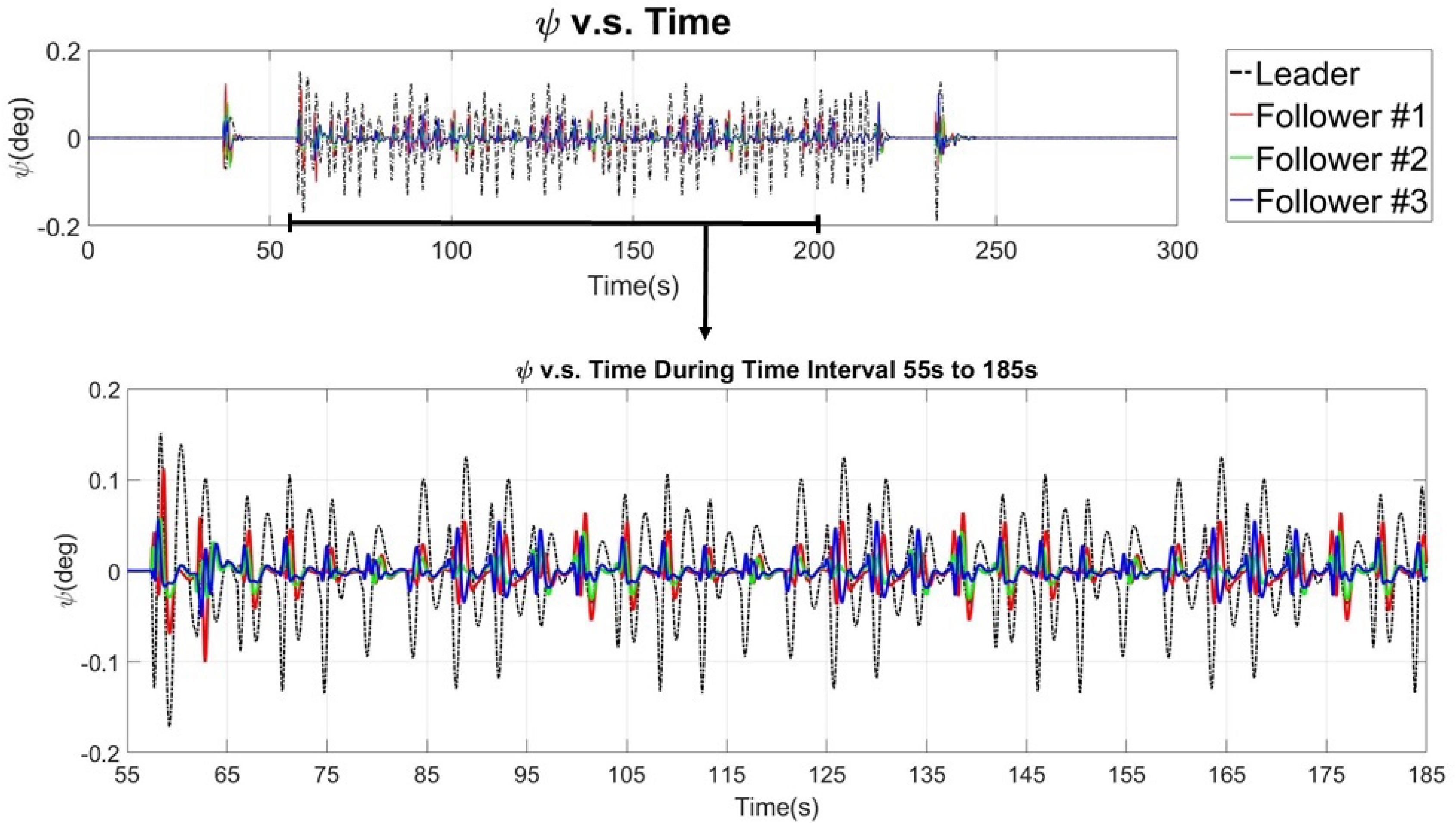
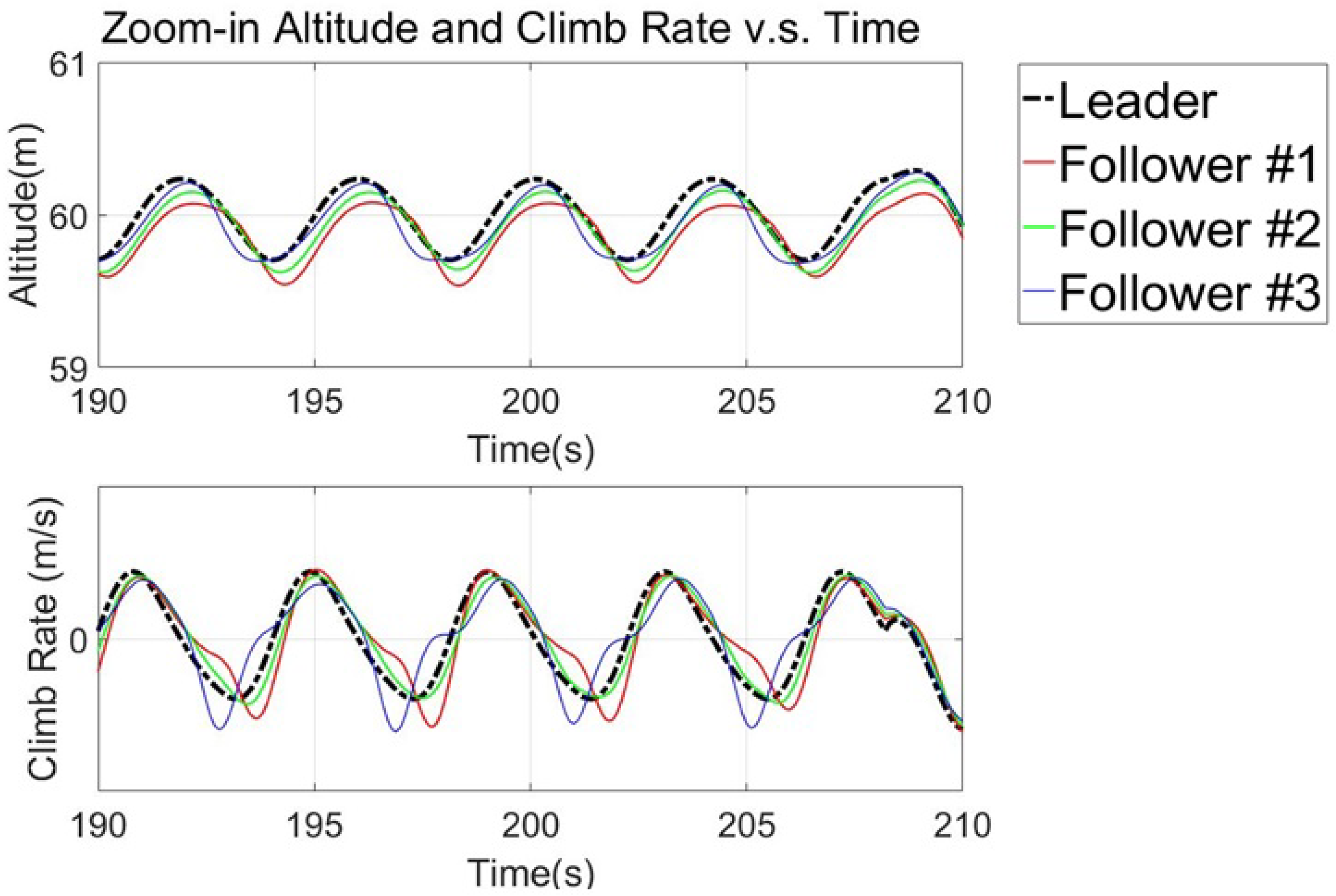
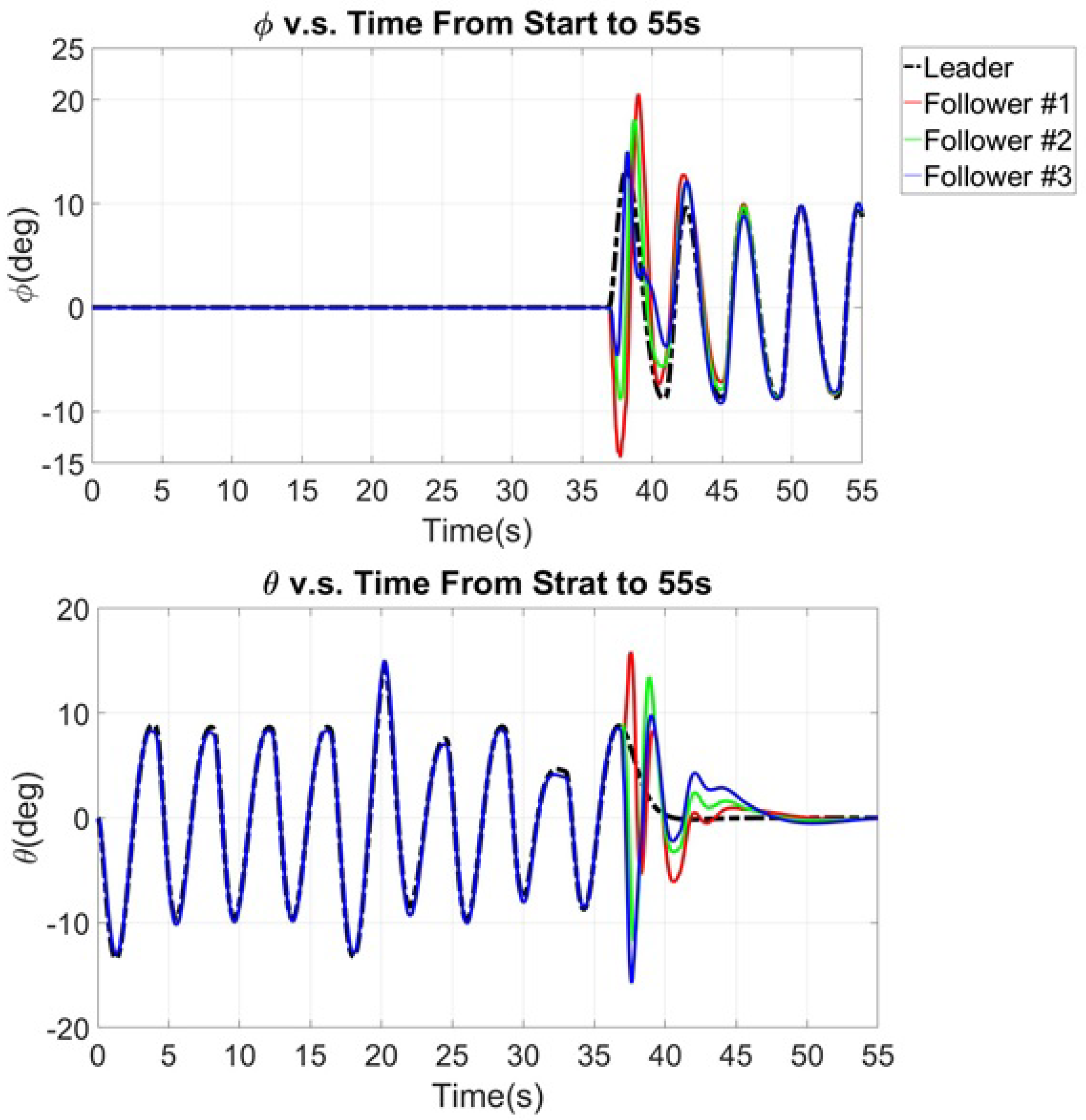
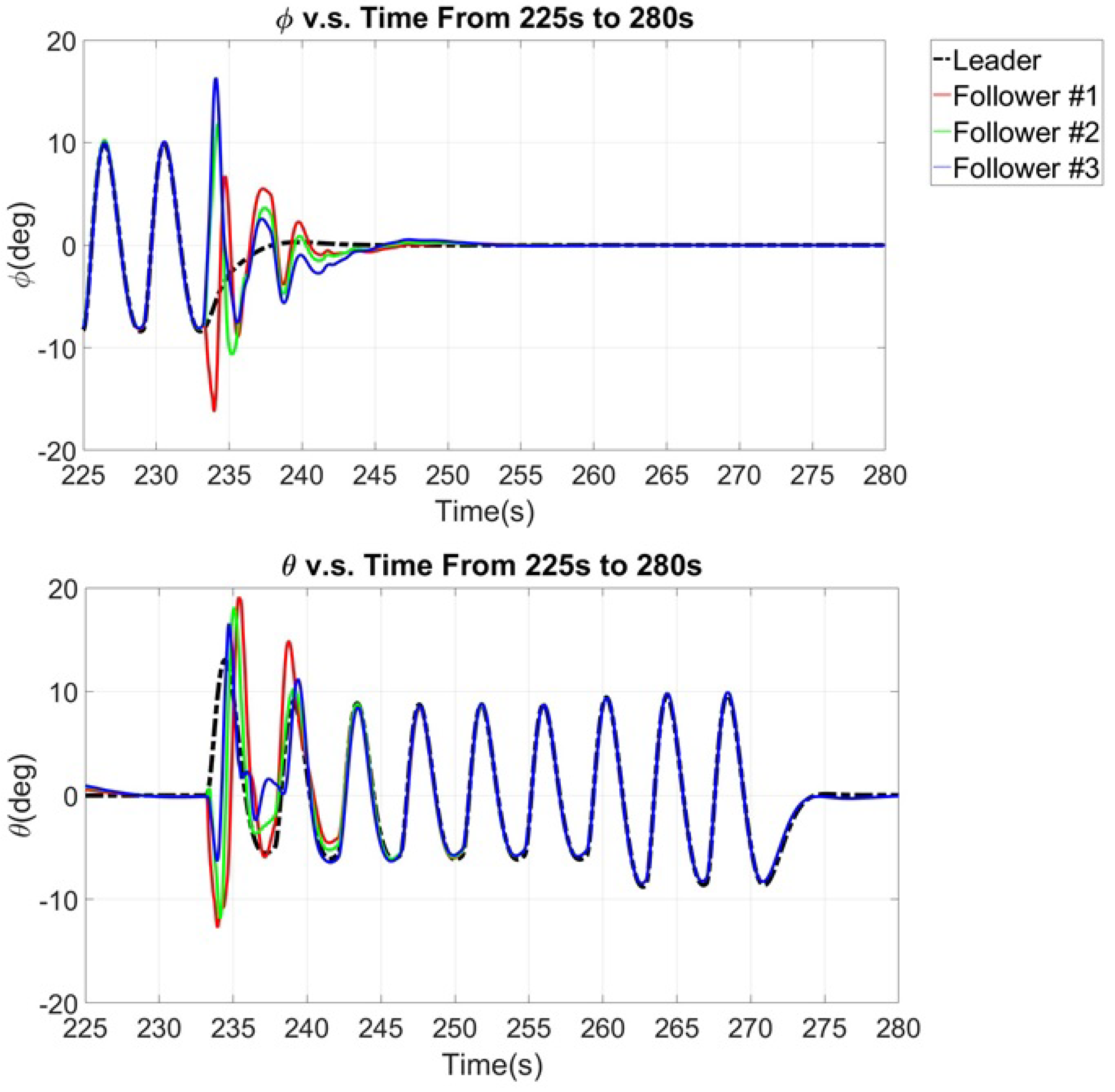
7.2. Simulation of the Comprehensive Maneuver
8. Discussion
9. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Scharf, D.P.; Hadaegh, F.Y.; Ploen, S.R. A survey of spacecraft formation flying guidance and control (Part II): Control. In Proceedings of the 2004 American Control Conference, Boston, MA, USA, 30 June–2 July 2004. [Google Scholar]
- Rinaldi, F.; Chiesa, S.; Quagliotti, F. Linear quadratic control for quadrotors UAVs dynamics and formation flight. J. Intell. Robot. Syst. 2013, 70, 203–220. [Google Scholar] [CrossRef]
- Mercado, D.; Castro, R.; Lozano, R. Quadrotors flight formation control using a leader-follower approach. In Proceedings of the 2013 European Control Conference (ECC), Zurich, Switzerland, 17–19 July 2013; pp. 3858–3863. [Google Scholar]
- Wu, F.; Chen, J.; Liang, Y. Leader-follower formation control for quadrotors. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2017; Volume 187, p. 012016. [Google Scholar]
- Roldão, V.; Cunha, R.; Cabecinhas, D.; Silvestre, C.; Oliveira, P. A leader-following trajectory generator with application to quadrotor formation flight. Robot. Auton. Syst. 2014, 62, 1597–1609. [Google Scholar] [CrossRef]
- Hou, Z.; Fantoni, I. Distributed leader-follower formation control for multiple quadrotors with weighted topology. In Proceedings of the 2015 10th IEEE System of Systems Engineering Conference (SoSE), San Antonio, TX, USA, 17–20 May 2015; pp. 256–261. [Google Scholar]
- Min, Y.X.; Cao, K.C.; Sheng, H.H.; Tao, Z. Formation tracking control of multiple quadrotors based on backstepping. In Proceedings of the 2015 34th Chinese Control Conference (CCC), Hangzhou, China, 28–30 July 2015; pp. 4424–4430. [Google Scholar]
- Lee, K.U.; Choi, Y.H.; Park, J.B. Backstepping Based Formation Control of Quadrotors with the State Transformation Technique. Appl. Sci. 2017, 7, 1170. [Google Scholar] [CrossRef]
- Zhao, W.; Go, T.H. Quadcopter formation flight control combining MPC and robust feedback linearization. J. Frankl. Inst. 2014, 351, 1335–1355. [Google Scholar] [CrossRef]
- Gulzar, M.M.; Rizvi, S.T.H.; Javed, M.Y.; Munir, U.; Asif, H. Multi-Agent Cooperative Control Consensus: A Comparative Review. Electronics 2018, 7, 22. [Google Scholar] [CrossRef]
- Olfati-Saber, R.; Fax, J.A.; Murray, R.M. Consensus and cooperation in networked multi-agent systems. Proc. IEEE 2007, 95, 215–233. [Google Scholar] [CrossRef]
- Ren, W. Consensus based formation control strategies for multi-vehicle systems. In Proceedings of the American Control Conference, Minneapolis, MN, USA, 14–16 June 2006. [Google Scholar]
- Kuriki, Y.; Namerikawa, T. Formation control with collision avoidance for a multi-UAV system using decentralized MPC and consensus-based control. SICE J. Control Meas. Syst. Integr. 2015, 8, 285–294. [Google Scholar] [CrossRef]
- Nelson, R.C. Flight Stability and Automatic Control; WCB/McGraw Hill: New York, NY, USA, 1998; Volume 2. [Google Scholar]
- Roskam, J. Airplane Flight Dynamics and Automatic Flight Controls; DARcorporation: Lawrence, KS, USA, 1998. [Google Scholar]
- Lewis, F.L.; Vrabie, D.; Syrmos, V.L. Optimal Control; John Wiley & Sons: New York, NY, USA, 2012. [Google Scholar]
- MathWorks. Aerospace ToolBox Release Notes. Available online: https://www.mathworks.com/help/aerotbx/release-notes.html (accessed on 16 October 2018).
- MathWorks. Solve Custom MPC Quadratic Programming Problem and Generate Code. Available online: https://www.mathworks.com/help/mpc/examples/solve-custom-mpc-quadratic-programming-problem-and-generate-code.html (accessed on 25 September 2018).

| State | Equilibrium pt. | Small Disturbance Expression | Unit |
|---|---|---|---|
| x | m | ||
| y | m | ||
| u | m/s | ||
| v | m/s | ||
| rad | |||
| rad | |||
| q | rad/s | ||
| p | rad/s | ||
| m · N | |||
| m · N |
| State | Equilibrium pt. | Small Disturbance Expression | Unit |
|---|---|---|---|
| z | m | ||
| w | m/s | ||
| rad | |||
| r | rad/s | ||
| m · N | |||
| N |
| Case | Desired Altitude | Climb Rate | Vertical Motion |
|---|---|---|---|
| I | Not Given | Not Given | Maintain current altitude. |
| Given | Not Given | Climb to desired altitude. | |
| Not Given | Given | Continuous climbing with given climb rate. | |
| Given | Given | Climb to desired altitude with given climb rate. |
| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Mass of the Quadrotor | m | 1.5 | |
| Acceleration of Gravity | g | 9.807 | |
| Quadrotor Arm Length | L | 0.225 | m |
| 0.022 | |||
| Moment of Inertia | 0.022 | ||
| 0.0018 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, C.-W.; Shiau, J.-K. Quadrotor Formation Strategies Based on Distributed Consensus and Model Predictive Controls. Appl. Sci. 2018, 8, 2246. https://doi.org/10.3390/app8112246
Chang C-W, Shiau J-K. Quadrotor Formation Strategies Based on Distributed Consensus and Model Predictive Controls. Applied Sciences. 2018; 8(11):2246. https://doi.org/10.3390/app8112246
Chicago/Turabian StyleChang, Chia-Wei, and Jaw-Kuen Shiau. 2018. "Quadrotor Formation Strategies Based on Distributed Consensus and Model Predictive Controls" Applied Sciences 8, no. 11: 2246. https://doi.org/10.3390/app8112246
APA StyleChang, C.-W., & Shiau, J.-K. (2018). Quadrotor Formation Strategies Based on Distributed Consensus and Model Predictive Controls. Applied Sciences, 8(11), 2246. https://doi.org/10.3390/app8112246




