Abstract
This paper investigates the postbuckling and free vibration response of geometrically imperfect multilayer nanobeams. The beam is assumed to be subjected to a pre-stress compressive load due to the manufacturing and its ends are kept at a fixed distance in space. The small-size effect is modeled according to the nonlocal elasticity differential model of Eringen within the nonlinear Bernoulli-Euler beam theory. The constitutive equations relating the stress resultants to the cross-section stiffness constants for a nonlocal multilayer beam are developed. The governing nonlinear equation of motion is derived and then manipulated to be given in terms of only the lateral displacement. The static problem is solved for the buckling load and the postbuckling deflection in terms of three parameters: Imperfection amplitude, size, and lamination. A closed-form solution for the buckling load in terms of all of the beam parameters is developed. With the presence of imperfection and size effects, it has been shown that the buckling load can be either less or greater than the Euler buckling load. Moreover, the free vibration in the pre and postbuckling domains are investigated for the first five modes. Numerical results show that the effects of imperfection, the nonlocal parameter, and layup on buckling loads and natural frequencies of the nanobeams are significant.
1. Introduction
Micro/nano-electro-mechanical systems (MEMS/NEMS) have received a great deal of attention in the last decade due to their promising functionality and features. MEMS and NEMS can be made of multilayer materials, which makes them modeled as multilayer structures. The lithography technique is one way to fabricate MEMS and NEMS structures that are composed of multilayers and masks. One method to make masks is to use an electron-beam (e-beam) lithography machine. A major advantage of e-beam masks is that there are few restrictions on the shapes of features. Layer-multiplying co-extrusion is a manufacturing technology capable of producing nano-layered optical polymer films having precisely controlled refractive-index distributions. This technology can be applied to the fabrication of spectral filters based on a variation of the Christiansen filter of Bortz and Shatz [1]. Legtenberg et al. [2] presented the design and performance of an electrostatic actuator consisting of a laterally compliant cantilever beam and a fixed curved electrode, both suspended above a ground plane. Torri et al. [3] studied mechanical properties, stress evolution, and high-temperature thermal stability of nano-layered Mo–Si–N/SiC thin films. Li et al. [4] analyzed the deformation of a single-wall carbon nanotube (SWCNT) interacting with a curved bundle of nanotubes. Verma and Jayaram [5] investigated the role of interface curvature on stress distribution under indentation for ZrN/Zr multilayer coating.
During fabrication, and due to heating and cooling processes, the structure may exhibit an initial curved shape as a form of imperfection. Many MEMS devices employ curved structures as well [6]. The initial curvature of a beam structure has been a source of difficulty in developing relations between stresses and deformations. In addition, there is a coupling consisting of the extension, flexure, shear, and twist in the vibration of curved beams that involve in-plane and out-of-plane motions [7]. Petyt and Fleischer [8] investigated radial vibrations of a curved beam by three finite element models. Based on the principle of virtual work, Palani and Rajasekaran [9] derived the equilibrium equation of thin-walled curved beams of open cross sections that is solved using the finite element method (FEM). Chidamparam and Leissa [7] organized and summarized the published literature on the vibrations of curved bars, beams, rings, and arches. Lacarbonara [10] presented a solution of thermal postbuckling and vibrations of imperfect fixed-fixed beams. Howson and Jemah [11] found the exact out-of-plane natural frequencies of curved Timoshenko beams directly using the stiffness method. Raveendranath et al. [12] solved the problem of membrane and shear locking by using a new two-node shear flexible curved beam element.
Lacarbonara and Yabuno [13] studied the nonlinear vibration of piezoceramic hinged-hinged actuators modeled as an imperfect beam. Lacarbonara et al. [14] presented a two-mode interaction activated in the vicinity of veering of the frequencies of the lowest two modes and results from the non-linear stretching of the imperfect beams. Gao et al. [15] developed a refined theory of rectangular curved beams by using Papkovich-Neuber solution in a polar coordinate system and Lur’e method without ad hoc assumptions. Chang and Hodges [16] studied coupled in-plane and out-of-plane vibrations of curved beams, whether the curvature is built-in or is caused by loading. Emam [17] presented a unified approach that handles the static and dynamic behavior of the postbuckling of imperfect multilayer beams. Shooshtari et al. [18] studied the mechanical behaviors, such as maximum stress, contact force, and fatigue life, of a specially designed metallic curved micro-cantilever beam, using analytical, numerical (FEM), and experimental methods. Stanciulescu et al. [19] presented a nonlinear finite element formulation for modeling dynamic snapthrough of beams with initial curvature under thermo-mechanical loads. Wang et al. [20] examined the dynamics of geometrically imperfect simply supported pipes conveying a fluid. The effect of a sinusoidal wave or parabolic variations of imperfections is investigated for a four-degree-of-freedom model of the system. Wu et al. [21] presented exact solutions for free in-plane vibrations of curved beams and arches carrying various concentrated elements. Dastgerdi et al. [22] calculated the effective stiffness of carbon nanotubes and shape memory polymer (SMP) composites using the Mori-Tanaka method and found that it is significantly reduced by waviness and aggregation in CNTs. Lee and Yan [23] derived an analytical solution for out-of-plane deflection of a curved Timoshenko beam.
Nano-mechanics, an emerging area of research in the field of computational mechanics, is focusing on the behavior of structures at the nano length scales. Nanobeam structure is widely used in NEMS, such as nanowires, nano-probes, atomic force microscopy (AFM), nanoactuators, and nanosensors. For designing nanodevices and nanostructures, the small-scale effects and the atomic forces should be included. The discrete nature of matter is usually associated with the long-range character of inter-atomic forces and may induce a nonlocal behavior, which conflicts with the postulated local character of classical elasticity [24]. One promising theory, which combines information about the forces between atoms and the internal length scale, is the nonlocal elasticity theory developed by Eringen [25,26,27].
Tunneling Electron Microscope (TEM) images for carbon nanotubes (CNTs) illustrate that these tiny structures have a certain degree of curvature along the nanotubes’ length, as shown by Qian et al. [28] and Wang et al. [29]. Mikata [30] presented an exact elastica solution for a clamped-hinged beam and its applications to a single-walled carbon nanotube by the elliptic integral technique. Mayoof and Hawwa [31] investigated nonlinear vibration of a CNT with waviness along its axis based on elastic continuum mechanics theory. Formica et al. [32] employed an equivalent continuum model based on the Eshelby–Mori–Tanaka approach to derive global elastic modal properties of nano-structured composite plates. Ouakad and Younis [33] used a 2D nonlinear curved beam model to simulate the coupled in-plane and out-of-plane motions of a CNT with curvature.
The nonlocal elasticity theory, developed by Eringen [25,26,27], assumes that the stress at a point is a function of strains at all points in the continuum. Such a model contains information about the forces between atoms, and the internal length scale is introduced into the constitutive equations as a material parameter. Eringen’s nonlocal elasticity theory, characterized by a strain-driven integral convolution, is inapplicable to nanomechanics [34], due to a conflict between constitutive and equilibrium requirements [35].
All difficulties can be overcome by adopting the stress-driven integral model proposed in [36], whose mathematical consistency and applicative effectiveness have been acknowledged in the literature.
Glavardanov et al. [37] presented optimal shapes against buckling of elastic nonlocal small-scale Pflüger beams with Eringen’s model. Eltaher et al. [38,39] presented static, buckling, and free vibration analysis of functionally graded (FG) nonlocal size-dependent nanobeams using the finite element method. Based on the nonlocal beam theory, Wang et al. [40,41] studied the vibrations of simply supported double-walled carbon nanotubes subjected to a moving harmonic load by using nonlocal Euler-Bernoulli and Timoshenko beam theories. Emam [42] presented a unified model for the nonlocal static response of nanobeams in buckling and postbuckling states. Thongyothee and Chucheepsakul [43] studied postbuckling behavior of curved nanorods including the effects of nonlocal elasticity theory and surface stress by elastica theory. Mohammadi et al. [44] investigated the static instability of an imperfect nonlocal Eringen nanobeam embedded in an elastic foundation. Khater et al. [45] studied the buckling behavior of curved nanowires, including surface energy under thermal loading. Eltaher et al. [46] exploited a nonlinear nonlocal Euler-Bernoulli beam to investigate the buckling of bonding wires under thermal loading. Eltaher et al. [47] presented a review on nonlocal elastic models for bending, buckling, vibrations, and wave propagation of nanoscale beams. Eltaher et al. [39] studied the effect of nonlinear von Karman strains on the static bending of CNTs modeled by nonlocal elasticity. Ghadiri and Shafiei [48] studied the small-scale effect on the nonlinear bending vibration of a rotating cantilever nanobeam modeled by Euler–Bernoulli beam theory with von Kármán geometric nonlinearity. The nonlocal models predict the stiffness softening with an increase in the nonlocal scale parameter. Kaghazian et al. [49] studied the free vibration of a piezoelectric nanobeam using nonlocal elasticity theory. Khetir et al. [50] developed a new nonlocal trigonometric shear deformation theory for thermal buckling analysis of embedded nanosize FG plates. Mohamed et al. [51] presented a novel numerical procedure to predict nonlinear free and steady state forced vibrations of a clamped–clamped curved beam in the vicinity of postbuckling configuration. Ebrahimi and Barati [52] investigated the buckling behavior of a multi-phase nanocrystalline nanobeam resting on a Winkler-Pasternak foundation in the framework of nonlocal couple stress elasticity and a higher order refined beam model. Eltaher [53] studied static bending and buckling of perforated nonlocal size-dependent nanobeams by using both Timoshenko and Euler–Bernoulli beam theories with a nonlocal differential form of the Eringen model. Eltaher et al. [54] investigated resonance frequencies of size dependent perforated nonlocal Euler–Bernoulli and Timoshenko nanobeams. Ebrahimi and Barati [55,56] presented a unified formulation for the modeling of inhomogeneous nonlocal beams to include a shear deformation.
Recently, several studies focusing on the bending behavior of cantilevered beams have produced insubstantial results [57,58]. Benvenuti and Simone [59] presented the equivalence between the nonlocal and the gradient elasticity models by making reference to one-dimensional boundary value problems equipped with two integral stress–strain laws proposed by Eringen. Fernández-Sáez et al. [60] studied the numerically static bending of Euler–Bernoulli beams using the Eringen’s integral form. They underlined that Eringen’s differential equation is not equivalent to the strain-driven integral convolution.
Romano et al. [34] further discussed the applicability of the strain-driven nonlocal model in simple beam problems, such as the cantilever with end-point loading. They found out that there is incompatibility between constitutive and equilibrium boundary conditions on the stress field. As a consequence, the resulting nonlocal structural problem does not admit a solution. This obstruction is confirmed by the evidence that the alleged closed-form solutions by Tuna and Kirca [61] violate kinematic boundary conditions.
Also, Romano and Barretta [35,36] proved that the stress-driven integral constitutive law provides the natural way to get well-posed nonlocal elastic problems for application to nano-structures. Apuzzo et al. [62] derived the equation of motion of Bernoulli-Euler nanobeams using effectively the stress-driven nonlocal integral model.
Implementing the nonlocal elasticity into the analysis of curved, size-dependent laminated composite nanobeams has not yet been accomplished to the best of the authors’ knowledge. The present model takes into account the initial curvature, small size, lamination layout, and geometric nonlinearity for the static and dynamic response of beams. Buckling loads, postbuckling, and free vibrations pre and postbuckling are investigated by exploiting the classical von Kármán theory and Eringen’s nonlocal elasticity differential law to capture size effects. The buckling load, postbuckling, and free vibrations pre and postbuckling are investigated. A parametric study is performed in order to show the significance of size parameter, imperfection, and lamination on the resulting response.
2. Problem Formulation
2.1. Kinematic Relations
We consider a geometrically imperfect multilayer beam of a nanoscale size whose ends are kept at a fixed distance in space. The beam has a thickness, ; initial curvature of amplitude, ; and a fixed length of, Figure 1. The beam is assumed to deform in the plane. The beam is assumed to be subjected to a pre-stress compressive load due to the manufacturing processes that typically induce such residual stresses upon curing due to the mismatch of thermal expansion coefficients, as shown by Fang and Wickert [63]. It is worth noting that if the pre-stress load is beyond the buckling load, the beam will buckle and stretch because the ends are fixed in space. As a result, the effective compression at the end will reduce. The formula relating the pre-stress load and the possible buckling amplitude is different from the classical formulas assuming moving ends. This behavior will be outlined in more detail in the subsequent sections.
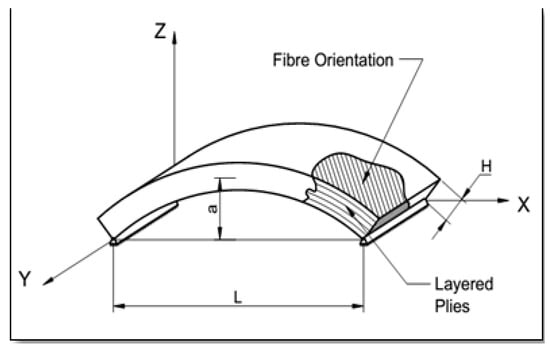
Figure 1.
A schematic of a curved, multilayer nanobeam with hinged boundaries.
Based on the classical Euler-Bernoulli beam theory, the axial and transverse displacements, and , of a point, , originally located at a distance, , from the origin at a height, , from the beam’s midplane are defined as
where and are the axial and transverse displacements along the midplane of the beam, and is the initial imperfection of the beam whose maximum amplitude is designated in Figure 1. The beam is assumed to be thin in order for the Euler-Bernoulli (EB) beam theory to be justified. Nevertheless, for multilayer beams, the aspect ratio is not the only parameter that contributes to the validity of the EB theory, but it is also the moduli of elasticity in the axial and lateral directions [64]. Generally, an aspect ratio of 20 and higher can justify the application of the EB beam theory. According to Eltaher et al. [65], the midplane stretching, which is depicted by the nonlinear von Karman strain, has a significant effect on the bending of nonlocal Euler-Bernoulli and Timoshenko nanobeams. So, the von Karman effect is considered in the current model and expressed as
where
are, respectively, the normal and bending strains.
2.2. Equations of Motion
The equations of motion of the beam are given as follows [66]:
where is the force stress resultant, is the moment stress resultant, is the normal stress, and is the mass per unit length. The boundary conditions are: Either or is prescribed at either or is prescribed at Neglecting the in-plane inertia term from Equation (4a), it is assumed hereafter that . Here, is the initial pre-stress that acts at the beam ends. It is important to emphasize that this load is not a mechanical load that can be increased beyond buckling. Since the beam ends are immovable, even if an external axial load is applied, it will be carried by the support. This is contrary to the case where one end is sliding towards the other as the load is increased.
2.3. Constitutive Equations
According to Eringen’s nonlocal elasticity differential model, the constitutive equation that describes the stress-strain relation for a laminated composite material is given by
where is the reduced transformed stiffness from the material coordinates to the problem coordinates, and is a size parameter such that , where is a constant and is an internal-length parameter. The length parameter, nm, for a single-wall carbon-nano tube [67]. Multiplying Equation (5) by the beam’s cross-sectional area, , and integrating over the area yields the nonlocal resultant force, , as follows:
where is the beam’s width, and and are the axial and coupling stiffness constants of the beam’s cross section, respectively. From the equilibrium equations, we have , and hence Equation (6) reduces to
which in light of Equation (3) reads as
Differentiating Equation (8) twice with respect to , and noting that , results in the following relation:
Similarly, the nonlocal resultant moment, , can be represented by
where is the bending stiffness of the cross section. Substituting the term, , from Equation (4b) into Equation (10) results in the moment stress resultant, , as a function of only the displacements as
Differentiating Equation (11) twice with respect to and substituting the result back into Equation (4b), we obtain
In order to eliminate the induced axial force, , from Equation (12), we integrate Equation (8) once with respect to and apply the non-moving end conditions, to get
Finally, by substituting , and into Equation (12), we obtain the equation of motion of a nonlocal, initially curved laminated multilayer nanobeam in terms of only the displacement, , as follows:
For a symmetric laminate, . Therefore, the equation of motion reduces to
In order to assess the significance of the size, layup, and initial curvature on the resulting static and dynamic response, we introduce the following nondimensional parameters:
The identifies dimensional quantities, which is understood to apply to all previous equations. As a result, the nondimensional equation of motion can be simplified and expressed as follows:
where the nondimensional size parameter, , pre-stress load, , and lamination coefficient, , are defined as
Investigating Equation (16), one can notice that the size parameter contributes to the inertia and the stiffness of the beam. Due to the nature of the buckling shape, the second derivative with respect to the spatial coordinate, , yields a minus sign, which causes the effect of the size parameter to increase the inertia. On the other hand, the size parameter reduces the stiffness, which means the small-size effect is of a softening type. Therefore, one concludes that as the size becomes smaller, the beam will end up having less buckling load and less natural frequencies. This will be clearly shown by the numerical results presenting lower buckling loads and lower natural frequencies in Section 4 and Section 5, where the significance of the size parameter, , the initial curvature, , and lamination coefficient, , on the buckling and free vibration of multilayer nanobeams is presented.
3. Static Analysis
The equation governing the static response of initially curved, multilayer nanobeams clamped at both ends can be obtained from Equation (16) by dropping the time-dependent terms. The result is
where is the lateral static deflection of the beam. Again, is the nondimensional initial pre-stress. Because geometric imperfection is present, Equation (17) governs all equilibrium positions that may exist at a given pre-load, This is not the classical buckling problem that is basically an eigenvalue problem. Indeed, when the beam exhibits some imperfection, and for any nonzero load, there exists a static equilibrium position that grows gradually as the load is increased. The problem with imperfection, as given by Equation (17), is a boundary-value problem. This is evident by the fact that the right-hand-side of Equation (17) is nonzero. The question is can we still find a buckling load in this case. The answer is yes. The point of buckling, in this case, will not refer to Euler buckling or bifurcation buckling, but it refers to a limit point, which may define a buckling load that is less or larger than the Euler buckling load. The structural dynamics community use the terms, bifurcation points and limit points, to refer to Euler buckling of initially straight columns and initially curved columns, respectively [68]. In the meantime, the nonlinear dynamics community use the terms, pitch-fork bifurcation and saddle-node bifurcations, to refer to these two points, respectively [69].
To gain insight, we define the effective compressive force that acts at the beam ends after buckling as
This is simply the initial pre-stress load minus the induced tensile midplane stretching due to buckling. Therefore, Equation (17) can be expressed as
As such, the size effect is about reducing the bending stiffness, which will result in reduced buckling loads and an increased postbuckling response, as will be shown next.
The initial configuration of a clamped-clamped imperfect beam is assumed to have the form [17]
where is the beam’s midspan initial rise, which is used as a control parameter representing the nondimensional imperfection amplitude. Emam [17] found that a general solution for the static deflection, , of a perfect or imperfect beam, can be expressed as follows
where is the buckling amplitude. Substituting Equations (20) and (21) into Equation (17) yields
Equation (22) governs the buckling amplitude, , for a given pre-stress load, initial imperfection amplitude, laminate layup coefficient, , and size parameter, . Buckling occurs when the two roots of Equation (22) coalesce. This condition is satisfied if the discriminant of Equation (22) is zero. Equation (22) takes the form
where the constants, , can be defined in light of Equation (22). In the prebuckling state, Equation (22) yields only one real solution that corresponds to the stable equilibrium position. On the other hand, once the beam buckles, Equation (22) yields three real solutions: Two solutions give the stable buckled positions and the third solution gives the unstable position. Consequently, buckling occurs when the two roots of Equation (22) coalesce. Following Emam [17], we set the discriminant of Equation (23) to equal zero to identify the buckling load
Solving Equation (24) for the buckling load, , we obtain
which defines the buckling load for a multilayer nonlocal beam with imperfection. Inspecting Equation (25), we notice that as the size effect becomes significant, the buckling load decreases, which is consistent with the remark that the nonlocal effect due to a small size has a softening effect. In the meantime, the imperfection amplitude, , appears in Equation (25) with different signs, which makes it possible to utilize it to enhance the buckling load. The maximum buckling load can be obtained by setting . It is found that the optimum initial imperfection that yields the maximum buckling load is defined as follows:
If the size effect is neglected and the material is isotropic (, the buckling load-initial imperfection relation is defined as
Additionally, the optimum initial imperfection is
Equations (27) and (28) are consistent with Lacarbonara [10] for clamped-clamped imperfect isotropic beams.
3.1. Buckling Load of Imperfect, Multilayer Nanobeams
In this section, we present the lowest buckling load for imperfect multilayer nanobeams. Namely three parameters are considered: The imperfection amplitude, the small-size parameter, and the lamination coefficient.
Before the numerical results are presented, we shed light on the range of the nanobeam length considered in this study. The nondimensional size parameter is varied from 0 to 0.1, which varies the beam length up to 6 nm, according to nm. The effects of the initial curvature and size parameter on the buckling load according to Equation (25) are given in Table 1 for . The first row of Table 1 is identical to the results reported by Aydogdu [70] and Emam [42] for nonlocal initially straight beams, which validates the current model. The table shows that as the size parameter increases, the buckling load decreases. On the other hand, the existence of the initial curvature may enhance the buckling load. For instance, the buckling load at is one-fifth of the classical buckling load () for a perfect beam. This means that the buckling load significantly decreases as the nonlocal parameter is increased for a given initial curvature. It is also noticed that the imperfection tends to increase the buckling load up to a certain limit then it inverses its effect. The buckling load increases from 39.48 to 78.86 as the initial curvature increases from 0 to 3 before the buckling loads drops with the increase of initial curvature. At a certain beam curvature, the buckling load may change its sense (i.e., from compression to tension), which is consistent with the shell structure theories [71]. The loads at which the buckling load changes sense are dubbed ‘null-loads’. The buckling load for for different values of the imperfection amplitude and the size parameter is shown in Table 2. First, one can notice the significance of the layup on the buckling load as the two parameters are varied. The beam shows the same trend as the case discussed before.

Table 1.
Nondimensional buckling load for a variety of initial curvatures and size parameter for

Table 2.
Non-dimensional buckling load for a variety of initial curvatures and size parameter for a
Now, we turn our attention to the significance of the initial imperfection on the buckling load, according to Equation (26). Figure 2 shows the variation of the buckling load with the beam’s imperfection amplitude as the nondimensional small-size parameter that is varied. Typically, the buckling load increases as the imperfection amplitude increases up to a threshold where the buckling load starts to decrease as the imperfection amplitude increases. It can also be noted that beyond the null-load, the buckling load switches from being positive (compressive) to being negative (tensile). The significance of the size parameter is evident from the figure where a considerable reduction in the buckling load is noticed.
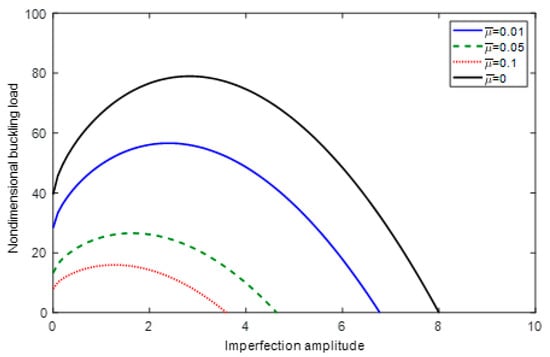
Figure 2.
Variation of the buckling load with the imperfection amplitude for = 1.
3.2. Postbuckling of Imperfect, Multilayer Nanobeams under Pre-Stress Loading
In this section, we present the postbuckling response of clamped-clamped nanobeams with imperfection. The beam is supposed to be under compressive pre-stress load due to manufacturing residual stresses. If this pre-stress load is beyond the buckling load, the beam buckles while its ends are kept fixed. As a result, a tensile force is created at the midplane due to bending. The net compressive force at the beam ends does not remain constant as the compressive pre-stress is reduced by the amount of the midplane stretching. First, we investigate the significance of the small size on the postbuckling for an initially straight column. Figure 3 shows the buckling amplitude as the pre-stress load is increased. Because the beam is perfect, the buckling point is called bifurcation or Euler buckling, where two symmetric stable equilibrium positions develop and grow gradually with the load. The initial straight position becomes unstable after buckling. The figure shows that as the size parameter becomes significant, i.e., size gets smaller and smaller, the buckling load reduces and more buckling amplitude is obtained at the same load. This is due to the softening effect of the nonlocal effect as highlighted before.
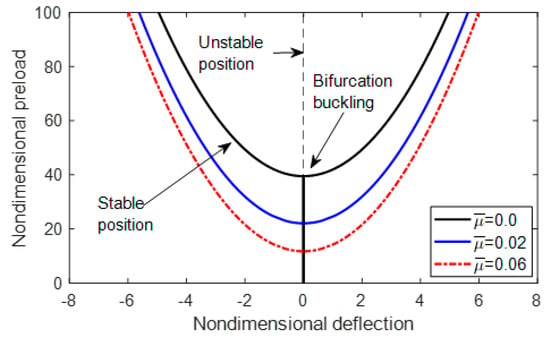
Figure 3.
Variation of the buckling amplitude with the axial pre-stress load of a perfect nanobeam with and a variety of the nonlocal parameter,
As pointed out earlier, as the beam exhibits imperfection, the onset of buckling occurs at a limit point rather than a bifurcation point. Figure 4, Figure 5, Figure 6 and Figure 7 show the postbuckling response of a beam with initial imperfection, , and size parameter, , respectively. In these figures, solid lines represent stable positions and dashed lines represent unstable positions. The load-deflection curves show the limit point where buckling occurs. It can be noticed that for the case in hand and for all size parameters the buckling load is greater than the Euler buckling load. As the beam size becomes smaller, the buckling load decreases and the buckling amplitude increases as a result of the nonlocal effect. In each figure, we plot the load-deflection curves for the perfect beam having the same size for the sake of comparison.
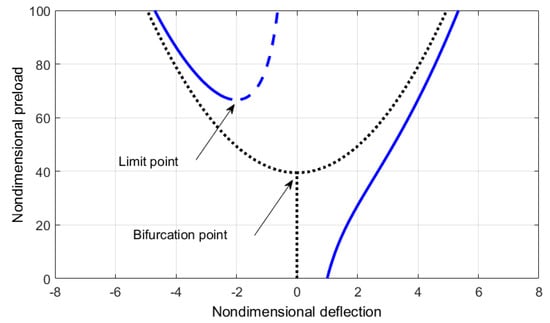
Figure 4.
Variation of the static deflection with the pre-load at and .
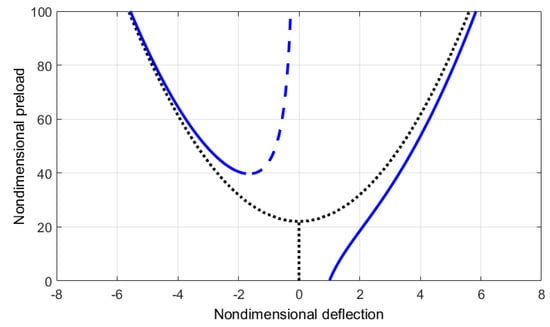
Figure 5.
Variation of the static deflection with the pre-load at , and .
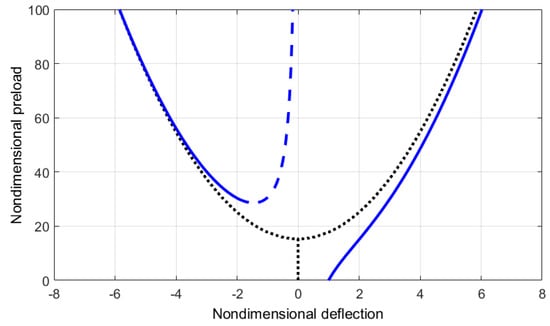
Figure 6.
Variation of the static deflection with the pre-load at and .
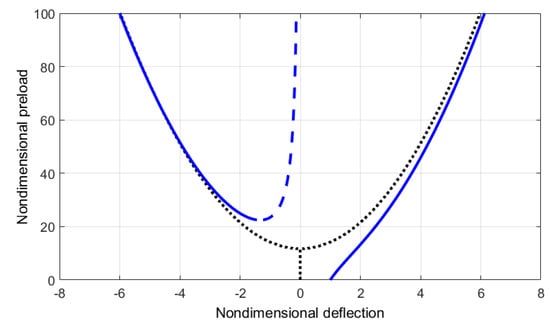
Figure 7.
Variation of the static deflection with the pre-load at and .
To investigate the significance of the lamination, we present the postbuckling response for () for the same imperfection amplitude (), as shown in Figure 8. As can be noted, the buckling load is higher than the Euler buckling as long as the imperfection amplitude is . The nonlocal effect of the size reduces the buckling load. The postbuckling response for beams with shows a smaller buckling amplitude compared with the case where , shown in Figure 9. In order to see cases where the buckling load becomes less than the Euler buckling load, we use an imperfection amplitude of Figure 9 shows the load-deflection curves for beams with an imperfection amplitude of , and a nonlocal parameter of , respectively. For the case where , the buckling amplitude is less than the Euler buckling load, as can be noticed from Figure 9d. This parametric study shows that the three parameters considered in this work, the size, lamination, and initial imperfection, have a significant effect on the buckling and postbuckling both qualitatively and quantitatively.
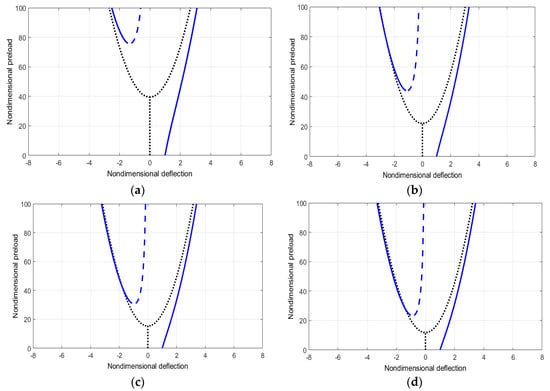
Figure 8.
Variation of the static deflection with the pre-load at . (a) (b) (c) (d)
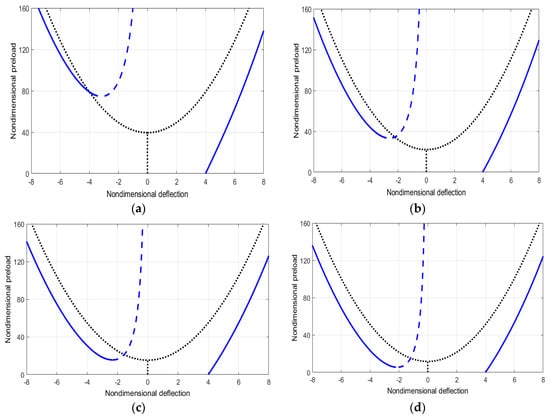
Figure 9.
Variation of the static deflection with the pre-load at and . (a) ; (b) (c) ; (d) .
4. Free Vibrations
The significance of the size parameter, imperfection, and lamination scheme on the free vibrations of nonlocal beams in the postbuckling regime is investigated. A small dynamic disturbance, , is assumed to take place around a static deflected position, , such that the total deflection measured from an initial configuration is defined as follows:
where the static position, , has been already defined for a given pre-load in the previous section. The linear free vibration problem in terms of the small dynamic disturbance, can be obtained by substituting Equation (25) into the governing equation, Equation (16). The result is
We note that the terms that have definite integrals can be dealt with as constants for any given functions, Assuming a harmonic solution in the form of , and solving Equation (26), yield the following general solution
where and are given by
where is the mode shape and is its frequency. This demands that the solution given by Equation (27) satisfies the boundary conditions and the equation of motion yields an eigenvalue problem that can be solved for the natural frequency, , and its associated mode shape. For more details, the reader is referred to Nayfeh and Emam [72].
Before the numerical results are presented, it is helpful to investigate the significance of the size parameter, , on the free vibrations to gain more insight. The size parameter, as can be seen from Equation (26), has an effect on the inertia, bending stiffness, and forcing terms. It can be noticed that the size parameter reduces the stiffness knowing that the constant, , is always positive. This means that the size effect has a kind of softening, which will in turn reduce the natural frequencies. The softening effect is noted from Figure 10, which represents the variation of the fundamental natural frequency with the pre-stress load for a unidirectional/cross-ply laminated beam. As the figure implies, for an initially straight multilayer nanobeam (), the natural frequency decreases as the pre-stress load increases in the prebuckling domain. This trend continues until the onset of buckling, where the fundamental frequency approaches zero. After that, the natural frequency increases as the pre-stress load is increased. This observation is noted for both classical and size-dependent nanobeams. The nonlocal effect on higher modes of perfect beams is further investigated and shown in Figure 10 for the third and fifth vibration modes, respectively. A greater reduction in the higher frequencies is noticed with the consideration of the size effect. However, the rate of change in the natural frequency in both the pre and postbuckling states is much less compared to the first mode. It is worth noting that for perfect beams, the natural frequencies of the even modes do not change with the pre-stress load in the postbuckling state (Nayfeh and Emam [72]). For instance, , respectively, and, respectively.
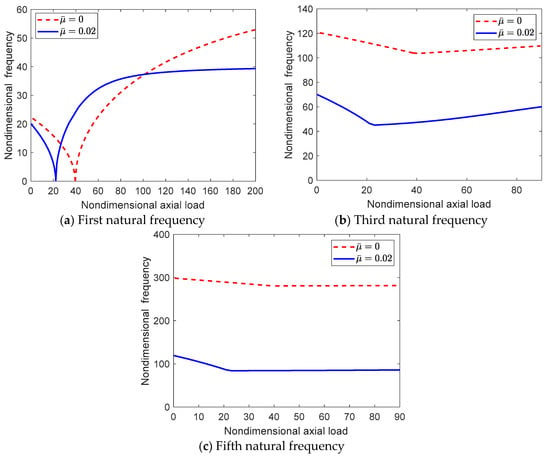
Figure 10.
The variation of the first, third, and fifth natural frequencies with the applied axial load for of the perfect nanobeam, , and .
Now, we investigate the effect of the initial curvature on the free vibration response. An initial imperfection of is introduced and the first five vibration modes are investigated for two values of the nonlocal parameter: . Figure 11 depicts the variation of the fundamental frequency with pre-stress load. Similar to perfect beams, the natural frequency exhibits a decrease in the prebuckling state, then it increases monotonically in the postbuckling state. It is noted that the inclusion of the nonlocal effect, , not only decreases the buckling load, but it also results in a leveling of the fundamental frequency as the axial load increases. This shows the hardening effect of nonlocal elasticity on the response of nanobeams.
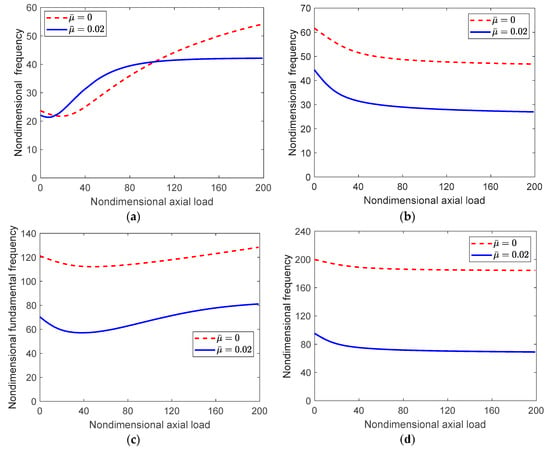
Figure 11.
The variation of the first four natural frequencies with the applied axial load for of the imperfect nanobeam, , and . (a) The first natural frequency; (b) The second natural frequency; (c) The third natural frequency; (d) The fourth natural frequency.
The nonlocal effect is more prominent for higher modes of vibration. Figure 11 shows the variation of the first to the fourth natural frequencies of the nanobeam with the pre-stress load. As can be seen from the figures, the natural frequencies significantly decrease with the inclusion of nonlocal effects. It is decreased by a factor of two for the second mode and by a factor of three for the fifth mode. It is also noted, except for the first and third modes, that the natural frequencies exhibit an initial decrease in the pre-buckling state then they level out in the post-buckling state.
5. Conclusions
An investigation into the postbuckling and free vibration response of size-dependent, geometrically imperfect multilayer nanobeams was introduced. The small-size effect was modeled according to the nonlocal elasticity differential model of Eringen within the nonlinear Bernoulli-Euler beam theory. It was found that the nonlocal effect reduces the buckling load and increases the postbuckling static response. The presence of initial imperfection changes the nature of the point at the onset of buckling from a bifurcation point to a limit point. The initial imperfection was found to be a key factor to enhance the buckling load; however, the optimum value of the initial imperfection that results in the maximum buckling load was found to be size dependent. The buckling load at different values of initial imperfection, a size parameter for a variety of lamination coefficients, was presented. Numerical results that show the buckling load and the load-deflection curves in the postbuckling domain for a variety of parameters were presented. It is shown that the buckling load with the presence of imperfection and a small-size effect can be less than or greater than the Euler buckling load. The linear free vibration problem has been solved for the vibration mode shapes and natural frequencies around the static postbuckling position. The fundamental natural frequency was found to be sensitive to the size effect, which has a significant qualitative and quantitative contribution. Moreover, the size effect was more prominent for higher modes of vibration where the buckling loads are significantly decreased. This study can be extended and supported by experimental testing to help design small-scale devices incorporating multilayered, initially curved beams at a nanoscale.
Author Contributions
S.A.E. and M.A.E. formulated the problem and generated the data. S.A.E. wrote the manuscript and presented the results, M.A.E. and W.S.A. reviewed the manuscript.
Funding
This research received no external funding.
Acknowledgments
The third author acknowledges KFUPM for their support.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bortz, J.; Shatz, N. Nanolayered polymer diffusive spectral filters. In Proceedings of the SPIE 8485, Nonimaging Optics: Efficient Design for Illumination and Solar Concentration IX, San Diego, CA, USA, 11 October 2012. [Google Scholar]
- Legtenberg, R.; Gilbert, J.; Senturia, S.D.; Elwenspoek, M. Electrostatic curved electrode actuators. J. Microelectromech. Syst. 1997, 6, 257–265. [Google Scholar] [CrossRef]
- Torri, P.; Hirvonen, J.P.; Kung, H.; Lu, Y.C.; Nastasi, M.; Gibson, P.N. Mechanical properties, stress evolution and high-temperature thermal stability of nanolayered Mo–Si–N/SiC thin films. J. Vac. Sci. Technol. B 1999, 17, 1329–1335. [Google Scholar] [CrossRef]
- Li, Z.; Dharap, P.; Nagarajaiah, S.; Nordgren, R.P.; Yakobson, B. Nonlinear analysis of a SWCNT over a bundle of nanotubes. Int. J. Solids Struct. 2004, 41, 6925–6936. [Google Scholar] [CrossRef]
- Verma, N.; Jayaram, V. Role of interface curvature on stress distribution under indentation for ZrN/Zr multilayer coating. Thin Solid Films 2014, 571, 283–289. [Google Scholar] [CrossRef]
- Senturia, S.D. Microsystem Design; Kluwer Academic Publishers: Boston, MA, USA, 2001. [Google Scholar]
- Chidamparam, P.; Leissa, A.W. Vibrations of planar curved beams, rings, and arches. Appl. Mech. Rev. 1993, 46, 467–483. [Google Scholar] [CrossRef]
- Petyt, M.; Fleischer, C.C. Free vibration of a curved beam. J. Sound Vib. 1971, 18, 17–30. [Google Scholar] [CrossRef]
- Palani, G.S.; Rajasekaran, S. Finite element analysis of thin-walled curved beams made of Composites. J. Struct. Eng. 1992, 118, 2039–2061. [Google Scholar] [CrossRef]
- Lacarbonara, W. A theoretical and experimental investigation of nonlinear vibrations of buckled beams. Ph.D. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 1997. [Google Scholar]
- Howson, W.P.; Jemah, A.K. Exact out-of-plane natural frequencies of curved Timoshenko beams. J. Eng. Mech. 1999, 125, 19–25. [Google Scholar] [CrossRef]
- Raveendranath, P.; Singh, G.; Pradhan, B. A two-noded locking-free shear flexible curved beam element. Int. J. Numer. Methods Eng. 1999, 44, 265–280. [Google Scholar] [CrossRef]
- Lacarbonara, W.; Yabuno, H. Closed-loop non-linear control of an initially imperfect beam with non-collocated input. J. Sound Vib. 2004, 273, 695–711. [Google Scholar] [CrossRef]
- Lacarbonara, W.; Arafat, H.N.; Nayfeh, A.H. Non-linear interactions in imperfect beams at veering. Int. J. Non-Linear Mech. 2005, 40, 987–1003. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, M.Z.; Zhao, B.S. The refined theory of rectangular curved beams. Acta Mech. 2007, 189, 141–150. [Google Scholar] [CrossRef]
- Chang, C.S.; Hodges, D. Vibration characteristics of curved beams. J. Mech. Mater. Struct. 2009, 4, 675–692. [Google Scholar] [CrossRef]
- Emam, S.A. A static and dynamic analysis of the postbuckling of geometrically imperfect beams. Structures 2009, 90, 247–253. [Google Scholar] [CrossRef]
- Shooshtari, A.; Kalhori, H.; Masoodian, A. Investigation for dimension effect on mechanical behavior of a metallic curved micro-cantilever beam. Measurement 2011, 44, 454–465. [Google Scholar] [CrossRef]
- Stanciulescu, I.; Mitchell, T.; Chandra, Y.; Eason, T.; Spottswood, M. A lower bound on snap-through instability of curved beams under thermomechanical loads. Int. J. Non-Linear Mech. 2012, 47, 561–575. [Google Scholar] [CrossRef]
- Wang, B.; Deng, Z.; Zhang, K.; Zhou, J. Dynamic analysis of embedded curved double-walled carbon nanotubes based on nonlocal Euler-Bernoulli Beam theory. Multidiscipl. Model. Mater. Struct. 2012, 8, 432–453. [Google Scholar] [CrossRef]
- Wu, J.S.; Lin, F.T.; Shaw, H.J. Free in-plane vibration analysis of a curved beam (arch) with arbitrary various concentrated elements. Appl. Math. Model. 2013, 37, 7588–7610. [Google Scholar] [CrossRef]
- Dastgerdi, J.; Marquis, G.; Salimi, M. The effect of nanotubes waviness on mechanical properties of CNT/SMP composites. Compos. Sci. Technol. 2013, 86, 164–169. [Google Scholar] [CrossRef]
- Lee, S.Y.; Yan, Q.Z. An analytical solution for out-of-plane deflection of a curved Timoshenko beam with strong nonlinear boundary conditions. Acta Mech. 2015, 226, 3679–3694. [Google Scholar] [CrossRef]
- Truesdell, C.; Noll, W. The Nonlinear Field Theories of Mechanics; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Eringen, A.C. Nonlocal polar elastic continua. Int. J. Eng. Sci. 1972, 10, 1–16. [Google Scholar] [CrossRef]
- Eringen, A.C.; Edelen, D. On nonlocal elasticity. Int. J. Eng. Sci. 1972, 10, 233–248. [Google Scholar] [CrossRef]
- Eringen, A.C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J. Appl. Phys. 1983, 54, 4703–4710. [Google Scholar] [CrossRef]
- Qian, D.; Dickey, E.C.; Andrews, R.; Rantell, T. Load transfer and deformation mechanisms in carbon nanotube-polystyrene Composites. Appl. Phys. Lett. 2000, 76, 2868–2870. [Google Scholar] [CrossRef]
- Wang, Z.L.; Poncharal, P.; De Heer, W.A. Nanomeasurements of individual carbon nanotubes by in situ TEM. Pure Appl. Chem. 2000, 72, 209–219. [Google Scholar] [CrossRef]
- Mikata, Y. Complete solution of elastica for a clamped-hinged beam, and its applications to a carbon nanotube. Acta Mech. 2007, 190, 133–150. [Google Scholar] [CrossRef]
- Mayoof, F.N.; Hawwa, M.A. Chaotic behavior of a curved carbon nanotube under harmonic excitation. Chaos Solitons Fractals 2009, 42, 1860–1867. [Google Scholar] [CrossRef]
- Formica, G.; Lacarbonara, W.; Alessi, R. Vibrations of carbon nanotube-reinforced s. J. Sound Vib. 2010, 329, 1875–1889. [Google Scholar] [CrossRef]
- Ouakad, H.M.; Younis, M.I. Natural frequencies and mode shapes of initially curved carbon nanotube resonators under electric excitation. J. Sound Vib. 2011, 330, 3182–3195. [Google Scholar] [CrossRef]
- Romano, G.; Barretta, R.; Diaco, M.; de Sciarra, F.M. Constitutive boundary conditions and paradoxes in nonlocal elastic nanobeams. Int. J. Mech. Sci. 2017, 121, 151–156. [Google Scholar] [CrossRef]
- Romano, G.; Barretta, R. Stress-driven versus strain-driven nonlocal integral model for elastic nano-beams. Compos. Part B 2017, 114, 184–188. [Google Scholar] [CrossRef]
- Romano, G.; Barretta, R. Nonlocal elasticity in nanobeams: The stress-driven integral model. Int. J. Eng. Sci. 2017, 115, 14–27. [Google Scholar] [CrossRef]
- Glavardanov, V.B.; Spasic, D.T.; Atanackovic, T.M. Stability and optimal shape of Pflüger micro/nano beam. Int. J. Solids Struct. 2012, 49, 2559–2567. [Google Scholar] [CrossRef]
- Eltaher, M.A.; Emam, S.A.; Mahmoud, F.F. Free vibration analysis of functionally graded size-dependent nanobeams. Appl. Math. Comput. 2012, 218, 7406–7420. [Google Scholar] [CrossRef]
- Eltaher, M.A.; Emam, S.A.; Mahmoud, F.F. Static and stability analysis of nonlocal functionally graded nanobeams. Compos. Struct. 2013, 96, 82–88. [Google Scholar] [CrossRef]
- Wang, L.; Dai, H.L.; Qian, Q. Dynamics of simply supported fluid-conveying pipes with geometric imperfections. J. Fluids Struct. 2012, 29, 97–106. [Google Scholar] [CrossRef]
- Wang, B.; Deng, Z.; Zhang, K.; Zhou, J. Nonlinear vibration of embedded single-walled carbon nanotube with geometrical imperfection under harmonic load based on nonlocal Timoshenko beam theory. Appl. Math. Mech. 2013, 34, 269–280. [Google Scholar] [CrossRef]
- Emam, S.A. A general nonlocal nonlinear model for buckling of nanobeams. Appl. Math. Model. 2013, 37, 6929–6939. [Google Scholar] [CrossRef]
- Thongyothee, C.; Chucheepsakul, S. Postbuckling behaviors of nanorods including the effects of nonlocal elasticity theory and surface stress. J. Appl. Phys. 2013, 114, 243507. [Google Scholar] [CrossRef]
- Mohammadi, H.; Mahzoon, M.; Mohammadi, M.; Mohammadi, M. Postbuckling instability of nonlinear nanobeam with geometric imperfection embedded in elastic foundation. Nonlinear Dyn. 2014, 76, 2005–2016. [Google Scholar] [CrossRef]
- Khater, M.; Eltaher, M.; Abdel-Rahman, E.; Yavuz, M. Surface and Thermal Load Effects on the Buckling of Curved Nanowires. J. Eng. Sci. Technol. 2014, 17, 279–283. [Google Scholar] [CrossRef][Green Version]
- Eltaher, M.A.; Khater, M.E.; Emam, S.A. A review on nonlocal elastic models for bending, buckling, vibrations, and wave propagation of nanoscale beams. Appl. Math. Model. 2016, 40, 4109–4128. [Google Scholar] [CrossRef]
- Eltaher, M.A.; El-Borgi, S.; Reddy, J.N. Nonlinear analysis of size-dependent and material-dependent nonlocal CNTs. Multilayer Struct. 2016, 153, 902–913. [Google Scholar] [CrossRef]
- Ghadiri, M.; Shafiei, N. Nonlinear bending vibration of a rotating nanobeam based on nonlocal Eringen’s theory using differential quadrature method. Microsyst. Technol. 2016, 22, 2853–2867. [Google Scholar] [CrossRef]
- Kaghazian, A.; Hajnayeb, A.; Foruzande, H. Free vibration analysis of a piezoelectric nanobeam using nonlocal elasticity theory. Struct. Eng. Mech. 2017, 61, 617–624. [Google Scholar] [CrossRef]
- Khetir, H.; Bouiadjra, M.B.; Houari, M.S.A.; Tounsi, A.; Mahmoud, S.R. A new nonlocal trigonometric shear deformation theory for thermal buckling analysis of embedded nanosize FG plates. Struct. Eng. Mech. 2017, 64, 391–402. [Google Scholar]
- Mohamed, N.; Eltaher, M.A.; Mohamed, S.A.; Seddek, L.F. Numerical analysis of nonlinear free and forced vibrations of buckled curved beams resting on nonlinear elastic foundations. Int. J. Non Linear Mech. 2018, 101, 157–173. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Barati, M.R. Axial magnetic field effects on dynamic characteristics of embedded multiphase nanocrystalline nanobeams. Microsyst. Technol. 2018, 24, 3521–3536. [Google Scholar] [CrossRef]
- Eltaher, M.A.; Kabeel, A.M.; Almitani, K.H.; Abdraboh, A.M. Static bending and buckling of perforated nonlocal size-dependent nanobeams. Microsyst. Technol. 2018, 24, 4881–4893. [Google Scholar] [CrossRef]
- Eltaher, M.A.; Abdraboh, A.M.; Almitani, K.H. Resonance frequencies of size dependent perforated nonlocal nanobeam. Microsyst. Technol. 2018, 24, 3925–3937. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Barati, M.R. Vibration analysis of embedded size dependent FG nanobeams based on third-order shear deformation beam theory. Struct. Eng. Mech. 2017, 61, 721–736. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Barati, M.R. A unified formulation for modeling of inhomogeneous nonlocal beams. Struct. Eng. Mech. 2018, 66, 369–377. [Google Scholar]
- Challamel, N.; Wang, C.M. The small length scale effect for a non-local cantilever beam: A paradox solved. Nanotechnology 2008, 19, 345703. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Yao, L.; Chen, W.; Li, S. Comments on nonlocal effects in nano-cantilever beams. Int. J. Eng. Sci. 2015, 87, 47–57. [Google Scholar] [CrossRef]
- Benvenuti, E.; Simone, A. One-dimensional nonlocal and gradient elasticity: Closed-form solution and size effect. Mech. Res. Commun. 2013, 48, 46–51. [Google Scholar] [CrossRef]
- Fernández-Sáez, J.; Zaera, R.; Loya, J.A.; Reddy, J.N. Bending of Euler–Bernoulli beams using Eringen’s integral formulation: A paradox resolved. Int. J. Eng. Sci. 2016, 99, 107–116. [Google Scholar] [CrossRef]
- Tuna, M.; Kirca, M. Exact solution of Eringen’s nonlocal integral model for bending of Euler-Bernoulli and Timoshenko beams. Int. J. Eng. Sci. 2016, 105, 80–92. [Google Scholar] [CrossRef]
- Apuzzo, A.; Barretta, R.; Luciano, R.; de Sciarra, F.M.; Penna, R. Free vibrations of Bernoulli-Euler nano-beams by the stress-driven nonlocal integral model. Compos. Part B Eng. 2017, 123, 105–111. [Google Scholar] [CrossRef]
- Fang, W.; Wickert, J.A. Post buckling of micromachined beams. J. Micromech. Microeng. 1994, 4, 116–122. [Google Scholar] [CrossRef]
- Emam, S.A. Analysis of shear-deformable composite beams in postbuckling. Compos. Struct. 2011, 94, 24–30. [Google Scholar] [CrossRef]
- Eltaher, M.; Khater, M.; Abdel-Rahman, E.; Yavuz, M. Model for nano-scale bonding wires under thermal loading. In Proceedings of the 14th IEEE International Conference on Nanotechnology, Toronto, ON, Canada, 18–21 August 2014; pp. 382–385. [Google Scholar]
- Reddy, J.N. On laminated plates with integrated sensors and actuators. Eng. Struct. 1999, 21, 568–593. [Google Scholar] [CrossRef]
- Wang, Q. Wave propagation in carbon nanotubes via nonlocal continuum mechanics. J. Appl. Phys. 2005, 98, 124301. [Google Scholar] [CrossRef]
- Jones, R.M. Buckling of Bars, Plates and Shells; Bull Ridge Publishing: Blacksburg, VA, USA, 2006. [Google Scholar]
- Nayfeh, A.H.; Balachandran, B. Applied Nonlinear Dynamics, Analytical, Computational, and Experimental Methods; Wiley Series in Nonlinear Sciences; Wiley Interscience: New York, NY, USA, 2000; ISBN 0471593486. [Google Scholar]
- Aydogdu, M. A general nonlocal beam theory: Its application to nanobeam bending, buckling and vibration. Phys. E Low Dimens. Syst. Nanostruct. 2009, 41, 1651–1655. [Google Scholar] [CrossRef]
- Srubshchik, L.S. Precritical equilibrium of a thin shallow shell of revolution and its stability. J. Appl. Math. Mech. 1980, 44, 229–235. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Emam, S.A. Exact solution and stability of postbuckling configurations of beams. Nonlinear Dyn. 2008, 54, 395–408. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).