Abstract
The vibrational behavior of viscoelastic nanoplates with a corrugated geometry is a key topic of practical interest. This problem is addressed here for wrinkled nanoplates with small corrugations related to incorrect manufacturing. To this end, a new One-Variable First-order Shear Deformation plate Theory (OVFSDT) is proposed in a combined form with a non-local strain gradient theory. The Kelvin–Voigt model is employed to describe the viscoelastic behavior of the nanoplate, whereby the frequency equations are solved numerically according to Navier’s approach, for simply-supported nanostructures. A comparative evaluation between the proposed theory and other approaches in the literature is successfully performed. It follows a large parametric study of the vibration response for varying geometry corrugations and non-local parameters.
1. Introduction
Wrinkles represent one of the major defects of metal sheets that can emerge during a manufacturing process (e.g., deep drawing, hot and cold rolling, etc.), with adverse effects on their mechanical performances. For instance, during a hot rolling process of a metal sheet, some possible corrugations can yield to deleterious residual stresses. Since the cooling coefficient at the mid-planes features a higher velocity than the one at the external surfaces, this can affect the microstructure of the plate. The wrinkles with large dimensions could be preventable, but fine corrugations remain almost unavoidable. In the last case, corrugated sheets with very fine corrugations are generally turned into pieces, while featuring an unpredictable behavior in machinery. This means that the effect of wrinkling can be of extreme importance for the mechanical behavior of metal sheets. Among many possible waviness configurations of a sheet, the sinusoidal waveform is one of the most common configuration after a cold rolling process, with an undefined wave number. These sinusoidal waves can be also characterized by different shapes, with one-side or more-side corrugations. A simple assumption of corrugated geometry considers the wave as a coil break, or as a central buckle [1].
With the advent of modern technologies such as nanotechnologies, the production of sheets with very small dimensions has increased significantly, including, for example, the adoption of nanosheets in advanced composites and electronic pieces, which make nanoparticles an extremely important component. Therefore, wrinkling and irregularities in nanosheets due to different manufacturing processes represent important issues to be treated. The great importance and complexity of waviness within nanosheets and nanoplates has attracted most researchers to the study of their vibration behavior, as it is useful for many practical engineering applications, as sensors, transducers or NanoElectroMechanical Systems (NEMS). Kamarian et al. [2] studied the natural frequencies of composite conical shells based on a Generalized Differential Quadrature (GDQ) method. The shells were reinforced with agglomerated nanotubes and a First-order Shear Deformation plate Theory (FSDT) was employed. The agglomeration effect on the free vibration behavior of laminated composite doubly-curved shells was also evaluated by Tornabene et al. [3], where the laminated structures were reinforced with nanotubes with a functionally graded distribution along the thickness. The additional work by Banić et al. [4] checked for the effect of the Winkler–Pasternak matrix on the vibrations of plates and shells strengthened by agglomerated nanotubes, while applying the GDQ approach to solve numerically the problem. The stability of nanocomposite-stiffened cylindrical shells was investigated by Nejati et al. [5], whose structures included a waviness geometry, and they were reinforced by functionally graded nanotubes with temperature-dependent properties. Malikan et al. [6] recently studied the thermal buckling behavior of double-layered nanoplates under a shear in-plane loading, and combined the FSDT with Eringen’s differential law to approach the problem and to determine the critical temperature. In a similar way, Malikan [7] applied the FSDT to study the coupled electro-mechanical behavior of nanoplates. To consider the small scale effect on the structural response, a modified couple stress theory was adopted successfully by the author. In two further works by Malikan [8,9], the non-uniform buckling response of composite nanoplates and microplates was analyzed both analytically and numerically. Malikan and Nguyen [10] also examined the electro-magnetic nanoplates in a hygrothermal environment, by using a new plate theory in conjunction with a non-local strain gradient model. In this context, many other analytical and numerical works have focused on the vibration and buckling response of nanocomposite materials and structures also in thermal conditions, see e.g., [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30], among others.
It is undoubted that the presence of damping within materials at different scales can affect significantly the overall structural response. For such a reason, the damping property must be carefully characterized and applied for the numerical study of actual nanomaterials and structures. Surprisingly, little attention has been devoted in the literature to this aspect, at least for nanoplates and nanoshells. As a result, Ahmadi-Hashemi et al. [20] analyzed a nanoplate in forced vibrational conditions, by assuming both an external and internal viscoelastic damping. The external damper was modeled as a visco-Pasternak foundation, whereby the internal damper was treated by a Kelvin–Voigt model. The Classical Plate Theory (CPT) in conjunction with the Eringen’s non-local continuum theory was successfully applied, whilst a rectangular nanoplate with simply-supported boundary conditions was examined according to the Navier’s technique. Wang et al. [21] investigated the eigen frequencies of a bi-layer viscoelastic nanoplate by means of a non-local elasticity theory. They applied the CPT on the non-linear strains, whereas the natural and resonant frequencies were computed by considering the Galerkin analytical method for clamped and simple boundaries. Zenkour and Sobhy [22] presented a free vibration analysis of a non-local viscoelastic nanoplate considering piezoelectricity placed on the viscoelastic medium in a hygrothermal environment. The Simple FSDT (S-FSDT) in a sinusoidal form was considered together with a non-local elasticity theory.
In the present work, instead, we propose an original study on the vibrational response of nanoplates with sinusoidal corrugations. The structural damping is considered by applying a Kelvin–Voigt linear model, whereas a modified version of FSDT is proposed in a combined form with the non-local strain gradient theory to tackle the problem. Besides this, the numerical results are extracted according to the Navier’s approach for simply supported nanoplates. For comparative purposes, the numerical results are verified against the outcomes of molecular dynamics-based simulations. Furthermore, the numerical results have been obtained for different geometrical and mechanical parameters, including a varying number of corrugations, as well as different viscoelastic coefficients and waviness configurations. The paper is organized as follows. First, we present the problem formulation and the governing equations in Section 2, whose solution procedure is proposed in Section 3. Next, the numerical parametric investigation is presented and discussed in Section 4, whereas the main conclusions are drawn in Section 5.
2. Modeling Assumptions
2.1. Problem Definition
The analysis considers a corrugated plate with length , width and thickness , as shown in Figure 1a. More details about the corrugations are shown in Figure 1b, where the parameter defines the length of half wave of a sinusoidal wave, and refers to the height of the sinusoidal wave. To derive the constitutive equations, we adopt a new One-Variable First-order Shear Deformation Theory (OVFSDT) which is compared to some further plate theories from literature. According to the proposed theory, the displacement field is defined as
where and are the rotations around the and axis, respectively, while , and denote the variations of the kinematic quantities along the , and axis, respectively. In addition, we define .
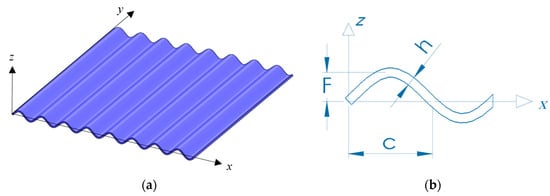
Figure 1.
Corrugated nanoplate: (a) 3D view, and (b) in-plane geometry.
By applying the Hamilton’s principle, we define the potential energy of the domain as [2,20]
where refers to the variation of the energy quantities, is the strain energy, is the kinetic energy, and is the work related to external forces or foundations, here neglected in the following.
The strain energy in Equation (2) can be computed as
and being the stress and strain tensors, respectively [6]. Based on the OVFSDT, the strain tensor is defined as follows
In addition, the kinetic energy can be determined as [2,20]
whose variation reads
The enforcement of yields to the following governing equations of the problem
The second moments of inertia in Equation (7) are defined as
The additional quantities , and in Equation (7) refer to the axial, flexural and shear internal actions along the , and axes, namely
2.2. Non-Local Strain Gradient Theory
Non-localities and small scales represent two important aspects that can be considered within a quantum mechanics approach. Since it is not straightforward to study the mechanical behavior of the nanostructures, many elasticity theories commonly require some strong simplifications according to continuum mechanics. In this framework, herein, we apply a non-local strain gradient model to investigate the nanoscale effects. A similar elasticity model includes both non-local and strain gradient impressive effects for nanoplates [10,31,32], as follows
l and μ being the length scale and non-local parameter, respectively.
In order to account for the wavy configuration of the nanoplate, we introduce an equivalent bending stiffness in the model [33,34,35]. Thus, for a sinusoidal wavy nanoplate, the corrugation is assumed as , whereas the equivalent mechanical properties for the orthotropic plate read
where L represents the length of the half wave of sinusoidal curve , and refer to the Poisson’s ratio and elasticity modulus, respectively, and Aij and Dij denote the extensional and flexural equivalent stiffness of the waviness nanoplate, respectively.
2.3. The Linear Viscoelastic Model
A Kelvin–Voigt linear model is herein applied in the equilibrium equations, according to the following procedure. The stress-strain relation for viscoelastic models reads as follows
and being the viscoelastic operators. A Kelvin–Voigt model includes the Newtonian damper and the Hookean elastic spring arranged in parallel [20,21,22]
where is the viscoelastic structural damping coefficient.
Thereafter, by substituting Equations (10), (11), (13) into Equation (9), the resulting non-local stresses are readily obtained as
3. Analytical Approach
The analytical treatment of the problem is based on the Navier’s approach. In detail, a simple supported plate is here studied, whose displacement field w is discretized by a double series function as follows [10]
where is the unknown amplitude, denotes the natural frequencies, and refer to the half-wave integers, and refers to time. By substituting Equation (15) into the motion equations and by neglecting the non-linear terms, we obtain the following algebraic equations
and being the mass and stiffness matrix, respectively.
4. Numerical Results and Discussion
In this section, we check first the accuracy of the proposed OVFSDT-based approach by means of a comparative evaluation between our numerical predictions and those available from the literature. More specifically, due to a complete lack of results about corrugated nanoplates, we here compare our results with those ones obtained for flat nanosheets. Among a large variety of possible approaches adopted in literature for the vibration study of graphene plates, the molecular dynamics and the non-local GDQ-based FSDT, as proposed in [36], have been here selected as efficient and accurate methods for comparative purposes.
The comparative results are summarized in Table 1 and Table 2, for a grapheme nanoplate with a zigzag hexagonal arrangement, or an armchair arrangement, respectively, assuming a Young’s modulus , a Poisson’s ratio , a constant thickness nm, two different non-local parameters nm2 and nm2. As visible in these two tables, the very good agreement between results reflects the accuracy of the proposed formulation to approach a similar problem, provided that non-local parameters are adequately selected. Note that few discrepancies between results can be mainly related to the different solution method of the governing equations, e.g., a Navier’s approach instead of a GDQ. These differences become even more negligible for increasing lengths as visible in Table 1 and Table 2. Some possible effects can be also related to the selected plate theory, as evaluated comparatively in Table 3 according to a CPT, FSDT, or a Third-order Shear Deformation Theory (TSDT) [23], as well as according to a three-dimensional elasticity [37] and the S-FSDT [38].

Table 1.
Numerical results based on the one-variable first-order shear deformation plate theory (OVFSDT), molecular dynamics, and non-local FSDT. , , , nm2.

Table 2.
Numerical results based on the OVFSDT, molecular dynamics, and non-local FSDT. , , , nm2.

Table 3.
Comparative evaluation between OVFSDT and other non-local plate models from literature. , , .
More specifically, the dimensionless natural frequency is computed for two different length-ratios (i.e., and , respectively), where two different length-to-thickness ratios and are assumed, while varying the non-local parameter . Based on Table 3, our results resemble very well those presented in [23,37,38], especially when treating thin plates. A general decrease in the natural frequency is also observed for an increasing non-local parameter, and a fixed geometry, independently of the selected plate theory.
After this preliminary check about the consistency of the proposed OVFSDT, we continue to apply this approach for a corrugated viscoelastic nanoplate with mechanical and geometrical properties, as summarized in Table 4.

Table 4.
Material properties of the viscoelastic nanoplate [36].
Figure 2 shows the variation of the natural frequency with the non-local parameter (Figure 2a) and dimensionless length scale (Figure 2b) within the proposed formulation, where both flat and curved geometries are compared in the presence or not of the viscoelastic damping parameter, namely Ns/m2 or Ns/m2. The nanoplate features two sinusoidal corrugations with amplitude (i.e., dimensionless amplitude ) and semi-length . Based on Figure 2, an increased non-local coefficient yields to a reduced natural frequency, whereas an increasing length scale parameter gets to an increased natural frequency of the nanostructure because of its increased stiffness, under the non-local strain gradient theory. This agrees with findings by Malikan and Nguyen [10]. Moreover, the natural frequency of the flat nanostructure is lower than the corrugated one, for the same fixed non-local coefficient (Figure 2a) and dimensionless length scale (Figure 2b). Remarkably, all the curves in Figure 2 are almost scalable with the varying geometry and damping parameter. A negligible increase in the natural frequency is also observed for an increasing viscoelastic damping parameter . Note that the equations based on the nonlocal strain gradient theory revert to the classical mechanics ones, when the length scale and nonlocal parameter are exactly the same (i.e., when is equal to ). Based on a comparative evaluation of Figure 2a,b, it is worth noting that the response of the nonlocal parameter compared to the length scale , is more sensitive for each fixed geometry and damping parameters of the nanostructure.
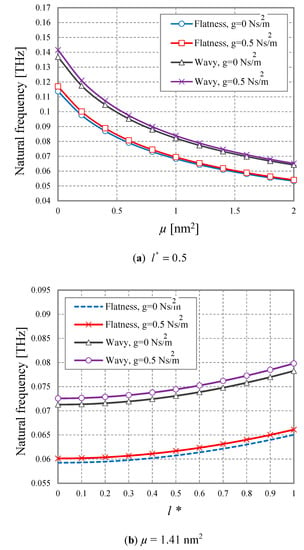
Figure 2.
Variation of the natural frequency with the nonlocal parameter (a) and the length scale (b).
A complete overview of the vibrating response of the corrugated nanosheet with varying geometries is plotted in Figure 3 and Figure 4. More specifically, a different number of waves is considered in Figure 3, while varying the amplitude between and . As visible in Figure 3, an increasing wave amplitude , for a fixed number of corrugations, leads to an increased frequency and stiffness of the nanoplate. The natural frequency seems to increase linearly up to a threshold value, moving from a flat to a corrugated nanoplate with just one corrugation. This threshold value clearly depends on the corrugation, since it increases for increasing magnitudes . A meaningless increase of the natural frequencies is also observed in Figure 3 after 1 corrugation, probably because further corrugations do not affect significantly the stiffness of the structure. Figure 4 also shows the effect of the damping on the structural response of a corrugated nanoplate with , nm2, , where the natural frequency of the structure increases proportionally with the viscoelastic damping. This increase is even more pronounced for increasing wave magnitudes . This means that the geometry of corrugations can affect the response of the nanostructure significantly, especially for higher values of viscosity. Thus, the exact geometry of wrinkles and imperfections resulting from a manufacturing process must carefully account for the structural study of a hyper-viscoelastic nanoplate.
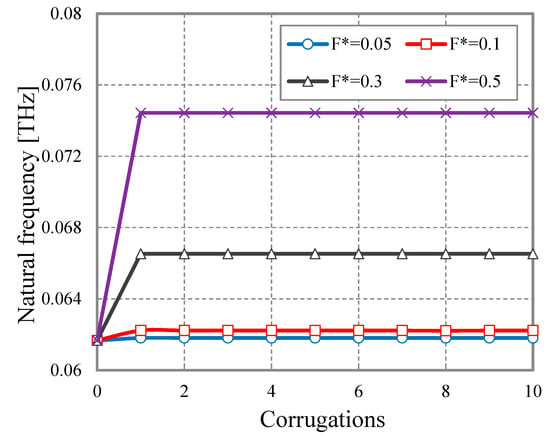
Figure 3.
Natural frequency vs. number of corrugations. , nm2, Ns/m2.
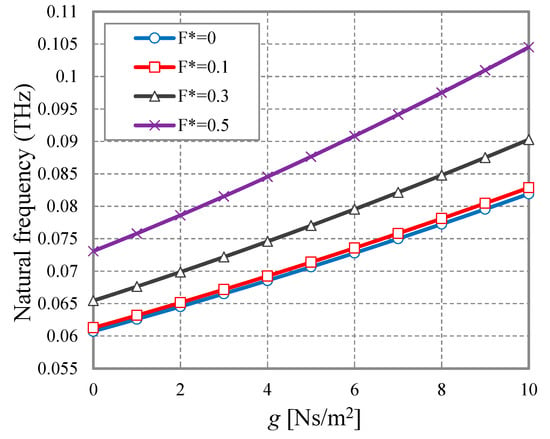
Figure 4.
Natural frequency vs. viscoelastic damping. , nm2, .
Another parametric investigation considers the combined effect of the dimensionless length scale and wave amplitude , for a corrugated nanoplate with 5 corrugations (i.e., for ), while keeping fixed the non-locality and the viscosity . This is shown in Figure 5, whose curves translate upwards constantly as the length scale parameter increases. Furthermore, the natural frequency increases monotonically as the dimensionless wave magnitude is increased, independently of the length scale . The results have been suitably repeated for a different number of corrugations, which are not reported here for the sake of brevity.
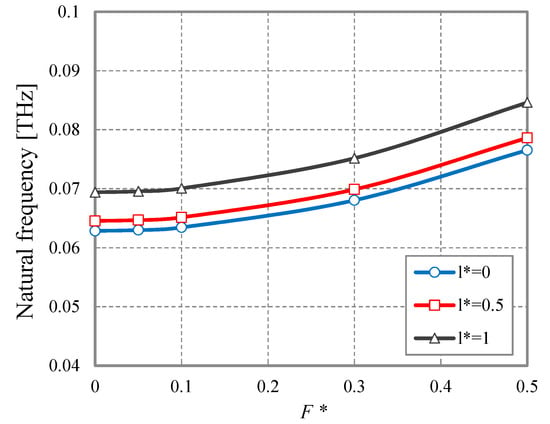
Figure 5.
Natural frequency vs. dimensionless wave amplitude . nm2, Ns/m2, .
5. Conclusions
The vibration response of viscoelastic nanoplates was investigated for different corrugation geometries, mainly related to incorrect manufacturing. To this end, the non-local strain gradient equations were incorporated into an OVFSDT, while applying the Kelvin–Voigt model for a realistic treatment of viscoelasticy. After a preliminary check of the accuracy of the proposed formulation, we employed a parametric investigation to analyze the sensitivity of the structural response at the nanoscale. Based on the numerical results, it is clear that the existence of corrugations within nanoplates can yield to a significant increase in their natural frequency and stiffness. More specifically, the structural response depends strictly on the corrugation geometry, especially for increasing values of the internal viscoelastic damping and non-local parameter.
Author Contributions
Conceptualization, Methodology, Software, Validation, Investigation, Writing-Review & Editing: M.M., R.D. and F.T. All the authors contributed equally to this work.
Funding
This research received no external funding.
Acknowledgments
The research topic is one of the subjects of the Centre of Study and Research for the Identification of Materials and Structures (CIMEST)-“M. Capurso” of the University of Bologna (Italy).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sunthorn, S.; Kittiphat, R. The effect on rolling mill of waviness in hot rolled steel, World academy of sciences, Engineering and technology. Int. J. Metall. Mater. Eng. 2014, 8, 2077–2082. [Google Scholar]
- Kamarian, S.; Salim, M.; Dimitri, R.; Tornabene, F. Free vibration analysis of conical shells reinforced with agglomerated carbon nanotubes. Int. J. Mech. Sci. 2016, 108–109, 157–165. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Viola, E. Effect of agglomeration on the natural frequencies of functionally graded carbon nanotube-reinforced laminated composite doubly-curved shells. Compos. Part B-Eng. 2016, 89, 187–218. [Google Scholar] [CrossRef]
- Banić, D.; Bacciocchi, M.; Tornabene, F.; Ferreira, A.J.M. Influence of Winkler-Pasternak foundation on the vibrational behavior of plates and shells reinforced by agglomerated carbon nanotubes. Appl. Sci. 2017, 7, 1228. [Google Scholar] [CrossRef]
- Nejati, M.; Dimitri, R.; Tornabene, F.; Hossein, Y.M. Thermal buckling of nanocomposite stiffened cylindrical shells reinforced by functionally graded wavy carbon nano-tubes with temperature-dependent properties. Appl. Sci. 2017, 7, 1223. [Google Scholar] [CrossRef]
- Malikan, M.; Jabbarzadeh, M.; Dastjerdi, S. Non-linear Static stability of bi-layer carbon nanosheets resting on an elastic matrix under various types of in-plane shearing loads in thermo-elasticity using nonlocal continuum. Microsyst. Technol. 2017, 23, 2973–2991. [Google Scholar] [CrossRef]
- Malikan, M. Electro-mechanical shear buckling of piezoelectric nanoplate using modified couple stress theory based on simplified first order shear deformation theory. Appl. Math. Model. 2017, 48, 196–207. [Google Scholar] [CrossRef]
- Malikan, M. Analytical predictions for the buckling of a nanoplate subjected to nonuniform compression based on the four-variable plate theory. J. Appl. Comput. Mech. 2017, 3, 218–228. [Google Scholar]
- Malikan, M. Buckling analysis of a micro composite plate with nano coating based on the modified couple stress theory. J. Appl. Comput. Mech. 2018, 4, 1–15. [Google Scholar]
- Malikan, M.; Nguyen, V.B. Buckling analysis of piezo-magnetoelectric nanoplates in hygrothermal environment based on a novel one variable plate theory combining with higher-order nonlocal strain gradient theory. Phys. E Low-Dimens. Syst. Nanostruct. 2018, 102, 8–28. [Google Scholar] [CrossRef]
- Malikan, M. Temperature influences on shear stability of a nanosize plate with piezoelectricity effect. Multidiscip. Model. Mater. Struct. 2018, 14, 125–142. [Google Scholar] [CrossRef]
- Golmakani, M.E.; Malikan, M.; Far, M.N.S.; Majidi, H.R. Bending and buckling formulation of graphene sheets based on nonlocal simple first order shear deformation theory. Mater. Res. Express 2018, 5, 065010. [Google Scholar] [CrossRef]
- Malikan, M.; Far, M.N.S. Differential quadrature method for dynamic buckling of graphene sheet coupled by a viscoelastic medium using neperian frequency based on nonlocal elasticity theory. J. Appl. Comput. Mech. 2018, 4, 147–160. [Google Scholar]
- Malikan, M.; Dastjerdi, S. Analytical buckling of FG nanobeams on the basis of a new one variable first-order shear deformation beam theory. Int. J. Eng. Appl. Sci. 2018, 10, 21–34. [Google Scholar] [CrossRef]
- Malikan, M. On the buckling response of axially pressurized nanotubes based on a novel nonlocal beam theory. J. Appl. Comput. Mech. 2018. [Google Scholar] [CrossRef]
- Fantuzzi, N.; Tornabene, F.; Bacciocchi, M.; Dimitri, R. Free vibration analysis of arbitrarily shaped Functionally Graded Carbon Nanotube-reinforced plates. Compos. Part B-Eng. 2017, 115, 384–408. [Google Scholar] [CrossRef]
- Nejati, M.; Asanjarani, A.; Dimitri, R.; Tornabene, F. Static and free vibration analysis of functionally graded conical shells reinforced by carbon nanotubes. Int. J. Mech. Sci. 2017, 130, 383–398. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. Linear static response of nanocomposite plates and shells reinforced by agglomerated carbon nanotubes. Compos. Part B-Eng. 2017, 115, 449–476. [Google Scholar] [CrossRef]
- Tornabene, F.; Bacciocchi, M.; Fantuzzi, N.; Reddy, J.N. Multiscale approach for three-Phase CNT/Polymer/Fiber laminated nanocomposite structures. Polym. Compos. 2017, in press. [Google Scholar] [CrossRef]
- Hashemi, S.H.; Mehrabani, H.; Ahmadi-Savadkoohi, A. Forced vibration of nanoplate on viscoelastic substrate with consideration of structural damping: An analytical solution. Compos. Struct. 2015, 133, 8–15. [Google Scholar] [CrossRef]
- Wang, Y.; Li, F.; Wang, Y. Nonlinear vibration of double layered viscoelastic nanoplates based on nonlocal theory. Physica E 2015, 67, 65–76. [Google Scholar] [CrossRef]
- Zenkour, A.M.; Sobhy, M. Nonlocal piezo-hygrothermal analysis for vibration characteristics of a piezoelectric Kelvin–Voigt viscoelastic nanoplate embedded in a viscoelastic medium. Acta Mech. 2018, 229, 3–19. [Google Scholar] [CrossRef]
- Aghababaei, R.; Reddy, J.N. Nonlocal third-order shear deformation plate theory with application to bending and vibration of plates. J. Sound Vib. 2009, 326, 277–289. [Google Scholar] [CrossRef]
- Malikan, M.; Tornabene, F.; Dimitri, R. Nonlocal three-dimensional theory of elasticity for buckling behavior of functionally graded porous nanoplates using volume integrals. Mater. Res. Express 2018, 5, 095006. [Google Scholar] [CrossRef]
- Malikan, M.; Nguyen, V.B.; Tornabene, F. Damped forced vibration analysis of single-walled carbon nanotubes resting on viscoelastic foundation in thermal environment using nonlocal strain gradient theory. Eng. Sci. Technol. Int. J. 2018, 21, 778–786. [Google Scholar] [CrossRef]
- Malikan, M.; Nguyen, V.B.; Tornabene, F. Electromagnetic forced vibrations of composite nanoplates using nonlocal strain gradient theory. Mater. Res. Express 2018, 5, 075031. [Google Scholar] [CrossRef]
- Malikan, M. Electro-thermal buckling of elastically supported double-layered piezoelectric nanoplates affected by an external electric voltage. Multidiscip. Model. Mater. Struct. 2018. [Google Scholar] [CrossRef]
- She, G.-L.; Yuan, F.-G.; Ren, Y.-R.; Xiao, W.-S. On buckling and postbuckling behavior of nanotubes. Int. J. Eng. Sci. 2017, 121, 130–142. [Google Scholar] [CrossRef]
- She, G.-L.; Yuan, F.-G.; Ren, Y.-R. Thermal buckling and post-buckling analysis of functionally graded beams based on a general higher-order shear deformation theory. Appl. Math. Model. 2017, 47, 340–357. [Google Scholar] [CrossRef]
- She, G.-L.; Yuan, F.-G.; Ren, Y.-R.; Liu, H.-B.; Xiao, W.-S. Nonlinear bending and vibration analysis of functionally graded porous tubes via a nonlocal strain gradient theory. Compos. Struct. 2018, 203, 614–623. [Google Scholar] [CrossRef]
- Lim, C.W.; Zhang, G.; Reddy, J.N. A Higher-order nonlocal elasticity and strain gradient theory and Its Applications in wave propagation. J. Mech. Phys. Solids 2015, 78, 298–313. [Google Scholar] [CrossRef]
- Barati, M.R.; Shahverdi, H. Hygro-thermal vibration analysis of graded double-refined-nanoplate systems using hybrid nonlocal stress-strain gradient theory. Compos. Struct. 2017, 176, 982–995. [Google Scholar] [CrossRef]
- Briassoulis, D. Equivalent orthotropic properties of corrugated sheets. Comput. Struct. 1986, 23, 129–138. [Google Scholar] [CrossRef]
- Liew, K.M.; Peng, L.X.; Kitipornchai, S. Buckling analysis of corrugated plates using a mesh-free Galerkin method based on the first-order shear deformation theory. Comput. Mech. 2006, 38, 61–75. [Google Scholar] [CrossRef]
- Liew, K.M.; Peng, L.X.; Kitipornchai, S. Vibration analysis of corrugated Reissner–Mindlin plates using a mesh-free Galerkin method. Int. J. Mech. Sci. 2009, 51, 642–652. [Google Scholar] [CrossRef]
- Ansari, R.; Sahmani, S.; Arash, B. Nonlocal plate model for free vibrations of single-layered graphene sheets. Phys. Lett. A 2010, 375, 53–62. [Google Scholar] [CrossRef]
- Wu, C.; Li, W. Free vibration analysis of embedded single-layered nanoplates and graphene sheets by using the multiple time scale method. Comput. Math. Appl. 2017, 73, 838–854. [Google Scholar] [CrossRef]
- Malekzadeh, P.; Shojaee, M. Free vibration of nanoplates based on a nonlocal two-variable refined plate theory. Compos. Struct. 2013, 95, 443–452. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).