Liquid Crystal Tunable Dielectric Metamaterial Absorber in the Terahertz Range
Abstract
1. Introduction
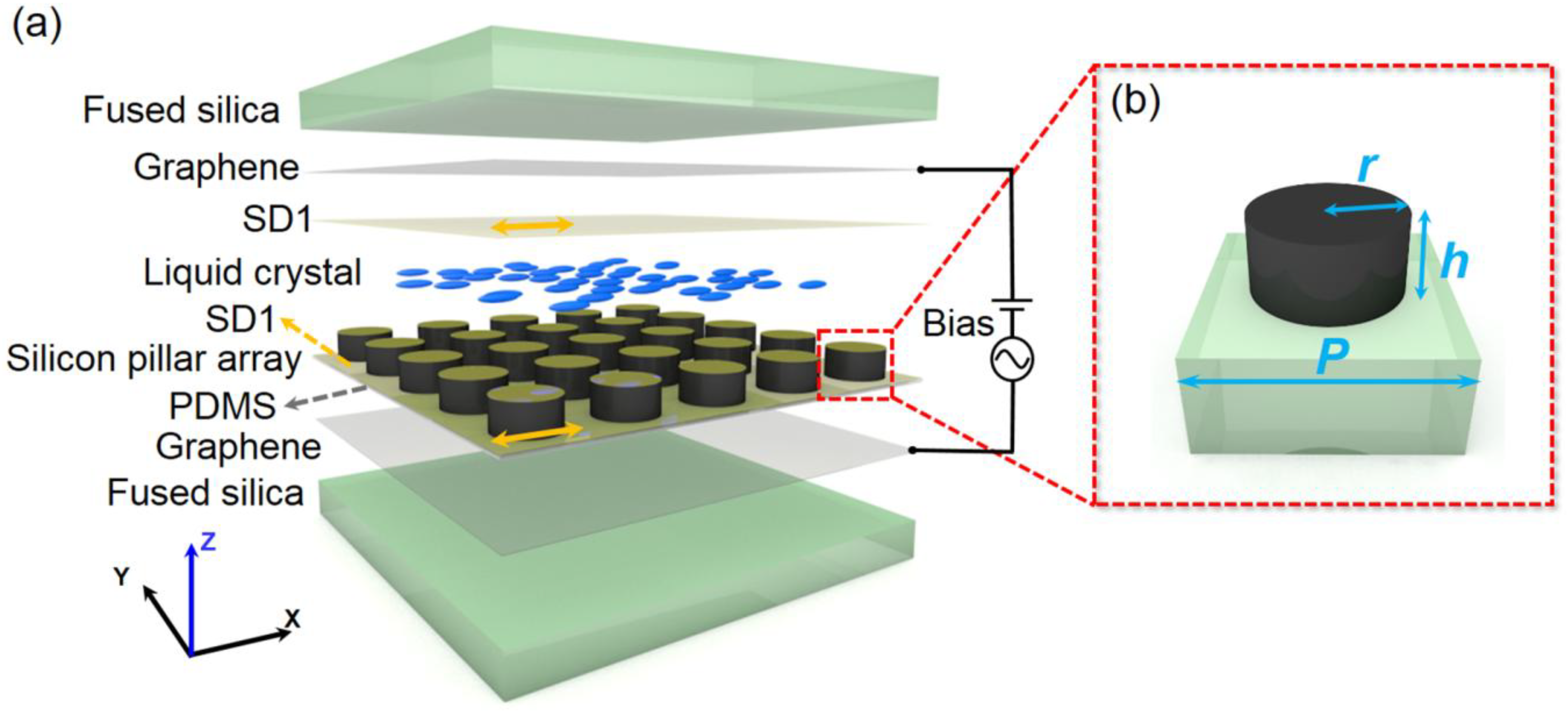
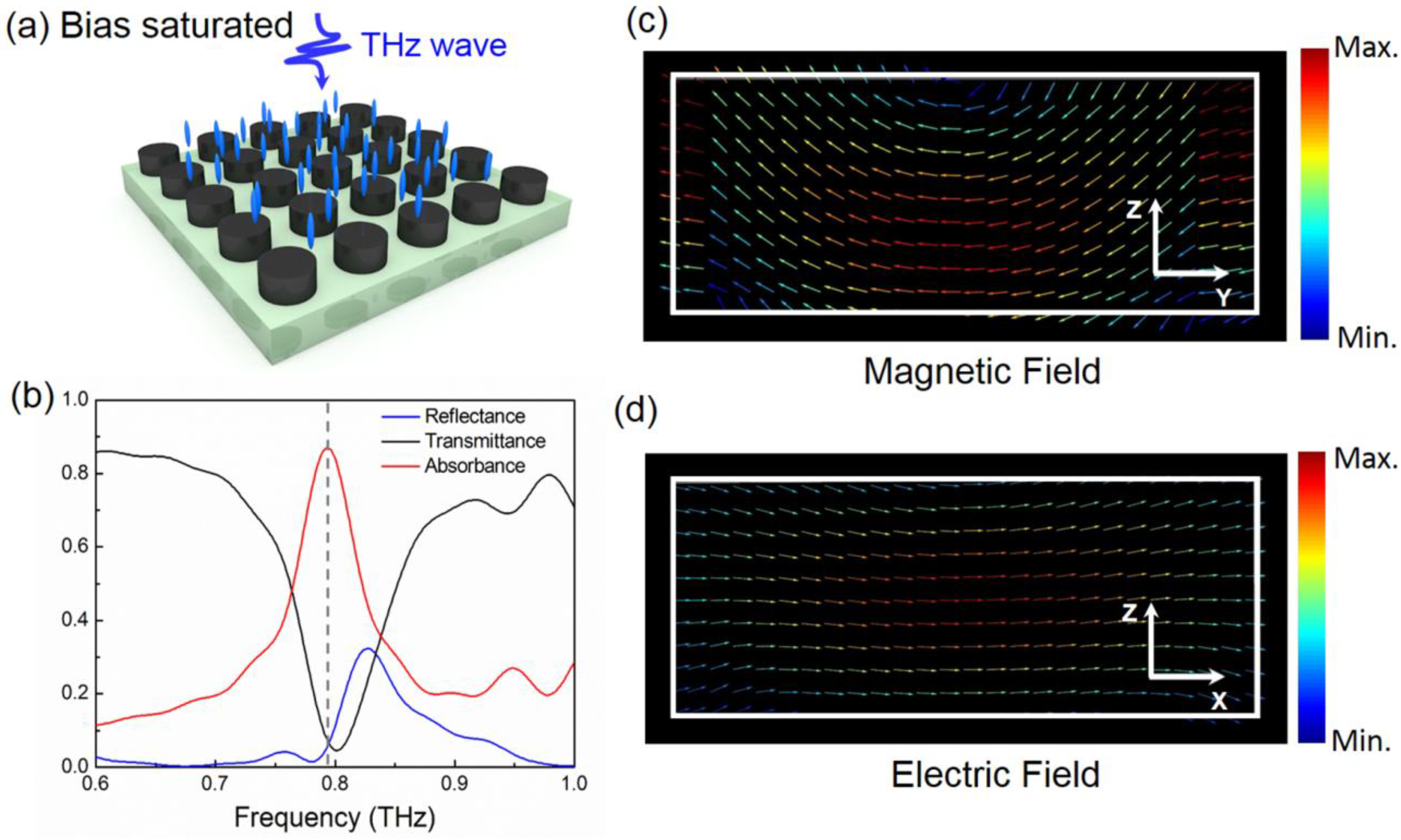
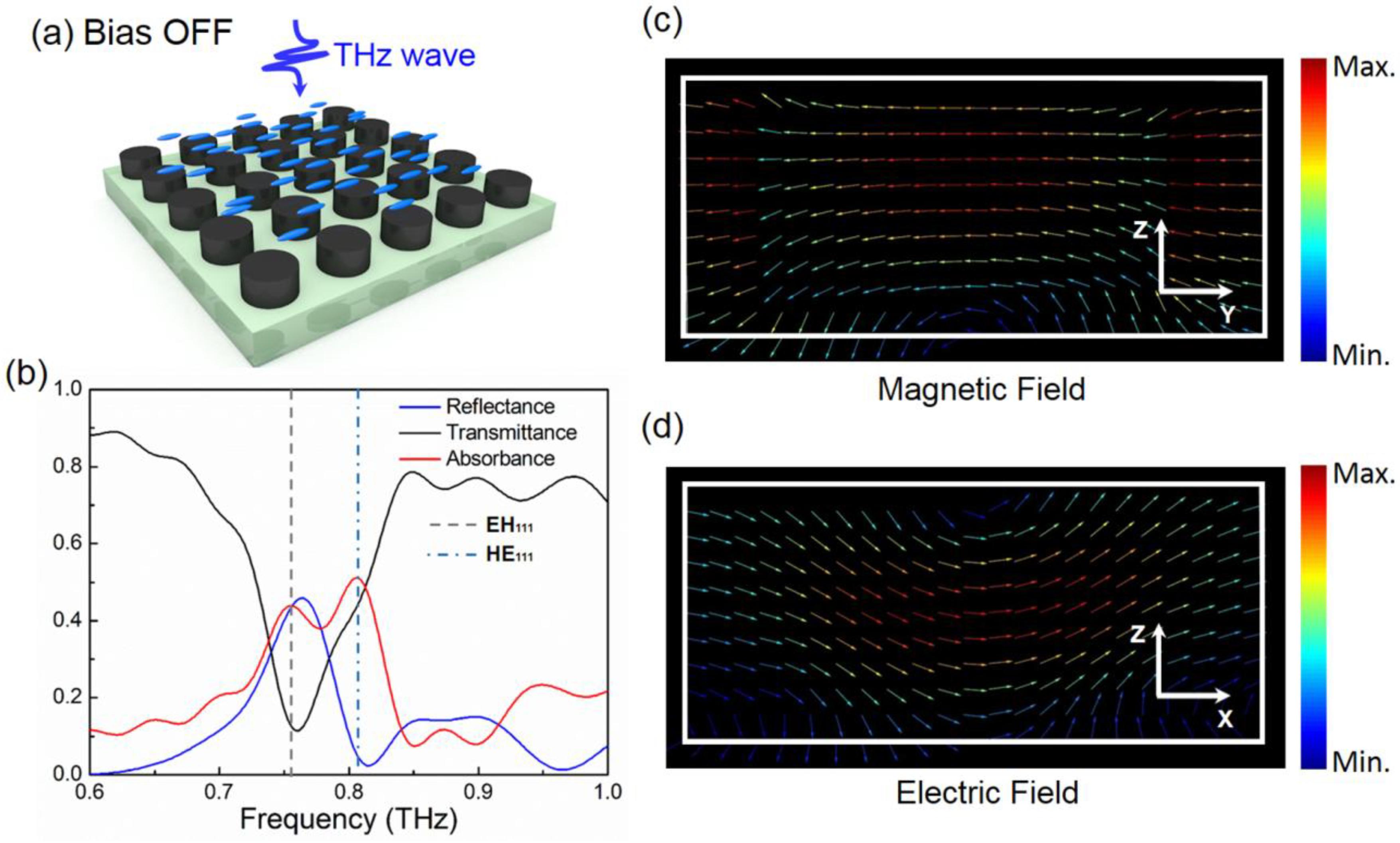
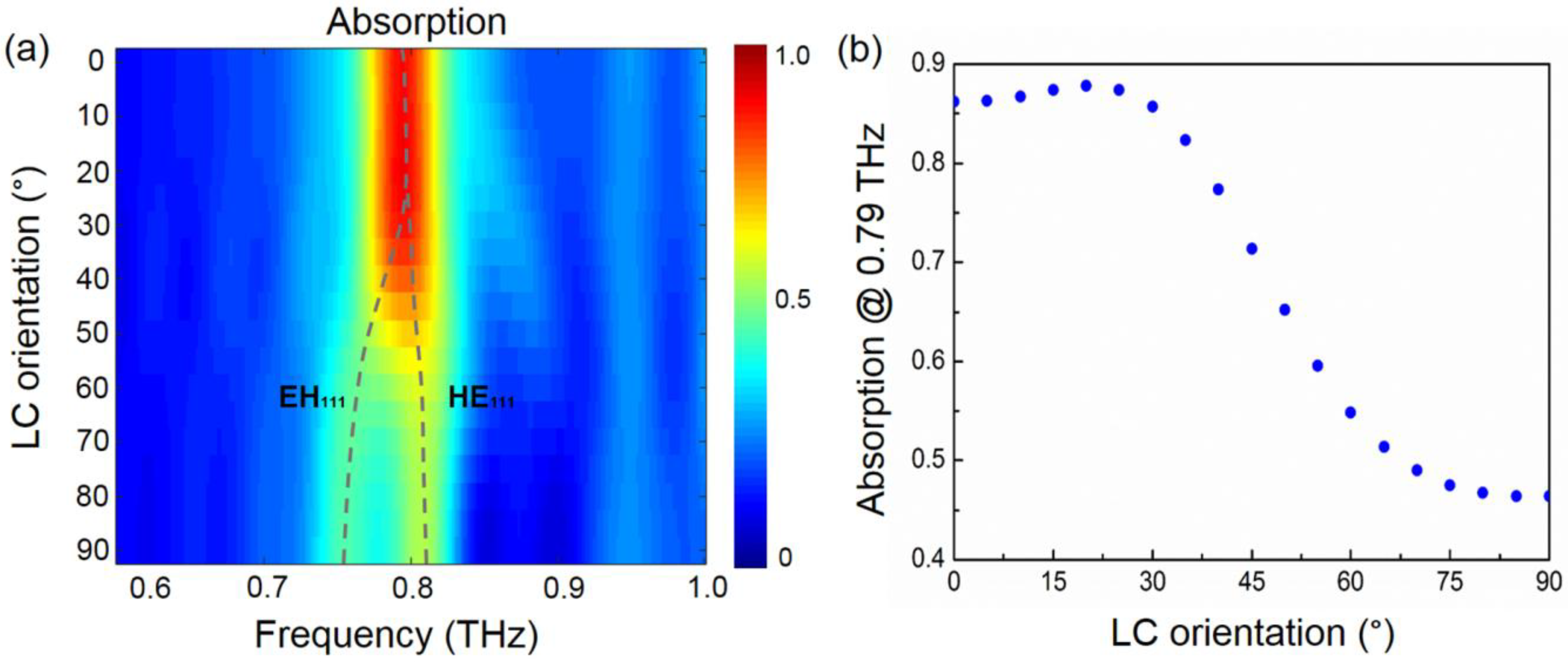
2. Tunable Dielectric Metamaterial Absorber
3. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Grossman, E.; Dietlein, C.; Ala-Laurinaho, J.; Leivo, M.; Gronberg, L.; Gronholm, M.; Lappalainen, P.; Rautiainen, A.; Tamminen, A.; Luukanen, A. Passive terahertz camera for standoff security screening. Appl. Opt. 2010, 49, E106–E120. [Google Scholar] [CrossRef] [PubMed]
- John, F.F.; Brian, S.; Feng, H.; Dale, G.; Robert, B.; Filipe, O.; David, Z. THz imaging and sensing for security applications—Explosives, weapons and drugs. Semicond. Sci. Technol. 2005, 20, S266. [Google Scholar] [CrossRef]
- Ferguson, B.; Zhang, X.-C. Materials for terahertz science and technology. Nat. Mater. 2002, 1, 26. [Google Scholar] [CrossRef] [PubMed]
- Fei, D.; Anders, P.; Sergey, I.B. Gradient metasurfaces: A review of fundamentals and applications. Rep. Prog. Phys. 2018, 81, 026401. [Google Scholar] [CrossRef]
- Tao, H.; Landy, N.I.; Bingham, C.M.; Zhang, X.; Averitt, R.D.; Padilla, W.J. A metamaterial absorber for the terahertz regime: Design, fabrication and characterization. Opt. Express 2008, 16, 7181–7188. [Google Scholar] [CrossRef] [PubMed]
- Shrekenhamer, D.; Chen, W.-C.; Padilla, W.J. Liquid Crystal Tunable Metamaterial Absorber. Phys. Rev. Lett. 2013, 110, 177403. [Google Scholar] [CrossRef] [PubMed]
- Driscoll, T.; Kim, H.-T.; Chae, B.-G.; Kim, B.-J.; Lee, Y.-W.; Jokerst, N.M.; Palit, S.; Smith, D.R.; Di Ventra, M.; Basov, D.N. Memory Metamaterials. Science 2009, 325, 1518–1521. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.-T.; Padilla, W.J.; Zide, J.M.O.; Gossard, A.C.; Taylor, A.J.; Averitt, R.D. Active terahertz metamaterial devices. Nature 2006, 444, 597. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.H.; Choi, M.; Kim, T.-T.; Lee, S.; Liu, M.; Yin, X.; Choi, H.K.; Lee, S.S.; Choi, C.-G.; Choi, S.-Y.; et al. Switching terahertz waves with gate-controlled active graphene metamaterials. Nat. Mater. 2012, 11, 936. [Google Scholar] [CrossRef] [PubMed]
- Savo, S.; Shrekenhamer, D.; Padilla, W.J. Liquid Crystal Metamaterial Absorber Spatial Light Modulator for THz Applications. Adv. Opt. Mater. 2014, 2, 275–279. [Google Scholar] [CrossRef]
- Shen, Z.; Zhou, S.; Ge, S.; Duan, W.; Chen, P.; Wang, L.; Hu, W.; Lu, Y. Liquid-crystal-integrated metadevice: Towards active multifunctional terahertz wave manipulations. Opt. Lett. 2018, 43, 4695–4698. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Fan, K.; Shadrivov, I.V.; Padilla, W.J. Experimental realization of a terahertz all-dielectric metasurface absorber. Opt. Express 2017, 25, 191–201. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Lin, X.-W.; Hu, W.; Shao, G.-H.; Chen, P.; Liang, L.-J.; Jin, B.-B.; Wu, P.-H.; Qian, H.; Lu, Y.-N.; et al. Broadband tunable liquid crystal terahertz waveplates driven with porous graphene electrodes. Light Sci. Appl. 2015, 4, e253. [Google Scholar] [CrossRef]
- Ge, S.; Chen, P.; Shen, Z.; Sun, W.; Wang, X.; Hu, W.; Zhang, Y.; Lu, Y. Terahertz vortex beam generator based on a photopatterned large birefringence liquid crystal. Opt. Express 2017, 25, 12349–12356. [Google Scholar] [CrossRef] [PubMed]
- Kowerdziej, R.; Olifierczuk, M.; Parka, J.; Wrobel, J. Terahertz characterization of tunable metamaterial based on electrically controlled nematic liquid crystal. Appl. Phys. Lett. 2014, 105, 022908. [Google Scholar] [CrossRef]
- Chen, C.C.; Chiang, W.F.; Tsai, M.C.; Jiang, S.A.; Chang, T.H.; Wang, S.H.; Huang, C.Y. Continuously tunable and fast-response terahertz metamaterials using in-plane-switching dual-frequency liquid crystal cells. Opt. Lett. 2015, 40, 2021–2024. [Google Scholar] [CrossRef] [PubMed]
- Borislav, V.; Dimitrios, C.Z.; Goran, I.; Romeo, B.; Radoš, G. Electrically tunable terahertz polarization converter based on overcoupled metal-isolator-metal metamaterials infiltrated with liquid crystals. Nanotechnology 2017, 28, 124002. [Google Scholar] [CrossRef]
- Ji, Y.-Y.; Fan, F.; Chen, M.; Yang, L.; Chang, S.-J. Terahertz artificial birefringence and tunable phase shifter based on dielectric metasurface with compound lattice. Opt. Express 2017, 25, 11405–11413. [Google Scholar] [CrossRef] [PubMed]
- Tang, K.C.; Liao, E.; Ong, W.L.; Wong, J.D.S.; Agarwal, A.; Nagarajan, R.; Yobas, L. Evaluation of bonding between oxygen plasma treated polydimethyl siloxane and passivated silicon. J. Phys. Conf. Ser. 2006, 34, 155. [Google Scholar] [CrossRef]
- Chen, P.; Ma, L.-L.; Duan, W.; Chen, J.; Ge, S.-J.; Zhu, Z.-H.; Tang, M.-J.; Xu, R.; Gao, W.; Li, T.; et al. Digitalizing Self-Assembled Chiral Superstructures for Optical Vortex Processing. Adv. Mater. 2018, 30, 1705865. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Lin, X.-W.; Liang, X.; Wu, J.-B.; Hu, W.; Zheng, Z.-G.; Jin, B.-B.; Qin, Y.-Q.; Lu, Y.-Q. Large birefringence liquid crystal material in terahertz range. Opt. Mater. Express 2012, 2, 1314–1319. [Google Scholar] [CrossRef]
- Mongia, R.K.; Bhartia, P. Dielectric resonator antennas—A review and general design relations for resonant frequency and bandwidth. Int. J. Microw. Millim.-Wave Comput.-Aided Eng. 1994, 4, 230–247. [Google Scholar] [CrossRef]
- Decker, M.; Staude, I.; Falkner, M.; Dominguez, J.; Neshev, D.N.; Brener, I.; Pertsch, T.; Kivshar, Y.S. High-Efficiency Dielectric Huygens’ Surfaces. Adv. Opt. Mater. 2015, 3, 813–820. [Google Scholar] [CrossRef]
- Fan, K.; Suen, J.Y.; Liu, X.; Padilla, W.J. All-dielectric metasurface absorbers for uncooled terahertz imaging. Optica 2017, 4, 601–604. [Google Scholar] [CrossRef]
- Buchnev, O.; Podoliak, N.; Kaczmarek, M.; Zheludev, N.I.; Fedotov, V.A. Metamaterials: Electrically Controlled Nanostructured Metasurface Loaded with Liquid Crystal: Toward Multifunctional Photonic Switch (Advanced Optical Materials 5/2015). Adv. Opt. Mater. 2015, 3, 595. [Google Scholar] [CrossRef]
- Staude, I.; Miroshnichenko, A.E.; Decker, M.; Fofang, N.T.; Liu, S.; Gonzales, E.; Dominguez, J.; Luk, T.S.; Neshev, D.N.; Brener, I.; et al. Tailoring Directional Scattering through Magnetic and Electric Resonances in Subwavelength Silicon Nanodisks. ACS Nano 2013, 7, 7824–7832. [Google Scholar] [CrossRef] [PubMed]
- Yeh, P. Optics of Liquid Crystal Displays. In Proceedings of the Conference on Lasers and Electro-Optics—Pacific Rim (CLEO/Pacific Rim 2007), Seoul, Korea, 26 August 2007. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, S.; Shen, Z.; Kang, R.; Ge, S.; Hu, W. Liquid Crystal Tunable Dielectric Metamaterial Absorber in the Terahertz Range. Appl. Sci. 2018, 8, 2211. https://doi.org/10.3390/app8112211
Zhou S, Shen Z, Kang R, Ge S, Hu W. Liquid Crystal Tunable Dielectric Metamaterial Absorber in the Terahertz Range. Applied Sciences. 2018; 8(11):2211. https://doi.org/10.3390/app8112211
Chicago/Turabian StyleZhou, Shenghang, Zhixiong Shen, Ruiyun Kang, Shijun Ge, and Wei Hu. 2018. "Liquid Crystal Tunable Dielectric Metamaterial Absorber in the Terahertz Range" Applied Sciences 8, no. 11: 2211. https://doi.org/10.3390/app8112211
APA StyleZhou, S., Shen, Z., Kang, R., Ge, S., & Hu, W. (2018). Liquid Crystal Tunable Dielectric Metamaterial Absorber in the Terahertz Range. Applied Sciences, 8(11), 2211. https://doi.org/10.3390/app8112211





