Planning of Partially Accelerated Degradation Test with Two Stress Variables for Practical Lifetime Estimation

Abstract

The reliability information for novel products and specimens available for various tests is limited during the development stage. In many real cases, the results of general tests under use and the maximum stress levels for checking performance and design are not utilized to obtain reliability information. To solve these problems, this paper proposes a practical partially accelerated degradation test (PADT) plans with two stress variables using a two-phase strategy. In addition, a sample scenario is introduced to demonstrate the feasibility of the proposed procedure. In the first phase, the ratios of the specimens used and the maximum stress levels for each variable are determined to estimate the parameters of an accelerated model based on the D-optimality criteria. To estimate the lifetime information and check the curvature effects of the accelerated model, practical PADT plans are developed in the second phase with three stress levels for each variable, which are based on the compromise concept. In this phase, the ratios for all test points and the middle-stress levels for two variables are determined. This information is used to minimize the asymptotic variance of the maximum likelihood estimator for the q-th quantile of the lifetime distribution under the use conditions. Thus, more accurate lifetime information and model validity can be obtained when using practical PADT plans. Finally, the statistical efficiency of the proposed test plan is demonstrated in a sample scenario.

1. Introduction

The functions of products have steadily increased and become more complex due to advances in technology and intense market competition. For this reason, the task of examining the reliability and performance of products has also increased in complexity. However, reliability evaluations tend to be time-consuming. It is also difficult to gather sufficient information about the product during the development stage and available specimens for testing may be limited. Thus, to increase the speed at which reliability information is acquired for a product, reliability test planning is necessary.

Conventional accelerated tests, in which all specimens are only allocated under accelerated conditions, have previously been used to plan and provide solutions to the above problems. However, various general tests should be performed under regular use (i.e., normal conditions), as well as under accelerated conditions. Therefore, an alternative test plan concept that includes realistic situations and use conditions is required. Partially accelerated tests provide a method of simultaneously testing products in the development stage simultaneously under both regular use and accelerated conditions.

Commonly, a partially accelerated test is classified either as a PALT or a partially accelerated degradation test (PADT) based on whether the product can observe a performance characteristic or not. Today, failures are rarely observed as the reliability of novel products has steadily improved. Commonly, these products are tested under general use conditions. The PADT, which observes a performance characteristic of a product over time, is more effective than the PALT at maximizing the advantages of partially accelerated tests. However, there are few studies for PADT designs [1], and no research has been published with two stress variables. In addition, Kim and Sung [1] mentioned the practical shortage problem of prototypes in the development phase and presented the PADT strategy to overcome this difficulty.

Thus, in this paper, to overcome the challenges described above, which include a low prototype quantity (i.e., a lack of test samples), the disadvantages of PALT, and the lack of prior information, we proposed a strategical approach for a constant stress-partially accelerated degradation test (CS-PADT) with two stress variables based on the Wiener process (WP). In particular, the proposed test plan can be simultaneously used for multipurpose tests such as design conformity, performance requirement and hot temperature operating test [1]. First, the parameters of an acceleration model are estimated by developing the CS-PADT plans with four test points. These test points are a combination of use and maximum stress levels for each stress variable and are based on the D-optimality criteria. Second, a practical PADT plan, which uses the stress levels of the first phase and the middle-stress conditions for two stress variables, is developed to examine the validity and curvature effects of the acceleration model. Subsequently, the lifetime, which is the q-th quantile of the lifetime distribution at the use condition, is estimated by minimizing the asymptotic variance of the maximum likelihood estimator (MLE). In addition, a scenario example is presented to demonstrate the validity of the proposed CS-PADT model.

The rest of this paper is organized as follows. Section 2 introduces the related works and Section 3 presents the planning strategy, basic assumptions, and model description. The model of CS-PADT plan with two stress and test plans is provided in Section 4. Section 5 presents the proposed test strategy through an example and in Section 6, the conclusions and future research directions are provided.

2. Related Works

In this section, the existing literature on designing partially accelerated test (PAT) plans including life test and degradation test are reviewed. Several previous studies have attempted to determine the optimal testing procedures for PATs. Most studies focused on the planning of the PALT [2,3,4,5,6,7,8,9,10,11,12,13,14]. In addition, these studies also considered constant stress (CS) loading [2,3,4,5,6,7] and step stress (SS) loading [2,8,9,10,11,12,13,14]. To design the test plans, the number of stress variables, degradation model, optimization criterion, and the decision variable were mainly considered along with the stress loading method [15,16]. In terms of failure distributions, exponential [2], lognormal [8], Gompertz [5,9], Weibull (or inverse Weibull) [3,6,10,12,13,14], logistic [4,11], and Burr XII [7] were adopted.

In PATs, since the lowest accelerated stress level is fixed with the normal use condition, no or few failures in the test samples are observed under test conditions including accelerated stress levels. However, in the case of degradation tests, reliability information such as degradation data can be obtained under the use and accelerated test conditions. Therefore, the PAT concept is more suitable for PADTs than PALTs [1,17].

Studies of PADT plans have been performed under CS loading [17] and SS loading [1]. A two-phase planning strategy for the design of CS-PADT plans that minimizes the Avar of the estimated $q$th quantile of the lifetime distribution was proposed [17]. In addition, practical SS-PADT planning with three stress levels was suggested [1]. However, almost all of the previous studies on the design of PALT and PADT plans have only considered a single stress variable. Thus, in this paper, practical PSSADT plans with two stress variables were developed.

Table 1 summarizes the literature on the design of PAT plans. In addition, decision variables were also considered as sample proportions were allocated to the allocation ratio ($\pi$), stress level ($s$), stress change time (SCT), and SCT based on the number of failures (SCF).

Table 1. The literature on the design of PAT (partially accelerated test) plans [1].

Authors	Test Type (The Number of Stress Variables)	Stress Loading Method	Lifetime Distribution or Degradation Model	Optimization Criterion	Decision Variable
Bai and Chung [2]	ALT (1)	Constant, Step	Exponential	Avar	$\pi$, SCT
Ismail [3]	ALT (1)	Constant	Weibull	Avar	$\pi$, $s$
Srivastava and Mittal [4]	ALT (1)	Constant	Logistic	Avar	$\pi$
Anwar and Islam [5]	ALT (1)	Constant	Gompertz	Avar	$\pi$, $s$
Ismail [6]	ALT (1)	Constant	Weibull	Avar	$\pi$
Srivastava and Mittal [7]	ALT (1)	Constant	Burr XII	Avar	$\pi$
Bai et al. [8]	ALT (1)	Step	Lognormal	Avar	SCT
Ismail [9]	ALT (1)	Step	Gompertz	Avar	SCT
Aly and Ismail [10]	ALT (1)	Step	Weibull	Avar	SCT
Srivastava and Mittal [11]	ALT (1)	Step	Logistic	Avar	SCT
Hassan and Al-Thobety [12]	ALT (1)	Step	Inverse Weibull	Avar	SCF
Ismail [13]	ALT (1)	Step	Weibull	Avar	SCT
Hassan [14]	ALT (1)	Step	Exponentiated inverse Weibull	D-opt	SCF
Kim and Sung [1]	ADT (1)	Step	WP	Avar	$s$
Lim et al. [17]	ADT (1)	Constant	WP	Avar	$\pi$, $s$

Note, WP: Wiener process, Avar: asymptotic variance, D-opt: D-optimality, $\pi$: sample proportions, $s$: stress level, SCT: stress change time, SCF: SCT based on the number of failures.

In addition to the design of optimal PAT plans, studies that estimated the parameters of probability distribution and compared performances of the estimators have been conducted. The MLEs and Bayesian estimators and credible intervals of the Weibull parameters were obtained to analyze the competing risks model in the PALTs under progressively type-I hybrid censoring [18]. Nassar et al. [19] analyzed performances of the estimators in the SS-PALTs under type-I and type-II progressive hybrid censoring. Soloman et al. [20] concentrated on the estimation of inverse Weibull parameters under progressive type-II censoring. Lone and Rahman [21] introduced a competing risk model with the SS-PADT plan under type-I progressively hybrid censoring. Abd and Fawzy [22] and Mohamed et al. [23] considered parameters estimations of two-parameters linear exponential [22] and Weibull-exponential distribution [23] with the CS-PALTs under progressively type-II censoring.

The WP degradation model is one of the stochastic processes for modeling of degradation pattern over time. The WP degradation model is often applied for degradation test planning and degradation analyses [1,17,24,25,26,27,28,29,30,31,32,33]. Recently, degradation data analysis and remaining useful life estimation approaches based on Wiener process were reviewed [33]. Sawik [34,35] applied the weighted-sum approach for four bi-objective vehicle routing problems and worker allocation problems with integer and mixed-integer programming. As seen above, studies have focused on PADT analysis, few studies on the design of PADT have not been published.

3. Planning Strategy and Basic Assumptions

3.1. Planning Strategy

General tests for multiple purposes should be performed to verify design conformity and the performance for novel products during the development stage. As the number of specimens is insufficient at this stage, the specimens must be used efficiently to maximize the specimen utility. If information from general tests can be applied to estimate the reliability of the novel product, it is possible to effectively use the specimens for reliability estimations. Therefore, the strategic planning of PADTs is required to gather sufficient reliability information for both use and accelerated conditions when two stress variables are applied.

This strategic approach is a two-phase process. In the first phase, the general tests are performed under use and accelerated conditions to obtain degradation data. For statistical efficiency, the accelerated condition of each stress variable is mostly determined at the maximum stress level; two stress levels of each stress variable are required. Four test points, which are combined with two stress variables, are considered to utilize the degradation data. The basic reliability information is gathered through these tests as there is no information when the novel products are developed. The information is used to estimate the parameters of the acceleration model. Thus, the allocation ratios for each of the test points are determined by the D-optimality criteria to minimize the variance of the estimated parameters [36].

In the above phase, each stress variable is tested at two levels to reduce the test time, cost, and specimen usage. However, this approach cannot identify the curvature effect of the model or estimate an accurate lifetime from the degradation data. Generally, three levels of each stress variable should be considered to provide reliable performance when solving this problem. In particular, the compromise concept with three levels has been used to resolve this problem in the accelerated degradation test (ADT) literature [24,37]. Therefore, an extra test point should be considered alongside the previously mentioned test points in the first and second phase. The new test point is tested at the combined middle level of each stress variable. In addition, the minimum and maximum stress levels are set to the use and maximum conditions, respectively, according to the PADT concept. In other words, in the second phase, the degradation data from the first phase (the use and maximum stress levels) is reused to identify the validity of the model and estimate the lifetime. Thus, the rest of the specimens are allocated to five test points according to the optimal ratios. In this case, the optimal ratio of the five test points and the middle-stress levels of each variable are determined to minimize the asymptotic variance of the MLE for the q-th quantile of lifetime distribution under use conditions with two stress variables. The two-phase process for the strategic PADT plan with two stress variables is shown in Figure 1.

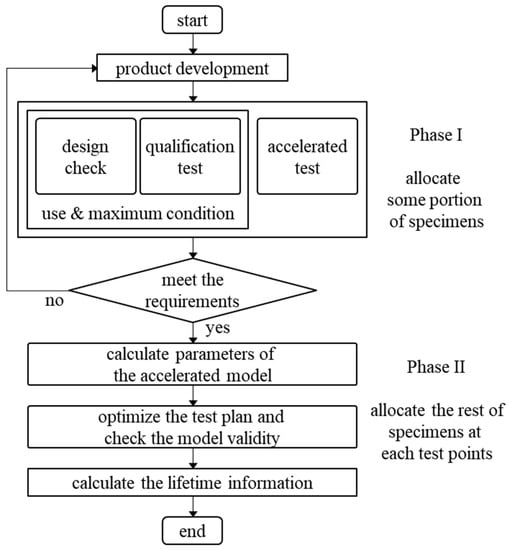
Figure 1. The two-phase process for the planning of PADT (practical partially accelerated degradation test).

3.2. Basic Assumptions

In this paper, we made the following two-phase PADT plan assumptions:

Assumption 1. 

Each stress level ($T_i^{\prime }$and$V_j^{\prime }$where$i=1,2,\cdots ,r_1$and$j=1,2,\cdots ,r_2$) is loaded following the CS loading scheme.$T_i^{\prime }$and$V_j^{\prime }$represent the i-th temperature stress level (in Kelvin) and j-th non-thermal stress level (voltage, vibration, etc.), respectively. $N$is the pre-determined total number of specimens andeach unit, and$n_{ij}$, is allocated to each stress level such that

$$n_{ij}={\pi }_{ij}N,{\displaystyle \sum _{i=1}^{r_1}{\displaystyle \sum _{j=1}^{r_2}{\pi }_{ij}}}=1,{\pi }_{ij}\ge 0$$

Assumption 2. 

The maximum test duration ($t_{M,ijk}$)andmeasurement times ($t_{ijkl}$,$k=1,2,\cdots ,n_{ij}$,$l=1,2,\cdots ,m$) are given, with their equivalent intervals ($t_l-t_{l-1}=\Delta t$). Thus, it is assumed that the maximum test duration is equal to$m\Delta t\left(=t_{M,ijk}\right)$for all$i$,$j$, and$k$.

Assumption 3. 

The degradation (or performance) characteristic$y_{ijk}\left(t\right)$of the k-th unit at the stress levels ($T_i^{\prime }$and$V_j^{\prime }$)follows the WP with a drift${\eta }^{\prime }\left(T_i^{\prime },V_j^{\prime }\right)$and diffusion constant${\sigma }^2$. It is assumed that a failure of the test item is reachedwhen$y_{ijk}\left(t\right)$becomes greater than the predetermined critical value$\omega$.

Assumption 4. 

The use and the maximum stress levels are given (or pre-specified) as ($T_1^{\prime }$and$V_1^{\prime }$) and($T_{r_1}^{\prime }=T_M^{\prime }$and$V_{r_2}^{\prime }=V_M^{\prime }$), respectively. In addition, the generalized Eyring model, which is one of the life-stress relationship models, is assumed to express the relationship between the drift${\eta }^{\prime }\left(T_i^{\prime },V_j^{\prime }\right)$and the two stress variables$T_i^{\prime }$and$V_j^{\prime }$, as follows [38].

$${\eta }^{\prime }\left(T_i^{\prime },V_j^{\prime }\right)={\delta }_1^{\prime }\exp \left(\frac{{\delta }_2^{\prime }}{T_i^{\prime }}+{\delta }_3^{\prime }{V}_j^{\prime }+{\delta }_4^{\prime }\frac{V_j^{\prime }}{T_i^{\prime }}\right)$$

where${\delta }_1^{\prime }\left(>0\right)$,${\delta }_2^{\prime }$,${\delta }_3^{\prime }$and${\delta }_4^{\prime }$are unknown constants which satisfy${\delta }_2^{\prime }+{\delta }_4^{\prime }{V}_j^{\prime }<0$and${\delta }_3^{\prime }+{\delta }_4^{\prime }/T_i^{\prime }>0$for all$i$and$j$.

Assumption 5. 

For each stress variable, the use and maximum stress levels were considered to estimate the parameters of the acceleration model in the first phase, and the middle-stress level was considered to identify the validity of the model and estimate the lifetime in the second phase.

The WP, which is one of the stochastic processes, is widely applied to degradation path modeling [25,26,27,28,39]. In addition, WP is often used with degradation test design due to its mathematical tractability [24,29,30,31,32,40,41]. The WP was also adopted for modeling the random behavior of the degradation characteristic in this paper. The WP, W(t) (with drift η and diffusion constant σ²) has the following properties:

(1)

W(0) = 0,

(2)

{W(t)|t ≥ 0} has stationary and independent increments, and

(3)

for 0 ≤ t₁ < t₂, the increment, ∆W (=W(t₂) − W(t₁)), is normally distributed with mean η(t₂ − t₁) and variance σ²(t₂ − t₁).

Let Y(t) be the degradation characteristic of the product at time t, and define y(t) = Y(t) − Y(0). In this paper, the degradation increment y(t) followed a WP, and we assumed that the drift η depends only on the stress level, whereas the diffusion constant σ² does not. At $t_{ijkl}$, the degradation characteristic, $y_{ijkl}$, follows a normal distribution with mean ${\eta }_{ij}{t}_{ijkl}$ and variance ${\sigma }^2{t}_{ijkl}$. In addition, each degradation increment between successive measurement times ($\Delta t_{ijkl}=t_{ijkl}-t_{ijk,l-1}$), $\Delta y_{ijkl}\left(=y_{ijkl}-y_{ijk,l-1}\right)$ also follows a normal distribution with mean ${\eta }_{ij}\Delta t_{ijkl}$ and variance ${\sigma }^2\Delta t_{ijkl}$. Thus, a probability density function, $f\left(\Delta y_{ijkl}\right)$, and the log-likelihood function, $\ln L$, of $\Delta y_{ijkl}$ are respectively expressed as:

$$f\left(\Delta y_{ijkl}\right)=\frac{1}{\sqrt{2\pi {\sigma }^2\Delta t_{ijkl}}}\exp \left[-\frac{{\left\{\Delta y_{ijkl}-{\eta }_{ij}\Delta t_{ijkl}\right\}}^2}{2{\sigma }^2\Delta t_{ijkl}}\right],-\infty <\Delta y_{ijkl}<\infty$$

$$\ln L={\displaystyle \sum _{i=1}^{r_1}{\displaystyle \sum _{j=1}^{r_2}{\displaystyle \sum _{k=1}^{n_{ij}}{\displaystyle \sum _{l=1}^m\left[-\frac{1}{2}\ln \left(2\pi \cdot \Delta t_{ijkl}\right)-\ln \sigma -\frac{{\left(\Delta y_{ijkl}-{\eta }_{ij}\Delta t_{ijkl}\right)}^2}{2{\sigma }^2\Delta t_{ijkl}}\right]}}}}$$

(1)

The stress levels of each variable, $T_i^{\prime }$ and $V_j^{\prime }$, were standardized as $T_i$ and $V_j$ respectively, for simplicity and without loss of generality. In terms of $T_i$ and $V_j$, the drift ${\eta }^{\prime }\left(T_i^{\prime },V_j^{\prime }\right)$ can be rewritten as

$$T_i=\frac{1/T_1^{\prime }-1/T_i^{\prime }}{1/T_1^{\prime }-1/T_M^{\prime }},V_j=\frac{V_j^{\prime }-V_1^{\prime }}{V_M^{\prime }-V_1^{\prime }}$$

$$\eta \left(T_i,V_j\right)=\exp \left({\delta }_1+{\delta }_2{T}_i+{\delta }_3{V}_j+{\delta }_4{T}_i{V}_j\right)={\eta }_{ij}$$

(2)

where ${\delta }_1=\ln {\delta }_1^{\prime }+\frac{{\delta }_2^{\prime }}{T_1^{\prime }}+{\delta }_3^{\prime }{V}_1^{\prime }+{\delta }_4^{\prime }\frac{V_1^{\prime }}{T_1^{\prime }}$, ${\delta }_2=\left({\delta }_2^{\prime }+{\delta }_4^{\prime }{V}_1^{\prime }\right)\left(\frac{1}{T_M^{\prime }}-\frac{1}{T_1^{\prime }}\right)$, ${\delta }_3=\left({\delta }_3^{\prime }+\frac{{\delta }_4^{\prime }}{T_1^{\prime }}\right)\left(V_M^{\prime }-V_1^{\prime }\right)$, ${\delta }_4={\delta }_4^{\prime }\left(\frac{1}{T_M^{\prime }}-\frac{1}{T_1^{\prime }}\right)\left(V_M^{\prime }-V_1^{\prime }\right)$. Equation (2) is a modified drift of the WP that organizes ${\eta }^{\prime }\left(T_i^{\prime }, V_j^{\prime }\right)$ by ${\delta }_1$, ${\delta }_2$, ${\delta }_3$ and ${\delta }_4$. Note that ${\delta }_2$, ${\delta }_3$, ${\delta }_2+{\delta }_4$ and ${\delta }_3+{\delta }_4$ are always positive since ${\delta }_2^{\prime }+{\delta }_4^{\prime }{V}_j^{\prime }<0$, ${\delta }_3^{\prime }+{\delta }_4^{\prime }/T_i^{\prime }>0$, $T_1^{\prime }<T_M^{\prime }$ and $V_1^{\prime }<V_M^{\prime }$.

For example, the relationship between the drift parameter and the stress variables, temperature, and voltage is assumed to follow the generalized Eyring model. The use and maximum stress levels $\left(r_1=r_2=3\right)$ of each stress variable were assumed to be $\left(45℃\left(=318\mathrm{K}\right),\mathrm{and}130℃\left(=403\mathrm{K}\right)\right)$ and $\left(3.8\mathrm{V},4.4\mathrm{V}\right)$, respectively. The stress levels standardized based on the above standardization equation are given below. If the middle-stress levels are given as 100 $℃$ ($T_2^{\prime }$) and 4.1 V ($V_2^{\prime }$), they also are standardized as follows.

$$\begin{array}{l}{45}^{\circ }\mathrm{C}\underset{\mathrm{use}\mathrm{condition}}{\stackrel{\mathrm{standardization}}{\to }}{T}_1=\frac{1/318-1/318}{1/318-1/398}=0,3.8V\underset{\mathrm{use}\mathrm{condition}}{\stackrel{\mathrm{standardization}}{\to }}{V}_1=\frac{3.8-3.8}{4.4-3.8}=0\\ \Rightarrow \eta \left(T_1,V_1\right)=\exp \left({\delta }_1+{\delta }_2{T}_1+{\delta }_3{V}_1+{\delta }_4{T}_1{V}_1\right)=\exp \left({\delta }_1\right)\end{array}$$

$$\begin{array}{l}{130}^{\circ }\mathrm{C}\underset{\mathrm{maximum}\mathrm{stress}\mathrm{level}}{\stackrel{\mathrm{standardization}}{\to }}{T}_M=\frac{1/318-1/403}{1/318-1/403}=1,4.4V\underset{\mathrm{maximum}\mathrm{stress}\mathrm{level}}{\stackrel{\mathrm{standardization}}{\to }}{V}_M=\frac{4.4-3.8}{4.4-3.8}=1\\ \Rightarrow \eta \left(T_M,V_M\right)=\exp \left({\delta }_1+{\delta }_2{T}_M+{\delta }_3{V}_M+{\delta }_4{T}_M{V}_M\right)=\exp \left({\delta }_1+{\delta }_2+{\delta }_3+{\delta }_4\right)\end{array}$$

$$\begin{array}{l}{100}^{\circ }\mathrm{C}\underset{\mathrm{middle}\mathrm{stress}\mathrm{level}}{\stackrel{\mathrm{standardization}}{\to }}{T}_2=\frac{1/318-1/373}{1/318-1/403}=0.7,4.1V\underset{\mathrm{middle}\mathrm{stress}\mathrm{level}}{\stackrel{\mathrm{standardization}}{\to }}{V}_2=\frac{4.1-3.8}{4.4-3.8}=0.5\\ \Rightarrow \eta \left(T_2,V_2\right)=\exp \left({\delta }_1+{\delta }_2{T}_2+{\delta }_3{V}_2+{\delta }_4{T}_2{V}_2\right)=\exp \left({\delta }_1+0.7{\delta }_2+0.5{\delta }_3+0.35{\delta }_4\right)\end{array}$$

In addition, an accelerated factor (AF) between the use ($T_1,V_1$) and maximum ($T_M,V_M$) stress levels of two stress variables can be calculated by Equation (2) as

$$\mathrm{AF}=\frac{\mathrm{drift}\mathrm{at}\mathrm{maximum}\mathrm{stress}\mathrm{level}}{\mathrm{drift}\mathrm{at}\mathrm{use}\mathrm{condition}}=\frac{\eta \left(T_M,V_M\right)}{\eta \left(T_1,V_1\right)}=\frac{\exp \left({\delta }_1+{\delta }_2+{\delta }_3+{\delta }_4\right)}{\exp \left({\delta }_1\right)}=\exp \left({\delta }_2+{\delta }_3+{\delta }_4\right)$$

According to Assumptions 5, we considered whether $r_1=r_2=2$ or $r_1=r_2=3$ should be the design for the test plan (Section 4). In the case of $r_1=r_2=2$, the accelerated model parameters were estimated. In the case of $r_1=r_2=3$, the planning of PADT plan with two stress variables was performed to identify the curvature effect of the model and to estimate the accurate lifetime of the novel product.

The mathematical notations and their descriptions are shown in Table 2.

Table 2. The list of symbols and descriptions.

Symbol	Description	Index
i	Index of temperature stress variable ($i=1,2,\cdots ,r_1$)	-
j	Index of non-thermal stress variable ($j=1,2,\cdots ,r_2$)	-
k	Index of test units	-
l	Index of measurement times	-
$T_i^{\prime }$	i-th temperature stress level (in Kelvin)	i
$V_j^{\prime }$	j-th non-thermal stress level (voltage, vibration, etc.)	j
$N$	Pre-determined total number of specimens	-
$n_{ij}$	Test unit at i-th and j-th stress level	i, j
$t_{M,ijk}$	Maximum test duration	i, j, k
$t_{ijkl}$	Measurement time	i, j, k, l
$y_{ijk}\left(t\right)$	Degradation characteristic of k-th test unit at i-th and j-th stress level and time t	i, j, k
${\eta }^{\prime }\left(T_i^{\prime },V_j^{\prime }\right)$	Drift of the Wiener process model	i, j
${\sigma }^2$	Diffusion constant of the Wiener process model	-
$\omega$	Pre-determined critical value	-
${\delta }_1^{\prime }$, ${\delta }_2^{\prime }$,${\delta }_3^{\prime }$,${\delta }_4^{\prime }$,	Parameters of generalized Eyring model	-
$T_i$	i-th standardized temperature stress level	i
$V_j$	j-th standardized non-thermal stress level (voltage, vibration, etc.)	j
$T_M$	Maximum standardized temperature stress level ($T_M=1)$	-
$V_M$	Maximum standardized non-thermal stress level ($V_M=1)$	-
${\delta }_1$, ${\delta }_2$, ${\delta }_3$, ${\delta }_4$	Modified parameters of generalized Eyring model by $T_i$ and $V_j$	-
$\eta \left(T_i, V_j\right)$	Modified drift by ${\delta }_1$, ${\delta }_2$, ${\delta }_3$ and ${\delta }_4$	i, j
AF	Accelerated factor	-

4. Design of Practical PADT Plan with Two Stress Variables

4.1. First Phase: PADT Plan with Two Stress Levels by Each Variable

In the development stage of novel products, the general tests under the use and maximum stress levels should be performed in order to acquire basic performance and reliability information such as the acceleration model parameter. Therefore, in the first phase, a PADT plan with two stress levels ($r_1=r_2=2$) is presented to estimate the parameters of the acceleration model. Two stress levels are assigned as the use and maximum stress levels by each variable (see Figure 2).

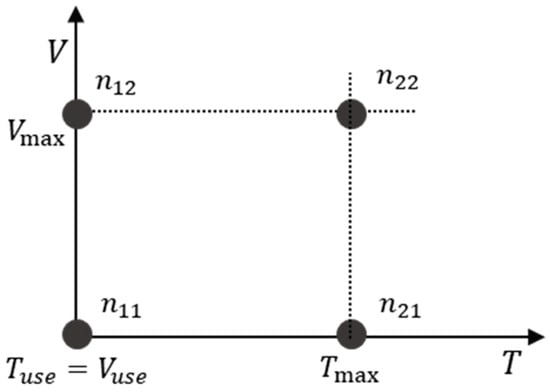
Figure 2. The test units and stress levels of four test points in the first phase.

To estimate the unknown parameters of the model (${\delta }_1,{\delta }_2,{\delta }_3,{\delta }_4$ and $\sigma$), the ratios (${\pi }_{11},{\pi }_{12},{\pi }_{21}$ and ${\pi }_{22}$) which were allocated to each test point, should be considered based on D-optimality criteria. Particularly, the ratios were determined to maximize the determinant of the Fisher information matrix for the model parameters. First, the maximum likelihood estimators (MLEs) for the unknown parameters can be obtained by calculating the first partial derivatives of $\ln L$ in Equation (1) of each parameter and solving the simultaneous equations: $\partial \ln L/\partial {\delta }_1=0$, $\partial \ln L/\partial {\delta }_2=0$, $\partial \ln L/\partial {\delta }_3=0$, $\partial \ln L/\partial {\delta }_4=0$ and $\partial \ln L/\partial \sigma =0$. The first partial derivatives of $\ln L$ are given as follows

$$\frac{\partial \ln L}{\partial {\delta }_1}={\displaystyle \sum _{i=1}^2{\displaystyle \sum _{j=1}^2{\displaystyle \sum _{k=1}^{n_{ij}}{\displaystyle \sum _{l=1}^m\left[\frac{\left(\Delta y_{ijkl}-{\eta }_{ij}\Delta t_{ijkl}\right){\eta }_{ij}}{{\sigma }^2}\right]}}}},$$

$$\frac{\partial \ln L}{\partial {\delta }_2}={\displaystyle \sum _{i=1}^2{\displaystyle \sum _{j=1}^2{\displaystyle \sum _{k=1}^{n_{ij}}{\displaystyle \sum _{l=1}^m\left[\frac{\left(\Delta y_{ijkl}-{\eta }_{ij}\Delta t_{ijkl}\right){\eta }_{ij}{T}_i}{{\sigma }^2}\right]}}}},$$

$$\frac{\partial \ln L}{\partial {\delta }_3}={\displaystyle \sum _{i=1}^2{\displaystyle \sum _{j=1}^2{\displaystyle \sum _{k=1}^{n_{ij}}{\displaystyle \sum _{l=1}^m\left[\frac{\left(\Delta y_{ijkl}-{\eta }_{ij}\Delta t_{ijkl}\right){\eta }_{ij}{V}_j}{{\sigma }^2}\right]}}}},$$

$$\frac{\partial \ln L}{\partial {\delta }_4}={\displaystyle \sum _{i=1}^2{\displaystyle \sum _{j=1}^2{\displaystyle \sum _{k=1}^{n_{ij}}{\displaystyle \sum _{l=1}^m\left[\frac{\left(\Delta y_{ijkl}-{\eta }_{ij}\Delta t_{ijkl}\right){\eta }_{ij}{T}_i{V}_j}{{\sigma }^2}\right]}}}},$$

$$\frac{\partial \ln L}{\partial \sigma }={\displaystyle \sum _{i=1}^2{\displaystyle \sum _{j=1}^2{\displaystyle \sum _{k=1}^{n_{ij}}{\displaystyle \sum _{l=1}^m\left[-\frac{1}{\sigma }+\frac{{\left(\Delta y_{ijkl}-{\eta }_{ij}\Delta t_{ijkl}\right)}^2}{{\sigma }^3\Delta t_{ijkl}}\right]}}}}.$$

Then, expectations of the negative second partial derivatives of $\ln L$ with each parameter were derived to obtain the Fisher information matrix, $F$ [42]. From above, the second partial derivatives of the $\ln L$ are shown in Appendix A.

Finally, $F$ and the determinant of $F$, $\left|F\right|$, are given by

$$F=\frac{N{t}_M}{{\sigma }^2}\left[\begin{array}{ccccc}{\displaystyle \sum _{i=1}^{r_1}{\displaystyle \sum _{j=1}^{r_2}{\pi }_{ij}{\eta }_{ij}^2}}& {\displaystyle \sum _{i=1}^{r_1}{\displaystyle \sum _{j=1}^{r_2}{\pi }_{ij}{\eta }_{ij}^2}}{T}_i& {\displaystyle \sum _{i=1}^{r_1}{\displaystyle \sum _{j=1}^{r_2}{\pi }_{ij}{\eta }_{ij}^2}}{V}_j& {\displaystyle \sum _{i=1}^{r_1}{\displaystyle \sum _{j=1}^{r_2}{\pi }_{ij}{\eta }_{ij}^2}}{T}_i{V}_j& 0\\ & {\displaystyle \sum _{i=1}^{r_1}{\displaystyle \sum _{j=1}^{r_2}{\pi }_{ij}{\eta }_{ij}^2}}{T}_i^2& {\displaystyle \sum _{i=1}^{r_1}{\displaystyle \sum _{j=1}^{r_2}{\pi }_{ij}{\eta }_{ij}^2}}{T}_i{V}_j& {\displaystyle \sum _{i=1}^{r_1}{\displaystyle \sum _{j=1}^{r_2}{\pi }_{ij}{\eta }_{ij}^2}}{T}_i^2{V}_j& 0\\ & & {\displaystyle \sum _{i=1}^{r_1}{\displaystyle \sum _{j=1}^{r_2}{\pi }_{ij}{\eta }_{ij}^2}}{V}_j^2& {\displaystyle \sum _{i=1}^{r_1}{\displaystyle \sum _{j=1}^{r_2}{\pi }_{ij}{\eta }_{ij}^2}}{T}_i{V}_j^2& 0\\ & & & {\displaystyle \sum _{i=1}^{r_1}{\displaystyle \sum _{j=1}^{r_2}{\pi }_{ij}{\eta }_{ij}^2}}{T}_i^2{V}_j^2& 0\\ & symmetric& & & 2m/t_M\end{array}\right]$$

(3)

$$\left|F\right|=\frac{2mN}{{\sigma }^2}{\eta }_{11}^2{\eta }_{12}^2{\eta }_{21}^2{\eta }_{22}^2{\pi }_{11}{\pi }_{12}{\pi }_{21}{\pi }_{22}=\frac{2mN}{{\sigma }^2}\exp \left(8{\delta }_1+4{\delta }_2+4{\delta }_3+2{\delta }_4\right){\pi }_{11}{\pi }_{12}{\pi }_{21}{\pi }_{22}.$$

(4)

The ratios (${\pi }_{11},{\pi }_{12},{\pi }_{21}$ and ${\pi }_{22}$) are decision variables and ${\delta }_1$, ${\delta }_2$, ${\delta }_3$, ${\delta }_4$ and $2mN/{\sigma }^2$ are constants in Equations (3) and (4). From Equation (4), it can be shown that $\left|F\right|$ is maximized when all decision variables are equal to 0.25. Therefore, a lemma was derived as follows.

Lemma 1. 

The optimal specimen ratios for four test points, which are a combination of the use and the maximum stress levels with two stress variables, are equal to 0.25 based on D-optimality criteria.

In this phase, for optimal test plans, the same specimen quantities were allocated to all test points according to Lemma 1. The parameters of the model were estimated based on information from the tests.

4.2. Second Phase: The Practical PADT Plan Based on the Concept of the Compromise Plan with Three Stress Levels

In the second phase, three stress levels with two stress variables were considered to detect the curvature effect of the acceleration model based on the concept of a compromise plan [1,24,37]. In addition, the lifetime information was precisely estimated through the relationship between the drift and stress variables. For these reasons, at least three stress levels are considered for most reliability tests in various manufacturing industries (Figure 3).

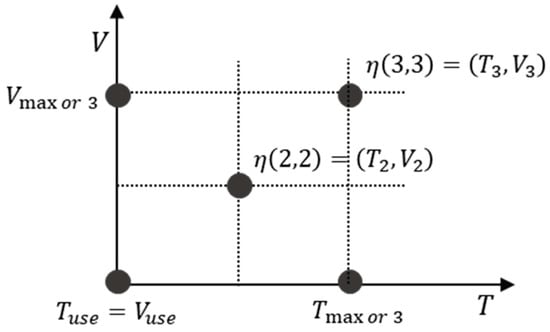
Figure 3. The test points and the individual stress levels in the second phase.

To optimize a PADT plan based on the compromise concept with three stress levels, that is, to find the decision variables of proposed PADT plans, the Fisher information matrix for the second phase should be derived in a similar fashion as the first phase. The degradation characteristic and the lifetime (or failure time) were defined according to Assumption 3. The lifetime was determined by the probability density function, $g_{ij}\left(t\right)$, of an inverse Gaussian distribution. If $t_{q,\left(i,j\right)}$ is the q-th quantile of the distribution at stress levels ($T_i,V_j$), then $t_{q,\left(i,j\right)}$ can be approximately defined as [37,43].

$$g_{ij}\left(t\right)=\sqrt{\frac{w^2}{2\pi {\sigma }^2{t}^3}}\exp \left[-\frac{{\left\{{\eta }_{ij}t-w\right\}}^2}{2{\sigma }^{2}t}\right],t>0$$

$$t_{q,\left(i,j\right)}\approx \frac{{\left[z_q\sigma +\sqrt{z_q^2{\sigma }^2+4{\eta }_{ij}w}\right]}^2}{4{\eta }_{ij}^2}$$

where $z_q$ is the q-th quantile of the standard normal distribution. In addition, given that the drift at the use conditions of the two stress variables is ${\eta }_{11}=\eta \left(T_1,V_1\right)=\eta \left(0,0\right)=\exp \left({\delta }_1\right)$, the MLE of $t_{q,\left(1,1\right)}$ is given by

$$\widehat{t_{q,\left(1,1\right)}}\approx \frac{{\left[z_q\widehat{\sigma }+\sqrt{z_q^2{\widehat{\sigma }}^2+4\exp \left({\widehat{\delta }}_1\right)w}\right]}^2}{4\exp \left(2{\widehat{\delta }}_1\right)}$$

where ${\widehat{\delta }}_1$ is the MLE of ${\delta }_1$ and $\widehat{\sigma }$ is the MLE of $\sigma$. Then, the first partial derivatives of $t_{q,\left(1,1\right)}$ with respect to each parameter, are given by

$$h=\left[\begin{array}{c}{h}_1\\ h_2\\ h_3\\ h_4\\ h_5\end{array}\right]=\left[\begin{array}{c}\frac{\partial t_{q,\left(1,1\right)}}{\partial {\delta }_1}\\ \frac{\partial t_{q,\left(1,1\right)}}{\partial {\delta }_2}\\ \frac{\partial t_{q,\left(1,1\right)}}{\partial {\delta }_3}\\ \frac{\partial t_{q,\left(1,1\right)}}{\partial {\delta }_4}\\ \frac{\partial t_{q,\left(1,1\right)}}{\partial \sigma }\end{array}\right]=\left[\begin{array}{c}\frac{w\left(z_q\sigma +\sqrt{4\exp \left({\delta }_1\right)w+z_q^2{\sigma }^2}\right)}{\exp \left({\delta }_1\right)\sqrt{4\exp \left({\delta }_1\right)w+z_q^2{\sigma }^2}}-\frac{{\left(z_q\sigma +\sqrt{4\exp \left({\delta }_1\right)w+z_q^2{\sigma }^2}\right)}^2}{2\exp \left(2{\delta }_1\right)}\\ 0\\ 0\\ 0\\ \frac{z_q\sigma +\sqrt{4\exp \left({\delta }_1\right)w+z_q^2{\sigma }^2}}{2\exp \left(2{\delta }_1\right)}\left(z_q+\frac{z_q^2{\sigma }^2}{\sqrt{4\exp \left({\delta }_1\right)w+z_q^2{\sigma }^2}}\right)\end{array}\right]$$

Let $F^{-1}$ be the inverse of the Fisher information matrix, then the asymptotic variance of the MLE of $t_{q,\left(1,1\right)}$ can be obtained by the inverse of the Fisher information matrix, $F^{-1}$, and the above vector $h$ as follows.

$$F^{-1}=\frac{{\sigma }^2}{N{t}_M}\left[\begin{array}{ccccc}{f}_{11}^{-1}& f_{12}^{-1}& f_{13}^{-1}& f_{14}^{-1}& 0\\ & f_{22}^{-1}& f_{23}^{-1}& f_{24}^{-1}& 0\\ & & f_{33}^{-1}& f_{34}^{-1}& 0\\ & & & f_{44}^{-1}& 0\\ & symmetric& & & f_{55}^{-1}\end{array}\right],$$

$$\mathrm{Avar}\left(\widehat{t_{q,\left(1,1\right)}}\right)=h^{\mathrm{T}}{F}^{-1}h=\frac{{\sigma }^2}{N{t}_M}\left[f_{11}^{-1}{h}_1^2+f_{55}^{-1}{h}_5^2\right]$$

(5)

where $f_{11}^{-1}=\frac{{\pi }_{22}{\pi }_{31}{\pi }_{33}{\eta }_{22}^2{\eta }_{31}^2{\eta }_{33}^2{\left(T_2-1\right)}^2{V}_2{}^2+{\pi }_{13}{\eta }_{13}^2\left(\begin{array}{l}{\pi }_{22}{\pi }_{33}{\eta }_{22}^2{\eta }_{33}^2{T}_2{}^2{\left(V_2-1\right)}^2\\ +{\pi }_{31}{\eta }_{31}^2\left({\pi }_{33}{\eta }_{33}^2+{\pi }_{22}{\eta }_{22}^2{T}_2{}^2{V}_2{}^2\right)\end{array}\right)}{{\pi }_{13}{\pi }_{22}{\pi }_{31}{\pi }_{33}{\eta }_{13}^2{\eta }_{22}^2{\eta }_{31}^2{\eta }_{33}^2{\left(T_2-1\right)}^2{\left(V_2-1\right)}^2+{\pi }_{11}{\eta }_{11}^2\left(\begin{array}{l}{\pi }_{22}{\pi }_{31}{\pi }_{33}{\eta }_{22}^2{\eta }_{31}^2{\eta }_{33}^2{\left(T_2-1\right)}^2{V}_2{}^2\\ +{\pi }_{13}{\eta }_{13}^2\left(\begin{array}{l}{\pi }_{22}{\pi }_{31}{\eta }_{22}^2{\eta }_{31}^2{T}_2{}^2{\left(V_2-1\right)}^2\\ +{\pi }_{31}{\eta }_{31}^2\left({\pi }_{33}{\eta }_{33}^2+{\pi }_{22}{\eta }_{22}^2{T}_2{}^2{V}_2{}^2\right)\end{array}\right)\end{array}\right)}$, $f_{55}^{-1}=2m/t_M$ and ‘$\mathrm{T}$’ indicate a transposition.

As a result, the objective function can be determined by only $f_{11}^{-1}$ because all terms in Equation (5) without $f_{11}^{-1}$ are constant terms in this case. Nevertheless, the objective function is sufficiently complicated to obtain analytic optimal solutions. Therefore, a genetic algorithm (GA) was adopted to determine the practical PADT plans with two stress variables. Table 3 presents the practical PADT plans in various combined cases of the model parameters, where ${\pi }_{33}=1-\left({\pi }_{11}+{\pi }_{13}+{\pi }_{22}+{\pi }_{31}\right)$. In Table 3, the parameters ${\delta }_2$, ${\delta }_3$, and ${\delta }_4$ were chosen to examine the effect of parameters on the acceleration model. The parameters ${\delta }_2$ and ${\delta }_3$ indicate the severity of $T$ (temperature) and $V$ (voltage), respectively. In addition ${\delta }_4$ represents the interaction effect of $T$ and $V$. That is, if ${\delta }_4$ is positive or negative, there is an interaction between T and V, whereas if ${\delta }_4$ is zero, there is no interaction. In thise study, the values of ${\delta }_4$ are assumed to be −3, 0, and 3. However, ${\delta }_1$ was not considered in Table 3 since it is a constant term and does not affect the design of the practical PADT plans.

Table 3. The practical PADT plans with two stress variables.

δ2	δ3	δ4	T2	V2	π11	π13	π22	π31	π33	${\mathit{f}}_{\mathbf{11}}^{-\mathbf{1}}$
3	4	−3	0.0004	0.6927	0.0456	0.1684	0.7566	0.0287	0.0007	6.480 × 10−2
3	4	0	0.4098	0.6566	0.0304	0.2162	0.5645	0.1839	0.0050	3.174 × 10−2
3	4	3	0.4251	0.6242	0.0376	0.2535	0.4073	0.2941	0.0075	1.392 × 10−2
3	6	−3	0.0001	0.8006	0.0503	0.1913	0.7063	0.0469	0.0052	2.912 × 10−3
3	6	0	0.1488	0.7867	0.0355	0.1796	0.6105	0.1663	0.0081	2.538$\times {10}^{-3}$
3	6	3	0.2029	0.7585	0.0396	0.1993	0.4757	0.2799	0.0055	1.621$\times {10}^{-3}$
3	8	−3	0.0006	0.8385	0.0620	0.1876	0.6945	0.0504	0.0055	9.856$\times {10}^{-5}$
3	8	0	0.0043	0.8454	0.0160	0.2015	0.6707	0.1079	0.0039	9.900$\times {10}^{-5}$
3	8	3	0.0136	0.8405	0.0453	0.1971	0.6529	0.0979	0.0068	9.757$\times {10}^{-5}$
5	4	−3	0.6896	0.3200	0.0199	0.0874	0.7126	0.1487	0.0314	1.183$\times {10}^{-2}$
5	4	0	0.6709	0.4761	0.0325	0.2948	0.4434	0.2275	0.0018	3.851$\times {10}^{-3}$
5	4	3	0.6403	0.4653	0.0281	0.3248	0.3280	0.3163	0.0028	1.789$\times {10}^{-3}$
5	6	−3	0.4737	0.7069	0.0082	0.1590	0.6032	0.1923	0.0373	1.373$\times {10}^{-3}$
5	6	0	0.4940	0.6838	0.0386	0.2516	0.3976	0.3115	0.0007	4.470$\times {10}^{-4}$
5	6	3	0.4500	0.6476	0.0484	0.3034	0.3031	0.3408	0.0043	2.292$\times {10}^{-4}$
5	8	−3	0.1610	0.8347	0.0403	0.1801	0.6065	0.1551	0.0180	8.763$\times {10}^{-5}$
5	8	0	0.2445	0.8167	0.0342	0.2155	0.4688	0.2791	0.0024	4.780$\times {10}^{-5}$
5	8	3	0.2336	0.7791	0.0311	0.2154	0.3774	0.3671	0.0090	2.956$\times {10}^{-5}$
7	4	−3	0.8170	0.0449	0.0432	0.0677	0.6879	0.1923	0.0089	5.439$\times {10}^{-4}$
7	4	0	0.7981	0.2074	0.0426	0.2461	0.5199	0.1819	0.0095	3.655$\times {10}^{-4}$
7	4	3	0.7845	0.2257	0.0505	0.3340	0.3975	0.2169	0.0011	2.233$\times {10}^{-4}$
7	6	−3	0.7263	0.5302	0.0265	0.2698	0.4784	0.2096	0.0157	1.425$\times {10}^{-4}$
7	6	0	0.6877	0.5022	0.0481	0.3249	0.3623	0.2614	0.0033	5.284$\times {10}^{-5}$
7	6	3	0.6542	0.4615	0.0327	0.4193	0.2351	0.2977	0.0152	2.906$\times {10}^{-5}$
7	8	−3	0.5498	0.7321	0.0347	0.2450	0.4179	0.2858	0.0166	1.463$\times {10}^{-5}$
7	8	0	0.4956	0.6942	0.0421	0.2975	0.2802	0.3791	0.0011	6.250$\times {10}^{-6}$
7	8	3	0.4577	0.6571	0.0502	0.3075	0.2838	0.3583	0.0002	3.748$\times {10}^{-6}$

In addition, some tendencies of the results of the practical PADT plan were derived from Table 3 as below.

(1)

As ${\delta }_2$ increases, $T_2$ increases and $V_2$ decreases.

(2)

As ${\delta }_3$ increases, $T_2$ decreases and $V_2$ increases.

(3)

As ${\delta }_2$, ${\delta }_3$, or ${\delta }_4$ increases, ${\pi }_{22}$ decreases.

First, when the parameter ${\delta }_2$ increases, $T_2$ simultaneously increases with $V_2$ decreasing. That is, if the mean degradation increment caused by temperature stress is greater than the mean degradation increment caused by voltage stress, the actual stress level $T_2$ increases in the PADT plans. However, when $T_2$ increases, $V_2$ should be decreased by ${\delta }_4$. Likewise, when ${\delta }_3$ increases, $V_2$ increases with $T_2$ decreasing simultaneously. In addition, an increase in ${\delta }_2$, ${\delta }_3$, and/or ${\delta }_4$ increases AF. When ${\delta }_2$, ${\delta }_3$, or ${\delta }_4$ increases, more test units at ${\pi }_{13}$, ${\pi }_{31}$ and/or ${\pi }_{33}$ are required corresponding to the parameters. As a result, ${\pi }_{22}$ decreases.

5. Example of a Sample Scenario

In this section, a sample scenario is introduced to demonstrate the practicality of the proposed procedure. The scenario is detailed as follows.

(1)

A total of 3000 samples from a novel semiconductor prototype were gathered for tests.

(2)

The degradation increment amount of the test units follows a normal distribution with mean ${\eta }_{ij}{t}_{ijkl}$ and variance

(3)

The generalized Eyring model for the accelerated model was assumed between the drift parameter and the stress variables.

(4)

The degradation characteristic was dependent on the temperature and the voltage stresses.

(5)

The maximum and use stress levels of the temperature were specified as 130 °C (=403 °K) and 45 °C (=318 °K), respectively.

(6)

The values of 4.4 and 3.8 V were determined as the maximum and use stress conditions for the voltage stress, respectively.

In the first phase, according to Lemma 1, 20 specimens were allocated to the design check to obtain the combination of typical use conditions, high temperature operating life (HTOL) under maximum temperature and use voltage, voltage limit tests under use temperature and maximum voltage, and biased highly accelerated stress test (HAST) for the combination of maximum stress levels. In other words, 80 specimens among the 3000 samples were used to estimate the parameters of the accelerated model. Thus, the model parameters were obtained using the degradation data from the above tests. The model parameters, δ₂, δ₃, and δ₄, were estimated as 5, 6, and −3, respectively, according to the first phase procedure.

After the model parameters were determined, the practical PADT plan with three stress levels for two stress variables was designed in the second phase. Thus, the ratios and middle-stress levels (Table 3) used were: ${\pi }_{11}=0.0082$, ${\pi }_{13}=0.1590$, ${\pi }_{22}=0.6032$, ${\pi }_{31}=0.1923$, ${\pi }_{33}=0.0373$, $T_2=0.4737$ and $V_2=0.7069$.

According to the above results, four specimens were added to the design check (${\pi }_{11}$). Additionally, 457, 557, and 92 specimens were allocated for the voltage limit test (${\pi }_{13}$), the HTOL (${\pi }_{31}$), and the HAST (${\pi }_{33}$), respectively. A total of 1810 specimens were tested (${\pi }_{22}$) under the middle-stress levels, 80.3 °C and 3.976 V, calculated based on Assumption 4. In the semiconductor area, qualification tests should be used to verify various item requirements. In particular, the HTOL and the HAST were included in the qualification tests, with 231 and 75 specimens, respectively, based on JEDEC standard JESD-47. Therefore, the specimens for the tests, as well as the reliability information, were more effectively applied during qualification.

A conventional test plan was also considered, in which the specimens were equally allocated to each test and the middle-stress levels were placed in the median between use and maximum levels [44]. This conventional test plan is one of the simplest test plans as 600 specimens are allocated to 5 test points. Thus, in this study, the practical PADT plan using the proposed procedure was compared with the conventional test plan to validate the statistical efficiency, using the equation below:

$$\mathrm{Relative}\mathrm{Efficiency}(\mathrm{RE})=\frac{v\mathrm{for}\mathrm{the}\mathrm{proposed}\mathrm{PADT}\mathrm{plan}}{v\mathrm{for}\mathrm{the}\mathrm{conventional}\mathrm{PADT}\mathrm{plan}}$$

(6)

A simplified objective function, $v$, for the conventional test plan was calculated as $3.20\times {10}^{-3}$, which was larger than the value $1.373\times {10}^{-3}$ of the proposed PADT plan. The relative efficiency between the proposed and conventional test plans was calculated as 0.4282 according to Equation (6). That is, the proposed practical PADT plan was superior to the conventional plan in terms of the statistical efficiency.

6. Conclusions

In this paper, CS-PADT plans with two stress variables are proposed using a strategic procedure composed of two phases. In particular, a real situation in the development stage is reflected in the PADT plans to minimize the issues of limited time, cost, and available specimen quantity for testing during the development stage. Several studies on the PATs have been conducted to solve the above issues. However, a study on the PADT plans with two stress variables has been not conducted. In the real situation with limited time and number of specimens, more than two stress variables can be considered, not a single stress variable, to obtain more reliable information. Therefore, this study developed the PADT plans with two stress variables for practical lifetime estimation. In addition, similar to Kim and Sung [1], the proposed test plan can be utilized for the various general tests such as conformity, performance, and operational feasibility tests. Therefore, the proposed test plan can be effectively utilized to solve the practical shortage problems of the prototype in the development phase.

In the first phase, two stress levels for each variable were considered to estimate the accelerated model parameters when the degradation characteristic follows the WP. Therefore, in this phase, four test points were considered, including the use and maximum stress levels. In addition, the optimal allocation ratio of the test units was determined to be 0.25 based on the D-optimality criteria. That is, the same specimen quantity was allocated to the four test points. The parameters of the model were then estimated using the reliability information from the tests of the first phase.

In the second phase, one more stress level for each stress variable was considered to check the acceleration model validity and also to identify the curvature effects. Additional stress levels were considered based on the compromise plans concept. Accordingly, a practical PADT plan with two stress variables was developed using the proposed procedure. Under use case conditions for all stress variables, the decision variables ratios were allocated based on a combination of all the test points and the middle-stress level of the two stress variables, which minimized the asymptotic variance of the MLE for the q-th quantile of the lifetime distribution. Therefore, it is expected that more accurate lifetime information is estimated. The presented sample scenario demonstrates the practicability of the proposed PADT plan and improved efficiency compared with conventional test plans in terms of statistical efficiency.

In future research, various stochastic degradation processes, such as the gamma process or inverse Gaussian process can be considered for the PADT plan with two stress variables. In addition, the proposed procedure may also be extended to design the SS-PADT plan.