Improving Bearing Fault Diagnosis Using Maximum Information Coefficient Based Feature Selection
Abstract
:1. Introduction
- (1)
- A new frame of feature selection is proposed for bearing fault diagnosis, which aims at considering the relevance among features and the relevance between features and fault categories. In the new feature selection frame, strong relevance features are eliminated by an FF-MIC matrix based on the relevance between features and features. On the contrary, strong relevance features are selected by the FC-MIC matrix based on the relevance between features and categories. The proposed frame can eliminate not only redundant features but also irrelevant features from the feature set.
- (2)
- In order to avoid computational complexity brought by wrapper methods, an intersection operation is applied to merge the obtained feature subsets. The intersection operation has advantages of forming a final subset with a lower dimension and saving time, instead of subset searching.
- (3)
- This paper applied two datasets to validate the effectiveness and adaptability of proposed method. It turned out the proposed method has a good applicability and stability.
2. Related Basic Theory and Algorithm
2.1. Maximum Information Coefficient
2.2. Merging Feature Subsets
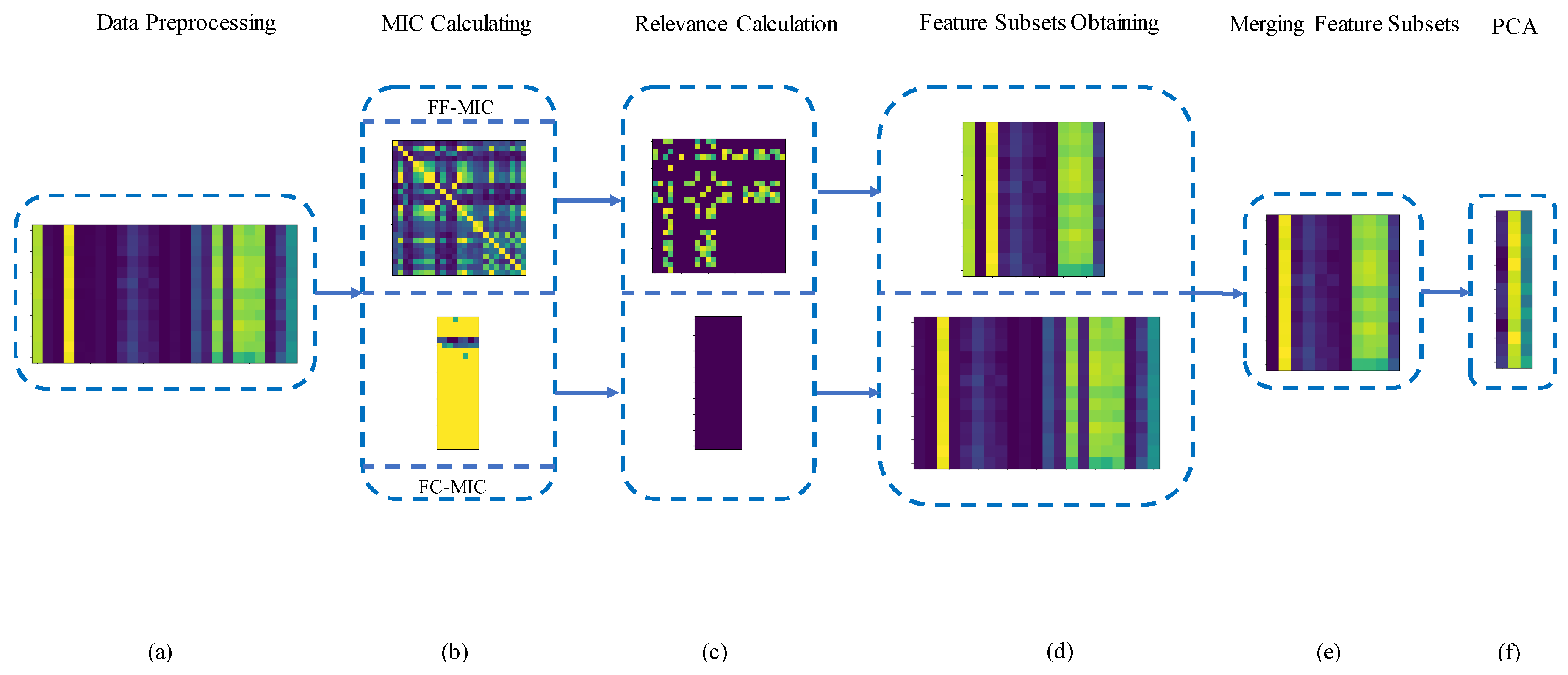
3. Proposed Method
3.1. Data Preprocessing
| Algorithm 1. Data preprocessing. |
| Input: samples: , where is the number of samples. Output: the preprocessed feature set .
|
3.2. MIC Calculation
| Algorithm 2. MIC calculation. |
| Input: where are fault categories, and is the number of fault categories. Output: FF-MIC and FC-MIC.
|
3.3. Relevance Calculation
| Algorithm 3. Relevance calculation |
| Input: , FF-MIC, and FC-MIC. Output: , and
|
3.4. Obtaining Feature Subsets
| Algorithm 4. Obtaining feature subsets |
| Input: , , and Output: and .
|
3.5. Merging Feature Subsets and Reducing Dimensions with PCA
| Algorithm 5. Merging feature subsets. |
| Input: and . Output: .
|
4. Experimental Results and Analysis
4.1. Experiments on CWRU Datasets
4.1.1. Experimental Setup and Datasets
4.1.2. Result Analysis of CWRU Datasets
4.2. Experiments on CUT-2 Datasets
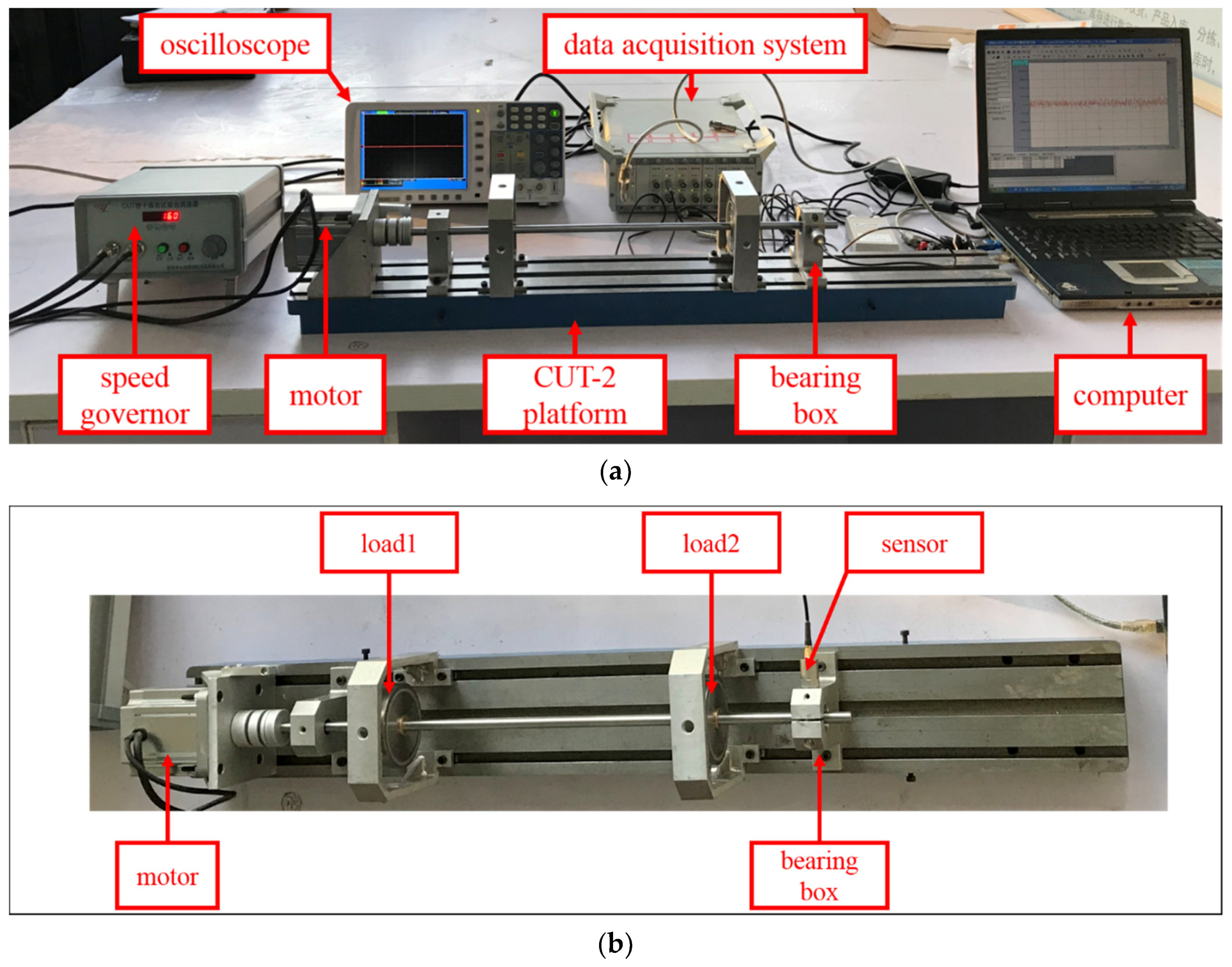
4.2.1. Experimental Setup and CUT-2 Datasets
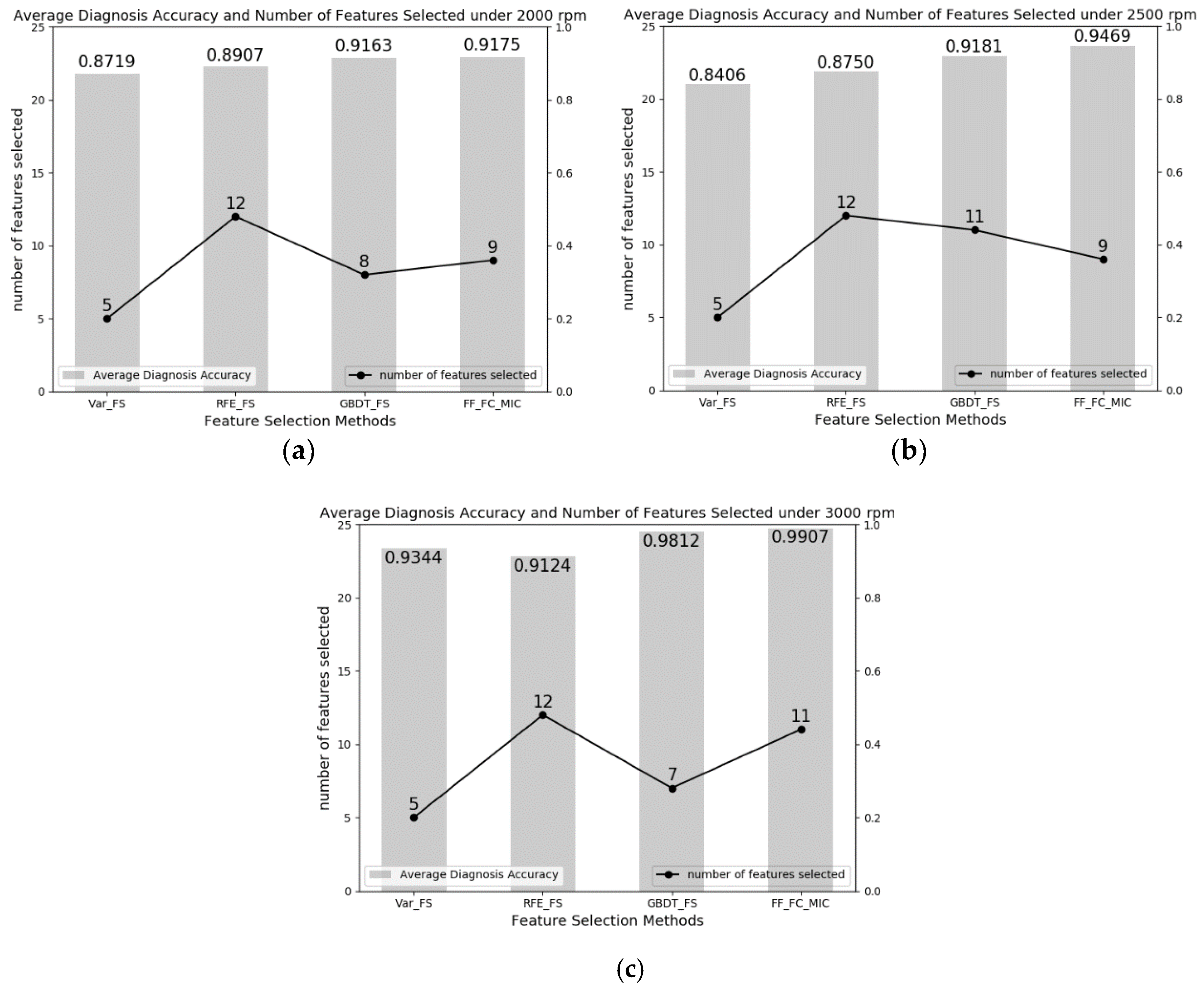
4.2.2. Result Analysis of CUT-2 Datasets
4.3. Comparison of Significant Differences
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ciabattoni, L.; Ferracuti, F.; Freddi, A.; Monteriu, A. Statistical Spectral Analysis for Fault Diagnosis of Rotating Machines. IEEE Trans. Ind. Electron. 2018, 65, 4301–4310. [Google Scholar] [CrossRef]
- Tra, V.; Kim, J.; Khan, S.A.; Kim, J. Bearing Fault Diagnosis under Variable Speed Using Convolutional Neural Networks and the Stochastic Diagonal Levenberg-Marquardt Algorithm. Sensors 2017, 17, 2834. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez-Galiano, V.F.; Luque-Espinar, J.A.; Chica-Olmo, M.; Mendes, M.P. Feature selection approaches for predictive modelling of groundwater nitrate pollution: An evaluation of filters, embedded and wrapper methods. Sci. Total Environ. 2018, 624, 661–672. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Li, T.; Liu, H. Recent advances in feature selection and its applications. Knowl. Inf. Syst. 2017, 53, 551–577. [Google Scholar] [CrossRef]
- Kashef, S.; Nezamabadi-Pour, H.; Nikpour, B. Multilabel feature selection: A comprehensive review and guiding experiments. Wiley Interdiscip. Rev.: Data Min. Knowl. Discov. 2018, 8, e1240. [Google Scholar] [CrossRef]
- Yao, X.; Wang, X.; Zhang, Y.; Quan, W. Summary of feature selection algorithms. Control. Decis. 2012, 27, 161–313. [Google Scholar]
- Fu, X.; Zhang, Y.; Zhu, Y. Rolling bearing fault diagnosis approach based on case-based reasoning. J. Xi’an Jiaotong Univ. 2011, 45, 79–84. [Google Scholar]
- Ou, L.; Yu, D. Rolling bearing fault diagnosis based on supervised laplaian score and principal component analysis. J. Mech. Eng. 2014, 88–94. [Google Scholar] [CrossRef]
- Ou, L.; Yu, D. Rolling bearing fault diagnosis based on laplaian score fuzzy C-means clustering. China Mech. Eng. 2014, 25, 1352–1357. [Google Scholar]
- Hui, K.H.; Ooi, C.S.; Lim, M.H.; Leong, M.S.; Al-Obaidi, S.M. An improved wrapper-based feature selection method for machinery fault diagnosis. PLOS ONE 2017, 12, e189143. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Zheng, H.; Zhu, T. Feature selection in machine fault diagnosis based on evolutionary Monte Carlo method. J. Vib. Shock 2011, 30, 98–101. [Google Scholar]
- Islam, R.; Khan, S.A.; Kim, J. Discriminant Feature Distribution Analysis-Based Hybrid Feature Selection for Online Bearing Fault Diagnosis in Induction Motors. J. Sens. 2016, 2016, 1–16. [Google Scholar] [CrossRef]
- Luo, M.; Li, C.; Zhang, X.; Li, R.; An, X. Compound feature selection and parameter optimization of ELM for fault diagnosis of rolling element bearings. ISA Trans. 2016, 65, 556–566. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.; Dong, F.; Ding, E.; Wu, S.; Fan, C. Rolling Bearing Fault Diagnosis Using Modified LFDA and EMD with Sensitive Feature Selection. IEEE Access 2018, 6, 3715–3730. [Google Scholar] [CrossRef]
- Liu, Y.; Hu, J.; Ren, L.; Yao, K.; Duan, J.; Chen, L. Study on the Bearing Fault Diagnosis based on Feature Selection and Probabilistic Neural Network. J. Mech. Transm. 2016, 40, 48–53. [Google Scholar]
- Yang, Y.; Pan, H.; Wei, J. The rolling bearing fault diagnosis method based on the feature selection and RRVPMCD. J. Vib. Eng. 2014, 27, 629–636. [Google Scholar]
- Atamuradov, V.; Medjaher, K.; Camci, F.; Dersin, P.; Zerhouni, N. Railway Point Machine Prognostics Based on Feature Fusion and Health State Assessment. IEEE Trans. Instrum. Meas. 2018, 1–14. [Google Scholar] [CrossRef]
- Cui, B.; Pan, H.; Wang, Z. Fault diagnosis of roller bearings base on the local wave and approximate entropy. J. North University China (Nat. Sci. Ed.) 2012, 33, 552–558. [Google Scholar]
- Shi, L. Correlation Coefficient of Simplified Neutrosophic Sets for Bearing Fault Diagnosis. Shock. Vib. 2016, 2016, 1–11. [Google Scholar] [CrossRef]
- Zheng, J.; Cheng, J.; Yang, Y.; Luo, S. A rolling bearing fault diagnosis method based on multi-scale fuzzy entropy and variable predictive model-based class discrimination. Mech. Mach. Theory 2014, 78, 187–200. [Google Scholar] [CrossRef]
- Zhang, N.; Wu, L.; Yang, J.; Guan, Y. Naive Bayes Bearing Fault Diagnosis Based on Enhanced Independence of Data. Sensors 2018, 18, 463. [Google Scholar] [CrossRef] [PubMed]
- Jiang, X.; Wu, L.; Ge, M. A Novel Faults Diagnosis Method for Rolling Element Bearings Based on EWT and Ambiguity Correlation Classifiers. Entropy 2017, 19, 231. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, L. Hybrid feature selection using component co-occurrence based feature relevance measurement. Expert Syst. Appl. 2018, 102, 83–99. [Google Scholar] [CrossRef]
- Bharti, K.K.; Singh, P.K. Hybrid dimension reduction by integrating feature selection with feature extraction method for text clustering. Expert Syst. Appl. 2015, 42, 3105–3114. [Google Scholar] [CrossRef]
- Xu, J.; Huang, F.; Mu, H.; Wang, Y.; Xu, Z. Tumor feature gene selection method based on PCA and information gain. J. Henan Univ. (Nat. Sci. Ed.) 2018, 46, 104–110. [Google Scholar]
- Zhu, L.; Wang, X.; Zhang, J. An engine fault diagnosis method based on ReliefF-PCA and SVM. J. Beijing Univ. Chem. Technol. (Nat. Sci.) 2018, 45, 55–59. [Google Scholar]
- Xiao, Y.; Liu, C. Improved PCA method for SAR target recognition based on sparse solution. J. Univ. Chin. Acad. Sci. 2018, 35, 84–88. [Google Scholar]
- Du, Z.; Xiang, C. A Wavelet Packet Decomposition and Principal Component Analysis Approach. Control Eng. China 2016, 23, 812–815. [Google Scholar]
- Fadda, M.L.; Moussaoui, A. Hybrid SOM–PCA method for modeling bearing faults detection and diagnosis. J. Braz. Soc. Mech. Sci. Eng. 2018, 40. [Google Scholar] [CrossRef]
- Wang, T.; Xu, H.; Han, J.; Elbouchikhi, E.; Benbouzid, M.E.H. Cascaded H-Bridge Multilevel Inverter System Fault Diagnosis Using a PCA and Multiclass Relevance Vector Machine Approach. IEEE Trans. Power Electron. 2015, 30, 7006–7018. [Google Scholar] [CrossRef]
- Sun, G.; Song, Z.; Liu, J.; Zhu, S.; He, Y. Feature Selection Method Based on Maximum Information Coefficient and Approximate Markov Blanket. Acta Autom. Sin. 2017, 43, 795–805. [Google Scholar]
- The Case Western Reserve University Bearing Data Center Bearing Data Center Seeded Fault Test Data[EB/OL]. Available online: http://csegroups.case.edu/bearingdatacenter/pages/download-data-file (accessed on 10 June 2016).
- Wei, Z.; Wang, Y.; He, S.; Bao, J. A novel intelligent method for bearing fault diagnosis based on affinity propagation clustering and adaptive feature selection. Knowl.-Based Syst. 2017, 116, 1–12. [Google Scholar] [CrossRef]
- Lei, Y.; He, Z.; Zi, Y. Fault Diagnosis Based on Novel Hybrid Intelligent Model. Chin. J. Mech. Eng. 2008, 44, 112–117. [Google Scholar] [CrossRef]



| Features in the Time Domain | Features in the Frequency Domain | ||
|---|---|---|---|
| is the time-domain signal sequence, , is the number of each sample points. | is the frequency-domain signal sequence, , is the number of spectral lines. | ||
| Conditions of the Bearings | Fault Size (inch) | Number of Samples | Class |
|---|---|---|---|
| Normal | 150 | 0 | |
| Inner race fault | 0.007 | 50 | 1 |
| 0.014 | 50 | ||
| 0.021 | 50 | ||
| Outer race fault | 0.007 | 50 | 2 |
| 0.014 | 50 | ||
| 0.021 | 50 | ||
| Baller fault | 0.007 | 50 | 3 |
| 0.014 | 50 | ||
| 0.021 | 50 |
| Motor Speed (rpm) | All Features | Selected Features | Selected Number |
|---|---|---|---|
| 1750 |  |  | 0, 3, 8, 9, 11, 16, 22 |
| 1772 | 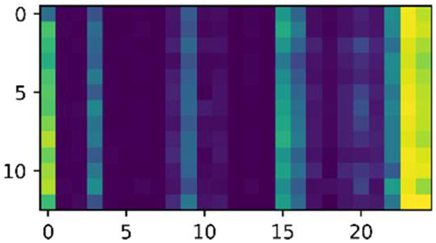 |  | 0, 3, 8, 9, 11, 15, 16, 20, 22 |
| Motor Speed (rpm) | Feature Selection Methods | Classification Models | |
|---|---|---|---|
| SVM | KNN | ||
| 1750 | Var_FS | 0.8750 | 0.8750 |
| RFE_FS | 0.8500 | 0.8333 | |
| GBDT_FS | 0.9417 | 0.9600 | |
| FF_FC_MIC | 0.9583 | 0.9750 | |
| 1772 | Var_FS | 0.7750 | 0.7417 |
| RFE_FS | 0.8000 | 0.7666 | |
| GBDT_FS | 0.9833 | 0.9917 | |
| FF_FC_MIC | 0.9917 | 1.0000 | |
| Conditions of the Bearings | Fault Size (mm) | Number of Samples | Class |
|---|---|---|---|
| Normal condition | 200 | 0 | |
| Inner race fault | 0.2 0.3 | 100 100 | 1 |
| Outer race fault | 0.2 0.3 | 100 100 | 2 |
| Baller fault | 0.2 0.3 | 100 100 | 3 |
| Motor Speed (rpm) | All Features | Selected Features | Selected Number |
|---|---|---|---|
| 2000 |  |  | 0, 2, 3, 8, 10, 11, 19, 20, 22 |
| 2500 | 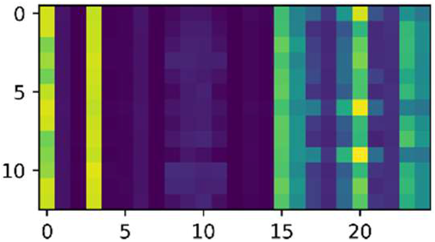 | 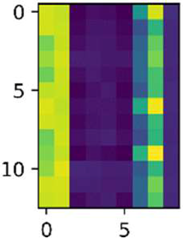 | 0, 3, 8, 9, 10, 11, 19, 20, 22 |
| 3000 | 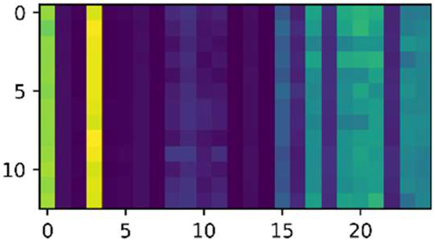 |  | 0, 3, 8, 9, 11, 14, 15, 16, 20, 21, 23 |
| Motor Speed (rpm) | Feature Selection Methods | Classification Models | |
|---|---|---|---|
| SVM | KNN | ||
| 2000 | Var_FS | 0.8688 | 0.8750 |
| RFE_FS | 0.8938 | 0.8875 | |
| GBDT_FS | 0.9313 | 0.9012 | |
| FF_FC_MIC | 0.9225 | 0.9125 | |
| 2500 | Var_FS | 0.8562 | 0.8250 |
| RFE_FS | 0.8688 | 0.8812 | |
| GBDT_FS | 0.9187 | 0.9175 | |
| FF_FC_MIC | 0.9625 | 0.9313 | |
| 3000 | Var_FS | 0.9437 | 0.9250 |
| RFE_FS | 0.9187 | 0.9062 | |
| GBDT_FS | 0.9750 | 0.9875 | |
| FF_FC_MIC | 0.9938 | 0.9875 | |
| Methods Compared | p-Value | Whether the Mean Difference between the Two Methods Is Significant (Y/N) |
|---|---|---|
| Var_FS, FF_FC_MIC | 1.166 × | Y |
| RFE_FS, FF_FC_MIC | 2.509 × | Y |
| GBDT_FS, FF_FC_MIC | 3.576 × | Y |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, X.; Wang, J.; Lu, J.; Liu, G.; Chen, J. Improving Bearing Fault Diagnosis Using Maximum Information Coefficient Based Feature Selection. Appl. Sci. 2018, 8, 2143. https://doi.org/10.3390/app8112143
Tang X, Wang J, Lu J, Liu G, Chen J. Improving Bearing Fault Diagnosis Using Maximum Information Coefficient Based Feature Selection. Applied Sciences. 2018; 8(11):2143. https://doi.org/10.3390/app8112143
Chicago/Turabian StyleTang, Xianghong, Jiachen Wang, Jianguang Lu, Guokai Liu, and Jiadui Chen. 2018. "Improving Bearing Fault Diagnosis Using Maximum Information Coefficient Based Feature Selection" Applied Sciences 8, no. 11: 2143. https://doi.org/10.3390/app8112143
APA StyleTang, X., Wang, J., Lu, J., Liu, G., & Chen, J. (2018). Improving Bearing Fault Diagnosis Using Maximum Information Coefficient Based Feature Selection. Applied Sciences, 8(11), 2143. https://doi.org/10.3390/app8112143






