Power Prediction of Bifacial Si PV Module with Different Reflection Conditions on Rooftop
Abstract
1. Introduction
Concept of Experiments
2. Modeling and Method
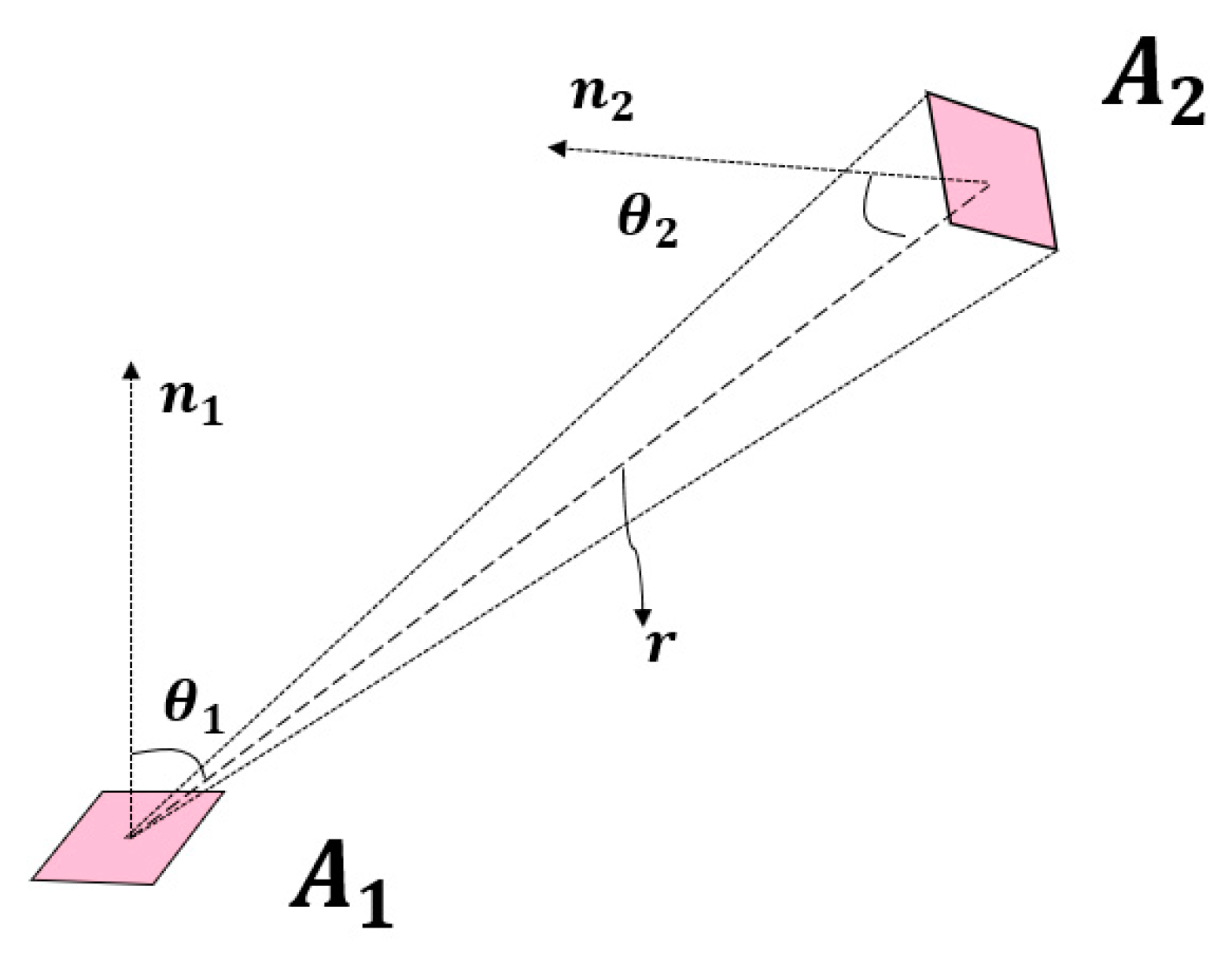
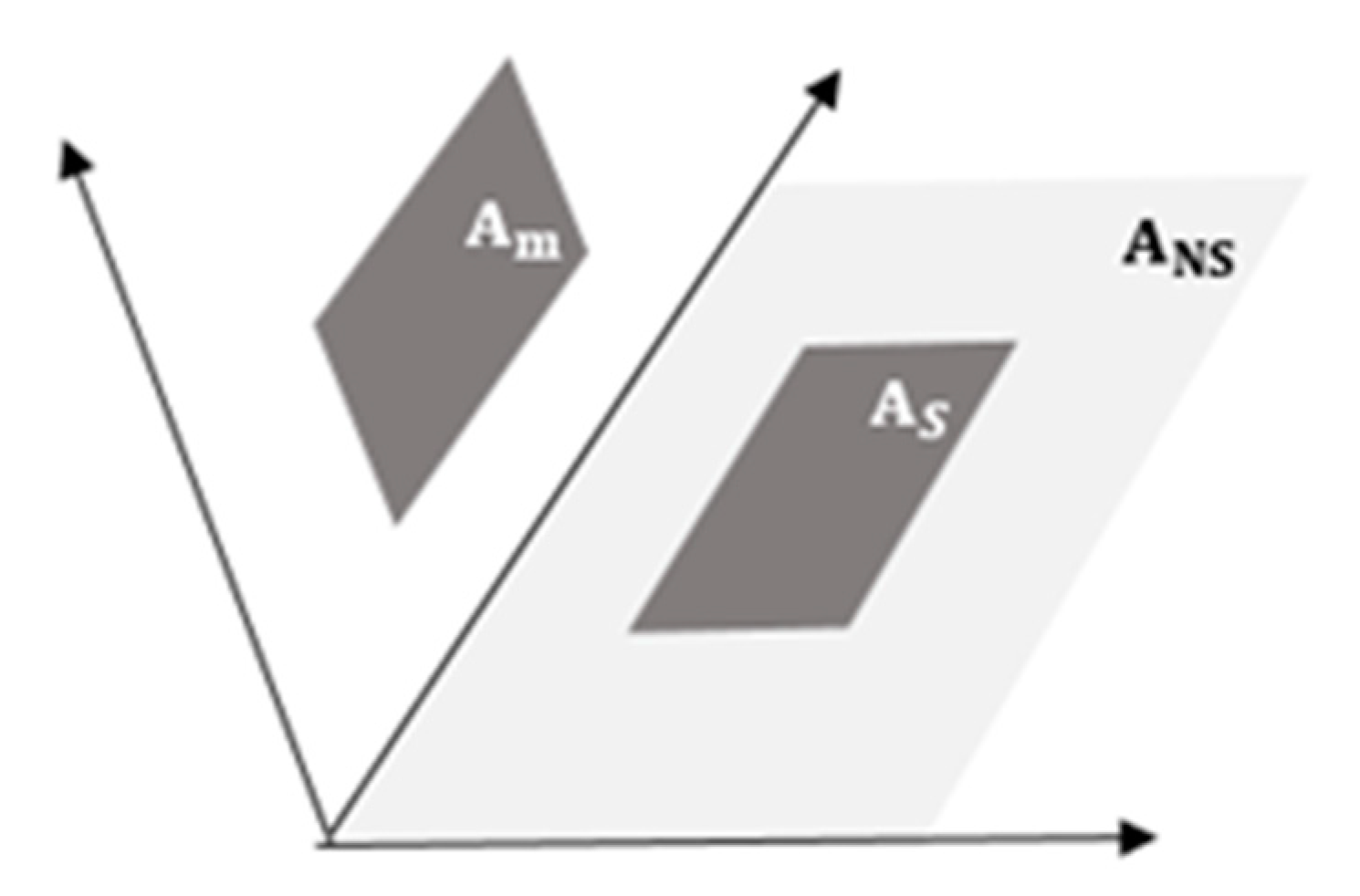
2.1. Rear Side Reflection
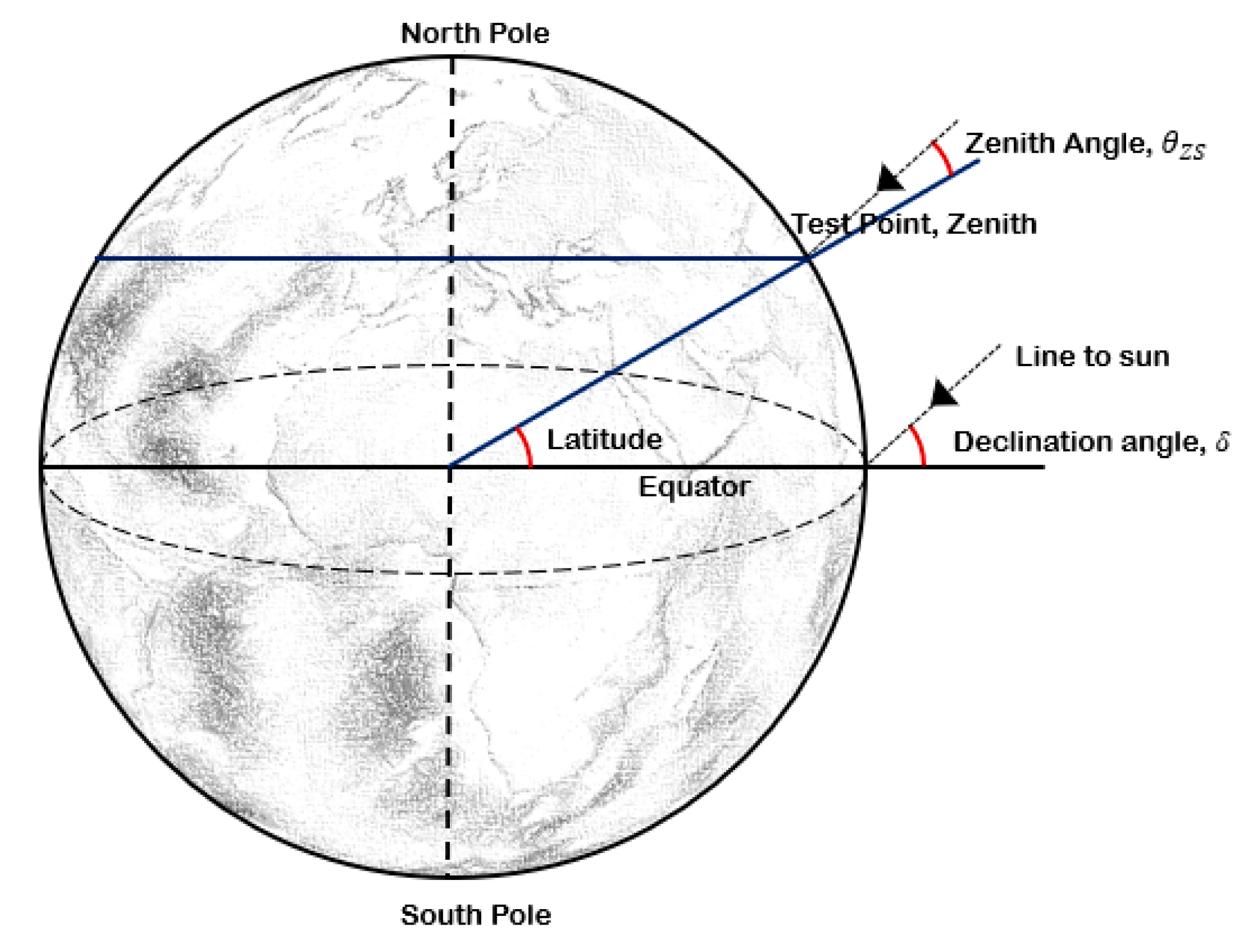
2.2. Irradiance Prediction of the Rear Side
2.3. Prediction of the Total Irradiation
2.4. Prediction of Output of the Bifacial Module
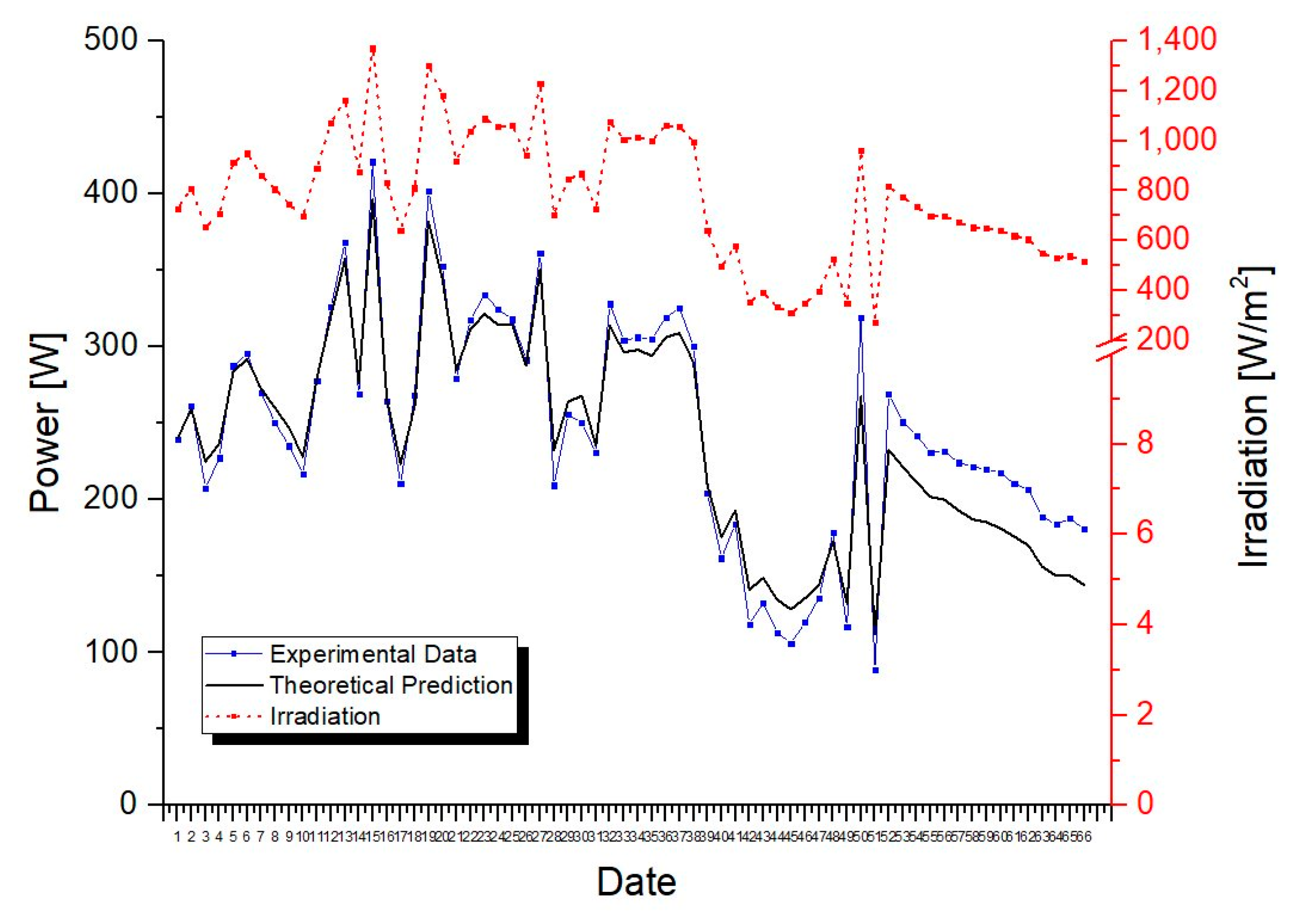
3. Proof of Theoretical Approach
3.1. Experimental Preparation
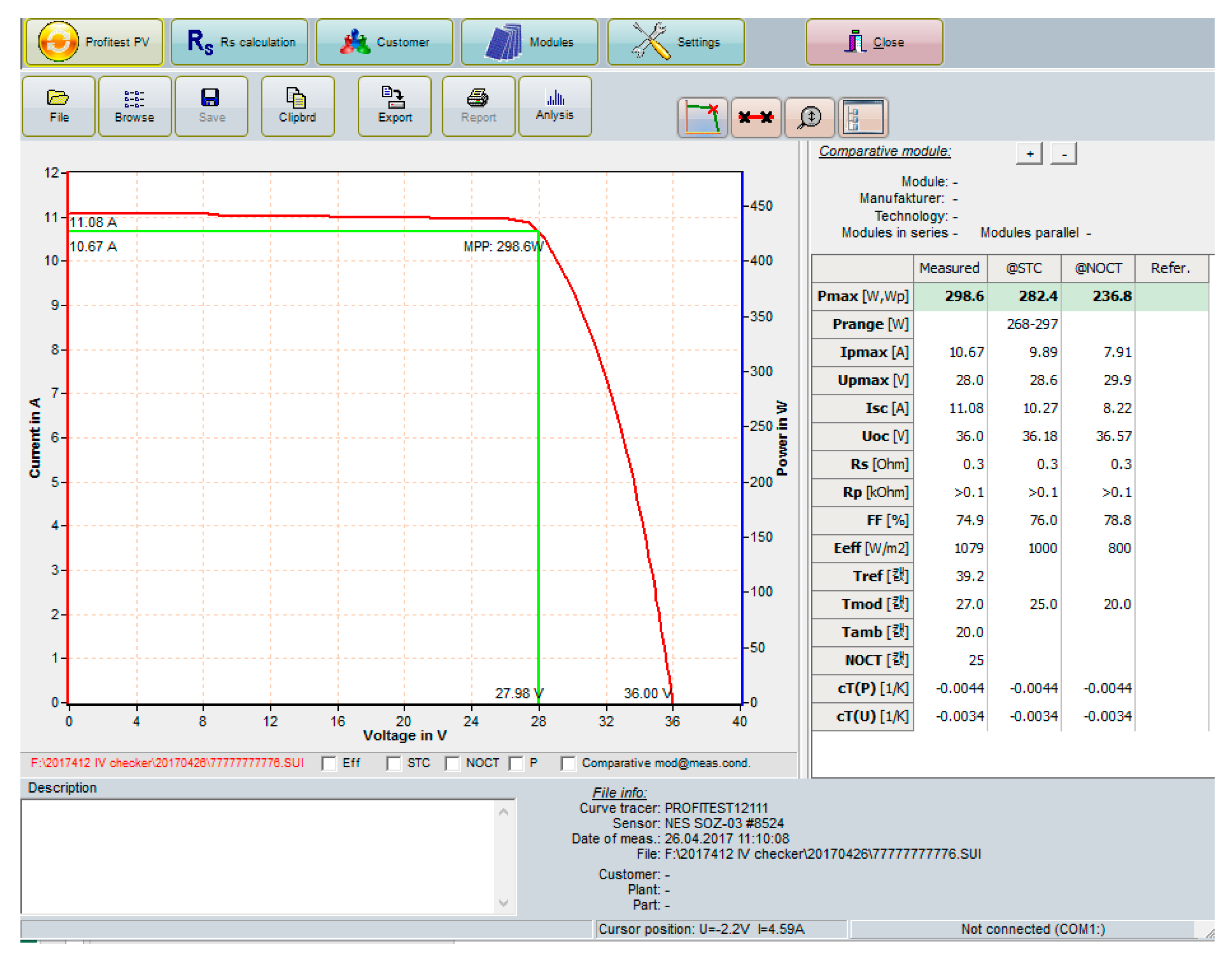
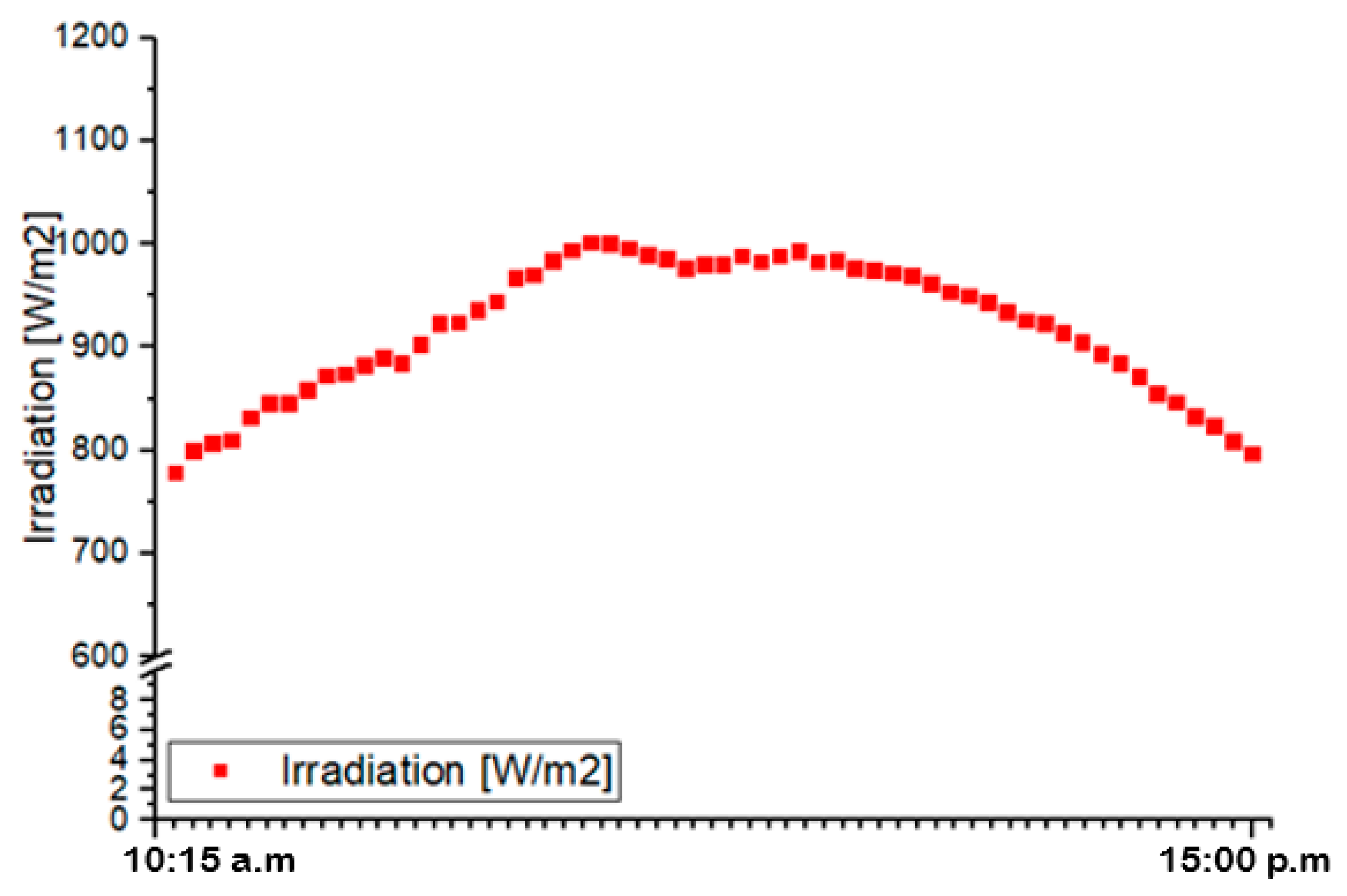
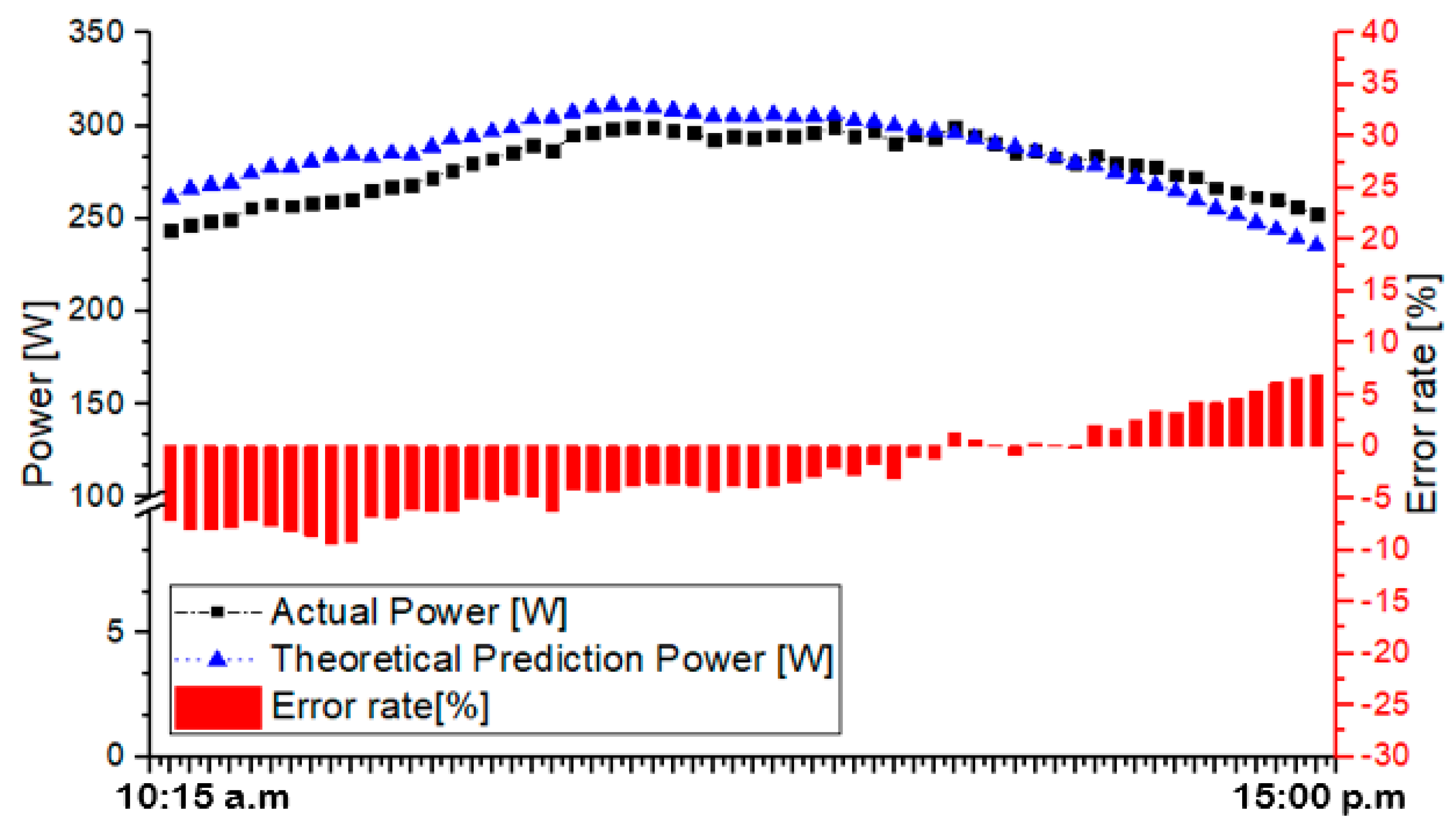
3.2. Test Results
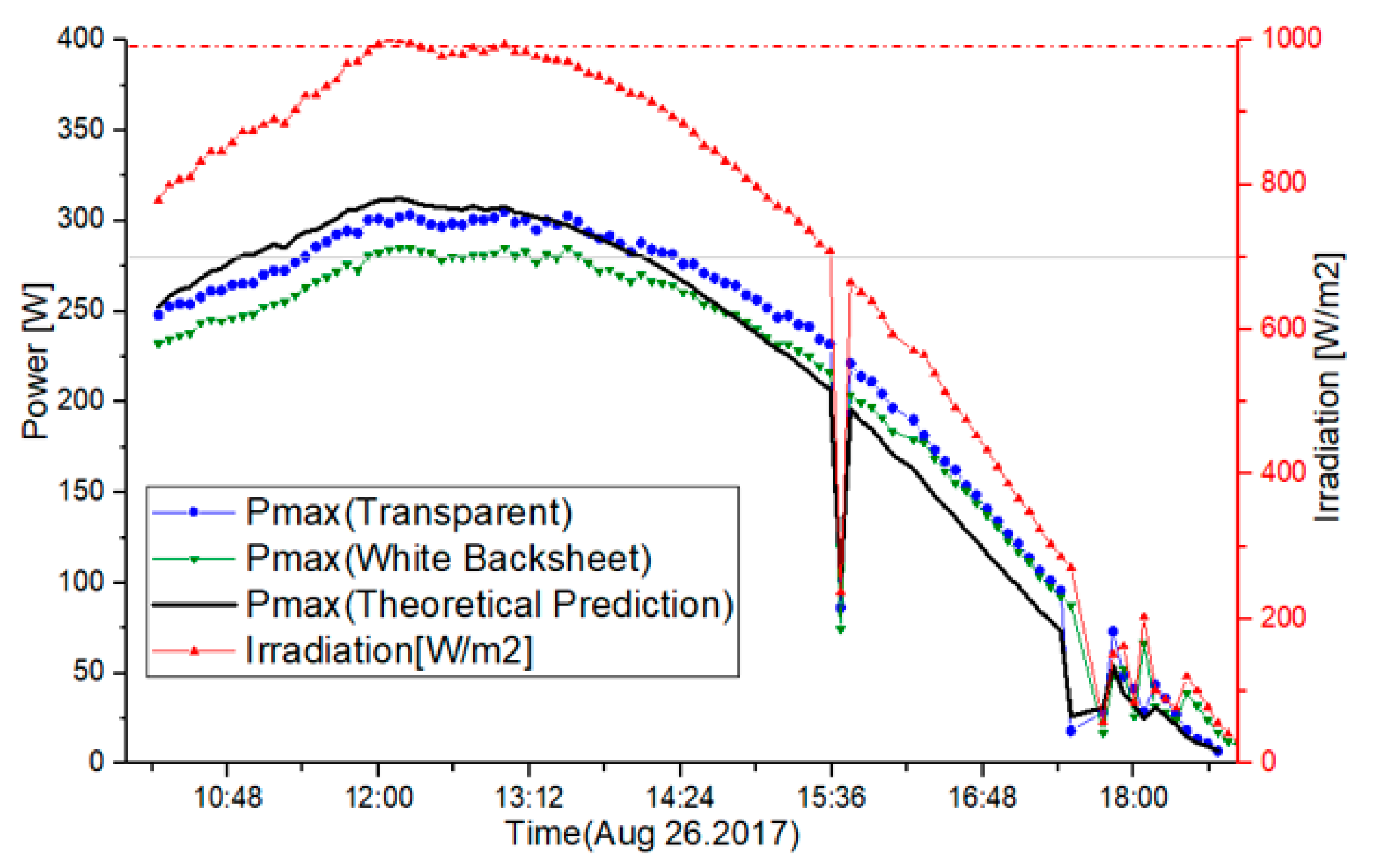
3.3. Application Test 1
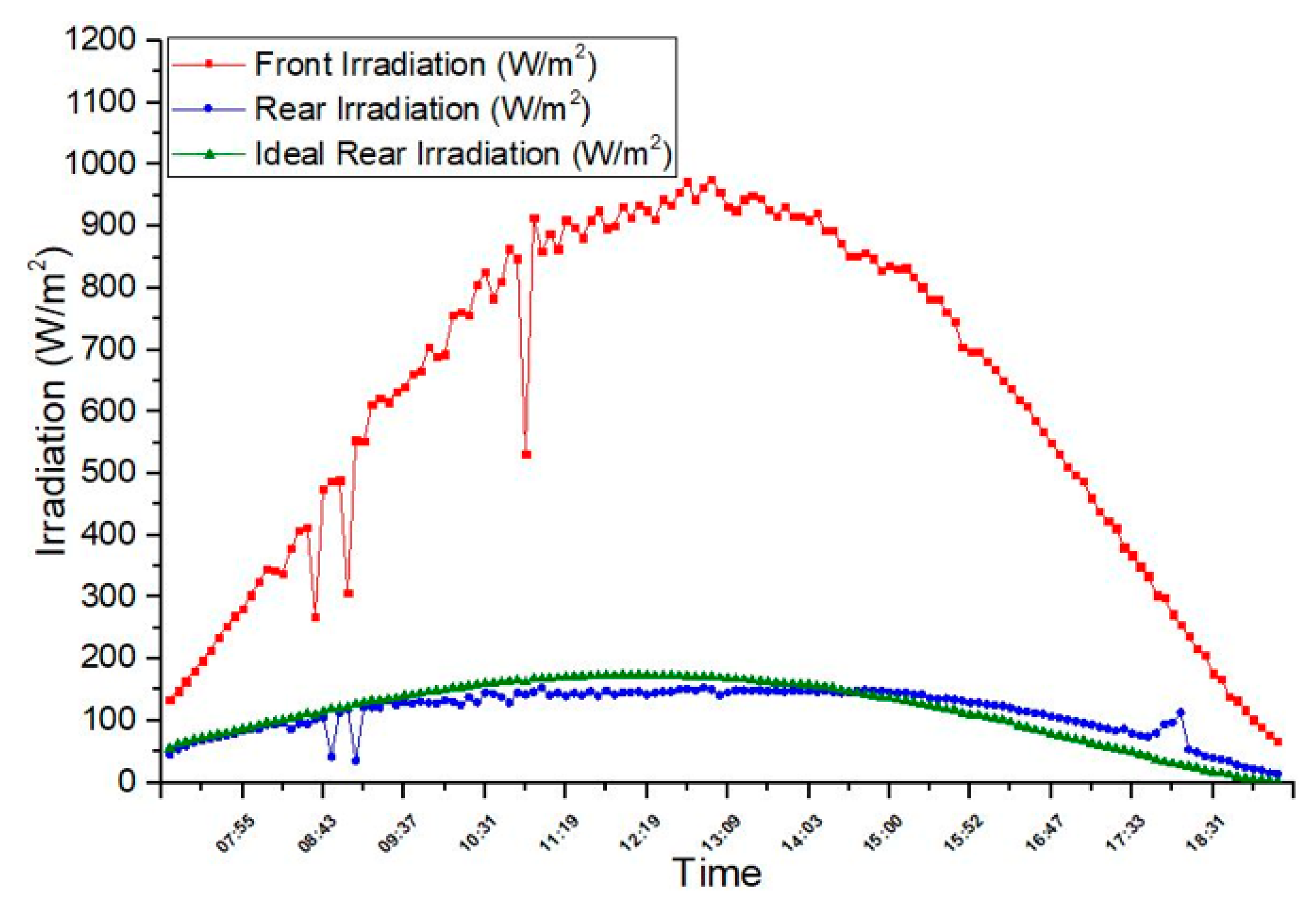
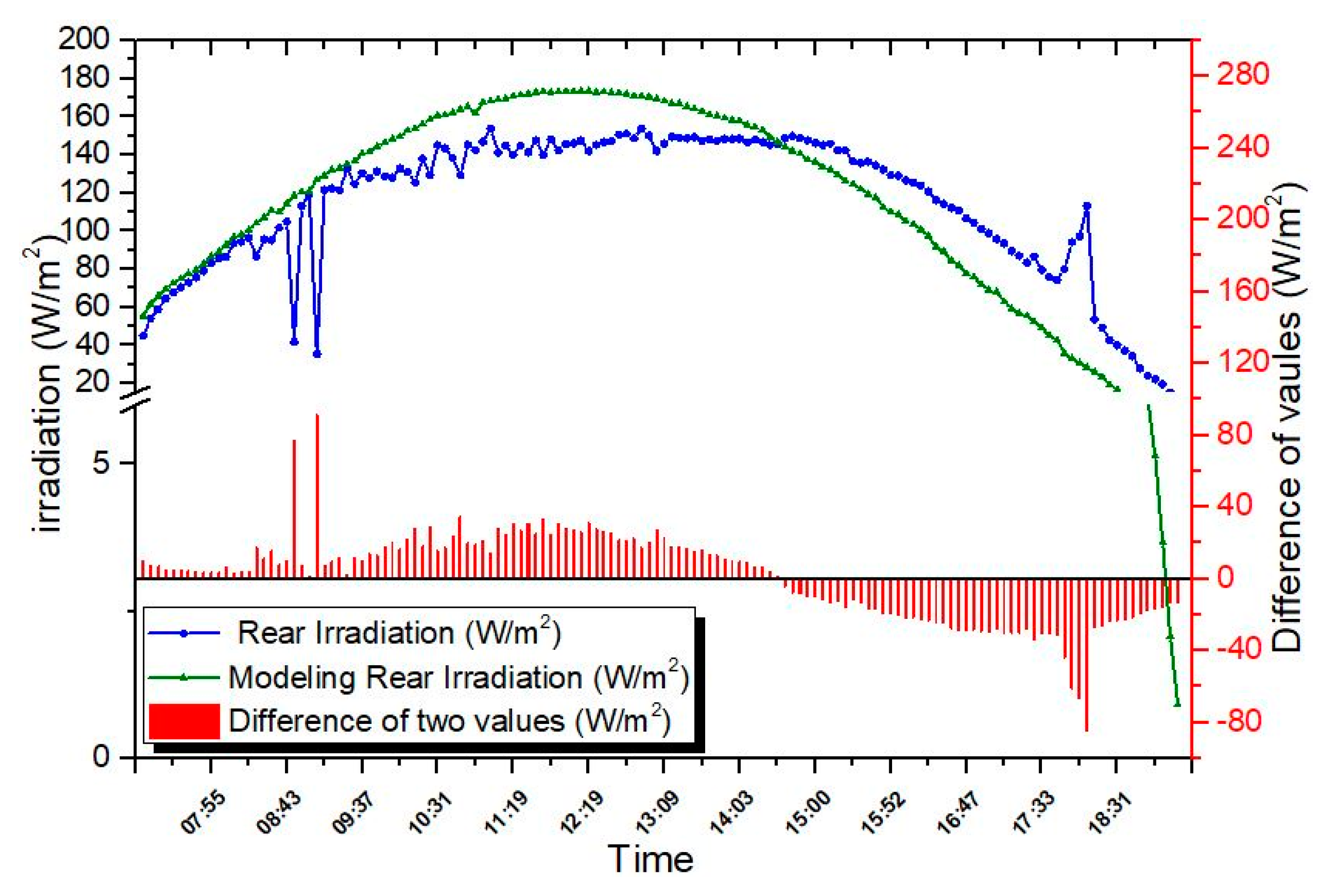
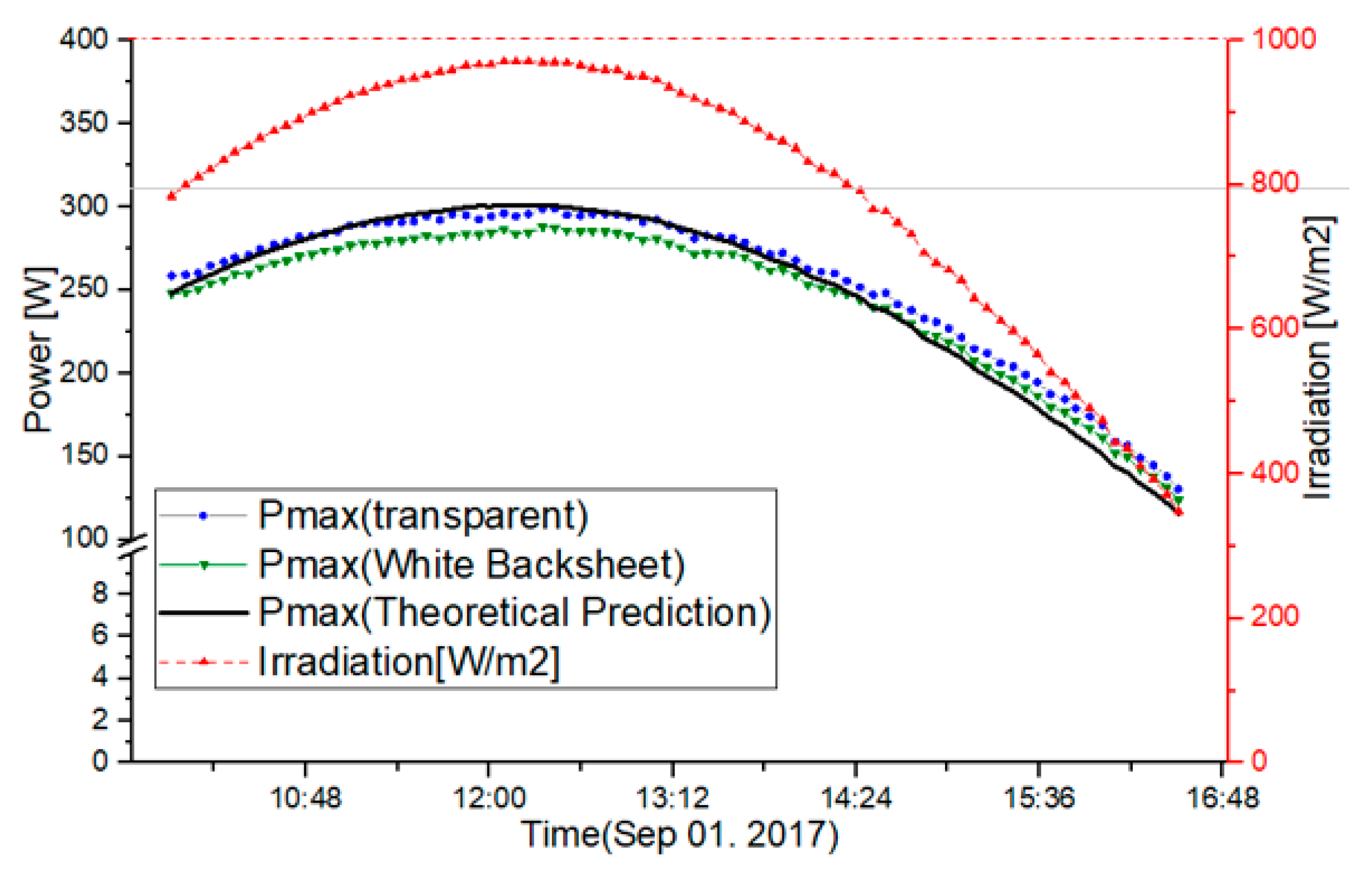
3.4. Application Test 2
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Total irradiance | |
| Direct irradiance | |
| Diffuse irradiance | |
| GHI | Global Horizontal Irradiance |
| DNI | Direct Normal Irradiance |
| DHI | Diffuse Horizontal Irradiance |
| View Factor of of irradiance affecting | |
| α | Albedo coefficient |
| Angle between the module and ground | |
| Front irradiance | |
| Rear irradiance | |
| G | Amount of solar irradiation |
| Angle between the direction perpendicular | |
| Eccentricity correction factor | |
| AM | Air Mass |
| Slope of the sun | |
| The solar time | |
| Latitude of measurement position | |
| Output power of bifacial module | |
| Front output power | |
| Rear output power | |
| Solar irradiance of the front | |
| Solar irradiance of the rear | |
| Front output power on STC | |
| Rear output power on STC | |
| Difference between predicted output and actual output |
References
- Kim, J.Y.; Kim, S.B.; Park, S.W. The Effect of the Renewal Portfolio Standards (RPS) on Electric Power Generation in Korea. Korean Soc. Public Adm. 2016, 27, 131–160. [Google Scholar]
- Wang, D.D.; Sueyoshi, T. Assessment of large commercial rooftop photovoltaic system installations: Evidence from California. Appl. Energy 2017, 188, 45–55. [Google Scholar] [CrossRef]
- Kamuyu, W.C.L.; Lim, J.R.; Won, C.S.; Ahn, H.K. Prediction Model of Photovoltaic Module Temperature for Power Performance of Floating PVs. Energies 2018, 11, 447. [Google Scholar] [CrossRef]
- Kang, J.G.; Kim, J.T. Development Trend of Bifacial Solar Cell Technology. Bull. Korea Photovolt. Soc. 2015, 1, 57–64. [Google Scholar]
- Bifacial Solar Photovoltaic Modules Program on Technology Innovation. Electric Power Research Institute. 2016. Available online: https://www.epri.com/#/pages/product/3002009163/ (accessed on 25 August 2018).
- Wang, S.; Wilkie, O.; Lam, J.; Steeman, R.; Zhang, W.; Khoo, K.S.; Sim, C.S.; Rostan, H. Bifacial photovoltaic systems energy yield modelling. Energy Procedia 2015, 77, 428–433. [Google Scholar] [CrossRef]
- Yusufoglu, U.A.; Pletzer, T.M.; Koduvelikulathu, L.J.; Comparotto, C.; Kopecek, R.; Kurz, H. Analysis of the annual performance of bifacial modules and optimization methods. IEEE J. Photovolt. 2015, 5, 320–328. [Google Scholar] [CrossRef]
- Singh, J.P.; Aberle, A.G.; Walsh, T.M. Electrical characterization method for bifacial photovoltaic modules. Sol. Energy Mater. Sol. Cells 2014, 127, 136–142. [Google Scholar] [CrossRef]
- Shoukry, I.; Libal, J.; Kopecek, R.; Wefringhaus, E.; Werner, J. Modelling of bifacial gain for stand-alone and in-field installed bifacial PV modules. Energy Procedia 2016, 92, 600–608. [Google Scholar] [CrossRef]
- Castillo-Aguilella, J.E.; Hauser, P.S. Bifacial Photovoltaic Module Best-Fit Annual Energy Yield Model with Azimuthal Correction. In Proceedings of the 2016 IEEE 43rd Photovoltaic Specialists Conference (PVSC), Portland, OR, USA, 5–10 June 2016. [Google Scholar]
- Steven, S.; Sung, J.S.; George, F. Characterizing Electrical Output of bifacial photovoltaic modules by altering reflective materials. J. Build. Constr. Plan. Res. 2016, 4, 41–55. [Google Scholar]
- Kreinin, L.; Bordin, N.; Karsenty, A.; Drori, A.; Grobgeld, D.; Eisenberg, N. PV Module Power Gain due to Bifacial Design. In Proceedings of the 35th IEEE Photovoltaic Specialists Conference, Honolulu, HI, USA, 20–25 June 2010. [Google Scholar]
- Kang, J.G.; Kim, J.H.; Kim, J.T. Analysis of Generation Characteristics of a Bifacial BIPV System According to Installation Methods. Curr. Photovolt. Res. (KPVS) 2015, 3, 121–125. [Google Scholar]
- Van Aken, B.B.; Okel, L.A.G.; Liu, J.; Luxembourg, S.L.; Van Roosmalen, J.A.M. White Bifacial Modules—Improved STC Performance Combined with Bifacial Energy Yield. In Proceedings of the 32nd European Photovoltaic Solar Energy Conference and Exhibition, Munich, Germany, 20–24 June 2016; 1BO.12.2. pp. 42–47. [Google Scholar]
- Appelbaum, J. Bifacial photovoltaic panels field. Renew. Energy 2016, 85, 338–343. [Google Scholar] [CrossRef]
- Yusufoglu, U.A.; Lee, T.H.; Pletzer, T.M.; Halm, A.; Koduveliklathu, L.J.; Comparotto, C.; Kurz, H. Simulation of energy production by bifacial modules with revision of ground reflection. Energy Procedia 2014, 55, 389–395. [Google Scholar] [CrossRef]
- Duran, C.; Buck, T.; Kopecek, R.; Libal, J.; Traverso, F. Bifacial solar cells with boron back surface field. In Proceedings of the 25th European Photovoltaic Solar Energy Conference and Exhibition, Valencia, Spain, 6–10 September 2010; pp. 2348–2352. [Google Scholar] [CrossRef]
- Werner, S.; Lohmüller, E.; Saint-Cast, P.; Greulich, J.; Weber, J.; Maier, S.; Wasmer, S. Key aspects for fabrication of p-type Cz-Si PERC solar cells exceeding 22% conversion efficiency. In Proceedings of the 33rd EUPVSEC—33rd European PV Solar Energy Conference and Exhibition, Amsterdam, The Netherlands, 25–29 September 2017. [Google Scholar]
- Guo, M.; Zang, H.; Gao, S.; Chen, T.; Xiao, J.; Cheng, L.; Sun, G. Optimal tilt angle and orientation of photovoltaic modules using HS algorithm in different climates of China. Appl. Sci. 2017, 7, 1028. [Google Scholar] [CrossRef]
- SolarWorld. How to Maximize Energy Yield with Bifacial Technology. White Paper. 2016. Available online: Https://solarkingmi.com/assets/How-to-Maximize-Energy-Yield-with-Bifacial-Solar-Technology-SW9001US.pdf (accessed on 9 August 2018).
- Hansen, C.W.; Stein, J.S.; Deline, C.; MacAlpine, S.; Marion, B.; Asgharzadeh, A. Analysis of irradiance models for bifacial PV modules. In Proceedings of the IEEE 43rd Photovoltaic Specialists Conference (PVSC), Portland, OR, USA, 5–10 June 2016; pp. 138–143. [Google Scholar] [CrossRef]
- Ineichen, P.; Guisan, O.; Perez, R. Ground-reflected radiation and albedo. Sol. Energy 1990, 44, 207–214. [Google Scholar] [CrossRef]
- Perez, R.; Ineichen, P.; Seals, R.; Michalsky, J.; Stewart, R. Modeling daylight availability and irradiance components from direct and global irradiance. Sol. Energy 1990, 44, 271–289. [Google Scholar] [CrossRef]
- Yunus, C.A.; Afshin, J.G. Heat and Mass Transfer: Fundamentals and Applications; McGraw-Hill Education: New York, NY, USA, 2011. [Google Scholar]
- John, A.D.; William, A.B. Solar Engineering of Thermal Processes, 4th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2013. [Google Scholar]
- Tang, R.; Yu, Y. Feasibility and optical performance of one axis three positions sun-tracking polar-axis aligned CPCs for photovoltaic applications. Sol. Energy 2010, 84, 1666–1675. [Google Scholar] [CrossRef]
- Zang, H.; Guo, M.; Wei, Z.; Sun, G. Determination of the optimal tilt angle of solar collectors for different climates of china. Sustainability 2016, 8, 654. [Google Scholar] [CrossRef]
- Peak Power Measuring Instrument and Curve Tracer for PV Modules and Strings. Available online: https://www.gossenmetrawatt.com/resources/p1/profitest-pv/profitest-pv-db_gb.pdf (accessed on 25 August 2018).
- Riley, D.; Hansen, C.; Stein, J.; Lave, M.; Marion, J.K.B.; Toor, F. A Performance Model for Bifacial PV Modules. In Proceedings of the 44th IEEE PVSC, Washington, DC, USA, 25–30 June 2017. [Google Scholar]
- Lee, H.G.; Kim, G.G.; Bhang, B.G.; Kim, D.K.; Park, N.S.; Ahn, H.K. Design Algorithm for Optimum Capacity of ESS Connected with PVs Under the RPS Program. IEEE Access 2018, 45899–45906. [Google Scholar] [CrossRef]






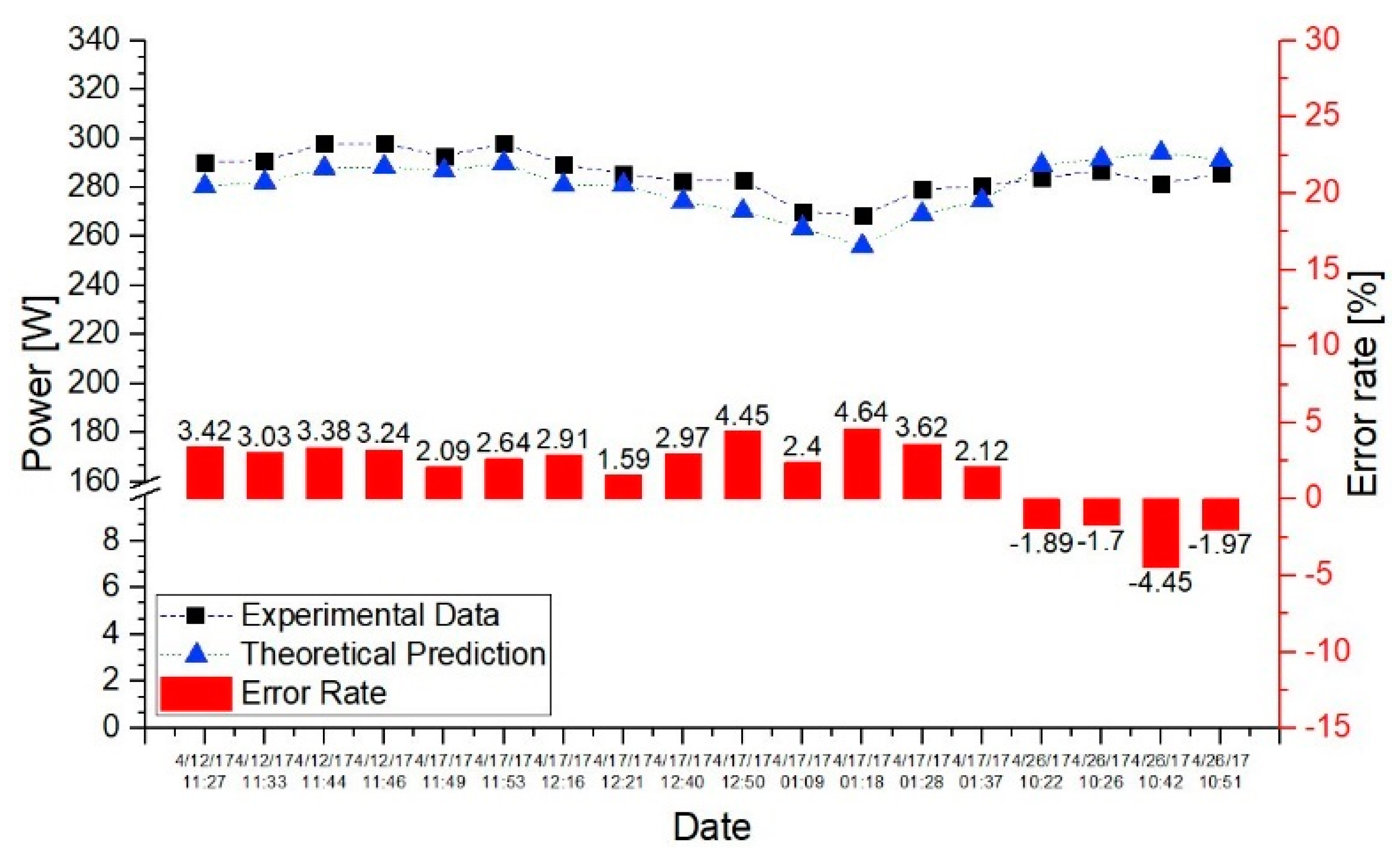
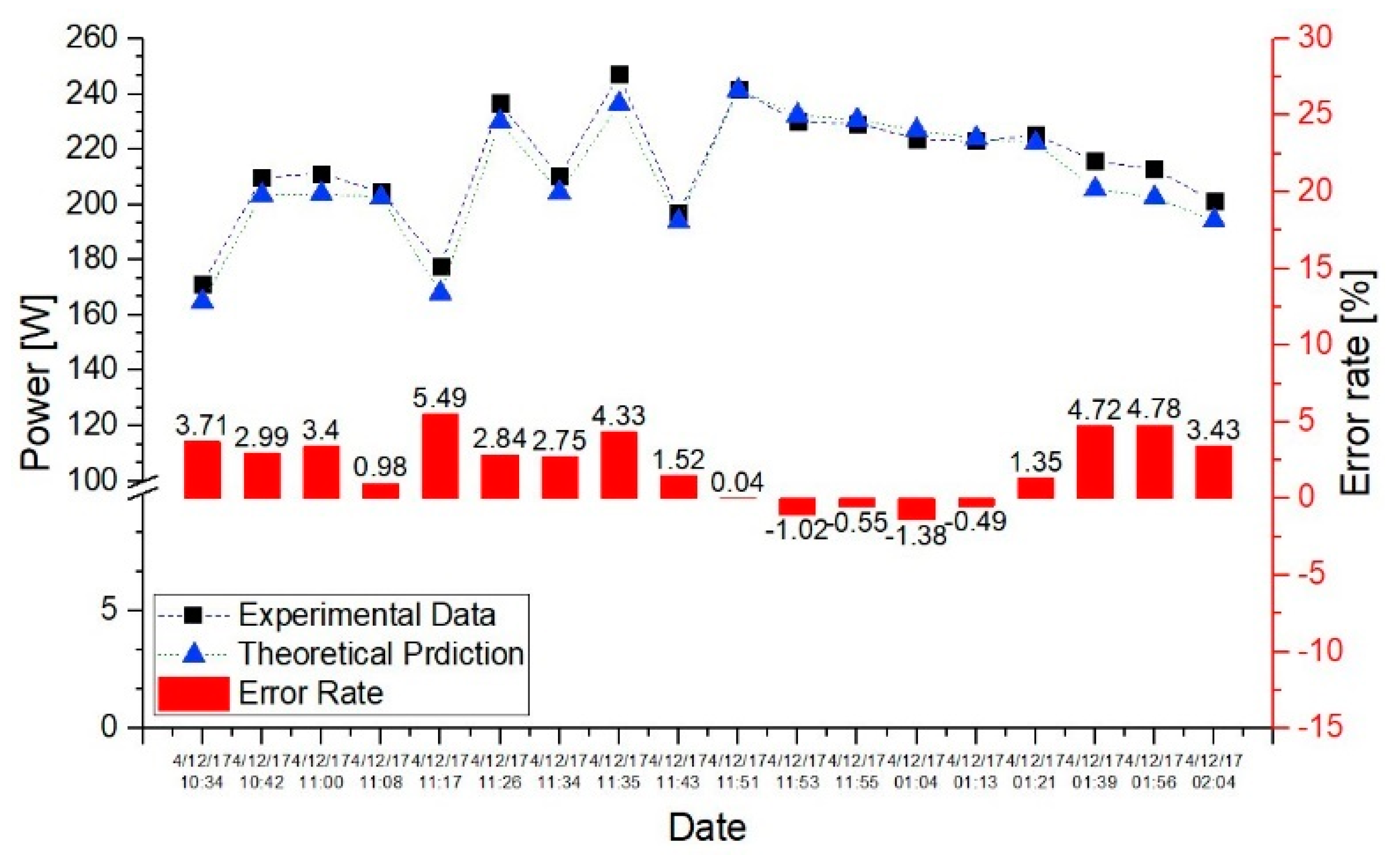
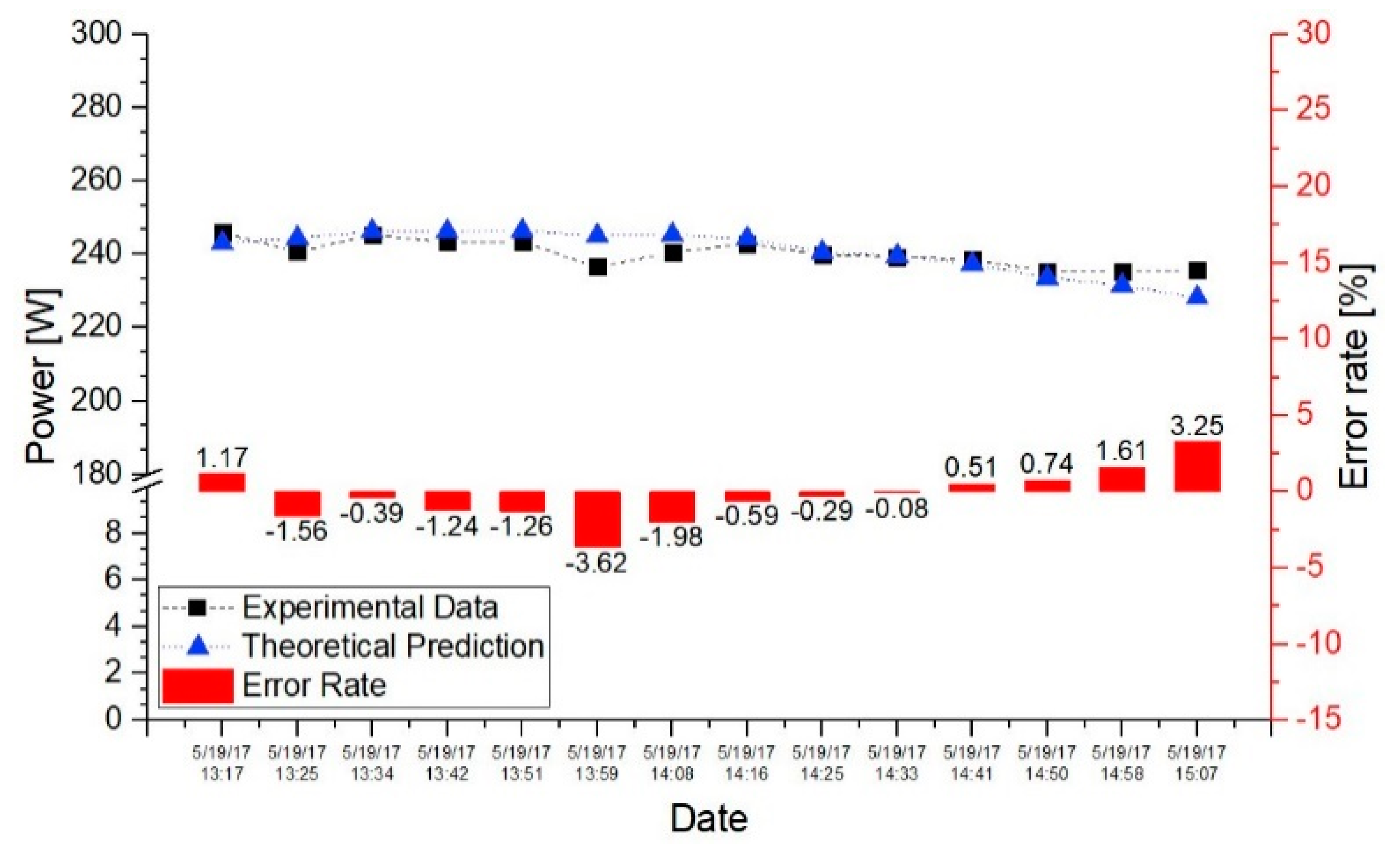
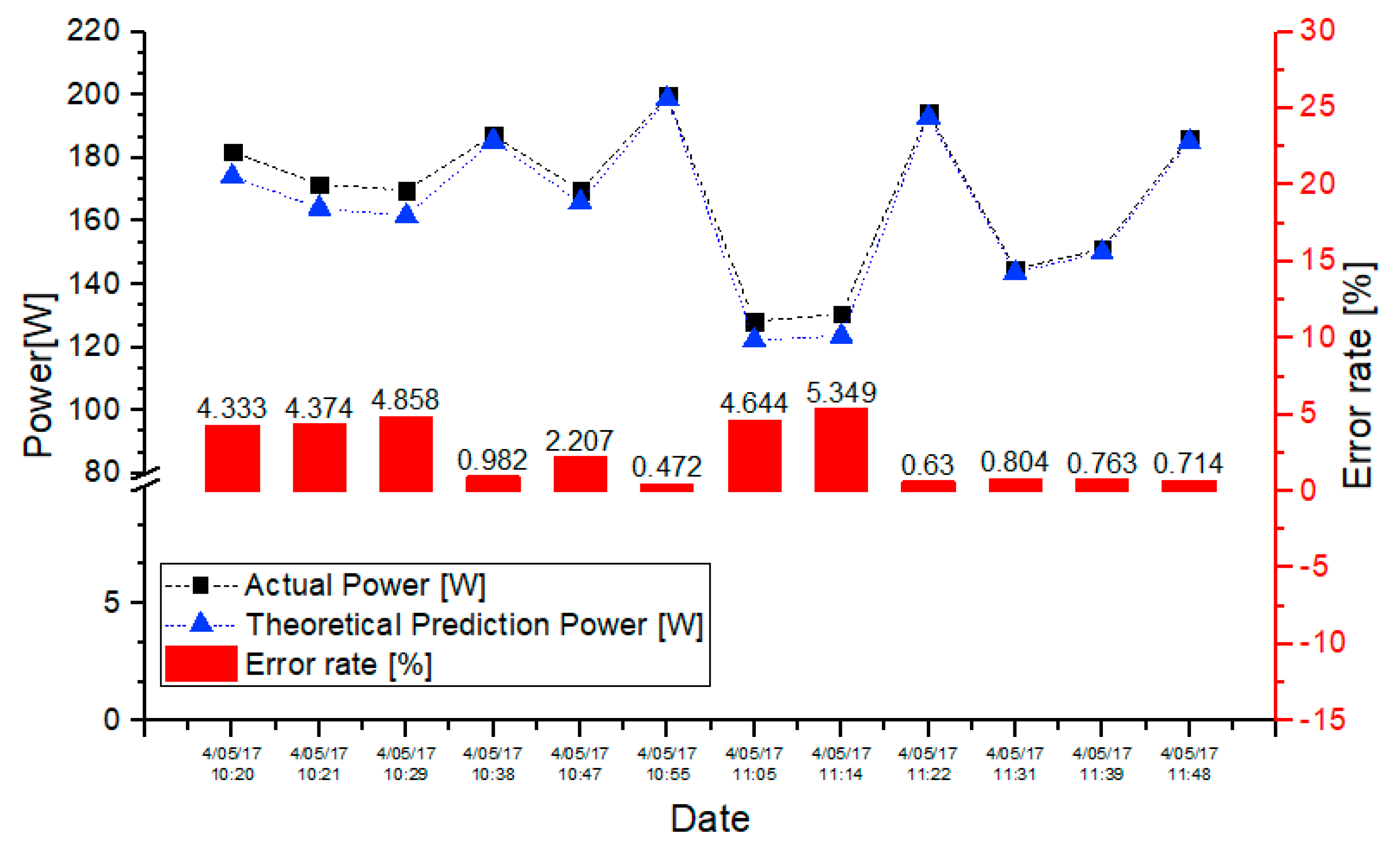


| Type | Floor Condition | Albedo | |
|---|---|---|---|
| Exp. 1 | White Paint | 0.85 | 262 |
| Exp. 2 | Green Paint | 0.25 | 262 |
| Exp. 3 | Black Paint | 0.1 | 262 |
| Exp. 4 | Cement | 0.4 | 262 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cha, H.L.; Bhang, B.G.; Park, S.Y.; Choi, J.H.; Ahn, H.K. Power Prediction of Bifacial Si PV Module with Different Reflection Conditions on Rooftop. Appl. Sci. 2018, 8, 1752. https://doi.org/10.3390/app8101752
Cha HL, Bhang BG, Park SY, Choi JH, Ahn HK. Power Prediction of Bifacial Si PV Module with Different Reflection Conditions on Rooftop. Applied Sciences. 2018; 8(10):1752. https://doi.org/10.3390/app8101752
Chicago/Turabian StyleCha, Hae Lim, Byeong Gwan Bhang, So Young Park, Jin Ho Choi, and Hyung Keun Ahn. 2018. "Power Prediction of Bifacial Si PV Module with Different Reflection Conditions on Rooftop" Applied Sciences 8, no. 10: 1752. https://doi.org/10.3390/app8101752
APA StyleCha, H. L., Bhang, B. G., Park, S. Y., Choi, J. H., & Ahn, H. K. (2018). Power Prediction of Bifacial Si PV Module with Different Reflection Conditions on Rooftop. Applied Sciences, 8(10), 1752. https://doi.org/10.3390/app8101752






