Correlation between the Golden Ratio and Nanowire Transistor Performance †
Abstract
:1. Introduction
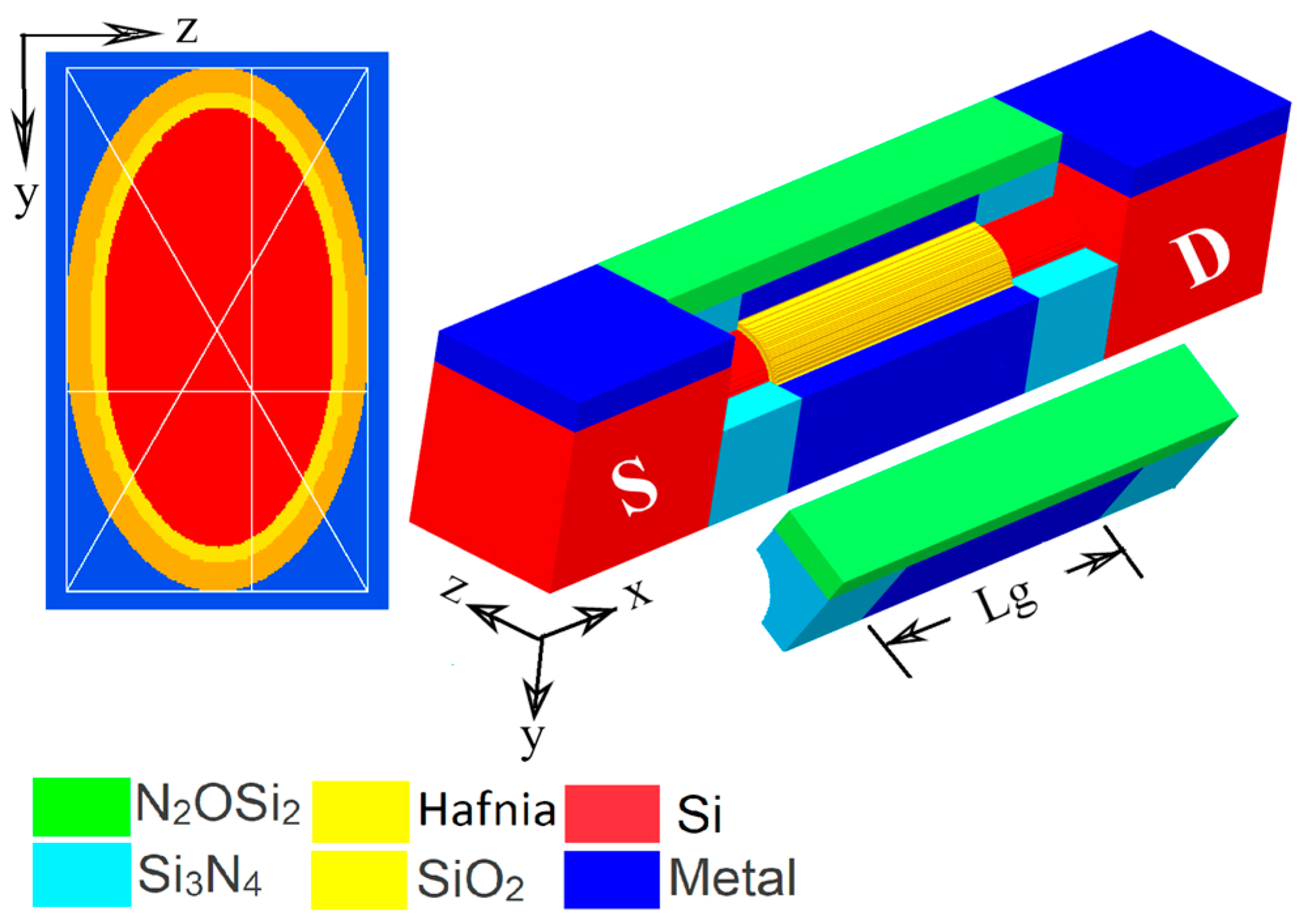
2. Device Description
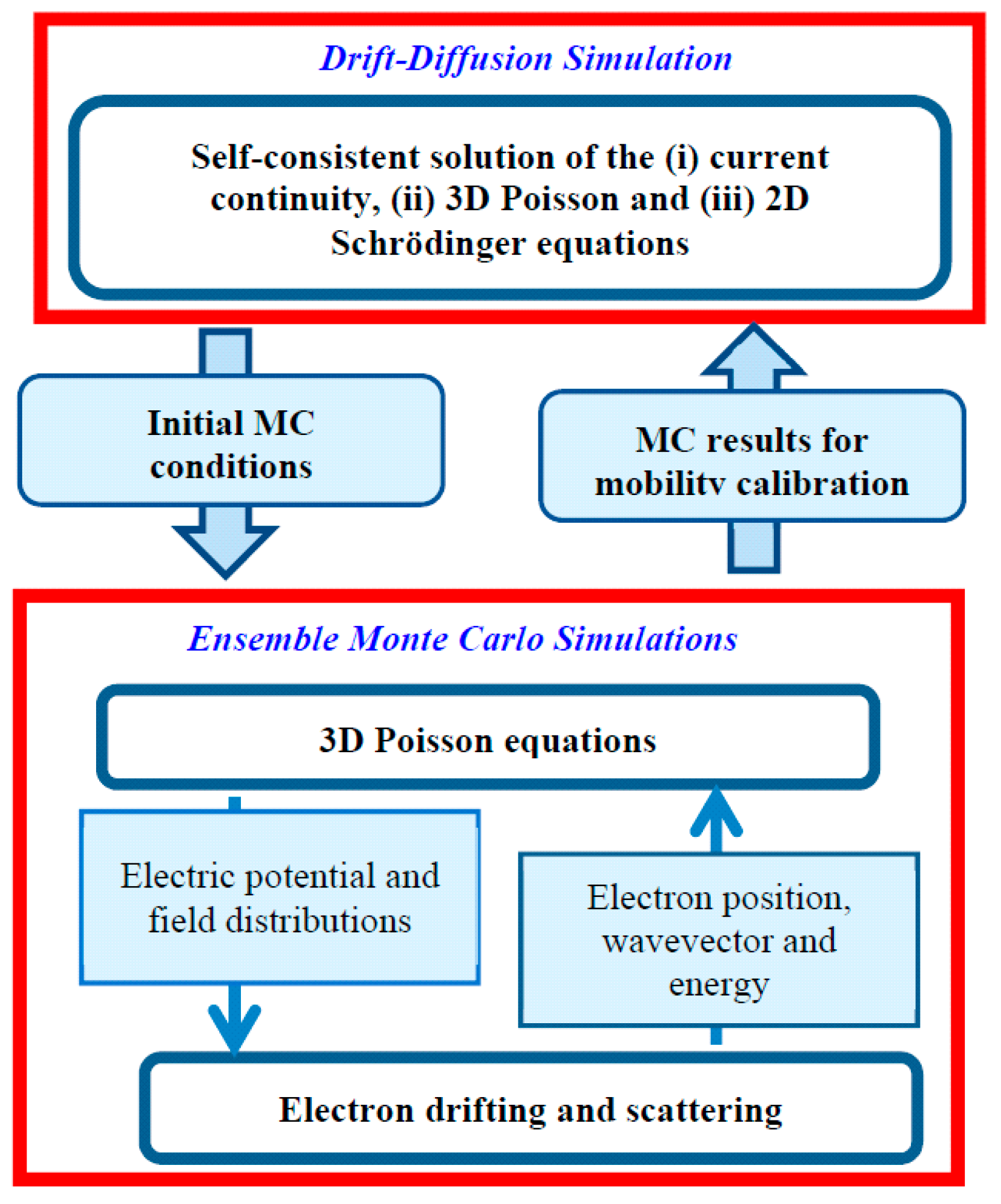
3. Methodology
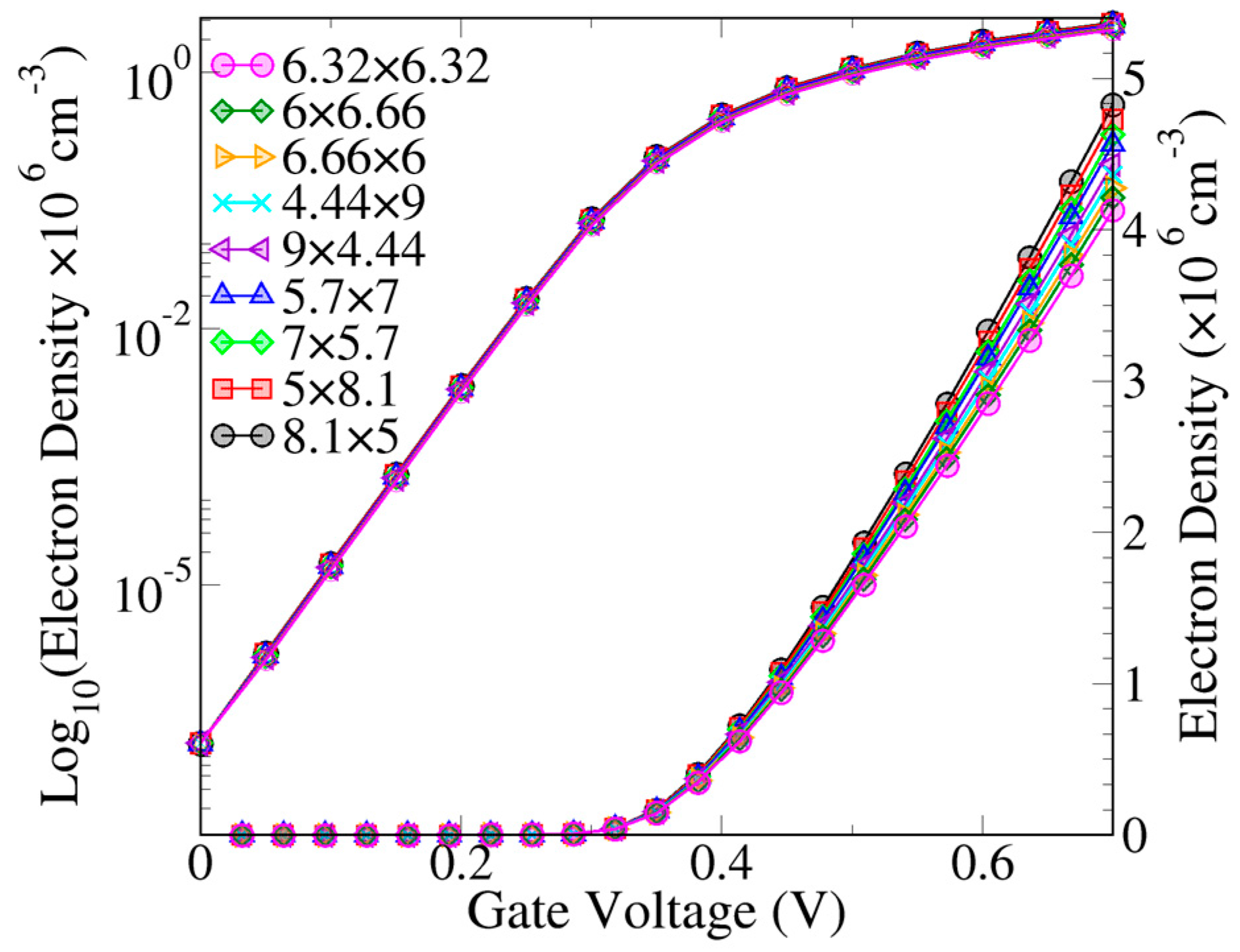
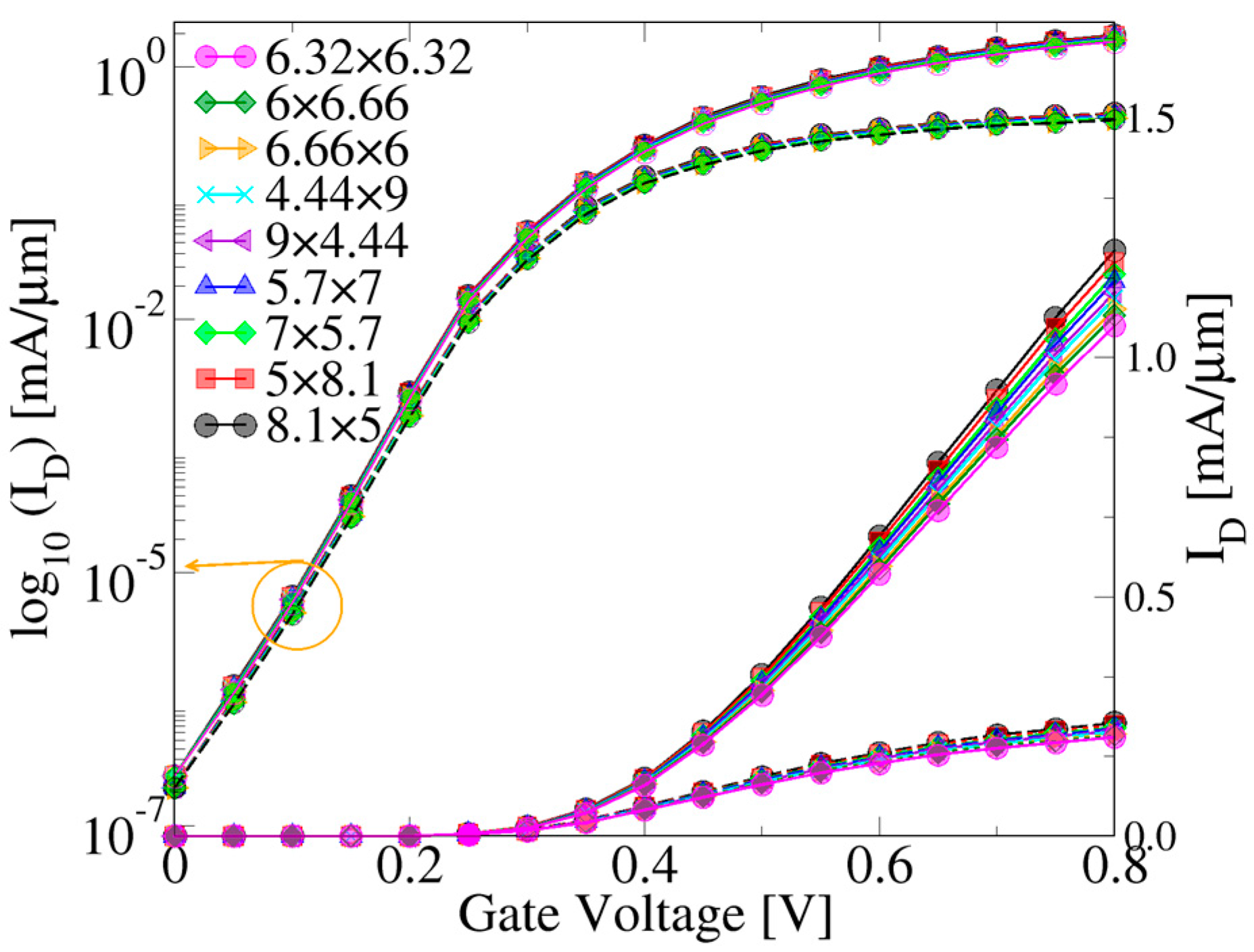
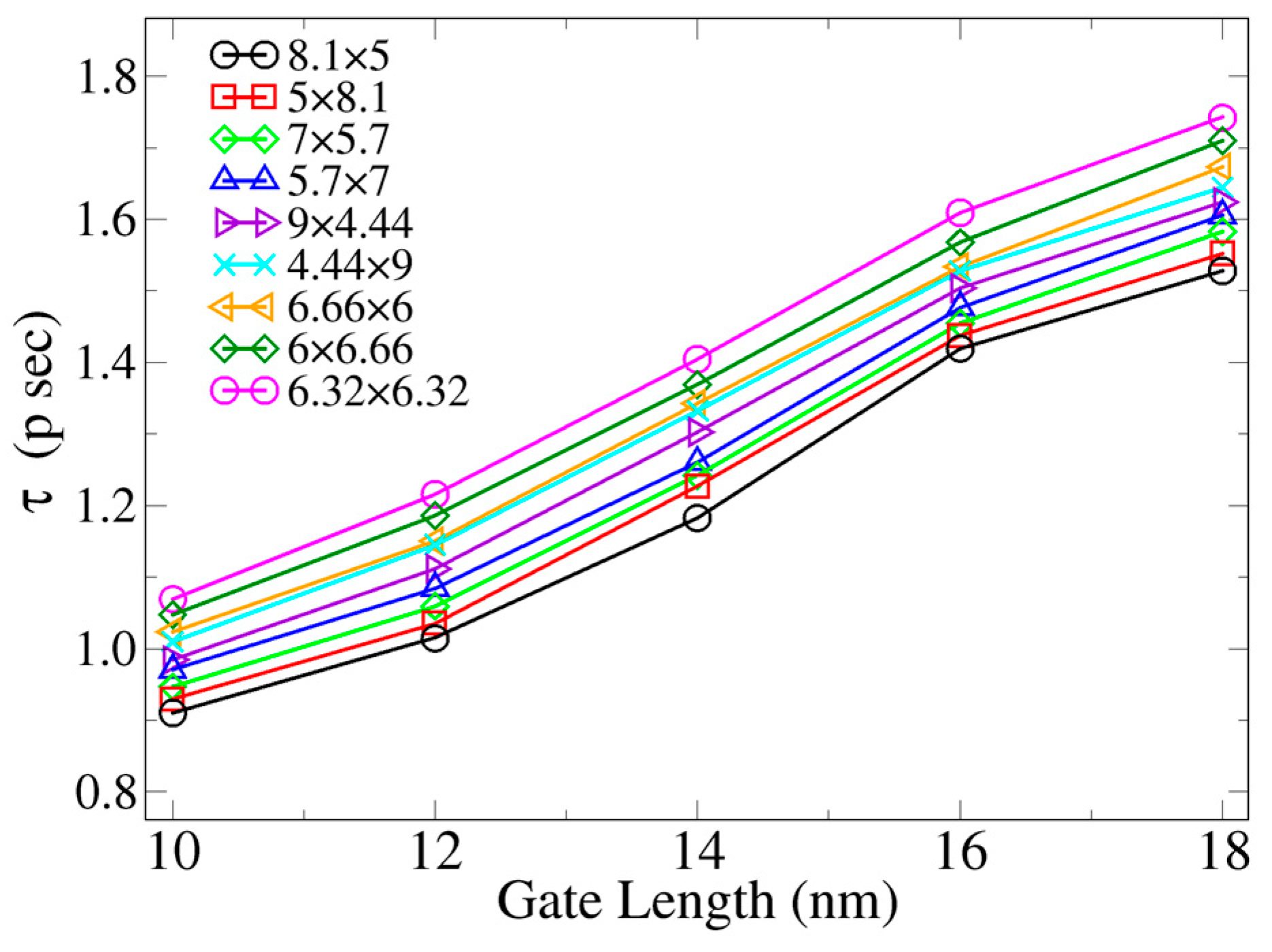
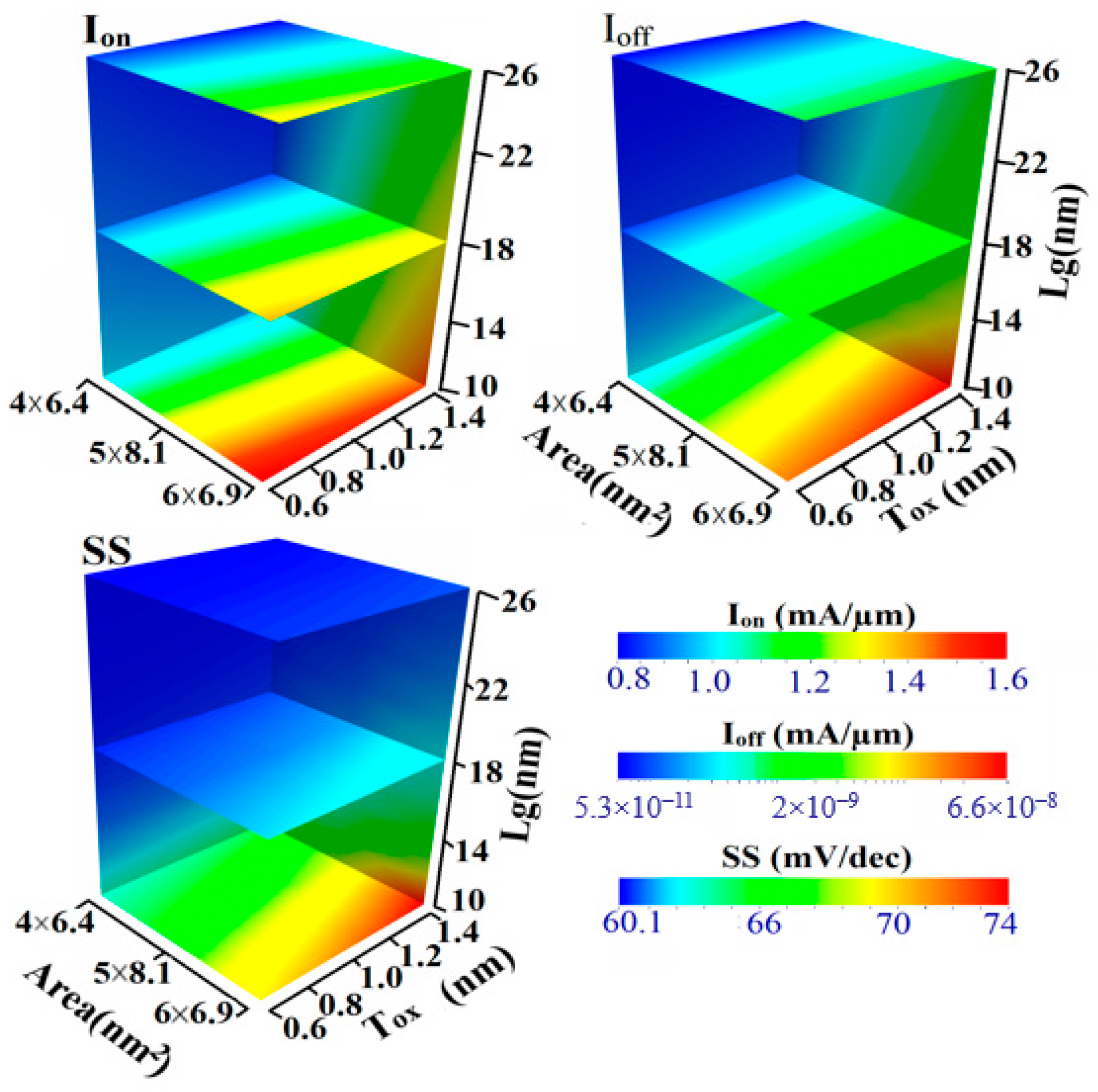
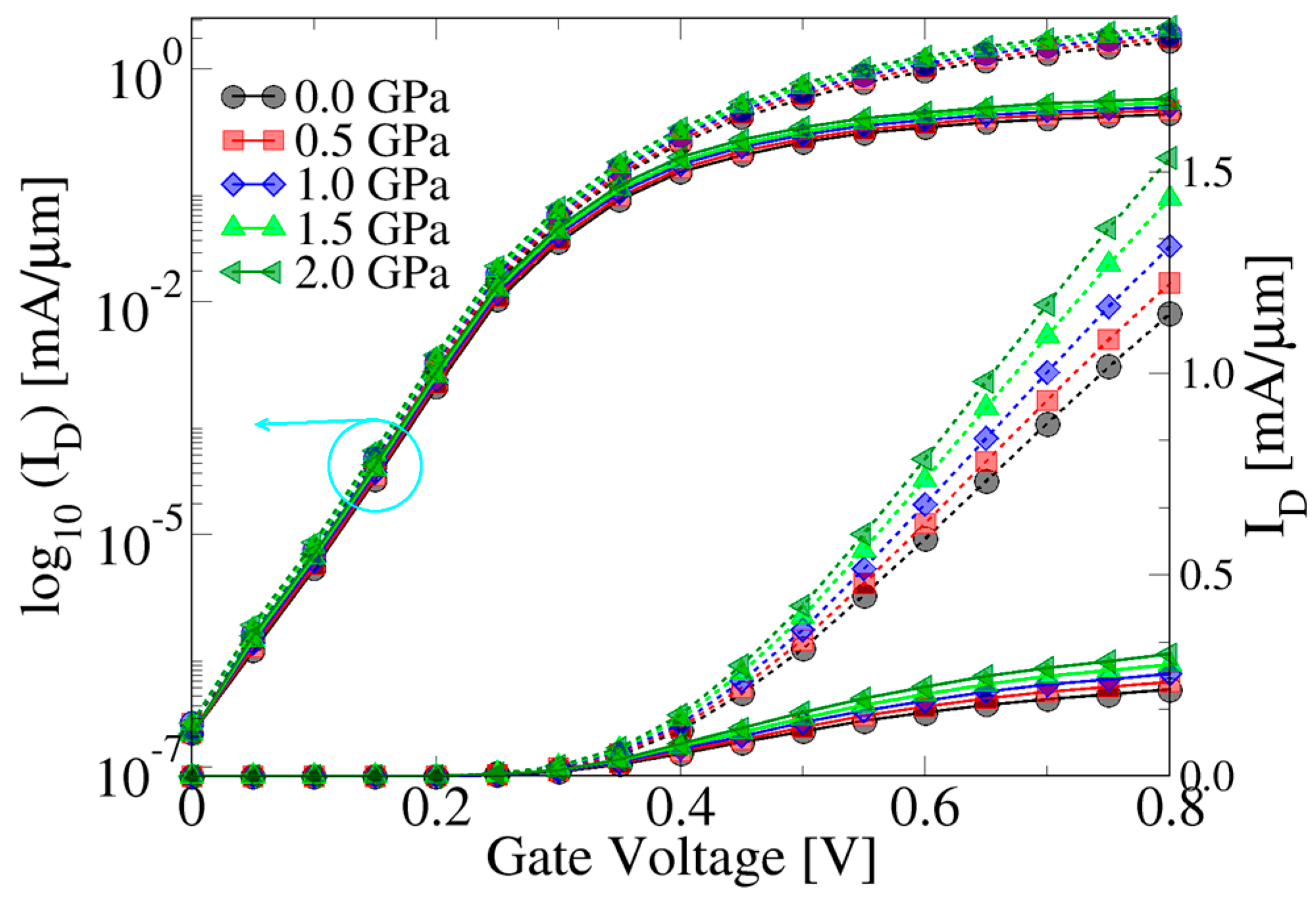
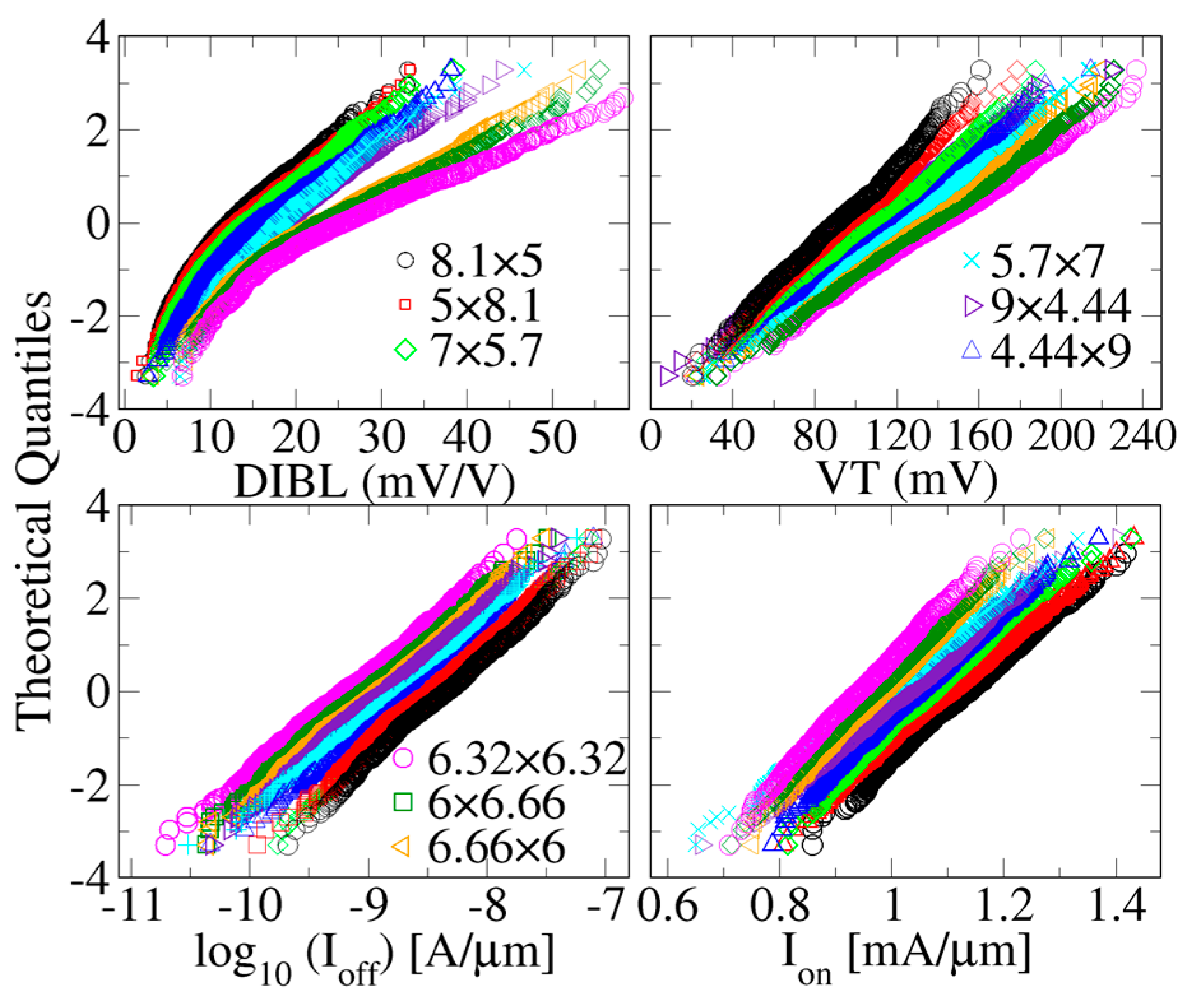
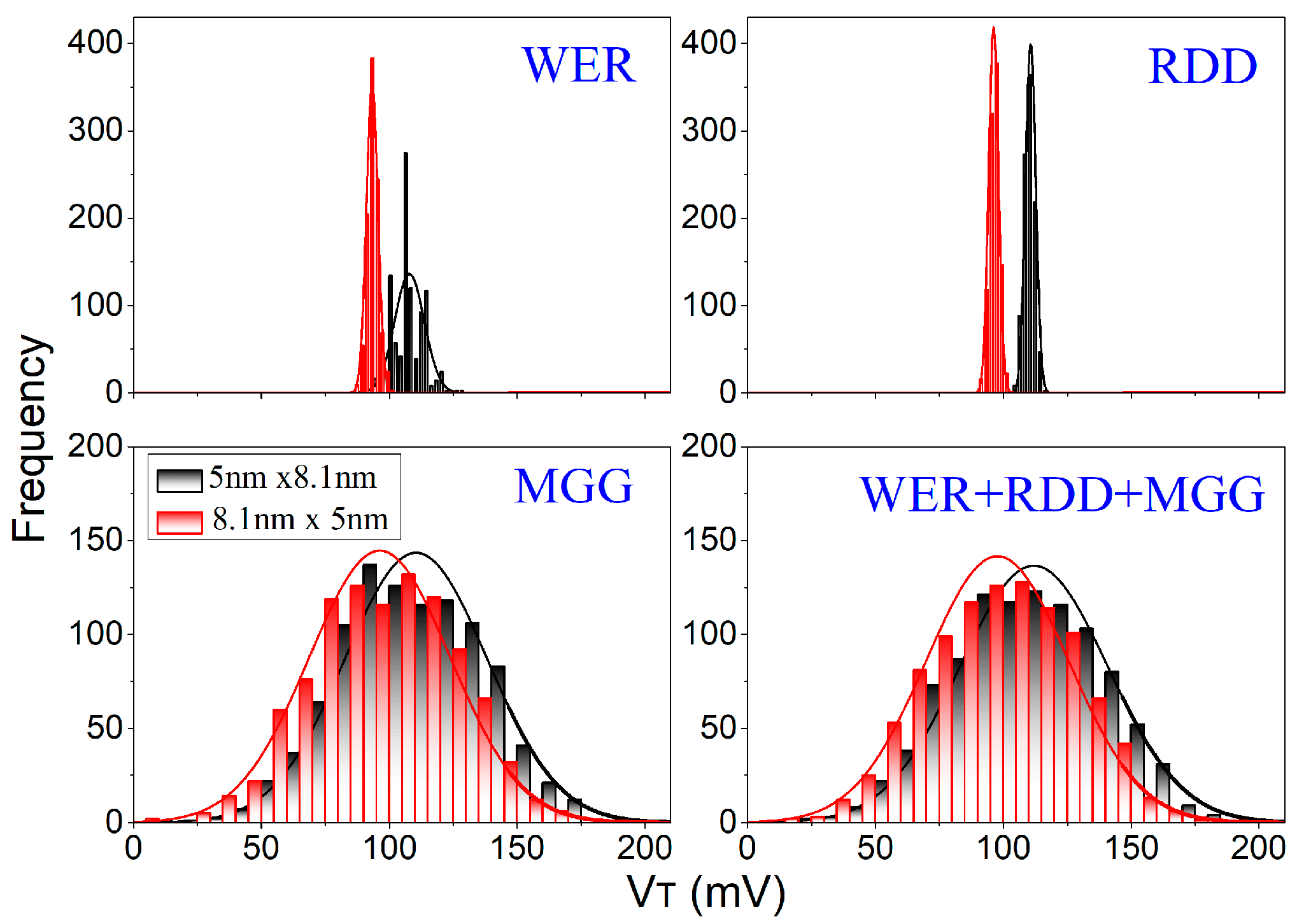
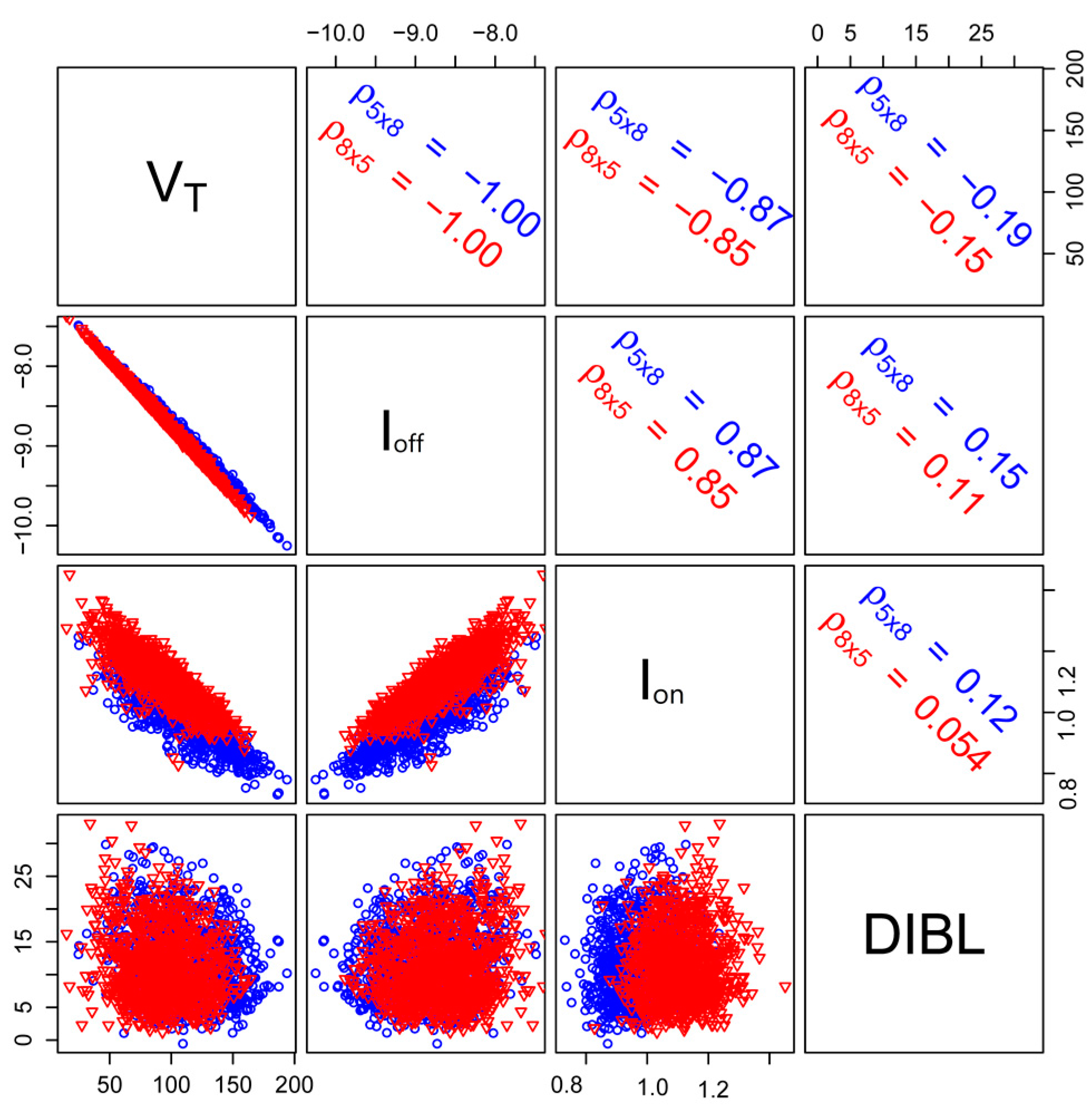
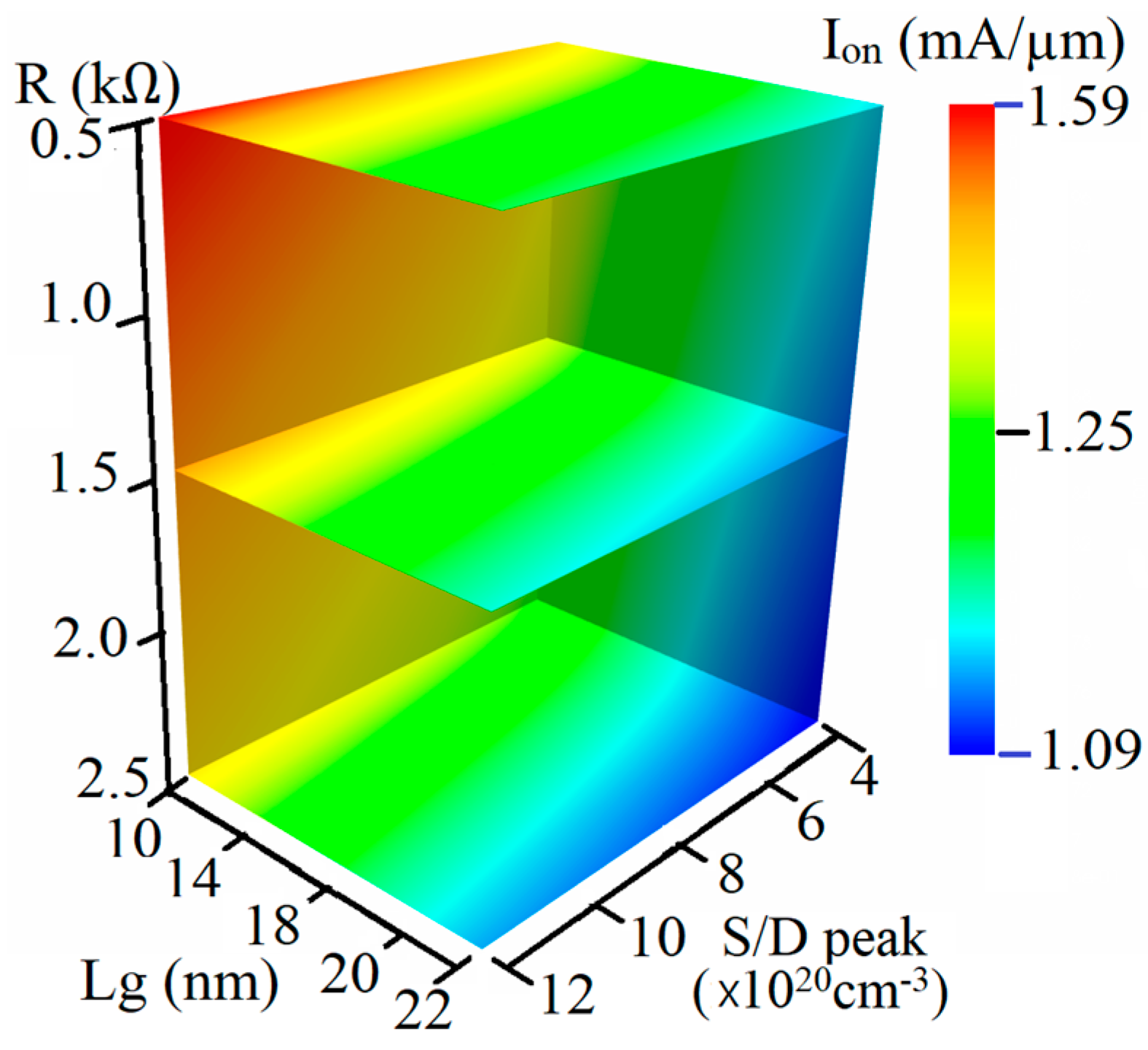
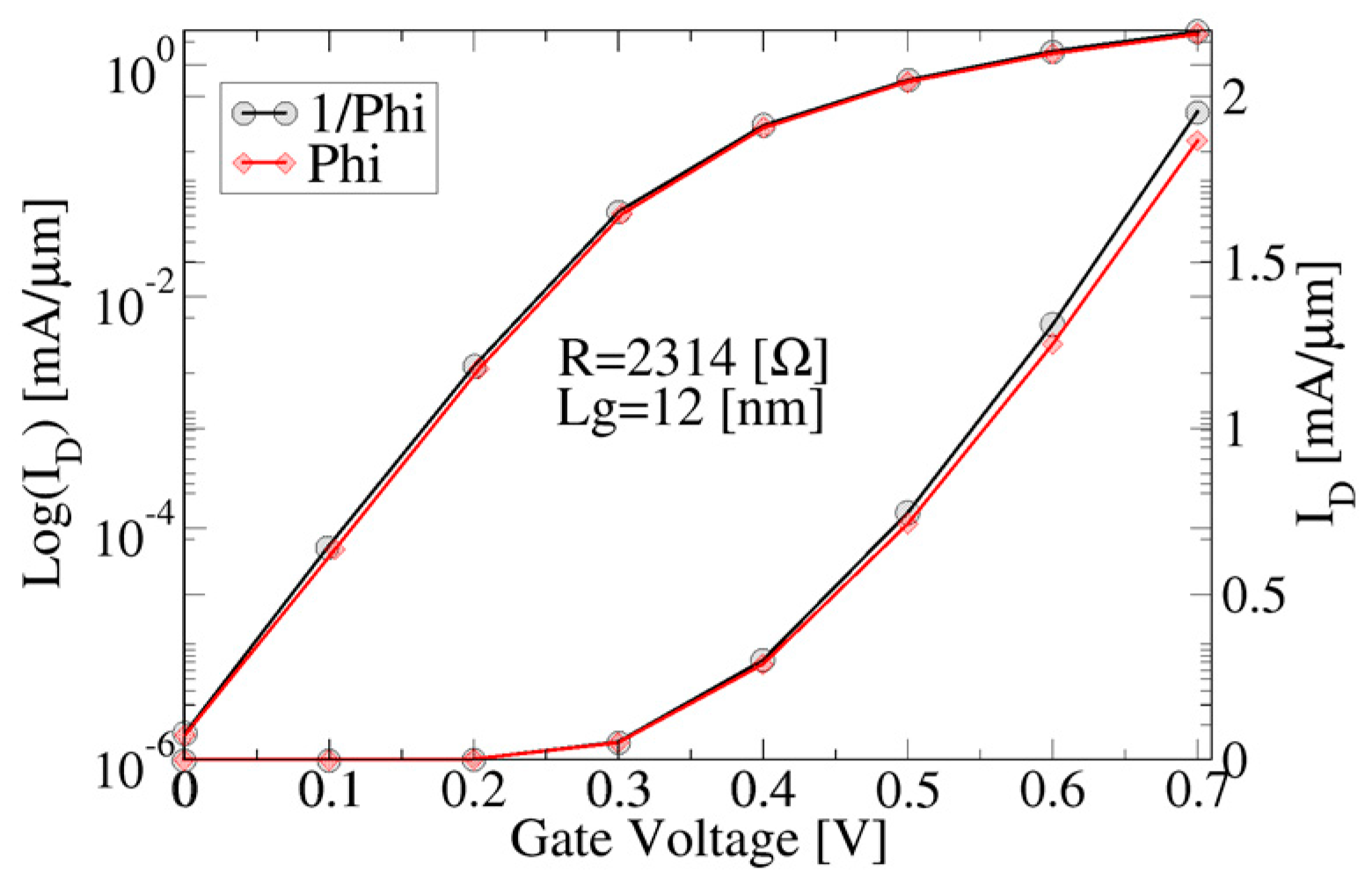
4. Results and Discussions
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Coldea, R.; Tennant, D.A.; Wheeler, E.M.; Wawrzynska, E.; Prabhakaran, D.; Telling, M.; Habicht, K.; Smeibidl, P.; Kiefer, K. Quantum Criticality in an Ising Chain: Experimental Evidence for Emergent E8 Symmetry. Science 2010, 327, 177–180. [Google Scholar] [CrossRef] [PubMed]
- Al-Ameri, T.; Georgiev, V.P.; Adamu-Lema, F.; Asenov, A. Does a nanowire transistor follow the golden ratio? A 2D Poisson-Schrödinger/3D Monte Carlo simulation study. In Proceedings of the International Conference on Simulation of Semiconductor Processes and Devices (SISPAD), Kamakura, Japan, 7–9 September 2017; pp. 57–60. [Google Scholar]
- Asenov, A.; Wang, Y.; Cheng, B.; Wang, X.; Asenov, P.; Al-Ameri, T.; Georgiev, V.P. Nanowire transistor solutions for 5 nm and beyond. In Proceedings of the 17th International Symposium on Quality Electronic Design (ISQED), Santa Clara, CA, USA, 15–16 March 2016; pp. 269–274. [Google Scholar]
- Al-Ameri, T.; Georgiev, V.P.; Adamu-Lema, F.; Asenov, A. Simulation Study of Vertically Stacked Lateral Si Nanowires Transistors for 5-nm CMOS Applications. IEEE J. Electron Devices Soc. 2017, 5, 466–472. [Google Scholar] [CrossRef]
- Wang, Y.; Al-Ameri, T.; Wang, X.; Georgiev, V.P.; Towie, E.; Amoroso, S.M.; Brown, A.R.; Cheng, B.; Reid, D.; Riddet, C.; et al. Simulation Study of the Impact of Quantum Confinement on the Electrostatically Driven Performance of n-type Nanowire Transistors. IEEE Trans. Electron Devices 2015, 62, 3229–3236. [Google Scholar] [CrossRef]
- Al-Ameri, T.; Wang, Y.; Georgiev, V.P.; Adamu-Lema, F.; Wang, X.; Asenov, A. Correlation between gate length, geometry and electrostatic driven performance in ultra-scaled silicon nanowire transistors. In Proceedings of the 2015 IEEE Nanotechnology Materials and Devices Conference (NMDC), Anchorage, AK, USA, 13–16 September 2015; pp. 1–5. [Google Scholar]
- Al-Ameri, T.; Georgiev, V.P.; Sadi, T.; Wang, Y.; Adamu-Lema, F.; Wang, X.; Amoroso, S.M.; Towie, E.; Brown, A.; Asenov, A. Impact of quantum confinement on transport and the electrostatic driven performance of silicon nanowire transistors at the scaling limit. Solid State Electron. 2017, 129, 73–80. [Google Scholar] [CrossRef]
- Mertens, H.; Ritzenthaler, R.; Chasin, A.; Schram, T.; Kunnen, E.; Hikavyy, A.; Ragnarsson, L.-A.; Dekkers, H.; Hopf, T.; Wostyn, K.; et al. Vertically stacked gate-all-around Si nanowire CMOS transistors with dual work function metal gates. In Proceedings of the 2016 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 3–7 December 2016; pp. 19.7.1–19.7.4. [Google Scholar]
- Mertens, H.; Ritzenthaler, R.; Hikavyy, A.; Kim, M.S.; Tao, Z.; Wostyn, K.; Chew, S.A.; De Keersgieter, A.; Mannaert, G.; Rosseel, E.; et al. Gate-all-around MOSFETs based on vertically stacked horizontal Si nanowires in a replacement metal gate process on bulk Si substrates. In Proceedings of the 2016 IEEE Symposium on VLSI Technology, Honolulu, HI, USA, 14–16 June 2016; pp. 1–2. [Google Scholar]
- Loubet, N.; Hook, T.; Montanini, P.; Yeung, C.-W.; Kanakasabapathy, S.; Guillom, M.; Yamashita, T.; Zhang, J.; Miao, X.; Wang, J.; et al. Stacked nanosheet gate-all-around transistor to enable scaling beyond FinFET. In Proceedings of the 2017 Symposium on VLSI Technology, Kyoto, Japan, 5–8 June 2017; Volume 5, pp. T230–T231. [Google Scholar]
- Na, M.H.; Nowak, E.J.; Haensch, W.; Cai, J. The effective drive current in CMOS inverters. In Proceedings of the Digest. International Electron Devices Meeting, San Francisco, CA, USA, USA, 8–11 December 2002; pp. 121–124. [Google Scholar]
- Asenov, A.; Brown, A.R.; Davies, J.H.; Kaya, S.; Slavcheva, G. Simulation of intrinsic parameter fluctuations in decananometer and nanometer-scale MOSFETs. IEEE Trans. Electron Devices 2003, 50, 1837–1852. [Google Scholar] [CrossRef]
- International Technology Roadmap for Semiconductors (ITRS). Available online: http://www.itrs2.net/ (accessed on 4 September 2017).
- Ghetti, A.; Rideau, D. 3D Monte Carlo Device Simulation of NanoWire MOSFETs including Quantum Mechanical and Strain Effects. In Proceedings of the 2006 International Conference on Simulation of Semiconductor Processes and Devices, Monterey, CA, USA, 6–8 September 2006; pp. 67–70. [Google Scholar]
- Asenov, A. Semiconductor Device Simulation. U.S. Patent 20170103153A1, 13 April 2017. [Google Scholar]
- Snowden, C. Introduction to semiconductor device modelling. Introd. Semicond. Device Model. 1986, 48, 1–27. [Google Scholar]
- Riddet, C.; Alexander, C.; Brown, A.R.; Roy, S.; Asenov, A. Simulation of Ab Initio & Quantum Confinement Scattering in UTB MOSFETs Using Three-Dimensional Ensemble Monte Carlo. IEEE Trans. Electron Devices 2011, 58, 600–608. [Google Scholar]
- Lindberg, J.; Aldegunde, M.; Nagy, D.; Dettmer, W.G.; Kalna, K.; Garcia-Loureiro, A.J.; Peric, D. Quantum corrections based on the 2-D Schr? Dinger equation for 3-D finite element monte carlo simulations of nanoscaled finfets. IEEE Trans. Electron Devices 2014, 61, 423–429. [Google Scholar] [CrossRef]
- Ezaki, T.; Werner, P.; Hane, M. Self-Consistent Quantum Mechanical Monte Carlo MOSFET Device Simulation. J. Comput. Electron. 2003, 2, 97–103. [Google Scholar] [CrossRef]
- Aldegunde, M.; García-Loureiro, A.J.; Kalna, K. 3D finite element monte carlo simulations of multigate nanoscale transistors. IEEE Trans. Electron Devices 2013, 60, 1561–1567. [Google Scholar] [CrossRef]
- Tanaka, H.; Suda, J.; Kimoto, T. Analysis of quasi-ballistic hole transport capability of Ge and Si nanowire pMOSFETs by quantum-corrected Boltzmann transport equation. In Proceedings of the 2017 International Conference on Simulation of Semiconductor and Devices (SISPAD), Kamakura, Japan, 7–9 September 2017; pp. 277–280. [Google Scholar]
- Liu, K.-M.; Register, L.F.; Banerjee, S.K. Quantum Transport Simulation of Strain and Orientation Effects in Sub-20 nm Silicon-on-Insulator FinFETs. IEEE Trans. Electron Devices 2011, 58, 4–10. [Google Scholar] [CrossRef]
- Wang, X.; Brown, A.R.; Binjie, C.; Asenov, A. Statical variability and reliability in nanoescale FinFETs. In Proceedings of the 2011 IEEE International Electron Devices Meeting (IEDM), Washington, DC, USA, 5–7 December 2011; pp. 103–106. [Google Scholar]
- Kovac, U.; Alexander, C.; Roy, G.; Riddet, C.; Cheng, B.; Asenov, A. Hierarchical Simulation of Statistical Variability: From 3-D MC With “ab initio” Ionized Impurity Scattering to Statistical Compact Models. IEEE Trans. Electron Devices 2010, 57, 2418–2426. [Google Scholar] [CrossRef]
- Bardon, M.G.; Sherazi, Y.; Schuddinck, P.; Jang, D.; Yakimets, D.; Debacker, P.; Baert, R.; Mertens, H.; Badaroglu, M.; Mocuta, A.; et al. Extreme scaling enabled by 5 tracks cells: Holistic design-device co-optimization for FinFETs and lateral nanowires. In Proceedings of the 2016 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 3–7 December 2016; pp. 28.2.1–28.2.4. [Google Scholar]
- Moroz, V.; Huang, J.; Choi, M. FinFET/nanowire design for 5 nm/3 nm technology nodes: Channel cladding and introducing a ‘bottleneck’ shape to remove performance bottleneck. In Proceedings of the 2017 IEEE Electron Devices Technology and Manufacturing Conference (EDTM), Toyama, Japan, 28 February–2 March 2017; Volume 3, pp. 67–69. [Google Scholar]
- Al-Ameri, T.; Georgiev, V.P.; Lema, F.; Sadi, T.; Wang, X.; Towie, E.; Riddet, C.; Alexander, C.; Asenov, A. Impact of strain on the performance of Si nanowires transistors at the scaling limit: A 3D Monte Carlo/2D poisson schrodinger simulation study. In Proceedings of the 2016 International Conference on Simulation of Semiconductor Processes and Devices (SISPAD), Nuremberg, Germany, 6–8 September 2016; pp. 213–216. [Google Scholar]
- Ragnarsson, L.-A.; Pantisano, L.; Kaushik, V.; Saito, S.-I.; Shimamoto, Y.; de Gendt, S.; Heyns, M. The impact of sub monolayers of HfO2 on the device performance of high-k-based transistors [MOSFETs]. In Proceedings of the IEEE International Electron Devices Meeting 2003, Washington, DC, USA, 8–10 December 2003; pp. 4.2.1–4.2.4. [Google Scholar]
- Sverdlov, V. Strain-Induced Effects in Advanced MOSFETs; Springer: Vienna, Austria, 2011; Volume 1. [Google Scholar]
- Gluschenkov, O.; Liu, Z.; Niimi, H.; Mochizuki, S.; Fronheiser, J.; Miao, X.; Li, J.; Demarest, J.; Zhang, C.; Niu, C.; et al. FinFET performance with Si:P and Ge:Group-III-Metal metastable contact trench alloys. In Proceedings of the 2016 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 3–7 December 2016; pp. 17.2.1–17.2.4. [Google Scholar]
- Das, U.K.; Bardon, M.G.; Jang, D.; Eneman, G.; Schuddinck, P.; Yakimets, D.; Raghavan, P.; Groeseneken, G. Limitations on Lateral Nanowire Scaling Beyond 7-nm Node. IEEE Electron Device Lett. 2017, 38, 2016–2018. [Google Scholar] [CrossRef]
- Moroz, V.; Huang, J.; Arghavani, R. Transistor design for 5nm and beyond: Slowing down electrons to speed up transistors. In Proceedings of the 17th International Symposium on Quality Electronic Design (ISQED), Santa Clara, CA, USA, 15–16 March 2016; Volume 2016, pp. 278–283. [Google Scholar]
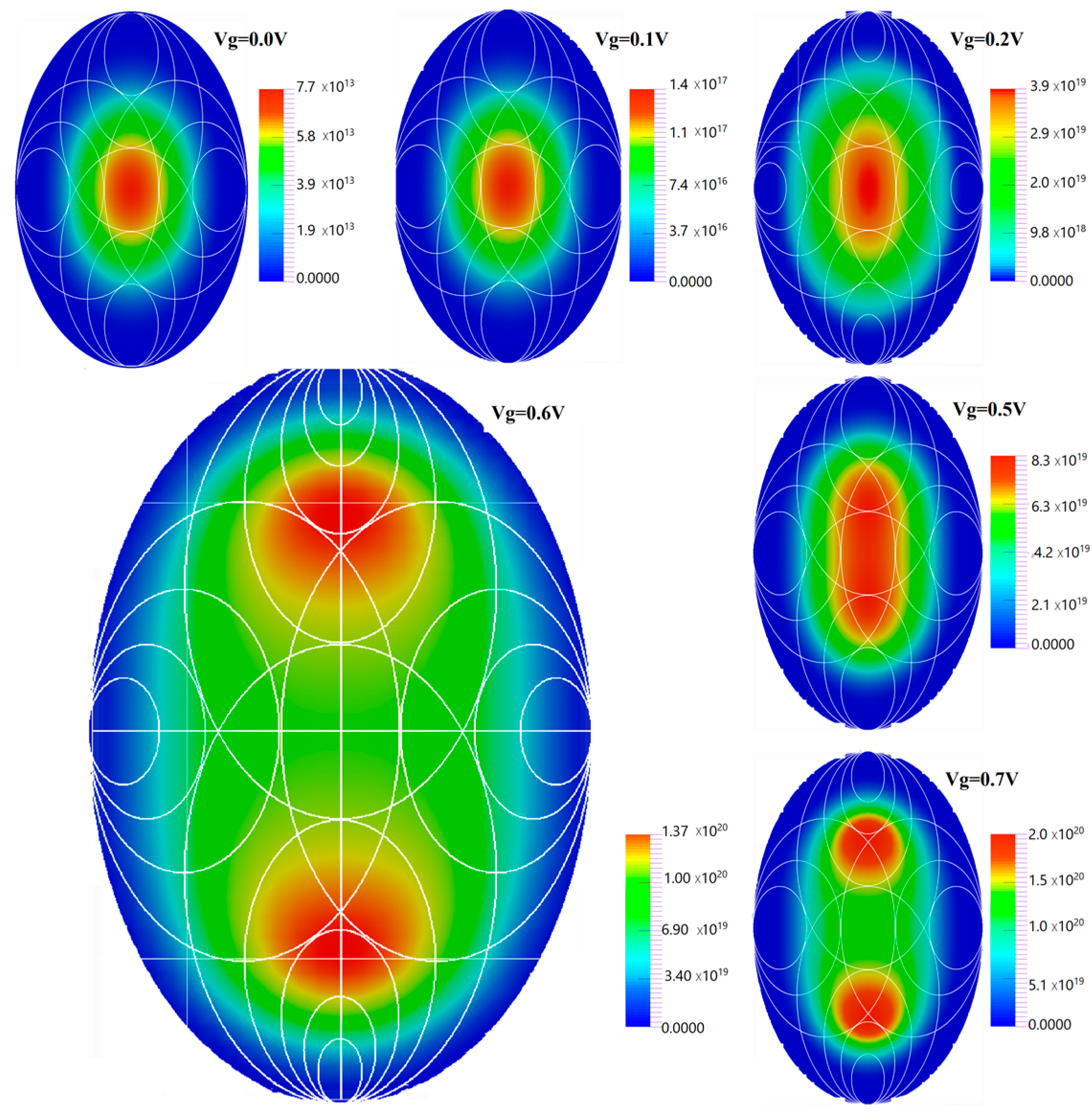

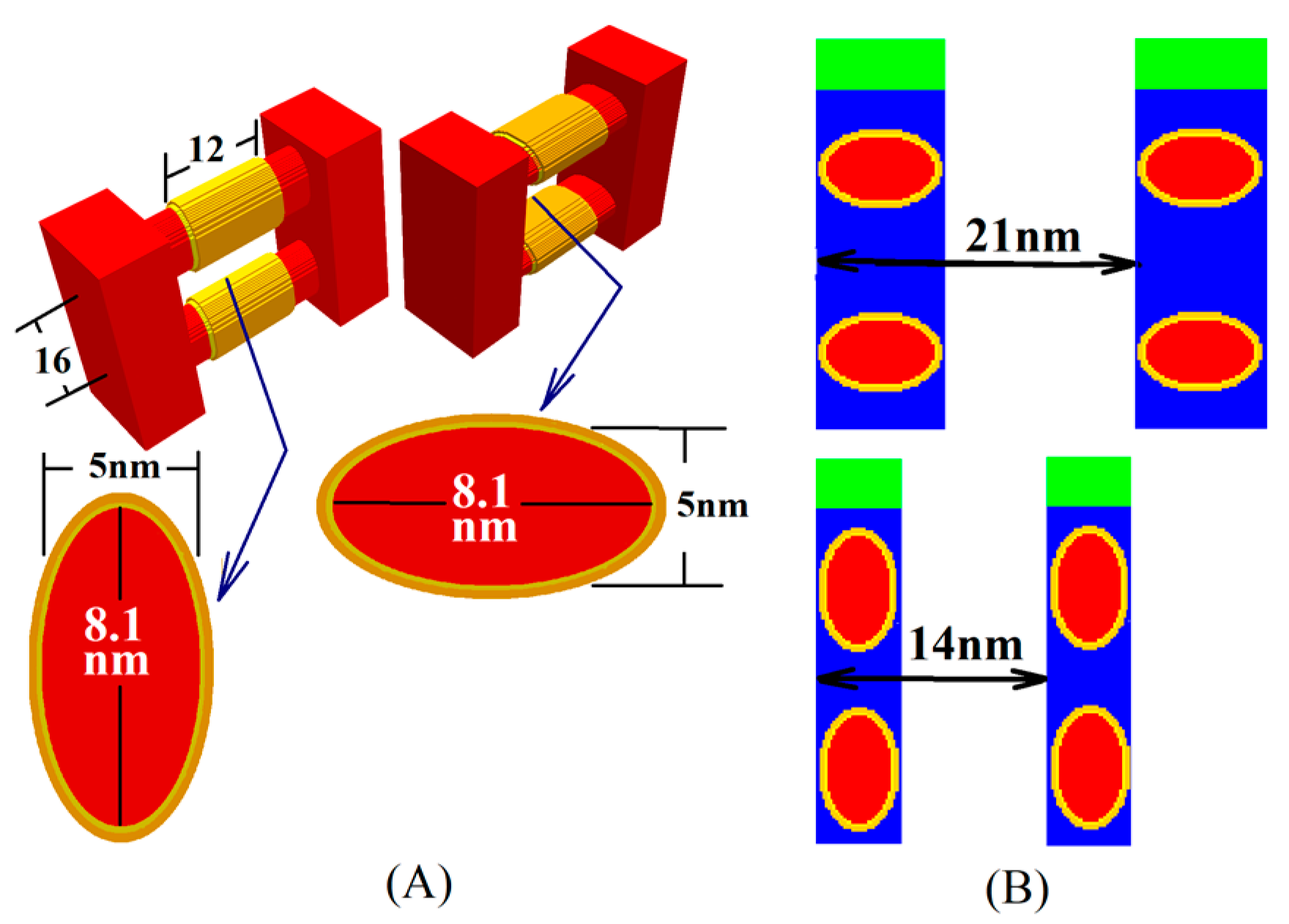
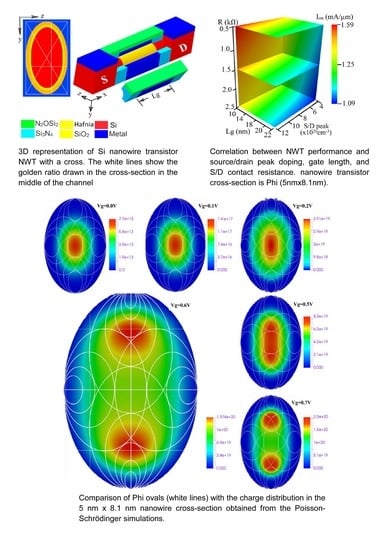
| Z (nm) × Y (nm) | Y/Z | Area (nm2) |
|---|---|---|
| 4.440 × 9.0 | 2.020 | 10π |
| 5 × 8.10 (Phi) | 1.620 | 10π |
| 5.7 × 7.0 | 0.810 | 10π |
| 6.0 × 6.66 | 0.900 | 10π |
| 6.32 × 6.32 | 1.000 | 10π |
| 6.66 × 6.0 | 1.110 | 10π |
| 7.0 × 5.7 | 1.220 | 10π |
| 8.10 × 5 (1/Phi) | 0.620 | 10π |
| 9.0 × 4.44 | 0.490 | 10π |
| Z (nm) × Y (nm) | QM (×107/cm) | CG (10−10 F/cm) | QM/CG (1017/F) | |
|---|---|---|---|---|
| <110> | ||||
| 4.44 × 9.0 | 2.73300 | 1.14010 | 2.3970 | Oblate NWT |
| 5 × 8.10 (Phi) | 2.84200 | 1.14740 | 2.4760 | |
| 5.7 × 7.0 | 2.75000 | 1.12900 | 2.4350 | |
| 6.0 × 6.66 | 2.58010 | 1.10930 | 2.3260 | |
| 6.320 × 6.320 | 2.54800 | 1.10920 | 2.2970 | Circular |
| 6.660 × 6.0 | 2.63160 | 1.11680 | 2.3560 | Prolate NWT |
| 7.0 × 5.70 | 2.77380 | 1.13520 | 2.4400 | |
| 8.10 × 5 (1/Phi) | 2.89200 | 1.16020 | 2.4910 | |
| 9.0 × 4.44 | 2.72700 | 1.13710 | 2.3980 | |
| Z (nm) × Y (nm) | QM (×107/cm) | CG (10−10 F/cm) | QM/CG (1017/F) | |
|---|---|---|---|---|
| <100> | ||||
| 4.44 × 90 | 2.73220 | 1.13500 | 2.40720 | Oblate NWT |
| 5 × 8.10 (Phi) | 2.89000 | 1.15970 | 2.49200 | |
| 5.7 × 7.0 | 2.77940 | 1.13840 | 2.44410 | |
| 6.0 × 6.66 | 2.64030 | 1.11840 | 2.36070 | |
| 6.320 × 6.320 | 2.61020 | 1.11600 | 2.33760 | Circular |
| 6.660 × 6.0 | 2.64020 | 1.11800 | 2.36150 | Prolate NWT |
| 7.0 × 5.70 | 2.77930 | 1.13800 | 2.44220 | |
| 8.10 × 5 (1/Phi) | 2.89100 | 1.15980 | 2.49100 | |
| 9.0 × 4.44 | 2.73210 | 1.13410 | 2.40900 | |
| Ion mA/µm | 5 nm × 8.1 nm | 8.1 nm × 5 nm | ||
|---|---|---|---|---|
| SD | Mean | SD | Mean | |
| WER | 0.0380 | 1.246 | 0.0276 | 1.310 |
| RDD | 0.0379 | 1.203 | 0.0401 | 1.265 |
| MGG | 0.0882 | 1.223 | 0.0893 | 1.286 |
| SV | 0.1031 | 1.171 | 0.0998 | 1.232 |
| VT mV | 5 nm × 8.1 nm | 8.1 nm × 5 nm | ||
|---|---|---|---|---|
| SD | Mean | SD | Mean | |
| WER | 5.807 | 107.85 | 2.247 | 93.29 |
| RDD | 2.001 | 110.66 | 1.91 | 96.18 |
| MGG | 27.82 | 110.41 | 27.59 | 96.24 |
| SV | 28.52 | 111.9 | 27.74 | 97.65 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Ameri, T. Correlation between the Golden Ratio and Nanowire Transistor Performance. Appl. Sci. 2018, 8, 54. https://doi.org/10.3390/app8010054
Al-Ameri T. Correlation between the Golden Ratio and Nanowire Transistor Performance. Applied Sciences. 2018; 8(1):54. https://doi.org/10.3390/app8010054
Chicago/Turabian StyleAl-Ameri, Talib. 2018. "Correlation between the Golden Ratio and Nanowire Transistor Performance" Applied Sciences 8, no. 1: 54. https://doi.org/10.3390/app8010054
APA StyleAl-Ameri, T. (2018). Correlation between the Golden Ratio and Nanowire Transistor Performance. Applied Sciences, 8(1), 54. https://doi.org/10.3390/app8010054