Temporal Response of Ultrafast Grating Monochromators

Featured Application

Grating monochromators for ultrafast pulses.

Abstract

The temporal response of double-grating monochromators is analyzed considering two effects on the ultrafast pulse given by the configuration. The first effect is the compensation of the pulse-front tilt, i.e., all the rays emitted by the source in different directions at the same wavelength have to travel the same optical path. The second effect is the group delay introduced by the two gratings, i.e., different wavelengths within the bandwidth transmitted by the slit travel different paths. The methodology to calculate the group delay introduced by the double-grating configuration is presented. Some practical design examples are provided to show the design rules and the achieved performances.

1. Introduction

Since its discovery, the process of high-order harmonic (HH) generation in gas has been at the center of experimental and theoretical investigations for studies of electronic structure and ultrafast dynamics of atoms, molecules and condensed matters [1]. Moreover, the radiation generated with the scheme of the HHs using few-optical-cycles laser pulses is at present the central tool for the investigation of matter with attosecond resolution [2]. HH generation occurs when an electron, liberated from an atom or molecule by an intense ultrashort laser fields, gains energy from the field and recombines with the parent ion [3]. The HH spectrum is described as a sequence of peaks corresponding to the odd harmonics of the fundamental laser wavelength with an intensity distribution characterized by a plateau spanning into extreme-ultraviolet (XUV) and soft X-rays whose extension is related to the pulse intensity. Thus, HH radiation can be used to perform a large variety of time-resolved experiments without the need for big facilities like synchrotrons or free-electron lasers.

The selection of a single harmonic from consecutive multiple harmonics is required for many spectroscopic applications. Various methods are used, such as multilayer mirrors [4], selected enhancement by laser pulse shaping [5], zone-plate monochromators [6], gratings at grazing incidence [7].

In particular, the use of gratings to realize monochromatic beamlines with ultrafast time response is well established not only for HHs [8], but also for intense free-electron laser pulses [9]. Gratings give broad tunability, covering the whole XUV spectral region, and high spectral selectivity. Different configurations have been already realized: single-stage grating monochromators with high efficiency and response in the few tens of femtoseconds time-scale [10,11,12] and double-stage reflective-grating monochromators with ultrafast response below ten femtoseconds [13,14,15,16]. In the first case, when using a single grating, a residual pulse-front tilt due to diffraction has to be accepted at the output of the monochromator. It can be minimized by choosing a suitable geometry to obtain temporal responses in the range of few tens of femtoseconds [17]. In the second case, two consecutive gratings are employed: the first one performs the spectral selection on an intermediate slit while the second one corrects for the pulse-front tilt introduced by the diffraction.

In this paper, the temporal response of double-grating monochromators is analyzed considering two effects on the ultrafast pulse given by the configuration. The first effect is the compensation of the pulse-front tilt, i.e., all the rays emitted by the source in different directions at the same wavelength have to travel the same optical path. Ideally the compensation is perfect for a double-grating configuration, although aberrations may give a residual distortion of the pulse-front. The second effect is the group delay (GD) introduced by the two gratings, i.e., different wavelengths within the bandwidth transmitted by the slit travel different paths. Similarly to grating pulse shapers for optical laser pulses, the pair of gratings in the time-delay-compensating configuration can be considered as a XUV pulse shaper, capable to introduce a controllable GD. The methodology to calculate the GD introduced by the double-grating configuration is presented in Section 2. In terms of temporal response, the best operative condition for a monochromator is found when the GD and the Fourier limit for the given bandwidth are almost equivalent. For a narrower bandwidth, the GD decreases but the Fourier limit increases, giving a longer temporal response. For a broader bandwidth, the Fourier limit decreases but the GD increases, giving again a longer temporal response. Some practical design examples are provided to show the design rules and the expected performances.

2. Ultrafast Response of Grating Monochromators

The monochromator demanded for the spectral selection of ultrashort pulses has to preserve the temporal duration as short as in the generation process. The monochromator can be modelled as a filter with a complex frequency response that includes both the non-uniform spectral transmission and the distortion in the spectral phase. Since the XUV pulse at the generation may be produced to be close to its transform limit, any modification of its complex spectrum results in a time broadening as described by its Fourier transform. For a Gaussian profile with no phase or frequency modulation, the half-height duration Δτ_F has a lower limit expressed as:

$$\Delta {\tau }_F=\frac{2\ln 2}{\pi c}\frac{{\lambda }^2}{\Delta \lambda }\cong \frac{0.44}{c}\frac{{\lambda }^2}{\Delta \lambda }$$

(1)

where λ is the pulse central wavelength, Δλ is the half-height spectral width of the pulse and c is the speed of light in vacuum.

In order to preserve the duration of the pulse at the output of the monochromator, the spectral transmission has to be constant within the bandwidth. This condition is always verified if the monochromator is realized by reflecting optics, since the reflectivity variations within the output bandwidth are usually negligible, so that the transfer function can be considered almost constant, although lower than unity.

Furthermore, the temporal response of the monochromator has to be shorter than Δτ_F. In case of a diffraction grating, the major mechanism that alters the time duration of the pulse is the difference in the lengths of the optical paths of the rays diffracted by different grating grooves. Indeed, a single grating gives inevitably a time broadening of the ultrafast pulse because of the pulse-front tilt due to diffraction, since the total difference in the optical paths of the rays diffracted at first order by N grooves illuminated by radiation at wavelength λ is Nλ. This effect can be dramatic in the femtosecond time scale. Let us consider a 300 grooves/mm grating illuminated by radiation at 30 nm over a length of 10 mm; the total number of grooves involved in the diffraction is 3000, corresponding to a pulse-front tilt of 90 μm, i.e., 300 fs. In case of femtosecond pulses, this reduces dramatically both the time resolution capability and the peak intensity at the exit of the monochromator.

Nevertheless, it is possible to realize grating monochromators that do not alter the temporal duration of ultrashort pulses by using two gratings in a time-delay-compensated (TDC) configuration: the first grating performs the spectral selection on an intermediate slit, then the second one corrects for the pulse-front tilt introduced by the diffraction. From the point of view of the ray paths, two are the conditions that the design must comply to: (1) the differences in the path lengths of rays having the same wavelength but with different entrance directions within the beam aperture that are caused by the diffraction from the first grating must be compensated by the second grating; (2) two rays at different wavelengths within the spectrum of the pulse to be selected have to be focused on the same point, i.e., the global spectral dispersion has to be zero. Both conditions are satisfied by a scheme with two equal gratings mounted in a symmetrical way. The spectral selection is performed by a slit placed in an intermediate position between the gratings, where the radiation is focused by the first grating.

Grazing-incidence gratings can be used in two geometries: the classical-diffraction mount (CDM) and the off-plane mount (OPM). The latter, also called conical diffraction mount, differs from the classical one in that the incident and diffracted wave vectors are almost parallel to the grooves [18]. The main advantage of the OPM when compared to the CDM is the much higher efficiency (up to a factor three), since it has been theoretically demonstrated and experimentally measured that the peak diffraction efficiency in the OPM is close to the reflectivity of the coating at the altitude angle, that makes the OPM suitable for the design of TDC monochromators with high throughput [19,20]. It is worth to mention here that the double-grating configuration is presently applied in the XUV, for wavelength that are typically longer than ≈10 nm. For shorter wavelengths, i.e., entering the soft X-ray region, the losses due to the decrease in reflectivity should be considered when balancing the advantages of the TDC configuration in terms of temporal response with the low photon throughput.

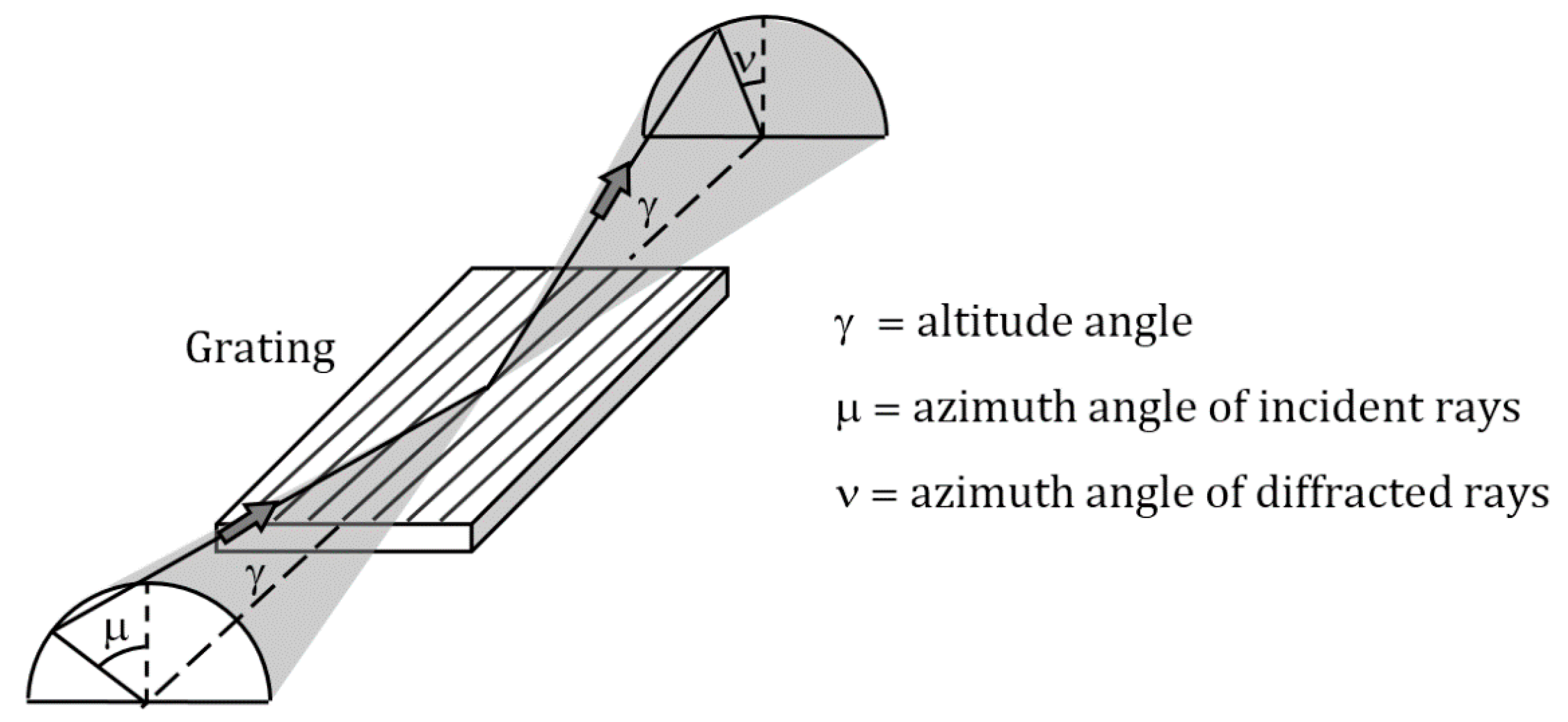
In the following, the paper will be focused on the OPM. The geometry is shown in Figure 1. The direction of the incoming rays is described by two parameters: the altitude and the azimuth. The altitude γ is defined as the angle between the direction of the incoming rays and the direction of the grooves. The azimuth μ of the incoming rays is defined to be zero if they lie in the plane perpendicular to the grating surface and parallel to the rulings. Let ν define the azimuth of the diffracted light at wavelength λ and order m. The grating equation is sinγ (sinμ + sinν) = mλδ, where δ is the groove density. For a monochromator, the grating is operated in the condition μ = ν and the resulting grating equation is μ = arcsin(½mλδ/sinγ).

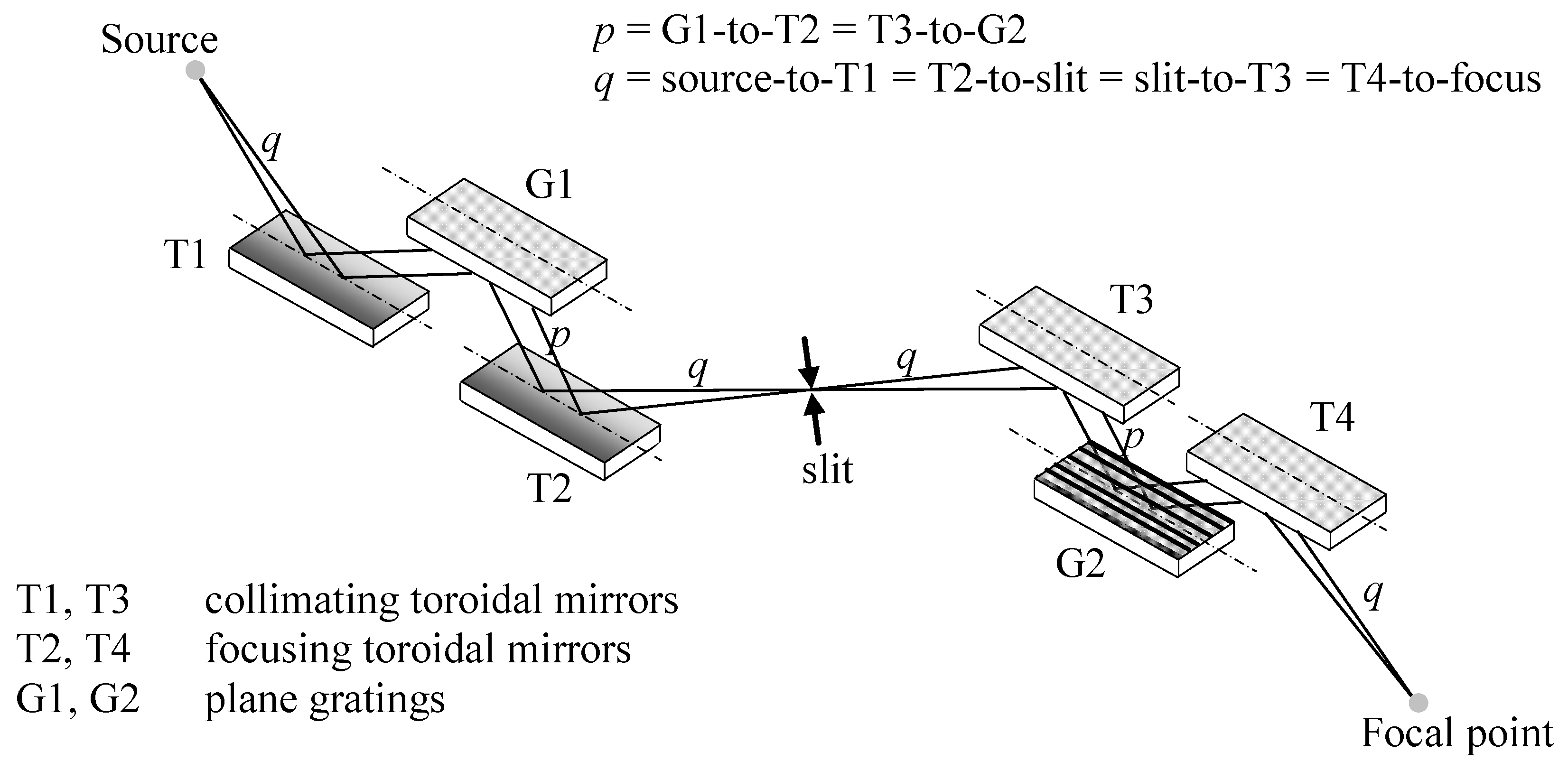
A schematic of a TDC monochromator with plane gratings in the OPM is shown in Figure 2. The gratings are used in collimated beams [21], therefore each of the two sections of the monochromator consists of three optical elements at grazing incidence: the collimating toroidal mirror, the plane grating and the focusing toroidal mirror.

Two are the effects to be considered when evaluating the temporal response of the TDC configuration: (1) the compensation of the pulse-front tilt and (2) the GD introduced within the bandwidth.

The pulse-front tilt is ideally fully compensated for a double-grating configuration, although residual aberrations introduced by the toroidal mirrors may give some distortion of the pulse-front, which has to be evaluated through ray-tracing simulations. With reference to Figure 2, in the following the term “input arm” will refer to the two collimators T1 and T3 and will indicate the distance between the source and the center of T1 or the distance between the intermediate slit and the center of T3; the term “output arm” will refer to the two focusing elements T2 and T4 and will indicate the distance between the center of T2 and the intermediate slit or the distance between the center of T4 and the output focal point. For the TDC configuration, the number of grooves illuminated on G2 has to be the same as G1. Since the gratings are equal and are operating at the same altitude angle, this condition is fulfilled if the output arm of T2 is equal to the input arm of T3. Furthermore, in order to minimize the aberrations, each of the two sections is operating with unity magnification, i.e., the input arm of the collimator is equal to the output arm of the successive focusing element. Therefore, all the arms are the same and the configuration is fully symmetrical. As shown in the following simulations, the pulse-front distortion due to aberrations in the symmetric TDC configuration is expected to be in the few-femtoseconds or even sub-femtosecond time scale, therefore it can be usually neglected.

The main instrumental effect on the time response of the TDC configuration is the GD introduced by the two gratings, i.e., different wavelengths within the bandwidth transmitted by the slit travel different optical paths, although all rays start from the source point and are finally focused on the same point to fulfill the condition of zero spectral dispersion. Indeed, the pair of gratings in the TDC configuration can be considered as a XUV pulse shaper capable to introduce a controllable GD [22,23], similarly to grating pulse shapers for optical laser pulses [24]. The GD is calculated as the difference in the optical paths within the bandwidth Δλ, as discussed in details in [25]. In case of Δλ/λ < 10%, the GD is linear with the wavelength and results:

$$GD(\lambda )=-\left(q-p\right)\frac{2\lambda {\sigma }^2}{c{\cos }^2\mu }\Delta \lambda \approx -\left(q-p\right)\frac{2\lambda {\sigma }^2}{c}\Delta \lambda$$

(2)

where the distances q and p are defined in Figure 2 and the term cos² μ can be neglected, since the azimuth μ is typically lower than 15°.

For q > p, as usual in experimental conditions, the GD decreases with the wavelength and this forces the group delay dispersion (GDD) to be almost constant and positive:

$$GDD=\frac{\partial GD(\omega )}{\partial \omega }=\frac{\left(q-p\right){\lambda }^3{\sigma }^2}{\pi c^2}$$

(3)

where ω = 2πc/λ is the angular frequency.

The GD is canceled for q = p, i.e., when the grating-to-mirror distance is equal to the mirror arm. Usually, this condition cannot be verified, since it would require an extremely large size to host the optical components.

In terms of temporal response, the GD introduced by the TDC monochromator within the output bandwidth has to be compared to the Fourier limit in the same bandwidth. For application to monochromatization of HHs, the monochromator can be used in two operative conditions: (1) low-resolution or (2) high-resolution option. In the first case, the bandwidth transmitted through the slit is wider than the intrinsic bandwidth of the single harmonic, although lower than the separation between consecutive harmonics, therefore the monochromator is used as a tunable filter to select one of the harmonics and the output bandwidth is limited by the bandwidth of the harmonic. In the second case, the output bandwidth is narrower than the bandwidth of the single harmonic and the spectral resolution is limited by the instrumental response.

2.1. Temporal Response of TDC Monochromators with Low Spectral Resolution

Low-resolution monochromators are typically used with HHs when the monochromator is required to select a single harmonic within a broad plateau and behaves as a tunable broad-band filter. The bandwidth transmitted by the slit has to be narrow enough to resolve two adjacent harmonics, that are separated by 2λ₀/[n(n + 2)], where λ₀ is the laser wavelength that is used to generate HHs and n is an odd integer (A single laser wavelength is assumed to be used to generate HHs, therefore only odd harmonics are generated.). Indeed, the output bandwidth is limited by the source itself and not by the monochromator. Comparing Equations (1) and (2), the GD results negligible with respect to the Fourier limit for:

$$\frac{\left(q-p\right){\sigma }^2\Delta {\lambda }^2}{0.22\lambda }<1$$

(4)

where Δλ is the bandwidth of the pulse.

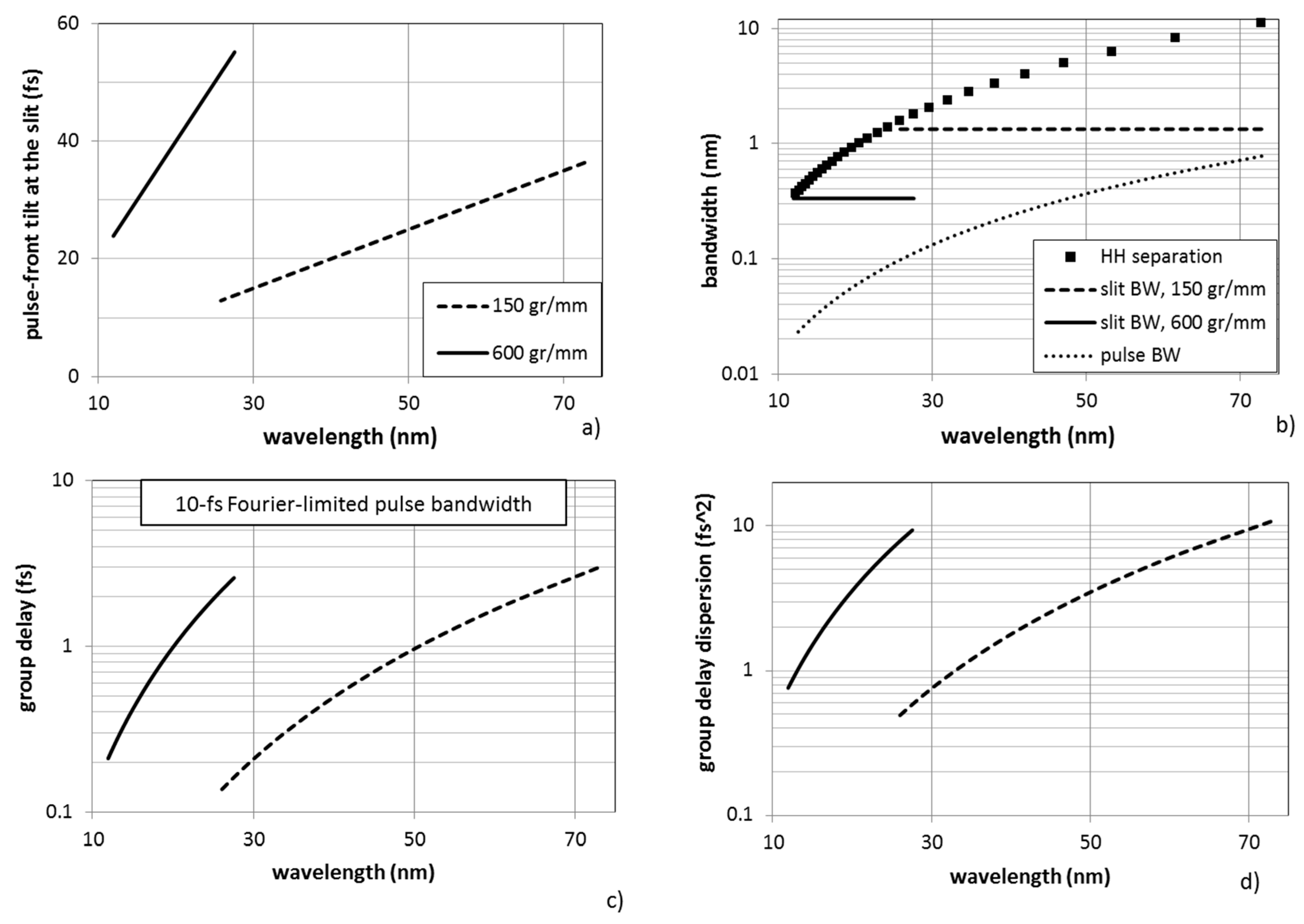
The calculations for typical parameters of low-resolution TDC monochromators are resumed in Figure 3. Two sets of gratings are used to span the 12–75 nm interval (i.e., harmonics H65-H11 of 800-nm Ti:Sa laser). XUV Fourier-limited 10 fs Gaussian pulses are assumed at the generation, of which the wavelength bandwidth is plotted in Figure 3a. The corresponding energy bandwidth is ΔE ≈ 180 meV. The bandwidth transmitted by the slit is also shown in Figure 3a: it is lower than the separation between consecutive harmonics, as requested for the selection of a single harmonic. The pulse-front tilt given by the first grating stage is plotted in Figure 3b for 4-mrad XUV divergence, that is a typical divergence for HHs generated by laser pulses in the millijoule range. The tilt is in the range 15–50 fs, therefore the original 10-fs pulse is stretched in time by the first grating. If monochromatic Fourier-limited pulses are requested at the output of the monochromator, a second grating stage is needed. The residual pulse-front distortion after the pulse-front tilt correction made by the second grating has been simulated through a ray-tracing procedure. For the parameters here assumed, it is lower than 0.5 fs within the whole interval of operation, therefore totally negligible. The GD and the GDD are plotted in Figure 3c,d for 10-fs Fourier-limited pulses. The GDD is below 10 fs² and the GD is definitely lower than the Fourier limit, confirming that the TDC monochromator, when used as a broad-band filter, does not sensibly alter the duration of the pulse.

2.2. Temporal Response of TDC Monochromators with High Spectral Resolution

In case of high resolution, the output bandwidth is limited by the monochromator and not by the intrinsic bandwidth of the single harmonic. Once the slit aperture W is fixed, the bandwidth transmitted through the slit is:

$$\Delta \lambda =\frac{W}{q\sigma }$$

(5)

In terms of temporal response, the best trade-off is found when the GD and the Fourier limit are almost equivalent. For a narrower bandwidth, the GD decreases but the Fourier limit increases. For a broader bandwidth, the Fourier limit decreases but the GD increases. The condition GD = Fourier is obtained combining Equations (1), (2) and (5) and, for Gaussian pulses, is expressed by:

$$W=q\sqrt{\frac{0.22\lambda }{q-p}}$$

(6)

Aim of the optical design is to find the parameters that fulfill Equation (6) to find the best trade-off between energy and temporal resolution.

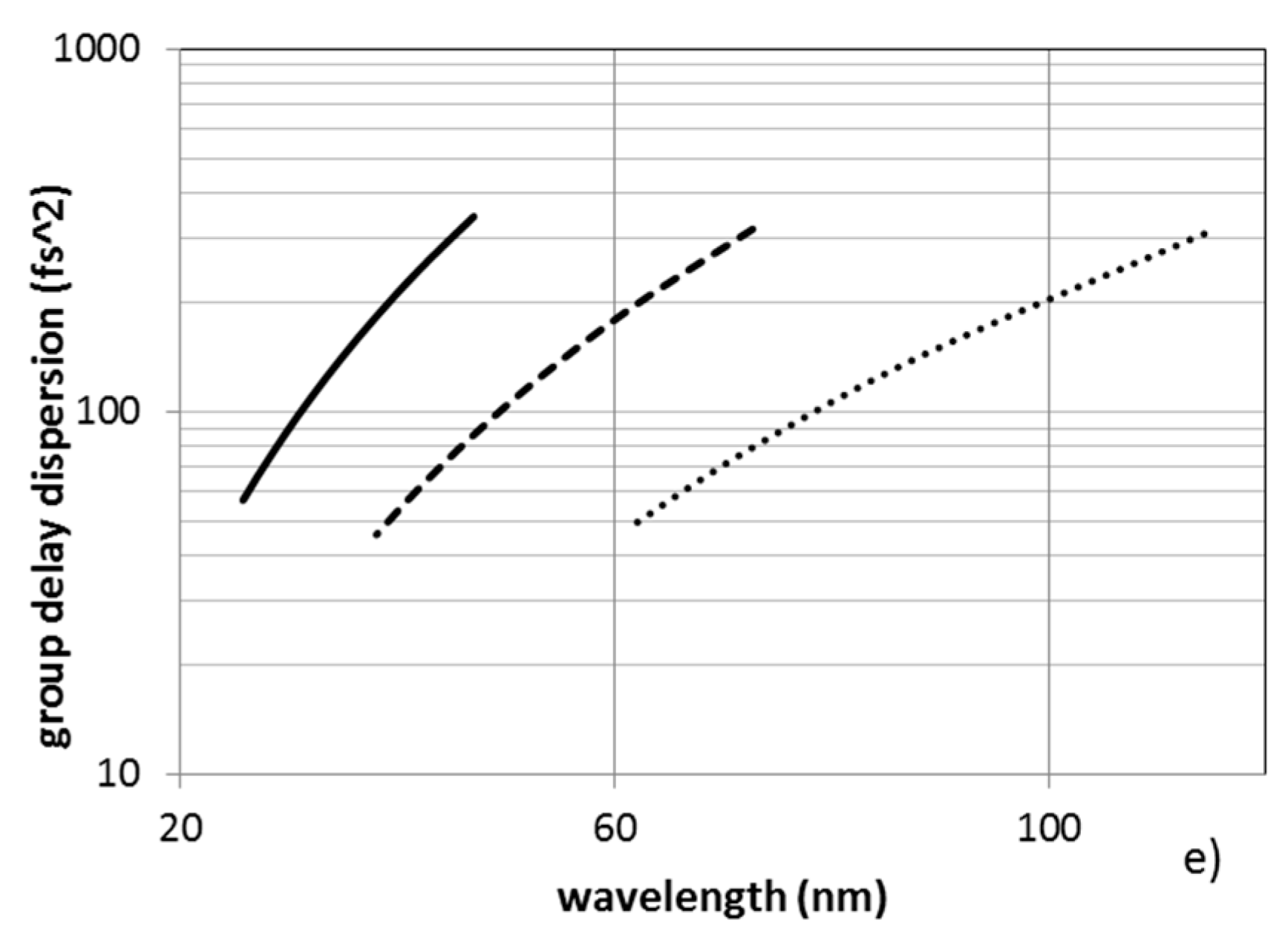
A test case is here discussed for sub-150 meV energy bandwidth and sub-50 fs temporal response in the 20–120 nm (62–10 eV) interval, that are typical values required for ultrafast photoelectron spectroscopy. The requirements are resumed in

Table 1. Requirements and parameters for a TDC monochromator with sub-150 meV energy bandwidth.

Requirements
Wavelength range	25–115 nm (10–50 eV)
Energy bandwidth	<150 meV
Temporal response	<50 fs
Parameters
Gratings	300/600/1200 grooves/mm
Exit arm q	800 mm
Mirror-to-grating p	150 mm
Slit aperture	75–160 μm

. A set of parameters, in terms of groove density and lengths of the arms, is also listed in Table 1.

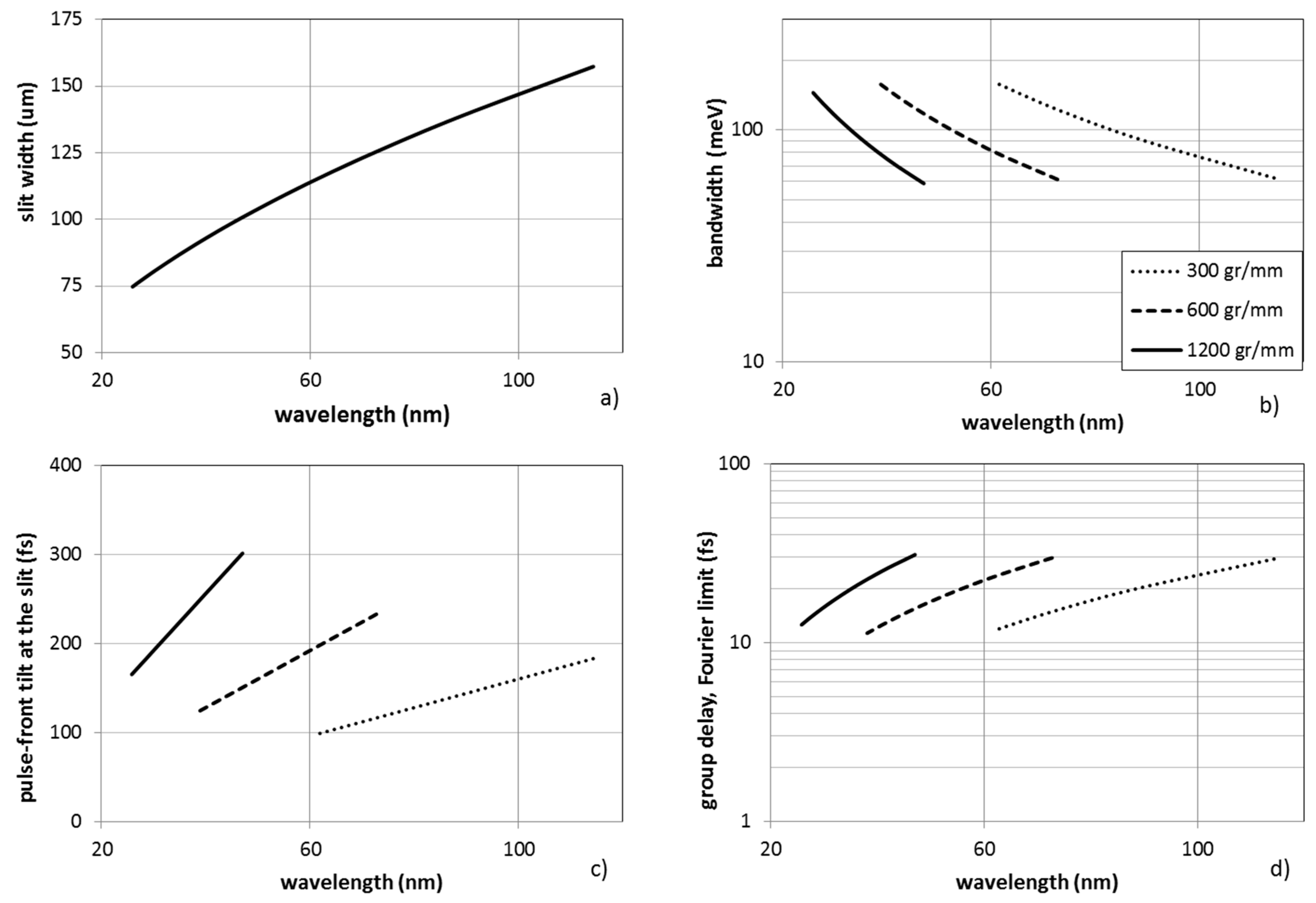
The performances, in terms of energy bandwidth and temporal response, are resumed in Figure 4. The slit width calculated by Equation (6) is shown in Figure 4a. It is the width giving an output bandwidth in which the GD is equal to the Fourier limit. The slit aperture is in the range 75–160 μm, that is a typical interval for practical operations. The corresponding bandwidth is shown in Figure 4b. By choosing the appropriate grating, the bandwidth is anyway below 100 meV for wavelengths longer than 32 nm. For shorter wavelengths, the bandwidth increases up to 150 meV at 25 nm. The pulse-front tilt given by the first grating stage is plotted in Figure 4c for 4-mrad XUV divergence. The tilt is definitely above 100 fs in the full range of operation. After the second grating, the residual pulse-front distortion, as simulated through a ray-tracing procedure, is lower than 2 fs within the whole interval of operation, i.e., fully negligible. The corresponding Fourier limit and GD are shown in Figure 4d,e and are in the range 10–30 fs in the whole interval of operation. The GDD is definitely higher than the low-resolution case, typically of the order of 100 fs². The GD can be reduced if the grating-to-mirror distance p is kept higher, that is, for a lower q–p value, at the expense of a larger size of the monochromator. In this case, the use of a second grating stage increases the temporal resolution by almost one order of magnitude when compared to a monochromator with a single grating for the same output bandwidth.

3. Conclusions

The temporal response of double-grating monochromators has been analyzed, in particular the group delay introduced by the two gratings within the bandwidth, i.e., different wavelengths travel different paths. The analysis has been focused on monochromators for high-order laser harmonics. Two operative conditions have been described: (1) the low-resolution configuration, when the monochromator is used as a broadband filter and the output bandwidth is limited by the source itself, i.e., by the intrinsic bandwidth of a single harmonic; (2) the high-resolution configuration, when the monochromator aims to a bandwidth narrower than that of the single harmonic. In the first case the group delay is typically negligible, being in the sub- or few-femtoseconds time scale, well beyond the Fourier limit. In the second case, the group delay is comparable to the Fourier limit and is the main factor limiting the temporal response of the monochromator. The best operative condition, in terms of temporal response, is found when the group delay and the Fourier limit for the given bandwidth are almost equivalent. Obviously, the final operative conditions depend on the users’ requirements that can be fulfilled by a suitable trade-off between energy and time resolution.