Experimental Tests and Aeroacoustic Simulations of the Control of Cavity Tone by Plasma Actuators
Abstract
:Featured Application
Abstract
1. Introduction
2. Methodologies
2.1. Experimental Tests
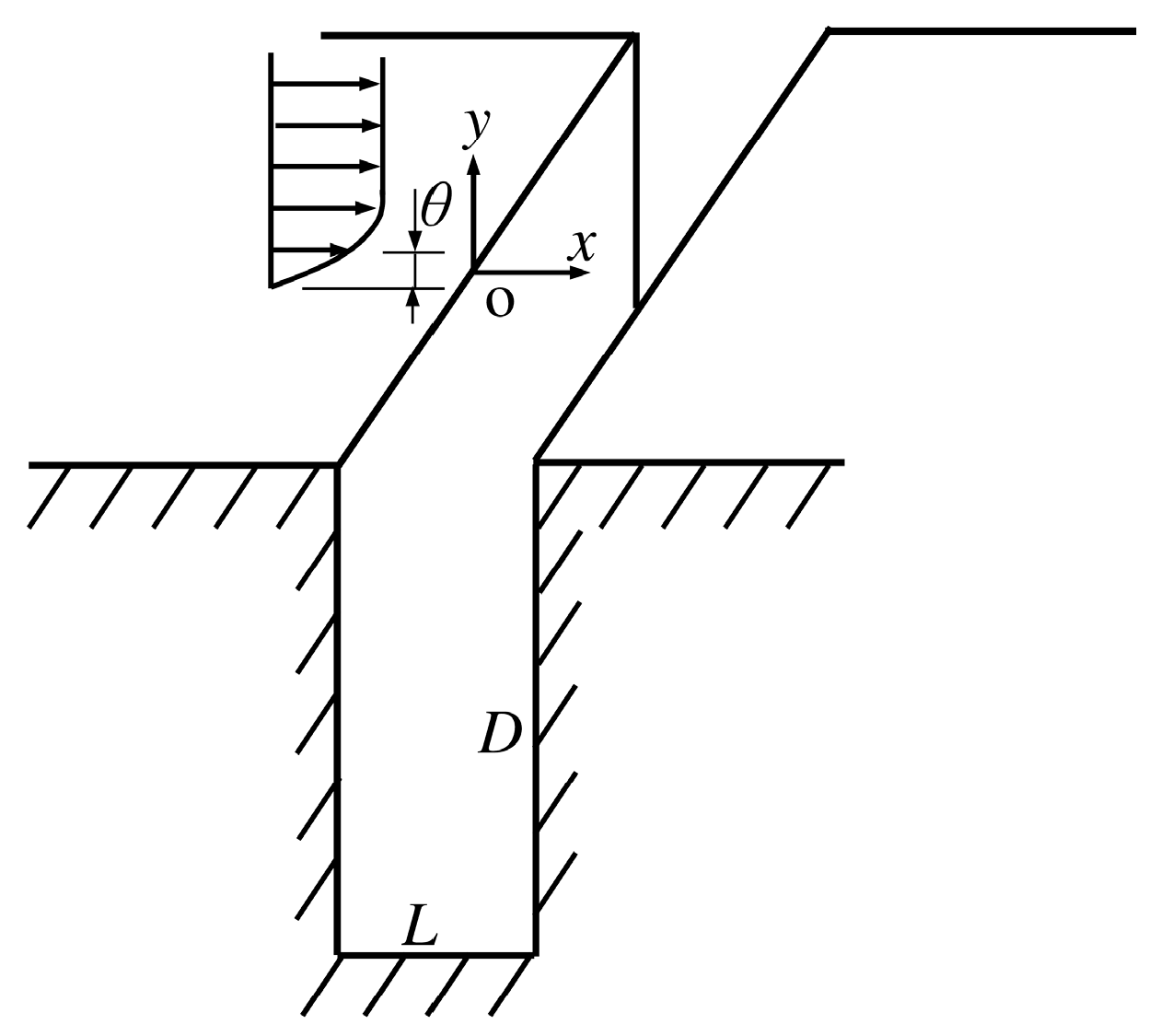
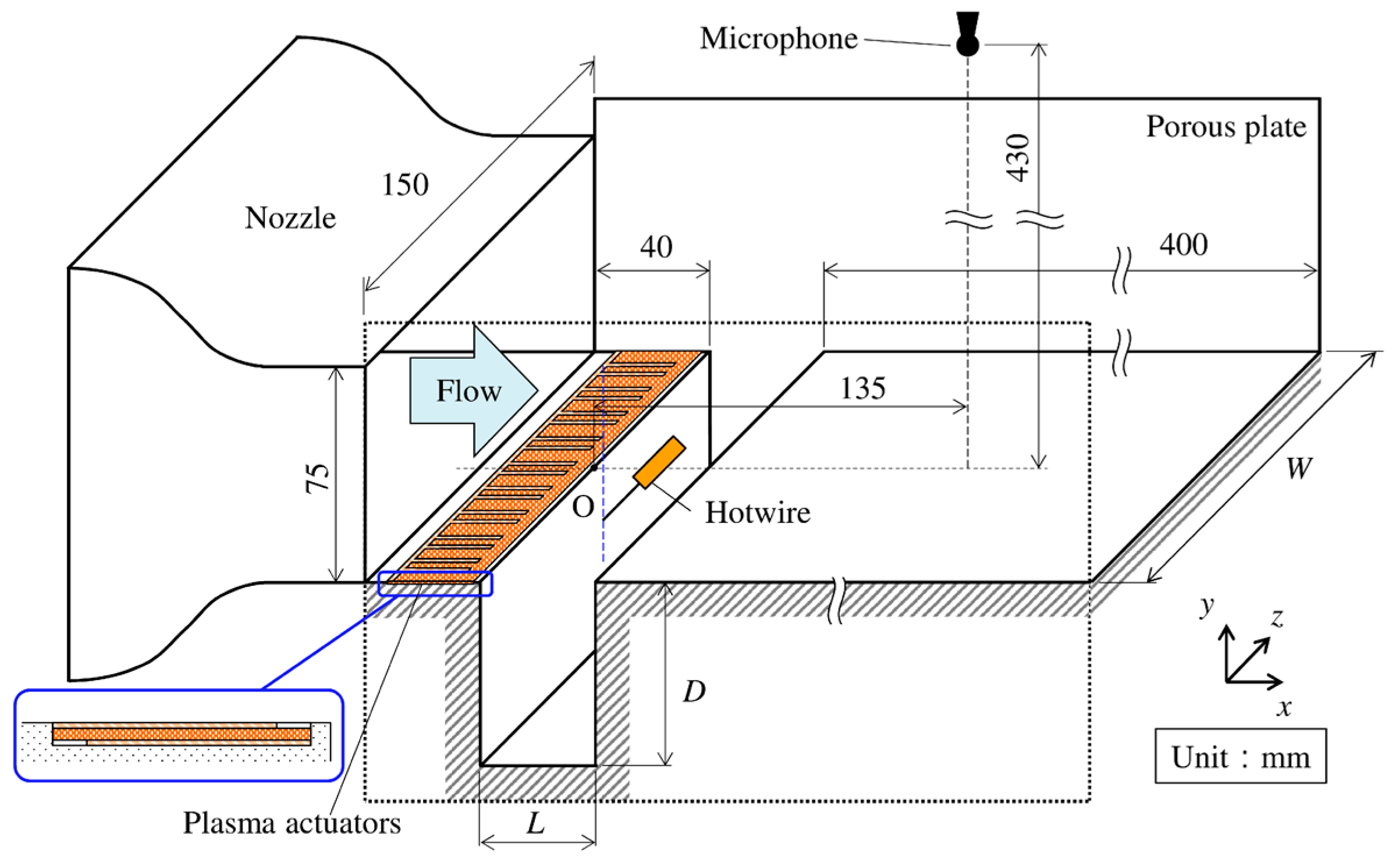
2.1.1. Wind Tunnel and Test Section
2.1.2. Measurement of Sound and Flow Fields
2.2. Test Case Descriptions
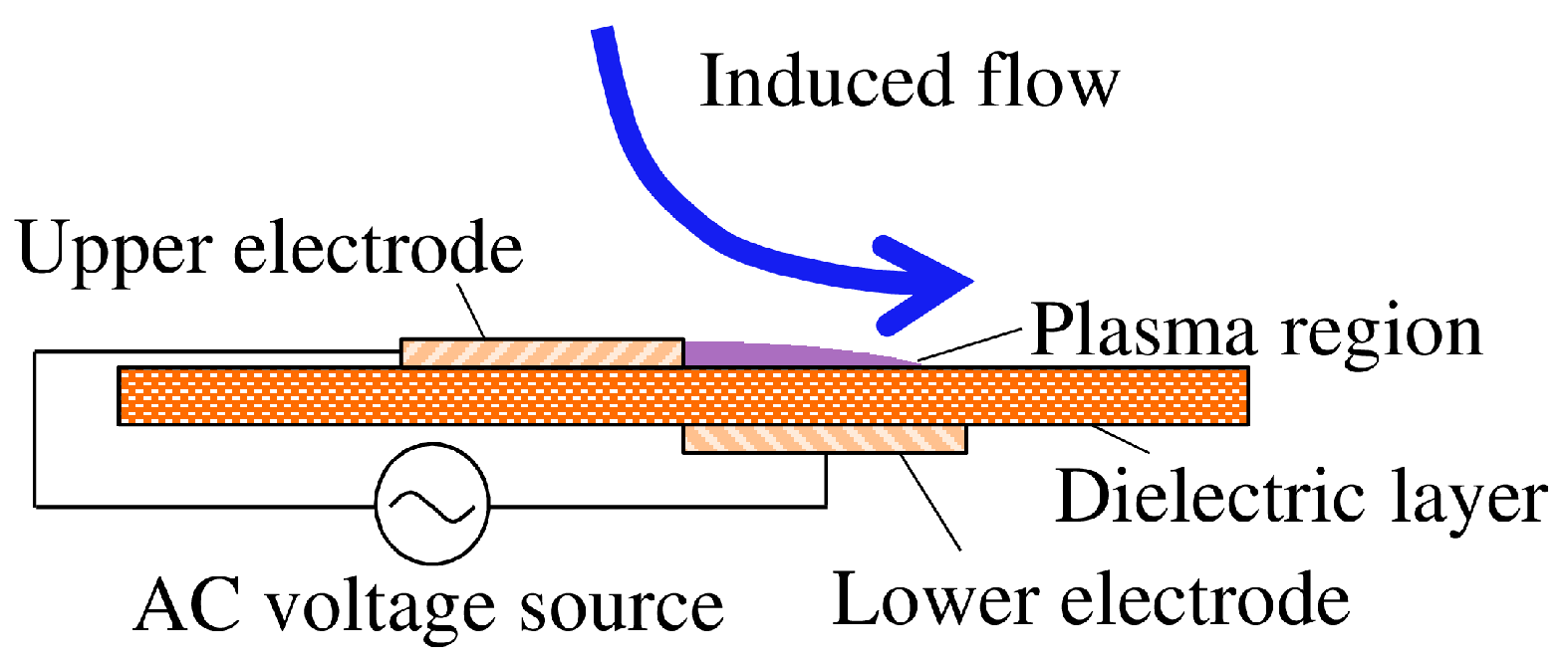
2.3. Plasma Actuator Control
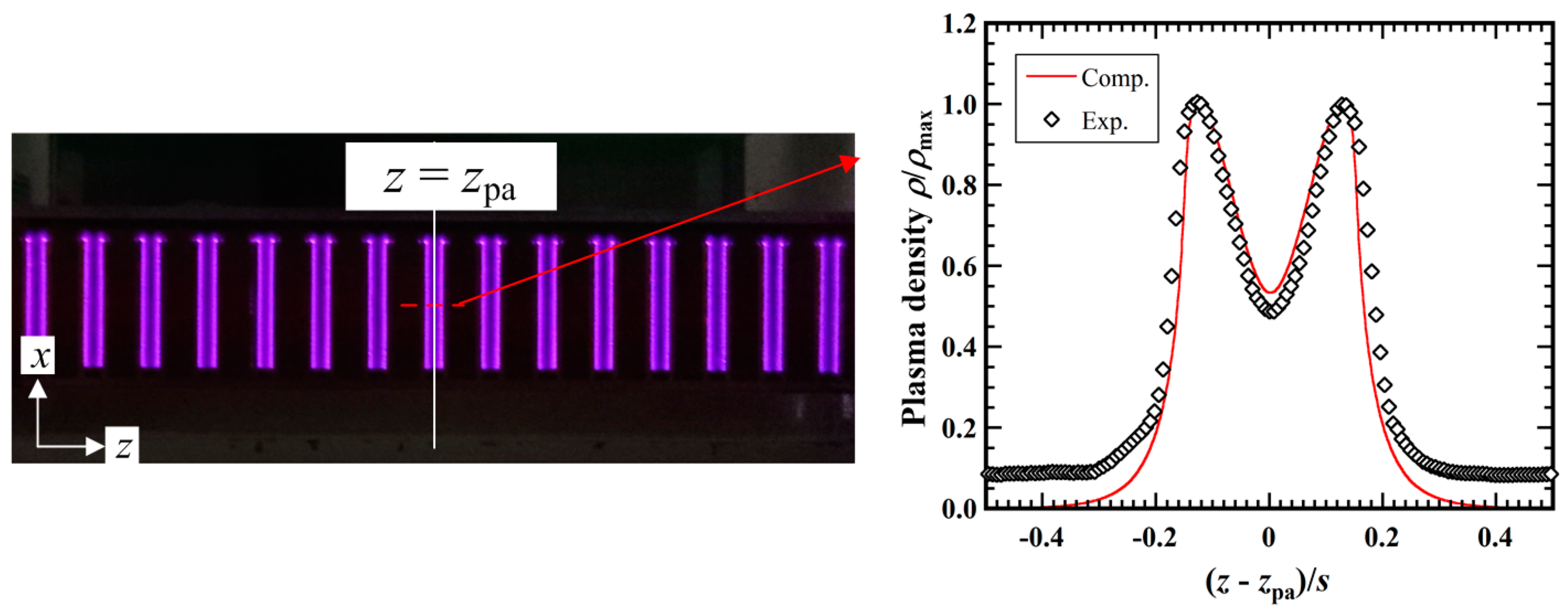
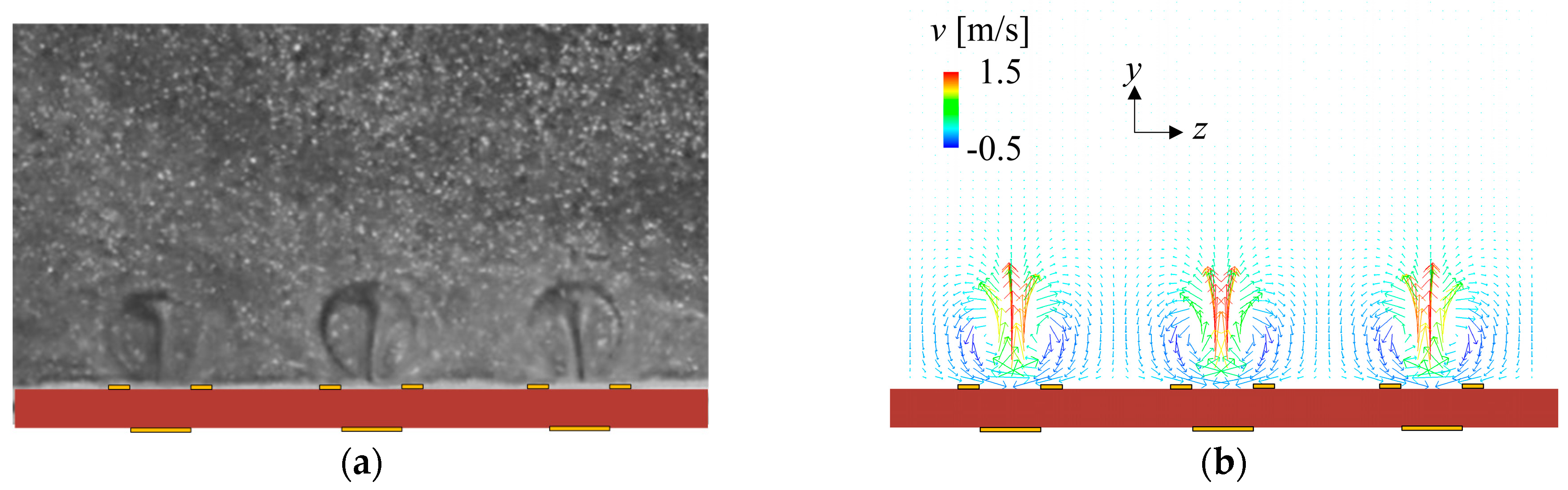
2.3.1. Control by Streamwise Plasma Actuators
2.3.2. Flush-Mounted Plasma Actuators
2.4. Numerical Simulations
2.4.1. Governing Equations and Finite-Difference Schemes
2.4.2. Body Force Exerted by Plasma Actuators
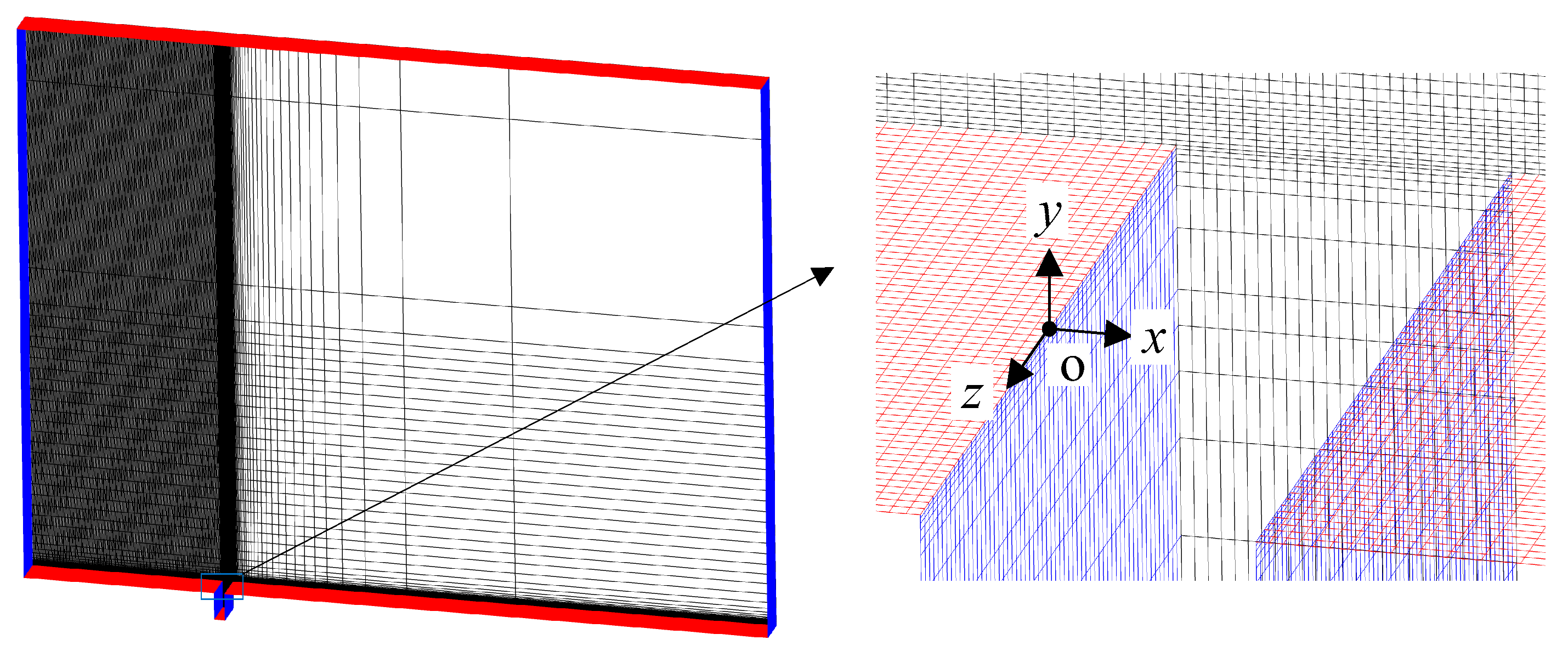
2.4.3. Computational Grid
2.4.4. Boundary Conditions
2.4.5. Prediction of the Far Acoustic Field
3. Comparison and Validation
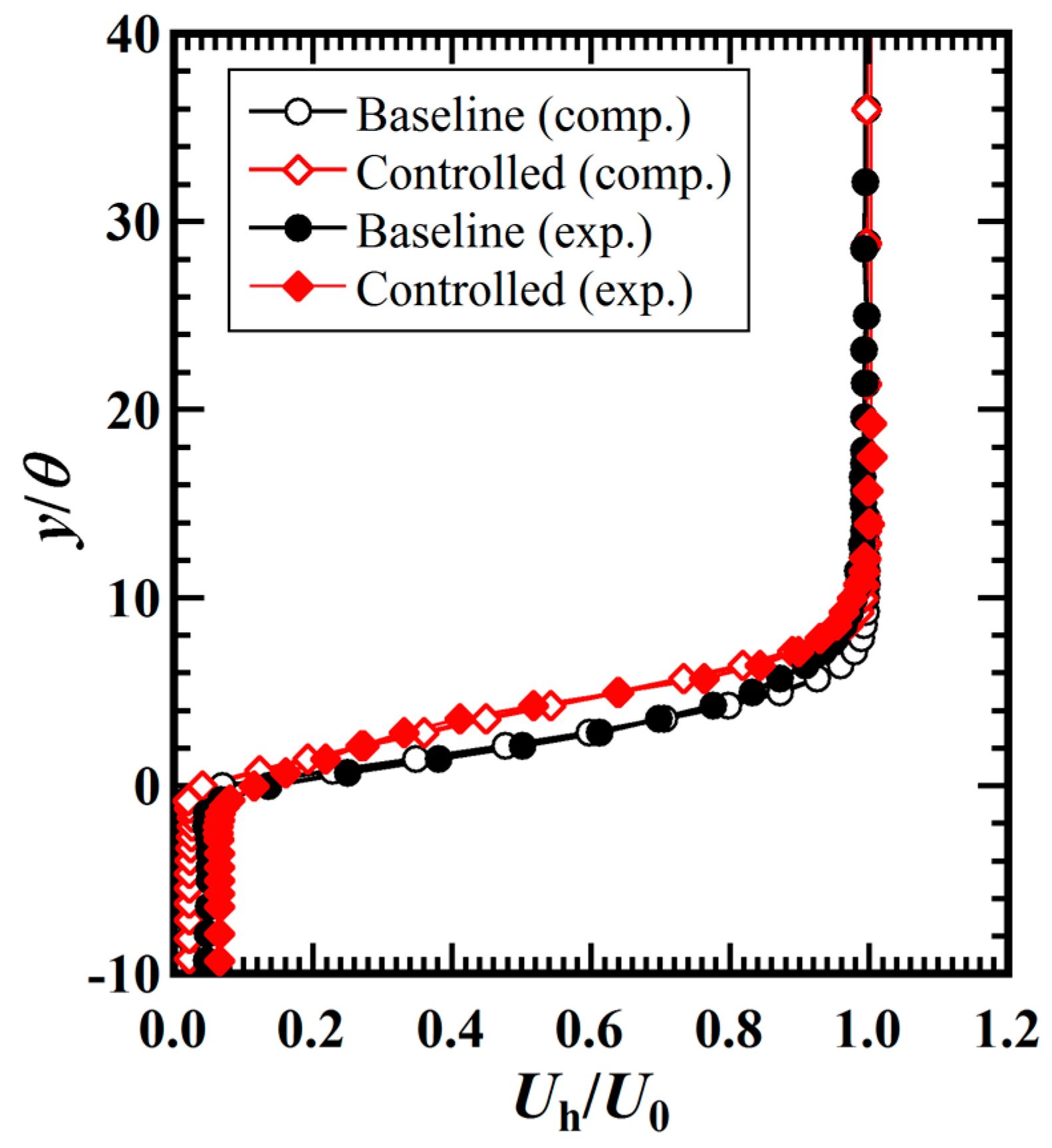
3.1. Flow Fields
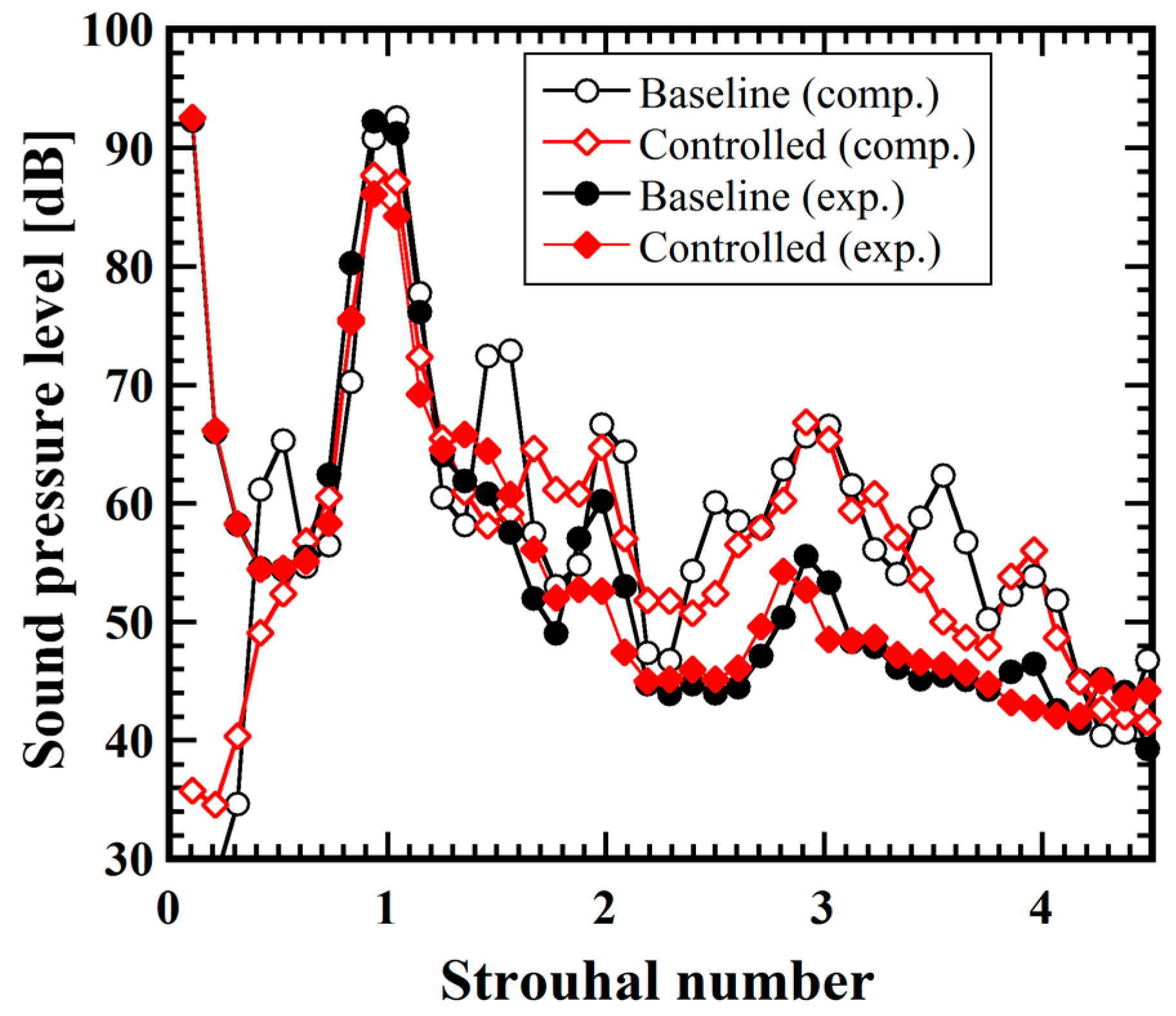
3.2. Sound-Pressure Spectra
4. Results and Discussions
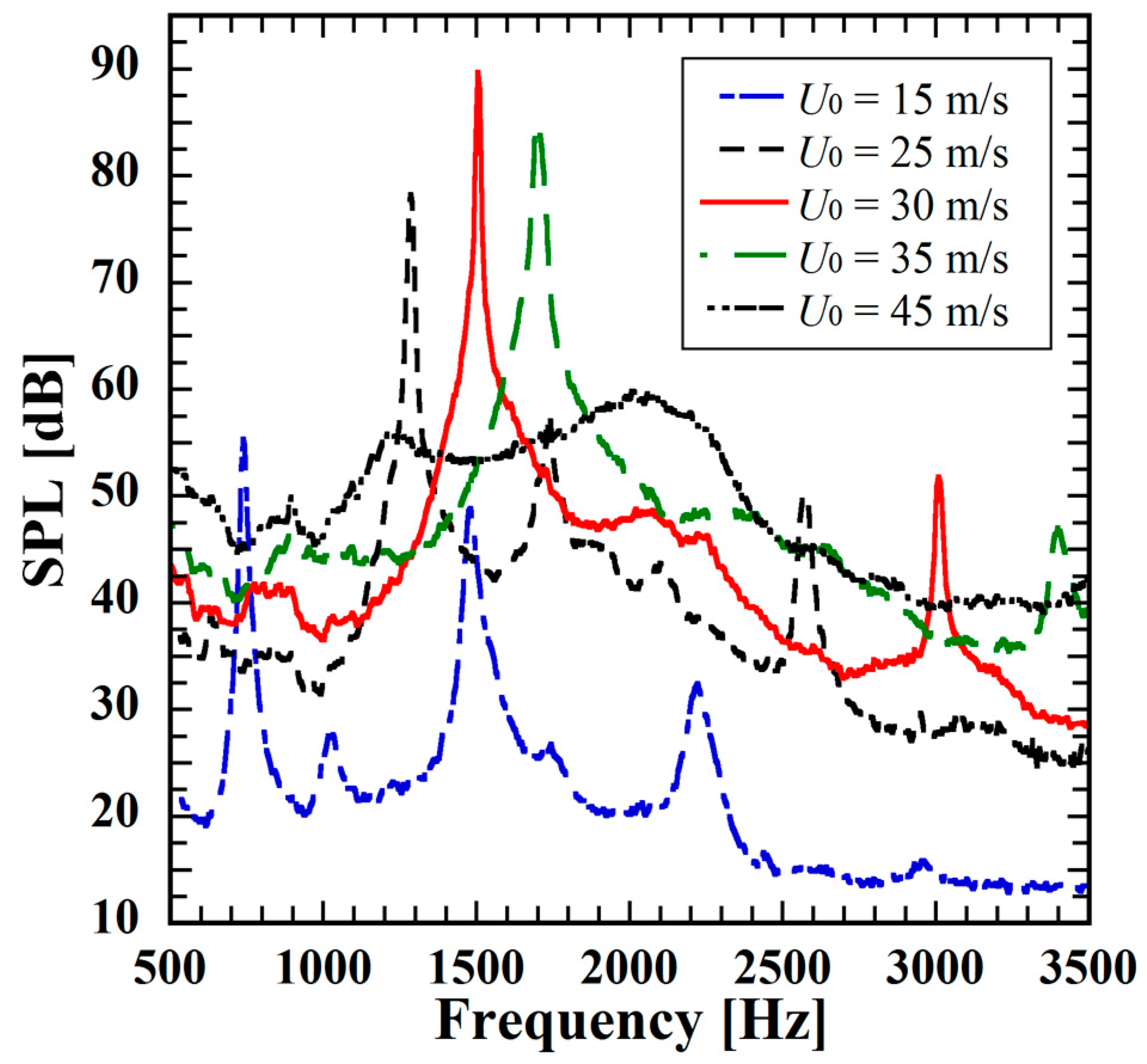
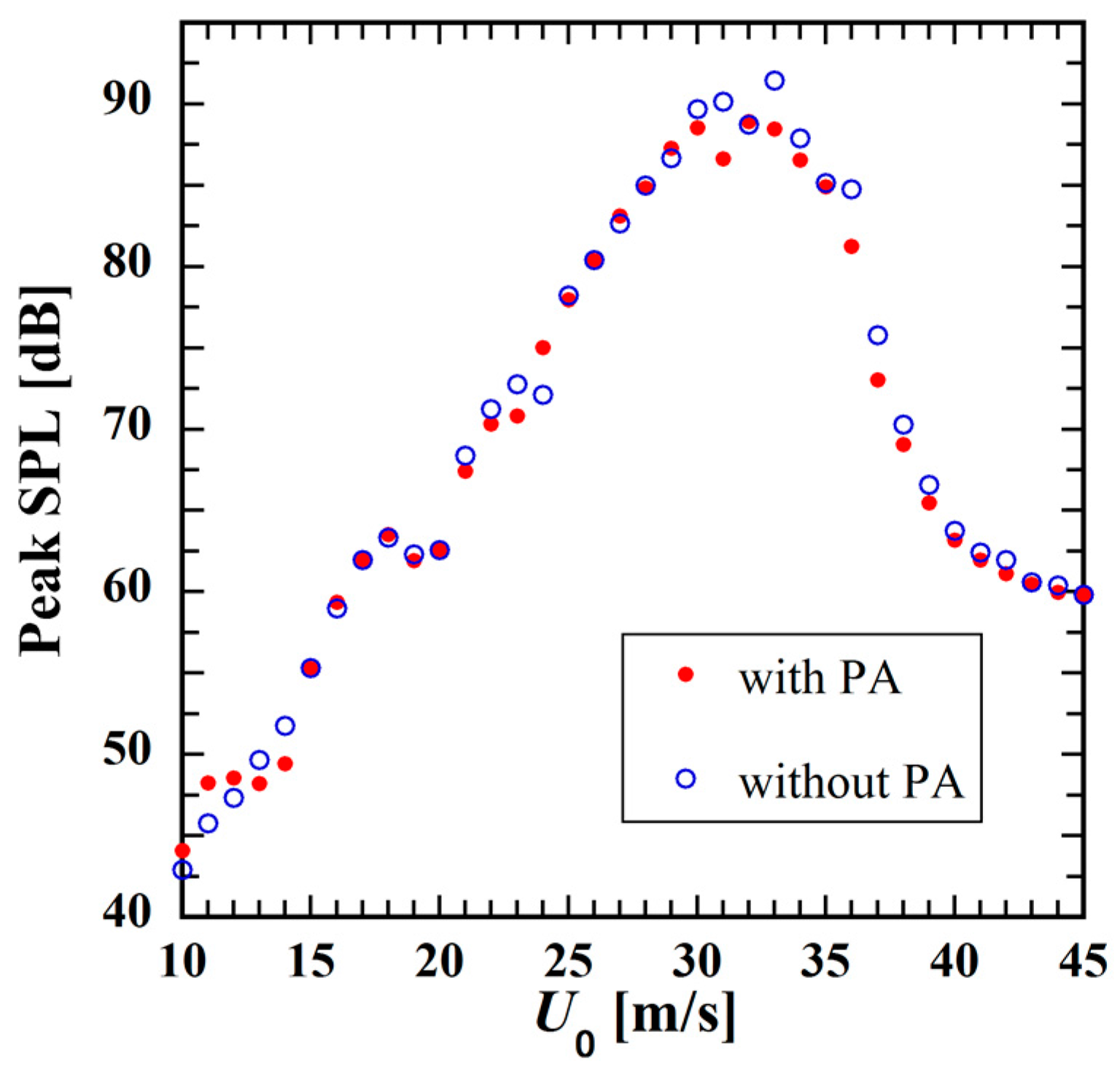
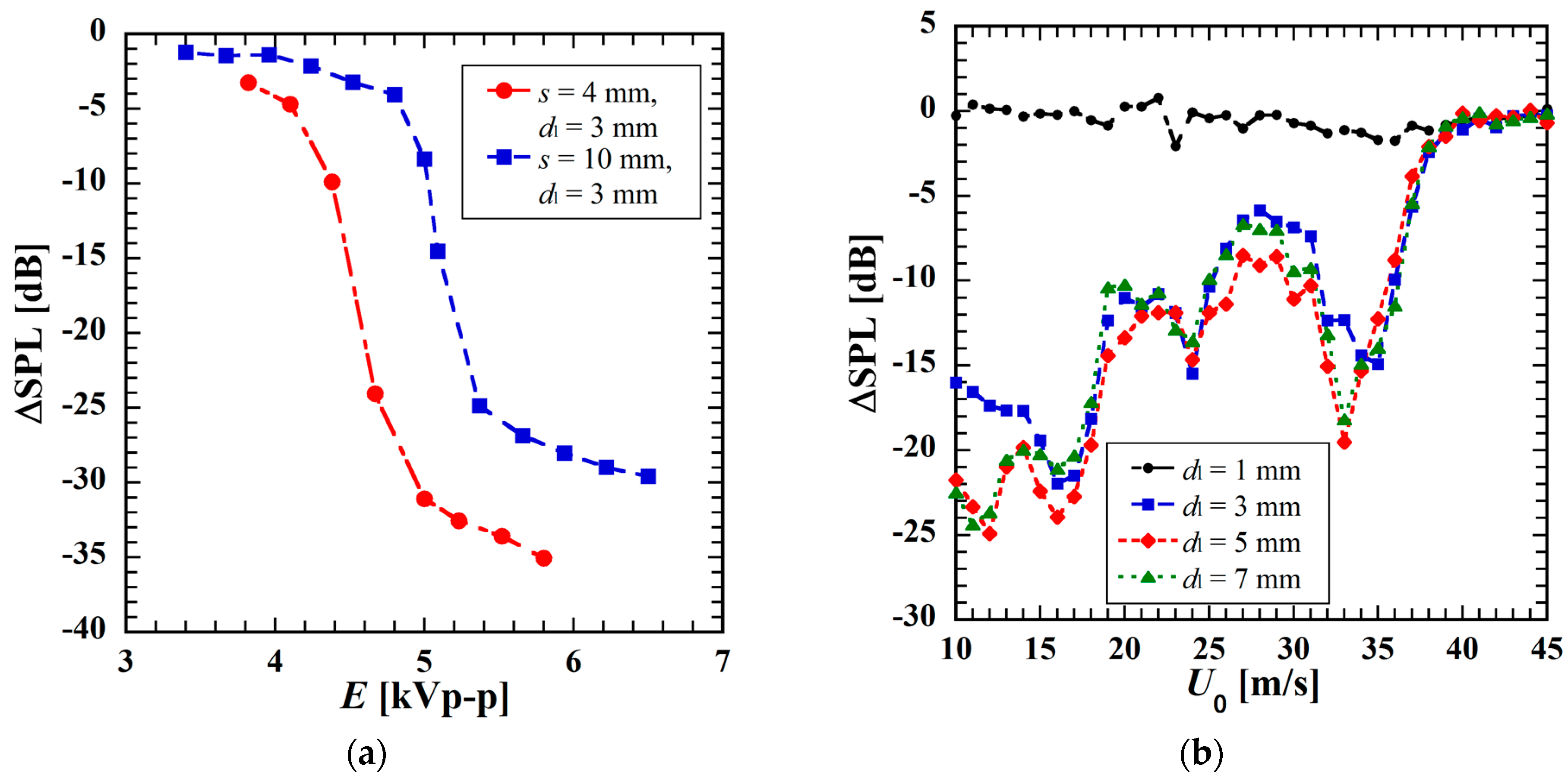
4.1. Measured Geometric Effects of Actuators on Control
4.2. Control Effects on Flow Structures and Pressure Fields
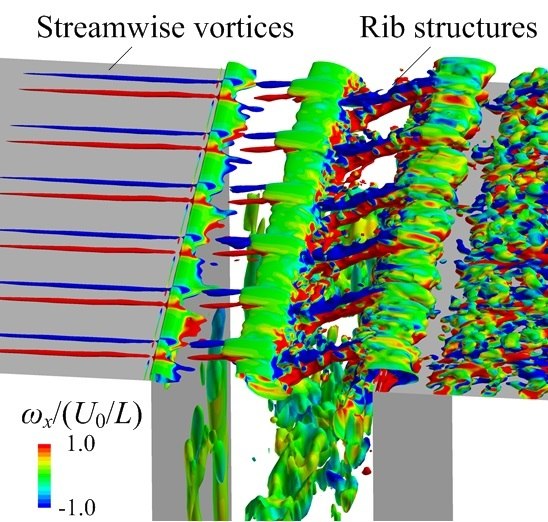
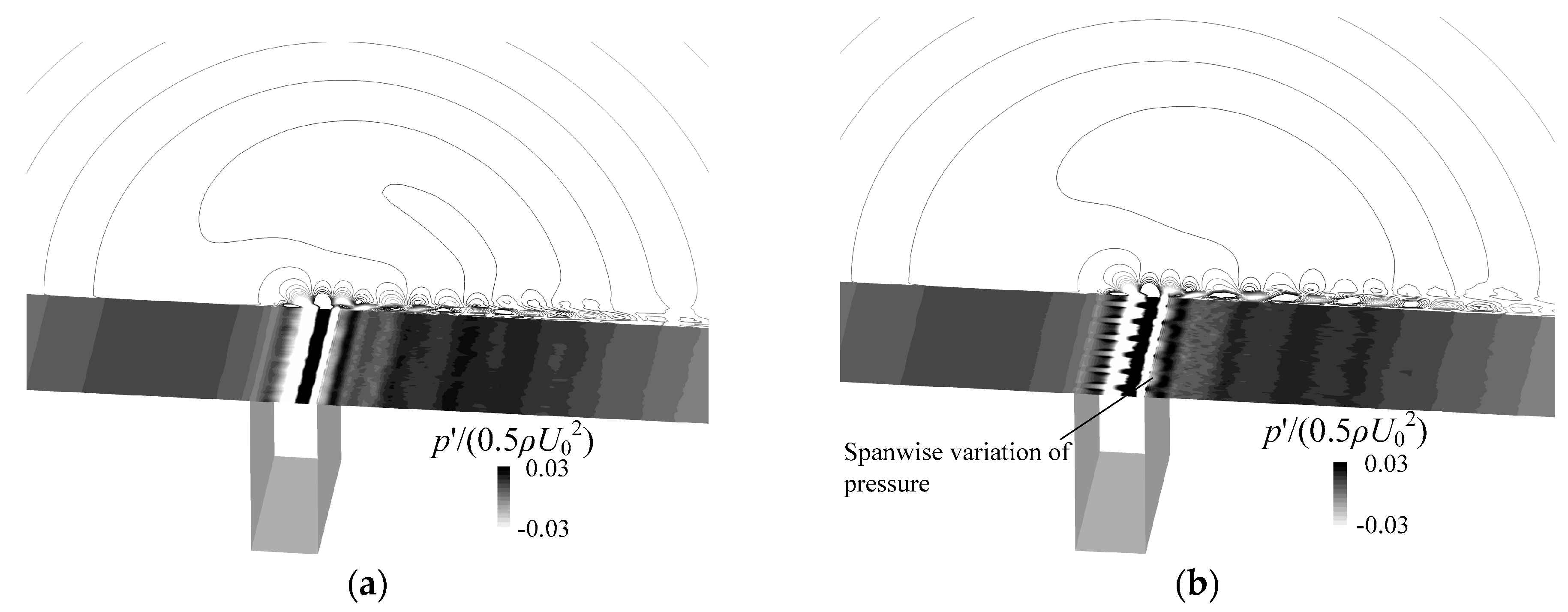
4.2.1. Vortical Structures
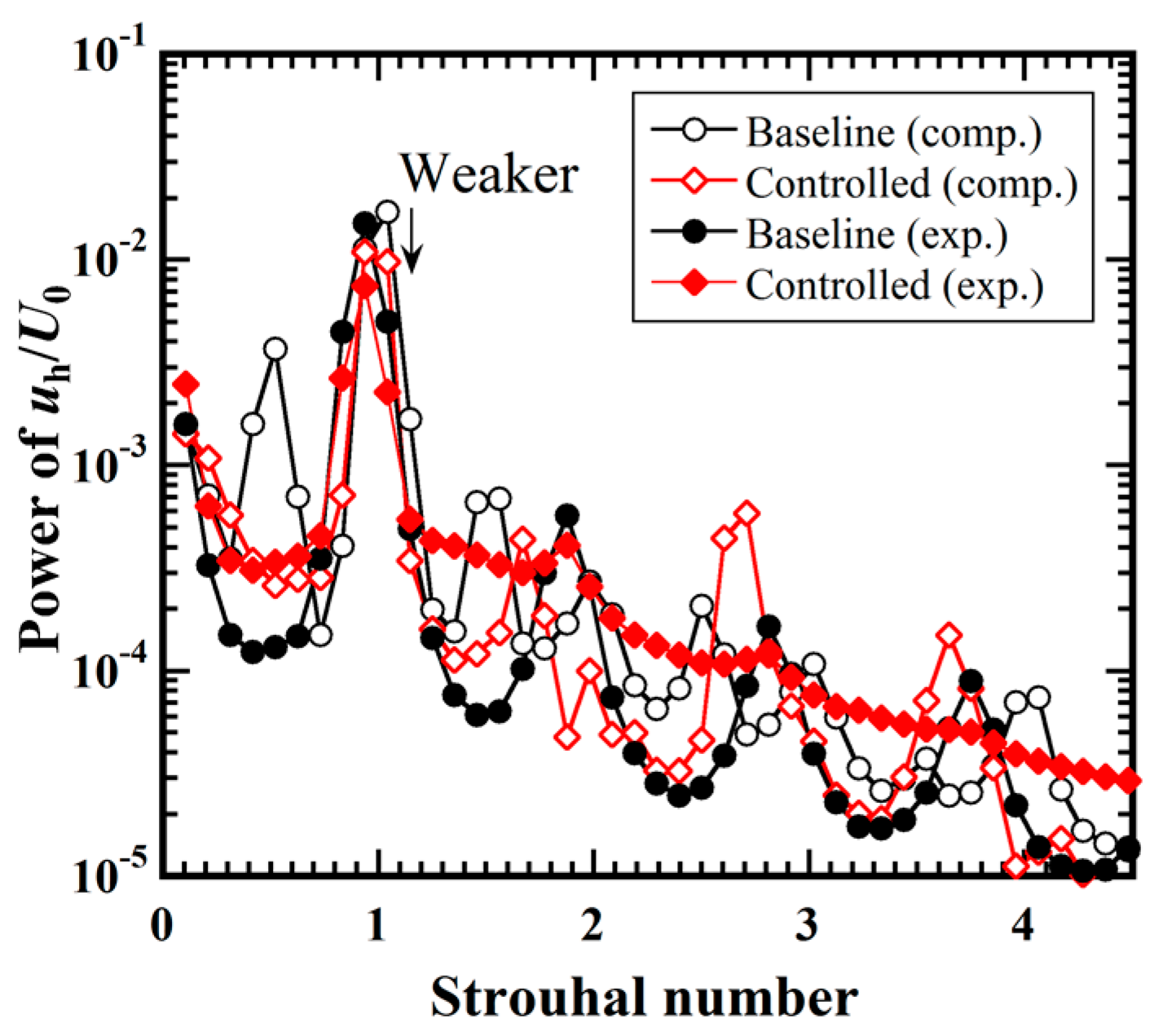
4.2.2. Power Spectra of Velocity Fluctuations
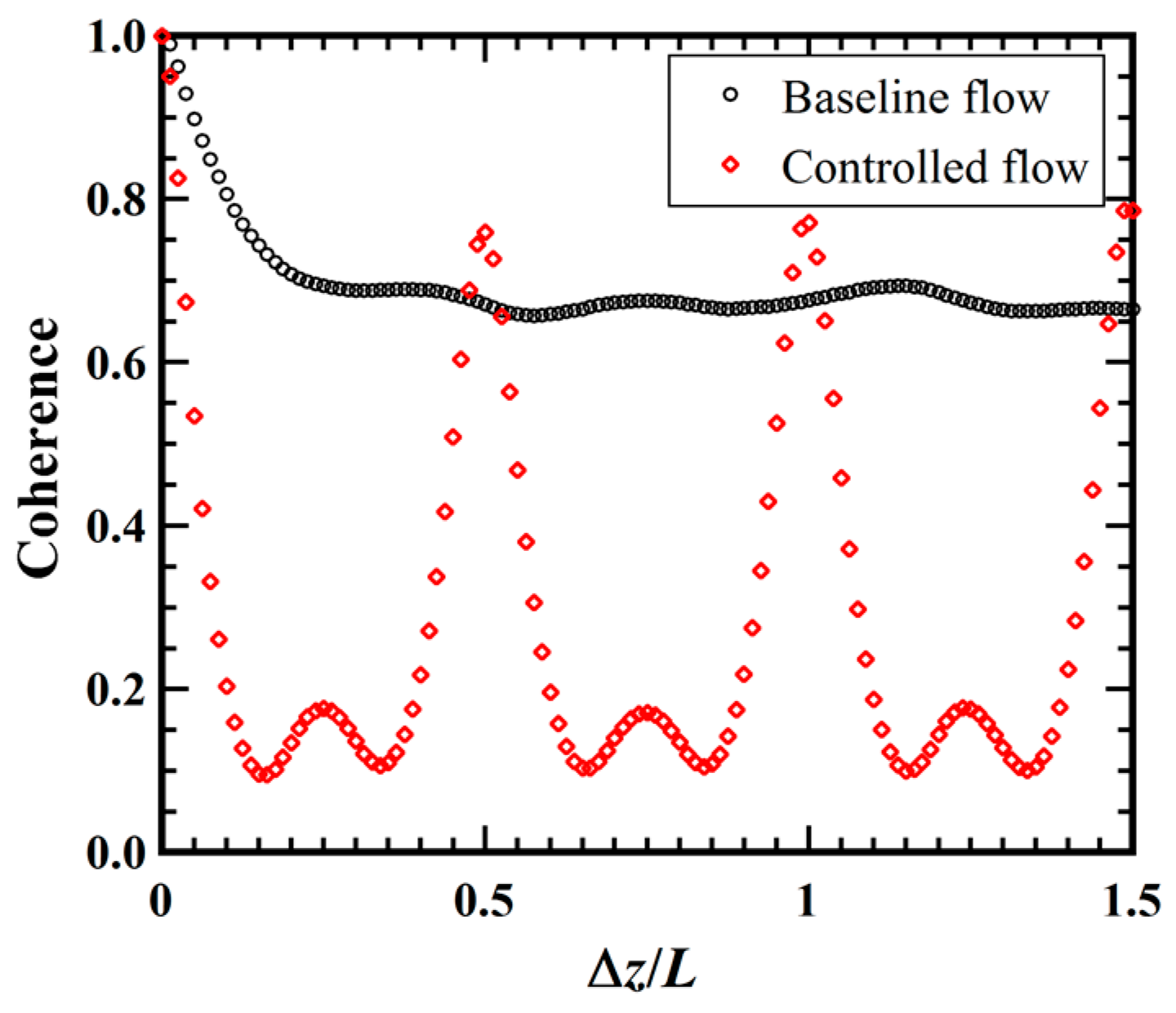
4.2.3. Spanwise Coherence
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Rossiter, J.E. Wind-Tunnel Experiments on the Flow over Rectangular Cavities at Subsonic and Transonic Speeds; No. 3438; Ministry of Aviation: New Delhi, India, 1964. Available online: http://naca.central.cranfield.ac.uk/reports/arc/rm/3438.pdf (accessed on 7 July 2017).
- Powell, A. On the edge tone. J. Acoust. Soc. Am. 1961, 33, 395–409. [Google Scholar] [CrossRef]
- East, L.F. Aerodynamically induced resonance in rectangular cavities. J. Sound Vib. 1966, 3, 277–287. [Google Scholar] [CrossRef]
- Zhuang, N.; Alvi, F.S.; Alkislar, M.B.; Shih, C. Supersonic cavity flows and their control. AIAA J. 2006, 44, 2118–2128. [Google Scholar] [CrossRef]
- Yokoyama, H.; Adachi, R.; Minato, T.; Iida, A. Experimental and Numerical Investigations on Control Methods of Cavity Tone by Blowing Jet in an Upstream Boundary Layer. SAE Int. J. Passeng. Cars Mech. Syst. 2017, 10, 13–21. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, X. Streamwise and spanwise plasma actuators for flow-induced cavity noise control. Phys. Fluids 2008, 20, 037101. [Google Scholar] [CrossRef]
- Gupta, A.D.; Roy, S. Noise control of subsonic cavity flows using plasma actuated receptive channels. J. Phys. D 2014, 47, 1–5. [Google Scholar] [CrossRef]
- Yokoyama, H.; Odawara, H.; Iida, A. Effects of freestream turbulence on cavity tone and sound source. Int. J. Aerosp. Eng. 2016, 2016, 7347106. [Google Scholar] [CrossRef]
- Kaneda, I.; Sekimoto, S.; Nonomura, T.; Asada, K.; Oyama, A.; Fujii, K. An effective three-dimensional layout of actuation body force for separation control. Int. J. Aerosp. Eng. 2012, 2012, 786960. [Google Scholar] [CrossRef]
- Lele, S.K. Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 1992, 103, 16–42. [Google Scholar] [CrossRef]
- Rizzetta, D.P.; Visbal, M.R. Large-eddy simulation of supersonic cavity flow fields including flow control. AIAA J. 2003, 41, 1452–1462. [Google Scholar] [CrossRef]
- Bogey, C.; Bailly, C. Large eddy simulations of round free jets using explicit filtering with/without dynamic Smagorinsky model. Int. J. Heat Fluid Flow 2006, 27, 603–610. [Google Scholar] [CrossRef]
- Bogey, C.; Bailly, C. Turbulence and energy budget in a self-preserving round jet: Direct evaluation using large eddy simulation. J. Fluid Mech. 2009, 627, 129–160. [Google Scholar] [CrossRef]
- Matsuura, K.; Kato, C. Large-eddy simulation of compressible transitional flows in a low-pressure turbine cascade. AIAA J. 2007, 45, 442–457. [Google Scholar] [CrossRef]
- Gaitonde, D.V.; Visbal, M.R. Pade-type higher-order boundary filters for the Navier-Stokes equations. AIAA J. 2000, 38, 2103–2112. [Google Scholar] [CrossRef]
- Yokoyama, H.; Kato, C. Fluid-acoustic interactions in self-sustained oscillations in turbulent cavity flows, I. Fluid-dynamic oscillations. Phys. Fluids 2009, 21, 105103. [Google Scholar] [CrossRef]
- Suzen, Y.B.; Huang, P.G.; Jacob, J.D.; Ashpis, D.E. Numerical Simulations of Plasma Based Flow Control Applications. In Proceedings of the 35th Fluid Dynamics Conference and Exhibition, Toronto, ON, Canada, 6–9 June 2005; No. AIAA 2005-4633. pp. 1–11. [Google Scholar] [CrossRef]
- Kusumoto, M.; Yokoyama, H.; Angland, D.; Iida, A. Control of aerodynamic noise from cascade of flat plates by plasma actuators. Trans. JSME 2017, 83, 16-00364. (In Japanese) [Google Scholar] [CrossRef]
- Forte, M.; Jolibois, J.; Pons, J.; Moreau, E.; Touchard, G.; Cazalens, M. Optimization of a dielectric barrier discharge actuator by stationary and non-stationary measurements of the induced flow velocity: Application to airflow control. Exp. Fluids 2007, 43, 917–928. [Google Scholar] [CrossRef]
- Thompson, K.W. Time dependent boundary conditions for hyperbolic systems. J. Comput. Phys. 1987, 68, 1–24. [Google Scholar] [CrossRef]
- Poinsot, T.J.; Lele, S.K. Boundary conditions for direct simulations of compressible viscous flows. J. Comput. Phys. 1992, 101, 104–129. [Google Scholar] [CrossRef]
- Kim, J.W.; Lee, D.J. Generalized characteristic boundary conditions for computational aeroacoustics. AIAA J. 1987, 38, 2040–2049. [Google Scholar] [CrossRef]
- Williams, J.E.F.; Hawkings, D.L. Sound generation by turbulence and surfaces in arbitrary motion. Philos. Trans. R. Soc. A 1968, 264, 321–342. [Google Scholar] [CrossRef]
- Lyrintzis, A.S. Surface integral methods in computational aeroacoustics—From the (CFD) near- field to the (Acoustic) far- field. Int. J. Aeroacoust. 2003, 2, 95–128. [Google Scholar] [CrossRef]
- Shur, M.L.; Spalart, P.R.; Strelets, M.K. Noise prediction for increasingly complex jets. Part I: Methods and tests. Int. J. Aeroacoust. 2005, 4, 213–246. [Google Scholar] [CrossRef]
- Yokoyama, H.; Kitamiya, K.; Iida, A. Flows around cascade of flat plates with acoustic resonance. Phys. Fluids 2013, 25, 106104. [Google Scholar] [CrossRef]
- Enloe, C.L.; McLaughlin, T.E.; VanDyken, R.D.; Kachner, K.D.; Jumper, E.J.; Corke, T.C.; Post, M.; Haddad, O. Mechanisms and Responses of a Single Dielectric Barrier Plasma Actuator: Geometric Effects. AIAA J. 2004, 42, 595–604. [Google Scholar] [CrossRef]





© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yokoyama, H.; Tanimoto, I.; Iida, A. Experimental Tests and Aeroacoustic Simulations of the Control of Cavity Tone by Plasma Actuators. Appl. Sci. 2017, 7, 790. https://doi.org/10.3390/app7080790
Yokoyama H, Tanimoto I, Iida A. Experimental Tests and Aeroacoustic Simulations of the Control of Cavity Tone by Plasma Actuators. Applied Sciences. 2017; 7(8):790. https://doi.org/10.3390/app7080790
Chicago/Turabian StyleYokoyama, Hiroshi, Isamu Tanimoto, and Akiyoshi Iida. 2017. "Experimental Tests and Aeroacoustic Simulations of the Control of Cavity Tone by Plasma Actuators" Applied Sciences 7, no. 8: 790. https://doi.org/10.3390/app7080790
APA StyleYokoyama, H., Tanimoto, I., & Iida, A. (2017). Experimental Tests and Aeroacoustic Simulations of the Control of Cavity Tone by Plasma Actuators. Applied Sciences, 7(8), 790. https://doi.org/10.3390/app7080790