Bonded-Particle Model with Nonlinear Elastic Tensile Stiffness for Rock-Like Materials
Abstract
:Featured Application
Abstract
1. Introduction
2. Method Description
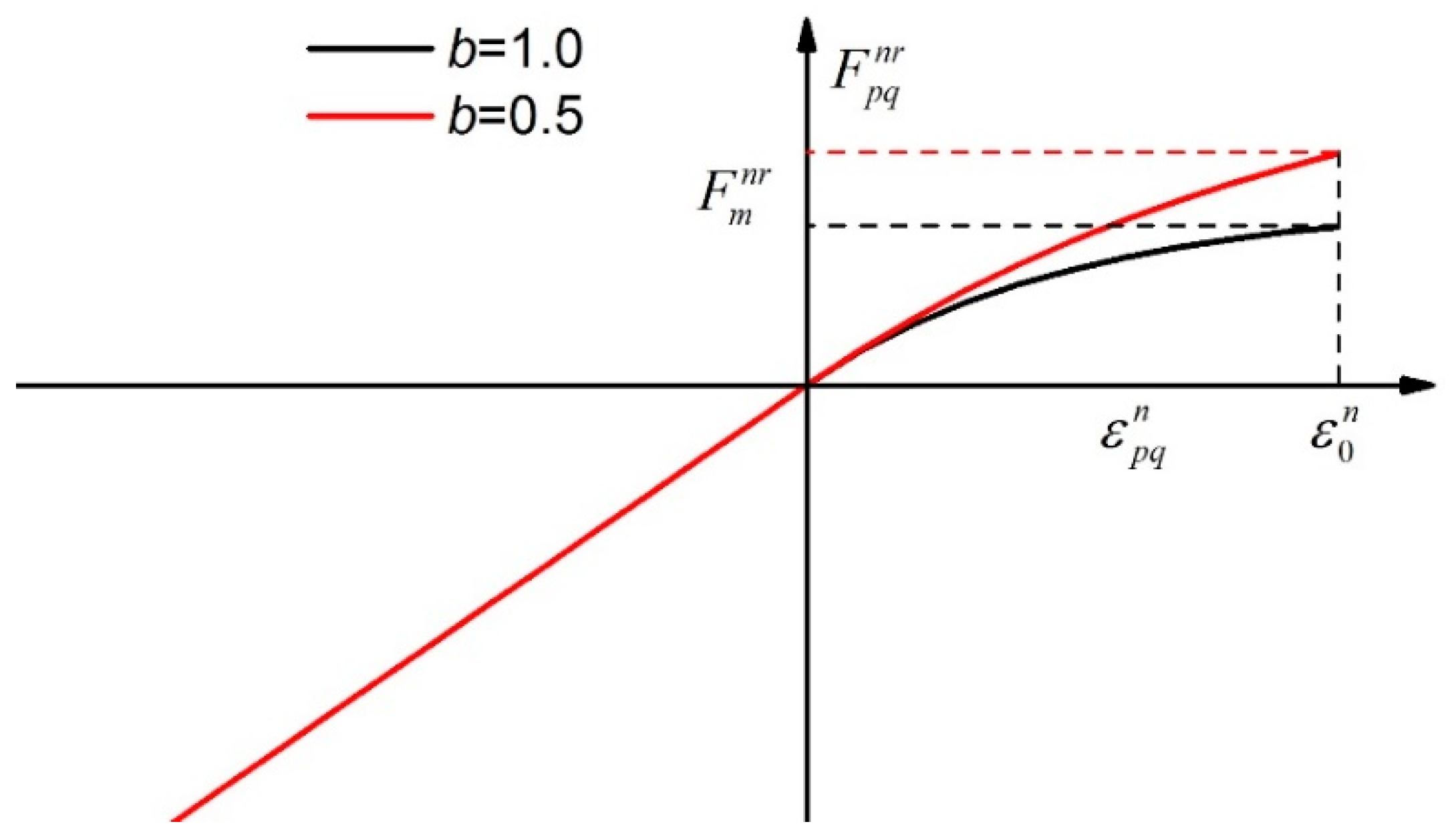
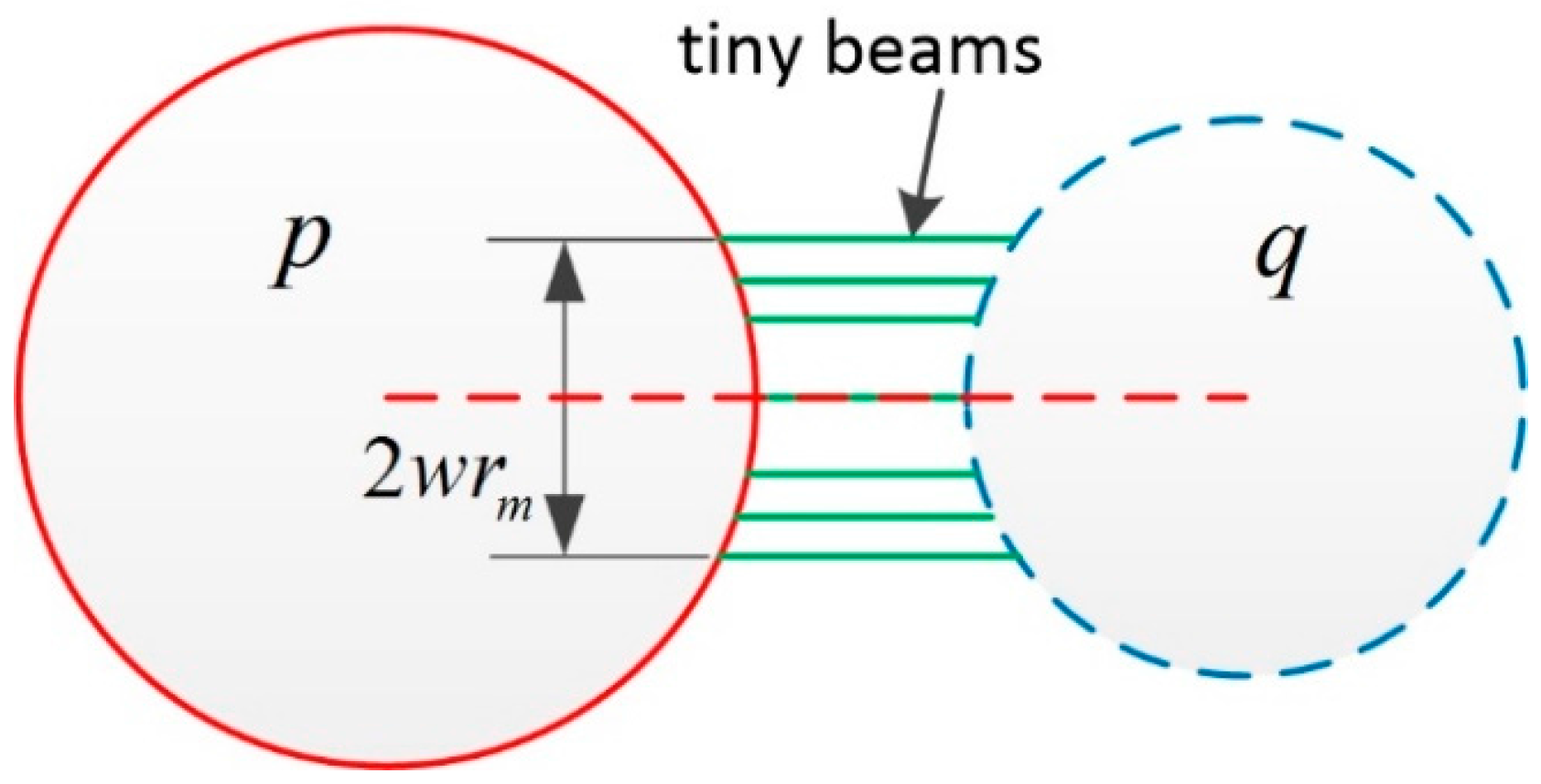
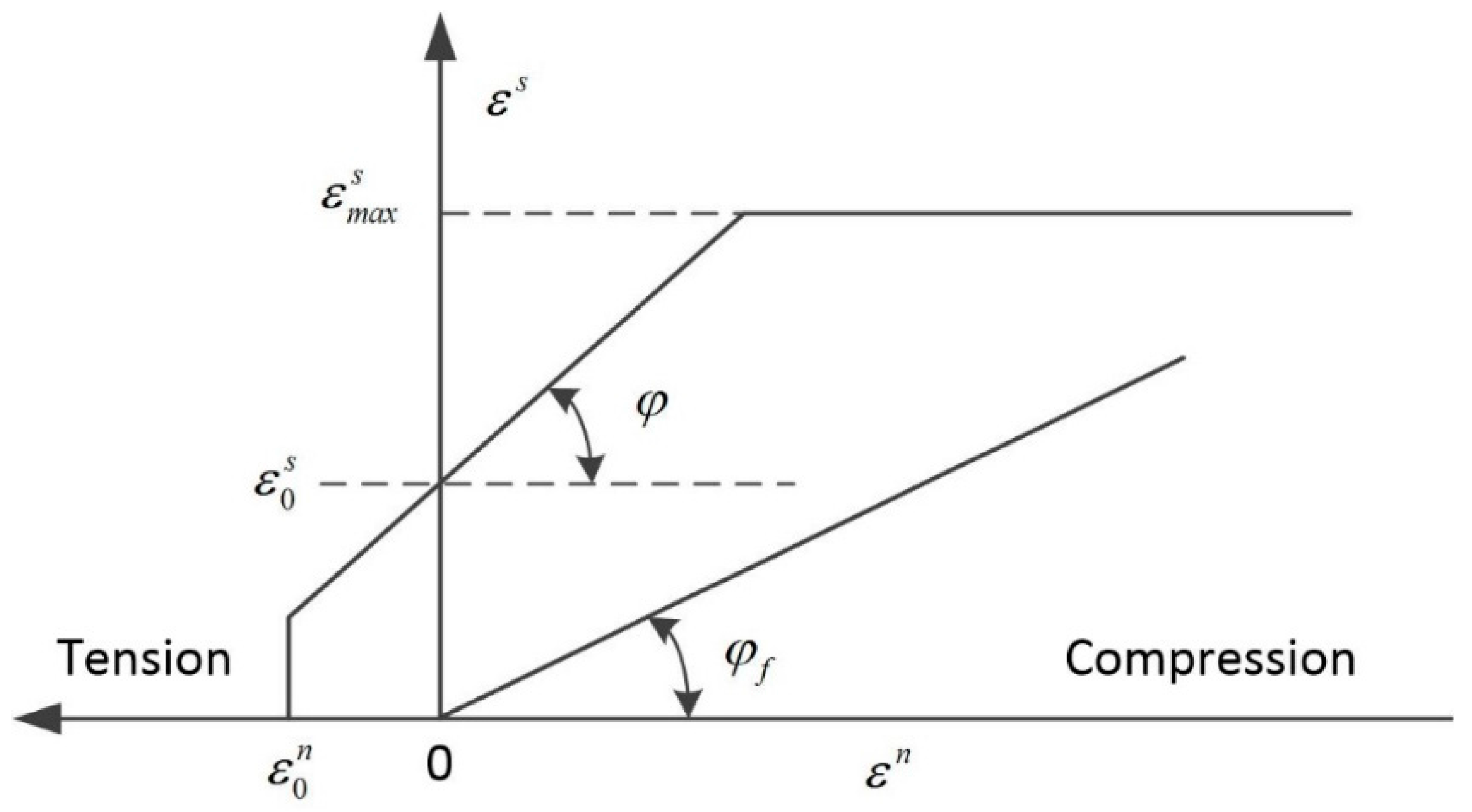
2.1. Contact Model
2.2. Numerical Simulation Model
2.3. Dimensionless Parameters in NET-BPM
2.4. Specimen Preparation
3. Relationship between Micro and Macro Parameter
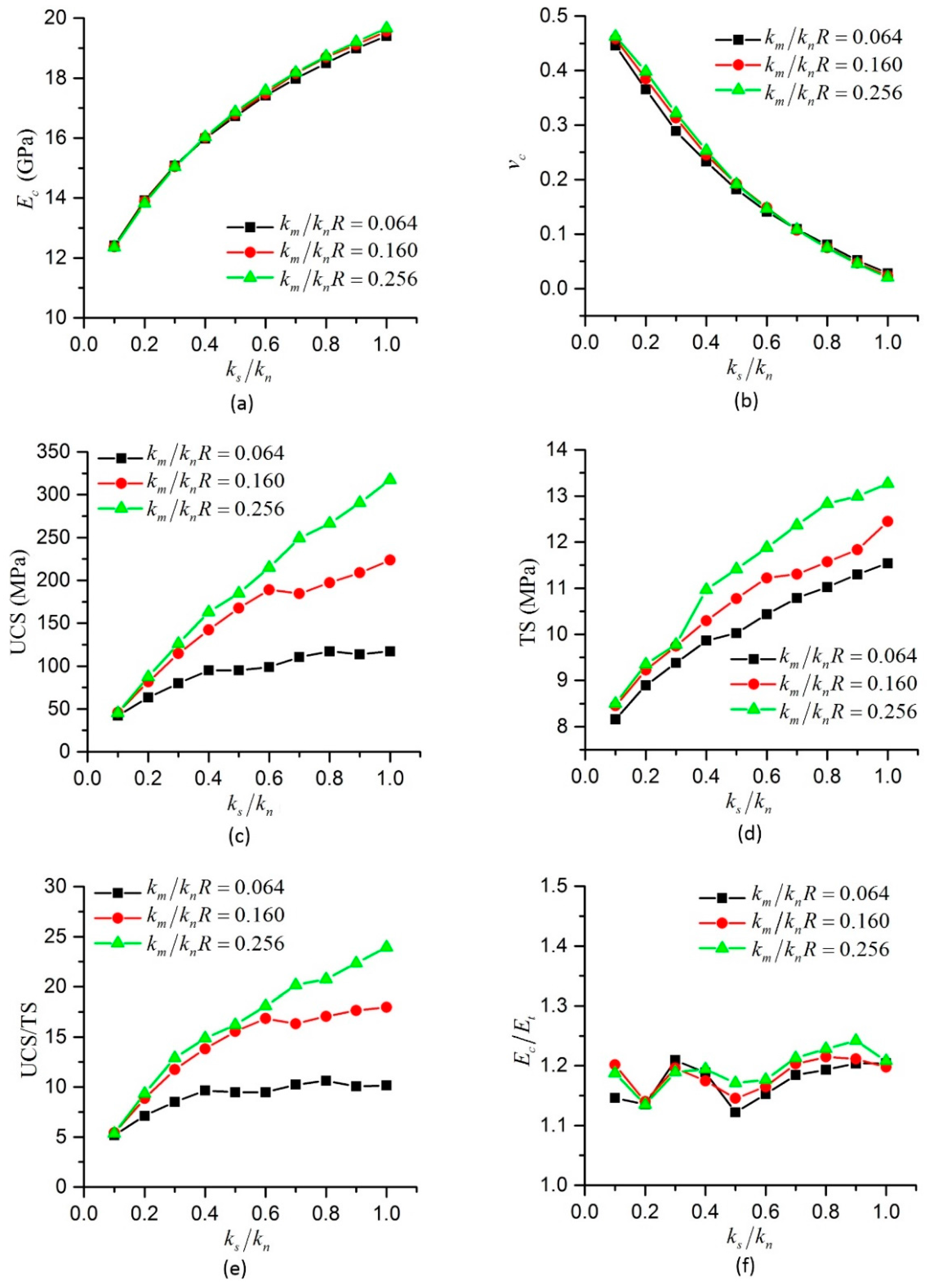
3.1. Effect of Bond Stiffness on Macro Parameters
3.2. Effect of Shape Coefficient on Macro Parameters
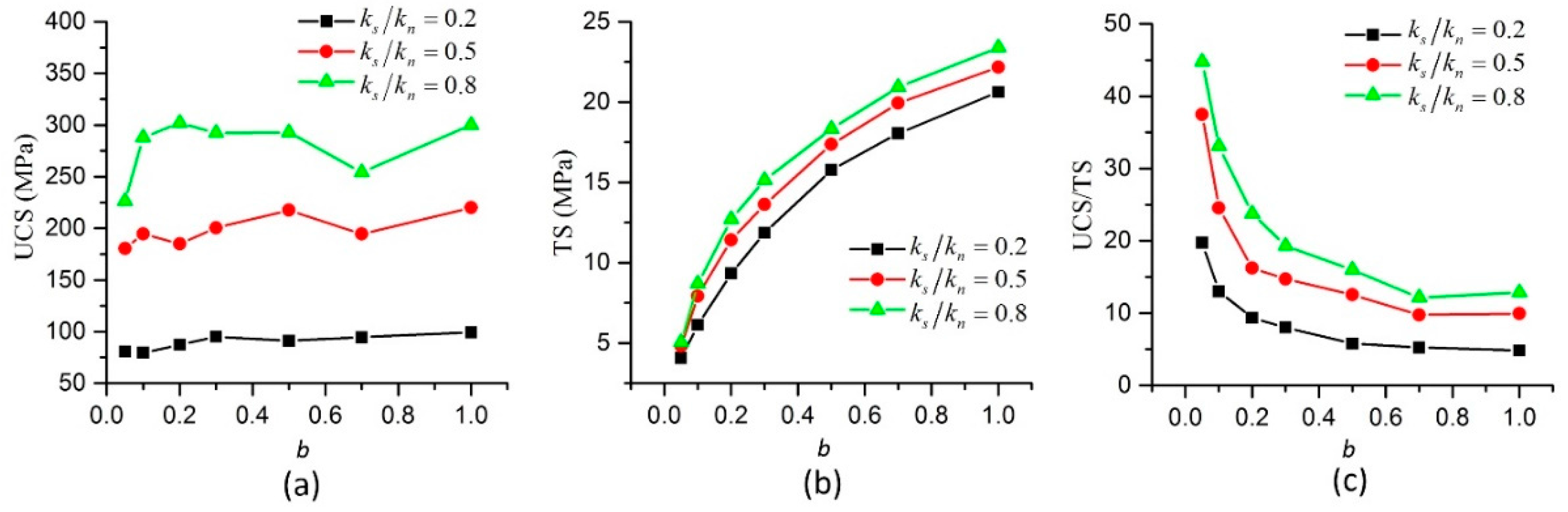
3.3. Effect of Bond Width Coefficient on Macro Parameters
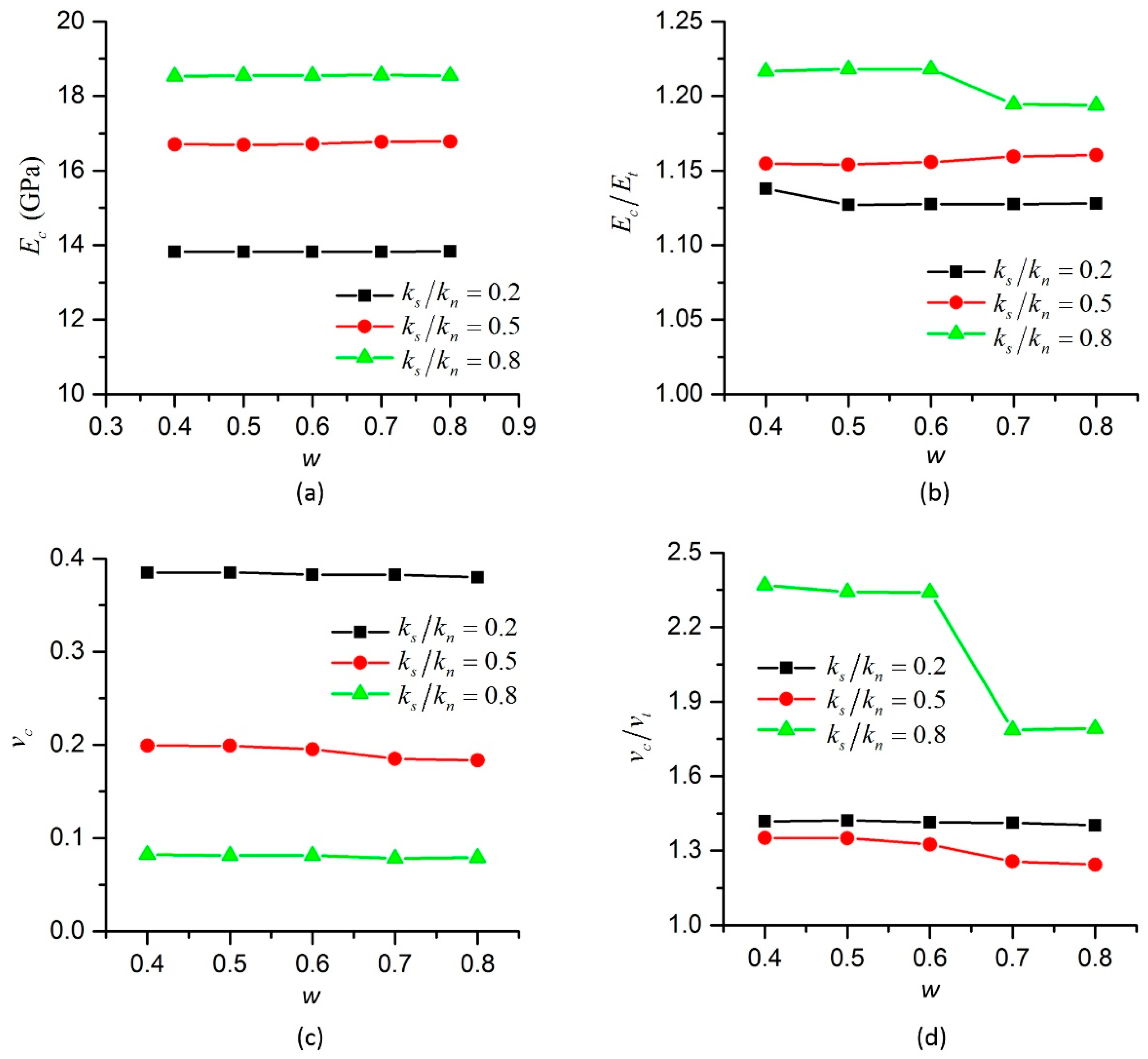
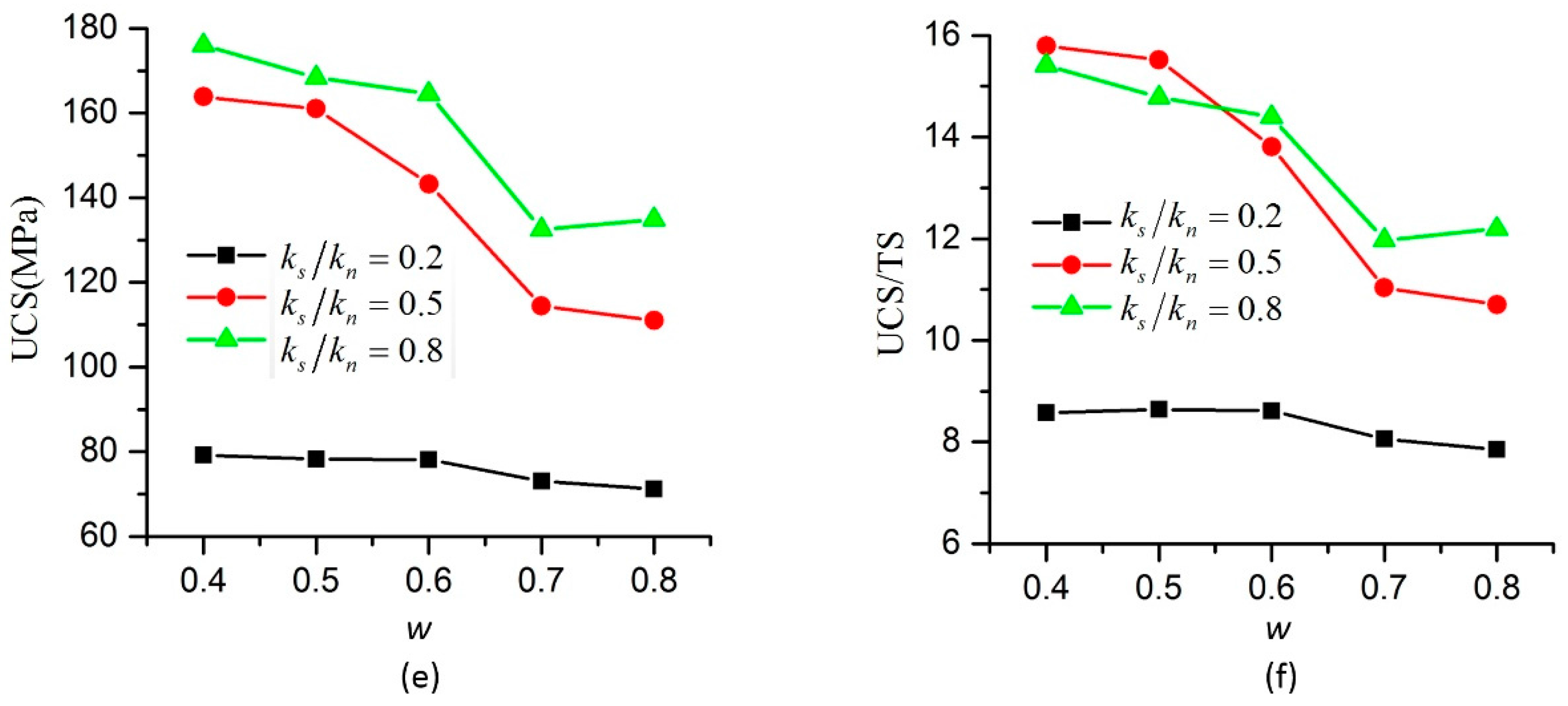
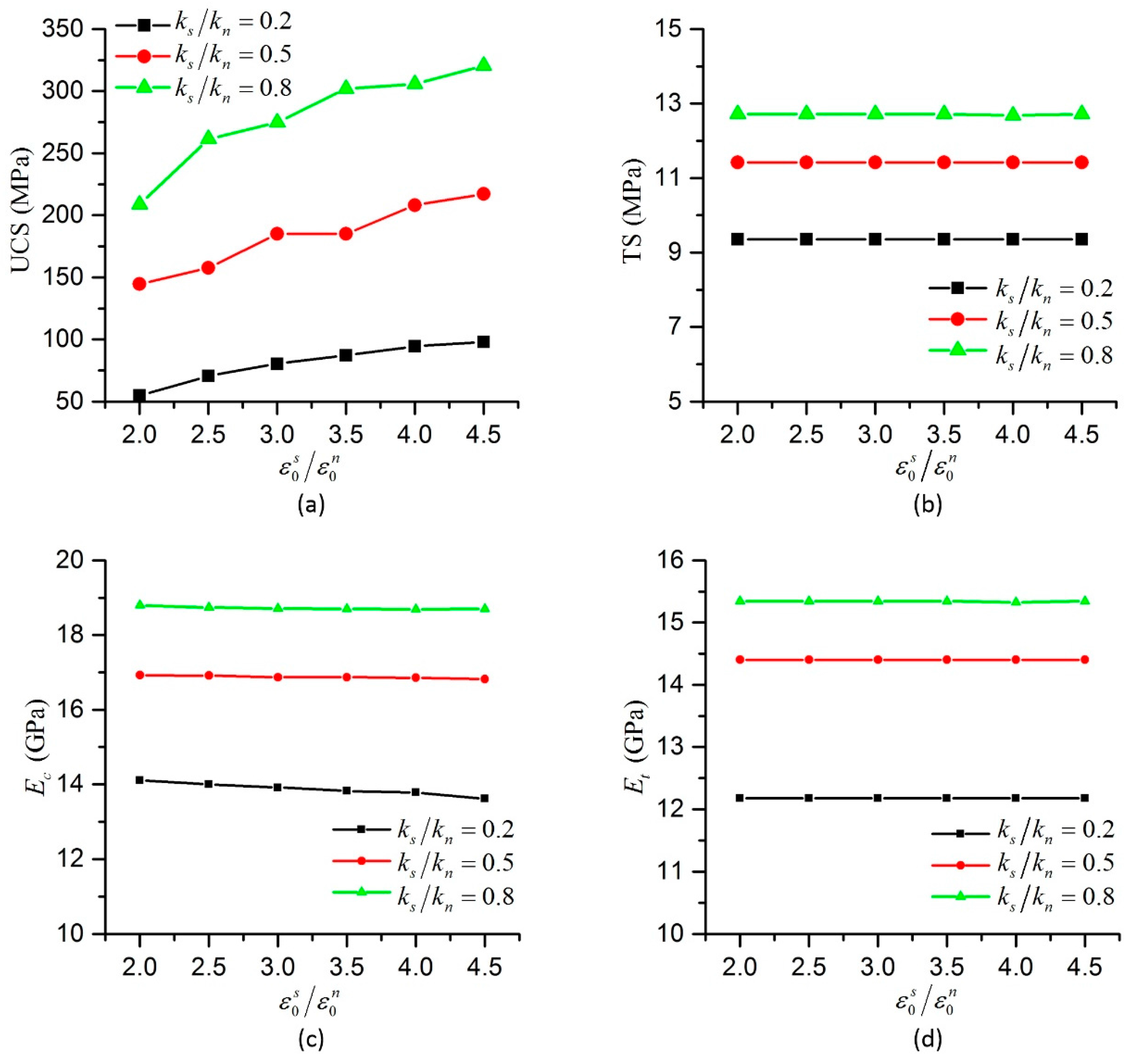
3.4. Effect of Ultimate Pure Shear Strain on Macro Parameters
4. Application of the NET-BPM
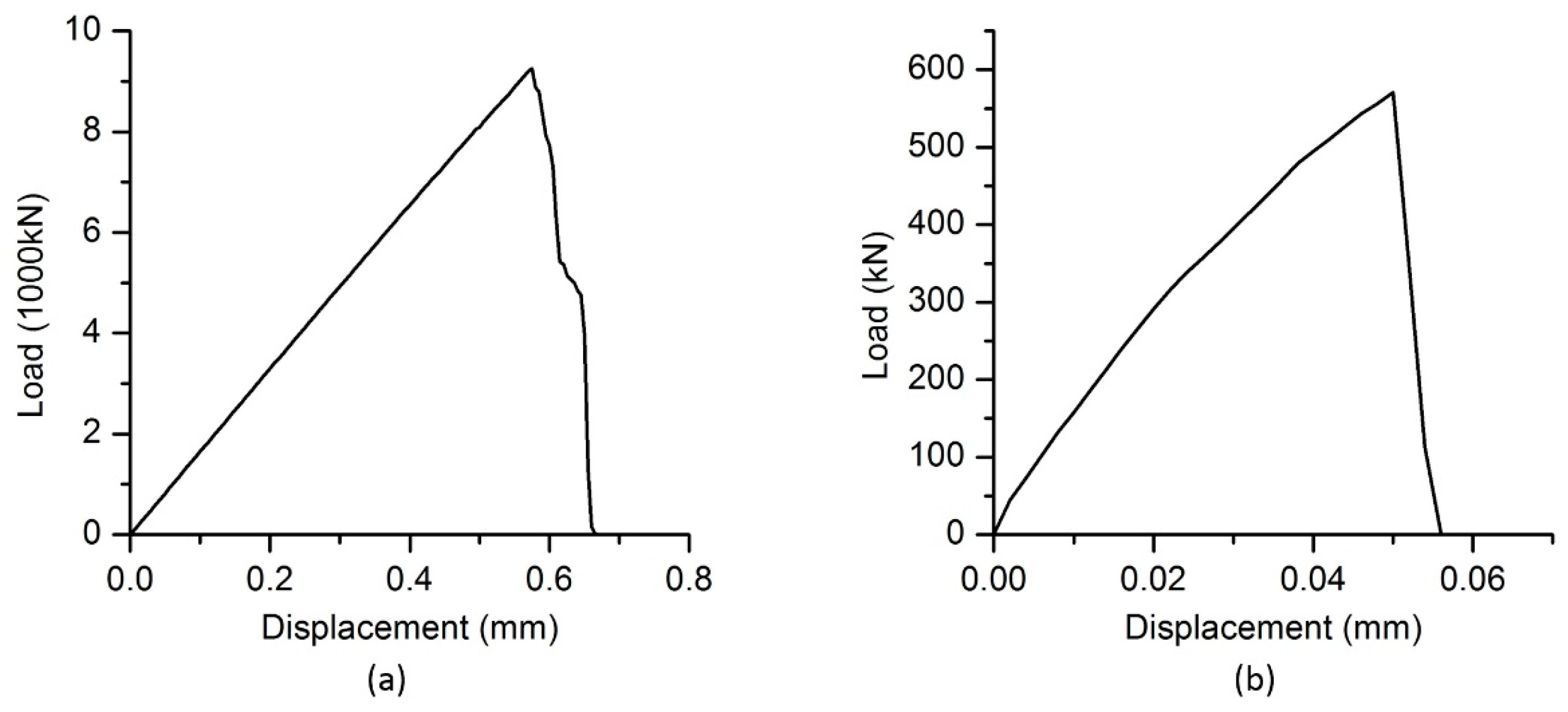
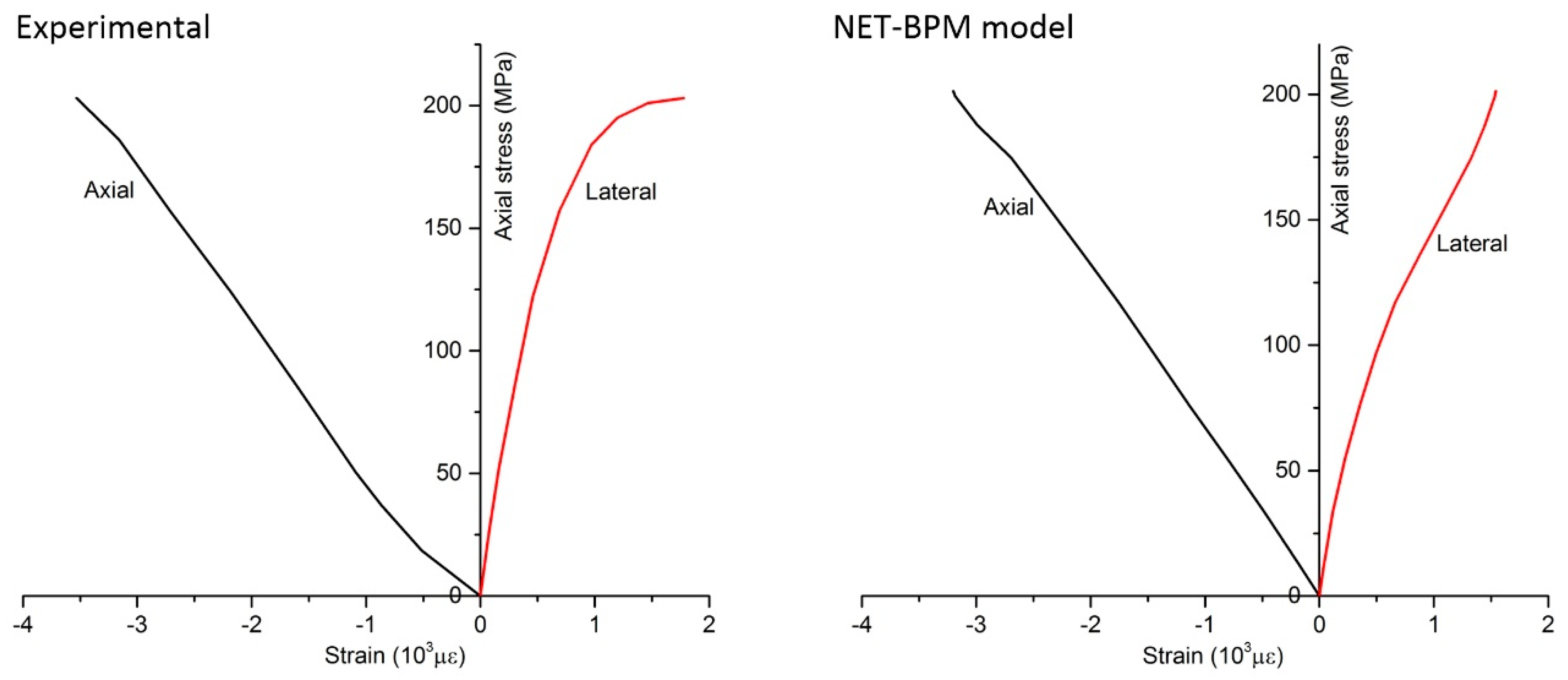
4.1. Modelling LDB Granite
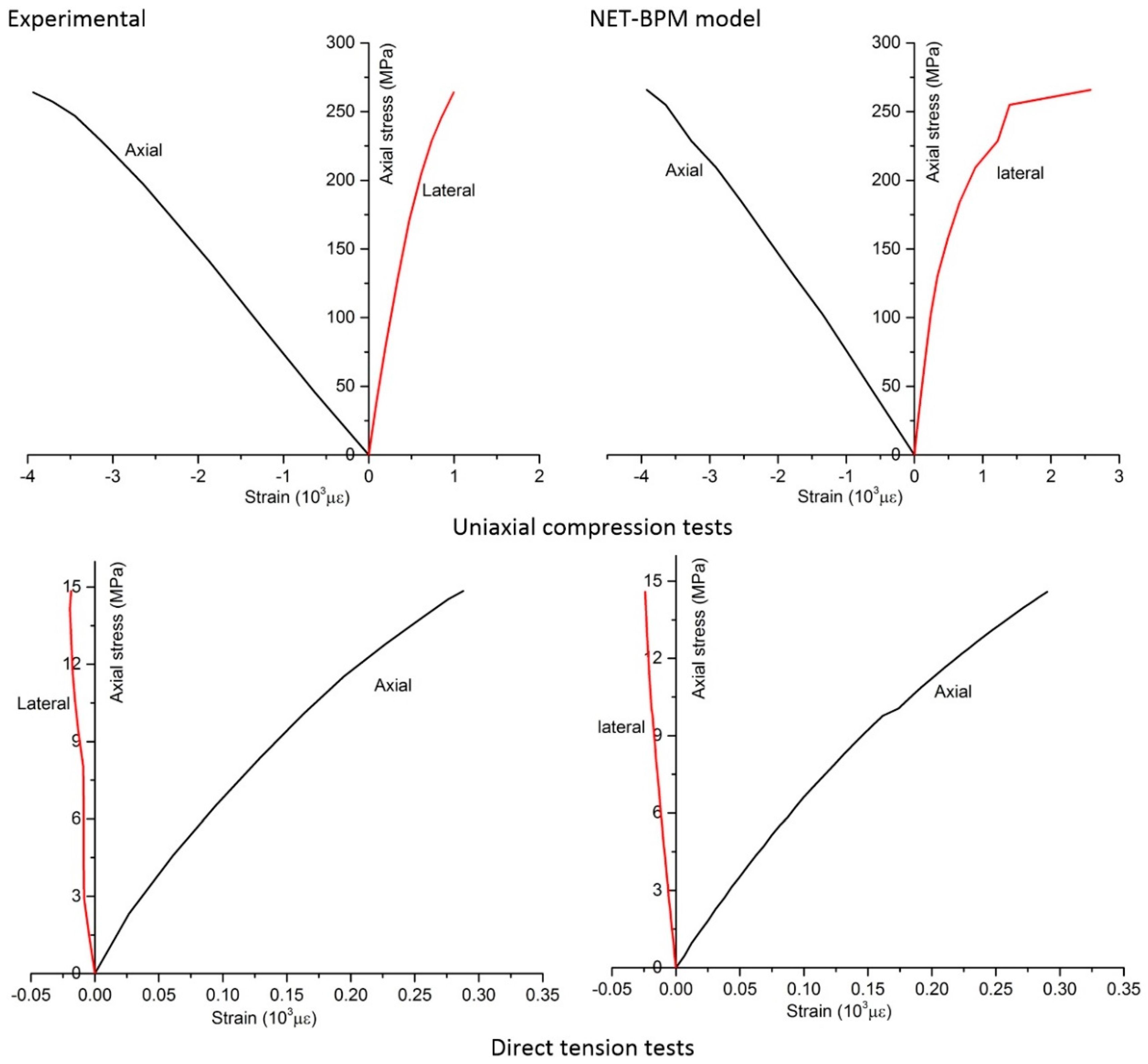
4.2. Modelling of Quartzite
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Potyondy, D.O.; Cundall, P.A. A bonded-particle model for rock. Int. J. Rock Mech. Min. Sci. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Cho, N.; Martin, C.D.; Sego, D.C. A clumped particle model for rock. Int. J. Rock Mech. Min. Sci. 2007, 44, 997–1010. [Google Scholar] [CrossRef]
- Potyondy, D.O. Simulating stress corrosion with a bonded-particle model for rock. Int. J. Rock Mech. Min. Sci. 2007, 44, 677–691. [Google Scholar] [CrossRef]
- Yoon, J. Application of experimental design and optimization to PFC model calibration in uniaxial compression simulation. Int. J. Rock Mech. Min. Sci. 2007, 44, 871–889. [Google Scholar] [CrossRef]
- Park, J.-W.; Song, J.-J. Numerical simulation of a direct shear test on a rock joint using a bonded-particle model. Int. J. Rock Mech. Min. Sci. 2009, 46, 1315–1328. [Google Scholar] [CrossRef]
- Schöpfer, M.P.J.; Abe, S.; Childs, C.; Walsh, J.J. The impact of porosity and crack density on the elasticity, strength and friction of cohesive granular materials: Insights from DEM modelling. Int. J. Rock Mech. Min. Sci. 2009, 46, 250–261. [Google Scholar] [CrossRef]
- Wang, Y.; Tonon, F. Modeling Lac du Bonnet granite using a discrete element model. Int. J. Rock Mech. Min. Sci. 2009, 46, 1124–1135. [Google Scholar] [CrossRef]
- Zhao, B.; Liu, D.; Xue, K. Experimental study on direct tension properties of red sandstone in Chongqing. Geotech. Investig. Surv. 2011, 2011, 9–12. [Google Scholar]
- Fakhimi, A.; Alavi Gharahbagh, E. Discrete element analysis of the effect of pore size and pore distribution on the mechanical behavior of rock. Int. J. Rock Mech. Min. Sci. 2011, 48, 77–85. [Google Scholar] [CrossRef]
- Su, O.; Ali Akcin, N. Numerical simulation of rock cutting using the discrete element method. Int. J. Rock Mech. Min. Sci. 2011, 48, 434–442. [Google Scholar] [CrossRef]
- Asadi, M.S.; Rasouli, V.; Barla, G. A bonded particle model simulation of shear strength and asperity degradation for rough rock fractures. Rock Mech. Rock Eng. 2012, 45, 649–675. [Google Scholar] [CrossRef]
- Scholtes, L.; Donze, F.-V. A DEM model for soft and hard rocks: Role of grain interlocking on strength. J. Mech. Phys. Solids 2013, 61, 352–369. [Google Scholar] [CrossRef]
- Brown, N.J.; Chen, J.-F.; Ooi, J. A bond model for DEM simulation of cementitious materials and deformable structures. Granul. Matter 2014, 16, 299–311. [Google Scholar] [CrossRef]
- Ding, X.; Zhang, L. A new contact model to improve the simulated ratio of unconfined compressive strength to tensile strength in bonded particle models. Int. J. Rock Mech. Min. Sci. 2014, 69, 111–119. [Google Scholar] [CrossRef]
- Park, B.; Min, K.-B. Bonded-particle discrete element modeling of mechanical behavior of transversely isotropic rock. Int. J. Rock Mech. Min. Sci. 2015, 76, 243–255. [Google Scholar] [CrossRef]
- Jiang, M.; Chen, H.; Crosta, G.B. Numerical modeling of rock mechanical behavior and fracture propagation by a new bond contact model. Int. J. Rock Mech. Min. Sci. 2015, 78, 175–189. [Google Scholar] [CrossRef]
- Scholtes, L.; Donze, F.-V. Modelling progressive failure in fractured rock masses using a 3D discrete element method. Int. J. Rock Mech. Min. Sci. 2012, 52, 18–30. [Google Scholar] [CrossRef]
- Zhu, H.P.; Zhou, Z.Y.; Yang, R.Y.; Yu, A.B. Discrete particle simulation of particulate systems: A review of major applications and findings. Chem. Eng. Sci. 2008, 63, 5728–5770. [Google Scholar] [CrossRef]
- Utili, S.; Nova, R. Dem analysis of bonded granular geomaterials. Int. J. Numer. Anal. Methods Geomech. 2008, 32, 1997–2031. [Google Scholar] [CrossRef]
- Fakhimi, A. Application of slightly overlapped circular particles assembly in numerical simulation of rocks with high friction angles. Eng. Geol. 2004, 74, 129–138. [Google Scholar] [CrossRef]
- Ergenzinger, C.; Seifried, R.; Eberhard, P. A discrete element model to describe failure of strong rock in uniaxial compression. Granul. Matter 2011, 13, 341–364. [Google Scholar] [CrossRef]
- Jiang, M.J.; Yu, H.-S.; Harris, D. A novel discrete model for granular material incorporating rolling resistance. Comput. Geotech. 2005, 32, 340–357. [Google Scholar] [CrossRef]
- Jiang, M.J.; Yu, H.S.; Harris, D. Bond rolling resistance and its effect on yielding of bonded granulates by DEM analyses. Int. J. Numer. Anal. Methods Geomech. 2006, 30, 723–761. [Google Scholar] [CrossRef]
- Jiang, M.; Shen, Z.; Wang, J. A novel three-dimensional contact model for granulates incorporating rolling and twisting resistances. Comput. Geotech. 2015, 65, 147–163. [Google Scholar] [CrossRef]
- Tran, V.T.; Marin, P. A discrete element model of concrete under high triaxial loading. Cement Concr. Compos. 2011, 33, 936–948. [Google Scholar] [CrossRef]
- Tavarez, F.A.; Plesha, M.E. Discrete element method for modelling solid and particulate materials. Int. J. Numer. Methods Eng. 2007, 70, 379–404. [Google Scholar] [CrossRef]
- Matsuda, Y.; Iwase, Y. Numerical simulation of rock fracture using three-dimensional extended discrete element method. Earth Planets Space 2002, 54, 367–378. [Google Scholar] [CrossRef]
- Fakhimi, A.; Villegas, T. Application of dimensional analysis in calibration of a discrete element model for rock deformation and fracture. Rock Mech. Rock Eng. 2007, 40, 193. [Google Scholar] [CrossRef]
- Yang, B.; Jiao, Y.; Lei, S. A study on the effects of microparameters on macroproperties for specimens created by bonded particles. Eng. Comput. 2006, 23, 607–631. [Google Scholar] [CrossRef]
- Morgan, J.K. Numerical simulations of granular shear zones using the distinct element method—2. Effects of particle size distribution and interparticle friction on mechanical behavior. J. Geophys. Res. 1999, 104, 2721–2732. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhu, H.; Zhang, L.; Ding, X. Study of scale effect on intact rock strength using particle flow modeling. Int. J. Rock Mech. Min. Sci. 2011, 48, 1320–1328. [Google Scholar] [CrossRef]
- Dondi, G.; Simone, A.; Vignali, V.; Manganelli, G. Numerical and experimental study of granular mixes for asphalts. Powder Tech. 2012, 232, 31–40. [Google Scholar] [CrossRef]
- Rojek, J.; Labra, C.; Su, O.; Oñate, E. Comparative study of different discrete element models and evaluation of equivalent micromechanical parameters. Int. J. Solids Struct. 2012, 49, 1497–1517. [Google Scholar] [CrossRef]
- Rojek, J.; Oñate, E.; Labra, C.; Kargl, H. Discrete element simulation of rock cutting. Int. J. Rock Mech. Min. Sci. 2011, 48, 996–1010. [Google Scholar] [CrossRef]
- Tropin, N.M.; Manakov, A.V.; Bocharov, O.B. Implementation of boundary conditions in discrete element modeling of rock cutting under pressure. Appl. Mech. Mater. 2014, 598, 114–118. [Google Scholar] [CrossRef]
- Lin, W.; Kamei, A.; Takahashi, M.; Kwasniewski, M.; Takagi, T.; Endo, H. Deformability of various granitic rocks from japan in uniaxial tension. In ISRM 2003—Technology Roadmap for Rock Mechanics; International Society for Rock Mechanics: Sandton, South Africa, 2003; pp. 787–790. [Google Scholar]
- Yu, X.-B.; Xie, Q.; Li, X.-Y.; Na, Y.-K.; Song, Z.-P. Cycle loading tests of rock samples under direct tension and compression and bi-modular constitutive model. Chin. J. Geotech. Eng. 2005, 27, 988–993. [Google Scholar]
- Yu, X.-B.; Wang, Q.-R.; Li, X.-Y.; Xie, Q.; Na, Y.-K.; Song, Z.-P. Experimental research on deformation of rocks in direct tension and compression. Rock Soil Mech. 2008, 29, 18–22. [Google Scholar]
- Li, D.; Li, X.; Li, C.C. Experimental studies of mechanical properties of two rocks under direct compression and tenslon. Chin. J. Rock Mech. Eng. 2010, 29, 624–632. [Google Scholar]
- Fujii, Y.; Takemura, T.; Takahashi, M.; Lin, W. Surface features of uniaxial tensile fractures and their relation to rock anisotropy in inada granite. Int. J. Rock Mech. Min. Sci. 2007, 44, 98–107. [Google Scholar] [CrossRef]
- Perkins, T.K.; Krech, W.W. The energy balance concept of hydraulic fracturing. Soc. Pet. Eng. 1968, 8, 1–12. [Google Scholar] [CrossRef]
- Martin, C.D. The Strength of Massive Lac du Bonnet Granite around Underground Openings; University of Manitoba: Winnipeg, MB, Canada, 1993. [Google Scholar]
- Koyama, T.; Jing, L. Effects of model scale and particle size on micro-mechanical properties and failure processes of rocks—A particle mechanics approach. Eng. Anal. Bound. Elem. 2007, 31, 458–472. [Google Scholar] [CrossRef]
- OuYang, Y.P.; Yang, Q.; Yu, L. An efficient dense and stable particular elements generation method based on geometry. Int. J. Numer. Methods Eng. 2017, 110, 1003–1020. [Google Scholar] [CrossRef]
- Fairhurst, C.E.; Hudson, J.A. Draft isrm suggested method for the complete stress-strain curve for intact rock in uniaxial compression. Int. J. Rock Mech. Min. Sci. 1999, 36, 279–289. [Google Scholar]
- Lin, W.; Manabu, T. Anisotropy of strength and deformation of inada granite under uniaxial tension. Chin. J. Rock Mech. Eng. 2008, 27, 2463–2472. [Google Scholar]
- Basu, A.; Mishra, D.A.; Roychowdhury, K. Rock failure modes under uniaxial compression, Brazilian, and point load tests. Bull. Eng. Geol. Environ. 2013, 72, 457–475. [Google Scholar] [CrossRef]
- Li, H.; Li, J.; Liu, B.; Li, J.; Li, S.; Xia, X. Direct tension test for rock material under different strain rates at quasi-static loads. Rock Mech. Rock Eng. 2013, 46, 1247–1254. [Google Scholar] [CrossRef]
- Stimpson, B.; Chen, R. Measurement of rock elastic moduli in tension and in compression and its practical significance. Can. Geotech. J. 1993, 30, 338–347. [Google Scholar] [CrossRef]
- Haimson, B.C.; Tharp, T.M. Stresses around boreholes in bilinear elastic rock. Soc. Pet. Eng. 1974, 14, 145–151. [Google Scholar] [CrossRef]







| Specimens | Ra (mm) | Particle Number | Bonded Contacts | Porosity (%) | Overlap Ratio (10−15) |
|---|---|---|---|---|---|
| Specimen A | 0.544 | 2031 | 5100 | 13.77 | 5.4 |
| Specimen B | 0.559 | 2006 | 5031 | 13.76 | 4.9 |
| Specimen C | 0.557 | 2023 | 5089 | 13.65 | 4.7 |
| Specimen D | 0.560 | 1996 | 5004 | 13.72 | 4.2 |
| Specimen E | 0.564 | 1960 | 4912 | 14.02 | 6.2 |
| (106 N) | ks/kn | km/(knR) | (10−3) | (°) | (°) | w | b | ||
|---|---|---|---|---|---|---|---|---|---|
| 30.0 | 0.5 | 0.256 | 4.0 | 3.5 | 10 | 45 | 39 | 0.8 | 0.2 |
| Specimens | Ec (GPa) | Et (GPa) | vc | vt | UCS (MPa) | TS (MPa) | UCS/TS | Ec/Et | vc/vt |
|---|---|---|---|---|---|---|---|---|---|
| Specimen A | 16.9 | 14.4 | 0.19 | 0.11 | 185.0 | 11.4 | 16.2 | 1.17 | 1.69 |
| Specimen B | 16.9 | 15.4 | 0.19 | 0.14 | 195.2 | 9.5 | 20.5 | 1.10 | 1.29 |
| Specimen C | 17.4 | 13.8 | 0.20 | 0.13 | 206.4 | 13.0 | 15.9 | 1.26 | 1.58 |
| Specimen D | 15.0 | 12.5 | 0.19 | 0.11 | 164.1 | 11.3 | 14.5 | 1.20 | 1.64 |
| Specimen E | 16.7 | 13.0 | 0.21 | 0.13 | 194.9 | 14.6 | 13.4 | 1.29 | 1.69 |
| Average | 16.6 | 13.8 | 0.19 | 0.12 | 189.1 | 12.0 | 16.1 | 1.20 | 1.58 |
| Stand deviation | 0.81 | 1.02 | 0.01 | 0.01 | 14.24 | 1.71 | 2.43 | 0.07 | 0.15 |
| Parameters | Size (mm) Width/Height | Ra (mm) | Particle Number | Bonded Contacts | Porosity (%) | Overlap Ratio (10−14) |
|---|---|---|---|---|---|---|
| LDB | 63/157.5 | 0.562 | 7892 | 20071 | 13.48 | 1.55 |
| Quartzite | 31/78 | 0.373 | 4365 | 11021 | 13.67 | 1.22 |
| Properties | UCS (MPa) | TS (MPa) | UCS/TS | Ec (GPa) | Et (GPa) | Ec/Et | vc | |
|---|---|---|---|---|---|---|---|---|
| LDB granite | Experimental | 200.0 | 9.3 | 21.5 | 68.1 | 47.5 | 1.43 | 0.35 |
| NET-BPM | 201.4 | 9.3 | 21.7 | 68.0 | 46.8 | 1.45 | 0.36 | |
| Quartzite | Experimental | 264.0 | 14.9 | 17.8 | 75.3 | 66.6 | 1.13 | 0.20 |
| NET-BPM | 265.8 | 14.8 | 18.0 | 75.7 | 62.0 | 1.22 | 0.20 | |
| Parameters | (106 N) | ks/kn | km/(knR) | (10−3) | (°) | (°) | w | b | ||
|---|---|---|---|---|---|---|---|---|---|---|
| LDB | 127 | 0.37 | 0.24 | 1.10 | 4.36 | 10 | 45 | 39 | 0.8 | 0.095 |
| Quartzite | 87 | 0.50 | 0.32 | 0.72 | 7.18 | 10 | 45 | 39 | 0.8 | 0.300 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ouyang, Y.; Yang, Q.; Chen, X. Bonded-Particle Model with Nonlinear Elastic Tensile Stiffness for Rock-Like Materials. Appl. Sci. 2017, 7, 686. https://doi.org/10.3390/app7070686
Ouyang Y, Yang Q, Chen X. Bonded-Particle Model with Nonlinear Elastic Tensile Stiffness for Rock-Like Materials. Applied Sciences. 2017; 7(7):686. https://doi.org/10.3390/app7070686
Chicago/Turabian StyleOuyang, Yiping, Qi Yang, and Xinquan Chen. 2017. "Bonded-Particle Model with Nonlinear Elastic Tensile Stiffness for Rock-Like Materials" Applied Sciences 7, no. 7: 686. https://doi.org/10.3390/app7070686
APA StyleOuyang, Y., Yang, Q., & Chen, X. (2017). Bonded-Particle Model with Nonlinear Elastic Tensile Stiffness for Rock-Like Materials. Applied Sciences, 7(7), 686. https://doi.org/10.3390/app7070686







