Observing Femtosecond Fragmentation Using Ultrafast X-ray-Induced Auger Spectra
Abstract
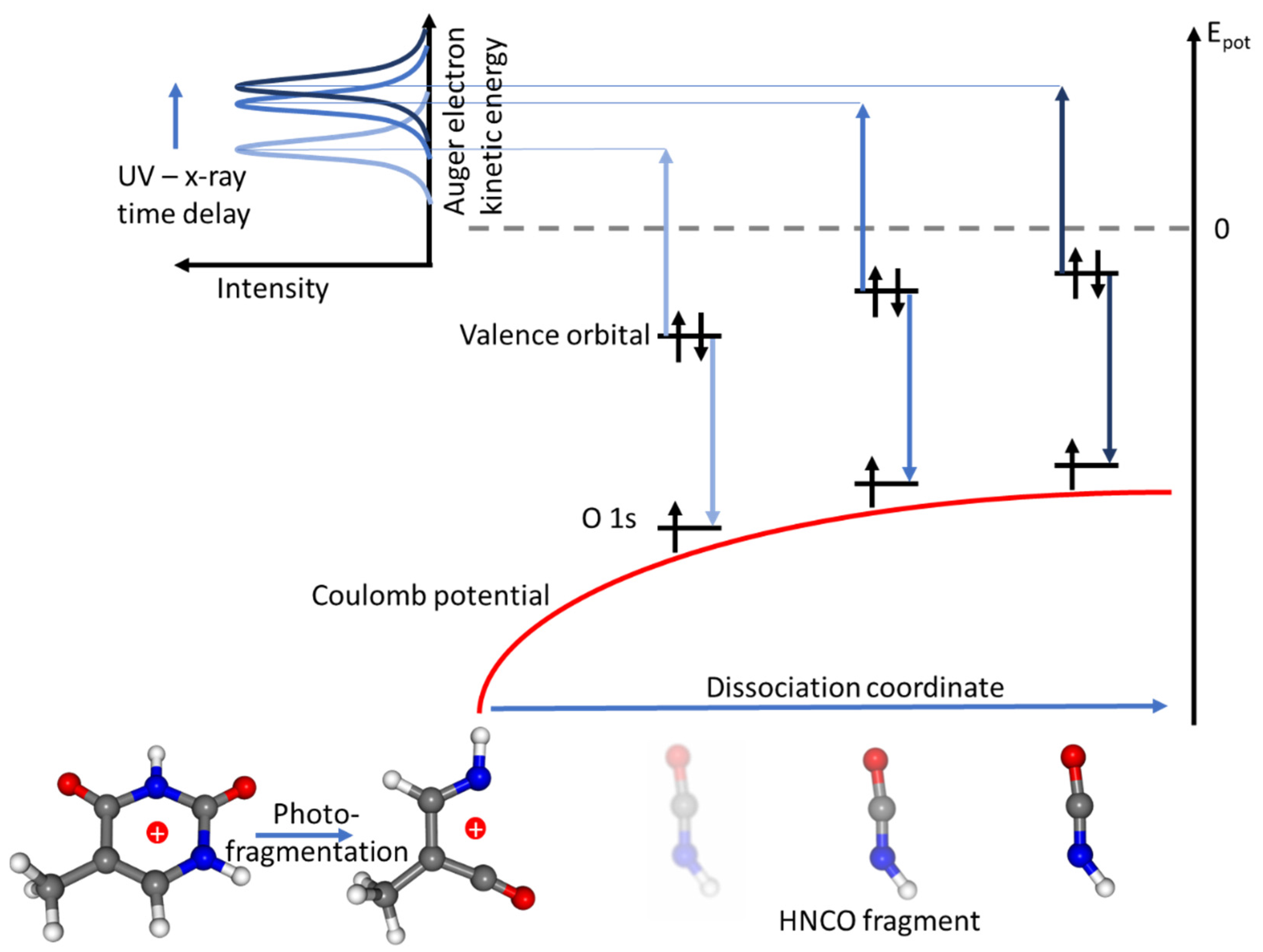
:1. Introduction
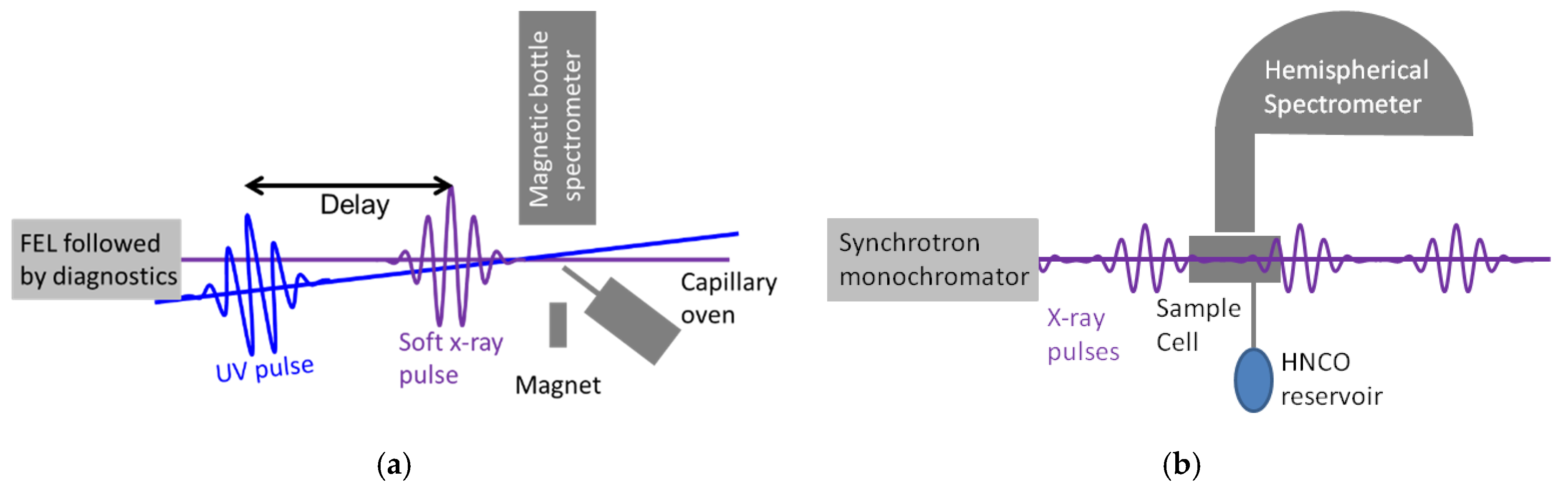
2. Experimental Methods and Theory
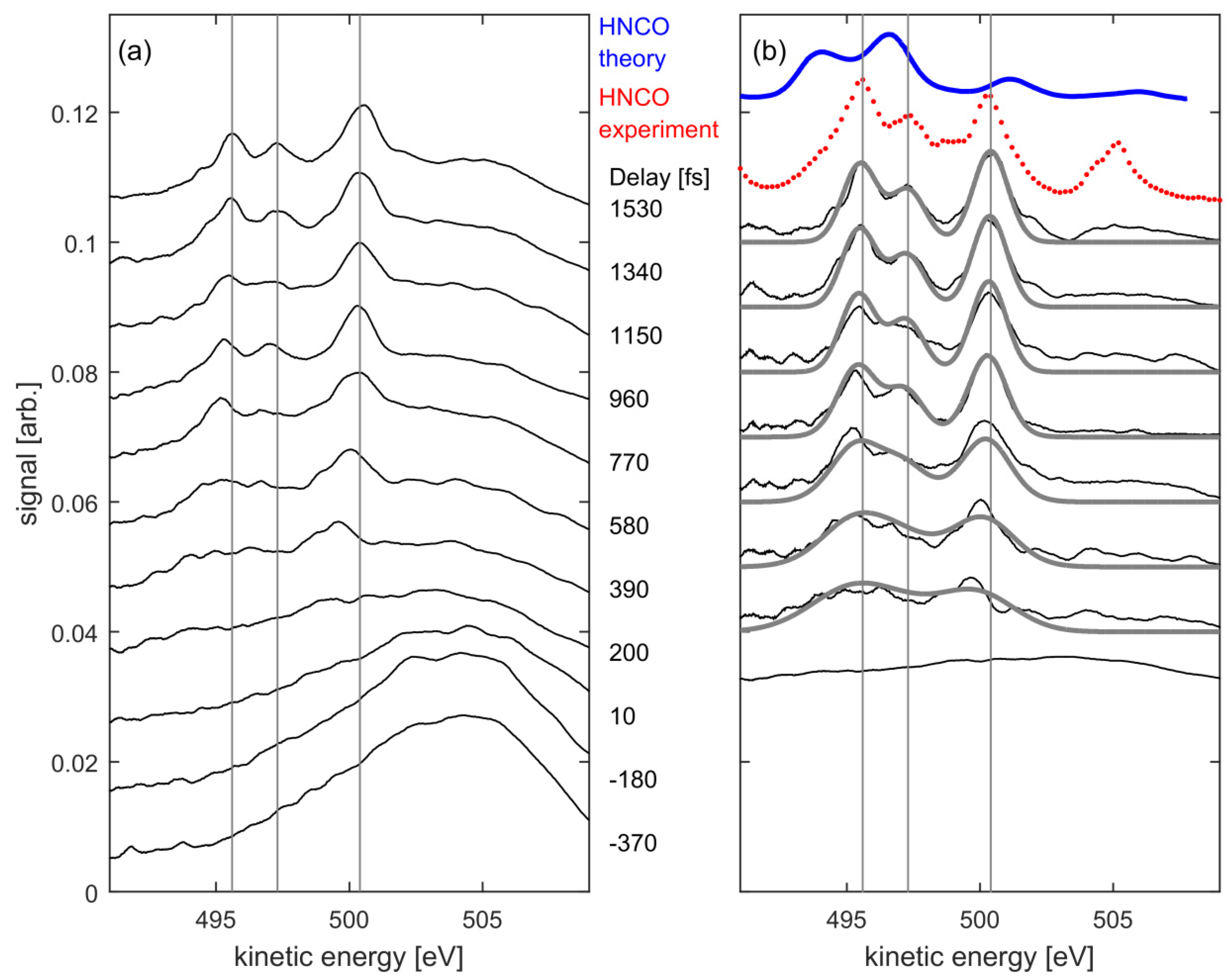
3. Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zewail, A.H. Femtochemistry: Atomic-Scale Dynamics of the Chemical Bond Using Ultrafast Lasers (Nobel Lecture). Angew. Chem. Int. Ed. 2000, 39, 2586–2631. [Google Scholar] [CrossRef]
- Mukamel, S. Principles of nonlinear optical spectroscopy; Oxford university press: Oxford, UK, 1995. [Google Scholar]
- Blanchet, V.; Zgierski, M.Z.; Seideman, T.; Stolow, A. Discerning vibronic molecular dynamics using time-resolved photoelectron spectroscopy. Nature 1999, 401, 52–54. [Google Scholar] [CrossRef]
- Srinivasan, R.; Lobastov, V.A.; Ruan, C.-Y.; Zewail, A.H. Ultrafast Electron Diffraction (UED). Helv. Chim. Acta 2003, 86, 1761–1799. [Google Scholar] [CrossRef]
- Yang, J.; Guehr, M.; Vecchione, T.; Robinson, M.S.; Li, R.; Hartmann, N.; Shen, X.; Coffee, R.; Corbett, J.; Fry, A.; et al. Diffractive imaging of a rotational wavepacket in nitrogen molecules with femtosecond megaelectronvolt electron pulses. Nat. Commun. 2016, 7, 11232. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Guehr, M.; Shen, X.; Li, R.; Vecchione, T.; Coffee, R.; Corbett, J.; Fry, A.; Hartmann, N.; Hast, C.; et al. Diffractive Imaging of Coherent Nuclear Motion in Isolated Molecules. Phys. Rev. Lett. 2016, 117, 153002. [Google Scholar] [CrossRef] [PubMed]
- Dishoeck, E.F. Astrochemistry of dust, ice and gas: introduction and overview. Faraday Discuss. 2014, 168, 9–47. [Google Scholar] [CrossRef] [PubMed]
- Koch, M.; Wolf, T.J.A.; Gühr, M. Understanding the modulation mechanism in resonance-enhanced multiphoton probing of molecular dynamics. Phys. Rev. A 2015, 91, 031403. [Google Scholar] [CrossRef]
- Ackermann, W.; Asova, G.; Ayvazyan, V.; Azima, A.; Baboi, N.; Bähr, J.; Balandin, V.; Beutner, B.; Brandt, A.; Bolzmann, A.; et al. Operation of a free-electron laser from the extreme ultraviolet to the water window. Nat. Photonics 2007, 1, 336–342. [Google Scholar] [CrossRef]
- Emma, P.; Akre, R.; Arthur, J.; Bionta, R.; Bostedt, C.; Bozek, J.; Brachmann, A.; Bucksbaum, P.; Coffee, R.; Decker, F.-J.; et al. First lasing and operation of an angstrom-wavelength free-electron laser. Nat. Photonics 2010, 4, 641–647. [Google Scholar] [CrossRef]
- Ishikawa, T.; Aoyagi, H.; Asaka, T.; Asano, Y.; Azumi, N.; Bizen, T.; Ego, H.; Fukami, K.; Fukui, T.; Furukawa, Y.; et al. A compact X-ray free-electron laser emitting in the sub-ångström region. Nat. Photonics 2012, 6, 540–544. [Google Scholar] [CrossRef]
- Allaria, E.; Appio, R.; Badano, L.; Barletta, W.A.; Bassanese, S.; Biedron, S.G.; Borga, A.; Busetto, E.; Castronovo, D.; Cinquegrana, P.; et al. Highly coherent and stable pulses from the FERMI seeded free-electron laser in the extreme ultraviolet. Nat. Photonics 2012, 6, 699–704. [Google Scholar] [CrossRef]
- Minitti, M.P.; Budarz, J.M.; Kirrander, A.; Robinson, J.S.; Ratner, D.; Lane, T.J.; Zhu, D.; Glownia, J.M.; Kozina, M.; Lemke, H.T.; et al. Imaging Molecular Motion: Femtosecond X-Ray Scattering of an Electrocyclic Chemical Reaction. Phys. Rev. Lett. 2015, 114, 255501. [Google Scholar] [CrossRef] [PubMed]
- Küpper, J.; Stern, S.; Holmegaard, L.; Filsinger, F.; Rouzée, A.; Rudenko, A.; Johnsson, P.; Martin, A.V.; Adolph, M.; Aquila, A.; et al. X-Ray Diffraction from Isolated and Strongly Aligned Gas-Phase Molecules with a Free-Electron Laser. Phys. Rev. Lett. 2014, 112, 083002. [Google Scholar] [CrossRef]
- Glownia, J.M.; Natan, A.; Cryan, J.P.; Hartsock, R.; Kozina, M.; Minitti, M.P.; Nelson, S.; Robinson, J.; Sato, T.; van Driel, T.; et al. Self-Referenced Coherent Diffraction X-Ray Movie of Ångstrom and Femtosecond-Scale Atomic Motion. Phys. Rev. Lett. 2016, 117, 153002. [Google Scholar] [CrossRef] [PubMed]
- Erk, B.; Boll, R.; Trippel, S.; Anielski, D.; Foucar, L.; Rudek, B.; Epp, S.W.; Coffee, R.; Carron, S.; Schorb, S.; et al. Imaging charge transfer in iodomethane upon x-ray photoabsorption. Science 2014, 345, 288–291. [Google Scholar] [CrossRef] [PubMed]
- McFarland, B.K.; Farrell, J.P.; Miyabe, S.; Tarantelli, F.; Aguilar, A.; Berrah, N.; Bostedt, C.; Bozek, J.D.; Bucksbaum, P.H.; Castagna, J.C.; et al. Ultrafast X-ray Auger probing of photoexcited molecular dynamics. Nat. Commun. 2014, 5, 4235. [Google Scholar] [CrossRef] [PubMed]
- Liekhus-Schmaltz, C.E.; Tenney, I.; Osipov, T.; Sanchez-Gonzalez, A.; Berrah, N.; Boll, R.; Bomme, C.; Bostedt, C.; Bozek, J.D.; Carron, S.; et al. Ultrafast isomerization initiated by X-ray core ionization. Nat Commun 2015, 6, 8199. [Google Scholar] [CrossRef] [PubMed]
- Petrovic, V.S.; Siano, M.; White, J.L.; Berrah, N.; Bostedt, C.; Bozek, J.D.; Broege, D.; Chalfin, M.; Coffee, R.N.; Cryan, J.; et al. Transient X-Ray Fragmentation: Probing a Prototypical Photoinduced Ring Opening. Phys. Rev. Lett. 2012, 108, 253006. [Google Scholar] [CrossRef] [PubMed]
- Berrah, N.; Fang, L.; Murphy, B.; Osipov, T.; Ueda, K.; Kukk, E.; Feifel, R.; van der Meulen, P.; Salen, P.; Schmidt, H.T.; et al. Double-core-hole spectroscopy for chemical analysis with an intense X-ray femtosecond laser. Proc. Natl. Acad. Sci. U. S. A. 2011, 108, 16912–16915. [Google Scholar] [CrossRef] [PubMed]
- Wolf, T.J.A.; Myhre, R.H.; Cryan, J.P.; Coriani, S.; Squibb, R.J.; Battistoni, A.; Berrah, N.; Bostedt, C.; Bucksbaum, P.; Coslovich, G.; et al. Probing ultrafast ππ*/nπ* internal conversion in organic chromophores via K-edge resonant absorption. Nat. Commun. 2017, 8, 29. [Google Scholar] [CrossRef] [PubMed]
- Ullrich, J.; Rudenko, A.; Moshammer, R. Free-Electron Lasers: New Avenues in Molecular Physics and Photochemistry. Annu. Rev. Phys. Chem. 2012, 63, 635–660. [Google Scholar] [CrossRef] [PubMed]
- Siegbahn, K. ESCA Applied to Free Molecules; North-Holland Pub. Co: Amsterdam, The Netherlands, 1969. [Google Scholar]
- Jochims, H.-W.; Schwell, M.; Baumgärtel, H.; Leach, S. Photoion mass spectrometry of adenine, thymine and uracil in the 6-22 eV photon energy range. Chem. Phys. 2005, 314, 263–282. [Google Scholar] [CrossRef]
- Improta, R.; Scalmani, G.; Barone, V. Radical cations of DNA bases: some insights on structure and fragmentation patterns by density functional methods. Int. J. Mass Spectrom. 2000, 201, 321–336. [Google Scholar] [CrossRef]
- Storchi, L.; Tarantelli, F.; Veronesi, S.; Bolognesi, P.; Fainelli, E.; Avaldi, L. The Auger spectroscopy of pyrimidine and halogen-substituted pyrimidines. J. Chem. Phys. 2008, 129, 154309. [Google Scholar] [CrossRef] [PubMed]
- Rennie, E.E.; Hergenhahn, U.; Kugeler, O. A core-level photoionization study of furan. J. Chem. Phys. 2002, 117, 6524–6532. [Google Scholar] [CrossRef]
- Sisourat, N.; Kryzhevoi, N.V.; Kolorenč, P.; Scheit, S.; Jahnke, T.; Cederbaum, L.S. Ultralong-range energy transfer by interatomic Coulombic decay in an extreme quantum system. Nat. Phys. 2010, 6, 508–511. [Google Scholar] [CrossRef]
- Moddeman, W.E.; Carlson, T.A.; Krause, M.O.; Pullen, B.P.; Bull, W.E.; Schweitzer, G.K. Determination of the K-LL Auger Spectra of N2, O2, CO, NO, H2O, and CO2. J. Chem. Phys. 1971, 55, 2317–2336. [Google Scholar] [CrossRef]
- Ferguson, K.R.; Bucher, M.; Bozek, J.D.; Carron, S.; Castagna, J.-C.; Coffee, R.; Curiel, G.I.; Holmes, M.; Krzywinski, J.; Messerschmidt, M.; et al. The Atomic, Molecular and Optical Science instrument at the Linac Coherent Light Source. J. Synchrotron Radiat. 2015, 22, 492–497. [Google Scholar] [CrossRef] [PubMed]
- Bozek, J.D. AMO instrumentation for the LCLS X-ray FEL. Eur. Phys. J.-Spec. Top. 2009, 169, 129–132. [Google Scholar] [CrossRef]
- McFarland, B.K.; Berrah, N.; Bostedt, C.; Bozek, J.; Bucksbaum, P.H.; Castagna, J.C.; Coffee, R.N.; Cryan, J.P.; Fang, L.; Farrell, J.P.; et al. Experimental strategies for optical pump: Soft X-ray probe experiments at the LCLS. J. Phys. Conf. Ser. 2014, 488, 12015. [Google Scholar] [CrossRef]
- Schorb, S.; Gorkhover, T.; Cryan, J.P.; Glownia, J.M.; Bionta, M.R.; Coffee, R.N.; Erk, B.; Boll, R.; Schmidt, C.; Rolles, D.; et al. X-ray–optical cross-correlator for gas-phase experiments at the Linac Coherent Light Source free-electron laser. Appl. Phys. Lett. 2012, 100, 121107. [Google Scholar] [CrossRef]
- Lindblad, A.; Söderström, J.; Nicolas, C.; Robert, E.; Miron, C. A multi-purpose source chamber at the PLEIADES beamline at SOLEIL for spectroscopic studies of isolated species: Cold molecules, clusters, and nanoparticles. Rev. Sci. Instrum. 2013, 84, 113105. [Google Scholar] [CrossRef] [PubMed]
- Fischer, G.; Geith, J.; Klapötke, T.M.; Krumm, B. Synthesis, Properties and Dimerization Study of Isocyanic Acid. Z. Für Naturforschung B 2002, 57, 19–24. [Google Scholar] [CrossRef]
- Schirmer, J.; Barth, A. Higher-order approximations for the particle-particle propagator. Z. Phys. At. Nucl. 1984, 317, 267–279. [Google Scholar] [CrossRef]
- Tarantelli, F. The calculation of molecular double ionization spectra by Green′s functions. Chem. Phys. 2006, 329, 11–21. [Google Scholar] [CrossRef]
- Kendall, R.A.; Dunning, T.H.; Harrison, R.J. Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions. J. Chem. Phys. 1992, 96, 6796–6806. [Google Scholar] [CrossRef]
| Delay (fs) | Peak 1, Distance (Å) | Peak 2, Distance (Å) | Peak 3, Distance (Å) | Model, Distance (Å) |
|---|---|---|---|---|
| 380 | - | - | 21 ± 3 | 17 |
| 580 | - | - | 36 ± 9 | 27 |
| 770 | 48 ± 16 | 24 ± 4 | 48 ± 16 | 35 |
| 960 | 72 ± 36 | 72 ± 36 | 144 ± 144 | 44 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wolf, T.J.A.; Holzmeier, F.; Wagner, I.; Berrah, N.; Bostedt, C.; Bozek, J.; Bucksbaum, P.; Coffee, R.; Cryan, J.; Farrell, J.; et al. Observing Femtosecond Fragmentation Using Ultrafast X-ray-Induced Auger Spectra. Appl. Sci. 2017, 7, 681. https://doi.org/10.3390/app7070681
Wolf TJA, Holzmeier F, Wagner I, Berrah N, Bostedt C, Bozek J, Bucksbaum P, Coffee R, Cryan J, Farrell J, et al. Observing Femtosecond Fragmentation Using Ultrafast X-ray-Induced Auger Spectra. Applied Sciences. 2017; 7(7):681. https://doi.org/10.3390/app7070681
Chicago/Turabian StyleWolf, Thomas J. A., Fabian Holzmeier, Isabella Wagner, Nora Berrah, Christoph Bostedt, John Bozek, Phil Bucksbaum, Ryan Coffee, James Cryan, Joe Farrell, and et al. 2017. "Observing Femtosecond Fragmentation Using Ultrafast X-ray-Induced Auger Spectra" Applied Sciences 7, no. 7: 681. https://doi.org/10.3390/app7070681
APA StyleWolf, T. J. A., Holzmeier, F., Wagner, I., Berrah, N., Bostedt, C., Bozek, J., Bucksbaum, P., Coffee, R., Cryan, J., Farrell, J., Feifel, R., Martinez, T. J., McFarland, B., Mucke, M., Nandi, S., Tarantelli, F., Fischer, I., & Gühr, M. (2017). Observing Femtosecond Fragmentation Using Ultrafast X-ray-Induced Auger Spectra. Applied Sciences, 7(7), 681. https://doi.org/10.3390/app7070681







