Surround by Sound: A Review of Spatial Audio Recording and Reproduction
Abstract
:1. Introduction
2. Binaural Recording and Rendering
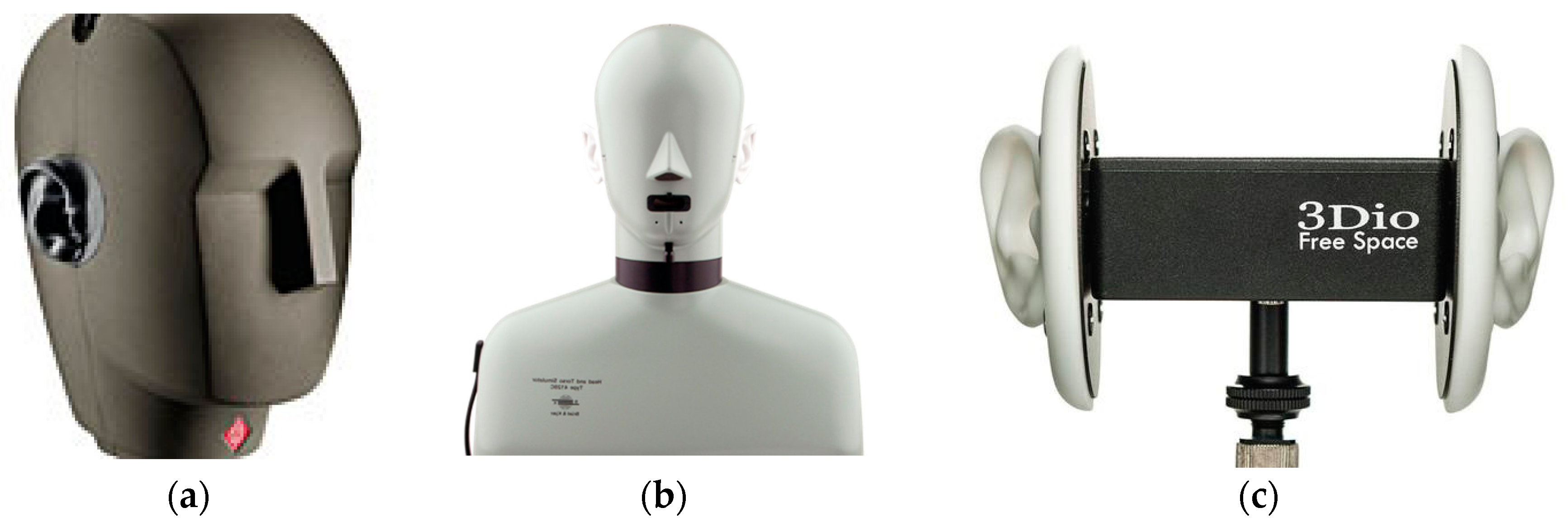
2.1. Binaural Recording and HRTF Measurement
2.1.1. Measurement Resolution
2.1.2. Test Signal and Post-Processing
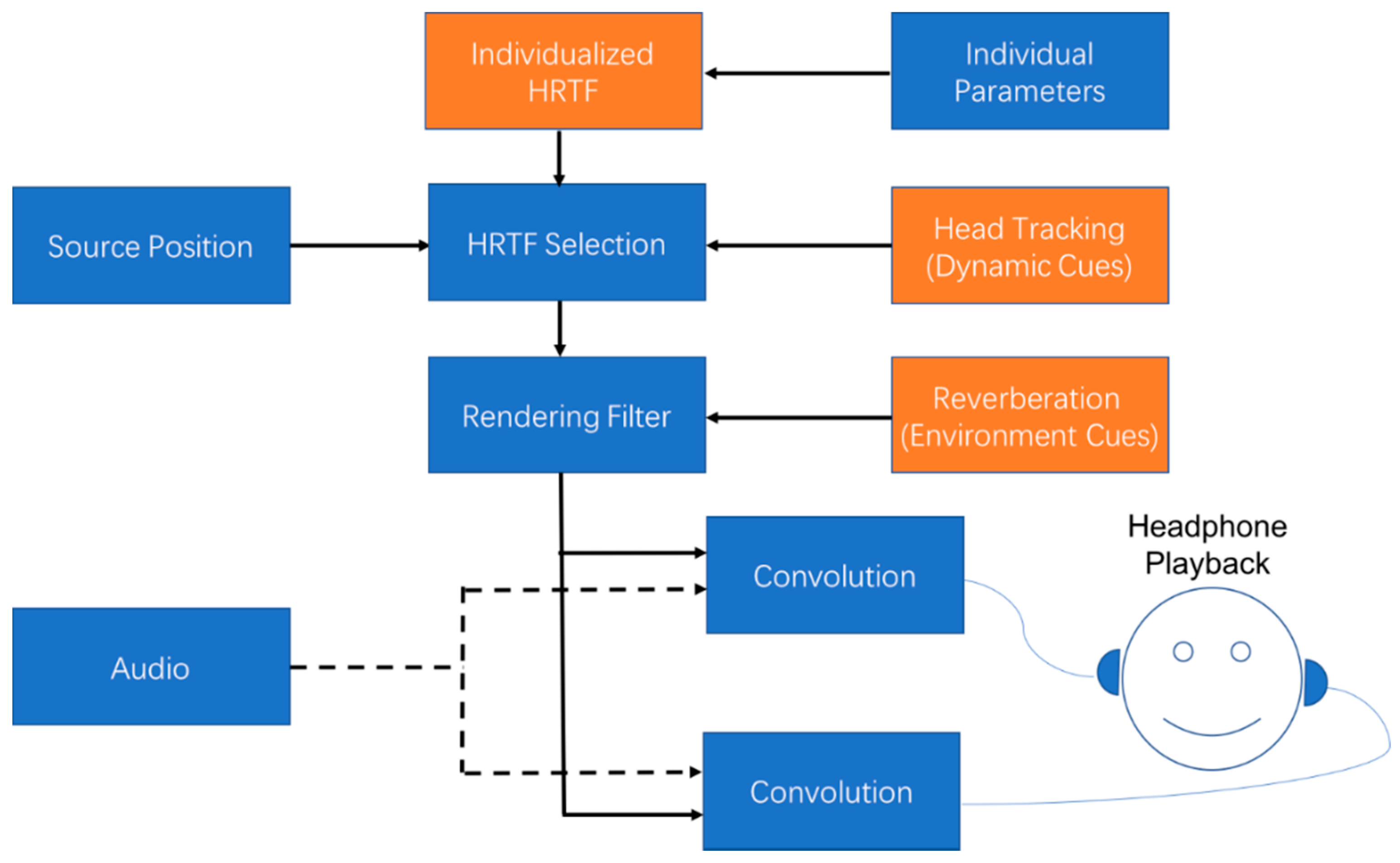
2.2. Binaural Rendering
2.2.1. Individualized HRTF
2.2.2. Dynamic Cues
2.2.3. Environment Cues
2.2.4. Rendering by Headphones or Loudspeakers
3. Soundfield Recording and Reproduction
3.1. Soundfield Representation
3.2. 3D Soundfield Recording
3.2.1. 3D Microphone Array
3.2.2. Plannar Microphone Array
3.2.3. Array of Higher Order Microphones
3.3. Soundfield Reproduction
3.3.1. Reproduction Methods
3.3.2. Listening Room Compensation
4. Multi-Zone Sound Reproduction
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Hammershoi, D.; Møller, H. Methods for binaural recording and reproduction. Acta Acust. United Acust. 2002, 88, 303–311. [Google Scholar]
- Møller, H. Fundamentals of binaural technology. Appl. Acoust. 1992, 36, 171–218. [Google Scholar] [CrossRef]
- Ranjan, R.; Gan, W.-S. Natural listening over headphones in augmented reality using adaptive filtering techniques. IEEE/ACM Trans. Audio Speech Lang. Process. 2015, 23, 1988–2002. [Google Scholar] [CrossRef]
- Sunder, K.; He, J.; Tan, E.-L.; Gan, W.-S. Natural sound rending for headphones: Integration of signal processing techniques. IEEE Signal Process. Mag. 2015, 23, 100–114. [Google Scholar] [CrossRef]
- Bauer, B.B. Stereophonic earphones and binaural loudspeakers. J. Acoust. Soc. Am. 1961, 9, 148–151. [Google Scholar]
- Huang, Y.; Benesty, J.; Chen, J. On crosstalk cancellation and equalization with multiple loudspeakers for 3-D sound reproduction. IEEE Signal Process. Lett. 2007, 14, 649–652. [Google Scholar] [CrossRef]
- Ahveninen, J.; Kopčo, N.K.; Jääskeläinen, I.P. Psychophysics and neuronal bases of sound localization in humans. Hear. Res. 2014, 307, 86–97. [Google Scholar] [CrossRef] [PubMed]
- Kolarik, A.J.; Moore, B.C.J.; Zahorik, P.; Cirstea, S.; Pardhan, S. Auditory distance perception in humans: A review of cues, development, neuronal bases and effects of sensory loss. Atten. Percept. Pyschophys. 2016, 78, 373–395. [Google Scholar] [CrossRef] [PubMed]
- Oculus Rift|Oculus. Available online: https://www.oculus.com/rift/ (accessed on 26 April 2017).
- PlayStation VR—Virtual Reality Headset for PS4. Available online: https://www.playstation.com/en-us/explore/playstation-vr/ (accessed on 26 April 2017).
- Abhayapala, T.D.; Ward, D.B. Theory and design of high order sound field microphones using spherical microphone array. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Orlando, FL, USA; 2002; pp. 1949–1952. [Google Scholar]
- Meyer, J.; Elko, G. A highly scalable spherical microphone array based on an orthonormal decomposition of the soundfield. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Orlando, FL, USA; 2002; pp. 1781–1784. [Google Scholar]
- Poletti, M.A. Three-dimensional surround sound systems based on spherical harmonics. J. Audio Eng. Soc. 2005, 53, 1004–1025. [Google Scholar]
- Samarasinghe, P.N.; Abhayapala, T.D.; Poletti, M.A. Spatial soundfield recording over a large area using distributed higher order microphones. In Proceedings of the IEEE Workshop on Applications of Signal Processing to Audio and Acoustics (WASPAA), New Paltz, NY, USA; 2011; pp. 221–224. [Google Scholar]
- Dolby Atmos Audio Technology. Available online: https://www.dolby.com/us/en/brands/dolby-atmos.html (accessed on 26 April 2017).
- Auro-3D/Auro Technologies: Three-dimensional Sound. Available online: http://www.auro-3d.com/ (accessed on 26 April 2017).
- Cheng, C.I.; Wakefield, G.H. Introduction to Head-Related Transfer Functions (HRTFs): Representations of HRTFs in time, frequency and space. J. Audio Eng. Soc. 2001, 49, 231–249. [Google Scholar]
- Schissler, C.; Nicholls, A.; Mehra, R. Efficient HRTF-based spatial audio for area and volumetric sources. IEEE Trans. Vis. Comput. Gr. 2016, 22, 1356–1366. [Google Scholar] [CrossRef] [PubMed]
- Neumann—Current Microphones, Dummy Head KU-100 Description. Available online: http://www.neumann.com/?lang=en&id=current_microphones&cid=ku100_description (accessed on 10 March 2017).
- Brüel & Kjær—4128C, Head and Torso Simulator HATS. Available online: http://www.bksv.com/Products/transducers/ear-simulators/head-and-torso/hats-type-4128c?tab=overview (accessed on 10 March 2017).
- 3Dio—The Free Space Binaural Microphone. Available online: http://3diosound.com/index.php?main_page=product_info&cPath=33&products_id=45 (accessed on 10 March 2017).
- Wenzel, E.M.; Arruda, M.; Kistler, D.J.; Wightman, F.L. Localization using nonindividualized head-related transfer functions. J. Acoust. Soc. Am. 1993, 94, 111–123. [Google Scholar] [CrossRef] [PubMed]
- Brungart, D.S. Near-field virtual audio displays. Presence Teleoper. Virtual Environ. 2002, 11, 93–106. [Google Scholar] [CrossRef]
- Otani, M.; Hirahara, T.; Ise, S. Numerical study on source distance dependency of head-related transfer functions. J. Acoust. Soc. Am. 2009, 125, 3253–3261. [Google Scholar] [CrossRef] [PubMed]
- Majdak, P.; Balazs, P.; Laback, B. Multiple exponential sweep method for fast measurment of head related transfer functions. J. Audio Eng. Soc. 2007, 55, 623–630. [Google Scholar]
- Andreopoulou, A.; Begault, D.R.; Katz, B.F.G. Inter-laboratory round robin HRTF measurement comparison. IEEE J. Sel. Top. Signal Process. 2015, 9, 895–906. [Google Scholar] [CrossRef]
- Duraiswami, R.; Zotkin, D.N.; Gumerov, N.A. Interpolation and range extrapolation of HRTFs. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Montreal, QC, Canada; 2004; pp. 45–48. [Google Scholar]
- Ajdler, T.; Faller, C.; Sbaiz, L.; Vetterli, M. Sound field analysis along a circle and its applications to HRTF interpolation. J. Audio Eng. Soc. 2008, 56, 156–175. [Google Scholar]
- Zhong, X.L.; Xie, B.S. Maximal azimuthal resolution needed in measurements of head-related transfer functions. J. Acoust. Soc. Am. 2009, 125, 2209–2220. [Google Scholar] [CrossRef] [PubMed]
- Minnaar, P.; Plogsties, J.; Christensen, F. Directional resolution of head-related transfer functions required in binaural synthesis. J. Audio Eng. Soc. 2005, 53, 919–929. [Google Scholar]
- Zhang, W.; Abhayapala, T.D.; Kennedy, R.A.; Duraiswami, R. Modal expansion of HRTFs: Continuous representation in frequency-range-angle. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Taipei, Taiwan, 19–24 April 2009; pp. 285–288. [Google Scholar]
- Zhang, M.; Kennedy, R.A.; Abhayapala, T.D. Empirical determination of frequency representation in spherical harmonics-based HRTF functional modeling. IEEE/ACM Trans. Audio Speech Lang. Process. 2015, 23, 351–360. [Google Scholar] [CrossRef]
- Zhang, W.; Abhayapala, T.D.; Kennedy, R.A.; Duraiswami, R. Insights into head-related transfer function: Spatial dimensionality and continuous representation. J. Acoust. Soc. Am. 2010, 127, 2347–2357. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Zhang, M.; Kennedy, R.A.; Abhayapala, T.D. On high-resolution head-related transfer function measurements: An efficient sampling scheme. IEEE Trans. Audio Speech Lang. Process. 2012, 20, 575–584. [Google Scholar] [CrossRef]
- Bates, A.P.; Khalid, Z.; Kennedy, R.A. Novel sampling scheme on the sphere for head-related transfer function measurements. IEEE/ACM Trans. Audio Speech Lang. Process. 2015, 23, 1068–1081. [Google Scholar] [CrossRef]
- Muller, A.; Massarani, P. Transfer-function measurement with sweeps. J. Audio Eng. Soc. 2001, 49, 443–471. [Google Scholar]
- Zotkin, D.N.; Duraiswami, R.; Grassi, E.; Gumerov, N.A. Fast head-related transfer function measurement via reciprocity. J. Acoust. Soc. Am. 2006, 120, 2202–2215. [Google Scholar] [CrossRef] [PubMed]
- Fukudome, K.; Suetsugu, T.; Ueshin, T.; Idegami, R.; Takeya, K. The fast measurment of head related impulse responses for all azimuthal directions using the continuous measurement method with a servoswiveled chair. Appl. Acoust. 2007, 68, 864–884. [Google Scholar] [CrossRef]
- He, J.; Ranjan, R.; Gan, W.-S. Fast continuous HRTF acquisition with unconstrained movements of human subjects. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Shanghai, China, 20–25 March 2016; pp. 321–325. [Google Scholar]
- Majdak, P.; Iwaya, Y.; Carpentier, T. Spatially oriented format for acoustics: A data exchange format representing head-related transfer functions. In Proceedings of the 134th Audio Engineering Society Convention, Rome, Italy, 4–7 May 2013; pp. 1–11. [Google Scholar]
- Zotkin, D.N.; Duraiswami, R.; Davis, L.S. Rendering localized spatial audio in a virtual auditory scene. IEEE Trans. Multimedia 2004, 6, 553–563. [Google Scholar] [CrossRef]
- Xie, B. Head-Related Transfer Function and Virtual Auditory Display; J Ross Publishing: Plantation, FL, USA, 2013. [Google Scholar]
- Gamper, H. Head-related transfer function interpolation in azimuth, elevation, and distance. J. Acoust. Soc. Am. 2013, 134. [Google Scholar] [CrossRef] [PubMed]
- Queiroz, M.; de Sousa, G.H.M.A. Efficient binaural rendering of moving sound sources using HRTF interpolation. J. New Music Res. 2011, 40, 239–252. [Google Scholar] [CrossRef]
- Savioja, L.; Huopaniemi, J.; Lokki, T.; Väänänen, R. Creating interactive virtual acoustic environments. J. Audio Eng. Soc. 1999, 47, 675–705. [Google Scholar]
- Freeland, F.P.; Biscinho, L.W.P.; Diniz, P.S.R. Efficient HRTF interpolation in 3D moving sound. In Proceedings of the 22nd AES International Conference: Virtual, Synthetic, and Entertainment Audio, Espoo, Finland, 15–17 June 2002; pp. 1–9. [Google Scholar]
- Kistler, D.J.; Wightman, F.L.L. A model of HeadRelated Transfer Functions based on Principal Components Analysis and Minimum-Phase reconstruction. J. Acoust. Soc. Am. 1992, 91, 1637–1647. [Google Scholar] [CrossRef] [PubMed]
- Romigh, G.D.; Brungart, D.S.; Stern, R.M.; Simpson, B.D. Efficient real spherical harmonic representation of head-related transfer function. IEEE J. Sel. Top. Signal Process. 2015, 9, 921–930. [Google Scholar] [CrossRef]
- Zotkin, D.N.; Hwang, J.; Duraiswami, R.; Davis, L.S. HRTF personalization using anthropometric measurements. In Proceedings of the IEEE Workshop on Applications of Signal Processing to Audio and Acoustics (WASPAA), New Paltz, NY, USA, 19–22 October 2003; pp. 157–160. [Google Scholar]
- Hu, H.; Zhou, L.; Ma, H.; Wu, Z. HRTF personalization based on airtificial neural network in individual virtual auditory space. Appl. Acoust. 2008, 69, 163–172. [Google Scholar] [CrossRef]
- Li, L.; Huang, Q. HRTF personalization modeling based on RBF neural network. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Vancouver, BC, Canada, 26–31 May 2013; pp. 3707–3710. [Google Scholar]
- Grindlay, G.; Vasilescu, M.A.O. A multilinear (tensor) framework for HRTF analysis and synthesis. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Honolulu, HI, USA, 16–20 April 2007; pp. 161–164. [Google Scholar]
- Spagnol, S.; Geronazzo, M.; Avanzini, F. On the relation between pinna reflection patterns and head-related transfer functon features. IEEE Trans. Audio Speech Lang. Process. 2013, 21, 508–519. [Google Scholar] [CrossRef]
- Geronazzo, M.; Spagnol, S.; Bedin, A.; Avanzini, F. Enhancing vertical localization with image-guided selection of non-individual head-related transfer functions. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Florence, Italy, 4–9 May 2014; pp. 4496–4500. [Google Scholar]
- Zhang, M.; Kennedy, R.A.; Abhayapala, T.D.; Zhang, W. Statistical method to identify key anthropometric parameters in HRTF individualization. In Proceedings of the Hands-free Speech Communication and Microphone Arrays (HSCMA), Edinburgh, UK, 30 May–1 June 2011; pp. 213–218. [Google Scholar]
- Bilinski, P.; Ahrens, J.; Thomas, M.R.P.; Tasheve, I.J.; Platt, J.C. HRTF magnitude synthesis via sparse representation of anthropometric features. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Florence, Italy, 4–9 May 2014; pp. 4468–4472. [Google Scholar]
- Tasheve, I.J. HRTF phase synthesis via sparse representation of anthropometric features. In Proceedings of the Information Theory and Applications Workshop (ITA), San Diego, CA, USA, 9–14 February 2014; pp. 1–5. [Google Scholar]
- He, J.; Gan, W.-S.; Tan, E.-L. On the preprocessing and postprocessing of HRTF individualizaion based on sparse representation of anthropometric features. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Brisbane, Australia, 19–24 April 2015; pp. 639–643. [Google Scholar]
- Fink, K.J.; Ray, L. Individualization of head related transfer functions using principal component analysis. Appl. Acoust. 2015, 87, 162–173. [Google Scholar] [CrossRef]
- Sunder, K.; Tan, E.-L.; Gan, W.-S. Individualization of binaural synthesis using frontal projection headphones. J. Audio Eng. Soc. 2013, 61, 989–1000. [Google Scholar]
- Cai, T.; Rakerd, B.; Hartmann, W.M. Computing interaural differences through finite element modeling of idealized human heads. J. Acoust. Soc. Am. 2015, 138, 1549–1560. [Google Scholar] [CrossRef] [PubMed]
- Katz, B.F.G. Boundary element method calculation of individual head-related transfer function. I. Rigid model calculation. J. Acoust. Soc. Am. 2001, 110, 2440–2448. [Google Scholar] [CrossRef] [PubMed]
- Otani, M.; Ise, S. Fast calculation system specialized for head-related transfer function based on boundary element method. J. Acoust. Soc. Am. 2006, 119, 2589–2598. [Google Scholar] [CrossRef] [PubMed]
- Prepeliță, S.; Geronazzo, M.; Avanzini, F.; Savioja, L. Influence of voxelization on finite difference time domain simulations of head-related transfer functions. J. Acoust. Soc. Am. 2016, 139, 2489–2504. [Google Scholar] [CrossRef] [PubMed]
- Mokhtari, P.; Takemoto, H.; Nishimura, R.; Kato, H. Preliminary estimation of the first peak of HRTFs from pinna anthropometry for personalized 3D audio. In Proceedings of the 5th International Conference on Three Dimensional Systems and Applications, Osaka, Japan, 26–28 June 2013; p. 3. [Google Scholar]
- Jin, C.T.; Guillon, P.; Epain, N.; Zolfaghari, R.; van Schaik, A.; Tew, A.I.; Hetherington, C.; Thorpe, J. Creating the sydney york morphological and acoustic recordings of ears database. IEEE Trans. Multimedia 2014, 16, 37–46. [Google Scholar] [CrossRef]
- Voss, P.; Lepore, F.; Gougoux, F.; Zatorre, R.J. Relevance of spectral cues for auditory spatial processing in the occipital cortex of the blind. Front. Psychol. 2011, 2, 48. [Google Scholar] [CrossRef] [PubMed]
- Kolarik, A.J.; Cirstea, S.; Pardhan, S. Discrimination of virtual auditory distance using level and direct-to-reverberant ratio cues. J. Acoust. Soc. Am. 2013, 134, 3395–3398. [Google Scholar] [CrossRef] [PubMed]
- Wightman, F.L.; Kistler, D.J. Resolution of front-back ambiguity in spatial hearing by listener and source movement. J. Acoust. Soc. Am. 1999, 102, 2325–2332. [Google Scholar] [CrossRef]
- Kolarik, A.J.; Cirstea, S.; Pardhan, S. Evidence for enhanced discrimination of virtual auditory distance among blind listeners using level and direct-to-reverberant cues. Exp. Brain Res. 2013, 224, 623–633. [Google Scholar] [CrossRef] [PubMed]
- Shinn-Cunningham, B.G. Distance cues for virtual auditory space. In Proceedings of the IEEE Pacific Rim Conference (PRC) on Multimedia, Sydney, Australia, 26-28 August 2001; pp. 227–230. [Google Scholar]
- Allen, J.B.; Berkeley, D.A. Image method for efficiently simulating small-room acoustics. J. Acoust. Soc. Am. 1979, 75, 943–950. [Google Scholar] [CrossRef]
- Valimaki, V.; Parker, J.D.; Savioja, L.; Smith, J.O.; Abel, J.S. Fifty years of artificial reverberation. IEEE Trans. Audio Speech Lang. Process. 2012, 20, 1421–1448. [Google Scholar] [CrossRef]
- Belloch, J.A.; Ferrer, M.; Gonzalez, A.; Martinez-Zaldivar, F.J.; Vidal, A.M. Headphone-based virtual spatialization of sound with a GPU accelerator. J. Audio Eng. Soc. 2013, 61, 546–561. [Google Scholar]
- Taylor, M.; Chandak, A.; Mo, Q.; Lauterbach, C.; Schissler, C.; Manocha, D. Guided multiview ray tracing for fast auralization. IEEE Trans. Vis. Comput. Gr. 2012, 18, 1797–1810. [Google Scholar] [CrossRef] [PubMed]
- Theile, G. On the standardization of the frequency response of high-quality studio headphones. J. Audio Eng. Soc. 1986, 34, 959–969. [Google Scholar]
- Hiipakka, M.; Kinnari, T.; Pulkki, V. Estimating head-related transfer functions of human subjects from pressure-velocity measurements. J. Acoust. Soc. Am. 2012, 13, 4051–4061. [Google Scholar] [CrossRef] [PubMed]
- Lindau, A.; Brinkmann, F. Perceptual evaluation of headphone compensation in binaural synthesis based on non-individual recordings. J. Audio Eng. Soc. 2012, 60, 54–62. [Google Scholar]
- Boren, B.; Geronazzo, M.; Brinkmann, F.; Choueiri, E. Coloration metrics for headphone equalization. In Proceedings of the 21st International Conference on Auditory Display, Graz, Austria, 6–10 July 2015; pp. 29–34. [Google Scholar]
- Takeuchi, T.; Nelson, P.A.; Hamada, H. Robustness to head misalignment of virtual sound imaging system. J. Acoust. Soc. Am. 2001, 109, 958–971. [Google Scholar] [CrossRef] [PubMed]
- Kirkeby, O.; Nelson, P.A.; Hamada, H. Local sound field reproduction using two closely spaced loudspeakers. J. Acoust. Soc. Am. 1998, 104, 1973–1981. [Google Scholar] [CrossRef]
- Takeuchi, T.; Nelson, P.A. Optimal source distribution for binaural synthesis over loudspeakers. J. Acoust. Soc. Am. 2002, 112, 2786–2797. [Google Scholar] [CrossRef] [PubMed]
- Bai, M.R.; Tung, W.W.; Lee, C.C. Optimal design of loudspeaker arrays for robust cross-talk cancellation using the Taguchi method and the generic algorithm. J. Acoust. Soc. Am. 2005, 117, 2802–2813. [Google Scholar] [CrossRef] [PubMed]
- Majdak, P.; Masiero, B.; Fels, J. Sound localization in individualized and non-individualized crosstalk cancellation systems. J. Acoust. Soc. Am. 2013, 133, 2055–2068. [Google Scholar] [CrossRef] [PubMed]
- Lacouture-Parodi, Y.; Habets, E.A. Crosstalk cancellation system using a head tracker based on interaural time differences. In Proceedings of the International Workshop on Acoustic Signal Enahcancement, Aachen, Germany, 4–6 September 2012; pp. 1–4. [Google Scholar]
- Williams, E.G. Fourier Acoustics: Sound Radiation and Nearfield Acoustical Holography; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Ward, D.B.; Abhayapala, T.D. Reproduction of a plane-wave sound field using an array of loudspeakers. IEEE Trans. Speech Audio Process. 2001, 9, 697–707. [Google Scholar] [CrossRef]
- Core Sound TetraMic. Available online: http://www.core-sound.com/TetraMic/1.php (accessed on 10 March 2017).
- Eigenmike Microphone. Available online: https://www.mhacoustics.com/products#eigenmike1 (accessed on 10 March 2017).
- Gerzon, M.A. The design of precisely conincident microphone arrays for stereo and surround sound. In Proceedings of the 50th Audio Engineering Society Covention, London, UK, 4–7 March 1975; pp. 1–5. [Google Scholar]
- Abhayapala, T.D.; Gupta, A. Spherical harmonic analysis of wavefields using multiple circular sensor arrays. IEEE Trans. Audio Speech Lang. Process. 2010, 18, 1655–1666. [Google Scholar] [CrossRef]
- Chen, H.; Abhayapala, T.D.; Zhang, W. Theory and design of compact hybrid microphone arrays on two-dimensional planes for three-dimensional soundfield analysis. J. Acoust. Soc. Am. 2015, 138, 3081–3092. [Google Scholar] [CrossRef] [PubMed]
- Samarasinghe, P.N.; Abhayapala, T.D.; Poletti, M.A. Wavefield analysis over large areas using distributed higher order microphones. IEEE/ACM Trans. Audio Speech Lang. Process. 2014, 22, 647–658. [Google Scholar] [CrossRef]
- Pulkki, V.; Karjalainen, M. Localization of amplitude-panned virtual sources, Part 1: Stereophonic panning. J. Audio Eng. Soc. 2001, 49, 739–752. [Google Scholar]
- Pulkki, V. Localization of amplitude-panned virtual sources, Part 2: Two and three dimensional panning. J. Audio Eng. Soc. 2001, 49, 753–767. [Google Scholar]
- Pulkki, V. Virtual sound source positioning using vector base amplitude panning. J. Audio Eng. Soc. 1997, 45, 456–466. [Google Scholar]
- Lossius, T.; Baltazar, P.; de la Hogue, T. DBAP—distance-based amplitude panning. In Proceedings of the 2009 International Computer Music Conference, Montreal, QC, Canada, 16–21 August 2009; pp. 1–4. [Google Scholar]
- VBAP Demo. Available online: http://legacy.spa.aalto.fi/software/vbap/VBAP_demo/ (accessed on 26 April 2017).
- Developers—3D Sound Labs. Available online: http://www.3dsoundlabs.com/category/developers/ (accessed on 26 April 2017).
- Cameras, M. Approach to recreating a sound field. J. Acoust. Soc. Am. 1967, 43, 1425–1431. [Google Scholar] [CrossRef]
- Gerzon, M.A. Periphony: With-height sound reproduction. J. Audio Eng. Soc. 1973, 21, 2–10. [Google Scholar]
- Gerzon, M.A. Ambisonics in multichannel broadcasting video. J. Audio Eng. Soc. 1985, 33, 859–871. [Google Scholar]
- Betlehem, T.; Abhayapala, T.D. Theory and design of sound field reproduction in reverberant rooms. J. Acoust. Soc. Am. 2005, 117, 2100–2111. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Abhayapala, T.D. Theory and design of soundfield reproducion using continuous loudspeakers concept. IEEE Trans. Audio Speech Lang. Process. 2009, 17, 107–116. [Google Scholar] [CrossRef]
- Daniel, J. Spatial sound encoding including near field effect: Introducing distance coding filters and a viable, new ambisonic format. In Proceedings of the 23rd AES International Conference: Signal Processing in Audio Recording and Reproduction, Copenhagen, Denmark, 23–25 May 2003. [Google Scholar]
- Ahrens, J.; Spors, S. Applying the ambisonics approach to planar and linear distributions of secondary sources and combinations thereof. Acta Acust. United Acust. 2012, 98, 28–36. [Google Scholar] [CrossRef]
- Ahrens, J.; Spors, S. Wave field synthesis of a sound field described by spherical harmonics expansion coefficients. J. Acoust. Soc. Am. 2012, 131, 2190–2199. [Google Scholar] [CrossRef] [PubMed]
- Bianchi, L.; Antonacci, F.; Sarti, A.; Turbaro, S. Model-based acoustic rendering based on plane wave decomposition. Appl. Acoust. 2016, 104, 127–134. [Google Scholar] [CrossRef]
- Okamoto, T. 2.5D higher-order Ambisonics for a sound field described by angular spectrum coefficients. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Shanghai, China, 20–25 March 2016; pp. 326–330. [Google Scholar]
- Berkhout, A.J. A holographic approach to acoustic control. J. Audio Eng. Soc. 1988, 36, 977–995. [Google Scholar]
- Berkhout, A.J.; de Vries, D.; Vogel, P. Acoustic control by wave field synthesis. J. Acoust. Soc. Am. 1993, 93, 2764–2778. [Google Scholar] [CrossRef]
- Spors, S.; Rabenstein, R.; Ahrens, J. The theory of wave field synthesis revisited. In Proceedings of the 124th Audio Engineering Society Convention, Amsterdam, The Netherlands, 17–20 May 2008. [Google Scholar]
- Spors, S.; Rabenstein, R. Spatial aliasing aritifacts produced by linear and circular loudspeaker arrays used for wave field synthesis. In Proceedings of the 120th Audio Engineering Society Convention, Paris, France, 20–23 May 2006. [Google Scholar]
- Boone, M.M.; Verheijen, E.N.G.; Tol, P.F.V. Spatial sound-field reproduction by wave-field synthesis. J. Audio Eng. Soc. 1995, 43, 1003–1012. [Google Scholar] [CrossRef]
- Boone, M.M. Multi-actuator panels (MAPs) as loudspeaker arrays for wave field synthesis. J. Audio Eng. Soc. 2004, 52, 712–723. [Google Scholar]
- Spors, S.; Ahrens, J. Analysis and improvement of pre-equalization in 2.5-dimensional wave field synthesis. In Proceedings of the 128 Audio Engineering Society Convention, London, UK, 23–25 May 2010. [Google Scholar]
- Firtha, G.; Fiala, P.; Schultz, F.; Spors, S. Improved referencing schemes for 2.5D wave field synthesis driving functions. IEEE/ACM Trans. Audio Speech Lang. Process. 2017, 25, 1117–1127. [Google Scholar] [CrossRef]
- Kirkeby, O.; Nelson, P.A. Reproduction of plane wave sound fields. J. Acoust. Soc. Am. 1993, 94, 2992–3000. [Google Scholar] [CrossRef]
- Tatekura, Y.; Urata, S.; Saruwatari, H.; Shikano, K. On-line relaxation algorithm applicable to acoustic fluctuation for inverse filter in multichannel sound reproduction system. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2005, E88-A, 1747–1756. [Google Scholar] [CrossRef]
- Spors, S.; Wierstorf, H.; Raake, A.; Melchior, F.; Frank, M.; Zotter, F. Spatial sound with loudspeakers and its perception: A review of the current state. Proc. IEEE 2013, 101, 1920–1938. [Google Scholar] [CrossRef]
- Wierstorf, H. Perceptual Assessment of Sound Field Synthesis; Technical University of Berlin: Berlin, Germany, 2014. [Google Scholar]
- Bharitkar, S.; Kyriakakis, C. Immersive Audio Signal Processing; Springer: New York, NY, USA, 2006. [Google Scholar]
- Corteel, E.; Nicol, R. Listening room compensation for wave field sysnthesis. What can be done? In Proceedings of the 23rd Audio Engineering Society Convention, Copenhagen, Denmark, 23–25 May 2003. [Google Scholar]
- Mourjopoulos, J.N. On the variation and invertibility of room impulse response functions. J. Sound Vib. 1985, 102, 217–228. [Google Scholar] [CrossRef]
- Hatziantoniou, P.D.; Mourjopoulos, J.N. Erros in real-time room acoustics dereverberation. J. Audio Eng. Soc. 2004, 52, 883–889. [Google Scholar]
- Spors, S.; Buchner, H.; Rabenstein, R.; Herbordt, W. Active listening room compensation for massive multichannel sound reproduction systems. J. Acoust. Soc. Am. 2007, 122, 354–369. [Google Scholar] [CrossRef] [PubMed]
- Talagala, D.; Zhang, W.; Abhayapala, T.D. Efficient multichannel adaptive room compensation for spatial soundfield reproduction using a modal decomposition. IEEE Trans. Audio Speech Lang. Process. 2014, 22, 1522–1532. [Google Scholar] [CrossRef]
- Schneider, M.; Kellermann, W. Multichannel acoustic echo cancellation in the wave domain with increased robustness to nonuniqueness. IEEE Trans. Audio Speech Lang. Process. 2016, 24, 518–529. [Google Scholar] [CrossRef]
- Poletti, M.A.; Fazi, F.M.; Nelson, P.A. Sound-field reproduction systems using fixed-directivity loudspeakers. J. Acoust. Soc. Am. 2010, 127, 3590–3601. [Google Scholar] [CrossRef] [PubMed]
- Poletti, M.A.; Abhayapala, T.D.; Samarasinghe, P.N. Interior and exterior sound field control using two dimensional higher-order variable-directivity sources. J. Acoust. Soc. Am. 2012, 131, 3814–3823. [Google Scholar] [CrossRef] [PubMed]
- Betlehem, T.; Poletti, M.A. Two dimensional sound field reproduction using higher-order sources to exploit room reflections. J. Acoust. Soc. Am. 2014, 135, 1820–1833. [Google Scholar] [CrossRef] [PubMed]
- Canclini, A.; Markovic, D.; Antonacci, F.; Sarti, A.; Tubaro, S. A room-compensated virtual surround sound system exploiting early reflections in a reverberant room. In Proceedings of the 20th European Signal Processing Conference (EUSIPCO), Bucharest, Romania, 27–31 August 2012; pp. 1029–1033. [Google Scholar]
- Samarasinghe, P.N.; Abhayapala, T.D.; Poletti, M.A. Room reflections assisted spatial sound field reproduction. In Proceedings of the European Signal Processing Conference (EUSIPCO), Lisbon, Portugal, 1–5 September 2014; pp. 1352–1356. [Google Scholar]
- Betlehem, T.; Zhang, W.; Poletti, M.A.; Abhayapala, T.D. Personal sound zones: Delivering interface-free audio to multiple listeners. IEEE Signal Process. Mag. 2015, 32, 81–91. [Google Scholar] [CrossRef]
- Choi, J.-W.; Kim, Y.-H. Generation of an acoustically bright zone with an illuminated region using multiple sources. J. Acoust. Soc. Am. 2002, 111, 1695–1700. [Google Scholar] [CrossRef] [PubMed]
- Shin, M.; Lee, S.Q.; Fazi, F.M.; Nelson, P.A.; Kim, D.; Wang, S.; Park, K.H.; Seo, J. Maximization of acoustic energy difference between two spaces. J. Acoust. Soc. Am. 2010, 128, 121–131. [Google Scholar] [CrossRef] [PubMed]
- Elliott, S.J.; Cheer, J.; Choi, J.-W.; Kim, Y.-H. Robustness and regularization of personal audio systems. IEEE Trans. Audio Speech Lang. Process. 2012, 20, 2123–2133. [Google Scholar] [CrossRef]
- Chang, J.-H.; Lee, C.-H.; Park, J.-Y.; Kim, Y.-H. A realization of sound focused personal audio system using acoustic contrast control. J. Acoust. Soc. Am. 2009, 125, 2091–2097. [Google Scholar] [CrossRef] [PubMed]
- Okamoto, T.; Sakaguchi, A. Experimental validation of spatial Fourier transform-based multiple sound zone generation with a linear loudspeaker array. J. Acoust. Soc. Am. 2017, 141, 1769–1780. [Google Scholar] [CrossRef] [PubMed]
- Cheer, J.; Elliott, S.J.; Gálvez, M.F.S. Design and implementation of a car cabin personal audio system. J. Audio Eng. Soc. 2013, 61, 414–424. [Google Scholar]
- Coleman, P.; Jackson, P.; Olik, M.; Pederson, J.A. Personal audio with a planar bright zone. J. Acoust. Soc. Am. 2014, 136, 1725–1735. [Google Scholar] [CrossRef] [PubMed]
- Coleman, P.; Jackson, P.; Olik, M.; M’øller, M.; Olsen, M.; Pederson, J.A. Acoustic contrast, planarity and robustness of sound zone methods using a circular loudspeaker array. J. Acoust. Soc. Am. 2014, 135, 1029–1940. [Google Scholar] [CrossRef] [PubMed]
- Poletti, M.A. An investigation of 2D multizone surround sound systems. In Proceedings of the 125th Audio Engineering Society Convention, San Francisco, CA, USA, 2–5 October 2008. [Google Scholar]
- Betlehem, T.; Withers, C. Sound field reproduction with energy constraint on loudspeaker weights. IEEE Trans. Audio Speech Lang. Process. 2012, 20, 2388–2392. [Google Scholar] [CrossRef]
- Radmanesh, N.; Burnett, I.S. Generation of isolated wideband soundfield using a combined two-stage Lasso-LS algorithm. IEEE Trans. Audio Speech Lang. Process. 2013, 21, 378–387. [Google Scholar] [CrossRef]
- Jin, W.; Kleijn, W.B. Theory and design of multizone soundfield reproduction using sparse methods. IEEE/ACM Trans. Audio Speech Lang. Process. 2015, 23, 2343–2355. [Google Scholar]
- Chang, J.-H.; Jacobsen, F. Sound field control with a circular double-layer array of loudspeakers. J. Acoust. Soc. Am. 2012, 131, 4518–4525. [Google Scholar] [CrossRef] [PubMed]
- Chang, J.-H.; Jacobsen, F. Experimental validation of sound field control with a circular double-layer array of loudspeakers. J. Acoust. Soc. Am. 2013, 133, 2046–2054. [Google Scholar] [CrossRef] [PubMed]
- Cai, Y.; Wu, M.; Yang, J. Sound reproduction in personal audio systems using the least-squares approach with acoustic contrast control constraint. J. Acoust. Soc. Am. 2014, 135, 734–741. [Google Scholar] [CrossRef] [PubMed]
- Gálvez, S.; Marcos, F.; Elliott, S.J.; Jordan, C. Time domain optimisation of filters used in a loudspeaker array for personal audio. IEEE/ACM Trans. Audio Speech Lang. Process. 2015, 23, 1869–1878. [Google Scholar] [CrossRef]
- Wu, Y.J.; Abhayapala, T.D. Spatial multizone soundfield reproduction: Theory and design. IEEE Trans. Audio Speech Lang. Process. 2011, 19, 1711–1720. [Google Scholar] [CrossRef]
- Poletti, M.A.; Fazi, F.M. An approach to generating two zones of silence with application to personal sound systems. J. Acoust. Soc. Am. 2015, 137, 1711–1720. [Google Scholar] [CrossRef] [PubMed]
- Menzies, D. Sound field synthesis with distributed modal constraints. Acta Acust. United Acust. 2012, 98, 15–27. [Google Scholar] [CrossRef]
- Helwani, K.; Spors, S.; Buchner, H. The synthesis of sound figures. Multidimens. Syst. Signal Process. 2014, 25, 379–403. [Google Scholar] [CrossRef]
- Zhang, W.; Abhayapala, T.D.; Betlehem, T.; Fazi, F.M. Analysis and control of multi-zone sound field reproduction using modal-domain approach. J. Acoust. Soc. Am. 2016, 140, 2134–2144. [Google Scholar] [CrossRef] [PubMed]


| Method | Typical Systems | Characteristics |
|---|---|---|
| Stereo/Surround | Dolby Stereo, Dolby 5.1/7.1 Dolby Atmos, NHK 22.2 Auro 3D |
|
| VBAP, DBAP | Software Demo [98] |
|
| Ambisonics (B-format) HOA | Youtube 360° VR Audio Kit [99] |
|
| WFS | IOSONO |
|
| Inverse Filtering | -- |
|
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Samarasinghe, P.N.; Chen, H.; Abhayapala, T.D. Surround by Sound: A Review of Spatial Audio Recording and Reproduction. Appl. Sci. 2017, 7, 532. https://doi.org/10.3390/app7050532
Zhang W, Samarasinghe PN, Chen H, Abhayapala TD. Surround by Sound: A Review of Spatial Audio Recording and Reproduction. Applied Sciences. 2017; 7(5):532. https://doi.org/10.3390/app7050532
Chicago/Turabian StyleZhang, Wen, Parasanga N. Samarasinghe, Hanchi Chen, and Thushara D. Abhayapala. 2017. "Surround by Sound: A Review of Spatial Audio Recording and Reproduction" Applied Sciences 7, no. 5: 532. https://doi.org/10.3390/app7050532
APA StyleZhang, W., Samarasinghe, P. N., Chen, H., & Abhayapala, T. D. (2017). Surround by Sound: A Review of Spatial Audio Recording and Reproduction. Applied Sciences, 7(5), 532. https://doi.org/10.3390/app7050532






