Fire Damage Assessment of Reinforced Concrete Structures Using Fuzzy Theory
Abstract
:1. Introduction
2. Previous Research
2.1. Fire Damage Inspection
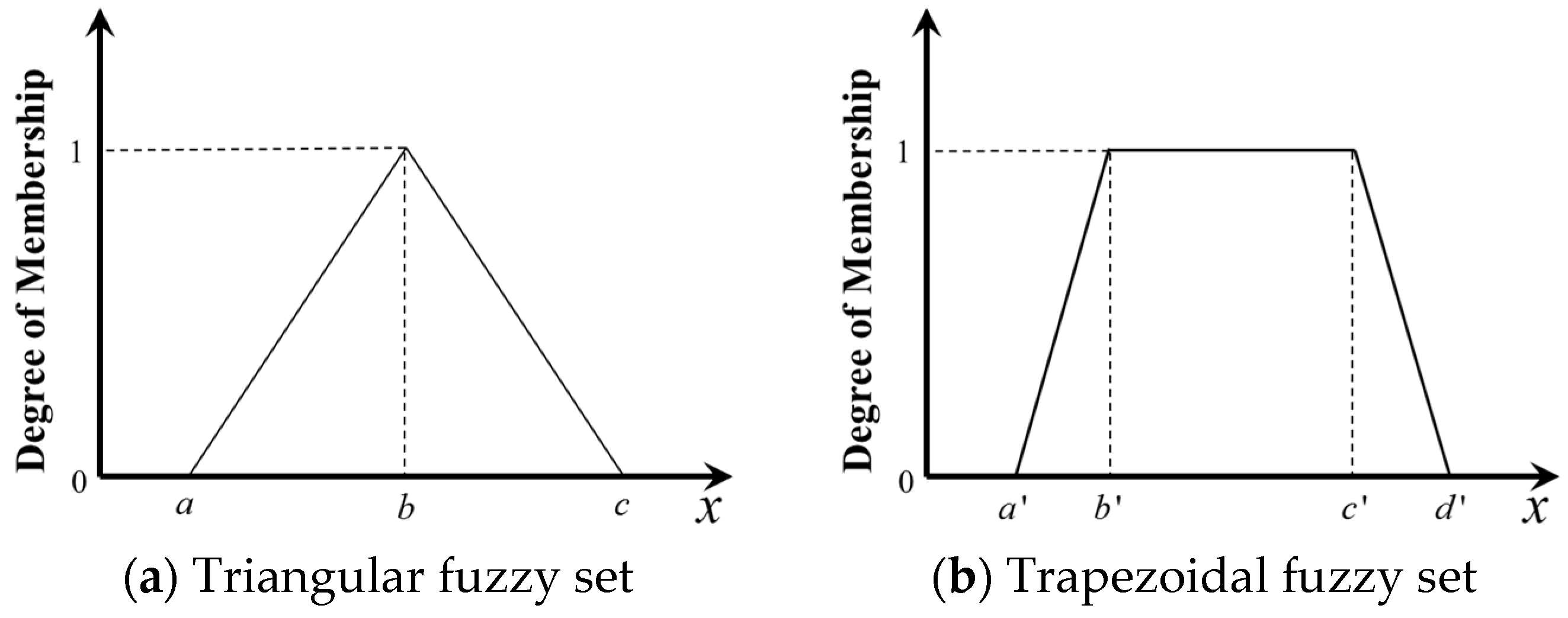
2.2. Fuzzy Theory
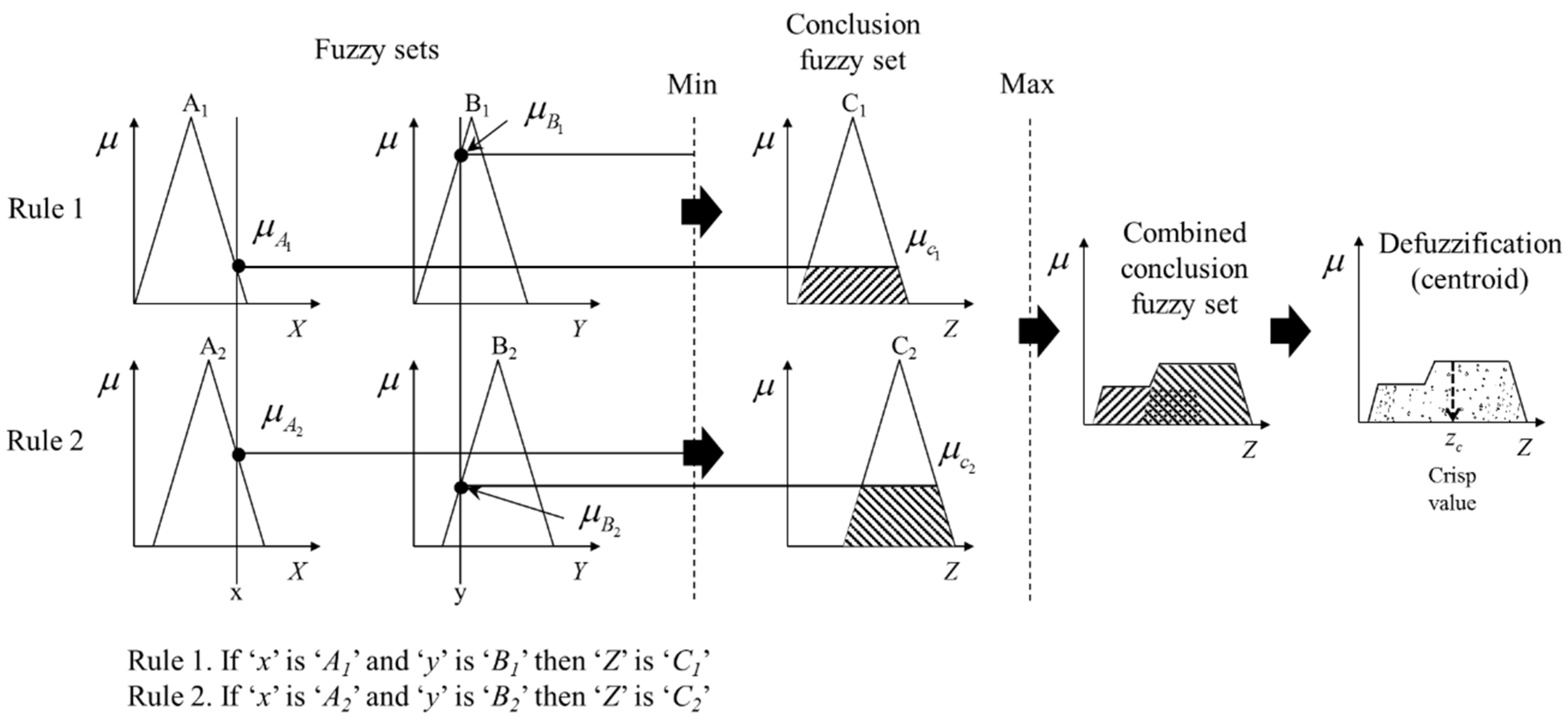
2.3. Fuzzy Inference
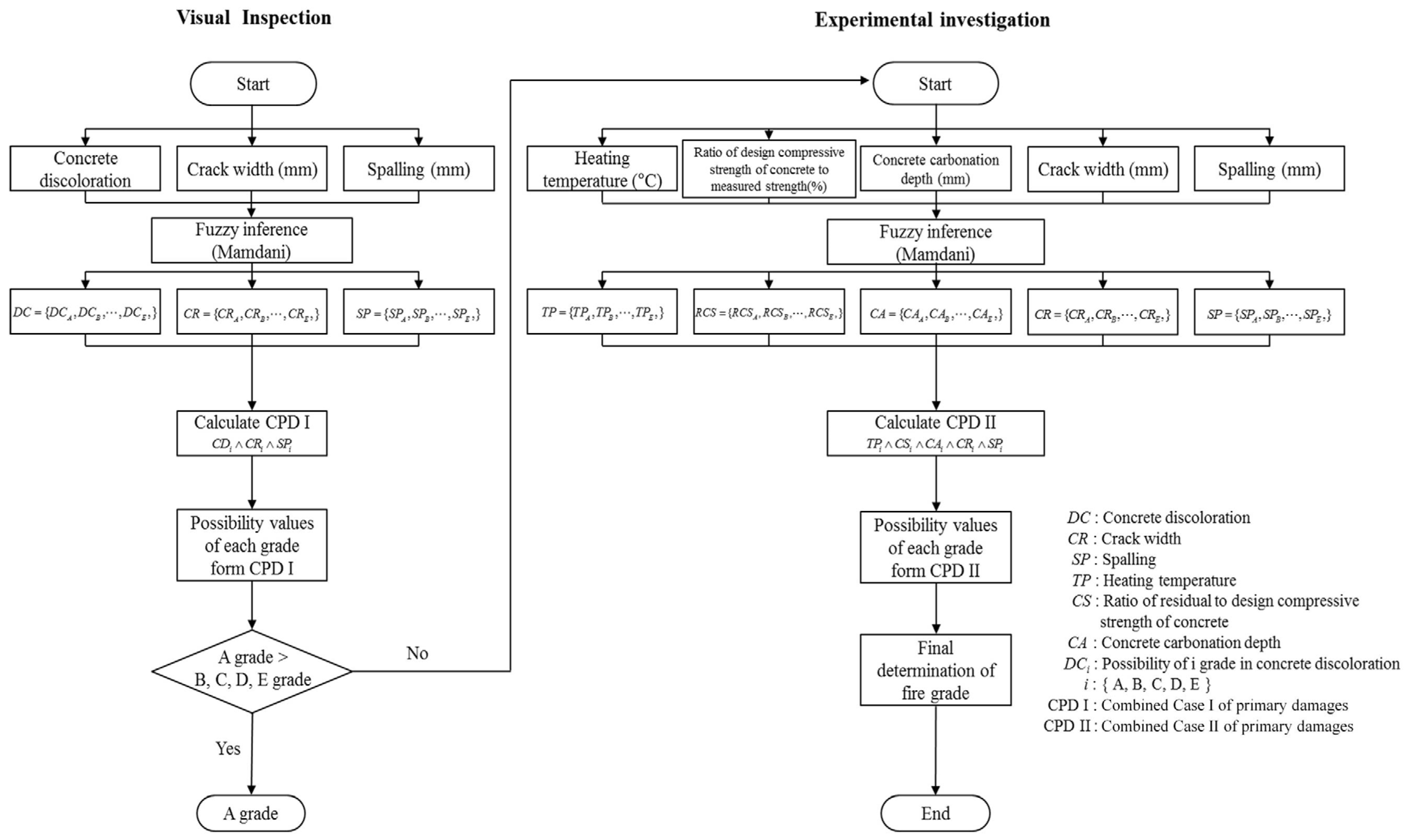
3. Fire Damage Diagnosis System Using Fuzzy Theory
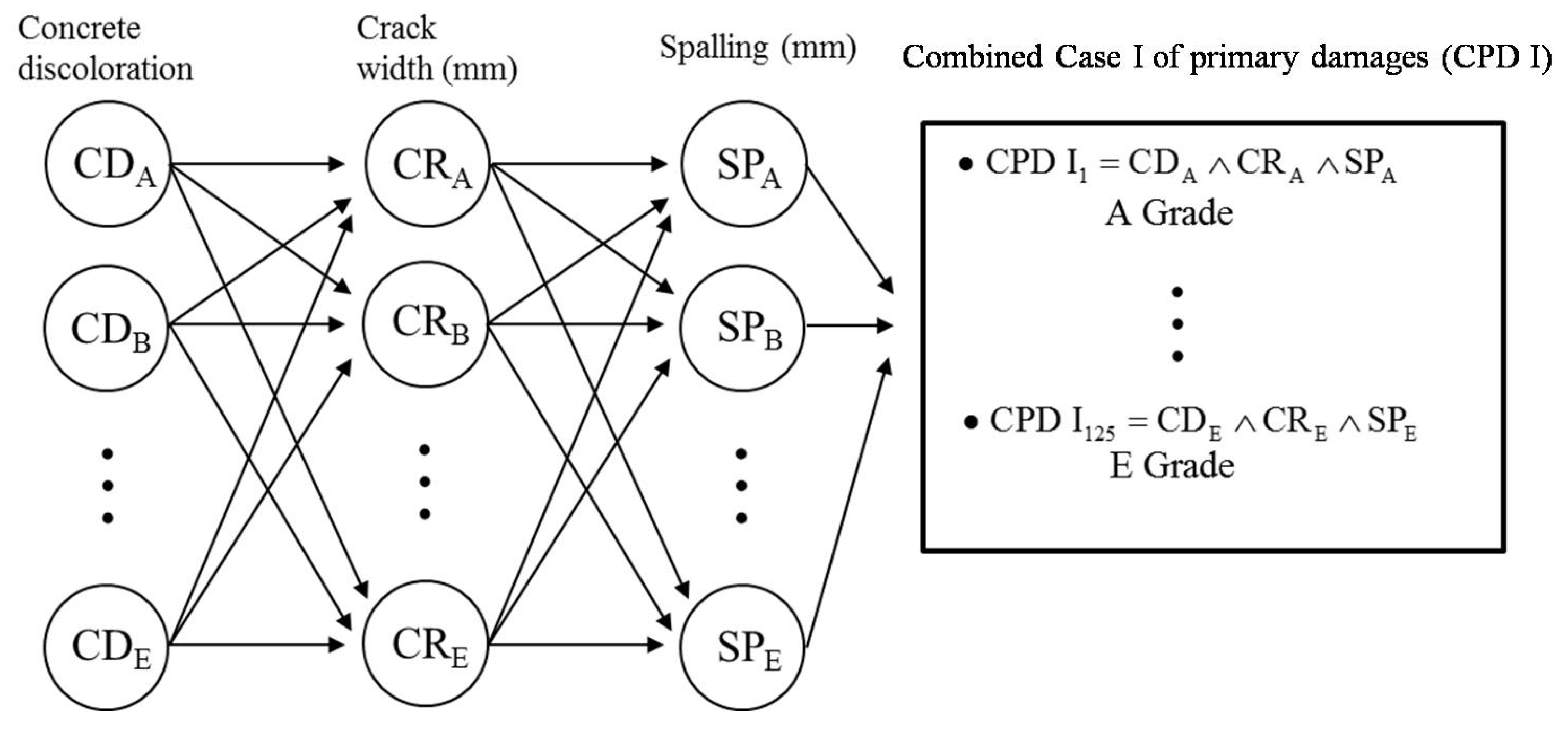
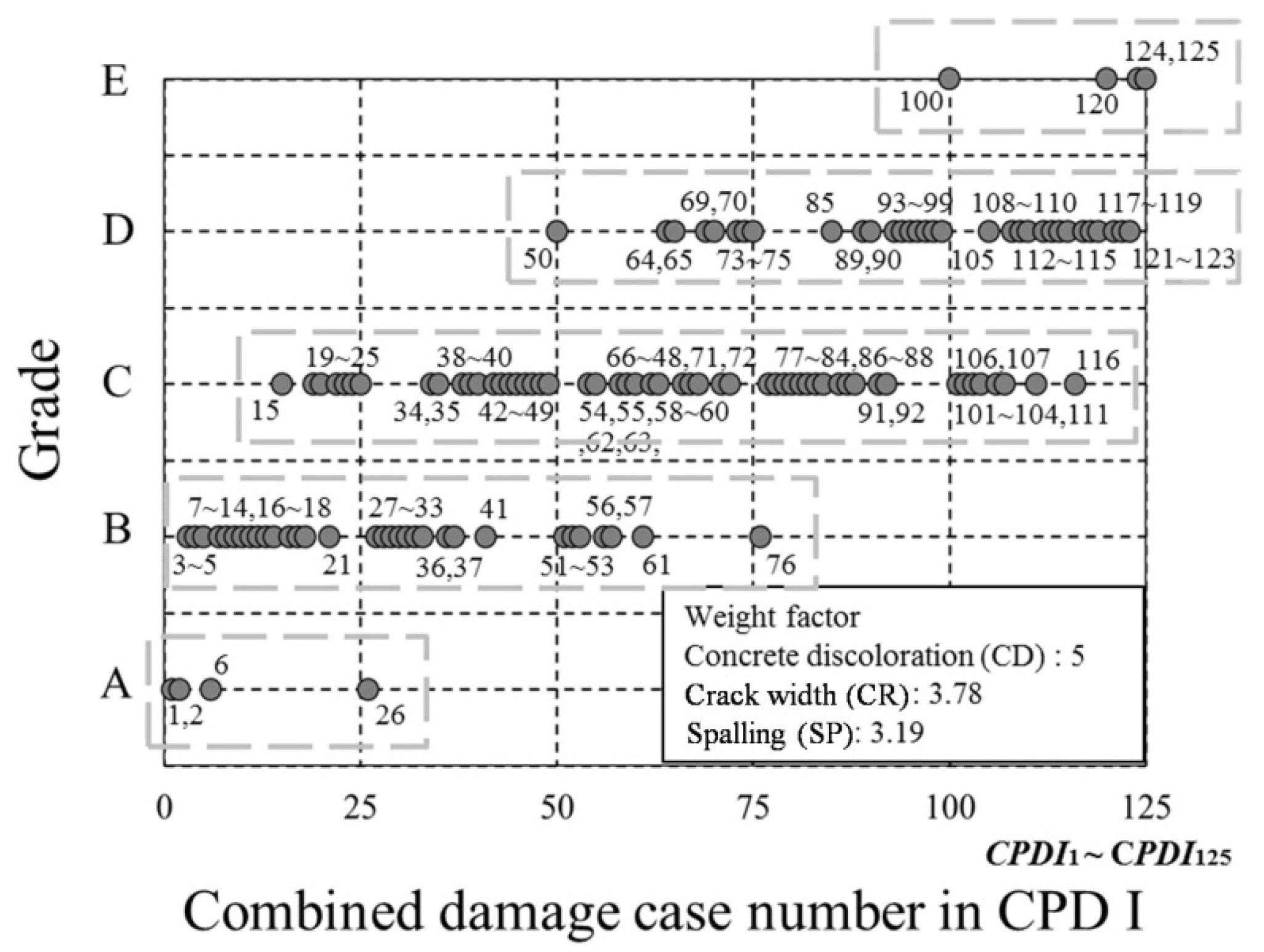
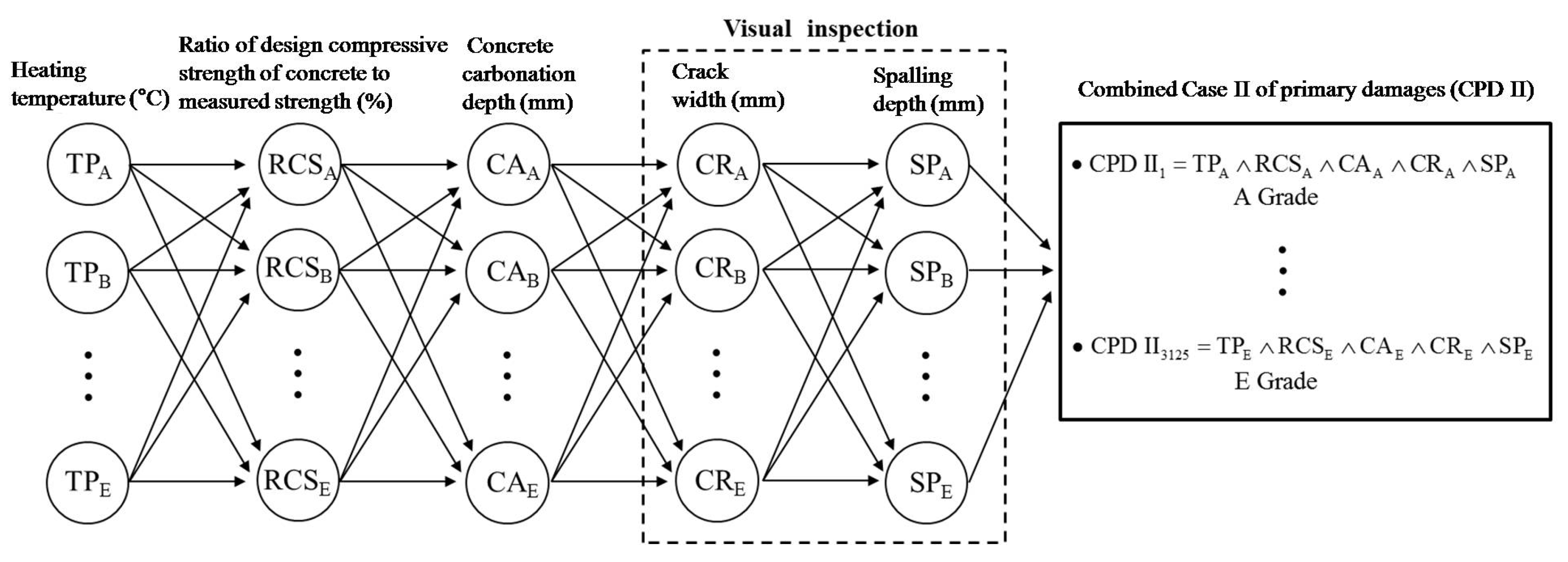
3.1. Combined Case of Primary Damages
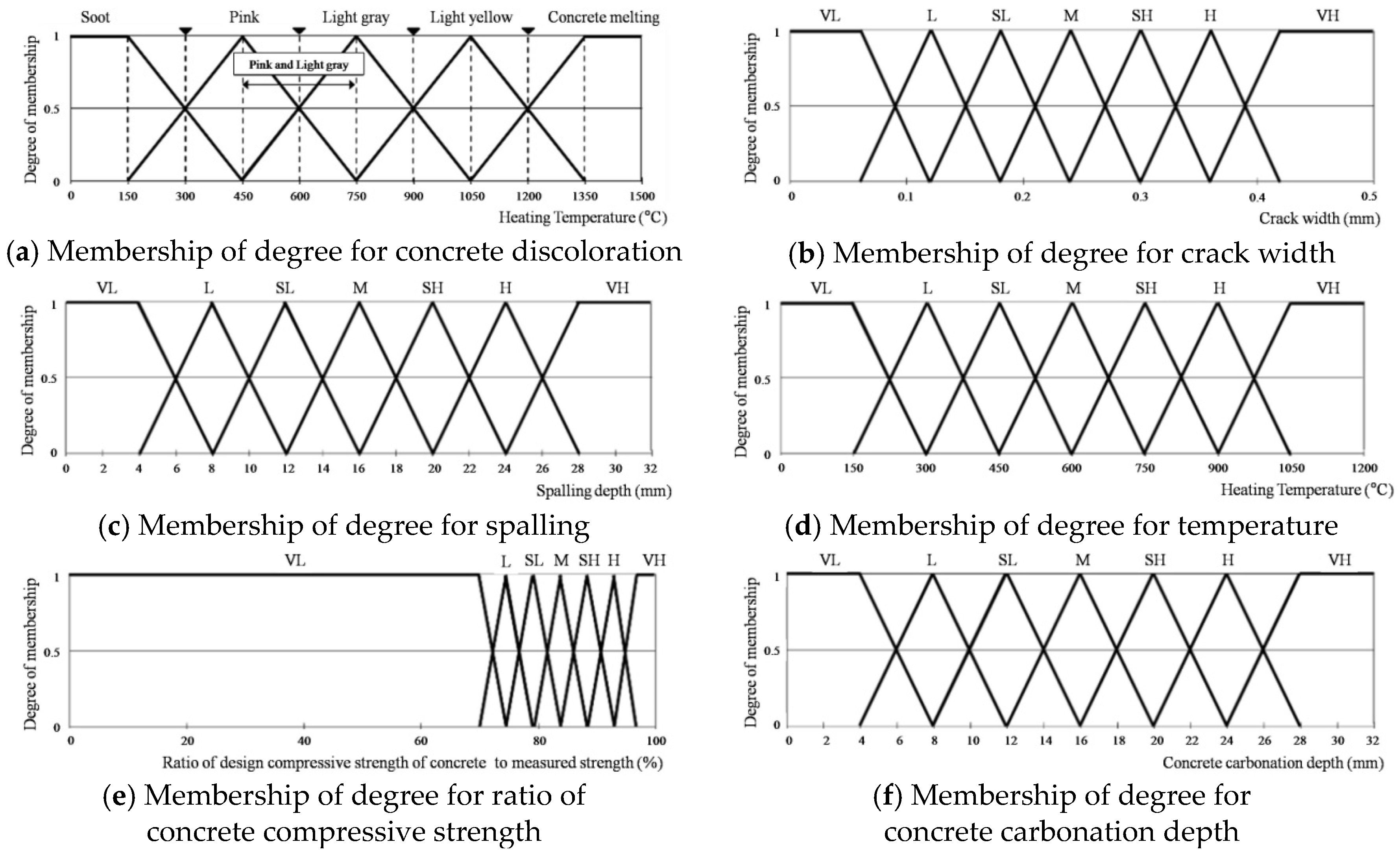
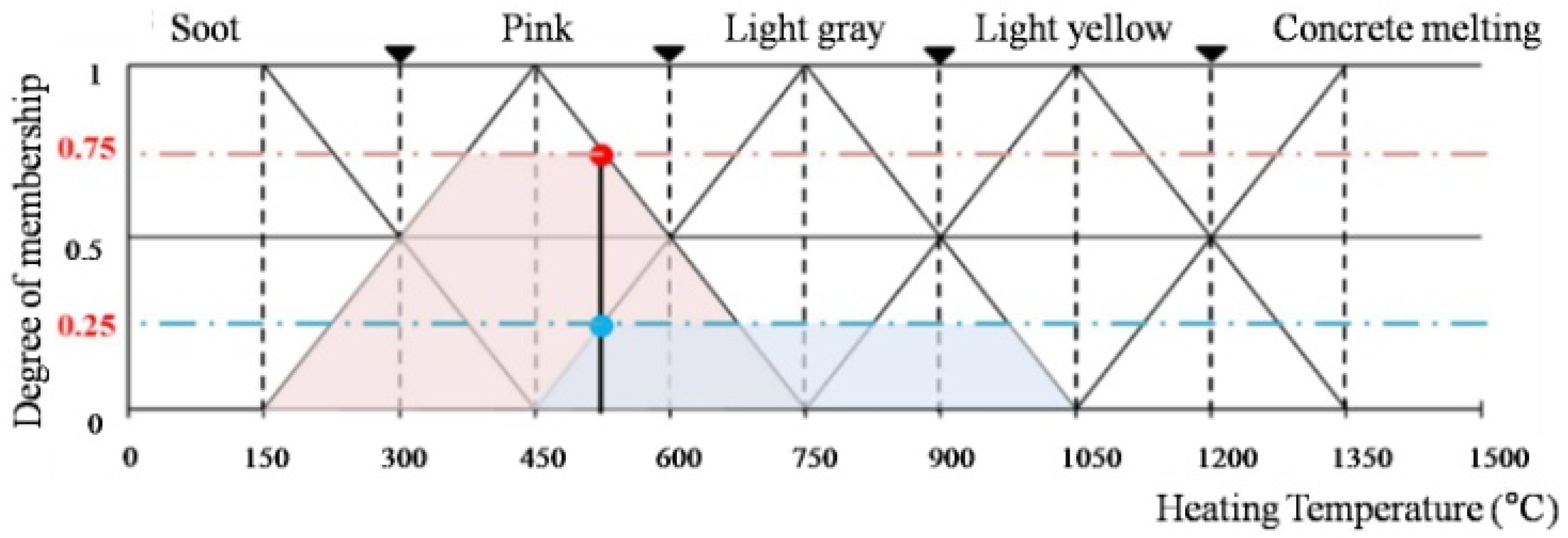
3.2. Membership Function
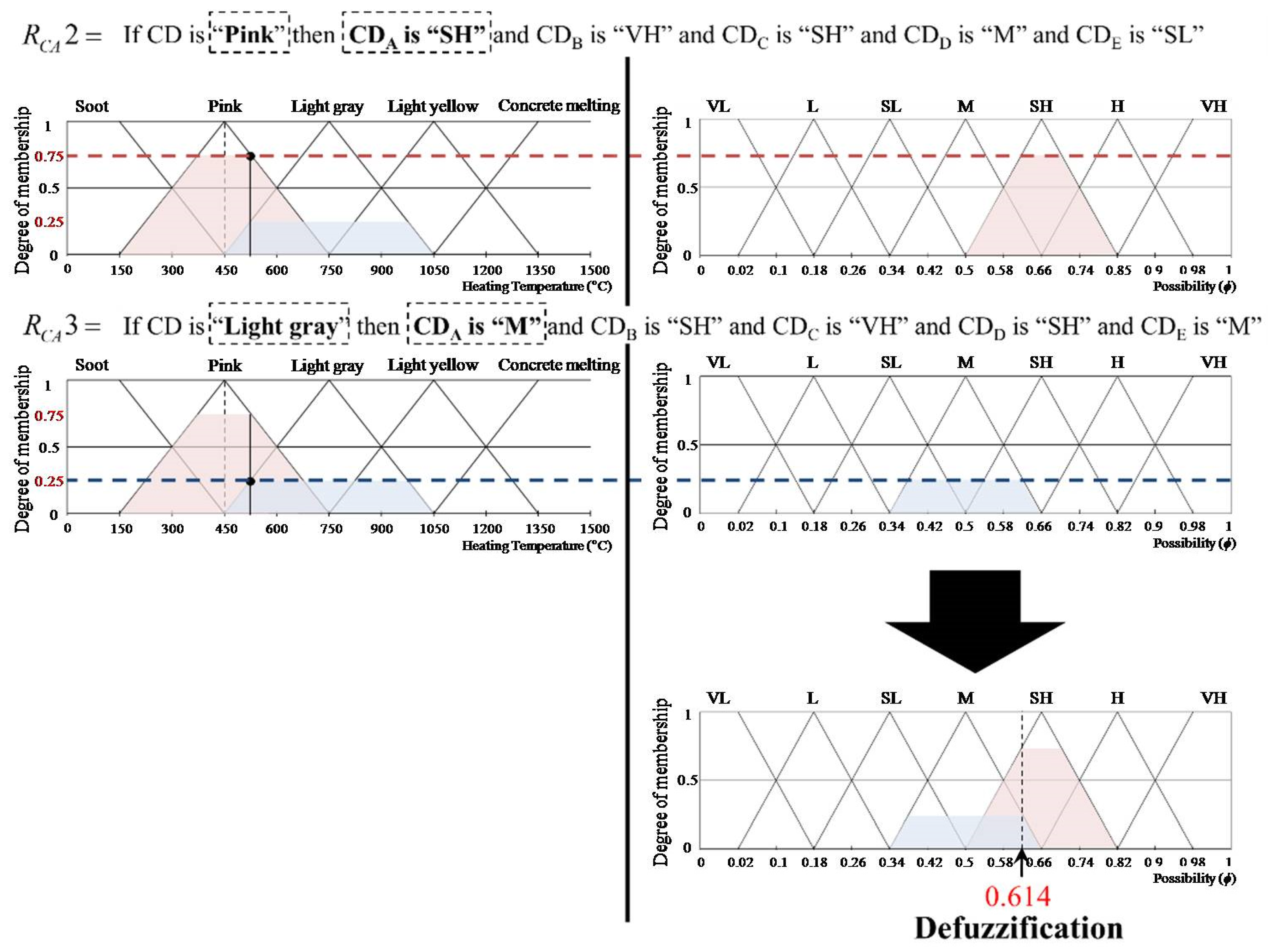
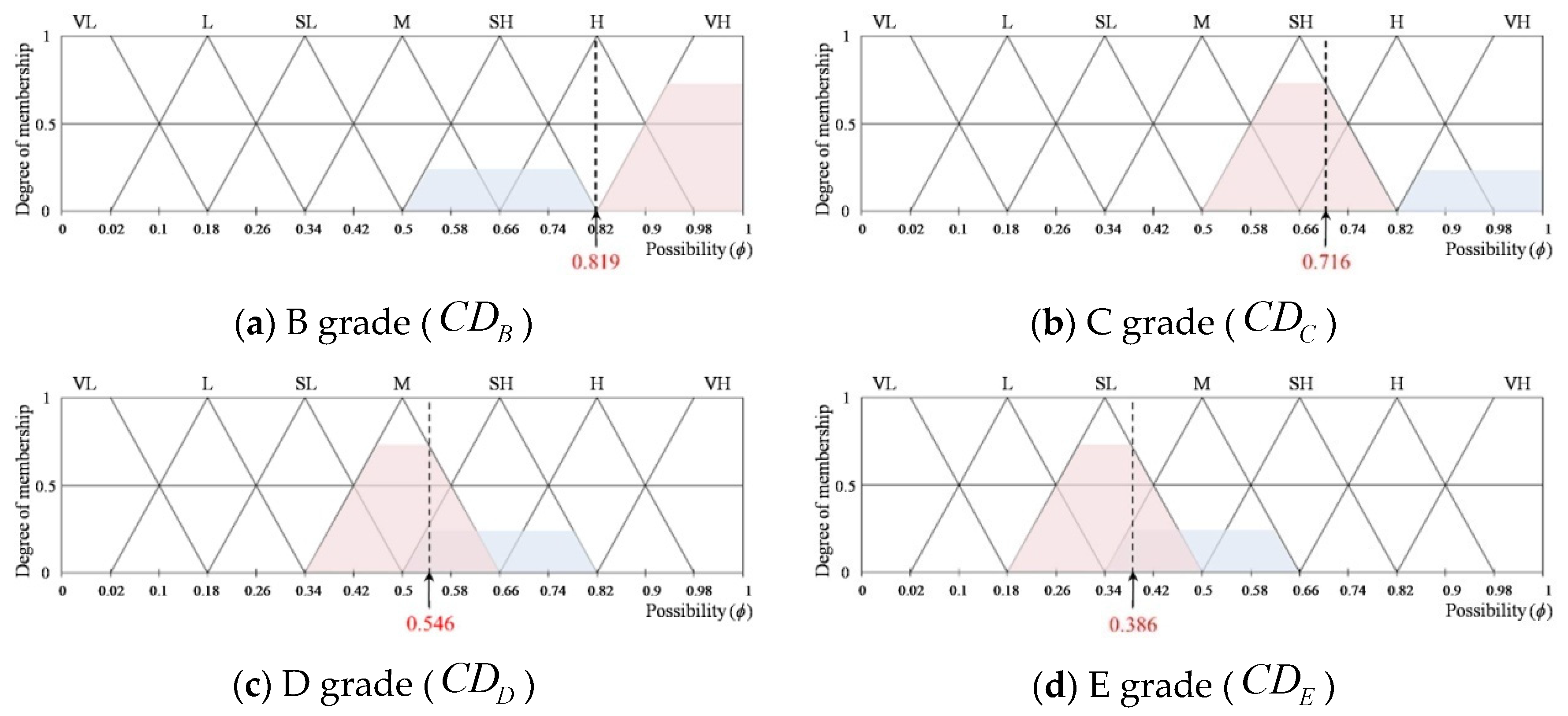
3.3. Process for CPD I
3.4. Process for CPD II
4. Comparison of Evaluation Results
5. Conclusions
- The existing fire damage evaluation methods highly rely on the experience and knowledge of the inspector, and thus, it is hard to ensure the objectiveness and reliability of his/her evaluation results. The fire damage diagnosis system (FDDS) proposed in this study, however, can provide consistent and objective evaluation results because it can ensure comprehensive considerations of the field inspection data in a systematic manner based on fuzzy theory.
- The FDDS evaluation results for the fire-damaged case examined in this study were the same or very close to those estimated by the fire inspection professionals based on the AIJ methods. As the FDDS provides very similar fire damage grades to the inspection method widely used in current practices, it can be now straightly adopted to the field inspection.
- The application of the FDDS can improve the reliability of the fire damage grades of RC members; it can be also very useful to establish appropriate post-fire actions, such as repairing or strengthening of the fire-damaged RC members.
- The fire damage diagnosis system proposed in this study provides the fire damage grades of individual RC members only, but it cannot give the overall fire damage grade of an RC structure at a structural level. Thus, additional research is yet necessary to extend its application to a building-level grade evaluation.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Korea Concrete Institute (KCI). Fire Resistance of Reinforced Concrete Structures; KCI: Seoul, Korea, 2005; 205p. [Google Scholar]
- Architectural Institute of Japan (AIJ). Diagnosis and Repair Methods of Fire-Damaged Buildings; AIJ: Tokyo, Japan, 2004; 140p. [Google Scholar]
- Architectural Institute of Korea (AIK). Repair and Reinforcement of Concrete Structures; AIK: Seoul, Korea, 1997; 181p. [Google Scholar]
- Kwon, Y.J.; Kim, M.H.; Kim, Y.R.; Jang, J.B. The Engineering Properties of Concrete Exposed at High Temperature. Korea Inst. Fire Sci. Eng. 2004, 18, 31–36. [Google Scholar]
- Kwon, Y.J.; Jang, J.B.; Kim, Y.R.; Kim, J.H.; Jang, J.H.; Kim, M.H. A Study on the Diagnosis and Repair Method of Deteriorated Concrete Structure by Fire Damage. Korea Inst. Fire Sci. Eng. 2003, 2003, 230–235. [Google Scholar]
- Zimmermann, H.J. Fuzzy Set Theory and Its Applications; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2001; 544p. [Google Scholar]
- Ross, T.J. Fuzzy Logic with Engineering Applications; Wiley: Hoboken, NJ, USA, 2010; 632p. [Google Scholar]
- Rao, S.S.; Sunsaraju, K.; Praksah, B.G.; Balakrishna, C. Multiobjective Fuzzy Optimization Techniques for Engineering Design. Comput. Struct. 1992, 42, 37–44. [Google Scholar] [CrossRef]
- Mo, Z.G.; Kang, M.M. Structural Optimization by Fuzzy Decision Making. Archit. Inst. Korea 1997, 13, 299–308. [Google Scholar]
- Kim, Y.M.; Kim, C.K.; Hong, G.H.; Hong, S.G. Fuzzy Based Assessment for Reinforced Concrete Building Structures. Archit. Inst. Korea 2001, 17, 123–132. [Google Scholar] [CrossRef]
- Kim, Y.M.; Kim, C.K.; Hong, S.G. Fuzzy set based crack diagnosis system for reinforced concrete structures. Comput. Struct. 2007, 85, 1828–1844. [Google Scholar] [CrossRef]
- Cho, H.C.; Lee, D.H.; Ju, H.; Kim, K.S.; Kim, K.-H.; Monteiro, P.J.M. Remaining service life estimation of reinforced concrete buildings based on fuzzy approach. Comput. Concr. 2015, 15, 879–902. [Google Scholar] [CrossRef]
- Cho, H.C.; Ju, H.; Oh, J.Y.; Lee, K.J.; Hahm, K.W.; Kim, K.S. Estimation of Concrete Carbonation Depth Considering Multiple Influencing Factors on the Deterioration of Durability for Reinforced Concrete Structures. Adv. Mater. Sci. Eng. 2016, 2016, 4814609. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy Sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Jang, J.S.R.; Sun, C.T.; Mizutani, E. Neuro-Fuzzy and Soft Computing; Prentice Hall: Upper Saddle River, NJ, USA, 1997; 614p. [Google Scholar]
- Mamdani, E.H.; Assilina, S. An Experiment in Linguistic Synthesis with a Fuzzy Logic Controller. Int. J. Man-Mach. Stud. 1975, 7, 1–13. [Google Scholar] [CrossRef]
- Jo, H. Fuzzy Based Condition Assessment Model of Middle and Small-Size Buildings. Master’s Thesis, Incheon National University, Incheon, Korea, 2011; 111p. [Google Scholar]
- Korea Infrastructure Safety and Technology Corporation (KISTEC). Safety Inspection Regulations; Ministry of Land, Transport and Maritime Affairs: Sejong, Korea, 2009; 202p. [Google Scholar]
- Kim, S.B.; Choi, S.G.; Han, S.H. Diagnosis and Repair Methods of Fire Damaged Buildings; Kimoondang: Soeul, Korea, 2009; 207p. [Google Scholar]
| Temperature | Damage Level | Grade |
|---|---|---|
| ~300 °C | No damage | I |
| Finishing material damage
(soot, surface exfoliation) | II | |
| 300~600 °C | Concrete damage without steel damage
(small cracks in concrete or spalling) | III |
| 600~950 °C | Bond damage of steel bars
(large cracks in concrete or exposure of steel bars) | IV |
| 950~1200 °C | Damage or buckling of steel bars
(large damage or deformation of structural members, heavy exposure of steel bars in a wide area) | V |
| ~1200 °C | Concrete melting |
| Investigation | Method | ||
|---|---|---|---|
| Primary investigation | Visual inspection | (1) Concrete discoloration | |
| (2) Crack width | |||
| (3) Spalling | |||
| Secondary investigation | Simple inspection | Simple method | (1) Schmidt hammer test |
| (2) Concrete carbonation test | |||
| Detailed inspection | Mechanical test | (1) Concrete core sampling | |
| (2) Steel bar sampling | |||
| (3) Vibration test | |||
| (4) Loading test | |||
| Material analysis | (1) UV spectrum method | ||
| (2)Microwave measurement | |||
| (3) Thermoluminescence measurement | |||
| (4) Ultrasonic test | |||
| (5) X-ray diffraction method | |||
| Numerical analysis | (1) Estimation of Heating temperature | ||
| (2)Evaluation of residual strength | |||
| (3) Structural analysis of fire damaged RC member | |||
| CPD I | Ranges of Grade | Grade | CPD II | Ranges of Grade | Grade |
|---|---|---|---|---|---|
| Concrete discoloration | Soot | A | Heating temperature (°C) | TP ≤ 300 | A |
| Pink | B | 300 ≤ TP < 600 | B | ||
| Light gray | C | 600 ≤ TP < 950 | C | ||
| Light yellow | D | 950 ≤ TP < 1200 | D | ||
| Concrete melting | E | 1200 ≤ TP | E | ||
| Crack width (mm) | CR ≤ 0.1 | A | Crack width (mm) | CR ≤ 0.1 | A |
| 0.1 ≤ CR < 0.2 | B | 0.1 ≤ CR < 0.2 | B | ||
| 0.2 ≤ CR < 0.3 | C | 0.2 ≤ CR < 0.3 | C | ||
| 0.3 ≤ CR < 0.5 | D | 0.3 ≤ CR < 0.5 | D | ||
| 0.5 ≤ CR | E | 0.5 ≤ CR | E | ||
| Spalling (mm) | No spalling | A | Spalling (mm) | No spalling | A |
| SP ≤ 15 | B | SP ≤ 15 | B | ||
| 15 ≤ SP < 20 | C | 15 ≤ SP < 20 | C | ||
| 20 ≤ SP < 25 | D | 20 ≤ SP < 25 | D | ||
| 25 ≤ SP | E | 25 ≤ SP | E | ||
| Ratio of design compressive strength of concrete to measured strength | RCS ≥ 100 (in perfect condition) | A | |||
| RCS ≥ 100 (with slight damage) | B | ||||
| 85 ≤ RCS < 100 | C | ||||
| 70 ≤ RCS < 85 | D | ||||
| 70 ≥ RCS | E | ||||
| Concrete carbonation depth (mm) | CA ≤ 5 | A | |||
| 5 ≤ CA < 10 | B | ||||
| 10 ≤ CA < 15 | C | ||||
| 15 ≤ CA < 30 | D | ||||
| 30 ≤ CA | E |
| Input Parameter | Rule No. | Fuzzy Rule |
|---|---|---|
| Concrete discoloration | RCD 1 | If CD is “soot”, then CDA is “VH” and CDB is “SH” and CDC is “M” and CDD is “SL” and CDE is “VL” |
| RCD 2 | If CD is “pink”, then CDA is “SH” and CDB is “VH” and CDC is “SH” and CDD is “M” and CDE is “SL” | |
| RCD 3 | If CD is “light gray”, then CDA is “M” and CDB is “SH” and CDC is “VH” and CDD is “SH” and CDE is “M” | |
| RCD 4 | If CD is “light blue”, then CDA is “SL” and CDB is “M” and CDC is “SH” and CDD is “VH” and CDE is “SH” | |
| RCD 5 | If CD is “concrete melting”, then CDA is “VH” and CDB is “SH” and CDC is “M” and CDD is “SL” and CDE is “VL” | |
| Crack width | RCR 1 | If CR is “VL”, then CRA is “VH” and CRB is “H” and CRC is “SL” and CRD is “L” and CRE is “VL” |
| RCR 2 | If CR is “L”, then CRA is “H” and CRB is “SH” and CRC is “M” and CRD is “SL” and CRE is “L” | |
| RCR 3 | If CR is “SL”, then CRA is “SH” and CRB is “H” and CRC is “SH” and CRD is “M” and CRE is “SL” | |
| RCR 4 | If CR is “M”, then CRA is “M” and CRB is “VH” and CRC is “H” and CRD is “SH” and CRE is “M” | |
| RCR 5 | If CR is “SH”, then CRA is “SL” and CRB is “H” and CRC is “VH” and CRD is “H” and CRE is “SH” | |
| RCR 6 | If CR is “H”, then CRA is “L” and CRB is “SH” and CRC is “H” and CRD is “VH” and CRE is “H” | |
| RCR 7 | If CR is “VH”, then CRA is “VL” and CRB is “M” and CRC is “SH” and CRD is “H” and CRE is “VH” | |
| Spalling | RSP 1 | If SP is “VL”, then SPA is “VH” and SPB is “H” and SPC is “SL” and SPD is “L” and SPE is “VL” |
| RSP 2 | If SP is “L”, then SPA is “H” and SPB is “SH” and SPC is “M” and SPD is “SL” and SPE is “L” | |
| RSP 3 | If SP is “SL”, then SPA is “SH” and SPB is “H” and SPC is “SH” and SPD is “M” and SPE is “SL” | |
| RSP 4 | If SP is “M”, then SPA is “M” and SPB is “VH” and SPC is “H” and SPD is “SH” and SPE is “M” | |
| RSP 5 | If SP is “SH”, then SPA is “SL” and SPB is “H” and SPC is “VH” and SPD is “H” and SPE is “SH” | |
| RSP 6 | If SP is “H”, then SPA is “L” and SPB is “SH” and SPC is “H” and SPD is “VH” and SPE is “H” | |
| RSP 7 | If SP is “VH”, then SPA is “VL” and SPB is “M”and SPC is “SH” and SPD is “H” and SPE is “VH” | |
| Heating temperature | RTP 1 | If TP is “VL”, then TPA is “VH” and TPB is “H” and TPC is “SL” and TPD is “L” and TPE is “VL” |
| RTP 2 | If TP is “L”, then TPA is “H” and TPB is “SH” and TPC is “M” and TPD is “SL” and TPE is “L” | |
| RTP 3 | If TP is “SL”, then TPA is “SH” and TPB is “H” and TPC is “SH” and TPD is “M” and TPE is “SL” | |
| RTP 4 | If TP is “M”, then TPA is “M” and TPB is “VH” and TPC is “H” and TPD is “SH” and TPE is “M” | |
| RTP 5 | If TP is “SH”, then TPA is “SL” and TPB is “H” and TPC is “VH” and TPD is “H” and TPE is “SH” | |
| RTP 6 | If TP is “H”, then TPA is “L” and TPB is “SH” and TPC is “H” and TPD is “VH” and TPE is “H” | |
| RTP 7 | If TP is “VH”, then TPA is “VL” and TPB is “M” and TPC is “SH” and TPD is “H” and TPE is “VH” | |
| Ratio of designed compressive strength of concrete to measured strength | RRCS 1 | If RCS is “VH”, then RCSA is “VH” and RCSB is “H” and RCSC is “SL” and RCSD is “L” and RCSE is “VL” |
| RRCS 2 | If RCS is “H”, then RCSA is “H” and RCSB is “SH” and RCSC is “M” and RCSD is “SL” and RCSE is “L” | |
| RRCS 3 | If RCS is “SH”, then RCSA is “SH” and RCSB is “H” and RCSC is “SH” and RCSD is “M” and RCSE is “SL” | |
| RRCS 4 | If RCS is “M”, then RCSA is “M” and RCSB is “VH” and RCSC is “H” and RCSD is “SH” and RCSE is “M” | |
| RRCS 5 | If RCS is “SL”, then RCSA is “SL” and RCSB is “H” and RCSC is “VH” and RCSD is “H” and RCSE is “SH” | |
| RRCS 6 | If RCS is “L”, then RCSA is “L” and RCSB is “SH” and RCSC is “H” and RCSD is “VH” and RCSE is “H” | |
| RRCS 7 | If RCS is “VL”, then RCSA is “VL” and RCSB is “M” and RCSC is “SH” and RCSD is “H” and RCSE is “VH” | |
| Concrete carbonation depth | RCA 1 | If CA is “VL”, then CAA is “VH” and CAB is “H” and CAC is “SL” and CAD is “L” and CAE is “VL” |
| RCA 2 | If CA is “L”, then CAA is “H” and CAB is “SH” and CAC is “M” and CAD is “SL” and CAE is “L” | |
| RCA 3 | If CA is “SL”, then CAA is “SH” and CAB is “H” and CAC is “SH” and CAD is “M” and CAE is “SL” | |
| RCA 4 | If CA is “M”, then CAA is “M” and CAB is “VH” and CAC is “H” and CAD is “SH” and CAE is “M” | |
| RCA 5 | If CA is “SH”, then CAA is “SL” and CAB is “H” and CAC is “VH” and CAD is “H” and CAE is “SH” | |
| RCA 1 | If CA is “H”, then CAA is “L” and CAB is “SH” and CAC is “H” and CAD is “VH” and CAE is “H” | |
| RCA 7 | If CA is “VH”, then CAA is “VL” and CAB is “M” and CAC is “SH”and CAD is “H” and CAE is “VH” |
| Survey Item | Weight Factor | |
|---|---|---|
| Concrete discoloration | 5.00 | |
| Heating temperature | ||
| Concrete compressive strength | 3.64 | |
| Concrete crack | 3.78 | |
| Concrete carbonation | 3.49 | |
| Surface condition | Peeling | 3.13 |
| Spalling | 3.19 | |
| Leakage | 3.33 | |
| Exposed steel bar | 3.40 | |
| Inspection Levels | Evaluation Items | Inspection Data | ||||
|---|---|---|---|---|---|---|
| Case 1 (Column) | Case 2 (Wall 1) | Case 3 (Wall 2) | Case 4 (Beam 1) | Case 5 (Beam 2) | ||
| CPD I | Concrete discoloration | Pink | Soot | Pink | Pink | Pink |
| Crack width (mm) | 0.21 | 0.23 | 0.37 | 0.29 | 0.32 | |
| Spalling (mm) | 7 | 19 | 0 | 27.50 | 0 | |
| CPD II | Heating temperature (°C) | 250 | 290 | 290 | 410 | 280 |
| Crack width (mm) | 0.21 | 0.23 | 0.37 | 0.29 | 0.32 | |
| Spalling (mm) | 7 | 19 | 0 | 27.50 | 0 | |
| Ratio of design compressive strength of concrete to measured strength (%) | 90.10 | 92.39 | 91.83 | 74.10 | 87.88 | |
| Concrete carbonation depth (mm) | 13.50 | 26.50 | 26.00 | 10.90 | 16.00 | |
| Case | Inspection Results by Professionals [2,19] | Fire Damage Diagnosis Results by FDDS | |||
|---|---|---|---|---|---|
| CPD I | Possibility | CPD II | Possibility | ||
| Case 1 (Column) | B | B grade | 0.787 | B grade | 0.757 |
| Case 2 (Wall 1) | B | B grade | 0.827 | B grade | 0.793 |
| Case 3 (Wall 2) | B | B grade | 0.852 | B grade | 0.773 |
| Case 4 (Beam 1) | B | C grade | 0.872 | C grade | 0.771 |
| Case 5 (Beam 2) | B | B grade | 0.872 | B grade | 0.824 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cho, H.-C.; Lee, D.H.; Ju, H.; Park, H.-C.; Kim, H.-Y.; Kim, K.S. Fire Damage Assessment of Reinforced Concrete Structures Using Fuzzy Theory. Appl. Sci. 2017, 7, 518. https://doi.org/10.3390/app7050518
Cho H-C, Lee DH, Ju H, Park H-C, Kim H-Y, Kim KS. Fire Damage Assessment of Reinforced Concrete Structures Using Fuzzy Theory. Applied Sciences. 2017; 7(5):518. https://doi.org/10.3390/app7050518
Chicago/Turabian StyleCho, Hae-Chang, Deuck Hang Lee, Hyunjin Ju, Hyun-Cheol Park, Heung-Youl Kim, and Kang Su Kim. 2017. "Fire Damage Assessment of Reinforced Concrete Structures Using Fuzzy Theory" Applied Sciences 7, no. 5: 518. https://doi.org/10.3390/app7050518
APA StyleCho, H.-C., Lee, D. H., Ju, H., Park, H.-C., Kim, H.-Y., & Kim, K. S. (2017). Fire Damage Assessment of Reinforced Concrete Structures Using Fuzzy Theory. Applied Sciences, 7(5), 518. https://doi.org/10.3390/app7050518







