Improved Image Denoising Algorithm Based on Superpixel Clustering and Sparse Representation
Abstract
:1. Introduction
2. Basics of Superpixel Clustering and Sparse Representation (SC-SR) Algorithm
2.1. Simple Linear Iterative Clustering Algorithm for Segmentation
2.2. Sparse Subspace Clustering for Noisy Data
2.3. Sparse Representation Based Image Denoising
3. Proposed SC-SR Algorithm
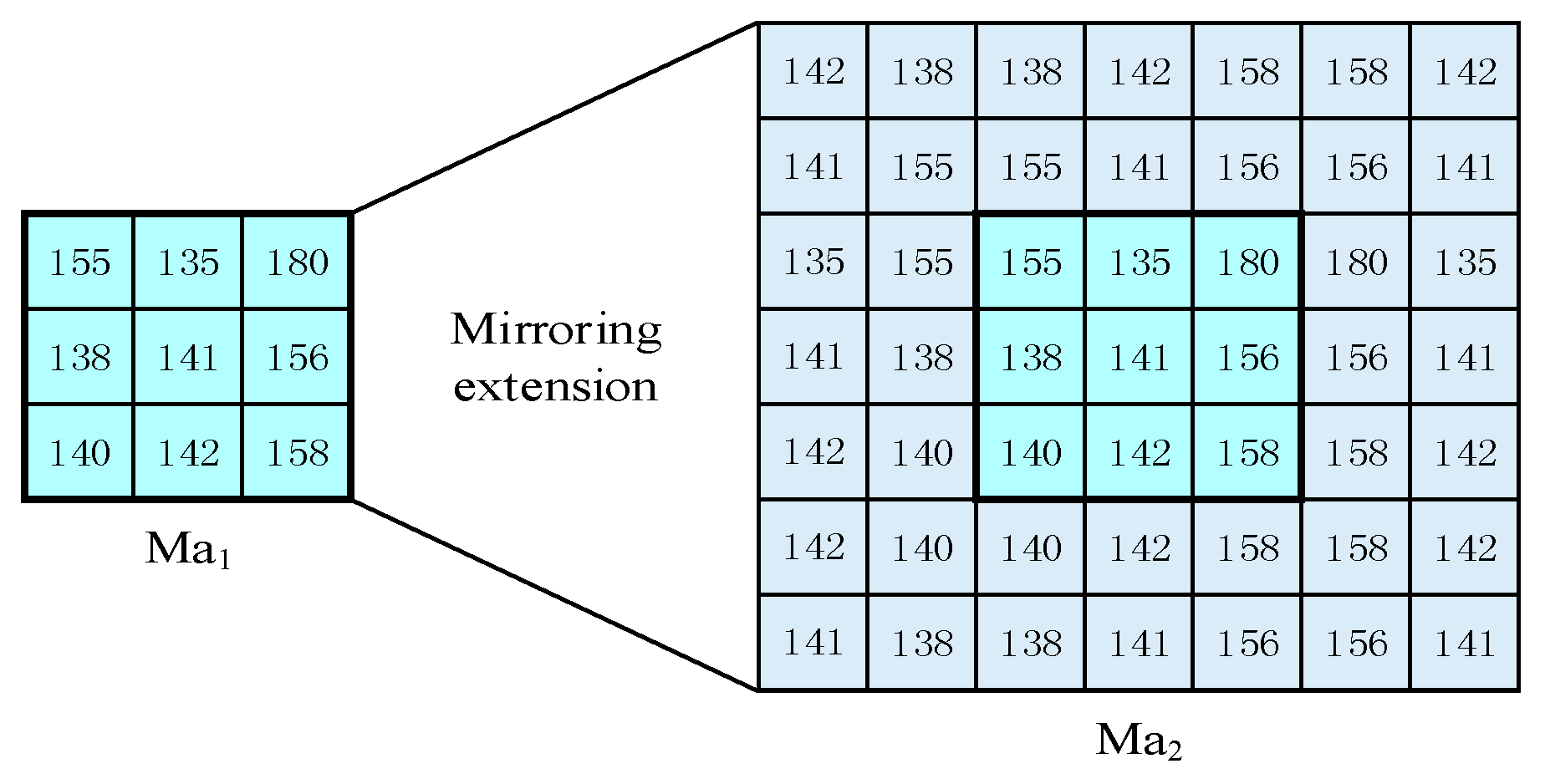
3.1. Superpixels Clustering
3.2. Learning Sub-Dictionaries for Each Cluster of Superpixels
3.3. Sparse Representation Model for Image Denoising
| Algorithm 1. The proposed algorithm called SC-SR |
|
4. Experimental Results
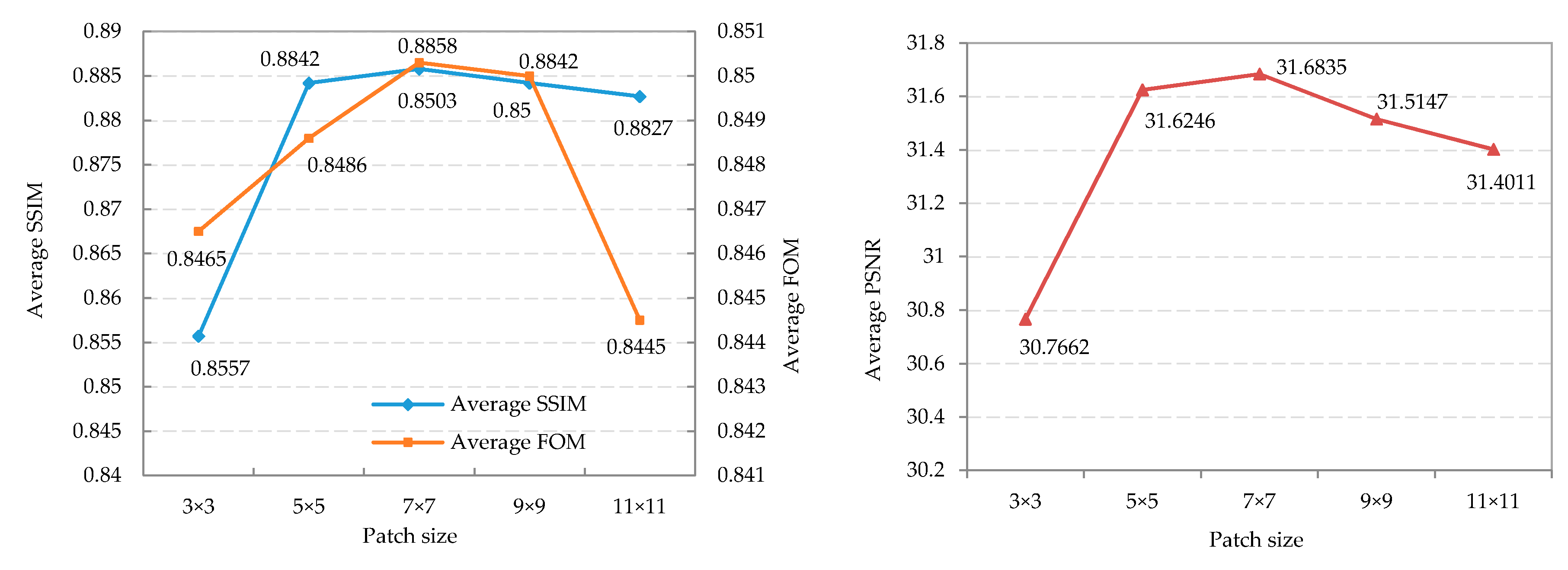
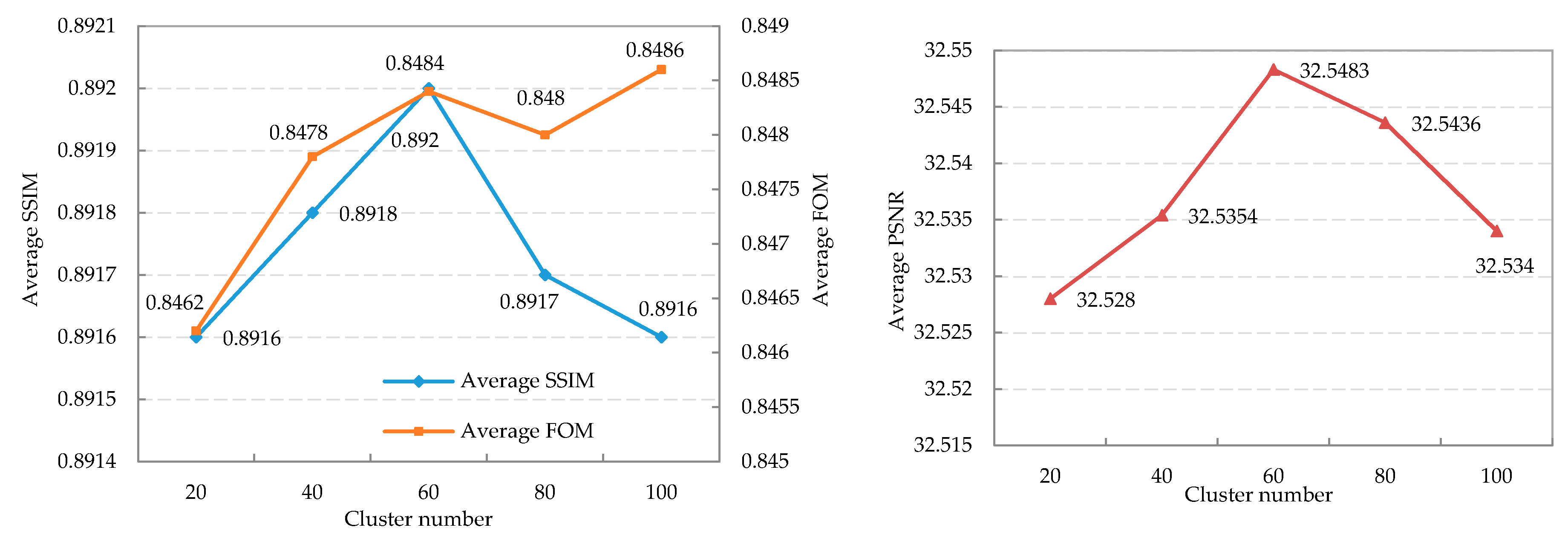
4.1. Parameters Setting
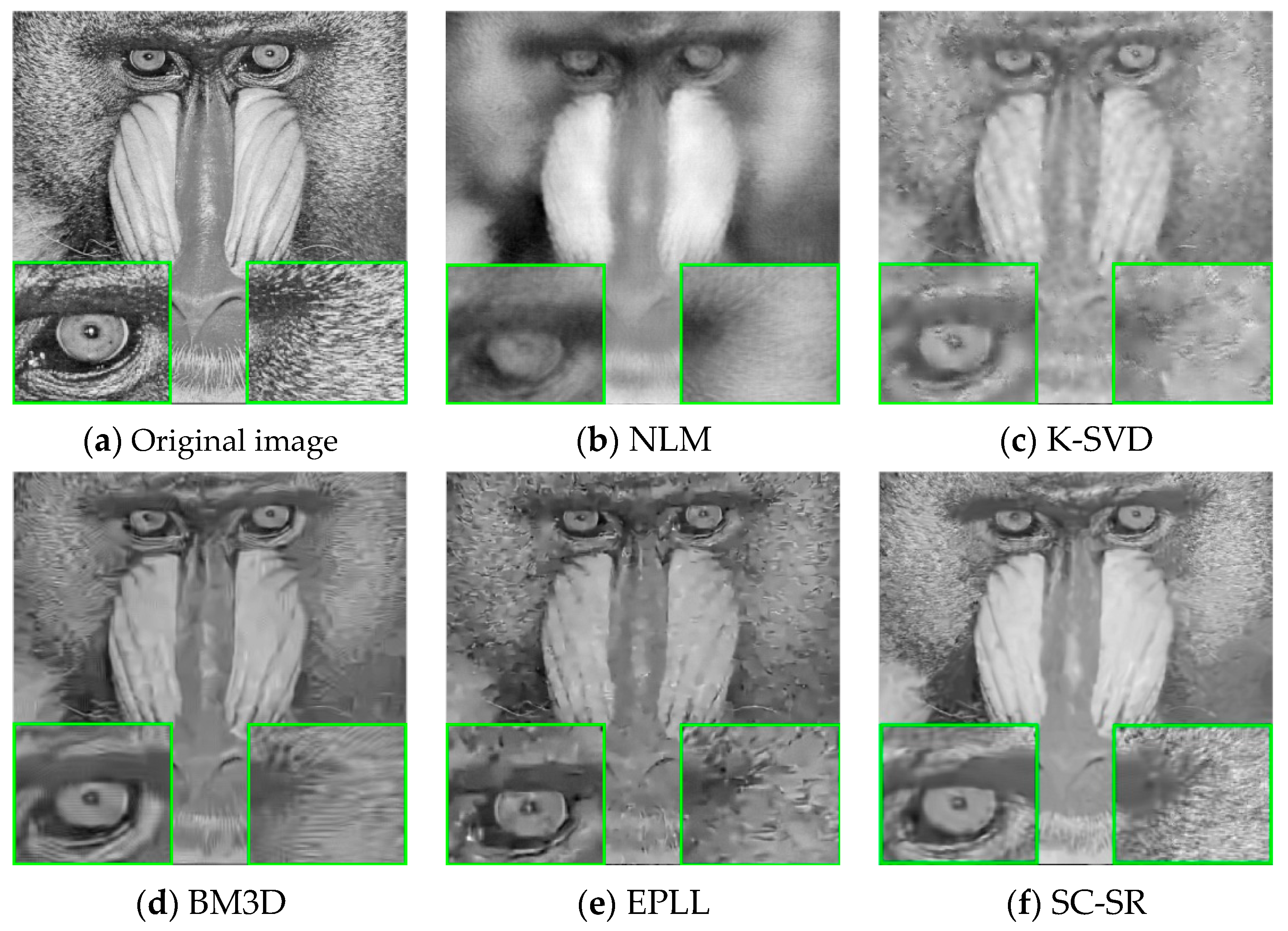
4.2. Qualitative Comparisons
4.3. Quantitative Comparisons
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Buades, A.; Coll, B.; Morel, J.M. A non-local algorithm for image denoising. In Proceedings of the International Conference on Computer Vision and Pattern Recognition (CVPR), San Diego, CA, USA, 20–25 June 2005. [Google Scholar]
- Dabov, K.; Foi, A.; Katkovnik, V.; Egiazarian, K. Image denoising by sparse 3-D transform-domain collaborative filtering. IEEE Trans. Image Process. 2007, 16, 2080–2095. [Google Scholar] [CrossRef] [PubMed]
- Elad, M.; Aharon, M. Image denoising via sparse and redundant representations over learned dictionaries. IEEE Trans. Image Process. 2006, 15, 3736–3745. [Google Scholar] [CrossRef] [PubMed]
- Aharon, M.; Elad, M.; Bruckstein, A. The K-SVD: An algorithm for designing overcomplete dictionaries for sparse representation. IEEE Trans. Signal Process. 2006, 54, 4311–4322. [Google Scholar] [CrossRef]
- Mairal, J.; Bach, F.; Ponce, J.; Sapiro, G.; Zisserman, A. Non-local sparse models for image restoration. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Kyoto, Japan, 27 September–4 October 2009. [Google Scholar]
- Chatterjee, P.; Milanfar, P. Clustering-Based Denoising with locally learned dictionaries. IEEE Trans. Image Process. 2009, 18, 1438–1451. [Google Scholar] [CrossRef] [PubMed]
- Dong, W.S.; Zhang, L.; Shi, G.M.; Li, X. Nonlocally centralized sparse representation for image restoration. IEEE Trans. Image Process. 2013, 22, 1620–1630. [Google Scholar] [CrossRef] [PubMed]
- Gu, S.H.; Zhang, L.; Zuo, W.M.; Feng, X.C. Weighted nuclear norm minimization with application to image denoising. In Proceedings of the International Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014. [Google Scholar]
- Ji, H.; Liu, C.Q.; Shen, Z.W.; Xu, Y.H. Robust video denoising using low rank matrix completion. In Proceedings of the IEEE International Conference on Computer Vision and Pattern Recognition (CVPR), San Francisco, CA, USA, 13–18 June 2010. [Google Scholar]
- Xu, J.; Zhang, L.; Zuo, W.M.; Zhang, D.; Feng, X.C. Patch Group Based Nonlocal Self-Similarity Prior Learning for Image Denoising. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015. [Google Scholar]
- Achanta, R.; Shaji, A.; Smith, K.; Lucchi, A.; Fua, P.; Susstrunk, S. SLIC Superpixels Compared to State-of-the-Art Superpixel Methods. IEEE Trans. Pattern Anal. 2012, 34, 2274–2282. [Google Scholar] [CrossRef] [PubMed]
- Achanta, R.; Shaji, A.; Smith, K.; Lucchi, A.; Fua, P.; Susstrunk, S. SLIC Superpixels; EPFL Technical Report No. 149300; EPFL: Lausanne, Switzerland, 2010. [Google Scholar]
- Elhamifar, E.; Vidal, R. Sparse subspace clustering. In Proceedings of the International Conference on Computer Vision and Pattern Recognition (CVPR), Miami, FL, USA, 20–25 June 2009. [Google Scholar]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. B 1996, 58, 267–288. [Google Scholar]
- Xie, Y.; Lu, H.; Yang, M.H. Bayesian Saliency via Low and Mid-Level Cues. IEEE Trans. Image Process. 2013, 22, 1689–1698. [Google Scholar] [PubMed]
- Dong, W.S.; Zhang, L.; Shi, G.M.; Wu, X.L. Image Deblurring and Super-resolution by Adaptive Sparse Domain Selection and Adaptive Regularization. IEEE Trans. Image Process. 2011, 20, 1838–1857. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Dong, W.; Zhang, D.; Shi, G.M. Two-stage image denoising by principal component analysis with local pixel grouping. IEEE Trans. Image Process. 2010, 43, 1531–1549. [Google Scholar] [CrossRef]
- Wang, J.; Kwon, S.; Shim, B. Generalized orthogonal matching pursuit. IEEE Trans. Signal Process. 2012, 60, 6202–6216. [Google Scholar] [CrossRef]
- Daubechies, I.; Defriese, M.; Mol, C.D. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint. Commun. Pure Appl. Math. 2004, 57, 1413–1457. [Google Scholar] [CrossRef]
- Dong, W.S.; Li, X.; Zhang, L.; Shi, G.M. Sparsity-based Image Denoising via Dictionary Learning and Structural Clustering. In Proceedings of the International Conference on Image Processing (ICIP), Brussels, Belgium, 11–14 September 2011. [Google Scholar]
- Zoran, D.; Weiss, Y. From learning models of natural image patches to whole image restoration. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Barcelona, Spain, 6–13 November 2011. [Google Scholar]
- Gao, X.; Lu, W.; Tao, D.; Li, X. Image quality assessment based on multiscale geometric analysis. IEEE Trans. Image Process. 2009, 18, 1409–1423. [Google Scholar] [PubMed]
- Beck, A.; Teboulle, M. A fast iterative shrinkage thresholding algorithm for linear inverse problems. SIAM J. Imaging Sci. 2009, 2, 183–202. [Google Scholar] [CrossRef]


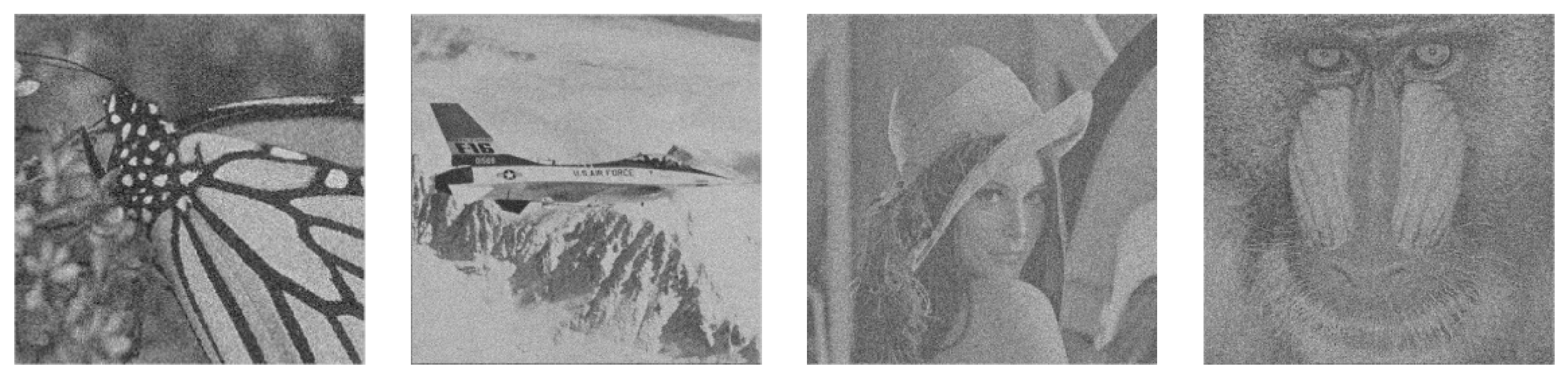




| Images | (a) | ||||
| NLM | KSVD | BM3D | EPLL | SC-SR | |
| Baboon | 34.48 | 35.44 | 35.49 | 35.49 | 35.49 |
| 0.9288 | 0.9536 | 0.9534 | 0.9552 | 0.9519 | |
| 0.9123 | 0.9326 | 0.9297 | 0.9332 | 0.9351 | |
| Fingerprint | 34.44 | 36.63 | 36.51 | 36.43 | 36.65 |
| 0.9807 | 0.9878 | 0.9876 | 0.9875 | 0.9887 | |
| 0.9056 | 0.8919 | 0.9876 | 0.9038 | 0.9642 | |
| Airplane | 37.40 | 39.07 | 39.25 | 39.21 | 39.31 |
| 0.9425 | 0.9584 | 0.9595 | 0.9604 | 0.9598 | |
| 0.9278 | 0.9251 | 0.9331 | 0.9372 | 0.9388 | |
| Monarch | 36.72 | 37.74 | 38.25 | 38.27 | 38.29 |
| 0.9677 | 0.9720 | 0.9756 | 0.9755 | 0.9758 | |
| 0.9789 | 0.9738 | 0.9762 | 0.9771 | 0.9751 | |
| Lena | 37.17 | 38.62 | 38.71 | 38.59 | 38.74 |
| 0.9239 | 0.9455 | 0.9444 | 0.9449 | 0.9450 | |
| 0.9113 | 0.9125 | 0.9303 | 0.9281 | 0.9289 | |
| House | 37.34 | 39.43 | 39.86 | 38.97 | 39.94 |
| 0.9164 | 0.9546 | 0.9568 | 0.9498 | 0.9584 | |
| 0.9383 | 0.9468 | 0.9535 | 0.9395 | 0.9442 | |
| Peppers | 36.70 | 37.81 | 38.10 | 37.98 | 38.15 |
| 0.9409 | 0.9550 | 0.9558 | 0.9562 | 0.9551 | |
| 0.9361 | 0.9378 | 0.9407 | 0.9508 | 0.9506 | |
| Straw | 34.40 | 35.49 | 35.43 | 35.36 | 35.52 |
| 0.9813 | 0.9850 | 0.9848 | 0.9846 | 0.9864 | |
| 0.9200 | 0.9218 | 0.9198 | 0.9143 | 0252 | |
| Hill | 35.53 | 37.00 | 37.13 | 37.03 | 37.18 |
| 0.9085 | 0.9423 | 0.9427 | 0.9437 | 0.9431 | |
| 0.8740 | 0.9181 | 0.9266 | 0.9216 | 0.9256 | |
| Woman | 36.06 | 37.26 | 37.45 | 37.33 | 37.42 |
| 0.9056 | 0.9336 | 0.9325 | 0.9347 | 0.9329 | |
| 0.9104 | 0.9291 | 0.9343 | 0.9306 | 0.9331 | |
| Average | 36.024 | 37.449 | 37.62 | 37.47 | 37.67 |
| 0.9396 | 0.95878 | 0.9593 | 0.9593 | 0.9597 | |
| 0.9215 | 0.92895 | 0.9432 | 0.9336 | 0.9421 | |
| Images | (b) | ||||
| NLM | KSVD | BM3D | EPLL | SC-SR | |
| Baboon | 25.95 | 28.42 | 28.67 | 28.70 | 28.77 |
| 0.6800 | 0.8227 | 0.8327 | 0.8421 | 0.8388 | |
| 0.7051 | 0.8234 | 0.8187 | 0.8117 | 0.7995 | |
| Fingerprint | 27.67 | 30.06 | 30.29 | 29.82 | 30.41 |
| 0.8935 | 0.9462 | 0.9495 | 0.9462 | 0.9510 | |
| 0.6968 | 0.7075 | 0.7760 | 0.7761 | 0.7946 | |
| Airplane | 31.31 | 33.60 | 33.89 | 33.78 | 33.97 |
| 0.8756 | 0.9100 | 0.9162 | 0.9163 | 0.9163 | |
| 0.7677 | 0.8095 | 0.8240 | 0.8540 | 0.8482 | |
| Monarch | 29.73 | 31.45 | 31.97 | 32.06 | 32.10 |
| 0.8999 | 0.9282 | 0.9384 | 0.9379 | 0.9407 | |
| 0.9016 | 0.9226 | 0.9281 | 0.9397 | 0.9386 | |
| Lena | 31.45 | 33.73 | 34.25 | 33.84 | 34.12 |
| 0.8454 | 0.8860 | 0.8953 | 0.8893 | 0.8928 | |
| 0.6457 | 0.7552 | 0.7920 | 0.8185 | 0.8093 | |
| House | 32.64 | 34.34 | 34.96 | 34.12 | 35.02 |
| 0.8561 | 0.8778 | 0.8901 | 0.8768 | 0.8922 | |
| 0.7430 | 0.8541 | 0.8878 | 0.8749 | 0.8769 | |
| Peppers | 30.23 | 32.25 | 32.69 | 32.55 | 32.64 |
| 0.8624 | 0.8998 | 0.9064 | 0.9054 | 0.9050 | |
| 0.8123 | 0.8260 | 0.8408 | 0.8869 | 0.8661 | |
| Straw | 26.67 | 28.57 | 28.65 | 28.53 | 28.72 |
| 0.8661 | 0.9270 | 0.9291 | 0.9281 | 0.9350 | |
| 0.6833 | 0.7960 | 0.8049 | 0.8060 | 0.7952 | |
| Hill | 28.89 | 31.45 | 31.85 | 31.69 | 31.88 |
| 0.7270 | 0.8227 | 0.8394 | 0.8382 | 0.8428 | |
| 0.5812 | 0.7682 | 0.7800 | 0.8013 | 0.7959 | |
| Woman | 29.91 | 31.92 | 32.42 | 32.23 | 32.38 |
| 0.7860 | 0.8433 | 0.8545 | 0.8537 | 0.8543 | |
| 0.6355 | 0.7834 | 0.8018 | 0.8363 | 0.8323 | |
| Average | 29.45 | 31.58 | 31.96 | 31.73 | 32.00 |
| 0.8292 | 0.8864 | 0.8952 | 0.8934 | 0.8969 | |
| 0.7172 | 0.8046 | 0.8254 | 0.8405 | 0.8357 | |
| Images | (c) | ||||
| NLM | KSVD | BM3D | EPLL | SC-SR | |
| Baboon | 22.85 | 25.79 | 26.04 | 26.18 | 26.13 |
| 0.4955 | 0.7081 | 0.7300 | 0.7483 | 0.7300 | |
| 0.4036 | 0.7245 | 0.7174 | 0.7245 | 0.7403 | |
| Fingerprint | 24.32 | 27.30 | 27.72 | 27.14 | 27.79 |
| 0.7979 | 0.8984 | 0.9117 | 0.9050 | 0.9117 | |
| 0.5974 | 0.6371 | 0.7034 | 0.6772 | 0.7321 | |
| Airplane | 28.17 | 30.97 | 31.44 | 31.27 | 31.45 |
| 0.8286 | 0.8719 | 0.8833 | 0.8794 | 0.8865 | |
| 0.6036 | 0.7306 | 0.7419 | 0.7904 | 0.7638 | |
| Monarch | 26.43 | 28.72 | 29.31 | 29.33 | 29.44 |
| 0.8336 | 0.8880 | 0.9031 | 0.9001 | 0.9045 | |
| 0.8066 | 0.8532 | 0.8821 | 0.9024 | 0.9076 | |
| Lena | 28.73 | 31.34 | 32.05 | 31.59 | 31.98 |
| 0.7964 | 0.8428 | 0.8607 | 0.8502 | 0.8615 | |
| 0.4242 | 0.6420 | 0.6885 | 0.7259 | 0.7178 | |
| House | 29.08 | 32.09 | 32.93 | 32.13 | 32.96 |
| 0.8114 | 0.8452 | 0.8595 | 0.8471 | 0.8604 | |
| 0.5850 | 0.7751 | 0.8319 | 0.8077 | 0.8202 | |
| Peppers | 26.79 | 29.68 | 30.21 | 30.07 | 30.18 |
| 0.8023 | 0.8564 | 0.8687 | 0.8652 | 0.8668 | |
| 0.6232 | 0.7385 | 0.7617 | 0.8168 | 0.791 | |
| Straw | 21.98 | 25.71 | 25.92 | 25.80 | 25.90 |
| 0.6225 | 0.8509 | 0.8631 | 0.8607 | 0.8739 | |
| 0.6160 | 0.7132 | 0.7162 | 0.7001 | 0.7155 | |
| Hill | 26.41 | 29.22 | 29.81 | 29.61 | 29.83 |
| 0.6400 | 0.7406 | 0.7748 | 0.7688 | 0.7721 | |
| 0.3723 | 0.6441 | 0.6607 | 0.6947 | 0.6723 | |
| Woman | 27.14 | 29.66 | 30.29 | 30.04 | 30.25 |
| 0.7245 | 0.7853 | 0.8069 | 0.7995 | 0.8053 | |
| 0.4585 | 0.6492 | 0.6854 | 0.7579 | 0.6990 | |
| Average | 26.19 | 29.05 | 29.57 | 29.32 | 29.59 |
| 0.7353 | 0.8288 | 0.8462 | 0.8424 | 0.8473 | |
| 0.5490 | 0.7108 | 0.7389 | 0.7598 | 0.7560 | |
| Images | (d) | ||||
| NLM | KSVD | BM3D | EPLL | SC-SR | |
| Baboon | 21.65 | 23.57 | 23.88 | 24.03 | 24.01 |
| 0.4072 | 0.5570 | 0.6029 | 0.6189 | 0.6057 | |
| 0.2764 | 0.5428 | 0.5252 | 0.5865 | 0.5758 | |
| Fingerprint | 21.31 | 24.71 | 25.29 | 24.72 | 25.45 |
| 0.6613 | 0.8179 | 0.8587 | 0.8433 | 0.8563 | |
| 0.5515 | 0.6274 | 0.6179 | 0.5513 | 0.6536 | |
| Airplane | 25.32 | 28.53 | 29.06 | 28.98 | 29.13 |
| 0.7797 | 0.8231 | 0.8401 | 0.8335 | 0.8515 | |
| 0.4750 | 0.6135 | 0.6570 | 0.7161 | 0.6792 | |
| Monarch | 23.12 | 26.56 | 26.72 | 27.03 | 26.77 |
| 0.7517 | 0.8344 | 0.8485 | 0.8487 | 0.8521 | |
| 0.6844 | 0.8143 | 0.8259 | 0.8537 | 0.8128 | |
| Lena | 26.53 | 29.06 | 29.86 | 29.43 | 29.92 |
| 0.7511 | 0.7928 | 0.8159 | 0.8005 | 0.8253 | |
| 0.3266 | 0.4858 | 0.5677 | 0.6164 | 0.5769 | |
| House | 25.96 | 29.59 | 30.64 | 29.74 | 30.71 |
| 0.7569 | 0.7996 | 0.8256 | 0.8020 | 0.8356 | |
| 0.4821 | 0.6676 | 0.7350 | 0.7058 | 0.7229 | |
| Peppers | 23.71 | 27.33 | 27.79 | 27.59 | 27.68 |
| 0.7328 | 0.8046 | 0.8181 | 0.8134 | 0.8223 | |
| 0.4603 | 0.6523 | 0.6862 | 0.7412 | 0.6686 | |
| Straw | 19.66 | 22.93 | 23.19 | 23.28 | 23.38 |
| 0.4039 | 0.6928 | 0.7435 | 0.7397 | 0.7425 | |
| 0.5265 | 0.5529 | 0.5933 | 0.5560 | 0.5950 | |
| Hill | 24.71 | 27.15 | 27.93 | 27.76 | 28.05 |
| 0.5766 | 0.6562 | 0.7053 | 0.6963 | 0.7039 | |
| 0.2446 | 0.4413 | 0.5207 | 0.5629 | 0.5388 | |
| Woman | 25.01 | 27.61 | 28.31 | 28.08 | 28.38 |
| 0.6722 | 0.7258 | 0.7501 | 0.7383 | 0.7556 | |
| 0.3546 | 0.5039 | 0.5578 | 0.6506 | 0.5694 | |
| Average | 23.70 | 26.70 | 27.27 | 27.06 | 27.35 |
| 0.6493 | 0.7504 | 0.7809 | 0.7735 | 0.7851 | |
| 0.4382 | 0.5902 | 0.6287 | 0.6541 | 0.6393 | |
| Images | (e) | ||||
| NLM | KSVD | BM3D | EPLL | SC-SR | |
| Baboon | 20.95 | 22.08 | 22.38 | 22.48 | 22.56 |
| 0.3568 | 0.4356 | 0.4685 | 0.4890 | 0.4901 | |
| 0.2680 | 0.3077 | 0.3173 | 0.4114 | 0.4358 | |
| Fingerprint | 18.95 | 21.77 | 23.59 | 22.65 | 23.63 |
| 0.4952 | 0.6804 | 0.7974 | 0.7597 | 0.7900 | |
| 0.5073 | 0.4908 | 0.5027 | 0.4514 | 0.5731 | |
| Airplane | 23.27 | 26.01 | 27.01 | 26.95 | 27.13 |
| 0.7273 | 0.7602 | 0.7860 | 0.7767 | 0.8163 | |
| 0.3625 | 0.4633 | 0.5389 | 0.6253 | 0.5881 | |
| Monarch | 20.43 | 24.22 | 24.58 | 24.72 | 24.81 |
| 0.6503 | 0.7618 | 0.7777 | 0.7795 | 0.8006 | |
| 0.5406 | 0.7315 | 0.7300 | 0.7614 | 0.7472 | |
| Lena | 24.59 | 26.90 | 27.98 | 27.60 | 28.05 |
| 0.6999 | 0.7328 | 0.7636 | 0.7465 | 0.7871 | |
| 0.2777 | 0.3298 | 0.4394 | 0.5013 | 0.4753 | |
| House | 23.59 | 26.75 | 28.49 | 27.90 | 28.53 |
| 0.6967 | 0.7252 | 0.7768 | 0.7636 | 0.7669 | |
| 0.3941 | 0.4638 | 0.6288 | 0.6379 | 0.6204 | |
| Peppers | 21.15 | 25.02 | 25.51 | 25.67 | 25.45 |
| 0.6634 | 0.7386 | 0.7479 | 0.7621 | 0.7717 | |
| 0.3990 | 0.5282 | 0.5401 | 0.6354 | 0.5801 | |
| Straw | 18.59 | 20.51 | 21.26 | 20.99 | 21.39 |
| 0.2785 | 0.4726 | 0.5824 | 0.5521 | 0.5970 | |
| 0.4419 | 0.4592 | 0.4804 | 0.4240 | 0.4837 | |
| Hill | 23.54 | 25.61 | 26.35 | 26.20 | 26.29 |
| 0.5283 | 0.5928 | 0.6332 | 0.6262 | 0.6355 | |
| 0.2153 | 0.2665 | 0.4002 | 0.4424 | 0.4223 | |
| Woman | 23.47 | 25.86 | 26.55 | 26.43 | 26.49 |
| 0.6251 | 0.6701 | 0.6948 | 0.6810 | 0.7063 | |
| 0.3299 | 0.3405 | 0.4232 | 0.5175 | 0.4604 | |
| Average | 21.85 | 24.47 | 25.37 | 25.16 | 25.43 |
| 0.5722 | 0.6570 | 0.7028 | 0.6936 | 0.7162 | |
| 0.3736 | 0.4381 | 0.5001 | 0.5408 | 0.5386 | |
| Images | (f) | ||||
| NLM | KSVD | BM3D | EPLL | SC-SR | |
| Baboon | 20.68 | 21.40 | 21.64 | 21.68 | 21.71 |
| 0.3379 | 0.3860 | 0.4049 | 0.4186 | 0.4137 | |
| 0.2387 | 0.2205 | 0.2224 | 0.2889 | 0.2988 | |
| Fingerprint | 17.75 | 19.55 | 22.39 | 21.12 | 22.39 |
| 0.3781 | 0.5355 | 0.7478 | 0.6770 | 0.7347 | |
| 0.4376 | 0.4397 | 0.4699 | 0.3869 | 0.4956 | |
| Airplane | 22.05 | 24.18 | 25.54 | 25.61 | 25.63 |
| 0.6723 | 0.6981 | 0.7453 | 0.7292 | 0.7902 | |
| 0.3280 | 0.3511 | 0.4741 | 0.5509 | 0.5399 | |
| Monarch | 22.52 | 22.52 | 23.20 | 23.42 | 23.29 |
| 0.5569 | 0.7050 | 0.7237 | 0.7313 | 0.7553 | |
| 0.4911 | 0.6201 | 0.6733 | 0.7203 | 0.6947 | |
| Lena | 23.41 | 25.44 | 26.65 | 26.14 | 26.71 |
| 0.6597 | 0.6846 | 0.7225 | 0.6952 | 0.7568 | |
| 0.2670 | 0.2793 | 0.3720 | 0.4114 | 0.3997 | |
| House | 22.29 | 24.80 | 26.94 | 26.22 | 26.74 |
| 0.6442 | 0.6584 | 0.7379 | 0.7098 | 0.7669 | |
| 0.3322 | 0.3521 | 0.5329 | 0.5557 | 0.5204 | |
| Peppers | 19.78 | 22.97 | 24.12 | 24.19 | 24.06 |
| 0.6038 | 0.6710 | 0.7006 | 0.7103 | 0.7391 | |
| 0.3690 | 0.4105 | 0.4783 | 0.5880 | 0.5396 | |
| Straw | 18.21 | 19.22 | 19.94 | 19.80 | 20.01 |
| 0.2248 | 0.3306 | 0.4410 | 0.4210 | 0.4584 | |
| 0.3582 | 0.3758 | 0.3812 | 0.3344 | 0.4187 | |
| Hill | 22.84 | 24.66 | 25.28 | 25.19 | 25.23 |
| 0.4993 | 0.5544 | 0.5865 | 0.5784 | 0.5967 | |
| 0.1925 | 0.2137 | 0.3179 | 0.3352 | 0.3349 | |
| Woman | 22.58 | 24.55 | 25.39 | 25.29 | 25.24 |
| 0.5967 | 0.6279 | 0.6551 | 0.6419 | 0.6739 | |
| 0.2998 | 0.2612 | 0.3610 | 0.4118 | 0.3976 | |
| Average | 21.21 | 22.93 | 24.10 | 23.87 | 24.11 |
| 0.5174 | 0.5852 | 0.6465 | 0.6313 | 0.6686 | |
| 0.3314 | 0.3524 | 0.4283 | 0.4584 | 0.4640 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Xiao, X.; Peng, X.; Liu, Y.; Zhao, W. Improved Image Denoising Algorithm Based on Superpixel Clustering and Sparse Representation. Appl. Sci. 2017, 7, 436. https://doi.org/10.3390/app7050436
Wang H, Xiao X, Peng X, Liu Y, Zhao W. Improved Image Denoising Algorithm Based on Superpixel Clustering and Sparse Representation. Applied Sciences. 2017; 7(5):436. https://doi.org/10.3390/app7050436
Chicago/Turabian StyleWang, Hai, Xue Xiao, Xiongyou Peng, Yan Liu, and Wei Zhao. 2017. "Improved Image Denoising Algorithm Based on Superpixel Clustering and Sparse Representation" Applied Sciences 7, no. 5: 436. https://doi.org/10.3390/app7050436
APA StyleWang, H., Xiao, X., Peng, X., Liu, Y., & Zhao, W. (2017). Improved Image Denoising Algorithm Based on Superpixel Clustering and Sparse Representation. Applied Sciences, 7(5), 436. https://doi.org/10.3390/app7050436







