Research on the Blind Source Separation Method Based on Regenerated Phase-Shifted Sinusoid-Assisted EMD and Its Application in Diagnosing Rolling-Bearing Faults
Abstract
:1. Introduction
2. Theoretical Descriptions
2.1. Regenerated Phase-Shifted Sinusoid-Assisted EMD Theory
- (a)
- Gaussian white noise with mean zero and standard deviation is added to the decomposed signal . Meanwhile, the normalization treatment is carried out;
- (b)
- The IMFs of all the scales are obtained by using EMD algorithm to decompose the normalized signal;
- (c)
- Repeat the above two steps (a)–(b) for n times, where the added random white noise for every time is required to obey normal distribution;
- (d)
- Make an average of n-groups totality of IMF components by EMD decomposition and obtain , where is the i-th IMF components obtained from the j-th decomposition and is the remainder.
- (a)
- Initialize ;
- (b)
- Apply standard EMD algorithm to and then determine and with the resulting IMFs. is acquired by uniformly sampling in with the phase shifting number (). After this, is obtained.
- (c)
- The standard EMD algorithm of is performed, which aims to obtain the first IMF. The final IMF is calculated by averaging all these first IMFs.
- (d)
- Remove from : . Let
- (e)
- Repeat the above steps (b)–(d) multiple times until no more IMF can be produced. Consequently, the final is regarded as the residue .
2.2. The Basic Principle of Blind Source Separation
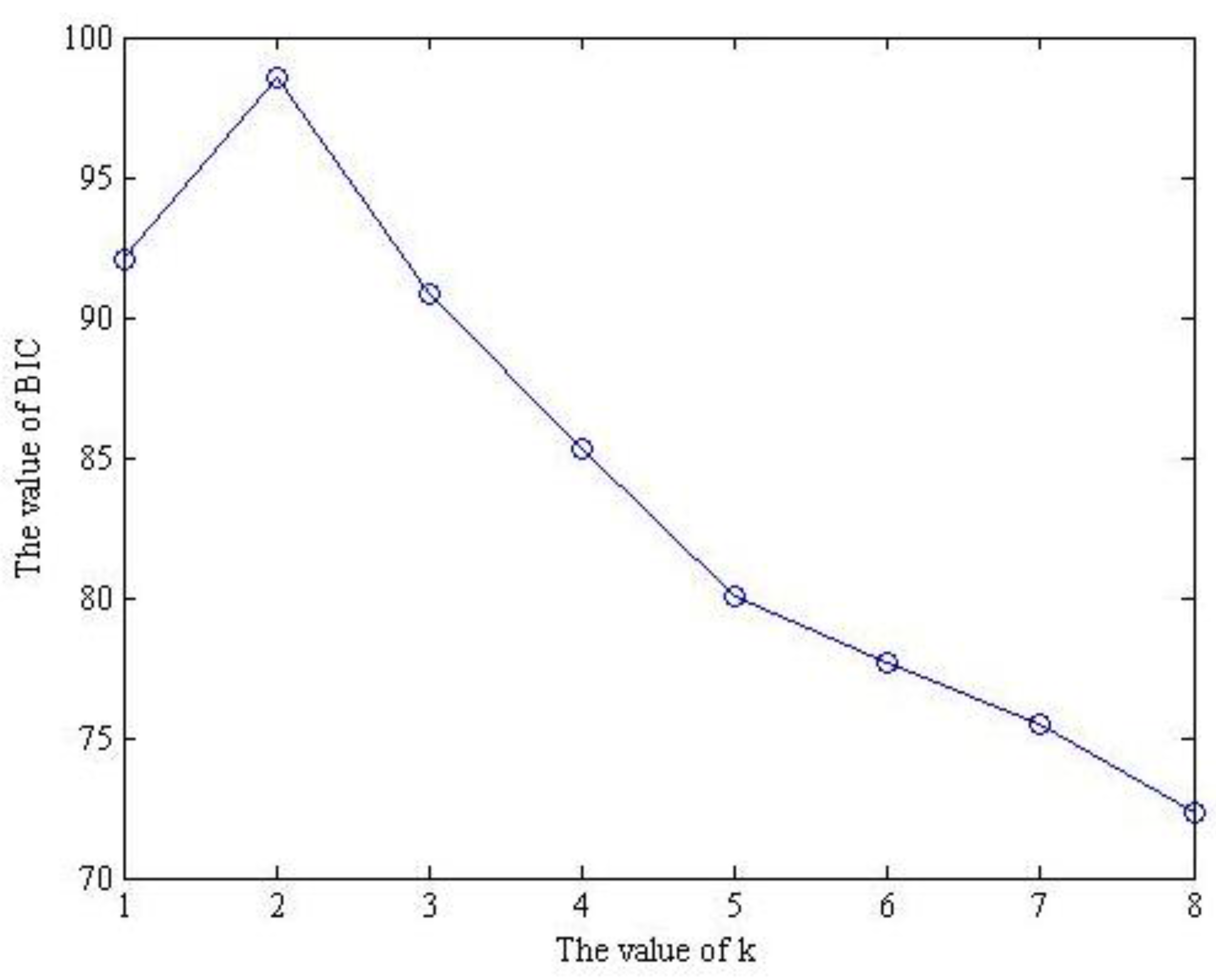
2.3. Source Number Estimation Based on Bayesian Information Criterion
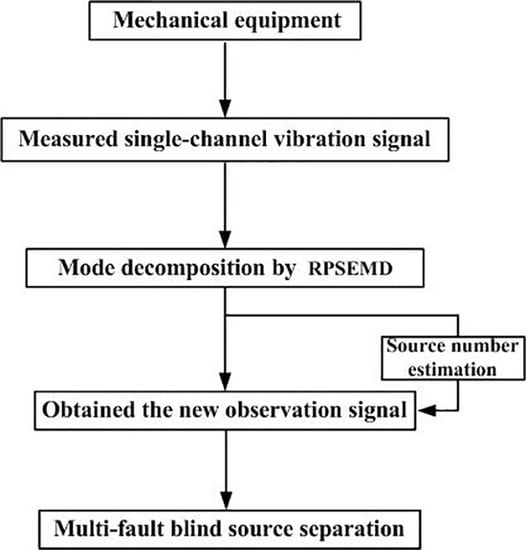
2.4. The Main Computational Steps of the Proposed Method
- (1)
- Decompose the single-channel observation signal by RPSEMD, with a series of linear and stationary IMFs and residual component being obtained;
- (2)
- The new multi-dimensional observation signal is composed by IMFs obtained from RPSEMD and the original signal itself. In this way, the dimension of the observation signal can be increased, so that the new observation signal can be analyzed in accordance with the blind source separation theory;
- (3)
- Estimate the number of source signals by employing the Bayes information criteria;
- (4)
- According to the estimation number of the source signal, the method of feature matrix joint diagonalization based on the four-order accumulation is used to perform blind source separation on the recombination observation signal , so as to obtain the estimation of the source signal .
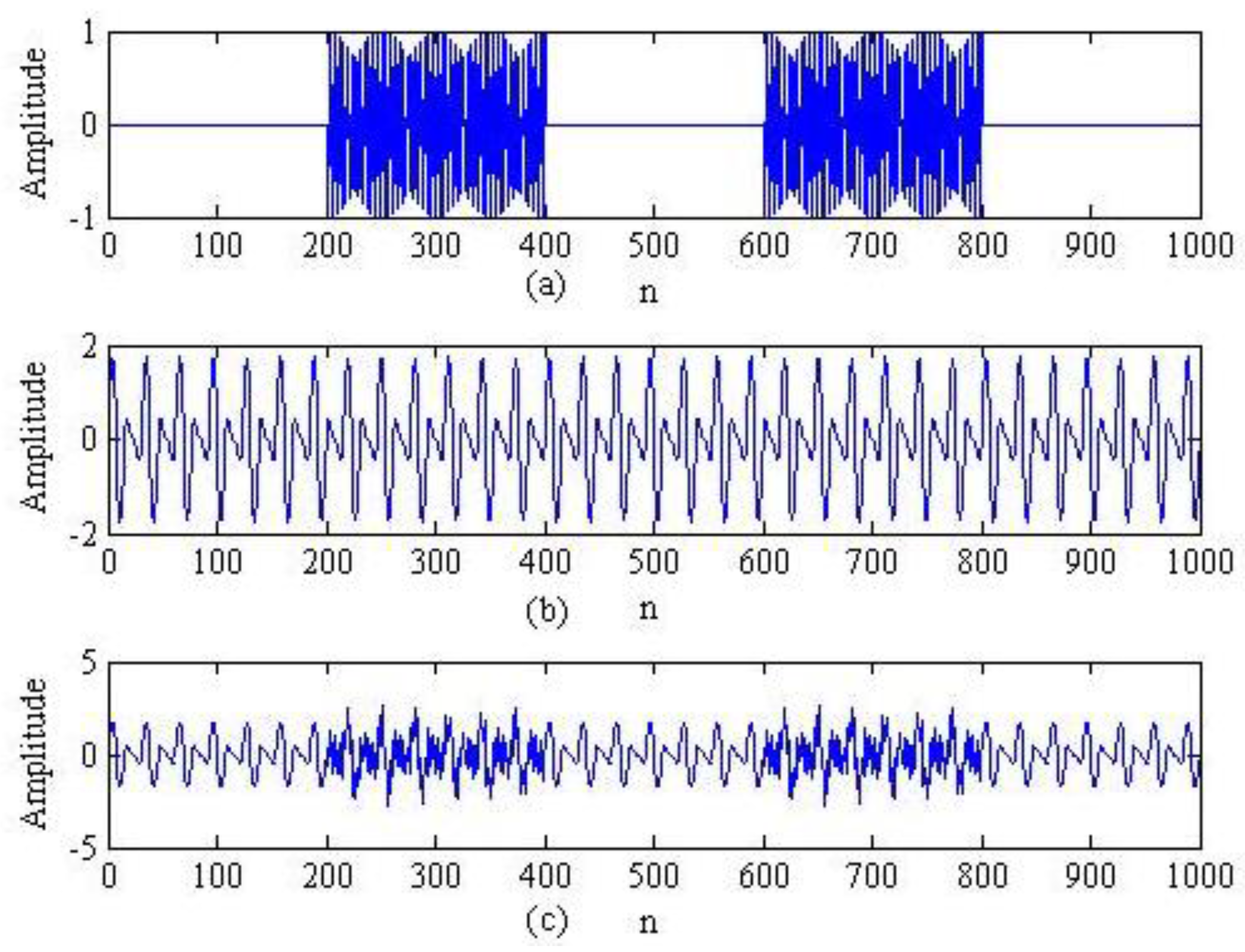
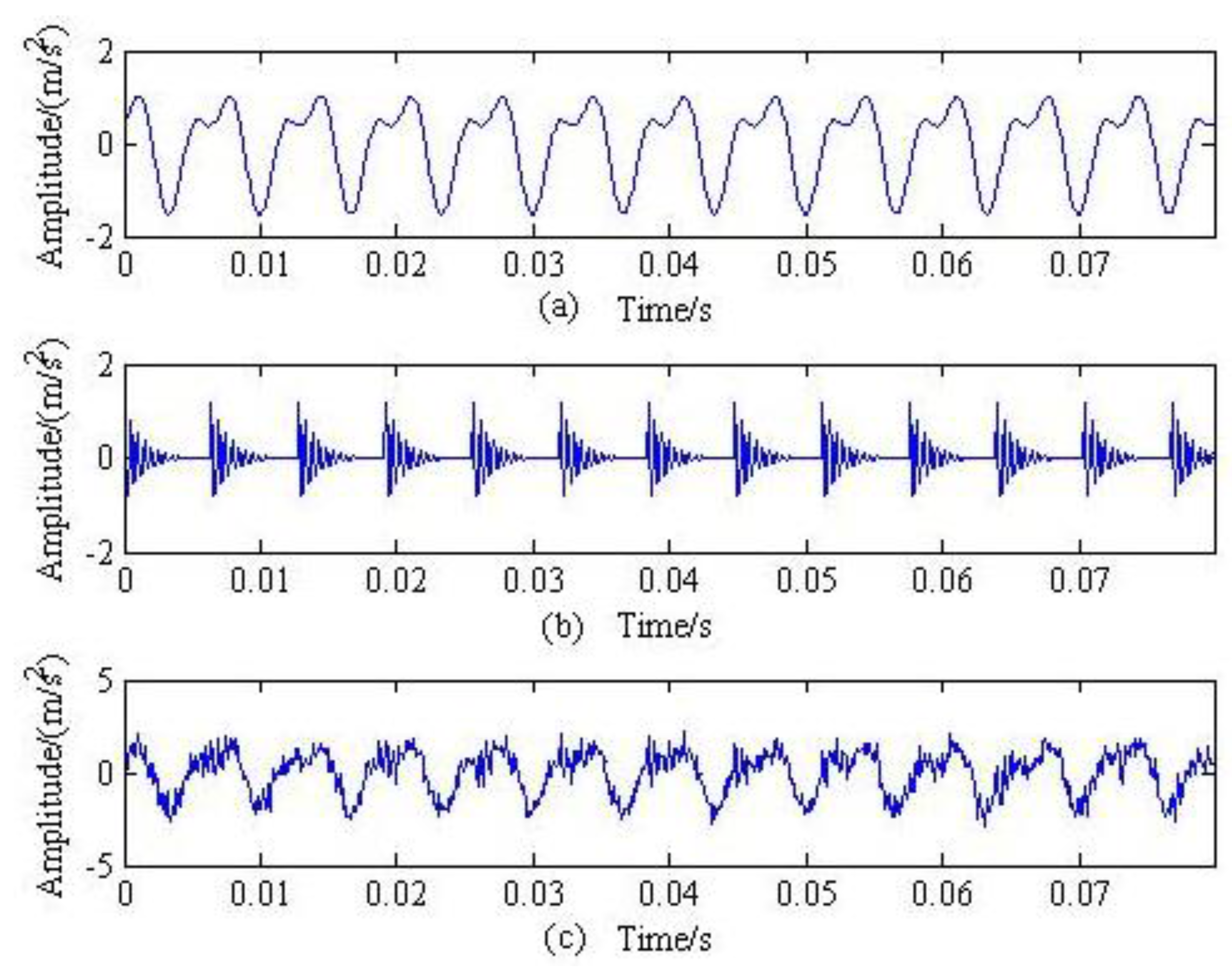
3. Simulation Signal Analysis
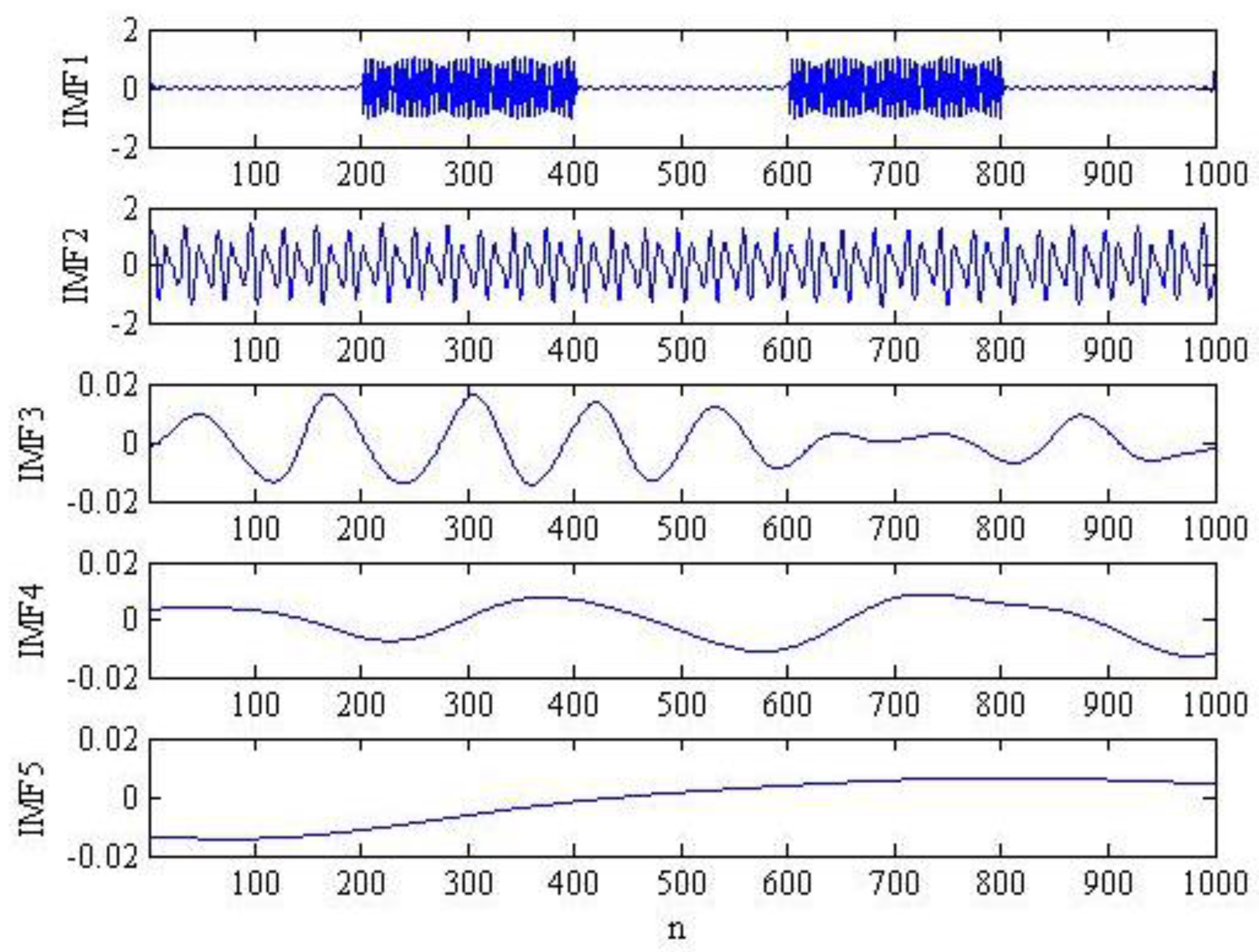
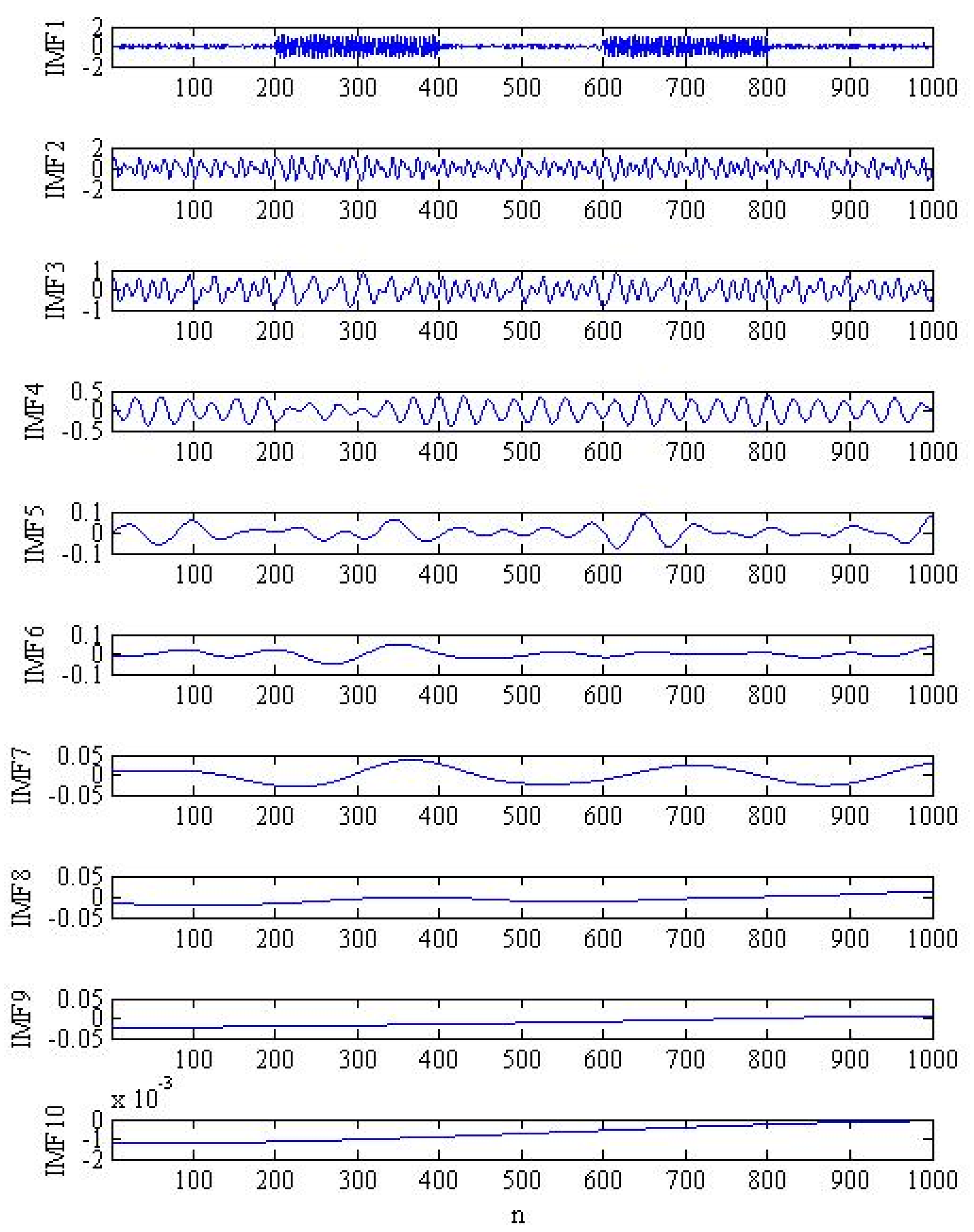
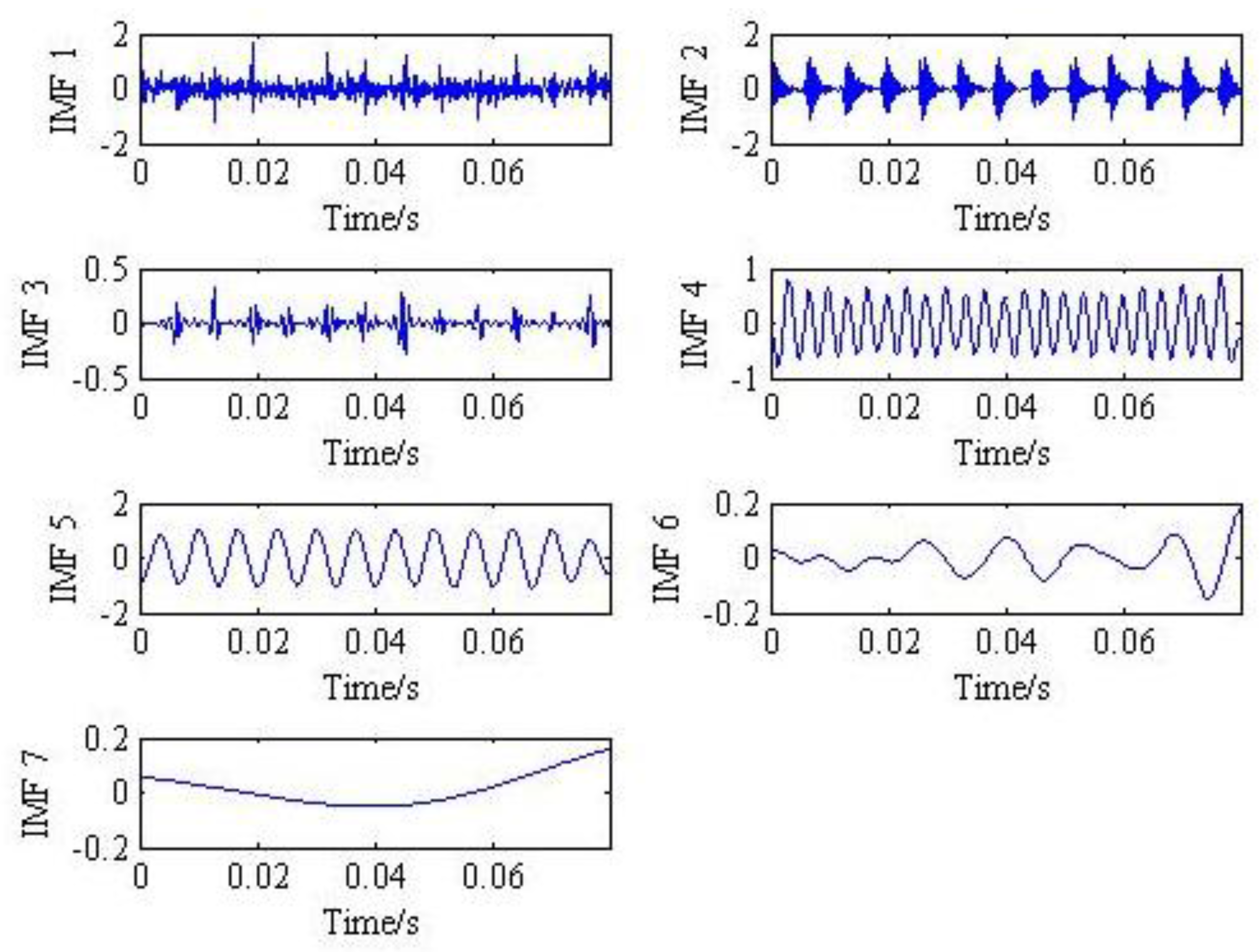
3.1. The Performance of Mode Decomposition Provided by the Proposed Method
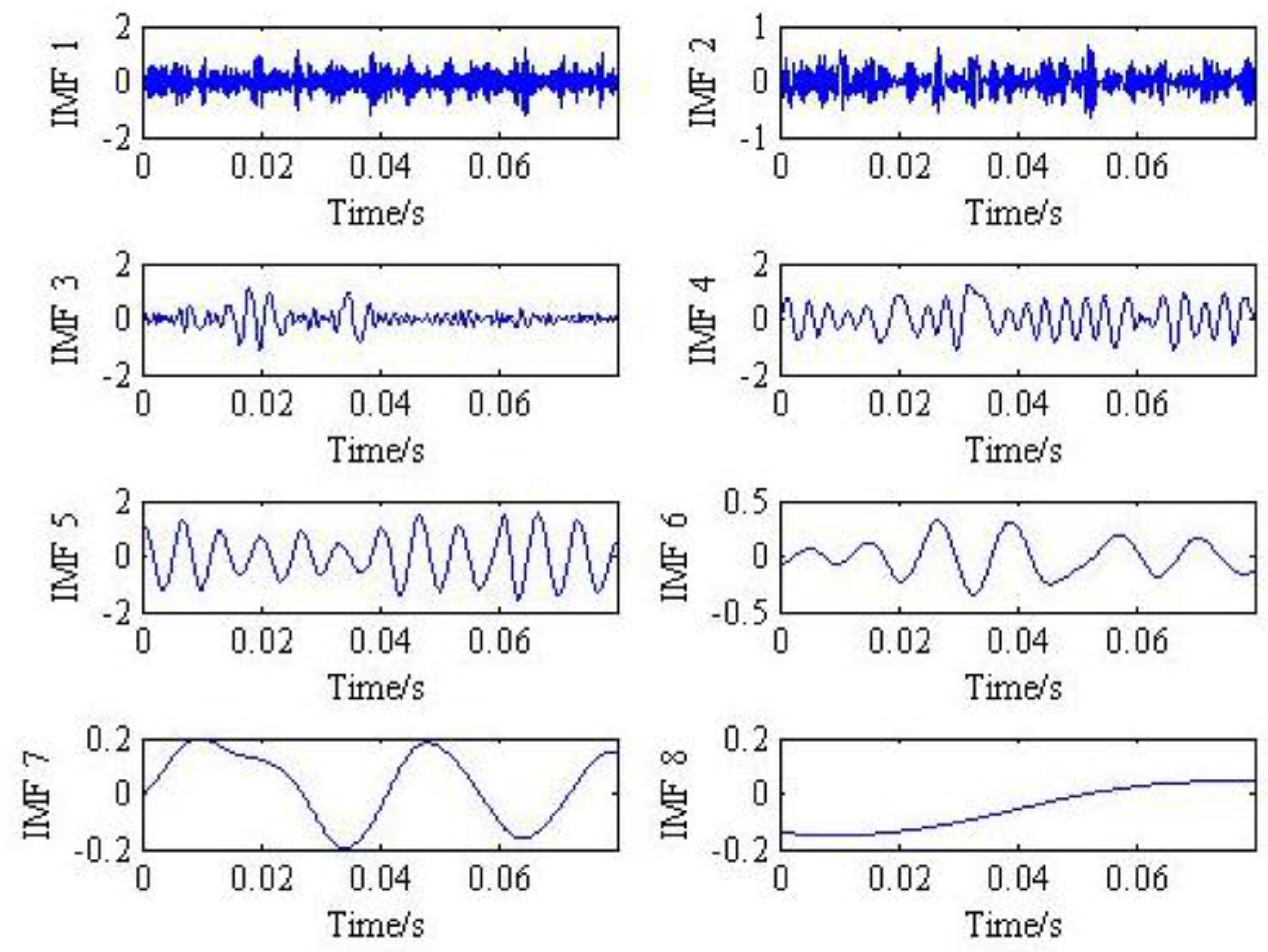
3.2. Multi-Fault Separation of Simulation Signal Analysis
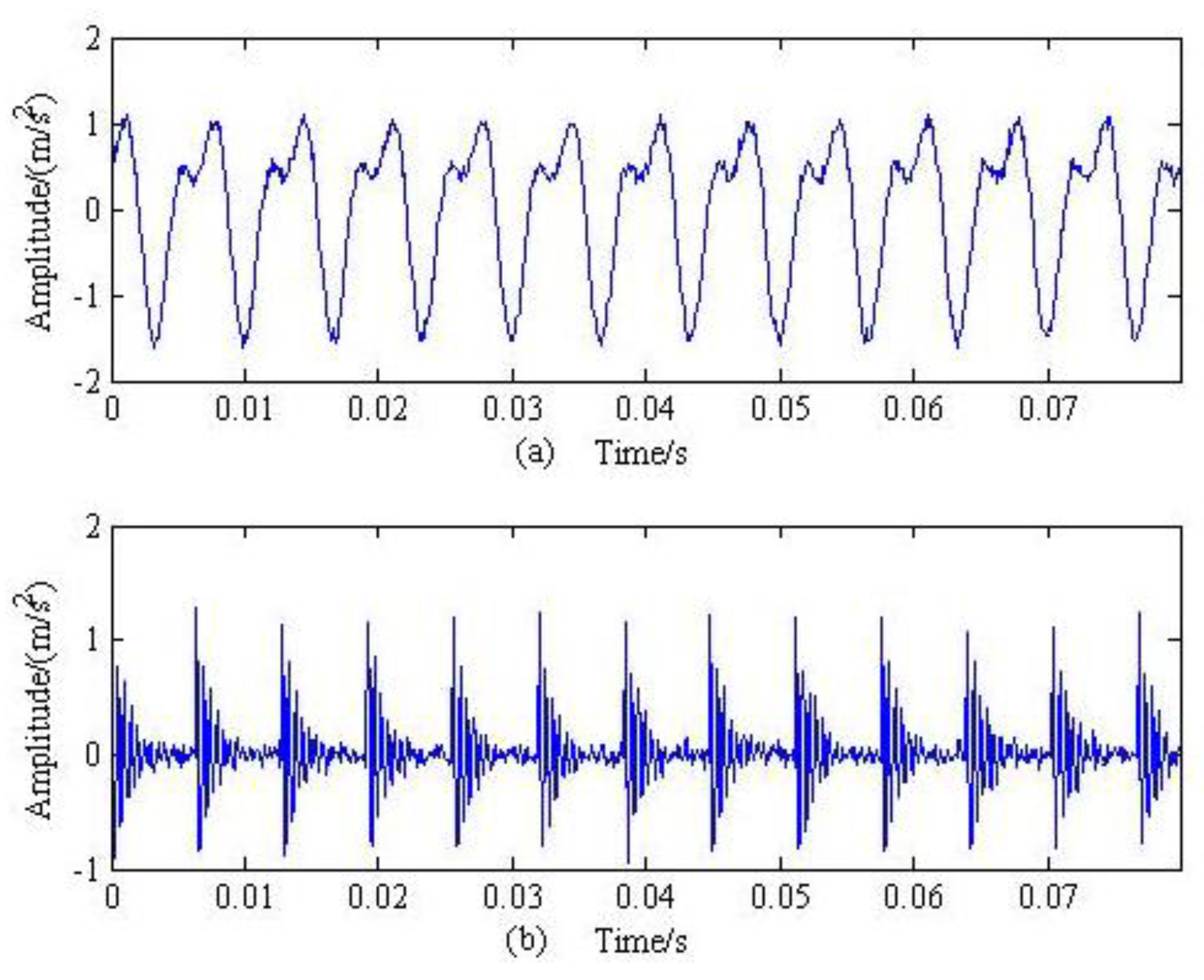
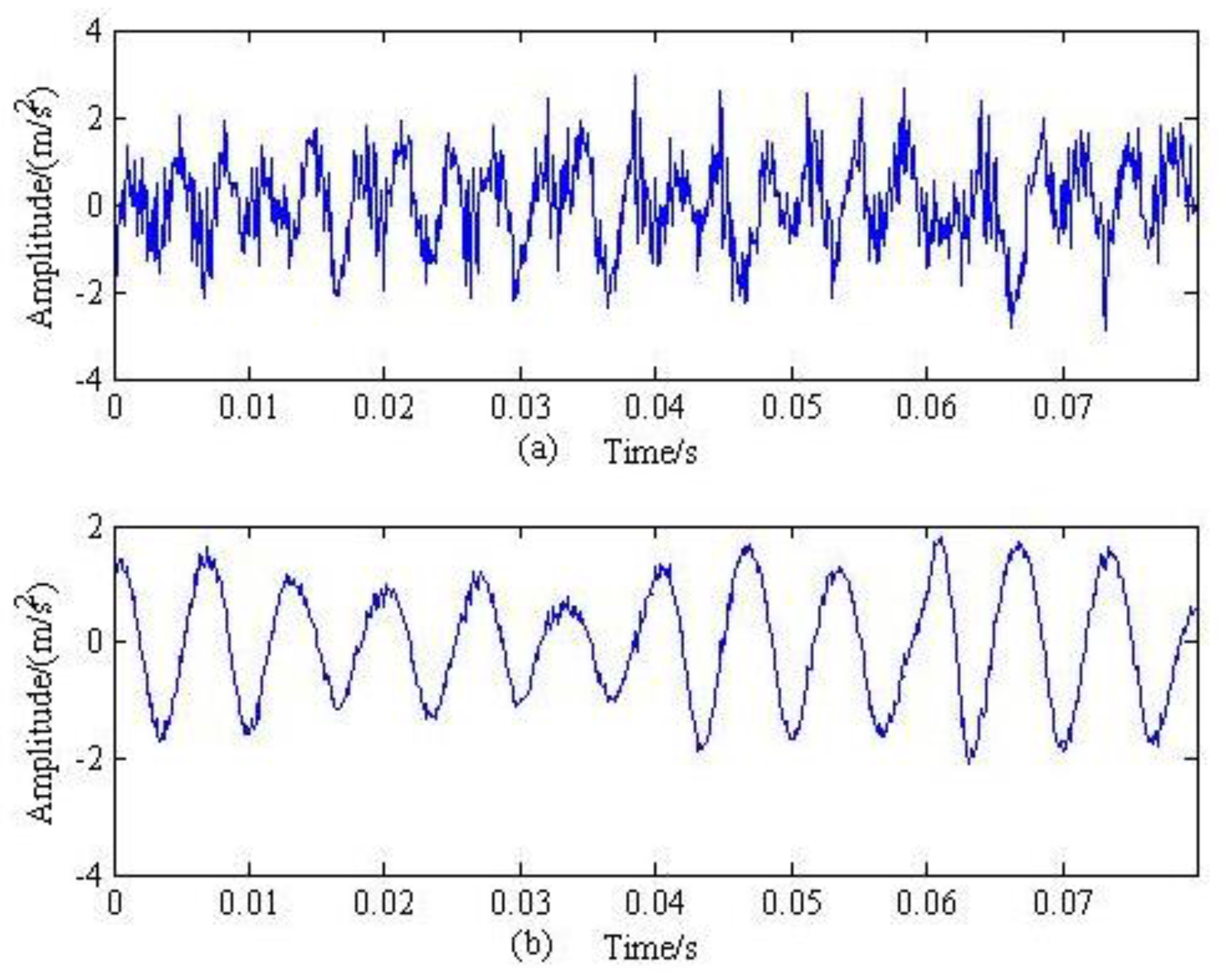
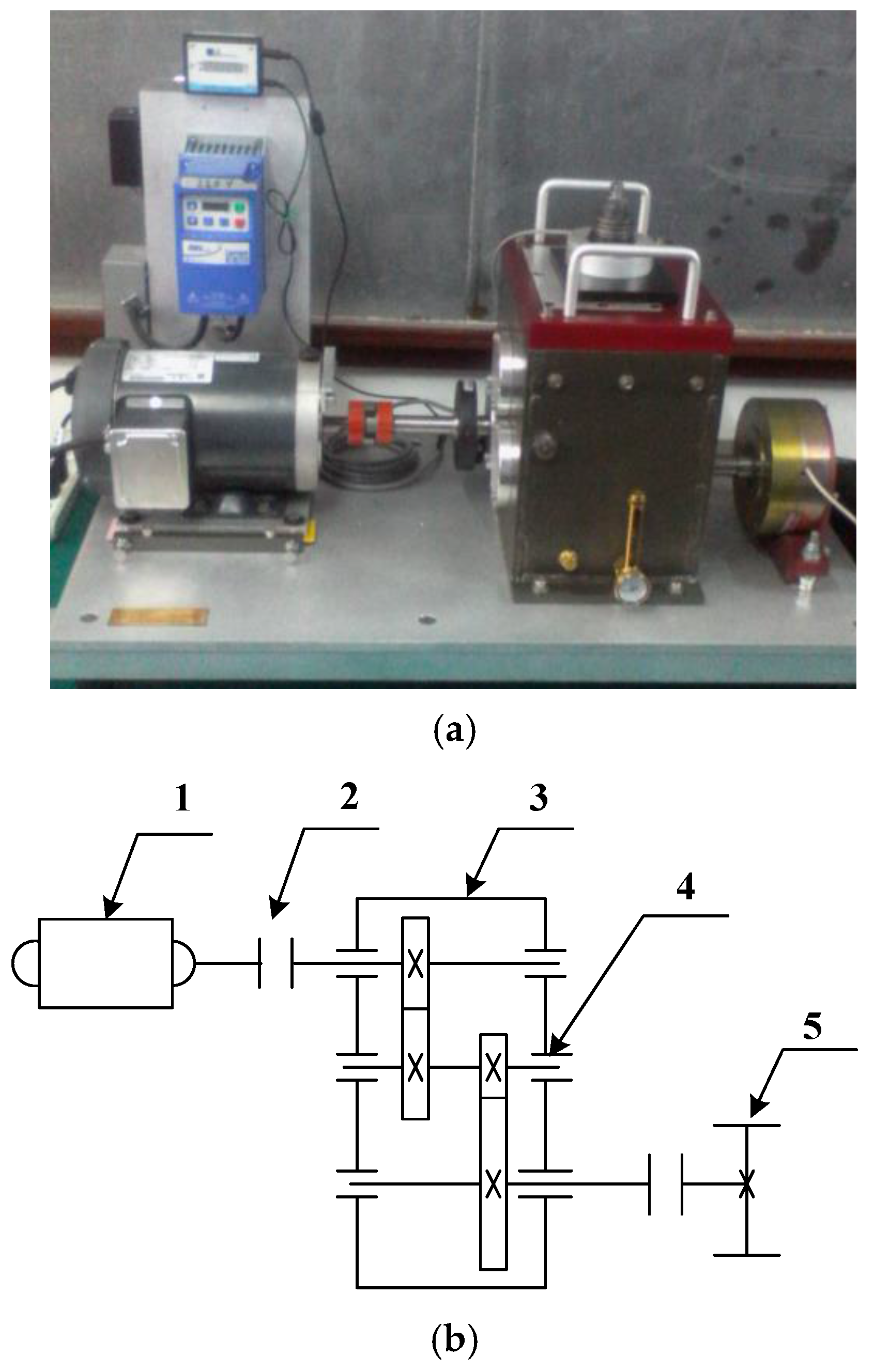
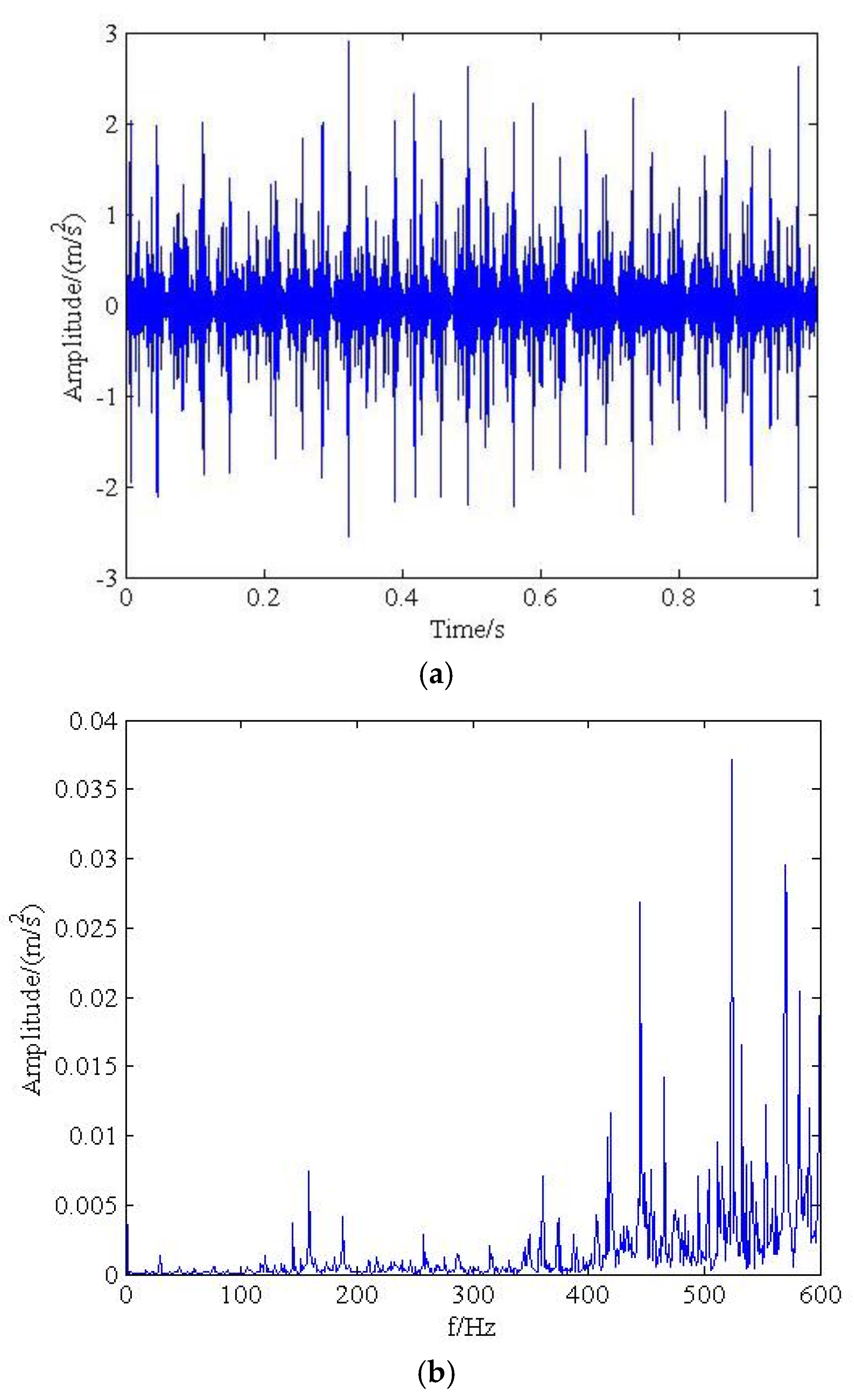
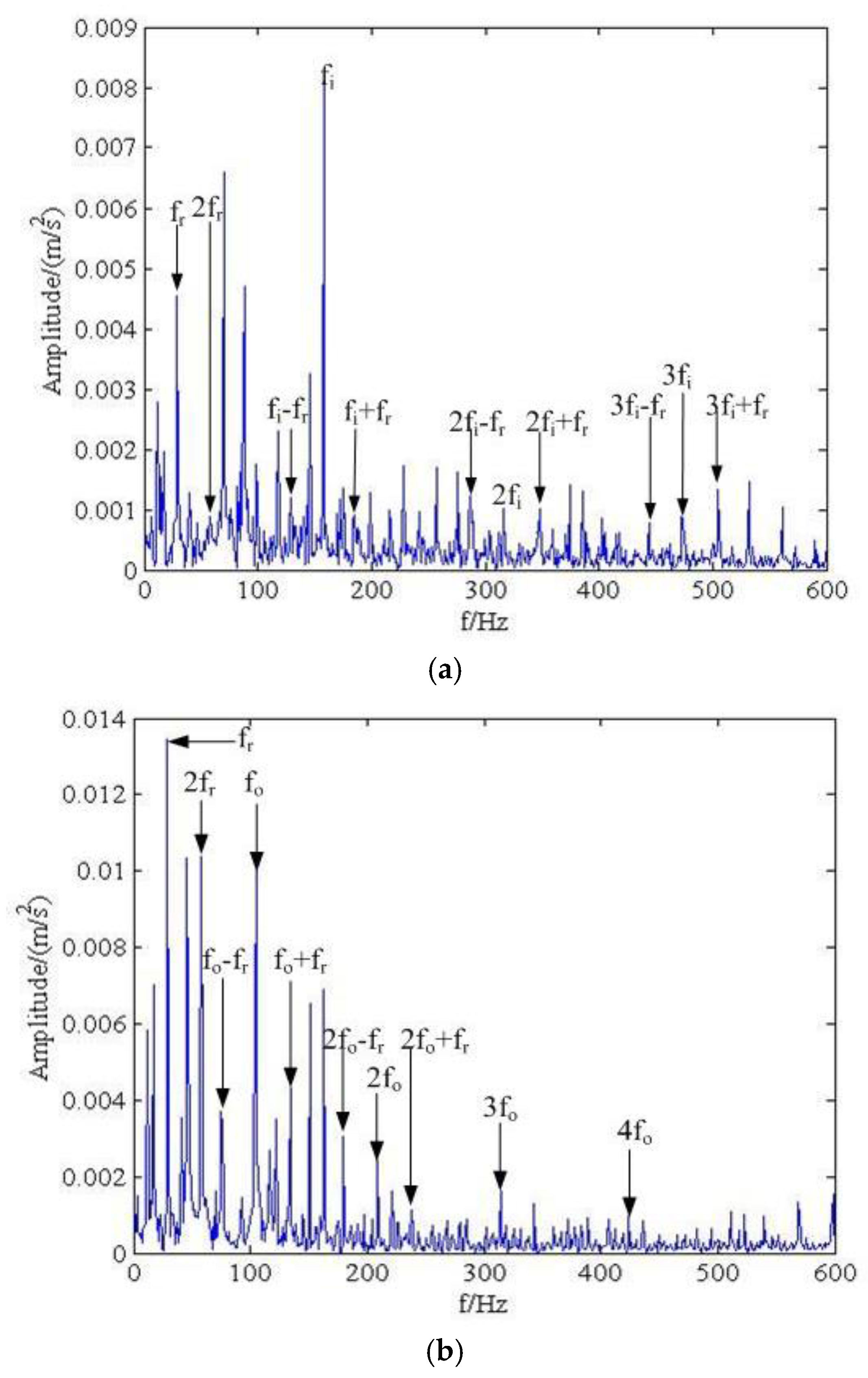
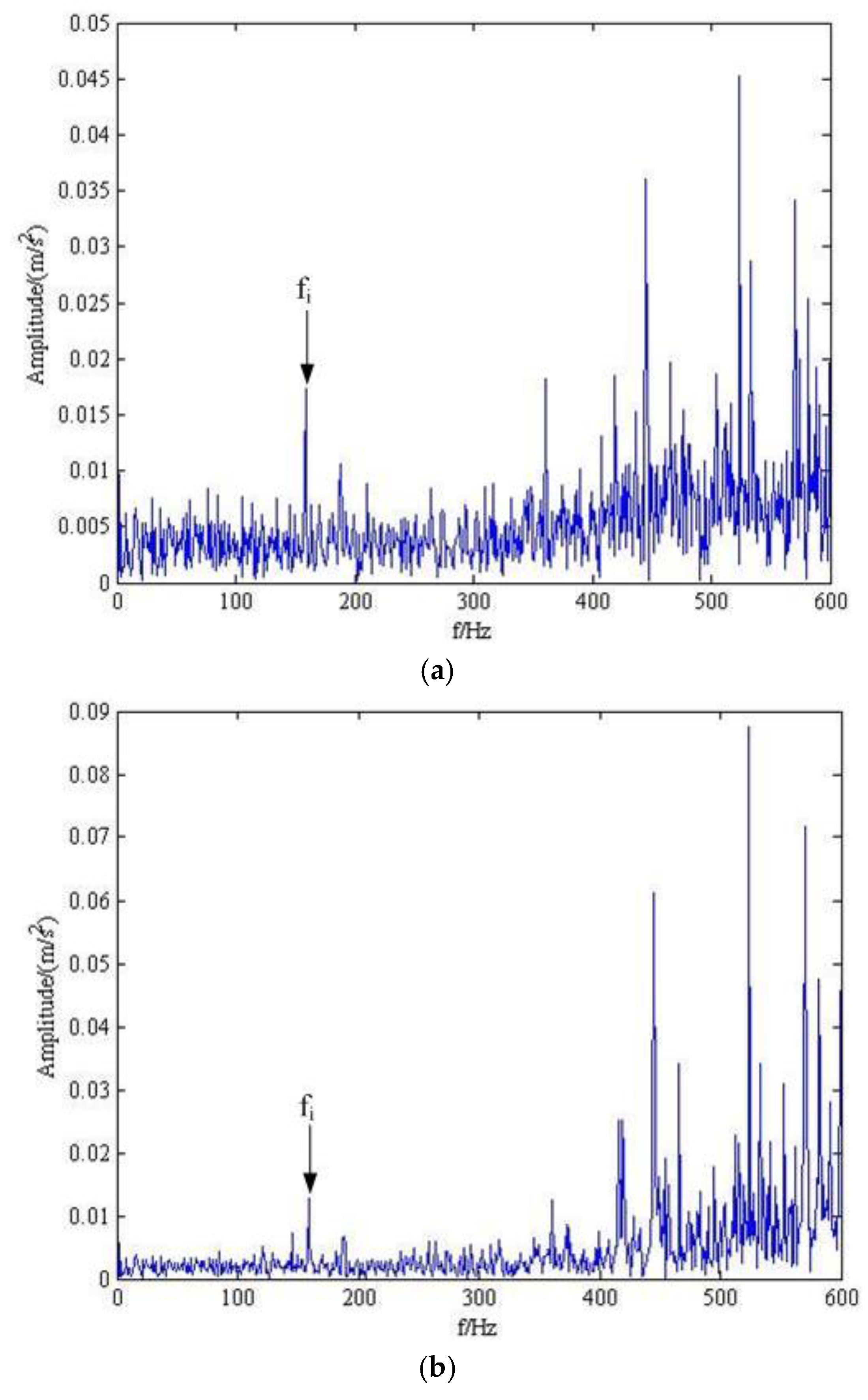
4. Analysis of the Rolling-Bearing on an Experimental Bench
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Li, Y.; Xu, M.; Wang, R.; Huang, W. A fault diagnosis scheme for rolling bearing based on local mean decomposition and improved multiscale fuzzy entropy. J. Sound Vib. 2016, 360, 277–299. [Google Scholar] [CrossRef]
- Yi, C.; Lv, Y.; Dang, Z.; Xiao, H. A Novel Mechanical Fault Diagnosis Scheme Based on the Convex 1-D Second-Order Total Variation Denoising Algorithm. Appl. Sci. 2016, 6, 403. [Google Scholar] [CrossRef]
- Yi, C.; Lv, Y.; Dang, Z. A Fault Diagnosis Scheme for Rolling Bearing Based on Particle Swarm Optimization in Variational Mode Decomposition. Shock Vib. 2016, 2016, 9372691. [Google Scholar] [CrossRef]
- Xu, B.; Song, G.; Masri, S.F. Damage detection for a frame structure model using vibration displacement measurement. Struct. Health Monit. 2012, 11, 281–292. [Google Scholar] [CrossRef]
- Yao, P.; Kong, Q.; Xu, K.; Jiang, T.; Hou, L.; Song, G. Structural health monitoring of multi-spot welded joints using a lead zirconate titanate based active sensing approach. Smart Mater. Struct. 2016, 25, 015031. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, C.; Song, G. Health Status Monitoring of Cuplock Scaffold Joint Connection Based on Wavelet Packet Analysis. Shock Vib. 2015, 2015, 695845. [Google Scholar] [CrossRef]
- Feng, Q.; Kong, Q.; Huo, L.; Song, G. Crack detection and leakage monitoring on reinforced concrete pipe. Smart Mater. Struct. 2015, 24, 115020. [Google Scholar] [CrossRef]
- Li, D.; Ho, S.C.M.; Song, G.; Ren, L.; Li, H. A review of damage detection methods for wind turbine blades. Smart Mater. Struct. 2015, 24, 033001. [Google Scholar] [CrossRef]
- Yi, C.; Lv, Y.; Dang, Z.; Xiao, H.; Yu, X. Quaternion singular spectrum analysis using convex optimization and its application to fault diagnosis of rolling bearing. Measurement 2017, 103, 321–332. [Google Scholar] [CrossRef]
- Belouchrani, A.; Abed-Meraim, K.; Cardoso, J.F.; Moulines, E. A blind source separation technique using second-order statistics. IEEE Trans. Signal Process. 1997, 45, 434–444. [Google Scholar] [CrossRef]
- Zhao, M.; Lin, J.; Xu, X.Q.; Li, X.J. Multi-fault detection of rolling element bearings under harsh working condition using IMF-based adaptive envelope order analysis. Sensors 2014, 14, 20320–20345. [Google Scholar] [CrossRef] [PubMed]
- Kouadri, A.; Baiche, K.; Zelmat, M. Blind source separation filters-based-fault detection and isolation in a three tank system. J. Appl. Stat. 2014, 41, 1799–1813. [Google Scholar] [CrossRef]
- Antoni, J. Blind separation of vibration components: Principles and demonstrations. Mech. Syst. Signal Process. 2005, 19, 1166–1180. [Google Scholar] [CrossRef]
- Gelle, G.; Colas, M.; Serviere, C. Blind source separation: A tool for rotating machine monitoring by vibrations analysis? J. Sound Vib. 2001, 248, 865–885. [Google Scholar] [CrossRef]
- Mowlaee, P.; Christensen, M.G.; Jensen, S.H. New results on single-channel speech separation using sinusoidal modeling. IEEE Trans. Audio Speech Lang. Process. 2011, 19, 1265–1277. [Google Scholar] [CrossRef]
- Gao, B.; Woo, W.L.; Dlay, S.S. Single channel source separation using EMD-subband variable regularized sparse features. IEEE Trans. Audio Speech Lang. Process. 2011, 19, 961–976. [Google Scholar] [CrossRef]
- Guo, Y.; Naik, G.R.; Nguyen, H. Single channel blind source separation based local mean decomposition for Biomedical applications. In Proceedings of the 2013 35th Annual International Conference of the IEEE, Osaka, Japan, 3–7 July 2013; pp. 6812–6815. [Google Scholar]
- Guo, Y.; Huang, S.; Li, Y.; Naik, G.R. Edge effect elimination in single-mixture blind source separation. Circuits Syst. Signal Process. 2013, 32, 2317–2334. [Google Scholar] [CrossRef]
- Pendharkar, G.; Naik, G.R.; Nguyen, H.T. Using blind source separation on accelerometry data to analyze and distinguish the toe walking gait from normal gait in ITW children. Biomed. Signal Process. Control 2014, 13, 41–49. [Google Scholar] [CrossRef]
- Davies, M.E.; James, C.J. Source separation using single channel ICA. Signal Process. 2007, 87, 1819–1832. [Google Scholar] [CrossRef]
- Chai, R.; Naik, G.; Nguyen, T.N.; Ling, S.; Tran, Y.; Craig, A.; Nguyen, H. Driver Fatigue Classification with Independent Component by Entropy Rate Bound Minimization Analysis in an EEG-based System. IEEE J. Biomed. Health Inform. 2016. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Chen, J.; Xiao, F. Application of Empirical Model Decomposition and Independent Component Analysis to Magnetic Anomalies Separation: A Case Study for Gobi Desert Coverage in Eastern Tianshan, China. In Geostatistical and Geospatial Approaches for the Characterization of Natural Resources in the Environment; Springer International Publishing: Berlin, Germany, 2016. [Google Scholar]
- Naik, G.; Altimemy, A.; Nguyen, H. Transradial Amputee Gesture Classification Using an Optimal Number of sEMG Sensors: An Approach Using ICA Clustering. IEEE Trans. Neural Syst. Rehabil. Eng. 2015, 24, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Maneshi, M.; Vahdat, S.; Gotman, J.; Grova, C. Validation of Shared and Specific Independent Component Analysis (SSICA) for Between-Group Comparisons in fMRI. Front. Neurosci. 2016, 10. [Google Scholar] [CrossRef] [PubMed]
- Di Persia, L.E.; Milone, D.H. Using multiple frequency bins for stabilization of FD-ICA algorithms. Signal Process. 2016, 119, 162–168. [Google Scholar] [CrossRef]
- Adali, T.; Calhoun, V.D. Complex ICA of brain imaging data. IEEE Signal Process. Mag. 2007, 24, 136. [Google Scholar] [CrossRef]
- Naik, G.R.; Kumar, D.K. Estimation of independent and dependent components of non-invasive EMG using fast ICA: Validation in recognising complex gestures. Comput. Methods Biomech. Biomed. Eng. 2011, 14, 1105–1111. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.; Deng, Y. A Time-Frequency Algorithm for Noisy ICA. In Geo-Informatics in Resource Management and Sustainable Ecosystem; Springer: Berlin/Heidelberg, Germany, 2015; pp. 357–365. [Google Scholar]
- Hong, H.; Liang, M. Separation of fault features from a single-channel mechanical signal mixture using wavelet decomposition. Mech. Syst. Signal Process. 2007, 21, 2025–2040. [Google Scholar] [CrossRef]
- Mijović, B.; de Vos, M.; Gligorijevic, I.; Taelman, J.; Van Huffel, S. Source separation from single-channel recordings by combining empirical-mode decomposition and independent component analysis. IEEE Trans. Biomed. Eng. 2010, 57, 2188–2196. [Google Scholar] [CrossRef] [PubMed]
- Naik, G.R.; Selvan, S.E.; Nguyen, H.T. Single-Channel EMG Classification with Ensemble-Empirical- Mode-Decomposition-Based ICA for Diagnosing Neuromuscular Disorders. IEEE Trans. Neural Syst. Rehabil. Eng. A Publ. IEEE Eng. Med. Biol. Soc. 2016, 24, 734–743. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Li, M.; Song, G.; Xu, J. Hierarchical ensemble-based data fusion for structural health monitoring. Smart Mater. Struct. 2010, 19, 126–134. [Google Scholar] [CrossRef]
- Lv, Y.; Yuan, R.; Song, G. Multivariate empirical mode decomposition and its application to fault diagnosis of rolling bearing. Mech. Syst. Signal Process. 2016, 81, 219–234. [Google Scholar] [CrossRef]
- Sadhu, A. An Integrated Multivariate Empirical Mode Decomposition Method towards Modal Identification of Structures. Available online: http://journals.sagepub.com/doi/abs/10.1177/1077546315621207 (accessed on 7 January 2017).
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Wang, H.; Li, R.; Tang, G.; Yuan, H.F.; Zhao, Q.L.; Cao, X. A compound fault diagnosis for rolling bearings method based on blind source separation and ensemble empirical mode decomposition. PLoS ONE 2014, 9, e109166. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Huang, S.; Li, Y. Single-mixture source separation using dimensionality reduction of ensemble empirical mode decomposition and independent component analysis. Circuits Syst. Signal Process. 2012, 31, 2047–2060. [Google Scholar] [CrossRef]
- Yeh, J.R.; Shieh, J.S.; Huang, N.E. Complementary Ensemble Empirical Mode Decomposition: A Novel Noise Enhanced Data Analysis Method. Adv. Adapt. Data Anal. 2011, 2, 135–156. [Google Scholar] [CrossRef]
- Kouchaki, S.; Sanei, S.; Arbon, E.L.; Dijk, D.J. Tensor based singular spectrum analysis for automatic scoring of sleep EEG. IEEE Trans. Neural Syst. Rehabil. Eng. 2015, 23, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Kemao, Q.; Da, F. Regenerated Phase-Shifted Sinusoid-Assisted Empirical Mode Decomposition. IEEE Signal Process. Lett. 2016, 23, 556–560. [Google Scholar] [CrossRef]
- Huang, L.; Xiao, Y.; Liu, K.; So, H.C. Bayesian information criterion for source enumeration in large-scale adaptive antenna array. IEEE Trans. Veh. Technol. 2016, 65, 3018–3032. [Google Scholar] [CrossRef]
- Cardoso, J.F.; Souloumiac, A. Blind Beamforming for non-Gaussian Signals. IEE Proc. F Radar Signal Process. 1994, 140, 362–370. [Google Scholar] [CrossRef]
- Ypma, A. Learning Methods for Machine Vibration Analysis and Health Monitoring; TU Delft: Delft, The Netherlands, 2001. [Google Scholar]
- Randall, R.B.; Antoni, J.; Chobsaard, S. The relationship between spectral correlation and envelope analysis in the diagnostics of bearing faults and other cyclostationary machine signals. Mech. Syst. Signal Process. 2001, 15, 945–962. [Google Scholar] [CrossRef]
| Noise Standard Deviation | Ensemble Size | Maximum Number of Sifting Iterations |
|---|---|---|
| 0.2 | 200 | 500 |
| (Hz) | (Hz) | (Hz) | ||||||
|---|---|---|---|---|---|---|---|---|
| 0.003 | 29 | 156 | 0.01 | 2000 | 1 | 0 | 0 | 800 |
| Rotating Frequency | Transmission Frequency | Output Frequency | Inner Ring Fault Frequency | Outer Ring Fault Frequency |
|---|---|---|---|---|
| f | 0.29f | 0.11f | 5.43f | 3.572f |
| Rotating Frequency /Hz | Inner Ring Fault Frequency /Hz | Outer Ring Fault Frequency /Hz |
|---|---|---|
| 29 | 157.47 | 130.59 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yi, C.; Lv, Y.; Xiao, H.; You, G.; Dang, Z. Research on the Blind Source Separation Method Based on Regenerated Phase-Shifted Sinusoid-Assisted EMD and Its Application in Diagnosing Rolling-Bearing Faults. Appl. Sci. 2017, 7, 414. https://doi.org/10.3390/app7040414
Yi C, Lv Y, Xiao H, You G, Dang Z. Research on the Blind Source Separation Method Based on Regenerated Phase-Shifted Sinusoid-Assisted EMD and Its Application in Diagnosing Rolling-Bearing Faults. Applied Sciences. 2017; 7(4):414. https://doi.org/10.3390/app7040414
Chicago/Turabian StyleYi, Cancan, Yong Lv, Han Xiao, Guanghui You, and Zhang Dang. 2017. "Research on the Blind Source Separation Method Based on Regenerated Phase-Shifted Sinusoid-Assisted EMD and Its Application in Diagnosing Rolling-Bearing Faults" Applied Sciences 7, no. 4: 414. https://doi.org/10.3390/app7040414
APA StyleYi, C., Lv, Y., Xiao, H., You, G., & Dang, Z. (2017). Research on the Blind Source Separation Method Based on Regenerated Phase-Shifted Sinusoid-Assisted EMD and Its Application in Diagnosing Rolling-Bearing Faults. Applied Sciences, 7(4), 414. https://doi.org/10.3390/app7040414